High-Resolution Gridded Livestock Projection for Western China Based on Machine Learning
Abstract
:1. Introduction
2. Study Area and Data
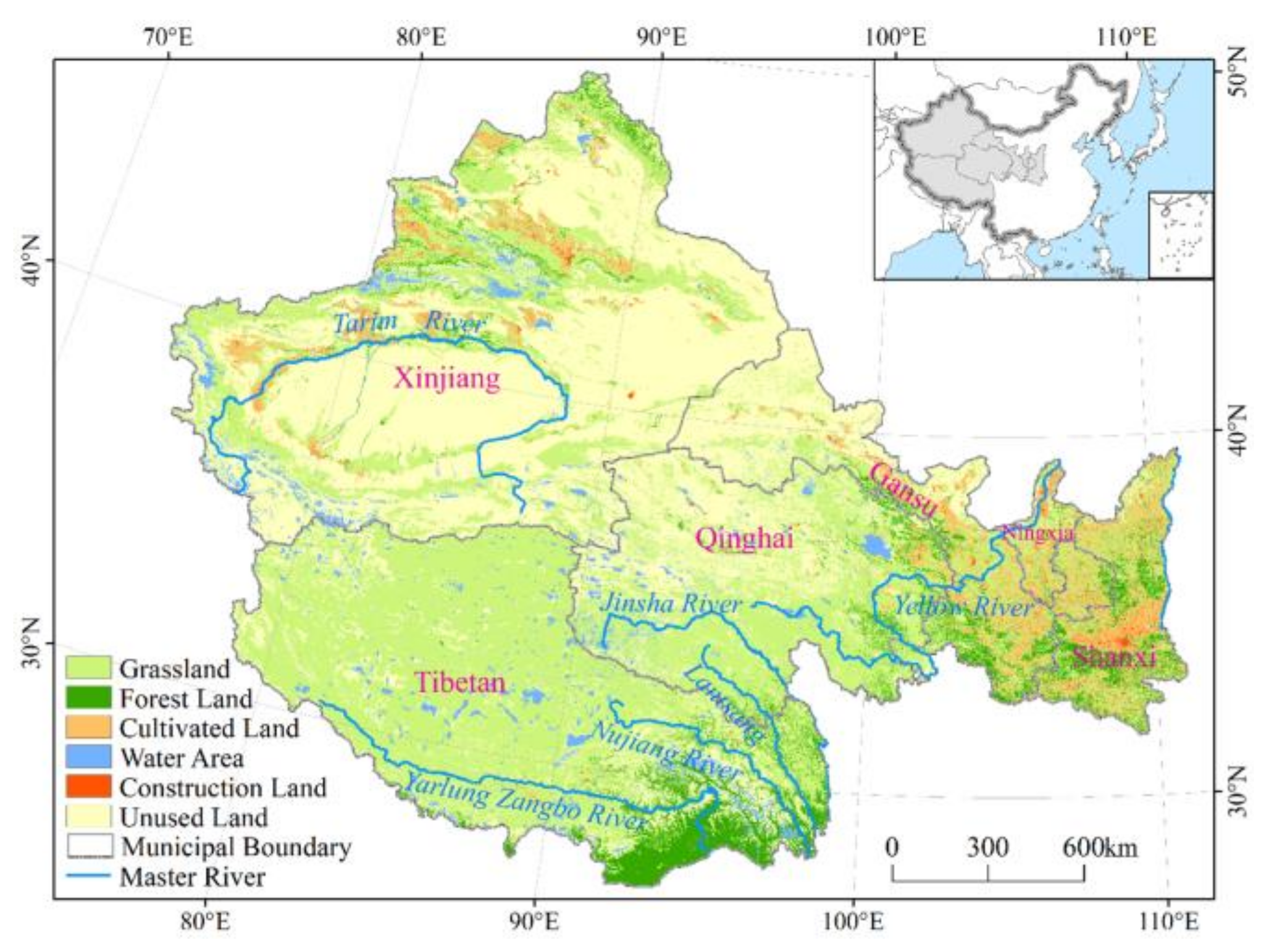
2.1. Study Area
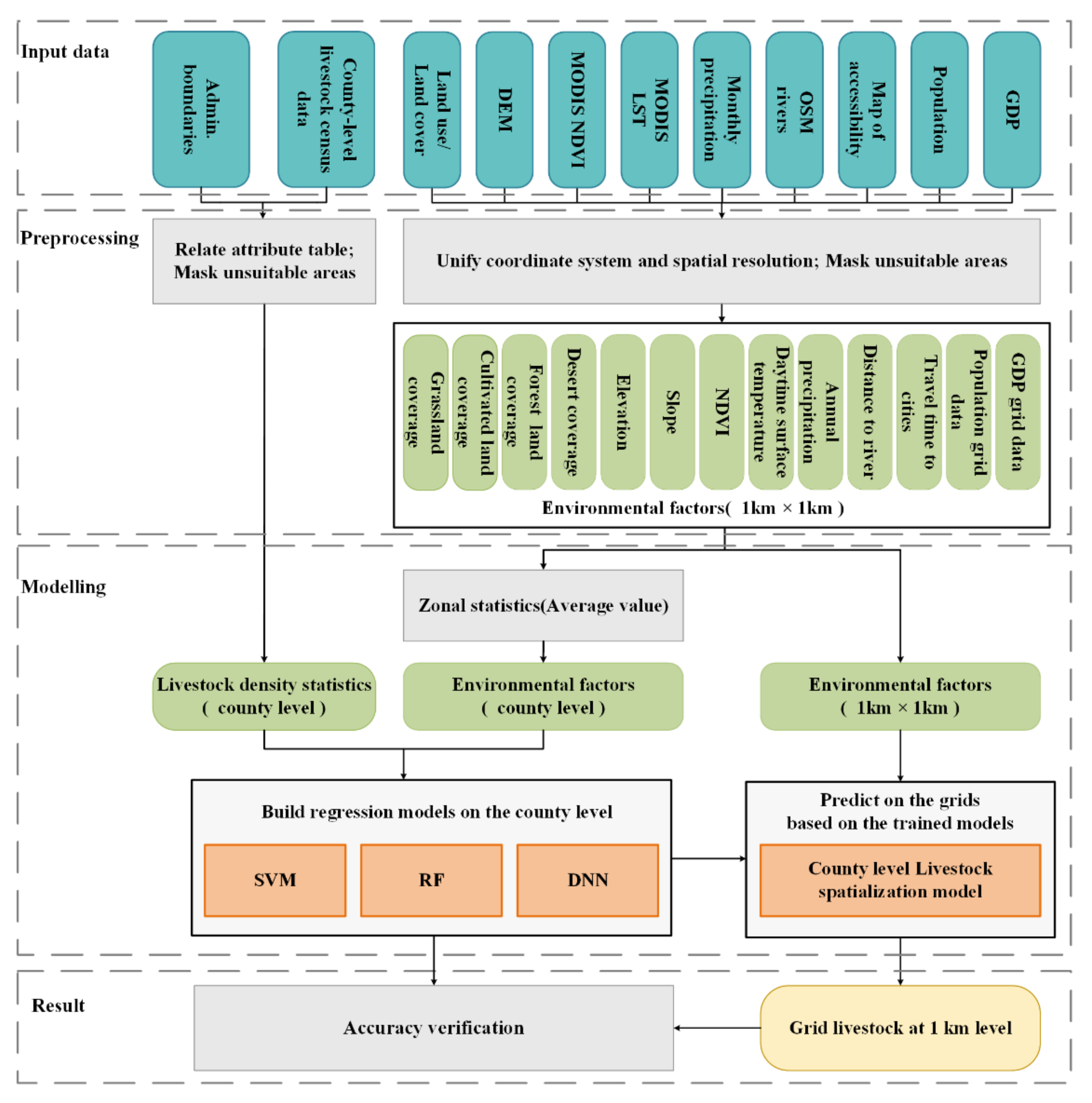
2.2. Data and Preprocessing
2.2.1. The Gridded Geographic Data
2.2.2. Livestock Statistics
3. Methodology
3.1. Machine Learning Methods
3.1.1. Support Vector Machine
3.1.2. Random Forest
3.1.3. Deep Neural Network
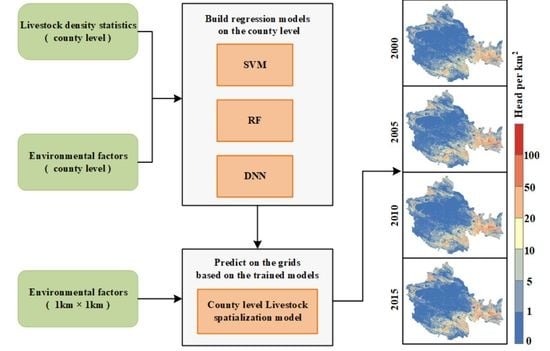
3.2. Livestock Density Estimation Models
3.2.1. Livestock Density Estimation
3.2.2. Livestock Density Adjustment
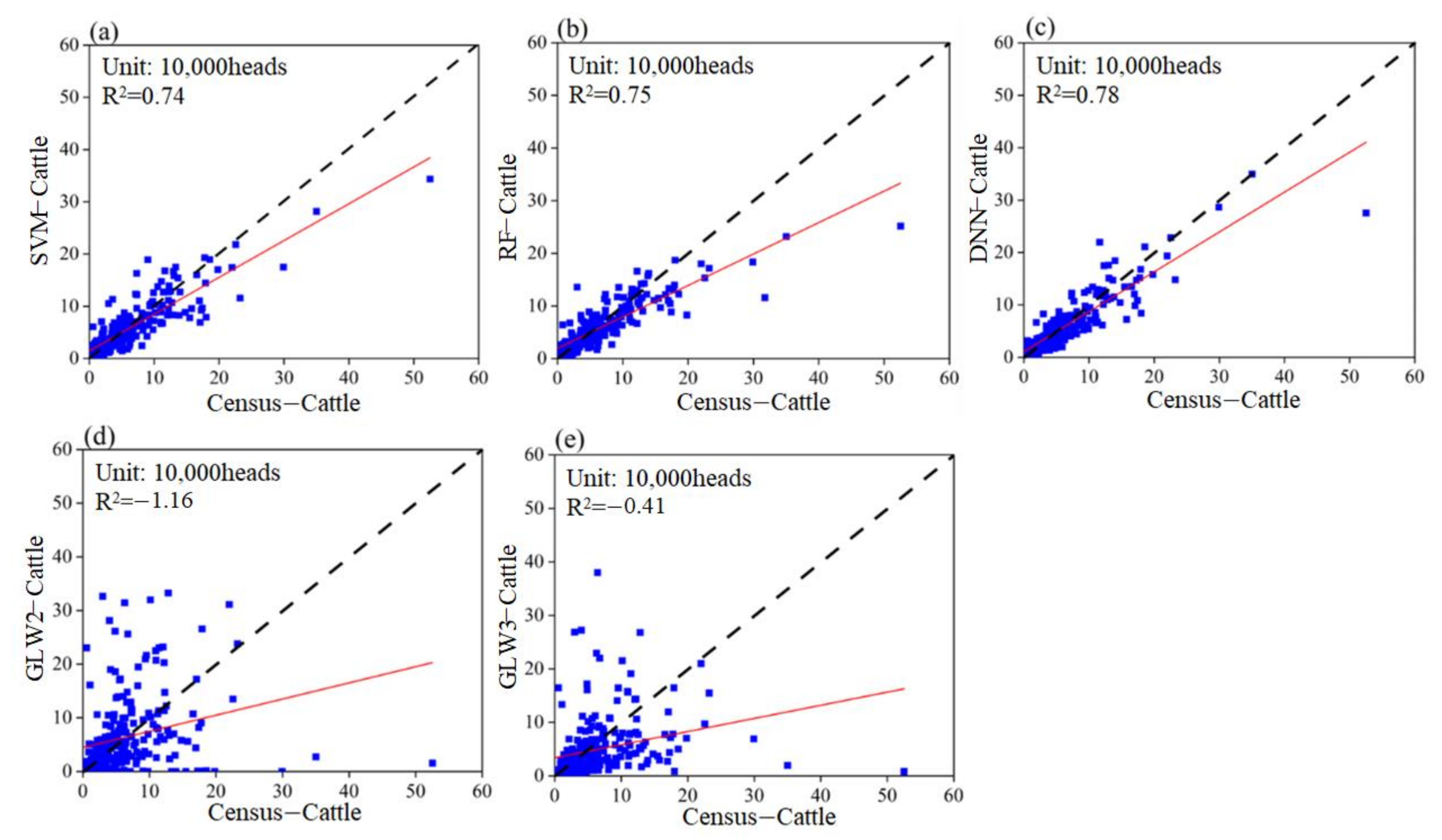
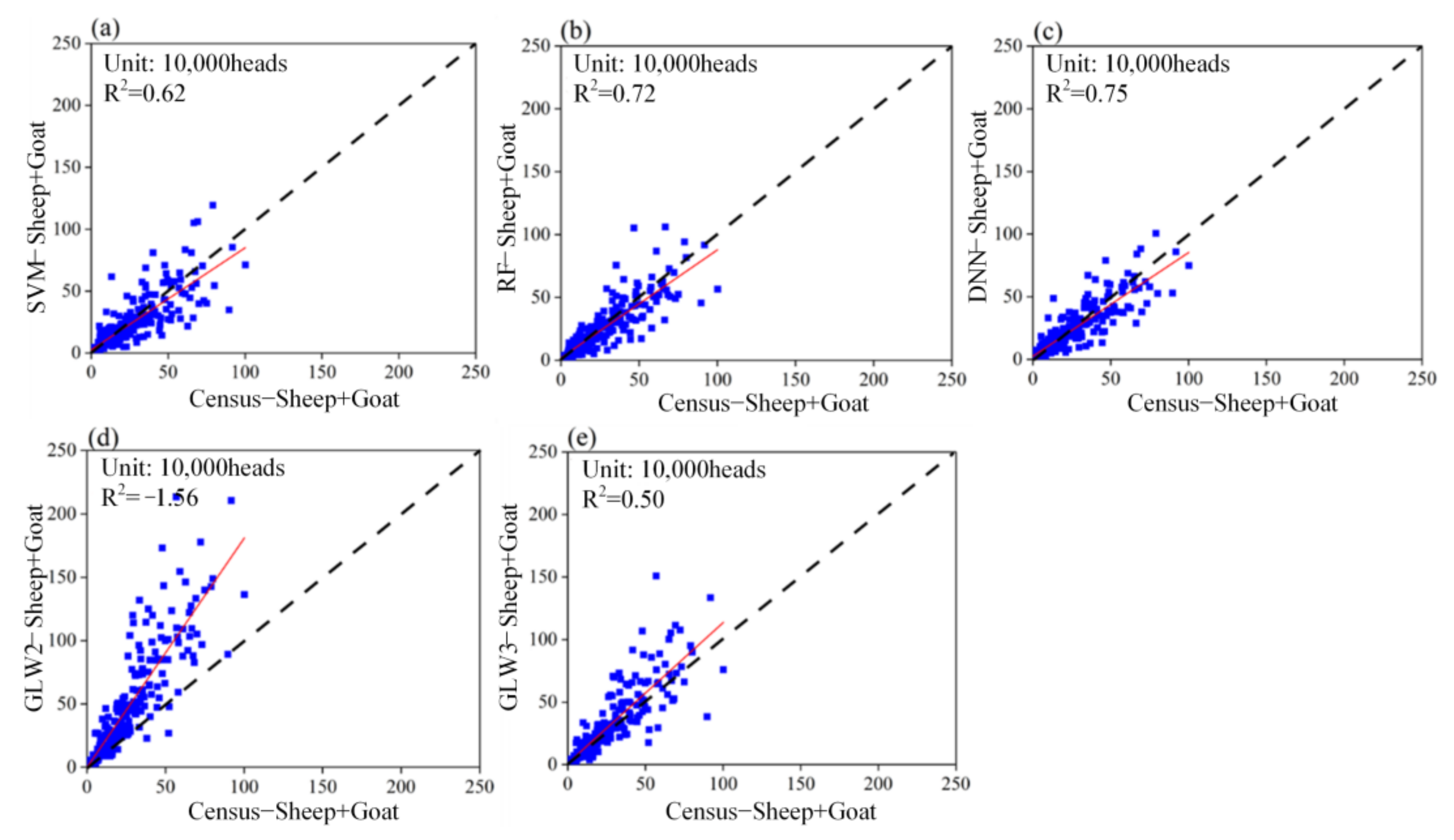
3.2.3. Performance Evaluation
4. Results
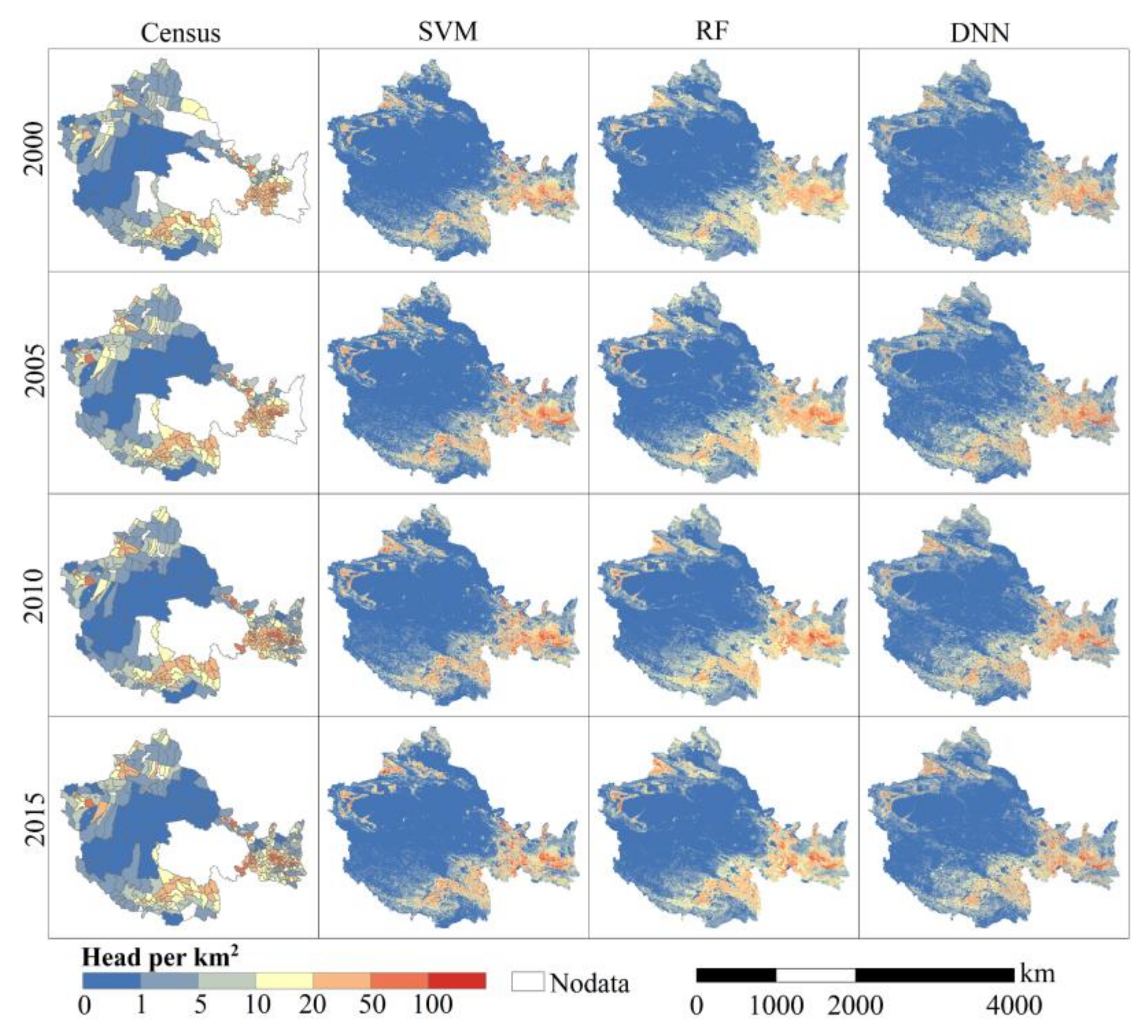
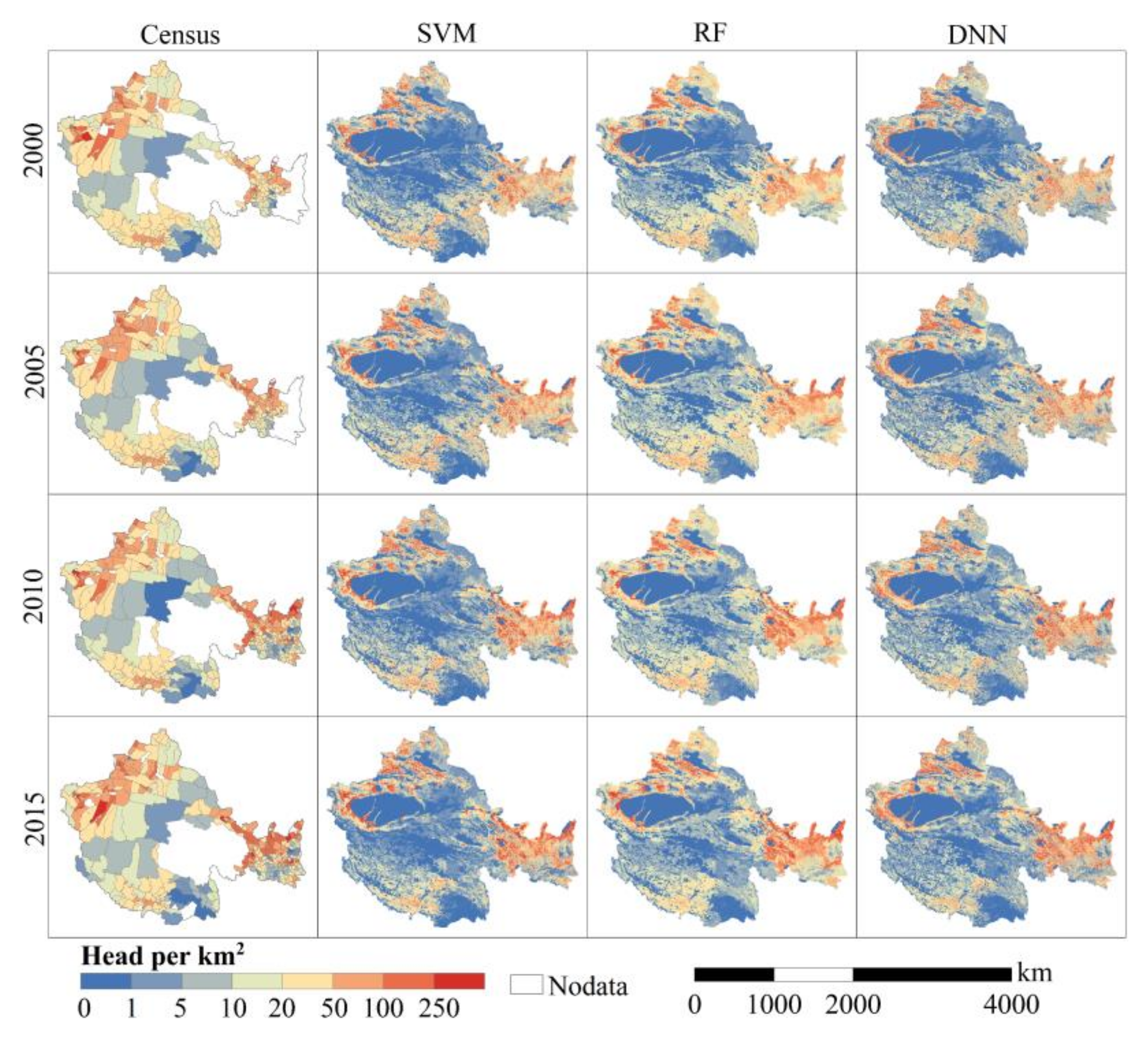
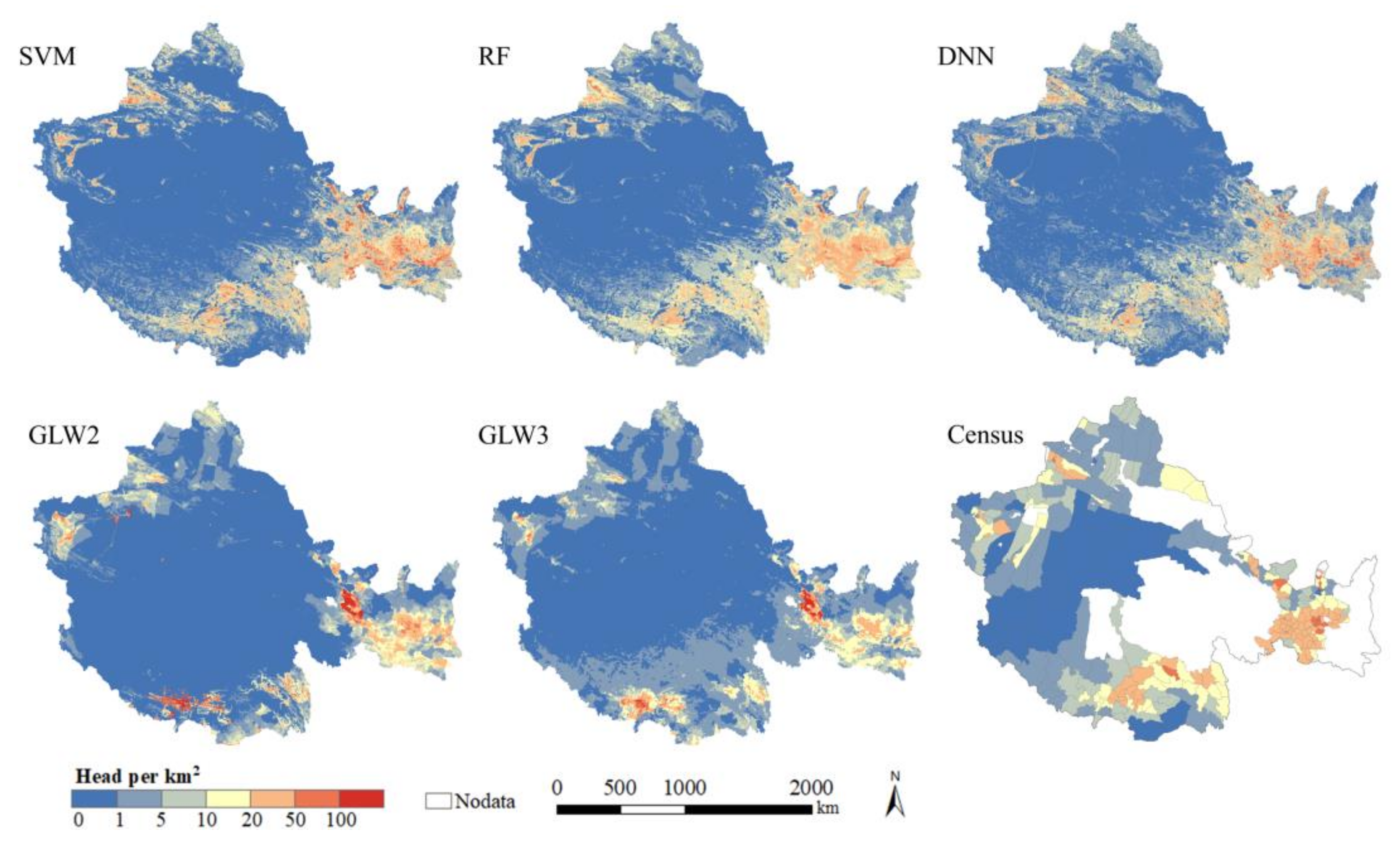
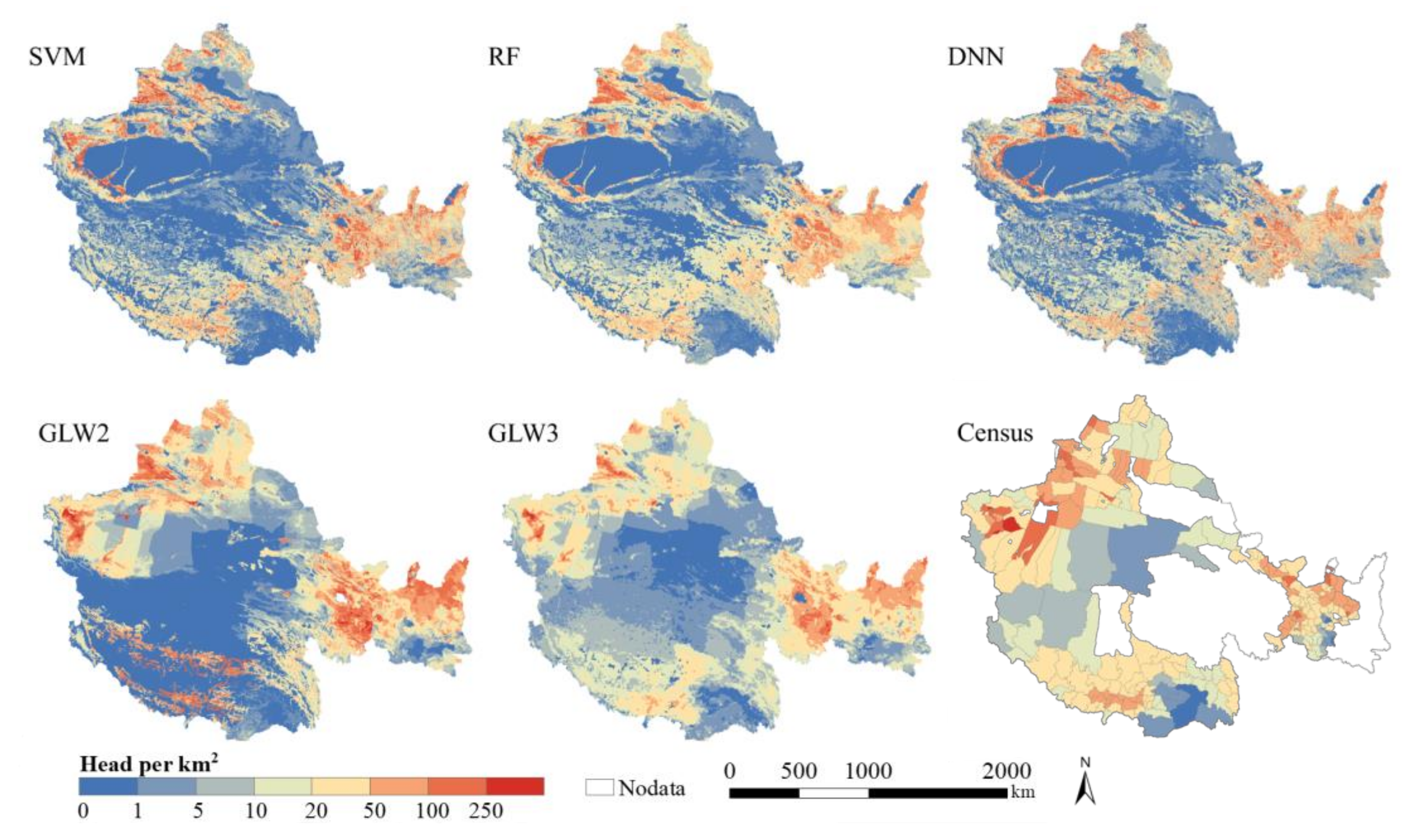
4.1. Gridded Livestock Distribution Maps
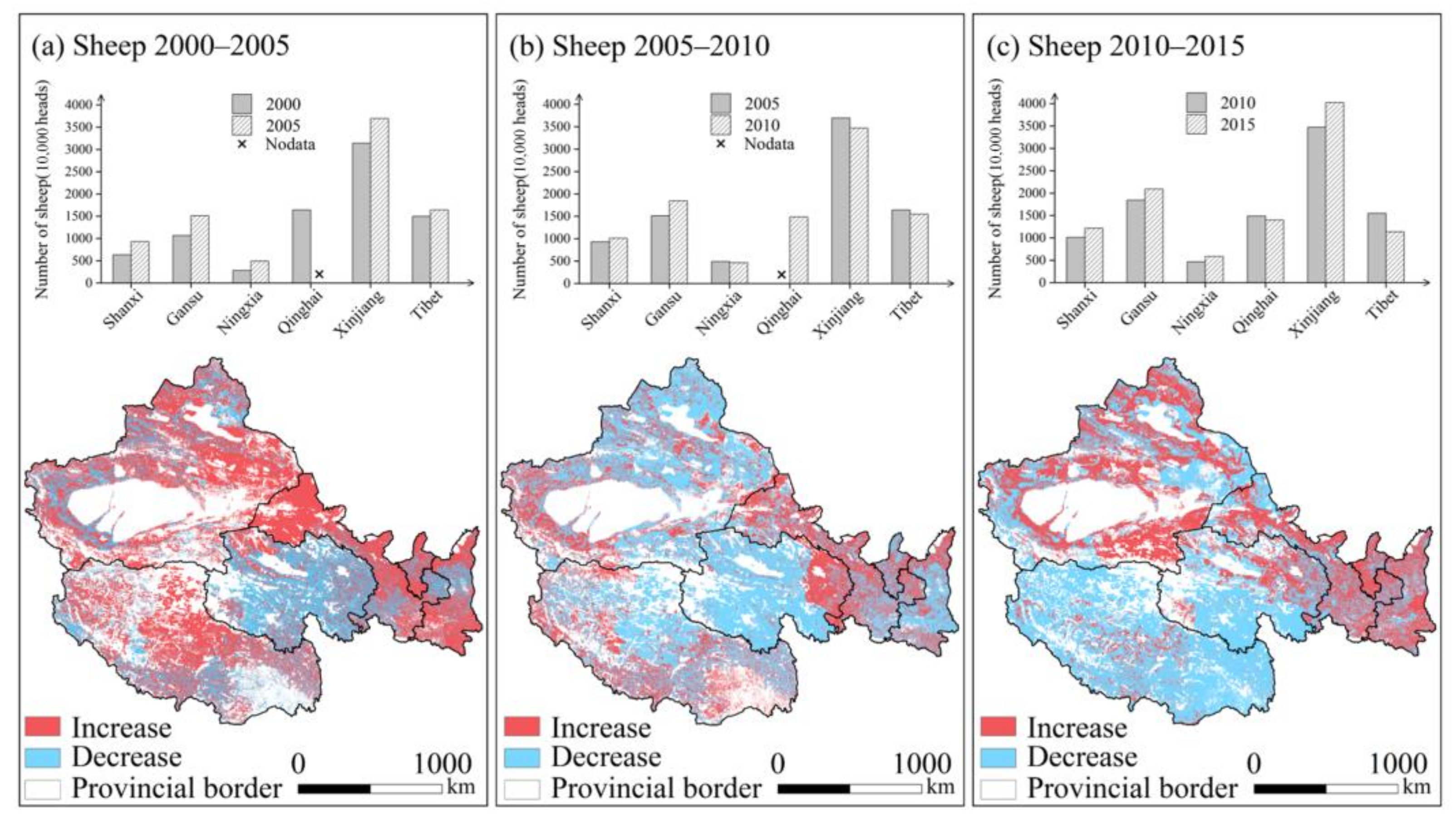
4.2. Spatiotemporal Changes of Livestock
5. Discussion
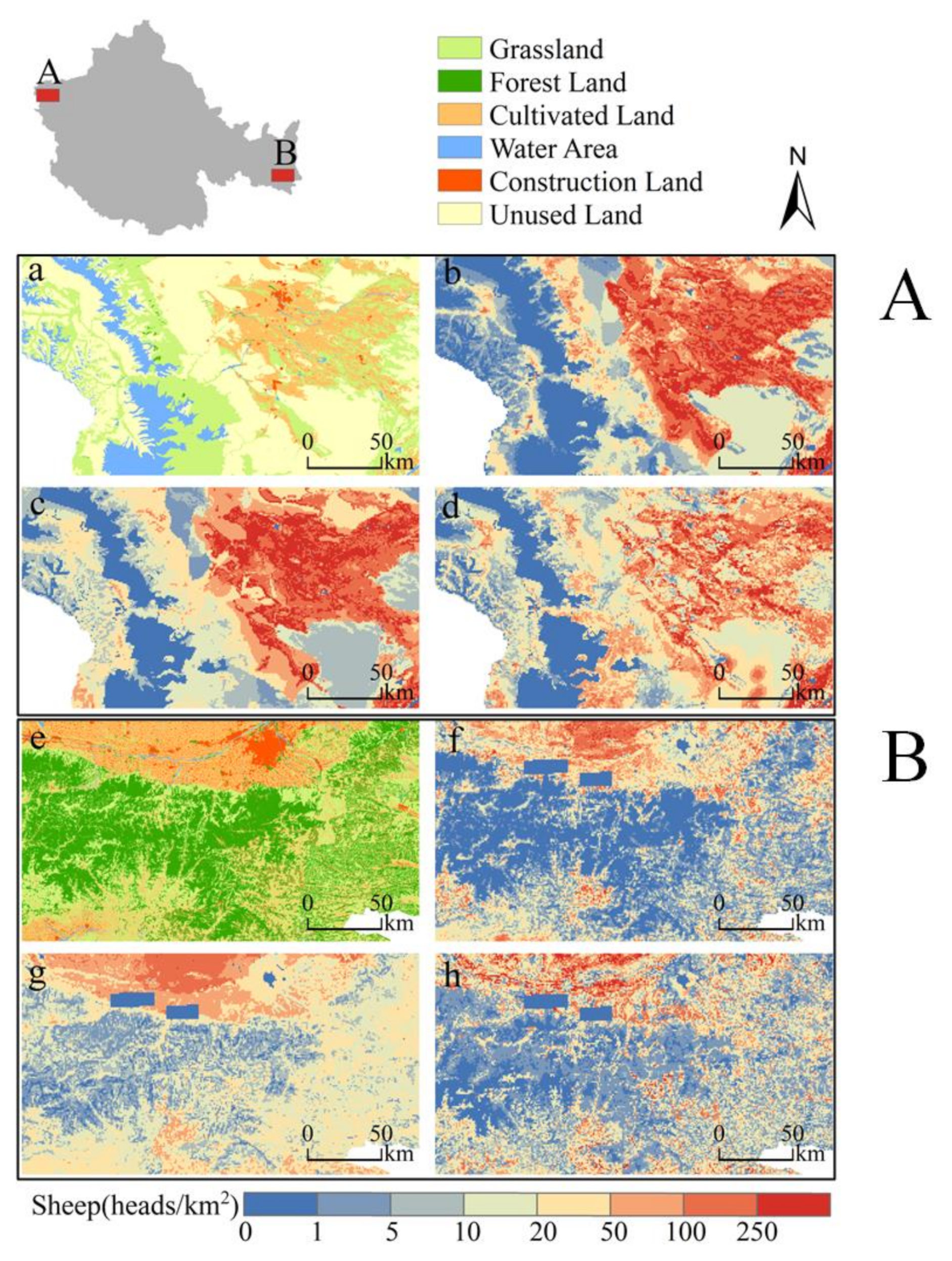
5.1. Comparison with the Open Access Gridded Livestock Datasets
5.2. The Reasonableness of the Hypothesis
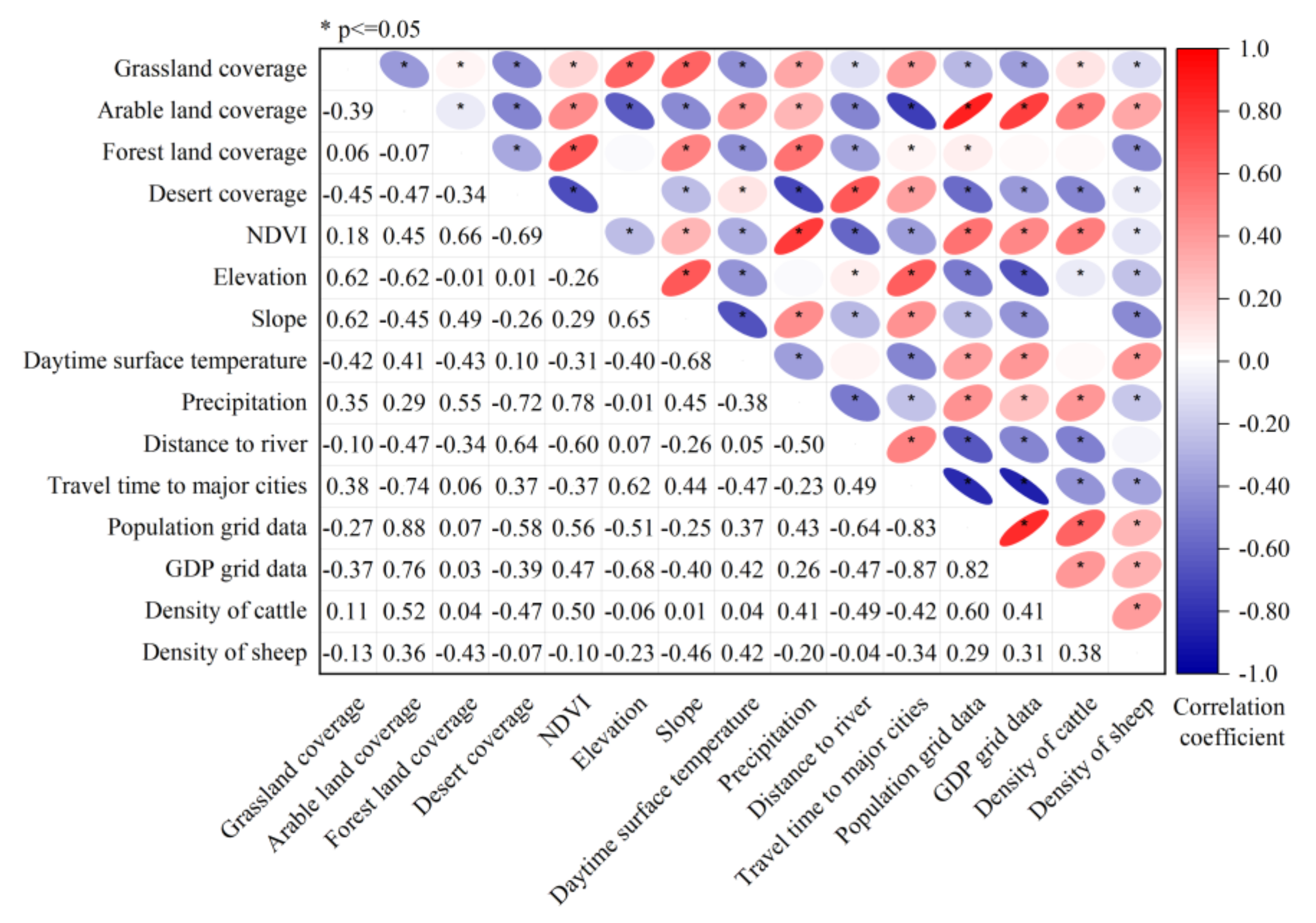
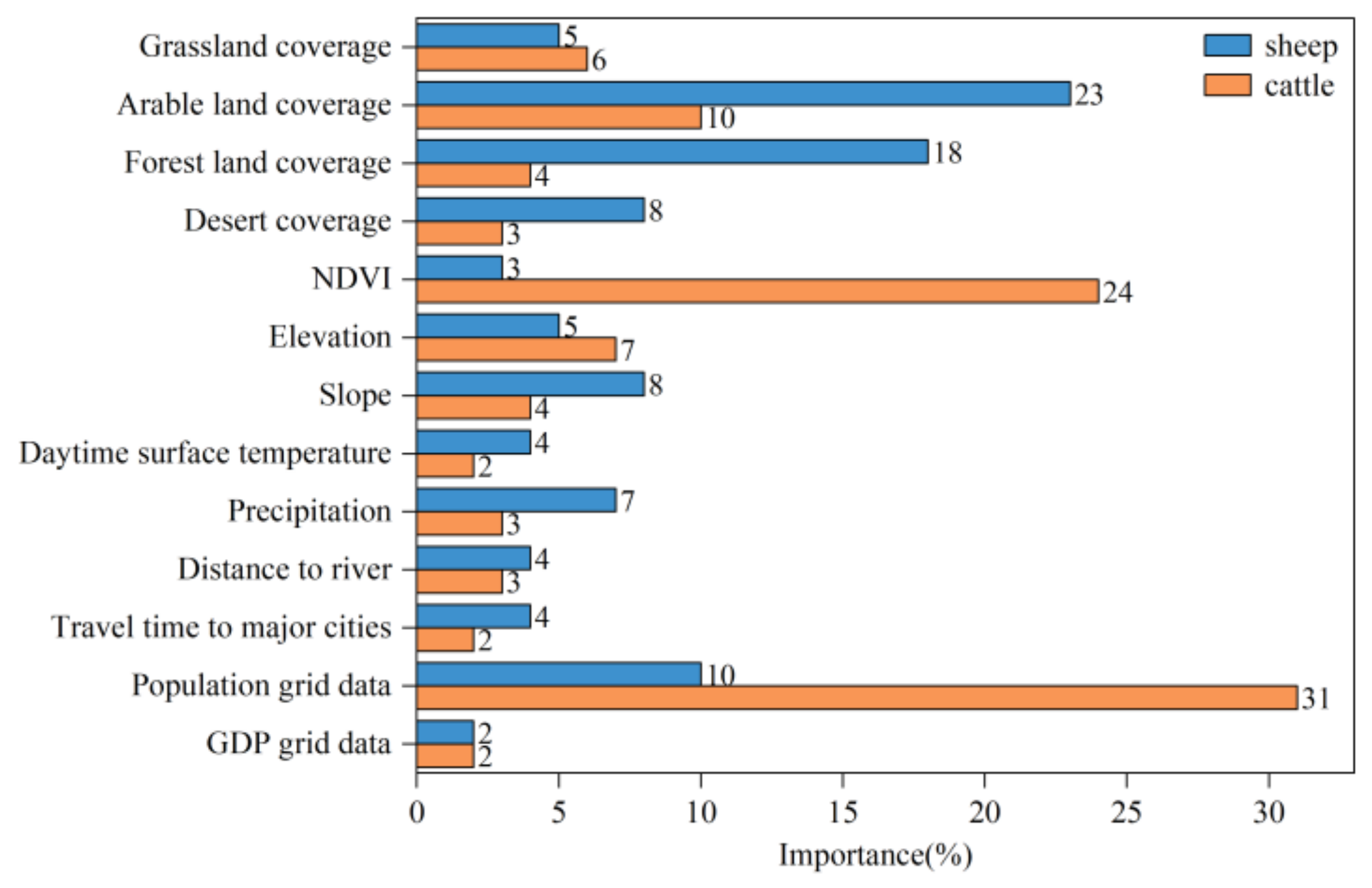
5.3. Selection and Contribution of Environmental Factors
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, M. China’s livestock industry development: Achievements, experiences and future trends. Chin. Issues Agric. Econ. 2018, 8, 60–70. [Google Scholar]
- Olesen, J.; Schelde, K.; Weiske, A.; Weisbjerg, M.; Asman, W.; Djurhuus, J. Modelling greenhouse gas emissions from European conventional and organic dairy farms. Agric. Ecosyst. Environ. 2006, 112, 207–220. [Google Scholar] [CrossRef]
- Monteny, G.-J.; Bannink, A.; Chadwick, D. Greenhouse gas abatement strategies for animal husbandry. Agric. Ecosyst. Environ. 2006, 112, 163–170. [Google Scholar] [CrossRef]
- Steinfeld, H.; Gerber, P.; Wassenaar, T.D.; Castel, V.; Rosales, M.; Rosales, M.; de Haan, C. Livestock’s Long Shadow: Environmental Issues and Options; Food & Agriculture Organization: Rome, Italy, 2006. [Google Scholar]
- Dong, N.; Yang, X.; Cai, H. Research progress and perspective on the spatialization of population data. J. Geo-Inf. Sci 2016, 18, 1295–1304. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Anselin, L.; Deichmann, U. A framework for the areal interpolation of socioeconomic data. Environ. Plan. A 1993, 25, 383–397. [Google Scholar] [CrossRef]
- Wint, W.; Robinson, T. Gridded Livestock of the World 2007; FAO: Roma, Italy, 2007. [Google Scholar]
- Robinson, T.P.; Wint, G.W.; Conchedda, G.; Van Boeckel, T.P.; Ercoli, V.; Palamara, E.; Cinardi, G.; D’Aietti, L.; Hay, S.I.; Gilbert, M. Mapping the global distribution of livestock. PLoS ONE 2014, 9, e96084. [Google Scholar] [CrossRef] [Green Version]
- Nicolas, G.; Robinson, T.P.; Wint, G.W.; Conchedda, G.; Cinardi, G.; Gilbert, M. Using random forest to improve the downscaling of global livestock census data. PLoS ONE 2016, 11, e0150424. [Google Scholar] [CrossRef] [Green Version]
- Gilbert, M.; Nicolas, G.; Cinardi, G.; Van Boeckel, T.P.; Vanwambeke, S.O.; Wint, G.W.; Robinson, T.P. Global distribution data for cattle, buffaloes, horses, sheep, goats, pigs, chickens and ducks in 2010. Sci. Data 2018, 5, 180227. [Google Scholar] [CrossRef] [Green Version]
- Neumann, K.; Elbersen, B.S.; Verburg, P.H.; Staritsky, I.; Pérez-Soba, M.; de Vries, W.; Rienks, W.A. Modelling the spatial distribution of livestock in Europe. Landsc. Ecol. 2009, 24, 1207–1222. [Google Scholar] [CrossRef]
- Prosser, D.J.; Wu, J.; Ellis, E.C.; Gale, F.; Van Boeckel, T.P.; Wint, W.; Robinson, T.; Xiao, X.; Gilbert, M. Modelling the distribution of chickens, ducks, and geese in China. Agric. Ecosyst. Environ. 2011, 141, 381–389. [Google Scholar] [CrossRef] [Green Version]
- Van Boeckel, T.P.; Prosser, D.; Franceschini, G.; Biradar, C.; Wint, W.; Robinson, T.; Gilbert, M. Modelling the distribution of domestic ducks in Monsoon Asia. Agric. Ecosyst. Environ. 2011, 141, 373–380. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Zhu, H.; Shao, X.; Zhong, H. Research on Gridding of Livestock Spatial Density Based on Multi-Source Information. China Sci. Technol. Res. Guide 2017, 49, 53–59. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Bailey, D.W.; Stephenson, M.B.; Pittarello, M. Effect of terrain heterogeneity on feeding site selection and livestock movement patterns. Anim. Prod. Sci. 2015, 55, 298–308. [Google Scholar] [CrossRef]
- Zhou, L.; Xiong, L.-Y. Natural topographic controls on the spatial distribution of poverty-stricken counties in China. Appl. Geogr. 2018, 90, 282–292. [Google Scholar] [CrossRef]
- Raynor, E.; Gersie, S.; Stephenson, M.; Clark, P.; Spiegal, S.; Boughton, R.; Bailey, D.; Cibils, A.; Smith, B.; Derner, J. Cattle grazing distribution patterns related to topography across diverse rangeland ecosystems of North America. Rangel. Ecol. Manag. 2021, 75, 91–103. [Google Scholar] [CrossRef]
- Kruska, R.; Reid, R.S.; Thornton, P.K.; Henninger, N.; Kristjanson, P.M. Mapping livestock-oriented agricultural production systems for the developing world. Agric. Syst. 2003, 77, 39–63. [Google Scholar] [CrossRef]
- Liu, J.; Kuang, W.; Zhang, Z.; Xu, X.; Qin, Y.; Ning, J.; Zhou, W.; Zhang, S.; Li, R.; Yan, C.; et al. Spatiotemporal characteristics, patterns, and causes of land-use changes in China since the late 1980s. J. Geogr. Sci. 2014, 24, 195–210. [Google Scholar] [CrossRef]
- Liu, J.; Liu, M.; Tian, H.; Zhuang, D.; Zhang, Z.; Zhang, W.; Tang, X.; Deng, X. Spatial and temporal patterns of China’s cropland during 1990–2000: An analysis based on Landsat TM data. Remote Sens. Environ. 2005, 98, 442–456. [Google Scholar] [CrossRef]
- National Tibetan Plateau Data Center. Available online: http://www.tpdc.ac.cn/zh-hans/data/12e91073-0181-44bf-8308-c50e5bd9a734/ (accessed on 21 December 2020).
- Peng, S. 1-km Monthly Precipitation Dataset for China (1901–2017); A Big Earth Data Platform for Three Poles; National Tibetan Plateau Data Center: Beijing, China, 2020. [Google Scholar]
- Nelson, A. Travel Time to Major Cities: A Global Map of Accessibility; Global Environment Monitoring Unit, Joint Research Centre of the European Commission: Enschede, The Netherlands, 2008. [Google Scholar]
- Weiss, D.J.; Nelson, A.; Gibson, H.S.; Temperley, W.; Peedell, S.; Lieber, A.; Hancher, M.; Poyart, E.; Belchior, S.; Fullman, N.; et al. A global map of travel time to cities to assess inequalities in accessibility in 2015. Nature 2018, 553, 333–336. [Google Scholar] [CrossRef] [PubMed]
- Resource and Environment Science and Data Center. China Population Spatial Distribution Kilometer Grid Dataset. Available online: https://www.resdc.cn/DOI/DOI.aspx?DOIid=32 (accessed on 10 April 2021).
- Resource and Environment Science and Data Center. China GDP Spatial Distribution Kilometer Grid Data Set. Available online: https://www.resdc.cn/DOI/doi.aspx?DOIid=33 (accessed on 10 April 2021).
- Van Velthuizen, H. Mapping Biophysical Factors that Influence Agricultural Production and Rural Vulnerability; Food & Agriculture Organization: Rome, Italy, 2007. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Thomas, S.; Pillai, G.; Pal, K. Prediction of peak ground acceleration using ϵ-SVR, ν-SVR and Ls-SVR algorithm. Geomat. Nat. Hazards Risk 2017, 8, 177–193. [Google Scholar] [CrossRef] [Green Version]
- Pasolli, L.; Notarnicola, C.; Bruzzone, L. Estimating soil moisture with the support vector regression technique. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1080–1084. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Scornet, E. Tuning parameters in random forests. ESAIM Proc. Surv. 2017, 60, 144–162. [Google Scholar] [CrossRef] [Green Version]
- Fang, K.; Wu, J.; Zhu, J.; Xie, B. Research review of random forest method. Stat. Inf. Forum 2011, 26, 32–38. [Google Scholar]
- Merkel, G.D.; Povinelli, R.J.; Brown, R.H. Short-term load forecasting of natural gas with deep neural network regression. Energies 2018, 11, 2008. [Google Scholar] [CrossRef] [Green Version]
- Kuwata, K.; Shibasaki, R. Estimating crop yields with deep learning and remotely sensed data. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 858–861. [Google Scholar]
- Zhao, S.; Liu, Y.; Zhang, R.; Fu, B. China’s population spatialization based on three machine learning models. J. Clean. Prod. 2020, 256, 120644. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, C.; Zhao, M.; Hou, J.; Zhang, Y.; Gu, J. Mapping the Population Density in Mainland China Using NPP/VIIRS and Points-Of-Interest Data Based on a Random Forests Model. Remote Sens. 2020, 12, 3645. [Google Scholar] [CrossRef]
- Cecchi, G.; Wint, W.; Shaw, A.; Marletta, A.; Mattioli, R.; Robinson, T. Geographic distribution and environmental characterization of livestock production systems in Eastern Africa. Agric. Ecosyst. Environ. 2010, 135, 98–110. [Google Scholar] [CrossRef]
- Ganskopp, D.; George, M.; Bailey, D.; Borman, M.; Surber, G.; Harris, N. Factors and practices that influence livestock distribution. Univ. Calif. Div. Agric. Nat. Resour. 2007, 8217, 20. [Google Scholar]
- Lloyd, C.T.; Sorichetta, A.; Tatem, A.J. High resolution global gridded data for use in population studies. Sci. Data 2017, 4, 170001. [Google Scholar] [CrossRef] [Green Version]
- Hollings, T.; Robinson, A.; van Andel, M.; Jewell, C.; Burgman, M. Species distribution models: A comparison of statistical approaches for livestock and disease epidemics. PLoS ONE 2017, 12, e0183626. [Google Scholar] [CrossRef] [Green Version]
- Piipponen, J.; Jalava, M.; de Leeuw, J.; Rizayeva, A.; Godde, C.; Herrero, M.; Kummu, M. Global assessment of grassland carrying capacities and relative stocking densities of livestock. Earth Space Sci. Open Arch. 2021. [Google Scholar] [CrossRef]
- Liu, X.; Huang, J.; Huang, J.; Li, C.; Ding, L.; Meng, W. Estimation of gridded atmospheric oxygen consumption from 1975 to 2018. J. Meteorol. Res. 2020, 34, 646–658. [Google Scholar] [CrossRef]
- Leng, G.; Hall, J.W. Where is the Planetary Boundary for freshwater being exceeded because of livestock farming? Sci. Total Environ. 2021, 760, 144035. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, H.; Shi, H.; Pan, S.; Qin, X.; Pan, N.; Dangal, S.R. Methane emissions from livestock in East Asia during 1961−2019. Ecosyst. Health Sustain. 2021, 7, 1918024. [Google Scholar] [CrossRef]
- El Moustaid, F.; Thornton, Z.; Slamani, H.; Ryan, S.J.; Johnson, L.R. Predicting temperature-dependent transmission suitability of bluetongue virus in livestock. Parasites Vectors 2021, 14, 382. [Google Scholar] [CrossRef]



| Type | Variables | Time 1 | Source | Initial Data Declaration |
|---|---|---|---|---|
| Environmental factors | Grassland coverage | 2000–2015 | Chinese Academy of Sciences Resource and Environmental Science Data Center (http://www.resdc.cn, accessed on 10 March 2021) | 100 m |
| Arable land coverage | 2000–2015 | 100 m | ||
| Forest land coverage | 2000–2015 | 100 m | ||
| Desert coverage | 2000–2015 | 100 m | ||
| NDVI | 2000–2015 | Geospatial Data Cloud (http://www.gscloud.cn, accessed on 19 March 2021) | 500 m | |
| Elevation | 2000 | National Tibetan Plateau Data Center (http://data.tpdc.ac.cn, accessed on 21 December 2020) | 1000 m | |
| Slope | 2000 | 1000 m | ||
| Daytime surface temperature | 2000–2015 | Geospatial Data Cloud (http://www.gscloud.cn, accessed on 19 March 2021) | 1000 m | |
| Precipitation | 2000–2015 | National Tibetan Plateau Data Center (http://data.tpdc.ac.cn, accessed on 25 March 2021) | 1000 m | |
| Distance to river | 2000–2015 | Open Street Map (https://www.openstreetmap.org, accessed on 7 April 2021) | shapefile | |
| Travel time to major cities | 2000, 2015 | Nelson A. D. et al., D. J. Weiss et al. | 1000 m | |
| Population grid data | 2000–2015 | Resource and Environment Science and Data Center (https://www.resdc.cn, accessed on 10 April 2021) | 1000 m | |
| GDP grid data | 2000–2015 | 1000 m | ||
| Unsuitable areas | Permanent water | 2000–2015 | Chinese Academy of Sciences Resource and Environmental Science Data Center (http://www.resdc.cn, accessed on 10 March 2021) | 100 m |
| Urban cores | 2000–2015 | Resource and Environment Science and Data Center (https://www.resdc.cn, accessed on 10 April 2021) | 1000 m | |
| Protected areas | 2000–2015 | World Database of Protected Areas (WDPA) (https://www.protectedplanet.net/country/CHN, accessed on 14 April 2021) | shapefile | |
| Pasture suitability | 2005 | United Nations Food and Agriculture Organization (https://data.apps.fao.org/map/catalog, accessed on 15 April 2021) | 10,000 m | |
| Census | Stock data of cattle | 2000–2015 | China Statistical Yearbooks (http://www.stats.gov.cn/tjsj/pcsj/, accessed on 27 November 2020) | County |
| Stock data of sheep | 2000–2015 | County |
| Species | Model | Training Set | Test Set | ||
|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | ||
| Cattle | SVM | 0.50 | 14.86 | 0.54 | 13.21 |
| RF | 0.92 | 5.82 | 0.74 | 9.57 | |
| DNN | 0.95 | 4.73 | 0.75 | 8.98 | |
| Sheep | SVM | 0.55 | 43.38 | 0.52 | 52.65 |
| RF | 0.93 | 19.59 | 0.72 | 34.58 | |
| DNN | 0.96 | 14.71 | 0.73 | 33.97 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Hou, J.; Huang, C. High-Resolution Gridded Livestock Projection for Western China Based on Machine Learning. Remote Sens. 2021, 13, 5038. https://doi.org/10.3390/rs13245038
Li X, Hou J, Huang C. High-Resolution Gridded Livestock Projection for Western China Based on Machine Learning. Remote Sensing. 2021; 13(24):5038. https://doi.org/10.3390/rs13245038
Chicago/Turabian StyleLi, Xianghua, Jinliang Hou, and Chunlin Huang. 2021. "High-Resolution Gridded Livestock Projection for Western China Based on Machine Learning" Remote Sensing 13, no. 24: 5038. https://doi.org/10.3390/rs13245038
APA StyleLi, X., Hou, J., & Huang, C. (2021). High-Resolution Gridded Livestock Projection for Western China Based on Machine Learning. Remote Sensing, 13(24), 5038. https://doi.org/10.3390/rs13245038