Improving the Spatial Resolution of GRACE-Derived Terrestrial Water Storage Changes in Small Areas Using the Machine Learning Spatial Downscaling Method
Abstract
:1. Introduction
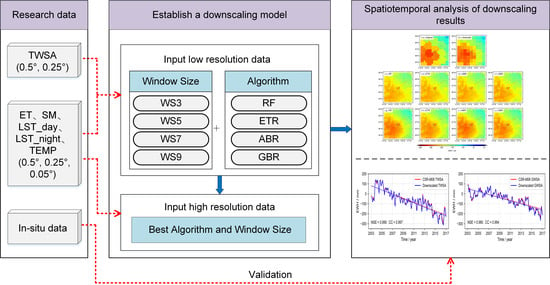
2. The MLSDM for Spatial Downscaling
3. Materials and Methods
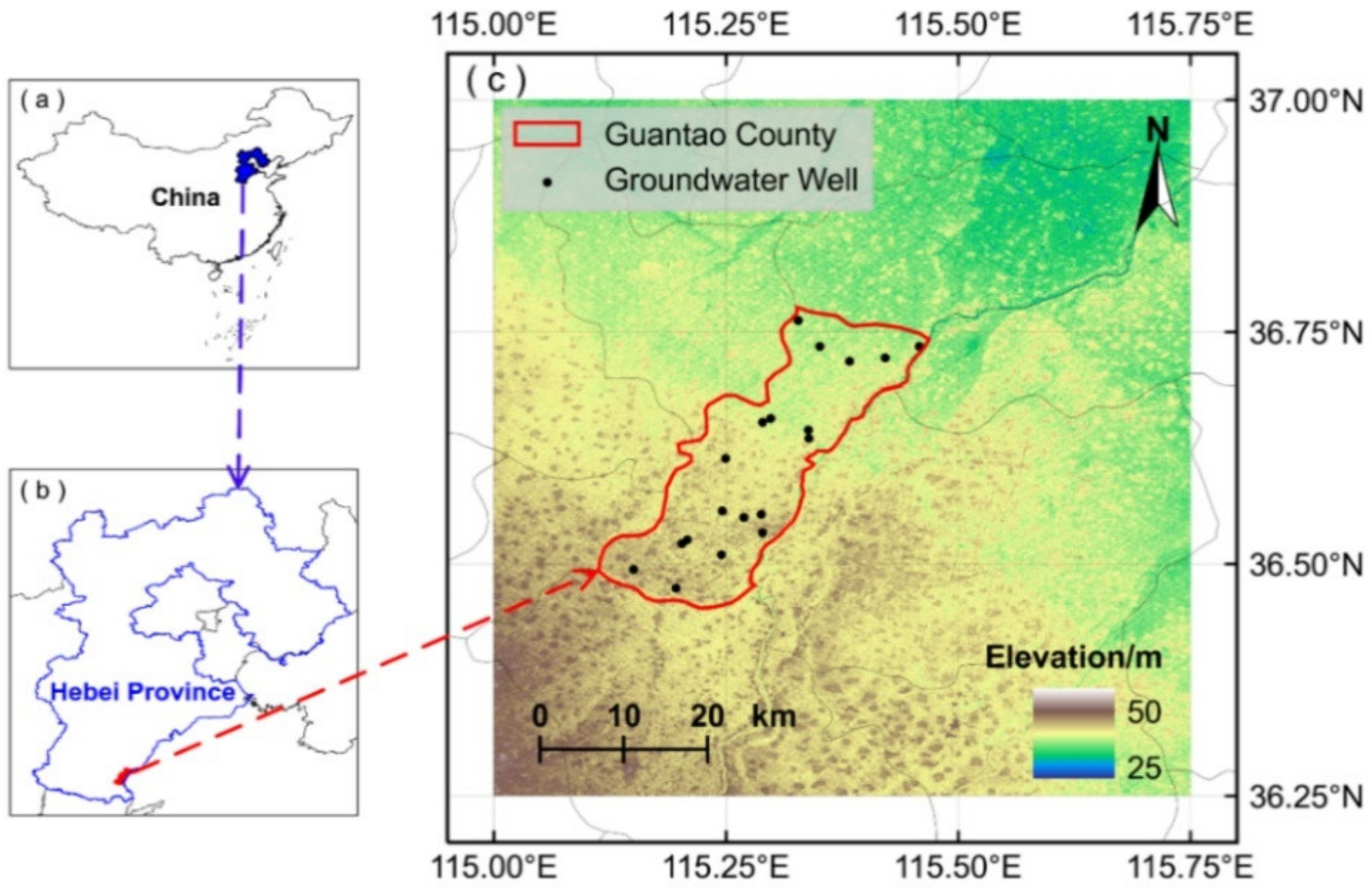
3.1. Study Area
3.2. Materials
3.2.1. GRACE Solutions
3.2.2. GLDAS Model
3.2.3. MODIS Data
3.2.4. TEMP Data
3.2.5. In Situ Observations
3.3. Machine Learning Algorithms
3.4. Data Processing Flow
- (1)
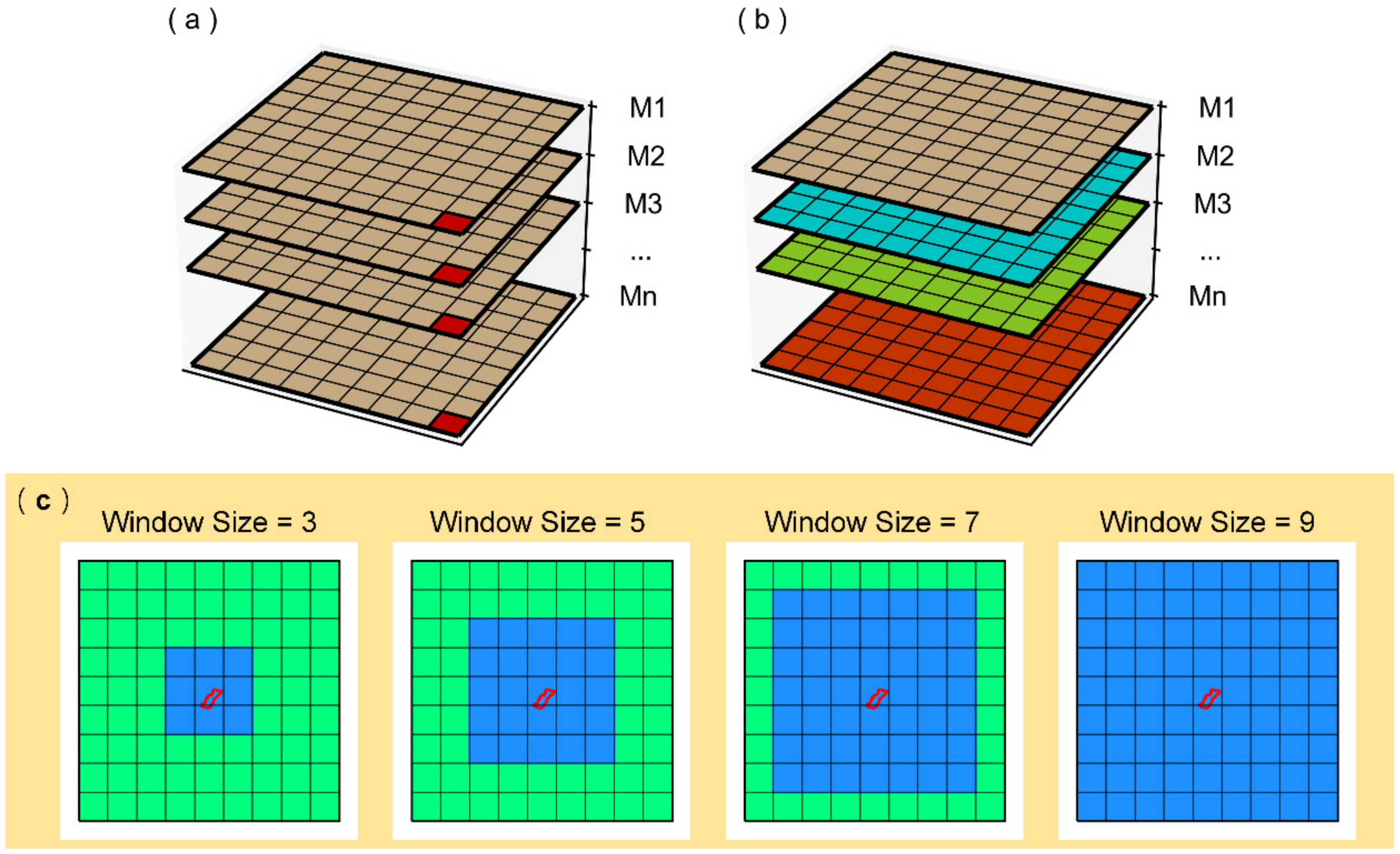
- Firstly, to analyze the influence of the modeling window on the downscaled results, we set up modeling windows with the sizes of 3 × 3 (WS3), 5 × 5 (WS5), 7 × 7 (WS7), and 9 × 9 (WS9) based on a 0.5° grid with Guantao County as the center (Figure 1c).
- (2)
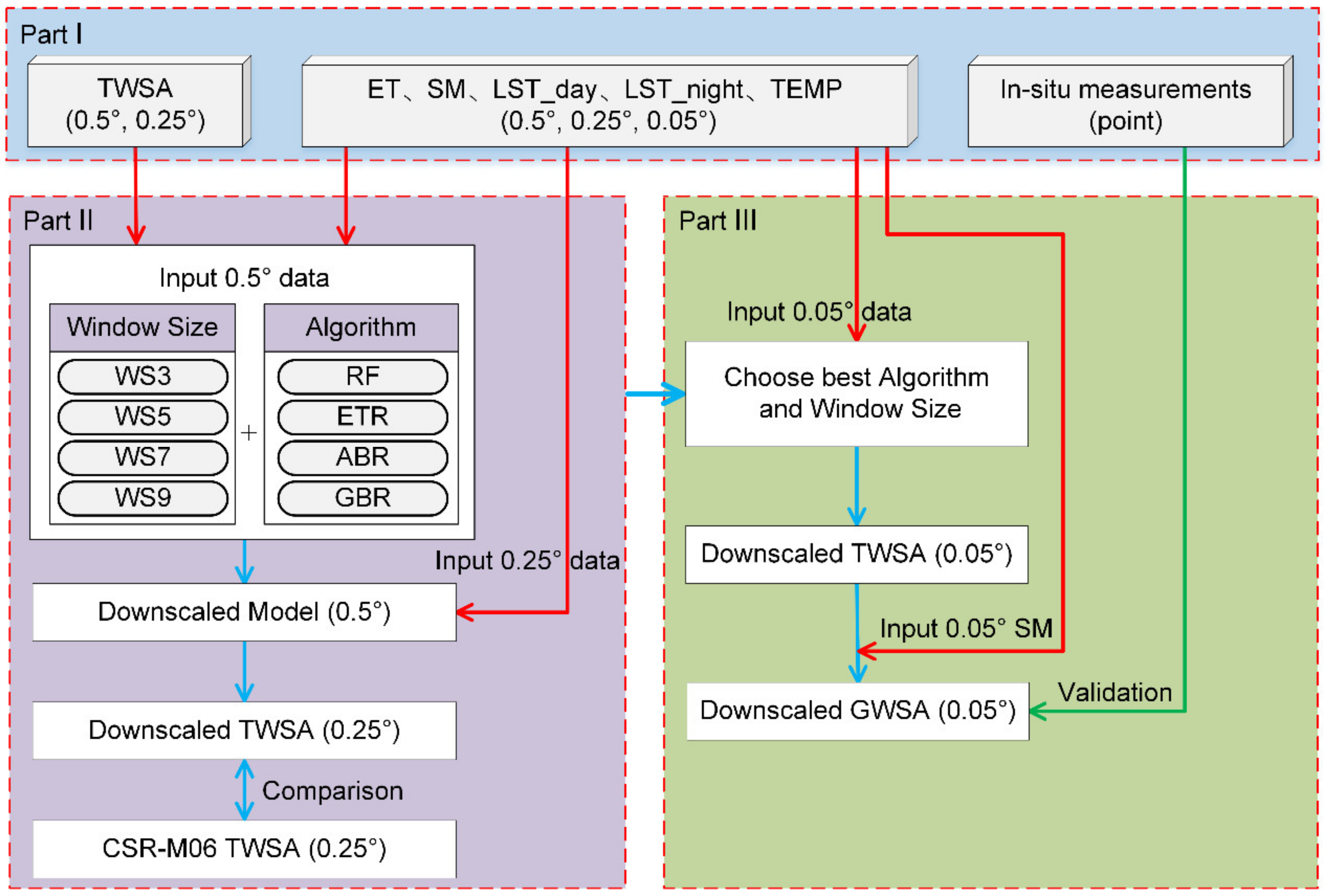
- Secondly, due to the inconsistent spatiotemporal resolution, the research data needed to be preprocessed (Part I). The spatial resolution of TWSA was resampled to 0.5° and 0.25°; the spatial resolution of ET, SM, LST_day, LST_night, and TEMP was resampled to 0.5°, 0.25°, and 0.05°. With the exception of the in situ groundwater well observations, the temporal resolution of other research data is unified as one month.
- (3)
- Thirdly, The MLSDM is employed to establish the regression models between TWSA and five hydrological variables at a spatiotemporal resolution of 0.5° × 0.5° and one month (Figure 1b,c and Part II) (WS3, WS5, WS7, WS9 modeling window cross joint RF, ETR, GBR, ABR algorithm, such as WS3 + RF). We input the hydrological variables of 0.25° into the regression model of the corresponding month (the red arrow in Part II) to obtain the downscaled 0.25° TWSA. Then, this study compared RMSE, MAE, NSE, and CC between downscaled 0.25° TWSA and CSR-M06-derived TWSA on spatiotemporal signals to determine the best combined model.
- (4)
- Finally, the optimal combined model in Part II was applied to the hydrological variables at a spatial resolution of 0.05° to obtain the estimated 0.05° TWSA. According to the water storage balance equation, the soil moisture anomalies (SMA) were subtracted from the TWSA to estimate a 0.05° GWSA. Subsequently, the in situ groundwater well observations in Guantao County were used to compare and verify the downscaled GWSA (Part III).
3.5. Model Evaluation Metrics
4. Results
4.1. Accuracy Analysis of Downscaling Method
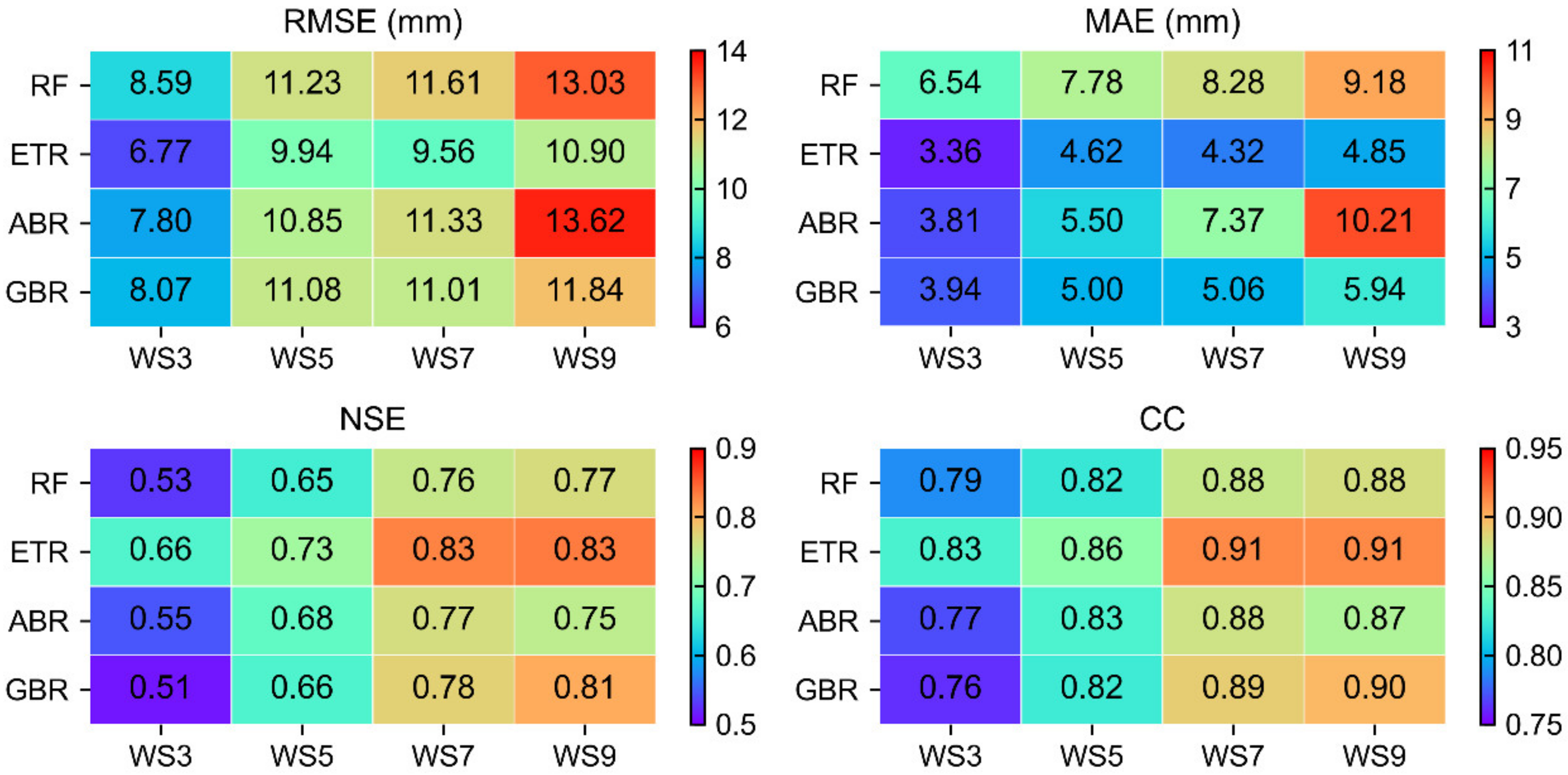
4.1.1. Performance of Downscaling Model
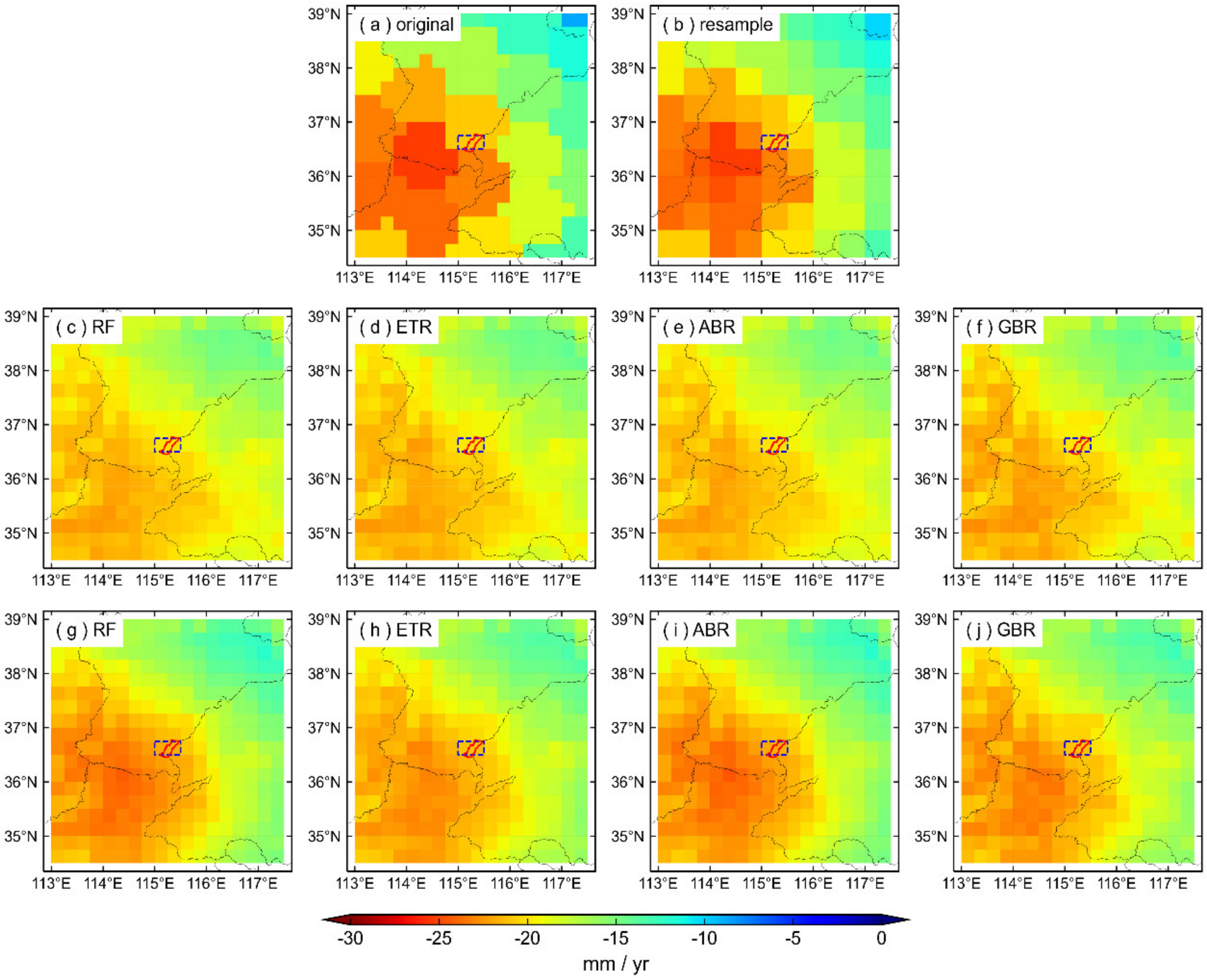
4.1.2. Spatial Analysis of Downscaled TWSA before and after Adding Residuals
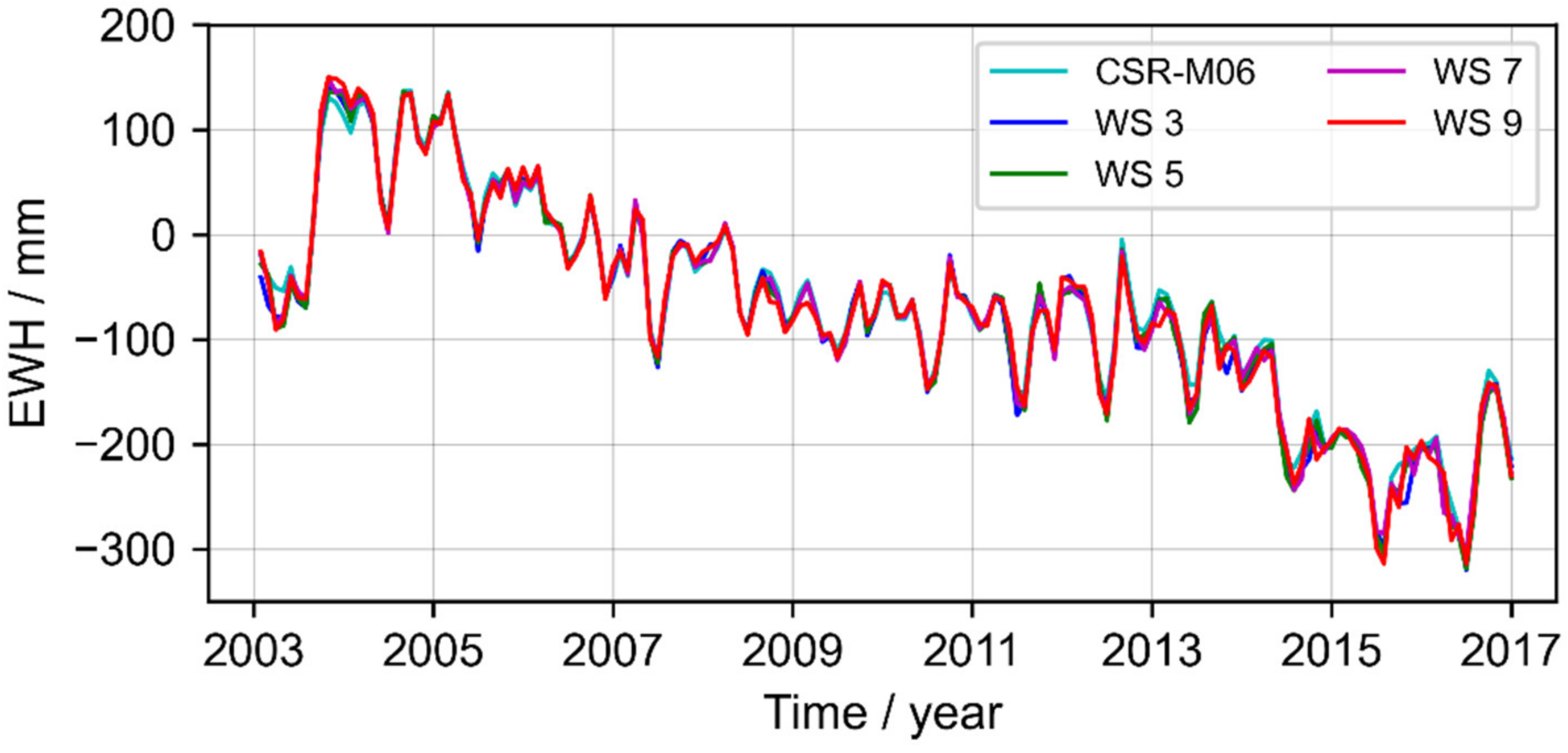
4.1.3. Time Series Analysis of TWSA in Guantao County before and after Downscaling
4.2. Downscaled Results with High Spatial Resolution
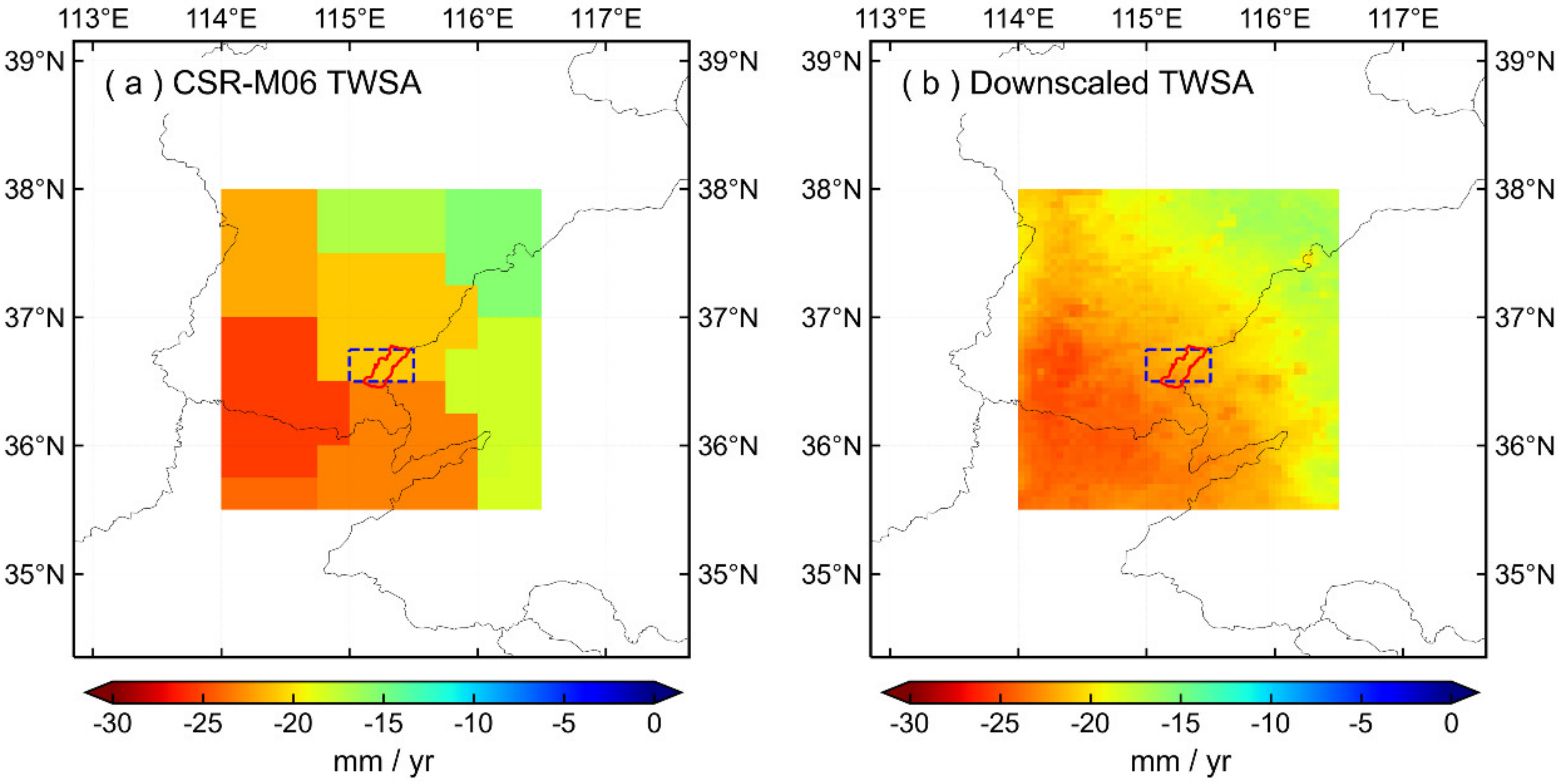
4.2.1. Spatiotemporal Distribution of TWSA Downscaled Signal
4.2.2. Spatiotemporal Distribution of GWSA Downscaled Signal
5. Discussion
5.1. Validation Analysis of In Situ Observations
5.2. Limitation and Outlook
6. Conclusions
- (1)
- To improve the spatial resolution of TWSA products, the MLSDM was constructed using different modeling windows combined with multiple machine learning algorithms. The verification results show that the downscaled results obtained by MLSDM are consistent with the original CSR-M06 model in the spatial distribution. Furthermore, after adding residuals, the downscaling accuracy of each combined model was improved, and the RMSE, MAE, NSE, and CC values increased by 20%~26%, 13%~27%, and 20%~82%, and 3%~7%. Specifically, the accuracy of RF in each modeling window is slightly better than ETR, ABR, and GBR.
- (2)
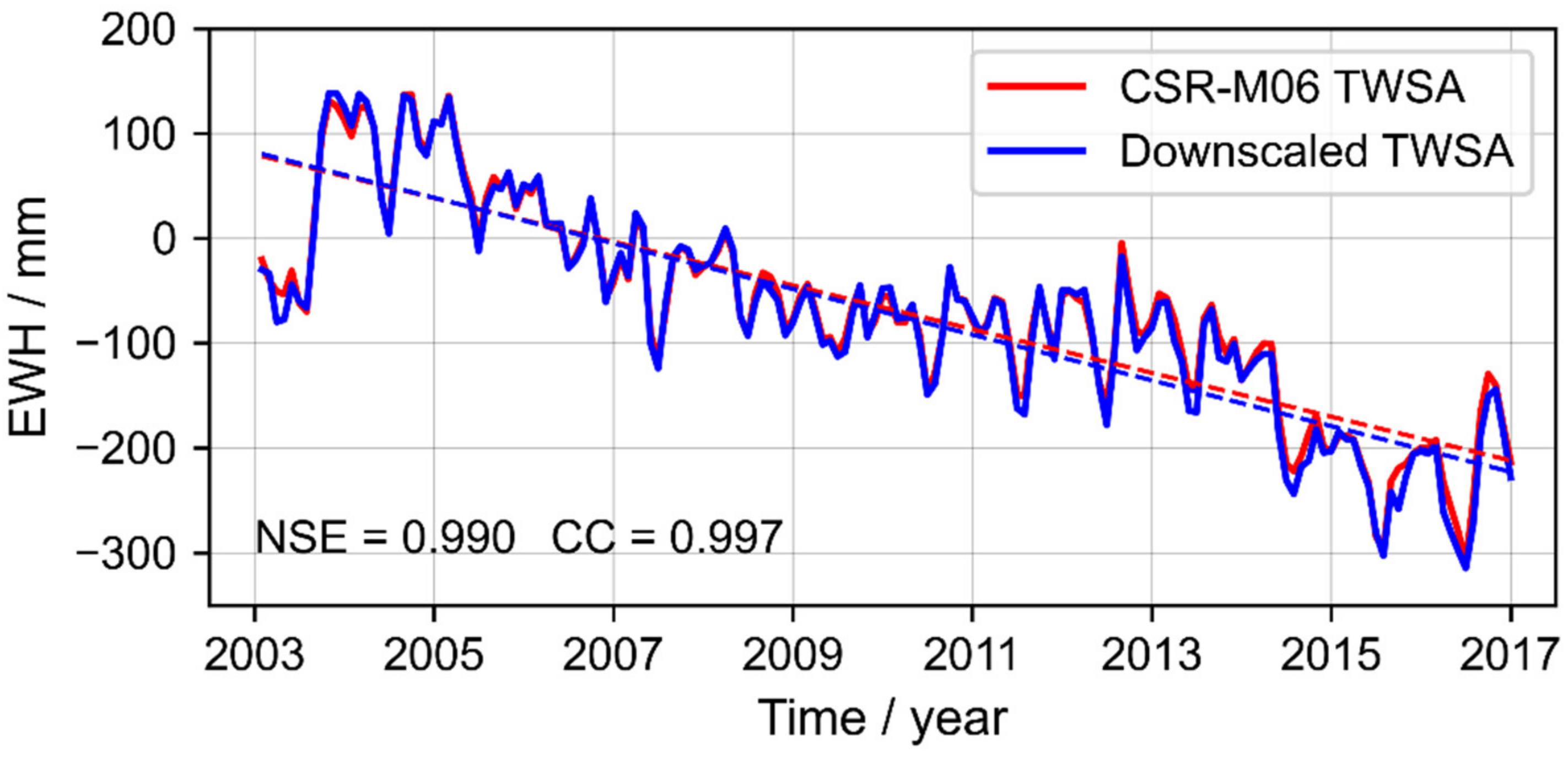
- To further analyze the impact of the modeling windows, this study compared the TWS time series changes in Guantao County that were derived from the downscaled results of RF combined with different modeling windows. The RMSE, MAE, NSE, and CC of WS5 combined with RF were 9.67 mm, 6.80 mm, 0.990, and 0.997, respectively, which are slightly superior to the downscaled results of WS3, WS7, and WS9.
- (3)
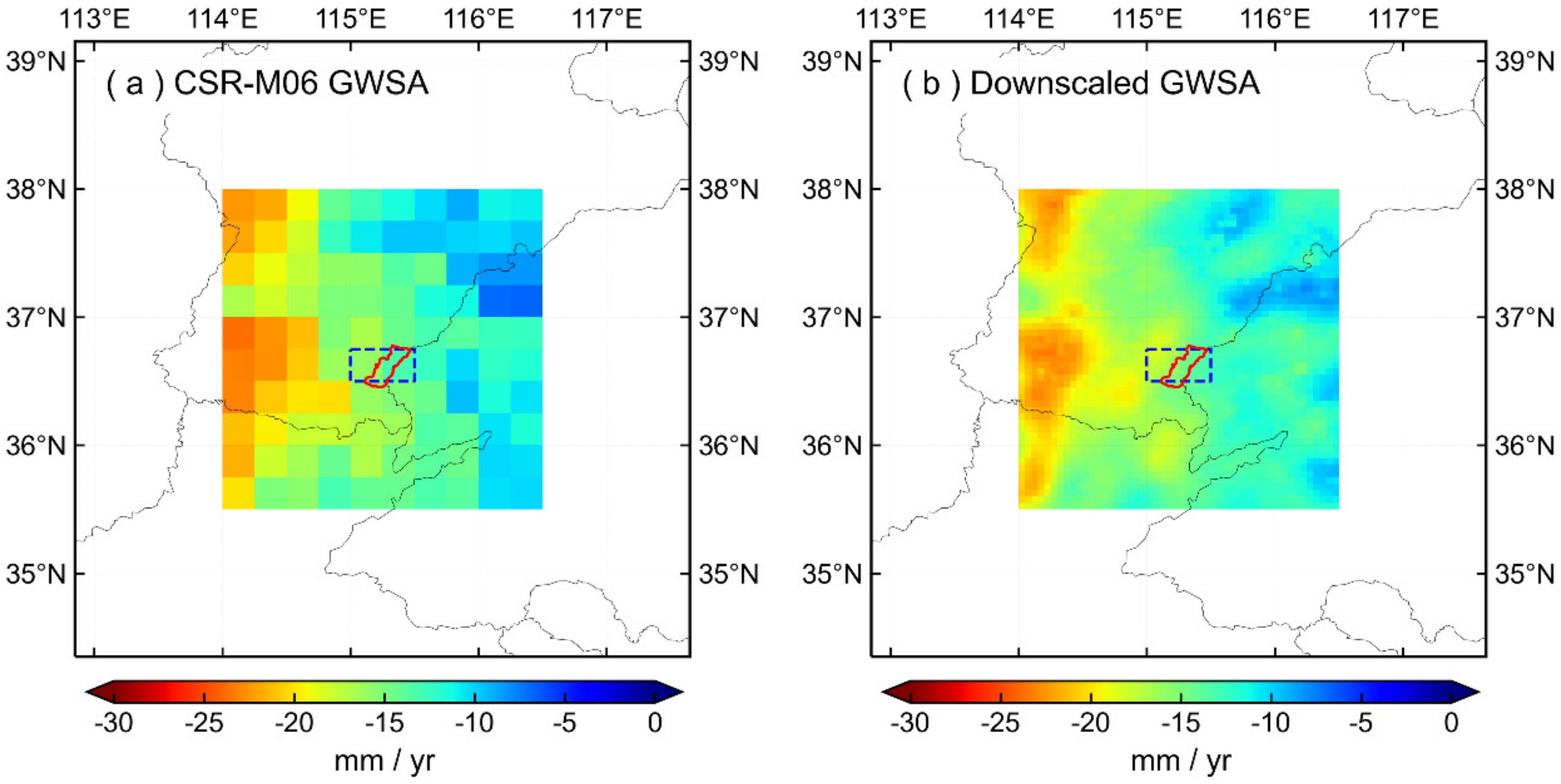
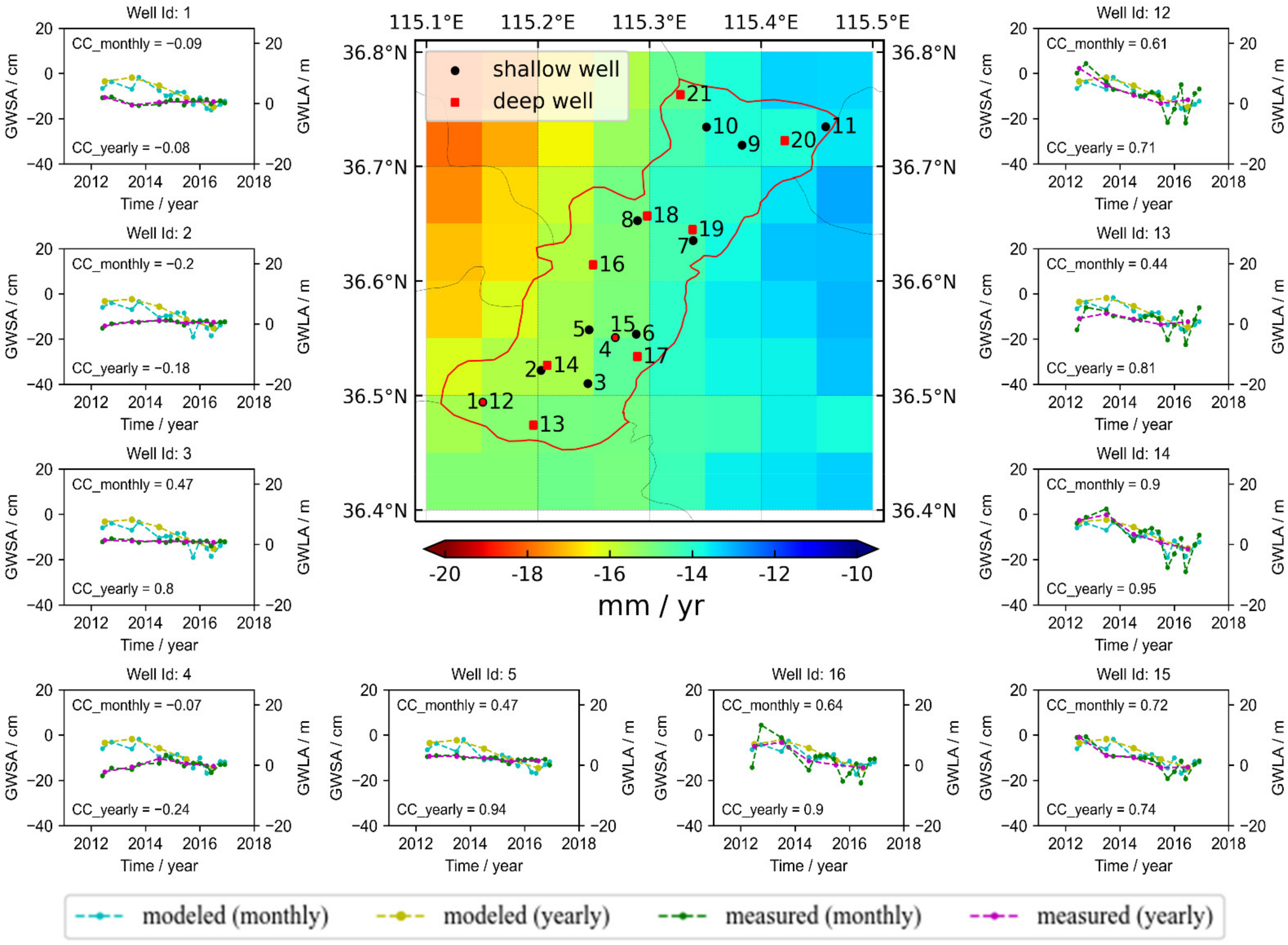
- The combined model of WS5 and RF was utilized to downscale the TWSA/GWSA data to 0.05°, and the signals before and after downscaling demonstrated high consistency. The NSE and CC of the TWSA time series before and after downscaling are 0.990 and 0.997, respectively, and the NSE and CC of GWSA time series before and after downscaling are 0.980 and 0.994, respectively. Subsequently, the measured groundwater level data was used to verify the high-resolution GWSA results. The CC between the high-resolution GWSA and 80% of the deep groundwater well data was above 0.70, but the correlation between shallow groundwater was relatively poor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59–60, 143–156. [Google Scholar] [CrossRef]
- Wada, Y.; Wisser, D.; Bierkens, M.F.P. Global modeling of withdrawal, allocation and consumptive use of surface water and groundwater resources. Earth Syst. Dyn. 2014, 5, 15–40. [Google Scholar] [CrossRef] [Green Version]
- Dangar, S.; Asoka, A.; Mishra, V. Causes and implications of groundwater depletion in India: A review. J. Hydrol. 2021, 596, 126103. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Lemoine, J.-M.; Biancale, R.; Hsu, H.-T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Longuevergne, L.; Long, D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA. Water Resour. Res. 2012, 48, W04520.04521–W04520.04529. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.A.; Zhao, Y.; Khan, J.; Rahman, G.; Rafiq, M.; Moazzam, M.F.U. Spatial and Temporal Analysis of Rainfall and Drought Condition in Southwest Xinjiang in Northwest China, Using Various Climate Indices. Earth Syst. Environ. 2021, 5, 201–216. [Google Scholar] [CrossRef]
- Valipour, M.; Bateni, S.M.; Jun, C. Global Surface Temperature: A New Insight. Climate 2021, 9, 81. [Google Scholar] [CrossRef]
- Bierkens, M.F.P.; Wada, Y. Non-renewable groundwater use and groundwater depletion: A review. Environ. Res. Lett. 2019, 14, 063002. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [Green Version]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, L11501. [Google Scholar] [CrossRef] [Green Version]
- Famiglietti, J.S.; Rodell, M. Water in the Balance. Science 2013, 340, 1300–1301. [Google Scholar] [CrossRef]
- Alley, W.M.; Konikow, L.F. Bringing GRACE Down to Earth. Groundwater 2015, 53, 826–829. [Google Scholar] [CrossRef]
- Hasan, E.; Tarhule, A.; Kirstetter, P.-E. Twentieth and Twenty-First Century Water Storage Changes in the Nile River Basin from GRACE/GRACE-FO and Modeling. Remote Sens. 2021, 13, 953. [Google Scholar] [CrossRef]
- Scanlon, B.; Zhang, Z.; Rateb, A.; Sun, A.; Wiese, D.; Save, H.; Beaudoing, H.; Lo, M.-H.; Müller Schmied, H.; Doell, P.; et al. Tracking Seasonal Fluctuations in Land Water Storage Using Global Models and GRACE Satellites. Geophys. Res. Lett. 2019, 46, 5254–5264. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, B.; Yao, Y.; Yang, Y.; Li, J.; Ran, Q. GRACE and land surface models reveal severe drought in eastern China in 2019. J. Hydrol. 2021, 601, 126640. [Google Scholar] [CrossRef]
- Xiong, J.; Guo, S.; Yin, J.; Gu, L.; Xiong, F. Using the Global Hydrodynamic Model and GRACE Follow-On Data to Access the 2020 Catastrophic Flood in Yangtze River Basin. Remote Sens. 2021, 13, 3023. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. Contribution of ice sheet and mountain glacier melt to recent sea level rise. Nat. Geosci. 2013, 6, 549. [Google Scholar] [CrossRef]
- Cazenave, A.; Chen, J. Time-variable gravity from space and present-day mass redistribution in theEarth system. Earth Planet. Sci. Lett. 2010, 298, 263–274. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2007, 15, 159–166. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Famigliett, J.S.; Scanlon, B.R.; Rodell, M. Groundwater Storage Changes: Present Status from GRACE Observations. Remote Sens. Water Resour. 2016, 207–227. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Yang, Z.L.; Niu, G.Y. 2005 drought event in the Amazon River basin as measured by GRACE and estimated by climate models. J. Geophys. Res. Solid Earth 2009, 114, B05404. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46, W12526. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Luo, Z.; Tangdamrongsub, N.; Wang, L.; He, L.; Xu, C.; Li, Q. Characterizing Drought and Flood Events over the Yangtze River Basin Using the HUST-Grace2016 Solution and Ancillary Data. Remote Sens. 2017, 9, 1100. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Guo, S.; Yin, J. Discharge Estimation Using Integrated Satellite Data and Hybrid Model in the Midstream Yangtze River. Remote Sens. 2021, 13, 2272. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Li, J.; Zhang, Z.; Ni, S. Long-term groundwater variations in Northwest India from satellite gravity measurements. Glob. Planet. Chang. 2014, 116, 130–138. [Google Scholar] [CrossRef] [Green Version]
- Joshi, S.K.; Gupta, S.; Sinha, R.; Densmore, A.L.; Rai, S.P.; Shekhar, S.; Mason, P.J.; van Dijk, W. Strongly heterogeneous patterns of groundwater depletion in Northwestern India. J. Hydrol. 2021, 598, 126492. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Y.; Gong, H.; Yeh, P.J.-F.; Li, X.; Zhou, D.; Zhao, W. Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain. Geophys. Res. Lett. 2015, 42, 1791–1799. [Google Scholar] [CrossRef]
- Gong, H.; Pan, Y.; Zheng, L.; Li, X.; Zhu, L.; Zhang, C.; Huang, Z.; Li, Z.; Wang, H.; Zhou, C. Long-term groundwater storage changes and land subsidence development in the North China Plain (1971–2015). Hydrogeol. J. 2018, 26, 1417–1427. [Google Scholar] [CrossRef] [Green Version]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Liu, P.-W.; Massoud, E.; Farr, T.G.; Lundgren, P.; Famiglietti, J.S. Monitoring Groundwater Change in California’s Central Valley Using Sentinel-1 and GRACE Observations. Geosciences 2019, 9, 436. [Google Scholar] [CrossRef] [Green Version]
- Vasco, D.W.; Farr, T.G.; Jeanne, P.; Doughty, C.; Nico, P. Satellite-based monitoring of groundwater depletion in California’s Central Valley. Sci. Rep. 2019, 9, 16053. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilby, R.L.; Wigley, T.M.L. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. Earth Environ. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- Fowler, H.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Wilby, R.L.; Wigley, T.M.L.; Conway, D.; Jones, P.D.; Hewitson, B.C.; Main, J.; Wilks, D.S. Statistical downscaling of general circulation model output: A comparison of methods. Water Resour. Res. 1998, 34, 2995–3008. [Google Scholar] [CrossRef]
- Yan, R.; Bai, J. A New Approach for Soil Moisture Downscaling in the Presence of Seasonal Difference. Remote Sens. 2020, 12, 2818. [Google Scholar] [CrossRef]
- Wen, F.; Zhao, W.; Wang, Q.; Sánchez, N. A Value-Consistent Method for Downscaling SMAP Passive Soil Moisture With MODIS Products Using Self-Adaptive Window. IEEE Trans. Geosci. Remote Sens. 2020, 58, 913–924. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Wang, F.; Tian, D.; Lowe, L.; Kalin, L.; Lehrter, J. Deep Learning for Daily Precipitation and Temperature Downscaling. Water Resour. Res. 2021, 57, e2020WR029308. [Google Scholar] [CrossRef]
- Yan, X.; Chen, H.; Tian, B.; Sheng, S.; Wang, J.; Kim, J.-S. A Downscaling–Merging Scheme for Improving Daily Spatial Precipitation Estimates Based on Random Forest and Cokriging. Remote Sens. 2021, 13, 2040. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. A Comparison of Different Regression Algorithms for Downscaling Monthly Satellite-Based Precipitation over North China. Remote Sens. 2016, 8, 835. [Google Scholar] [CrossRef] [Green Version]
- Fasbender, D.; Ouarda, T. Spatial Bayesian Model for Statistical Downscaling of AOGCM to Minimum and Maximum Daily Temperatures. J. Clim. 2010, 23, 5222–5242. [Google Scholar] [CrossRef] [Green Version]
- Tan, S.; Wu, B.; Yan, N. A method for downscaling daily evapotranspiration based on 30-m surface resistance. J. Hydrol. 2019, 577, 123882. [Google Scholar] [CrossRef]
- Liu, Y.G.; Wang, S.X.; Wang, Y.; Hu, H.N. Evaluation of potential evapotranspiration in the Weihe River Basin based on statistical downscaling. IOP Conf. Ser. Earth Environ. Sci. 2018, 191, 012025. [Google Scholar] [CrossRef]
- Wan, Z.; Zhang, K.; Xue, X.; Hong, Z.; Hong, Y.; Gourley, J.J. Water balance-based actual evapotranspiration reconstruction from ground and satellite observations over the Conterminous United States. Water Resour. Res. 2015, 51, 6485–6499. [Google Scholar] [CrossRef]
- Ning, S.; Ishidaira, H.; Wang, J. Statistical Downscaling of GRACE-derived Terrestrial Water Storage Using Satellite and GLDAS Products. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2014, 70, I_133–I_138. [Google Scholar] [CrossRef]
- Karunakalage, A.; Sarkar, T.; Kannaujiya, S.; Chauhan, P.; Pranjal, P.; Taloor, A.K.; Kumar, S. The appraisal of groundwater storage dwindling effect, by applying high resolution downscaling GRACE data in and around Mehsana district, Gujarat, India. Groundw. Sustain. Dev. 2021, 13, 100559. [Google Scholar] [CrossRef]
- Miro, M.E.; Famiglietti, J.S. Downscaling GRACE Remote Sensing Datasets to High-Resolution Groundwater Storage Change Maps of California’s Central Valley. Remote Sens. 2018, 10, 143. [Google Scholar] [CrossRef] [Green Version]
- Seyoum, M.W.; Kwon, D.; Milewski, M.A. Downscaling GRACE TWSA Data into High-Resolution Groundwater Level Anomaly Using Machine Learning-Based Models in a Glacial Aquifer System. Remote Sens. 2019, 11, 824. [Google Scholar] [CrossRef] [Green Version]
- Milewski, A.M.; Thomas, M.B.; Seyoum, W.M.; Rasmussen, T.C. Spatial Downscaling of GRACE TWSA Data to Identify Spatiotemporal Groundwater Level Trends in the Upper Floridan Aquifer, Georgia, USA. Remote Sens. 2019, 11, 2756. [Google Scholar] [CrossRef] [Green Version]
- Sahour, H.; Sultan, M.; Vazifedan, M.; Abdelmohsen, K.; Karki, S.; Yellich, J.A.; Gebremichael, E.; Alshehri, F.; Elbayoumi, T.M. Statistical Applications to Downscale GRACE-Derived Terrestrial Water Storage Data and to Fill Temporal Gaps. Remote Sens. 2020, 12, 533. [Google Scholar] [CrossRef] [Green Version]
- The People’s Government of Guantao County. Available online: http://www.guantao.gov.cn/channel-4-9.html (accessed on 1 September 2020).
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Watkins, M.; Wiese, D.; Yuan, D.N.; Boening, C.; Landerer, F. Improved Methods for Observing Earth’s Time Variable Mass Distribution with GRACE using Spherical Cap Mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2016, 52, 9412–9429. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef] [Green Version]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Monteith, J. Evaporation and Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Wan, Z.; Hook, S.; Hulley, G. MOD11C3 MODIS/Terra Land Surface Temperature/Emissivity Monthly L3 Global 0.05 Deg CMG V006. Available online: https://lpdaac.usgs.gov/products/mod11c3v006/ (accessed on 3 July 2021).
- Peng, S.; Ding, D.; Liu, W. 1 km monthly temperature and precipitation dataset for China from 1901 to 2017. Earth Syst. Sci. Data 2019, 11, 1931–1946. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.Z. 1-km Monthly Mean Temperature Dataset for China (1901–2017); National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar] [CrossRef]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble Machine Learning. Scholarpedia 2009, 4, 2776. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely Randomized Trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Drucker, H. Improving Regressors Using Boosting Techniques. In Proceedings of the 14th International Conference on Machine Learning, Nashville, TN, USA, 8–12 July 1997. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
- Chai, T.; Draxler, R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- McCuen, R.; Knight, Z.; Cutter, A. Evaluation of the Nash–Sutcliffe Efficiency Index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Rodgers, L.; Nicewander, A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Willmott, C.; Matsuura, K. Advantages of the Mean Absolute Error (MAE) over the Root Mean Square Error (RMSE) in Assessing Average Model Performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Wang, M. Downscaling Groundwater Storage Data in China to a 1-km Resolution Using Machine Learning Methods. Remote Sens. 2021, 13, 523. [Google Scholar] [CrossRef]
- Chen, S.; She, D.; Zhang, L.; Guo, M.; Liu, X. Spatial Downscaling Methods of Soil Moisture Based on Multisource Remote Sensing Data and Its Application. Water 2019, 11, 1401. [Google Scholar] [CrossRef] [Green Version]



| Variables | Sources | Scale | Unit | Website |
|---|---|---|---|---|
| TWSA | CSR RL06 Mascon | 0.25°; Monthly | cm | http://www2.csr.utexas.edu/grace/RL06_mascons.html (accessed on 1 May 2021) |
| Soil Moisture | GLDAS | 0.25°; Monthly | mm | https://disc.gsfc.nasa.gov/datasets?keywords=GLDAS (accessed on 1 May 2021) |
| Evapotranspiration | MODIS 16A2 | 500 m; 8 day | kg/m2/8 day | https://lpdaac.usgs.gov/products/mod16a2v006/ (accessed on 1 May 2021) |
| Day Land Surface Temperature | MODIS 11C3 | 0.05°; Monthly | Kelvin | https://lpdaac.usgs.gov/products/mod11c3v006/ (accessed on 1 May 2021) |
| Night Land Surface Temperature | MODIS 11C3 | 0.05°; Monthly | Kelvin | https://lpdaac.usgs.gov/products/mod11c3v006/ (accessed on 1 May 2021) |
| TEMP | TPDC | 1 km; Monthly | °C | http://data.tpdc.ac.cn/zh-hans/ (accessed on 1 May 2021) |
| Groundwater Level | In situ observations | point; sub-yearly | m | -- |
| Shallow Groundwater Well | Deep Groundwater Well | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Well Id | Before Downscaling | After Downscaling 1 | Well Id | Before Downscaling | After Downscaling 1 | ||||
| CC_monthly | CC_yearly | CC_monthly | CC_yearly | CC_monthly | CC_yearly | CC_monthly | CC_yearly | ||
| 1 | 0.27 | 0.29 | −0.09 | −0.08 | 12 | 0.38 | 0.76 | 0.61↑ | 0.71 |
| 2 | −0.24 | −0.35 | −0.20↑ | −0.18↑ | 13 | 0.05 | 0.47 | 0.44↑ | 0.81↑ |
| 3 | 0.21 | 0.91 | 0.47↑ | 0.80 | 14 | 0.43 | 0.88 | 0.90↑ | 0.95↑ |
| 4 | −0.16 | −0.28 | −0.07↑ | −0.24↑ | 15 | 0.51 | 0.81 | 0.72↑ | 0.74 |
| 5 | 0.69 | 0.82 | 0.47 | 0.94↑ | 16 | 0.30 | 0.83 | 0.64↑ | 0.90↑ |
| 6 | 0.45 | 0.71 | 0.67↑ | 0.87↑ | 17 | 0.40 | 0.81 | 0.69↑ | 0.76 |
| 7 | −0.55 | −0.65 | −0.28↑ | −0.56↑ | 18 | −0.05 | 0.01 | 0.05↑ | 0.09↑ |
| 8 | −0.82 | −0.87 | −0.70↑ | −0.84↑ | 19 | 0.12 | 0.33 | 0.42↑ | 0.48↑ |
| 9 | −0.68 | −0.70 | −0.34↑ | −0.65↑ | 20 | 0.43 | 0.90 | 0.65↑ | 0.86 |
| 10 | −0.39 | −0.56 | −0.34↑ | −0.52↑ | 21 | 0.37 | 0.95 | 0.43↑ | 0.91 |
| 11 | −0.63 | −0.64 | −0.26↑ | −0.59↑ | -- | -- | -- | -- | -- |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zheng, W.; Yin, W.; Li, X.; Zhang, G.; Zhang, J. Improving the Spatial Resolution of GRACE-Derived Terrestrial Water Storage Changes in Small Areas Using the Machine Learning Spatial Downscaling Method. Remote Sens. 2021, 13, 4760. https://doi.org/10.3390/rs13234760
Chen Z, Zheng W, Yin W, Li X, Zhang G, Zhang J. Improving the Spatial Resolution of GRACE-Derived Terrestrial Water Storage Changes in Small Areas Using the Machine Learning Spatial Downscaling Method. Remote Sensing. 2021; 13(23):4760. https://doi.org/10.3390/rs13234760
Chicago/Turabian StyleChen, Zhiwei, Wei Zheng, Wenjie Yin, Xiaoping Li, Gangqiang Zhang, and Jing Zhang. 2021. "Improving the Spatial Resolution of GRACE-Derived Terrestrial Water Storage Changes in Small Areas Using the Machine Learning Spatial Downscaling Method" Remote Sensing 13, no. 23: 4760. https://doi.org/10.3390/rs13234760
APA StyleChen, Z., Zheng, W., Yin, W., Li, X., Zhang, G., & Zhang, J. (2021). Improving the Spatial Resolution of GRACE-Derived Terrestrial Water Storage Changes in Small Areas Using the Machine Learning Spatial Downscaling Method. Remote Sensing, 13(23), 4760. https://doi.org/10.3390/rs13234760