Predicting Days to Maturity, Plant Height, and Grain Yield in Soybean: A Machine and Deep Learning Approach Using Multispectral Data
Abstract
:1. Introduction
2. Materials and Methods
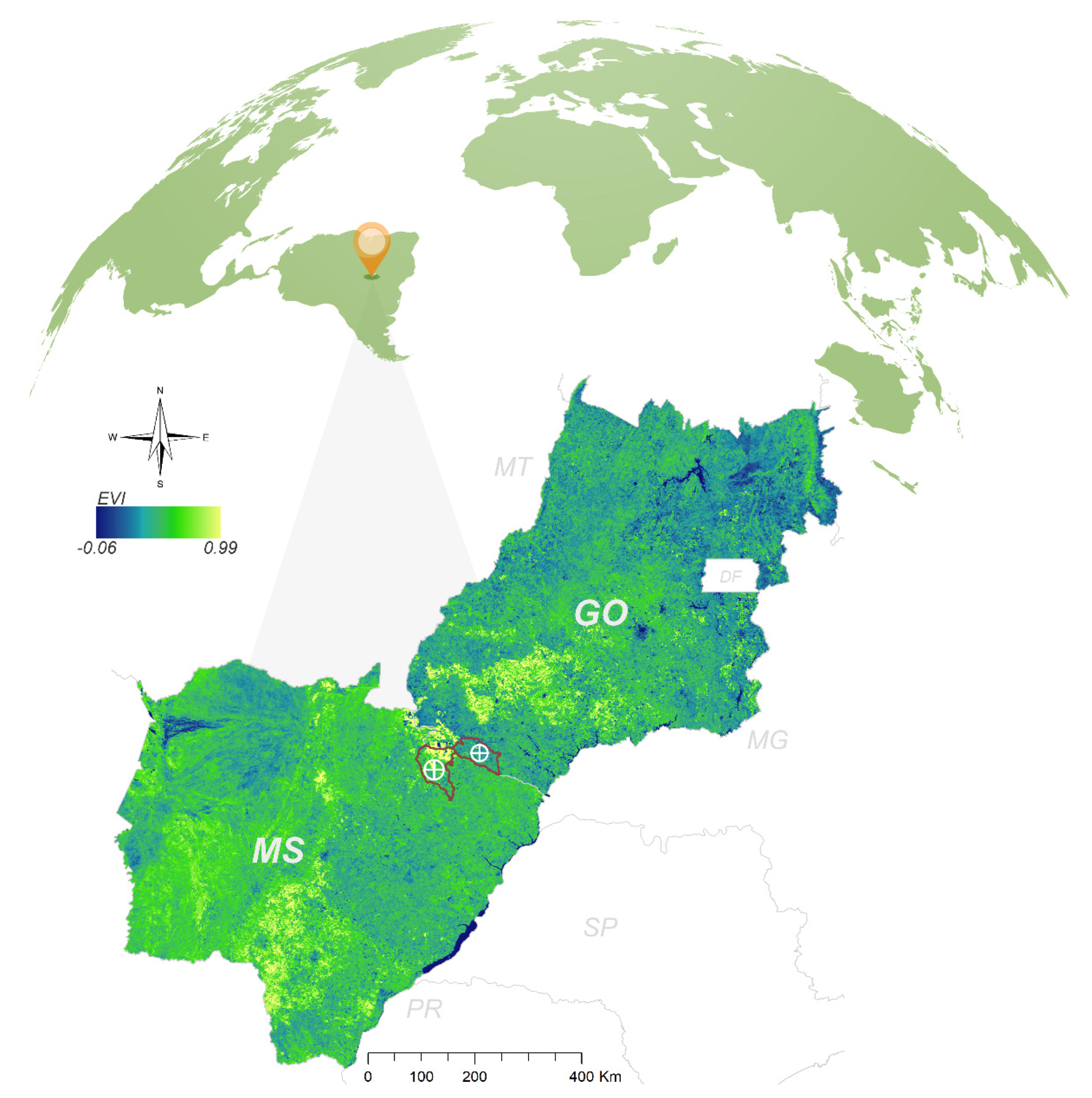
2.1. Field Trials
2.2. Aerial Multispectral Image Acquisition and Vegetation Indices Calculation
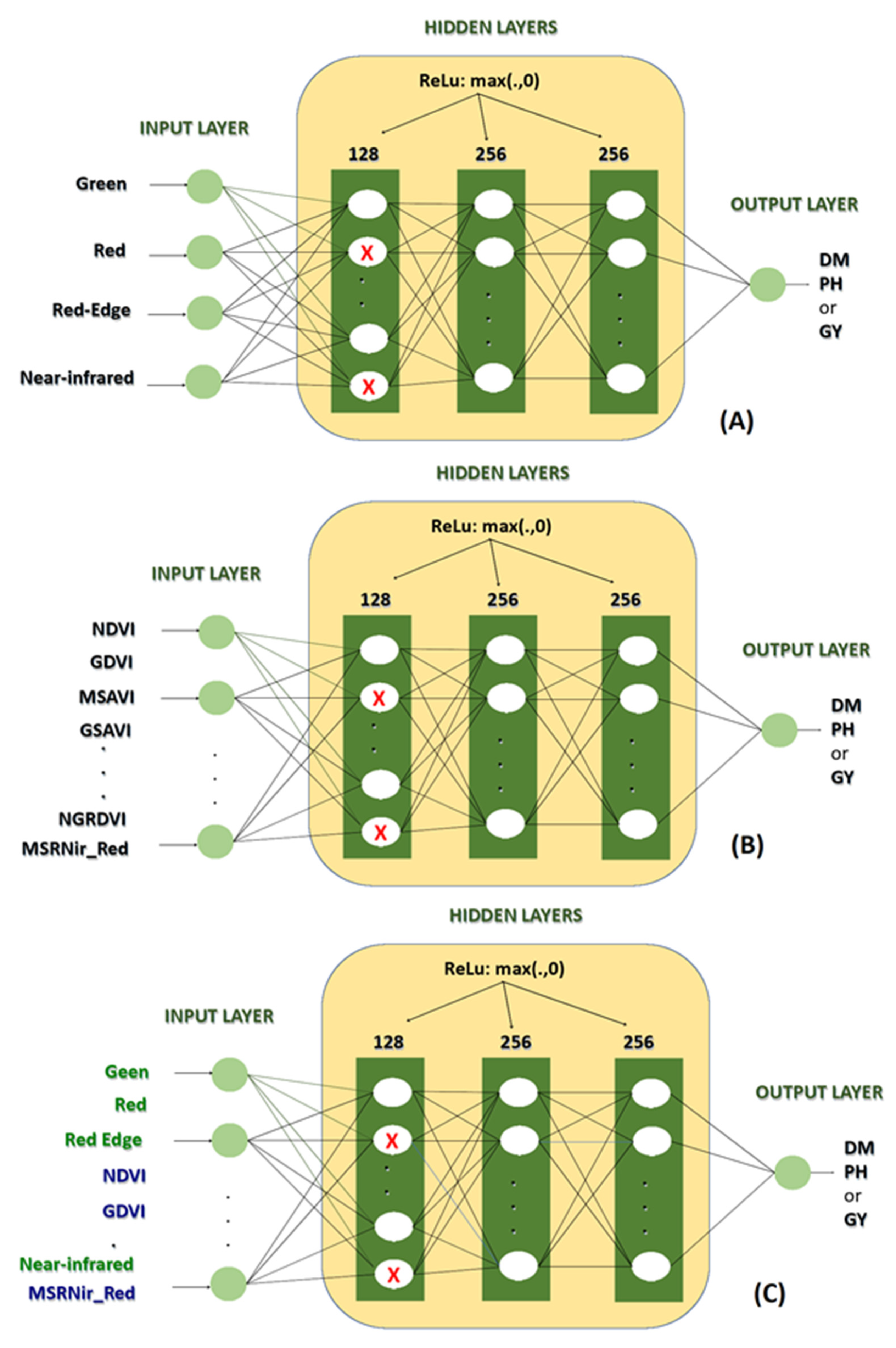
2.3. Machine Learning
2.4. Statistical Analyses
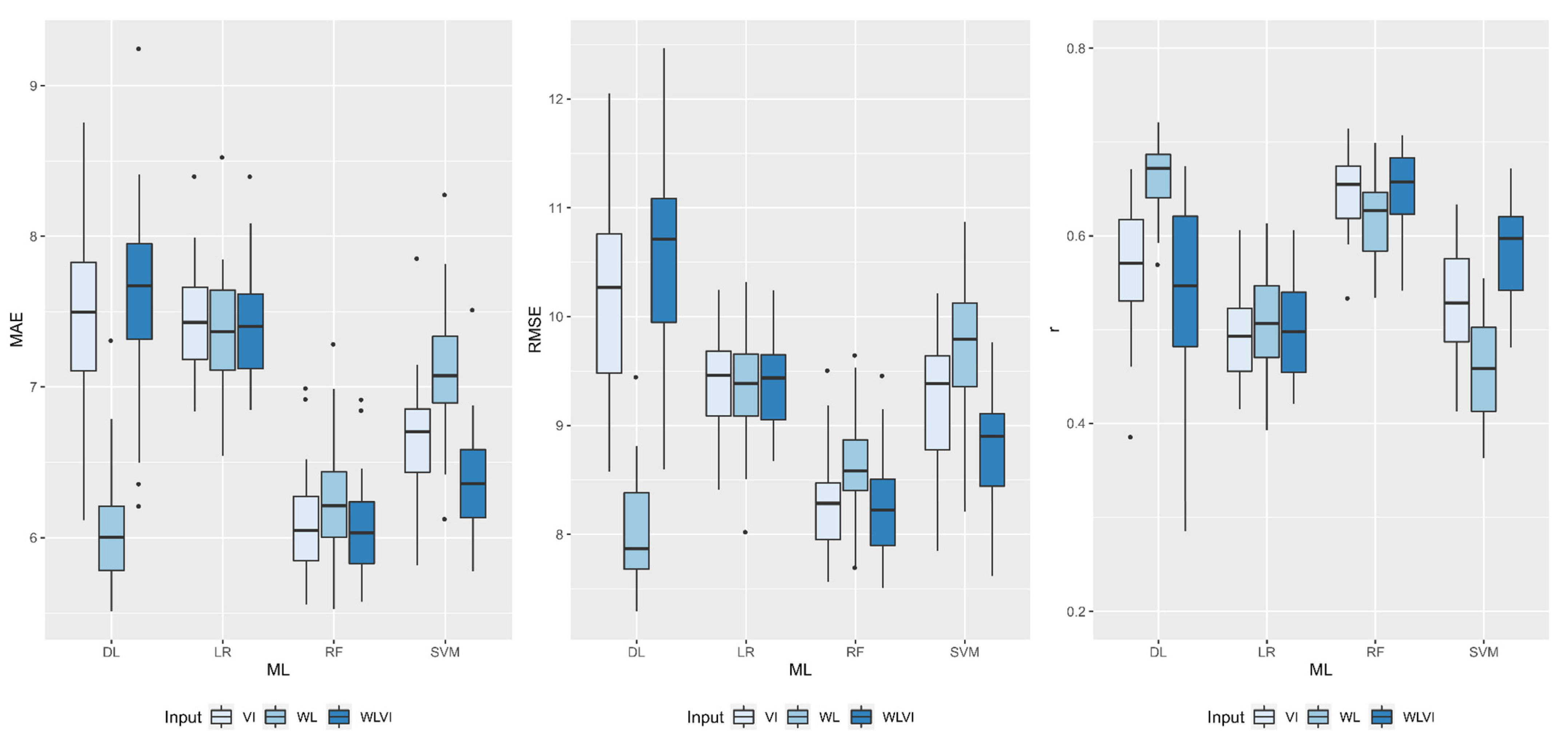
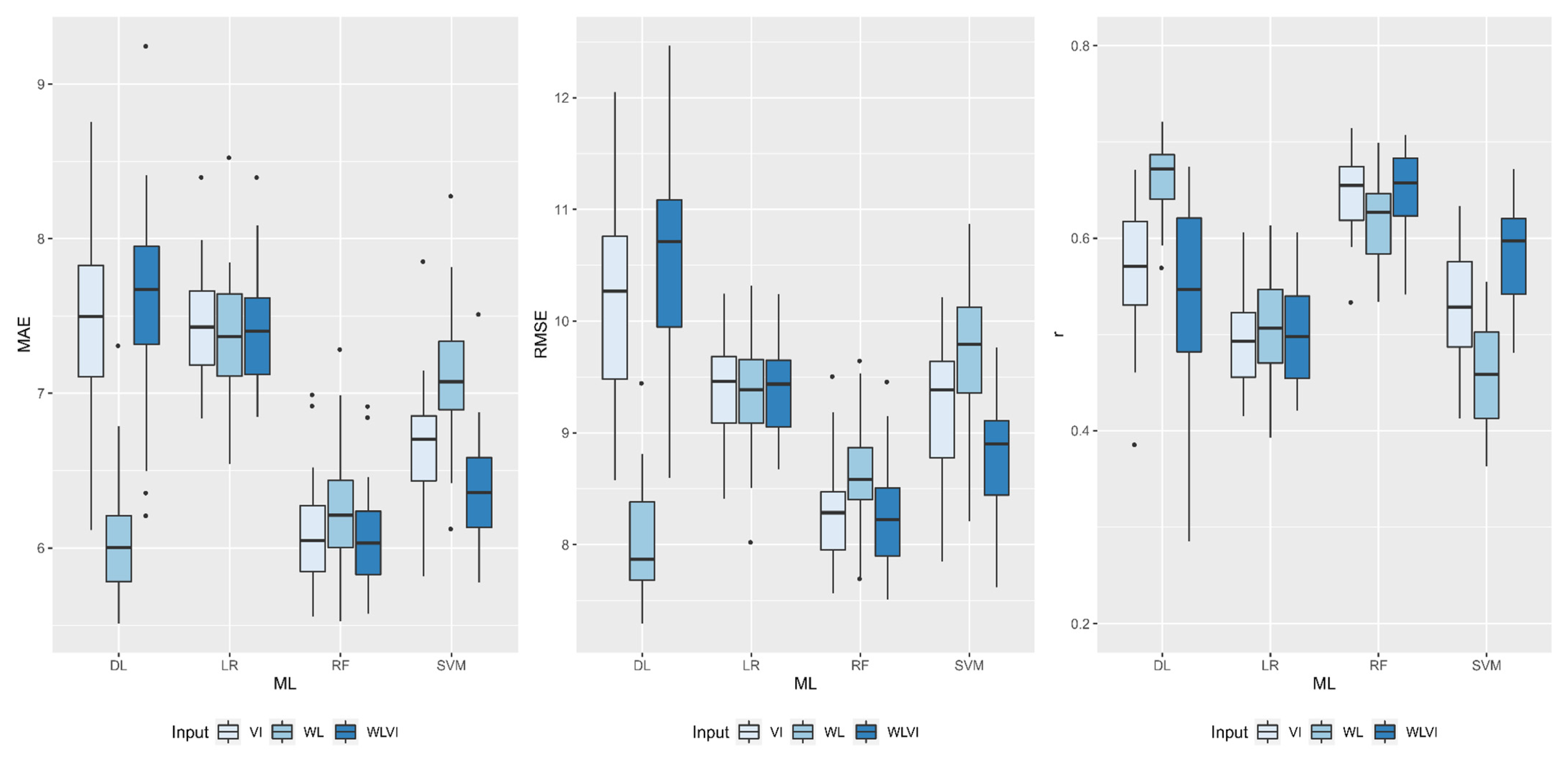
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khaki, S.; Wang, L.; Archontoulis, S.V. A CNN-RNN Framework for Crop Yield Prediction. Front. Plant Sci. 2020, 10, 1750. [Google Scholar] [CrossRef]
- da Silva, E.E.; Baio, F.H.R.; Teodoro, L.P.R.; Junior, C.A.D.S.; Borges, R.S.; Teodoro, P.E. UAV-multispectral and vegetation indices in soybean grain yield prediction based on in situ observation. Remote Sens. Appl. Soc. Environ. 2020, 18, 100318. [Google Scholar] [CrossRef]
- Osco, L.P.; Ramos, A.P.M.; Pereira, D.R.; Moriya, A.S.; Imai, N.N.; Matsubara, E.T.; Estrabis, N.; De Souza, M.; Junior, J.M.; Gonçalves, W.N.; et al. Predicting Canopy Nitrogen Content in Citrus-Trees Using Random Forest Algorithm Associated to Spectral Vegetation Indices from UAV-Imagery. Remote Sens. 2019, 11, 2925. [Google Scholar] [CrossRef] [Green Version]
- Osco, L.; Junior, J.; Ramos, A.; Furuya, D.; Santana, D.; Teodoro, L.; Gonçalves, W.; Baio, F.; Pistori, H.; Junior, C.; et al. Leaf Nitrogen Concentration and Plant Height Prediction for Maize Using UAV-Based Multispectral Imagery and Machine Learning Techniques. Remote Sens. 2020, 12, 3237. [Google Scholar] [CrossRef]
- Osco, L.P.; Ramos, A.P.M.; Moriya, É.A.S.; Bavaresco, L.G.; De Lima, B.C.; Estrabis, N.; Pereira, D.R.; Creste, J.E.; Júnior, J.M.; Gonçalves, W.N.; et al. Modeling Hyperspectral Response of Water-Stress Induced Lettuce Plants Using Artificial Neural Networks. Remote Sens. 2019, 11, 2797. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Yungbluth, D.C.; Vong, C.N.; Scaboo, A.M.; Zhou, J. Estimation of maturity date of soybean breeding lines using UAV-based imagery. Remote Sens. 2019, 11, 2075. [Google Scholar] [CrossRef] [Green Version]
- Osco, L.P.; Ramos, A.P.M.; Pinheiro, M.M.F.; Moriya, A.S.; Imai, N.N.; Estrabis, N.; Ianczyk, F.; De Araújo, F.F.; Liesenberg, V.; Jorge, L.A.D.C.; et al. A Machine Learning Framework to Predict Nutrient Content in Valencia-Orange Leaf Hyperspectral Measurements. Remote Sens. 2020, 12, 906. [Google Scholar] [CrossRef] [Green Version]
- Amatya, S.; Karkee, M.; Gongal, A.; Zhang, Q.; Whiting, M.D. Detection of cherry tree branches with full foliage in planar architecture for automated sweet-cherry harvesting. Biosyst. Eng. 2015, 146, 3–15. [Google Scholar] [CrossRef] [Green Version]
- Vani, S.; Sukumaran, R.; Savithri, S. Prediction of sugar yields during hydrolysis of lignocellulosic biomass using artificial neural network modeling. Bioresour. Technol. 2015, 188, 128–135. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.; Mueller, N.D.; Fleisher, D.; Yun, K.; Butler, E.E.; Timlin, D.; Shim, K.-M.; Gerber, J.; Reddy, V.R.; et al. Random Forests for Global and Regional Crop Yield Predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef]
- Pantazi, X.; Moshou, D.; Alexandridis, T.; Whetton, R.; Mouazen, A. Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Hunt, M.L.; Blackburn, G.A.; Carrasco, L.; Redhead, J.W.; Rowland, C.S. High resolution wheat yield mapping using Sentinel-2. Remote Sens. Environ. 2019, 233, 111410. [Google Scholar] [CrossRef]
- Ramos, P.; Prieto, F.; Montoya, E.; Oliveros, C. Automatic fruit count on coffee branches using computer vision. Comput. Electron. Agric. 2017, 137, 9–22. [Google Scholar] [CrossRef]
- Su, Y.-X.; Xu, H.; Yan, L.-J. Support vector machine-based open crop model (SBOCM): Case of rice production in China. Saudi J. Biol. Sci. 2017, 24, 537–547. [Google Scholar] [CrossRef]
- Ramos, A.P.M.; Osco, L.P.; Furuya, D.E.G.; Gonçalves, W.N.; Santana, D.C.; Teodoro, L.P.R.; Junior, C.A.D.S.; Capristo-Silva, G.F.; Li, J.; Baio, F.H.R.; et al. A random forest ranking approach to predict yield in maize with uav-based vegetation spectral indices. Comput. Electron. Agric. 2020, 178, 105791. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine Learning Approaches for Crop Yield Prediction and Nitrogen Status Estimation in Precision Agriculture: A Review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sakamoto, T. Incorporating environmental variables into a MODIS-based crop yield estimation method for United States corn and soybeans through the use of a random forest regression algorithm. ISPRS J. Photogramm. Remote Sens. 2019, 160, 208–228. [Google Scholar] [CrossRef]
- Sun, J.; Di, L.; Sun, Z.; Shen, Y.; Lai, Z. County-Level Soybean Yield Prediction Using Deep CNN-LSTM Model. Sensors 2019, 19, 4363. [Google Scholar] [CrossRef] [Green Version]
- Yu, N.; Li, L.; Schmitz, N.; Tian, L.F.; Greenberg, J.A.; Diers, B.W. Development of methods to improve soybean yield estimation and predict plant maturity with an unmanned aerial vehicle based platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
- Taha, R.S.; Seleiman, M.F.; Alotaibi, M.; Alhammad, B.A.; Rady, M.M.; Mahdi, A.H.A. Exogenous potassium treatments elevate salt tolerance and performances of Glycine max L. by boosting antioxidant defense system under actual saline field conditions. Agronomy 2020, 10, 1741. [Google Scholar] [CrossRef]
- Conab—Monitoramento Agrícola. Available online: https://www.conab.gov.br/index.php/info-agro/safras/graos/monitoramento-agricola (accessed on 15 April 2021).
- Wei, M.; Molin, J. Soybean Yield Estimation and Its Components: A Linear Regression Approach. Agriculture 2020, 10, 348. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Klopfenstein, A.; Douridas, N.; Shearer, S. Integration of high resolution remotely sensed data and machine learning techniques for spatial prediction of soil properties and corn yield. Comput. Electron. Agric. 2018, 153, 213–225. [Google Scholar] [CrossRef]
- Soltis, P.S.; Nelson, G.; Zare, A.; Meineke, E.K. Plants meet machines: Prospects in machine learning for plant biology. Appl. Plant Sci. 2020, 8, e11371. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Ball, J.E.; Anderson, D.T.; Chan, C.S. Comprehensive survey of deep learning in remote sensing: Theories, tools, and challenges for the community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef] [Green Version]
- Castro, W.; Junior, J.M.; Polidoro, C.; Osco, L.P.; Gonçalves, W.; Rodrigues, L.; Santos, M.; Jank, L.; Barrios, S.; Valle, C.; et al. Deep Learning Applied to Phenotyping of Biomass in Forages with UAV-Based RGB Imagery. Sensors 2020, 20, 4802. [Google Scholar] [CrossRef]
- Chen, Y.; Ribera, J.; Boomsma, C.; Delp, E.J. Plant Leaf Segmentation for Estimating Phenotypic Traits; Video and Image Processing Laboratory (VIPER); Purdue University: West Lafayette, IN, USA, 2017; pp. 3884–3888. [Google Scholar]
- Jin, Z.; Azzari, G.; You, C.; Di Tommaso, S.; Aston, S.; Burke, M.; Lobell, D.B. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 2019, 228, 115–128. [Google Scholar] [CrossRef]
- Nevavuori, P.; Narra, N.; Lipping, T. Crop yield prediction with deep convolutional neural networks. Comput. Electron. Agric. 2019, 163, 104859. [Google Scholar] [CrossRef]
- Barbosa, A.; Trevisan, R.; Hovakimyan, N.; Martin, N.F. Modeling yield response to crop management using convolutional neural networks. Comput. Electron. Agric. 2020, 170, 105197. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Finoto, E.L.; Sediyama, T.; Carrega, W.C.; De Albuquerque, J.A.A.; Cecon, P.R.; Reis, M.S. Efeito da aplicação de fungicida sobre caracteres agronômicos e severidade das doenças de final de ciclo na cultura da soja. Rev. Agro@Mbiente On-Line 2011, 5, 44. [Google Scholar] [CrossRef]
- Masuka, B.; Atlin, G.N.; Olsen, M.; Magorokosho, C.; Labuschagne, M.; Crossa, J.; Bänziger, M.; Pixley, K.V.; Vivek, B.S.; von Biljon, A.; et al. Gains in Maize Genetic Improvement in Eastern and Southern Africa: I. CIMMYT Hybrid Breeding Pipeline. Crop. Sci. 2017, 57, 168–179. [Google Scholar] [CrossRef] [Green Version]
- Morrison, M.J.; Voldeng, H.D.; Cober, E.R. Agronomic Changes from 58 Years of Genetic Improvement of Short-Season Soybean Cultivars in Canada. Agron. J. 2000, 92, 780–784. [Google Scholar] [CrossRef]
- Jin, J.; Liu, X.; Wang, G.; Mi, L.; Shen, Z.; Chen, X.; Herbert, S.J. Agronomic and physiological contributions to the yield improvement of soybean cultivars released from 1950 to 2006 in Northeast China. Field Crop. Res. 2010, 115, 116–123. [Google Scholar] [CrossRef]
- Todeschini, M.H.; Milioli, A.S.; Rosa, A.C.; Dallacorte, L.V.; Panho, M.C.; Marchese, J.A.; Benin, G. Soybean genetic progress in South Brazil: Physiological, phenological and agronomic traits. Euphytica 2019, 215, 124. [Google Scholar] [CrossRef]
- Xie, C.; Yang, C. A review on plant high-throughput phenotyping traits using UAV-based sensors. Comput. Electron. Agric. 2020, 178, 105731. [Google Scholar] [CrossRef]
- Eugenio, F.C.; Grohs, M.; Venancio, L.P.; Schuh, M.; Bottega, E.L.; Ruoso, R.; Schons, C.; Mallmann, C.L.; Badin, T.L.; Fernandes, P. Estimation of soybean yield from machine learning techniques and multispectral RPAS imagery. Remote Sens. Appl. Soc. Environ. 2020, 20, 100397. [Google Scholar] [CrossRef]

| Index | Equation |
|---|---|
| ARVI2 (Atmospherically Resistant Vegetation Index 2) | |
| ATSAVI (Adjusted Transformed soil-adjusted VI) | |
| BWDRVI (Blue-wide dynamic range vegetation index) | |
| CCCI (Canopy Chlorophyll Content Index) | |
| CIgreen (Chlorophyll Index Green) | |
| CIrededge (Chlorophyll Index RedEdge) | |
| CVI (Chlorophyll Vegetation Index) | |
| DVI (Difference Vegetation Index) | |
| EVEI2 (Enhanced Vegetation Index 2) | |
| GDVI (Difference NIR/Green Difference Vegetation Index) | |
| GEMI (Global Environment Monitoring Index) | |
| GNDVI (Green Normalized Difference Vegetation Index) | |
| GRNDVI (Green-Red NDVI) | |
| GRVI (Green-Red Vegetation Index) | |
| GSAVI (Green Soil Adjusted Vegetation Index) | |
| GTVI (Green Triangle Vegetation Index) | |
| IPVI (Infrared Percentage Vegetation Index) | |
| LogR (Log Ratio) | ) |
| MSAVI (Modified Soil Adjusted Vegetation Index) | |
| MSRNir_Red (Modified Simple Ratio NIR/RED) | |
| NDRE (Normalized Difference Red-Edge Index) | |
| NDVI (Normalized Difference Vegetation Index) | |
| NGRDI (Normalized Green-Red Difference Index) | |
| NormR1 (Normalized G) | |
| NormR2 (Normalized NIR) | |
| NormR3 (Normalized R) | |
| RGR (Red Green Ratio Index) | |
| RI (Redness Index) | |
| RRI 1 | |
| SRQT_IR_R (Square root of the NIR/Red ratio) | |
| SRRed_NIR | |
| TNDVI (Transformed NDVI) | |
| TVI (Transformed Vegetation Index) | |
| WDRVI (Wide Dynamic Range Vegetation Index) | (0.1 ∗ ()) |
| Model | Input | ||
|---|---|---|---|
| WL | VI | WLVI | |
| MAE | |||
| DL | 6.05 Bc | 7.45 Aa | 7.62 Aa |
| RF | 6.24 Ac | 6.09 Ac | 6.04 Ac |
| SVM | 7.11 Ab | 6.65 Bb | 6.38 Bb |
| LR | 7.37 Aa | 7.43 Aa | 7.41 Aa |
| RMSE | |||
| DL | 8.01 Cd | 10.23 Ba | 10.58 Aa |
| RF | 8.58 Ac | 8.28 Ac | 8.23 Ad |
| SVM | 9.76 Aa | 9.25 Bb | 8.82 Cc |
| LR | 9.34 Ab | 9.41 Ab | 9.39 Ab |
| r | |||
| DL | 0.66 Aa | 0.57 Bb | 0.54 Cc |
| RF | 0.62 Ab | 0.65 Aa | 0.65 Aa |
| SVM | 0.46 Cd | 0.53 Bc | 0.58 Ab |
| LR | 0.51 Ac | 0.50 Ad | 0.50 Ad |
| Model | Input | ||
|---|---|---|---|
| WL | VI | WLVI | |
| MAE | |||
| DL | 8.32 Cb | 10.89 Ba | 11.92 Aa |
| RF | 8.38 Ab | 8.09 Ac | 8.11 Ac |
| SVM | 8.98 Aa | 8.55 Bb | 8.49 Bb |
| LR | 9.03 Aa | 8.65 Bb | 8.67 Bb |
| RMSE | |||
| DL | 10.51 Cb | 13.38 Ba | 14.55 Aa |
| RF | 10.88 Ab | 10.49 Ac | 10.51 Ac |
| SVM | 11.77 Aa | 11.05 Bb | 10.97 Bb |
| LR | 11.78 Aa | 11.24 Bb | 11.21 Bb |
| r | |||
| DL | 0.79 Aa | 0.77 Ab | 0.75 Bb |
| RF | 0.77 Ba | 0.79 Aa | 0.79 Aa |
| SVM | 0.73 Bb | 0.76 Ac | 0.77 Ab |
| LR | 0.73 Bb | 0.75 Ac | 0.75 Ab |
| Model | MAE | RMSE | r |
|---|---|---|---|
| DL | 788.31 b | 1000.48 b | 0.45 a |
| RF | 807.16 a | 1025.59 a | 0.42 a |
| SVM | 787.87 b | 1010.11 b | 0.44 a |
| LR | 790.88 b | 105.06 b | 0.43 a |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teodoro, P.E.; Teodoro, L.P.R.; Baio, F.H.R.; da Silva Junior, C.A.; dos Santos, R.G.; Ramos, A.P.M.; Pinheiro, M.M.F.; Osco, L.P.; Gonçalves, W.N.; Carneiro, A.M.; et al. Predicting Days to Maturity, Plant Height, and Grain Yield in Soybean: A Machine and Deep Learning Approach Using Multispectral Data. Remote Sens. 2021, 13, 4632. https://doi.org/10.3390/rs13224632
Teodoro PE, Teodoro LPR, Baio FHR, da Silva Junior CA, dos Santos RG, Ramos APM, Pinheiro MMF, Osco LP, Gonçalves WN, Carneiro AM, et al. Predicting Days to Maturity, Plant Height, and Grain Yield in Soybean: A Machine and Deep Learning Approach Using Multispectral Data. Remote Sensing. 2021; 13(22):4632. https://doi.org/10.3390/rs13224632
Chicago/Turabian StyleTeodoro, Paulo Eduardo, Larissa Pereira Ribeiro Teodoro, Fábio Henrique Rojo Baio, Carlos Antonio da Silva Junior, Regimar Garcia dos Santos, Ana Paula Marques Ramos, Mayara Maezano Faita Pinheiro, Lucas Prado Osco, Wesley Nunes Gonçalves, Alexsandro Monteiro Carneiro, and et al. 2021. "Predicting Days to Maturity, Plant Height, and Grain Yield in Soybean: A Machine and Deep Learning Approach Using Multispectral Data" Remote Sensing 13, no. 22: 4632. https://doi.org/10.3390/rs13224632
APA StyleTeodoro, P. E., Teodoro, L. P. R., Baio, F. H. R., da Silva Junior, C. A., dos Santos, R. G., Ramos, A. P. M., Pinheiro, M. M. F., Osco, L. P., Gonçalves, W. N., Carneiro, A. M., Junior, J. M., Pistori, H., & Shiratsuchi, L. S. (2021). Predicting Days to Maturity, Plant Height, and Grain Yield in Soybean: A Machine and Deep Learning Approach Using Multispectral Data. Remote Sensing, 13(22), 4632. https://doi.org/10.3390/rs13224632













