Risk Assessment of Urban Floods Based on a SWMM-MIKE21-Coupled Model Using GF-2 Data
Abstract
:1. Introduction
2. Materials and Methods
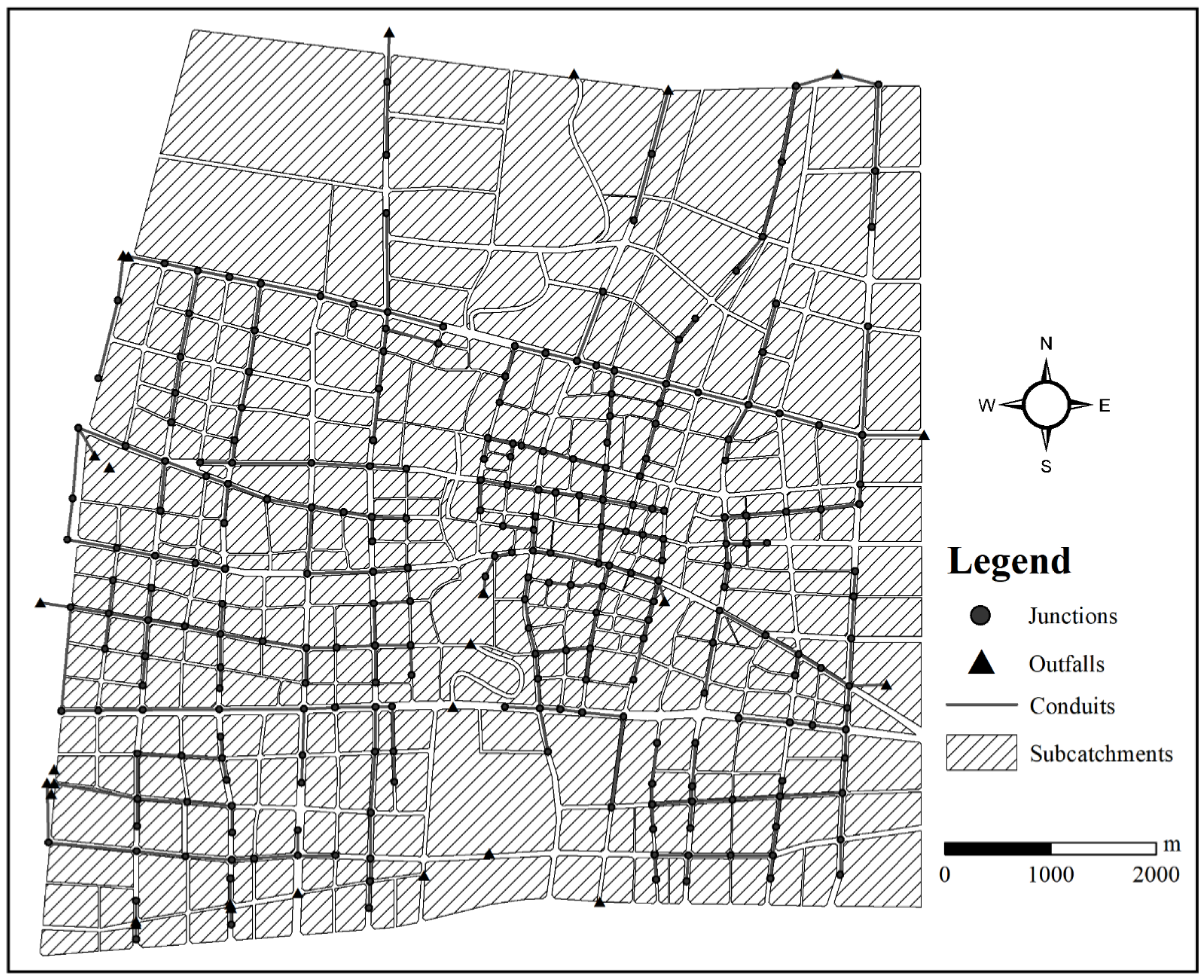
2.1. Study Area and Data Sets
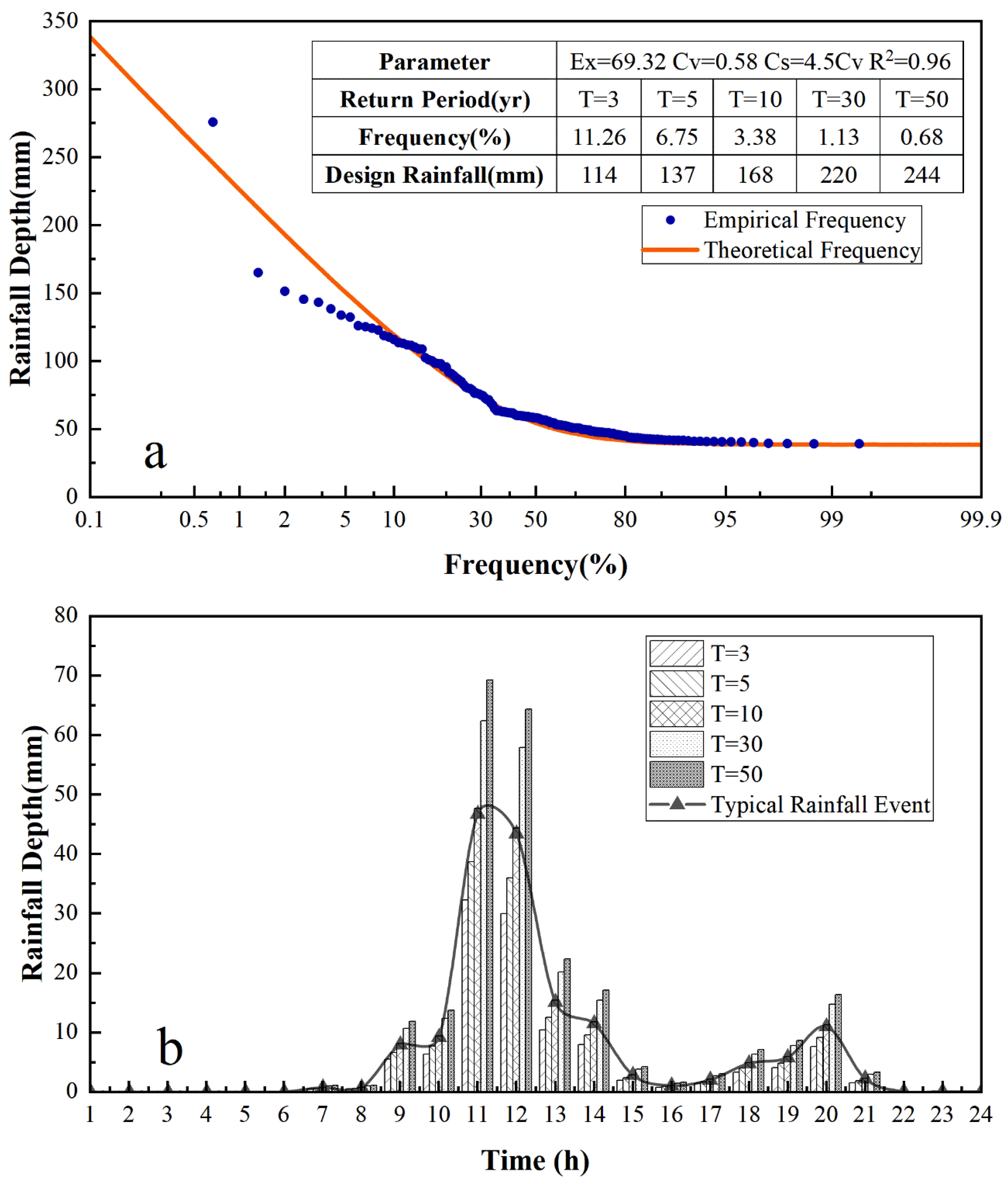
2.2. Designing Rainfall Events
2.3. The Linkage of the SWMM and MIKE21
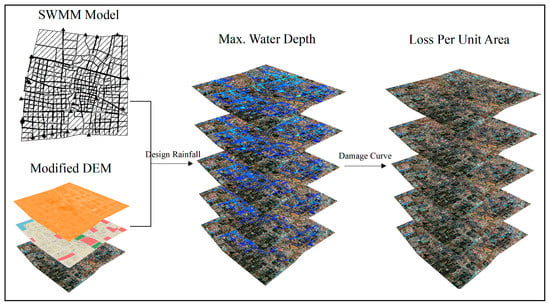
2.4. Damage Assessment
3. Results
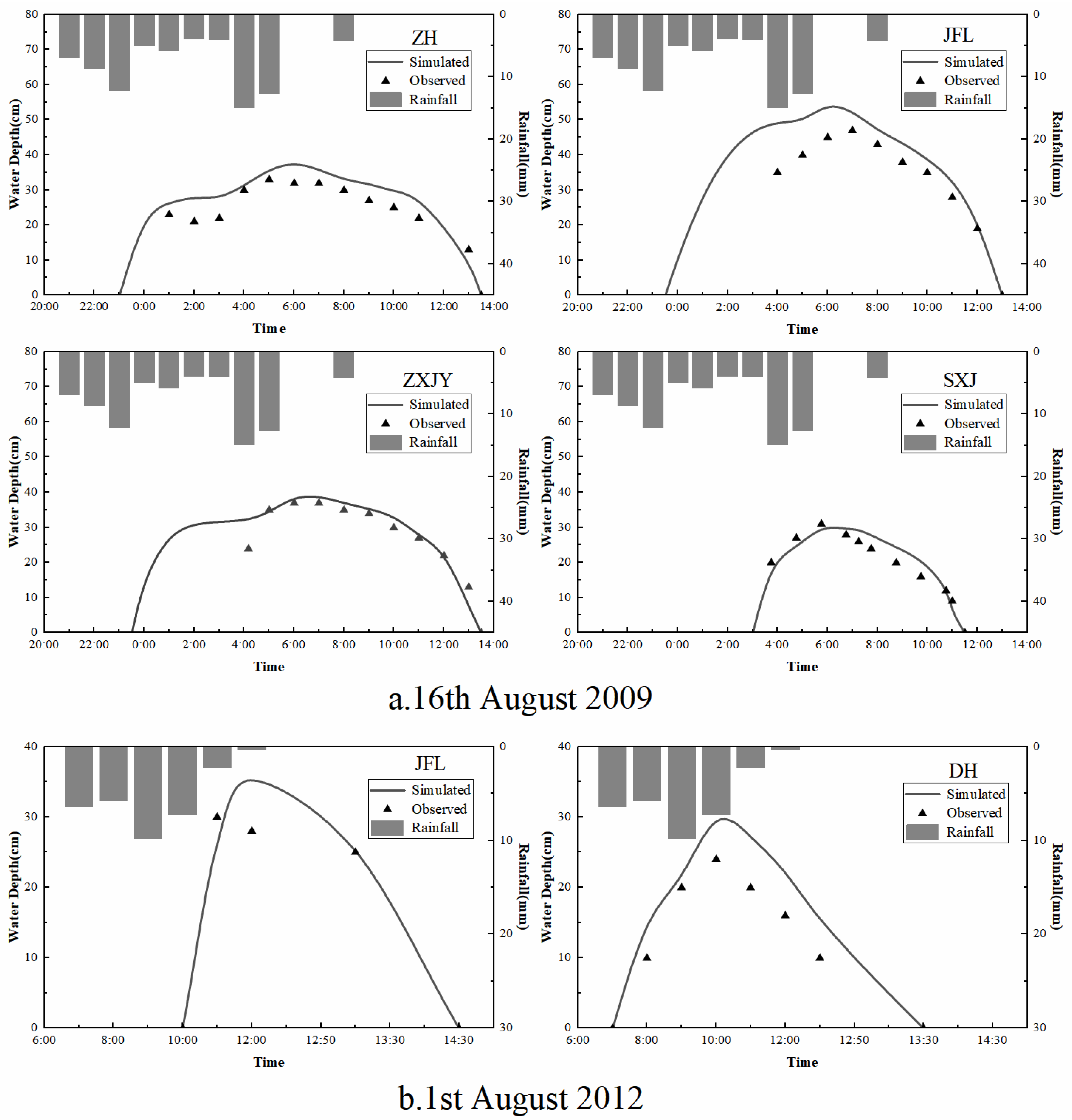
3.1. Model Construction and Verification
3.2. Urban Flood Simulations for Different Return Periods
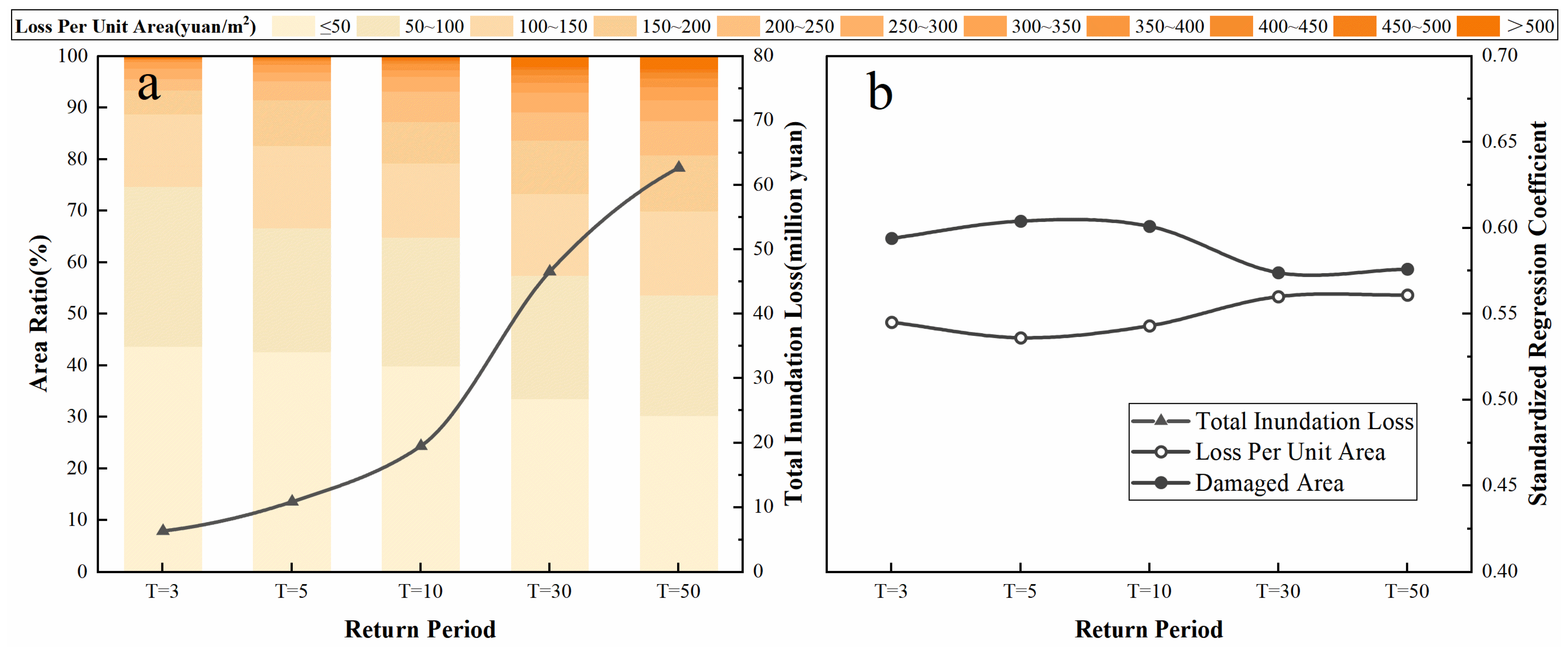
3.3. Risk Assessment of Urban Flood
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- AR6 Climate Change 2021: The Physical Science Basis. Available online: https://www.ipcc.ch/report/ar6/wg1/#FullReport (accessed on 15 August 2021).
- Hoegh-Guldberg, O.; Jacob, D.; Taylor, M.; Guillén Bolaños, T.; Bindi, M.; Brown, S.; Camilloni, I.A.; Diedhiou, A.; Djalante, R.; Ebi, K.; et al. The human imperative of stabilizing global climate change at 1.5 °C. Science 2019, 365, w6974. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, Y.; Luo, P.; Zhang, S.; Sun, B. Spatiotemporal Analysis of Hydrological Variations and Their Impacts on Vegetation in Semiarid Areas from Multiple Satellite Data. Remote Sens. 2020, 12, 4177. [Google Scholar] [CrossRef]
- Cohen, J.E. Human Population: The Next Half Century. Science 2003, 302, 1172–1175. [Google Scholar] [CrossRef] [PubMed]
- Luo, P.; Xu, C.; Kang, S.; Huo, A.; Lyu, J.; Zhou, M.; Nover, D. Heavy metals in water and surface sediments of the Fenghe River Basin, China: Assessment and source analysis. Water Sci. Technol. 2021. [Google Scholar] [CrossRef]
- Wei, X.; Wang, N.; Luo, P.; Yang, J.; Zhang, J.; Lin, K. Spatiotemporal Assessment of Land Marketization and Its Driving Forces for Sustainable UrbanRural Development in Shaanxi Province in China. Sustainability 2021, 13, 7755. [Google Scholar] [CrossRef]
- Xie, D.; Duan, L.; Si, G.; Liu, W.; Zhang, T.; Mulder, J. Long–Term 15N Balance After Single–Dose Input of 15N–Labeled NH4+ and NO3– in a Subtropical Forest Under Reducing N Deposition. Global Biogeochem. Cycles 2021, 35, e2021GB006959. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, Y.; Wang, H.; Jiang, Z. Depth prediction of urban flood under different rainfall return periods based on deep learning and data warehouse. Sci. Total Environ. 2020, 716, 137077. [Google Scholar] [CrossRef]
- Chang, X.; Xu, Z.; Zhao, G.; Li, H. Simulation of urban rainfall-runoff in piedmont cities: Case study of Jinan city, China. J. Hydroelectr. Eng. 2018, 37, 107–116. [Google Scholar] [CrossRef]
- Qiu, J. Urbanization contributed to Beijing storms. Nature 2012. [Google Scholar] [CrossRef]
- Zha, X.; Luo, P.; Zhu, W.; Wang, S.; Lyu, J.; Zhou, M.; Huo, A.; Wang, Z. A bibliometric analysis of the research on Sponge City: Current situation and future development direction. Ecohydrology 2021, 14, e2328. [Google Scholar] [CrossRef]
- Milanesi, L.; Pilotti, M.; Ranzi, R. A conceptual model of people’s vulnerability to floods. Water Resour. Res. 2015, 51, 182–197. [Google Scholar] [CrossRef]
- Feng, P.; Cui, G.; Zhon, Y. On the evaluation and prediction of urban flood economic loss. J. Hydraul. Eng. 2001, 8, 64–68. [Google Scholar] [CrossRef]
- Benito, G.; Lang, M.; Barriendos, M.; Llasat, M.C.; Francés, F.; Ouarda, T.; Thorndycraft, V.; Enzel, Y.; Bardossy, A.; Coeur, D.; et al. Use of Systematic, Palaeoflood and Historical Data for the Improvement of Flood Risk Estimation. Review of Scientific Methods. Nat. Hazards 2004, 31, 623–643. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, C.C.; Tan, Z.; Chen, Y.; Qiu, H.; Huang, C.; Li, Y.; Zhang, Y.; Li, X.; Shulmeister, J.; et al. Prehistoric and historic overbank floods in the Luoyang Basin along the Luohe River, middle Yellow River basin, China. Quatern. Int. 2019, 521, 118–128. [Google Scholar] [CrossRef]
- Kandilioti, G.; Makropoulos, C. Preliminary flood risk assessment: The case of Athens. Nat. Hazards 2012, 61, 441–468. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, T.; Hong, S.; Wang, L. Review on applications of remote sensing in urban flood modeling. Chin. Sci. Bull. 2018, 63, 2156–2166. [Google Scholar] [CrossRef]
- Jamali, B.; Löwe, R.; Bach, P.M.; Urich, C.; Arnbjerg-Nielsen, K.; Deletic, A. A rapid urban flood inundation and damage assessment model. J. Hydrol. 2018, 564, 1085–1098. [Google Scholar] [CrossRef]
- Mu, D.; Luo, P.; Lyu, J.; Zhou, M.; Huo, A.; Duan, W.; Nover, D.; He, B.; Zhao, X. Impact of temporal rainfall patterns on flash floods in Hue City, Vietnam. J. Flood Risk Manag. 2021, 14, e12668. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, P.; Zhao, S.; Kang, S.; Wang, P.; Zhou, M.; Lyu, J. Control and remediation methods for eutrophic lakes in the past 30 years. Water Sci. Technol. 2020, 81, 1099–1113. [Google Scholar] [CrossRef]
- Huang, G.; Huang, J.; Yu, H.; Yang, S. Secondary Development of Storm Water Management Model SWMM Based GIS. Water Resour. Power 2011, 29, 43–45. [Google Scholar] [CrossRef]
- He, X.; Chen, C.; Liu, Y.; Chu, Y. Inundation Analysis Method for Urban Mountainous Areas Based on Soil Conservation Service Curve Number (SCS-CN) Model Using Remote Sensing Data. Sens. Mater 2020, 32, 3813–3822. [Google Scholar] [CrossRef]
- Storm Water Management Model User’s Manual Version 5.1. Available online: https://www.epa.gov/sites/production/files/2019-02/documents/epaswmm5_1_manual_master_8-2-15.pdf (accessed on 15 August 2021).
- Tsihrintzis, V.A.; Sidan, C.B. ILLUDAS and PSRM-QUAL predictive ability in small urban areas and comparison with other models. Hydrol. Process 2008, 22, 3321–3336. [Google Scholar] [CrossRef]
- Choo, Y.M.; Sim, S.B.; Choe, Y.W. A Study on Urban Inundation Using SWMM in Busan, Korea, Using Existing Dams and Artificial Underground Waterways. Water 2021, 13, 1708. [Google Scholar] [CrossRef]
- Barszcz, M. Radar Data Analyses for a Single Rainfall Event and Their Application for Flow Simulation in an Urban Catchment Using the SWMM Model. Water 2018, 10, 1007. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Ye, Z.; Shibata, S. Assessment of Rain Garden Effects for the Management of Urban Storm Runoff in Japan. Sustainability 2020, 12, 9982. [Google Scholar] [CrossRef]
- He, S.; Chen, W.; Liu, Y.; Mu, X. Study on design method of the initial rainwater storage tank based on ANN and PSO. J. Hydraul. Eng. 2020, 51, 1558–1566. [Google Scholar] [CrossRef]
- Sañudo, E.; Cea, L.; Puertas, J. Modelling Pluvial Flooding in Urban Areas Coupling the Models Iber and SWMM. Water 2020, 12, 2647. [Google Scholar] [CrossRef]
- Tavakolifar, H.; Abbasizadeh, H.; Nazif, S.; Shahghasemi, E. Development of 1D–2D Urban Flood Simulation Model Based on Modified Cellular Automata Approach. J. Hydrol. Eng. 2021, 26, 04020065. [Google Scholar] [CrossRef]
- Bisht, D.S.; Chatterjee, C.; Kalakoti, S.; Upadhyay, P.; Sahoo, M.; Panda, A. Modeling urban floods and drainage using SWMM and MIKE URBAN: A case study. Nat. Hazards 2016, 84, 749–776. [Google Scholar] [CrossRef]
- Yang, L.; Li, J.; Kang, A.; Li, S.; Feng, P. The Effect of Nonstationarity in Rainfall on Urban Flooding Based on Coupling SWMM and MIKE21. Water Resour. Manag. 2020, 34, 1535–1551. [Google Scholar] [CrossRef]
- Ahn, J.; Na, Y.; Park, S.W. Development of Two-Dimensional Inundation Modelling Process using MIKE 21 Model. Ksce. J. Civ. Eng. 2019, 23, 3968–3977. [Google Scholar] [CrossRef]
- Chen, P.; Fu, C.; Yu, J.; Ji, X. Research on the Numerical Simulation of Flood Routing for the Flood Detention Basin Based on Mike 21. China Rural. Water Hydropower 2017, 113–116. [Google Scholar] [CrossRef]
- Li, M.; Wu, W.; Wang, J.; Che, Z.; Xie, Y. Simulating and mapping the risk of surge floods in multiple typhoon scenarios: A case study of Yuhuan County, Zhejiang Province, China. Stoch. Env. Res. Risk A 2017, 31, 645–659. [Google Scholar] [CrossRef]
- Zuo, J.; Zhang, H.X.; Deng, S.; Gu, P.; Lian, L.L. Analysis of influence of mesh partition on Mike 21 calculation in flood impact assessment. IOP Conf. Ser. Earth Environ. Sci. 2020, 612, 012060. [Google Scholar] [CrossRef]
- Wang, N.; Hou, J.; Du, Y.; Jing, H.; Wang, T.; Xia, J.; Gong, J.; Huang, M. A dynamic, convenient and accurate method for assessing the flood risk of people and vehicle. Sci. Total Environ. 2021, 797, 149036. [Google Scholar] [CrossRef]
- Muhadi, N.A.; Abdullah, A.F.; Bejo, S.K.; Mahadi, M.R.; Mijic, A. The Use of LiDAR-Derived DEM in Flood Applications: A Review. Remote Sens. 2020, 12, 2308. [Google Scholar] [CrossRef]
- Li, B.; Hou, J.; Li, D.; Yang, D.; Han, H.; Bi, X.; Wang, X.; Hinkelmann, R.; Xia, J. Application of LiDAR UAV for High-Resolution Flood Modelling. Water Resour. Manag. 2021, 35, 1433–1447. [Google Scholar] [CrossRef]
- Hang, L.; Cai, G.Y. Cnn Based Detection of Building Roofs from High Resolution Satellite Images. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2020, 42, 187–192. [Google Scholar] [CrossRef] [Green Version]
- Lyu, H. Impacts of Urban Complex Conditions on Detailed Hydrological Processes. Ph.D. Thesis, Tsinghua University, Beijing, China, May 2018. [Google Scholar]
- Zhang, M.; Chen, F.; Liang, D.; Tian, B.; Yang, A. Use of Sentinel-1 GRD SAR Images to Delineate Flood Extent in Pakistan. Sustainability 2020, 12, 5784. [Google Scholar] [CrossRef]
- Choi, G.W.; Lee, H.S.; Lee, S.Y. Urban Inundation Analysis using the Integrated Model of MOUSE and MIKE 21. J. Korean Soc. Hazard Mitig. 2007, 7, 75–83. [Google Scholar]
- Flood Damage Assessment-Literature Review and Recommended Procedure. Available online: https://watersensitivecities.org.au/content/flood-damage-assessment-literature-review-recommended-procedure/ (accessed on 15 August 2021).
- Hammond, M.J.; Chen, A.S.; Djordjević, S.; Butler, D.; Mark, O. Urban flood impact assessment: A state-of-the-art review. Urban Water J. 2015, 12, 14–29. [Google Scholar] [CrossRef] [Green Version]
- Velasco, M.; Cabello, À.; Russo, B. Flood damage assessment in urban areas. Application to the Raval district of Barcelona using synthetic depth damage curves. Urban Water J. 2016, 13, 426–440. [Google Scholar] [CrossRef]
- Scawthorn, C.; Flores, P.; Blais, N.; Blais, H.; Tate, E.; Chang, S.; Mifflin, E.; Thomas, W.; Murphy, J.; Jones, C.; et al. HAZUS-MH Flood Loss Estimation Methodology. II. Damage and Loss Assessment. Nat. Hazards Rev. 2016, 7, 72–81. [Google Scholar] [CrossRef]
- Yin, Z.; Xu, S. Study on Risk Assessment of Urban Natural Hazards, 1st ed.; Science press: Beijing, China, 2012; pp. 100–102. [Google Scholar]
- Wang, L.; Qin, Q.; Li, J.; Li, Z.; Jin, C.; Li, J. Study on the Disaster Analysis Model of Waterlogging in City Based on Gis. Sci. Surv. Mapp. 2004, 29, 48–52. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Z.; Xiong, L. Establishment of Simplified Urban Waterlogging Model Using Spatial Analysis. J. Nat. Disasters 2004, 13, 8–14. [Google Scholar] [CrossRef]
- Detailed Control Plan of the Central District in Cangzhou City. Available online: https://www.hebghy.com/news/1895.cshtml (accessed on 15 August 2021).
- General Rules for Civil Building Design. Available online: https://wenku.baidu.com/view/1701002ae2bd960590c677f1.html (accessed on 15 August 2021).
- Analyzing the Contribution of High Resolution Water Range in Dividing Catchment Based on D8 Algorithm. Available online: https://www.researchgate.net/publication/328985516_Analyzing_the_Contribution_of_High_Resolution_Water_Range_in_Dividing_Catchment_Based_on_D8_Algorithm (accessed on 15 August 2021).
- Cangzhou House Demolition Management Regulations and Demolition Compensation Standards. Available online: http://www.cangzhou.gov.cn/zwbz/zwdt/cxwj/632632.shtml (accessed on 15 August 2021).
- Yao, S. Risk Assessment of Urban Rainstorm Disaster–A Case Study of Beijing-Tianjin-Hebei Region. Master’s Thesis, Tsinghua University, Beijing, China, May 2016. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting Through Conceptual Models Part I–A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Muthusamy, M.; Casado, M.R.; Butler, D.; Leinster, P. Understanding the effects of Digital Elevation Model resolution in urban fluvial flood modelling. J. Hydrol. 2021, 596, 126088. [Google Scholar] [CrossRef]
- Chen, T. Study on the Simulation of Flood/Waterlogging and the Effect of Reduction Measures in the Sponge city Demonstration Area of Jinan City. Ph.D. Thesis, Beijing Normal University, Beijing, China, May 2019. [Google Scholar]
- Wu, M. Research on Waterlogging Simulation and Risk Assessment Base on Coupled Waterlogging Model in Jinan City. Master’s Thesis, Shandong University, Jinan, China, June 2020. [Google Scholar]
- Goldshleger, N.; Karnibad, L.; Shoshany, M.; Asaf, L. Generalising urban runoff and street network density relationship: A hydrological and remote-sensing case study in Israel. Urban Water J. 2012, 9, 189–197. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, J. Drainage Design Manual, 1st ed.; China Architecture & Building Press: Beijing, China, 1990; p. 161. [Google Scholar]
- Wang, R. Urban Waterlogging Risk Level Assessment Methods and Case Study. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, June 2016. [Google Scholar]
- Huang, G. Discrimination of relationship between urban storm waterlogging prevention and sponge city construction. China Flood Drought Manag. 2018, 28, 8–14. [Google Scholar] [CrossRef]
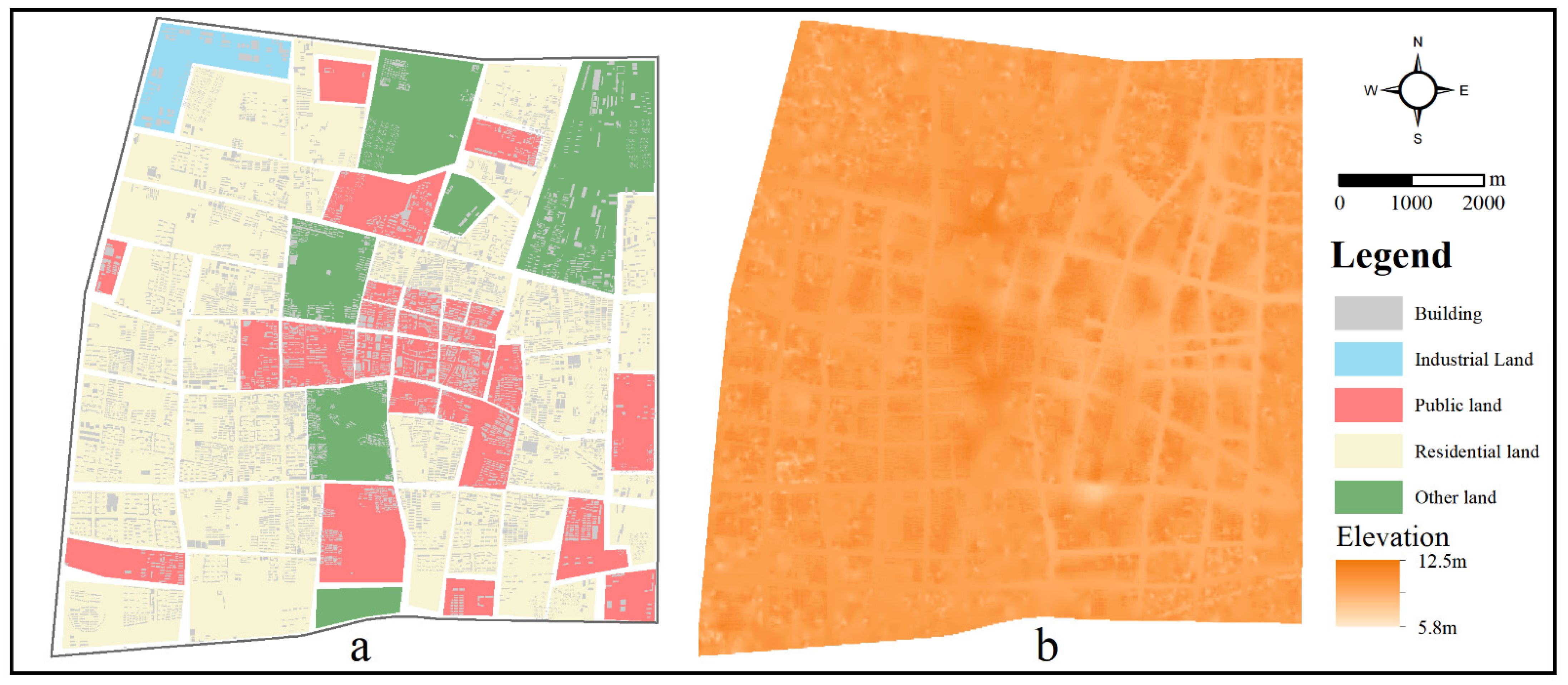



| Land-Use Type | Building Type | Step Height (cm) |
|---|---|---|
| Public land | Administration, commerce, education, etc. | 35 |
| Industrial Land | Industrial buildings | 20 |
| Residential land | Residential buildings | 15 |
| Other land | Other buildings | 15 |
| Type | Parameter | Value |
|---|---|---|
| Subcatchments | Area (ha) | 2.3~299.7 |
| Slope (%) | 0.01~0.6 | |
| Width (m) | 40.6~1333.2 | |
| Depression storage * (mm) | 1.27~6 | |
| Manning’s roughness * | Impervious area | 0.014 |
| Pervious area | 0.2 | |
| Pipelines | 0.013 | |
| Horton infiltration parameters * | Maximum rate (mm/h) | 36 |
| Minimum rate (mm/h) | 2.5 | |
| Decay constant | 3 | |
| Drying time (d) | 5 |
| Stage | Flooding Data | Measured Site | R2 | NSE | RMSE (cm) |
|---|---|---|---|---|---|
| Calibration | 16 August 2009 | ZH | 0.95 | 0.75 | 4.33 |
| JFL | 0.96 | 0.71 | 7.3 | ||
| ZXJY | 0.94 | 0.91 | 3.22 | ||
| SXJ | 0.93 | 0.89 | 2.84 | ||
| Verification | 1 August 2012 | JFL | 0.91 | 0.88 | 4.06 |
| DH | 0.95 | 0.61 | 5.29 |
| Return Period (yr) | T = 3 | T = 5 | T = 10 | T = 30 | T = 50 |
|---|---|---|---|---|---|
| Mean Inundation Depth (cm) | 9.41 | 10.53 | 12.18 | 15.68 | 17.31 |
| Maximum inundation Area (km2) | 5.12 | 6.74 | 8.91 | 11.95 | 13.18 |
| Runoff Coefficient | 0.84 | 0.85 | 0.87 | 0.89 | 0.9 |
| Total Damage Area (ha) | 8.07 | 12.53 | 20.29 | 39.47 | 48.73 |
| Total Inundation Loss (million yuan) | 6.29 | 10.84 | 19.46 | 46.55 | 62.67 |
| Return Period (yr) | Dependent Variables | Independent Variables | Standardized Regression Coefficient |
|---|---|---|---|
| T = 3 | Total Loss | Loss Per Unit Area | 0.545 |
| Damaged Area | 0.594 | ||
| T = 5 | Total Loss | Loss Per Unit Area | 0.536 |
| Damaged Area | 0.604 | ||
| T = 10 | Total Loss | Loss Per Unit Area | 0.543 |
| Damaged Area | 0.601 | ||
| T = 30 | Total Loss | Loss Per Unit Area | 0.560 |
| Damaged Area | 0.574 | ||
| T = 50 | Total Loss | Loss Per Unit Area | 0.561 |
| Damaged Area | 0.576 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Zhang, T.; Fu, J.; Li, J.; Cao, Z.; Feng, P. Risk Assessment of Urban Floods Based on a SWMM-MIKE21-Coupled Model Using GF-2 Data. Remote Sens. 2021, 13, 4381. https://doi.org/10.3390/rs13214381
Zhao L, Zhang T, Fu J, Li J, Cao Z, Feng P. Risk Assessment of Urban Floods Based on a SWMM-MIKE21-Coupled Model Using GF-2 Data. Remote Sensing. 2021; 13(21):4381. https://doi.org/10.3390/rs13214381
Chicago/Turabian StyleZhao, Lidong, Ting Zhang, Jun Fu, Jianzhu Li, Zhengxiong Cao, and Ping Feng. 2021. "Risk Assessment of Urban Floods Based on a SWMM-MIKE21-Coupled Model Using GF-2 Data" Remote Sensing 13, no. 21: 4381. https://doi.org/10.3390/rs13214381
APA StyleZhao, L., Zhang, T., Fu, J., Li, J., Cao, Z., & Feng, P. (2021). Risk Assessment of Urban Floods Based on a SWMM-MIKE21-Coupled Model Using GF-2 Data. Remote Sensing, 13(21), 4381. https://doi.org/10.3390/rs13214381