Joint Radar-Communications Exploiting Optimized OFDM Waveforms

Abstract

We propose novel Joint Radar-communication spectrum sharing strategies exploiting orthogonal frequency-division multiplexing (OFDM) waveforms that concurrently achieve the objectives of both radar and communication systems. An OFDM transmitter is considered that transmits dual-purpose OFDM subcarriers such that all the subcarriers are exploited for the primary radar function and further exclusively allocated to the secondary communication function serving multiple users. The waveform optimization is performed by employing mutual information (MI) as the optimization criterion for both radar and communication operations. For the purpose of radar performance optimization, we consider the MI between the frequency-dependent target response and the transmit OFDM waveforms. On the other hand, communication system performance is evaluated in terms of the MI between the frequency-dependent communication channels of communication users with the transmit OFDM subcarriers. These optimization objectives not only enable the transmit power allocation of the OFDM subcarriers, but also govern the subcarrier distribution among the communication users. Two resource optimization scenarios are considered, resulting in radar-centric and cooperative resource allocation strategies that exploit convex and mixed-integer linear programming optimization problems for power allocation and subcarrier distribution, respectively. We further present a chunk subcarrier allocation approach that applies to both optimization strategies to reduce the computational complexity with a trivial performance loss. Simulation results are presented to illustrate the effectiveness of the proposed strategies.

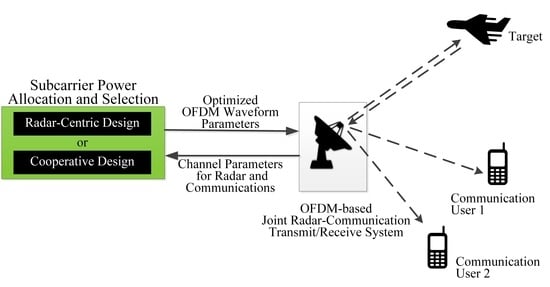
1. Introduction

Wireless spectrum sharing has attracted significant attention from researchers due to the ever-increasing demand for spectral resources for existing and emerging applications [1,2,3,4,5,6]. Modern wireless communication systems require extensive expansion in allocated spectral resources in order to enhance data rates and quality of service. Emerging technical fields, such as the Internet of Things, call for new dedicated spectral allocations to bring new products onto the market. The problem of spectral congestion has traditionally been addressed by enhancing the spectral efficiency using cognitive radio [7] and cognitive radar [8]. On the other hand, recent efforts towards spectrum-efficient systems have mostly focused on spectrum sharing approaches that enable multiple disparate applications within the same spectrum bands [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

There are two main classes of radar–communication spectrum sharing strategies that have been considered in the literature. The first type consists of co-existing radar and communication systems in the same spectrum bands where the mutual interference is mitigated via exploiting extensive cooperation and/or information sharing between the two systems. On the other hand, the second strategy enables Joint Radar-communication (JRC) by utilizing dual-purpose waveforms that serve the objective of both subsystems. The information embedding in JRC systems is enabled either by embedding communication information in radar waveforms or by dedicating separate waveforms to radar and communications [1,2,3,5,9,10,11,12,13,14,15,17,18,19,20,21,22,23,24,25,26,28,29,30,31].

The basic principle of a JRC system is to transmit waveforms that simultaneously achieve both radar and communication objectives by using the same physical platform as illustrated in Figure 1. Such systems achieve their objectives either by employing spatial multiplexing using smart antenna arrays [4,12,13,14,15,20], waveform diversity [1,2,3,9,18,23,25,26,28,32], or their combination [5,17,19,21,22,24]. JRC systems are inherently robust against mutual interference since both the radar and communication systems exploit the same waveforms. However, waveform optimization still remains a challenge in such systems especially if the waveforms have to be designed in real time.

To perform optimized waveform design, mutual information (MI) has been extensively used in the literature as a quantitative performance measure for both radar and communication systems [18,33,34,35,36]. For radar systems, MI maximization is directly linked to maximizing the probability of detection while maintaining a constant false alarm rate [33]. On the other hand, for communication systems, MI maximization is analogous to maximizing the channel capacity for the systems [35]. As such, we adopted MI as a quantitative measure to evaluate the performance of JRC systems. The convex nature of MI maximization makes it better for performance analysis and optimization than nonconvex measures such as the Cramer–Rao bound and the probability of detection.

Our contributions in this paper are summarized as follows:

• We propose a method for exploiting OFDM waveforms in JRC operation where all the subcarriers are used for the primary radar operation. At the same time, the subcarriers are further used for secondary communications and are distributed to multiple communication users in a mutually exclusively manner;
• Considering frequency-selective radar target characteristics and communication channels, we derive the mathematical formulation of the MI for both radar and communication subsystems;
• We devise solutions to the problem of subcarrier power allocation, as well as subcarrier distribution by exploiting the MI for both the radar and communication subsystems. In this context, we develope two optimization strategies respectively implementing radar-centric and cooperative JRC system designs. We show that the optimization strategy for power allocation is a convex optimization problem, whereas the optimization for the subcarrier distribution for multiple communication users is a mixed-integer linear programming (MILP) problem;
• In order to reduce the computational complexity of the optimization problems, we introduce chunk power allocation and subcarrier assignment techniques. These techniques group close subcarriers in the form of chunks, leading to a reduction in the computational complexity without noticeable performance loss in both the radar and communication subsystems.

The paper is organized as follows. The system model of the JRC system exploiting OFDM waveforms is described in Section 2. In Section 3, we derive the mathematical formulations of the MI for the radar and communication subsystems by considering frequency-selective channels. Section 4 discuses optimal power allocation and subcarrier assignment for radar-centric and cooperative JRC system designs. Section 5 discusses the power allocation and subcarrier assignment for the chunk of subcarriers. Simulation examples are provided in Section 6 to demonstrate the effectiveness of the proposed methods. Finally, conclusions are drawn in Section 7.

Notations: We use lowercase (uppercase) bold characters to describe vectors (matrices). In particular, ${\mathbf{I}}_K$ stands for the $K\times K$ identity matrix, whereas ${\mathbf{1}}_K$ and ${\mathbf{0}}_K$ respectively represent the $K\times 1$ vectors of all ones and zeros. The operations ${(·)}^{\mathrm{T}}$ and ${(·)}^{\mathrm{H}}$ denote the transpose and conjugate transpose, respectively, while the symbol ∗ denotes the convolution operator. The notation $h\left(\mathbf{x}\right)$ denotes the differential entropy of $\mathbf{x}$, $I(\mathbf{x};\mathbf{s})$ denotes mutual information between $\mathbf{x}$ and $\mathbf{s}$, whereas $\mathbb{E}\left[·\right]$ and $log(·)$ stand for statistical expectation and the logarithm of base two, respectively. Finally, $\mathrm{diag}\left(\mathbf{x}\right)$ denotes the diagonal matrix whose main diagonal is comprised of the entries from x, while $\mathrm{tr}(·)$ denotes the trace of a matrix.

2. System Model

Consider a JRC system consisting of a single-antenna transmitter that transmits dual-purpose OFDM radar–communication waveforms [32]. We assume one radar target and R communication receivers present in the vicinity of the JRC transmitter. The target response to the OFDM waveform and the characteristics of the communication channels are assumed to vary with the frequency. All the OFDM subcarriers are exploited for the radar system, whereas they are allocated to the R communication users. Figure 2 illustrates an example of the power allocation for the OFDM subcarriers and their assignment to two communication receivers.

The L-symbol OFDM signal vector $\mathbf{x}$, emitted from the dual-purpose transmitter, can be represented as:

$$\mathbf{x}={\mathbf{F}}_{}\mathbf{s},$$

(1)

where $\mathbf{s}={[s_1,\cdots ,s_K]}^{\mathrm{T}}$ denotes a $K\times 1$ signal vector, $K\le L$, with each $s_k,\forall k$ corresponding to the amplitude and phase of the kth subcarrier. In addition, ${\mathbf{F}}_{}$ is the $L\times K$ inverse discrete Fourier transform (IDFT) matrix such that each column of ${\mathbf{F}}_{}$ corresponds to an OFDM subcarrier having a unique frequency. Note that the columns of ${\mathbf{F}}_{}$ are orthogonal to each other, i.e.,

$${\mathbf{F}}_{}^{\mathrm{H}}{\mathbf{F}}_{}={\mathbf{I}}_K.$$

(2)

We exploit the quadratic phase shift keying (QPSK) scheme for each subcarrier. As such, the phase of $s_k$ carries the communication information in the kth subcarrier, whereas its magnitude determines the corresponding transmit energy $|s_k{|}^2$. Our objective is to allocate subcarrier powers and assign them to the communication users so as to optimize the performance of the JRC system.

The total transmit power of the transmitted OFDM waveform can be expressed as:

$$P_{\mathrm{total}}={\mathbf{x}}^{\mathrm{H}}\mathbf{x}={\mathbf{s}}^{\mathrm{H}}{\mathbf{F}}_{}^{\mathrm{H}}{\mathbf{F}}_{}\mathbf{s}={\mathbf{s}}^{\mathrm{H}}\mathbf{s}=\sum _{k=1}^K{p}_k=\mathrm{tr}\left\{\mathbf{P}\right\},$$

(3)

such that $\mathbf{P}=\mathrm{diag}\left\{\mathbf{p}\right\}$ is a diagonal matrix with diagonal elements given as:

$$\mathbf{p}={[p_1,\cdots ,p_K]}^{\mathrm{T}},$$

(4)

where $p_k={\left|s_k\right|}^2$. The maximum total transmit power by the dual-purpose JRC transmitter is represented by $P_{\mathrm{total},\max }$. We further denote the maximum and minimum transmit powers for the kth subcarrier as $p_{k,\max }$ and $p_{k,\min }$, respectively, and define the following maximum and minimum transmit power vectors:

$$\begin{array}{cc}\hfill {\mathbf{p}}_{\max }& ={[p_{1,\max },\cdots ,p_{K,\max }]}^{\mathrm{T}},\hfill \\ \hfill {\mathbf{p}}_{\min }& ={[p_{1,\min },\cdots ,p_{K,\min }]}^{\mathrm{T}}.\hfill \end{array}$$

(5)

Note that all the subcarriers having nonzero power are used for the radar function, and the same subcarriers are further allocated to the communication receivers. Thus, the dual-purpose waveform used by the radar also fulfills the communication objectives by transmitting distinct QPSK communication symbols described as the OFDM subcarrier signal vector $\mathbf{s}$ to the communication receivers.

The dual-purpose OFDM signal is reflected by the target having a frequency-dependent radar cross-section (RCS) and reaches the radar receiver. The radar channel vector is denoted as:

$$\mathbf{h}={[h_1,\cdots ,h_K]}^{\mathrm{T}},$$

(6)

where $h_k$ denotes the radar channel coefficient for the kth OFDM subcarrier, which includes the RCS, as well as the propagation loss. The received signal reflected by the target and received at the radar can be expressed as:

$${\tilde{\mathbf{y}}}_{\mathrm{rad}}=\tilde{\mathbf{h}}\ast \mathbf{x}+\tilde{\mathbf{n}},$$

(7)

where $\tilde{\mathbf{h}}={\mathbf{F}}_{}\mathbf{h}$ is the impulse response of the radar channel and $\tilde{\mathbf{n}}$ is the zero-mean circularly complex additive white Gaussian noise vector.

After performing the discrete Fourier transform (DFT), the K subcarriers of the OFDM signal are recovered at the radar receiver as:

$${\mathbf{y}}_{\mathrm{rad}}=\mathbf{Hs}+\mathbf{n},$$

(8)

where $\mathbf{H}=\mathrm{diag}\left(\mathbf{h}\right)$ and $\mathbf{n}$ is the Fourier transform of $\tilde{\mathbf{n}}$ and denotes the zero-mean circularly complex additive white Gaussian noise vector. We assume that the noise components in the K subcarriers are independent and identically distributed with known covariance matrix ${\mathsf{\Sigma }}_{\mathrm{n}}=\mathrm{diag}\{{\sigma }_{\mathrm{n},1}^2,\cdots ,{\sigma }_{\mathrm{n},K}^2\}$.

The communication channel response vector for the rth communication user is expressed as:

$${\mathbf{g}}_r={[g_{r,1},\dots ,g_{r,K}]}^{\mathrm{T}},$$

(9)

where $g_{r,k}$ is the communication channel response associated with the kth OFDM subcarrier. The transmit signal reaching the rth communication receiver is given as:

$${\mathbf{y}}_{\mathrm{com},r}={\mathbf{G}}_r\mathbf{s}+{\mathbf{m}}_r,r=1,\dots ,R,$$

(10)

where ${\mathbf{G}}_r=\mathrm{diag}\left({\mathbf{g}}_r\right)$. Moreover, ${\mathbf{m}}_r$ is the zero-mean additive white complex Gaussian noise vector with a known covariance matrix ${\mathsf{\Sigma }}_{{\mathrm{m}}_r}=\mathrm{diag}\{{\sigma }_{{\mathrm{m}}_{r,1}}^2,\cdots ,{\sigma }_{{\mathrm{m}}_{r,K}}^2\}$. In addition, the statistical properties of the radar and communication channels are known to be $\mathbf{h}\sim \mathcal{CN}\left({\mathbf{0}}_K,{\mathsf{\Sigma }}_{\mathbf{h}}\right)$ and ${\mathbf{g}}_r\sim \mathcal{CN}\left({\mathbf{0}}_K,{\mathsf{\Sigma }}_{{\mathrm{g}}_r}\right)$, where ${\mathsf{\Sigma }}_{\mathrm{h}}=\mathrm{diag}\{{\sigma }_{{\mathrm{h}}_1}^2,\cdots ,{\sigma }_{{\mathrm{h}}_K}^2\}$ and ${\mathsf{\Sigma }}_{{\mathrm{g}}_r}=\mathrm{diag}\{{\sigma }_{{\mathrm{g}}_{r,1}}^2,\cdots ,{\sigma }_{{\mathrm{g}}_{r,K}}^2\}$ are $K\times K$ diagonal matrices. We assume that $\mathbf{h}$ and $\mathbf{n}$, as well as ${\mathbf{g}}_r$ and ${\mathbf{m}}_r$, $r=1,\cdots ,R$, are mutually independent.

3. Optimization Criteria Based on Mutual Information

In this section, we derive the mathematical relation for the MI-based optimization criteria respectively for the radar and communication subsystems.

3.1. Radar Subsystem

Consider the MI between the dual-purpose OFDM transmit waveform and the frequency-dependent target response $\mathbf{h}$ as the performance criterion for the radar subsystem. It is expressed as [35]:

$$I\left({\mathbf{y}}_{\mathrm{rad}};\mathbf{h}|\mathbf{s}\right)=h\left({\mathbf{y}}_{\mathrm{rad}}\right|\mathbf{s})-h\left({\mathbf{y}}_{\mathrm{rad}}\right|\mathbf{h},\mathbf{s})=h\left({\mathbf{y}}_{\mathrm{rad}}\right|\mathbf{s})-h\left(\mathbf{n}\right).$$

(11)

The covariance matrix of ${\mathbf{y}}_{\mathrm{rad}}$ can be derived by exploiting Equation (8) as follows [34]:

$$\mathbb{E}\left[{\mathbf{y}}_{\mathrm{rad}}{\mathbf{y}}_{\mathrm{rad}}^{\mathrm{H}}\right]=\mathbb{E}\left[\mathbf{H}\mathbf{s}{\mathbf{s}}^{\mathrm{H}}{\mathbf{H}}^{\mathrm{H}}+\mathbf{n}{\mathbf{n}}^{\mathrm{H}}\right]=\mathbf{P}{\mathsf{\Sigma }}_{\mathrm{h}}+{\mathsf{\Sigma }}_{\mathrm{n}}.$$

(12)

Thus, ${\mathbf{y}}_{\mathrm{rad}}|\mathbf{s}\sim \mathcal{CN}\left({\mathbf{0}}_K,\mathbf{P}{\mathsf{\Sigma }}_{\mathrm{h}}+{\mathsf{\Sigma }}_{\mathrm{n}}\right)$. Equation (11) takes the following form [35]:

$$\begin{array}{cc}\hfill I({\mathbf{y}}_{\mathrm{rad}};\mathbf{h}|\mathbf{s})& =log\left[{\left(\pi e\right)}^{K}det\left(\mathbf{P}{\mathsf{\Sigma }}_{\mathrm{h}}+{\mathsf{\Sigma }}_{\mathrm{n}}\right)\right]-log\left[{\left(\pi e\right)}^{K}det\left({\mathsf{\Sigma }}_{\mathrm{n}}\right)\right]\hfill \\ \hfill & =log\left(det\left(\mathbf{P}{\mathsf{\Sigma }}_{\mathrm{h}}+{\mathsf{\Sigma }}_{\mathrm{n}}\right)\right)-logdet\left({\mathsf{\Sigma }}_{\mathrm{n}}\right).\hfill \end{array}$$

(13)

Since $\mathbf{P}{\mathsf{\Sigma }}_{\mathrm{h}}$ is a diagonal matrix, we can express its determinant as the product of its diagonal entries. Thus, Equation (13) takes the following form:

$$I({\mathbf{y}}_{\mathrm{rad}};\mathbf{h}|\mathbf{s})=log\left(\prod _{k=1}^K\frac{p_k{\sigma }_{{\mathrm{h}}_k}^2+{\sigma }_{\mathrm{n},k}^2}{{\sigma }_{\mathrm{n},k}^2}\right)=\sum _{k=1}^{K}log\left(1+\frac{p_k{\sigma }_{{\mathrm{h}}_k}^2}{{\sigma }_{\mathrm{n},k}^2}\right).$$

(14)

3.2. Communication Subsystem

In communication systems, maximizing the MI is analogous to maximizing the data rate [35]. The MI between the communication receivers and the dual-purpose OFDM transmit waveform can be derived by exploiting the same procedure as used for the radar subsystem. The MI between the transmitted OFDM signal vector s and the communication channel vector ${\mathbf{g}}_r$ of the rth communication receiver is given by [35]:

$$\begin{array}{cc}\hfill I\left({\mathbf{y}}_{\mathrm{com},r};{\mathbf{g}}_r|\mathbf{s}\right)& =h\left({\mathbf{y}}_{\mathrm{com},r}\right|\mathbf{s})-h\left({\mathbf{y}}_{\mathrm{com},r}\right|{\mathbf{g}}_r,\mathbf{s})\hfill \\ \hfill & =h\left({\mathbf{y}}_{\mathrm{com},r}\right|\mathbf{s})-h\left({\mathbf{m}}_r\right).\hfill \end{array}$$

(15)

Because ${\mathbf{y}}_{\mathrm{com},r}|\mathbf{s}\sim \mathcal{CN}\left({\mathbf{0}}_K,{\mathbf{P}\mathsf{\Sigma }}_{{\mathrm{g}}_r}+{\mathsf{\Sigma }}_{{\mathrm{m}}_r}\right)$, we can rewrite Equation (15) as [35]:

$$\begin{array}{cc}\hfill & I({\mathbf{y}}_{\mathrm{com},r};{\mathbf{g}}_r|\mathbf{s})=log\left(det\left({\mathbf{P}\mathsf{\Sigma }}_{{\mathrm{g}}_r}+{\mathsf{\Sigma }}_{{\mathrm{m}}_r}\right)\right)-log\left(det\left({\mathsf{\Sigma }}_{{\mathrm{m}}_r}\right)\right).\hfill \end{array}$$

(16)

Since ${\mathbf{P}\mathsf{\Sigma }}_{{\mathrm{g}}_r}$ is a diagonal matrix, Equation (16) can be expressed as:

$$\begin{array}{cc}\hfill & I({\mathbf{y}}_{\mathrm{com},r};{\mathbf{g}}_r|\mathbf{s})=log\left[\prod _{k=1}^K\frac{p_k^{\mathrm{H}}{\sigma }_{{\mathrm{g}}_{r,k}}^2+{\sigma }_{{\mathrm{m}}_{r,k}}^2}{{\sigma }_{{\mathrm{m}}_{r,k}}^2}\right]=\sum _{k=1}^{K}log\left(1+\frac{p_k{\sigma }_{{\mathrm{g}}_{r,k}}^2}{{\sigma }_{{\mathrm{m}}_{r,k}}^2}\right).\hfill \end{array}$$

(17)

4. Optimal Power Distribution and Subcarrier Allocation

In this section, we optimize the transmit power allocated for each subcarrier and assign all the subcarriers exclusively among the communication receivers so that the MI is maximized. All the subcarriers are used for the radar function and are also optimally assigned exclusively to the communication users such that an individual subcarrier serves only one communication receiver. This enables interference-free multiple access by transmitting distinct data streams to different communication receivers using the subcarriers dedicated to them.

We consider two optimization strategies for power allocation and subcarrier assignment. The first approach performs a radar-centric operation where the power allocation to subcarriers is solely to maximize the radar MI based on the radar channel conditions and is irrespective of the communication channels. In the second scenario, the radar subsystem cooperates with the communication subsystem by sacrificing some of the achievable radar MI in order to provide more flexibility in the optimization and offer better performance for the communication subsystem. We provide optimization problems for both power allocation and subcarrier allotment to the communication receivers. These two scenarios are respectively considered in Section 4.1 and Section 4.2.

Considering that the computational complexity of these optimization problems increases with an increase of the number of OFDM subcarriers, in order to reduce the computational complexity involved in subcarrier power allocation and allotment, we further develop a grouped or chunk-based processing strategy. Such a strategy is considered in Section 5.

4.1. Radar-Centric Design

In this scenario, our objective is to maximize the MI for radar, as described in Equation (14), irrespective of the communication channel conditions. Such a design gives supreme precedence to the radar function, and the resulting subcarrier power allocation provides the maximum MI for the radar operation. However, this strategy does not guarantee that the communication objectives will be satisfied. As we further allocate the subcarriers to different communication users whose transmit power is determined based solely on the radar-centric operation, the transmit dual-purpose OFDM waveform can still be used by the communication receivers.

4.1.1. Power Allocation

The MI in Equation (14) is a concave function of $\mathbf{p}$. Therefore, the resulting convex optimization that tends to maximize the radar MI can be expressed as follows [32]:

$$\begin{array}{cccc}\hfill & \underset{\mathbf{p}}{\max }\hfill & \hfill & \sum _{k=1}^{K}log\left(1+\frac{p_k{\sigma }_{{\mathrm{h}}_k}^2}{{\sigma }_{\mathrm{n},k}^2}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & {\mathbf{1}}_K^{\mathrm{T}}\mathbf{p}\le P_{\mathrm{total},\max },\hfill \\ \hfill & \hfill & & {\mathbf{p}}_{\min }\le \mathbf{p}\le {\mathbf{p}}_{\max }.\hfill \end{array}$$

(18)

The constraints in the above optimization problem emphasize the fact that the power of all OFDM subcarriers is bounded by the total available power $P_{\mathrm{total},\max }$, whereas the power of the subcarriers is bounded by the respective maximum possible transmit power described in vector ${\mathbf{p}}_{\max }$.

4.1.2. Subcarrier Assignment

We assign each subcarrier to a unique communication user. For this purpose, we exploit MILP optimization, which allots the OFDM subcarriers to the individual communication users such that the total communication MI is maximized. The assignment of each subcarrier for only one communication user ensures interference-free multiple access for all communication users.

Note that, in the underlying radar-centric operation, the transmit power of each subcarrier is already determined by exploiting the optimization problem (18), and the following optimization problems only assign each subcarrier to a communication receiver. For this purpose, we use two different optimization criteria, respectively maximizing the sum communication MI and the worst-case communication MI.

In the first criterion, the total communication MI that can be collectively achieved by the communication users is expressed as:

$$\begin{array}{cccc}\hfill & \underset{{\mathbf{w}}_k}{\max }\hfill & \hfill & \sum _{r=1}^R\sum _{k=1}^K{w}_{r,k}log\left(1+\frac{p_k{\sigma }_{{\mathrm{g}}_{r,k}}^2}{{\sigma }_{{\mathrm{m}}_{r,k}}^2}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & {\mathbf{1}}_K^{\mathrm{T}}{\mathbf{w}}_k=1,w_{r,k}\in \{0,1\},\forall r,\forall k,\hfill \end{array}$$

(19)

where $w_{r,k}$ is a binary assignment variable, which takes a value of $w_{r,k}=1$ when the kth subcarrier is assigned to the rth communication user. Furthermore, we define ${\mathbf{w}}_k={[w_{1,k},\cdots ,w_{R,k}]}^{\mathrm{T}}$ as the vector illustrating the assignment of the kth subcarrier.

Note that in this optimization scenario, it is possible that some communication users having poor channel conditions are ignored, resulting in negligible communication MI for them, even though the overall communication MI is maximized.

In order to mitigate the above-mentioned problem, the second optimization criterion maximizes the worst-case communication MI that ensures that all the communication users are fed with a fair value of the communication MI irrespective of their channel conditions. This is important for the critical communication infrastructure, which cannot tolerate being ignored in case it has bad channel conditions. The worst-case MI criterion can be ensured by employing the following max-min MILP optimization problem:

$$\begin{array}{cccc}\hfill & \underset{{\mathbf{w}}_k}{\max }\underset{r}{\min }\hfill & \hfill & \sum _{k=1}^K{w}_{r,k}log\left(1+\frac{p_k{\sigma }_{{\mathrm{g}}_{r,k}}^2}{{\sigma }_{{\mathrm{m}}_{r,k}}^2}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & {\mathbf{1}}_K^{\mathrm{T}}{\mathbf{w}}_k=1,w_{r,k}\in \{0,1\},\forall r,\forall k.\hfill \end{array}$$

(20)

The above optimization problem can also be expressed as follows:

$$\begin{array}{cccc}\hfill & \underset{{\mathbf{w}}_k}{\max }\hfill & \hfill & t\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & \sum _{k=1}^K{w}_{r,k}log\left(1+\frac{p_k{\sigma }_{{\mathrm{g}}_{r,k}}^2}{{\sigma }_{{\mathrm{m}}_{r,k}}^2}\right)\ge t,\forall r,\hfill \\ \hfill & \hfill & & {\mathbf{1}}_K^{\mathrm{T}}{\mathbf{w}}_k=1,w_{r,k}\in \{0,1\},\forall r,\forall k.\hfill \end{array}$$

(21)

Note again that the allocated power $p_k$ in the above optimizations is a constant and has already been derived from the optimization problem (18). Although the optimization in Problems (20) and (21) ensures the worst-case MI for each communication user, we should be careful that, if some communication users have extremely poor channel conditions, a worst-case optimization might drain significant power in the poor communication channels, rendering the overall communication performance to be very low.

4.2. Cooperative Design

We discussed earlier that the subcarrier power allocation in the radar-centric design solely depends on the radar channel conditions and results in the maximum possible MI for radar function. In this subsection, we consider the scenario where the radar shows some flexibility for the maximum possible MI that it can achieve. Such flexibility in the radar subsystem with an insignificant radar performance loss enables the communications users to achieve significantly higher MI.

4.2.1. Power Distribution

The first step is to determine the maximum possible MI ${\alpha }_{\mathrm{opt}}$ that can be achieved for the radar function determined by the optimization problem (18). Subsequently, the radar subsystem decides its flexibility parameter $\gamma$ whose value varies between zero and one, where a higher value of $\gamma$ favors the radar objectives. The new radar objective of the JRC system is to achieve a radar MI of at least $\gamma {\alpha }_{\mathrm{opt}}$. In this way, the radar function allows some flexibility for the dual-purpose transmitters to adjust the transmit powers depending on the communication channels.

An iterative approach can be used for power distribution and subcarrier allocation. First, the initial values of the subcarrier allocation coefficients $w_{r,k}$ are either randomly chosen or extracted by exploiting the optimization problems (19) or (21). Subsequently, the following optimization problem then achieves the acceptable radar objective while maximizing the overall communication MI:

$$\begin{array}{cccc}\hfill & \underset{\mathbf{p}}{\max }\hfill & \hfill & \sum _{r=1}^R\sum _{k=1}^K{w}_{r,k}log\left(1+\frac{p_k{\sigma }_{{\mathrm{g}}_{r,k}}^2}{{\sigma }_{{\mathrm{m}}_{r,k}}^2}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & \sum _{k=1}^{K}log\left(1+\frac{p_k{\sigma }_{{\mathrm{h}}_k}^2}{{\sigma }_{\mathrm{n},k}^2}\right)\ge \gamma {\alpha }_{\mathrm{opt}},\hfill \\ \hfill & \hfill & & {\mathbf{1}}_K^{\mathrm{T}}\mathbf{p}\le P_{\mathrm{total},\max },\hfill \\ \hfill & \hfill & & {\mathbf{0}}_K\le \mathbf{p}\le {\mathbf{p}}_{\max }.\hfill \end{array}$$

(22)

Note that the subcarrier allocation coefficients $w_{r,k}$ are constant in the above optimization problem. This optimization problem results in the optimized power allocation for individual OFDM subcarriers at this stage. A similar optimization problem can be formulated for the case of worst-case communication MI optimization by replacing ${\max }_{\mathbf{p}}{\sum }_{r=1}^R(·)$ in the optimization problem (22) with ${\max }_{\mathbf{p}}{min}_r(·)$.

4.2.2. Subcarrier Allocation

The optimal value of $p_k$ obtained from the optimization problem (22) is fed back to (19) or (21), depending on which type of communication optimization criterion is desired. The optimization for the power distribution (22) and that for subcarrier allocation (19) or (21) are repeated iteratively until there is no significant change in the achieved power distribution and subcarrier assignment profiles.

5. Chunk Subcarrier Processing

The number of optimization variables increases with the number of subcarriers, resulting in higher computational complexity. This problem becomes more serious for MILP optimization problems as the computational complexity approaches the brute-force search complexity for a high number of variables. We mitigate this issue by grouping multiple neighboring subcarriers together as a single variable. As the neighboring channel for the radar and communication subsystems shows close channel conditions, such an approach naturally leads to a good approximation of the optimized solution. However, the performance degradation is expected to increase with an increase in the chunk size.

Assume that the set of all K available OFDM subcarriers is evenly partitioned into Q nonoverlapping chunks of M subcarriers each. We can employ the following optimization problem for radar-centric power allocation:

$$\begin{array}{cccc}\hfill & \underset{\mathbf{p}}{\max }\hfill & \hfill & \sum _{k=1}^{K}log\left(1+\frac{p_k{\sigma }_{{\mathrm{h}}_k}^2}{{\sigma }_{\mathrm{n},k}^2}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & {\mathbf{1}}_K^{\mathrm{T}}\mathbf{p}\le P_{\mathrm{total},\max },\hfill \\ \hfill & \hfill & & {\mathbf{p}}_{\min }\le \mathbf{p}\le {\mathbf{p}}_{\max },\hfill \\ \hfill & \hfill & & p_n=p_{n+m},\hfill \end{array}$$

(23)

where $m=1,\cdots ,M-1$ and $n=1,M,2M,\cdots ,K$.

Similarly, we can address the chunk subcarrier assignment problem for radar-centric design that results in the maximum communication MI by exploiting the MILP optimization as follows:

$$\begin{array}{cccc}\hfill & \underset{{\mathbf{w}}_k}{\max }\hfill & \hfill & \sum _{r=1}^R\sum _{k=1}^K{w}_{r,k}log\left(1+\frac{p_k{\sigma }_{{\mathrm{g}}_{r,k}}^2}{{\sigma }_{{\mathrm{m}}_{r,k}}^2}\right)\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\hfill & \hfill & {\mathbf{1}}_K^{\mathrm{T}}{\mathbf{w}}_k=1,w_{r,k}\in \{0,1\},\forall r,\forall k,\hfill \\ \hfill & \hfill & & w_{r,n}=w_{r,n+m},\forall r,\hfill \end{array}$$

(24)

where $m=1,\cdots ,M-1$ and $n=1,M,2M,\cdots ,K$.

Similar optimization strategies can be developed for cooperative power allocation and subcarrier assignment.

6. Numerical Results

Consider a JRC transmitter exploiting sixty-four subcarriers, and there are one radar target and two communication receivers in the scene. The maximum individual subcarrier power and the total maximum power are normalized to 10 units and 250 units, respectively. The normalized target and communication channel gains, respectively expressed as ${\sigma }_{{\mathrm{h}}_k}/{\sigma }_{{\mathrm{n}}_k}$ and ${\sigma }_{{\mathrm{g}}_{r,k}}/{\sigma }_{{\mathrm{m}}_{r,k}}$, are illustrated in Figure 3. We used the Gurobi solver [37] to solve all the optimization problems, and the achieved MI for all the cases is expressed in bit/s/Hz as the unit.

First, we consider the radar-centric design for power allocation and subcarrier assignment problems. Figure 4 shows the power allocation for different subcarriers using the radar-centric optimization problem (18) that maximizes the MI for the radar function. It can be observed that most of the power is allocated to the subcarriers that have a high target reflection coefficient, resulting in the maximum MI for the radar function. We then employed the optimization problem (20) to assign the OFDM subcarriers to the two communication users so as to achieve the maximum total communication MI using the OFDM subcarriers whose power is already allocated using (18). The subcarriers in the red and blue colors depict the OFDM subcarriers respectively allocated to Communication Users 1 and 2, respectively. It is observed that, although the overall communication MI is maximized, Communication User 1 achieves only 36% of the total communication MI. In order to democratize the achieved communication MI by both communication users irrespective of their channel conditions, we employed the optimization problem (21), which performs max-min optimization to achieve this purpose. The results for this worst-case optimization are shown in Figure 4b, illustrating that a fair share of 49.5% of the total communication MI is now allocated to Communication User 1. Note that the MI distribution among the two users is not exactly the same because the powers are already allocated in the radar-centric design and the optimization problem (21) only tends to democratize the MI distribution between the two users.

Next, we discuss the cooperative radar–communication design where the radar flexibility parameter is set as $\gamma =0.9$. Figure 5a shows the power allocation and subcarrier distribution for the case of the maximum communication MI. We note in

Table 1. Achieved mutual information for the proposed strategies.

	Radar-Centric Design		Cooperative Design ($\mathit{\gamma }=0.9$)
	Maximum	Worst-Case	Maximum	Worst-Case
	Comm. MI	Comm. MI	Comm. MI	Comm. MI
$I({\mathbf{y}}_{\mathrm{rad}};\mathbf{h}|\mathbf{s})$	31.56	31.56	28.41	28.41
$I({\mathbf{y}}_{\mathrm{com},1};{\mathbf{g}}_1|\mathbf{s})$	12.67	13.16	23.02	19.65
$I({\mathbf{y}}_{\mathrm{com},2};{\mathbf{g}}_2|\mathbf{s})$	18.27	13.42	17.22	19.65

that, at the expense of reducing the radar MI by 10%, the overall communication MI is improved by 30%. Similarly, Figure 5b illustrates the results, which maximize the worst-case communication MI for both communication users at the expense of reduced sum communication MI. Compared to the worst-case optimization results in the radar-centric case, we observed almost a 50% improvement in the overall communication MI. Moreover, the worst-case optimization strategy resulted in exactly the same MI of 19.65 for both communication users. Table 1 summarizes the achieved MI for the radar-centric and cooperative JRC designs without using the chunk power allocation. It can be observed that, compared to the radar-centric design, the cooperative design resulted in overall better performance for both the radar and communication systems.

Figure 6 and Figure 7 show the results of the chunk-based resource allocation strategies for both the radar-centric and cooperative JRC system designs. For this purpose, we use the neighboring subcarriers grouped into a set of $M=4$ subcarriers, resulting in a total of $Q=16$ groups. The achieved MI for all chunk-based resource allocation strategies is summarized in

Table 2. Achieved mutual information for the proposed chunk-based strategies.

	Radar-Centric Design		Cooperative Design ($\mathit{\gamma }=0.9$)
	Maximum	Worst-Case	Maximum	Worst-Case
	Comm. MI	Comm. MI	Comm. MI	Comm. MI
$I({\mathbf{y}}_{\mathrm{rad}};\mathbf{h}|\mathbf{s})$	31.30	31.30	28.17	28.17
$I({\mathbf{y}}_{\mathrm{com},1};{\mathbf{g}}_1|\mathbf{s})$	12.86	13.08	22.50	17.71
$I({\mathbf{y}}_{\mathrm{com},2};{\mathbf{g}}_2|\mathbf{s})$	17.46	15.87	16.58	17.71

. It can be observed that the chunk-based resource allocation strategy shows exactly the same performance trends compared to the resource allocation without using chunks of subcarriers as in Table 1, except the fact that the achieved JRC performance is slightly lower for the chunk-based scenarios. However, the number of total optimization variables is reduced by a factor of four, thereby effectively reducing the computational complexity of the system and highlighting the benefit of using the chunk-based optimization approach.

Figure 8 shows the achieved MI for the cooperative JRC system design by varying the radar flexibility parameter $\gamma$ from 0.8–1. It is observed that the communication MI advantage increased as the value of $\gamma$ reduced, but such a communication advantage saturated when $\gamma$ is below 0.9. A similar trend is observed in Figure 9, which shows the achieved MIs for the cooperative design using the chunk-based strategy. These results showed that the only an insignificant performance reduction is required for the radar subsystem to enable the optimized performance for the communication subsystem.

Finally, we investigate the power allocation and subcarrier assignment for the cooperative JRC system where the radar and communication channel responses are relatively flat, as shown in Figure 10a. Note that User 1 had higher communication channel gains for all the subcarriers compared to User 2. Such a situation can arise particularly if User 1 is located closer to the transmitter compared to User 2. In such a case, it is natural to use the JRC strategy employing the worst-case communication MI because the sum communication MI maximization will allocate all the subcarriers to User 1, which has better channel conditions, leaving User 2 with a communication outage.

Figure 10b shows the power allocation and subcarrier assignment resulting from the worst-case cooperative JRC strategy. It can be observed that more subcarriers are allocated to User 2 so that both communication users are provided the same communication MI of 20.58. A similar trend can been observed in Figure 10c, where chunk subcarrier allocation is considered. Since each chunk consisted of four consecutive subcarriers that can be assigned to either of the communication users, chunk association with either of the communication users can create a significant communication MI advantage. Therefore, the resulting power allocation is less uniform for this approach compared to Figure 10b. It can also be noted that both users are provided with an equal communication MI of 20.42.

Now, we compare the complexity of the proposed strategies in terms of the computational time. All the simulations are performed on a computer equipped with an Intel(R) Core(TM) i7-9750H (2.60 GHz) processor and 16 GB RAM. We used MATLAB R2021a (64-bit), the CVX toolbox (Version 2.2, Build 1148) [38], and the Gurobi solver (Version 9.1) [37] for all optimization problems.

Table 3. Average computation time (ms) for the proposed resource allocation strategies: $K=$ 1024 subcarriers, $R=2$ users, and channel conditions from Figure 3.

	Power Allocation (Radar-Centric) (18)	Subcarrier Assignment (Sum com. MI) (19)	Subcarrier Assignment (Worst-Case com. MI) (20) or (21)	Power Allocation (Sum com. MI) (22)	Power Allocation (Worst-Case com. MI)
Without chunks	276	232	321	80,605	80,999
2 subcarrier chunks	214	220	251	34,415	34,812
4 subcarrier chunks	177	218	235	15,650	16,288
8 subcarrier chunks	166	214	221	7291	8204

shows the average computation time, rounded off to the nearest millisecond, for the proposed optimization strategies. Note that the JRC power allocations are the most computationally expensive because they involve both the radar and communication objectives.

7. Conclusions

In this paper, we presented a novel JRC system that exploits OFDM waveforms to perform both radar and communication operations simultaneously. A dual-purpose OFDM transmitter was exploited that optimizes the transmit power of different subcarriers to fulfil the objectives of the radar function. Subsequently, the same OFDM subcarriers were then allocated to different communication receivers to enable the communication function of the JRC system. The MI between the frequency-sensitive radar target and communication channels was used as the criteria for the optimization of the JRC system performance. The radar-centric and cooperative designs were extended to chunk-based resource allocation, which reduced the computational cost of the desired performance optimizations. The simulation results verified the effectiveness of the proposed strategies.

The proposed JRC strategies can be readily extended to the multiple target case where the targets have similar channel responses. However, more involved research efforts are needed for multiple target cases where the channel response varies from one target to another. Such scenarios face challenging problems such as missed target detection, target prioritization, and increased computational complexity. In addition, further research efforts are required in the domain of mathematical optimization to reduce the computational cost of the resource allocation problems. Moreover, quantitative studies of the impact of channel uncertainties in both the radar and communication systems would help better understand the advantages offered by the proposed resource optimization approaches.