Next Article in Journal
Application of the Comparison of Multibeam Echo-Sound Records to the Study of Stability of a Toxic Waste Stockpile Located on the Margin of a Tidal System: Tinto Estuary, Huelva, SW Spain
Next Article in Special Issue
Investigating the Effects of k and Area Size on Variance Estimation of Multiple Pixel Areas Using a k-NN Technique for Forest Parameters
Previous Article in Journal
Accuracy Verification and Correction of D-InSAR and SBAS-InSAR in Monitoring Mining Surface Subsidence
Previous Article in Special Issue
Measurement of Forest Inventory Parameters with Apple iPad Pro and Integrated LiDAR Technology
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 21
10.3390/rs13214367
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Consumer Grade UAV-Based Framework to Estimate Structural Attributes of Coppice and High Oak Forest Stands in Semi-Arid Regions

by
Arvin Fakhri
1 and
Hooman Latifi
1,2,*
1
Department of Photogrammetry and Remote Sensing, Faculty of Geodesy and Geomatics Engineering, K.N. Toosi University of Technology (KNTU), Tehran 19967-15433, Iran
2
Department. of Remote Sensing, Institute of Geography and Geology, University of Wuerzburg, 97074 Wuerzburg, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(21), 4367; https://doi.org/10.3390/rs13214367
Submission received: 15 September 2021 / Revised: 27 October 2021 / Accepted: 27 October 2021 / Published: 29 October 2021
(This article belongs to the Special Issue Optimizing the Usages of High-Spatial Resolution Remote Sensing Data: From Precision Resources Inventory to Operational Forestry)
Browse Figures
Versions Notes

Abstract

:
Semi-arid tree covers, in both high and coppice growth forms, play an essential role in protecting water and soil resources and provides multiple ecosystem services across fragile ecosystems. Thus, they require continuous inventories. Quantification of forest structure in these tree covers provides important measures for their management and biodiversity conservation. We present a framework, based on consumer-grade UAV photogrammetry, to separately estimate primary variables of tree height (H) and crown area (A) across diverse coppice and high stands dominated by Quercus brantii Lindl. along the latitudinal gradient of Zagros mountains of western Iran. Then, multivariate linear regressions were parametrized with H and A to estimate the diameter at breast height (DBH) of high trees because of its importance to accelerate the existing practical DBH inventories across Zagros Forests. The estimated variables were finally applied to a model tree aboveground biomass (AGB) for both vegetative growth forms by local allometric equations and Random Forest models. In each step, the estimated variables were evaluated against the field reference values, indicating practically high accuracies reaching root mean square error (RMSE) of 0.68 m and 4.74 cm for H and DBH, as well as relative RMSE < 10% for AGB estimates. The results generally suggest an effective framework for single tree-based attribute estimation over mountainous, semi-arid coppice, and high stands.

1. Introduction

Forests significantly contribute to the global carbon cycle by providing the largest reserves of terrestrial carbon [1]. Therefore, quantifying forest structure, particularly across fragile and erosion-prone forest sites, is of major importance for their conservation and management [2,3]. The structural analysis of such vegetation is also a prerequisite to assess their current condition and evaluate their ecosystem services such as carbon stocks, CO2 uptake [4,5], and aboveground biomass (AGB) [6] as affected by disturbances and land use changes. The primary structural attributes that are common among forest ecosystems include the number of trees, species composition, tree size, and the AGB [7], which are considered inputs to derive secondary attributes such as total leaf area, tree and leaf biomasses, and multiple other ecosystem services [3]. Tree height and diameter at breast height (DBH) are among the basic forest inventory attributes [8,9], which are integrated by many allometric equations for estimating the AGB [10,11] and are therefore essential information for quantifying forest carbon cycle [12], carbon stock [13], and global climate change [14]. Traditional methods of measuring tree height are costly and time-consuming, and they are particularly infeasible for spatial upscaling to larger domains [15]. In addition, one of the main obstacles of these measurements is the lack of sufficient visibility to the tree top, particularly for broadleaves with circular crowns. One way to bypass this is via the possibility of using high-resolution nadir view to enable two- and three-dimensional measurements by fully observing the surface of the tree canopy, which is commonly enabled by remote sensing data and methods [16,17,18]. In addition to height estimation, they can be rather intuitively applied to estimate a range of other tree canopy variables, including the crown area [19] and its diameter [20]. The list of studies on tree height estimations, by 3D remote sensing methods, is enormous [21], which includes studies that applied data from both active and passive sensors. LiDAR [13,22,23] and RADAR [24,25] data have been extensively studied, which are yet financially prohibitive despite their generally high estimation accuracies [26]. On the other hand, passive high-resolution sensors, such as photogrammetric Unmanned Aerial Vehicles (UAVs), offer possibilities to derive three-dimensional models at, comparatively, much lower costs [27] that allow for capturing the forest canopy surface via image matching and the subsequent post-processing techniques [28]. On the one hand, multi-rotor drones are easier to take off and land, so they are therefore preferred by researchers because they are usually cheaper and more flexible for scientific purposes [29]. On the other hand, larger-scale studies have been carried out with the help of fixed-wing drones equipped with optical cameras [30]. A number of studies have been performed on fixed-wing drones in measuring the vertical structural attributes of forests for large-scale areas [31,32,33]. Although passive sensors do not penetrate the crown layer and thus cannot provide information from understories, they are beneficial in measuring the horizontal and vertical structural attributes for single-story forest stands.
Furthermore, DBH is another essential forest structural variable [34,35] that is obtained by measuring the diameter of the trunk at a height of 1.3 m [36]. Although DBH can be conveniently measured with traditional methods such as caliper [35], problems are faced towards its spatial upscaling, particularly across remote and difficult-to-access areas with variations in tree growth forms [37]. In such cases, the use of remote sensing methods is considered as a reliable alternative [38,39,40]. In general, studies on direct estimation of DBH by remote sensing have mainly focused on using LIDAR data [41,42], while passive optical data fail to deliver sub-canopy observations due to tree foliage cover [37,43]. This entails an indirect estimation of the DBH, using 3D photogrammetric data, for example, by relating DBH and tree height [44] or DBH and canopy area [45]. Additionally, Benjamin and Russell, 2021 [46] estimated DBH using complementary measurements on UAV-derived models. Therefore, they first created a regression model using the area of tree canopies, calculated the canopy diameter by fitting a circle to the canopy of each tree, followed by fitting against the ground reference data. This yielded relative errors ranging between 19.7% and 33.7%. Whereas methods based on under-canopy UAV flights have returned promising results for estimating single tree DBH [47], they commonly entail an additional LiDAR payload that is prohibitive for budget applications designed and applied by most forest administrations. Moreover, AGB reserves are mainly related to forest structure and species composition [48,49]. The AGB is thus an important indicator for measuring the carbon sequestration capacity [50]. Direct methods to estimate AGB include destructive methods [51], while allometric equations are generally used as alternative indirect methods [52].
The UAV technology has enabled producing accurate small-scale estimates based on derivations such as digital surface models (DSMs), which can be further applied to derive side-products such as DTMs, and calibrate spatial models of forest structural attributes. The process of producing DTM in forested areas commonly involves interpolations [53,54,55,56] with the main problem being the lack of empty areas, i.e., areas without trees, in dense stands [57]. On the contrary, sparse tree covers enable photogrammetric models that lead to the high accuracy of canopy height models (CHM = DSM-DTM), which are crucial to estimating tree structural variables. For example, Vahid et al. (2021) [58] estimated tree height from CHM using high-pass and local maximum filters across a test site, located within the Hyrcanian mixed forests of northern Iran, followed by estimation of the tree canopy area using the Invert Watershed Segmentation (IWS) algorithm. This consequently led to calculating crown diameter with a relative RMSE of 10.1% and 7.02% for estimating the height and crown diameter, respectively.
The Middle East and West Asia are currently facing one of the worldwide harshest heatwaves, also termed as a heat dome (see https://earthobservatory.nasa.gov/images/148430/heatwave-scorches-the-middle-east access on 15 September 2021). They are considered obvious signs of climate change that have largely affected fauna, flora, and human communities. The Zagros Forests located in western Iran (with marginal expansion into southeastern Turkey and northern Iraq) are among the most fragile ecosystems in west Asia. In Iran, they cover ca. 20% of the total countrywide vegetated area. These forests play a key role in maintaining the harsh climate, supplying water, and economic and social balance of Iran and the region [59]. These forests are dominated by three oak species Q. infectoria Olivier, Q. libani Olivier, and Q. brantii Lindl., with the relative dominance of the latter species increasing along the latitudinal gradient [59,60,61]. The vertical structures of these species occur in both high and coppice forms, where coppice stands generally have a vertical one-story structure. The tremendous power of sprouting and asexual regeneration of Q. brantii, and the incompetence of other species for the establishment, has led to almost pure dominance of Q. brantii in central and south Zagros zones, yet with different proportions of high and coppice stands affected by both the climate and lifestyles of local populations (nomadic or sedentary). Due to their unique historical development and multiple anthropogenic influential phenomena, their crucial structural characteristics include species, the origin of trees (high or coppice), number of sprouts per sprout-clumps for coppices, sprout diameter and tree canopy diameters, DBH for high trees, as well as tree height and AGB for trees in both vegetative forms. Despite all associated challenges, continuous monitoring of Zagros Forests is largely constrained by accessibility, lack of logistics, and financial capabilities, leading to hitherto available sporadic and insufficient quantitative structural information, even on small-scale spatial domains.
In this study, we suggest a consumer grade UAV-based framework to retrieve a number of the most important primary and secondary structural attributes of Q. brantii–dominated stands in both high and coppice forms along the north-south gradient of Zagros Mountains. We focused on the height and area of tree canopies as directly estimable attributes, whereas the DBH of high trees and AGB were indirectly estimated. We estimated DBH via its relationship with crown area and height. Finally, we estimated the AGB by both allometric models with tree height and DBH as independent variables, as well as nonlinear regression models (random forest regression, RFR) with crown surface area and height as predictors. The aim was to provide both science and practice with objective comparative estimates of single tree-based Q. brantii AGB across these extremely fragile ecosystems that have been continuously under climatic and anthropogenic pressures.
The commonly-applied field methods of measuring the structural attributes of Zagros Forests are costly and time consuming due to their mountainous topography and limited accessibility. Therefore, there is an interest in facilitating rapid field measurements of the structural attributes, particularly by means of 3D remote sensing methods. To the best of our knowledge, no international study has been published, so far, on the use of remote sensing in measuring the structural attributes of trees in the Zagros region. Therefore, here, we addressed the basic research question of whether UAV photogrammetric methods can serve as a complementary method in ground measurements of Zagros Forests. In particular, the innovative aspects of this study are that (1) it focuses on a rich dataset of plot measurements that are distributed across the latitudinal gradient of Zagros Forests, (2) it differentiates high and coppice growth forms for all analyses, (3) it compares AGB estimations from machine learning and allometric methods to serve both science and practice. This includes surveys to answer the following questions:
-
Are 3D photogrammetric models accurate enough to estimate the height of single trees in Zagros?
-
Can DBH (as an essential variable that is unable to be directly derived from photogrammetric models) be estimated using other UAV-measured primary attributes?
-
How do the available single-attribute allometric equations for Q. brantii in Zagros Forests perform compared to commonly-applied nonlinear models (RFR) on UAV-extracted variables to predict AGB?

2. Materials and Methods

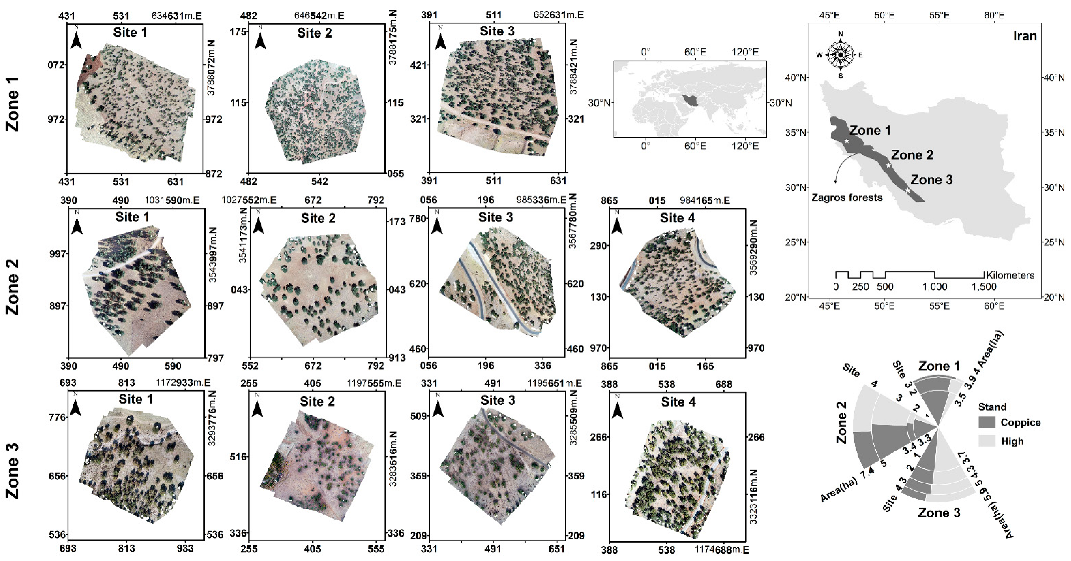
2.1. Study Area

Zagros Forests consist of ca. 1300 and ca. 200 km extensions along the latitudinal and longitudinal gradients, respectively. These semi-arid ecosystems comprise an area of ca. 6 million ha and cover about 44% of Iran’s total area of forests [59,62]. The average annual temperature ranges between 9 and 25 degrees Celsius, with the maximum 74 degree difference between the coldest and warmest temperatures, which indicates a continental climate [62]. In general, the northern zone of Zagros is associated with comparatively wetter and cooler climate compared with the central and southern zones [59].
We divided Zagros Forests into three regions, based on both general climatic conditions and administrative division, in which we established our sampling locations: northern zone (zone 1), middle zone (zone 2), and southern zone (zone 3). Then, 11 study sites across all three regions with dominance of Q. brantii were selected with the aim of deriving their structural attributes in both high and coppice forms by covering a representative latitudinal gradient (Figure 1).

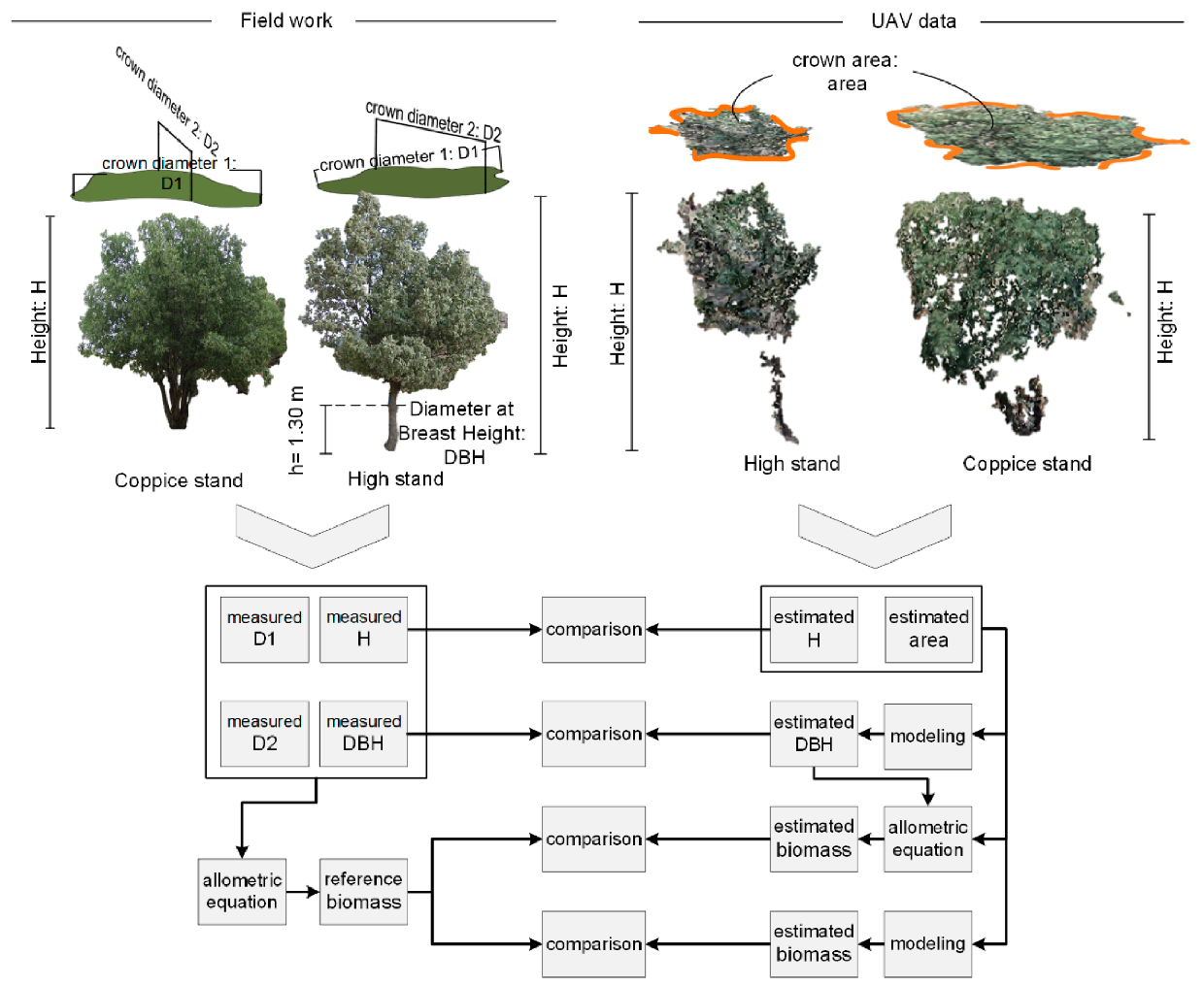
2.2. Field Measurements

The reference data on a set of tree structural features, including height (H), canopy area (A), diameter at breast height (DBH), and the AGB were either field-sampled or estimated as described below [63]. The inventories were conducted within the 11 study sites established along the latitudinal gradient of Zagros mountains during 4 months in 2019, i.e., close to UAV imaging dates (Section 2.3) within the framework of provincial sub-projects of “the National Zagros Forest Monitoring Plan” coordinated by the Research Institute of Forests and Rangelands (RIFR) of Iran (Figure 1). The reference AGB was indirectly calculated using the allometric equations (Table 1) [64,65] with the independent variables of H, DBH, and average diameter of the canopy (D) for each of the high and coppice forms separately (Table 2). We relied on the available field records when assigning the stands to each of coppice or high vegetative forms, since single trees in all sites, except those in Zone 1, were tagged with either coppice or high origin, which we further adopted in our analysis. Due to the absence of this designation in all three sites in Zone 1, we took all trees with a single sprout as high trees and those with the number of sprouts > 1 as coppice trees. Thus, we partly deviated from the pure ecological principle in defining the vegetative form, which is primarily based on sexual or asexual growth origin.

2.3. UAV Imaging

We applied a consumer-grade DJI Phantom 4 pro multi-rotor UAV (DJI, 2016) for aerial imaging. The device included a 3-axis stabilization gimbal, 1’’ CMOS sensor camera and FOV 84° 8.8 mm/24 mm lens. The full list of technical specifications can be found at https://www.dji.com/phantom-4-pro/info (access on 15 September 2021). The flights for different sites were designed according to the site-specific topographic conditions and tree cover but generally as double-grid networks with 80% horizontal/vertical overlaps conducted with an iOS version of Pix4DCapture (https://support.pix4d.com/hc/en-us/articles/204010419-iOS-Pix4Dcapture-Manual-and-Settings access on 15 September 2021) installed on an iPad 2018 tablet. The flights were carried out during 2nd–5th of September 2019 for northern and central zones and 6th–7th of November 2019 for southern zone with a resolution of 5472 × 3648 pixels at 70 m flight altitude. In general, images were taken with a resolution of 5 cm, although there were slight differences in image resolution at various sites. This resulted in ca. 125 image tiles per forest site.
Five control points that were recorded per site (four corners and a centroid) that included GPS-measured latitudes, longitudes, and altitudes. The coordinates were measured using the real-time kinematic (RTK) method for northern and central plots and the post-processing kinematic (PPK) method for southern plots by applying two GPS receivers of Trimble 5700 and 5800 and a Zephyr Geodetic antenna. For the PPK method, the recorded points were post-processed using geodetic fixed reference points within Shamim National Geodetic Platform (https://shamim.ssaa.ir/sbc access on 15 September 2021).

2.4. Methodology

Figure 2 shows the general flowchart of this research. Based on the field-measured variables of tree height, DBH, the first diameter, and the second diameter of the tree crown, allometric equations (Table 1) were parametrized to estimate the AGB values (see the left side of Figure 2). Furthermore, UAV-derived CHMs and orthophotos were applied to extract the height and crown surface as primary variables, using which multivariate linear regressions were developed to estimate the DBH with H and A as independent variables. Consequently, the AGB values were predicted by (1) allometric equations as a function of H, DBH, and D (Table 1) and (2) nonlinear regressions with H and A as independent variables (see Figure 2 right wing). We divided the entire reference data into separate training and test datasets for all three stages for which estimations were carried out. These three stages included (1) derivation of UAV-based models, (2) segmentation of individual tree crowns, and (3) derivation of single tree structural variables.

2.4.1. UAV-Derived Terrain and Surface Models

The raw UAV images were processed in Agisoft Metashape 1.7 (https://www.agisoft.com access on 15 September 2021). The products from UAV data comprised DTM, DSM, and orthophoto for each site. Then, we derived the CHM using CHM = DSM-DTM.

2.4.2. Individual Tree Crown Segmentation

Individual trees were segmented in order to extract the height and crown area of individual trees. Despite the high dominance of Q. brantii within all sites, the individual trees were highly diverse in terms of their height and crown shape, resulting in the use of CHM for tree segmentation [19,66]. We applied the Marker-Controlled Watershed Segmentation (MCWS,) as a previously-tested and efficient method, across sparse tree stands [67,68]. We abstained from using the classical watershed as an unsupervised classification method due to the over-estimations raised by the presence of noise in images [69], which necessitates variable levels of pre- and post-processing. The MCWS method has been previously used to detect single tree crowns by applying a set of pre- and post-processors [67,70], with more technical details in [69] to which the reader is referred.

2.4.3. Extracting the Height and Canopy Area of Individual Trees

After delineating the crown boundary of each tree, the variables of height and crown area for each tree were calculated as the maximum value of CHM in the tree polygon and the polygon area, respectively. The fact that the field reference data included the measured tree heights enabled a comparison of the CHM-derived and field-measured heights for high and coppice trees separately.

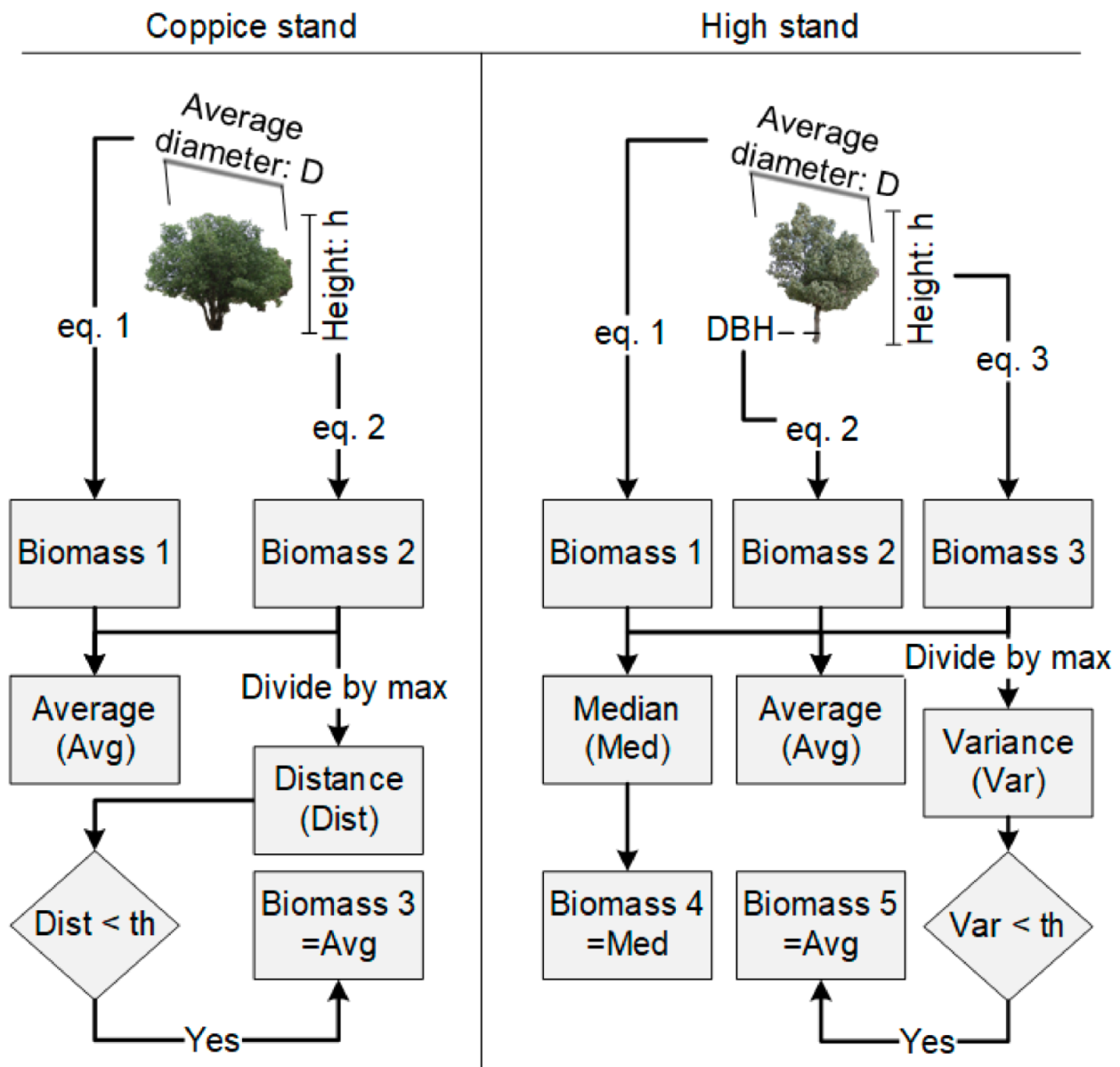
2.4.4. DBH Estimation

Since the DBH was infeasible to be directly derived from UAV photogrammetric data, we estimated it as a function of H and A [71,72,73] to serve its practical implementation. To this aim, multivariate linear regression models, using these two parameters (H and A) that were extracted in the previous steps, were applied [74]. The field-measured DBH values (for high trees) were used to train and test the model with random 50% partitioning within each forest site.

2.4.5. AGB Estimation

Allometric equations for estimating the biomass of Q. brantii trees in both high and coppice forms, using independent variables of H, DBH, and D followed [64] (Table 1). The H was directly extracted from UAV-based CHM, while the DBH was indirectly derived as described above. We directly applied the last two equations in Table 1 to estimate the AGB for trees in high stands, while the remainder of the equations were applied to the coppice stands. Moreover, we additionally included the A variable in AGB estimation, whereas it was not originally included in the allometric equations listed in Table 1. Therefore, a nonlinear machine learning model, with H and A as independent variables, was applied for each of the tree vegetative forms. We employed RFR, a supervised algorithm based on ensemble learning by using a combination of a set of regression trees [75,76]. It converges by (1) randomly drawing numerous initial bootstrap samples with replacements from the original training dataset, (2) fitting each regression tree to each of the bootstrap samples, and (3) predicting all trees by constructing decision trees during training [77]. The RFR was numerously reported as a powerful and accurate approach, followed by its compatibility with nonlinear relationships [78]. The number of regression trees, identified as the number of estimators, was defined as hyperparameter by testing the RMSE on training data for values ranging between 100 and 1000 at intervals of 50 [79]. This resulted in selecting 700 trees as the optimal number of estimators. According to the number of existing allometric equations that were used to calculate the reference AGB values, the total three and two AGB values were obtained for each high and coppice tree, respectively. Moreover, the average of those models was also calculated as an additional AGB value.
Here, obtaining different AGB values for a given tree was inherent, since each allometric equation in Table 1 features a different independent variable (H, D, and DBH). Therefore, we performed a numerical modification to derive an average instead of an average that possibly does not incorporate different possible values for AGB. We did this modification by first defining a threshold value and then checking the variance of different AGB values prior to calculating the final reference value. This ensured that the AGB value was ignored, i.e., it was treated as an outlier, if the variance (for high trees) or distance (for coppice trees) was higher than the defined threshold value. Otherwise, we calculated the mean value of the applied multiple AGB equations and considered it as the modified average. This resulted in the final four AGB values for high stands and three values for coppice stands. In addition, the median of the three AGB values of high stands was considered to be an additional AGB value (Figure 3).
Following the generation of reference AGB values, the RFR was trained for each group. These models were evaluated using the Leave-One-Out-Cross-Validation (LOOCV) [80].

3. Results

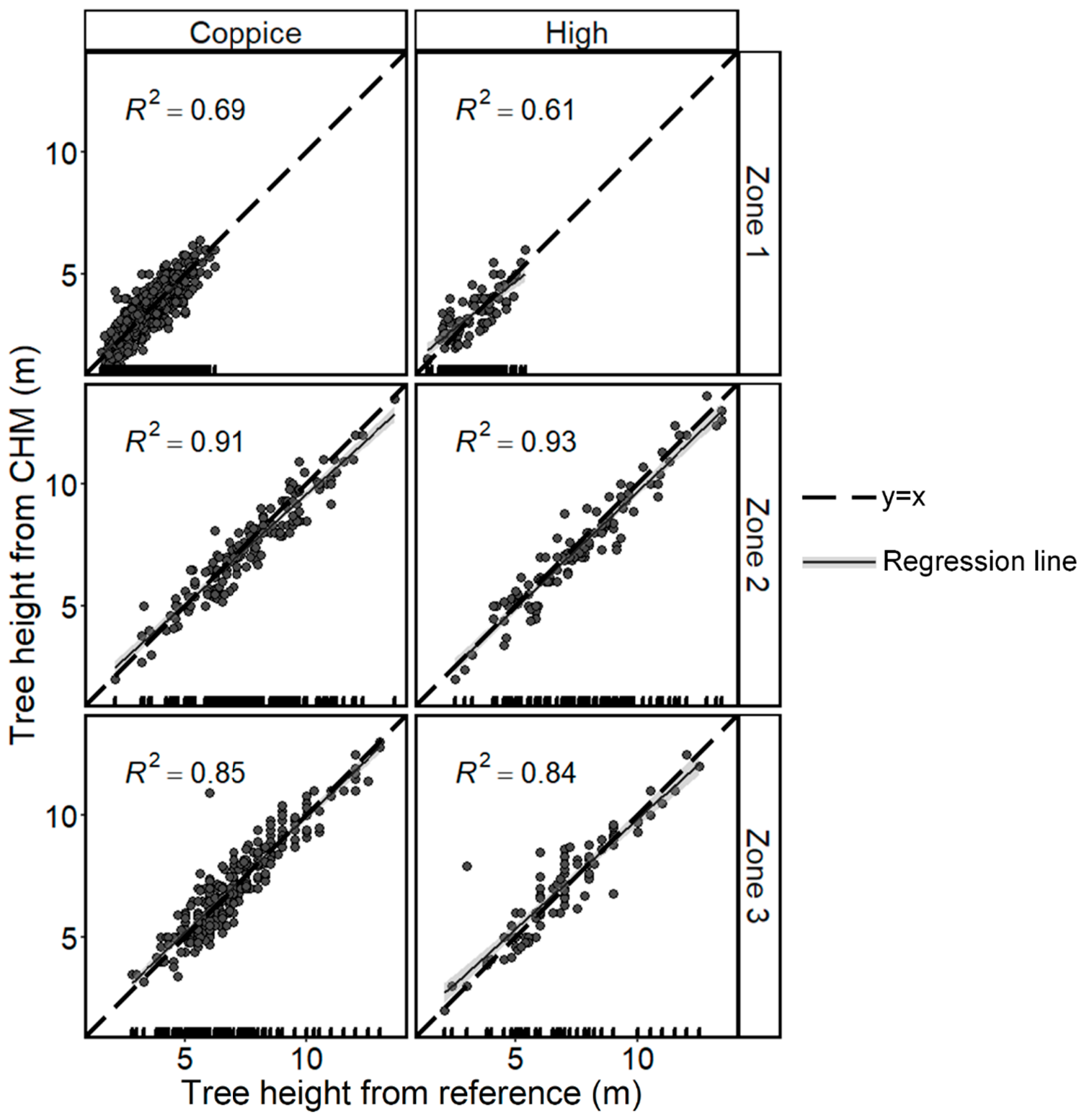
3.1. Tree Height Estimation

The results of tree height estimation for both vegetative forms were obtained in each zone (Figure 4). The reader is referred to the Appendix A for the site-specific results. The results suggested the R2 values of 0.69, 0.91, and 0.85 for high stands and 0.61, 0.93, and 0.84 for coppice stands for CHM-derived tree heights compared with the reference values in Zones 1–3, respectively. Apart from the practically accurate fits, it also suggested a high-quality segmentation that was previously carried out by MCWS prior to height estimation.
As shown in Figure 4, different values of tree height, from 1 m to 15 m in all three zones, were extracted with high accuracy.

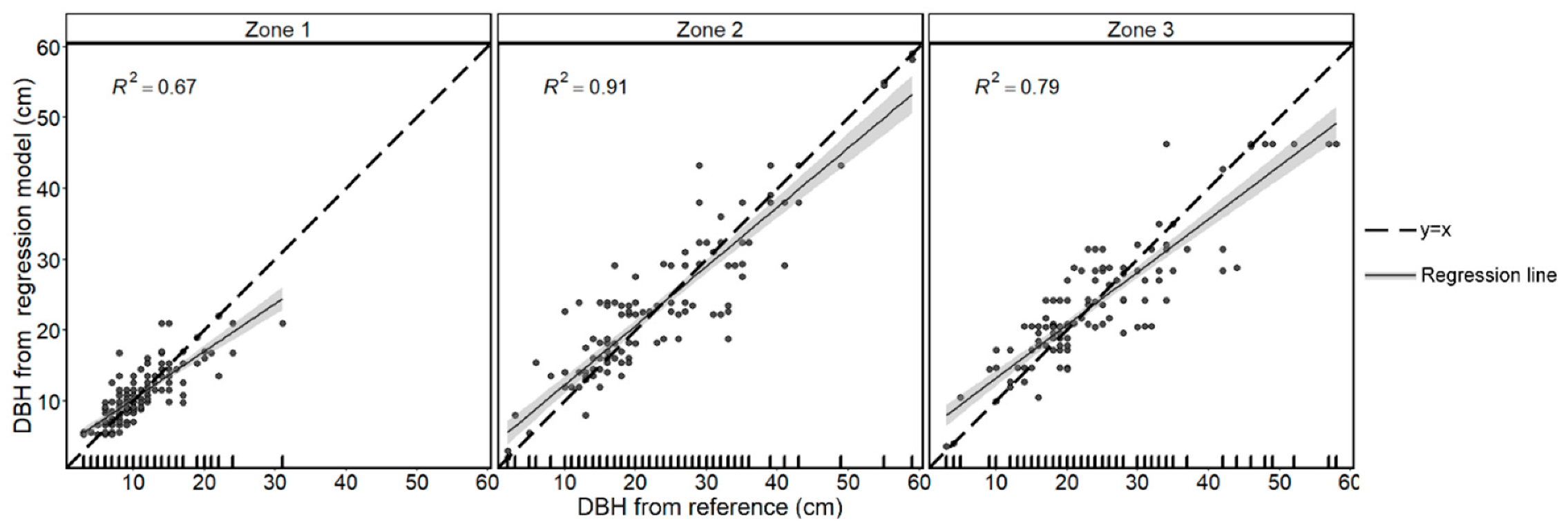
3.2. DBH Estimation

The results of multivariate linear regression, as a comparison between the modelled DBH and the terrestrial reference values, showed a high linear correlation of estimated values with the reference values (Figure 5). The site-specific results are included in the Appendix B.

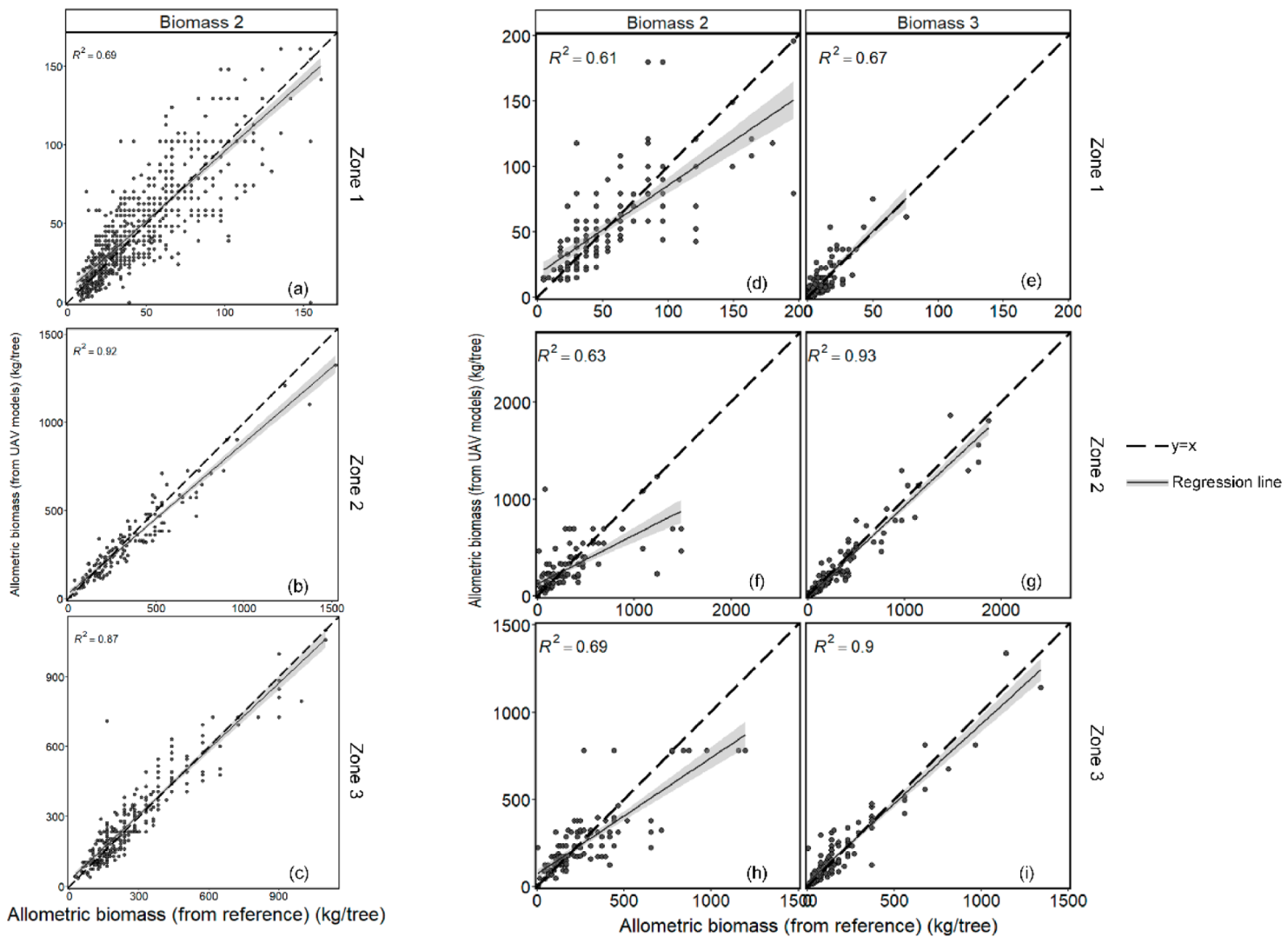
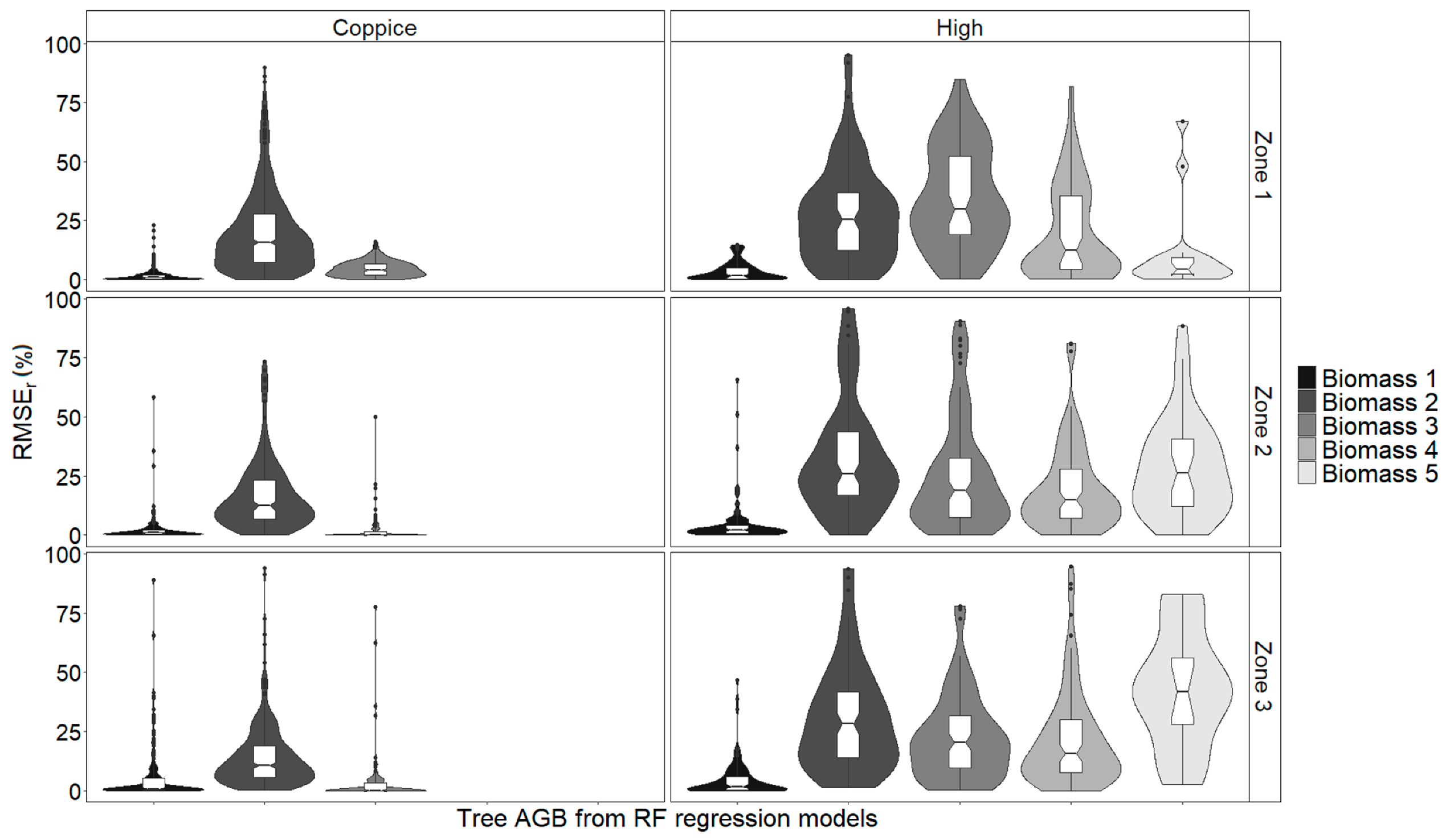
3.3. AGB Estimation

3.3.1. AGB estimation by allometric equations

The results of allometric equations, with H, D, and DBH as independent variables, were partially affected by the prediction accuracy of H and DBH from UAV data (Table 3). In addition, the results of AGB estimations, when comparing field- and UAV-derived variables, are summarized in Figure 6. We directly extracted the crown area (A) and tree height (H) from the UAV models (CHM and orthophoto), while we indirectly estimated the DBH using the regression models on H and A. Therefore, only allometric equations on DBH and H were used. For the site-specific results, the reader is referred to the Appendix C.
The results suggested that the AGB model 3, with H as an independent variable, showed a better fit with the reference data compared with the model 2 that used DBH as an independent variable.

3.3.2. AGB Estimation by RFR

We only used H and A to estimate AGB using RFR, since the UAV-modelled DBH was a function of H and A. The relative RMSE values of LOOCV, for different reference AGB models, suggested comparatively higher performance of model 1 in mean rRMSE of AGB estimation for both high and coppice stands (Figure 7).
As expected, model 3 returned intermediate results for coppice trees, since it was averaged from models 1 and 2. This was also partially the case for high stands. Among models 2 and 3, i.e., models based on DBH and H, the model with allometry on height in high trees outperformed the model with DBH for Zones 2 and 3. This was indicated by the lower mean rRMSE and the higher density of error distribution in the lower values for model 3. The allometric model 4, i.e., the median of models 1, 2, and 3, showed higher accuracy than model 5 for Zones 2 and 3, as resulted by its comparatively lower average value and the higher density of error distribution in the mid-range. In all three zones, the DBH model for the high stands was shown to perform weaker than almost all other models (except for Zone 1). Furthermore, model 1, i.e., the allometry on D, performed better than all other models. For coppice stands in all three zones, D and H were the most and least influential variables in allometric models, respectively (the site-specific results are presented in Appendix D).

4. Discussion

Zagros Forests are among the most ecologically diverse, yet most degraded ecosystems in Iran and the Middle East. Upon first reports from early 2000, the region has been severely affected by a multi-agent oak dieback. This phenomenon mostly occurred across the central and southern parts of the Zagros region [81,82]. This necessitates rapid and cost-effective quantification and monitoring of their structural attributes to maintain their sustainability. However, harsh topography and infeasibility of field works, over remote and partly inaccessible areas, majorly constrain providing detailed structural information, which can be alleviated by locally adjustable UAV-based approaches. These benefits are mainly valid across small-scale areas. Due to the problems raised by limited flight duration, limited areal coverage and fixed gimbals, the use of consumer grade UAVs are commonly limited to small-scale areas and plot-based inventories [83,84]. On the other hand, due to the sensitivity to weather conditions, it is necessary to ensure the weather stability before starting the flight operation [29]. Another major limitation of UAVs concerns the legal restrictions on flying, which avoids their use in many areas, including those close to country borders [85]. Despite those critical limitations, the advantages of using UAVs in small areas outweigh their disadvantages [86] and thus argument their use as alternatives or complements to other remote sensing data.
Here, we mainly focused on indirect methods for estimating essential structural variables of trees in natural Q. brantii dominated stands, in high and coppice vegetative forms that were spread over three distant biogeographical zones, along the latitudinal gradient of Zagros Forests. The canopy surface parameters and tree height for Q. brantii dominated stands were directly measured on UAV-based photogrammetric models. However, the AGB is generally calculated in practice by allometric equations, based on either height (H), average crown diameter (D), or diameter at breast height (DBH) of the trees in single-factor allometric equations [64]. Whereas we relied on a range of previously available local AGB models for trees grown within coppice and high stands, we primarily tested the possibility to parametrize the models with UAV-estimated tree variables to serve the practical implementation of our results. To this aim, DBH was estimated, by linear regression of the H and A, and was then used within the allometric equations to derive the AGB. Apart from that, we also followed the commonly-tested RFR approach based on nonparametric spatial models with UAV-estimated input variables. We deliberately avoided using a large feature space, with multiple textural and spectral indices, to maintain the parsimony of the models as well as their comparability against the allometric models (see, for example, [87]). This might be contrary to some relevant studies in which larger feature spaces were applied at the cost of applying exhaustive variable selection techniques (see [88]), which, however, are associated with limited comparability between allometric and RFR modeling approaches.
With the rationale to minimize the potential error of tree height that occurred in field measurements (due to insufficient visibility of top crown in broadleaves, human errors, and device errors) [89,90,91,92] numerous former studies applied high resolution remote sensing data (mostly LiDAR). Other relevant studies using UAV photogrammetry reported RMSEs of 0.28 m [28] 0.34 m [93] 1.30 m [19] and 3.04 m, respectively. Our results of 0.82 and 0.64 m RMSE, within high- and coppice-dominated stands, were in-line with those studies, though we generally do not recommend direct comparisons of absolute error rates among studies conducted in areas with different ecosystem properties and varying standards for field data collection.
One of the main challenges in estimating the tree height is the production of CHM in dense forests [94]. To produce an accurate CHM, Vahid et al. (2021) [58] acquired UAV data in two different seasons corresponding to leaf-off and leaf-on conditions, followed by estimating single-tree heights. The estimations resulted in R2 = 0.808. Although leaf abundance was stated to be an influential factor on single tree height estimation [95], we used only leaf-on season images in our study within multiple sites of the Zagros Forests, due to different density of trees ranging from semi-dense to sparse, while there was no fully dense forest stand in our study sites. We reached R2 values ranging between 0.61 and 0.93, depending on both factors of site and growth form. Despite the fact that the tree species were largely similar across all surveyed forest sites, the difference in accuracy across the three zones of Zagros Forests can be attributed to two factors of (1) the imaging conditions and (2) the applied RFR machine learning method. Although we attempted to capture imagery, possibly under constant weather conditions and flight planning in all three Zones, the difference in accuracy may be due to differences in the number of trees, i.e., density in each area (see Table 2), slightly different times of the flight and partially different topography of the sites. The latter factor can introduce variable levels of artifacts in digital terrain modeling [96], single tree detection [97], and the subsequent AGB estimation [98] when generally working on all 3D sources of airborne data. However, this was out of the scope of our study.
In terms of DBH, it is among the most conveniently-measured variables in the field. Its direct derivation from passive UAV imagery is infeasible, but it is possible to be estimated by models incorporating image-based UAV measurements, such as tree height and canopy area [99]. Here, we estimated H and A from UAV data across areas with high trees, which was in line with previous studies that estimated DBH using passive photogrammetry data [45]. Our linear model reached an R2 in range of [0.67, 0.91] for Zones 1, 2, and 3, which was comparatively in line with [100] that reported R2 of 0.738 in a nonlinear model of DBH as a function of canopy diameter and tree height.
Partly relevant studies such as [99] reported inferior predictions of AGB as a function of UAV-based tree height and canopy area compared with those based on DBH. However, the latter study was conducted in a mangrove ecosystem, in which both height and canopy area are less influential on the AGB compared to most terrestrial tree ecosystems, mainly due to their comparatively more complex structure and coppice-only vegetative forms. Here, our AGB models for both vegetative forms showed superiority of tree height to DBH when estimating AGB from UAV data by allometric equations. To the best of our knowledge, this is the first study that (1) differentiated between estimates of coppice and high stands and (2) estimated AGB based on photogrammetric data in the Zagros region, whereas even field-based studies on AGB in the Zagros region are rare [101]. Allometric equations, with DBH as an independent variable, were reported to be mostly correlated with AGB [102]. This was mostly the case for average canopy diameter (D) in field-based studies carried out within the Zagros ecosystem [103], which can be mainly attributed to the coppice and multi-stem origin of the majority of its forest stands. Similarly, the highest performances in both high and coppice forms in our UAV-based study were observed for models that were parametrized with average crown diameter. Apart from the dominant coppice origin, a further reason could be the generally extensive crown of Q. brantii trees within commonly sparse Zagros stands, which leads to the formation of a major part of the variance described for the AGB. Comparable UAV-based studies that combined spectral information and H, extracted from UAV photogrammetric data, include, for example, [104] for poplar plantations, with R2 values reaching 0.54 and RMSE = 0.23 kg/m2 for the AGB (in a site with average AGB of 1.68 kg/m2). Furthermore, Lin et al. (2018) [105] suggested a nonlinear regression model for estimating AGB with height as a single independent variable extracted from UAV oblique photography, which resulted in RMSE = 54 kg and rRMSE = 34% when compared with allometric equations on H. Here, our UAV-based models delivered RMSE values < 10%, using only H and A as the independent variables. Although we are aware of the general limitation of reference data calculations using allometric equations [106], we attempted to compensate for this by (1) using diverse allometries, including three equations for high-dominated and two for coppice-dominated stands, and (2) additionally averaging the resulted reference values via using the modified mean and median values.
Finally, our UAV photogrammetric models to estimate a set of essential structural attributes can be tested across not only the Zagros region, but also over other similarly structured semi-arid forest stands. In forests similar to the Zagros Forests, the single trees extraction is more accurate due to the sparse tree distribution. Moreover, the height of each tree can be estimated with higher accuracy compared with denser tree ecosystems. In dense forests, deriving an accurate UAV-based DTM is mostly challenged by (1) difficulty in separating the trees and (2) ground invisibility caused by tree density. Both constraints have a direct negative effect on the estimation of crown area and height, as well as indirectly on the estimation of DBH and AGB. However, in some cases, high resolution images can be helpful in extracting dense trees, but this adds another limitation: namely, the infeasibility of imaging large areas with consumer-grade UAVs. We tested direct and indirect methods to estimate the height, crown area, DBH, and AGB, separately, for stands dominated by trees with coppice and high vegetative forms. When comparing the estimates against detailed site-based results (see the Appendix A, Appendix B, Appendix C and Appendix D), the results suggested comparatively high accuracies, achieved by the photogrammetric method, applied on consumer grade UAV datasets. This can further support both forest scientific and practical administrative applications within the Zagros region, which already largely lacks such estimates and thus cannot be quantitatively monitored following the occurrence of multiple diminishing factors including land-use change, tree decline, increased cattle grazing, and frequent wildfires.

5. Conclusions

Sustainable management of fragile semi-arid mountainous forests entails quantitative monitoring of tree attributes on various spatial scales. Currently, sparsely available field estimates in Zagros is exacerbated by weak technical infrastructure, e.g., infeasibility of using Terrestrial LiDAR, GeoSLAM, or airborne LiDAR, which entail relying on methods based on a combination of limited field data and passive photogrammetry or remote sensing data. We suggested a UAV-assisted workflow to measure and estimate a range of primary and secondary structural attributes on single tree-level across multiple forest sites, located along the latitudinal gradient of Zagros Forests. Differentiation between high and coppice growth forms is highly relevant in Zagros and other oak-dominated ecosystems due to the strong anthropogenic pressure on tree regeneration, as well as high ability of oak trees for asexual regeneration. Despite the reported uncertainties, the results largely support the use of UAVs for plot-based measurements of single trees over such difficult-to-reach areas. Our results for direct estimation of H and A from three-dimensional models were practically accurate over almost the entire forest sites, which justified their further application in estimating the single tree AGB using both allometric equations and machine learning. Moreover, estimating the DBH by regression on A and H as input variables was done to suggest a practical workflow for both science and forest administration in Zagros, where regular field-based methods are infeasible due to inaccessibility and lack of logistic facilities for frequent monitoring. However, this is associated with an unknown amount of aggregated error. We also showed that high resolution UAV data enable an indirect retrieval of single tree DBH using UAV-extracted A and H as independent variables with negligible correlation. Finally, we suggest further research on (1) the use of consumer-grade UAV photogrammetry for tree measurements, in particular across coppice trees to reduce the existing uncertainties via testing the effects of topography, data acquisition time, and shadow on model performance and (2) to follow spatial upscaling methods, based on a combination of UAV and satellite multispectral data for larger spatial scales.

Author Contributions

Conceptualization, H.L. and A.F.; methodology, A.F. and H.L.; software, A.F.; validation, A.F.; formal analysis, A.F. and H.L; investigation, A.F. and H.L; data curation, H.L.; writing—original draft preparation, A.F. and H.L; writing—review and editing, A.F. and H.L.; visualization, A.F.; supervision, H.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Zagros Monitoring Project of the Research Institute of Forests and Rangelands (RIFR) (grant number 01-09-09-047-97012) within the sub-project “UAV-assisted Forest Structure Monitoring” (grant number: 013-09-0951-048-97012-970548).

Data Availability Statement

Not applicable.

Acknowledgments

The authors are grateful to diverse field crews in three provinces of Kermanshah, Chaharmahal-and-Bakhtiari and Fars who collected the field data on oak decline. We are particularly grateful for the assistance of Mehdi Pourhashemi from RIFR, Yaghoub Iranmanesh, Hassan Jahanbazi, Seyed Kazem Bordbar, Mehrdad Zarafshar and Habibollah Rahimi at the provincial bureaus of RIFR, as well as our patient driver Mohammad Qarliqi and our GPS assistants Mohammad Ali Bahavar and Javad Sabaei. The UAV and GPS measurement campaigns were logistically supported by the National Zagros Monitoring Project of the Research Institute of Forests and Rangelands (Project No. 01-09-09-047-97012) within the sub-project “UAV-assisted Forest Structure Monitoring” (Project No. 013-09-0951-048-97012-970548). The authors also thank Marziye Ghasemi Mobaraki for her supports in terms of UAV and field data processing. This research was conducted within the “Remote Sensing for Ecology and Ecosystem Conservation (RSEEC)” research lab of the KNTU (https://www.researchgate.net/lab/Research-Lab-Remote-Sensing-for-Ecology-and-Ecosystem-Conservation-RSEEC-Hooman-Latifi) (accessed date 27 October 2021).

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

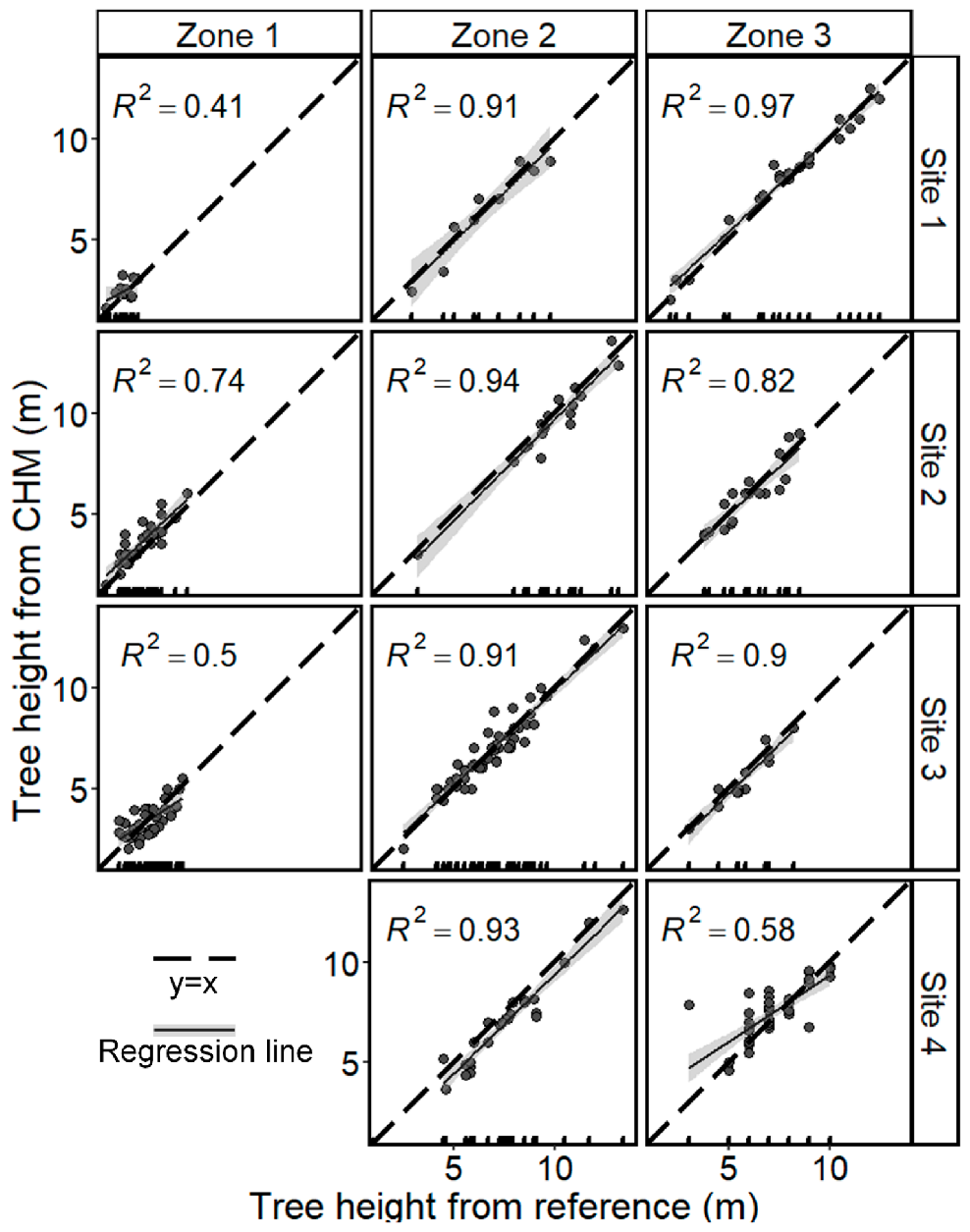
Remotesensing 13 04367 g0a1
Figure A1. Site-specific comparison of H from CHM with actual measured values (reference values) in trees with high stand form.
Figure A1. Site-specific comparison of H from CHM with actual measured values (reference values) in trees with high stand form.
Remotesensing 13 04367 g0a1
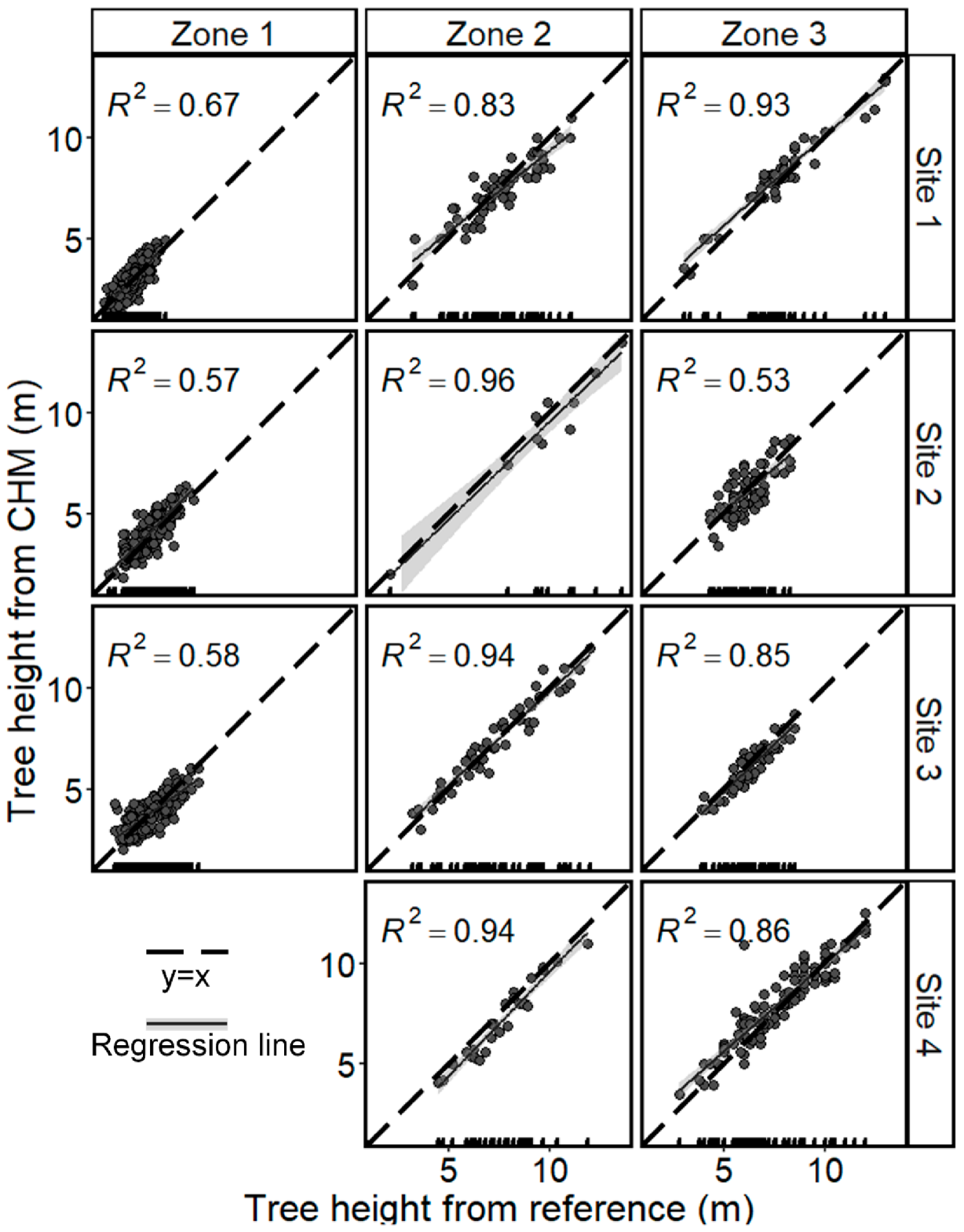
Remotesensing 13 04367 g0a2
Figure A2. Site-specific comparison of H from CHM with actual measured values (reference values) in trees with coppice stand form.
Figure A2. Site-specific comparison of H from CHM with actual measured values (reference values) in trees with coppice stand form.
Remotesensing 13 04367 g0a2
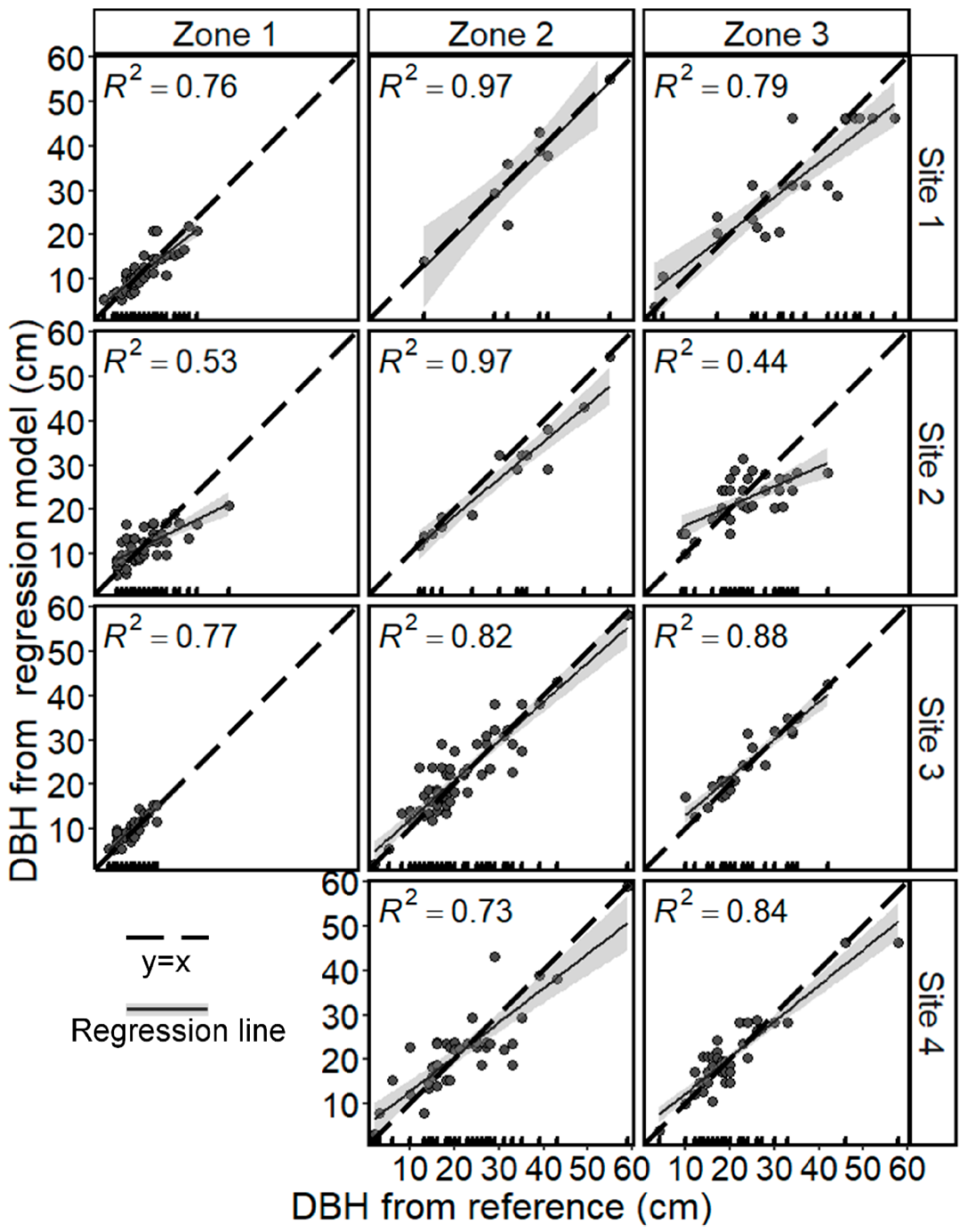
Remotesensing 13 04367 g0a3
Figure A3. Site-specific comparison of DBH estimated from multivariate linear regression model with independent variables of height (H) and canopy area (A) in trees with high stand form.
Figure A3. Site-specific comparison of DBH estimated from multivariate linear regression model with independent variables of height (H) and canopy area (A) in trees with high stand form.
Remotesensing 13 04367 g0a3

Appendix B

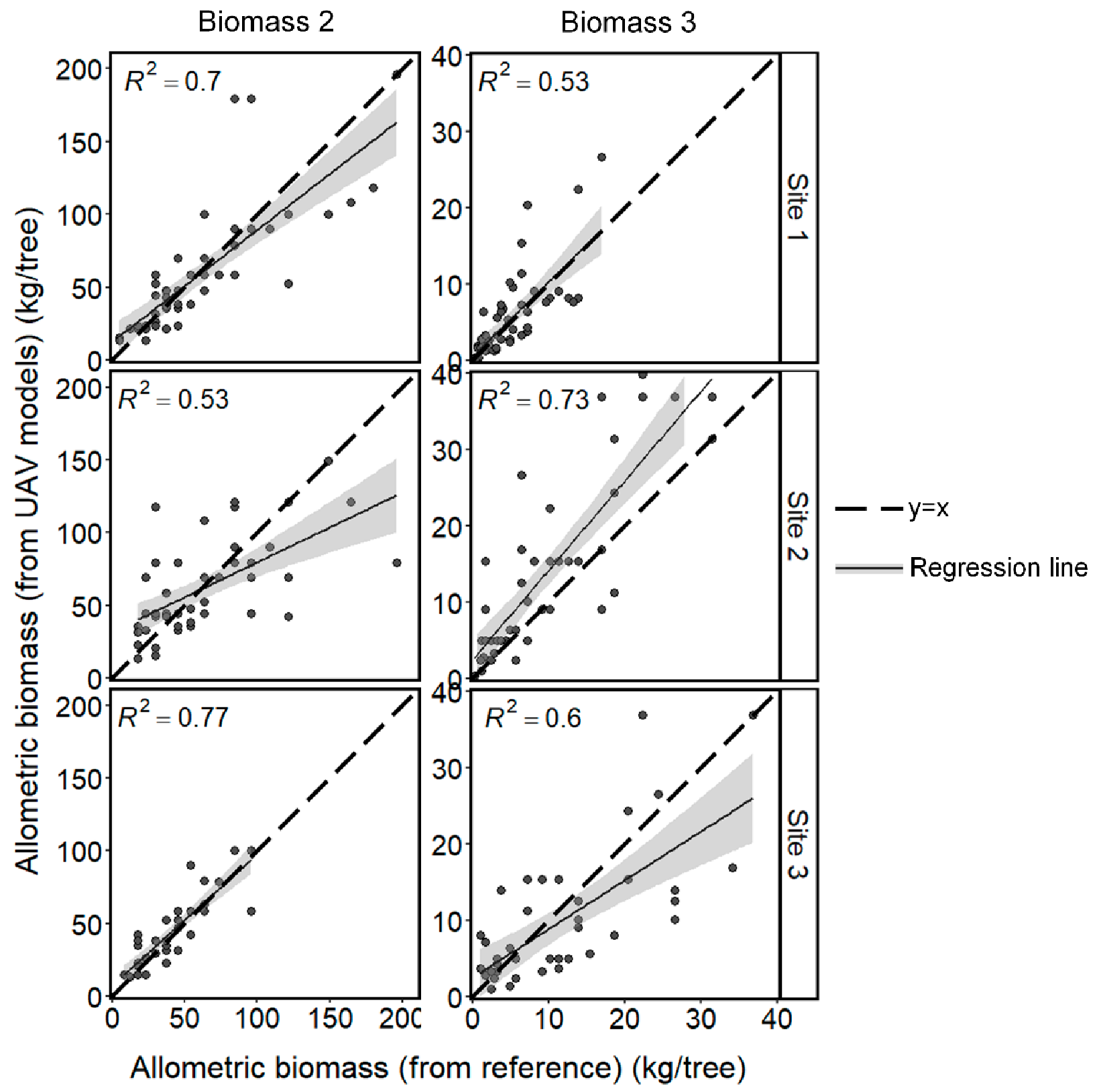
Remotesensing 13 04367 g0a4
Figure A4. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in high stands in Zone 1.
Figure A4. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in high stands in Zone 1.
Remotesensing 13 04367 g0a4

Appendix C

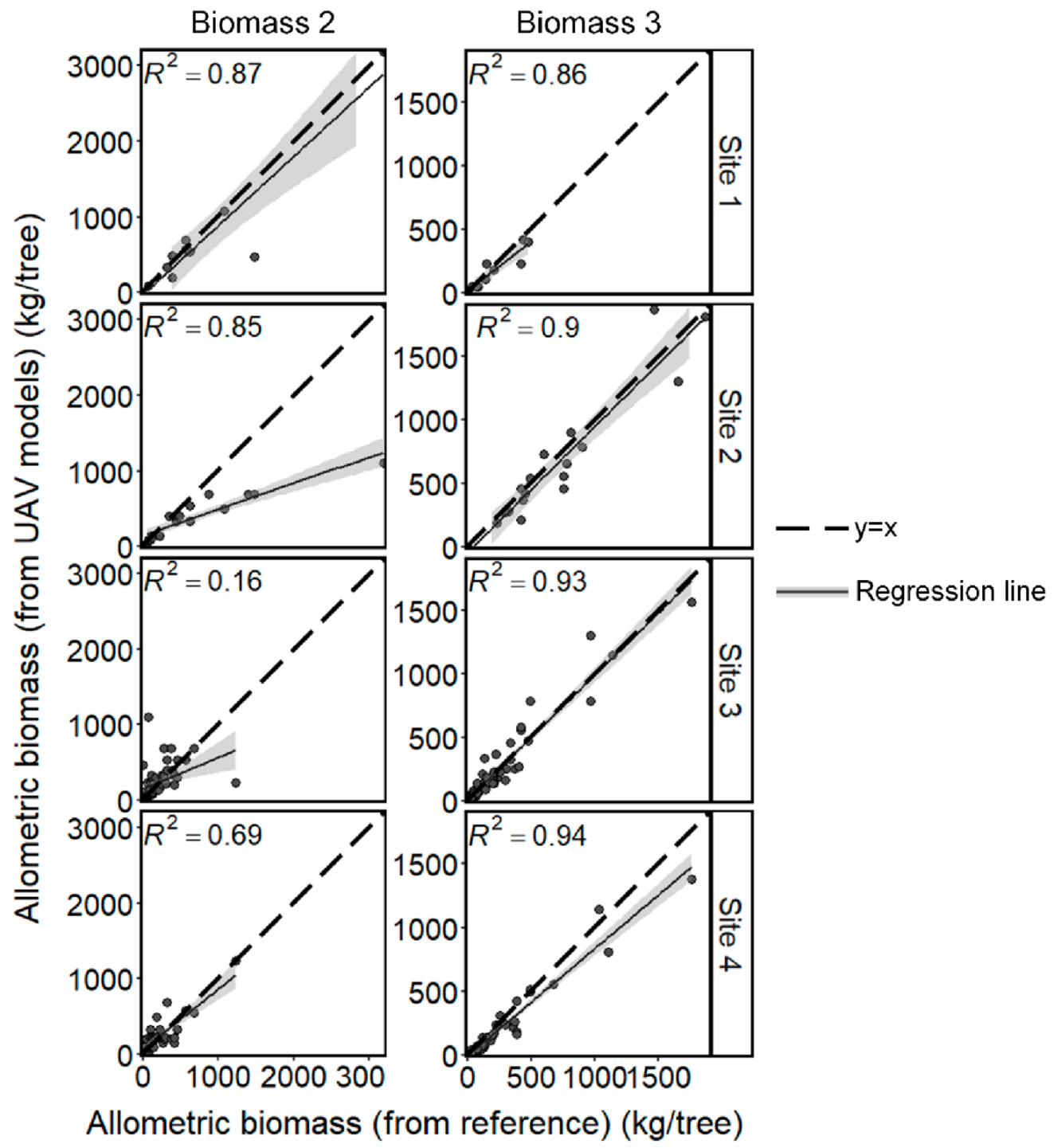
Remotesensing 13 04367 g0a5
Figure A5. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in high stands in Zone 2.
Figure A5. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in high stands in Zone 2.
Remotesensing 13 04367 g0a5
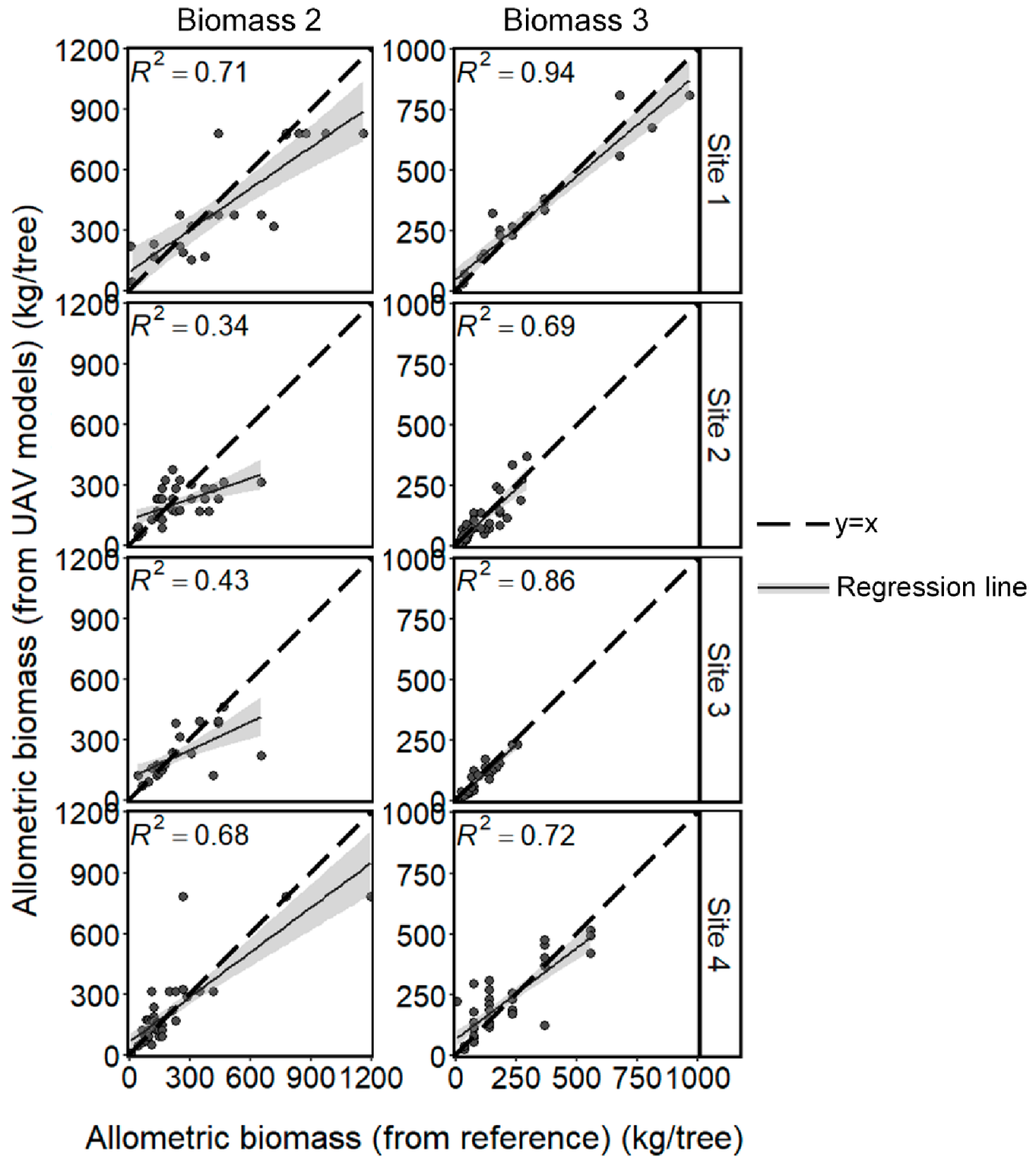
Remotesensing 13 04367 g0a6
Figure A6. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in high stands in Zone 3.
Figure A6. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in high stands in Zone 3.
Remotesensing 13 04367 g0a6
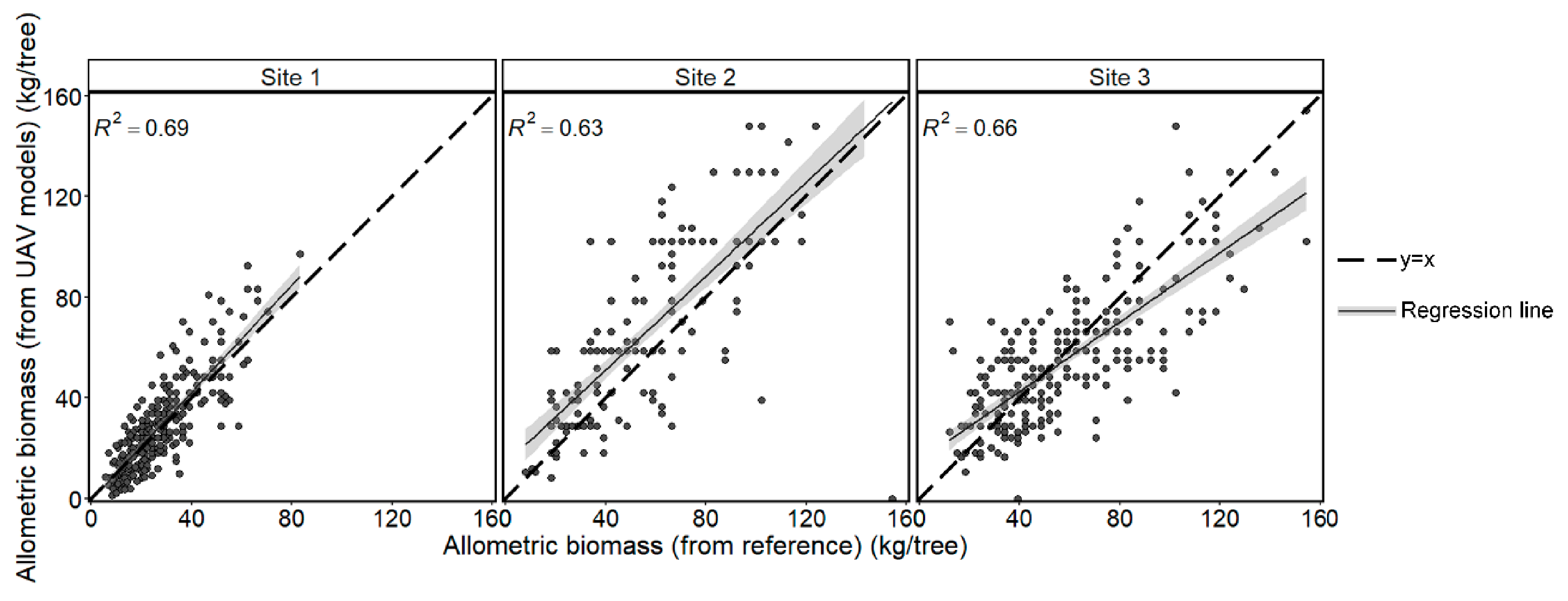
Remotesensing 13 04367 g0a7
Figure A7. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands in Zone 1.
Figure A7. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands in Zone 1.
Remotesensing 13 04367 g0a7
Remotesensing 13 04367 g0a8
Figure A8. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands in Zone 2.
Figure A8. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands in Zone 2.
Remotesensing 13 04367 g0a8
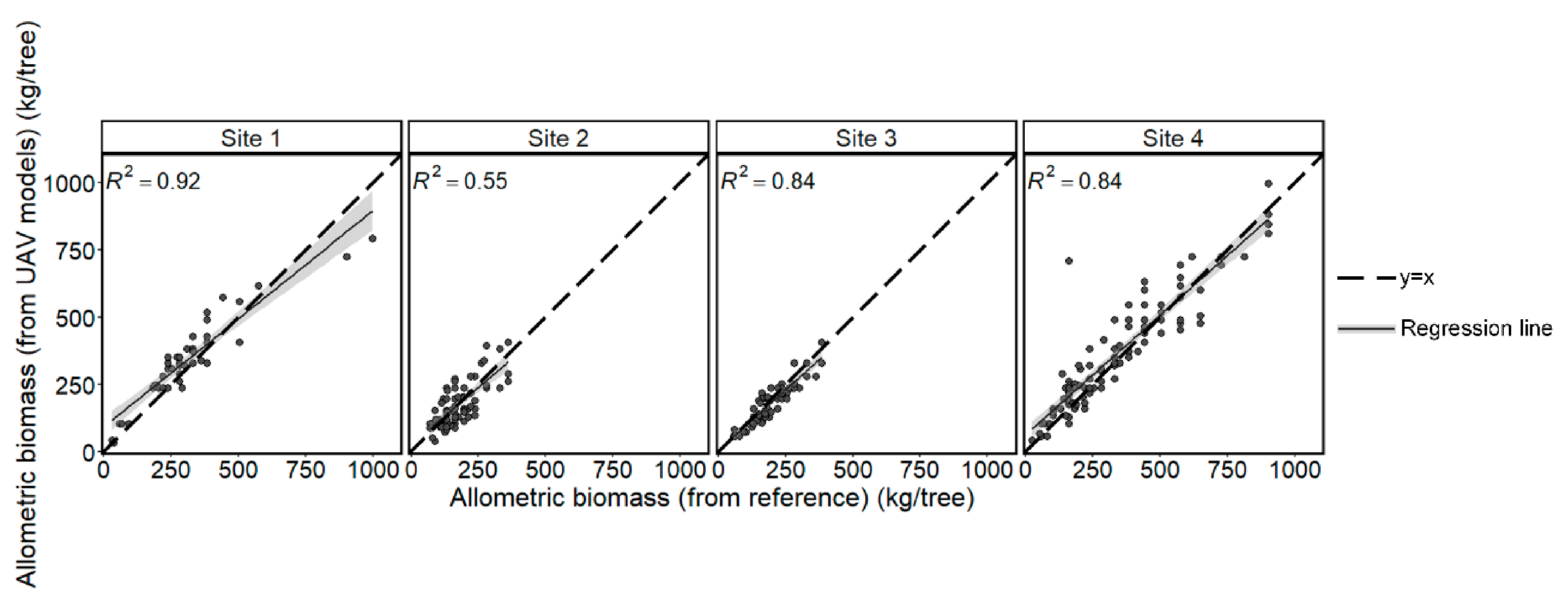
Remotesensing 13 04367 g0a9
Figure A9. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands in Zone 3.
Figure A9. Site-specific AGB values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands in Zone 3.
Remotesensing 13 04367 g0a9

Appendix D

Remotesensing 13 04367 g0a10
Figure A10. Site-specific relative RSME values of RFR models for AGB estimation in high stands.
Figure A10. Site-specific relative RSME values of RFR models for AGB estimation in high stands.
Remotesensing 13 04367 g0a10
Remotesensing 13 04367 g0a11
Figure A11. Site-specific relative RSME values of RFR models for AGB estimation in coppice stands.
Figure A11. Site-specific relative RSME values of RFR models for AGB estimation in coppice stands.
Remotesensing 13 04367 g0a11

References

  1. Quéré, C.L.; Andrew, R.M.; Canadell, J.G.; Sitch, S.; Korsbakken, J.I.; Peters, G.P.; Manning, A.C.; Boden, T.A.; Tans, P.P.; Houghton, R.A. Global Carbon Budget 2016. Earth Syst. Sci. Data 2016, 8, 605–649. [Google Scholar] [CrossRef]
  2. Kint, V.; Robert, D.W.; Noël, L. Evaluation of sampling methods for the estimation of structural indices in forest stands. Ecol. Model. 2004, 180, 461–476. [Google Scholar] [CrossRef]
  3. Nowak, D.J.; Crane, D.E.; Stevens, J.C.; Hoehn, R.E.; Walton, J.T.; Bond, J. A ground-based method of assessing urban forest structure and ecosystem services. Aboriculture Urban For. 2008, 34, 347–358. [Google Scholar]
  4. Jung, J.; Kim, S.; Hong, S.; Kim, K.; Kim, E.; Im, J.; Heo, J. Effects of national forest inventory plot location error on forest carbon stock estimation using k-nearest neighbor algorithm. ISPRS J. Photogramm. Remote Sens. 2013, 81, 82–92. [Google Scholar] [CrossRef]
  5. Iizuka, K.; Tateishi, R. Estimation of CO2 Sequestration by the forests in Japan by discriminating precise tree age category using remote sensing techniques. Remote Sens. 2015, 7, 15082–15113. [Google Scholar] [CrossRef]
  6. Rana, P.; Korhonen, L.; Gautam, B.; Tokola, T. Effect of field plot location on estimating tropical forest above-ground bi-omass in Nepal using airborne laser scanning data. ISPRS J. Photogramm. Remote Sens. 2014, 94, 55–62. [Google Scholar] [CrossRef]
  7. Garcia, M.; Saatchi, S.; Ustin, S.; Balzter, H. Modelling Forest canopy height by integrating airborne LiDAR samples with satellite Radar and multispectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 159–173. [Google Scholar] [CrossRef]
  8. Goodbody, T.R.; Coops, N.C.; Marshall, P.L.; Tompalski, P.; Crawford, P. Unmanned aerial systems for precision forest in-ventory purposes: A review and case study. For. Chron. 2017, 93, 71–81. [Google Scholar] [CrossRef]
  9. Ganz, S.; Käber, Y.; Adler, P. Measuring Tree height with remote sensing—A comparison of photogrammetric and lidar data with different field measurements. Forests 2019, 10, 694. [Google Scholar] [CrossRef]
  10. Phalla, T.; Ota, T.; Mizoue, N.; Kajisa, T.; Yoshida, S.; Vuthy, M.; Heng, S. The importance of tree height in estimating indi-vidual tree biomass while considering errors in measurements and allometric models. AGRIVITA J. Agric. Sci. 2017, 40, 131–140. [Google Scholar]
  11. Kebede, B.; Soromessa, T. Allometric equations for aboveground biomass estimation of Olea Europaea L. subsp. cuspidata in Mana Angetu Forest. Ecosyst. Health Sustain. 2018, 4, 1–12. [Google Scholar] [CrossRef]
  12. Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef]
  13. Andersen, H.-E.; Reutebuch, S.E.; McGaughey, R.J. A rigorous assessment of tree height measurements obtained using airborne lidar and conventional field methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
  14. Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
  15. Fieber, K.D.; Davenport, I.; Tanase, M.A.; Ferryman, J.M.; Gurney, R.J.; Becerra, V.M.; Walker, J.; Hacker, J.M. Validation of Canopy Height Profile methodology for small-footprint full-waveform airborne LiDAR data in a discontinuous canopy environment. ISPRS J. Photogramm. Remote Sens. 2015, 104, 144–157. [Google Scholar] [CrossRef]
  16. Nilsson, M. Estimation of tree heights and stand volume using an airborne lidar system. Remote Sens. Environ. 1996, 56, 1–7. [Google Scholar] [CrossRef]
  17. Naesset, E. Estimating Timber Volume of Forest Stands Using Airborne Laser Scanner Data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
  18. Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res. 1998, 28, 1016–1031. [Google Scholar] [CrossRef]
  19. Panagiotidis, D.; Abdollahnejad, A.; Surový, P.; Chiteculo, V. Determining tree height and crown diameter from high-resolution UAV imagery. Int. J. Remote Sens. 2017, 38, 2392–2410. [Google Scholar] [CrossRef]
  20. Falkowski, M.J.; Smith, A.; Hudak, A.T.; Gessler, P.E.; Vierling, L.A.; Crookston, N.L. Automated estimation of individual conifer tree height and crown diameter via two-dimensional spatial wavelet analysis of lidar data. Can. J. Remote Sens. 2006, 32, 153–161. [Google Scholar] [CrossRef]
  21. Camarretta, N.; Harrison, P.; Bailey, T.; Potts, B.; Lucieer, A.; Davidson, N.; Hunt, M. Monitoring Forest structure to guide adaptive management of forest restoration: A review of remote sensing approaches. New For. 2020, 51, 573–596. [Google Scholar] [CrossRef]
  22. Vauhkonen, J.; Maltamo, M.; McRoberts, R.E.; Næsset, E. Introduction to forestry applications of airborne laser scanning. Concepts Case Studies. Manag. For. Ecosyst. 2014, 27, 2014. [Google Scholar]
  23. Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An international comparison of individual tree detection and extraction using airborne laser scanning. Remote Sens. 2012, 4, 950–974. [Google Scholar] [CrossRef]
  24. Luo, H.; Chen, E.; Cheng, J.; Li, X. Forest height estimation methods using polarimetric SAR Interferometry. J. Remote Sens. 2010, 14, 806–821. [Google Scholar]
  25. Pohl, C.; Loong, C. In-Situ Data Collection for Oil Palm Tree Height Determination Using Synthetic Aperture Radar; IOP Publishing: Bistol, UK, 2016; Volume 34, p. 01 2027.
  26. Goodbody, T.R.; Coops, N.C.; White, J.C. Digital aerial photogrammetry for updating area-based forest inventories: A review of opportunities, challenges, and future directions. Curr. For. Rep. 2019, 5, 55–75. [Google Scholar] [CrossRef]
  27. Puliti, S.; Solberg, S.; Granhus, A. Use of UAV Photogrammetric data for estimation of biophysical properties in forest stands under regeneration. Remote Sens. 2019, 11, 233. [Google Scholar] [CrossRef]
  28. Krause, S.; Sanders, T.G.; Mund, J.-P.; Greve, K. UAV-based photogrammetric tree height measurement for intensive forest monitoring. Remote Sens. 2019, 11, 758. [Google Scholar] [CrossRef]
  29. Pádua, L.; Vanko, J.; Hruška, J.; Adão, T.; Sousa, J.J.; Peres, E.; Morais, R. UAS, sensors, and data processing in agroforestry: A review towards practical applications. Int. J. Remote Sens. 2017, 38, 2349–2391. [Google Scholar] [CrossRef]
  30. Gómez, C.; Alejandro, P.; Hermosilla, T.; Montes, F.; Pascual, C.; Ruiz, L.A.; Álvarez-Taboada, F.; Tanase, M.; Valbuena, R. Remote sensing for the Spanish forests in the 21st century: A review of advances, needs, and opportunities. For. Syst. 2019, 28, 1–33. [Google Scholar] [CrossRef]
  31. Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A Photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
  32. Zarco-Tejada, P.J.; Diaz-Varela, R.; Angileri, V.; Loudjani, P. Tree height quantification using very high resolution imagery acquired from an Unmanned Aerial Vehicle (UAV) and Automatic 3D photo-reconstruction methods. Eur. J. Agron. 2014, 55, 89–99. [Google Scholar] [CrossRef]
  33. Dandois, J.P.; Ellis, E.C. High Spatial Resolution Three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
  34. Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F. Terrestrial Laser Scanning in Forest Inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
  35. Liu, C.; Xing, Y.; Duanmu, J.; Tian, X. Evaluating different methods for estimating diameter at breast height from terrestrial laser scanning. Remote Sens. 2018, 10, 513. [Google Scholar] [CrossRef]
  36. US Department of Agriculture Forest Service (USDA FS). Forest Inventory and Analysis National Core Field Guide; Field Data Collection Procedures for Phase 2 Plots; USDA FS: Washington, DC, USA, 2017; Volume 1. [Google Scholar]
  37. Iizuka, K.; Yonehara, T.; Itoh, M.; Kosugi, Y. Estimating tree height and diameter at breast height (DBH) from digital sur-face models and orthophotos obtained with an unmanned aerial system for a Japanese cypress (Chamaecyparis Obtusa) Forest. Remote Sens. 2018, 10, 13. [Google Scholar] [CrossRef]
  38. Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in Forest Inventory Using Airborne Laser Scanning. Remote Sens. 2012, 4, 1190–1207. [Google Scholar] [CrossRef]
  39. Widyorini, R.; Kobayashi, S.; Kawai, S.; Omura, Y.; Sanga-Ngoie, K.; Supriadi, B. Backscattering characteristics of L-band polarimetric and optical satellite imagery over planted acacia forests in Sumatra, Indonesia. J. Appl. Remote Sens. 2012, 6, 063525. [Google Scholar] [CrossRef]
  40. Ota, T.; Ogawa, M.; Shimizu, K.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; Sano, T.; et al. Aboveground biomass estimation using structure from motion approach with aerial photographs in a seasonal tropical forest. Forests 2015, 6, 3882–3898. [Google Scholar] [CrossRef]
  41. Corte, A.P.D.; Rex, F.E.; De Almeida, D.R.A.; Sanquetta, C.R.; Silva, C.A.; Moura, M.M.; Wilkinson, B.; Zambrano, A.M.A.; Neto, E.M.D.C.; Veras, H.F.P.; et al. Measuring individual tree diameter and height using GatorEye High-Density UAV-Lidar in an Integrated Crop-Livestock-Forest System. Remote Sens. 2020, 12, 863. [Google Scholar] [CrossRef]
  42. Puliti, S.; Breidenbach, J.; Astrup, R. Estimation of Forest Growing Stock Volume with UAV Laser Scanning Data: Can It Be Done without Field Data? Remote Sens. 2020, 12, 1245. [Google Scholar] [CrossRef]
  43. Machimura, T.; Fujimoto, A.; Hayashi, K.; Takagi, H.; Sugita, S. A novel tree biomass estimation model applying the pipe model theory and adaptable to UAV-Derived Canopy Height Models. Forests 2021, 12, 258. [Google Scholar] [CrossRef]
  44. Jucker, T.; Caspersen, J.; Chave, J.; Antin, C.; Barbier, N.; Bongers, F.; Dalponte, M.; van Ewijk, K.Y.; Forrester, D.I.; Haeni, M. Allometric Equations for Integrating Remote Sensing Imagery into Forest Monitoring Programmes. Glob. Chang. Biol. 2017, 23, 177–190. [Google Scholar] [CrossRef]
  45. Zagalikis, G.; Cameron, A.D.; Miller, D.R. The application of digital photogrammetry and image analysis techniques to derive tree and stand characteristics. Can. J. For. Res. 2005, 35, 1224–1237. [Google Scholar] [CrossRef]
  46. Fraser, B.; Congalton, R. Estimating Primary Forest Attributes and Rare Community Characteristics Using Unmanned Aerial Systems (UAS): An Enrichment of Conventional Forest Inventories. Remote Sens. 2021, 13, 2971. [Google Scholar] [CrossRef]
  47. Chisholm, R.; Rodríguez-Ronderos, M.; Lin, F. Estimating Tree Diameters from an Autonomous Below-Canopy UAV with Mounted LiDAR. Remote Sens. 2021, 13, 2576. [Google Scholar] [CrossRef]
  48. Baker, T.R.; Phillips, O.L.; Malhi, Y.; Almeida, S.; Arroyo, L.; Di Fiore, A.; Erwin, T.; Killeen, T.J.; Laurance, S.G.; Laurance, W.F.; et al. Variation in wood density determines spatial patterns inAmazonian forest biomass. Glob. Chang. Biol. 2004, 10, 545–562. [Google Scholar] [CrossRef]
  49. Lewis, S.L.; Sonké, B.; Sunderland, T.; Begne, S.K.; Lopez-Gonzalez, G.; Van Der Heijden, G.M.; Phillips, O.L.; Affum-Baffoe, K.; Baker, T.R.; Banin, L. Above-Ground Biomass and Structure of 260 African Tropical Forests. Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20120295. [Google Scholar] [CrossRef]
  50. Brahma, B.; Nath, A.J.; Sileshi, G.W.; Das, A.K. Estimating biomass stocks and potential loss of biomass carbon through clear-felling of rubber plantations. Biomass Bioenergy 2018, 115, 88–96. [Google Scholar] [CrossRef]
  51. Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error propagation and scaling for tropical forest biomass estimates. Philos. Trans. R. Soc. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef]
  52. Pothong, T.; Elliott, S.; Chairuangsri, S.; Chanthorn, W.; Shannon, D.P.; Wangpakapattanawong, P. New Allometric Equations for Quantifying Tree Biomass and Carbon Sequestration in Seasonally Dry Secondary Forest in Northern Thailand. New Forests 2021, 1–20. [Google Scholar] [CrossRef]
  53. Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
  54. Vosselman, G. Slope based filtering of laser altimetry data. Int. Arch. Photogramm. Remote Sens. 2000, 33, 935–942. [Google Scholar]
  55. Sithole, G.; Vosselman, G. Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
  56. Bandara, K.R.; Samarakoon, L.; Shrestha, R.P.; Kamiya, Y. Automated generation of digital terrain model using point clouds of digital surface model in forest area. Remote Sens. 2011, 3, 845–858. [Google Scholar] [CrossRef]
  57. Mlambo, R.; Woodhouse, I.H.; Gerard, F.; Anderson, K. Structure from Motion (SfM) Photogrammetry with Drone Data: A low cost method for monitoring greenhouse gas emissions from Forests in Developing Countries. Forests 2017, 8, 68. [Google Scholar] [CrossRef]
  58. Nasiri, V.; Darvishsefat, A.A.; Arefi, H.; Pierrot-Deseilligny, M.; Namiranian, M.; Le Bris, A. Unmanned aerial vehicles (UAV)-based canopy height modeling under leaf-on and leaf-off conditions for determining tree height and crown diameter (case study: Hyrcanian mixed forest). Can. J. For. Res. 2021, 51, 962–971. [Google Scholar] [CrossRef]
  59. Jazirehi, M.; Ebrahimi Rostaghi, M. Silviculture in Zagros; University of Tehran: Tehran, Iran, 2003. [Google Scholar]
  60. Khalyani, A.H.; Falkowski, M.J.; Mayer, A.L. Classification of Landsat images based on spectral and topographic variables for land-cover change detection in Zagros forests. Int. J. Remote Sens. 2012, 33, 6956–6974. [Google Scholar] [CrossRef]
  61. Sajad, G.; Sefidi, K. Comparison of sustainable forest management (SFM) trends at global and country levels: Case study in Iran. J. For. Res. 2012, 23, 311–317. [Google Scholar] [CrossRef]
  62. Sagheb-Talebi, K.; Pourhashemi, M.; Sajedi, T. Forests of Iran: A Treasure from the Past, a Hope for the Future; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 94-007-7370-6. [Google Scholar]
  63. Avery, T.E.; Burkhart, H.E. Forest Measurements; Waveland Press: Long Grove, IL, USA, 2015; ISBN 1-4786-2974-6. [Google Scholar]
  64. Iranmanesh, Y. Assessment on Biomass Estimation Methods and Carbon Sequestration of Quercus brantii Lindl. Chaharmahal & Bakhtiari Forests. Ph.D. thesis, Tarbiat Modares University, Tehran, Iran, 2013; p. 107. [Google Scholar]
  65. Mahdavi, A.; Saidi, S.; Iranmanesh, Y.; Naderi, M. Biomass and Carbon Stocks in Three Types of Persian Oak (Quercus brantii var. persica) of Zagros Forests in a Semi-Arid Area, Iran. J. Arid. Land 2020, 12, 766–774. [Google Scholar]
  66. Nuijten, R.J.; Coops, N.C.; Goodbody, T.R.; Pelletier, G. Examining the Multi-Seasonal Consistency of Individual Tree Seg-mentation on Deciduous Stands Using Digital Aerial Photogrammetry (DAP) and Unmanned Aerial Systems (UAS). Remote Sens. 2019, 11, 739. [Google Scholar] [CrossRef]
  67. Meyer, F.; Beucher, S. Morphological Segmentation. J. Vis. Commun. Image Represent. 1990, 1, 21–46. [Google Scholar] [CrossRef]
  68. Gomes, M.F.; Maillard, P. Detection of Tree Crowns in Very High Spatial Resolution Images. Environ. Appl. Remote Sens. 2016, 41–71. [Google Scholar] [CrossRef]
  69. Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 2nd ed.; Publishing House of Electronics Industry: Beijing, China, 2002; p. 455. [Google Scholar]
  70. Amiri, N. Assessment of Marker-Controlled Watershed Segmentation Algorithm for Individual Tree Top Detection and Crown Delineation. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2014. [Google Scholar]
  71. Gonzalez-Benecke, C.A.; Gezan, S.A.; Samuelson, L.J.; Cropper, W.P.; LeDuc, D.J.; Martin, T.A. Estimating Pinus palustris tree diameter and stem volume from tree height, crown area and stand-level parameters. J. For. Res. 2014, 25, 43–52. [Google Scholar] [CrossRef]
  72. Blanchard, E.; Birnbaum, P.; Ibanez, T.; Boutreux, T.; Antin, C.; Ploton, P.; Vincent, G.; Pouteau, R.; Vandrot, H.; Hequet, V.; et al. Contrasted allometries between stem diameter, crown area, and tree height in five tropical biogeographic areas. Trees 2016, 30, 1953–1968. [Google Scholar] [CrossRef]
  73. Verma, N.K.; Lamb, D.W.; Reid, N.; Wilson, B. An Allometric Model for Estimating DBH of Isolated and Clustered Eucalyp-tus Trees from Measurements of Crown Projection Area. For. Ecol. Manag. 2014, 326, 125–132. [Google Scholar] [CrossRef]
  74. Aiken, L.S.; West, S.G.; Pitts, S.C.; Baraldi, A.N.; Wurpts, I.C. Multiple Linear Regression. In Handbook of Psychology, 2nd ed.; American Cancer Society: Washington, DC, USA, 2012; ISBN 978-1-118-13388-0. [Google Scholar] [CrossRef]
  75. Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
  76. Quinlan, J.R. C4.5: Programs for Machine Learning; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 0-08-050058-7. [Google Scholar]
  77. Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of Biomass in Wheat using Random Forest Regression Algorithm and Remote Sensing Data. Crop J. 2016, 4, 212–219. [Google Scholar]
  78. Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; Center for Bioinformatics and Molecular Biostatistics, University of California: San Francisco, CA, USA, 2004. [Google Scholar]
  79. Prasad, A.; Iverson, L.; Liaw, A.; Ecosystems, S.; Mar, N. Newer Tree Classification and Techniques: Forests Random Prediction Bagging for Ecological Regression. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
  80. Mitchell, T.M. Machine Learning; McGraw Hill: Burr Ridge, IL, USA, 1997; Volume 45, pp. 870–877. [Google Scholar]
  81. Arsalani, M.; Pourtahmasi, K.; Azizi, G.; Bräuning, A.; Mohammadi, H. Tree-ring based December–February precipitation reconstruction in the southern Zagros Mountains, Iran. Dendrochronologia 2018, 49, 45–56. [Google Scholar] [CrossRef]
  82. Boloorani, A.D.; Ranjbareslamloo, S.; Mirzaie, S.; Bahrami, H.A.; Mirzapour, F.; Tehrani, N.A. Spectral behavior of Persian oak under compound stress of water deficit and dust storm. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102082. [Google Scholar] [CrossRef]
  83. Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Madrigal, V.P.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
  84. Surový, P.; Kuželka, K. Acquisition of Forest Attributes for Decision Support at the Forest Enterprise Level Using Remote-Sensing Techniques—A Review. Forests 2019, 10, 273. [Google Scholar] [CrossRef]
  85. Xiang, T.-Z.; Xia, G.-S.; Zhang, L. Mini-Unmanned Aerial Vehicle-Based Remote Sensing: Techniques, applications, and prospects. IEEE Geosci. Remote Sens. Mag. 2019, 7, 29–63. [Google Scholar] [CrossRef]
  86. Dainelli, R.; Toscano, P.; Di Gennaro, S.F.; Matese, A. Recent advances in unmanned aerial vehicle forest remote sensing—A systematic review. Part I: A general framework. Forests 2021, 12, 327. [Google Scholar] [CrossRef]
  87. Fassnacht, F.E.; Mangold, D.; Schäfer, J.; Immitzer, M.; Kattenborn, T.; Koch, B.; Latifi, H. Estimating Stand density, biomass and tree species from very high resolution stereo-imagery–towards an all-in-one sensor for forestry applications? For. Int. J. For. Res. 2017, 90, 613–631. [Google Scholar] [CrossRef]
  88. Vorster, A.G.; Evangelista, P.H.; Stovall, A.E.L.; Ex, S. Variability and uncertainty in forest biomass estimates from the tree to landscape scale: The role of allometric equations. Carbon Balance Manag. 2020, 15, 1–20. [Google Scholar] [CrossRef]
  89. Bragg, D.C. An Improved Tree Height Measurement Technique Tested on Mature Southern Pines. South. J. Appl. For. 2008, 32, 38–43. [Google Scholar] [CrossRef]
  90. Goetz, S.; Dubayah, R. Advances in Remote Sensing Technology and Implications for Measuring and Monitoring Forest Car-bon Stocks and Change. Carbon Manag. 2011, 2, 231–244. [Google Scholar] [CrossRef]
  91. Larjavaara, M.; Muller-Landau, H.C. Measuring Tree Height: A Quantitative Comparison of Two Common Field Methods in a Moist Tropical Forest. Methods Ecol. Evol. 2013, 4, 793–801. [Google Scholar] [CrossRef]
  92. Sibona, E.; Vitali, A.; Meloni, F.; Caffo, L.; Dotta, A.; Lingua, E.; Motta, R.; Garbarino, M. Direct Measurement of Tree Height Provides Different Results on the Assessment of LiDAR Accuracy. Forests 2017, 8, 7. [Google Scholar] [CrossRef]
  93. Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Tech-niques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
  94. He, H.; Yan, Y.; Chen, T.; Cheng, P. Tree Height Estimation of Forest Plantation in Mountainous Terrain from Bare-Earth Points Using a DoG-Coupled Radial Basis Function Neural Network. Remote Sens. 2019, 11, 1271. [Google Scholar] [CrossRef]
  95. Huang, H.; He, S.; Chen, C. Leaf Abundance Affects Tree Height Estimation Derived from UAV Images. Forests 2019, 10, 931. [Google Scholar] [CrossRef]
  96. Aryal, R.R.; Latifi, H.; Heurich, M.; Hahn, M. Impact of Slope, Aspect, and Habitat-Type on LiDAR-Derived Digital Terrain Models in a near Natural, Heterogeneous Temperate Forest. PPFG J. Photogramm. Remote Sens. Geoinf. Sci. 2017, 85, 243–255. [Google Scholar] [CrossRef]
  97. Duan, Z.; Zhao, D.; Zeng, Y.; Zhao, Y.; Wu, B.; Zhu, J. Assessing and Correcting Topographic Effects on Forest Canopy Height Retrieval Using Airborne LiDAR Data. Sensors 2015, 15, 12133–12155. [Google Scholar] [CrossRef]
  98. Poley, L.G.; McDermid, G.J. A Systematic Review of the Factors Influencing the Estimation of Vegetation Aboveground Bi-omass Using Unmanned Aerial Systems. Remote Sens. 2020, 12, 1052. [Google Scholar] [CrossRef]
  99. Jones, A.R.; Segaran, R.R.; Clarke, K.D.; Waycott, M.; Goh, W.S.H.; Gillanders, B.M. Estimating Mangrove Tree Biomass and Carbon Content: A Comparison of Forest Inventory Techniques and Drone Imagery. Front. Mar. Sci. 2020, 6, 784. [Google Scholar] [CrossRef]
  100. Rabadán, M.Á.V.; Peña, J.S.; Adán, F.S. Estimation of Diameter and Height of Individual Trees for Pinus Sylvestris L. Based on the Individualising of Crowns Using Airborne LiDAR and the National Forestry Inventory Data. For. Syst. 2016, 25, 1. [Google Scholar]
  101. Ebrahimi, S.; Valipour, A.; Sohrabi, H.; Ghahramany, L. Modelling the Biomass of Lebanon Oak Sprouts and it’s response to thinning in Northern Zagros Forests (the Case of Baneh, Kurdistan Province). Iran. J. For. 2019, 10, 431–447. [Google Scholar]
  102. Zianis, D.; Mencuccini, M. On simplifying allometric analyses of forest biomass. For. Ecol. Manag. 2004, 187, 311–332. [Google Scholar] [CrossRef]
  103. Alinezhadi, S.; Basiri, R.; Tahmasebi, P.; Askari, U. Estimation of biomass of different parts of Persian oak (Quercus brantii Lindl.) through allometric equations (in Persian). In Proceedings of the 4th National Conference on Environment, Energy and Biodefense, Tehran, Iran, 27 December 2015. [Google Scholar]
  104. Peña, J.M.; de Castro, A.I.; Torres-Sánchez, J.; Andújar, D.; Martín, C.S.; Dorado, J.; Fernández-Quintanilla, C.; López-Granados, F. Estimating tree height and biomass of a poplar plantation with image-based UAV technology. AIMS Agric. Food 2018, 3, 313–323. [Google Scholar] [CrossRef]
  105. Lin, J.; Wang, M.; Ma, M.; Lin, Y. Aboveground Tree Biomass Estimation of Sparse Subalpine Coniferous Forest with UAV Oblique Photography. Remote Sens. 2018, 10, 1849. [Google Scholar] [CrossRef]
  106. Han, S.H.; Park, B.B. Comparison of Allometric Equation and Destructive Measurement of Carbon Storage of Naturally Re-generated Understory in a Pinus Rigida Plantation in South Korea. Forests 2020, 11, 425. [Google Scholar] [CrossRef]
Remotesensing 13 04367 g001
Figure 1. The study area includes 11 sites from the three northern (Zone 1), middle (Zone 2), and southern (Zone 3) regions of the Zagros Forests. Each site is represented by UAV orthophotos. The locations are in the UTM zone 38N coordinate system. According to the pie-chart, all sites comprise both high and coppice trees, while in Zone 1, the predominant form is coppice.
Figure 1. The study area includes 11 sites from the three northern (Zone 1), middle (Zone 2), and southern (Zone 3) regions of the Zagros Forests. Each site is represented by UAV orthophotos. The locations are in the UTM zone 38N coordinate system. According to the pie-chart, all sites comprise both high and coppice trees, while in Zone 1, the predominant form is coppice.
Remotesensing 13 04367 g001
Remotesensing 13 04367 g002
Figure 2. General workflow of the study.
Figure 2. General workflow of the study.
Remotesensing 13 04367 g002
Remotesensing 13 04367 g003
Figure 3. Flowchart of generating different AGB values.
Figure 3. Flowchart of generating different AGB values.
Remotesensing 13 04367 g003
Remotesensing 13 04367 g004
Figure 4. Comparison of H from CHM with actual measured values (reference values).
Figure 4. Comparison of H from CHM with actual measured values (reference values).
Remotesensing 13 04367 g004
Remotesensing 13 04367 g005
Figure 5. Comparison of DBH, estimated from the multivariate linear regression model with independent variables of height (H) and canopy area (A) in trees with high stand form.
Figure 5. Comparison of DBH, estimated from the multivariate linear regression model with independent variables of height (H) and canopy area (A) in trees with high stand form.
Remotesensing 13 04367 g005
Remotesensing 13 04367 g006
Figure 6. Biomass values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands (a–c) and high stands (d–i).
Figure 6. Biomass values obtained from allometric equations on variables measured by UAV (vertical axis) and reference values (horizontal axis) in coppice stands (a–c) and high stands (d–i).
Remotesensing 13 04367 g006
Remotesensing 13 04367 g007
Figure 7. Relative RSME values of RFR models for AGB estimation.
Figure 7. Relative RSME values of RFR models for AGB estimation.
Remotesensing 13 04367 g007
Table 1. Allometric equations for estimating biomass in Persian oak species.
Table 1. Allometric equations for estimating biomass in Persian oak species.
StandIndependent VariableEquation
HighAverage tree crown diameter (m)Y = 0.881x3.228
DBH (cm)Y = 0.615x1.865
Tree height (m)Y = 0.067x3.921
CoppiceAverage tree crown diameter (m)Y = 2.534x2.383
Tree height (m)Y = 1.868x2.487
Table 2. Summary of ground measured values.
Table 2. Summary of ground measured values.
ZoneSiteStandNumber of TreesSymbol MinimumMaximum MeanSTD
11Coppice295H (m)1.554.62.8280.58
D (m)1.19.553.91.43
High54H (m)1.44.12.8430.64
D (m)0.856.753.5491.67
DBH (cm)32411.024.68
2Coppice200H (m)1.863.7750.85
D (m)1.156.653.7871.05
High50H (m)1.463.3780.94
D (m)0.855.552.9021.2
DBH (cm)63112.145.05
3Coppice252H (m)2.16.23.8960.86
D (m)1.17.43.71.19
High40H (m)25.23.5380.85
D (m)0.63.752.0360.71
DBH (cm)4158.9252.97
21Coppice59H (m)3.211.17.4361.78
D (m)2.813.36.9331.92
High10H (m)3.29.67.081.96
D (m)3.9510.36.841.94
DBH (cm)139844.322.4
2Coppice12H (m)2.114.810.443.25
D (m)1.916.69.5043.37
High19H (m)3.21510.272.46
D (m)2.2516.69.6293.45
DBH (cm)129836.7921.8
3Coppice49H (m)3.2127.3882.23
D (m)2.49.66.3491.95
High62H (m)2.513.47.1952.12
D (m)211.85.4061.8
DBH (cm)25920.279.41
4Coppice26H (m)4.511.97.651.74
D (m)3.512.98.212.37
High39H (m)4.513.47.6972.01
D (m)3.712.957.6242.19
DBH (cm)25921.4910.9
31Coppice44H (m)3137.7662.14
D (m)1.614.56.3782.62
High23H (m)2.112.57.8352.86
D (m)0.75126.0243.18
DBH (cm)35732.6513.9
2Coppice75H (m)4.38.36.10.94
D (m)1.6510.754.7641.91
High36H (m)3.88.56.051.3
D (m)1.2594.2651.9
DBH (cm)94223.177.56
3Coppice63H (m)3.98.56.3221.04
D (m)1.5125.6572.02
High29H (m)38.26.1831.12
D (m)1115.5452.08
DBH (cm)104222.347.6
4Coppice107H (m)2.8127.6862.03
D (m)2.75145.9322.28
High48H (m)3106.9581.53
D (m)1.7593.7381.57
DBH (cm)45819.318.63
Table 3. RMSE value of H and DBH parameters, estimated from photogrammetric models.
Table 3. RMSE value of H and DBH parameters, estimated from photogrammetric models.
ParameterStandUAV VariablesBest RMSEUnit
HeightCoppiceCHM0.573m
High0.572
DBHHighCHM, Orthophoto2.620cm
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Fakhri, A.; Latifi, H. A Consumer Grade UAV-Based Framework to Estimate Structural Attributes of Coppice and High Oak Forest Stands in Semi-Arid Regions. Remote Sens. 2021, 13, 4367. https://doi.org/10.3390/rs13214367

AMA Style

Fakhri A, Latifi H. A Consumer Grade UAV-Based Framework to Estimate Structural Attributes of Coppice and High Oak Forest Stands in Semi-Arid Regions. Remote Sensing. 2021; 13(21):4367. https://doi.org/10.3390/rs13214367

Chicago/Turabian Style

Fakhri, Arvin, and Hooman Latifi. 2021. "A Consumer Grade UAV-Based Framework to Estimate Structural Attributes of Coppice and High Oak Forest Stands in Semi-Arid Regions" Remote Sensing 13, no. 21: 4367. https://doi.org/10.3390/rs13214367

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop