Abstract
Rising sea levels pose one of the greatest threats to coastal zones. However, sea-level changes near the coast, particularly absolute sea-level changes, have been less well monitored than those in the open ocean. In this study, we aim to investigate the potential of Global Navigation Satellite Systems Interferometric Reflectometry (GNSS-IR) to measure coastal absolute sea-level changes and tie on-land (coastal GNSS) and offshore (satellite altimetry) observations into the same framework. We choose three coastal GNSS stations, one each in regions of subsidence, uplift and stable vertical land motions, to derive both relative sea levels and sea surface heights (SSH) above the satellite altimetry reference ellipsoid from 2008 to 2020. Our results show that the accuracy of daily mean sea levels from GNSS-IR is <1.5 cm compared with co-located tide-gauge records, and amplitudes of annual cycle and linear trends estimated from GNSS-IR measurements and tide-gauge data agree within uncertainty. We also find that the de-seasoned and de-trended SSH time series from GNSS-IR and collocated satellite altimetry are highly correlated and the estimated annual amplitudes and linear trends statistically agree well, indicating that GNSS-IR has the potential to monitor coastal absolute sea-level changes and provide valuable information for coastal sea-level and climate studies.
1. Introduction
Rising seas due to global warming present a major threat to coastal zones [1,2,3,4]. It is increasingly important to monitor and quantify coastal sea-level rise, and thus to determine the potential impact of climate changes on coasts (e.g., from sea-level rise). However, coastal zones, where most human interactions with the ocean occur, remain an observational gap in our sea-level knowledge [5]. The two most commonly used systems for directly measuring sea levels are land-based tide gauges and satellite altimetry. Tide gauges have been providing valuable information about sea-level changes at the coast since 1831, when the first operational automatic tide gauge was installed [6], whereas satellite altimetry has been continuously monitoring open-ocean sea surface heights since 1992, when the first satellite mission specifically designed for sea-level studies was launched [7]. However, sea-level observations from these two observing systems suffer from several limitations.
Tide gauges measure changes in sea level relative to the land on which they are located; therefore, supplemental information on vertical land motion (VLM) is required to isolate sea-level signals associated with climate change in tide-gauge records [8,9]; there is no common reference level for individual tide-gauge records, making stacking records difficult [10]. Satellite altimetry measures absolute sea-level variations (i.e., sea-surface height) with respect to a reference ellipsoid; however, the measurements in coastal zones (a few kilometers from the coast) are not yet reliable due to contamination of altimetric waveforms with the land, or inadequate geophysical corrections [11]. Additional efforts are therefore needed to study sea-level trends in coastal zones using past and present satellite altimeters [12,13].
Over the past decade, a geodetic Global Navigation Satellite Systems (GNSS) station placed at the coast has been emerging as an alternative coastal sea-level observing system with several important advantages: (1) it can obtain both relative sea-level changes from the reflected satellite signals off the water surface through GNSS Interferometric Reflectometry (GNSS-IR) [14] and VLM from the direct satellite signals through precise point positioning [9], thus overcoming the limitations of tide gauges lacking VLM and the unreliable measurements from satellite altimetry in the coastal zones; (2) it senses changes of the sea surface in a swath extending some distance from the coast, which is substantially greater than a traditional tide gauge [15]. A distance of 0.5 km is possible with a GNSS antenna placed high enough, ~20 m above sea level. Therefore, GNSS-IR measurements have the potential to fill the sea-level observational gap in coastal zones, especially if they are specifically designed for such purposes; (3) GNSS-IR measures coastal sea level directly in a geocentric frame that is consistent with satellite altimetry and does not require in situ calibration unless equipment changes cause large offsets, hence, potentially linking the satellite altimeter measurements of sea-level rise with tide-gauge measurements by bridging the open-ocean measurements with those in close proximity to the coast.
GNSS-IR has been proven to be effective for detecting storm surges [16,17], tsunami [18], sea state [19] and astronomical tides [20,21,22]. However, all these previous studies focused on short-term, i.e., sub-daily sea-level variations. Considering the aforementioned advantages of GNSS-IR compared with tide gauges and satellite altimetry, we aim to address in this study the following questions: (1) Can GNSS-IR measure the seasonal cycle in sea level—one of the most important non-tidal components of sea-level records—and how well does it measure the seasonal cycle compared to co-located tide-gauge records? (2) Can coastal GNSS stations provide reliable geocentric sea-level changes to quantify long-term sea-level trends, one of the essential indicators of climate change? We investigate both relative sea-level changes from GNSS-IR and absolute sea-level changes from a combination of relative sea-level changes and VLM from the same GNSS equipment and compare them with co-located tide-gauge records and satellite altimeter measurements.
2. Data and Methods
2.1. Data
To study absolute rates of sea-level rise and seasonal sea-level changes at the locations of interest, we use a combination of three data sets: GNSS data, satellite altimeter measurements and tide-gauge records. For GNSS data, we selected three coastal geodetic stations with record lengths >7 years and differing types of vertical land motions in the United States of America (USA) and France. They are PBAY (uplifting) at Alaska, USA, SC02 (relatively stable) at Friday Harbor, Washington State, USA, and BRST (subsiding) at Brest in northwestern France. Geographic locations of the three sites are shown in Figure A1. We obtained 1-Hz GNSS data for the three sites with the longest possible record length from public GNSS archives. BRST is located in a very busy harbor, which is far from ideal for a method that requires coherent reflections from a water surface. PBAY, on the other hand, is located in a fairly remote bay. SC02 at Friday Harbor is set back from the water, which reduces the number of observations that can be used for reflectometry.
For tide-gauge records, we obtained the measurements at Seldovia (29 km from PBAY) and Friday Harbor (345 m from SC02) from the National Oceanic and Atmospheric Administration (NOAA); they have a sampling interval of 6 minutes. Hourly tide-gauge records at Brest (293 m from BRST) were provided by the University of Hawaii Sea Level Center. For satellite altimeter measurements, we obtained reprocessed multi-mission altimetric gridded sea-level anomaly (SLA) with daily temporal resolution and spatial sampling of 0.25 degree produced by the Copernicus Climate Change Service (C3S) from the Copernicus Marine Environment Monitoring Service (CMEMS). Various geophysical corrections including dynamic atmospheric corrections were applied to the merged gridded SLA products. It should be noted that the recent progress in reprocessing radar waveforms in coastal areas and the use of new altimetry techniques (e.g., Ka band altimetry and synthetic aperture radar mode) have enabled the satellite community to develop new coastal altimetry data sets that have better accuracy than gridded products near the coast. [23] demonstrated that the coastal amplitude of the annual cycle at the Baltic Sea–North Sea transition zone estimated from a dedicated re-tracked coastal altimetry solution is in better agreement with estimations derived from tide-gauge records than the one from the gridded sea-level products generated by the European Space Agency Sea Level Climate Change Initiative community. However, those coastal altimetry products are not readily available for most of the coasts including our study regions, and they need to be assessed regionally in terms of trends over multi-decadal timescales [10]. We therefore use the gridded satellite altimetry products for this study.
2.2. SSH from Satellite Altimetry and Coastal GNSS Stations
Figure 1 illustrates how a coastal GNSS station measures RSL and SSH above a reference ellipsoid. To be consistent with the satellite altimeter measurements, we converted the coastal GNSS sea-level measurement to the satellite altimetry reference ellipsoid (the T/P reference ellipsoid). SLA provided by the CMEMS is the anomaly of the signal around the mean sea surface (MSS) above the satellite altimetry reference ellipsoid. To calculate SSH above the ellipsoid (i.e., ), we obtained MSS with spatial sampling of 1 minute from Aviso+, and down-sampled the MSS to the grid points of SLA.
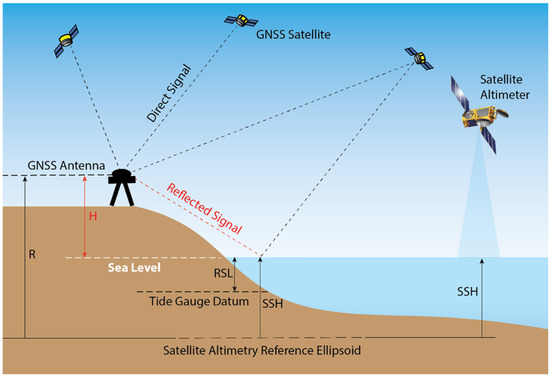
Figure 1.
Schematic of coastal land-based GNSS, tide gauges and satellite altimeter measurements. The land-based GNSS receiver records the phase of the electromagnetic wave of the GNSS signal, and this signal arrives both directly from the satellite and from reflections off the nearby water surface. Those two signals interfere with each other, creating a characteristic oscillating pattern overlain on a long-term trend in the SNR data. By analyzing the frequency of the SNR oscillation in low elevation angle data, we can estimate the vertical distance (H) from the water surface to the GNSS antenna phase center. Additionally, the precise position of the antenna reference point (R) can be obtained through the analysis of direct carrier phase signals. Combining results from the direct and the reflected signals, we then obtain sea surface height above the satellite altimetry reference ellipsoid (SSH = R- H) as long as the offset between the geodetic antenna reference point and the reflection phase center is known.
To obtain SSH from coastal GNSS stations, we need to first estimate their positions. We processed the Global Positioning System (GPS) data using the GipsyX/RTGx precise point positioning software version 1.2 from the Jet Propulsion Laboratory (JPL), and JPL final precise satellite orbits and clocks [24]. The processing strategy is similar to those used in [25] and [26], although they used GIPSY-OASIS, a predecessor of GipsyX/RTGx, for processing. The IGS14 absolute phase center model (igs14.atx) was applied to both satellite and receiver antennas [27]. The GipsyX results are the daily positions of the antenna reference point in the International Terrestrial Reference Frame 2014 (ITRF2014) [28]. We then converted the GipsyX results from ITRF2014 to the T/P reference ellipsoid coordinate system to obtain .
Secondly, we used the GPS signal-to-noise ratio (SNR) data at the L1 frequency to calculate H. Although in principle other frequencies can be used, their availability and quality have been highly variable in the past ten years. For the sake of consistency, here we focus on L1. To restrict the reflected satellite signals from the land, we applied azimuth and elevation angle masks to isolate signals reflected off the water surface where the GNSS stations were installed. For PBAY, we only used data with azimuth between 90° and 240°, and elevation angles between 12° and 25°. The masks applied to SC02 and BRST are ((100°, 200°), (5°, 15°)) and ((145°, 300°), (15°, 25°)), respectively. Additionally, the antenna height above the water surface is approximately 6.0 m at PBAY, 5.2 m at SC02, and 16.7 m at BRST, making the average zones of water surface that can be sensed by the GNSS antennas 40 m away from the coast at PBAY, 100 m at SC02, and 80 m at BRST. The sensing zones are shown in Figure A2. We corrected the biases caused by tropospheric delay and the height change over a satellite pass using standard models following the methods in [16]. In this study, we did not model phase center variations in the estimation of from SNR data. The reference point of is the mean phase center of the reflected signals, which is different from the antenna reference point which R is referenced to; hence, the resulting SSH (= R - H) includes a vertical offset between the antenna reference point and the mean phase center. However, if there is no change of equipment over the analysis period, this offset can be considered as a constant, therefore not hindering the estimation of seasonal cycle or linear trends. The number of observations depends on the location of the sites. On average, we obtained 39 observations per day for PBAY, 28 for SC02 and 24 for BRST. We note that these numbers can be increased substantially by using multi-GNSS and multi-frequency data. We also examined the potential impact of sea ice as for GNSS stations located in regions where there is annual sea ice variability, sea ice will contaminate GNSS-IR signals, resulting biases in long-term tidal constituents [22]. We found that the number of observations at PBAY in winter is not reduced compared with other seasons, suggesting that seawater in the vicinity of PBAY is not iced up in winter.
At daily and sub-daily time scales, astronomical tides are the major component to drive sea-level oscillations, but they are not the focus of this work. To be consistent with both the daily solutions of and the CMEMS SLA products, we therefore removed the tidal effects and subsequently averaged the residuals over 24 hours to obtain daily solutions of relative sea levels from GNSS-IR. It should be noted that a daily mean computed by simply averaging data over 24 hours is contaminated by the tidal signal. For conventional tide-gauge records, daily means are calculated from hourly records by using either a Demerliac filter or Doodson X0 filters [29]. The purpose of the filters is to remove tidal effects from the four main tidal constituents (, , and ) and low-pass filter the residuals with minimum computational effort. Since GNSS-IR observations are not evenly sampled in time as conventional tide-gauge records are, and computational cost is no longer an issue for post processing, we alternatively adopted harmonic analysis to first estimate the four main tidal constituents and then subtract the predicted tides based on the four main tidal constituents from to remove the tidal effects. We used the Utide software package to perform tidal harmonic analysis and tides prediction [30]. We tested our method of removing tides and calculating daily means by using tide-gauge records at PBAY and compared with the daily means calculated from the two filters. The root-mean-square (RMS) difference is around 1 mm, suggesting that our method of daily mean calculation is reliable.
2.3. Artificial Offset Caused by Change of GNSS Equipment
It is well known in the geodetic literature that changing any part of a geodetic GNSS instrument (receiver, antenna or radome) will almost always cause offsets in position time series [31,32,33]. After decades of research the geodetic community has developed methods for significantly reducing the size of these offsets. The best geodetic results use carefully measured phase center offsets and variations (e.g., IGS14.atx) [27]. That being said, residual errors almost always remain in the position time series, as is the case at one of our sites, BRST, for a change from one Leica antenna (LEIAT504GG) to one Trimble antenna (TRM57971.00). We find equipment changes could also cause offsets in the estimations of . We have removed this equipment-related bias using daily means of GNSS-IR relative sea-level measurements with those generated from the co-located hourly tide-gauge records. We further discuss the importance of antenna biases in the discussion section.
3. Results
3.1. Relative Sea-Level Changes from GNSS-IR and Tide Gauges
Both GNSS-IR and tide gauges measure sea levels relative to the land. It has been demonstrated that GNSS-IR measurements at daily and sub-daily time scales have a comparable accuracy to tide-gauge records [14,34]. In this study, we explore the potential application of GNSS-IR in detecting seasonal cycle and long-term trends of sea-level changes.
For consistency, we used the same approach as was mentioned in Section 2.2 to calculate daily means of sea level from the GNSS-IR measurements and tide-gauge records. Additionally, we filtered out high-frequency signals with periods <2 months by applying a 59-day moving average to daily means of both GNSS-IR and tide-gauge measurements. GNSS-IR measurements are anticorrelated with sea-level heights measured by a conventional tide gauge, and tide-gauge records are referenced to a local datum, which is different from that of GNSS-IR measurements. A mean is therefore removed, meaning that sea levels for both systems are referenced to an arbitrary datum.
Figure 2 shows the smoothed daily means of GNSS-IR measurements superimposed with daily means of nearby tide-gauge records. Taking tide-gauge records as the reference, no systematic biases are found, and the root-mean-square error (RMSE) of daily means of GNSS-IR measurements is 2.9 cm, 2.0 cm, and 3.4 cm for PBAY, SC02, and BRST, respectively. After applying the filter of 59-day moving average, the RMSEs for PBAY, SC02 and BRST are 1.4 cm, 0.9 cm and 1.5 cm.
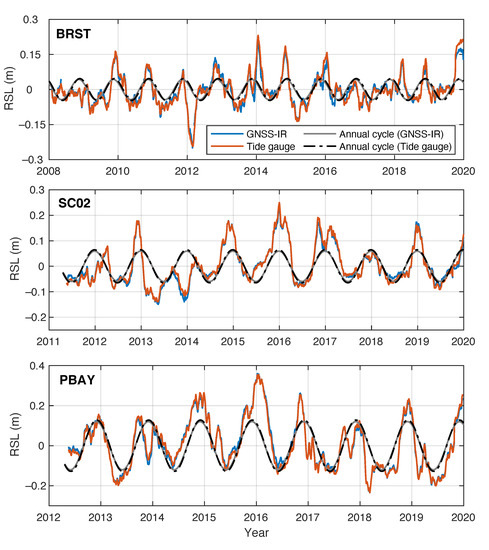
Figure 2.
Time series of smoothed relative sea levels from GNSS-IR and tide gauge, and the corresponding fitted annual cycle, showing close agreement between measurements from the two observing systems.
To estimate the seasonal cycle and linear trend, we employ a common least squares approach to fit the data with a model including annual and semiannual harmonics, a rate and an offset in the following form:
where is the smoothed relative sea level at epoch . and are the amplitudes of annual and semi-annual cycles, and are the phases of annual and semi-annual cycles in days, with zero phase corresponding to 1 January. is the linear trend. is an offset. Given that tide gauge and GNSS-IR observations are independent from epoch-to-epoch, we assumed white noise for error estimations.
For our three sites, annual sea-level changes are the dominant seasonal signal, and their amplitudes measured by tide gauges are comparable to, but slightly larger than, those from GNSS-IR measurements (see Table 1), which is consistent with the findings from [35], showing that annual amplitudes measured by tide gauges are larger than those in the nearby shallow ocean. The differences between annual phases in tide-gauge and GNSS-IR measurements are less than one month, reflecting the overall agreement between the two observing systems at seasonal timescales. Table 1 also shows that linear trends of RSL calculated from GNSS-IR measurements and tide-gauge records are in good agreement within uncertainty, and correlation coefficients of de-seasoned and de-trended time series of GNSS-IR measurements and tide-gauge records (Figure A3) are 0.99, 0.99 and 0.97 for PBAY, SC02 and BRST, respectively. This indicates that GNSS-IR can detect the seasonal cycle of sea-level changes and the associated long-term trends in coastal zones with a comparable accuracy as tide gauges.

Table 1.
Comparison of estimations of annual amplitudes, annual phases and linear trends from GNSS-IR and tide gauges. Uncertainties indicate a 1-sigma standard deviation.
3.2. Absolute Sea-Level Changes from GNSS-IR and Satellite Altimetry
Sea-level changes result from a combination of different influencing factors, including atmospheric effects, vertical land movements and oceanic processes. Atmospheric effects on measured sea surface height are the response of sea surface to atmospheric wind and pressure forcing, and can reach about 15 cm [36]. To be consistent with SSH obtained from CMEMS, we removed such effects in the daily mean sea levels produced from GNSS-IR by using the dynamic atmospheric correction (DAC) products that CMEMS used to generate SSH products. The DAC accounts for variations in sea surface height due to a low-frequency inverse barometer response and high-frequency wind and pressure effects [37]. We obtained the DAC products with a temporal resolution of six hours and spatial sampling of 0.25 degree from Aviso+. We averaged the 6-hourly DAC solutions to obtain daily DAC. For a particular site, we used DAC extracted from the nearest grid point to the site.
Over the selected period, the vertical position of SC02 is fairly stable, with an estimated rate of vertical land movement −0.1 0.03 mm/yr. However, PBAY is uplifting at an estimated rate of 12.7 0.05 mm/yr due to the combined elastic and viscoelastic response of the Earth to the mass loss of glaciers and icefields [38], while BRST is subsiding at an estimated rate of −1.2 0.02 mm/yr resulting from the land reclamation to create and develop the surrounding harbors [39]. For consistency, these uncertainties were calculated using the same technique as for GNSS-IR and tide-gauge uncertainties but are comparable with those assuming colored noise.
To isolate sea surface height from oceanic causes and to be consistent with the measurements from satellite altimetry, both atmospheric effects and vertical land movements in the sea-level measurements from coastal GNSS need to be corrected. Figure 3 shows the time series of GPS vertical displacements, DAC, RSL, RSL with DAC removed and absolute sea level (ASL) at PBAY. Both DAC and vertical land movements at PBAY exhibit seasonality, and the corresponding annual amplitudes are 5.3 cm and 0.4 cm. After removing DAC, the estimated amplitude of annual cycle from GNSS-IR decreases from 12.0 cm to 7.1 cm, while estimated slope increases from −10.7 mm/yr to −8.9 mm/yr. Further removing vertical land movements, estimated annual amplitude increases to 7.6 cm, and sea level is rising at an estimated rate of 3.1 mm/yr. It should be noted that the computed sea level trends may change with a different time window of the data because of the multi-decadal oscillations: a robust trend estimation requires 60 to 70 years of data [40]. Results for the other two stations are shown in Figure A4 and Figure A5.
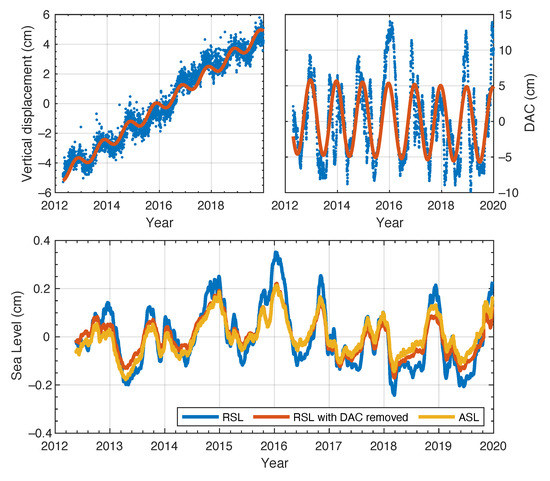
Figure 3.
Top left panel: vertical displacements from GPS (blue dots) and the fit of vertical displacements (red line); top right panel: DAC time series at the nearest grid point of PBAY (blue dots) and the fit of DAC (red line); bottom panel: relative sea levels from GNSS-IR with and without DAC removed, and absolute sea levels referenced to satellite altimetry reference ellipsoid at PBAY.
In order to compare with satellite altimetry, we choose three types of satellite altimeter data that are commonly used in studies related to coastal vertical land movements and coastal absolute sea-level changes: (1) the nearest grid point [41]; (2) the grid point from which the de-seasoned and de-trended sea levels at a distance of less than 100 km from the GNSS station has the highest correlation coefficient with that from the coastal GNSS [42]; (3) the spatial average of sea levels from the grid points within 100 km from the GNSS station [39]. Since an offset was introduced to the SSH from coastal GNSS observations and our focus is absolute sea level change, we do not directly compare SSH from the two observing systems; we instead compare the estimated annual amplitudes and phases, and linear trends.
Figure 4 shows the spatial variability of amplitudes, and linear trends from satellite altimetry near PBAY. The amplitudes of grid points within 100 km from PBAY range from 5 cm to 9 cm, and the corresponding correlation coefficients vary between 0.70 and 0.93 (Figure A6). Both the annual amplitudes of the nearest grid point and the one with the highest correlation coefficient agree well with that from coastal GNSS observations. However, the linear trend from the grid point with the highest correlation coefficient is in better agreement with that from coastal GNSS measurements. Additionally, due to the presence of considerable spatial variability in the annual cycle and linear trend in this region, spatial average is not a suitable approach for comparison. The annual amplitudes and phases, and linear trends estimated from SSH time series from coastal GNSS and the grid point of satellite altimetry with the highest correlation coefficient, are summarized in Table 2. It shows that annual amplitudes and linear trends agree within uncertainty, and the difference of annual phases at PBAY are around 12 days, consistent with the results of [35], who used satellite altimeter and tide-gauge data to demonstrate that differences of 1–2 months in annual phase for coastal, shallow and deep ocean are typical.
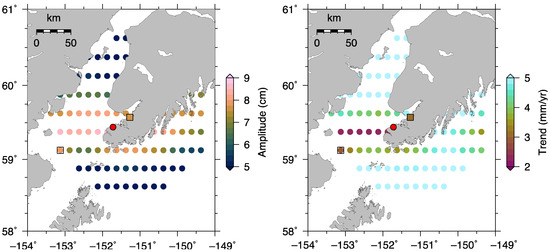
Figure 4.
Annual amplitudes (left panel) and linear trends (right panel) estimated from the satellite altimeter data within 100 km from PBAY. The filled square represents the GNSS station while the filled red circle is the tide gauge. The colored dot with a black square is the grid point from which the de-seasoned and de-trended satellite altimeter data has the highest correlation coefficient with those from the coastal GNSS.

Table 2.
Annual amplitudes and phases, and linear trends estimated from coastal GNSS and satellite altimeter SSH time series, Uncertainties indicate a 1-sigma standard deviation.
SC02 is located within the San Juan islands where the accuracy of satellite altimetry products in this region likely decreases significantly due to land contamination. Our results show that the annual amplitudes and linear trends estimated from satellite altimeter data within 100 km from SC02 are generally smaller than those from coastal GNSS observations and the nearby open ocean (Figure 5). If we broaden the search area to 200 km, we find that both annual amplitude and phase, and linear trend derived from the grid point with highest correlation coefficient (0.90, Figure A7) are in good agreement with those estimated from coastal GNSS (Table 2).
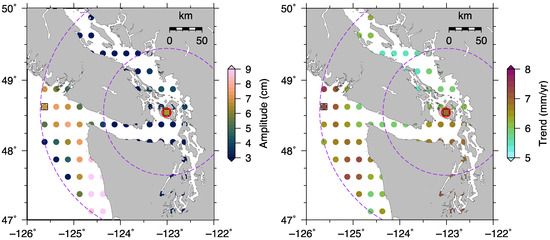
Figure 5.
Annual amplitudes (left panel) and linear trends (right panel) estimated from the satellite altimeter data within 200 km from SC02. The purple dash lines are circles with radius of 100 km and 200 km from SC02.The filled square represents the GNSS station, and the open black circle is the tide gauge. The colored dot with a black square is the grid point from which the de-seasoned and de-trended satellite altimeter data has the highest correlation coefficient with those from the coastal GNSS.
Ref. [39] demonstrated that sea-level time series from satellite altimetry near BRST are spatially coherent; they therefore concluded that there is no significant land contamination and used a spatial average for an area of 1-degree radius around the tide gauge location as absolute sea level and combined it with vertical land motions from Interferometric Synthetic Aperture Radar (InSAR) to estimate relative sea-level changes along the coast. Our results also show that annual amplitudes estimated from the nearest grid point, the grid point with highest correlation coefficient (Figure A8) and the spatial average are similar. However, they are all larger than that estimated from the SSH time series derived from coastal GNSS (Figure 6). One possible reason could be errors in the DAC that was applied to remove dynamic atmospheric effects in the coastal GNSS measurements. Although it is acknowledged that the DAC provides a significant overall improvement to satellite altimetry products, [37] observed that significant errors in the correction remain due to a lack of resolution of the model (in shelf areas but also in some deep ocean regions), remaining bathymetry errors and atmospheric forcing field uncertainties. Changes of equipment at BRST not only caused offsets in reflector heights (Figure A9), but also in vertical displacements (Figure A10). Additionally, besides the vertical component of antenna electrical phase center offset, there may be horizontal offsets; therefore, the offset in the reflector heights calculated by comparison with co-located tide-gauge records is not applicable to SSH. We first removed offsets in the vertical displacements; secondly, we calculated offset caused by change of antenna on October 26, 2011, by comparing with SSH from the spatial average of sea-level time series within 100 km from BRST. After those offsets were corrected, linear trends estimated from coastal GNSS measurements and satellite altimeter data agree well statistically (Table 2).
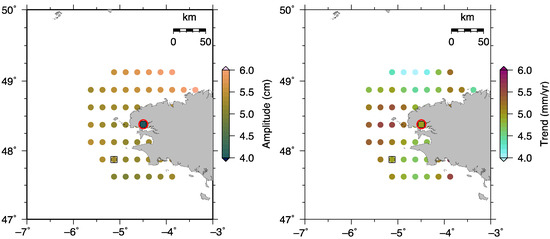
Figure 6.
Annual amplitudes (left panel) and linear trends (right panel) estimated from the satellite altimeter data within 100 km from BRST. The filled square represents the GNSS station, and the open black circle is the tide gauge. The colored dot with a black square is the grid point from which the de-seasoned and de-trended satellite altimeter data has the highest correlation coefficient with those from the coastal GNSS.
4. Discussion
Vertical land motions are a key element in understanding how sea levels have changed and how future sea level may impact coastal areas. Sources to quantify this effect include direct observing systems (e.g., GNSS and InSAR) and indirect approaches. One of the widely used indirect approaches is to combine tide-gauge records and satellite altimetry to calculate the rates of VLM [41]. The disadvantage of this approach is that the difference between satellite altimetry and the tide-gauge records can reveal drifts in the altimeter-derived SSH or in its geophysical corrections. An important assumption is that these are negligible, so that the trend in the differences can be attributed to VLM. Additionally, given the fact that the performance of satellite altimetry near the coast decreases significantly, a certain number of studies instead used a direct observing system—i.e., GNSS—to correct vertical land motions in the tide-gauge records to obtain absolute sea level at the coast [43]. However, there are also disadvantages of this method, including (1) requirement of two sets of equipment; (2) record lengths of the two types of measurements are usually different, with GNSS record lengths much shorter than that of tide gauges; (3) GNSS and tide gauge are generally not co-located and the vertical land movements at the two locations often behave differently (even over short distances if the monument bases are different); and (4) an assumption that VLM manifests in a linear fashion over the period of interest.
To compare with the results estimated from coastal GNSS-IR, we also used GNSS observations to correct VLM in the tide-gauge records near the three selected sites. Here we assume that the measured GNSS land motion is appropriate for the tide gauges, though in no case are they truly collocated. For example, while they are <300 meters apart, the GNSS site at Friday Harbor (SC02) is drilled into bedrock while the tide gauge is on a dock. We first removed dynamic atmospheric effects from the tide-gauge data, and the corresponding linear trends are −8.9 ± 0.5 mm/yr at Seldovia (near PBAY), 7.2 ± 0.4 mm/yr at Friday Harbor (near SC02) and 4.5 ± 0.1 mmm/yr at Brest (near BRST). Further correcting VLM, the estimated linear trends of absolute sea-level changes at Seldovia, Friday Harbor and Brest are 3.4 ± 0.5 mm/yr, 7.1 ± 0.4 mm/yr and 3.3 mm/yr ± 0.1, respectively. Comparing with linear trends derived from GNSS-IR and satellite altimetry in Table 2, the largest difference is found at Brest. There are two possible reasons for this difference. One is that the DAC applied to tide-gauge data might be inaccurate; and the other is that two linear trend periods can be distinguished in the time series of vertical displacements at BRST (Figure A10) over the period of 2008–2020: (1) 2008 – 2012, over which the subsidence rate is estimated at −0.4 ± 0.09 mm/yr and (2) 2013 – 2020, –1.4 ± 0.03 mm/yr, breaking the assumption that VLM behaves linearly at a rate of –1.2 mm/yr over 2008–2020.
Here, we used a consistent dataset (L1 GPS SNR) for 8+ years at three sites. As noted previously, this uniformity was broken at BRST when an antenna change caused a bias in the estimates. When the vertical phase center offset from the IGS14.atx document was used, the bias was reduced but not eliminated. This is consistent with what has been shown in previous studies [44,45]. Although not shown here, there are also frequency dependent biases, with L2 generally showing better agreement with tide gauge leveling measurements than L1. Some of this frequency variation can be predicted by using a simulator [46], but those simulators require gain pattern information that is simply unavailable for the GNSS antennae being used for coastal studies. While the GNSS antenna and frequency-dependent biases can be estimated and removed, for GNSS-IR to provide a true measurement of sea level in ITRF, it is important the GNSS-IR community fully document best practices for achieving it.
5. Conclusions
Observing sea-level changes at the coast and quantifying its drivers is the first step to understanding the complex dynamics of the coastal region, to link the response of the coastal environment to sea-level changes and to anticipate how projected sea-level variations will impact the coastal areas. In this study, we demonstrate that coastal GNSS can complement tide gauges and satellite altimetry to measure both relative and absolute sea-level changes at the coast at seasonal and longer timescales with several important advantages. However, some technical issues of GNSS-IR remain a challenge, including antenna and frequency biases. Although such biases do not affect studies about relative sea-level changes, if left uncorrected, they will cause an offset in SSH estimates. Offsets in reflector heights caused by changes of equipment have less of an impact on estimations of tides and seasonal cycles, but they will bias linear trends derived from both relative sea level and absolute sea levels. Efforts are needed to address those issues to further improve the performance of GNSS-IR.
Recent results from new altimetry re-processing algorithms indicate that coastal satellite altimetry products can now be as close as 0.9 km to the coast in Australia, Southeast Asia and Mediterranean Sea [47]. Coastal GNSS stations with an antenna height of ~60 m with respect to the water surface can sense sea-level changes up to ~1 km away from the coast. GNSS-IR may therefore play a key role in filling the observational gap in the coastal zones.
Author Contributions
Conceptualization, D.P.; formal analysis, D.P. and L.F.; writing—original draft preparation, D.P.; writing—review and editing, K.M.L., L.F. and E.M.H.; supervision, K.M.L. and E.M.H.; project administration, E.M.H.; funding acquisition, E.M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Singapore Ministry of Education Academic Research Fund Tier 3 (MOE 2019-T3-1-004), and by the National Research Foundation Singapore under its NRF Investigatorship scheme (National Research Investigatorship Award No. NRF-NRFI05-2019-0009), the Earth Observatory of Singapore (EOS), the National Research Foundation of Singapore and the Singapore Ministry of Education under the Research Centers of Excellence initiative.
Data Availability Statement
Tide-gauge records are publicly available here: https://tidesandcurrents.noaa.gov/ and https://uhslc.soest.hawaii.edu/ (accessed on 31 August 2021). GNSS data are freely available here: ftp://gps.alaska.edu/, https://www.unavco.org/ and https://earthdata.nasa.gov/ (accessed on 31 August 2021). DAC products and MSS are freely available here: https://www.aviso.altimetry.fr/en/home.html (accessed on 31 August 2021). Satellite altimetry data are freely available here: https://marine.copernicus.eu/ (accessed on 31 August 2021).
Acknowledgments
We thank the reviewers and editors for their valuable comments which helped to improve the manuscript. This is EOS paper number 406.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Figure A1.
Geographic locations of the three GNSS sites we selected for this study.

Figure A2.
Locations of the three GNSS stations PBAY, SC02 and BRST (yellow dots), and the corresponding reflection areas (white ellipses), which were approximated by the first Fresnel zone for a reflector height of 6 m for PBAY, 5 m for SC02 and 16 m for BRST. The white ellipses for each satellite track are the sensing zones for GPS observations for elevation angles 12° (longest ellipse), 20° (second ellipse) and 25° (shortest ellipse) for PBAY, for elevation angles 5° (longest ellipse), 10° (second ellipse), and 15° (shortest ellipse) for SC02, and for elevation angles 15° (longest ellipse), 20° (second ellipse), and 15° (shortest ellipse) for BRST. We made the figures using Google Earth. PBAY was equipped with TRM57971.00 antenna and SCIT radome without equipment change from 2012 to 2020. SC02 was equipped with TRM29659.00 antenna and SCIT radome from 2011 to 29 April 2015, and afterward changed to TRM59800.80. BRST was initially equipped with LEIAT504GG antenna, and changed to LEIAT504GG antenna on 11 June 2008, and TRM57971.00 antenna on 16 October 2011.
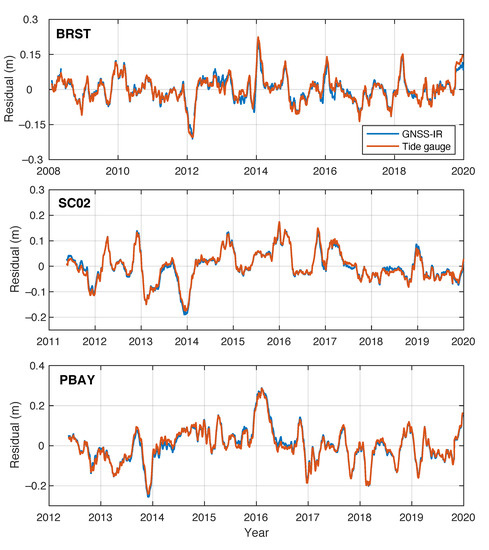
Figure A3.
De-seasoned and de-trended time series of relative sea levels from GNSS-IR and tide gauges.
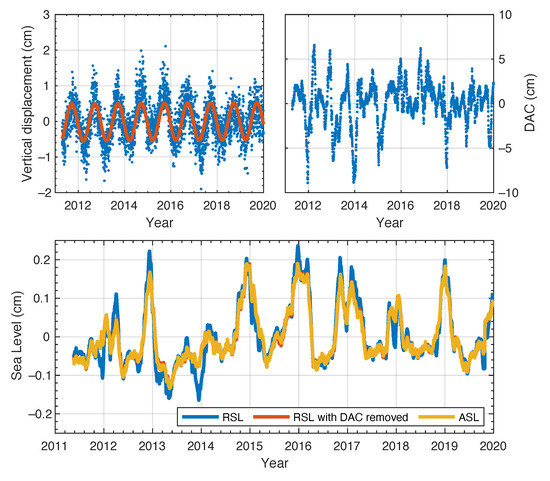
Figure A4.
Same as Figure 5, but for SC02.
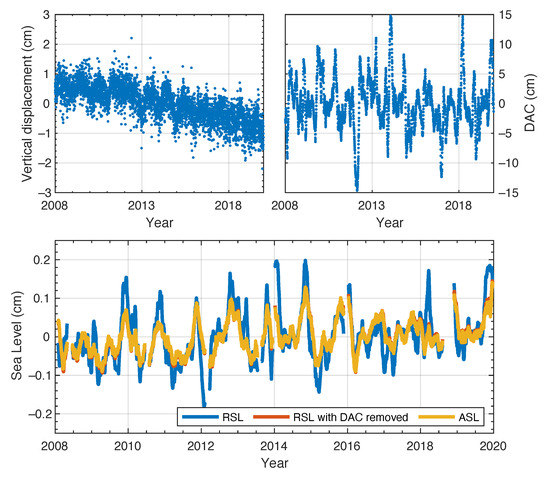
Figure A5.
Same as Figure 5 but for BRST.
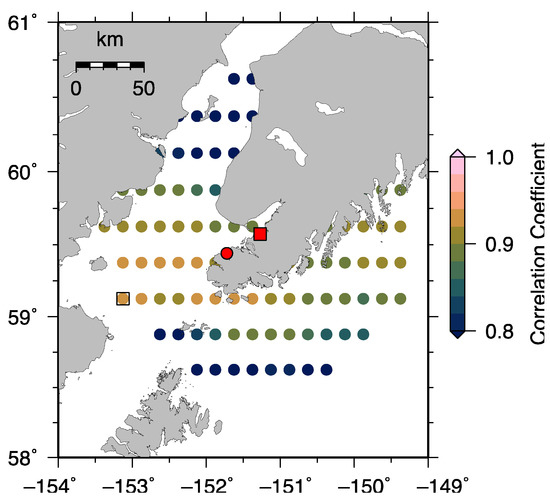
Figure A6.
Correlation coefficient at PBAY. The filled red circle represents the tide gauge while the filled red square is the GNSS station. The colored dot with a black square is the grid point from which the de-seasoned and de-trended satellite altimeter data has the highest correlation coefficient with those from the coastal GNSS.
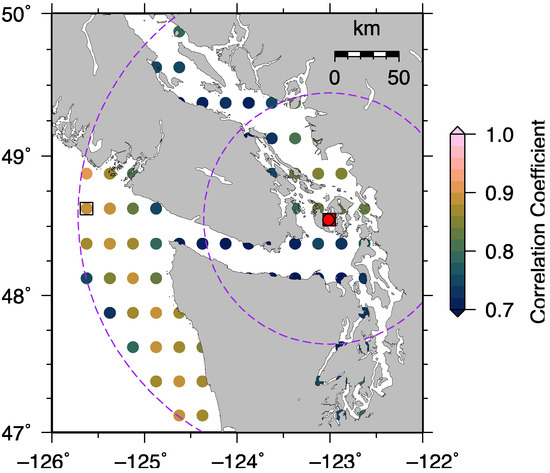
Figure A7.
Correlation coefficient at SC02. The filled red circle represents the tide gauge while the open square represents the GNSS station. The colored dot with a black square is the grid point from which the de-seasoned and de-trended satellite altimeter data has the highest correlation coefficient with those from the coastal GNSS.
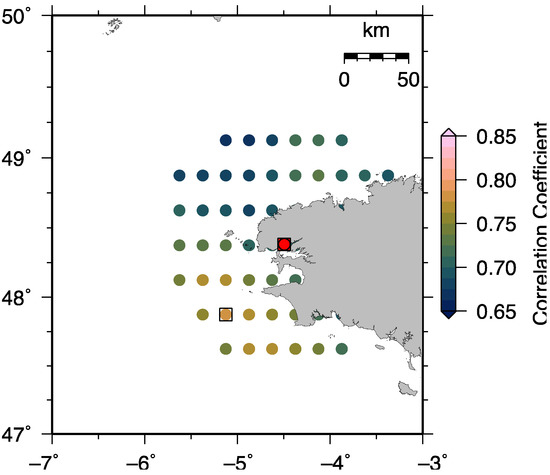
Figure A8.
Same as Figure A7, but for BRST.
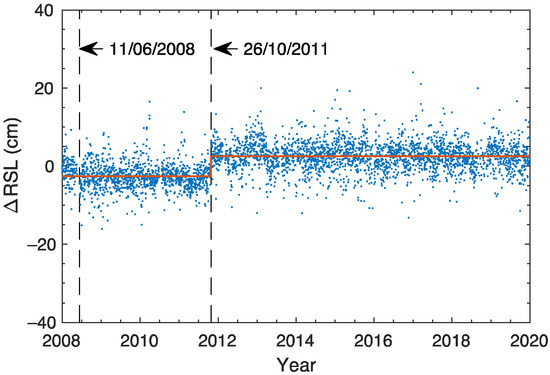
Figure A9.
The differences in relative sea levels measured by GNSS-IR at BRST and the co-located tide-gauge records. GNSS station and tide gauge are 293 m apart. Blue dots are the difference between the two types of measurements, while the red line is the fit to the differences. The two dash lines indicate change of equipment: the GNSS antenna changed from LEIAT504 to LEIAT504GG on 11 June 2008, and from LEICA (LEIAT504GG) to TRIMBLE (TRM57971.00) on 26 October 2011.
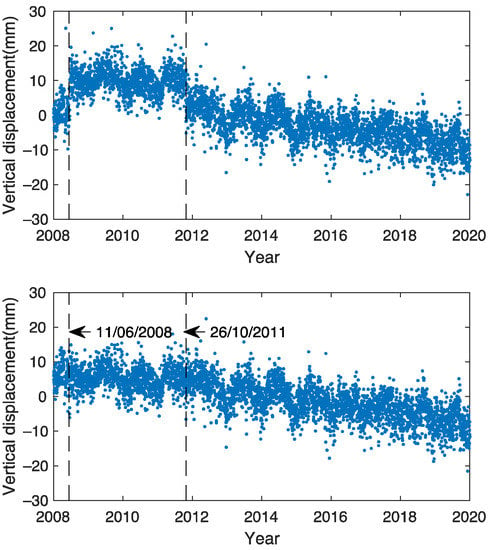
Figure A10.
GPS measured vertical displacement at BRST with (bottom panel) and without (Top panel) offset corrected.
References
- Li, L.; Switzer, A.D.; Wang, Y.; Chan, C.-H.; Qiu, Q.; Weiss, R. A modest 0.5-m rise in sea level will double the tsunami hazard in Macau. Sci. Adv. 2018, 4, eaat1180. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kulp, S.A.; Strauss, B.H. New elevation data triple estimates of global vulnerability to sea-level rise and coastal flooding. Nat. Commun. 2019, 10, 1–12. [Google Scholar]
- Befus, K.; Barnard, P.L.; Hoover, D.J.; Hart, J.F.; Voss, C.I. Increasing threat of coastal groundwater hazards from sea-level rise in California. Nat. Clim. Chang. 2020, 10, 946–952. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Felfelani, F.; Satoh, Y.; Boulange, J.; Burek, P.; Gädeke, A.; Gerten, D.; Gosling, S.N.; Grillakis, M.; Gudmundsson, L. Global terrestrial water storage and drought severity under climate change. Nat. Clim. Chang. 2021, 11, 226–233. [Google Scholar] [CrossRef]
- Benveniste, J.; Cazenave, A.; Vignudelli, S.; Fenoglio-Marc, L.; Shah, R.; Almar, R.; Andersen, O.; Birol, F.; Bonnefond, P.; Bouffard, J.; et al. Requirements for a Coastal Hazards Observing System. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef] [Green Version]
- Pugh, D.; Woodworth, P. Sea-Level Science: Understanding Tides, Surges, Tsunamis and Mean Sea-Level Changes; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Fu, L.L.; Christensen, E.J.; Yamarone, C.A.; Lefebvre, M.; Menard, Y.; Dorrer, M.; Escudier, P. TOPEX/POSEIDON mission overview. J. Geophys. Res. Ocean. 1994, 99, 24369–24381. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Marcos, M. Vertical land motion as a key to understanding sea level change and variability. Rev. Geophys. 2016, 54, 64–92. [Google Scholar] [CrossRef] [Green Version]
- Santamaría-Gómez, A.; Gravelle, M.; Collilieux, X.; Guichard, M.; Míguez, B.M.; Tiphaneau, P.; Wöppelmann, G. Mitigating the effects of vertical land motion in tide gauge records using a state-of-the-art GPS velocity field. Glob. Planet. Chang. 2012, 98, 6–17. [Google Scholar] [CrossRef]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring sea level in the coastal zone with satellite altimetry and tide gauges. In Integrative Study of the Mean Sea Level and Its Components; Springer: Berlin/Heidelberg, Germany, 2017; pp. 35–59. [Google Scholar]
- Benveniste, J.; Birol, F.; Calafat, F.; Cazenave, A.; Dieng, H.; Gouzenes, Y.; Legeais, J.F.; Léger, F.; Niño, F.; Passaro, M.; et al. Coastal sea level anomalies and associated trends from Jason satellite altimetry over 2002–2018. Sci. Data 2020, 7, 357. [Google Scholar] [CrossRef]
- Cazenave, A.; Palanisamy, H.; Ablain, M. Contemporary sea level changes from satellite altimetry: What have we learned? What are the new challenges? Adv. Space Res. 2018, 62, 1639–1653. [Google Scholar] [CrossRef]
- Marti, F.; Cazenave, A.; Birol, F.; Passaro, M.; Léger, F.; Niño, F.; Almar, R.; Benveniste, J.; Legeais, J.F. Altimetry-based sea level trends along the coasts of western Africa. Adv. Space Res. 2019, 68, 504–522. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Löfgren, J.S.; Haas, R. Coastal sea level measurements using a single geodetic GPS receiver. Adv. Space Res. 2013, 51, 1301–1310. [Google Scholar] [CrossRef] [Green Version]
- Roesler, C.; Larson, K.M. Software tools for GNSS interferometric reflectometry (GNSS-IR). GPS Solut. 2018, 22, 80. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Hill, E.M.; Li, L.; Switzer, A.D.; Larson, K.M. Application of GNSS interferometric reflectometry for detecting storm surges. GPS Solut. 2019, 23, 47. [Google Scholar] [CrossRef] [Green Version]
- Vu, P.L.; Ha, M.C.; Frappart, F.; Darrozes, J.; Ramillien, G.; Dufrechou, G.; Gegout, P.; Morichon, D.; Bonneton, P. Identifying 2010 Xynthia Storm Signature in GNSS-R-Based Tide Records. Remote Sens. 2019, 11, 782. [Google Scholar] [CrossRef] [Green Version]
- Larson, K.M.; Lay, T.; Yamazaki, Y.; Cheung, K.F.; Ye, L.; Williams, S.D.; Davis, J.L. Dynamic Sea Level Variation from GNSS: 2020 Shumagin Earthquake Tsunami Resonance and Hurricane Laura. Geophys. Res. Lett. 2020, 48, e2020GL091378. [Google Scholar]
- Roussel, N.; Ramillien, G.; Frappart, F.; Darrozes, J.; Gay, A.; Biancale, R.; Striebig, N.; Hanquiez, V.; Bertin, X.; Allain, D. Sea level monitoring and sea state estimate using a single geodetic receiver. Remote Sens. Environ. 2015, 171, 261–277. [Google Scholar] [CrossRef]
- Zeiger, P.; Frappart, F.; Darrozes, J.; Roussel, N.; Bonneton, P.; Bonneton, N.; Detandt, G. SNR-Based Water Height Retrieval in Rivers: Application to High Amplitude Asymmetric Tides in the Garonne River. Remote Sens. 2021, 13, 1856. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Williams, S.D. A 10-year comparison of water levels measured with a geodetic GPS receiver versus a conventional tide gauge. J. Atmos. Ocean. Technol. 2017, 34, 295–307. [Google Scholar] [CrossRef] [Green Version]
- Tabibi, S.; Geremia-Nievinski, F.; Francis, O.; van Dam, T. Tidal analysis of GNSS reflectometry applied for coastal sea level sensing in Antarctica and Greenland. Remote Sens. Environ. 2020, 248, 111959. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Benveniste, J. Annual sea level variability of the coastal ocean: The Baltic Sea-North Sea transition zone. J. Geophys. Res. Ocean. 2015, 120, 3061–3078. [Google Scholar] [CrossRef] [Green Version]
- Bertiger, W.; Bar-Sever, Y.; Dorsey, A.; Haines, B.; Harvey, N.; Hemberger, D.; Heflin, M.; Lu, W.; Miller, M.; Moore, A.W. GipsyX/RTGx, a new tool set for space geodetic operations and research. Adv. Space Res. 2020, 66, 469–489. [Google Scholar] [CrossRef]
- Feng, L.; Hill, E.M.; Banerjee, P.; Hermawan, I.; Tsang, L.L.; Natawidjaja, D.H.; Suwargadi, B.W.; Sieh, K. A unified GPS-based earthquake catalog for the Sumatran plate boundary between 2002 and 2013. J. Geophys. Res. Solid Earth 2015, 120, 3566–3598. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, T.; Koh, T.-Y.; Hill, E.M. Selected Years of Monsoon Variations and Extratropical Dry-Air Intrusions Compared with the Sumatran GPS Array Observations in Indonesia. J. Meteorol. Soc. Japan Ser. II 2021, 99, 505–535. [Google Scholar] [CrossRef]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08. atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Woodworth, P.L.; Aarup, T. Manual on Sea Level Measurement and Interpretation. Volume III-Reappraisals and Recommendations as of the Year 2000; UNESCO-IOC: Paris, France, 2002. [Google Scholar]
- Codiga, D.L. Unified Tidal Analysis and Prediction Using the UTide Matlab Functions; Graduate School of Oceanography, University of Rhode Island Narragansett: Kingston, RI, USA, 2011. [Google Scholar]
- Collilieux, X.; Métivier, L.; Altamimi, Z.; van Dam, T.; Ray, J. Quality assessment of GPS reprocessed terrestrial reference frame. GPS Solut. 2011, 15, 219–231. [Google Scholar] [CrossRef]
- Métivier, L.; Altamimi, Z.; Rouby, H. Past and present ITRF solutions from geophysical perspectives. Adv. Space Res. 2020, 65, 2711–2722. [Google Scholar] [CrossRef]
- Rebischung, P.; Altamimi, Z.; Ray, J.; Garayt, B. The IGS contribution to ITRF2014. J. Geod. 2016, 90, 611–630. [Google Scholar] [CrossRef]
- Larson, K.M.; Ray, R.D.; Nievinski, F.G.; Freymueller, J.T. The accidental tide gauge: A GPS reflection case study from Kachemak Bay, Alaska. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1200–1204. [Google Scholar] [CrossRef] [Green Version]
- Vinogradov, S.V.; Ponte, R.M. Annual cycle in coastal sea level from tide gauges and altimetry. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Carrère, L.; Lyard, F. Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing-comparisons with observations. Geophys. Res. Lett. 2003, 30, 1275. [Google Scholar] [CrossRef] [Green Version]
- Carrère, L.; Faugère, Y.; Ablain, M. Major improvement of altimetry sea level estimations using pressure-derived corrections based on ERA-Interim atmospheric reanalysis. Ocean. Sci. 2016, 12, 825–842. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.; Freymueller, J.T. Geodetic observations of time-variable glacial isostatic adjustment in Southeast Alaska and its implications for Earth rheology. J. Geophys. Res. Solid Earth 2019, 124, 9870–9889. [Google Scholar] [CrossRef]
- Poitevin, C.; Wöppelmann, G.; Raucoules, D.; Le Cozannet, G.; Marcos, M.; Testut, L. Vertical land motion and relative sea level changes along the coastline of Brest (France) from combined space-borne geodetic methods. Remote Sens. Environ. 2019, 222, 275–285. [Google Scholar] [CrossRef]
- Dangendorf, S.; Calafat, F.M.; Arns, A.; Wahl, T.; Haigh, I.D.; Jensen, J. Mean sea level variability in the North Sea: Processes and implications. J. Geophys. Res. Ocean. 2014, 119. [Google Scholar] [CrossRef] [Green Version]
- Watson, P.J. An assessment of the utility of satellite altimetry and tide gauge data (ALT-TG) as a proxy for estimating vertical land motion. J. Coast. Res. 2019, 35, 1131–1144. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Gravelle, M.; Wöppelmann, G. Long-term vertical land motion from double-differenced tide gauge and satellite altimetry data. J. Geod. 2014, 88, 207–222. [Google Scholar] [CrossRef]
- Montillet, J.P.; Melbourne, T.I.; Szeliga, W.M. GPS vertical land motion corrections to sea-level rise estimates in the Pacific Northwest. J. Geophys. Res. Ocean. 2018, 123, 1196–1212. [Google Scholar] [CrossRef]
- Santamaría-Gómez, A.; Watson, C.; Gravelle, M.; King, M.; Wöppelmann, G. Levelling co-located GNSS and tide gauge stations using GNSS reflectometry. J. Geod. 2015, 89, 241–258. [Google Scholar] [CrossRef]
- Williams, S.; Nievinski, F. Tropospheric delays in ground-based GNSS multipath reflectometry—Experimental evidence from coastal sites. J. Geophys. Res. Solid Earth 2017, 122, 2310–2327. [Google Scholar] [CrossRef] [Green Version]
- Nievinski, F.G.; Larson, K.M. An open source GPS multipath simulator in Matlab/Octave. Gps Solut. 2014, 18, 473–481. [Google Scholar] [CrossRef]
- Birol, F.; Léger, F.; Passaro, M.; Cazenave, A.; Niño, F.; Calafat, F.M.; Shaw, A.; Legeais, J.-F.; Gouzenes, Y.; Schwatke, C. The X-TRACK/ALES multi-mission processing system: New advances in altimetry towards the coast. Adv. Space Res. 2021, 67, 2398–2415. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).