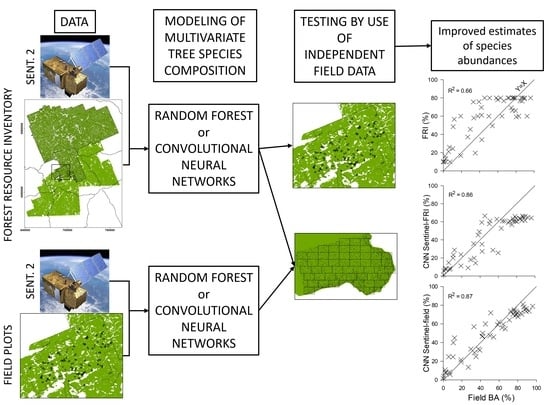
Use of Sentinel-2 Data to Improve Multivariate Tree Species Composition in a Forest Resource Inventory
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. The Forest Resource Inventory
2.3. Sentinel-2 Data
2.4. Field Data
2.5. Data Pre-Processing
2.6. Model Creation
2.7. Model Testing
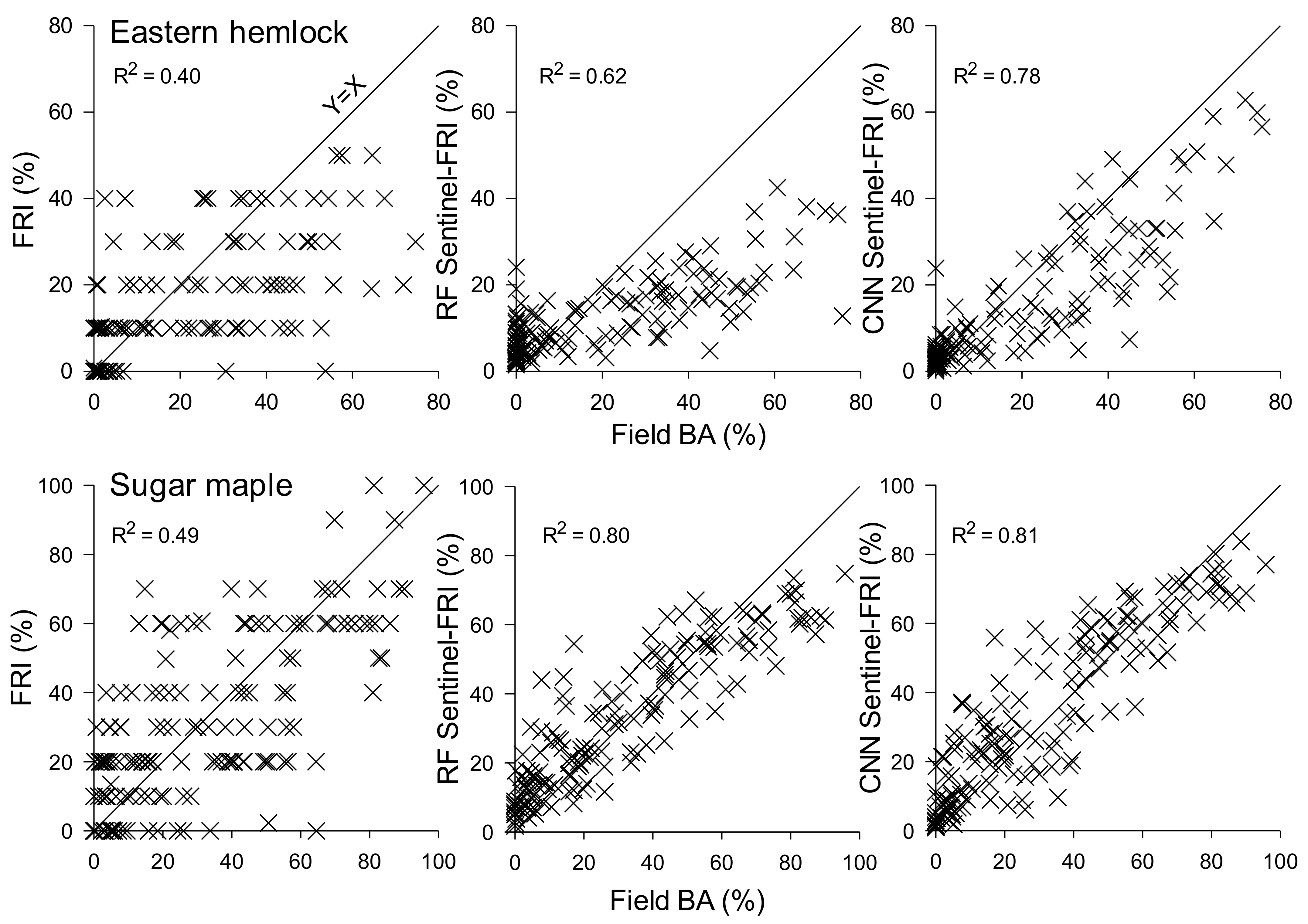
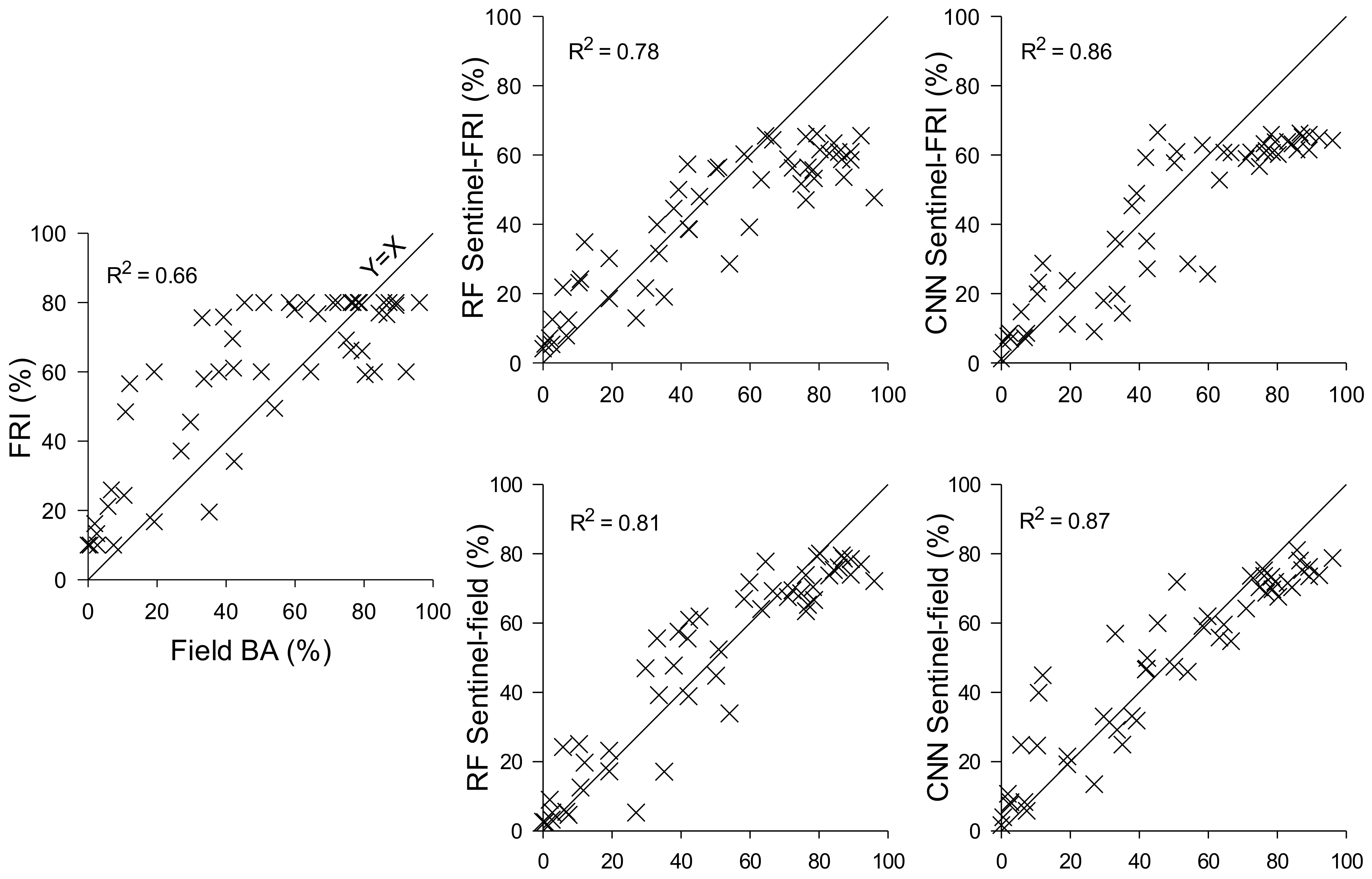
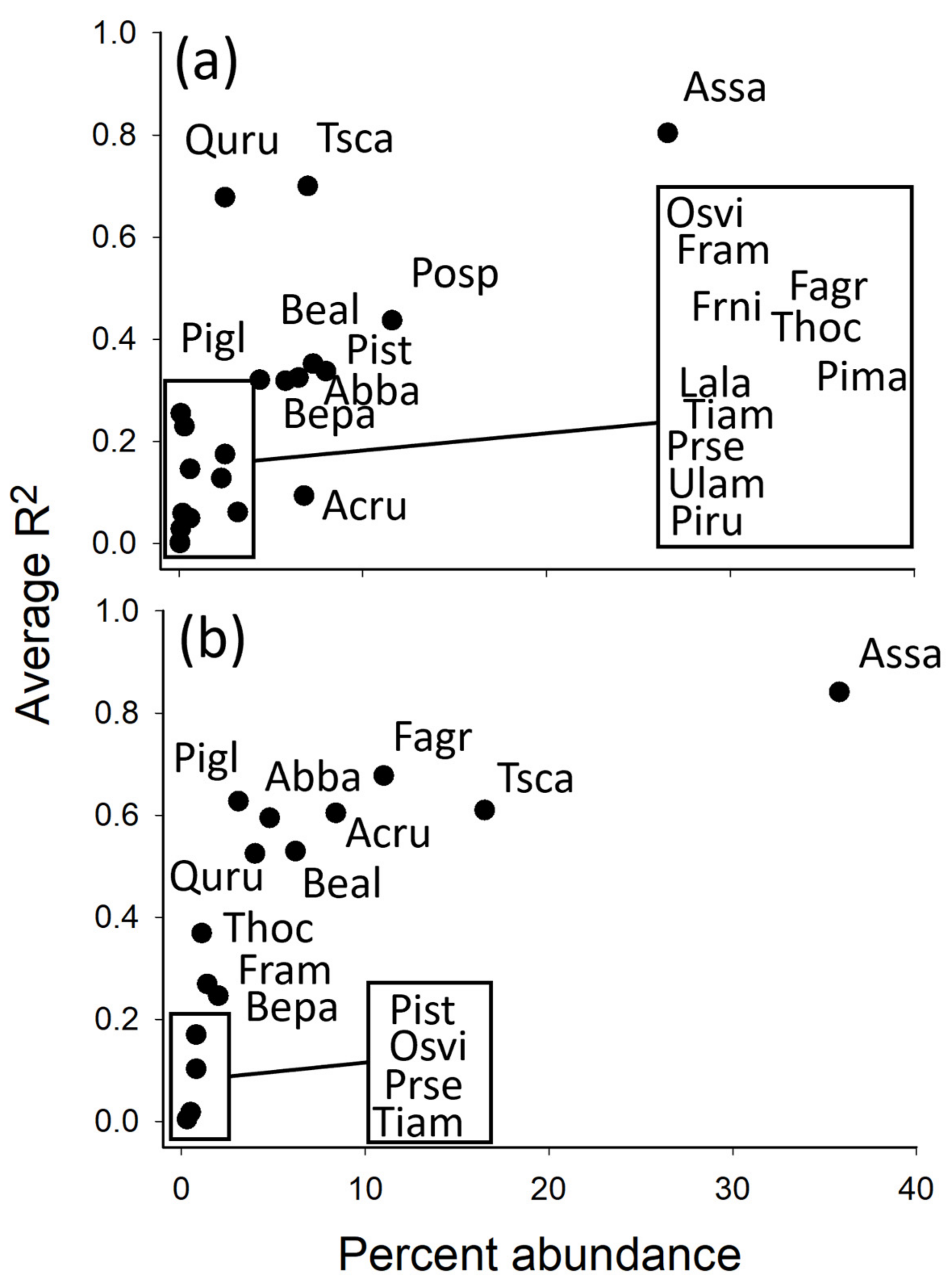
3. Results
| Species | FRI 1 | RF Sentinel-FRI | CNN Sentinel-FRI | |||
|---|---|---|---|---|---|---|
| R2 | p | R2 | p | R2 | p | |
| Sugar maple (Acer saccharum Marsh.) | 0.494 | <0.001 | 0.803 | <0.001 | 0.805 | <0.001 |
| Red oak (Quercus rubra L.) | 0.655 | <0.001 | 0.633 | <0.001 | 0.723 | <0.001 |
| Eastern hemlock (Tsuga canadensis (L.) Carrière) | 0.396 | <0.001 | 0.617 | <0.001 | 0.783 | <0.001 |
| Poplar (Populus spp.) | 0.172 | <0.001 | 0.398 | <0.001 | 0.476 | <0.001 |
| Yellow birch (Betula alleghaniensis Britt.) | 0.190 | <0.001 | 0.271 | <0.001 | 0.433 | <0.001 |
| Balsam fir (Abies balsamea (L.)) | 0.133 | <0.001 | 0.275 | <0.001 | 0.375 | <0.001 |
| White pine (Pinus strobus L.) | 0.099 | <0.001 | 0.113 | <0.001 | 0.562 | <0.001 |
| White spruce (Picea glauca (Moench) Voss) | 0.075 | <0.001 | 0.300 | <0.001 | 0.341 | <0.001 |
| White birch (Betula papyrifera Marsh.) | 0.005 | ns 2 | 0.221 | <0.001 | 0.416 | <0.001 |
| White ash (Fraxinus americana L.) | 0.066 | 0.001 | 0.229 | <0.001 | 0.230 | <0.001 |
| Ironwood (Ostrya virginiana (Mill.) K. Koch) | 0.005 | ns | 0.151 | <0.001 | 0.359 | <0.001 |
| American beech (Fagus grandifolia Ehrh.) | 0.041 | 0.011 | 0.124 | <0.001 | 0.226 | <0.001 |
| Black ash (Fraxinus nigra Marsh.) | 0.043 | 0.010 | 0.002 | ns | 0.290 | <0.001 |
| Eastern white cedar (Thuja occidentalis L.) | 0.049 | 0.006 | 0.160 | <0.001 | 0.096 | <0.001 |
| Red maple (Acer rubrum L.) | 0.018 | ns | 0.108 | <0.001 | 0.079 | <0.001 |
| Black spruce (Picea mariana (Mill.) BSP) | 0.044 | 0.009 | 0.075 | <0.001 | 0.048 | 0.006 |
| Eastern larch (Larix laricina (Du Roi) K. Koch) | 0 | - | 0.011 | ns | 0.108 | <0.001 |
| Basswood (Tilia americana L.) | 0 | - | 0.031 | 0.029 | 0.068 | 0.001 |
| Black cherry (Prunus serotina Ehrh.) | 0 | - | 0.024 | ns | 0.034 | 0.022 |
| White elm (Ulmus americana L.) | 0.046 | 0.007 | 0.004 | ns | <0.001 | ns |
| Red spruce (Picea rubens Sarg.) | 0.002 | ns | 0.001 | ns | <0.001 | ns |
| Mean | 0.141 | 0.217 | 0.307 | |||
| Species | FRI 1 | RF Sentinel-FRI | CNN Sentinel-FRI | RF Sentinel-Field | CNN Sentinel-Field | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | p | R2 | p | R2 | p | R2 | p | R2 | p | |
| Sugar maple (Acer saccharum) | 0.659 | <0.001 | 0.782 | <0.001 | 0.864 | <0.001 | 0.810 | <0.001 | 0.873 | <0.001 |
| Eastern hemlock (Tsuga canadensis) | 0.666 | <0.001 | 0.640 | <0.001 | 0.827 | <0.001 | 0.528 | <0.001 | 0.692 | <0.001 |
| Red oak (Quercus rubra) | 0 | - | 0.641 | <0.001 | 0.714 | <0.001 | 0.402 | <0.001 | 0.648 | <0.001 |
| Red maple (Acer rubrum) | 0.245 | <0.001 | 0.224 | <0.001 | 0.469 | <0.001 | 0.528 | <0.001 | 0.681 | <0.001 |
| Balsam fir (Abies balsamea) | 0 | - | 0.395 | <0.001 | 0.534 | <0.001 | 0.492 | <0.001 | 0.698 | <0.001 |
| Yellow birch (Betula alleghaniensis) | 0.160 | 0.004 | 0.313 | <0.001 | 0.421 | <0.001 | 0.465 | <0.001 | 0.594 | <0.001 |
| American beech (Fagus grandifolia) | 0.003 | ns 2 | 0.149 | 0.005 | 0.225 | <0.001 | 0.452 | <0.001 | 0.903 | <0.001 |
| White spruce (Picea glauca) | 0 | - | 0.360 | <0.001 | 0.045 | ns | 0.659 | <0.001 | 0.596 | <0.001 |
| Eastern white cedar (Thuja occidentalis) | 0.467 | <0.001 | 0.168 | 0.003 | 0.205 | <0.001 | 0.264 | <0.001 | 0.474 | <0.001 |
| White birch (Betula papyrifera) | 0 | - | 0.441 | <0.001 | 0.328 | <0.001 | 0.403 | <0.001 | 0.089 | 0.033 |
| White pine (Pinus strobus) | 0.289 | <0.001 | 0.250 | <0.001 | 0.187 | 0.002 | 0.117 | 0.014 | 0.223 | <0.001 |
| White ash (Fraxinus americana) | 0 | - | 0.015 | ns | 0.417 | <0.001 | 0.143 | 0.006 | 0.395 | <0.001 |
| Ironwood (Ostrya virginiana) | 0.044 | 0.141 | 0.012 | ns | 0.036 | ns | 0.044 | ns | 0.162 | 0.003 |
| Black cherry (Prunus serotina) | 0 | - | 0.022 | ns | 0.006 | ns | 0.029 | ns | 0.007 | ns |
| Basswood (Tilia americana) | 0 | - | 0.014 | ns | 0.005 | ns | 0.005 | ns | 0.004 | ns |
| Mean | 0.169 | 0.295 | 0.352 | 0.356 | 0.469 | |||||
| Comparison 1 | Stand 1 (3.9 ha) | Stand 2 (0.8 ha) | Stand 3 (6.0 ha) | Stand 4 (3.1 ha) |
|---|---|---|---|---|
| Field vs. FRI | 6.95 | 12.12 | 3.83 | 4.27 |
| Field vs. RF Sentinel-FRI | 4.43 | 8.96 | 1.93 | 2.30 |
| Field vs. CNN Sentinel-FRI | 4.06 | 8.69 | 1.98 | 3.48 |
| Field vs. RF Sentinel-field | 3.60 | 6.13 | 1.74 | 1.69 |
| Field vs. CNN Sentinel-field | 4.72 | 2.84 | 1.21 | 2.70 |
| FRI | RF Sentinel-FRI | CNN Sentinel-FRI | RF Sentinel-Field | CNN Sentinel-Field | |
|---|---|---|---|---|---|
| FRI | - | 0.163 | 0.178 | 0.107 | 0.114 |
| RF Sentinel-FRI | - | 0.441 | 0.365 | 0.239 | |
| CNN Sentinel-FRI | - | 0.237 | 0.253 | ||
| RF Sentinel-field | - | 0.334 | |||
| CNN Sentinel-field | - |
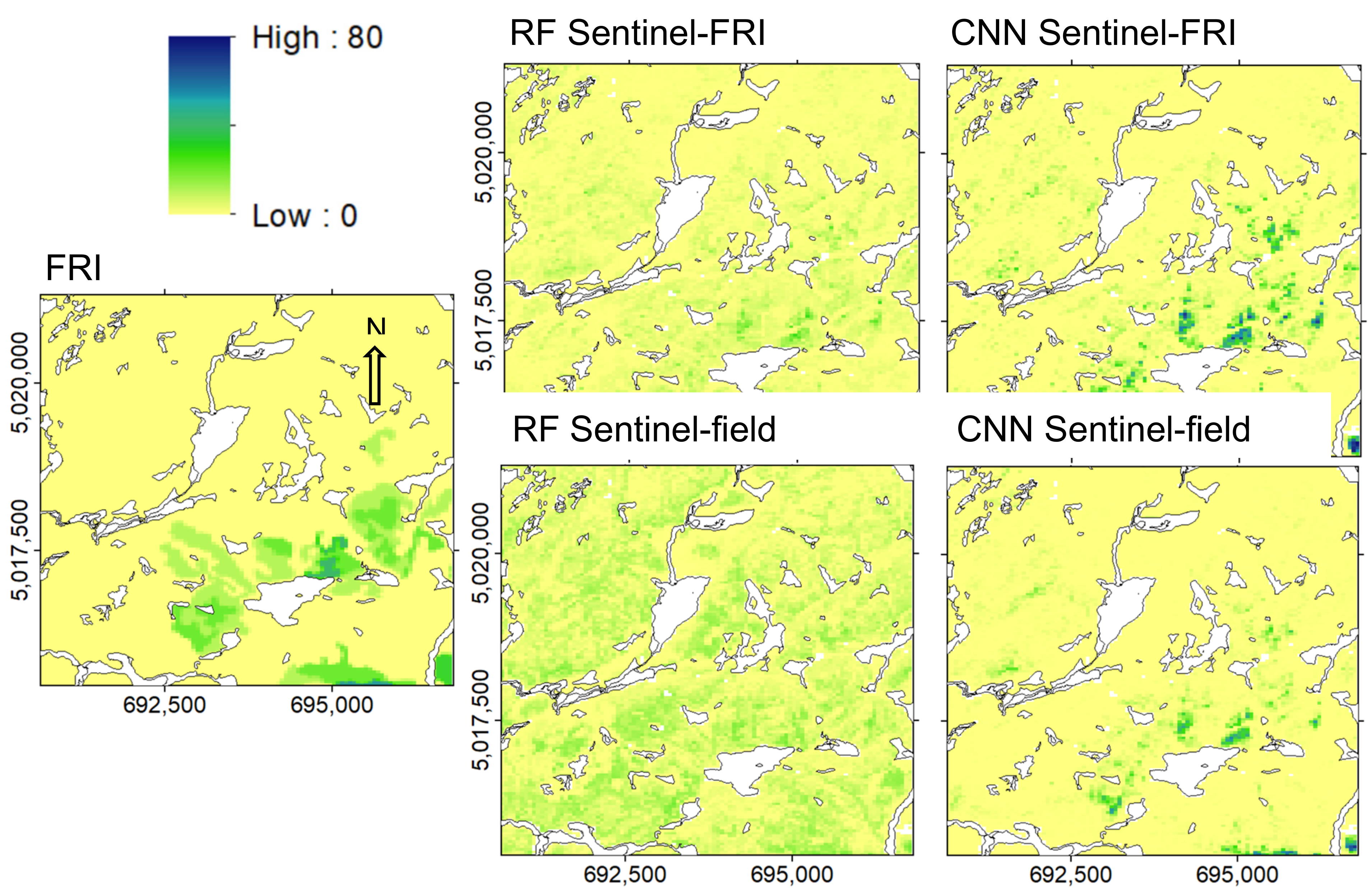
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McDermid, G.J.; Hall, R.J.; Sanchez-Azofeifa, G.A.; Franklin, S.E.; Stenhouse, G.B.; Kobliuk, T.; LeDrew, E.F. Remote sensing and forest inventory for wildlife habitat assessment. For. Ecol. Manag. 2009, 257, 2262–2269. [Google Scholar] [CrossRef]
- Pinto, F.; Rouillard, D.; Sobze, J.M.; Ter-Mikaelian, M. Validating tree species composition in forest resource inventory for Nipissing Forest, Ontario, Canada. For. Chron. 2007, 83, 247–251. [Google Scholar] [CrossRef]
- Penner, M. Yield prediction for mixed species stands in boreal Ontario. For. Chron. 2008, 84, 46–52. [Google Scholar] [CrossRef]
- Stoffels, J.; Mader, S.; Hill, J.; Werner, W.; Ontrup, G. Satellite-based stand-wise forest cover type mapping using a spatially adaptive classification approach. Eur. J. For. Res. 2012, 131, 1071–1089. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalen, P.; Kangas, A. From comprehensive field inventories to remotely sensed wall-to-wall stand attribute data—A brief history of management inventories in the Nordic countries. Can. J. For. Res. 2021, 51, 257–266. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalen, P. Species-specific management inventory in Finland. In Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies; Maltamo, M., Naesset, E., Vaukhonen, J., Eds.; Managing Forest Ecosystems; Springer: Dordrecht, The Netherlands, 2014; Volume 27, pp. 241–252. [Google Scholar] [CrossRef]
- Rettie, W.J.; Sheard, J.W.; Messier, F. Identification and description of forested vegetation communities available to woodland caribou: Relating wildlife habitat to forest cover data. For. Ecol. Manag. 1997, 93, 245–260. [Google Scholar] [CrossRef]
- Malcolm, J.R.; Campbell, B.D.; Kuttner, B.G.; Sugar, A.; Malcolm, J.R.; Kuttner, B.G. Potential indicators of the impacts of forest management on wildlife habitat in northeastern Ontario: A multivariate application of wildlife habitat suitability matrices. For. Chron. 2004, 80, 91–106. [Google Scholar] [CrossRef][Green Version]
- Hennigar, C.R.; MacLean, D.A.; Amos-Binks, L.J. A novel approach to optimize management strategies for carbon stored in both forests and wood products. For. Ecol. Manag. 2008, 256, 786–797. [Google Scholar] [CrossRef]
- Malcolm, J.R.; Holtsmark, B.; Piascik, P.W. Forest harvesting and the carbon debt in boreal east-central Canada. Clim. Chang. 2020, 161, 433–449. [Google Scholar] [CrossRef]
- Magnussen, S.; Russo, G. Uncertainty in photo-interpreted forest inventory variables and effects on estimates of error in Canada’s national forest inventory. For. Chron. 2012, 88, 439–447. [Google Scholar] [CrossRef]
- Thompson, I.D.; Maher, S.C.; Rouillard, D.P.; Fryxell, J.M.; Baker, J.A. Accuracy of forest inventory mapping: Some implications for boreal forest management. For. Ecol. Manag. 2007, 252, 208–221. [Google Scholar] [CrossRef]
- Maxie, A.J.; Hussey, K.F.; Lowe, S.J.; Middel, K.R.; Pond, B.A.; Obbard, M.E.; Patterson, B.R. A comparison of forest resource inventory, provincial land cover maps and field surveys for wildlife habitat analysis in the Great Lakes—St. Lawrence forest. For. Chron. 2010, 86, 77–86. [Google Scholar] [CrossRef]
- Potvin, F.; Belanger, L.; Lowell, K. The validity of forest maps for the description of wildlife habitats on the local level—A case study in the Abitibi-Temiscamingue region. For. Chron. 1999, 75, 851–859. [Google Scholar] [CrossRef]
- Féret, J.B.; Asner, G.P. Semi-supervised methods to identify individual crowns of lowland tropical canopy species using imaging spectroscopy and Lidar. Remote Sens. 2012, 4, 2457–2476. [Google Scholar] [CrossRef]
- Hartling, S.; Sagan, V.; Sidike, P.; Maimaitijiang, M.; Carron, J. Urban tree species classification using a Worldview-2/3 and LiDAR data fusion approach and deep learning. Sensors 2019, 19, 1284. [Google Scholar] [CrossRef]
- Immitzer, M.; Neuwirth, M.; Böck, S.; Brenner, H.; Vuolo, F.; Atzberger, C. Optimal input features for tree species classification in central Europe based on multi-temporal Sentinel-2 data. Remote Sens. 2019, 11, 2599. [Google Scholar] [CrossRef]
- Bolyn, C.; Michez, A.; Gaucher, P.; Lejeune, P.; Bonnet, S. Forest mapping and species composition using supervised per pixel classification of Sentinel-2 imagery. Biotech. Agron. Soc. 2018, 22, 172–187. [Google Scholar] [CrossRef]
- Tomppo, E.; Olsson, H.; Ståhl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining national forest inventory field plots and remote sensing data for forest databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Chen, Q.; Walters, B.F. Multivariate inference for forest inventories using auxiliary airborne laser scanning data. For. Ecol. Manag. 2017, 401, 295–303. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăgu, L. Random Forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Hu, X.; Gong, J. Forest type identification with Random Forest using Sentinel-1A, Sentinel-2A, multi-temporal Landsat-8 and DEM data. Remote Sens. 2018, 10, 946. [Google Scholar] [CrossRef]
- Rezaee, M.; Zhang, Y.; Mishra, R.; Tong, F.; Tong, H. Using a VGG-16 Network for individual tree species detection with an object-based approach. In Proceedings of the 2018 10th IAPR Workshop on Pattern Recognition in Remote Sensing, PRRS 2018, Beijing, Chinas, 19–20 August 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Rowe, J.S. Forest Regions of Canada; Canadian Forestry Service: Ottawa, ON, Canada, 1972.
- Environment Canada, Canadian Climate Normals 1981–2010, Haliburton, Ontario. Available online: https://climate.weather.gc.ca/climate_normals/ (accessed on 15 August 2020).
- OMNR. Forest Information Manual; Queen’s Printer for Ontario: Peterborough, ON, Canada, 2001.
- Persson, M.; Lindberg, E.; Reese, H. Tree species classification with multi-temporal Sentinel-2 data. Remote Sens. 2018, 10, 1794. [Google Scholar] [CrossRef]
- Ranghetti, L.; Boschetti, M.; Nutini, F.; Busetto, L. “sen2r”: An R toolbox for automatically downloading and preprocessing Sentinel-2 satellite data. Comput. Geosci. 2020, 139, 104473. [Google Scholar] [CrossRef]
- Spriggs, R.S.; Vanderwel, M.C.; Jones, T.A.; Caspersen, J.P.; Coomes, D.A. A simple area-based model for predicting airborne LiDAR first returns from stem diameter distributions: An example study in an uneven-aged, mixed temperate forest. Can. J. For. Res. 2015, 45, 1338–1350. [Google Scholar] [CrossRef]
- Condit, R.S. Tropical Forest Census Plots—Methods and Results from Barro Colorado Island, Panama and a Comparison with Other Plots; Springer: Berlin/Heidelberg, Germany; R G. Landes Company: Georgetown, TX, USA, 1998. [Google Scholar]
- Anderson-Teixeira, K.J.; Davies, S.J.; Bennett, A.C.; Gonzalez-Akre, E.B.; Muller-Landau, H.C.; Wright, S.J.; Abu Salim, K.; Almeyda Zambrano, A.M.; Alonso, A.; Baltzer, J.L.; et al. CTFS-ForestGEO: A worldwide network monitoring forests in an era of global change. Glob. Chang. Biol. 2015, 21, 528–549. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.C. Photosynthetic capacity peaks at intermediate size in temperate deciduous trees. Tree Physiol. 2010, 30, 555–573. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Segal, M.; Xiao, Y. Multivariate random forests. WIRES Data Min. Knowl. 2011, 1, 80–87. [Google Scholar] [CrossRef]
- Ishwaran, H.; Kogalur, U.B. Fast Unified Random Forests for Survival, Regression, and Classification (RF-SRC) 2020. R Package Version 2.9.3. Available online: https://cran.r-project.org/web/packages/randomForestSRC/randomForestSRC.pdf (accessed on 16 January 2020).
- Shang, C.; Treitz, P.; Caspersen, J.; Jones, T. Estimation of forest structural and compositional variables using ALS data and multi-seasonal satellite imagery. Int. J. Appl. Earth Obs. 2019, 78, 360–371. [Google Scholar] [CrossRef]
- Lim, J.; Kim, K.M.; Jin, R. Tree species classification using Hyperion and Sentinel-2 data with machine learning in South Korea and China. ISPRS Int. Geo-Inf. 2019, 8, 150. [Google Scholar] [CrossRef]
- Oksanen, J.; Blanchet, F.G.; Friendly, M.; Kindt, R.; Legendre, P.; McGlinn, D.; Minchin, P.R.; O’Hara, R.B.; Simpson, G.L.; Solymos, P.; et al. Vegan: Community Ecology Package 2019. R Package Version 2.5-6. Available online: https://cran.r-project.org/web/packages/vegan/vegan.pdf (accessed on 16 January 2020).
- Khan, S.; Hossein, R.; Syed, A.S.; Mohammed, B.; Gerard, M.; Dickinson, S. A Guide to Convolutional Neural Networks for Computer Vision; Morgan & Claypool: San Rafael, CA, USA, 2018. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hamraz, H.; Jacobs, N.B.; Contreras, M.A.; Clark, C.H. Deep learning for conifer/deciduous classification of airborne LiDAR 3D point clouds representing individual trees. ISPRS J. Photogramm. 2019, 158, 219–230. [Google Scholar] [CrossRef]
- Wang, S.; Cao, J.; Yu, P. Deep learning for spatio-temporal data mining: A survey. IEEE Trans. Knowl. Data Eng. 2020. [Google Scholar] [CrossRef]
- Ping, W.; Peng, K.; Gibiansky, A.; Arik, S.Ö.; Kannan, A.; Narang, S.; Raiman, J.; Miller, J. Deep voice 3: 2000-speaker neural text-to-speech. arXiv 2018, arXiv:1710.07654. [Google Scholar]
- Brousseau, B.; Rose, J.; Eizenman, M. Hybrid eye-tracking on a smartphone with CNN feature extraction and an infrared 3D model. Sensors 2020, 20, 543. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D.D. Hyperopt: A Python library for optimizing the hyperparameters of machine learning algorithms. In Proceedings of the 12th Python in Science Conference, Austin, TX, USA, 24–29 June 2013. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020; Available online: https://www.R-project.org/ (accessed on 18 December 2019).
- Grabska, E.; Hostert, P.; Pflugmacher, D.; Ostapowicz, K. Forest stand species mapping using the Sentinel-2 time series. Remote Sens. 2019, 11, 1197. [Google Scholar] [CrossRef]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data. pp. 1–12. Available online: https://statistics.berkeley.edu/sites/default/files/tech-reports/666.pdf (accessed on 22 April 2021).
- Rejou-Mechain, M.; Muller-Landau, H.C.; Detto, M.; Thomas, S.C.; le Toan, T.; Saatchi, S.S.; Barreto-Silva, J.S.; Bourg, N.A.; Bunyavejchewin, S.; Butt, N.; et al. Local spatial structure of forest biomass and its consequences for remote sensing of carbon stocks. Biogeosciences 2014, 11, 6827–6840. [Google Scholar] [CrossRef]
- Bohlman, S.; Pacala, S. A forest structure model that determines crown layers and partitions growth and mortality rates for landscape-scale applications of tropical forests. J. Ecol. 2012, 100, 508–518. [Google Scholar] [CrossRef]
- Axelsson, A.; Lindberg, E.; Reese, H.; Olsson, H. Tree species classification using Sentinel-2 imagery and Bayesian inference. Int. J. Appl. Earth Obs. Geoinf. 2021, 100, 102318. [Google Scholar] [CrossRef]
- Pan, L.; Xia, H.; Yang, J.; Niu, W.; Wang, R.; Song, H.; Guo, Y.; Qin, Y. Mapping cropping intensity in Huaihe basin using phenology algorithm, all Sentinel-2 and Landsat images in Google Earth Engine. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102376. [Google Scholar] [CrossRef]
- Leckie, D.G.; Tinis, S.; Nelson, T.; Burnett, C.; Gougeon, F.A.; Cloney, E.; Paradine, D. Issues in species classification of trees in old growth conifer stands. Can. J. Remote Sens. 2005, 31, 175–190. [Google Scholar] [CrossRef]
- Isaac, E.; Easwarakumar, K.S.; Isaac, J. Urban landcover classification from multispectral image data using optimized adaboosted random forests. Remote Sens. Lett. 2017, 8, 350–359. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded Random Forest for hyperspectral image classification. IEEE J. Sel. Top. Appl. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Hościło, A.; Lewandowska, A. Mapping forest type and tree species on a regional scale using multi-temporal Sentinel-2 data. Remote Sens. 2019, 11, 929. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2016, arXiv:1511.07289. [Google Scholar]
- Kingma, D.P.; Ba, J.L.B. ADAM: A Method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Tieleman, T.; Hinton, G. Lecture 6.5-Rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA Neural Netw. Mach. Learn. 2012, 4, 26–31. [Google Scholar]
- Bottou, L. Large-scale machine learning with stochastic gradient descent. In Proceedings of COMPSTAT’2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malcolm, J.R.; Brousseau, B.; Jones, T.; Thomas, S.C. Use of Sentinel-2 Data to Improve Multivariate Tree Species Composition in a Forest Resource Inventory. Remote Sens. 2021, 13, 4297. https://doi.org/10.3390/rs13214297
Malcolm JR, Brousseau B, Jones T, Thomas SC. Use of Sentinel-2 Data to Improve Multivariate Tree Species Composition in a Forest Resource Inventory. Remote Sensing. 2021; 13(21):4297. https://doi.org/10.3390/rs13214297
Chicago/Turabian StyleMalcolm, Jay R., Braiden Brousseau, Trevor Jones, and Sean C. Thomas. 2021. "Use of Sentinel-2 Data to Improve Multivariate Tree Species Composition in a Forest Resource Inventory" Remote Sensing 13, no. 21: 4297. https://doi.org/10.3390/rs13214297
APA StyleMalcolm, J. R., Brousseau, B., Jones, T., & Thomas, S. C. (2021). Use of Sentinel-2 Data to Improve Multivariate Tree Species Composition in a Forest Resource Inventory. Remote Sensing, 13(21), 4297. https://doi.org/10.3390/rs13214297