A Framework for Actual Evapotranspiration Assessment and Projection Based on Meteorological, Vegetation and Hydrological Remote Sensing Products
Abstract
:1. Introduction
- How does actual evapotranspiration dynamically evolve?
- What are the relevant and decisive factors that affect the AET changes?
- What kind of input and which machine learning algorithms can simulate the most intense future AET?
- How to integrate the results of multiple machine learning algorithms to generate an optimal set of AET future prediction products?
2. Materials and Methods
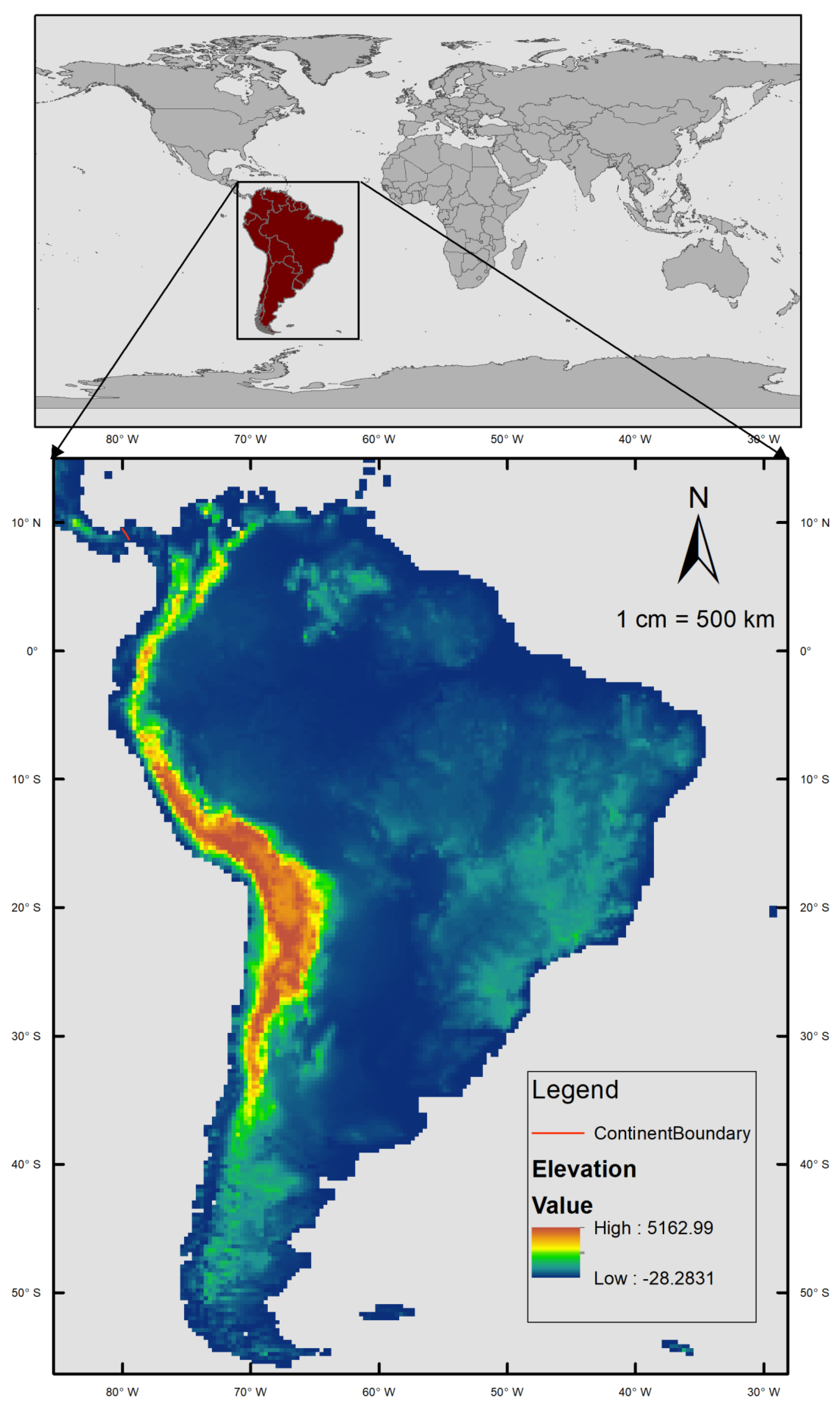
2.1. Case Study
2.2. Data
2.2.1. Meteorological Data (Temperature, Precipitation, and Potential Evapotranspiration)
2.2.2. Hydrological Data (Actual Evapotranspiration, Total Water Storage, and Runoff)
2.2.3. Vegetation Index (NDVI)
2.2.4. Future Climate Scenarios (CMIP6)
2.3. Methods
2.3.1. Man-Kendall Test
2.3.2. Boruta Algorithm
- Copy all features to build random shadow features. Shuffle all the features in the data randomly and rearrange the order of the features.
- Input the features and their copies into the random forest classifier to calculate the Z-scores.
- Remove features with lower Z-scores than the shadow attributes. The important variables, whose Z-scores are over the set of shadow features, are verified.
- Repeat steps 1–3 until all variables are identified.
2.3.3. Support Vector Regression (SVR)
2.3.4. Random Forest (RF)
2.3.5. Research Framework
3. Results
3.1. Assess the Evolution Tendency of AET
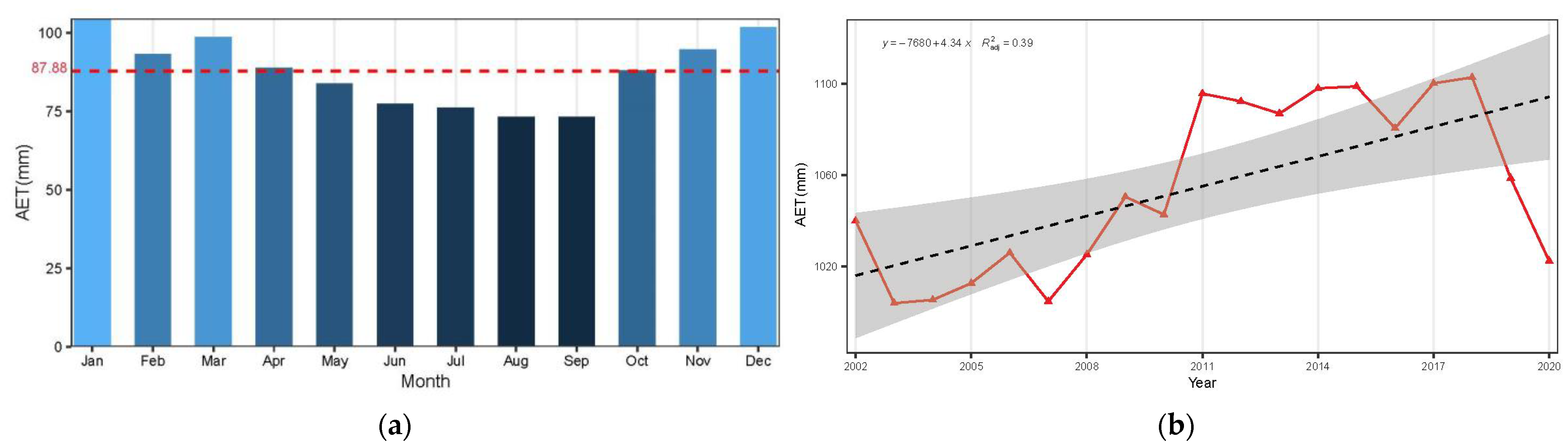
3.1.1. Temporal Evolution
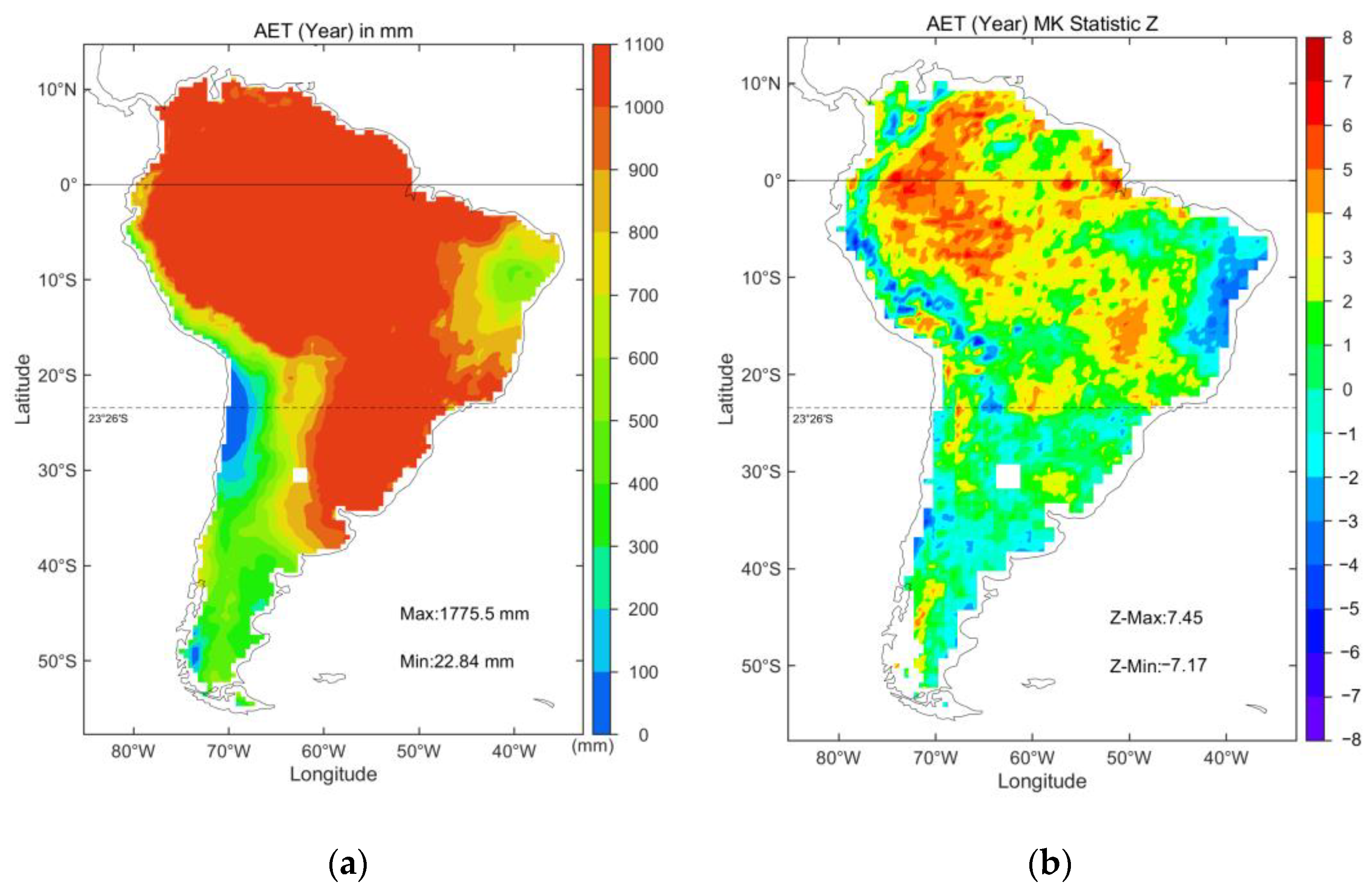
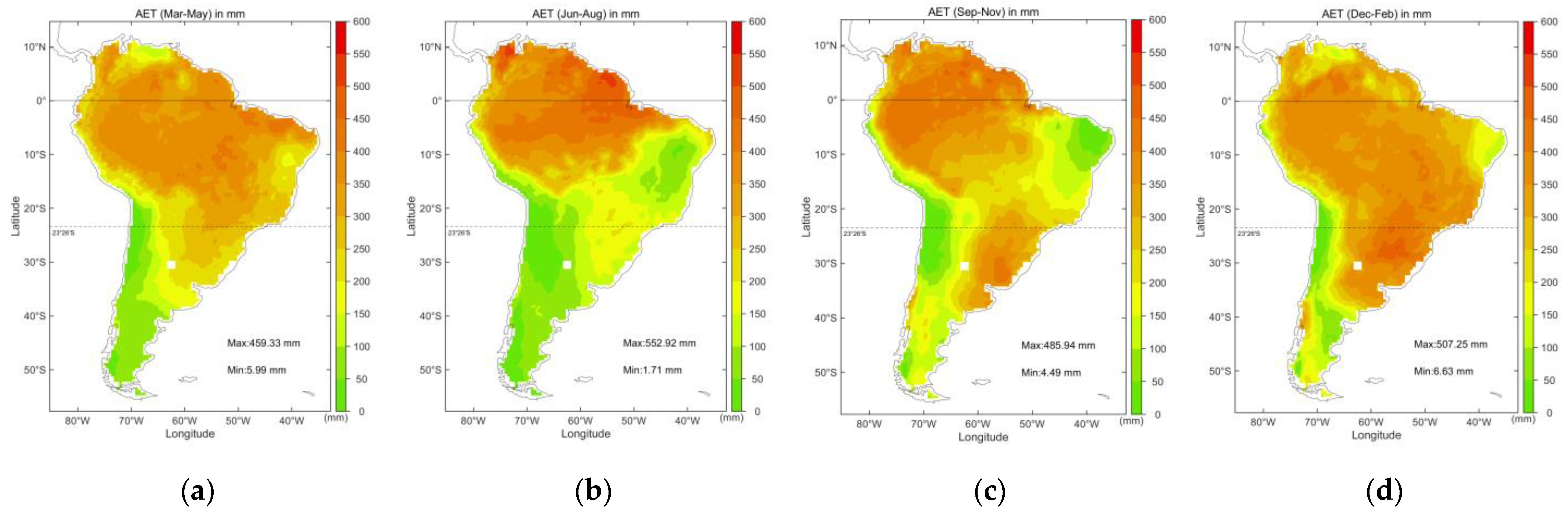
3.1.2. Spatial Evolution
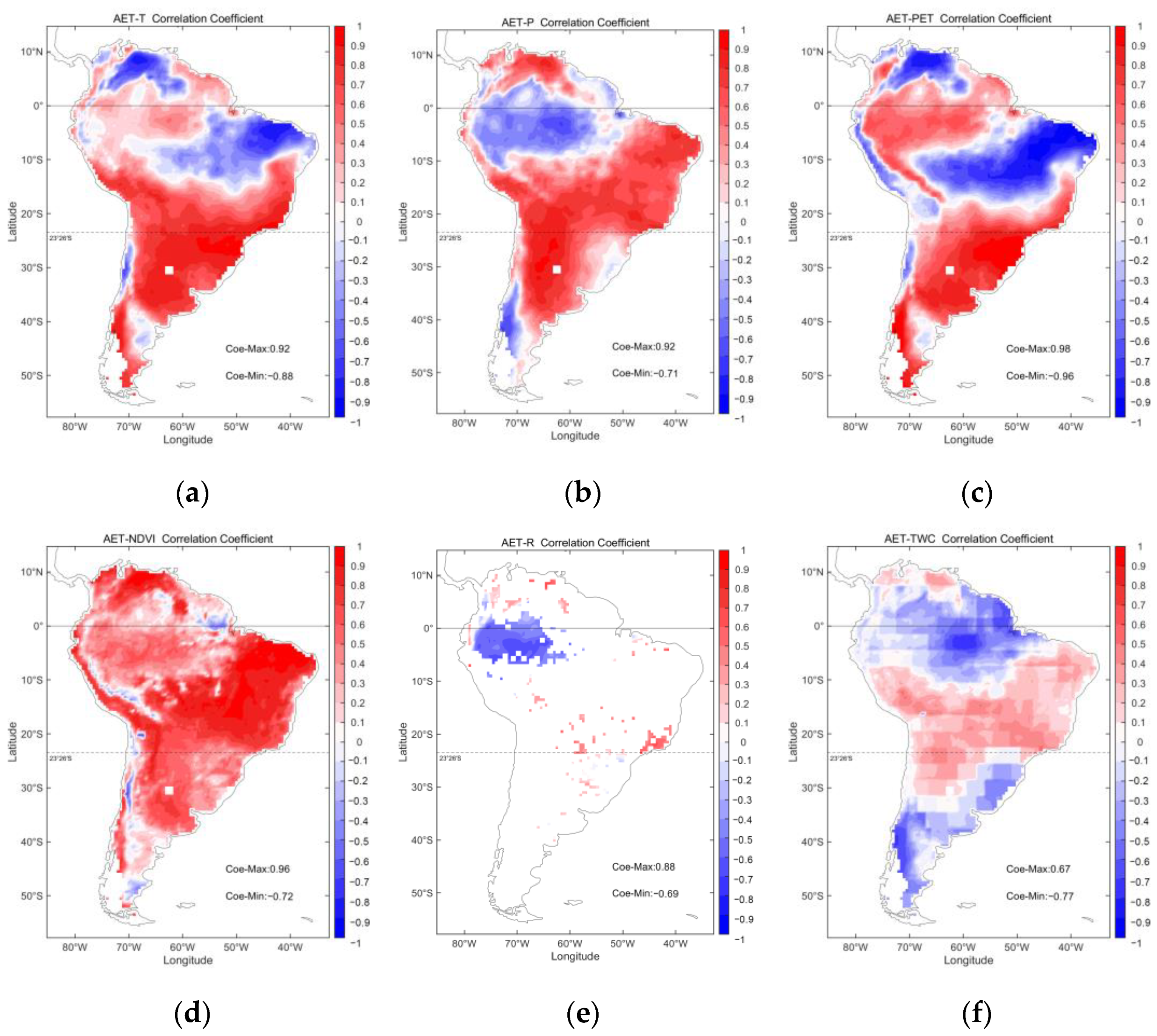
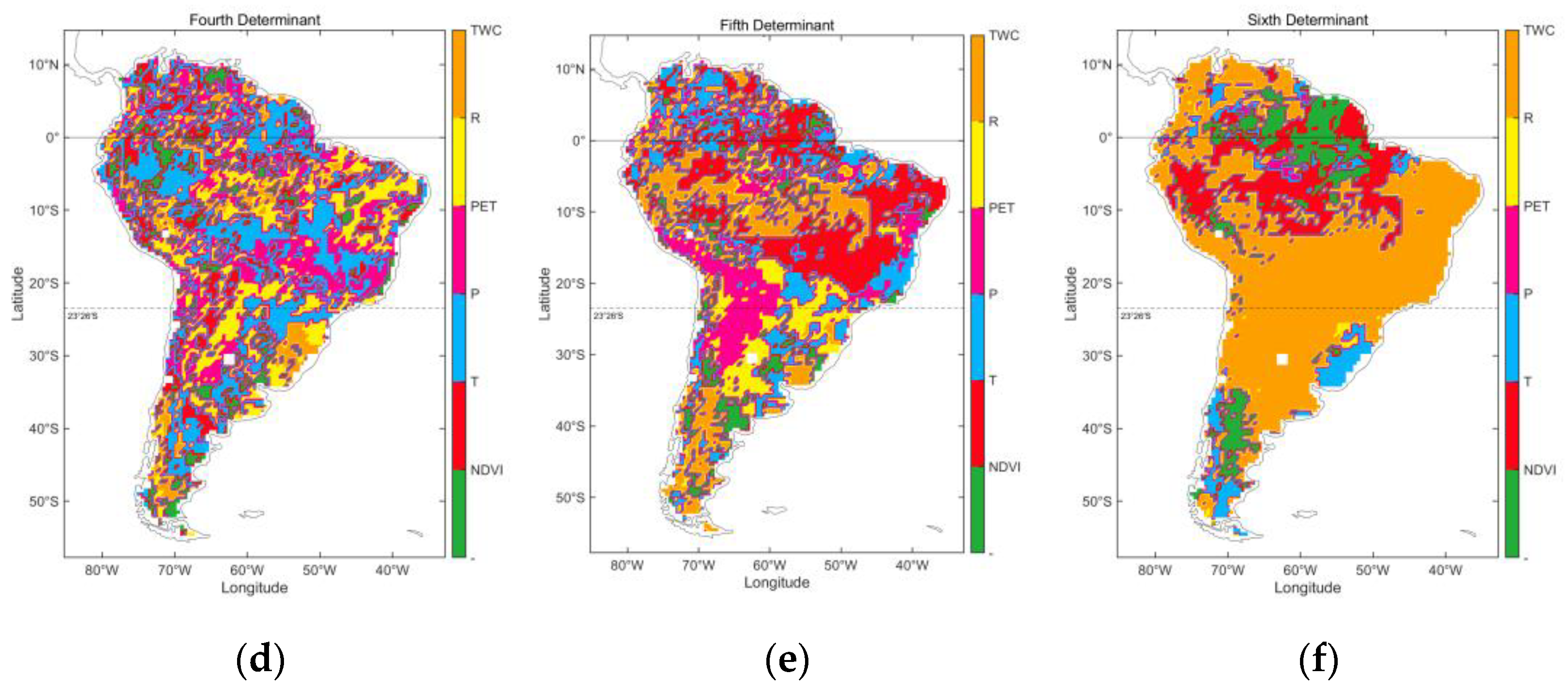
3.2. Assess the Relevant Factors and Determinant Order of AET
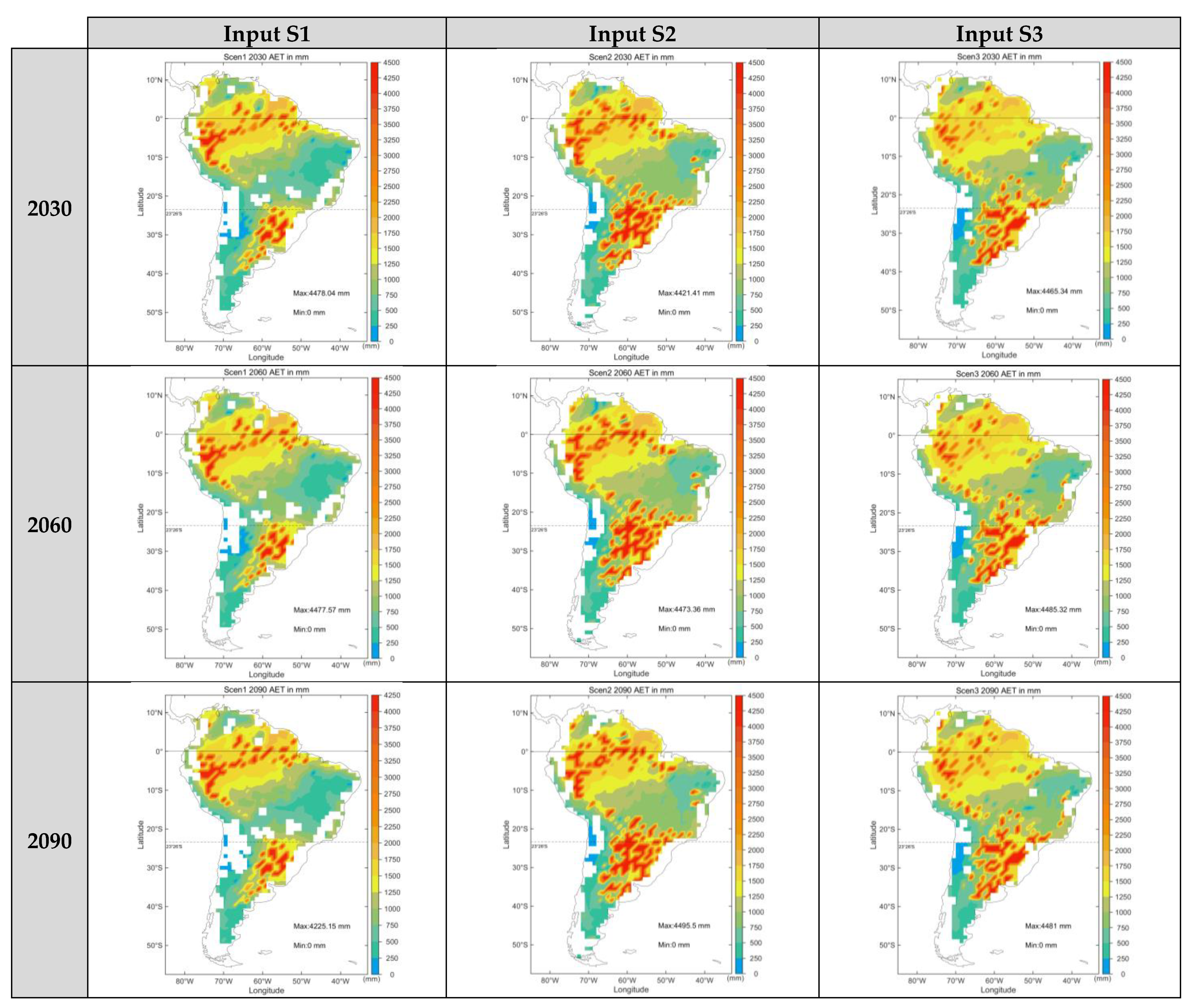
3.3. Projection of AET under Different Input Strategies
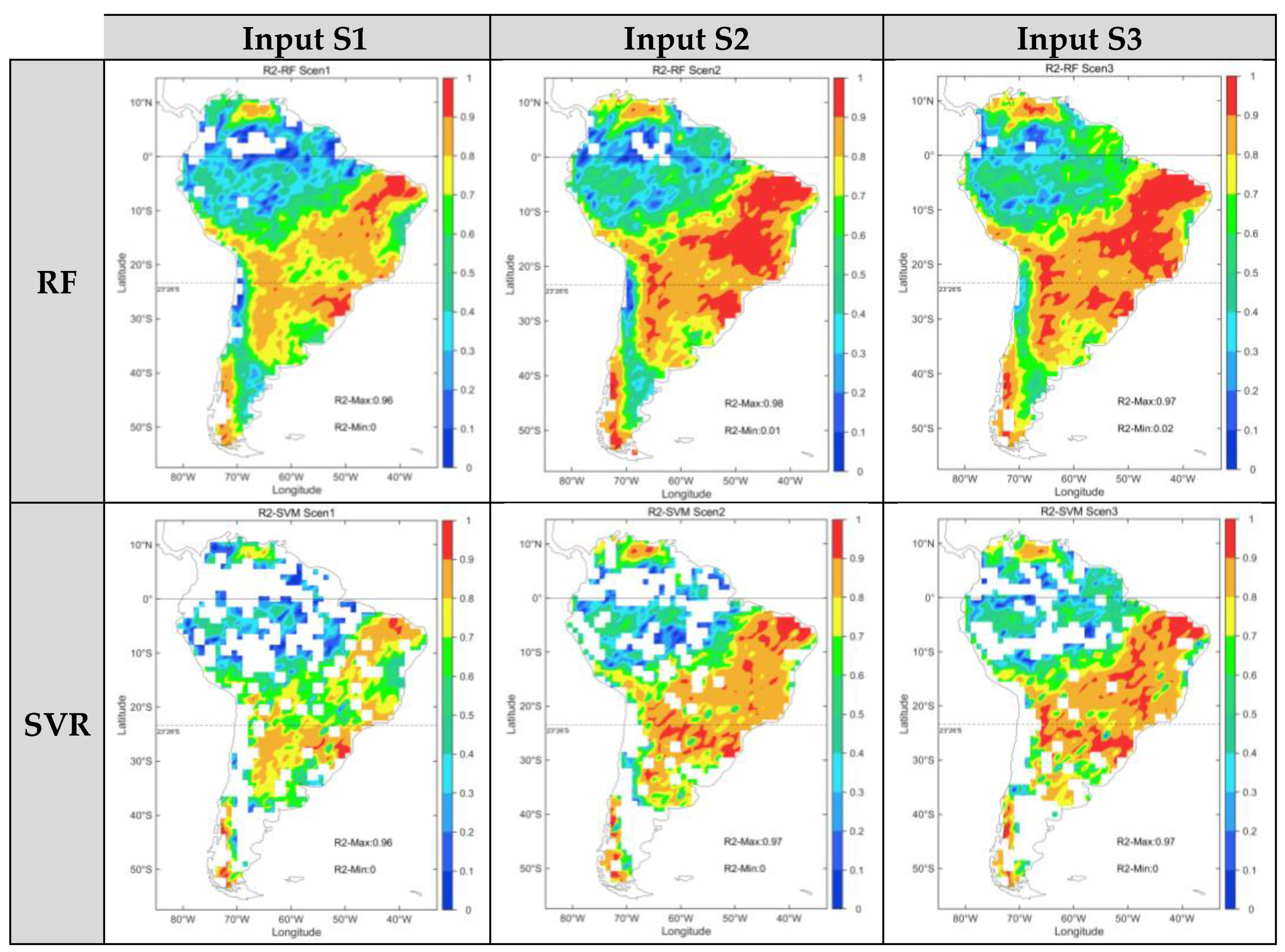
3.3.1. Accuracy of the Models under Different Input Strategies
3.3.2. Joint Optimal Prediction of Two Models
4. Discussion
4.1. The Framework of Trend Assessment
4.2. The Framework about the Relevant and Dominant Factor Assessment of AET
4.3. The Framework about the Joint Optimal Projection of AET
5. Conclusions
- In South America, AET increased significantly at a rate of 43.4 mm/10a recently and experienced an obvious decline in 2020 due to water shortage. In terms of spatial distribution, AET values tended to be lower on both sides while higher (>1000 mm) in the middle. AET in most areas of SA exhibited a significant ascending trend, especially in the Amazon area.
- With the P-coefficient exceeding 0.8, the correlation between AET and T, P, and NDVI was closer. The decisive factors obtained by Boruta algorithm were ranked as T > NDVI > P > PET > TWC > R, and NDVI controlled the largest area range. However, R was the primary determinant in the upper and middle reaches of the Amazon. It could be concluded that rapid runoff is the limiting factor for AET here due to the negative correlation.
- SVR paled in comparison to the RF in South America. By comparing the of the two models on the pixel scale and selecting the optimal model for simulation, the joint optimal prediction datasets were obtained. Furthermore, the S2 considering meteorological and vegetation data derived from MODIS simulated the most intensive future evaporation in the three input strategies.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Z.; Li, S.; Zhu, K.; Yang, T.; Shao, C. Does actual cropland water consumption change with evaporation potential in the Lower Yellow River? Agric. Ecosyst. Environ. 2021, 316, 107468. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef] [Green Version]
- Nistor, M.M.; Rai, P.K.; Carebia, I.A.; Singh, P.; Shahi, A.P.R.A.T.A.P.; Mishra, V.N. Comparison of the effectiveness of two budyko-based methods for actual evapotranspiration in Uttar Pradesh, India. Geogr. Tech. 2020, 15, 1–15. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Poon, P.K.; Kinoshita, A.M. Estimating evapotranspiration in a post-fire environment using remote sensing and machine learning. Remote Sens. 2018, 10, 1728. [Google Scholar] [CrossRef] [Green Version]
- Good, S.P.; Noone, D.; Bowen, G. Hydrologic connectivity constrains partitioning of global terrestrial water fluxes. Science 2015, 349, 175–177. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Wang, Q.; Yao, X.; Jiang, Q.; Yu, J.; Jiang, W. Variation in reference evapotranspiration over the Tibetan plateau during 1961–2017: Spatiotemporal variations, future trends and links to other climatic factors. Water 2020, 12, 3178. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to MSG-SEVIRI data in the Senegal River basin. Remote Sens. Environ. 2008, 112, 1242–1255. [Google Scholar] [CrossRef]
- Jin, X.; Guo, R.; Xia, W. Distribution of actual evapotranspiration over Qaidam basin, an Arid area in China. Remote Sens. 2013, 5, 6976–6996. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Lemeur, R. Evaluation of daily evapotranspiration estimates from instantaneous measurements. Agric. For. Meteorol. 1995, 74, 139–154. [Google Scholar] [CrossRef]
- Tandoǧdu, Y.; Camgöz, O. An experimental approach for estimating evapotranspiration. CIM Bull. 1999, 92, 55–60. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Gao, J.; Qiao, M.; Qiu, X.; Zeng, Y.; Hua, H.; Ye, X.; Adamu, M. Estimation of Actual Evapotranspiration Distribution in the Huaihe River Upstream Basin Based on the Generalized Complementary Principle. Adv. Meteorol. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Bouchet, R.J. Évapotranspiration Réelle Et Potentielle Signification Climatique. Int. Assoc. Sci. Hydrol. 1963, 62, 134–142. [Google Scholar]
- Xu, C.Y.; Chen, D. Comparison of seven models for estimation of evapotranspiration and groundwater recharge using lysimeter measurement data in Germany. Hydrol. Process. 2005, 19, 3717–3734. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. Measurement and estimation of actual evapotranspiration in the field under Mediterranean climate: A review. Eur. J. Agron. 2000, 13, 125–153. [Google Scholar] [CrossRef]
- Sarma, A.; Bharadwaj, K. Determination of crop-coefficients and estimation of evapotranspiration of rapeseed using lysimeter and different reference evapotranspiration models. J. Agrometeorol. 2020, 22, 172–178. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Gao, G.; Chen, D.; Xu, C.Y.; Simelton, E. Trend of estimated actual evapotranspiration over China during 1960–2002. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Singh Rawat, K.; Kumar Singh, S.; Bala, A.; Szabó, S. Estimation of crop evapotranspiration through spatial distributed crop coefficient in a semi-arid environment. Agric. Water Manag. 2019, 213, 922–933. [Google Scholar] [CrossRef]
- Seiler, C.; Moene, A.F. Estimating actual evapotranspiration from satellite and meteorological data in central Bolivia. Earth Interact. 2011, 15, 1–24. [Google Scholar] [CrossRef]
- Sawadogo, A.; Gündoğdua, K.S.; Tim, H.; Demir, A.O.; Ünlü, M.; Zwart, S.J. Comparative analysis of the pysebal model and lysimeter for estimating actual evapotranspiration of soybean crop in Adana, Turkey. Int. J. Eng. Geosci. 2020, 5, 60–65. [Google Scholar] [CrossRef]
- Tofigh, S.; Rahimi, D.; Zakerinejad, R. A comparison of actual evapotranspiration estimates based on Remote Sensing approaches with a classical climate data driven method. Acta Univ. Carol. Geogr. 2020, 55, 165–182. [Google Scholar] [CrossRef]
- Wu, B.; Zhu, W.; Yan, N.; Xing, Q.; Xu, J.; Ma, Z.; Wang, L. Regional actual evapotranspiration estimation with land and meteorological variables derived from multi-source satellite data. Remote Sens. 2020, 12, 332. [Google Scholar] [CrossRef] [Green Version]
- Ansari, H.; Marofi, S.; Mohamadi, M. Topography and Land Cover Effects on Snow Water Equivalent Estimation Using AMSR-E and GLDAS Data. Water Resour. Manag. 2019, 33, 1699–1715. [Google Scholar] [CrossRef]
- Moghim, S. Assessment of Water Storage Changes Using GRACE and GLDAS. Water Resour. Manag. 2020, 34, 685–697. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Chen, X.; Qiao, Y. Analysis on impacts of hydro-climatic changes and human activities on available water changes in Central Asia. Sci. Total Environ. 2020, 737, 139779. [Google Scholar] [CrossRef]
- Andam-Akorful, S.A.; Ferreira, V.G.; Awange, J.L.; Forootan, E.; He, X.F. Multi-model and multi-sensor estimations of evapotranspiration over the Volta Basin, West Africa. Int. J. Clim. 2015, 35, 3132–3145. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Khan, M.S.; Baik, J.; Choi, M. Inter-comparison of evapotranspiration datasets over heterogeneous landscapes across Australia. Adv. Space Res. 2020, 66, 533–545. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Bai, X.; Tang, H.; Cao, Y.; Wang, M.; Wu, L. Inversion and spatiotemporal evolution of actual evapotranspiration in southwest China for the past 50 years. Shengtai Xuebao/Acta Ecol. Sin. 2018, 38, 8835–8848. [Google Scholar] [CrossRef]
- Liu, J.; Meng, X.; Ma, Y.; Liu, X. Introduce canopy temperature to evaluate actual evapotranspiration of green peppers using optimized ENN models. J. Hydrol. 2020, 590, 125437. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Filgueiras, R.; Almeida, T.S.; Mantovani, E.C.; Dias, S.H.B.; Fernandes-Filho, E.I.; da Cunha, F.F.; Venancio, L.P. Soil water content and actual evapotranspiration predictions using regression algorithms and remote sensing data. Agric. Water Manag. 2020, 241, 106346. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Shukla, S. Support vector machine based modeling of evapotranspiration using hydro-climatic variables in a sub-tropical environment. Agric. For. Meteorol. 2015, 200, 172–184. [Google Scholar] [CrossRef]
- Hu, S.; Mo, X. Attribution of long-term evapotranspiration trends in the mekong river basin with a remote sensing-based process model. Remote Sens. 2021, 13, 303. [Google Scholar] [CrossRef]
- Gao, X.; Sun, M.; Luan, Q.; Zhao, X.; Wang, J.; He, G.; Zhao, Y. The spatial and temporal evolution of the actual evapotranspiration based on the remote sensing method in the Loess Plateau. Sci. Total Environ. 2020, 708, 135111. [Google Scholar] [CrossRef]
- Scornet, E. Random forests and kernel methods. IEEE Trans. Inf. Theory 2016, 62, 1485–1500. [Google Scholar] [CrossRef] [Green Version]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- He, W.; Wang, Z.; Jiang, H. Model optimizing and feature selecting for support vector regression in time series forecasting. Neurocomputing 2008, 72, 600–611. [Google Scholar] [CrossRef]
- Salati, E.; Vose, P.B. Amazon Basin: A system in equilibrium. Science 1984, 225, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Marengo, J.A.; Tomasella, J.; Alves, L.M.; Soares, W.R.; Rodriguez, D.A. The drought of 2010 in the context of historical droughts in the Amazon region. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Hill, K.J.; Taschetto, A.S.; England, M.H. South American rainfall impacts associated with inter-El Niño variations. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Gloor, M.; Brienen, R.J.W.; Galbraith, D.; Feldpausch, T.R.; Schöngart, J.; Guyot, J.L.; Espinoza, J.C.; Lloyd, J.; Phillips, O.L. Intensification of the Amazon hydrological cycle over the last two decades. Geophys. Res. Lett. 2013, 40, 1729–1733. [Google Scholar] [CrossRef]
- Marengo, J.A.; Liebmann, B.; Grimm, A.M.; Misra, V.; Silva Dias, P.L.; Cavalcanti, I.F.A.; Carvalho, L.M.V.; Berbery, E.H.; Ambrizzi, T.; Vera, C.S.; et al. Recent developments on the South American monsoon system. Int. J. Climatol. 2012, 32, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Polade, S.D.; Pierce, D.W.; Cayan, D.R.; Gershunov, A.; Dettinger, M.D. The key role of dry days in changing regional climate and precipitation regimes. Sci. Rep. 2014, 4, 1–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Zheng, K.; Wei, J.Z.; Pei, J.Y.; Cheng, H.; Zhang, X.L.; Huang, F.Q.; Li, F.M.; Ye, J.S. Impacts of climate change and human activities on grassland vegetation variation in the Chinese Loess Plateau. Sci. Total Environ. 2019, 660, 236–244. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.R.; Reichstein, M. Trend Change detection in NDVI time series: Effects of inter-annual variability and methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef] [Green Version]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model. Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef] [Green Version]
- O’Neill, B.C.; Kriegler, E.; Ebi, K.L.; Kemp-Benedict, E.; Riahi, K.; Rothman, D.S.; van Ruijven, B.J.; van Vuuren, D.P.; Birkmann, J.; Kok, K.; et al. The roads ahead: Narratives for shared socioeconomic pathways describing world futures in the 21st century. Glob. Environ. Chang. 2017, 42, 169–180. [Google Scholar] [CrossRef] [Green Version]
- Ayugi, B.; Ngoma, H.; Babaousmail, H.; Karim, R.; Iyakaremye, V.; Lim Kam Sian, K.T.C.; Ongoma, V. Evaluation and projection of mean surface temperature using CMIP6 models over East Africa. J. Afr. Earth Sci. 2021, 181, 104226. [Google Scholar] [CrossRef]
- Rehana, S.; Sireesha Naidu, G. Development of hydro-meteorological drought index under climate change—Semi-arid river basin of Peninsular India. J. Hydrol. 2021, 594, 125973. [Google Scholar] [CrossRef]
- Hůnová, I.; Bäumelt, V.; Modlík, M. Long-term trends in nitrogen oxides at different types of monitoring stations in the Czech Republic. Sci. Total Environ. 2020, 699, 134378. [Google Scholar] [CrossRef] [PubMed]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, X.; Wang, Q.; Yu, J.; Jiang, Q.; Jiang, W.; Li, L. Differences in reference evapotranspiration variation and climate-driven patterns in different altitudes of the Qinghai–Tibet plateau (1961–2017). Water 2021, 13, 1749. [Google Scholar] [CrossRef]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Weekly soil moisture forecasting with multivariate sequential, ensemble empirical mode decomposition and Boruta-random forest hybridizer algorithm approach. Catena 2019, 177, 149–166. [Google Scholar] [CrossRef]
- Alresheedi, A.A.; Al-Hagery, M.A. Forecasting the global horizontal irradiance based on boruta algorithm and artificial neural networks using a lower cost. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 11. [Google Scholar] [CrossRef]
- Kursa, M.B.; Jankowski, A.; Rudnicki, W.R. Boruta—A system for feature selection. Fundam. Inform. 2010, 101, 271–285. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Qu, J.; Ren, K.; Shi, X. Binary Grey Wolf Optimization-Regularized Extreme Learning Machine Wrapper Coupled with the Boruta Algorithm for Monthly Streamflow Forecasting. Water Resour. Manag. 2021, 35, 1029–1045. [Google Scholar] [CrossRef]
- Drucker, H.; Surges, C.J.C.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Salcedo-Sanz, S.; Ortiz-García, E.G.; Pérez-Bellido, Á.M.; Portilla-Figueras, A.; Prieto, L. Short term wind speed prediction based on evolutionary support vector regression algorithms. Expert Syst. Appl. 2011, 38, 4052–4057. [Google Scholar] [CrossRef]
- Santamaría-Bonfil, G.; Reyes-Ballesteros, A.; Gershenson, C. Wind speed forecasting for wind farms: A method based on support vector regression. Renew. Energy 2016, 85, 790–809. [Google Scholar] [CrossRef]
- Zhong, S.; Xie, X.; Lin, L. Two-layer random forests model for case reuse in case-based reasoning. Expert Syst. Appl. 2015, 42, 9412–9425. [Google Scholar] [CrossRef]
- Mohammadi, B.; Mehdizadeh, S. Modeling daily reference evapotranspiration via a novel approach based on support vector regression coupled with whale optimization algorithm. Agric. Water Manag. 2020, 237, 106145. [Google Scholar] [CrossRef]
- Arlot, S.; Genuer, R. Comments on: A random forest guided tour. Test 2016, 25, 228–238. [Google Scholar] [CrossRef] [Green Version]
- Marceau, D.J.; Howarth, P.J.; Gratton, D.J. Remote sensing and the measurement of geographical entities in a forested environment. 1. The scale and spatial aggregation problem. Remote Sens. Environ. 1994, 49, 93–104. [Google Scholar] [CrossRef]
- Jin, Z.; Ma, Y.; Chu, L.; Liu, Y.; Dubrow, R.; Chen, K. Predicting spatiotemporally-resolved air temperature over Sweden from satellite data using an ensemble model. ISEE Conf. Abstr. 2021, 2021. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, Q.; Hao, X.; Yue, P. Changes in Evapotranspiration Over Global Semiarid Regions 1984–2013. J. Geophys. Res. Atmos. 2019, 124, 2946–2963. [Google Scholar] [CrossRef]
- Elder, R.C.; Balling, R.C.; Cerveny, R.S.; Krahenbuhl, D. Regional Variability in Drought as a Function of the Atlantic Multidecadal Oscillation. Caribb. J. Sci. 2014, 48, 31–43. [Google Scholar] [CrossRef]
- de Oliveira, R.G.; Valle Júnior, L.C.G.; da Silva, J.B.; Espíndola, D.A.L.F.; Lopes, R.D.; Nogueira, J.S.; Curado, L.F.A.; Rodrigues, T.R. Temporal trend changes in reference evapotranspiration contrasting different land uses in southern Amazon basin. Agric. Water Manag. 2021, 250, 106815. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Chura, O.; López-Moreno, J.I.; Azorin-Molina, C.; Sanchez-Lorenzo, A.; Aguilar, E.; Moran-Tejeda, E.; Trujillo, F.; Martínez, R.; Nieto, J.J. Spatio-temporal variability of droughts in Bolivia: 1955–2012. Int. J. Clim. 2015, 35, 3024–3040. [Google Scholar] [CrossRef] [Green Version]
- de Carvalho Alves, M.; de Carvalho, L.G.; Vianello, R.L.; Sediyama, G.C.; de Oliveira, M.S.; de Sá Junior, A. Geostatistical improvements of evapotranspiration spatial information using satellite land surface and weather stations data. Theor. Appl. Climatol. 2013, 113, 155–174. [Google Scholar] [CrossRef]
- Martinez, C.J.; Thepadia, M. Estimating Reference Evapotranspiration with Minimum Data in Florida. J. Irrig. Drain. Eng. 2010, 136, 494–501. [Google Scholar] [CrossRef]
- Ghilain, N.; Arboleda, A.; Sepulcre-Cantò, G.; Batelaan, O.; Ardö, J.; Gellens-Meulenberghs, F. Improving evapotranspiration in a land surface model using biophysical variables derived from MSG/SEVIRI satellite. Hydrol. Earth Syst. Sci. 2012, 16, 2567–2583. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.H.; Souza-Filho, J.D.C.; Ribeiro, A. Comments on “The regional evapotranspiration of the Amazon”. J. Hydrometeorol. 2004, 5, 1279–1280. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, X. Climate change impacts on global agricultural water deficit. Geophys. Res. Lett. 2013, 40, 1111–1117. [Google Scholar] [CrossRef]
- Thaler, V.; Loikith, P.C.; Mechoso, C.R.; Pampuch, L.A. A multivariate assessment of climate change projections over South America using the fifth phase of the Coupled Model Intercomparison Project. Int. J. Clim. 2021, 41, 4265–4282. [Google Scholar] [CrossRef]
- Brêda, J.P.L.F.; de Paiva, R.C.D.; Collischon, W.; Bravo, J.M.; Siqueira, V.A.; Steinke, E.B. Climate change impacts on South American water balance from a continental-scale hydrological model driven by CMIP5 projections. Clim. Chang. 2020, 159, 503–522. [Google Scholar] [CrossRef]



| Variables | Abbr. | Version | Spatial Resolutions | Time Span | Data Source (11 July 2021) |
|---|---|---|---|---|---|
| Temperature | T | CRU TS Version 4.05 | 0.5 degrees | 2001–2020 | https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.05/ge/ |
| Precipitation | P | CRU TS Version 4.05 | 0.5 degrees | 2001–2020 | https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.05/ge/ |
| Potential evapotranspiration | PET | CRU TS Version 4.05 | 0.5 degrees | 2001–2020 | https://crudata.uea.ac.uk/cru/data/hrg/cru_ts_4.05/ge/ |
| Actual evapotranspiration | AET | GLDAS Noah2.1 | 0.25 degrees | 2000–2020 | https://disc.gsfc.nasa.gov/datasets/ |
| Surface runoff | Qs | GLDAS Noah2.1 | 0.25 degrees | 2000–2020 | https://disc.gsfc.nasa.gov/datasets/ |
| Subface runoff | Qsb | GLDAS Noah2.1 | 0.25 degrees | 2000–2020 | https://disc.gsfc.nasa.gov/datasets/ |
| Snowmelt runoff | Qsm | GLDAS Noah2.1 | 0.25 degrees | 2000–2020 | https://disc.gsfc.nasa.gov/datasets/ |
| Total water storage changes | TWC | JPL GRACE(-FO) RL06 | 0.5 degrees | 2002–2020 | https://grace.jpl.nasa.gov/ |
| Normalized Difference Vegetation Index | NDVI | MOD13C2 Version6 | 0.05 degrees | 2000–2020 | https://lpdaac.usgs.gov/products/mod13c2v006/ |
| Temperature | T | CMIP6-NCAR SSP245 | 100 km | 2020–2090 | https://esgf-node.llnl.gov/projects/cmip6/ |
| Precipitation | P | CMIP6-NCAR SSP245 | 100 km | 2020–2090 | https://esgf-node.llnl.gov/projects/cmip6/ |
| Potential evapotranspiration | PET | IPSL-CM6A-LR SSP245 | 250 km | 2020–2090 | https://cmc.ipsl.fr/all-projects/ |
| Month | Z-Value | Climate Change Rate (mm/10a) |
|---|---|---|
| January | 3.15 | 5.59 |
| February | 3.43 | 5.31 |
| March | 2.38 | 4.52 |
| April | 3.15 | 4.97 |
| May | 2.87 | 5.61 |
| June | 2.59 | 4.78 |
| July | 2.03 | 3.28 |
| August | 1.68 | 2.72 |
| September | 0.28 | 0.62 |
| October | 0.77 | 0.15 |
| November | 1.75 | 2.61 |
| December | 2.03 | 3.23 |
| T | P | PET | NDVI | R | TWC | |
|---|---|---|---|---|---|---|
| Correlation coefficient | 0.832 | 0.813 | 0.587 | 0.822 | 0.267 | 0.638 |
| Boruta-order of importance | First | Third | Fourth | Second | Sixth | Fifth |
| Order | T | P | PET | NDVI | R | TWC |
|---|---|---|---|---|---|---|
| First | 10.34 | 13.97 | 23.22 | 24.85 | 21.52 | 6.10 |
| Second | 20.02 | 15.41 | 21.39 | 16.61 | 22.46 | 4.13 |
| Third | 14.69 | 16.59 | 21.34 | 21.49 | 21.27 | 4.63 |
| Fourth | 12.46 | 26.98 | 18.35 | 13.23 | 21.22 | 7.75 |
| Fifth | 25.73 | 17.94 | 14.25 | 11.04 | 12.50 | 18.53 |
| Sixth | 16.76 | 9.11 | 1.45 | 12.78 | 1.04 | 58.86 |
| Input Strategies | Meteorological Factors | Vegetation Index | Hydrological Factors | Description |
|---|---|---|---|---|
| Input S1 | T, P, and PET From CMIP6 | Not input | Not input | Only Forced by the meteorological Factors during 2020–2090 |
| Input S2 | T, P, and PET From CMIP6 | Monthly historical average NDVI | Not input | The future monthly NDVI roughly represented by the historical mean value |
| Input S3 | T, P, and PET From CMIP6 | Monthly historical average NDVI | Monthly historical average R and TWC | The future monthly NDVI, R, and TWC roughly represented by the historical mean value |
| Input Strategies | Model | |||
|---|---|---|---|---|
| Input S1 | RF | 4.73 | 42.09 | 59.17 |
| SVR | 2.52 | 28.67 | 45.43 | |
| Input S2 | RF | 16.95 | 51.61 | 64.84 |
| SVR | 9.26 | 42.85 | 54.95 | |
| Input S3 | RF | 16.57 | 53.94 | 70.70 |
| SVR | 10.27 | 42.79 | 55.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yue, Q.; Wang, Q.; Yu, J.; Zheng, Y.; Yao, X.; Xu, S. A Framework for Actual Evapotranspiration Assessment and Projection Based on Meteorological, Vegetation and Hydrological Remote Sensing Products. Remote Sens. 2021, 13, 3643. https://doi.org/10.3390/rs13183643
Liu Y, Yue Q, Wang Q, Yu J, Zheng Y, Yao X, Xu S. A Framework for Actual Evapotranspiration Assessment and Projection Based on Meteorological, Vegetation and Hydrological Remote Sensing Products. Remote Sensing. 2021; 13(18):3643. https://doi.org/10.3390/rs13183643
Chicago/Turabian StyleLiu, Yuan, Qimeng Yue, Qianyang Wang, Jingshan Yu, Yuexin Zheng, Xiaolei Yao, and Shugao Xu. 2021. "A Framework for Actual Evapotranspiration Assessment and Projection Based on Meteorological, Vegetation and Hydrological Remote Sensing Products" Remote Sensing 13, no. 18: 3643. https://doi.org/10.3390/rs13183643
APA StyleLiu, Y., Yue, Q., Wang, Q., Yu, J., Zheng, Y., Yao, X., & Xu, S. (2021). A Framework for Actual Evapotranspiration Assessment and Projection Based on Meteorological, Vegetation and Hydrological Remote Sensing Products. Remote Sensing, 13(18), 3643. https://doi.org/10.3390/rs13183643






