A Parallel Method for Open Hole Filling in Large-Scale 3D Automatic Modeling Based on Oblique Photography
Abstract
:1. Introduction
- Hierarchical relationships between open holes are established in accordance with the topological proximity relations between holes in various partitioning cells as elementary units for hole filling.
- A general algorithm is constructed to convert open holes into closed holes based on the topological closure principle.
- Hole filling is performed layer by layer from the external boundary holes using adjacency information, and the filling results at the cell boundaries are smoothed using the Laplacian operator.
2. Related Work
2.1. Existing Open Hole Filling Method for Oblique Photography
2.2. Limitations of the Existing Method
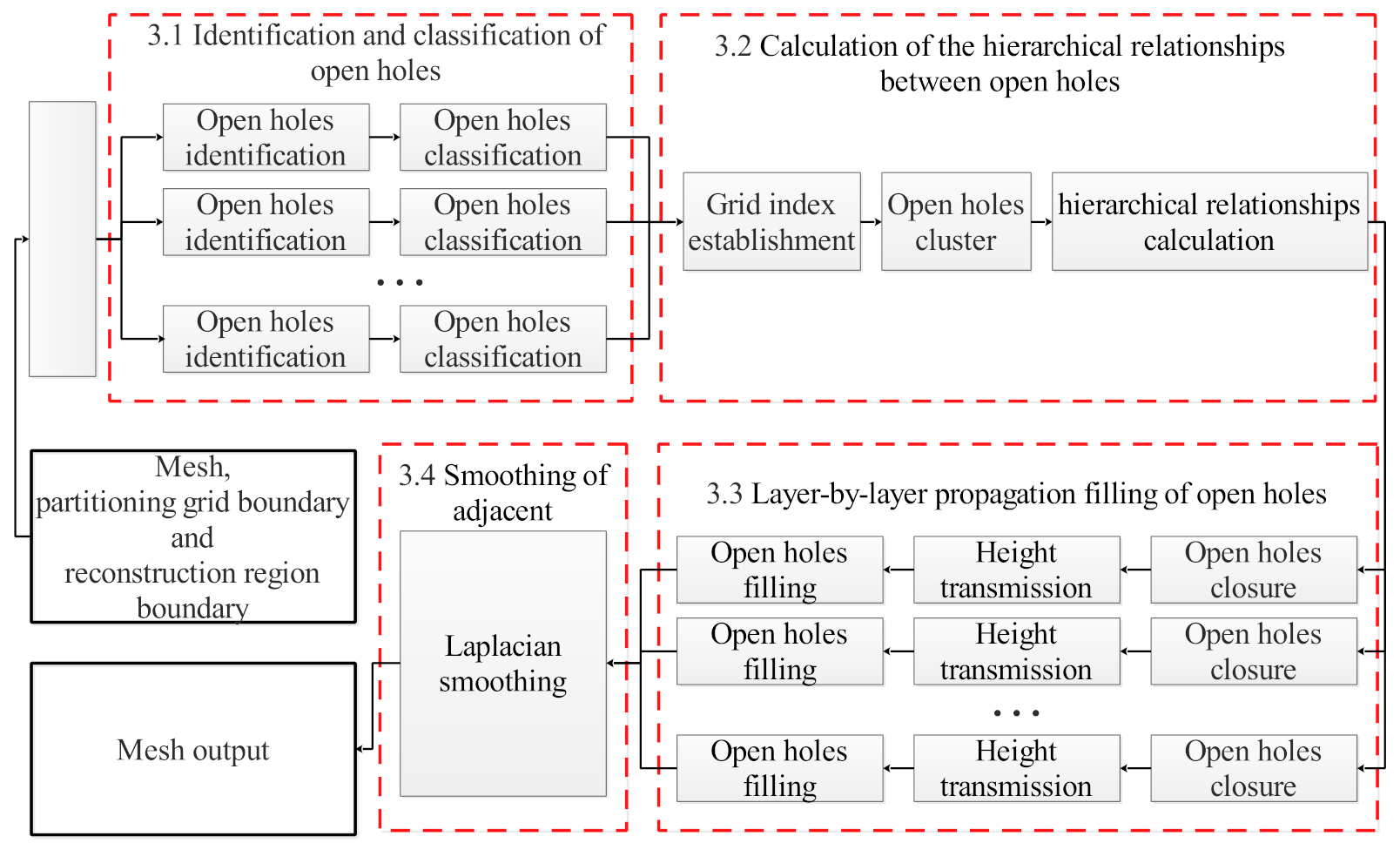
3. Methodology
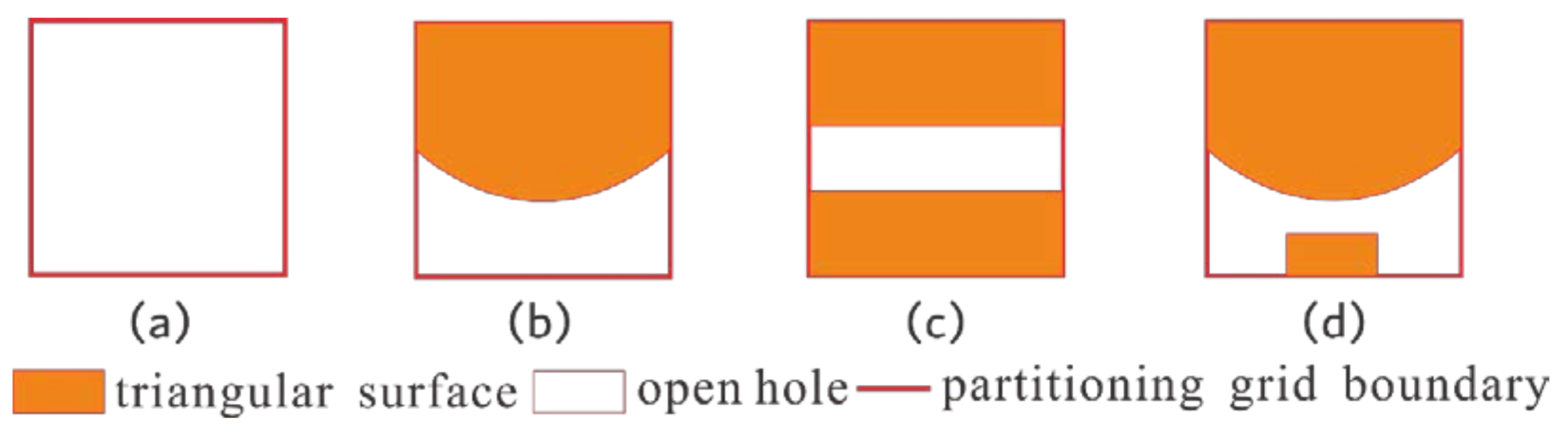
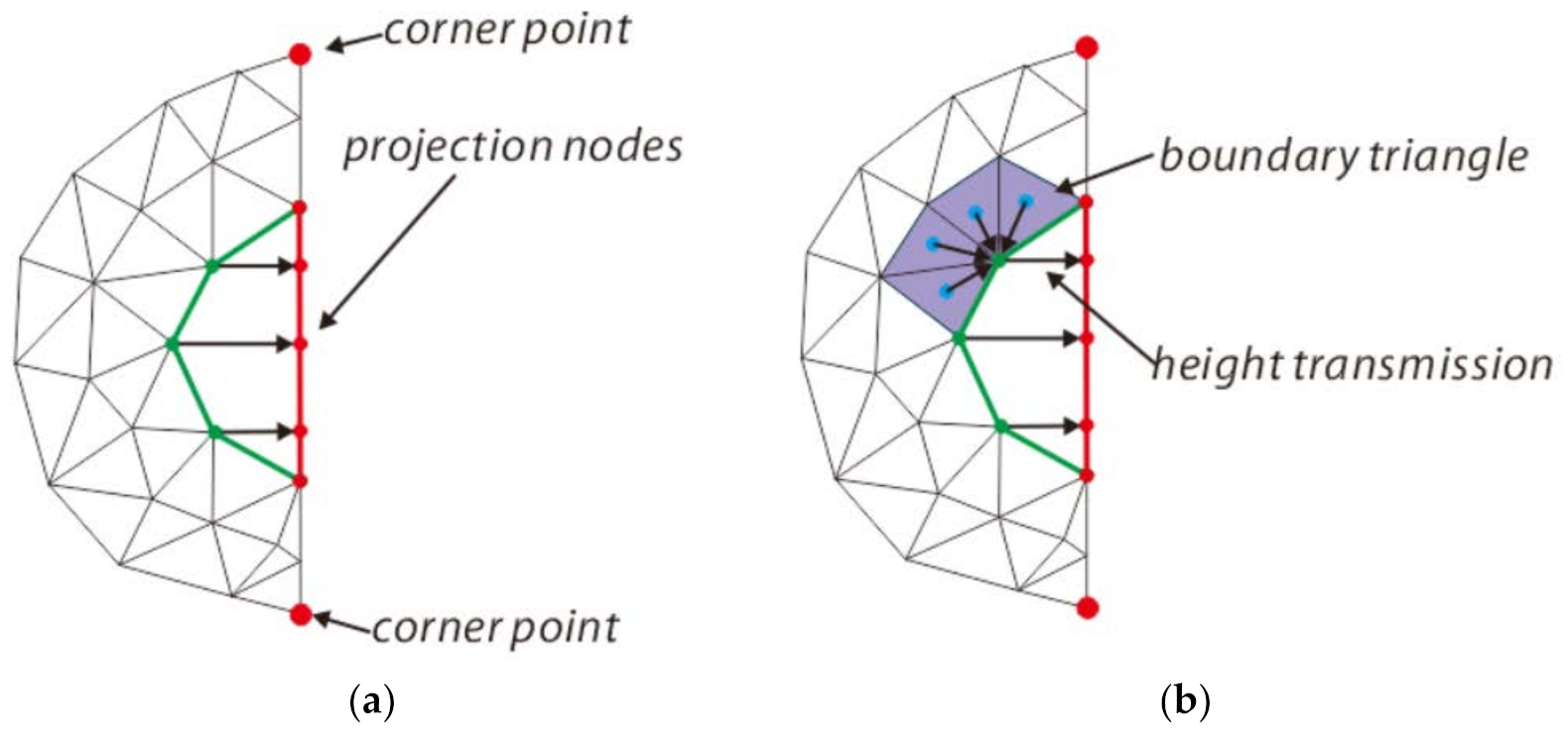
3.1. Identification and Classification of Open Holes
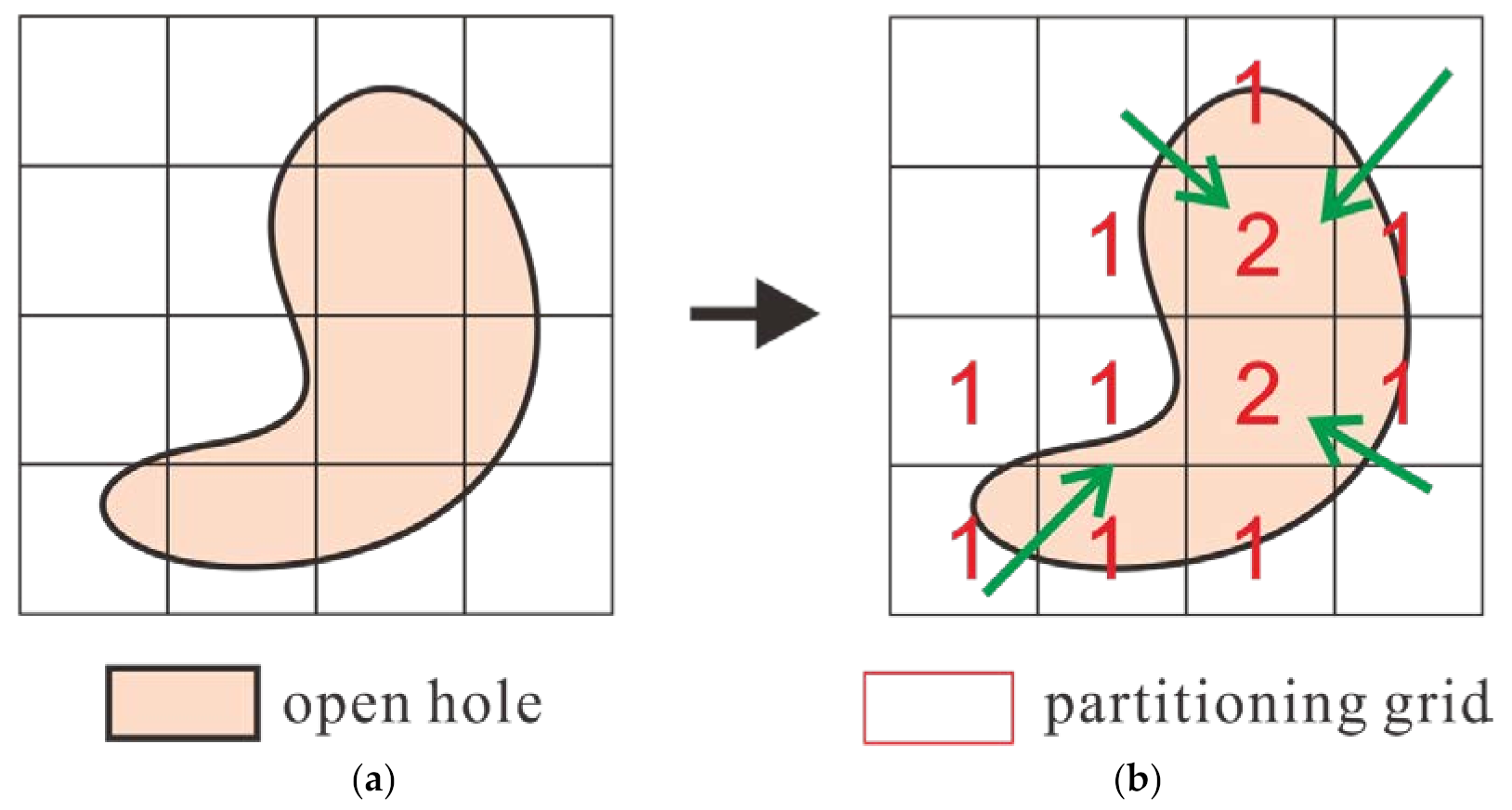
3.2. Calculation of the Hierarchical Relationships between Open Holes
3.3. Layer-by-Layer Propagation Filling of Open Holes
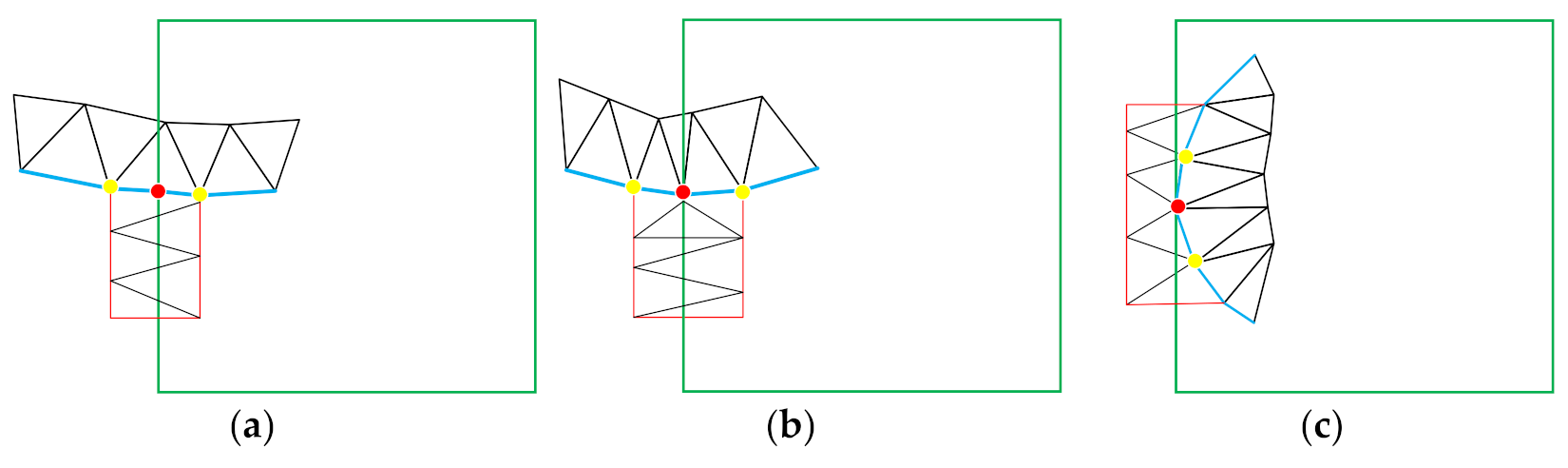
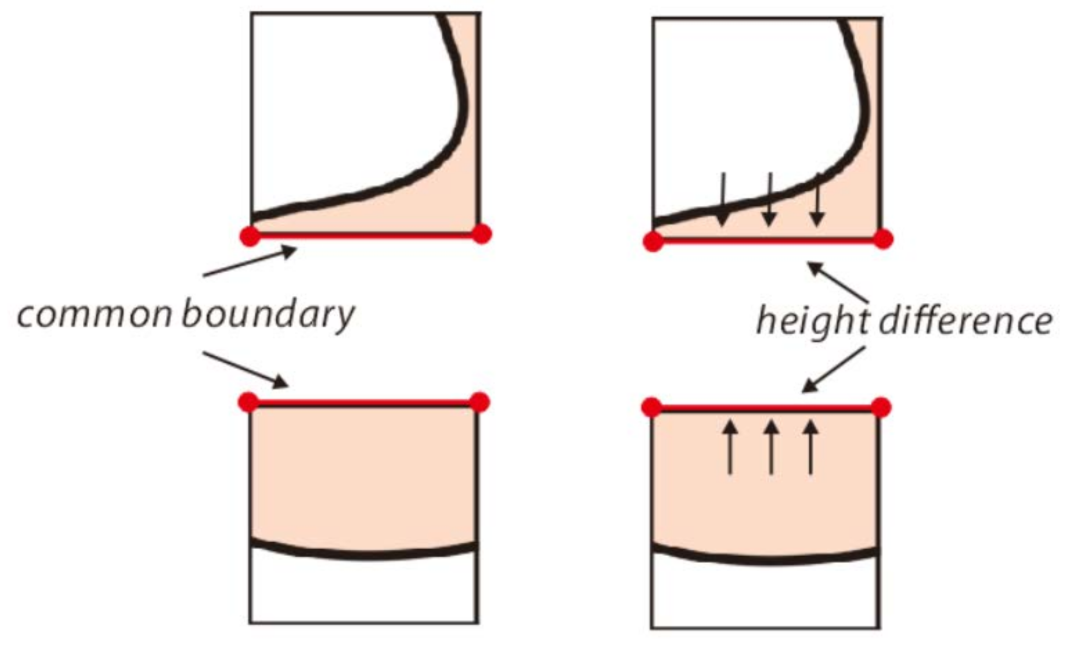
3.4. Smoothing of Adjacent Holes
4. Experiments and Analyses
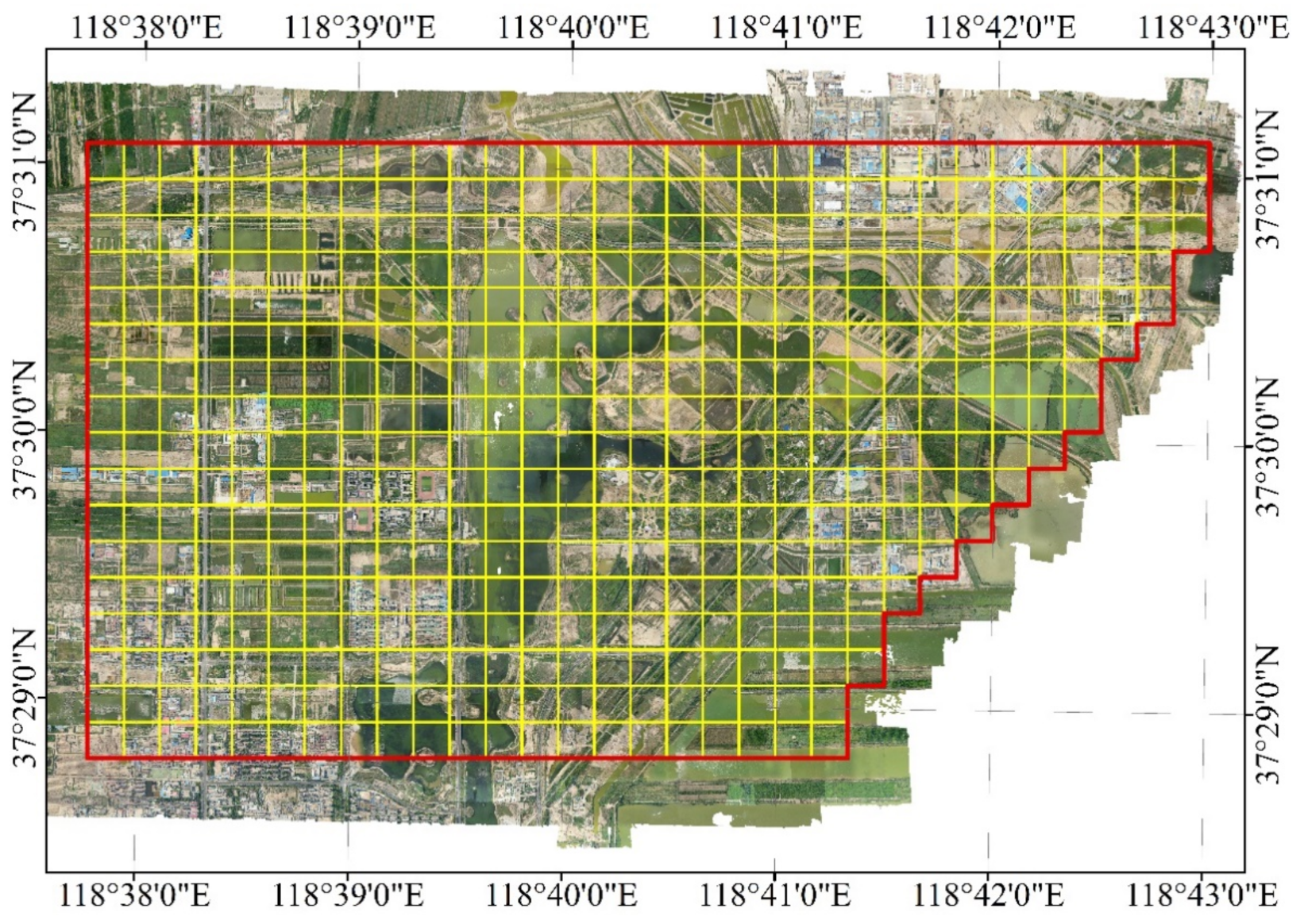
4.1. Experimental Data and Running Environment
4.2. Comparative Analysis of Filling Success Rate
- Comparison of the filling success rates in a local experimental area
- 2.
- Comparison of the filling success rates in the global experimental area
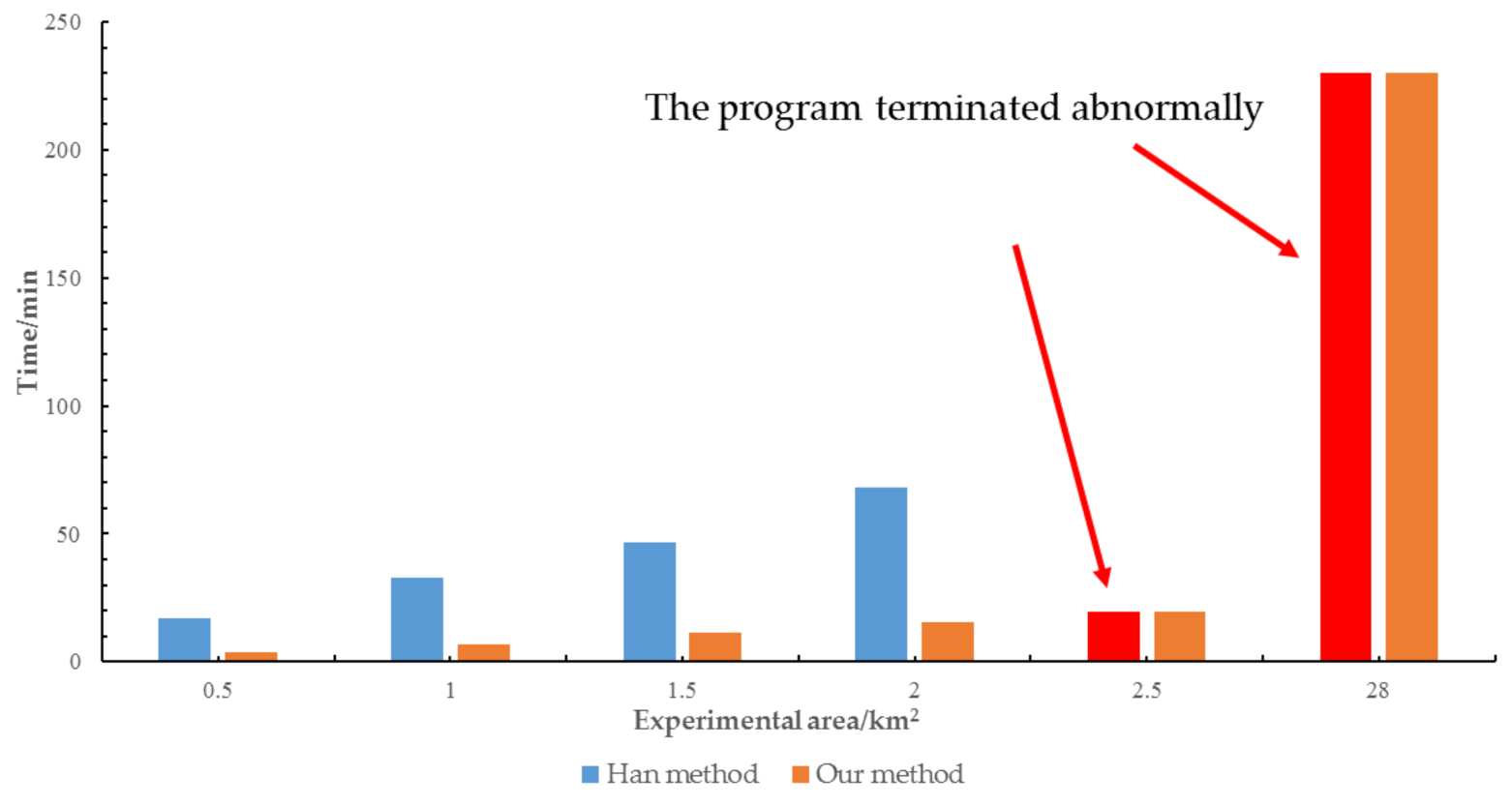
4.3. Comparative Analysis of Filling Efficiency
- Comparison of hole filling time consumption
- 2.
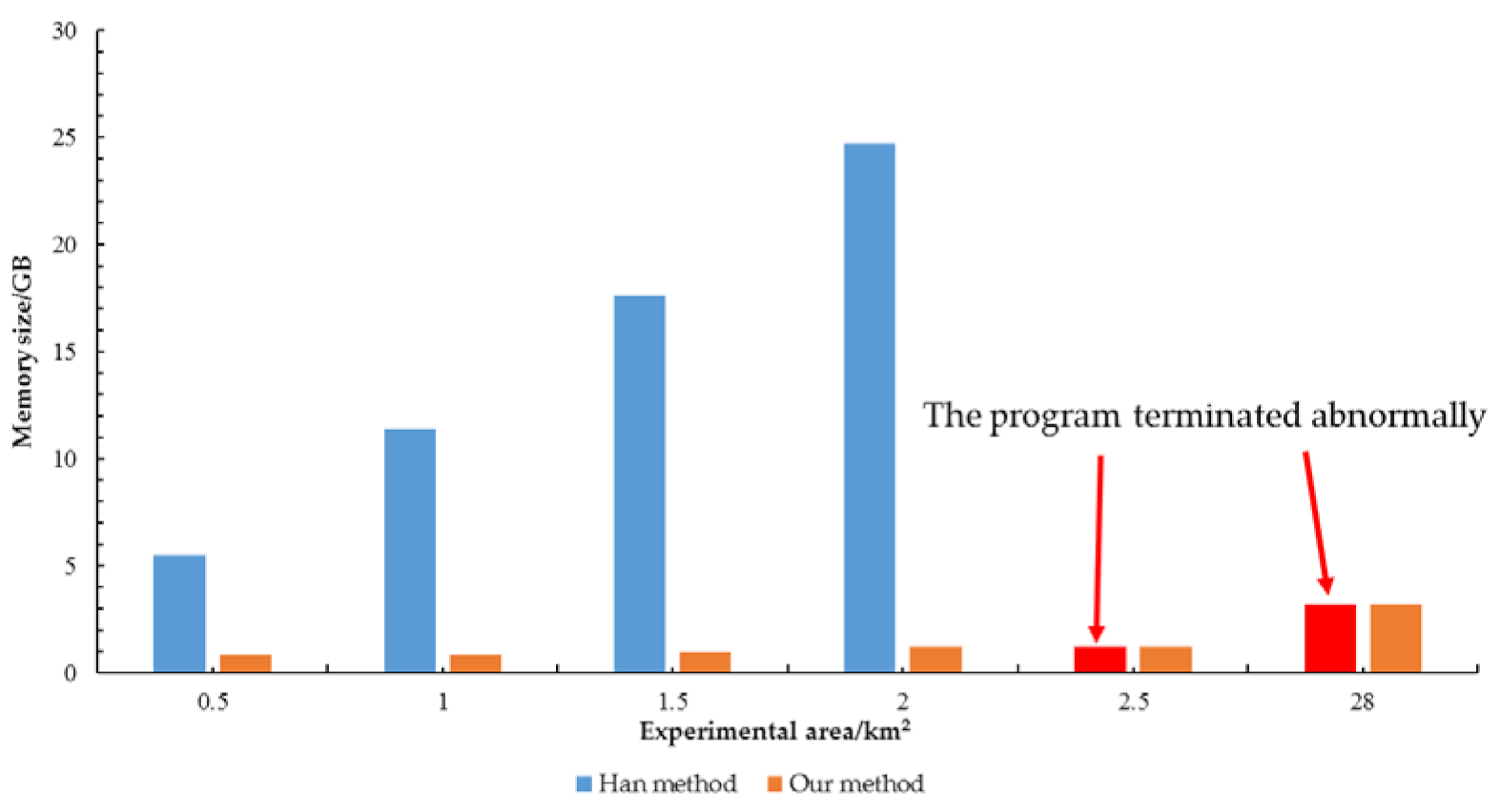
- Comparison of memory consumption for hole filling
4.4. Comparative Analysis of Filling Accuracy
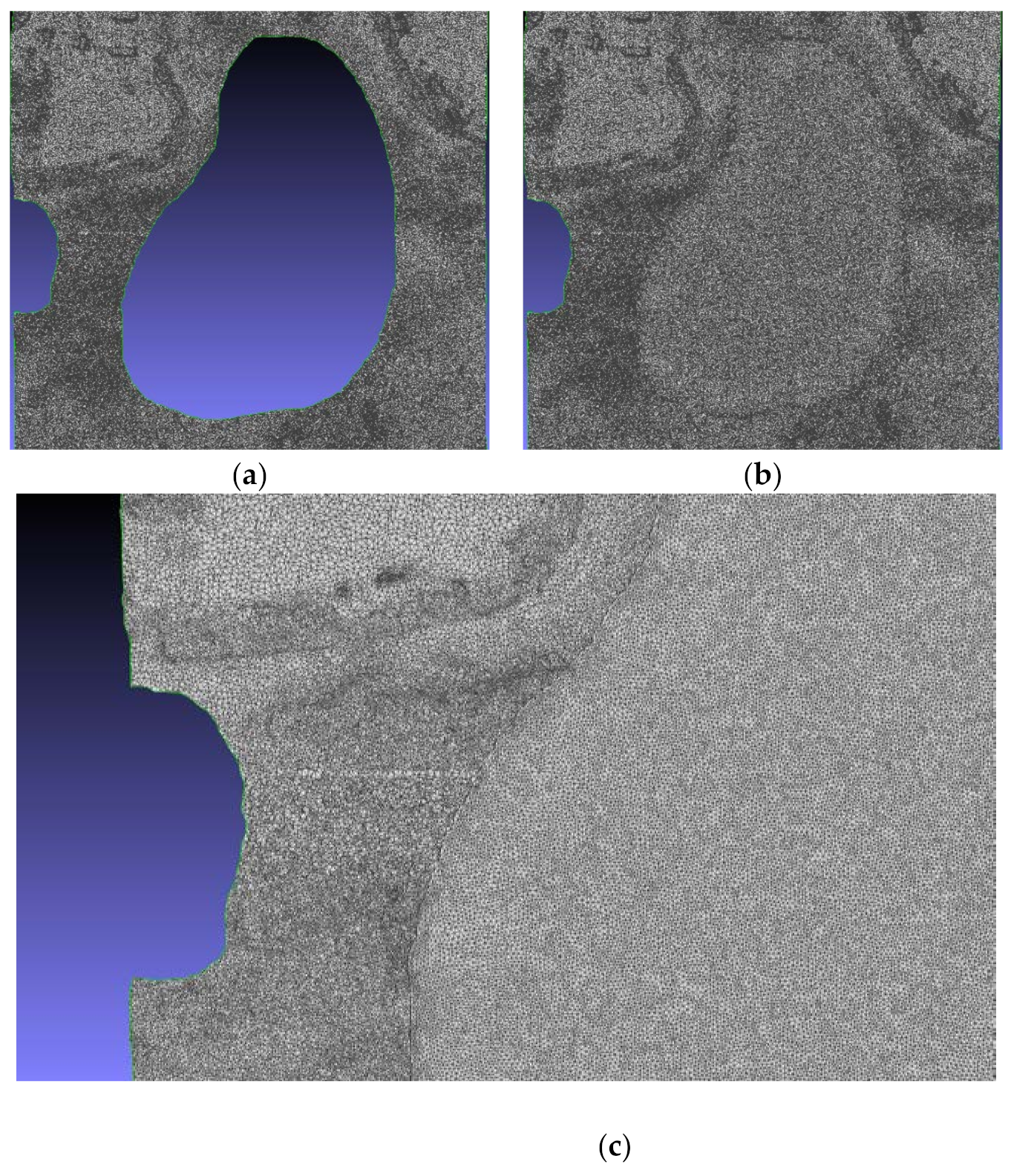
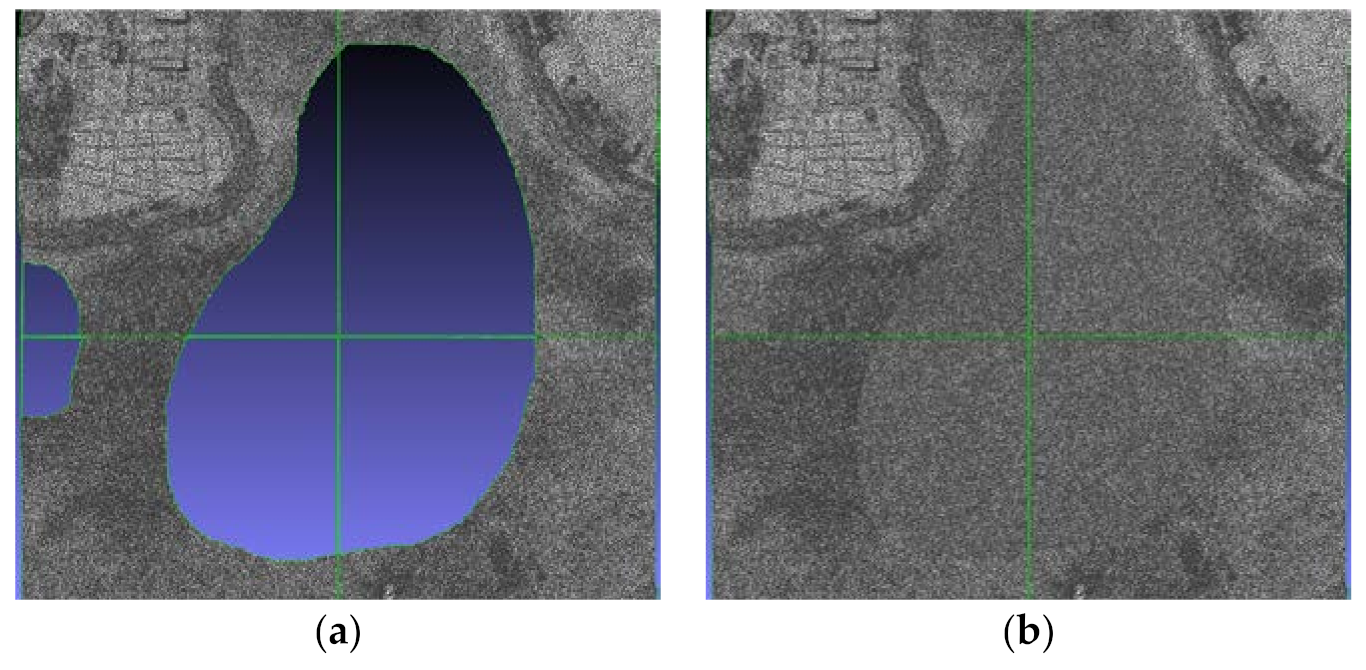
- Comparison of Hole Filling Results
- 2.
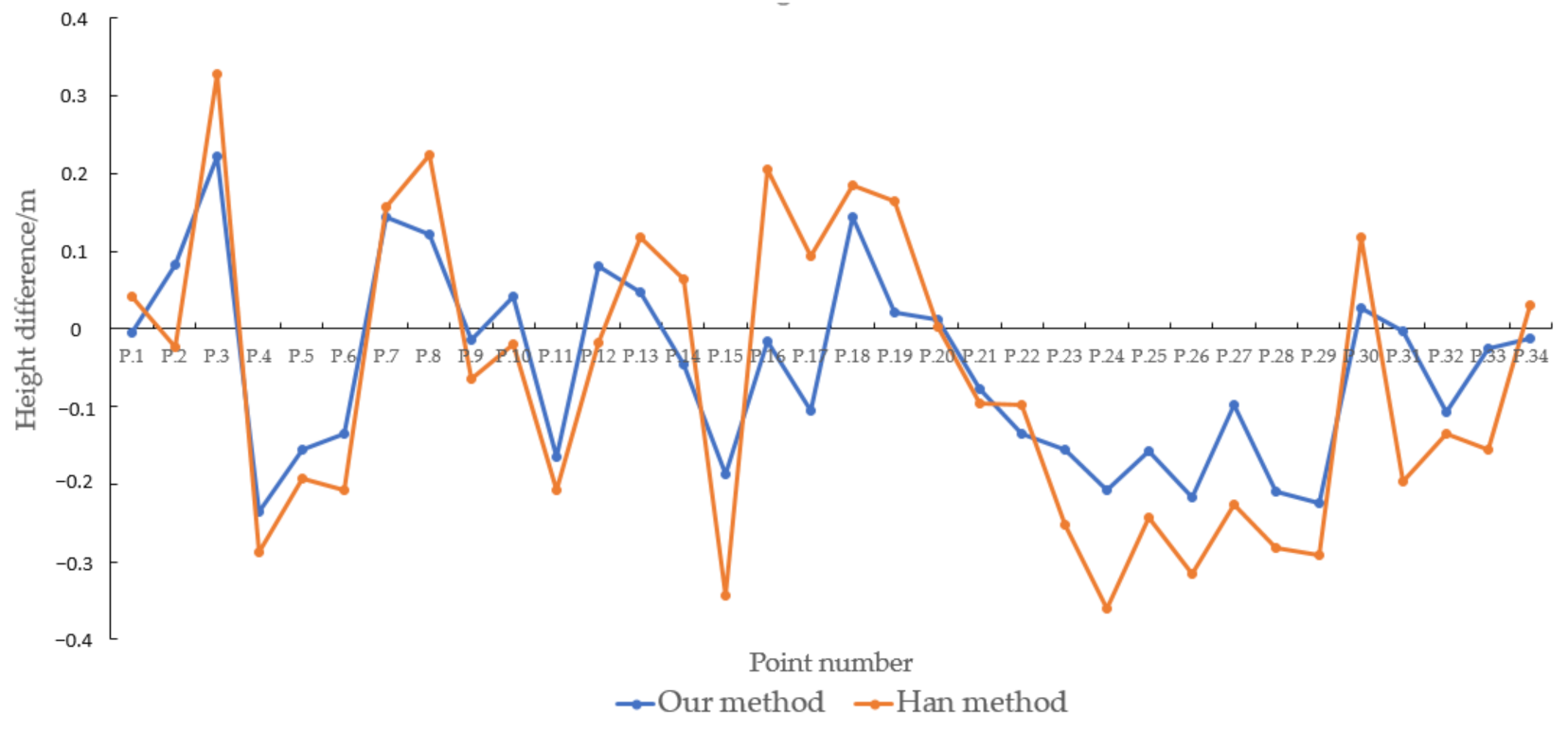
- Comparison of Hole Filling Accuracy
5. Conclusions
- Concerning the filling success rate, for closed holes, which are commonly encountered in large-scale 3D automatic modeling, the proposed method is consistent with the state-of-the-art Han method. Additionally, the proposed approach has a 12.4% higher success rate for filling type I open holes than the Han method and successfully compensates for the limitations of the existing method in the filling of type II open holes.
- In terms of the efficiency of hole filling, when implemented on a standard personal computer, the Han method is applicable only for hole filling in a small area (≤2 km2). When the experimental area is large (>2 km2), the use of the Han method leads to computer crashes because of the excessive amount of data to be processed. Moreover, even within the repairable scope, the time consumption of the Han method is approximately 4–5 times greater than that of the proposed method, and its memory consumption is approximately 7–21 times greater.
- Regarding the repair accuracy, the proposed method exhibits high height accuracy and minor errors, with the average and standard deviation of the height differences being 37.5% and 38.9% lower than those of the Han method, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bendels, G.H.; Schnabel, R.; Klein, R. Detecting holes in point set surfaces. J. WSCG 2006, 14, 89–96. [Google Scholar]
- Chalmovianský, P.; Jüttler, B. Filling Holes in Point Clouds. In Mathematics of Surfaces; Springer: Berlin/Heidelberg, Germany, 2003; pp. 196–212. [Google Scholar]
- Guo, X.; Xiao, J.; Wang, Y. A survey on algorithms of hole filling in 3D surface reconstruction. Vis. Comput. 2018, 34, 93–103. [Google Scholar] [CrossRef]
- Argudo, O.; Brunet, P.; Chica, A.; Vinacua, À. Biharmonic fields and mesh completion. Graph. Models 2015, 82, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Davis, J.; Marschner, S.R.; Garr, M.; Levoy, M. Filling Holes in Complex Surfaces using Volumetric Diffusion. In Proceedings of the First International Symposium on 3D Data Processing Visualization and Transmission, Padua, Italy, 19–21 June 2002; pp. 428–441. [Google Scholar]
- Guo, T.-Q.; Li, J.-J.; Weng, J.-G.; Zhuang, Y.-T. Filling Holes in Complex Surfaces using Oriented Voxel Diffusion. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 4370–4375. [Google Scholar]
- Ju, T. Robust repair of polygonal models. ACM Trans. Graph. 2004, 23, 888–895. [Google Scholar] [CrossRef] [Green Version]
- Altantsetseg, E.; Khorloo, O.; Matsuyama, K.; Konno, K. Complex Hole-Filling Algorithm for 3D Models. In Proceedings of the Computer Graphics International Conference, Yokohama, Japan, 27–30 June 2017; pp. 1–6. [Google Scholar]
- Jun, Y. A piecewise hole filling algorithm in reverse engineering. Comput. Aided Des. 2005, 37, 263–270. [Google Scholar] [CrossRef]
- Kobbelt, L.; Schröder, P.; Hoppe, H. Filling Holes in Meshes. In Proceedings of the Eurographics Symposium on Geometry Processing, Aachen, Germany, 23–25 June 2003; Available online: https://dl.acm.org/doi/proceedings/10.5555/882370 (accessed on 16 August 2021).
- Wu, X.; Chen, W. A Scattered Point Set Hole-Filling Method Based on Boundary Extension and Convergence. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2014; pp. 5329–5334. [Google Scholar]
- Huang, H.; Zhou, L.; Chen, X.; Gong, Z. SMART robotic system for 3D profile turbine vane airfoil repair. Int. J. Adv. Manuf. Technol. 2003, 21, 275–283. [Google Scholar] [CrossRef]
- Li, E.; Zhang, X.; Chen, Y. Sampling and Surface Reconstruction of Large Scale Point Cloud. In Proceedings of the 13th ACM SIGGRAPH International Conference on Virtual-Reality Continuum and its Applications in Industry, Shenzhen, China, 30 November–2 December 2014; pp. 35–41. [Google Scholar]
- Marton, Z.C.; Rusu, R.B.; Beetz, M. On Fast Surface Reconstruction Methods for Large and Noisy Point Clouds. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3218–3223. [Google Scholar]
- Qi, Z.; ShuZhen, L.; Jialu, B.; Jiarang, Z. Opening-hole repairing in point cloud based on improved curve contraction flows. Laser Optoelectron. Prog. Las. Optoelect. Prog. 2018, 119–125. [Google Scholar] [CrossRef]
- Mostegel, C.; Prettenthaler, R.; Fraundorfer, F.; Bischof, H. Scalable Surface Reconstruction from Point Clouds with Extreme Scale and Density Diversity. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 904–913. [Google Scholar]
- Han, J.; Shen, S. Scalable point cloud meshing for image-based large-scale 3D modeling. Vis. Comput. Ind. Biomed. Art 2019, 2, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Vu, H.-H.; Labatut, P.; Pons, J.-P.; Keriven, R. High accuracy and visibility-consistent dense multiview stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 889–901. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Liang, J.; Ren, M.; Qiao, G.; Lu, W.; Liu, S. A fast hole-filling method for triangular mesh in additive repair. Appl. Sci. 2020, 10, 969. [Google Scholar] [CrossRef] [Green Version]
- Desbrun, M.; Meyer, M.; Schröder, P.; Barr, A.H. Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 317–324. [Google Scholar]
- Liepa, P. Filling Holes in Meshes. In Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Aachen, Germany, 23–25 June 2003; pp. 200–206. Available online: http://diglib.eg.org/handle/10.2312/SGP.SGP03.200-206 (accessed on 16 August 2021).
- Liao, T.; Li, X.; Xu, G.; Zhang, Y.J. Secondary Laplace operator and generalized Giaquinta–Hildebrandt operator with applications on surface segmentation and smoothing. Comput. Aided Des. 2016, 70, 56–66. [Google Scholar] [CrossRef]






| Closed Holes | Open Holes—Type I | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type A | Type B | Type C | Type D | |||||||
| No. R. | 16 | 4 | 17 | 0 | 1 | |||||
| No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | |
| Han method | 16 | 100% | 1 | 25% | 9 | 52.9% | / | / | 1 | 100% |
| Our method | 16 | 100% | 4 | 100% | 17 | 100% | / | / | 1 | 100% |
| Open Holes—Type II | ||||||||
|---|---|---|---|---|---|---|---|---|
| Type A | Type B | Type C | Type D | |||||
| No. R. | 0 | 2 | 0 | 0 | ||||
| No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | |
| Han method | / | / | 0 | 0 | / | / | / | / |
| Our method | / | / | 2 | 100% | / | / | / | / |
| Closed Holes | Open Holes-Type I | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type A | Type B | Type C | Type D | |||||||
| No. R. | 20 | 5 | 20 | 4 | 4 | |||||
| No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | |
| Han method | 20 | 100% | 2 | 40% | 12 | 60% | 4 | 100% | 4 | 100% |
| Our method | 20 | 100% | 5 | 100% | 20 | 100% | 4 | 100% | 4 | 100% |
| Closed Holes | Open Holes-Type I | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Type A | Type B | Type C | Type D | |||||||
| No. R. | 56 | 17 | 43 | 4 | 3 | |||||
| No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | |
| Han method | / | / | / | / | / | / | / | / | / | / |
| Our method | 56 | 100% | 17 | 100% | 43 | 100% | 4 | 100% | 3 | 100% |
| Open Holes—Type II | ||||||||
|---|---|---|---|---|---|---|---|---|
| Type A | Type B | Type C | Type D | |||||
| No. R. | 0 | 5 | 0 | 1 | ||||
| No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | No. F. | S.T. (%) | |
| Han method | / | / | / | / | / | / | / | / |
| Our method | / | / | 5 | 100% | / | / | 1 | 100% |
| 0.5 km2 | 1.0 km2 | 1.5 km2 | 2.0 km2 | 2.5 km2 | 28 km2 | |
|---|---|---|---|---|---|---|
| Han method | 17.2 | 32.8 | 46.5 | 68.2 | / | / |
| Our method | 3.9 | 6.7 | 11.6 | 15.2 | 19.3 | 230 |
| 0.5 km2 | 1.0 km2 | 1.5 km2 | 2.0 km2 | 2.5 km2 | 28 km2 | |
|---|---|---|---|---|---|---|
| Han method | 5.5 | 11.4 | 17.6 | 24.7 | / | / |
| Our method | 0.8 | 0.8 | 1.0 | 1.2 | 1.2 | 3.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Liu, Z.; Zhu, H.; Wu, P. A Parallel Method for Open Hole Filling in Large-Scale 3D Automatic Modeling Based on Oblique Photography. Remote Sens. 2021, 13, 3512. https://doi.org/10.3390/rs13173512
Wang F, Liu Z, Zhu H, Wu P. A Parallel Method for Open Hole Filling in Large-Scale 3D Automatic Modeling Based on Oblique Photography. Remote Sensing. 2021; 13(17):3512. https://doi.org/10.3390/rs13173512
Chicago/Turabian StyleWang, Fei, Zhendong Liu, Hongchun Zhu, and Pengda Wu. 2021. "A Parallel Method for Open Hole Filling in Large-Scale 3D Automatic Modeling Based on Oblique Photography" Remote Sensing 13, no. 17: 3512. https://doi.org/10.3390/rs13173512
APA StyleWang, F., Liu, Z., Zhu, H., & Wu, P. (2021). A Parallel Method for Open Hole Filling in Large-Scale 3D Automatic Modeling Based on Oblique Photography. Remote Sensing, 13(17), 3512. https://doi.org/10.3390/rs13173512






