Evaluating the Performance of sUAS Photogrammetry with PPK Positioning for Infrastructure Mapping
Abstract
1. Introduction
Contributions
2. Materials and Methods
2.1. Study Area and Reference Data
2.2. sUAS Image Acquisition
2.3. Postprocess Kinematic (PPK) Direct Geopositioning
2.4. Continuously Operating Reference Stations (CORSs)
2.5. sUAS Image Processing
2.6. Surface Model and Orthophoto Generation
2.7. sUAS and Robotic Total Station Comparison
2.8. Tests of GCP and PPK Influence on Accuracy
3. Results
3.1. Camera Calibration
3.2. Survey and Processing Time Costs
3.3. Tiepoint Distribution
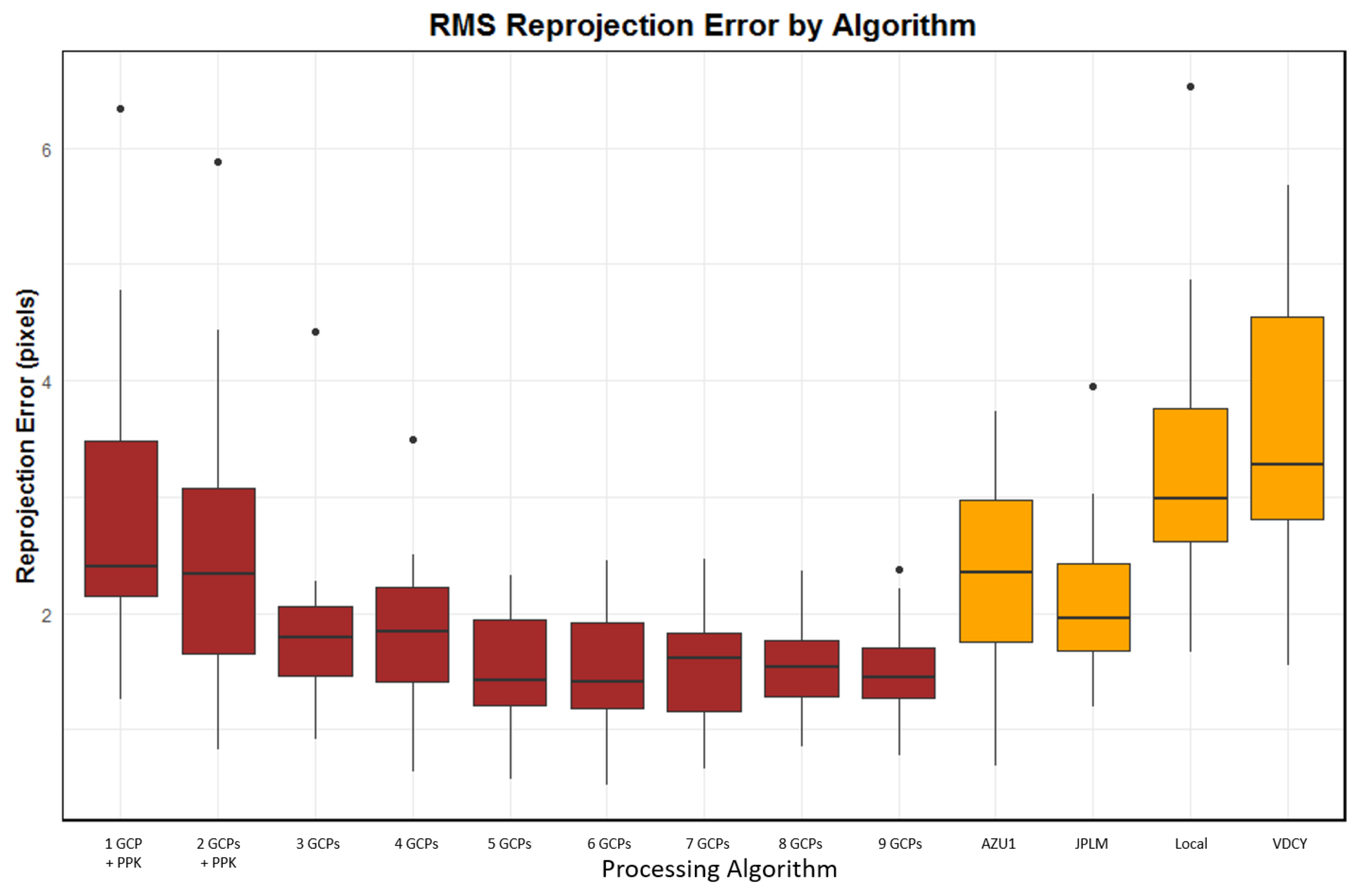
3.4. Reprojection Error
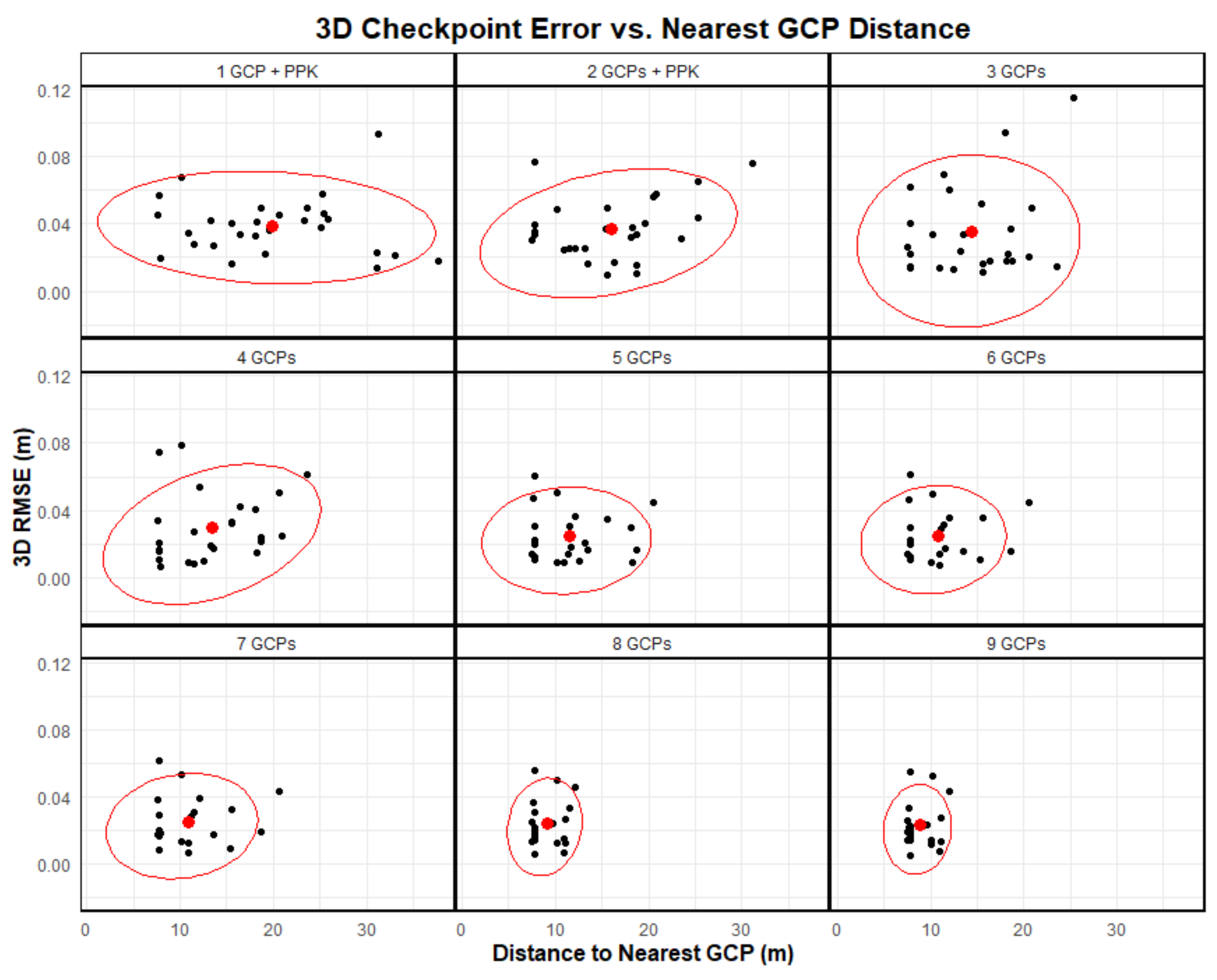
3.5. Checkpoint Location Error
3.6. Error Differences Across Checkpoints
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PPK | Postprocessing Kinematic |
| GCP | Ground Control Point |
| CORS | Continuously Operating Reference Station |
References
- Wang, J.; Sun, W.; Shou, W.; Wang, X.; Wu, C.; Chong, H.Y.; Liu, Y.; Sun, C. Integrating BIM and LiDAR for Real-Time Construction Quality Control. J. Intell. Robot. Syst. Theory Appl. 2015, 79, 417–432. [Google Scholar] [CrossRef]
- Gikas, V. Three-dimensional laser scanning for geometry documentation and construction management of highway tunnels during excavation. Sensors 2012, 12, 11249–11270. [Google Scholar] [CrossRef]
- Mora, O.E.; Chen, J.; Stoiber, P.; Koppanyi, Z.; Pluta, D.; Josenhans, R.; Okubo, M. Accuracy of stockpile estimates using low-cost sUAS photogrammetry. Int. J. Remote Sens. 2020, 41, 1–16. [Google Scholar] [CrossRef]
- Nuchter, A.; Surmann, H.; Lingemann, K.; Hertzberg, J.; Thrun, S. 6D SLAM with an application in autonomous mine mapping. In Proceedings of the IEEE International Conference on Robotics and Automation—ICRA’04, New Orleans, LA, USA, 26 April–1 May 2004; Volume 2, pp. 1998–2003. [Google Scholar] [CrossRef]
- Eschmann, C.; Kuo, C.; Kuo, C.; Boller, C. Unmanned Aircraft Systems for Remote Building. In Proceedings of the European Workshop on Structural Health Monitoring, Dresden, Germany, 3–6 July 2012; pp. 1–8. [Google Scholar]
- Kang, Z.; Chen, J.; Wang, B. Global Registration of Subway Tunnel Point Clouds Using an Augmented Extended Kalman Filter and Central-Axis Constraint. PLoS ONE 2015, 10, e0126862. [Google Scholar] [CrossRef]
- Agnisarman, S.; Lopes, S.; Chalil Madathil, K.; Piratla, K.; Gramopadhye, A. A survey of automation-enabled human-in-the-loop systems for infrastructure visual inspection. Autom. Constr. 2019, 97, 52–76. [Google Scholar] [CrossRef]
- Leingartner, M.; Maurer, J.; Ferrein, A.; Steinbauer, G. Evaluation of Sensors and Mapping Approaches for Disasters in Tunnels. J. Field Robot. 2016, 33, 1037–1057. [Google Scholar] [CrossRef]
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Varhola, A.; Vastaranta, M.; Coops, N.C.; Cook, B.D.; Pitt, D.; Woods, M. A best practices guide for generating forest inventory attributes from airborne laser scanning data using an area-based approach. For. Chron. 2013, 89, 722–723. [Google Scholar] [CrossRef]
- Varhola, A.; Coops, N.C. Estimation of watershed-level distributed forest structure metrics relevant to hydrologic modeling using LiDAR and Landsat. J. Hydrol. 2013, 487, 70–86. [Google Scholar] [CrossRef]
- Wu, Q.; Lane, C.R. Delineating wetland catchments and modeling hydrologic connectivity using lidar data and aerial imagery. Hydrol. Earth Syst. Sci. 2017, 21, 3579–3595. [Google Scholar] [CrossRef] [PubMed]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- North, M.P.; Kane, J.T.; Kane, V.R.; Asner, G.P.; Berigan, W.; Churchill, D.J.; Conway, S.; Gutiérrez, R.J.; Jeronimo, S.; Keane, J.; et al. Cover of tall trees best predicts California spotted owl habitat. For. Ecol. Manag. 2017, 405, 166–178. [Google Scholar] [CrossRef]
- Lucieer, A.; Turner, D.; King, D.H.; Robinson, S.A. Using an unmanned aerial vehicle (UAV) to capture micro-topography of antarctic moss beds. Int. J. Appl. Earth Obs. Geoinform. 2014, 27, 53–62. [Google Scholar] [CrossRef]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. High-resolution mapping of aboveground shrub biomass in Arctic tundra using airborne lidar and imagery. Remote Sens. Environ. 2016, 184, 361–373. [Google Scholar] [CrossRef]
- Estornell, J.; Ruiz, L.A.; Velázquez-Martí, B.; Fernández-Sarría, A. Estimation of shrub biomass by airborne LiDAR data in small forest stands. For. Ecol. Manag. 2011, 262, 1697–1703. [Google Scholar] [CrossRef]
- McCarley, T.R.; Kolden, C.A.; Vaillant, N.M.; Hudak, A.T.; Smith, A.M.; Kreitler, J. Landscape-scale quantification of fire-induced change in canopy cover following mountain pine beetle outbreak and timber harvest. For. Ecol. Manag. 2017, 391, 164–175. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Orem, C.A. How do sediment yields from post-wildfire debris-laden flows depend on terrain slope, soil burn severity class, and drainage basin area? Insights from airborne-LiDAR change detection. Earth Surf. Process. Landf. 2014, 39, 1822–1832. [Google Scholar] [CrossRef]
- Daba, S.; Rieger, W.; Strauss, P. Assessment of gully erosion in eastern Ethiopia using photogrammetric techniques. Catena 2003, 50, 273–291. [Google Scholar] [CrossRef]
- Tran, C.J.; Mora, O.E.; Fayne, J.V.; Gabriela Lenzano, M. Unsupervised classification for landslide detection from airborne laser scanning. Geosciences 2019, 9, 221. [Google Scholar] [CrossRef]
- Qiu, W.; Cheng, Y.J. High-Resolution DEM Generation of Railway Tunnel Surface Using Terrestrial Laser Scanning Data for Clearance Inspection. J. Comput. Civ. Eng. 2017, 31. [Google Scholar] [CrossRef]
- Mora, O.E.; Suleiman, A.; Chen, J.; Pluta, D.; Okubo, M.H.; Josenhans, R. Comparing sUAS Photogrammetrically-Derived Point Clouds with GNSS Measurements and Terrestrial Laser Scanning for Topographic Mapping. Drones 2019, 3, 64. [Google Scholar] [CrossRef]
- Agüera-vega, F.; Carvajal-ramírez, F.; Martínez-Carricondo, P. Assessment of photogrammetric mapping accuracy based on variation ground control points number using unmanned aerial vehicle. Measurement 2017, 98, 221–227. [Google Scholar] [CrossRef]
- Gerke, M.; Przybilla, H.J. Accuracy analysis of photogrammetric UAV image blocks: Influence of onboard RTK-GNSS and cross flight patterns. Photogramm. Fernerkund. Geoinf. 2016, 2016, 17–30. [Google Scholar] [CrossRef]
- Tomaštík, J.; Mokroš, M.; Surov, P.; Grzn, A. UAV RTK/PPK Method—An Optimal Solution for Mapping Inaccessible Forested Areas? Remote Sens. 2019, 11, 721. [Google Scholar] [CrossRef]
- Benassi, F.; Asta, E.D.; Diotri, F.; Forlani, G.; Morra, U.; Roncella, R.; Santise, M. Testing Accuracy and Repeatability of UAV Blocks Oriented with GNSS-Supported Aerial Triangulation. Remote Sens. 2017, 9, 172. [Google Scholar] [CrossRef]
- Bolkas, D.; Sichler, T.J.; Mcmarlin, W. A Case Study on the Accuracy Assessment of a Small UAS Photogrammetric Survey Using Terrestrial Laser Scanning. Surv. Land Inf. Sci. 2019, 78, 31–44. [Google Scholar]
- Bolkas, D. Assessment of GCP Number and Separation Distance for Small UAS Surveys with and without GNSS-PPK Positioning. J. Surv. Eng. 2019, 145, 1–17. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Reindl, T.; Seidl, J.; Brouček, J. Evaluation of the georeferencing accuracy of a photogrammetric model using a quadrocopter with onboard GNSS RTK. Sensors 2020, 20, 2318. [Google Scholar] [CrossRef]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; di Cella, U.M.; Roncella, R.; Santise, M. Quality assessment of DSMs produced from UAV flights georeferenced with on-board RTK positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]
- Przybilla, H.J.; Bäumker, M.; Luhmann, T.; Hastedt, H.; Eilers, M. Interaction between direct georeferencing, control point configuration and camera self-calibration for RTK-based UAV photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2020, 43, 485–492. [Google Scholar] [CrossRef]
- Starek, M.J.; Davis, T.; Prouty, D.; Berryhill, J. Small-scale UAS for geoinformatics applications on an island campus. In Proceedings of the 2014 Ubiquitous Positioning Indoor Navigation and Location Based Service, UPINLBS 2014—Conference Proceedings, Corpus Christi, TX, USA, 20–21 November 2014; pp. 120–127. [Google Scholar] [CrossRef]
- Javadnejad, F.; Slocum, R.K.; Gillins, D.T.; Olsen, M.J.; Parrish, C.E. Dense Point Cloud Quality Factor as Proxy for Accuracy Assessment of Image-Based 3D Reconstruction. J. Surv. Eng. 2021, 147, 04020021. [Google Scholar] [CrossRef]
- DroneDeploy. Drone Mapping Software: Drone Mapping App. Available online: https://www.dronedeploy.com/ (accessed on 14 May 2021).
- Bentley Systems. 3D Reality Modeling Software. 2021. Available online: https://www.bentley.com/en/products/brands/contextcapture (accessed on 14 May 2021).




| Treatment | GCP Count | Checkpoint Count | PPK Base |
|---|---|---|---|
| 1 GCP + PPK | 1 | 20 | Local |
| 2 GCPs + PPK | 2 | 20 | Local |
| 3 GCPs | 3 | 20 | none |
| 4 GCPs | 4 | 20 | none |
| 5 GCPs | 5 | 20 | none |
| 6 GCPs | 6 | 20 | none |
| 7 GCPs | 7 | 20 | none |
| 8 GCPs | 8 | 20 | none |
| 9 GCPs | 9 | 20 | none |
| JPLM | 0 | 20 | JPLM |
| AZU1 | 0 | 20 | AZU1 |
| VDCY | 0 | 20 | VDCY |
| Local | 0 | 20 | Local |
| Station | Sample Rate | GNSS | Distance (km) | Location |
|---|---|---|---|---|
| JPLM | 1 s | GPS + GLO | 18.36 | 34°12′17.34″ N, 118°10′23.57″ W |
| AZU1 | 15 s | GPS | 8.69 | 34°07′33.66″ N, 117°53′47.31″ W |
| VDCY | 15 s | GPS | 21.65 | 34°10′42.82″ N, 118°13′11.95″ W |
| Treatment (Units) | Focal Length (mm) | Pixel Size (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| - | - | - | - | - | |||||
| Local | 10.02 | 0.0109 | −0.0324 | 0.0341 | 0.0012 | 0.00020 | 8.54 | 2449 | 1845 |
| JPLM | 10.02 | 0.0107 | −0.0323 | 0.0339 | 0.0012 | 0.00020 | 8.54 | 2449 | 1845 |
| AZUI | 9.98 | 0.0109 | −0.0324 | 0.0335 | 0.0012 | 0.00020 | 8.54 | 2449 | 1845 |
| VDCY | 10.00 | 0.0111 | −0.0344 | 0.0358 | 0.0012 | 0.00020 | 8.55 | 2449 | 1845 |
| 1 GCP + PPK | 10.01 | 0.0105 | −0.0306 | 0.0319 | 0.0012 | 0.00024 | 8.52 | 2449 | 1845 |
| 2 GCPs + PPK | 10.00 | 0.0106 | −0.0314 | 0.0328 | 0.0011 | 0.00022 | 8.53 | 2449 | 1845 |
| 3 GCPs | 8.80 | 0.0061 | −0.0170 | 0.0134 | 0.0010 | 0.00005 | 8.54 | 2435 | 1832 |
| 4 GCPs | 8.80 | 0.0066 | −0.0160 | 0.0126 | 0.0010 | 0.00001 | 8.54 | 2435 | 1831 |
| 5 GCPs | 8.80 | 0.0068 | −0.0169 | 0.0132 | 0.0010 | −0.00006 | 8.54 | 2434 | 1830 |
| 6 GCPs | 8.80 | 0.0071 | −0.0175 | 0.0137 | 0.0010 | −0.00009 | 8.54 | 2434 | 1830 |
| 7 GCPs | 8.80 | 0.0070 | −0.0175 | 0.0137 | 0.0009 | −0.00013 | 8.54 | 2434 | 1829 |
| 8 GCPs | 8.80 | 0.0090 | −0.0217 | 0.0169 | 0.0010 | −0.00012 | 8.54 | 2434 | 1833 |
| 9 GCPs | 8.80 | 0.0089 | −0.0216 | 0.0169 | 0.0009 | −0.00014 | 8.54 | 2434 | 1833 |
| Treatment | Total Time | Field Labor | Flight | Survey | Photogrammetry | PPK |
|---|---|---|---|---|---|---|
| Local | 2230 | 330 | 330 | 0 | 100 | 1800 |
| JPLM | 2222 | 330 | 330 | 0 | 92 | 1800 |
| AZU1 | 2242 | 330 | 330 | 0 | 112 | 1800 |
| VDCY | 2272 | 330 | 330 | 0 | 142 | 1800 |
| 1 GCP + PPK | 2511 | 578 | 330 | 248 | 133 | 1800 |
| 2 GCPs + PPK | 2739 | 827 | 330 | 497 | 112 | 1800 |
| 3 GCPs | 1190 | 1075 | 330 | 745 | 115 | 0 |
| 4 GCPs | 1441 | 1323 | 330 | 993 | 118 | 0 |
| 5 GCPs | 1691 | 1571 | 330 | 1241 | 120 | 0 |
| 6 GCPs | 1940 | 1820 | 330 | 1490 | 120 | 0 |
| 7 GCPs | 2189 | 2068 | 330 | 1738 | 121 | 0 |
| 8 GCPs | 2438 | 2316 | 330 | 1986 | 122 | 0 |
| 9 GCPs | 2685 | 2564 | 330 | 2234 | 121 | 0 |
| Treatment | Keypoints | Tiepoints | Tiepoints per Photo |
|---|---|---|---|
| Local | 18,991 | 20,385 | 1348 |
| JPLM | 18,991 | 20,356 | 1352 |
| AZU1 | 18,991 | 19,582 | 1294 |
| VDCY | 18,991 | 19,661 | 1318 |
| 1 GCP + PPK | 18,991 | 20,621 | 1427 |
| 2 GCPs + PPK | 18,991 | 19,223 | 1344 |
| 3 GCPs | 18,991 | 21,598 | 1500 |
| 4 GCPs | 18,991 | 21,629 | 1499 |
| 5 GCPs | 18,991 | 21,587 | 1495 |
| 6 GCPs | 18,991 | 21,582 | 1496 |
| 7 GCPs | 18,991 | 21,552 | 1487 |
| 8 GCPs | 18,991 | 21,694 | 1510 |
| 9 GCPs | 18,991 | 21,674 | 1514 |
| Treatment | Horizontal | RMSE (m) Vertical | 3D | Horizontal | Bias (m) Vertical | 3D |
|---|---|---|---|---|---|---|
| Local | 0.026 | 0.047 | 0.054 | 0.023 | −0.039 | 0.045 |
| JPLM | 0.017 | 0.027 | 0.032 | 0.016 | −0.003 | 0.016 |
| AZU1 | 0.016 | 0.054 | 0.056 | 0.014 | 0.044 | 0.046 |
| VDCY | 0.024 | 0.074 | 0.077 | 0.022 | −0.066 | 0.070 |
| 1 GCP + PPK | 0.025 | 0.031 | 0.039 | 0.021 | −0.011 | 0.023 |
| 2 GCPs + PPK | 0.024 | 0.031 | 0.040 | 0.020 | 0.005 | 0.021 |
| 3 GCPs | 0.012 | 0.037 | 0.039 | 0.011 | 0.006 | 0.013 |
| 4 GCPs | 0.013 | 0.033 | 0.035 | 0.012 | −0.003 | 0.012 |
| 5 GCPs | 0.014 | 0.026 | 0.028 | 0.012 | 0.006 | 0.013 |
| 6 GCPs | 0.011 | 0.026 | 0.028 | 0.010 | 0.007 | 0.012 |
| 7 GCPs | 0.011 | 0.026 | 0.028 | 0.010 | 0.004 | 0.011 |
| 8 GCPs | 0.011 | 0.025 | 0.027 | 0.010 | 0.001 | 0.010 |
| 9 GCPs | 0.011 | 0.024 | 0.027 | 0.010 | −0.001 | 0.010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
McMahon, C.; Mora, O.E.; Starek, M.J. Evaluating the Performance of sUAS Photogrammetry with PPK Positioning for Infrastructure Mapping. Drones 2021, 5, 50. https://doi.org/10.3390/drones5020050
McMahon C, Mora OE, Starek MJ. Evaluating the Performance of sUAS Photogrammetry with PPK Positioning for Infrastructure Mapping. Drones. 2021; 5(2):50. https://doi.org/10.3390/drones5020050
Chicago/Turabian StyleMcMahon, Conor, Omar E. Mora, and Michael J. Starek. 2021. "Evaluating the Performance of sUAS Photogrammetry with PPK Positioning for Infrastructure Mapping" Drones 5, no. 2: 50. https://doi.org/10.3390/drones5020050
APA StyleMcMahon, C., Mora, O. E., & Starek, M. J. (2021). Evaluating the Performance of sUAS Photogrammetry with PPK Positioning for Infrastructure Mapping. Drones, 5(2), 50. https://doi.org/10.3390/drones5020050







