Diurnal and Seasonal Mapping of Water Deficit Index and Evapotranspiration by an Unmanned Aerial System: A Case Study for Winter Wheat in Denmark
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Design and Field Measurements
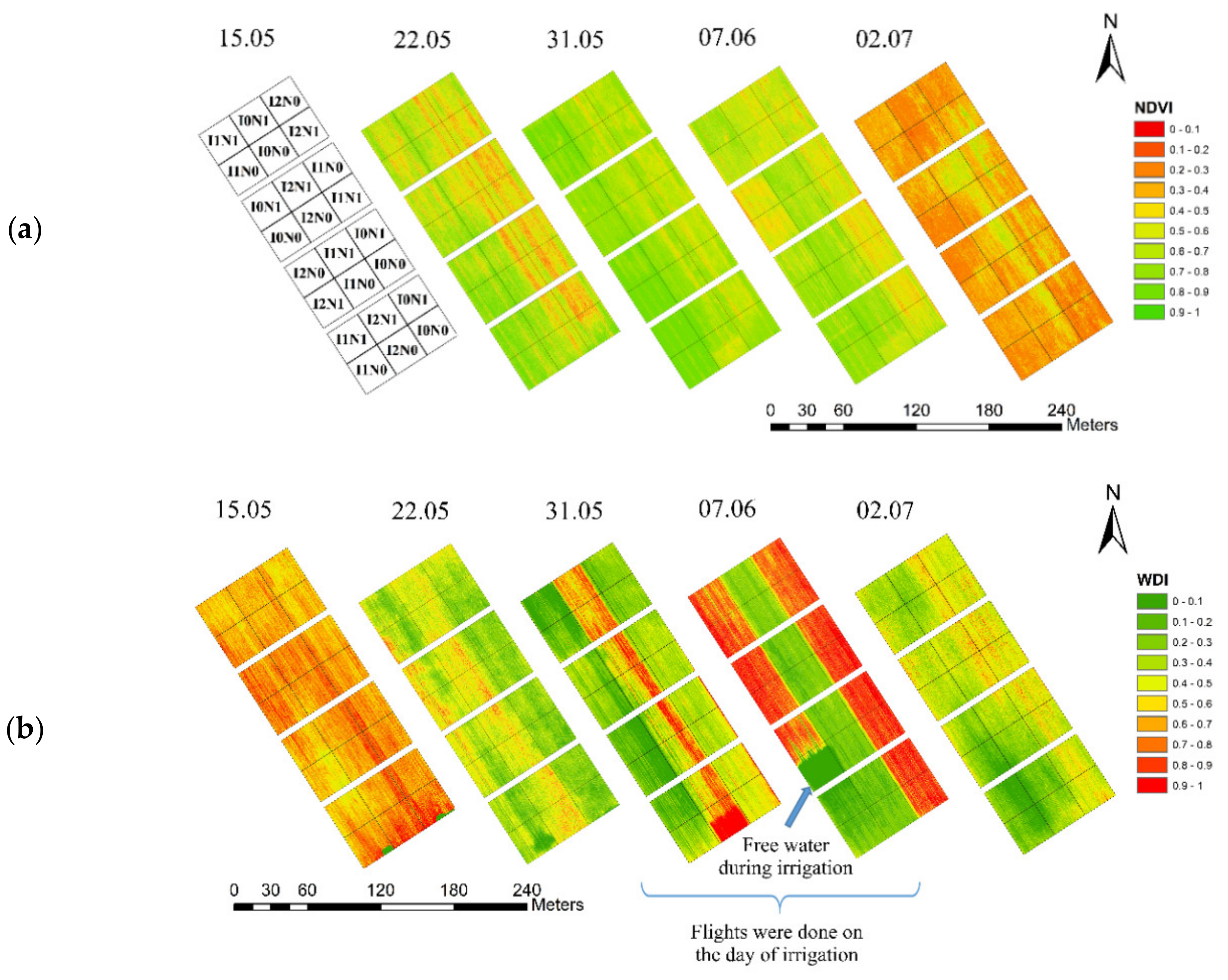
2.2. Unmanned Aerial System and Acquisition of Multispectral and Thermal Images
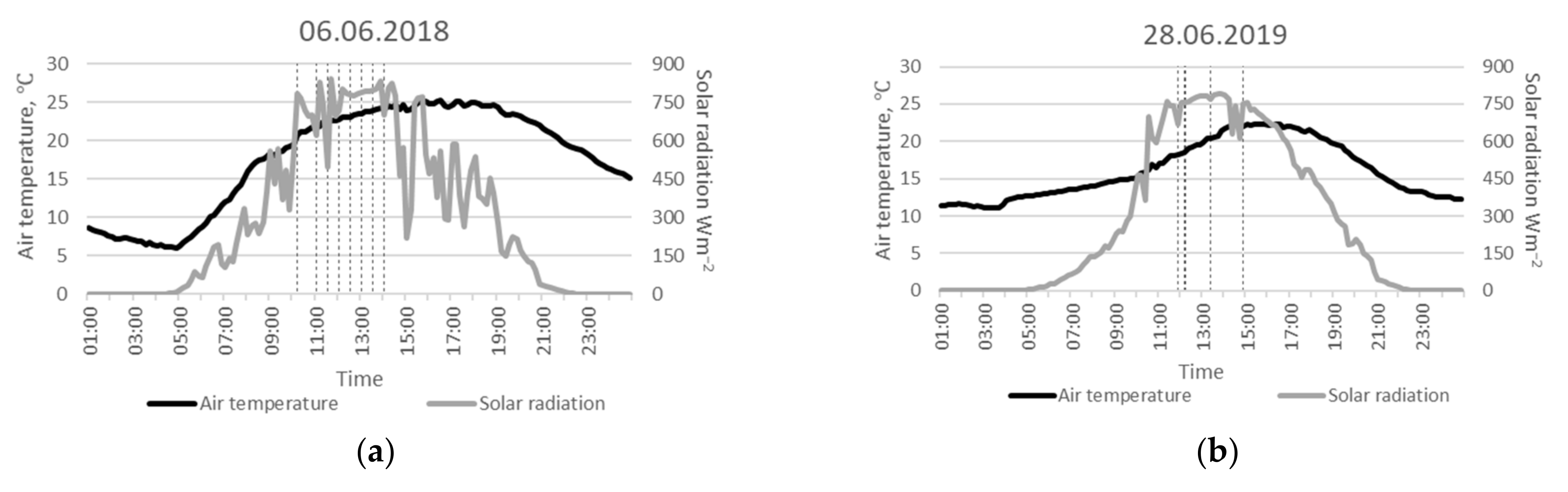
2.2.1. Data Acquisition Times
2.2.2. Data Processing
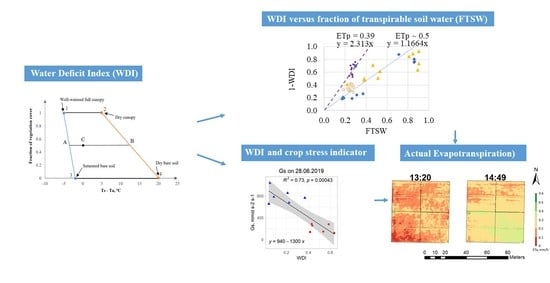
2.3. Calculation of the Water Deficit Index
2.4. Calculation of Seasonal and Diurnal Evapotranspiration
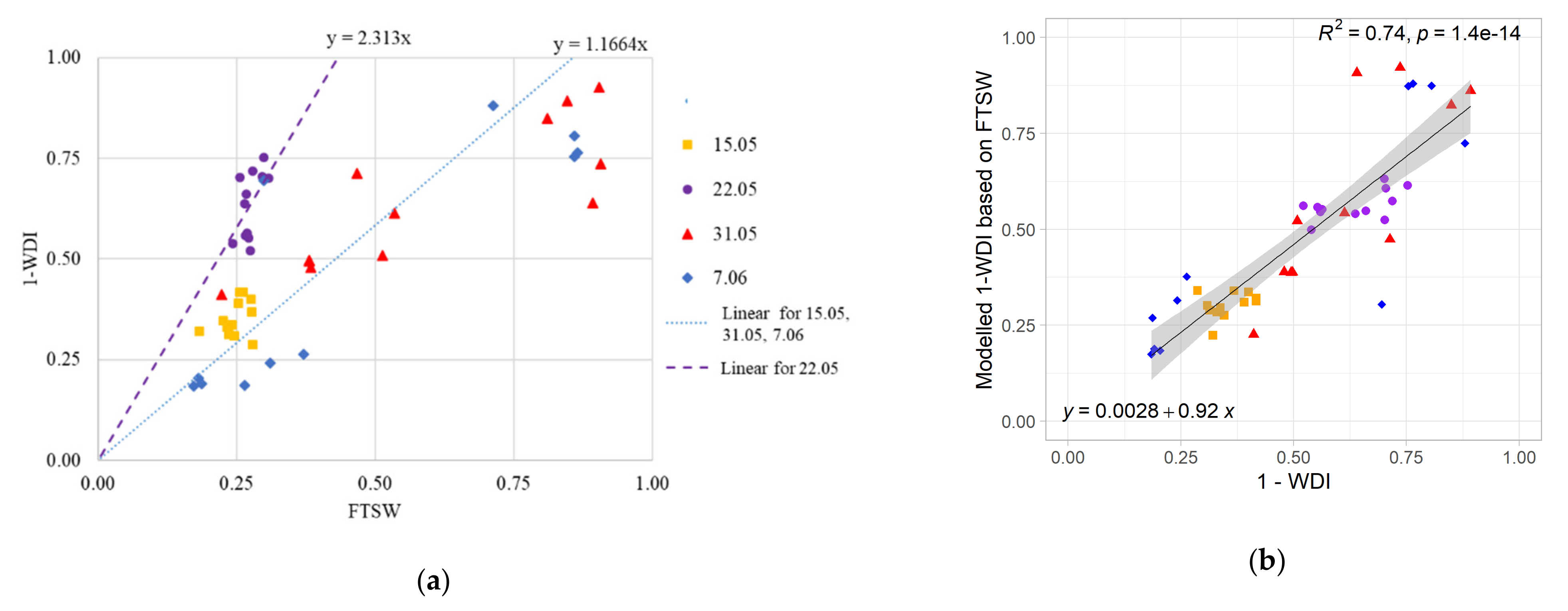
2.5. Calculation of Fraction of Transpirable Soil Water
2.6. Statistical Analyses
3. Results
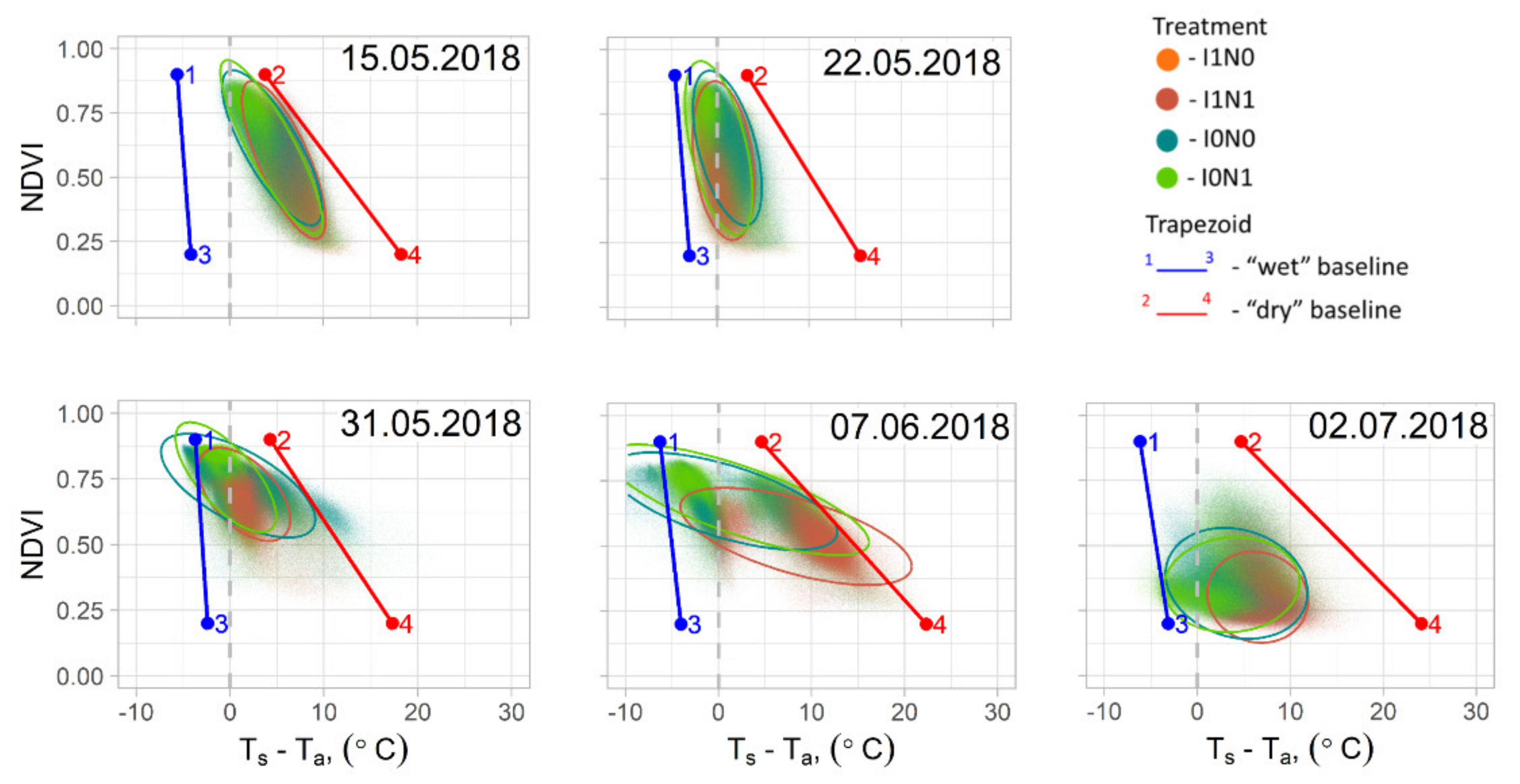
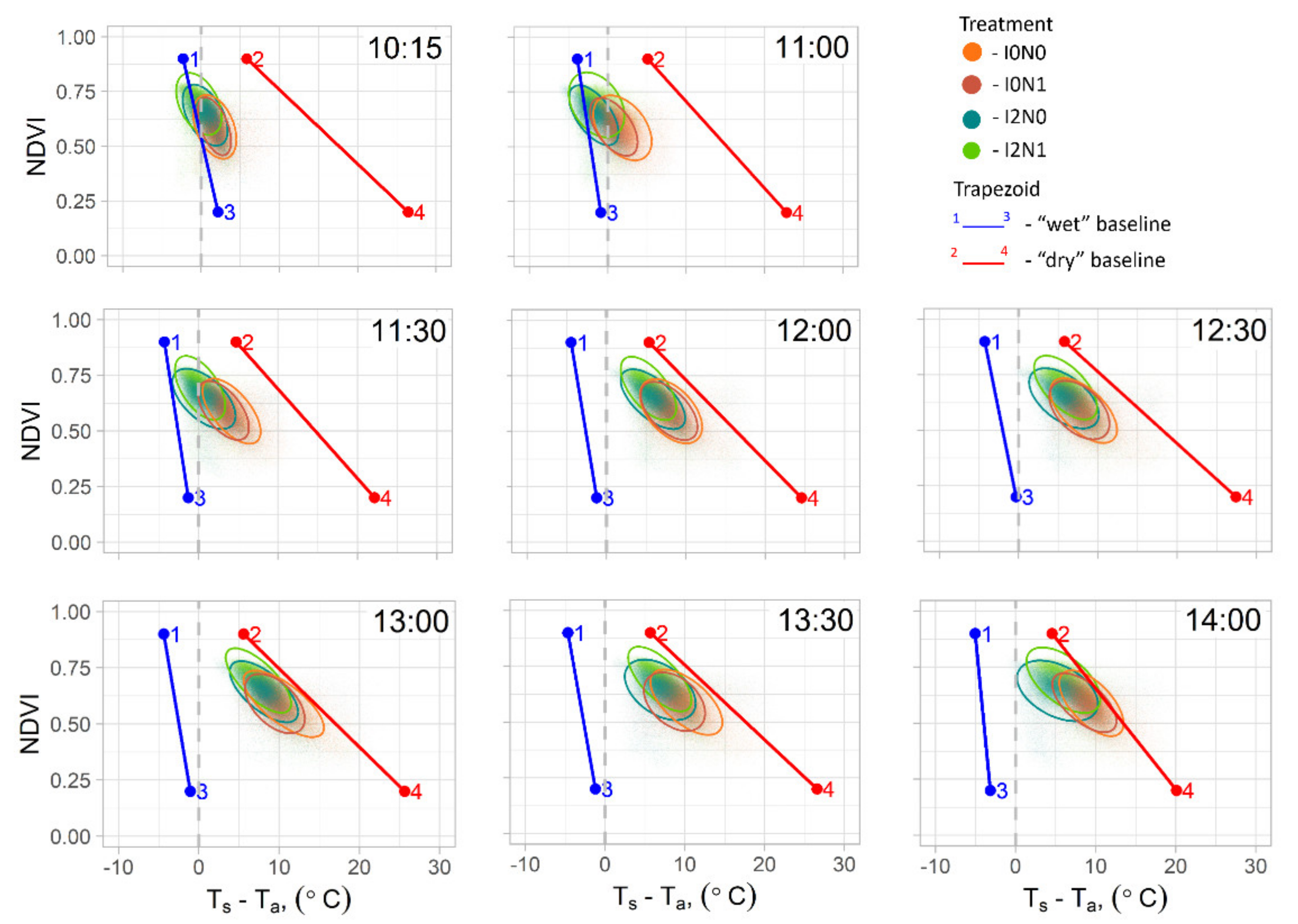
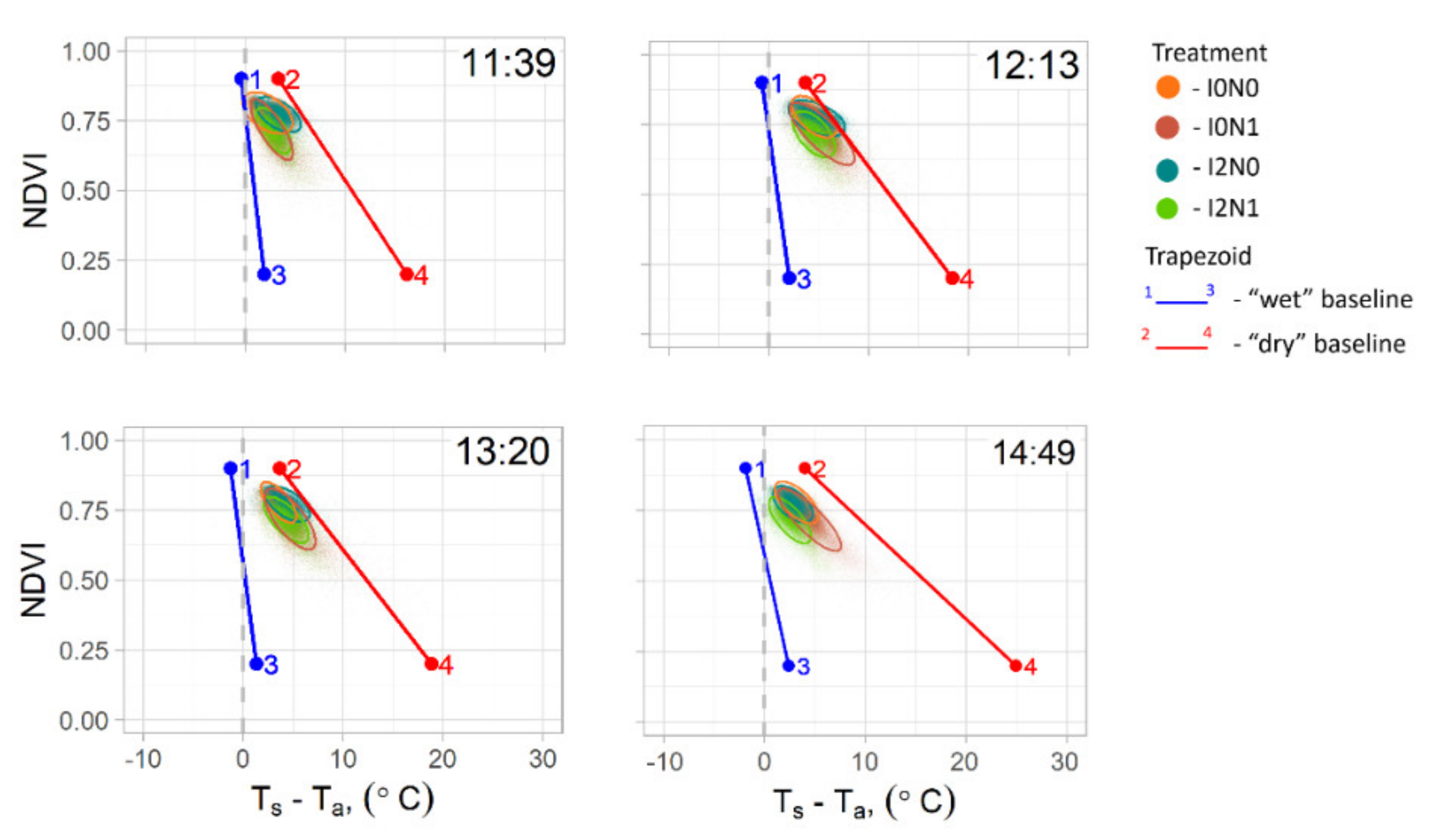
3.1. Vegetation Index/Temperature Trapezoid on Seasonal and Diurnal Scale
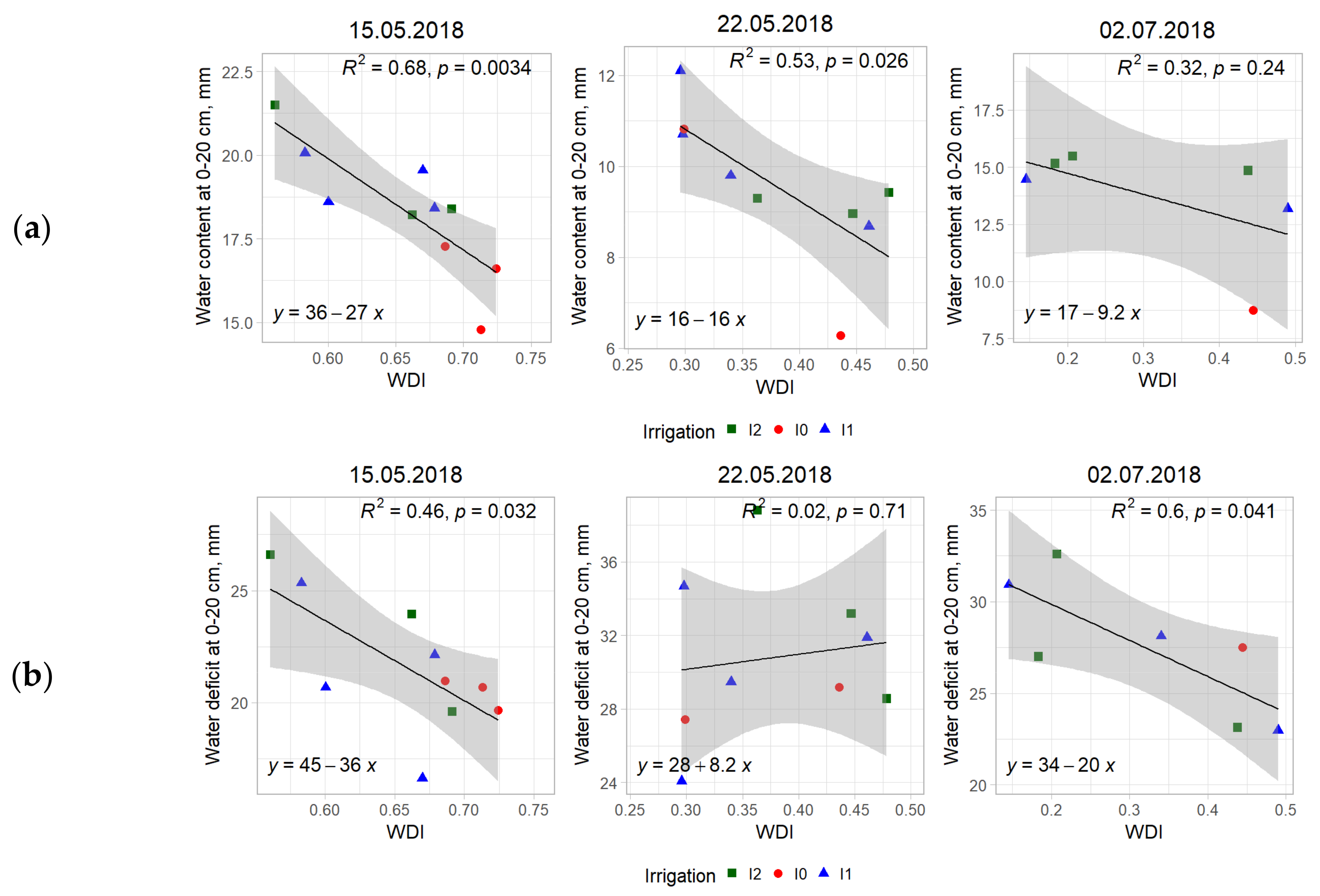
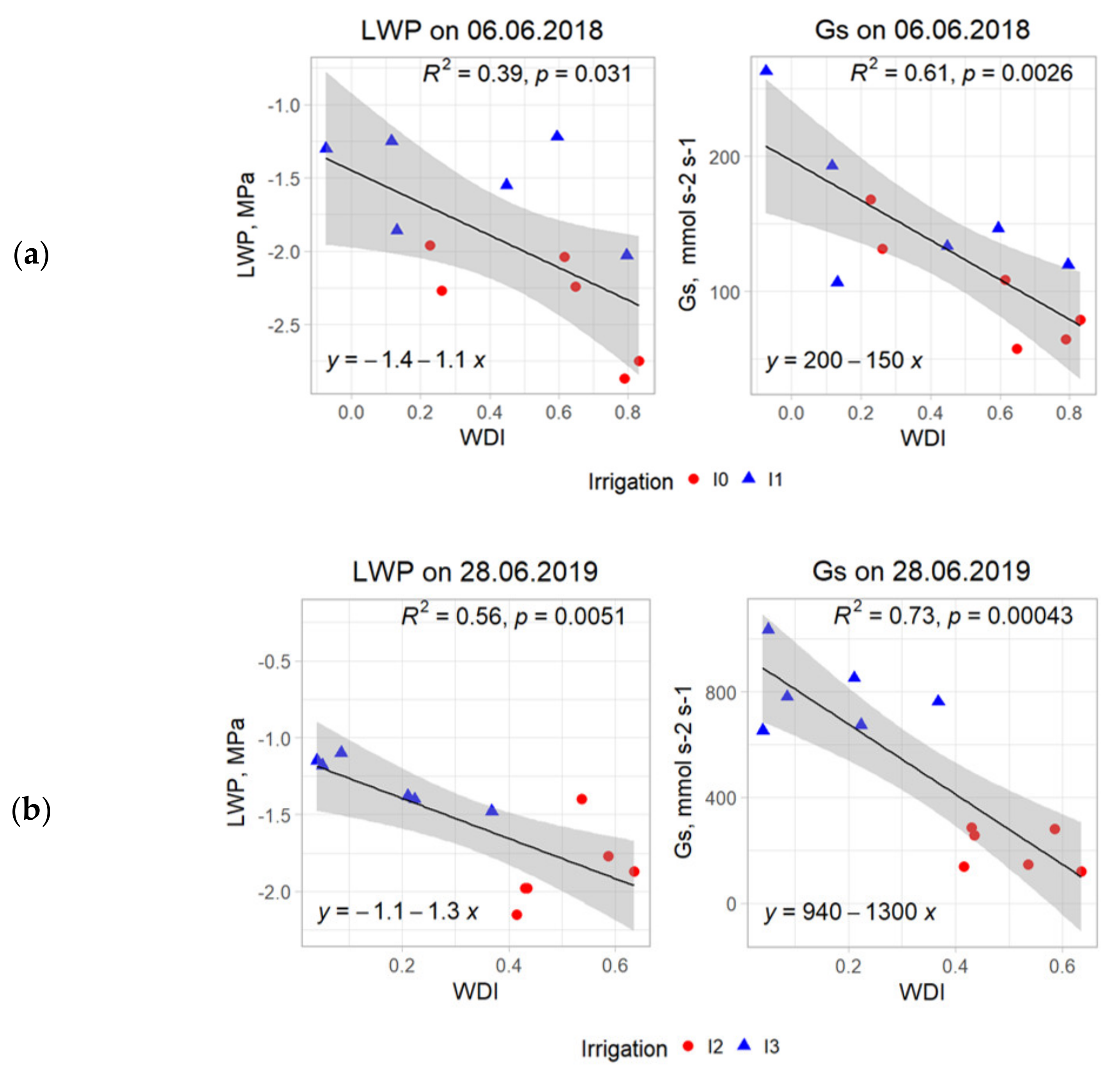
3.2. Water Deficit Index at Seasonal Scale and Correlation to Field Data
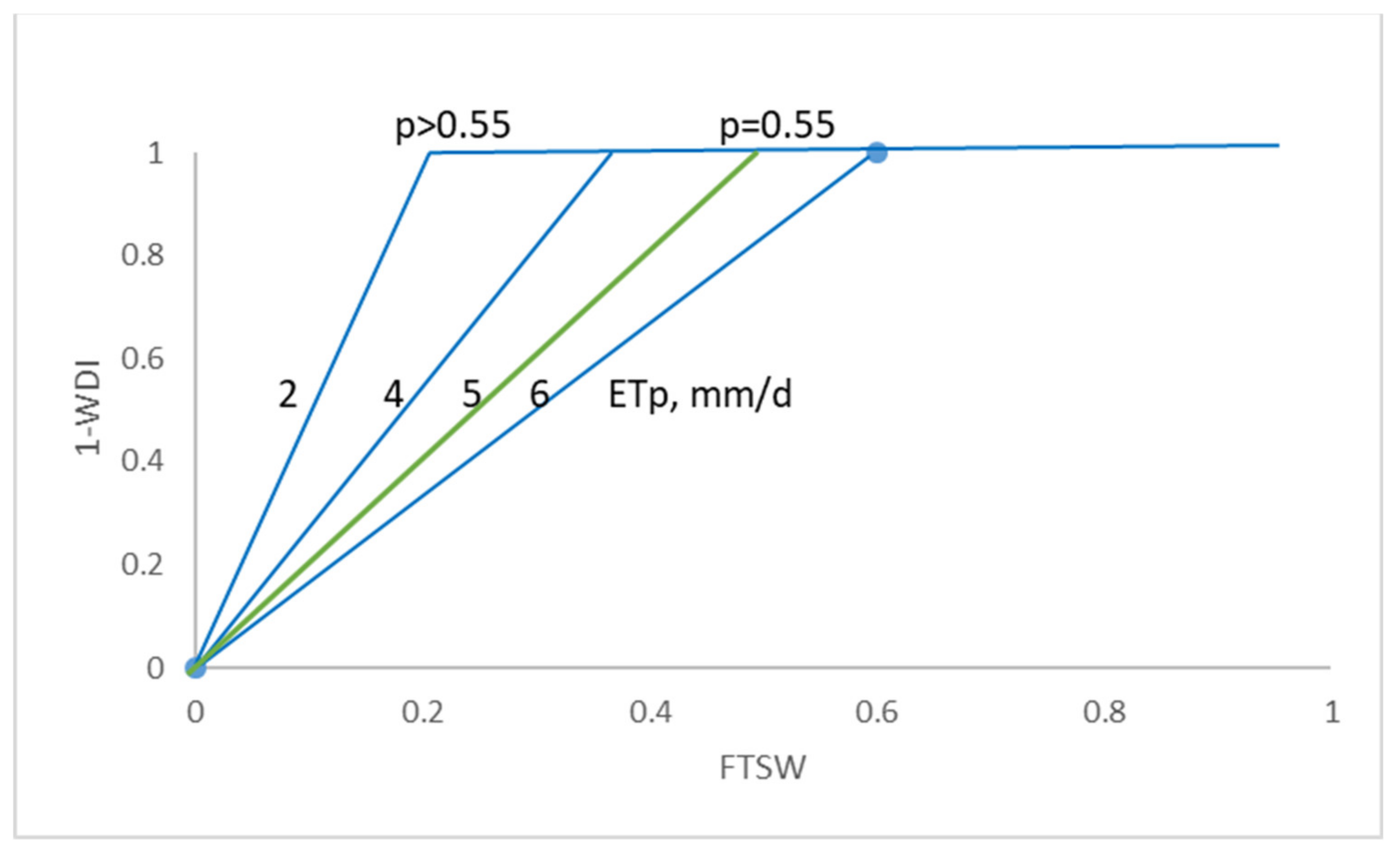
3.3. Relation between the WDI and the Fraction of Transpirable Soil Water and ETp
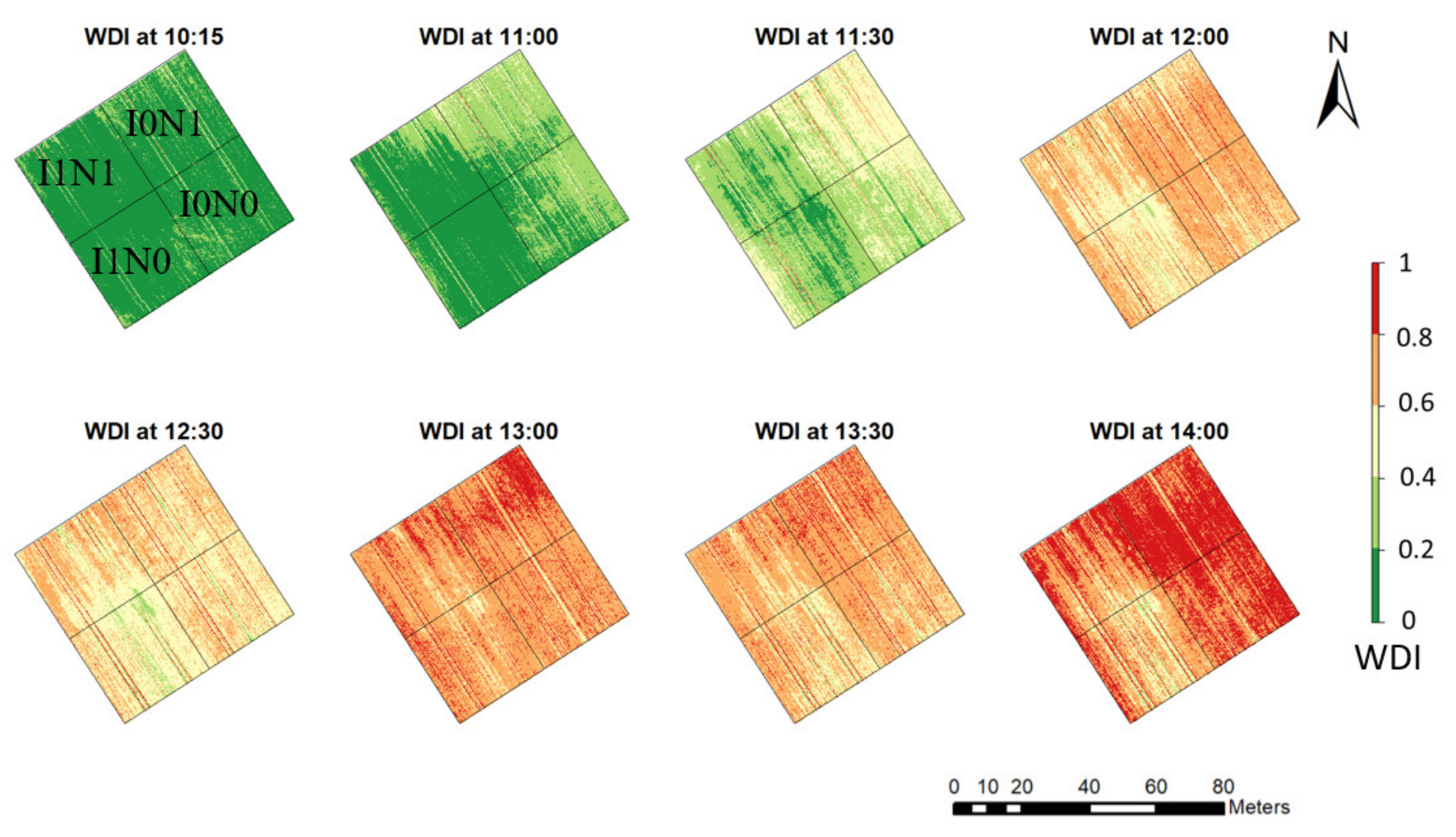
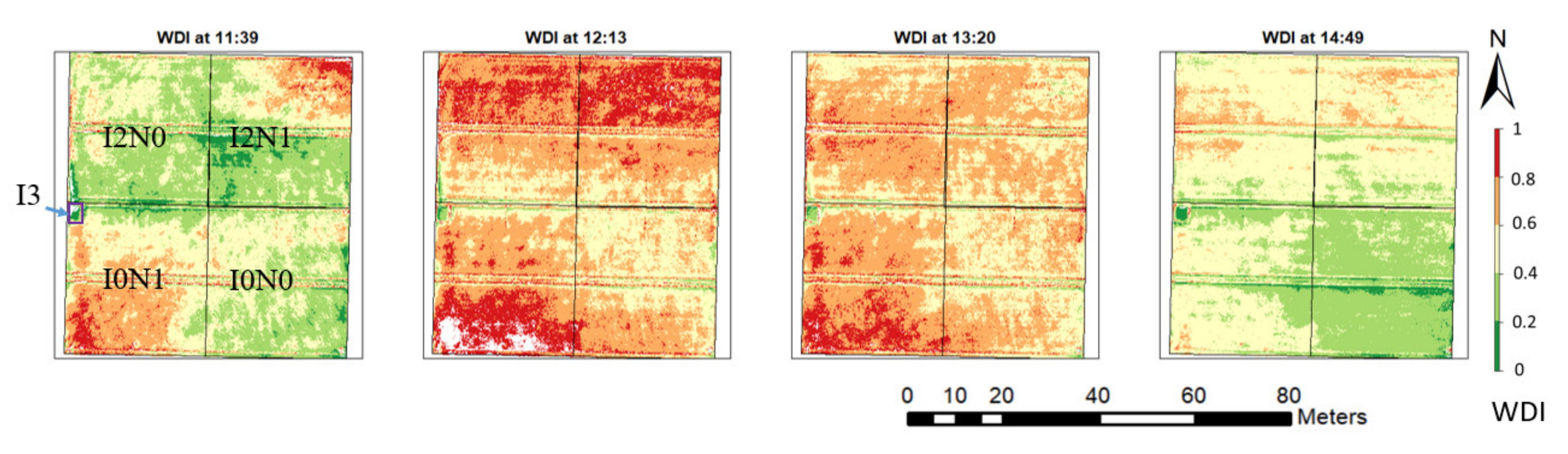
3.4. Modelling Water Deficit Index at Diurnal Scale
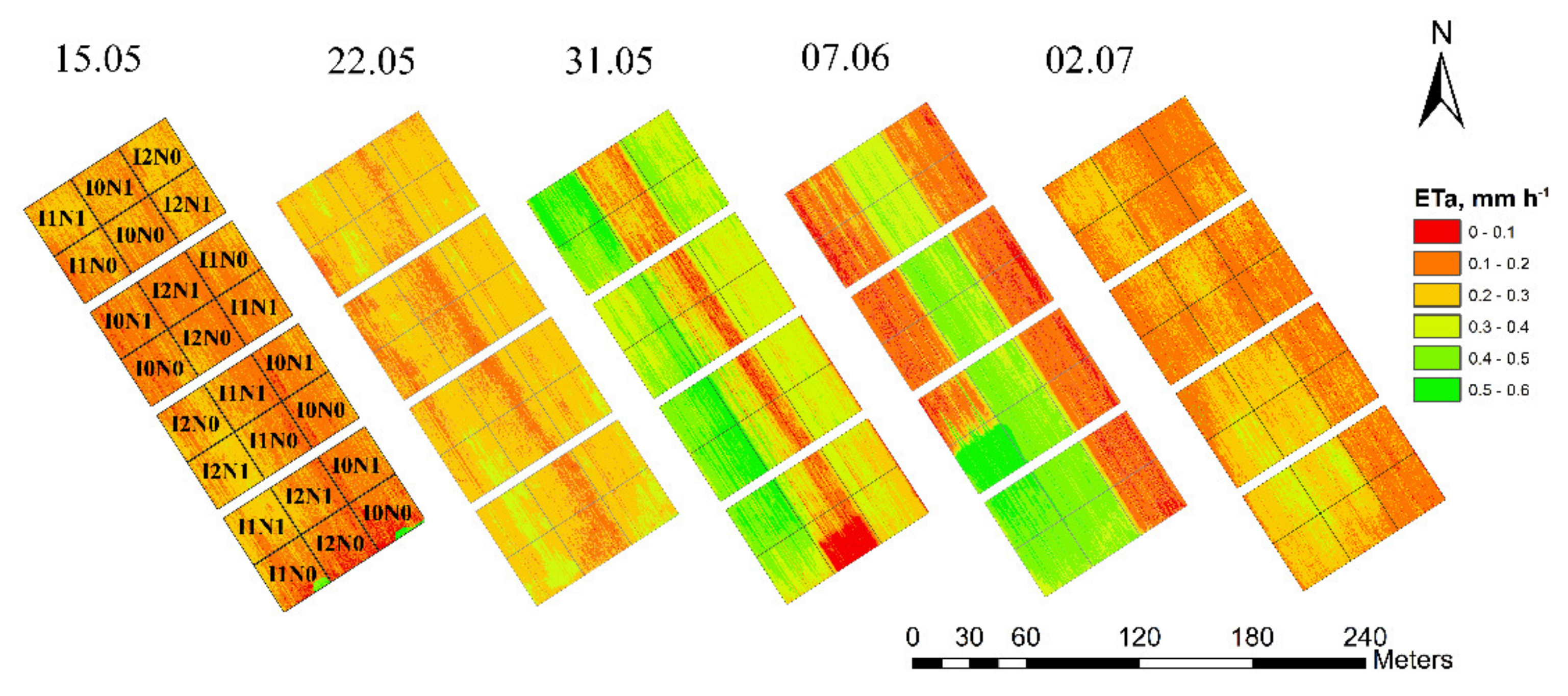
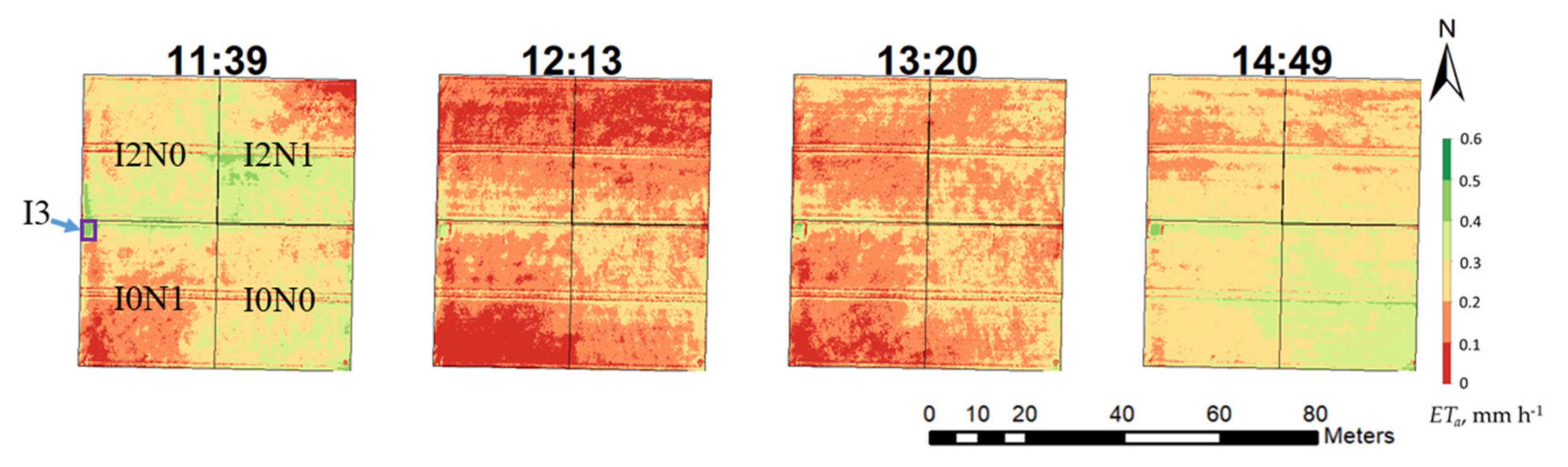
3.5. High-Resolution Mapping of Actual Evapotranspiration at the Seasonal and Diurnal Scale
4. Discussion
4.1. Seasonal Dynamics of the Water Deficit Index and Correlation to Soil Water Status
4.2. Water Deficit Index on the Diurnal Scale and Correlation to Leaf Water Status
4.3. Links between Evapotranspiration and Water Deficit Index
5. Conclusions
- (i)
- The WDI has high potential to accurately depict soil water status. It is sensitive to the topsoil water status. A semiphysical relationship was established between the FTSW in the root zone and the WDI based on ETp, which allows the direct calculation of soil water deficit from the WDI.
- (ii)
- Significant correlation of the WDI to plant stomatal conductance and leaf water potential indicates the possibility to detect early drought signals. The diurnal variation of WDI and ETa suggests that the ETa/ETp ratio varies during the day, being higher in the morning and lower at noon hours. Additionally, the largest difference between crops was seen later in the afternoon, as healthier plants started to recover faster compared to more stressed plants that demonstrated higher WDI values for a longer period. This can be used in further studies to improve the temporal upscaling of ETa with higher precision for irrigation planning.
- (iii)
- Since most of the parameters for the calculations of WDI, ETa and FTSW were derived from only a few initial variables routinely measured by the weather station, the WDI-based method allows for rapid calculation of the field energy balance and evaluation of soil and crop water status.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
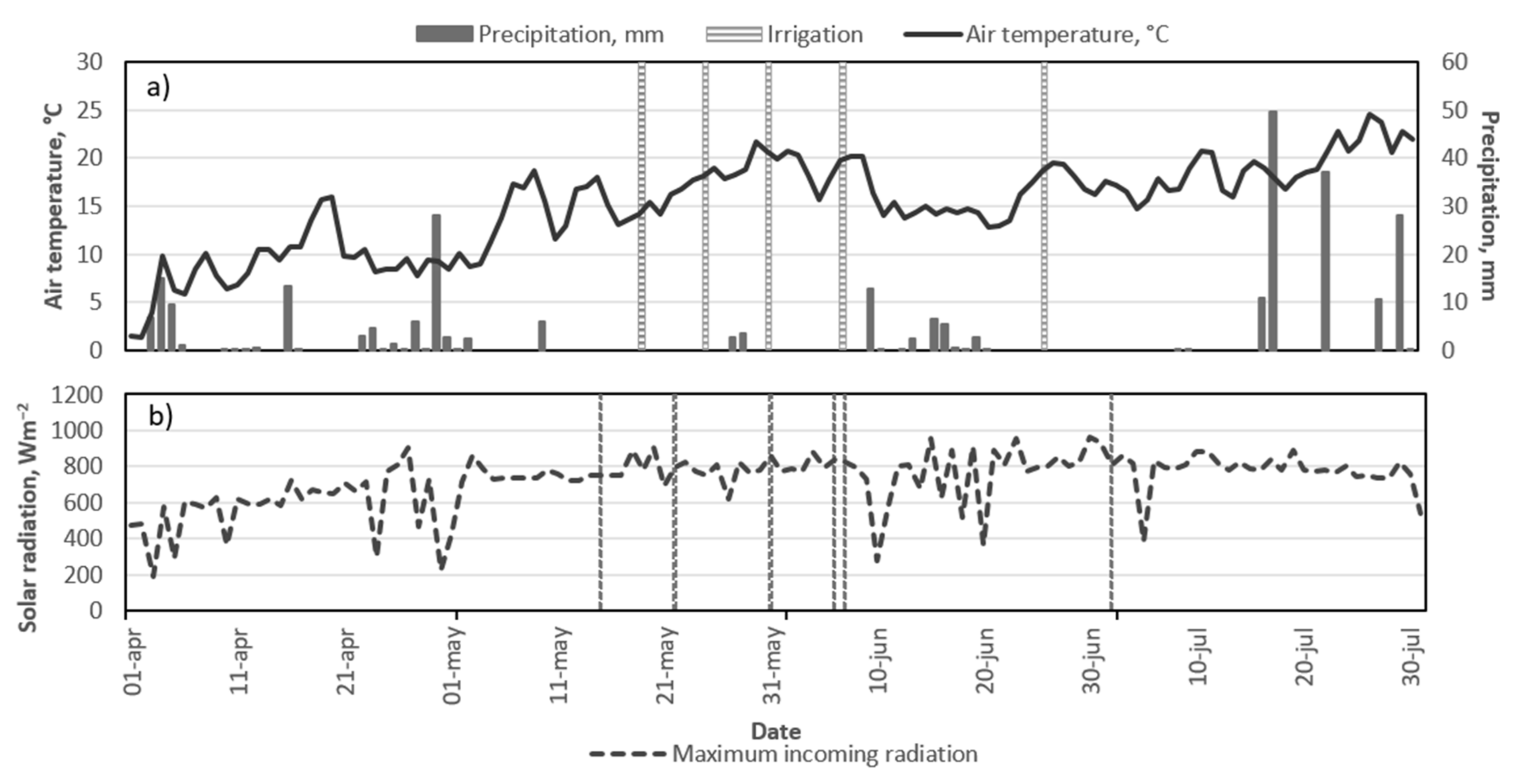
Appendix A. Initial Weather Parameters
| Date | Acquisition Time | Air Temperature Ta (°C) | Solar Radiation Rs (Wm−2) | Relative Humidity RH (%) | Wind Speed u [(m s−1) | Air Pressure pa (mbar) | |
|---|---|---|---|---|---|---|---|
| 15 May 2018 | 14:35 | 25.04 | 716.13 | 34.14 | 1.59 | 1059 | |
| 22 May 2018 | 15:35 | 22.14 | 574.50 | 40.81 | 1.43 | 1060 | |
| 31 May 2018 | 14:20 | 23.81 | 780.60 | 48.07 | 2.12 | 1019 | |
| 6 June 2018 | 10:15 | 20.45 | 702.33 | 50.51 | 0.76 | 1018 | |
| 11:00 | 22.03 | 729.07 | 40.36 | 1.11 | 1018 | ||
| 11:30 | 22.49 | 678.00 | 38.81 | 1.00 | 1018 | ||
| 12:00 | 22.96 | 768.27 | 35.66 | 1.05 | 1018 | ||
| 12:30 | 23.32 | 779.47 | 36.67 | 0.85 | 1018 | ||
| 13:00 | 23.65 | 791.30 | 37.18 | 1.03 | 1017 | ||
| 13:30 | 24.09 | 809.80 | 34.91 | 0.99 | 1017 | ||
| 14:00 | 24.30 | 777.33 | 35.59 | 1.58 | 1017 | ||
| 7 June 2018 | 14:42 | 25.98 | 787.73 | 27.25 | 1.29 | 1016 | |
| 2 July 2018 | 15:35 | 25.39 | 730.63 | 26.85 | 0.94 | 1018 | |
| 28 June 2019 | 11:49 | 18.12 | 717.70 | 78.64 | 1.87 | 1023 | |
| 12:13 | 18.65 | 756.03 | 74.83 | 1.65 | 1023 | ||
| 13:20 | 20.16 | 777.07 | 70.09 | 1.65 | 1023 | ||
| 14:49 | 22.03 | 702.97 | 65.48 | 0.81 | 1023 | ||
| Treatment | Irrigation in 2018, mm | Irrigation in 2019, mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 19.05 | 25.05 | 31.05 | 06.06 | 26.06 | Total 2018 | 24.04 | 15.05 | 01.07 | Total 2019 | |
| I0 | 20 | 15 | 15 | 10 | 25 | 85 | 50 | 0 | 0 | 50 |
| I1 | 20 | 40 | 45 | 30 | 25 | 160 | 50 | 15 | 20 | 85 |
| I2 | 20 | 40 | 45 | 30 | 25 | 160 | 50 | 25 | 35 | 110 |
Appendix B. Energy Balance Components and Calculations
Appendix C
References
- Jones, H.G. Imaging for precision agriculture—The mixed pixel problem with special reference to thermal imagery. In Proceedings of the 9th Conference of the Asian Federation for Information Technology in Agriculture, Peth, Australia, 29 September–2 October 2014. [Google Scholar]
- Matese, A.; Baraldi, R.; Berton, A.; Cesaraccio, C.; Di Gennaro, S.F.; Duce, P.; Facini, O.; Mameli, M.G.; Piga, A.; Zaldei, A. Estimation of water stress in grapevines using proximal and remote sensing methods. Remote Sens. 2018, 10, 114. [Google Scholar] [CrossRef] [Green Version]
- Franch, B.; Vermote, E.F.; Skakun, S.; Roger, J.C.; Becker-Reshef, I.; Murphy, E.; Justice, C. Remote sensing based yield monitoring: Application to winter wheat in United States and Ukraine. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 112–127. [Google Scholar] [CrossRef]
- Burton, I.; Lim, B. Achieving adequate adaptation in agriculture. In Increasing Climate Variability and Change; Springer: Berlin/Heidelberg, Germany, 2005; pp. 191–200. [Google Scholar]
- Liu, F.; Jensen, C.R.; Andersen, M.N. A review of drought adaptation in crop plants: Changes in vegetative and reproductive physiology induced by ABA-based chemical signals. Aust. J. Agric. Res. 2005, 56, 1245–1252. [Google Scholar] [CrossRef]
- Jones, H.G. Drought and other abiotic stresses. In Plants and Microclimate; Cambridge University Press: Cambridge, UK, 2014; pp. 255–289. [Google Scholar]
- Li, Y.; Li, H.; Li, Y.; Zhang, S. Improving water-use efficiency by decreasing stomatal conductance and transpiration rate to maintain higher ear photosynthetic rate in drought-resistant wheat. Crop J. 2017, 5, 231–239. [Google Scholar] [CrossRef]
- Kulkarni, M.; Soolanayakanahally, R.; Ogawa, S.; Uga, Y. Drought response in wheat: Key genes and regulatory mechanisms controlling root system architecture and transpiration efficiency. Front. Chem. 2017, 5, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Krishna, G.; Sahoo, R.N.; Singh, P.; Patra, H.; Bajpai, V.; Das, B.; Kumar, S.; Dhandapani, R.; Vishwakarma, C.; Pal, M.; et al. Application of thermal imaging and hyperspectral remote sensing for crop water deficit stress monitoring. Geocarto Int. 2021, 36, 481–498. [Google Scholar] [CrossRef]
- Legg, B.J.; Day, W.; Lawlor, D.W.; Parkinson, K.J. The effects of drought on barley growth: Models and measurements showing the relative importance of leaf area and photosynthetic rate. J. Agric. Sci. 1979, 92, 703–716. [Google Scholar] [CrossRef]
- Kim, S.W.; Lee, S.K.; Jeong, H.J.; An, G.; Jeon, J.S.; Jung, K.H. Crosstalk between diurnal rhythm and water stress reveals an altered primary carbon flux into soluble sugars in drought-treated rice leaves. Sci. Rep. 2017, 7, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Yu, Q.; Li, J.; Li, L.H.; Li, X.G.; Yu, G.R.; Sun, X.M. Simulation of diurnal variations of CO2, water and heat fluxes over winter wheat with a model coupled photosynthesis and transpiration. Agric. For. Meteorol. 2006, 137, 194–219. [Google Scholar] [CrossRef]
- Messina, G.; Modica, G. Applications of UAV thermal imagery in precision agriculture: State of the art and future research outlook. Remote Sens. 2020, 12, 1491. [Google Scholar] [CrossRef]
- Maes, W.; Huete, A.; Steppe, K. Optimizing the processing of UAV-based thermal imagery. Remote Sens. 2017, 9, 476. [Google Scholar] [CrossRef] [Green Version]
- Santesteban, L.G.; Di Gennaro, S.F.; Herrero-Langreo, A.; Miranda, C.; Royo, J.B.; Matese, A. High-resolution UAV-based thermal imaging to estimate the instantaneous and seasonal variability of plant water status within a vineyard. Agric. Water Manag. 2017, 183, 49–59. [Google Scholar] [CrossRef]
- Sagan, V.; Maimaitijiang, M.; Sidike, P.; Eblimit, K.; Peterson, K.; Hartling, S.; Esposito, F.; Khanal, K.; Newcomb, M.; Pauli, D.; et al. UAV-based high resolution thermal imaging for vegetation monitoring, and plant phenotyping using ICI 8640 P, FLIR Vue Pro R 640, and thermo map cameras. Remote Sens. 2019, 11, 330. [Google Scholar] [CrossRef] [Green Version]
- Gago, J.; Douthe, C.; Coopman, R.E.; Gallego, P.P.; Ribas-Carbo, M.; Flexas, J.; Escalona, J.; Medrano, H. UAVs challenge to assess water stress for sustainable agriculture. Agric. Water Manag. 2015, 153, 9–19. [Google Scholar] [CrossRef]
- Jackson, R.D.; Kustas, W.P.; Choudhury, B.J. A reexamination of the crop water stress index. Irrig. Sci. 1988, 9, 309–317. [Google Scholar] [CrossRef]
- Hoffmann, H.; Jensen, R.; Thomsen, A.; Nieto, H.; Rasmussen, J.; Friborg, T. Crop water stress maps for an entire growing season from visible and thermal UAV imagery. Biogeosciences 2016, 13, 6545–6563. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Dugo, V.; Zarco-Tejada, P.; Nicolás, E.; Nortes, P.A.; Alarcón, J.J.; Intrigliolo, D.S.; Fereres, E. Using high resolution UAV thermal imagery to assess the variability in the water status of five fruit tree species within a commercial orchard. Precis. Agric. 2013, 14, 660–678. [Google Scholar] [CrossRef]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Mzid, N.; Cantore, V.; De Mastro, G.; Albrizio, R.; Sellami, M.H.; Todorovic, M. The application of ground-based and satellite remote sensing for estimation of bio-physiological parameters of wheat grown under different water regimes. Water 2020, 12, 2095. [Google Scholar] [CrossRef]
- El-Shirbeny, M.A.; Ali, A.M.; Rashash, A.; Badr, M.A. Wheat yield response to water deficit under central pivot irrigation system using remote sensing techniques. World J. Eng. Technol. 2015, 3, 65–72. [Google Scholar] [CrossRef] [Green Version]
- Köksal, E.S. Irrigation water management with water deficit index calculated based on oblique viewed surface temperature. Irrig. Sci. 2008, 27, 41–56. [Google Scholar] [CrossRef]
- Tang, J.; Han, W.; Zhang, L. UAV multispectral imagery combined with the FAO-56 dual approach for maize evapotranspiration mapping in the north china plain. Remote Sens. 2019, 11, 2519. [Google Scholar] [CrossRef] [Green Version]
- De Bruin, H.; Trigo, I. A new method to estimate reference crop evapotranspiration from geostationary satellite imagery: Practical considerations. Water 2019, 11, 382. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO: Quebec City, QC, Canada, 1998. [Google Scholar]
- Kjaersgaard, J.H.; Plauborg, F.; Mollerup, M.; Petersen, C.T.; Hansen, S. Crop coefficients for winter wheat in a sub-humid climate regime. Agric. Water Manag. 2008, 95, 918–924. [Google Scholar] [CrossRef]
- González-Dugo, M.P.; Moran, M.S.; Mateos, L.; Bryant, R. Canopy temperature variability as an indicator of crop water stress severity. Irrig. Sci. 2006, 24, 233–240. [Google Scholar] [CrossRef]
- Gerhards, M.; Schlerf, M.; Mallick, K.; Udelhoven, T. Challenges and future perspectives of multi-/hyperspectral thermal infrared remote sensing for crop water-stress detection: A review. Remote Sens. 2019, 11, 1240. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Müller, C.; Elliot, J.; Mueller, N.D.; Ciais, P.; Jägermeyr, J.; Gerber, J.; Dumas, P.; Wang, C.; Yang, H.; et al. Global irrigation contribution to wheat and maize yield. Nat. Commun. 2021, 12, 1–8. [Google Scholar] [CrossRef]
- Jacobsen, O.H.; Schjønning, P. A laboratory calibration of time domain reflectometry for soil water measurement including effects of bulk density and texture. J. Hydrol. 1993, 151, 147–157. [Google Scholar] [CrossRef]
- Hansen, L. Soil types at the Danish State experimental stations. Tidsskr. Planteavl 1976, 80, 742–758. [Google Scholar]
- Turner, N.C. Measurement of plant water status by the pressure chamber technique. Irrig. Sci. 1988, 9, 289–308. [Google Scholar] [CrossRef]
- Hack, H.; Bleiholder, H.; Buhr, L.; Meier, U.; Schnock-Fricke, U.; Weber, E.; Witzenberger, A. Einheitliche Codierung der phänologischen Entwicklungsstadien mono- und Allgemein. Nachrichtenbl. Deut. Pflanzenschutzd. 1992, 44, 256–270. [Google Scholar]
- Jensen, C.R.; Svendsen, H.; Andersen, M.N.; Lösch, R. Use of the root contact concept, an empirical leaf conductance model and pressure-volume curves in simulating crop water relations. Plant Soil 1993, 149, 1–26. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteorol. 1990, 49, 205–223. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E. AquaCrop—The FAO crop model to simulate yield response to water: II. main algorithms and software description. Agron. J. 2009, 101, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Sagan, V.; Maimaitijiang, M.; Sidike, P.; Maimaitiyiming, M.; Erkbol, H.; Hartling, S.; Peterson, K.T.; Peterson, J.; Burken, J.; Fritschi, F. UAV/satellite multiscale data fusion for crop monitoring and early stress detection. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Enschede, The Netherlands, 10–14 June 2019. [Google Scholar]
- Colaizzi, P.D.; Barnes, E.M.; Clarke, T.R.; Choi, C.Y.; Waller, P.M.; Haberland, J.; Kostrzewski, M. Water stress detection under high frequency sprinkler irrigation with water deficit index. J. Irrig. Drain. Eng. 2003, 9437. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Garcia, M.; Ibrom, A.; Jakobsen, J.; Köppl, C.J.; Mallick, K.; Looms, M.C.; Bauer-Gottwein, P. Mapping root-zone soil moisture using a temperature-vegetation triangle approach with an unmanned aerial system: Incorporating surface roughness from structure from motion. Remote Sens. 2018, 10, 1978. [Google Scholar] [CrossRef] [Green Version]
- Barbedo, J.G.A. A review on the use of unmanned aerial vehicles and imaging sensors for monitoring and assessing plant stresses. Drones 2019, 3, 40. [Google Scholar] [CrossRef] [Green Version]
- Gerhards, M.; Schlerf, M.; Rascher, U.; Udelhoven, T.; Juszczak, R.; Alberti, G.; Miglietta, F.; Inoue, Y. Analysis of airborne optical and thermal imagery for detection of water stress symptoms. Remote Sens. 2018, 10, 1139. [Google Scholar] [CrossRef] [Green Version]
- Cohen, Y.; Alchanatis, V.; Meron, M.; Saranga, Y.; Tsipris, J. Estimation of leaf water potential by thermal imagery and spatial analysis. J. Exp. Bot. 2005, 56, 1843–1852. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, T.; Schreiner, R.P. Appropriate time to measure leaf and stem water potential in North-South Oriented, vertically shoot-positioned vineyards. Am. J. Enol. Vitic. 2021, 72, 64–72. [Google Scholar] [CrossRef]
- Wang, X.G.; Kang, Q.; Chen, X.H.; Wang, W.; Fu, Q.H. Wind speed-independent two-source energy balance model based on a theoretical trapezoidal relationship between land surface temperature and fractional vegetation cover for evapotranspiration estimation. Adv. Meteorol. 2020, 2020. [Google Scholar] [CrossRef]
- Foster, T.; Mieno, T.; Brozović, N. Satellite-based monitoring of irrigation water use: Assessing measurement errors and their implications for agricultural water management policy. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Wang, S.; Garcia, M.; Ibrom, A.; Bauer-Gottwein, P. Temporal interpolation of land surface fluxes derived from remote sensing—Results with an unmanned aerial system. Hydrol. Earth Syst. Sci. 2020, 24, 3643–3661. [Google Scholar] [CrossRef]
- Hu, X.; Shi, L.; Lin, L.; Zha, Y. Nonlinear boundaries of land surface temperature–vegetation index space to estimate water deficit index and evaporation fraction. Agric. For. Meteorol. 2019, 279, 107736. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Legg, B.J.; Long, I.F. Turbulent diffusion within a wheat canopy: II. Results and interpretation. Q. J. R. Meteorol. Soc. 1975, 101, 611–628. [Google Scholar] [CrossRef]

| Date | Acquisition Time | Air Temperature Ta (°C) | ET0 (mm h−1) | Trapezoid x-Points (°C) | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| 15 May 2018 | 14:35 | 25.04 | 0.45 | −5.65 | 3.76 | −4.15 | 15.17 |
| 22 May 2018 | 15:35 | 22.14 | 0.36 | −4.59 | 3.26 | −3.03 | 13.05 |
| 31 May 2018 | 14:20 | 23.81 | 0.49 | −3.73 | 4.27 | −2.42 | 13.90 |
| 6 June 2018 | 10:15 | 20.45 | 0.42 | −2.32 | 5.81 | 2.15 | 24.58 |
| 11:00 | 22.03 | 0.44 | −3.90 | 5.09 | −0.91 | 20.32 | |
| 11:30 | 22.49 | 0.41 | −4.30 | 4.73 | −1.30 | 20.22 | |
| 12:00 | 22.96 | 0.46 | −4.48 | 5.35 | −1.26 | 22.31 | |
| 12:30 | 23.32 | 0.48 | −4.29 | 5.78 | −0.32 | 25.77 | |
| 13:00 | 23.65 | 0.48 | −4.39 | 5.56 | −1.07 | 23.36 | |
| 13:30 | 24.09 | 0.50 | −4.68 | 5.68 | −1.22 | 24.46 | |
| 14:00 | 24.30 | 0.48 | −5.05 | 4.56 | −3.17 | 17.23 | |
| 7 June 2018 | 14:42 | 25.98 | 0.49 | −6.30 | 4.63 | −4.05 | 20.18 |
| 2 July 2018 | 15:35 | 25.39 | 0.45 | −6.18 | 4.69 | −3.15 | 22.98 |
| 28 June 2019 | 11:49 | 18.12 | 0.44 | −0.39 | 3.29 | 1.92 | 12.27 |
| 12:13 | 18.65 | 0.46 | −0.66 | 3.63 | 2.06 | 14.23 | |
| 13:20 | 20.16 | 0.48 | −1.26 | 3.63 | 1.33 | 14.72 | |
| 14:49 | 22.03 | 0.44 | −1.85 | 3.99 | 2.42 | 21.82 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antoniuk, V.; Manevski, K.; Kørup, K.; Larsen, R.; Sandholt, I.; Zhang, X.; Andersen, M.N. Diurnal and Seasonal Mapping of Water Deficit Index and Evapotranspiration by an Unmanned Aerial System: A Case Study for Winter Wheat in Denmark. Remote Sens. 2021, 13, 2998. https://doi.org/10.3390/rs13152998
Antoniuk V, Manevski K, Kørup K, Larsen R, Sandholt I, Zhang X, Andersen MN. Diurnal and Seasonal Mapping of Water Deficit Index and Evapotranspiration by an Unmanned Aerial System: A Case Study for Winter Wheat in Denmark. Remote Sensing. 2021; 13(15):2998. https://doi.org/10.3390/rs13152998
Chicago/Turabian StyleAntoniuk, Vita, Kiril Manevski, Kirsten Kørup, Rene Larsen, Inge Sandholt, Xiying Zhang, and Mathias Neumann Andersen. 2021. "Diurnal and Seasonal Mapping of Water Deficit Index and Evapotranspiration by an Unmanned Aerial System: A Case Study for Winter Wheat in Denmark" Remote Sensing 13, no. 15: 2998. https://doi.org/10.3390/rs13152998
APA StyleAntoniuk, V., Manevski, K., Kørup, K., Larsen, R., Sandholt, I., Zhang, X., & Andersen, M. N. (2021). Diurnal and Seasonal Mapping of Water Deficit Index and Evapotranspiration by an Unmanned Aerial System: A Case Study for Winter Wheat in Denmark. Remote Sensing, 13(15), 2998. https://doi.org/10.3390/rs13152998