Snow Cover Variability in the Greater Alpine Region in the MODIS Era (2000–2019)
Abstract
:1. Introduction
2. Materials and Methods
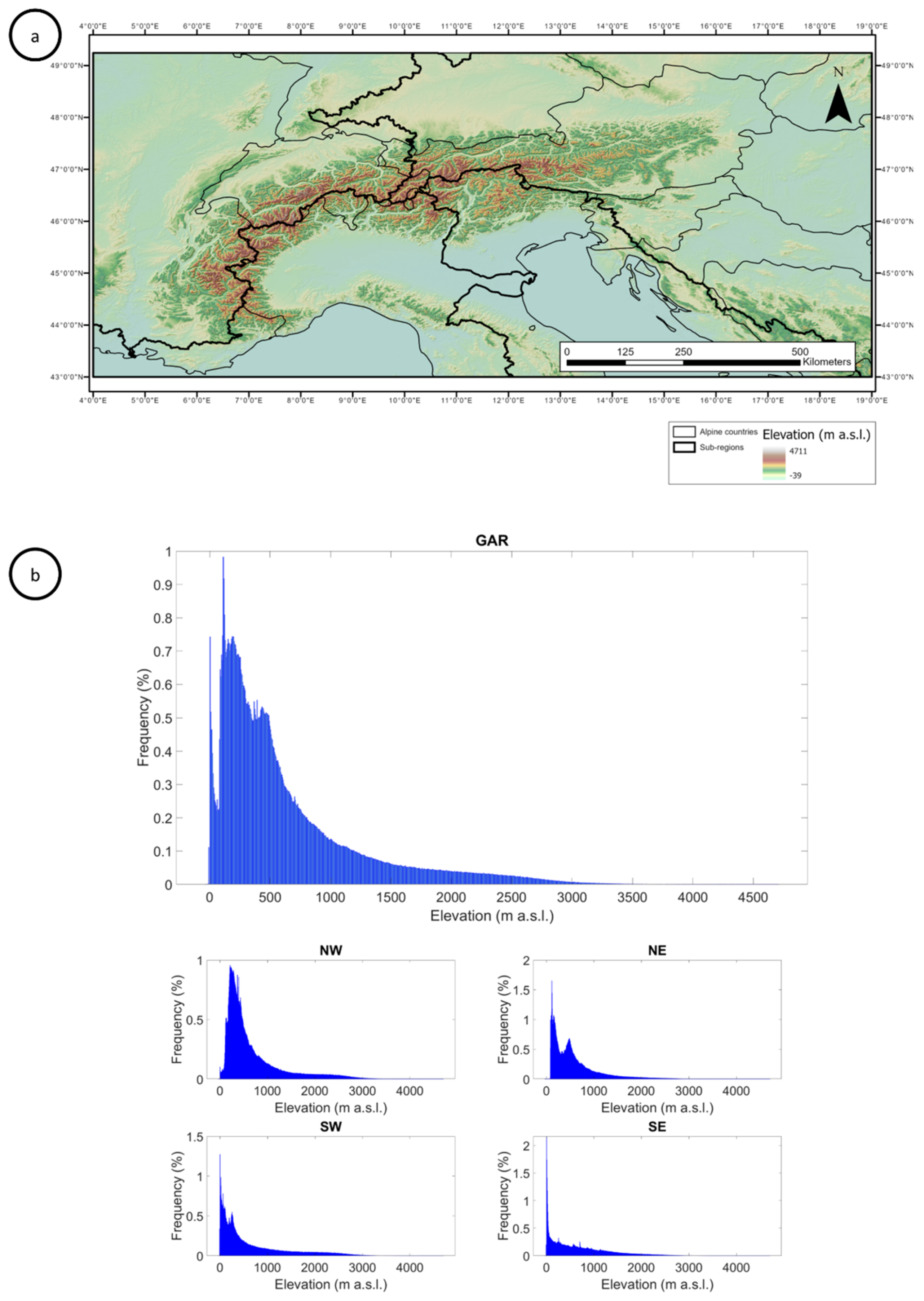
2.1. Study Area
2.2. Snow Cover and Ancillary Data
2.3. Cloud Cover and Gap Filtering
- Step 1: Combination of MOD10A1 and MYD10A1 products. By taking advantage of the different overpass time of Terra and Aqua satellites and the movement of clouds in between, the surfaces beneath clouds can be partly revealed. Let MODi,j,t be the snow cover grid point of the MOD10A1 product at each date t for grid row i and column j and MYDi,j,t the corresponding value of MYD10A1 for the same date and grid location. This step assumes that no snowmelt or snowfall occurred during the overpass of the two satellites on the same day. Snow cover from the MOD10A1 product forms the basis of the snow grid used in further processing steps, as this product is considered more accurate than its counterpart obtained from Aqua observations [44]. Thus, if MODi,j,t is cloud-free, the combination grid Si,j,t will retain its value, while if MODi,j,t is covered by clouds, Si,j,t will use the value of the MYDi,j,t grid point, i.e.,
- Step 2: Temporal combination of adjacent dates. Cloud cover can vary greatly from one day to the other. Thus, a combination of snow cover data from adjacent dates can be used to infer the presence of snow on a cloud-covered date, assuming that no snowmelt or snowfall occurred on the adjacent dates. For each grid point Si,j at date t, the grids at date t − 1 and t + 1 are considered. If a grid point is snow-covered on both dates, Si,j,t becomes snow-covered. The same occurs for snow-free pixels. If the surface conditions on date t − 1 and t + 1 are different, the pixel is left unchanged.
- Step 3: Calculation of the snow transition elevation. This step is based on finding the snow cover elevation range on a certain date. For each date t, the elevation of the maximum snowline (above which all pixels are snow-covered) and minimum snowline (elevation below which all pixels are snow-free) are calculated. This step then assumes that no snow should be found in cloudy pixels below the minimum snowline and that all cloudy pixels above the maximum snowline should be covered by snow. A grid point is then reclassified as snow if its elevation Hi,j is higher than the maximum snowline and as snow-free if its elevation is lower than the minimum snowline, following Equation (5):
- Step 4: Spatial interpolation. In this step, a plus sign-shaped neighborhood of four points around each grid point is considered (i.e., points Si−1,j, Si+1,j, Si,j−1 and Si,j+1). If at least 3 out of four of these points are snow-covered (snow-free), the grid point is reclassified as snow-covered (snow-free). The assumption of this point is based on spatial autocorrelation, so that the middle grid point will, with high probability, have the same surface type as the nearby grid points.
- Step 5: Combination of snowline elevation and spatial interpolation. In this step, the 3 × 3 neighborhood of each grid point is examined, and the elevation and snow cover of each non-cloudy pixel is considered; the central point is reclassified as snow-covered if any of the neighboring points is snow-covered and its elevation is lower than that of the central point, i.e.,
- Step 6: Temporal combination. In the final step, we iteratively consider the subsequent dates for all points that have remained cloud covered after the application of steps 1–5. For each grid point, dates (t + 1, …, t + n) are considered until a date is found where the point Si,j,t+n is snow-covered or snow-free. The value of the grid point on date t + n is then assigned to grid point Si,j,t. This step might introduce the largest uncertainty, since it assumes no snowfall or snowmelt occurred during the interpolation period, which might not necessarily be true if the number of cloud-covered days is large.
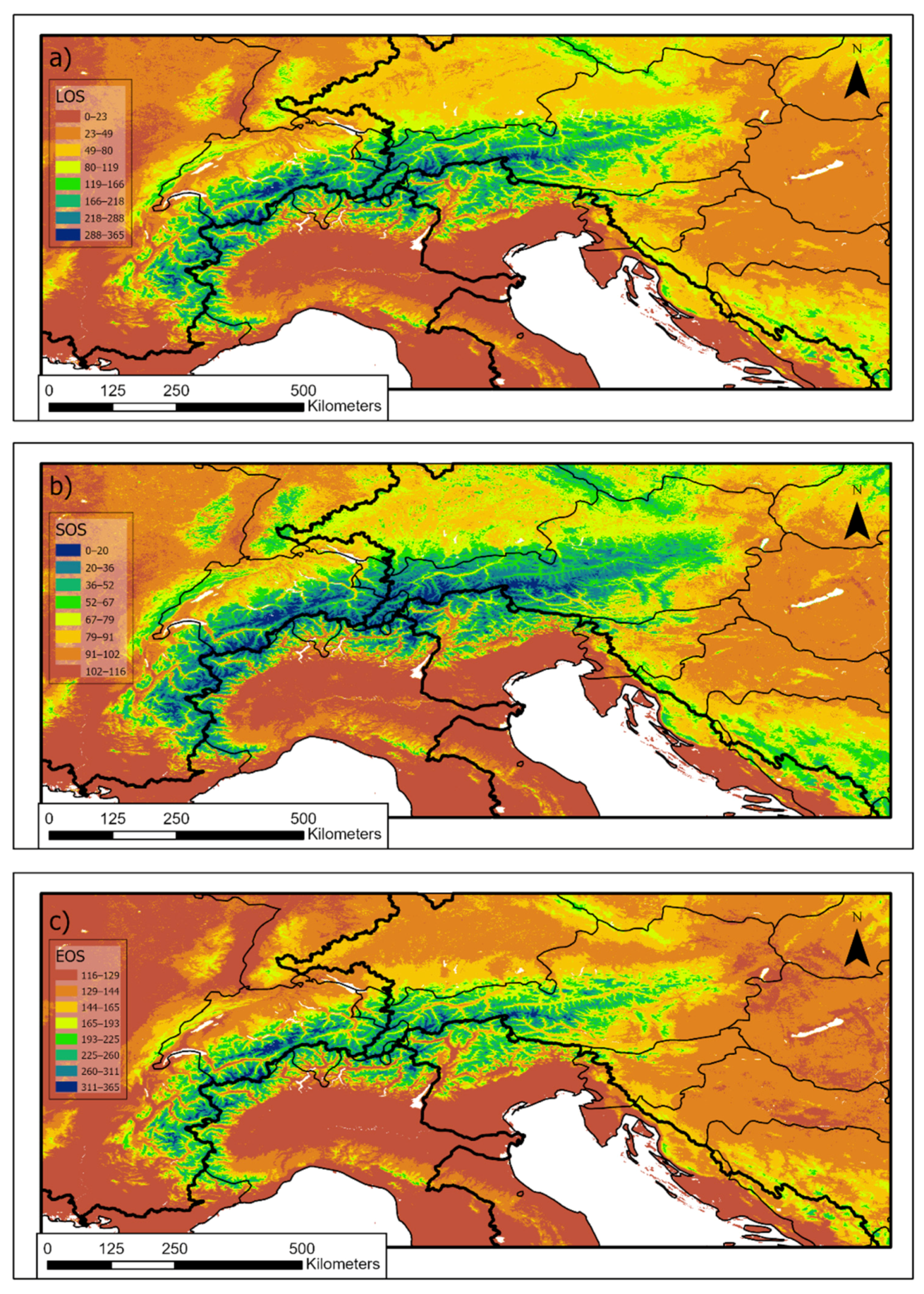
2.4. Calculation of Snow Cover Metrics (Length, Start and End of the Snow Season)
3. Results
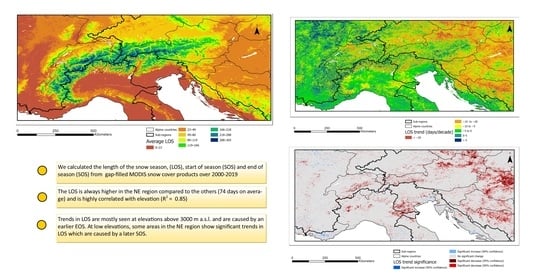
3.1. Means of Snow Cover Metrics over the GAR
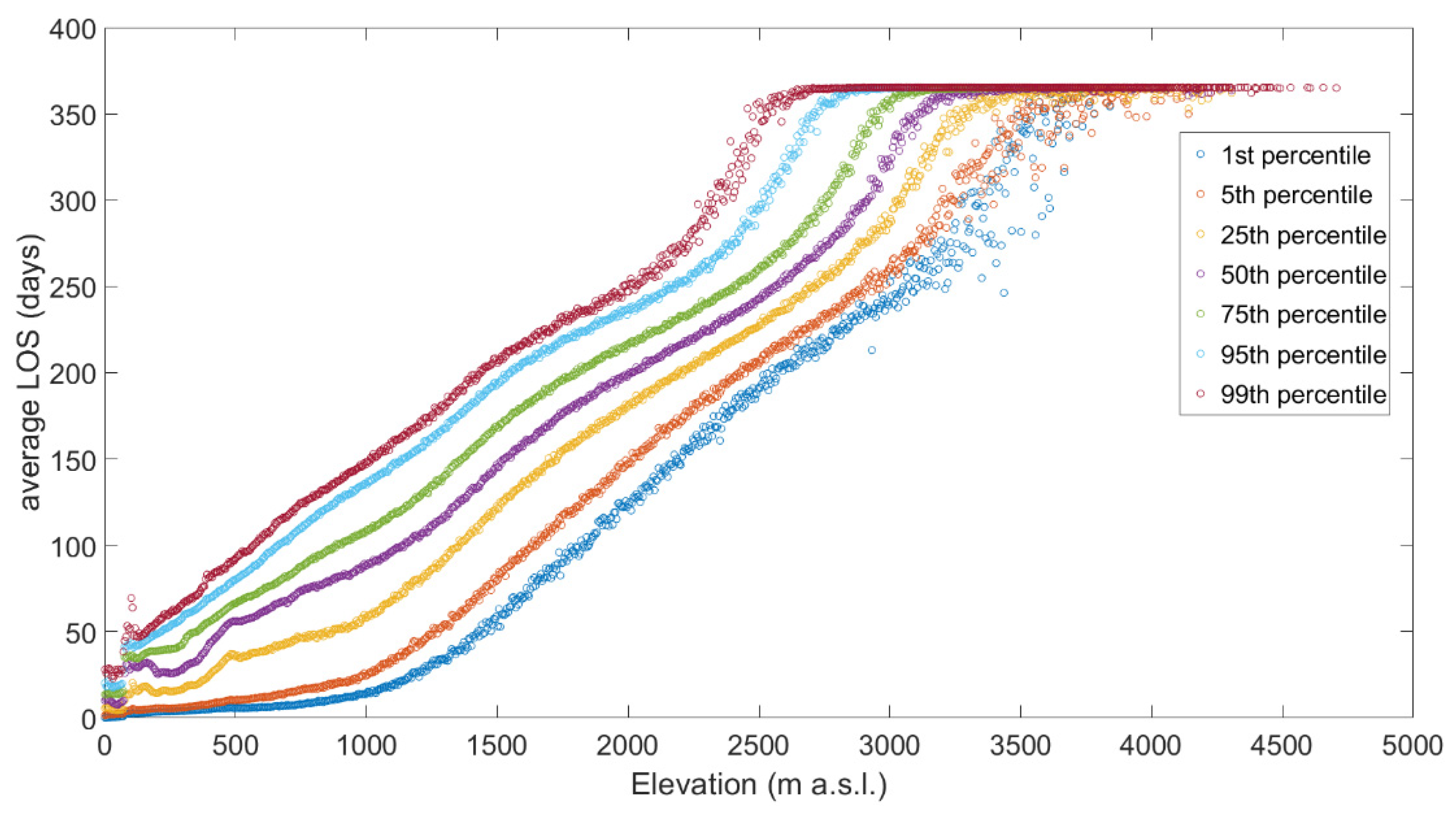
3.2. Factors Explaining the Spatial Variability in the Snow Cover
3.3. Interannual Variability in Snow Cover Metrics and Trend Analysis
4. Discussion
4.1. The Role of Glaciers
4.2. Snow Cover Variability in the Alps and Other Mountain Regions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Flanner, M.; Shell, K.; Barlage, M.; Perovich, D.K.; Tschudi, M.A. Radiative forcing and albedo feedback from the Northern Hemisphere cryosphere between 1979 and 2008. Nat. Geosci. 2011, 4, 151–155. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Bormann, K.J.; Brown, R.D.; Derksen, C.; Painter, T.H. Estimating snow-cover trends from space. Nat. Clim. Chang. 2018, 8, 924–928. [Google Scholar] [CrossRef]
- Senese, A.; Azzoni, R.S.; Maragno, D.; D’Agata, C.; Fugazza, D.; Mosconi, B.; Trenti, A.; Meraldi, E.; Smiraglia, C.; Diolaiuti, G. The non-woven geotextiles as strategies for mitigating the impacts of climate change on glaciers. Cold Reg. Sci. Technol. 2020, 173, 103007. [Google Scholar] [CrossRef]
- Zhang, T. Influence of the seasonal snow cover on the ground thermal regime: An overview. Rev. Geophys. 2005, 43, 43. [Google Scholar] [CrossRef]
- Sandvik, S.M.; Heegaard, E.; Elven, R.; Vandvik, V. Responses of alpine snowbed vegetation to long-term experimental warming. Écoscience 2004, 11, 150–159. [Google Scholar] [CrossRef]
- Vanin, S.; Turchetto, M. Winter activity of spiders and pseudoscorpions in the South-Eastern Alps (Italy). Ital. J. Zool. 2007, 74, 31–38. [Google Scholar] [CrossRef]
- Hågvar, S. A review of Fennoscandian arthropods living on and in snow. Eur. J. Èntomol. 2010, 107, 281–298. [Google Scholar] [CrossRef] [Green Version]
- Phoenix, G. Arctic plants threatened by winter snow loss. Nat. Clim. Chang. 2018, 8, 942–943. [Google Scholar] [CrossRef]
- Resano-Mayor, J.; Korner-Nievergelt, F.; Vignali, S.; Horrenberger, N.; Barras, A.G.; Braunisch, V.; Pernollet, C.A.; Arlettaz, R. Snow cover phenology is the main driver of foraging habitat selection for a high-alpine passerine during breeding: Implications for species persistence in the face of climate change. Biodivers. Conserv. 2019, 28, 2669–2685. [Google Scholar] [CrossRef]
- D’Agata, C.; Bocchiola, D.; Soncini, A.; Maragno, D.; Smiraglia, C.; Diolaiuti, G.A. Recent area and volume loss of Alpine glaciers in the Adda River of Italy and their contribution to hydropower production. Cold Reg. Sci. Technol. 2018, 148, 172–184. [Google Scholar] [CrossRef]
- Schaefli, B.; Manso, P.; Fischer, M.; Huss, M.; Farinotti, D. The role of glacier retreat for Swiss hydropower production. Renew. Energy 2019, 132, 615–627. [Google Scholar] [CrossRef] [Green Version]
- Marty, C. Climate Change and Snow Cover in the European Alps. In The Impact of Skiing on Mountain Environments; Rixen, C., Rolando, A., Eds.; Bentham Science Publishers: Sharjah, United Arab Emirates, 2013. [Google Scholar]
- Kapnick, S.; Hall, A. Causes of recent changes in western North American snowpack. Clim. Dyn. 2011, 38, 1885–1899. [Google Scholar] [CrossRef]
- Muntán, E.; García, C.; Oller, P.; Martí, G.; García, A.; Gutierrez, E. Reconstructing snow avalanches in the Southeastern Pyrenees. Nat. Hazards Earth Syst. Sci. 2009, 9, 1599–1612. [Google Scholar] [CrossRef] [Green Version]
- Fugazza, D.; Shaw, T.E.; Mashtayeva, S.; Brock, B. Inter-annual variability in snow cover depletion patterns and atmospheric circulation indices in the Upper Irtysh basin, Central Asia. Hydrol. Process. 2020, 34, 3738–3757. [Google Scholar] [CrossRef]
- Valt, M.; Cianfarra, P. Recent snow cover variability in the Italian Alps. Cold Reg. Sci. Technol. 2010, 64, 146–157. [Google Scholar] [CrossRef]
- Bocchiola, D.; Diolaiuti, G. Evidence of climate change within the Adamello Glacier of Italy. Theor. Appl. Clim. 2009, 100, 351–369. [Google Scholar] [CrossRef]
- Lejeune, Y.; Dumont, M.; Panel, J.-M.; Lafaysse, M.; Lapalus, P.; Le Gac, E.; Lesaffre, B.; Morin, S. 57 years (1960–2017) of snow and meteorological observations from a mid-altitude mountain site (Col de Porte, France, 1325 m of altitude). Earth Syst. Sci. Data 2019, 11, 71–88. [Google Scholar] [CrossRef] [Green Version]
- Marty, C. Regime shift of snow days in Switzerland. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Matiu, M.; Crespi, A.; Bertoldi, G.; Carmagnola, C.M.; Marty, C.; Morin, S.; Schöner, W.; Berro, D.C.; Chiogna, G.; De Gregorio, L.; et al. Observed snow depth trends in the European Alps: 1971 to 2019. Cryosphere 2021, 15, 1343–1382. [Google Scholar] [CrossRef]
- Rohrer, M.; Salzmann, N.; Stoffel, M.; Kulkarni, A.V. Missing (in-situ) snow cover data hampers climate change and runoff studies in the Greater Himalayas. Sci. Total. Environ. 2013, 468–469, S60–S70. [Google Scholar] [CrossRef]
- Hüsler, F.; Jonas, T.; Riffler, M.; Musial, J.P.; Wunderle, S. A satellite-based snow cover climatology (1985–2011) for the European Alps derived from AVHRR data. Cryosphere 2014, 8, 73–90. [Google Scholar] [CrossRef] [Green Version]
- Dietz, A.J.; Conrad, C.; Kuenzer, C.; Gesell, G.; Dech, S. Identifying Changing Snow Cover Characteristics in Central Asia between 1986 and 2014 from Remote Sensing Data. Remote Sens. 2014, 6, 12752–12775. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Riggs, G.A. Accuracy assessment of the MODIS snow products. Hydrol. Process. 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Redpath, T.A.N.; Sirguey, P.; Cullen, N.J. Characterising spatio-temporal variability in seasonal snow cover at a regional scale from MODIS data: The Clutha Catchment, New Zealand. Hydrol. Earth Syst. Sci. 2019, 23, 3189–3217. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Yan, W.; Zhao, C.; Kundzewicz, Z.W. Snow-Cover Area and Runoff Variation under Climate Change in the West Kunlun Mountains. Water 2019, 11, 2246. [Google Scholar] [CrossRef] [Green Version]
- Dietz, A.J.; Wohner, C.; Kuenzer, C. European Snow Cover Characteristics between 2000 and 2011 Derived from Improved MODIS Daily Snow Cover Products. Remote Sens. 2012, 4, 2432–2454. [Google Scholar] [CrossRef] [Green Version]
- Notarnicola, C. Hotspots of snow cover changes in global mountain regions over 2000–2018. Remote Sens. Environ. 2020, 243, 111781. [Google Scholar] [CrossRef]
- Brunetti, M.; Lentini, G.; Maugeri, M.; Nanni, T.; Auer, I.; Boehm, R.; Schoener, W. Climate variability and change in the Greater Alpine Region over the last two centuries based on multi-variable analysis. Int. J. Clim. 2009, 29, 2197–2225. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Nanni, T.; Auer, I.; Böhm, R.; Schöner, W. Precipitation variability and changes in the greater Alpine region over the 1800–2003 period. J. Geophys. Res. Space Phys. 2006, 111, 111. [Google Scholar] [CrossRef]
- Manara, V.; Bassi, M.; Brunetti, M.; Cagnazzi, B.; Maugeri, M. 1990–2016 surface solar radiation variability and trend over the Piedmont region (northwest Italy). Theor. Appl. Clim. 2019, 136, 849–862. [Google Scholar] [CrossRef]
- Manara, V.; Brunetti, M.; Gilardoni, S.; Landi, T.C.; Maugeri, M. 1951–2017 changes in the frequency of days with visibility higher than 10 km and 20 km in Italy. Atmos. Environ. 2019, 214, 116861. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Solomonson, V. NASA MODAPS SIPS MODIS/Terra Snow Cover Daily L3 Global 500m SIN Grid, 2015. Available online: http://nsidc.org/data/MOD10A1/versions/6 (accessed on 26 July 2021).
- Platnick, S.; King, M.; Ackerman, S.; Menzel, W.P.; Baum, B.; Riedi, J.; Frey, R. The MODIS cloud products: Algorithms and examples from terra. IEEE Trans. Geosci. Remote Sens. 2003, 41, 459–473. [Google Scholar] [CrossRef] [Green Version]
- Platnick, S.; Meyer, K.G.; King, M.; Wind, G.; Amarasinghe, N.; Marchant, B.; Arnold, G.T.; Zhang, Z.; Hubanks, P.A.; Holz, R.E.; et al. The MODIS Cloud Optical and Microphysical Products: Collection 6 Updates and Examples From Terra and Aqua. IEEE Trans. Geosci. Remote Sens. 2017, 55, 502–525. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise Global DEM Generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-4, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Senese, A.; Maugeri, M.; Ferrari, S.; Confortola, G.; Soncini, A.; Bocchiola, D.; Diolaiuti, G.A. Modelling Shortwave and Longwave Downward Radiation and Air Temperature Driving Ablation at the Forni Glacier (Stelvio National Park, Italy). Geogr. Fis. Din. Quat. 2016, 39, 89–100. [Google Scholar]
- Kästner, M.; Kriebel, K.T. Alpine cloud climatology using long-term NOAA-AVHRR satellite data. Theor. Appl. Clim. 2001, 68, 175–195. [Google Scholar] [CrossRef]
- Tran, H.; Nguyen, P.; Ombadi, M.; Hsu, K.-L.; Sorooshian, S.; Qing, X. A cloud-free MODIS snow cover dataset for the contiguous United States from 2000 to 2017. Sci. Data 2019, 6, 180300. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Jing, Y.; Shen, H.; Zhang, L. The recent developments in cloud removal approaches of MODIS snow cover product. Hydrol. Earth Syst. Sci. 2019, 23, 2401–2416. [Google Scholar] [CrossRef] [Green Version]
- Maskey, S.; Uhlenbrook, S.; Ojha, S. An analysis of snow cover changes in the Himalayan region using MODIS snow products and in-situ temperature data. Clim. Chang. 2011, 108, 391–400. [Google Scholar] [CrossRef]
- Gafurov, A.; Bárdossy, A. Cloud removal methodology from MODIS snow cover product. Hydrol. Earth Syst. Sci. 2009, 13, 1361–1373. [Google Scholar] [CrossRef] [Green Version]
- Hall, D.K.; Riggs, G.A.; DiGirolamo, N.E.; Román, M.O. Evaluation of MODIS and VIIRS cloud-gap-filled snow-cover products for production of an Earth science data record. Hydrol. Earth Syst. Sci. 2019, 23, 5227–5241. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Xie, H. New methods for studying the spatiotemporal variation of snow cover based on combination products of MODIS Terra and Aqua. J. Hydrol. 2009, 371, 192–200. [Google Scholar] [CrossRef]
- Sneyers, R. Über den Einsatz von statistischen Methoden zum objektiven Nachweis von Klimaschwankungen. Meteorol. Z. 1992, 1, 247–256. [Google Scholar] [CrossRef]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. In Henri Theil’s Contributions to Economics and Econometrics: Econometric Theory and Methodology; Raj, B., Koerts, J., Eds.; Advanced Studies in Theoretical and Applied Econometrics; Springer: Dordrecht, The Netherlands, 1992; pp. 345–381. ISBN 978-94-011-2546-8. [Google Scholar]
- Paul, F.; Rastner, P.; Azzoni, R.S.; Diolaiuti, G.; Fugazza, D.; Le Bris, R.; Nemec, J.; Rabatel, A.; Ramusovic, M.; Schwaizer, G.; et al. Glacier shrinkage in the Alps continues unabated as revealed by a new glacier inventory from Sentinel-2. Earth Syst. Sci. Data 2020, 12, 1805–1821. [Google Scholar] [CrossRef]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier Inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef] [Green Version]
- Azzoni, R.S.; Fugazza, D.; Zerboni, A.; Senese, A.; D’Agata, C.; Maragno, D.; Carzaniga, A.; Cernuschi, M.; Diolaiuti, G.A. Evaluating high-resolution remote sensing data for reconstructing the recent evolution of supra glacial debris. Prog. Phys. Geogr. Earth Environ. 2018, 42, 3–23. [Google Scholar] [CrossRef] [Green Version]
- Fugazza, D.; Senese, A.; Azzoni, R.S.; Maugeri, M.; Maragno, D.; Diolaiuti, G.A. New evidence of glacier darkening in the Ortles-Cevedale group from Landsat observations. Glob. Planet. Chang. 2019, 178, 35–45. [Google Scholar] [CrossRef]
- Hori, M.; Sugiura, K.; Kobayashi, K.; Aoki, T.; Tanikawa, T.; Kuchiki, K.; Niwano, M.; Enomoto, H. A 38-year (1978–2015) Northern Hemisphere daily snow cover extent product derived using consistent objective criteria from satellite-borne optical sensors. Remote Sens. Environ. 2017, 191, 402–418. [Google Scholar] [CrossRef]
- Terzago, S.; Cassardo, C.; Cremonini, R.; Fratianni, S. Snow Precipitation and Snow Cover Climatic Variability for the Period 1971–2009 in the Southwestern Italian Alps: The 2008–2009 Snow Season Case Study. Water 2010, 2, 773–787. [Google Scholar] [CrossRef]
- Scherrer, S.C.; Wüthrich, C.; Croci-Maspoli, M.; Weingartner, R.; Appenzeller, C. Snow variability in the Swiss Alps 1864–2009. Int. J. Clim. 2013, 33, 3162–3173. [Google Scholar] [CrossRef] [Green Version]
- Gafurov, A.; Vorogushyn, S.; Farinotti, D.; Duethmann, D.; Merkushkin, A.; Merz, B. Snow-cover reconstruction methodology for mountainous regions based on historic in situ observations and recent remote sensing data. Cryosphere 2015, 9, 451–463. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Orsolini, Y.; Wegmann, M.; Dutra, E.; Liu, B.; Balsamo, G.; Yang, K.; De Rosnay, P.; Zhu, C.; Wang, W.; Senan, R.; et al. Evaluation of snow depth and snow cover over the Tibetan Plateau in global reanalyses using in situ and satellite remote sensing observations. Cryosphere 2019, 13, 2221–2239. [Google Scholar] [CrossRef] [Green Version]
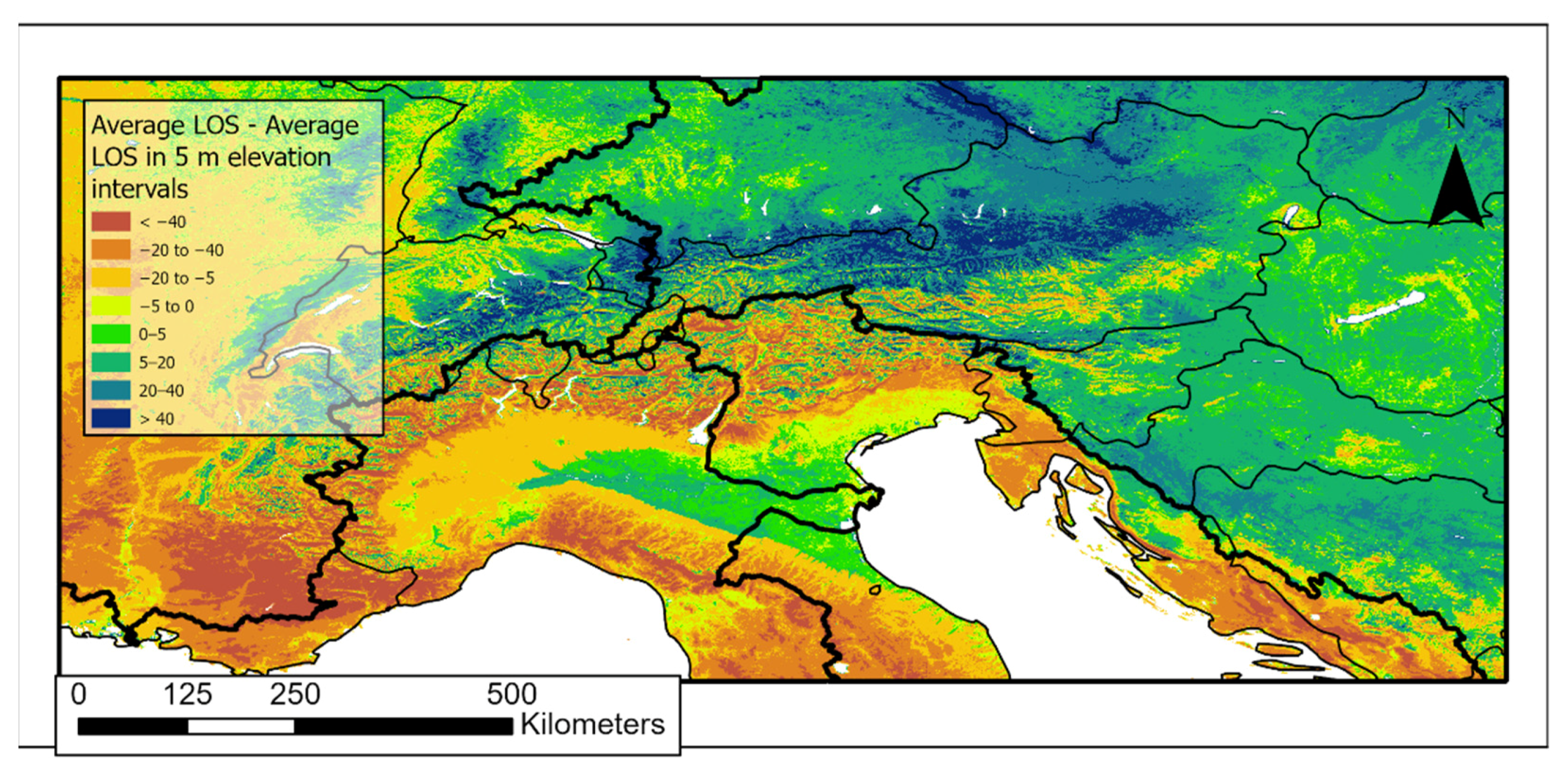
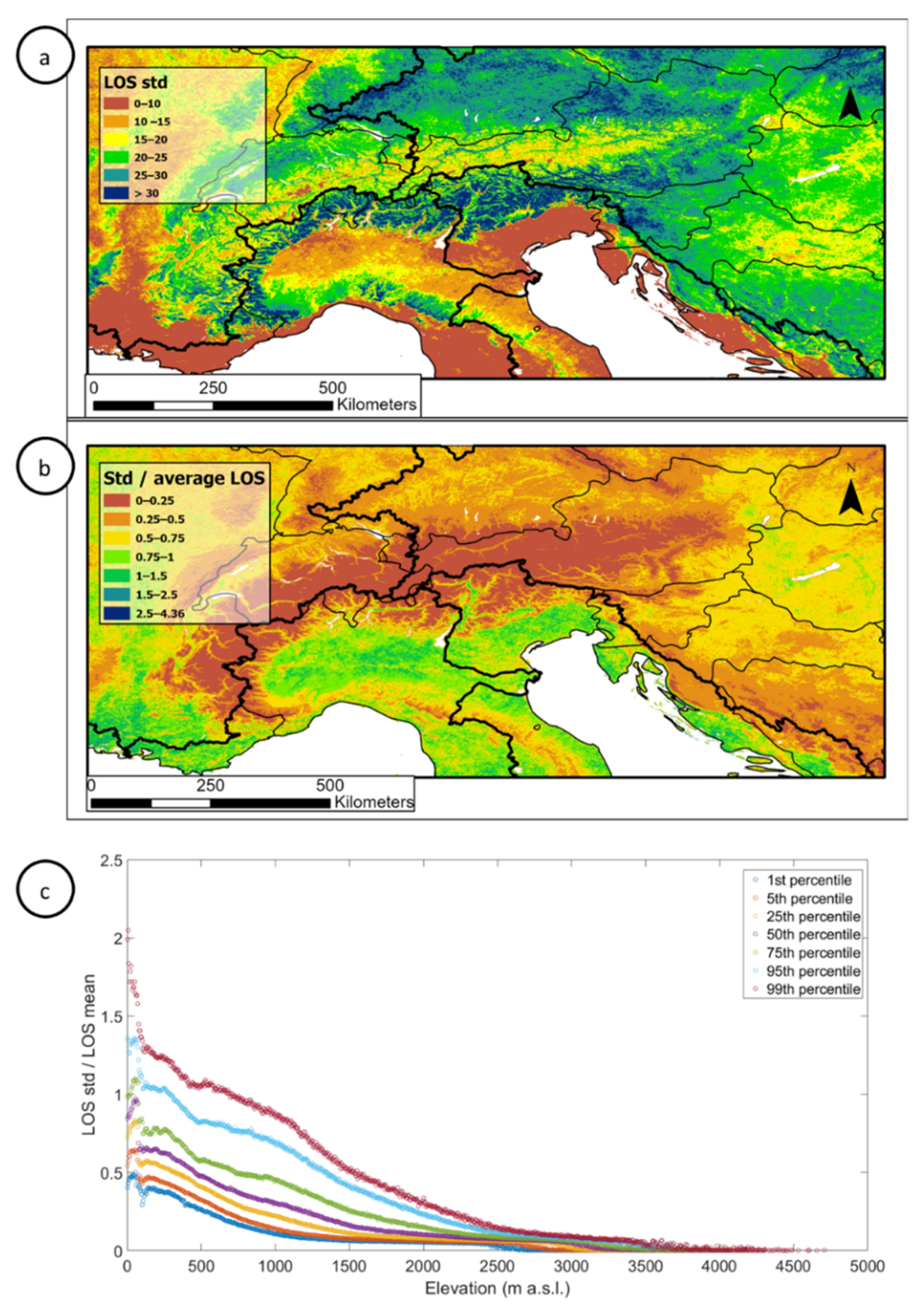


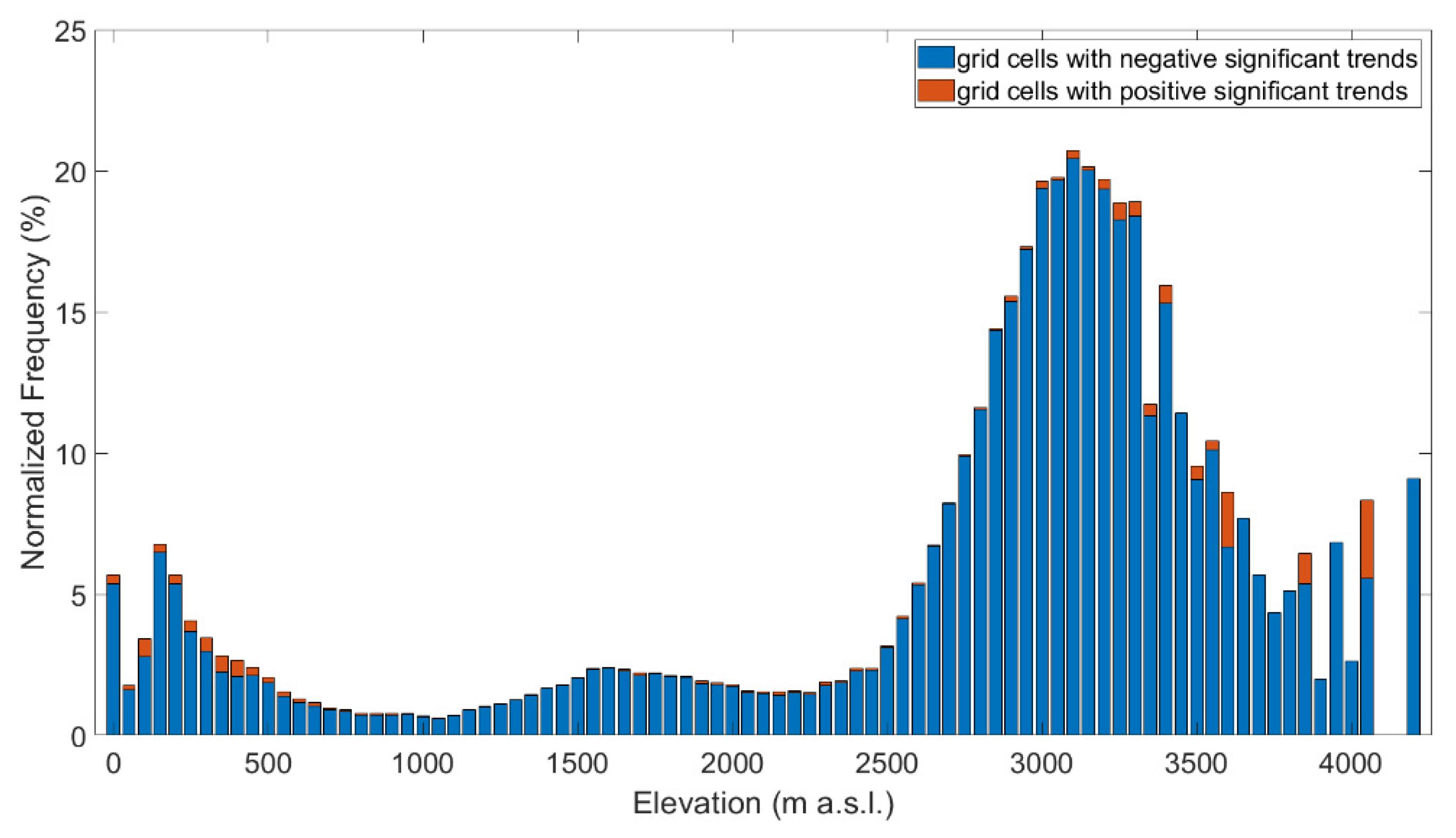

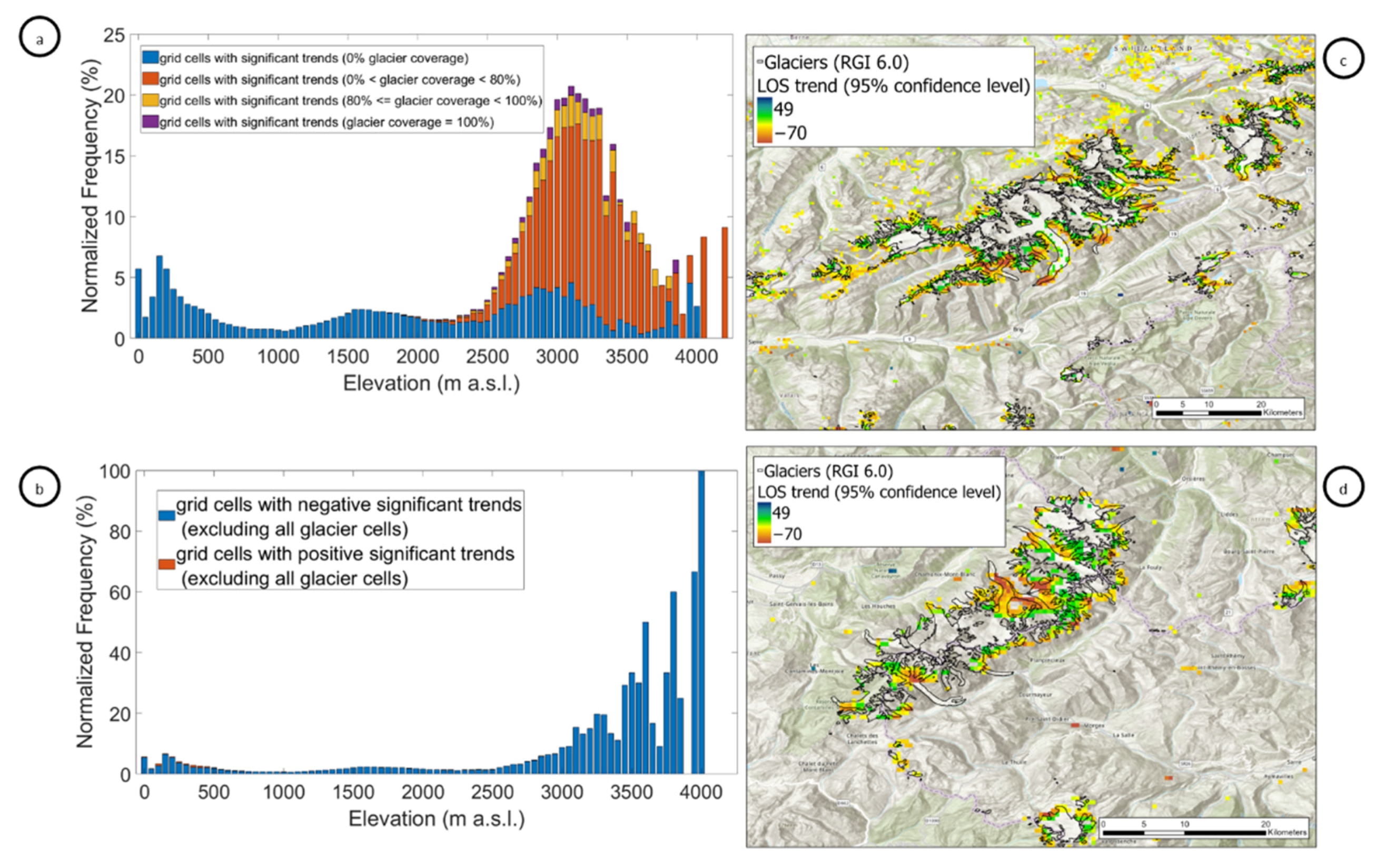
| Date | Corresponding Day |
|---|---|
| 1 October | 1 |
| 16 October | 16 |
| 31 October | 31 |
| 15 November | 46 |
| 30 November | 61 |
| 15 December | 76 |
| 30 December | 91 |
| 14 January | 106 |
| 29 January | 121 |
| 13 February | 136 |
| 28 February | 151 |
| 15 March | 166 |
| 30 March | 181 |
| 14 April | 196 |
| 29 April | 211 |
| 14 May | 226 |
| 29 May | 241 |
| 13 June | 256 |
| 28 June | 271 |
| 13 July | 286 |
| 28 July | 301 |
| 12 August | 316 |
| 27 August | 331 |
| 11 September | 346 |
| 26 September | 361 |
| Metric | Multilinear Regression | Elevation | Aspect | Slope | Shading Index | Latitude | Longitude |
|---|---|---|---|---|---|---|---|
| LOS | 0.91 | 0.85 | 0.00 | 0.36 | 0.22 | 0.02 | 0.00 |
| SOS | 0.89 | 0.76 | 0.01 | 0.34 | 0.23 | 0.06 | 0.00 |
| EOS | 0.89 | 0.86 | 0.00 | 0.36 | 0.20 | 0.01 | 0.00 |
| Length of Season | ||||||
|---|---|---|---|---|---|---|
| Elevation Class | Multivariate Regression | Aspect | Slope | Shading | Latitude | Longitude |
| z < 1000 | 0.55 | 0.02 | 0.03 | 0.00 | 0.30 | 0.21 |
| 1000 < z < 2000 | 0.55 | 0.11 | 0.00 | 0.07 | 0.34 | 0.07 |
| 2000 < z < 3000 | 0.34 | 0.12 | 0.00 | 0.07 | 0.20 | 0.06 |
| 3000 < z < 4000 | 0.22 | 0.03 | 0.00 | 0.02 | 0.17 | 0.07 |
| z > 4000 | 0.14 | 0.05 | 0.00 | 0.04 | 0.06 | 0.00 |
| Start of Season | ||||||
| Elevation Class | Multivariate Regression | Aspect | Slope | Shading | Latitude | Longitude |
| z < 1000 | 0.55 | 0.02 | 0.02 | 0.01 | 0.34 | 0.17 |
| 1000 < z < 2000 | 0.57 | 0.12 | 0.00 | 0.08 | 0.33 | 0.08 |
| 2000 < z < 3000 | 0.48 | 0.18 | 0.00 | 0.13 | 0.29 | 0.13 |
| 3000 < z < 4000 | 0.27 | 0.05 | 0.00 | 0.02 | 0.22 | 0.12 |
| z > 4000 | 0.13 | 0.06 | 0.00 | 0.03 | 0.04 | 0.00 |
| End of Season | ||||||
| Elevation Class | Multivariate Regression | Aspect | Slope | Shading | Latitude | Longitude |
| z < 1000 | 0.52 | 0.01 | 0.03 | 0.00 | 0.22 | 0.25 |
| 1000 < z < 2000 | 0.47 | 0.09 | 0.00 | 0.05 | 0.30 | 0.05 |
| 2000 < z < 3000 | 0.28 | 0.10 | 0.00 | 0.04 | 0.16 | 0.04 |
| 3000 < z < 4000 | 0.21 | 0.03 | 0.00 | 0.02 | 0.16 | 0.06 |
| z > 4000 | 0.14 | 0.04 | 0.01 | 0.04 | 0.06 | 0.00 |
| Length of Season | ||||||
|---|---|---|---|---|---|---|
| LOS Class | Multivariate Regression | Aspect | Slope | Shading | Latitude | Longitude |
| LOS < 180 | 0.52 | 0.03 | 0.03 | 0.00 | 0.28 | 0.17 |
| 180 < LOS < 330 | 0.40 | 0.12 | 0.00 | 0.09 | 0.28 | 0.14 |
| LOS > 330 | 0.32 | 0.04 | 0.00 | 0.14 | 0.12 | 0.03 |
| Start of Season | ||||||
| LOS Class | Multivariate Regression | Aspect | Slope | Shading | Latitude | Longitude |
| LOS < 180 | 0.53 | 0.03 | 0.02 | 0.00 | 0.32 | 0.15 |
| 180 < LOS < 330 | 0.53 | 0.16 | 0.01 | 0.15 | 0.35 | 0.18 |
| LOS > 330 | 0.32 | 0.05 | 0.00 | 0.15 | 0.13 | 0.04 |
| End of Season | ||||||
| LOS Class | Multivariate Regression | Aspect | Slope | Shading | Latitude | Longitude |
| LOS < 180 | 0.45 | 0.02 | 0.05 | 0.00 | 0.20 | 0.17 |
| 180 < LOS < 330 | 0.31 | 0.09 | 0.00 | 0.06 | 0.23 | 0.11 |
| LOS > 330 | 0.31 | 0.04 | 0.00 | 0.14 | 0.12 | 0.03 |
| Length of Season | |||||
|---|---|---|---|---|---|
| NW Trend | NE Trend | SW Trend | SE Trend | GAR Trend | |
| 0–500 | − | − | − | − | − |
| 500–1000 | − | − | − | − | − |
| 1000–1500 | + | − | − | − | − |
| 1500–2000 | − | − | − | − | − |
| 2000–2500 | + | − | + | − | − |
| 2500–3000 | − | − | + | − | − |
| 3000–3500 | −6.3 ** | −5.4 ** | − | − | −5.2 * |
| 3500–4000 | −1.1 * | − | −1.6 * | − | −1.2 ** |
| 4000–4500 | − | N/A | − | N/A | − |
| >4500 | + | N/A | + | N/A | + |
| Start of Season | |||||
| NW Trend | NE Trend | SW Trend | SE Trend | GAR Trend | |
| 0–500 | − | + | + | + | + |
| 500–1000 | + | + | + | + | + |
| 1000–1500 | − | + | + | + | + |
| 1500–2000 | + | + | + | + | + |
| 2000–2500 | + | + | + | + | + |
| 2500–3000 | + | + | + | + | + |
| 3000–3500 | 1.6 * | 0.6 ** | + | 0.1 * | + |
| 3500–4000 | 0.1 ** | + | + | 0.1 * | + |
| 4000–4500 | + | N/A | + | N/A | 0.1 |
| >4500 | + | N/A | + | N/A | + |
| End of Season | |||||
| NW Trend | NE Trend | SW Trend | SE Trend | GAR Trend | |
| 0–500 | + | - | + | - | - |
| 500–1000 | + | + | + | + | − |
| 1000–1500 | + | + | + | + | + |
| 1500–2000 | + | − | + | + | + |
| 2000–2500 | − | − | + | + | − |
| 2500–3000 | − | − | + | − | − |
| 3000–3500 | − | − | − | − | − |
| 3500–4000 | − | − | − | − | − |
| 4000–4500 | − | N/A | − | N/A | − |
| >4500 | + | N/A | + | N/A | + |
| NW Trend | NE Trend | SW Trend | SE Trend | GAR Trend | |
|---|---|---|---|---|---|
| Length of Season | |||||
| 2500–3000 | − | − | + | − | − |
| 3000–3500 | − | −11.7 ** | − | − | − |
| 3500–4000 | −4.9 ** | N/A | −7.7 ** | N/A | −6.3 ** |
| 4000–4500 | + | N/A | −5.6 ** | N/A | −2.7 ** |
| Start of Season | |||||
| 2500–3000 | + | + | + | + | + |
| 3000–3500 | + | +2.5 ** | + | + | + |
| 3500–4000 | 0.6 ** | N/A | + | N/A | + |
| 4000–4500 | + | N/A | 1.1 * | N/A | 0.5 * |
| End of Season | |||||
| 2500–3000 | − | − | + | − | − |
| 3000–3500 | − | − | − | − | − |
| 3500–4000 | −4.1 ** | N/A | −5.5 * | N/A | −5.2 * |
| 4000–4500 | + | N/A | −5.0 ** | N/A | −2.5 ** |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fugazza, D.; Manara, V.; Senese, A.; Diolaiuti, G.; Maugeri, M. Snow Cover Variability in the Greater Alpine Region in the MODIS Era (2000–2019). Remote Sens. 2021, 13, 2945. https://doi.org/10.3390/rs13152945
Fugazza D, Manara V, Senese A, Diolaiuti G, Maugeri M. Snow Cover Variability in the Greater Alpine Region in the MODIS Era (2000–2019). Remote Sensing. 2021; 13(15):2945. https://doi.org/10.3390/rs13152945
Chicago/Turabian StyleFugazza, Davide, Veronica Manara, Antonella Senese, Guglielmina Diolaiuti, and Maurizio Maugeri. 2021. "Snow Cover Variability in the Greater Alpine Region in the MODIS Era (2000–2019)" Remote Sensing 13, no. 15: 2945. https://doi.org/10.3390/rs13152945
APA StyleFugazza, D., Manara, V., Senese, A., Diolaiuti, G., & Maugeri, M. (2021). Snow Cover Variability in the Greater Alpine Region in the MODIS Era (2000–2019). Remote Sensing, 13(15), 2945. https://doi.org/10.3390/rs13152945