Ten Years of SNPP VIIRS Reflective Solar Bands On-Orbit Calibration and Performance
Abstract
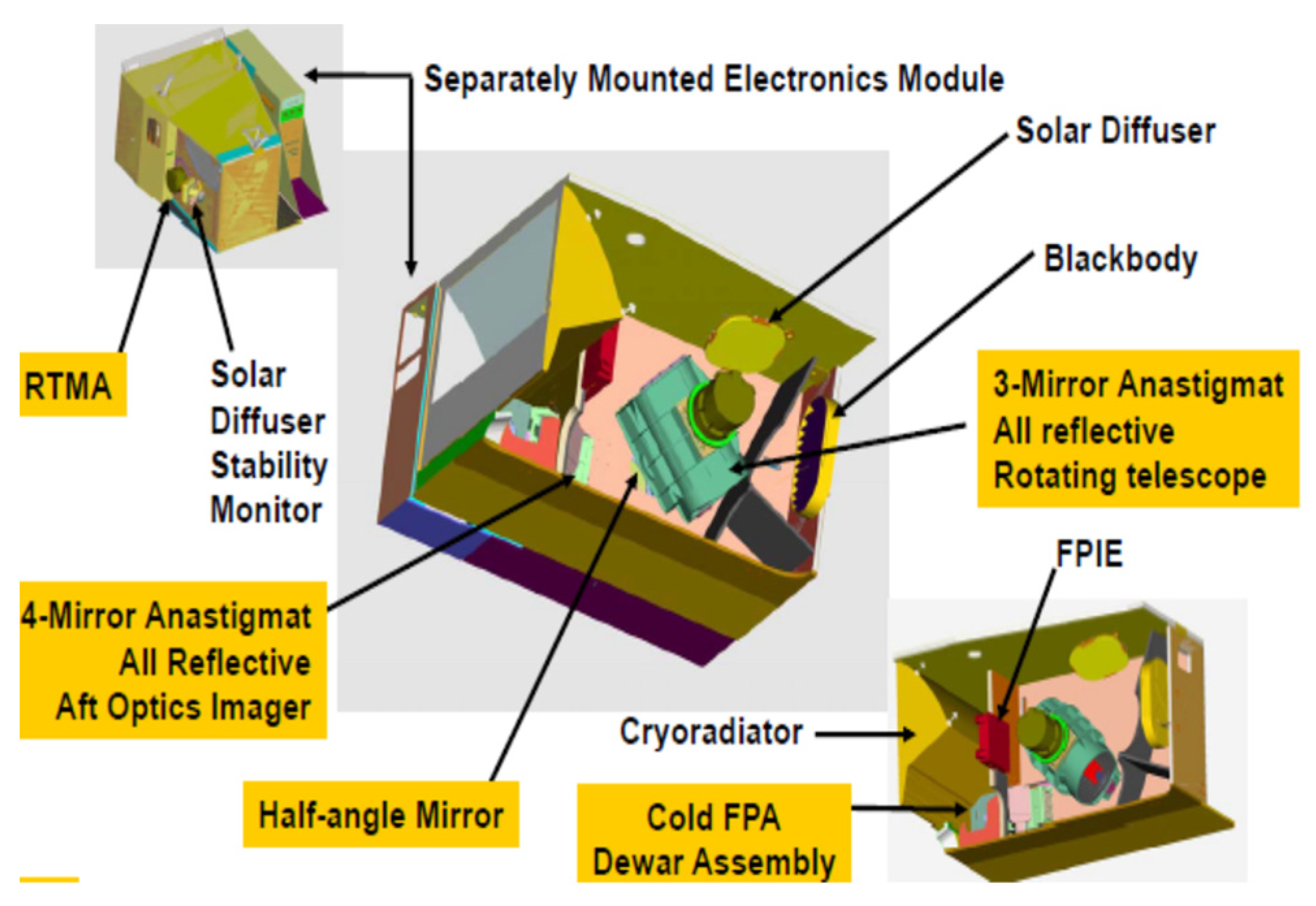
:1. Introduction
2. Calibration Algorithms
2.1. Radiance
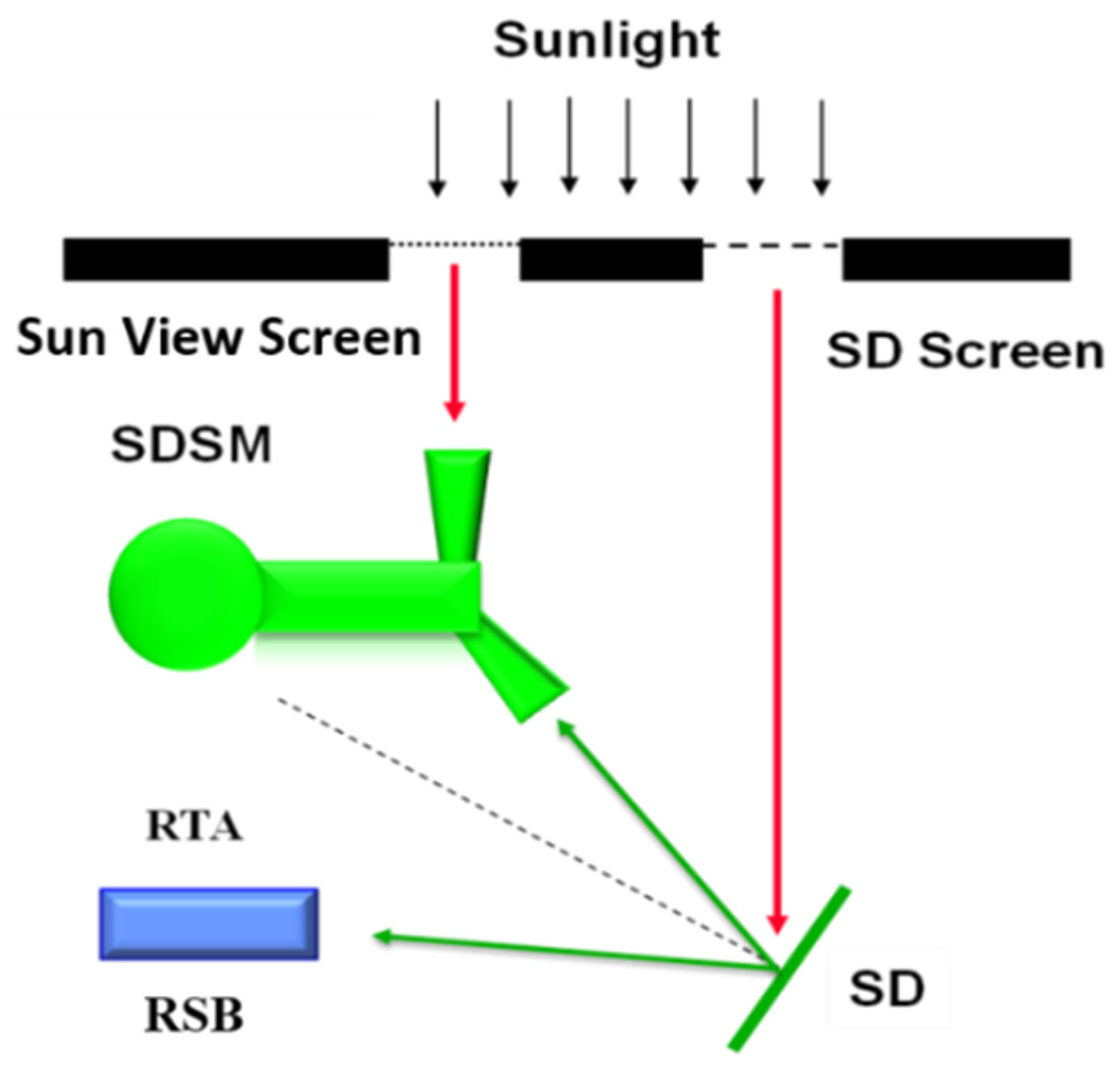
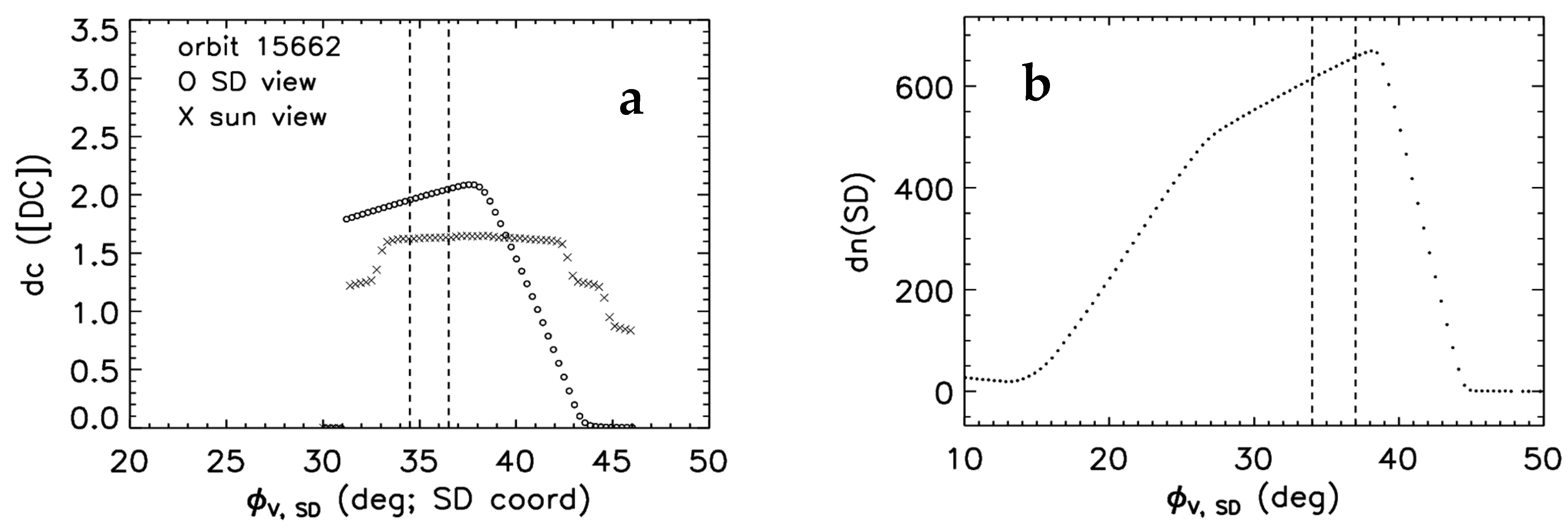
2.2. SDSM Calibration
2.3. SD Calibration
2.4. Lunar Calibration
2.5. SD and Lunar Calibration Comparison
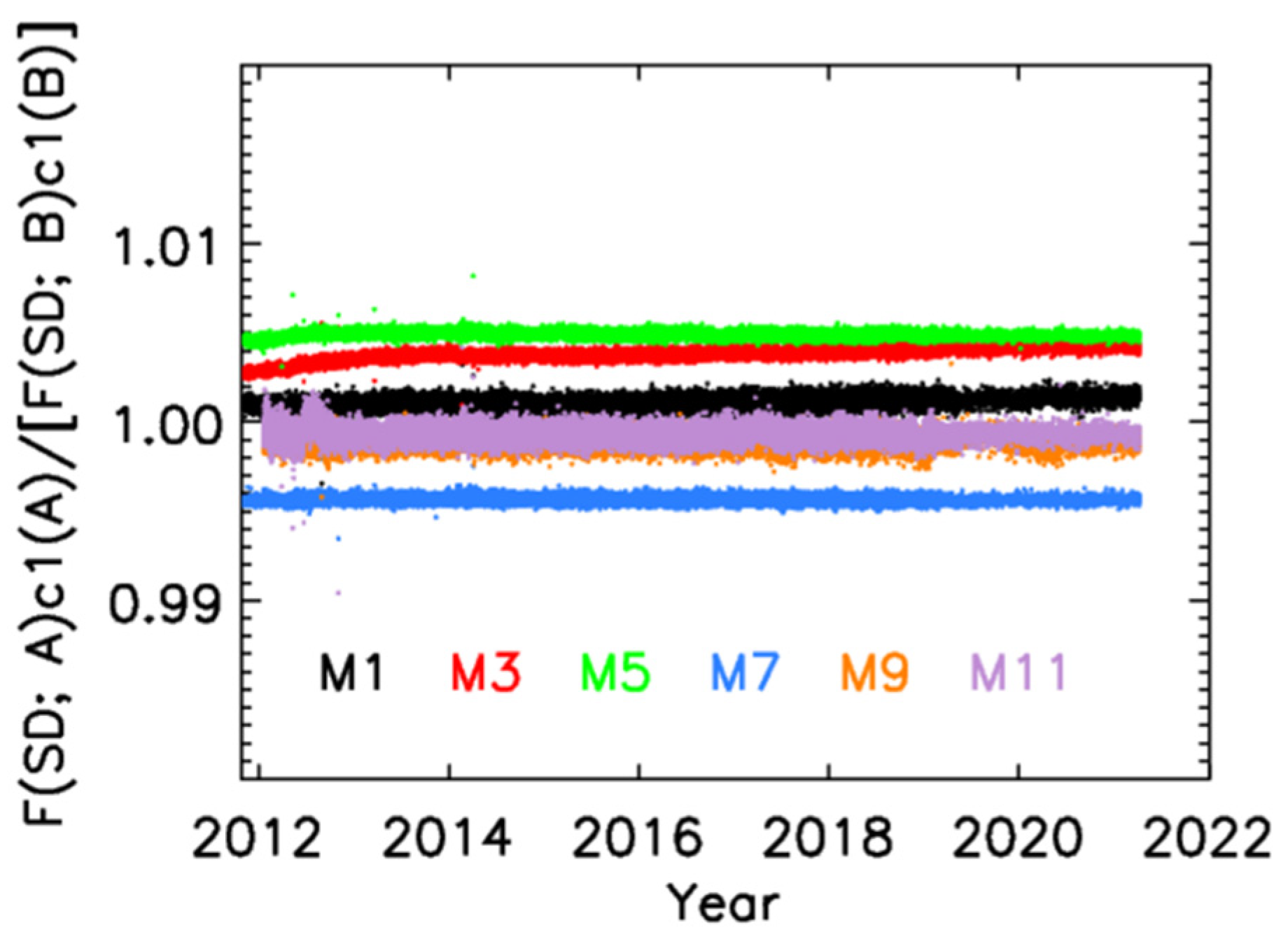
2.6. SDSM and SD Calibration Correction
2.7. EV Striping and Its Removal
3. Calibration Results and Performance
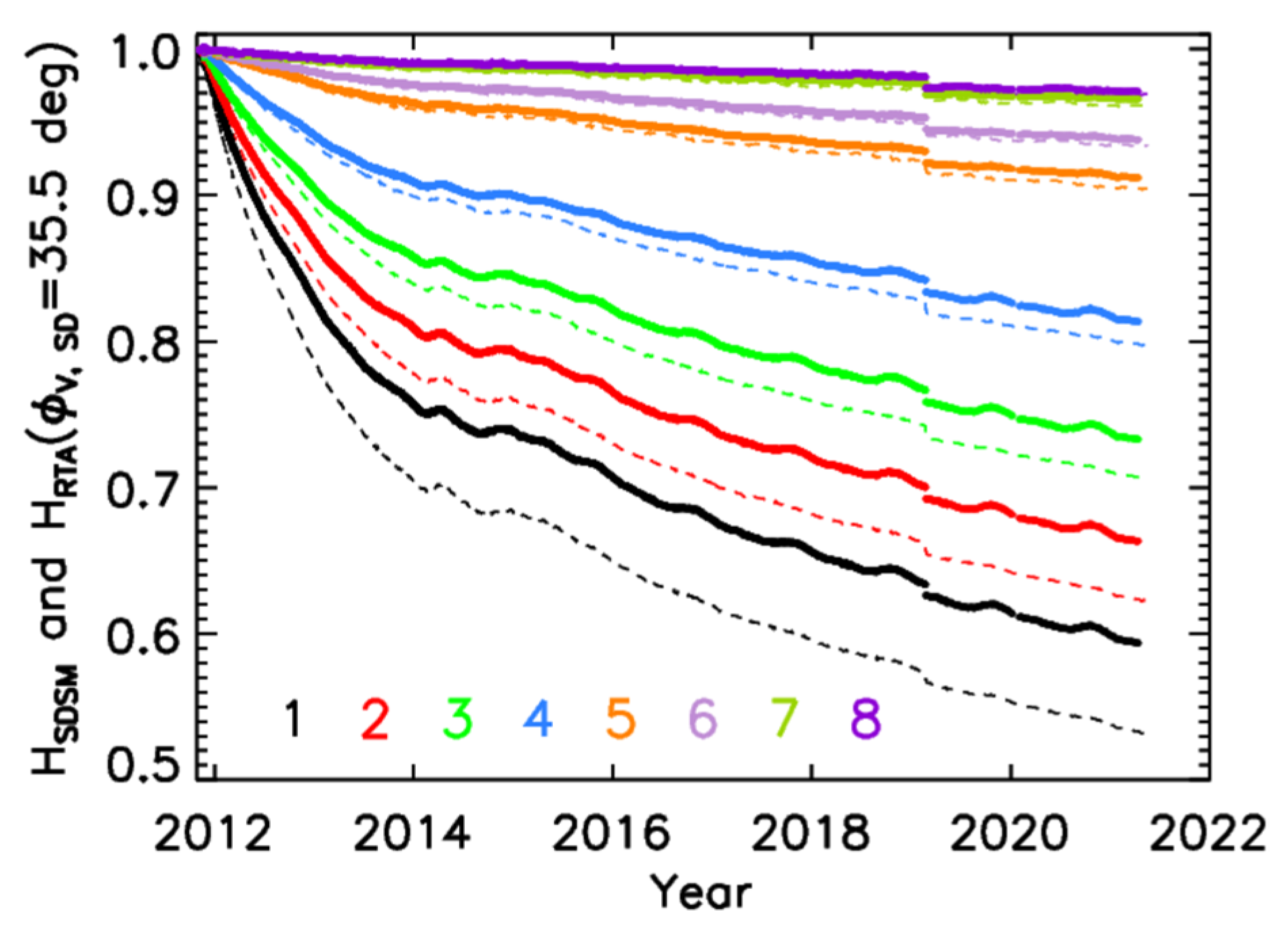
3.1. H-Factors
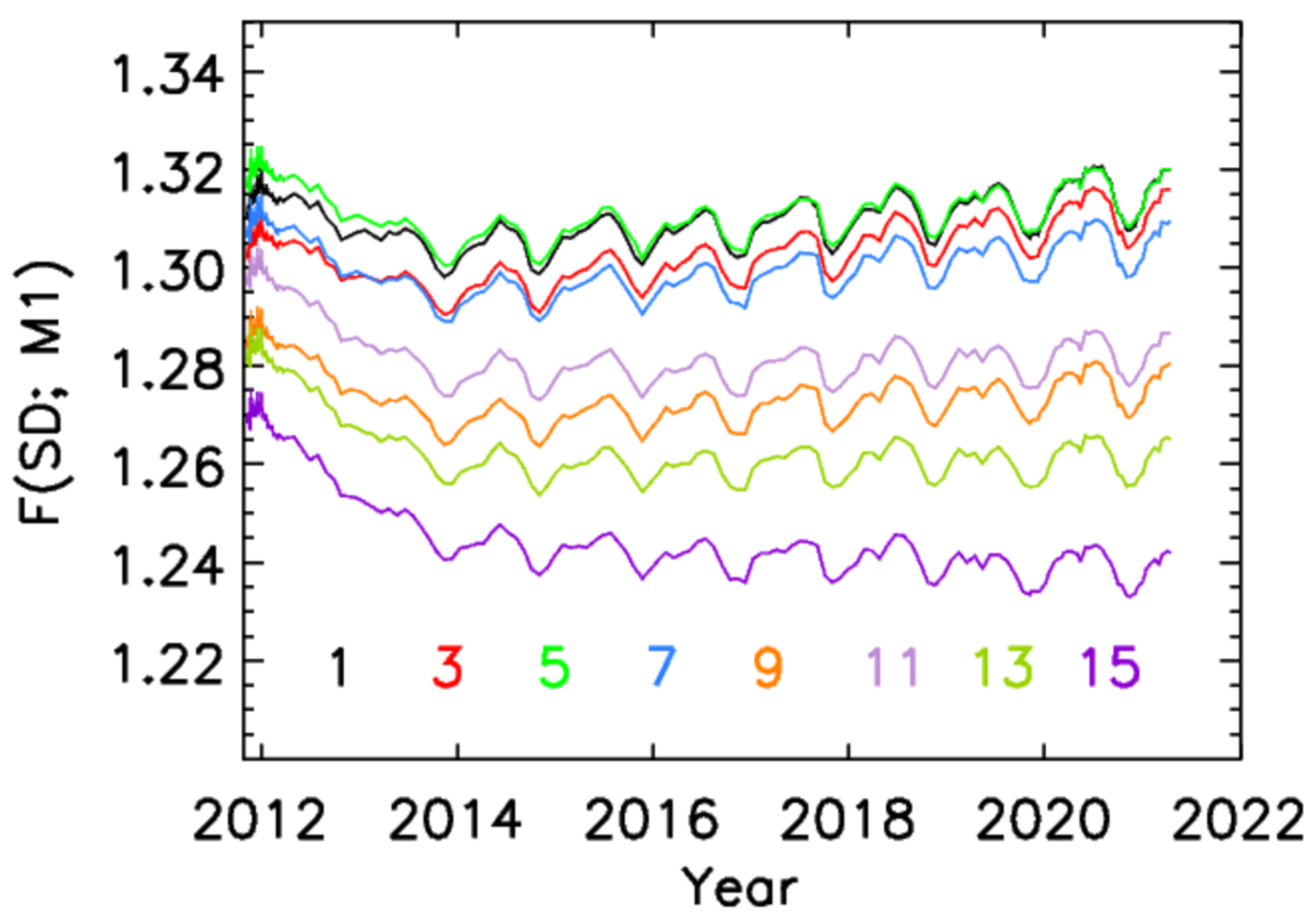
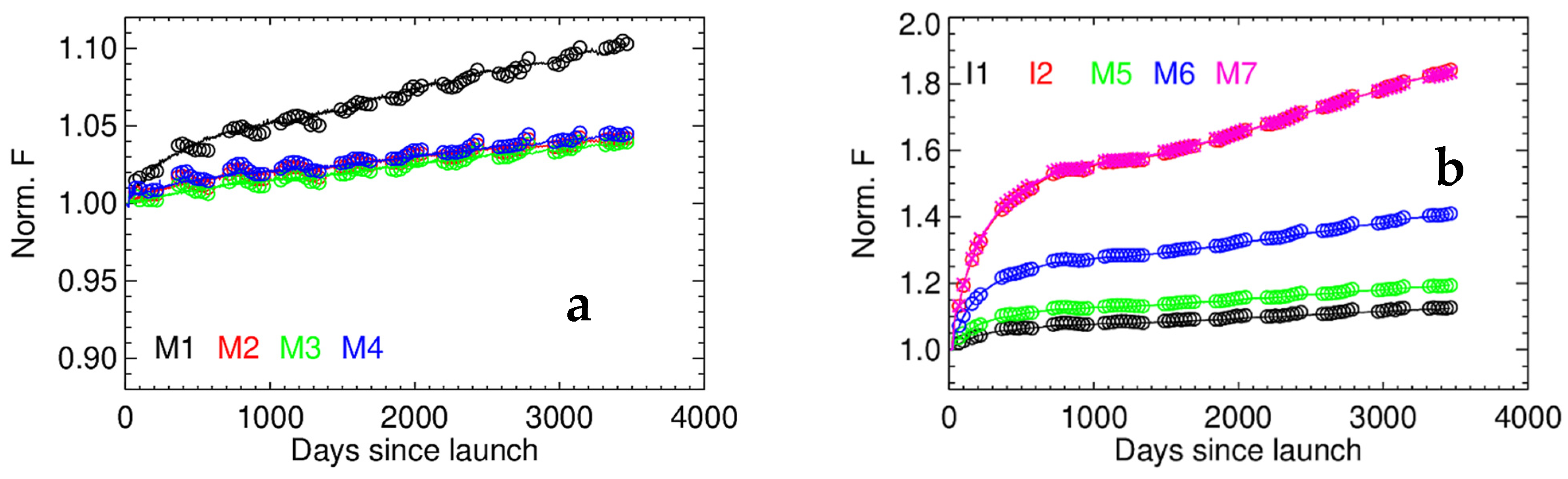
3.2. Time-Dependent RSR and SD F-Factors
3.3. Lunar F-Factors
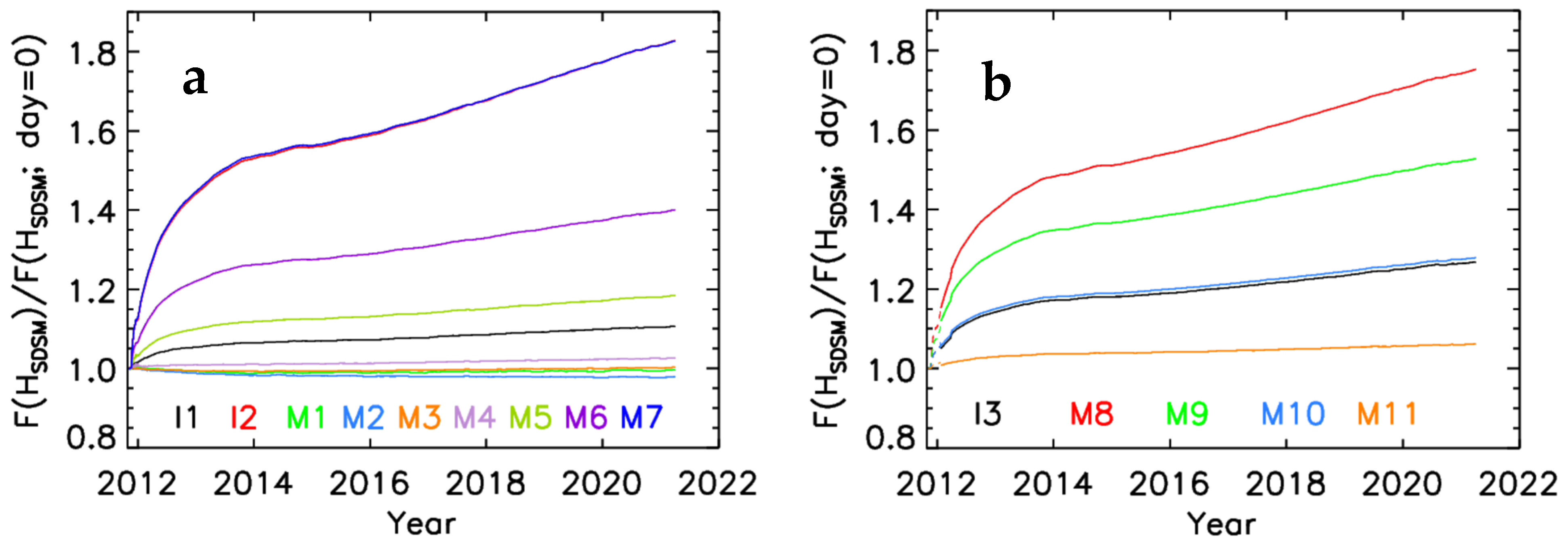
3.4. SD and Lunar F-Factor Comparison
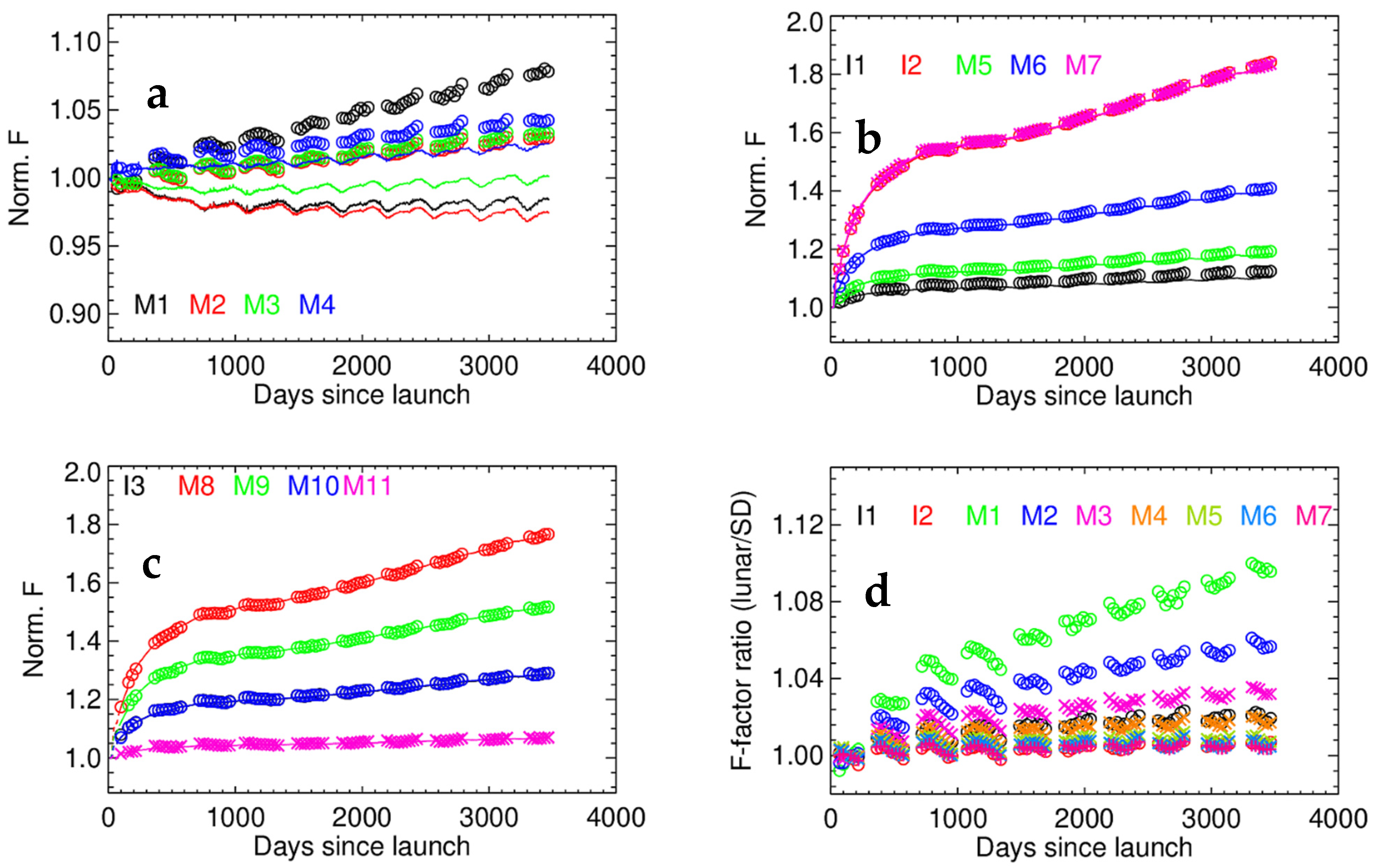
3.5. Corrected H-Factors and F-Factors
3.6. Improved EV Imagery with Striping Removal
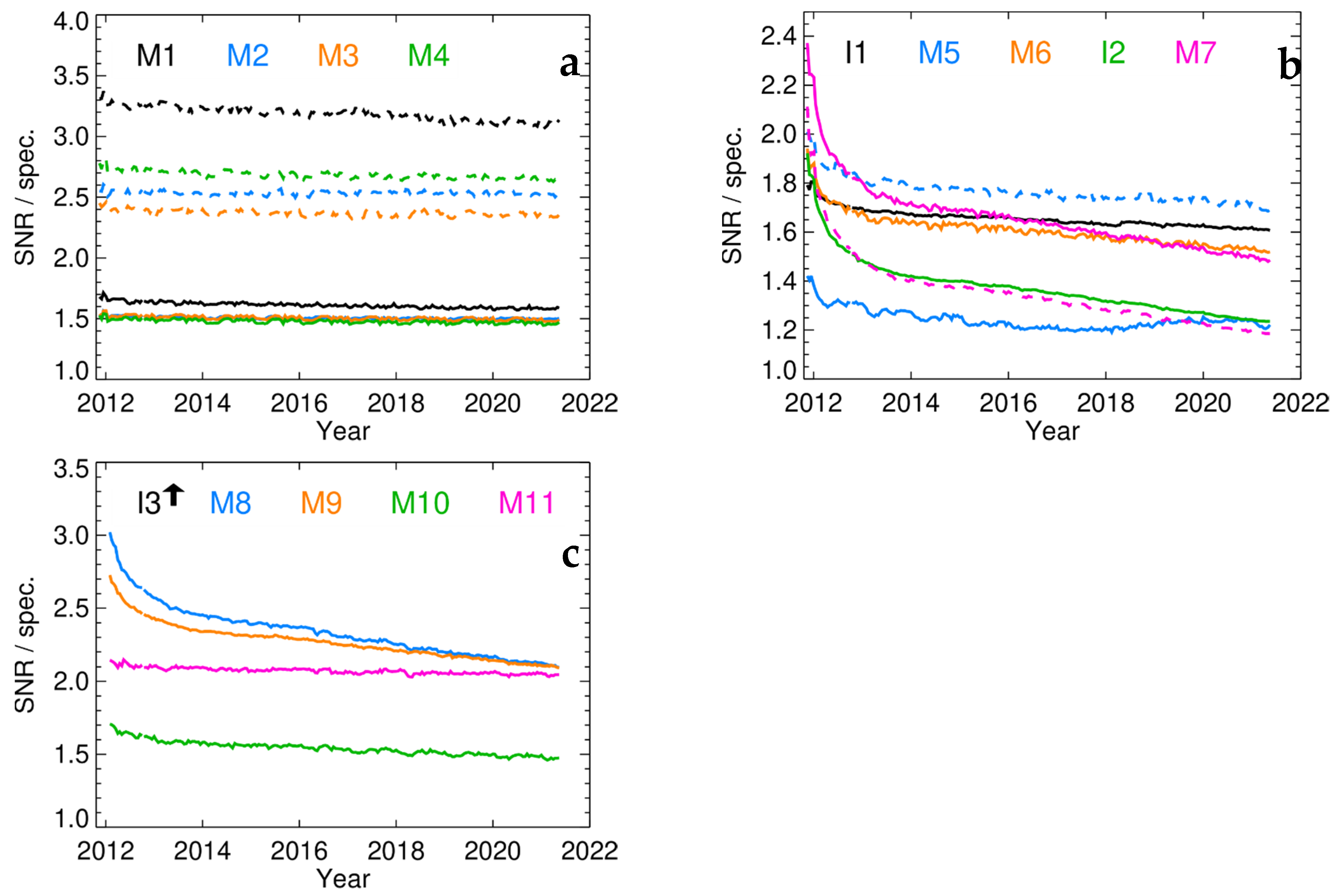
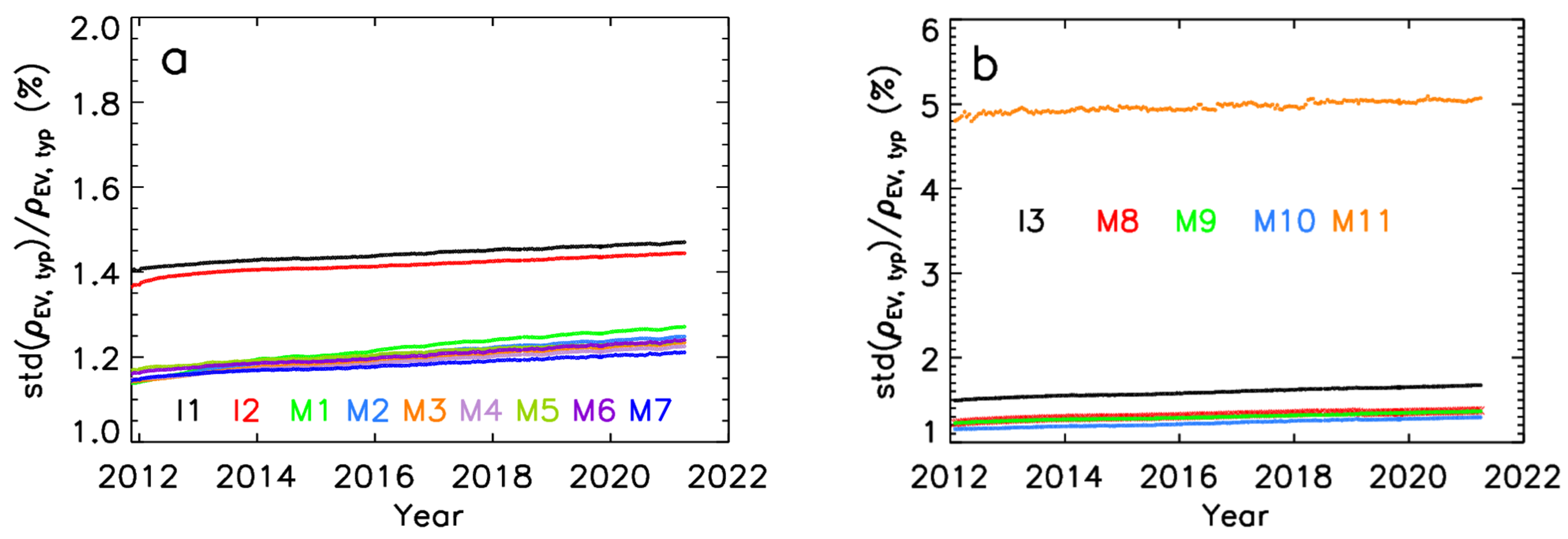
3.7. Uncertainty
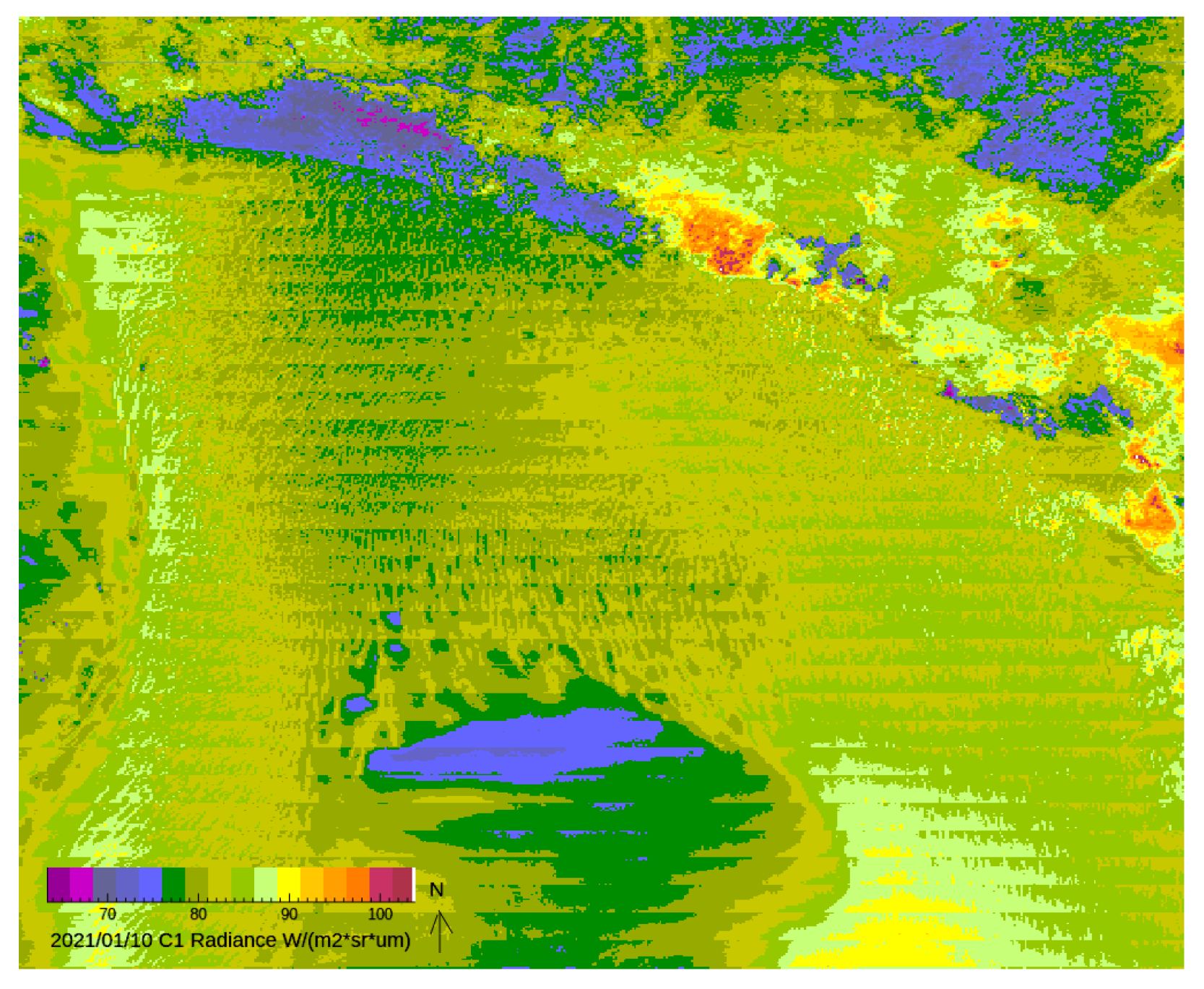
3.8. Desert Monitoring
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Cao, C.; Zhang, B.; Shao, X.; Wang, W.; Uprety, S.; Choi, T.; Blonski, S.; Gu, Y.; Bai, Y.; Lin, L.; et al. Mission-Long Recalibrated Science Quality Suomi NPP VIIRS Radiometric Dataset Using Advanced Algorithms for Time Series Studies. Remote Sens. 2021, 13, 1075. [Google Scholar] [CrossRef]
- Xiong, X.; Angal, A.; Chang, T.; Chiang, K.; Lei, N.; Li, Y.; Sun, J.; Twedt, K.; Wu, A. MODIS and VIIRS Calibration and Characterization in Support of Producing Long-Term High-Quality Data Products. Remote Sens. 2020, 12, 3167. [Google Scholar] [CrossRef]
- Ardanuy, P.E.; Schueler, C.F.; Miller, S.W.; Kealy, P.M.; Cota, S.A.; Haas, M.; Welsch, C. NPOESS VIIRS design process. Int. Symp. Opt. Sci. Technol. 2002, 4483, 24–34. [Google Scholar] [CrossRef]
- Schueler, C.; Clement, J.; Darnton, L.; Deluccia, F.; Scalione, T.; Swenson, H. VIIRS sensor performance. In Proceedings of the IGARSS 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2003; Volume 1, pp. 369–372. [Google Scholar]
- Murphy, R.E.; Ardanuy, P.; Deluccia, F.J.; Clement, J.E.; Schueler, C.F. The Visible Infrared Imaging Radiometer Suite. In Earth Science Satellite Remote Sensing; Springer: New York, NY, USA, 2007; Volume 1, pp. 199–223. [Google Scholar]
- Zhou, L.; Divakarla, M.; Liu, X.; Layns, A.; Goldberg, M. An Overview of the Science Performances and Calibration/Validation of Joint Polar Satellite System Operational Products. Remote Sens. 2019, 11, 698. [Google Scholar] [CrossRef] [Green Version]
- Justice, C.O.; Román, M.O.; Csiszar, I.; Vermote, E.F.; Wolfe, R.; Hook, S.J.; Friedl, M.; Wang, Z.; Schaaf, C.; Miura, T.; et al. Land and cryosphere products from Suomi NPP VIIRS: Overview and status. J. Geophys. Res. Atmos. 2013, 118, 9753–9765. [Google Scholar] [CrossRef] [Green Version]
- Vargas, M.; Miura, T.; Shabanov, N.; Kato, A. An initial assessment of Suomi NPP VIIRS vegetation index EDR. J. Geophys. Res. Atmos. 2013, 118, 12,301–12,316. [Google Scholar] [CrossRef] [Green Version]
- Csiszar, I.; Schroeder, W.; Giglio, L.; Ellicott, E.; Vadrevu, K.; Justice, C.O.; Wind, B. Active fires from the Suomi NPP Visible Infrared Imaging Radiometer Suite: Product status and first evaluation results. J. Geophys. Res. Atmos. 2014, 119, 803–816. [Google Scholar] [CrossRef]
- Wang, M.; Jiang, L. VIIRS-derived ocean color product using the imaging bands. Remote Sens. Environ. 2018, 206, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Minnett, P.J.; Evans, R.H.; Podestá, G.; Kilpatrick, K.A. Sea-surface temperature from Suomi-NPP VIIRS: Algorithm development and uncertainty estimation. Proc. SPIE 2014, 9111, 91110C. [Google Scholar]
- Bouali, M.; Ignatov, A. Adaptive Reduction of Striping for improved SST Imagery from S-NPP VIIRS. J. Tech. 2014, 31, 150–163. [Google Scholar]
- Meyer, K.; Platnick, S.; Holz, R.; Dutcher, S.; Quinn, G.; Nagle, F. Derivation of Shortwave Radiometric Adjustments for SNPP and NOAA-20 VIIRS for the NASA MODIS-VIIRS Continuity Cloud Products. Remote Sens. 2020, 12, 4096. [Google Scholar] [CrossRef]
- Lee, J.; Hsu, N.C.; Bettenhausen, C.; Sayer, A.; Seftor, C.J.; Jeong, M. Retrieving the height of smoke and dust aerosols by synergistic use of VIIRS, OMPS, and CALIOP observations. J. Geophys. Res. Atmos. 2015, 120, 8372–8388. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Wang, M. Radiometric calibration of the Visible Infrared Imaging Radiometer Suite reflective solar bands with robust characterizations and hybrid calibration coefficients. Appl. Opt. 2015, 54, 9331–9342. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. VIIRS Reflective Solar Bands Calibration Progress and Its Impact on Ocean Color Products. Remote Sens. 2016, 8, 194. [Google Scholar] [CrossRef] [Green Version]
- Eplee, R.E.; Turpie, K.R.; Meister, G.; Patt, F.S.; Franz, B.A.; Bailey, S. On-orbit calibration of the Suomi National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite for ocean color applications. Appl. Opt. 2015, 54, 1984–2006. [Google Scholar] [CrossRef] [PubMed]
- Baker, N. Joint Polar Satellite System (JPSS) VIIRS Radiometric Calibration Algorithm Theoretical Basis Document (ATBD); NASA Goddard Space Flight Center: Greenbelt, MA, USA, 2013.
- Oudrari, H.; McIntire, J.; Xiong, X.; Butler, J.; Lee, S.; Lei, N.; Schwarting, T.; Sun, J. Prelaunch Radiometric Characterization and Calibration of the S-NPP VIIRS Sensor. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2195–2210. [Google Scholar] [CrossRef]
- Cardema, J.C.; Rausch, K.W.; Lei, N.; Moyer, D.I.; De Luccia, F.J. Operational calibration of VIIRS reflective solar band sensor data records. Earth Obs. Syst. XVII 2012, 8510, 851019. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. On-orbit calibration of Visible Infrared Imaging Radiometer Suite reflective solar bands and its challenges using a solar diffuser. Appl. Opt. 2015, 54, 7210–7223. [Google Scholar] [CrossRef]
- Choi, T.; Shao, X.; Cao, C. On-orbit radiometric calibration of Suomi NPP VIIRS reflective solar bands using the Moon and solar diffuser. Appl. Opt. 2018, 57, 9533–9542. [Google Scholar] [CrossRef] [PubMed]
- Haas, E.; Moyer, D.; De Luccia, F.; Rausch, K.; Fulbright, J. VIIRS solar diffuser bidirectional reflectance distribution function (BRDF) degradation factor operational trending and update. Earth Obs. Syst. XVII 2012, 8510, 851016. [Google Scholar] [CrossRef]
- Fulbright, J.; Lei, N.; Efremova, B.; Xiong, X. Suomi-NPP VIIRS Solar Diffuser Stability Monitor Performance. IEEE Trans. Geosci. Remote Sens. 2015, 54, 631–639. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. Visible Infrared Imaging Radiometer Suite solar diffuser calibration and its challenges using a solar diffuser stability monitor. Appl. Opt. 2014, 53, 8571–8584. [Google Scholar] [CrossRef]
- Sun, J.; Xiong, X. Solar and lunar observation planning for Earth-observing sensor. Sens. Syst. Next-Gener. Satell. XV 2011, 8176, 817610. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, J.; Fulbright, J.; Wang, Z.; Butler, J.J. Lunar Calibration and Performance for S-NPP VIIRS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1052–1061. [Google Scholar] [CrossRef]
- Sun, J.; Xiong, X. SNPP VIIRS Reflective Solar Bands On-Orbit Calibration Using the Moon. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4499–4512. [Google Scholar] [CrossRef]
- Li, S.C.; Xiong, X.; Lei, N. S-NPP and N20 VIIRS RSB bands detector-to-detector calibration differences assessment using a homogeneous ground target. Proc. SPIE 2020, 11501, 115011N. [Google Scholar]
- Lei, N.; Xiong, X.; Mu, Q.; Li, S.; Chang, T. Positional Dependence of SNPP VIIRS Solar Diffuser BRDF Change Factor: An Empirical Approach. IEEE Trans. Geosci. Remote Sens. 2021, 1–6. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X.; Wang, Z.; Li, S.; Twedt, K. SNPP VIIRS RSB on-orbit radiometric calibration algorithms Version 2.0 and the performances, part 1: The algorithms. J. Appl. Remote Sens. 2020, 14, 047501. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X.; Wang, Z.; Li, S.; Twedt, K. SNPP VIIRS RSB on-orbit radiometric calibration algorithms Version 2.0 and the performances, part 2: The performances. J. Appl. Remote Sens. 2020, 14, 047502. [Google Scholar] [CrossRef]
- Sun, J.; Wang, M. On-orbit characterization of the VIIRS solar diffuser and solar diffuser screen. Appl. Opt. 2015, 54, 236–252. [Google Scholar] [CrossRef] [PubMed]
- Lei, N.; Chen, X.; Xiong, X. Determination of the SNPP VIIRS SDSM Screen Relative Transmittance From Both Yaw Maneuver and Regular On-Orbit Data. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1390–1398. [Google Scholar] [CrossRef]
- Choi, T.; Cao, C. S-NPP VIIRS on-orbit calibration coefficient improvements with yaw maneuver reanalysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7460–7465. [Google Scholar] [CrossRef]
- Sun, J.; Chu, M.; Wang, M. Degradation nonuniformity in the solar diffuser bidirectional reflectance distribution function. Appl. Opt. 2016, 55, 6001–6016. [Google Scholar] [CrossRef] [PubMed]
- Lei, N.; Xiong, X. Impacts of the Angular Dependence of the Solar Diffuser BRDF Degradation Factor on the SNPP VIIRS Reflective Solar Band On-Orbit Radiometric Calibration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1537–1543. [Google Scholar] [CrossRef]
- Lane, A.P.; Irvine, W.M. Monochromatic phase curves and albedos for the lunar disk. Astron. J. 1973, 78, 267. [Google Scholar] [CrossRef]
- Kieffer, H.H.; Wildey, R.L. Establishing the Moon as a Spectral Radiance Standard. J. Atmos. Oce. Technol. 1996, 13, 360–375. [Google Scholar] [CrossRef] [Green Version]
- Kieffer, H.H. Photometric Stability of the Lunar Surface. Icarus 1997, 130, 323–327. [Google Scholar] [CrossRef]
- Stone, T.C.; Kieffer, H.H.; Becker, K.J. Modeling the radiance of the moon for on-orbit calibration. Proc. SPIE 2003, 5151, 463–470. [Google Scholar]
- Kieffer, H.H.; Stone, T.C. The Spectral Irradiance of the Moon. Astron. J. 2005, 129, 2887–2901. [Google Scholar] [CrossRef] [Green Version]
- Stone, T.C.; Kieffer, H.H. Use of the Moon to support on-orbit sensor calibration for climate change measurements. Proc. SPIE 2006, 6296, 62960Y. [Google Scholar] [CrossRef]
- Moeller, C.; McIntire, J.; Schwarting, T.; Moyer, D.; Costa, J. Suomi NPP VIIRS spectral characterization: Understanding multiple RSR releases. Proc. SPIE 2012, 8510, 85101S. [Google Scholar]
- Lei, N.; Guenther, B.; Wang, Z.; Xiong, X. Modeling SNPP VIIRS reflective solar bands optical throughput degradation and its impacts on the relative spectral response. Proc. SPIE 2013, 8866, 88661H. [Google Scholar]
- Cao, C.; Xiong, J.; Blonski, S.; Liu, Q.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F. Suomi NPP VIIRS sensor data record verification, validation, and long-term performance monitoring. J. Geophys. Res. Atmos. 2013, 118, 11664–11678. [Google Scholar] [CrossRef]
- Lei, N.; Wang, Z.; Fulbright, J.; Xiong, X. Effect of the SDSM detector relative spectral response in determining the degradation coefficient of the SNPP VIIRS solar diffuser reflectance. Earth Obs. Syst. XVIII 2013, 8866, 88661I. [Google Scholar] [CrossRef]
- Lei, N.; Xiong, X. Suomi NPP VIIRS Solar Diffuser BRDF Degradation Factor at Short-Wave Infrared Band Wavelengths. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6212–6216. [Google Scholar] [CrossRef]
- Sun, J.; Xiong, X.; Waluschka, E.; Wang, M. Suomi National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite polarization sensitivity analysis. Appl. Opt. 2016, 55, 7645–7658. [Google Scholar] [CrossRef]
- Barrie, J.D.; Fuqua, P.D.; Meshishnek, M.J.; Ciofalo, M.R.; Chu, C.T.; Chaney, J.A.; Moision, R.M.; Graziani, L. Root cause determination of on-orbit degradation of the VIIRS rotating telescope assembly. In Earth Observing Systems XVII; SPIE: San Diego, CA, USA, 2012; Volume 8510, p. 85101B. [Google Scholar] [CrossRef] [Green Version]
- Iona, G.; Butler, J.; Guenther, B.; Graziani, L.; Johnson, E.; Kennedy, B.; Kent, C.; Lambeck, R.; Waluschka, E.; Xiong, X. VIIRS on-orbit optical anomaly: Investigation, analysis, root cause determination and lessons learned. Earth Obs. Syst. XVII 2012, 8510, 85101C. [Google Scholar] [CrossRef] [Green Version]
- Lessel, L.; McClain, S. Low Uncertainty Measurements of Bidirectional Reflectance Factor on the NPOESS/VIIRS Solar Diffuser. Proc. SPIE 2007, 6677, 667710. [Google Scholar]
- Twedt, K.; Lei, N.; Xiong, X.J. On-orbit noise characterization of the SNPP VIIRS reflective solar bands. Earth Obs. Syst. XXII 2017, 10402, 104021X. [Google Scholar] [CrossRef]
- Lei, N.; Twedt, K.; McIntire, J.; Xiong, X. SNPP VIIRS RSB earth view reflectance uncertainty. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5916–5919. [Google Scholar] [CrossRef] [Green Version]
- Wu, A.; Xiong, X.; Cao, C.; Chiang, K.-F. Assessment of SNPP VIIRS VIS/NIR Radiometric Calibration Stability Using Aqua MODIS and Invariant Surface Targets. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2918–2924. [Google Scholar] [CrossRef]
- Mu, Q.; Xiong, X.; Chang, T.; Wu, A. Exploring the stability and residual response versus scan angle effects in SNPP VIIRS sensor data record reflectance products using deep convective clouds. J. Appl. Remote Sens. 2018, 12, 034006. [Google Scholar] [CrossRef]

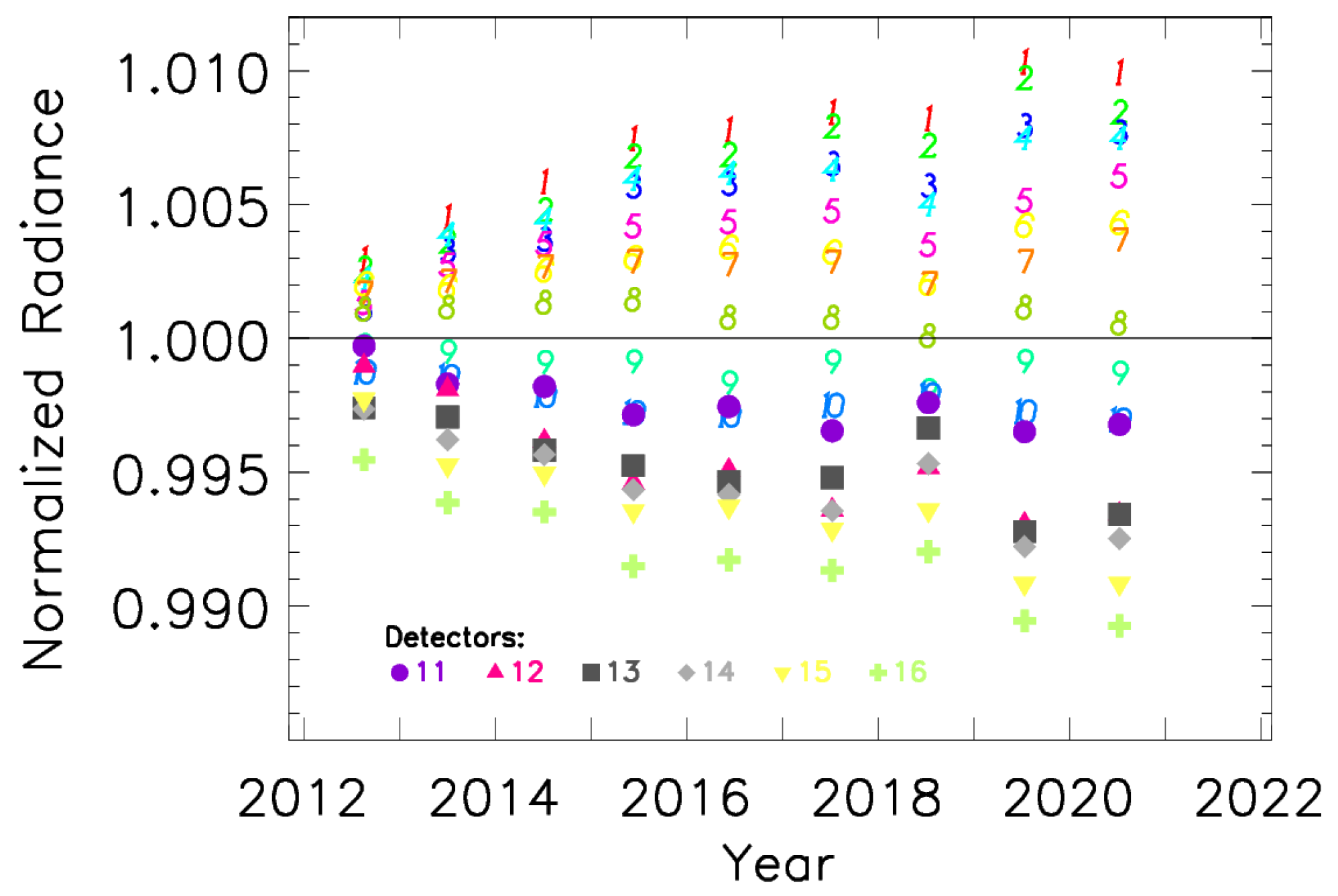
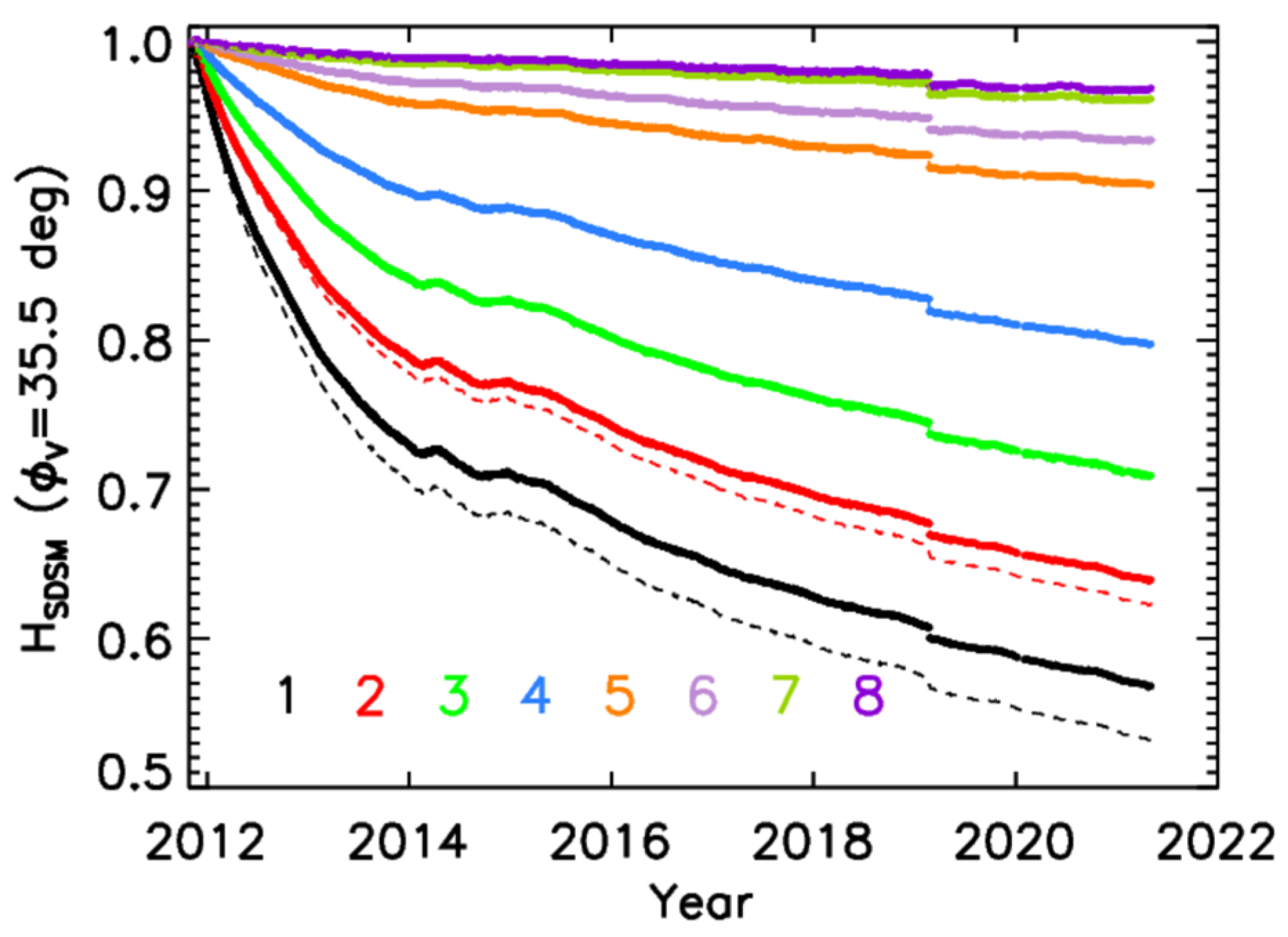
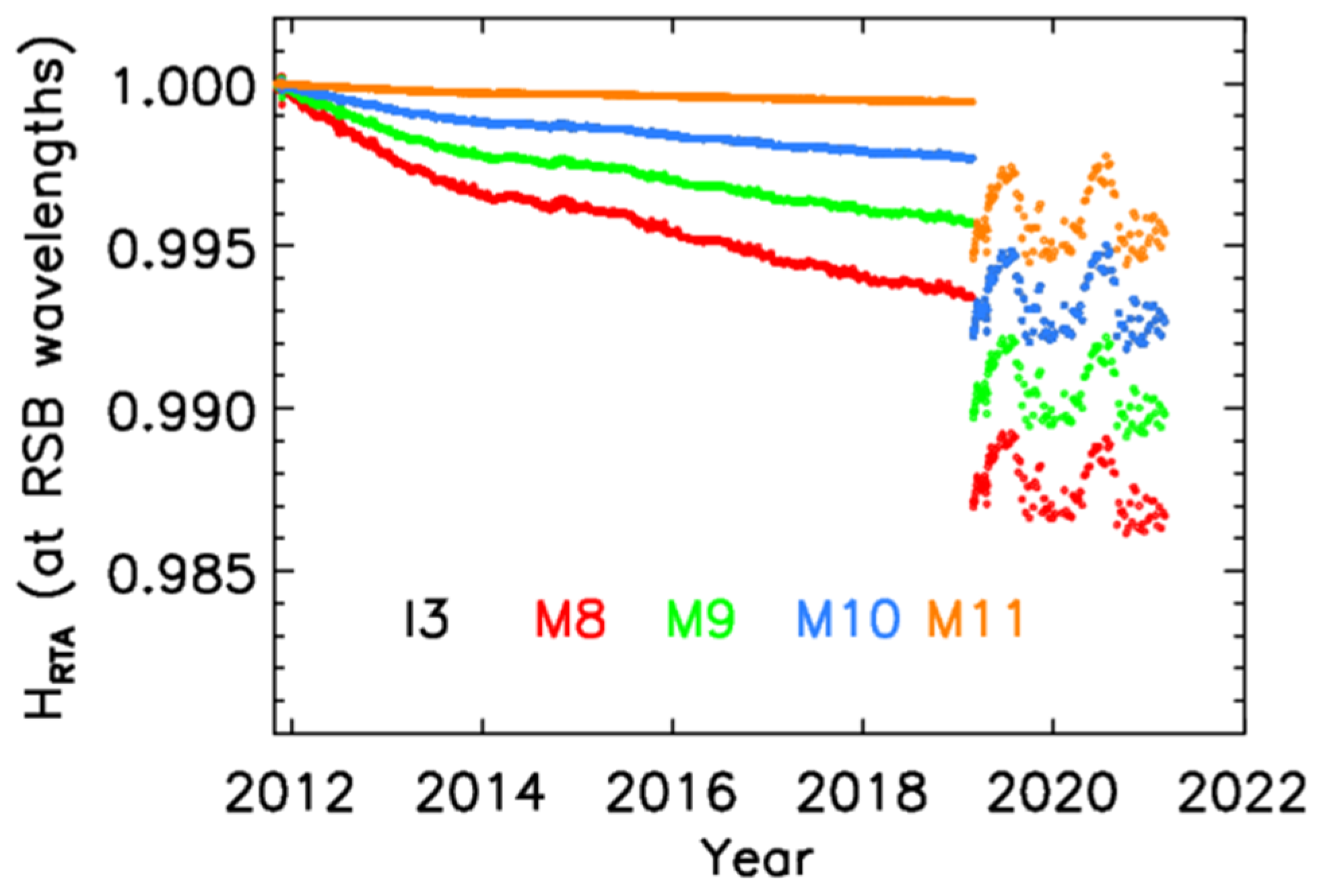
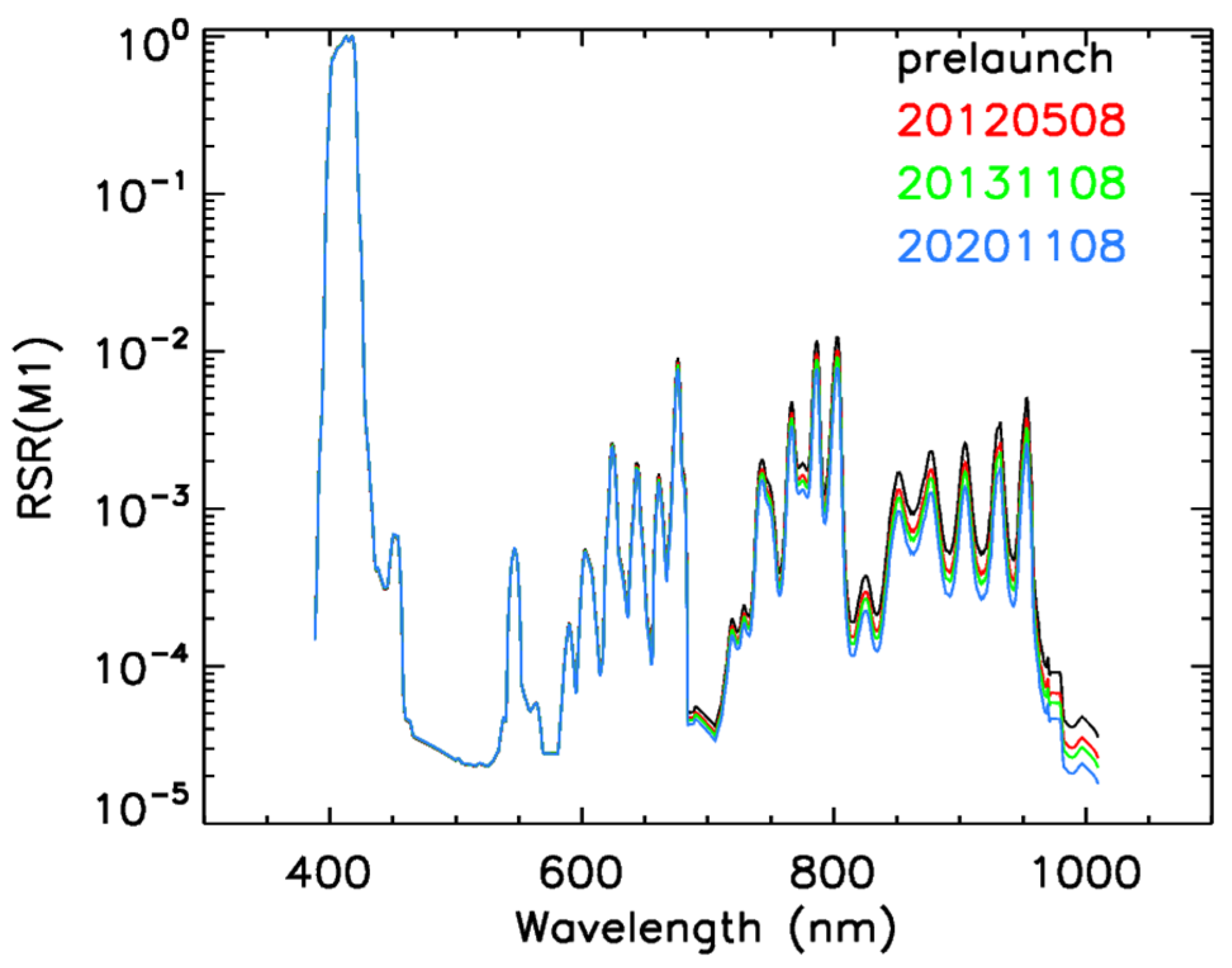


| SDSM | VIIRS RSB | |||||
|---|---|---|---|---|---|---|
| Detector | CW (nm) | Band | CW (nm) | BW (nm) | Gain | SNR Spec. |
| D1 | 412 | M1 | 410 | 20 | DG | 352, 316 |
| D2 | 450 | M2 | 443 | 18 | DG | 380, 409 |
| D3 | 488 | M3 | 486 | 20 | DG | 416, 414 |
| D4 | 555 | M4 | 551 | 20 | DG | 362, 315 |
| N/A | I1 | 640 | 80 | SG | 119 | |
| D5 | 672 | M5 | 671 | 20 | DG | 242, 360 |
| D6 | 746 | M6 | 745 | 15 | SG | 199 |
| D7 | 865 | M7 | 862 | 39 | DG | 215, 340 |
| D7 | 865 | I2 | 862 | 39 | SG | 150 |
| D8 | 935 | |||||
| M8 | 1238 | 20 | SG | 74 | ||
| M9 | 1378 | 15 | SG | 83 | ||
| M10 | 1610 | 60 | SG | 342 | ||
| I3 | 1610 | 60 | SG | 6 | ||
| M11 | 2250 | 50 | SG | 10 | ||
| Acronym | Full Description | Acronym | Full Description |
|---|---|---|---|
| AOI | AOI Angle of incidence | OBC | On-board calibrators |
| AU | Astronomical Unit | OBPG | Ocean Biology Processing Group |
| BRF | Bidirectional reflectance factor | OOB | Out-of-band |
| C1 | Collection 1 | PEATE | Product Evaluation and Algorithm Test Element |
| C2 | Collection 2 | PICS | Pseudo-invariant calibration sites |
| DCC | Deep convective clouds | ROLO | Robotic Lunar Observatory |
| EDR | Environmental data records | RSB | Reflective solar band |
| EV | Earth view | RSR | Relative spectral response |
| FPA | Focal plane assembly | RTA | Rotating telescope assembly |
| GSFC | Goddard Space Flight Center | RVS | Response-versus-scan-angle |
| HAM | Half-angle-mirror | SD | Solar diffuser |
| I-bands | Imaging bands | SDR | Sensor data records |
| JPSS | Joint Polar Satellite System | SDSM | Solar diffuser stability monitor |
| L1B | Level 1B | SNPP | Suomi national polar-orbiting partnership |
| LUT | Look-up-table | SNR | Signal-to-noise ratio |
| M-bands | Moderate resolution bands | SV | Space view |
| MODIS | Moderate Resolution Imaging Spectroradiometer | SWIR | Shortwave infrared |
| NIST | National Institute of Standards and Technology | TOA | Top-of-atmosphere |
| VIS | Visible | VCST | VIIRS Calibration Support Team |
| NIR | Near infrared | VIIRS | Visible Infrared Imaging Radiometer Suite |
| VNIR | VIS and NIR |
| Band | ||||
|---|---|---|---|---|
| I1 | 0.55 | 0.29 | 0.11 | 0.01 |
| I2 | 1.17 | 0.77 | 0.09 | 0.04 |
| M1 | −0.96 | 0.33 | 0.24 | 0.01 |
| M2 | 0.70 | 0.37 | 0.29 | 0.01 |
| M3 | 2.94 | 0.19 | 0.17 | 0.01 |
| M4 | 2.54 | 0.28 | 0.12 | 0.01 |
| M5 | 0.00 | 0.00 | 0.12 | 0.02 |
| M7 | 2.66 | 0.50 | 0.11 | 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Xiong, X.; Lei, N.; Li, S.; Twedt, K.; Angal, A. Ten Years of SNPP VIIRS Reflective Solar Bands On-Orbit Calibration and Performance. Remote Sens. 2021, 13, 2944. https://doi.org/10.3390/rs13152944
Sun J, Xiong X, Lei N, Li S, Twedt K, Angal A. Ten Years of SNPP VIIRS Reflective Solar Bands On-Orbit Calibration and Performance. Remote Sensing. 2021; 13(15):2944. https://doi.org/10.3390/rs13152944
Chicago/Turabian StyleSun, Junqiang, Xiaoxiong Xiong, Ning Lei, Sherry Li, Kevin Twedt, and Amit Angal. 2021. "Ten Years of SNPP VIIRS Reflective Solar Bands On-Orbit Calibration and Performance" Remote Sensing 13, no. 15: 2944. https://doi.org/10.3390/rs13152944
APA StyleSun, J., Xiong, X., Lei, N., Li, S., Twedt, K., & Angal, A. (2021). Ten Years of SNPP VIIRS Reflective Solar Bands On-Orbit Calibration and Performance. Remote Sensing, 13(15), 2944. https://doi.org/10.3390/rs13152944







