An Adaptive Surface Interpolation Filter Using Cloth Simulation and Relief Amplitude for Airborne Laser Scanning Data
Abstract
:1. Introduction
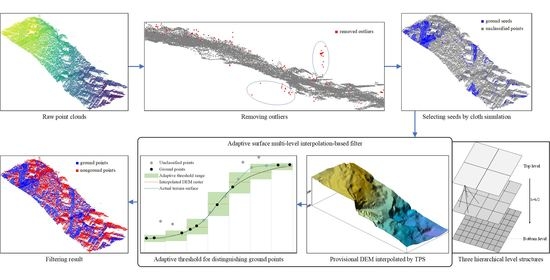
2. Methods
2.1. Removal of Outliers
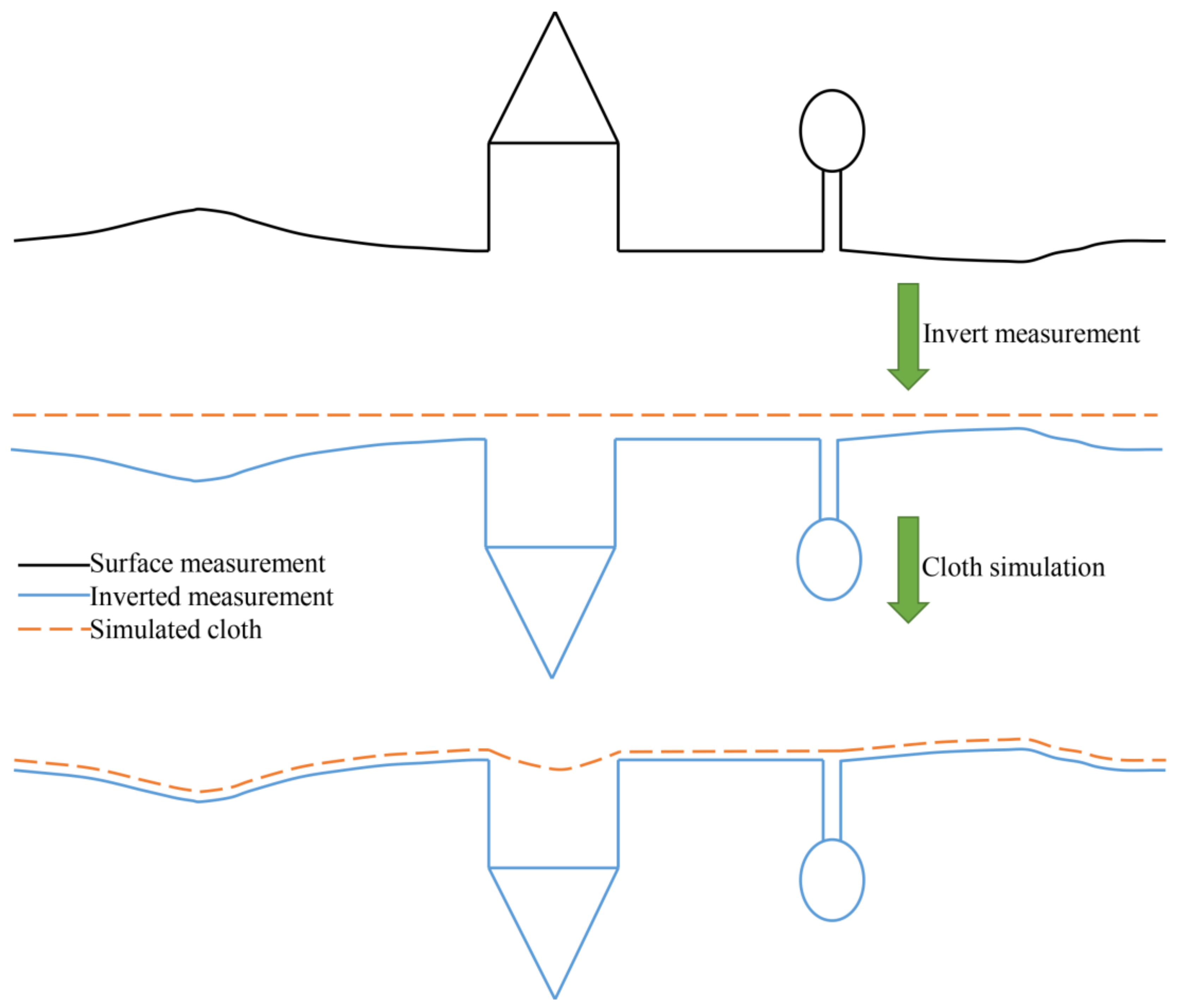
2.2. CSF for Ground Seed Selection
2.3. Local TPS Surface Interpolation Using Kdtree
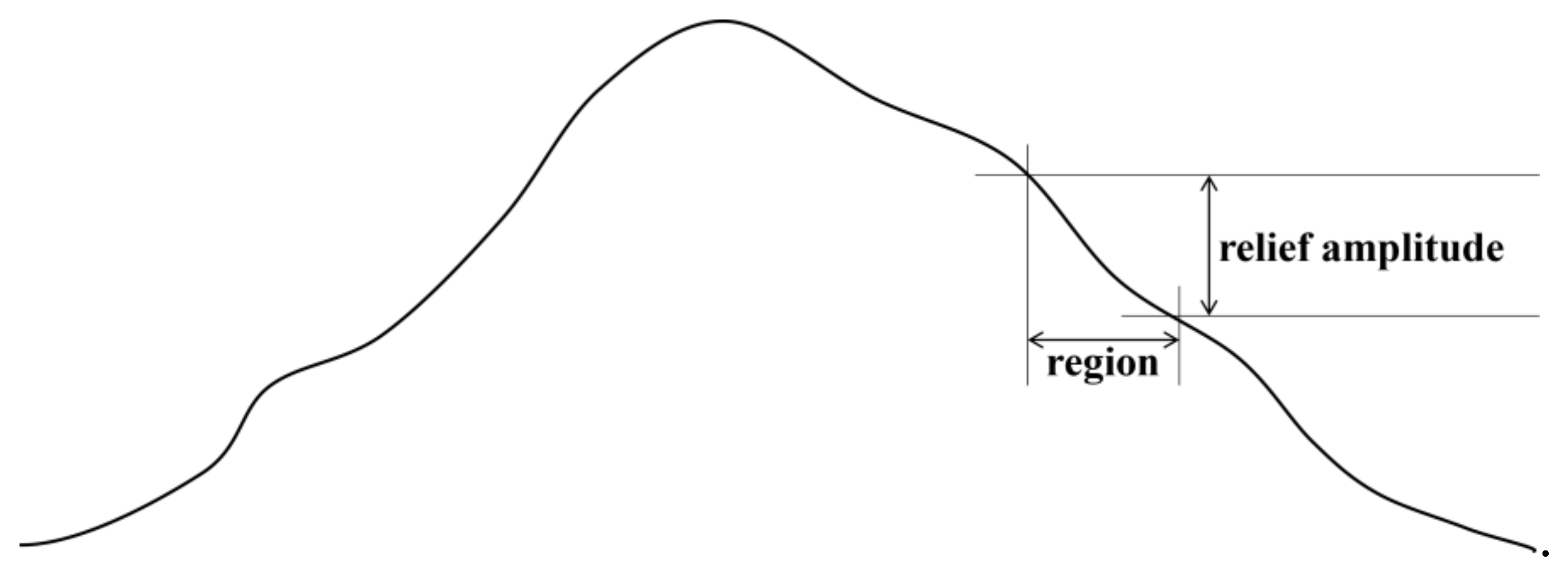
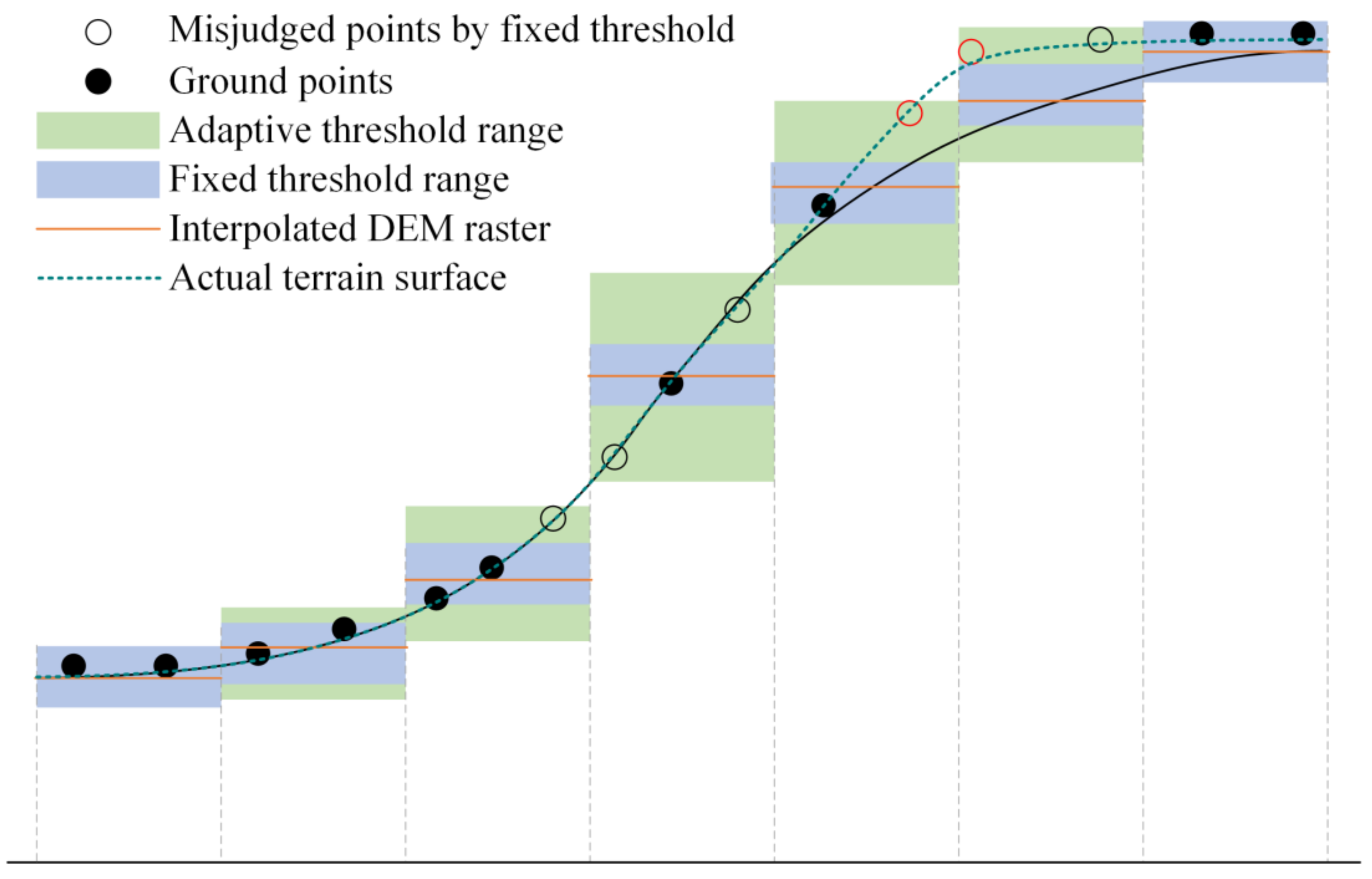
2.4. Relief Amplitude for Threshold Adaption
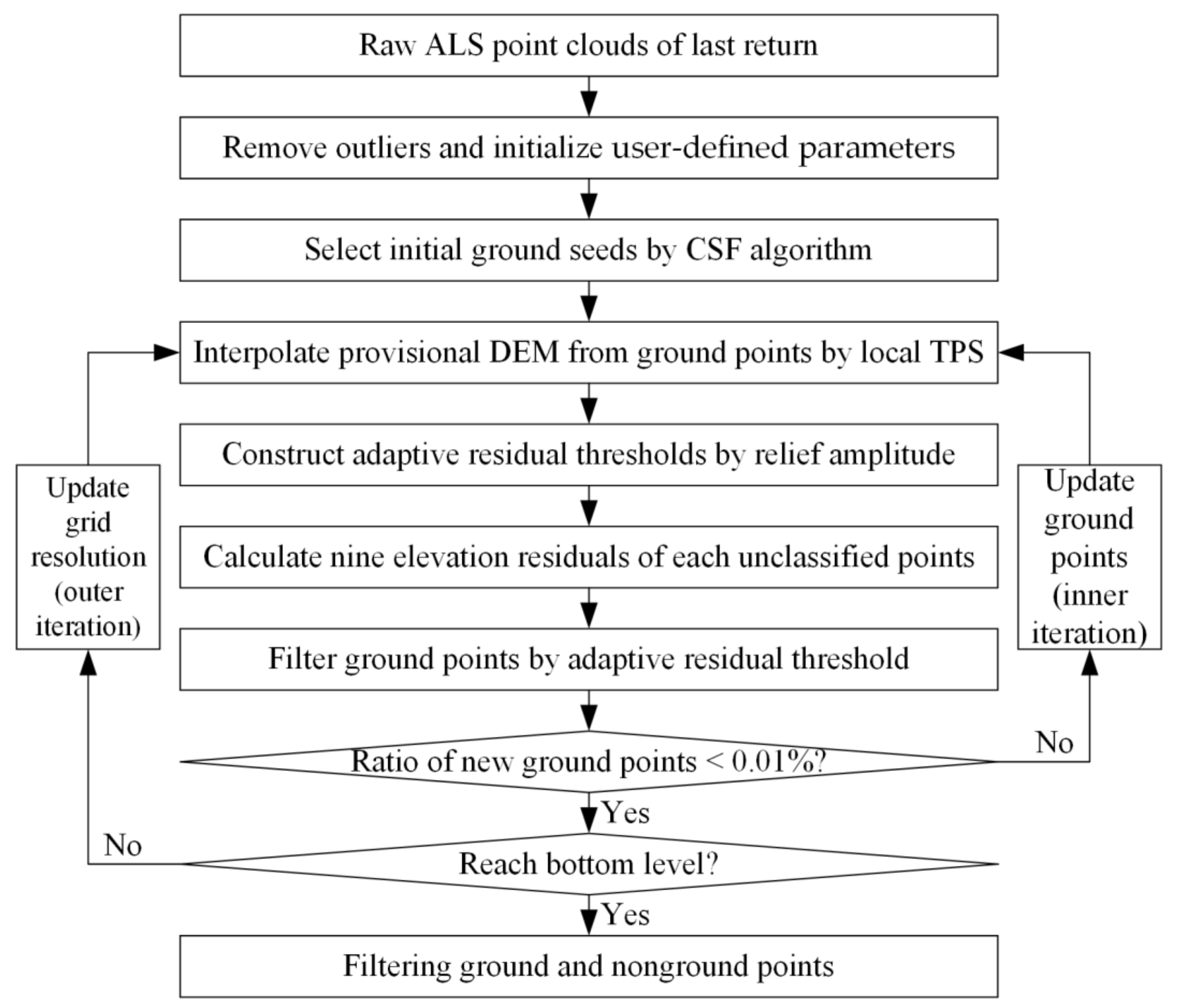
2.5. Adaptive Surface Interpolation Filter
- (1)
- Removing outliers from the raw ALS point clouds by SOR and initializing three user-defined parameters , and .
- (2)
- Initial ground seeds are selected from the point clouds without outliers by using the CSF algorithm, and the ground and unclassified points are updated.
- (3)
- The ground points are used to interpolate the provisional DEM raster surface by a TPS with a grid resolution and a smoothing factor .
- (4)
- The mean relief amplitude is computed from the provisional DEM, and the adaptive residual thresholds is constructed.
- (5)
- The elevation residuals are calculated from the unclassified points to corresponding nine neighbor cells of the provisional DEM.
- (6)
- The ground points are separated from the unclassified points if at least 4 of 9 values are smaller than the adaptive residual thresholds . In addition, the ground and unclassified points are updated.
- (7)
- Steps (3)–(6) are repeated until the new ground points are less than a certain number.
- (8)
- Steps (3)–(7) are repeated in the next hierarchy level with updating grid resolution and scale parameter . This outer iterative process terminates until the bottom hierarchy level is reached and the remaining unclassified points are labeled as nonground points.
3. Results
3.1. Experimental Data
3.2. Performance Measurement
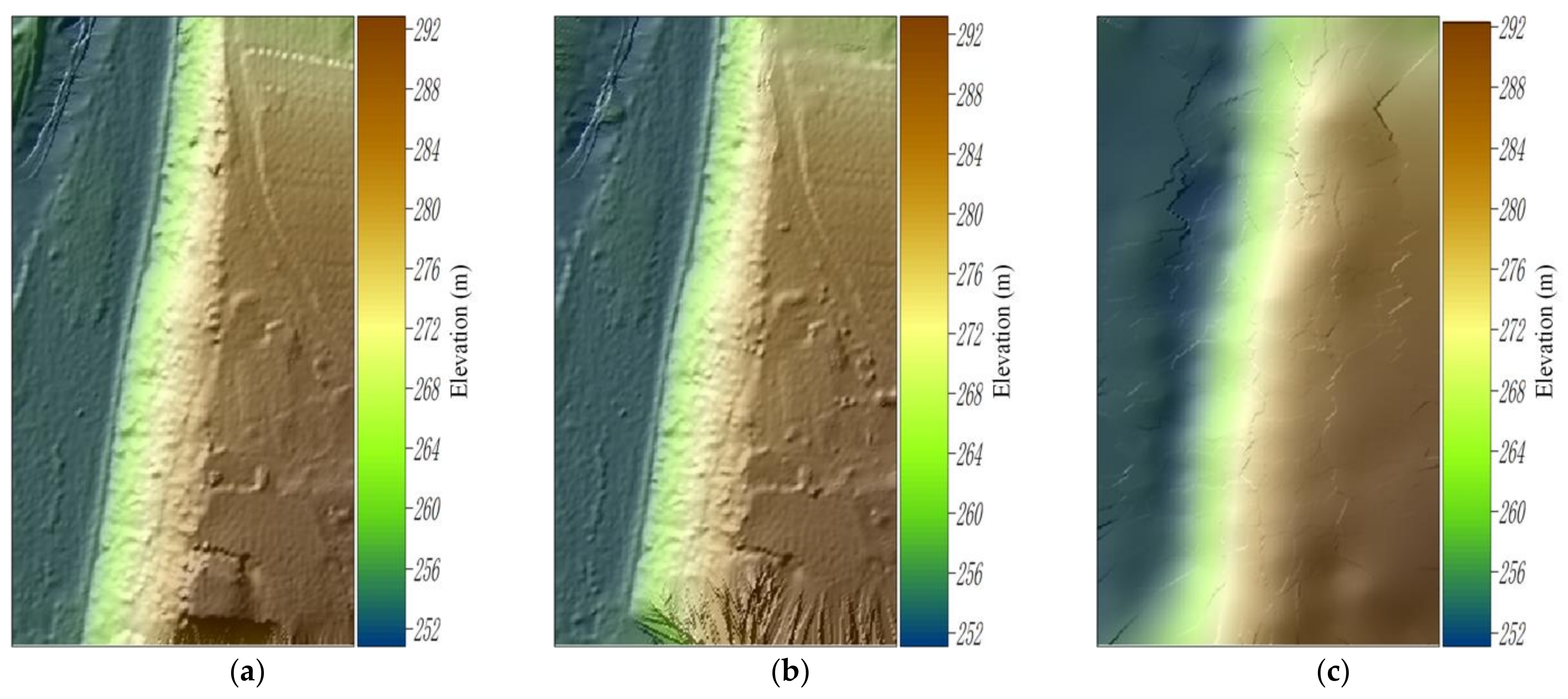
3.3. Results and Analysis
4. Discussion
4.1. Performance of Seed Selection Strategy
4.2. Effect of Adaptive Residual Thresholds
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-Art: DTM Generation Using Airborne LIDAR Data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, X.; Currit, N.; Zhao, K. Ground Filtering Algorithms for Airborne LiDAR Data: A Review of Critical Issues. Remote. Sens. 2010, 2, 833–860. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Li, Y. A Fast Global Interpolation Method for Digital Terrain Model Generation from Large LiDAR-Derived Data. Remote Sens. 2019, 11, 1324. [Google Scholar] [CrossRef] [Green Version]
- Tarolli, P. High-Resolution Topography for Understanding Earth Surface Processes: Opportunities and Challenges. Geomorphology 2014, 216, 295–312. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for DEM Generation: Some Critical Issues. Prog. Phys. Geogr. Earth Environ. 2008, 32, 31–49. [Google Scholar] [CrossRef]
- Wang, R.; Peethambaran, J.; Chen, D. LiDAR Point Clouds to 3-D Urban Models: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 606–627. [Google Scholar] [CrossRef]
- Wu, B.; Yu, B.; Wu, Q.; Yao, S.; Zhao, F.; Mao, W.; Wu, J. A Graph-Based Approach for 3D Building Model Reconstruction from Airborne LiDAR Point Clouds. Remote. Sens. 2017, 9, 92. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Brenner, C.; Sester, M. A Generative Statistical Approach to Automatic 3D Building Roof Reconstruction from Laser Scanning Data. ISPRS J. Photogramm. Remote. Sens. 2013, 79, 29–43. [Google Scholar] [CrossRef]
- Fischer, F.J.; Labrière, N.; Vincent, G.; Hérault, B.; Alonso, A.; Memiaghe, H.; Bissiengou, P.; Kenfack, D.; Saatchi, S.; Chave, J. A Simulation Method to Infer Tree Allometry and Forest Structure from Airborne Laser Scanning and Forest Inventories. Remote. Sens. Environ. 2020, 251, 112056. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M. Generating Spike-Free Digital Surface Models Using LiDAR Raw Point Clouds: A New Approach for Forestry Applications. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 104–114. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating Pit-free Canopy Height Models from Airborne Lidar. Photogramm. Eng. Remote. Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Pfeifer, N.T.R.; Briese, C.; Rieger, W. Interpolation of High Quality Ground Models from Laser Scanner Data in Forested Areas. Int. Arch. Photogramm. Remote Sens. 1999, 32, 31–36. [Google Scholar]
- Li, Y.; Wang, J.; Li, B.; Sun, W.; Li, Y. An Adaptive Filtering Algorithm of Multilevel Resolution Point Cloud. Surv. Rev. 2021, 53, 300–311. [Google Scholar] [CrossRef]
- Meng, X.; Lin, Y.; Yan, L.; Gao, X.; Yao, Y.; Wang, C.; Luo, S. Airborne LiDAR Point Cloud Filtering by a Multilevel Adaptive Filter Based on Morphological Reconstruction and Thin Plate Spline Interpolation. Electronics 2019, 8, 1153. [Google Scholar] [CrossRef] [Green Version]
- Cheng, P.; Hui, Z.; Xia, Y.; Ziggah, Y.Y.; Hu, Y.; Wu, J. An Improved Skewness Balancing Filtering Algorithm Based on Thin Plate Spline Interpolation. Appl. Sci. 2019, 9, 203. [Google Scholar] [CrossRef] [Green Version]
- Hui, Z.; Li, D.; Jin, S.; Ziggah, Y.Y.; Wang, L.; Hu, Y. Automatic DTM Extraction from Airborne LiDAR Based on Expectation-Maximization. Opt. Laser Technol. 2019, 112, 43–55. [Google Scholar] [CrossRef]
- Qin, L.; Wu, W.; Tian, Y.; Xu, W. LiDAR Filtering of Urban Areas with Region Growing Based on Moving-Window Weighted Iterative Least-Squares Fitting. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 841–845. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved Progressive TIN Densification Filtering Algorithm for Airborne LiDAR Data in Forested Areas. ISPRS J. Photogramm. Remote. Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef] [Green Version]
- Su, W.; Sun, Z.; Zhong, R.; Huang, J.; Li, M.; Zhu, J.; Zhang, K.; Wu, H.; Zhu, D. A New Hierarchical Moving Curve-Fitting Algorithm for Filtering Lidar Data for Automatic DTM Generation. Int. J. Remote. Sens. 2015, 36, 3616–3635. [Google Scholar] [CrossRef]
- Hu, H.; Ding, Y.; Zhu, Q.; Wu, B.; Lin, H.; Du, Z.; Zhang, Y.; Zhang, Y. An Adaptive Surface Filter for Airborne Laser Scanning Point Clouds by Means of Regularization and Bending Energy. ISPRS J. Photogramm. Remote. Sens. 2014, 92, 98–111. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Li, W.; Dai, H. A Multiresolution Hierarchical Classification Algorithm for Filtering Airborne LiDAR Data. ISPRS J. Photogramm. Remote. Sens. 2013, 82, 1–9. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. Parameter-Free Ground Filtering of LiDAR Data for Automatic DTM Generation. ISPRS J. Photogramm. Remote. Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Evans, J.; Hudak, A.T. A Multiscale Curvature Algorithm for Classifying Discrete Return LiDAR in Forested Environments. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 1029–1038. [Google Scholar] [CrossRef]
- Pfeifer, N.; Stadler, P.; Briese, C. Derivation of Digital Terrain Models in the SCOP++ Environment. In Proceedings of the OEEPE Workshop on Airborne Laserscanning and Interferometric SAR for Digital Elevation Models, Stockholm, Sweden, 1–3 March 2001. [Google Scholar]
- Axelsson, P. Processing of Laser Scanner Data—Algorithms and Applications. ISPRS J. Photogramm. Remote. Sens. 1999, 54, 138–147. [Google Scholar] [CrossRef]
- Kraus, K.; Pfeifer, N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote. Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Yang, Y.B.; Zhang, N.N.; Li, X.L. Adaptive Slope Filtering for Airborne Light Detection and Ranging Data in Urban Areas Based on Region Growing Rule. Surv. Rev. 2016, 1–8. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Yu, Y.; Zhong, L.; Ji, Z. DEM Generation from Lidar Data in Wooded Mountain Areas by Crosssection-Plane Analysis. Int. J. Remote. Sens. 2014, 35, 927–948. [Google Scholar] [CrossRef]
- Susaki, J. Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation. Remote. Sens. 2012, 4, 1804–1819. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.K.; Tseng, Y.H. Dem Generation from Airborne Lidar Data by an Adaptive Dual-Directional Slope Filter. In Proceedings of the ISPRS TC VII Symposium—100 Years ISPRS, Vienna, Austria, 5–7 July 2010. [Google Scholar]
- Meng, X.; Wang, L.; Silván-Cárdenas, J.L.; Currit, N. A Multi-Directional Ground Filtering Algorithm for Airborne LIDAR. ISPRS J. Photogramm. Remote. Sens. 2009, 64, 117–124. [Google Scholar] [CrossRef] [Green Version]
- Sithole, G. Filtering of Laser Altimetry Data Using a Slope Adaptive Filter. Int. Arch. Photogramm. Remote Sens. 2001, 34, 203–210. [Google Scholar]
- Vosselman, G. Slope Based Filtering of Laser Altimetry Data. Int. Arch. Photogramm. Remote Sens. 2000, 33, 935–942. [Google Scholar]
- Hui, Z.; Wang, L.; Ziggah, Y.Y.; Cai, S.; Xia, Y. Automatic Morphological Filtering Algorithm for Airborne Lidar Data in Urban Areas. Appl. Opt. 2019, 58, 1164–1173. [Google Scholar] [CrossRef]
- Li, Y.; Yong, B.; Van Oosterom, P.; Lemmens, M.; Wu, H.; Ren, L.; Zheng, M.; Zhou, J. Airborne LiDAR Data Filtering Based on Geodesic Transformations of Mathematical Morphology. Remote. Sens. 2017, 9, 1104. [Google Scholar] [CrossRef] [Green Version]
- Hui, Z.; Hu, Y.; Yevenyo, Y.Z.; Yu, X. An Improved Morphological Algorithm for Filtering Airborne LiDAR Point Cloud Based on Multi-Level Kriging Interpolation. Remote. Sens. 2016, 8, 35. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Yong, B.; Wu, H.; An, R.; Xu, H. An Improved Top-Hat Filter with Sloped Brim for Extracting Ground Points from Airborne Lidar Point Clouds. Remote. Sens. 2014, 6, 12885–12908. [Google Scholar] [CrossRef] [Green Version]
- Pingel, T.J.; Clarke, K.C.; McBride, W.A. An Improved Simple Morphological Filter for the Terrain Classification of Airborne LIDAR Data. ISPRS J. Photogramm. Remote. Sens. 2013, 77, 21–30. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering Airborne Laser Scanning Data with Morphological Methods. Photogramm. Eng. Remote. Sens. 2007, 73, 175–185. [Google Scholar] [CrossRef] [Green Version]
- Zhang, K.; Chen, S.-C.; Whitman, D.; Shyu, M.-L.; Yan, J.; Zhang, C. A Progressive Morphological Filter for Removing Nonground Measurements from Airborne LIDAR Data. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 872–882. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Zhang, C.; Fraser, C.S. Progressive Filtering of Airborne LiDAR Point Clouds Using Graph Cuts. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 2933–2944. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.; Liying, W.; Yan, X.; Yu, L. Aerial Lidar Point Cloud Voxelization with its 3D Ground Filtering Application. Photogramm. Eng. Remote. Sens. 2017, 83, 95–107. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y.; Li, J. Two-Step Adaptive Extraction Method for Ground Points and Breaklines from Lidar Point Clouds. ISPRS J. Photogramm. Remote. Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J. Segmentation-Based Filtering of Airborne LiDAR Point Clouds by Progressive Densification of Terrain Segments. Remote. Sens. 2014, 6, 1294–1326. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Li, X.; Zhang, Y. Fast Filtering of LiDAR Point Cloud in Urban Areas Based on Scan Line Segmentation and GPU Acceleration. IEEE Geosci. Remote. Sens. Lett. 2012, 10, 308–312. [Google Scholar] [CrossRef]
- Yan, M.; Blaschke, T.; Liu, Y.; Wu, L. An Object-Based Analysis Filtering Algorithm for Airborne Laser Scanning. Int. J. Remote. Sens. 2012, 33, 7099–7116. [Google Scholar] [CrossRef]
- Chang, L.-D.; Slatton, K.C.; Krekeler, C. Bare-Earth Extraction from Airborne LiDAR Data Based on Segmentation Modeling and Iterative Surface Corrections. J. Appl. Remote. Sens. 2010, 4, 041884. [Google Scholar] [CrossRef]
- Filin, S.; Pfeifer, N. Segmentation of Airborne Laser Scanning Data Using a Slope Adaptive Neighborhood. ISPRS J. Photogramm. Remote. Sens. 2006, 60, 71–80. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Filtering of Airborne Laser Scanner Data Based on Segmented Point Clouds. Int. Arch. Photogram. Remote Sens. Spat. Inform. Sci. 2005, 36, 66–71. [Google Scholar]
- Mahphood, A.; Arefi, H. Tornado Method for Ground Point Filtering from LiDAR Point Clouds. Adv. Space Res. 2020, 66, 1571–1592. [Google Scholar] [CrossRef]
- Ma, W.; Li, Q. An Improved Ball Pivot Algorithm-Based Ground Filtering Mechanism for LiDAR Data. Remote. Sens. 2019, 11, 1179. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote. Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Shao, Y.-C.; Chen, L.-C. Automated Searching of Ground Points from Airborne Lidar Data Using a Climbing and Sliding Method. Photogramm. Eng. Remote. Sens. 2008, 74, 625–635. [Google Scholar] [CrossRef] [Green Version]
- Sithole, G.; Vosselman, G. Experimental Comparison of Filter Algorithms for Bare-Earth Extraction from Airborne Laser Scanning Point Clouds. ISPRS J. Photogramm. Remote. Sens. 2004, 59, 85–101. [Google Scholar] [CrossRef]
- Lu, H.; Liu, X.; Bian, L. Terrain Complexity: Definition, Index, and DEM Resolution. Geoinform. Geospat. Inform. Sci. 2007, 6753, 675323. [Google Scholar] [CrossRef]
- Twidale, C.R. A Model of Landscape Evolution Involving Increased and Increasing Relief Amplitude. Z. Für Geomorphol. 1991, 35, 85–109. [Google Scholar] [CrossRef]
- Rusu, R.B.; Cousins, S. 3D is Here: Point Cloud Library (pcl). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Zandifar, A.; Lim, S.-N.; Duraiswami, R.; Gumerov, N.; Davis, L. Multi-Level Fast Multipole Method for Thin Plate Spline Evaluation. In Proceedings of the 2004 International Conference on Image Processing, Singapore, 24–27 October 2004; pp. 1683–1686. [Google Scholar] [CrossRef]
- Wahba, G. Spline Models for Observational Data; SIAM: Philadelphia, PA, USA, 1990. [Google Scholar]
- Garcia, G.P.; Grohmann, C.H. DEM-Based Geomorphological Mapping and Landforms Characterization of a Tropical Karst Environment in Southeastern Brazil. J. S. Am. Earth Sci. 2019, 93, 14–22. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.R.; Dong, K. Neighborhood Analysis-Based Calculation and Analysis of Multi-Scales Relief Amplitude. Adv. Mater. Res. 2012, 468–471, 2086–2089. [Google Scholar] [CrossRef]
- Sithole, G.; Vosselman, G. Report: ISPRS Comparison of Filters; ISPRS Commission III, Working Group 3: Enschede, The Netherlands, 2003. [Google Scholar]
- Congalton, R.G. A Review of Assessing the Accuracy of Classifications of Remotely Sensed Data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, W.; Liang, X.; Wan, P.; Qi, J.; Yu, S.; Yan, G.; Shao, J. Filtering Airborne LiDAR Data Through Complementary Cloth Simulation and Progressive TIN Densification Filters. Remote. Sens. 2019, 11, 1037. [Google Scholar] [CrossRef] [Green Version]



| Region | Spacing | Site | Sample | Features |
|---|---|---|---|---|
| Urban | 1–1.5 m | 1 | samp11 | Mixture of vegetation and buildings on hillside |
| samp12 | Mixture of vegetation and buildings | |||
| 2 | samp21 | Road with bridge | ||
| samp22 | Irregularly shaped buildings and bridge | |||
| samp23 | Large, irregularly shaped buildings | |||
| samp24 | Steep slopes with vegetation | |||
| 3 | samp31 | Complex buildings | ||
| 4 | samp41 | Data gaps and irregularly shaped buildings | ||
| samp42 | Railway station with trains | |||
| Rural | 2–3.5 m | 5 | samp51 | Mixture of vegetation and buildings on hillside |
| samp52 | Steep, terraced slopes | |||
| samp53 | Steep, terraced slopes | |||
| samp54 | Irregularly shaped buildings | |||
| 6 | samp61 | Data gaps, discontinuity | ||
| 7 | samp71 | Underpass and bridge |
| Filtered | Ground | Nonground | ||
|---|---|---|---|---|
| References | ||||
| ground | a | b | f = (a + b)/e | |
| nonground | c | d | g = (c + d)/e | |
| h = (a + c)/e | i = (b + d)/e | e = a + b + c + d | ||
| Sample | h (m) | t (m) | st (Bool) |
|---|---|---|---|
| samp11 | 2 | 0.2 | False |
| samp12 | 4 | 0 | True |
| samp21 | 2 | 0 | False |
| samp22 | 2 | 0.2 | True |
| samp23 | 4 | 0.2 | True |
| samp24 | 2 | 0.1 | True |
| samp31 | 4 | 0 | True |
| samp41 | 4 | 0.1 | True |
| samp42 | 4 | 0.4 | True |
| samp51 | 2 | 0.1 | False |
| samp52 | 4 | 0.2 | True |
| samp53 | 4 | 0.3 | True |
| samp54 | 4 | 0.2 | False |
| samp61 | 2 | 0.5 | False |
| samp71 | 2 | 0.3 | False |
| Sample | T.I (%) | T.II (%) | T.E. (%) | Kappa (%) |
|---|---|---|---|---|
| samp11 | 9.00 | 12.93 | 10.68 | 78.16 |
| samp12 | 2.33 | 2.91 | 2.61 | 94.77 |
| samp21 | 0.52 | 3.17 | 1.10 | 96.79 |
| samp22 | 0.73 | 7.72 | 2.91 | 93.10 |
| samp23 | 4.33 | 4.70 | 4.50 | 90.97 |
| samp24 | 1.09 | 9.62 | 3.43 | 91.21 |
| samp31 | 0.27 | 2.00 | 1.07 | 97.85 |
| samp41 | 8.03 | 5.22 | 6.62 | 86.75 |
| samp42 | 0.18 | 1.28 | 0.96 | 97.70 |
| samp51 | 0.25 | 6.62 | 1.64 | 95.09 |
| samp52 | 1.35 | 16.38 | 2.93 | 84.07 |
| samp53 | 2.34 | 23.11 | 3.18 | 64.49 |
| samp54 | 1.18 | 4.04 | 2.72 | 94.55 |
| samp61 | 1.22 | 12.19 | 1.60 | 78.27 |
| samp71 | 0.37 | 7.23 | 1.15 | 94.16 |
| mean | 2.21 | 7.94 | 3.14 | 89.20 |
| std | 2.69 | 5.83 | 2.49 | 9.06 |
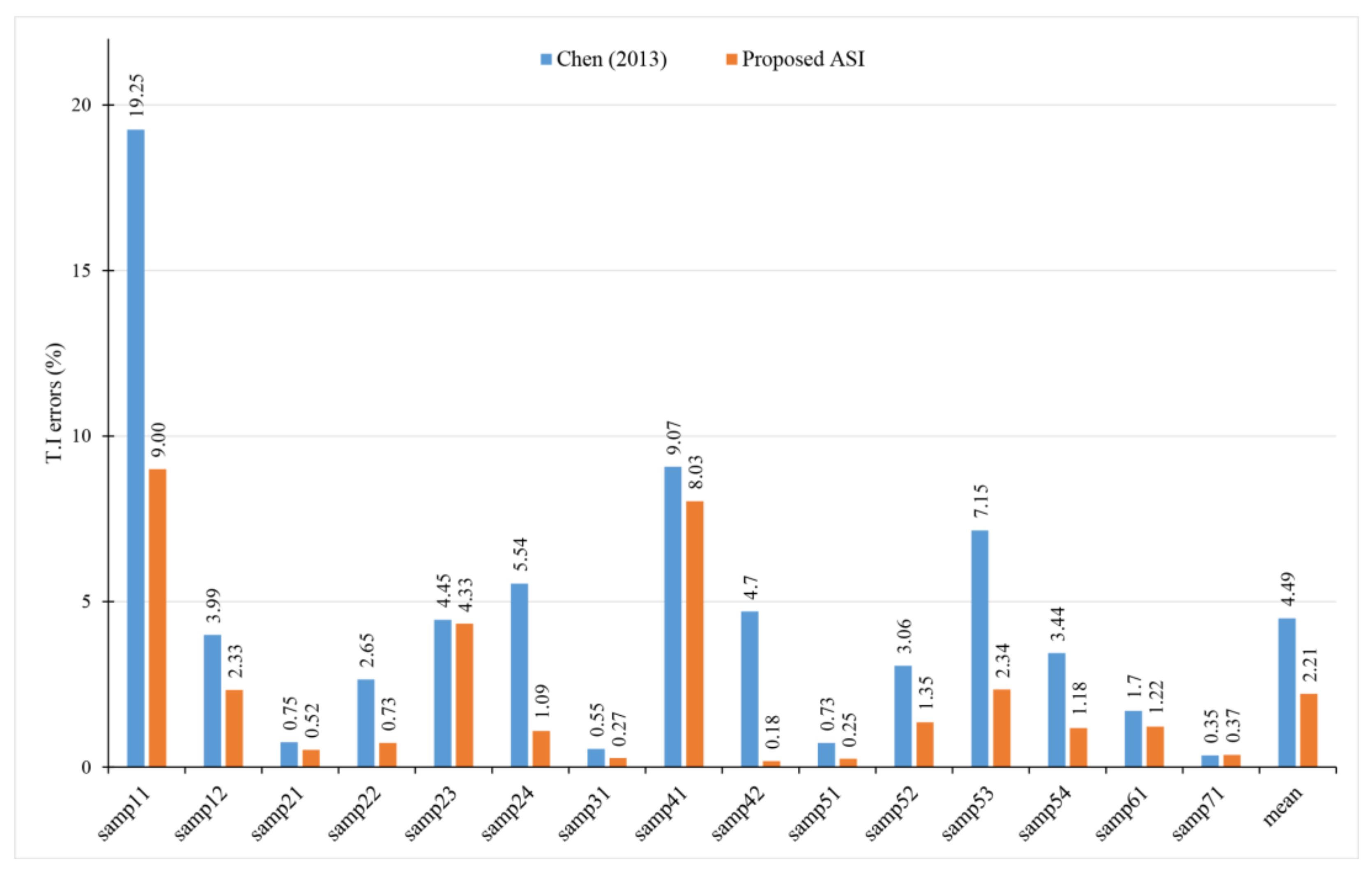
| Sample | Mongus (2012) | Chen (2013) | Meng (2019) | Li (2020) | Proposed ASI |
|---|---|---|---|---|---|
| samp11 | 11.01 | 13.01 | 10.20 | 9.44 | 10.68 |
| samp12 | 5.17 | 3.38 | 2.97 | 3.34 | 2.61 |
| samp21 | 1.98 | 1.34 | 1.35 | 1.50 | 1.10 |
| samp22 | 6.56 | 4.67 | 3.82 | 4.93 | 2.91 |
| samp23 | 5.83 | 5.24 | 5.03 | 4.42 | 4.50 |
| samp24 | 7.98 | 6.29 | 5.22 | 6.87 | 3.43 |
| samp31 | 3.34 | 1.11 | 2.13 | 1.39 | 1.07 |
| samp41 | 3.71 | 5.58 | 6.40 | 4.82 | 6.62 |
| samp42 | 5.72 | 1.72 | 0.66 | 0.81 | 0.96 |
| samp51 | 2.59 | 1.64 | 1.71 | 1.79 | 1.64 |
| samp52 | 7.11 | 4.18 | 3.39 | 3.47 | 2.93 |
| samp53 | 8.52 | 7.29 | 6.58 | 5.96 | 3.18 |
| samp54 | 6.73 | 3.09 | 2.93 | 2.95 | 2.72 |
| samp61 | 4.85 | 1.81 | 2.10 | 1.69 | 1.60 |
| samp71 | 3.14 | 1.33 | 1.34 | 1.60 | 1.15 |
| mean | 5.62 | 4.11 | 3.72 | 3.67 | 3.14 |
| std | 2.39 | 3.06 | 2.48 | 2.35 | 2.49 |
| Sample | Mongus (2012) | Chen (2013) | Meng (2019) | Li (2020) | Proposed ASI |
|---|---|---|---|---|---|
| samp11 | 77.31 | 74.12 | 79.09 | 80.74 | 78.16 |
| samp12 | 89.66 | 93.23 | 94.05 | 93.31 | 94.77 |
| samp21 | 94.09 | 96.10 | 96.02 | 95.62 | 96.79 |
| samp22 | 84.74 | 89.03 | 91.05 | 88.35 | 93.10 |
| samp23 | 88.29 | 89.49 | 89.92 | 91.12 | 90.97 |
| samp24 | 80.07 | 84.53 | 86.86 | 82.78 | 91.21 |
| samp31 | 93.25 | 97.76 | 95.69 | 97.21 | 97.85 |
| samp41 | 92.61 | 88.83 | 87.19 | 90.36 | 86.75 |
| samp42 | 86.95 | 95.81 | 98.42 | 98.06 | 97.70 |
| samp51 | 92.18 | 95.17 | 94.89 | 94.66 | 95.09 |
| samp52 | 68.45 | 78.91 | 82.82 | 82.42 | 84.07 |
| samp53 | 42.18 | 46.69 | 49.12 | 43.43 | 64.49 |
| samp54 | 86.63 | 93.90 | 94.11 | 94.08 | 94.55 |
| samp61 | 65.05 | 77.36 | 74.82 | 77.81 | 78.27 |
| samp71 | 85.04 | 93.19 | 93.33 | 92.08 | 94.16 |
| mean | 81.77 | 86.27 | 87.16 | 86.80 | 89.20 |
| std | 13.50 | 12.72 | 12.05 | 13.08 | 9.06 |
| Sample | Chen (2013) | Zhang (2016) | Cai (2019) | Proposed ASI |
|---|---|---|---|---|
| samp11 | 13.01 | 12.01 | 16.24 | 10.68 |
| samp12 | 3.38 | 2.97 | 8.85 | 2.61 |
| samp21 | 1.34 | 3.42 | 14.18 | 1.10 |
| samp22 | 4.67 | 8.94 | 4.25 | 2.91 |
| samp23 | 5.24 | 4.79 | 8.52 | 4.50 |
| samp24 | 6.29 | 2.87 | 15.59 | 3.43 |
| samp31 | 1.11 | 1.61 | 7.28 | 1.07 |
| samp41 | 5.58 | 5.14 | 13.04 | 6.62 |
| samp42 | 1.72 | 1.58 | 4.75 | 0.96 |
| samp51 | 1.64 | 3.08 | 3.51 | 1.64 |
| samp52 | 4.18 | 3.93 | 4.65 | 2.93 |
| samp53 | 7.29 | 5.20 | 3.95 | 3.18 |
| samp54 | 3.09 | 3.18 | 2.58 | 2.72 |
| samp61 | 1.81 | 1.49 | 0.86 | 1.60 |
| samp71 | 1.33 | 5.71 | 2.03 | 1.15 |
| mean | 4.11 | 4.39 | 7.35 | 3.14 |
| std | 3.06 | 2.76 | 4.98 | 2.49 |
| Sample | MHC | Proposed ASI | ||
|---|---|---|---|---|
| Points | RMSE (m) | Points | RMSE (m) | |
| samp11 | 55 | 3.17 | 9322 | 3.53 |
| samp12 | 63 | 1.66 | 24,233 | 0.99 |
| samp21 | 20 | 0.55 | 9561 | 0.11 |
| samp22 | 49 | 2.01 | 21,668 | 0.43 |
| samp23 | 35 | 3.56 | 11,196 | 1.47 |
| samp24 | 28 | 2.26 | 5016 | 0.60 |
| samp31 | 81 | 0.73 | 15,449 | 0.17 |
| samp41 | 24 | 3.50 | 4688 | 1.67 |
| samp42 | 56 | 0.85 | 11,119 | 0.54 |
| samp51 | 120 | 1.10 | 11,927 | 0.51 |
| samp52 | 346 | 1.91 | 13,827 | 3.07 |
| samp53 | 500 | 4.54 | 21,594 | 5.74 |
| samp54 | 140 | 0.60 | 2061 | 0.92 |
| samp61 | 516 | 1.37 | 26,460 | 1.26 |
| samp71 | 108 | 2.17 | 8489 | 1.57 |
| mean | 143 | 2.00 | 13,107 | 1.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhu, H.; Luo, Z.; Shen, H.; Li, L. An Adaptive Surface Interpolation Filter Using Cloth Simulation and Relief Amplitude for Airborne Laser Scanning Data. Remote Sens. 2021, 13, 2938. https://doi.org/10.3390/rs13152938
Li F, Zhu H, Luo Z, Shen H, Li L. An Adaptive Surface Interpolation Filter Using Cloth Simulation and Relief Amplitude for Airborne Laser Scanning Data. Remote Sensing. 2021; 13(15):2938. https://doi.org/10.3390/rs13152938
Chicago/Turabian StyleLi, Feng, Haihong Zhu, Zhenwei Luo, Hang Shen, and Lin Li. 2021. "An Adaptive Surface Interpolation Filter Using Cloth Simulation and Relief Amplitude for Airborne Laser Scanning Data" Remote Sensing 13, no. 15: 2938. https://doi.org/10.3390/rs13152938
APA StyleLi, F., Zhu, H., Luo, Z., Shen, H., & Li, L. (2021). An Adaptive Surface Interpolation Filter Using Cloth Simulation and Relief Amplitude for Airborne Laser Scanning Data. Remote Sensing, 13(15), 2938. https://doi.org/10.3390/rs13152938