Bearings-Only Target Tracking with an Unbiased Pseudo-Linear Kalman Filter

Abstract

In bearings-only target tracking, the pseudo-linear Kalman filter (PLKF) attracts much attention because of its stability and its low computational burden. However, the PLKF’s measurement vector and the pseudo-linear noise are correlated, which makes it suffer from bias problems. Although the bias-compensated PLKF (BC–PLKF) and the instrumental variable-based PLKF (IV–PLKF) can eliminate the bias, they only work well when the target behaves with non-manoeuvring movement. To extend the PLKF to the manoeuvring target tracking scenario, an unbiased PLKF (UB–PLKF) algorithm, which splits the noise away from the measurement vector directly, is proposed. Based on the results of the UB–PLKF, we also propose its velocity-constrained version (VC–PLKF) to further improve the performance. Simulations show that the UB–PLKF and VC–PLKF outperform the BC–PLKF and IV–PLKF both in non-manoeuvring and manoeuvring scenarios.

1. Introduction

Bearings-only tracking (BOT) comprises estimating a target’s state from bearing measurements received by an observer [1]. It plays an important role in both military and civil applications, for example, underwater surveillance [2,3], 3-D passive target tracking [4,5,6,7] and UAV (unmanned aerial vehicle) path planning [8,9,10,11]. However, the nonlinear relationship between the bearing measurements and the target state vector makes BOT a typical nonlinear filtering problem [12].

There are two common ways to deal with the nonlinearity in the BOT problem. The first way is to choose the nonlinear Bayesian filtering algorithms. Early approaches are based on the extended Kalman filter and its improved versions [1,13,14]. However, the extended Kalman filter uses the first-order Taylor expansion to replace the corresponding nonlinear function, which will certainly lead to truncation errors. Other more sophisticated Kalman filters, such as the unscented Kalman filter [15] and the cubature Kalman filter [16], applied to the BOT problem, can be found in [17,18]. Another important approach is based upon particle filtering (see, for instance, [19,20]). However, the high computational requirements of the particle filter would involve high-performance expensive hardware that discourages its implementation in BOT applications. It is important to also mention here the non-Bayesian-based shadowing filter that, recently, has been applied to the BOT problem [21]. However, such a filter is a kind of gradient descent algorithm, hence, it is highly sensitive to the step size as well as the computation of the Jacobian matrix [22].

Another way to cope with the nonlinearlity in BOT is to convert it into linear form, and the most common method used is the pseudo-linear Kalman filter (PLKF) [23]. It has lower computational complexity and is more robust compared with the nonlinear Bayesian filtering algorithms introduced above [24], and no other prior parameters are required compared with the shadowing filter. These advantages make the PLKF an attractive method for engineering. However, unlike the traditional Kalman filter, the PLKF measurement vector contains the bearing noise, which makes it correlated with the pseudo-linear noise. This correlation leads to bias problems for the PLKF. To improve the PLKF performance, the instantaneous bias of PLKF is analysed in [25], and two improved PLKF algorithms, the bias-compensated PLKF (BC–PLKF) and the instrumental variable-based PLKF (IV–PLKF), are proposed. The BC–PLKF subtracts the approximated bias from the estimate of the PLKF to reduce the bias. The IV–PLKF utilizes the results of the BC–PLKF to construct a noise-free measurement vector, and its asymptotic unbiasedness has been proved in [25,26]. Although BC–PLKF and IV–PLKF effectiveness has been verified in [25] when the target moves without manoeuvring, their performance in the manoeuvring target tracking scenario may be unsatisfactory. It is not surprising because the measurement vector and the noise are still correlated in BC–PLKF, and its performance cannot be guaranteed by only subtracting the bias when the target manoeuvres. IV–PLKF also suffers from this problem because it uses the results of the BC–PLKF as its input parameters.

To extend the PLKF algorithm to the case of the BOT problem with a manoeuvring target and at the same time make an excellent compromise between computational load and accuracy, we first propose an unbiased PLKF (UB–PLKF) algorithm which splits the bearing noise away from the measurement vector directly to eliminate their correlation, thus avoiding the bias compensation operation in BC–PLKF. The unbiasedness makes the UB–PLKF more adaptable to the abrupt changes in the target state and ensures the UB–PLKF’s convergence when the target manoeuvres. Then, for further improving its performance, the target velocity range information is incorporated into the UB–PLKF to construct the velocity-constrained PLKF (VC–PLKF) based on [27]. Incorporating some prior information about the target state into the Kalman filter to construct the state-constrained Kalman filter [28] is common; however, this method is rarely seen in PLKF. Although [29,30,31] have introduced the constraints into BOT, they are all based on the batch algorithms which can hardly handle the manoeuvring target tracking problem. To the best of the authors’ knowledge, this is the first time that a velocity-constrained PLKF has been proposed. Simulations will verify the effectiveness of the UB–PLKF and VC–PLKF both in non-manoeuvring and manoeuvring target tracking scenarios.

This paper is organised as follows: In Section 2, we first formulate the BOT problem to be solved and generally review the PLKF, BC–PLKF, and IV–PLKF, then we propose the UB–PLKF and VC–PLKF. Section 3 presents the simulation results to verify the effectiveness of the proposed algorithms.

Notations

Throughout the paper, vectors and matrices are denoted by boldface lower-case and upper-case letters, respectively. $\mathbb{E}\{·\}$ and tr$\{·\}$ denote the expectation operator and trace operator, respectively; ${\mathit{I}}_{n\times n}$ denotes the $n\times n$ identity matrix; $0_{n\times m}$ denotes the $n\times m$ zero matrix; the superscript “BC”, “IV”, “UB” and “VC” denote, respectively, the vector or matrix in BC–PLKF, IV–PLKF, UB–PLKF and VC–PLKF, and any vector or matrix with this kind of superscript has the same dimension as its original form in PLKF; the superscript “T” denotes the transpose operation of a vector or matrix; the superscript “$-1$” denotes the inverse operation of a matrix; the superscript “+” means that the vector or matrix belongs to the posterior estimate, and “−” means that the vector or matrix belongs to the predictive estimate; $\mathit{y}=\mathit{x}(i:j)$ means that y consists of the ith through the jth element of x, and $\parallel ·\parallel$ denotes the $l$-2 norm of a vector.

2. Materials and Methods

In this section, we first formulate the 2D BOT problem, then we provide brief reviews of the PLKF and its two improved versions—the BC–PLKF and the IV–PLKF. After these, we propose the UB–PLKF to cope with the biased estimate problem in PLKF. Then, we incorporate the velocity constraint information into the UB–PLKF to construct the VC–PLKF.

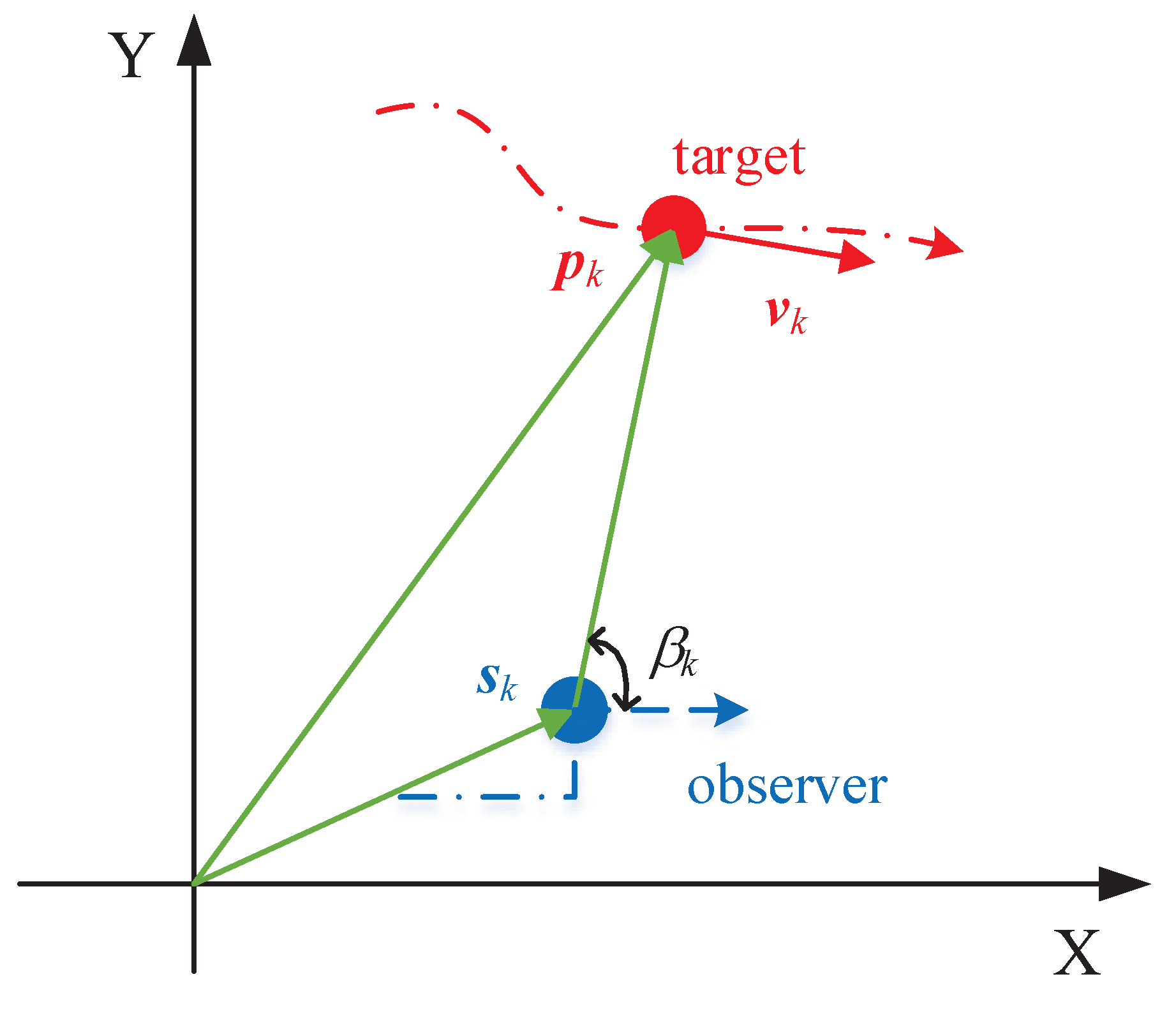
2.1. Problem Formulation

We focus on the BOT problem in 2D-plane with the bearing measurements received by a moving observer, which is shown in Figure 1. We denote by ${\mathit{p}}_k={[p_{x,k},p_{y,k}]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$ and ${\mathit{v}}_k={[v_{x,k},v_{y,k}]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$ the position and velocity of the target at the discrete time index $k=1,\cdots ,N$, respectively. We then have target state vector ${\mathit{x}}_k={[{\mathit{p}}_k^{\mathrm{T}},{\mathit{v}}_k^{\mathrm{T}}]}^{\mathrm{T}}\in {\mathbb{R}}^{4\times 1}$. The observer position is represented by the vector ${\mathit{s}}_k={[s_{x,k},s_{y,k}]}^{\mathrm{T}}\in {\mathbb{R}}^{2\times 1}$, which is assumed to be known.

In the following, we assume that the target is moving under the constant velocity model as discussed in [32], then the target dynamic model is:

$${\mathit{x}}_k=\mathit{F}{\mathit{x}}_{k-1}+{\mathit{w}}_{k-1},$$

(1)

where $\mathit{F}\in {\mathbb{R}}^{4\times 4}$ is the transition matrix, and ${\mathit{w}}_{k-1}\in {\mathbb{R}}^{4\times 1}$ is the process noise, which is assumed to be a Gaussian random vector with mean $0_{4\times 1}$ and covariance matrix $\mathit{Q}\in {\mathbb{R}}^{4\times 4}$. The matrices $\mathit{F}$ and $\mathit{Q}$ are given by [32]

$$\begin{array}{c}\mathit{F}=\left[\begin{array}{cccc}1& 0& T& 0\\ 0& 1& 0& T\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],\end{array}$$

(2)

$$\begin{array}{c}\mathit{Q}=\left[\begin{array}{cccc}{q}_x\frac{T^3}{3}& 0& q_x\frac{T^2}{2}& 0\\ 0& q_y\frac{T^3}{3}& 0& q_y\frac{T^2}{2}\\ q_x\frac{T^2}{2}& 0& q_{x}T& 0\\ 0& q_y\frac{T^2}{2}& 0& q_{y}T,\end{array}\right]\end{array}$$

(3)

where T is the sample interval, which is assumed to be equal to 1 s throughout the paper. $q_x$ and $q_y$ are respectively the power spectral densities of ${\mathit{w}}_k$ in two coordinates.

We adopt ${\tilde{\beta }}_k$ to denote the bearing collected by the observer at k. It can be written as

$$\begin{array}{cc}\hfill {\tilde{\beta }}_k& ={\beta }_k+n_k,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\beta }_k& ={tan}^{-1}\frac{\Delta y_k}{\Delta x_k},\hfill \end{array}$$

(5)

where $\Delta x_k=p_{x,k}-s_{x,k}$, $\Delta y_k=p_{y,k}-s_{y,k}$, ${tan}^{-1}$ is the four-quadrant inverse tangent function, and $n_k$ is the bearing noise, which is assumed to be Gaussian with zero mean and variance ${\sigma }_k^2$. ${\sigma }_k$ is assumed to be known, and $n_k$ is independent of the process noise ${\mathit{w}}_k$ throughout the paper.

2.2. Overview of the PLKF, BC–PLKF, and IV–PLKF

This subsection first discusses the PLKF algorithm and then analyses its bias. Afterwards, the improved PLKF algorithms–BC–PLKF and IV–PLKF in [25] are introduced.

2.2.1. PLKF

Obviously, we have the following equation:

$$\begin{array}{cc}\hfill sin{n}_k& =sin({\tilde{\beta }}_k-{\beta }_k)\hfill \\ & =sin{\tilde{\beta }}_{k}cos{\beta }_k-cos{\tilde{\beta }}_{k}sin{\beta }_k,\hfill \end{array}$$

(6)

multiplying $d_k=\sqrt{\Delta x_k^2+\Delta y_k^2}$ to both sides of (6), and notice that $d_k\times cos{\beta }_k=\Delta x_k$, $d_k\times sin{\beta }_k=\Delta y_k$, we have

$$\begin{array}{cc}\hfill d_{k}sin{n}_k& =sin{\tilde{\beta }}_k\Delta x_k-cos{\tilde{\beta }}_k\Delta y_k\hfill \\ & =sin{\tilde{\beta }}_k(p_{x,k}-s_{x,k})-cos{\tilde{\beta }}_k(p_{y,k}-s_{y,k})\hfill \\ & =[sin{\tilde{\beta }}_k,-cos{\tilde{\beta }}_k]{\mathit{p}}_k-[sin{\tilde{\beta }}_k,-cos{\tilde{\beta }}_k]{\mathit{s}}_k\hfill \\ & =[sin{\tilde{\beta }}_k,-cos{\tilde{\beta }}_k,0,0]{\mathit{x}}_k-[sin{\tilde{\beta }}_k,-cos{\tilde{\beta }}_k]{\mathit{s}}_k.\hfill \end{array}$$

(7)

Then we have the following pseudo-linear measurement equation:

$$z_k={\mathit{H}}_k{\mathit{x}}_k+{\eta }_k,$$

(8)

where $z_k=[sin{\tilde{\beta }}_k,-cos{\tilde{\beta }}_k]{\mathit{s}}_k$, ${\mathit{H}}_k=[sin{\tilde{\beta }}_k,-cos{\tilde{\beta }}_k,0,0]$, and ${\eta }_k=-d_{k}sin{n}_k$ is the pseudo-linear noise. The variance of ${\eta }_k$ is denoted by $R_k=\mathbb{E}\left\{{\eta }_k^2\right\}=d_k^2·\mathbb{E}\left\{{sin}^2{n}_k\right\}\approx d_k^2{\sigma }_k^2$ for small bearing noise $n_k$.

Combining (1) and (8), the PLKF is given by

step 1

Predicting the state:

$${\widehat{\mathit{x}}}_{k|k-1}=\mathit{F}{\widehat{\mathit{x}}}_{k-1|k-1};$$

(9)

step 2

Predicting the covariance matrix:

$${\mathit{P}}_{k|k-1}=\mathit{F}{\mathit{P}}_{k-1|k-1}{\mathit{F}}^{\mathrm{T}}+\mathit{Q};$$

(10)

step 3

Calculating the gain matrix:

$${\mathit{K}}_k={\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}}{\left(R_k+{\mathit{H}}_k{\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}}\right)}^{-1};$$

(11)

step 4

Updating the state:

$${\widehat{\mathit{x}}}_{k|k}={\widehat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k(z_k-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k-1});$$

(12)

step 5

Updating the covariance matrix:

$${\mathit{P}}_{k|k}=({\mathit{I}}_{4\times 4}-{\mathit{K}}_k{\mathit{H}}_k){\mathit{P}}_{k|k-1},$$

(13)

where ${\widehat{\mathit{x}}}_{k|k-1}\in {\mathbb{R}}^{4\times 1}$ and ${\mathit{P}}_{k|k-1}\in {\mathbb{R}}^{4\times 4}$ denote, respectively, the one-step prediction and the corresponding prediction error covariance matrix, and ${\mathit{K}}_k\in {\mathbb{R}}^{4\times 1}$ denotes the Kalman gain, and ${\widehat{\mathit{x}}}_{k|k}\in {\mathbb{R}}^{4\times 1}$ and ${\mathit{P}}_{k|k}\in {\mathbb{R}}^{4\times 4}$ are, respectively, the posterior state estimate and corresponding estimation error covariance matrix. Since the true values of $d_k$ and $R_k$ are not available, the approximated values are used,

$$\begin{array}{cc}\hfill {\widehat{d}}_k& =\parallel {\widehat{\mathit{x}}}_{k|k-1}(1:2)-{\mathit{s}}_k\parallel ,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\widehat{R}}_k& ={\widehat{d}}_k^2{\sigma }_k^2.\hfill \end{array}$$

(15)

2.2.2. BC–PLKF

According to [25], the posterior bias ${\mathit{e}}_k={\widehat{\mathit{x}}}_{k|k}-{\mathit{x}}_k$ of the PLKF can be written as:

$${\mathit{e}}_k={\mathit{A}}_k+{\mathit{B}}_k+{\mathit{C}}_k$$

(16)

where

$$\begin{array}{c}\hfill {\mathit{A}}_k={\left({\mathit{P}}_{k|k-1}^{-1}+{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\mathit{H}}_k\right)}^{-1}{\mathit{P}}_{k|k-1}^{-1}\mathit{F}\left({\widehat{\mathit{x}}}_{k-1|k-1}-{\mathit{x}}_{k-1}\right),\end{array}$$

(17)

$${\mathit{B}}_k=-{\left({\mathit{P}}_{k|k-1}^{-1}+{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\mathit{H}}_k\right)}^{-1}{\mathit{P}}_{k|k-1}^{-1}{\mathit{w}}_{k-1},$$

(18)

$${\mathit{C}}_k={\left({\mathit{P}}_{k|k-1}^{-1}+{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\mathit{H}}_k\right)}^{-1}{\mathit{P}}_{k|k-1}^{-1}{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\eta }_k.$$

(19)

The first term ${\mathit{A}}_k$ propagates the error from the last time $k-1$, and it is not the cause that leads to the biased estimate in PLKF. The second term ${\mathit{B}}_k$ propagates the bias from the correlation between ${\mathit{H}}_k$ and ${\mathit{w}}_{k-1}$. If we assume the process noise ${\mathit{w}}_k$ is relatively small, then ${\mathit{B}}_k$ can be ignored. When it comes to the third term ${\mathit{C}}_k$, it propagates the bias from the correlation between ${\mathit{H}}_k$ and ${\eta }_k$, which cannot be ignored since they all contain the bearing noise $n_k$. Thus, we can have the conclusion that it is the correlation between the ${\mathit{H}}_k$ and ${\eta }_k$ that leads to the biased estimate, and if we can compensate the bias from ${\mathit{C}}_k$, the bias in ${\widehat{\mathit{x}}}_{k|k}$ can be reduced.

So the bias compensation can be achieved by

$${\widehat{\mathit{x}}}_{k|k}-{\left({\mathit{P}}_{k|k-1}^{-1}+{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\mathit{H}}_k\right)}^{-1}{\mathit{P}}_{k|k-1}^{-1}{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\eta }_k.$$

(20)

However, the true value of ${\mathit{C}}_k$ cannot be obtained; we are supposed to replace it with its conditional expectation based on ${\widehat{\mathit{x}}}_{k|k}$, which can be formulated as: [25]

$$\begin{array}{cc}\hfill {\widehat{\mathit{C}}}_k& ={\left({\mathit{P}}_{k|k-1}^{-1}+{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\mathit{H}}_k\right)}^{-1}{\mathit{P}}_{k|k-1}^{-1}\mathbb{E}\left\{{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\eta }_k|{\widehat{\mathit{x}}}_{k|k}\right\}\hfill \\ \hfill & =-{\mathit{P}}_{k|k}{\widehat{R}}_k^{-1}{\sigma }_k^2{\mathit{M}}^{\mathrm{T}}(\mathit{M}{\widehat{\mathit{x}}}_{k|k}-{\mathit{s}}_k),\hfill \end{array}$$

(21)

where $\mathit{M}=\left[{\mathit{I}}_{2\times 2},0_{2\times 2}\right]$, and we use the formula ${\mathit{P}}_{k|k}={\left({\mathit{P}}_{k|k-1}^{-1}+{\mathit{H}}_k^{\mathrm{T}}{\widehat{R}}_k^{-1}{\mathit{H}}_k\right)}^{-1}$.

Finally, the BC–PLKF is summarized below [25]:

step 1

Predicting the state:

$${\widehat{\mathit{x}}}_{k|k-1}=\mathit{F}{\widehat{\mathit{x}}}_{k-1|k-1}^{\mathrm{BC}};$$

(22)

step 2

Predicting the covariance matrix:

$${\mathit{P}}_{k|k-1}=\mathit{F}{\mathit{P}}_{k-1|k-1}^{\mathrm{BC}}{\mathit{F}}^{\mathrm{T}}+\mathit{Q};$$

(23)

step 3

Calculating the gain matrix:

$${\mathit{K}}_k^{\mathrm{BC}}={\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}}{\left({\widehat{R}}_k+{\mathit{H}}_k{\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}}\right)}^{-1};$$

(24)

step 4

Updating the state:

$${\widehat{\mathit{x}}}_{k|k}={\widehat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k^{\mathrm{BC}}(z_k-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k-1});$$

(25)

step 5

Updating the covariance matrix:

$${\mathit{P}}_{k|k}^{\mathrm{BC}}=({\mathit{I}}_{4\times 4}-{\mathit{K}}_k^{\mathrm{BC}}{\mathit{H}}_k){\mathit{P}}_{k|k-1};$$

(26)

step 6

Bias compensation:

$${\widehat{\mathit{x}}}_{k|k}^{\mathrm{BC}}={\widehat{\mathit{x}}}_{k|k}+{\mathit{P}}_{k|k}^{\mathrm{BC}}{\widehat{R}}_k^{-1}{\sigma }_k^2{\mathit{M}}^{\mathrm{T}}(\mathit{M}{\widehat{\mathit{x}}}_{k|k}-{\mathit{s}}_k).$$

(27)

2.2.3. IV–PLKF

Unlike the BC–PLKF, the IV–PLKF tries to construct a vector ${\mathit{G}}_k$, which is chosen to be independent of ${\eta }_k$, and at the same time is strongly correlated with ${\mathit{H}}_k$. The optimal form of ${\mathit{G}}_k$ is the noise-free version of ${\mathit{H}}_k$ [25]:

$${\mathit{G}}_k^{\mathrm{opt}}=[sin{\beta }_k,-cos{\beta }_k]\mathit{M}.$$

(28)

Since the true bearing measurement ${\beta }_k$ is unavailable, a suboptimal vector based upon the estimate ${\widehat{\beta }}_k^{\mathrm{BC}}$ from BC–PLKF is chosen:

$$\begin{array}{c}{\widehat{\beta }}_k^{\mathrm{BC}}={tan}^{-1}\frac{{\widehat{\mathit{x}}}_{k|k}^{\mathrm{BC}}\left(2\right)-s_{y,k}}{{\widehat{\mathit{x}}}_{k|k}^{\mathrm{BC}}\left(1\right)-s_{x,k}},\end{array}$$

(29)

$$\begin{array}{c}{\mathit{G}}_k=\left[sin{\widehat{\beta }}_k^{\mathrm{BC}},-cos{\widehat{\beta }}_k^{\mathrm{BC}}\right]\mathit{M}.\end{array}$$

(30)

The complete IV–PLKF algorithm is [25]:

step 1

Predicting the state:

$${\widehat{\mathit{x}}}_{k|k-1}=\mathit{F}{\widehat{\mathit{x}}}_{k-1|k-1}^{\mathrm{IV}};$$

(31)

step 2

Predicting the covariance matrix:

$${\mathit{P}}_{k|k-1}=\mathit{F}{\mathit{P}}_{k-1|k-1}^{\mathrm{IV}}{\mathit{F}}^{\mathrm{T}}+\mathit{Q};$$

(32)

step 3

Calculating the gain matrix:

$${\mathit{K}}_k={\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}}{\left({\widehat{R}}_k+{\mathit{H}}_k{\mathit{P}}_{k|k-1}{\mathit{H}}_k^{\mathrm{T}}\right)}^{-1};$$

(33)

step 4

Updating the state:

$${\widehat{\mathit{x}}}_{k|k}={\widehat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k(z_k-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k-1});$$

(34)

step 5

Updating the covariance matrix:

$${\mathit{P}}_{k|k}=({\mathit{I}}_{4\times 4}-{\mathit{K}}_k{\mathit{H}}_k){\mathit{P}}_{k|k-1};$$

(35)

step 6

Bias compensation:

$${\widehat{\mathit{x}}}_{k|k}^{\mathrm{BC}}={\widehat{\mathit{x}}}_{k|k}+{\mathit{P}}_{k|k}{\widehat{R}}_k^{-1}{\sigma }_k^2{\mathit{M}}^{\mathrm{T}}(\mathit{M}{\widehat{\mathit{x}}}_{k|k}-{\mathit{s}}_k);$$

(36)

step 7

IV estimation:

$$\begin{array}{c}{\mathit{G}}_k=[sin{\widehat{\beta }}_k^{\mathrm{BC}},-cos{\widehat{\beta }}_k^{\mathrm{BC}}]\mathit{M}\end{array}$$

(37)

$$\begin{array}{c}{\mathit{K}}_k^{\mathrm{IV}}={\mathit{P}}_{k|k-1}{\mathit{G}}_k^{\mathrm{T}}{\left({\widehat{R}}_k+{\mathit{H}}_k{\mathit{P}}_{k|k-1}{\mathit{G}}_k^{\mathrm{T}}\right)}^{-1}\end{array}$$

(38)

$$\begin{array}{c}{\widehat{\mathit{x}}}_{k|k}^{\mathrm{IV}}={\widehat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k^{\mathrm{IV}}(z_k-{\mathit{H}}_k{\widehat{\mathit{x}}}_{k|k-1})\end{array}$$

(39)

$$\begin{array}{c}{\mathit{P}}_{k|k}^{\mathrm{IV}}={\mathit{P}}_{k|k-1}-{\mathit{K}}_k^{\mathrm{IV}}{\mathit{H}}_k{\mathit{P}}_{k|k-1}.\end{array}$$

(40)

We shall notice that, although the asymptotic convergence of the IV based method is verified in [26], the performance of the IV–PLKF is still limited by the BC–PLKF due to the usage of ${\widehat{\mathit{x}}}_{k|k}^{\mathrm{BC}}$ in calculating ${\widehat{\beta }}_k^{\mathrm{BC}}$. When the BC–PLKF performance deteriorates in the manoeuvring scenario, the IV–PLKF will also suffer.

2.3. The Proposed UB–PLKF and VC–PLKF

We first propose the UB–PLKF to cope with the biased estimate problem in PLKF. Then we incorporate the velocity constraint information into the UB–PLKF to construct the VC–PLKF.

2.3.1. UB–PLKF

Revisiting the matrix ${\mathit{H}}_k$ in (8), we can rewrite it as follows:

$$\begin{array}{cc}\hfill {\mathit{H}}_k=& [sin{\tilde{\beta }}_k,-cos{\tilde{\beta }}_k,0,0]\hfill \\ \hfill =& [sin{\beta }_{k}cos{n}_k,-cos{\beta }_{k}cos{n}_k,0,0]\hfill \\ & +[cos{\beta }_{k}sin{n}_k,sin{\beta }_{k}sin{n}_k,0,0]\hfill \\ \hfill \approx & [sin{\beta }_k,-cos{\beta }_k,0,0]+n_k[cos{\beta }_k,sin{\beta }_k,0,0],\hfill \end{array}$$

(41)

where we assume $cos{n}_k\approx 1$ and $sin{n}_k\approx n_k$ for small bearing noise.

Substituting (41) into (8), we get:

$$\begin{array}{c}\hfill z_k\approx [sin{\beta }_k,-cos{\beta }_k,0,0]{\mathit{x}}_k+n_k\left(\left[cos{\beta }_k,sin{\beta }_k,0,0\right]{\mathit{x}}_k-d_k\right);\end{array}$$

(42)

here we also assume that ${\eta }_k=-d_{k}sin{n}_k\approx -d_k{n}_k$. Let $m_k=[cos{\beta }_k,sin{\beta }_k,0,0]{\mathit{x}}_k-d_k$, and multiplying $1/m_k$ to both sides of (42), we have:

$${\overline{z}}_k={\overline{\mathit{H}}}_k{\mathit{x}}_k+n_k,$$

(43)

where ${\overline{z}}_k=z_k/m_k$, ${\overline{\mathit{H}}}_k=[sin{\beta }_k,-cos{\beta }_k,0,0]/m_k$. Notice that in (43), the measurement vector is independent of the noise, and the noise here is the bearing noise $n_k$, not the pseudo-linear noise ${\eta }_k$.

Based on (43), the expectation of ${\mathit{C}}_k$ is

$$\mathbb{E}\left\{{\mathit{C}}_k\right\}=\mathbb{E}\left\{{\left({\mathit{P}}_{k|k-1}^{-1}+{\overline{\mathit{H}}}_k^{\mathrm{T}}{\sigma }_k^{-2}{\overline{\mathit{H}}}_k\right)}^{-1}\right\}\mathbb{E}\left\{{\overline{\mathit{H}}}_k^{\mathrm{T}}{\sigma }_k^{-2}{n}_k\right\}.$$

(44)

It is clear that (44) equals 0 because ${\overline{\mathit{H}}}_k$ is no longer correlated with $n_k$. Then, an unbiased PLKF algorithm is obtained as follows:

step 1

Predicting the state:

$${\widehat{\mathit{x}}}_{k|k-1}=\mathit{F}{\widehat{\mathit{x}}}_{k-1|k-1}^{\mathrm{UB}};$$

(45)

step 2

Predicting the covariance matrix:

$${\mathit{P}}_{k|k-1}=\mathit{F}{\mathit{P}}_{k-1|k-1}^{\mathrm{UB}}{\mathit{F}}^{\mathrm{T}}+\mathit{Q};$$

(46)

step 3

Calculating the gain matrix:

$${\mathit{K}}_k^{\mathrm{UB}}={\mathit{P}}_{k|k-1}{\overline{\mathit{H}}}_k^{\mathrm{T}}{\left({\sigma }_k^2+{\overline{\mathit{H}}}_k{\mathit{P}}_{k|k-1}{\overline{\mathit{H}}}_k^{\mathrm{T}}\right)}^{-1};$$

(47)

step 4

Updating the state:

$${\widehat{\mathit{x}}}_{k|k}^{\mathrm{UB}}={\widehat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k^{\mathrm{UB}}({\overline{z}}_k-{\overline{\mathit{H}}}_k{\widehat{\mathit{x}}}_{k|k-1});$$

(48)

step 5

Updating the covariance matrix:

$${\mathit{P}}_{k|k}^{\mathrm{UB}}=({\mathit{I}}_{4\times 4}-{\mathit{K}}_k^{\mathrm{UB}}{\overline{\mathit{H}}}_k){\mathit{P}}_{k|k-1}.$$

(49)

Obviously, the true values of the bearing ${\beta }_k$ and $m_k$ in (43) cannot be obtained, we replace them with corresponding approximated versions ${\widehat{\beta }}_k^{\mathrm{UB}}$ and ${\widehat{m}}_k$, which are defined as follows:

$$\begin{array}{c}{\widehat{\beta }}_k^{\mathrm{UB}}={tan}^{-1}\frac{{\widehat{\mathit{x}}}_{k|k-1}\left(2\right)-s_{y,k}}{{\widehat{\mathit{x}}}_{k|k-1}\left(1\right)-s_{x,k}},\end{array}$$

(50)

$$\begin{array}{c}{\widehat{m}}_k=\left[cos{\widehat{\beta }}_k^{\mathrm{UB}},sin{\widehat{\beta }}_k^{\mathrm{UB}},0,0\right]{\widehat{\mathit{x}}}_{k|k-1}-{{\widehat{d}}_k}^{\mathrm{UB}},\end{array}$$

(51)

$$\begin{array}{c}{\widehat{d}}_k^{\mathrm{UB}}=\parallel {\widehat{\mathit{x}}}_{k|k-1}(1:2)-{\mathit{s}}_k\parallel .\end{array}$$

(52)

We emphasise here that the main idea behind the IV–PLKF and the UB–PLKF is similar. They both try to construct a noise-free measurement vector. However, the IV–PLKF performance is limited by the BC–PLKF, while the UB–PLKF does not suffer from this. The advantages of the UB–PLKF will be verified in the simulation part.

2.3.2. VC–PLKF

Based on the UB–PLKF, we develop its velocity constrained version in this part. First, we shall handle an optimisation problem with an equality constraint. Let ${\mathit{v}}_{k|k}={\widehat{\mathit{x}}}_{k|k}^{\mathrm{UB}}$(3:4) and ${\mathit{e}}_{v,k}={\mathit{v}}_k-{\mathit{v}}_{k|k}$, we have:

$$\begin{array}{cc}\hfill & \underset{{\mathit{K}}_{v,k}}{min}\mathbb{E}\left\{{\mathit{e}}_{v,k}^{\mathrm{T}}{\mathit{e}}_{v,k}\right\}\hfill \\ \hfill & s_{·}{t}_{·}\parallel {\mathit{v}}_{k|k}\parallel =v,\hfill \end{array}$$

(53)

where ${\mathit{K}}_k^{\mathrm{UB}}={\left[{\mathit{K}}_{p,k}^{\mathrm{T}},{\mathit{K}}_{v,k}^{\mathrm{T}}\right]}^{\mathrm{T}}$, and ${\mathit{K}}_{v,k}\in {\mathbb{R}}^{2\times 1}$. $v$ is the velocity constraint, which is a positive constant. Note that $\mathbb{E}\{{\mathit{e}}_{v,k}^{\mathrm{T}}{\mathit{e}}_{v,k}\}=tr\{{\mathit{P}}_{vv,k}^{+}\}$, and ${\mathit{P}}_{k|k}^{\mathrm{UB}}=\left[\begin{array}{cc}{\mathit{P}}_{pp,k}^{+}& {\mathit{P}}_{pv,k}^{+}\\ {\mathit{P}}_{vp,k}^{+}& {\mathit{P}}_{vv,k}^{+}\end{array}\right]$. Then (53) can be rewritten as

$$\begin{array}{cc}\hfill & \underset{{\mathit{K}}_{v,k}}{min}tr\{{\mathit{P}}_{vv,k}^{+}\}\hfill \\ \hfill & s_{·}{t}_{·}\parallel {\mathit{v}}_{k|k}\parallel =v.\hfill \end{array}$$

(54)

Let ${\mathit{v}}_{k|k-1}={\widehat{\mathit{x}}}_{k|k-1}$(3:4) in (45), and according to the Kalman formula, we have:

$${\mathit{v}}_{k|k}={\mathit{v}}_{k|k-1}+{\mathit{K}}_{v,k}{ϵ}_k,$$

(55)

where ${ϵ}_k={\overline{z}}_k-{\overline{\mathit{H}}}_k{\widehat{\mathit{x}}}_{k|k-1}^{\mathrm{UB}}$. Substituting (55) into the velocity constraint in (54), we have:

$${ϵ}_k^2{\mathit{K}}_{v,k}^{\mathrm{T}}{\mathit{K}}_{v,k}+2{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{K}}_{v,k}{ϵ}_k+{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{v}}_{k|k-1}-v^2=0.$$

(56)

According to the Joseph formula [33], the update formula of the partitioned $posterior$ covariance matrix can be written as:

$${\mathit{P}}_{vv,k}^{+}={\mathit{P}}_{vv,k}^{-}-{\mathit{K}}_{v,k}{\overline{\mathit{H}}}_k{\mathit{P}}_{2,k}-{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}{\mathit{K}}_{v,k}^{\mathrm{T}}+{\mathit{K}}_{v,k}{W}_k{\mathit{K}}_{v,k}^{\mathrm{T}},$$

(57)

where

$$\begin{array}{cc}\hfill {\mathit{P}}_{k|k-1}=& \left[{\mathit{P}}_{1,k},{\mathit{P}}_{2,k}\right]\hfill \\ \hfill =& \left[\begin{array}{cc}{\mathit{P}}_{pp,k}^{-}& {\mathit{P}}_{pv,k}^{-}\\ {\mathit{P}}_{vp,k}^{-}& {\mathit{P}}_{vv,k}^{-}\end{array}\right]\hfill \end{array}$$

(58)

and

$$W_k={\overline{\mathit{H}}}_k{\mathit{P}}_{k|k-1}{\overline{\mathit{H}}}_k^{\mathrm{T}}+{\sigma }_k^2.$$

(59)

Utilising (56) and (57) and the Lagrange multiplier method, we can construct the performance index $j_k$ as follows:

$$\begin{array}{cc}\hfill j_k=& tr\left\{{\mathit{P}}_{vv,k}^{-}-{\mathit{K}}_{v,k}{\overline{\mathit{H}}}_k{\mathit{P}}_{2,k}-{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}{\mathit{K}}_{v,k}^{\mathrm{T}}+{\mathit{K}}_{v,k}{W}_k{\mathit{K}}_{v,k}^{\mathrm{T}}\right\}\hfill \\ \hfill & +{\lambda }_k\left[{ϵ}_k^2{\mathit{K}}_{v,k}^{\mathrm{T}}{\mathit{K}}_{v,k}+2{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{K}}_{v,k}{ϵ}_k+{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{v}}_{k|k-1}-v^2\right].\hfill \end{array}$$

(60)

Taking the first derivative of $j_k$ with respect to ${\mathit{K}}_{v,k}$ and setting it to zero yields:

$$-{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}+{\mathit{K}}_{v,k}{W}_k+{\lambda }_k({\mathit{v}}_{k|k-1}{ϵ}_k+{\mathit{K}}_{v,k}{ϵ}_k^2)=0.$$

(61)

Then we have the first-order condition:

$${\mathit{K}}_{v,k}=\frac{{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}-{\lambda }_k{\mathit{v}}_{k|k-1}{ϵ}_k}{W_k+{\lambda }_k{ϵ}_k^2}.$$

(62)

Substituting (62) into (56), and according to [27], the scalar equation with ${\lambda }_k$ can be obtained as:

$$\begin{array}{c}\hfill -{\lambda }_k^2{\widetilde{ϵ}}_k^2{v}^2-2{\lambda }_k{\widetilde{ϵ}}_k{v}^2+\left(\frac{{ϵ}_k^2{\overline{\mathit{H}}}_k{\mathit{P}}_{2,k}{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}}{W_k^2}+\frac{2{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}{ϵ}_k}{W_k}+{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{v}}_{k|k-1}-v^2\right)=0,\end{array}$$

(63)

where ${\widetilde{ϵ}}_k={ϵ}_k^2/W_k$.

Then, ${\lambda }_k$ can be written as

$${\lambda }_k=\frac{-b-\sqrt{b^2-4ac}}{2a},$$

(64)

where

$$\begin{array}{c}\hfill a=-v^2{\widetilde{ϵ}}_k^2,\end{array}$$

(65)

$$\begin{array}{c}\hfill b=-2{\widetilde{ϵ}}_k{v}^2,\end{array}$$

(66)

$$c={ϵ}_k^2{\overline{\mathit{H}}}_k{\mathit{P}}_{2,k}{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}/W_k^2+2{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{P}}_{2,k}^{\mathrm{T}}{\overline{\mathit{H}}}_k^{\mathrm{T}}{ϵ}_k/W_k+{\mathit{v}}_{k|k-1}^{\mathrm{T}}{\mathit{v}}_{k|k-1}-v^2.$$

(67)

Notice that we use $-b-\sqrt{b^2-4ac}$, not $-b\pm \sqrt{b^2-4ac}$, because the minimum performance index $j_k$ occurs when the minus sign is chosen according to [27].

Substituting (64)–(67) into (62) we get:

$${\mathit{K}}_{v,k}^{*}={\mathit{K}}_{v,k}+\left(\frac{v}{\parallel {\mathit{v}}_{k|k}\parallel }-1\right)\frac{{\mathit{v}}_{k|k}}{{ϵ}_k},$$

(68)

where the asterisk was added to distinguish from the unconstrained form ${\mathit{K}}_{v,k}$. (see Appendix A).

Now we have the VC–PLKF with an equality constraint as follows:

step 1

Predicting the state:

$${\widehat{\mathit{x}}}_{k|k-1}=\mathit{F}{\widehat{\mathit{x}}}_{k-1|k-1}^{\mathrm{VC}};$$

(69)

step 2

Predicting the covariance matrix:

$${\mathit{P}}_{k|k-1}=\mathit{F}{\mathit{P}}_{k-1|k-1}^{\mathrm{VC}}{\mathit{F}}^{\mathrm{T}}+\mathit{Q};$$

(70)

step 3

Calculating the gain matrix for UB–PLKF:

$${\mathit{K}}_k^{\mathrm{UB}}={\mathit{P}}_{k|k-1}{\overline{\mathit{H}}}_k^{\mathrm{T}}/\left({\sigma }_k^2+{\overline{\mathit{H}}}_k{\mathit{P}}_{k|k-1}{\overline{\mathit{H}}}_k^{\mathrm{T}}\right);$$

(71)

step 4

Calculating the innovation:

$${ϵ}_k={\overline{z}}_k-{\overline{\mathit{H}}}_k{\widehat{\mathit{x}}}_{k|k-1};$$

(72)

step 5

Updating the state:

$${\widehat{\mathit{x}}}_{k|k}^{\mathrm{UB}}={\widehat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k^{\mathrm{UB}}{ϵ}_k;$$

(73)

step 6

Updating the covariance for UB–PLKF:

$${\mathit{P}}_{k|k}^{\mathrm{UB}}=({\mathit{I}}_{4\times 4}-{\mathit{K}}_k^{\mathrm{UB}}{\overline{\mathit{H}}}_k){\mathit{P}}_{k|k-1};$$

(74)

step 7

Constructing the VC–PLKF:

$$\begin{array}{c}{\mathit{v}}_{k|k}={\widehat{\mathit{x}}}_{k|k}^{\mathrm{UB}}(3:4)\end{array}$$

(75)

$$\begin{array}{c}{\mathit{K}}_{v,k}^{*}={\mathit{K}}_k^{\mathrm{UB}}(3:4)+\left(\frac{\mathit{v}}{\parallel {\mathit{v}}_{k|k}\parallel }-1\right)\frac{{\mathit{v}}_{k|k}}{{ϵ}_k}\end{array}$$

(76)

$$\begin{array}{c}{\mathit{K}}_k^{\mathrm{VC}}=\left[{\mathit{K}}_k^{\mathrm{UB}}(1:2);{\mathit{K}}_{v,k}^{*}\right]\end{array}$$

(77)

$$\begin{array}{c}{\widehat{\mathit{x}}}_{k|k}^{\mathrm{VC}}={\widehat{\mathit{x}}}_{k|k-1}+{\mathit{K}}_k^{\mathrm{VC}}{ϵ}_k\end{array}$$

(78)

$$\begin{array}{c}{\mathit{P}}_{k|k}^{\mathrm{VC}}=({\mathit{I}}_{4\times 4}-{\mathit{K}}_k^{\mathrm{VC}}{\overline{\mathit{H}}}_k){\mathit{P}}_{k|k-1}.\end{array}$$

(79)

In most cases, however, what we know is the target velocity range, and this means we should handle a problem with inequality constraints. To translate the inequality constraint into the equality constraint, we adopt the rule in [29], that is,

$${\widehat{\mathit{x}}}_{k|k}^{\mathrm{VC}}=\left\{\begin{array}{cc}{\widehat{\mathit{x}}}_{k|k}^{\mathrm{VC}}{\mid }_{v=v_{\max }}\hfill & \mathrm{if}\parallel {\mathit{v}}_{k|k}\parallel >v_{\max },\hfill \\ {\widehat{\mathit{x}}}_{k|k}^{\mathrm{VC}}{\mid }_{v=v_{\min }}\hfill & \mathrm{if}\parallel {\mathit{v}}_{k|k}\parallel <v_{\min },\hfill \\ {\widehat{\mathit{x}}}_{k|k}^{\mathrm{VC}}={\widehat{\mathit{x}}}_{k|k}^{\mathrm{UB}}\hfill & \mathrm{if}{v}_{\min }\le \parallel {\mathit{v}}_{k|k}\parallel \le v_{\max }.\hfill \end{array}\right.$$

(80)

Here, $v_{\min }$ and $v_{\max }$ denote the lower and upper bounds of the velocity, respectively. Equation (80) means that if $\parallel {\mathit{v}}_{k|k}\parallel \in [v_{\min },v_{\max }]$, the steps after (75) are avoided, and we just output ${\widehat{\mathit{x}}}_{k|k}^{\mathrm{VC}}={\widehat{\mathit{x}}}_{k|k}^{\mathrm{UB}}$ and ${\mathit{P}}_{k|k}^{\mathrm{VC}}={\mathit{P}}_{k|k}^{\mathrm{UB}}$. Otherwise, if $\parallel {\mathit{v}}_{k|k}\parallel$ is less than $v_{\min }$ or greater than $v_{\max }$, we do the VC–PLKF with the equality constraint with $v=v_{\min }$ or $v=v_{\max }$, respectively.

We shall emphasise that, although the VC–PLKF and the algorithms in [29] all make use of the velocity constraints, the VC–PLKF constructs a norm-constrained Kalman filter, which is an iterative algorithm; however, algorithms in [29] are all based on the batch algorithms, which are computationally expensive and can hardly handle the manoeuvring target tracking problem.

3. Results

In this section, the proposed UB–PLKF and VC–PLKF are compared with the BC–PLKF and the IV–PLKF via Monte Carlo (MC) simulations. We adopt the root mean square error (RMSE) and the time-averaged RMSE as the performance metrics.

Assuming that ${\widehat{\mathit{x}}}_{k|k}^i$ is the state vector that we estimate at k via i th MC simulation. We can define the RMSEs obtained from $M=300$ MC simulations as follows:

$$\begin{array}{c}\hfill {\mathrm{RMSE}}_k^{\mathrm{pos}}={\left(\frac{1}{M}\sum _{i=1}^M\parallel {\widehat{\mathit{p}}}_{k|k}^i-{\mathit{p}}_k{\parallel }^2\right)}^{1/2}\end{array}$$

(81)

$$\begin{array}{c}\hfill {\mathrm{RMSE}}_k^{\mathrm{vel}}={\left(\frac{1}{M}\sum _{i=1}^M\parallel {\widehat{\mathit{v}}}_{k|k}^i-{\mathit{v}}_k{\parallel }^2\right)}^{1/2}\end{array}$$

(82)

where ${\widehat{\mathit{p}}}_{k|k}^i={\widehat{\mathit{x}}}_{k|k}^i(1:2)$, ${\widehat{\mathit{v}}}_{k|k}^i={\widehat{\mathit{x}}}_{k|k}^i$(3:4).

The time-averaged RMSEs are also adopted and are computed as [25]:

$$\begin{array}{c}\hfill {\mathrm{RMSE}}_{\mathrm{avg}}^{\mathrm{pos}}={\left(\frac{1}{MU}\sum _{i=1}^M\sum _{k=P}^N\parallel {\widehat{\mathit{p}}}_{k|k}^i-{\mathit{p}}_k{\parallel }^2\right)}^{1/2}\end{array}$$

(83)

$$\begin{array}{c}\hfill {\mathrm{RMSE}}_{\mathrm{avg}}^{\mathrm{vel}}={\left(\frac{1}{MU}\sum _{i=1}^M\sum _{k=P}^N\parallel {\widehat{\mathit{v}}}_{k|k}^i-{\mathit{v}}_k{\parallel }^2\right)}^{1/2},\end{array}$$

(84)

where $U=N-P+1$ is the effective time that takes into account the computation of time-averaged RMSEs, $N=350$ is the total number of time index k, and $P=60$ is chosen to eliminate the influence of the initial error according to [25].

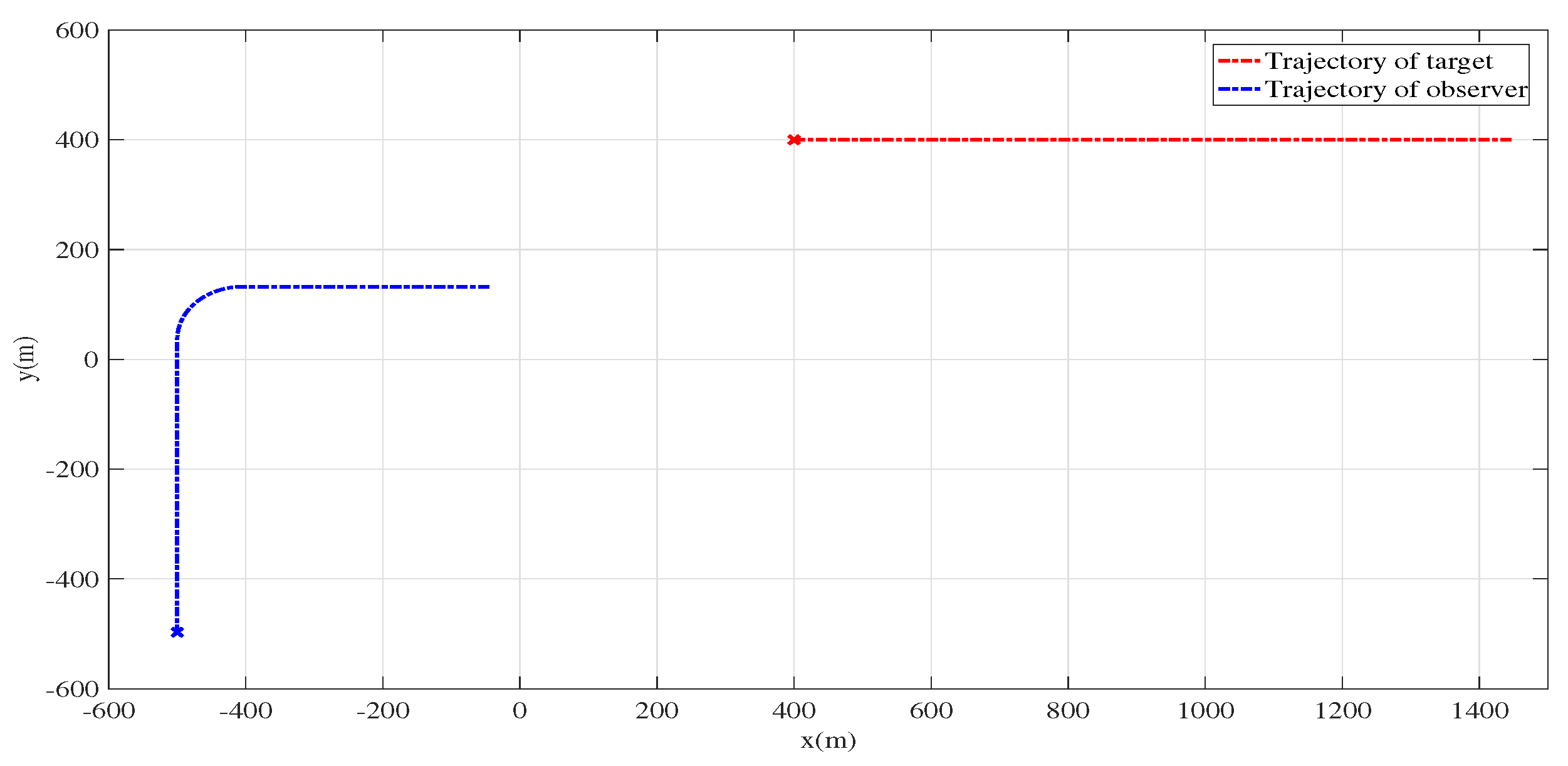
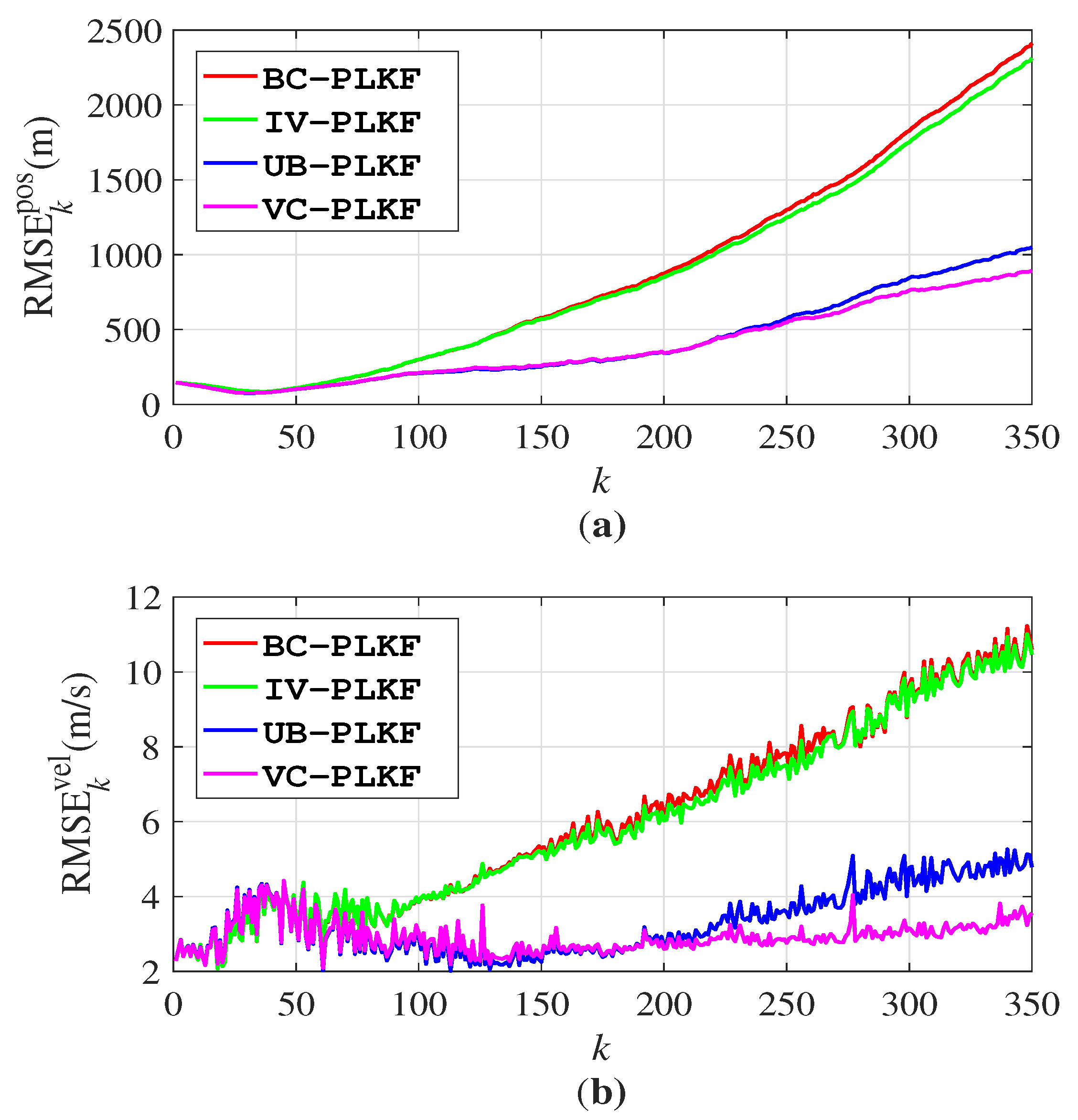
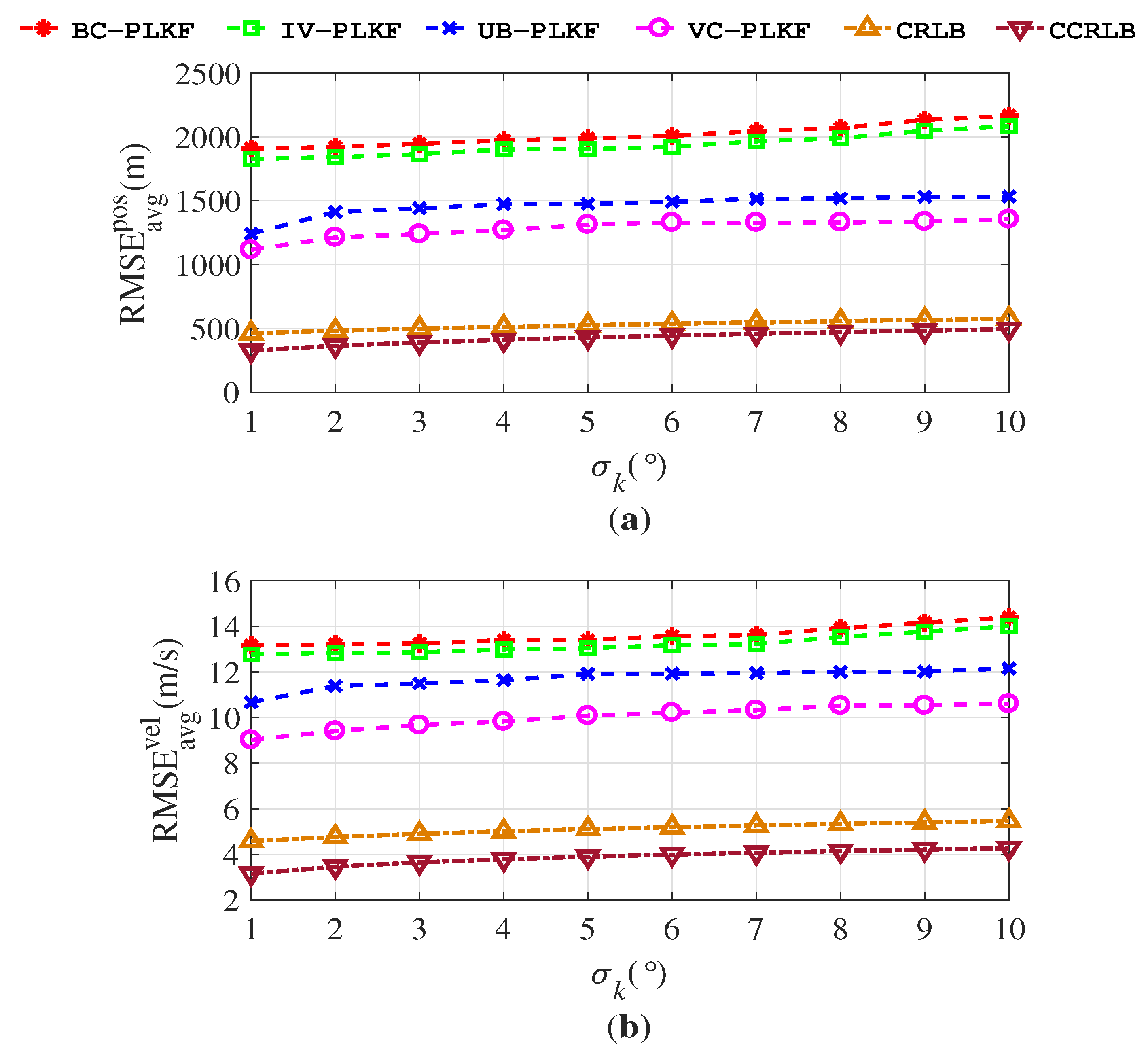
3.1. Scenario 1: Non-Manoeuvring Target Tracking

We first test the filters’ performance against poor initialisation and poor target sensor geometry with a non-manoeuvring scenario, which is given in Figure 2. The initial state vector of the target is ${\mathit{x}}_0={[400,400,3,0]}^{\mathrm{T}}$, and to test the performance against poor initialisation, we set the initial state of the estimate ${\widehat{\mathit{x}}}_{0|-1}$ Gaussian, and its mean is ${[500,300,2,-1]}^{\mathrm{T}}$ and the covariance matrix is ${\mathit{P}}_{0|-1}=\mathrm{diag}(625,625,4,4)$. The observer starts at ${[-500,-500]}^{\mathrm{T}}\mathrm{m}$ and follows a linear path with a constant speed of ${[0,3]}^{\mathrm{T}}\mathrm{m}/\mathrm{s}$ for the first 180 scans. Then, it executes a coordinated turn for 50 scans with a turn rate of $1.8{}^{\circ }/\mathrm{s}$ followed by 120 scans, where it moves in a straight line with velocity ${[3,0]}^{\mathrm{T}}\mathrm{m}/\mathrm{s}$. Notice that at the last 120 scans, the bearing rate between the target and the observer is 0, which constructs the case of poor target sensor geometry. $q_x$ and $q_y$ in (3) are $q_x=q_y=0.2{\mathrm{m}}^2/{\mathrm{s}}^3$. The standard deviation ${\sigma }_k=5^{\circ }$ is assumed to be time invariant. The upper bound of the velocity is $v_{\max }=6\mathrm{m}/\mathrm{s}$, while the lower bound is $v_{\min }=1\mathrm{m}/\mathrm{s}$.

Figure 3 shows the RMSEs for different algorithms. The IV–PLKF and BC–PLKF show similar performances in RMSEs of both the position and velocity, and so do the UB–PLKF and VC–PLKF. However, the biases of the UB–PLKF and VC–PLKF are much smaller than the BC–PLKF and IV–PLKFs, and this suggests that splitting the noise $n_k$ away from the ${\mathit{H}}_k$ is more effective than subtracting the bias from PLKF. Divergence problems have not been present in RMSEs of UB–PLKF and VC–PLKF, and this suggests that the proposed UB–PLKF and VC–PLKF can work well in conditions of poor initialisation and poor target sensor geometry.

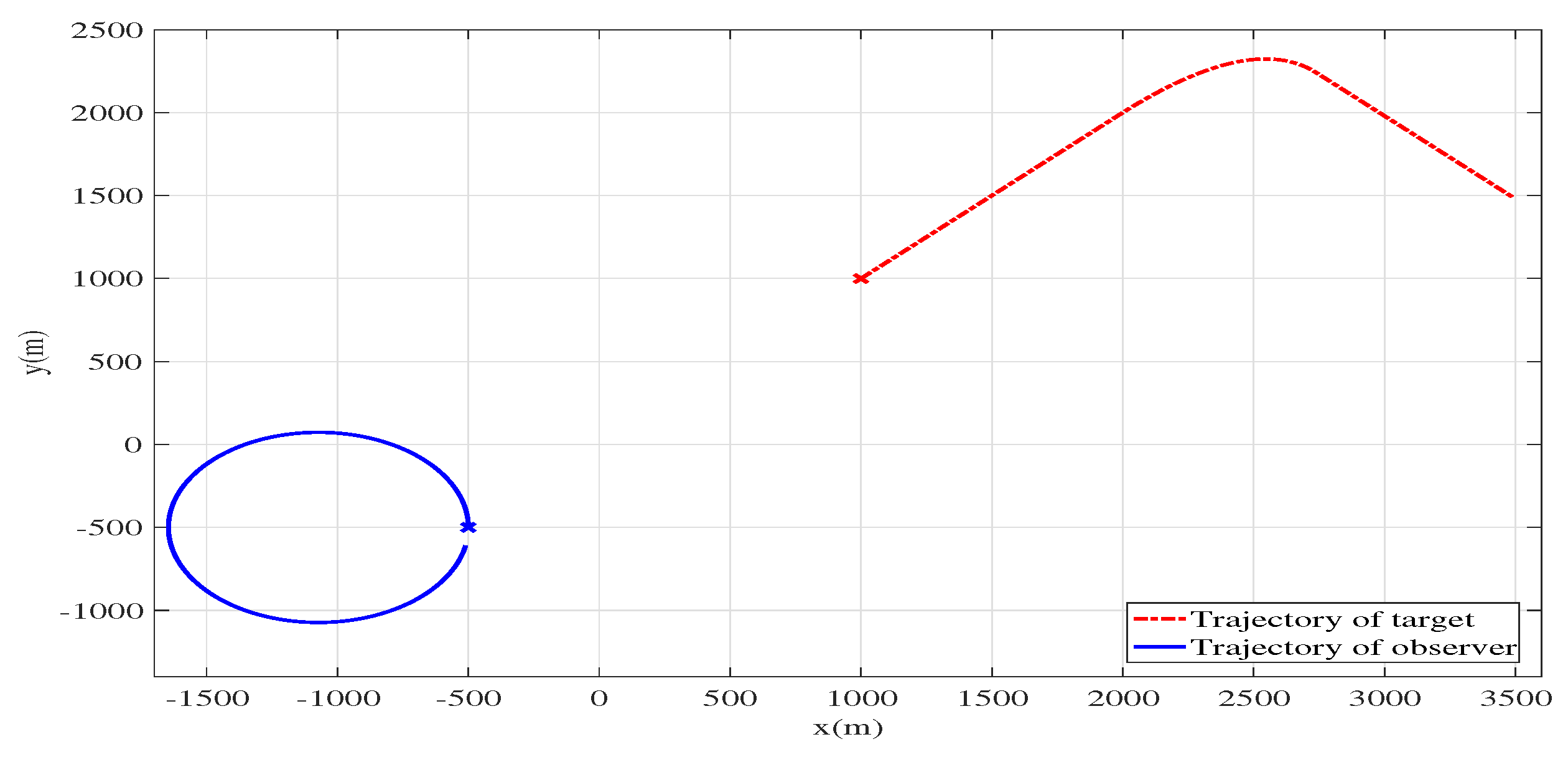
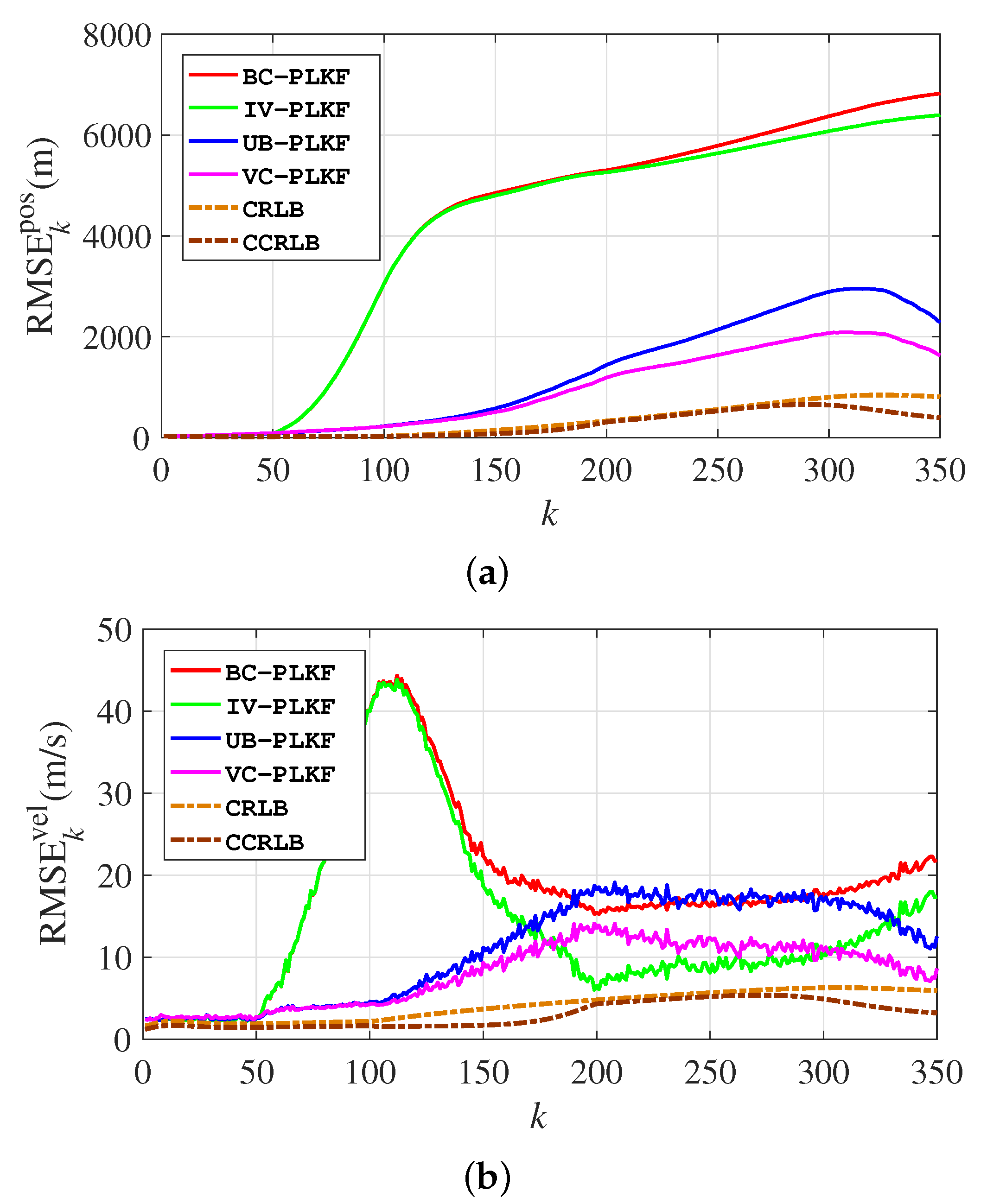
3.2. Scenario 2: Manoeuvring Target Tracking

Figure 4 represents the geometry of scenario 2. The initial state of the target is ${\mathit{x}}_0={[1000,1000,10,10]}^{\mathrm{T}}$, and it moves in a straight line for the first 100 scans. Then it performs a constant acceleration movement [32] with acceleration ${[-0.05,-0.15]}^{\mathrm{T}}$$\mathrm{m}/{\mathrm{s}}^2$ in the following 100 scans. In the final 150 scans, it moves along a straight line at a constant speed ${[5,-5]}^{\mathrm{T}}\mathrm{m}/\mathrm{s}$. The initial state of the estimate ${\widehat{\mathit{x}}}_{0|-1}$ is a Gaussian random vector with mean ${[1000,1000,10,10]}^{\mathrm{T}}$, and the rest of the settings are the same as those of scenario 1, except that $v_{\min }=5\mathrm{m}/\mathrm{s}$ and $v_{\max }=16\mathrm{m}/\mathrm{s}$. The observer begins at ${[-500,-500]}^{\mathrm{T}}\mathrm{m}$ with velocity ${[0,9.45]}^{\mathrm{T}}\mathrm{m}/\mathrm{s}$, and executes a coordinated turn for the whole 350 scans with a turn rate of $-1.8{}^{\circ }/\mathrm{s}$, where “−” means the anticlockwise direction. We also adopt the Cramer–Rao lower bound (CRLB) [34] and the constrained Cramer–Rao lower bound (CCRLB) [35] in this scenario to evaluate the performance of the four algorithms (the derivation of CRLB and CCRLB can be found in Appendix B).

Figure 5 plots the RMSEs and CRLB for the four algorithms. The RMSEs of the VC–PLKF are closest to the CRLB and CCRLB, followed by UB–PLKF. We also find that the velocity RMSEs of UB–PLKF and VC–PLKF decrease after the manoeuvring, which means that the proposed algorithms are more adaptable to abrupt changes in the velocity. Figure 6 shows the time-averaged RMSEs for ${\sigma }_k\in \{1^{\circ },\cdots ,{10}^{\circ }\}$; it also verifies that the VC–PLKF and UB–PLKF outperform the BC–PLKF and IV–PLKF. The time-averaged RMSEs of the four algorithms are also flat, which proves that the four algorithms all have good robustness to the different levels of the bearing noise.

To test the performance of the proposed algorithms in the case in which there exists a noise statistics mismatch, we again assume that the deviation ${\sigma }_k$ is time-varying. When $k<51$ or $k>201$, ${\sigma }_k=3^{\circ }$, whereas ${\sigma }_k=7^{\circ }$ at the other times. The other settings remain unchanged. Figure 7 shows the RMSEs of different algorithms. It is clear that the position RMSEs of the BC–PLKF and IV–PLKF get worse when the mismatch begins, and retain high levels the rest of the time. However, the mismatch has little influence on the proposed UB–PLKF and VC–PLKF. The shapes of their positions and velocity RMSE curves are basically the same as those in Figure 5. This verifies that the UB–PLKF and VC–PLKF are more robust to the noise statistics mismatch. When it comes to the velocity RMSEs, some differences may occur. We can find that, although the velocity RMSEs of the IV–PLKF gets worse after the mismatch begins, it becomes smaller after the 100th scan. The possible reason is that at the 100th scan, the target starts to manoeuvre, and at this time, large measurement errors occur. So the large variance may more adaptable to this case. However, after the 201st scan, the velocity RMSEs of the BC–PLKF and IV–PLKF get worse again and finally exceed the RMSEs of UB–PLKF and VC–PLKF.

Table 1. Settings for 4 different cases in VC–PLKF.

	Case 1	Case 2	Case 3	Case 4
$v_{\max }$(m/s)	21	19	17	16
$v_{\min }$(m/s)	1	3	5	7

lists four different cases of velocity constraints to compare the influence of different constraints in VC–PLKF. The time-averaged RMSEs are given by Figure 8. The closer the constraint is to the true speed, the smaller the RMSE of the VC–PLKF is. However, this improvement is at the cost of reducing the application scope of the algorithm. Thus, the choices of the upper and lower bounds depend on our prior knowledge of the target, otherwise it is suggested to choose a large range of constraints.

4. Discussion

Section 3 compares the algorithms’ performances in terms of RMSE and time-averaged RMSE. Figure 3 and Figure 5 show that the proposed algorithms outperform the BC–PLKF and IV–PLKF in [25] both in non-manoeuvring and manoeuvring scenarios. This is not surprising since the BC–PLKF just subtracts the approximated bias and does not split the noise away from the ${\mathit{H}}_k$. When the target manoeuvres or the target sensor geometry becomes poor, the approximated bias may not be accurate, which leads to huge biases in BC–PLKF. The IV–PLKF also suffers from this, since it utilizes the results of the BC–PLKF to calculate the approximated bearings. However, the proposed algorithms are unbiased and can be rapidly adapted to the changes in the scenarios.

Table 2. Normalised runtimes for the 4 algorithms.

Algorithm	BC–PLKF	IV–PLKF	UB–PLKF	VC–PLKF
Runtime	1.35	2.12	1	1.21

records the runtimes of the four algorithms, which are normalised by the UB–PLKF runtime. It shows that the UB–PLKF costs the least time among the four improved algorithms because it avoids the bias compensation step in BC–PLKF. The VC–PLKF and BC–PLKF have similar complexity, while the IV–PLKF takes the longest time to run. Considering the RMSEs, the time-averaged RMSEs and the runtimes, we can draw the conclusion that the proposed UB–PLKF and VC–PLKF outperform the BC–PLKF and IV–PLKF, both in terms of tracking accuracy and real-time application.

In this paper, we assume that the statistical characteristics of noise are known a priori; however, this is not true in practical application. So, future research may contain the construction of the UB–PLKF in terms of the unknown statistical characteristics of noise by variational inference [36].

5. Conclusions

To handle the bias problem in the traditional PLKF algorithm, we propose the UB–PLKF algorithm. Unlike the existing BC–PLKF and IV–PLKF, the UB–PLKF splits the noise away from the measurement vector directly, which can lead to an unbiased estimate. We then develop the VC–PLKF by solving a partial norm-constrained optimisation problem with an inequality relation to improve the performance of UB–PLKF. Simulation results show that the UB–PLKF and VC–PLKF outperform the BC–PLKF and IV–PLKF according to the RMSE, the time-averaged RMSE, and the computational complexity. The results also verify that the proposed algorithms can adapt to the abrupt changes of the target velocity, and thus are more suitable for the manoeuvring target tracking scenario.