Hyperanalytic Wavelet-Based Robust Edge Detection
Abstract
1. Introduction
- (a)
- To have a low error rate,
- (b)
- The edge points should be well localized,
- (c)
- To circumvent the possibility to have multiple responses for a single edge.
- (1)
- To reduce the sensitivity of the edge detector to noise, a Gaussian filter is applied first;
- (2)
- To compute the gradient magnitude and direction, the derivative operators are used;
- (3)
- To get edges with a one-pixel width, non-maximum suppression is used;
- (4)
- To eliminate weak edges, the threshold with hysteresis is applied.
1.1. Motivation
- (A)
- The wavelet transforms (WT) are sparse representations of images and can be implemented with fast algorithms [6];
- (B)
- There is an inter-scale dependency between the wavelet detail coefficients from two consecutive scales [8]. In the following, the parent coefficients will be indexed by 1 and the child coefficients will be indexed by 2;
- (C)
- The probability density functions (pdf) of wavelet detail coefficients or parent-children pairs of wavelet detail coefficients are invariant to input image transformations [9];
- (D)
- The WT decorrelates the noise component of the input image [6];
- (E)
- (F)
- The CoWT have good directional selectivity and low redundancy.
1.2. Contribution
1.3. Related Work
- 1.
- Detecting the step and linear edges from images corrupted by mixed noise (exponential and impulse) without smoothing. The authors of [15] substituted the Gaussian smoothing filter with a statistical classification technique;
- 2.
- Detecting thin-line edges, as a series of outliers using the Dixon’s r-test;
- 3.
- Suppressing the spurious edge elements and connecting the isolated missing edge elements.
2. Materials and Methods
2.1. Hyperanalytic Wavelet Transform
- Since wavelets are bandpass functions, the wavelet coefficients tend to oscillate around singularities;
- The wavelet coefficients oscillation pattern around singularities is significantly perturbed even by small shift of the signal;
- The wide spacing of the wavelet coefficient samples (the calculation of the wavelet coefficients involves interleaved sampling operations in discrete time and high-pass filtering), resulting in a substantial aliasing. The inverse DWT transformation (IDWT) cancels this aliasing, of course, if the wavelet coefficients are not changed. Any wavelet coefficient processing operation, as seen in thresholding; filtering; or quantization, leading to artifacts in the reconstructed signal.
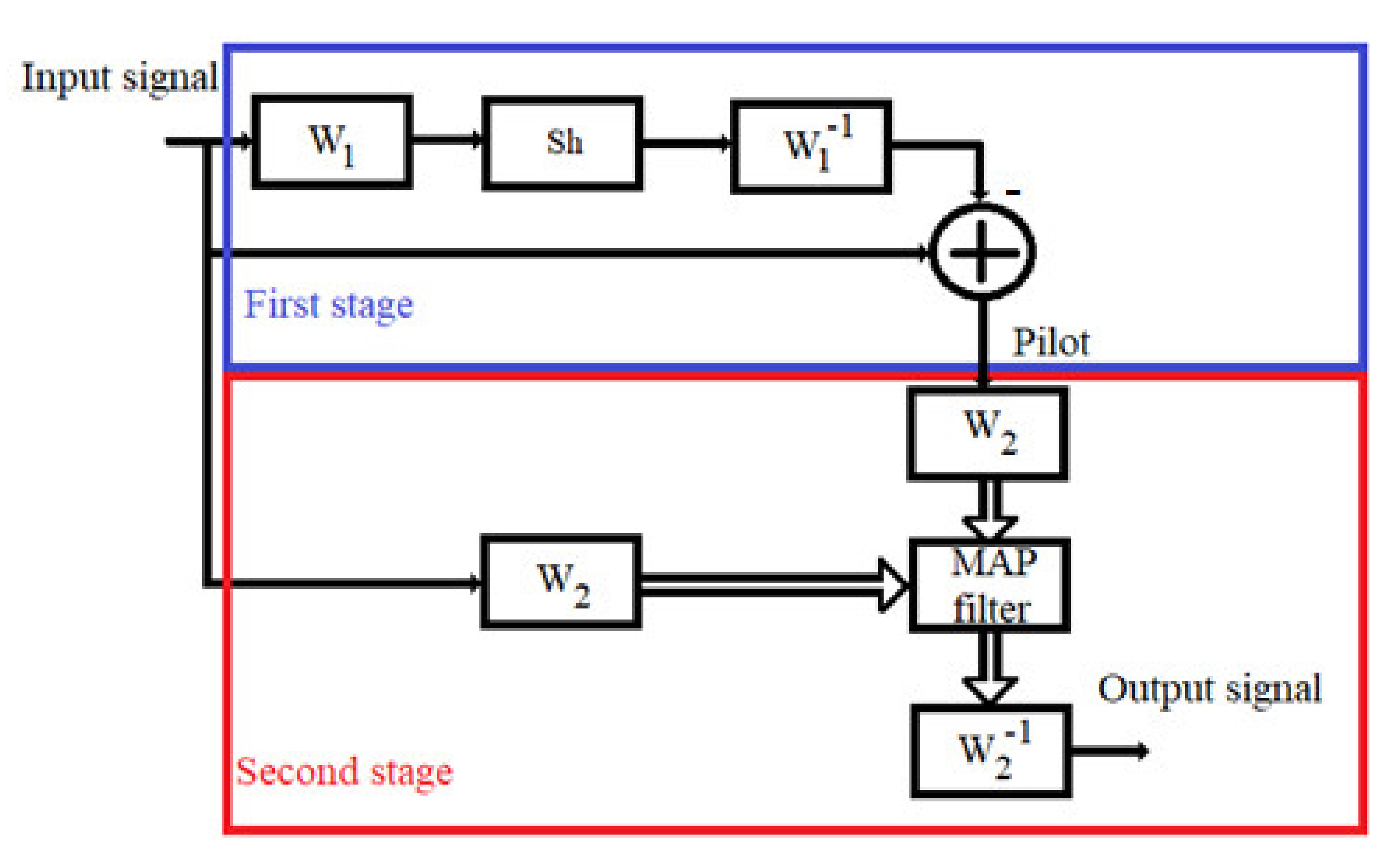
2.2. Global MAP Filters Applied in Wavelet Domain
- 1.
- Computation of the WT of the observation: and separation of approximation and detail coefficients;
- 2.
- Non-linear filtering of detail coefficients and restructuration of WT by the concatenation of approximation coefficients with the new detail coefficients;
- 3.
- Computation of the inverse WT (IWT).
Bishrink Filter
2.3. Multiplicative Noise
2.4. Proposed Denoising Method
2.5. Performance Measures
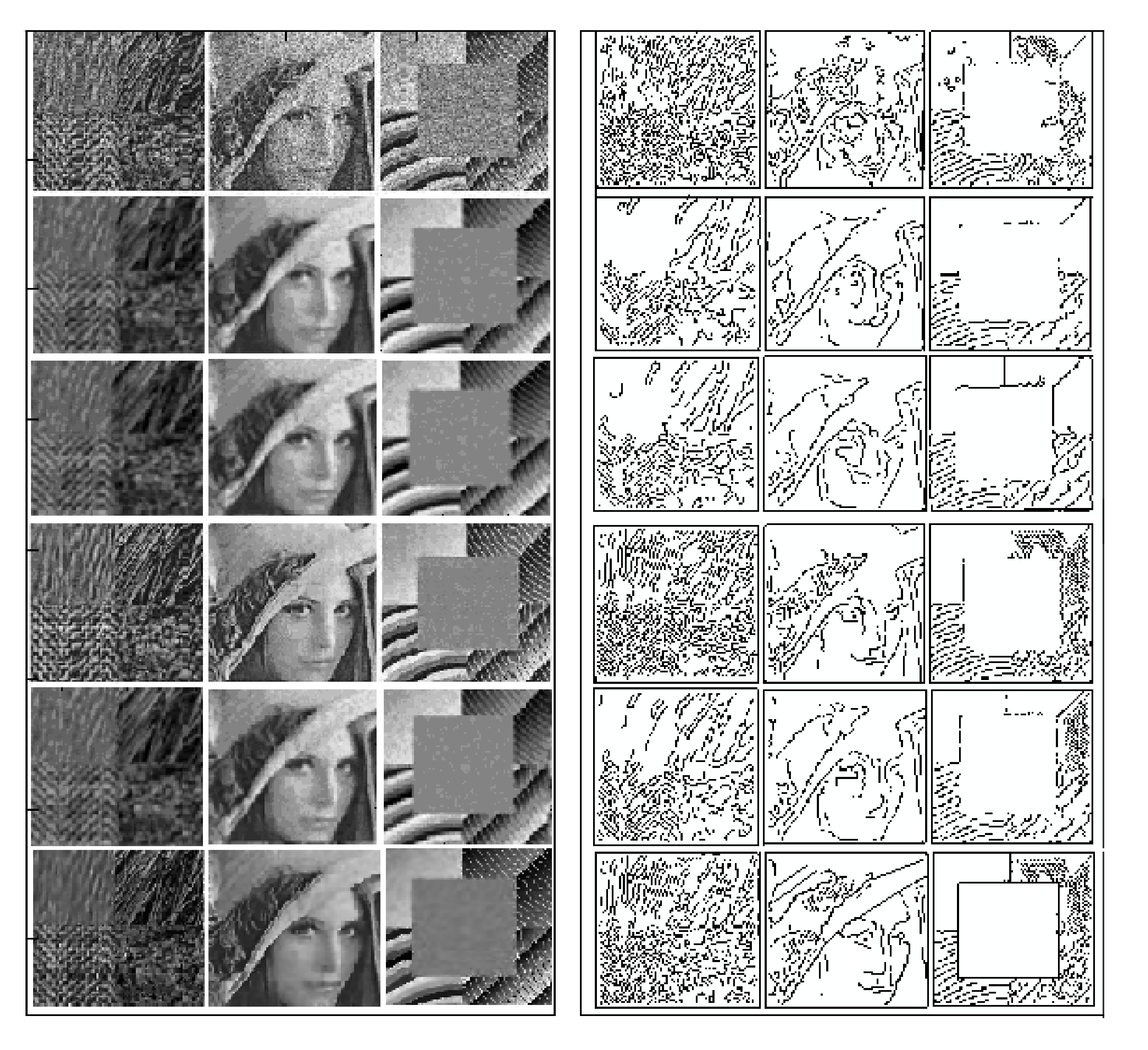
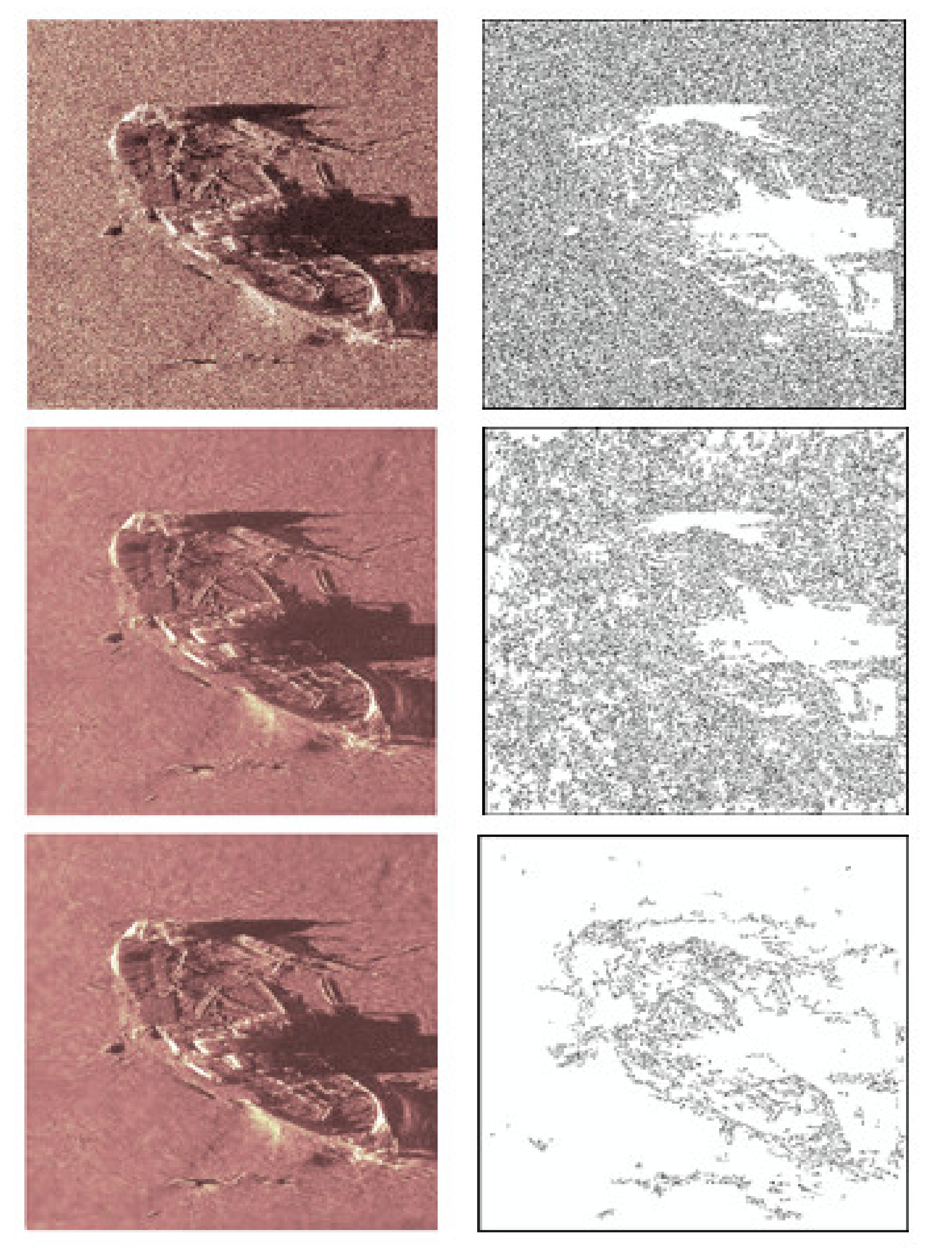
3. Results
3.1. Images Affected by Synthesized Noise
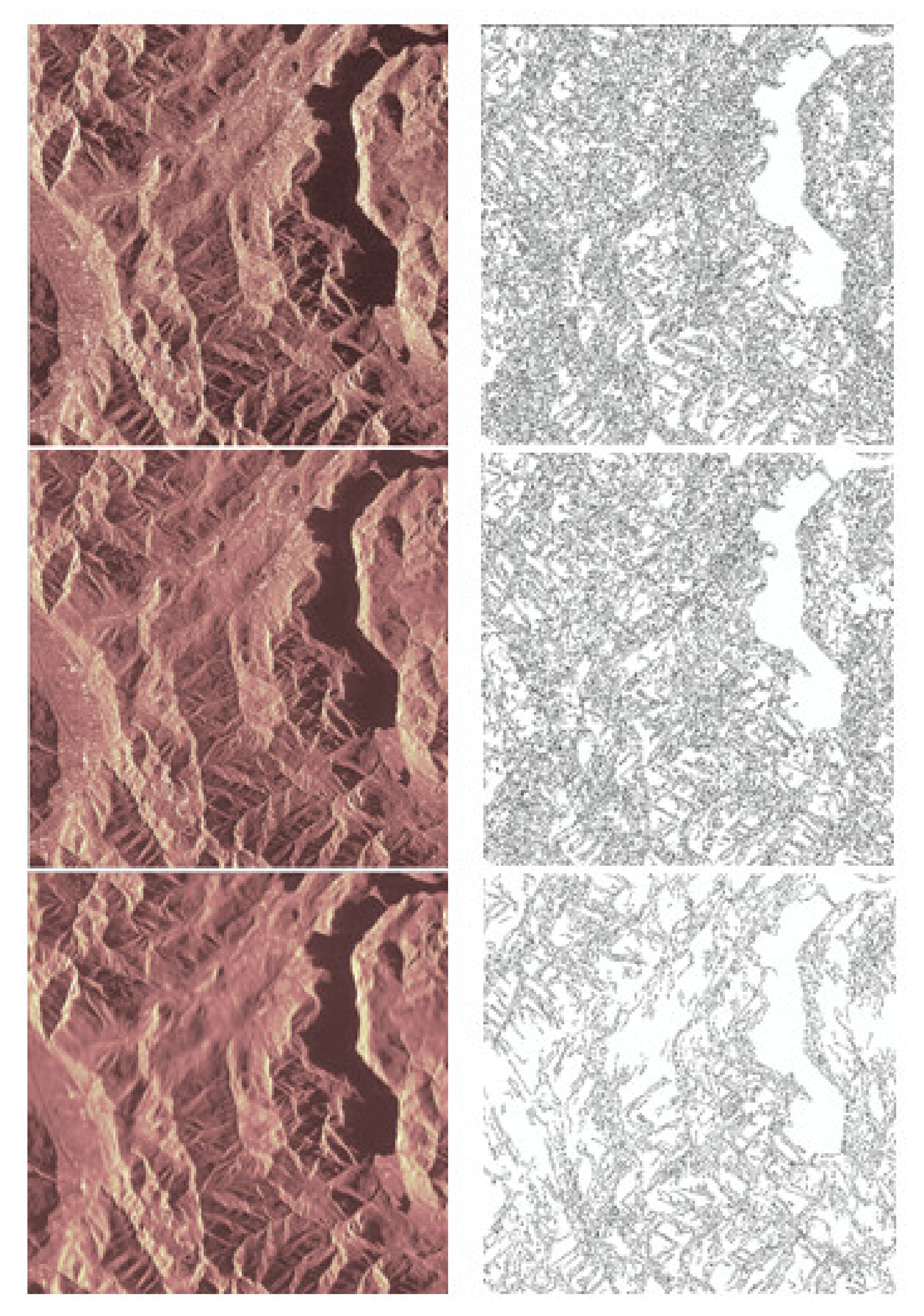
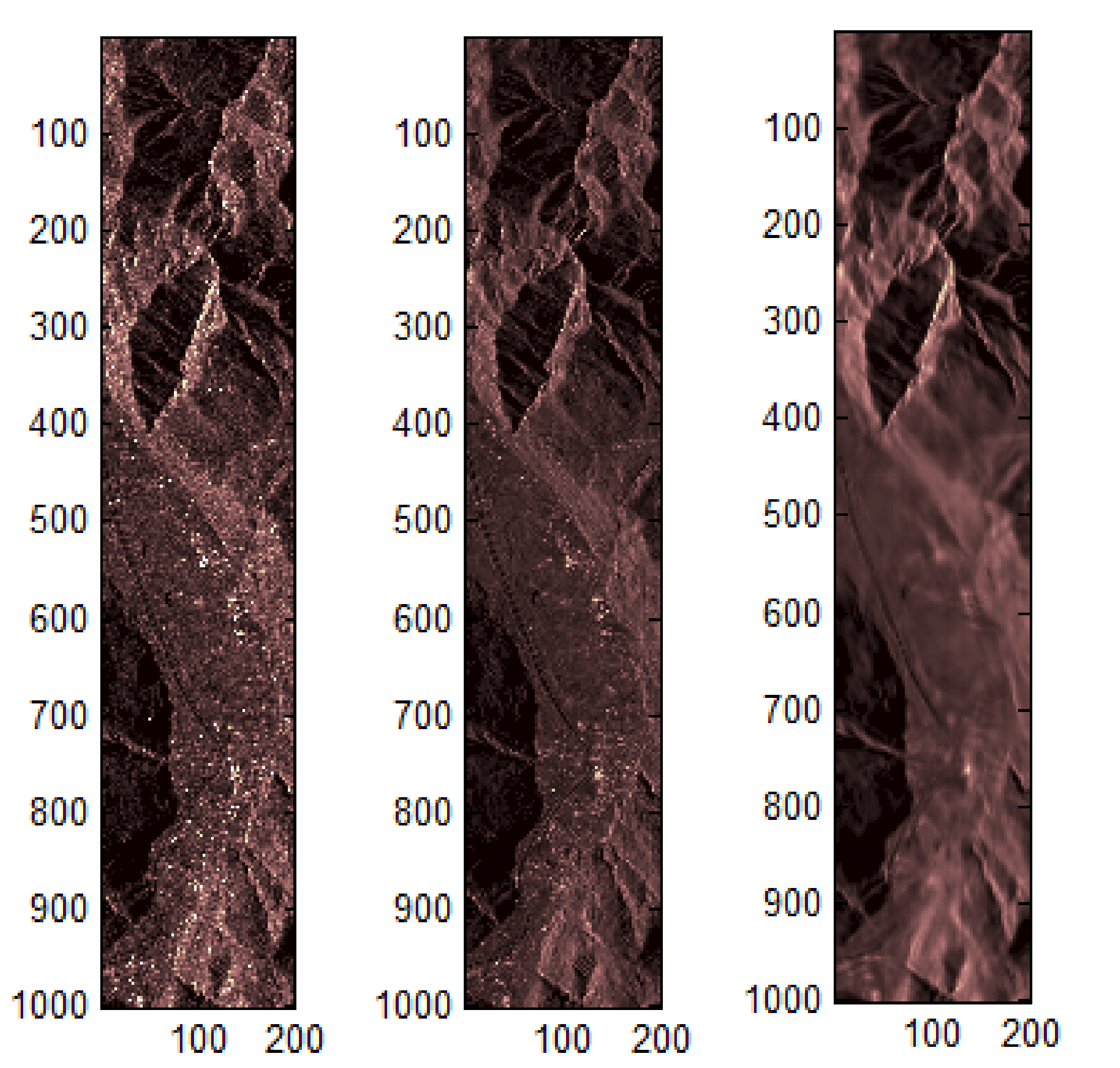
3.2. Real Remote Sensing Images
4. Discussion
4.1. Images Affected by Synthesized Speckle
4.2. Real Remote Sensing Images
4.3. Comparison with Modern Despeckling Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Hagara, M.; Kubinec, P. About Edge Detection in Digital Images. Radioengineering 2018, 27, 919–929. [Google Scholar] [CrossRef]
- Canny, J. A Computational Approach to Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 6, 679–698. [Google Scholar] [CrossRef]
- Marr, D.; Hildreth, E. Theory of edge detection. Proc. R. Soc. London Ser. B Boil. Sci. 1980, 207, 187–217. [Google Scholar] [CrossRef]
- Lee, J.; Haralick, R.; Shapiro, L. Morphologic edge detection. IEEE J. Robot. Autom. 1987, 3, 142–156. [Google Scholar] [CrossRef]
- Chanda, B.; Kundu, M.K.; Padmaja, Y.V. A multi-scale morphologic edge detector. Pattern Recognit. 1998, 31, 1469–1478. [Google Scholar] [CrossRef]
- Stéphane, M. A Wavelet Tour of Signal Processing. The Sparse Way, 3rd ed.; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar] [CrossRef]
- Firoiu, I.; Nafornita, C.; Boucher, J.-M.; Isar, A. Image Denoising Using a New Implementation of the Hyperanalytic Wavelet Transform. IEEE Trans. Instrum. Meas. 2009, 58, 2410–2416. [Google Scholar] [CrossRef]
- Sendur, L.; Selesnick, I. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Trans. Signal Process. 2002, 50, 2744–2756. [Google Scholar] [CrossRef]
- Selesnick, I.W. The Estimation of Laplace Random Vectors in Additive White Gaussian Noise. IEEE Trans. Signal Process. 2008, 56, 3482–3496. [Google Scholar] [CrossRef]
- Holschneider, M.; Kronland-Martinet, R.; Morlet, J.; Tchmitchian, P. Wavelets, Time-Frequency Methods and Phase Space, Chapter A Real-Time Algorithm for Signal Analysis with the Help of the Wavelet Transform; Springer: Berlin/Heidelberg, Germany, 1989; pp. 289–297. [Google Scholar]
- Kingsbury, N. The Dual-Tree Complex Wavelet Transform: A New Efficient Tool For Image Restoration And Enhancement. Proc. EUSIPCO 1998, 319–322. [Google Scholar] [CrossRef]
- Ghael, S.P.; Sayeed, A.M.; Baraniuk, R.G. Improved wavelet denoising via empirical Wiener filtering. Proc. SPIE 1997, 389–399. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Shui, P.-L.; Zhang, W.-C. Noise-robust edge detector combining isotropic and anisotropic Gaussian kernels. Pattern Recognit. 2012, 45, 806–820. [Google Scholar] [CrossRef]
- Kundu, A. Robust edge detection. In Proceedings of the CVPR 1989: IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 4–8 June 1989. [Google Scholar] [CrossRef]
- Lim, D.H. Robust edge detection in noisy images. Comput. Stat. Data Anal. 2006, 50, 803–812. [Google Scholar] [CrossRef]
- Brooks, R.A.; Bovik, A.C. Robust techniques for edge detection in multiplicative weibull image noise. Pattern Recognit. 1990, 23, 1047–1057. [Google Scholar] [CrossRef]
- Lin, W.-C.; Wang, J.-W. Edge detection in medical images with quasi high-pass filter based on local statistics. Biomed. Signal Process. Control. 2018, 39, 294–302. [Google Scholar] [CrossRef]
- Mafi, M.; Rajaei, H.; Cabrerizo, M.; Adjouadi, M. A Robust Edge Detection Approach in the Presence of High Impulse Noise Intensity Through Switching Adaptive Median and Fixed Weighted Mean Filtering. IEEE Trans. Image Process. 2018, 27, 5475–5490. [Google Scholar] [CrossRef]
- Isar, A.; Nafornita, C. On the statistical decorrelation of the 2D discrete wavelet transform coefficients of a wide sense stationary bivariate random process. Digit. Signal Process. 2014, 24, 95–105. [Google Scholar] [CrossRef]
- Olhede, S.C.; Metikas, G. The Hyperanalytic Wavelet Transform. IEEE Transact. Signal Process. 2009, 57, 3426–3441. [Google Scholar] [CrossRef]
- Alfsmann, D.; Göckler, H.G.; Sangwine, S.J.; Ell, T.A. Hypercomplex Algebras in Digital Signal Processing: Benefits and Drawbaks. In Proceedings of the 2007 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007. [Google Scholar]
- Clyde, C.; Davenport, M. A Commutative Hypercomplex Algebra with Associated Function Theory. In Clifford Algebras with Numeric and Symbolic Computations; Ablamowicz, R., Ed.; Birkhäuser: Boston, MA, USA, 1996; pp. 213–227. [Google Scholar]
- Nafornita, C.; Isar, A. A complete second order statistical analysis of the Hyperanalytic Wavelet Transform. In Proceedings of the 2012 10th International Symposium on Electronics and Telecommunications, Timisoara, Romania, 15–16 November 2012; pp. 227–230. [Google Scholar]
- Tomassi, D.; Milone, D.; Nelson, J.D. Wavelet shrinkage using adaptive structured sparsity constraints. Signal Process. 2015, 106, 73–87. [Google Scholar] [CrossRef]
- Starck, J.-L.; Donoho, D.L.; Fadili, M.J.; Rassat, A. Sparsity and the Bayesian perspective. Astron. Astrophys. 2013, 552, A133. [Google Scholar] [CrossRef]
- Foucher, S.; Benie, G.; Boucher, J.-M. Multiscale MAP filtering of SAR images. IEEE Trans. Image Process. 2001, 10, 49–60. [Google Scholar] [CrossRef]
- Pižurica, A. Image Denoising Algorithms: From Wavelet Shrinkage to Nonlocal Collaborative Filtering; Wiley: Hoboken, NJ, USA, 2017; pp. 1–17. [Google Scholar]
- Luisier, F.; Blu, T.; Unser, M. A New SURE Approach to Image Denoising: Interscale Orthonormal Wavelet Thresholding. IEEE Trans. Image Process. 2007, 16, 593–606. [Google Scholar] [CrossRef]
- Achim, A.; Kuruoglu, E. Image denoising using bivariate α-stable distributions in the complex wavelet domain. IEEE Signal Process. Lett. 2005, 12, 17–20. [Google Scholar] [CrossRef]
- Isar, A.; Nafornita, C. Sentinel 1 Stripmap GRDH image despeckling using two stages algorithms. In Proceedings of the 2016 12th IEEE International Symposium on Electronics and Telecommun, ISETC, Timisoara, Romania, 27–28 October 2016; pp. 343–348. [Google Scholar] [CrossRef]
- Achim, A.; Tsakalides, P.; Bezerianos, A. SAR image denoising via Bayesian wavelet shrinkage based on heavy-tailed modeling. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1773–1784. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.G.; Zhang, B.; Hong, W.; Wu, Y.-R. Adaptive Total Variation Regularization Based SAR Image Despeckling and Despeckling Evaluation Index. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2765–2774. [Google Scholar] [CrossRef]
- Firoiu, I.; Nafornita, C.; Isar, D.; Isar, A. Bayesian Hyperanalytic Denoising of SONAR Images. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1065–1069. [Google Scholar] [CrossRef]
- Isar, A.; Firoiu, I.; Nafornita, C.; Mog, S. SONAR Images Denoising. Sonar Syst. 2011. [Google Scholar] [CrossRef][Green Version]
- Lee, J.-S. Refined filtering of image noise using local statistics. Comput. Graph. Image Process. 1981, 15, 380–389. [Google Scholar] [CrossRef]
- Kuan, D.T.; Sawchuk, A.A.; Strand, T.C.; Chavel, P. Adaptive Noise Smoothing Filter for Images with Signal-Dependent Noise. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 165–177. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 157–166. [Google Scholar] [CrossRef]
- Lopes, A.; Nezry, E.; Touzi, R.; Laur, H. Maximum A Posteriori Speckle Filtering And First Order Texture Models In Sar Images. In Proceedings of the 10th Annual International Symposium on Geoscience and Remote Sensing, College Park, MD, USA, 20–24 May 1990; pp. 2409–2412. [Google Scholar]
- Walessa, M.; Datcu, M. Model-based despeckling and information extraction from SAR images. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2258–2269. [Google Scholar] [CrossRef]
- Achim, A.; Kuruoğlu, E.E.; Zerubia, J. SAR image filtering based on the heavy-tailed Rayleigh model. IEEE Trans. Image Process. 2006, 15, 2686–2693. [Google Scholar] [CrossRef]
- Buades, A. Image and Film Denoising by Non-Local Means. Ph.D. Thesis, Universitat de les Iles Baleares, Illes Balears, Spain, 2007. [Google Scholar]
- Coupé, P.; Hellier, P.; Kervrann, C.; Barillot, C. Bayesian non local means-based speckle filtering. In Proceedings of the 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Paris, France, 14–17 May 2008; pp. 1291–1294. [Google Scholar] [CrossRef]
- Zhong, H.; Xu, J.; Jiao, L. Classification based nonlocal means despeckling for SAR image. Proc. SPIE 2009, 7495. [Google Scholar] [CrossRef]
- Gleich, D.; Datcu, M. Gauss–Markov Model for Wavelet-Based SAR Image Despeckling. IEEE Signal Process. Lett. 2006, 13, 365–368. [Google Scholar] [CrossRef]
- Bhuiyan, M.I.H.; Ahmad, M.O.; Swamy, M.N.S. Spatially Adaptive Wavelet-Based Method Using the Cauchy Prior for Denoising the SAR Images. IEEE Trans. Circuits Syst. Video Technol. 2007, 17, 500–507. [Google Scholar] [CrossRef]
- Solbø, S.; Eltoft, T. Homomorphic wavelet-based statistical despeckling of SAR images. IEEE Trans. Geosci. Remote Sens. 2004, 42, 711–721. [Google Scholar] [CrossRef]
- Argenti, F.; Bianchi, T.; Alparone, L. Multiresolution MAP Despeckling of SAR Images Based on Locally Adaptive Generalized Gaussian pdf Modeling. IEEE Trans. Image Process. 2006, 15, 3385–3399. [Google Scholar] [CrossRef]
- Bianchi, T.; Argenti, F.; Alparone, L. Segmentation-Based MAP Despeckling of SAR Images in the Undecimated Wavelet Domain. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2728–2742. [Google Scholar] [CrossRef]
- Gagnon, L.; Jouan, A. Speckle filtering of SAR images: A comparative study between complex-wavelet-based and standard filters. Proc. SPIE 1997, 3169, 80–91. [Google Scholar]
- Xing, S.; Xu, Q.; Ma, D. Speckle Denoising Based On Bivariate Shrinkage Functions and Dual-Tree Complex Wavelet Transform, The Int. Arch. of the Photogrammetry. Remote Sens. Spat. Inform. Sci. 2008, 38, 1–57. [Google Scholar]
- Maggioni, M.; Sánchez-Monge, E.; Foi, A.; Danielyan, A.; Dabov, K.; Katkovnik, V.; Egiazarian, K. Image and Video Denoising by Sparse 3D Transform-Domain Collaborative Filtering Block-Matching and 3D Filtering (BM3D) Algorithm and Its Extensions. 2014. Available online: http://www.cs.tut.fi/~foi/GCF-BM3D/ (accessed on 21 June 2021).
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A Nonlocal SAR Image Denoising Algorithm Based on LLMMSE Wavelet Shrinkage. IEEE Trans. Geosci. Remote Sens. 2012, 50, 606–616. [Google Scholar] [CrossRef]
- Fjortoft, R.; Lopes, A.; Adragna, F. Radiometric and spatial aspects of speckle filtering. In Proceedings of the IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120), Honolulu, HI, USA, 24–28 July 2002; Volume 4, pp. 1660–1662. [Google Scholar]
- Shui, P.-L. Image denoising algorithm via doubly local Wiener filtering with directional windows in wavelet domain. IEEE Signal Process. Lett. 2005, 12, 681–684. [Google Scholar] [CrossRef]
- Pratt, W.K. Digital Image Processing; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Buckheit, J.B.; Donoho, D.L. WaveLab and Reproducible Research. Depend. Probab. Stat. 1995, 103, 55–81. [Google Scholar] [CrossRef]
- Firoiu, I. Complex Wavelet Transform: Application to Denoising. Ph.D. Thesis, Politehnica University Timisoara, Timisoara, Romania, 2010. [Google Scholar]
- Nafornita, C.; Isar, A.; Dehelean, T. Multilook SAR Image Enhancement Using the Dual Tree Complex Wavelet Transform. In Proceedings of the 2018 International Conference on Communications (COMM), Bucharest, Romania, 14–16 June 2018; pp. 151–156. [Google Scholar]
- Nafornita, C.; Isar, A.; Nelson, J.D.B. Regularised, semi-local hurst estimation via generalised lasso and dual-tree complex wavelets. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 2689–2693. [Google Scholar]
- Nelson, J.D.B.; Nafornita, C.; Isar, A. Generalised M-Lasso for robust, spatially regularised hurst estimation. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; pp. 1265–1269. [Google Scholar]
- Nelson, J.D.B.; Nafornita, C.; Isar, A. Semi-Local Scaling Exponent Estimation With Box-Penalty Constraints and Total-Variation Regularization. IEEE Trans. Image Process. 2016, 25, 3167–3181. [Google Scholar] [CrossRef]
- Nafornita, C.; Isar, A.; Nelson, J.D.B. Denoising of Single Look Complex SAR Images using Hurst Estimation. In Proceedings of the 12th International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 26–27 October 2016; pp. 333–338. [Google Scholar] [CrossRef]
- Nafornita, C.; Nelson, J.; Isar, A. Performance analysis of SAR image denoising using scaling exponent estimator. In Proceedings of the 2016 International Conference on Communications (COMM), Bucharest, Romania, 9–10 June 2016. [Google Scholar] [CrossRef]
- Zhu, X.; Montazeri, S.; Ali, M.; Hua, Y.; Wang, Y.; Mou, L.; Shi, Y.; Xu, F.; Bamler, R. Deep Learning Meets SAR: Concepts, Models, Pitfalls, and Perspectives. IEEE Geosci. Remote Sens. Mag. 2021. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Chierchia, G.; Cozzolino, D.; Poggi, G.; Verdoliva, L. SAR image despeckling through convolutional neural networks. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5438–5441. [Google Scholar]
- Wang, P.; Zhang, H.; Patel, V.M. SAR Image Despeckling Using a Convolutional Neural Network. IEEE Signal Process. Lett. 2017, 24, 1763–1767. [Google Scholar] [CrossRef]
- Yue, D.-X.; Xu, F.; Jin, Y.-Q. SAR despeckling neural network with logarithmic convolutional product model. Int. J. Remote Sens. 2018, 39, 7483–7505. [Google Scholar] [CrossRef]
- Vitale, S.; Ferraioli, G.; Pascazio, V. Multi-Objective CNN-Based Algorithm for SAR Despeckling. IEEE Trans. Geosci. Remote Sens. 2020, 1–14. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, L.; Ding, X. SAR image despeckling with a multilayer perceptron neural network. Int. J. Digit. Earth 2018, 12, 354–374. [Google Scholar] [CrossRef]
- Lattari, F.; Leon, B.G.; Asaro, F.; Rucci, A.; Prati, C.; Matteucci, M. Deep Learning for SAR Image Despeckling. Remote Sens. 2019, 11, 1532. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Cozzolino, D.; Verdoliva, L.; Scarpa, G.; Poggi, G. Nonlocal CNN SAR Image Despeckling. Remote Sens. 2020, 12, 1006. [Google Scholar] [CrossRef]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2noise: Learning image restoration without clean data, 2018, Proceedings of the 35th International Conference on Machine Learning. arXiv 2018, arXiv:1803.04189. [Google Scholar]
- Ma, X.; Wang, C.; Yin, Z.; Wu, P. SAR Image Despeckling by Noisy Reference-Based Deep Learning Method. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 8807–8818. [Google Scholar] [CrossRef]
- Fracastoro, G.; Magli, E.; Poggi, G.; Scarpa, G.; Valsesia, D.; Verdoliva, L. Deep Learning Methods For Synthetic Aperture Radar Image Despeckling: An Overview Of Trends And Perspectives. IEEE Geosci. Remote Sens. Mag. 2021, 9, 29–51. [Google Scholar] [CrossRef]





| Proposed Method | Canny’s Method | ||||
|---|---|---|---|---|---|
| First Step | Final Result | Directly on Noisy Image | |||
| Input PSNR | Output PSNR | Output SSIM | Edges’ MSE | Edges’ MSE | |
| 10 | 28.13 | 35.19 | 0.9989 | 0.04 | 0.07 |
| 15 | 24.59 | 33.41 | 0.9983 | 0.06 | 0.09 |
| 20 | 22.10 | 32.06 | 0.9977 | 0.07 | 0.14 |
| 25 | 20.21 | 31.06 | 0.9971 | 0.07 | 0.2 |
| 30 | 18.61 | 30.20 | 0.9964 | 0.08 | 0.21 |
| Proposed Method | Canny’s Method | ||||
|---|---|---|---|---|---|
| First Step | Final Result | Directly on Noisy Image | |||
| Input PSNR | Output PSNR | Output SSIM | Edges’ MSE/no. of missed pixels | Edges’ MSE/no. of false edge pixels | |
| 10 | 28.13 | 33.11 | 0.9981 | 0.05/1122 | 0.06/1218 |
| 15 | 24.59 | 31.20 | 0.9970 | 0.07/2828 | 0.09/5247 |
| 20 | 22.10 | 29.86 | 0.9959 | 0.09/5443 | 0.14/13,538 |
| 25 | 20.21 | 28.82 | 0.9948 | 0.1/6893 | 0.18/17,130 |
| 30 | 18.61 | 28.08 | 0.9935 | 0.1/6978 | 0.20/26,644 |
| Proposed Method | Canny’s Method | ||||
|---|---|---|---|---|---|
| First Step | Final Result | Directly on Noisy Image | |||
| Input PSNR | Output PSNR | Output SSIM | Edges’ MSE/no. of missed pixels | Edges’ MSE/no. of false edge pixels | |
| 10 | 28.13 | 33.23 | 0.9987 | 0.05/516 | 0.06/3672 |
| 15 | 24.59 | 31.31 | 0.9978 | 0.06/523 | 0.09/7995 |
| 20 | 22.10 | 29.41 | 0.9968 | 0.07/2052 | 0.14/16,922 |
| 25 | 20.21 | 28.21 | 0.9956 | 0.08/3235 | 0.17/25,815 |
| 30 | 18.61 | 27.06 | 0.9943 | 0.09/4335 | 0.2/29,272 |
| NL | Noisy | Result in [48] | HWT - | HWT - | |||
|---|---|---|---|---|---|---|---|
| Marginal ASTF | Bishrink | ||||||
| D4 | B9/7 | D4 | B9/7 | D4 | B9/7 | ||
| 1 | 12.1 | 26.0 | 26.2 | 25.4 | 25.6 | 25.7 | 26.2 |
| 4 | 17.8 | 29.3 | 29.6 | 29.9 | 30.0 | 29.9 | 30.4 |
| 16 | 23.7 | 32.9 | 33.1 | 33.2 | 32.9 | 33.0 | 33.3 |
| NL | Noisy | SA-WB MMAE | MAP-S | PPB | SAR-BM3D | H-BM3D | Prop. |
|---|---|---|---|---|---|---|---|
| 1 | 12.1 | 25.0 | 26.3 | 26.7 | 27.9 | 26.4 | 26.4 |
| 4 | 17.8 | 29.0 | 29.8 | 29.8 | 29.6 | 31.2 | 30.6 |
| 16 | 23.7 | 32.4 | 33.2 | 32.7 | 34.1 | 34.5 | 33.5 |
| Method | Parameters | |
|---|---|---|
| ENL | Noise Rejection | |
| Input image | 2 | Unavailable |
| First stage (HWT-marginal ASTF) | 3.4 | Worst result |
| Entire System | 7.61 | Best result |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isar, A.; Nafornita, C.; Magu, G. Hyperanalytic Wavelet-Based Robust Edge Detection. Remote Sens. 2021, 13, 2888. https://doi.org/10.3390/rs13152888
Isar A, Nafornita C, Magu G. Hyperanalytic Wavelet-Based Robust Edge Detection. Remote Sensing. 2021; 13(15):2888. https://doi.org/10.3390/rs13152888
Chicago/Turabian StyleIsar, Alexandru, Corina Nafornita, and Georgiana Magu. 2021. "Hyperanalytic Wavelet-Based Robust Edge Detection" Remote Sensing 13, no. 15: 2888. https://doi.org/10.3390/rs13152888
APA StyleIsar, A., Nafornita, C., & Magu, G. (2021). Hyperanalytic Wavelet-Based Robust Edge Detection. Remote Sensing, 13(15), 2888. https://doi.org/10.3390/rs13152888






