Abstract
Daily evapotranspiration (ETd) plays a key role in irrigation water management and is particularly important in drought-stricken areas, such as California and high-value crops. Remote sensing allows for the cost-effective estimation of spatial evapotranspiration (ET), and the advent of small unmanned aerial systems (sUAS) technology has made it possible to estimate instantaneous high-resolution ET at the plant, row, and subfield scales. sUAS estimates ET using “instantaneous” remote sensing measurements with half-hourly/hourly forcing micrometeorological data, yielding hourly fluxes in W/m2 that are then translated to a daily scale (mm/day) under two assumptions: (a) relative rates, such as the ratios of ET-to-net radiation (Rn) or ET-to-solar radiation (Rs), are assumed to be constant rather than absolute, and (b) nighttime evaporation (E) and transpiration (T) contributions are negligible. While assumption (a) may be reasonable for unstressed, full cover crops (no exposed soil), the E and T rates may significantly vary over the course of the day for partially vegetated cover conditions due to diurnal variations of soil and crop temperatures and interactions between soil and vegetation elements in agricultural environments, such as vineyards and orchards. In this study, five existing extrapolation approaches that compute the daily ET from the “instantaneous” remotely sensed sUAS ET estimates and the eddy covariance (EC) flux tower measurements were evaluated under different weather, grapevine variety, and trellis designs. Per assumption (b), the nighttime ET contribution was ignored. Each extrapolation technique (evaporative fraction (EF), solar radiation (Rs), net radiation-to-solar radiation (Rn/Rs) ratio, Gaussian (GA), and Sine) makes use of clear skies and quasi-sinusoidal diurnal variations of hourly ET and other meteorological parameters. The sUAS ET estimates and EC ET measurements were collected over multiple years and times from different vineyard sites in California as part of the USDA Agricultural Research Service Grape Remote Sensing Atmospheric Profile and Evapotranspiration eXperiment (GRAPEX). Optical and thermal sUAS imagery data at 10 cm and 60 cm, respectively, were collected by the Utah State University AggieAir sUAS Program and used in the Two-Source Energy Balance (TSEB) model to estimate the instantaneous or hourly sUAS ET at overpass time. The hourly ET from the EC measurements was also used to validate the extrapolation techniques. Overall, the analysis using EC measurements indicates that the Rs, EF, and GA approaches presented the best goodness-of-fit statistics for a window of time between 1030 and 1330 PST (Pacific Standard Time), with the Rs approach yielding better agreement with the EC measurements. Similar results were found using TSEB and sUAS data. The 1030–1330 time window also provided the greatest agreement between the actual daily EC ET and the extrapolated TSEB daily ET, with the Rs approach again yielding better agreement with the ground measurements. The expected accuracy of the upscaled TSEB daily ET estimates across all vineyard sites in California is below 0.5 mm/day, (EC extrapolation accuracy was found to be 0.34 mm/day), making the daily scale results from TSEB reliable and suitable for day-to-day water management applications.
Keywords:
evapotranspiration (ET); daily ET; remote sensing; sUAS; vineyards; GRAPEX; eddy covariance (EC); TSEB; energy balance 1. Introduction
Evapotranspiration (ET) is a key component in the hydro-ecological process, which couples water and energy budgets, links the land surface and the atmosphere [1], and represents water consumption for biomass production [2]. Routine monitoring of actual ET is important for a variety of applications, including water resource management, drought monitoring, climate change, and the efficiency of crop irrigation [3,4,5,6]. Numerous methods have been used over the past decades to measure ET, including lysimeters, Bowen ratio, and eddy covariance (EC) flux towers. However, these methods represent limited sampling areas [7], and the measurements are best interpreted for homogeneous surfaces [8]. Spatial techniques are needed to accurately quantify ET for improved irrigation scheduling and water management decision support, particularly in complex canopies such as vineyards, which have non-uniform and complex vertical canopy structure, wide and variable row spacing, and deep and complex rooting systems [9]. This canopy structure produces large diurnal changes in solar radiation exposure to soil and plants [9] and requires sophisticated radiation extinction modeling [10,11]. Meanwhile, row spacing ranges between 2.4 m and 3.6 m for vineyards [12], and between 3.6 m and 6 m for orchards trees [13]. Water-limiting conditions across different vineyards in drought-stricken areas, such as California, necessitate the assessment of irrigation demand to set up agricultural water management strategies and decisions [14]. According to the USDA, California produces over 90% of US wine, with a steady growth reaching 635,000 acres [15] in 2019. The high evaporative demand with limited rainfall in the vineyard growing season (May–September), along with the need to achieve grapevine stress targets, constitutes a significant challenge for irrigation scheduling to ensure vineyard productivity [16].
Advances in methods for measuring and modeling the interactions of vineyards with the environment require a better understanding of the processes influencing energy, water, and carbon exchange for highly organized and complex structure perennial crops. Various remote sensing platforms, including satellites, manned aircraft, and small unmanned aerial systems (sUAS), improve the potential availability of surface information for estimating ET at different spatial scales [17]. However, spatial information from satellites has limitations for ET estimation, including spatial and temporal resolutions, the presence of clouds at overpass time, and imagery delivery time [18]. These issues make satellite data challenging to use for the continuous mapping of daily ET (ETd) and for real-time irrigation scheduling [19]. However, data fusion methodologies using multiple satellite platforms have improved capabilities for generating daily ET on a more routine basis [20,21] and for irrigation scheduling [22]. While manned aircraft have the ability to gather high-resolution data on demand at different times of the day, they are usually cost-prohibitive and, therefore, unlikely to be used to conduct multiple flights over an area of interest [23]. The advent of advanced sUAS remote sensing technology with lightweight sensors could overcome some of the previously mentioned remote sensing platform limitations. Compared to satellites, sUAS can be described as “flexible in timing”, in that they can be operated as needed at almost any time [7]. Additionally, sUAS can provide high spatial and temporal resolution data at sub-meter and multispectral resolutions, although data quality and data processing workflows must be enhanced before sUAS can become an efficient data collection platform [24]. Moreover, the areal coverage from sUAS is limited compared to satellites. For example, the Landsat 8 scene size is 185 km × 180 km, while an sUAS is nearly 1.6 km × 1.6 km, depending on the sensor type and flight height.
Whether using satellite or aerial imagery, the ability to reliably extrapolate from one-time-of-day instantaneous ET (ETi) to daily ET (ETd) is most useful [25] and relevant for the water management of agricultural crops [3]. Although numerous daily ET datasets are available for different applications, these products are often calculated based on the Penman-Monteith approach, the Priestley-Taylor method, or the integration of multiple ET estimates at a coarse resolution (≥0.25°) [26]. EEFLUX (Earth Engine Evapotranspiration Flux) is another source for obtaining daily ET information at 30-m spatial resolution using Landsat data and an energy balance model. However, its temporal resolution of 16 days [27] limits its capability for continuously monitoring ET and identifying the spatial variability in irrigation practices that can occur in less than one week. Many current research efforts are being directed towards daily ET estimation using surface energy balance models, among them the Two-Source Energy Balance (TSEB) model. However, the TSEB model provides hourly surface energy fluxes, which requires a scaling/extrapolation approach for generating daily ET information. Several studies have compared different daily ET methods with an assumption that the ratio of latent heat flux (LE) to one energy balance term is constant throughout the day, yet no universal approach has been identified as suitable for all types of land surfaces. Previous studies have indicated that the accuracy of that approach (upscaling daily ET) is a function of land surface type. For example, the evaporative fraction (EF) approach produced the best agreement in bare soil [28] and soybean [19], while the incoming solar radiation (Rs) approach was deemed to be more efficient in estimating daily ET in grassland and woody savanna [29]. Another crucial issue for precise daily ET estimation is the proper selection of the time-of-day window. In the study conducted by Colaizzi et al. [28], the best time window for extrapolating the hourly ET to a daily scale was shown to be within 1 or 2 h of solar noon. This conclusion was also supported by Jackson et al. [30], who identified the time-of-day window for acquiring the ET for daily ET estimation as within 2 h of solar noon. Therefore, some concerns, such as actual and potential satellite overpass times and cloudiness vs. time of day, should be identified clearly to avoid any error propagation in the daily ET estimation.
The need for accurate daily ET (ETd) estimates raises two fundamental questions: (1) which daily ET extrapolation approach at grapevine row scales can provide reliable values under a variety of crop and environmental conditions and thermal-based ET models like TSEB? and (2) what time window for acquiring a remotely-sensed ET provides the most reliable daily ET using an extrapolation approach? Multiple efforts have been made to estimate ETd for different crops; however, computing ETd for complex canopies, such as vineyards and grapevine row scales, has not been adequately addressed. In this study, different extrapolation approaches from the literature were assessed for estimating daily ET from instantaneous sUAS ET estimates for several vineyard sites across California. Specifically, this paper (a) assessed the performance of several daily ET extrapolation approaches using EC observations and sUAS information, and (b) determined an optimal time window for ET upscaling from a single to a daily estimate.
1.1. Daily ET Upscaling Approaches
ET upscaling is commonly performed by assuming conservation of some ET metric over the daytime, generally known as a ratio between instantaneous ET and a reference variable at a specific time of day, and that nighttime E and T contributions (soil evaporation and plant transpiration) are negligible or represent some small percentage of the daytime ET (on the order of 10%). This hypothesis is commonly known as energy self-preservation [29,31,32] and includes EF, Rs, and Rn/Rs ratio approaches. The second assumption in flux upscaling procedures is that cloud-free conditions persist throughout the daytime [28,33]. However, the clear-sky condition cannot be assured necessarily throughout the season. Other ETd extrapolation approaches are characterized by a quasi-sinusoidal shape, such as Gaussian (GA) and Sine. These approaches assume that the diurnal variation of ET is similar to the solar irradiance, with the peak value at solar noon. A description of each approach is presented below.
1.1.1. Evaporative Fraction (EF) Approach
One of the most common schemes to extrapolate instantaneous evapotranspiration to a daily value is the evaporative fraction (EF) [34]. EF is defined as the ratio of latent heat flux (LE) to the available energy (the difference between net radiation, Rn, and soil heat flux, G), assumed to be constant throughout daytime hours. The EF approach is presented in Equation (1), as follows:
where ETd is the daily ET (mm/day), LE is the instantaneous latent heat flux (W/m2), Rn is the instantaneous net radiation (W/m2), G is the instantaneous soil heat flux (W/m2), is the water density (kg/m3), is the latent heat of vaporization for water (MJ/kg), is the total daily available energy (MJ/m2/day), and c is a factor equal to 1000 to convert meters to millimeters.
Numerous studies have considered the tendency of the EF to be nearly constant during the daytime [35]; however, the combination of soil moisture, weather conditions, topography, and biophysical conditions has an impact on the conservation (or variability) of the EF in the daytime [31]. According to Hoedjes et al. [36], self-preservation of the EF approach is applicable under dry conditions, while under wet conditions, the EF is no longer valid. Nonetheless, a previous study by Crago [32], which used Bowen ratio stations over natural grassland, indicated that, for clear days, the midday EF is a good indicator of the daytime average value of the EF compared with cloudy days, but the values are still underestimated from the daytime average EF due to the concave-up shape of the diurnal variation of the EF. This finding is also supported by Li et al. [37], who found that the EF is relatively close to the daily average EF in the 1000 to 1500 timeframe, and could be used to guide vineyard irrigation practices in arid regions. However, the study by Zhang and Lemeur [38], which used 12 surface network stations called Système Automatique de Mesure de l’Evaporation Rèelle (SAMER) over an area composed of forest (40%) and mixed agriculture (60%), indicated that the EF varies during the daytime and could not be used as a guide for ETd estimates due to factors such as available energy, soil moisture, and other environmental variables. According to the study by Gentine et al. [39], which examined the influence of environmental factors (incoming solar radiation, wind speed, air temperature, soil water content, and leaf area index) on the diurnal behavior of the EF over wheat and olive, indicated that EF is strongly linked to soil moisture availability and canopy cover. As such, the EF increases with increasing the soil moisture and/or fractional cover. On the other hand, they found that the phase difference between net radiation (Rn) and the soil heat flux (G) must be well-characterized in application models that invoke the EF daytime self-preservation.
1.1.2. Solar Radiation (Rs) Approach
Another approach for extrapolating ETi to ETd is the Rs approach, which is similar to the EF but replaces the available energy ((Rn − G), instantaneous or daily) term with the incoming solar radiation (Rs) as a reference variable. This approach, developed by Jackson et al. [30], assumes that the diurnal ET variation is similar to the solar radiation (ET~Rs), that is, the ET is highly correlated and proportional to the Rs. Equation (2) demonstrates the expressions for calculating ETd using the Rs approach.
where is the daily solar radiation (MJ/m2/day), and is the instantaneous solar radiation (W/m2). Other parameters are similar to the EF approach.
According to Van Neil et al. [40], the Rs approach is robust when upscaling ETi to multiple timeframes (e.g., daily, 8-day, and monthly). Moreover, many studies have indicated that solar radiation (Rs) is the most robust scalar approach that explains the ratio between the ETd and ETi [41].
1.1.3. Ratio of Net Radiation-to-Solar Radiation (Rn/Rs) Approach
The Rn/Rs approach is another approach to scale up ETi to ETd using the evaporative fraction (EF) and the ratio of net radiation-to-solar radiation (Rn/Rs) [42]. The Rn/Rs approach is presented in Equation (3).
The parameters of this approach are explained in the EF and Rs approaches.
1.1.4. Sine Approach
The Sine approach, developed by Jackson et al. [30], showed that the generic trend of the ETi during the daylight period is similar to the solar irradiance and could be approximated by a Sine function, where the maximum irradiance occurs at solar noon (~12 p.m.). For cloudy days, the daily ET estimates using the Sine approach are less reliable or may be invalid. This implies that the ETi responds strongly to solar radiation [38]. The approach has been investigated by Zhang and Lemeur [38], who found the Sine approach to be preferable to others for upscaling instantaneous ET values.
where ETi represents the instantaneous ET (mm/hr), N is the total time from sunrise to sunset (h) and can be calculated using Equation (5), and t is the time elapsed since sunrise (h).
In Equation (5), a and b are latitude-dependent constants, while D is the day of the year. For parameters a and b, Jackson et al. [30] developed a regression model that is a function of the latitude of the location, as shown in Equations (6) and (7), respectively.
and
where L is the latitude in decimal degrees.
1.1.5. Gaussian (GA) Approach
The Gaussian (GA) approach has been used recently by Liu et al. [43] to retrieve the ETd from remotely sensed instantaneous ET. The study used ETi observations from an EC system and found that the ET diurnal variation follows a Gaussian-fitting curve. When comparing this approach to the Sine and EF approaches, results from the study of Liu et al. [43] indicated that GA is more accurate using the eddy covariance (EC) system.
where w is the width that equals 2δ, δ is the standard deviation of ETi values, ti is the time of the instantaneous ET (ETi), and tc is the time when ETi arrives at maximum value in the diurnal variation.
1.2. Two-Source Energy Balance (TSEB) Model
The TSEB model was developed by Norman et al. [44] to explicitly accommodate the difference between radiometric and aerodynamic surface temperatures that affect the energy exchange between soil and canopy systems and the lower atmosphere at instantaneous time scales. In the TSEB model, turbulent energy fluxes are partitioned between canopy and soil, with different versions applied to separate between those components. These versions include the TSEB-PT (Priestly-Taylor), the TSEB-DTD (Dual Time Difference), TSEB-2T-DMS (Data-Mining Sharpening of temperature), and TSEB-2T (Dual Temperature). The TSEB-PT version assumes a composite radiometric temperature (Trad) that contains temperature contributions from the soil/substrate and canopy and is decomposed based on the vegetation fractional cover (fc). The TSEB-DTD version, developed by Norman et al. [45], uses two observations of Trad: the first observation obtained 1.5 h after the sunrise (Trad,0), and the second one during the daytime (Trad,1). The TSEB-DTD version uses the same approach as TSEB-PT to divide the composite Trad between the soil/substrate and canopy temperatures. Using TSEB-DTD could reduce the error in flux estimations when uncertainty exists in local air temperature observations and absolute Trad [46]. TSEB-2T-DMS uses a data-mining fusion algorithm to sharpen the land surface temperature (LST), which allows better discrimination between the soil/substrate and canopy temperatures [47]. The TSEB-2T approach was originally developed by Kustas and Norman [48] and was further refined and tested by Nieto et al. [49]. The main concept underpinning the TSEB-2T approach is to estimate the Ts and Tc from composite LST imagery using the relationship between the vegetation index (VI) and the LST to extract the Ts and Tc within a spatial domain. An early attempt at estimating vineyard water use at a field scale using aerial imagery with TSEB and a simple thermal-based contextual scheme suggests the TSEB is a robust approach for vineyard ET estimation [50]. In this study, the TSEB model was used to calculate the instantaneous ET at the time of the sUAS overpass, and the various schemes were used to extrapolate this one-time-of-day ET to a daily value. The TSEB-2T model was used for the Sierra Loma vineyard analysis, while the TSEB-PT was used for Ripperdan and Barrelli due to limitations in applying the TSEB-2T model to those two sites. The average value of the LAI was used for these sites, but the TSEB-2T requires the LAI spatial information to identify the threshold values of NDVI of soil, which is based on the empirical relationship between the NDVI and LAI. More details about the TSEB-2T can be found in Nieto et al. [49]. Applying the energy conservation and balance principles, the energy budget in the TSEB model can be described in the following equations:
where Rn is the net radiation, and G is the soil heat flux. H and LE are heat fluxes, where H is the sensible heat flux and LE is the latent heat flux. All flux units are expressed in W/m2. Subscripts of c and s represent the canopy and soil components, respectively. To estimate the sensible heat flux for soil and canopy, Norman et al. [44] proposed a series of soil vegetation resistive schemes (following an analogy with Ohm’s law), as illustrated in Figure 1.
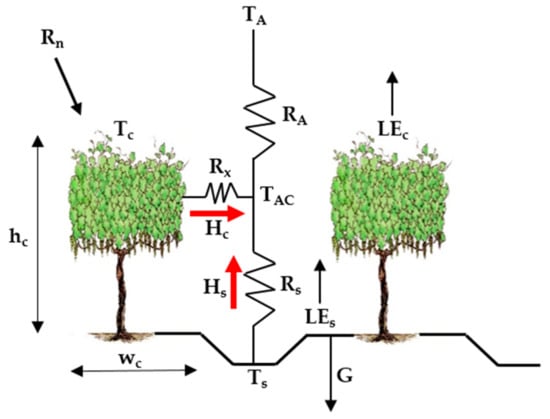 where is the air density (kg/m3), is the heat capacity of the air at constant pressure (J/kg/K), TA is the air temperature (Kelvins), Tc and Ts are the canopy and soil temperatures (Kelvins), respectively, and TAC is the temperature of the canopy air space (Kelvins), which is calculated with Equation (13).
where RA is the aerodynamic resistance to heat transport from the soil/canopy system, Rx is the boundary layer resistance of the canopy leaves, and Rs is the aerodynamic resistance to heat transport in the boundary layer close to the soil surface. All resistances are expressed in (s/m). The mathematical expressions used to compute the resistance network are detailed in Equations (14)–(16).
where is the friction velocity, calculated as the following:
where is the air density (kg/m3), is the heat capacity of the air at constant pressure (J/kg/K), TA is the air temperature (Kelvins), Tc and Ts are the canopy and soil temperatures (Kelvins), respectively, and TAC is the temperature of the canopy air space (Kelvins), which is calculated with Equation (13).
where RA is the aerodynamic resistance to heat transport from the soil/canopy system, Rx is the boundary layer resistance of the canopy leaves, and Rs is the aerodynamic resistance to heat transport in the boundary layer close to the soil surface. All resistances are expressed in (s/m). The mathematical expressions used to compute the resistance network are detailed in Equations (14)–(16).
where is the friction velocity, calculated as the following:

Figure 1.
Schematic representation of the Two-Source Energy Balance (TSEB) model.
In Equation (17), and are the measurement heights for wind speed (u) and air temperature (, respectively, is the zero-plane displacement height, and is the roughness length for momentum. The unit of is expressed in m. In the TSEB model versions, the roughness length of momentum () is assumed to equal the roughness length for heat transport , as the aerodynamic resistance of the canopy elements (Rx) already takes into account the different efficiencies between momentum and heat transport. represents the von Karman’s constant, which is equal to . and are the adiabatic correction factors for heat and momentum, respectively. The details of these two factors are described in Brutsaert [51]. In Equation (15), is assumed to be 90 s1/2/m and represents the average width of leaf (m). The coefficients (b and c) in Equation (16) depend on the turbulent length scale in the canopy, the soil-surface roughness, and the turbulence intensity in the canopy. More details can be found in the work by Nieto et al. (2019a), Nieto et al. (2019b), Kustas et al., and Kondo and Ishida [11,49,52,53].
2. Methodology
2.1. Study Area
The experiment was conducted within three different climate regions located in California, as shown in Figure 2. All of these sites are part of the Grape Remote Sensing Atmospheric Profile and Evapotranspiration eXperiment (GRAPEX) project [54], led by the USDA ARS in collaboration with E&J Gallo Winery, University of California in Davis, Utah State University, NASA, and others. The overall objective of the GRAPEX project is to provide the vineyard manager and grower with spatially distributed, remotely sensed ET information for improving irrigation water use efficiency and detecting crop stress in multiple vineyard blocks. This would facilitate water conservation efforts in California’s Central Valley, which has been experiencing frequent and severe drought conditions. The project began in 2013 at two pinot noir blocks located within the Sierra Loma Vineyard near Lodi, California () in Sacramento County (see Figure 2) [7]. The two vineyard blocks, north and south, differed in maturity and age, having been implemented in 2009 and 2011, respectively. The configuration of the trellising system in both fields is the same, with vine trellises 3.35 m apart and an east–west orientation. In 2017, the GRAPEX project extended the observations to include two additional vineyards: Barrelli vineyard (), located near Cloverdale, California, and Ripperdan vineyard (), located near Madera, California. With the expansion of the GRAPEX project from Sierra Loma to the Barrelli site to the north and Ripperdan to the south, a large range in trellis designs, climate regions, vine varieties, canopy structure, and vine physiology are represented. The Ripperdan vineyard was planted in 2009, whereas the Barrelli vineyard was implemented in 2010. Both the Barrelli and Ripperdan vineyards employ different plantation structures and vine varieties. The vine rows in Barrelli have a northeast–southwest row orientation, with a row spacing of 3.35 m and predominately Cabernet Sauvignon vine variety, while in Ripperdan, the row direction is east–west, with a row spacing of 2.74 m growing Chardonnay and Merlot. Data collection campaigns/intensive observation periods (IOPs) in these sites were conducted in the veraison period (from mid-July to early August), when the crop evaporative demand increases.
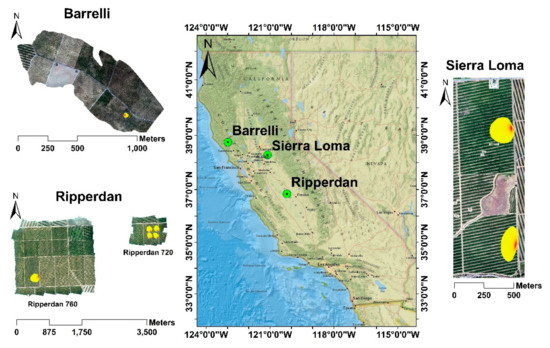
Figure 2.
Layout of study vineyards in Central Valley, California with estimated typical flux footprint/source area for the EC towers.
2.2. Procedure
Figure 3 illustrates the procedure used for this study. First, available eddy covariance (EC) flux tower data was filtered to select cloud-free days only. Then, five different ETd approaches were applied to the LE fluxes from the EC measurements for upscaling the ET to the daily timescale. The analysis was performed using EC observations at different vine phenological stages (April–May, June–August, and September–October). Finally, daily sUAS ET information, produced using the TSEB model, and results from the five approaches for upscaling/extrapolating the daily ET were compared against the measured ETd from the EC tower data. Two time windows were selected for the daily ET estimation: the first was near solar noon (1030–1330), and the second was in the afternoon (1430–1630). The reasons for these selections were (a) satellite overpass time, (b) sUAS flexibility, which allows for flights at different hours, including mid to late afternoon, and (c) an opportunity to assess the suitability of using later (2+ hours after solar noon) sUAS flights for the estimation of daily ET.
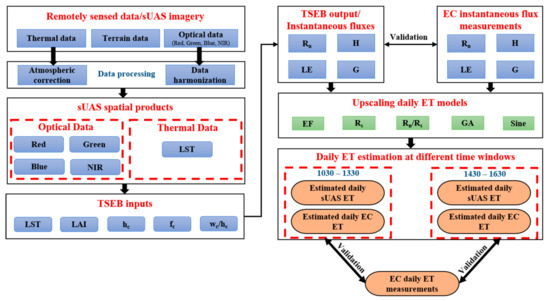
Figure 3.
Study methodology for assessing different upscaling daily ET methods in sUAS.
2.2.1. sUAS Data Processing
The AggieAir sUAS Program at Utah State University (https://uwrl.usu.edu/aggieair/ accessed on 10 December 2020) [55] acquired high-resolution imagery at 450 m above ground level (agl), resulting in visible and near-infrared data at a 0.10 m spatial resolution, and a thermal spatial resolution at 0.6 m. The spectral range of the visible and near-infrared data was similar to Landsat; however, the thermal band range was wider, with a bandwidth spanning from 7 to 14 µm. Thermal data was acquired using a radiometrically calibrated micro-bolometer camera. Table 1 lists the information concerning the different AggieAir sUAS flights. In this study, the obtained sUAS images were georectified using ground control points (GCPs). Details of the optical and thermal information are presented below.

Table 1.
Dates and times of AggieAir sUAS flights used in this study.
Thermal Data
Changes in the transmissivity and atmospheric radiance can adversely affect the sUAS thermal data [56]. Details about thermal data calibration can be found in the work by Torres-Rua [56], while the work by Torres-Rua et al. [57] shows that the TSEB model is insensitive to surface emissivity. The AggieAir sUAS Program has a thermal protocol to use over 90% of overlap for thermal raw imagery collected after sUAS launching but before mission data collection upon internal lens temperature stabilization of the microbolometer camera. These two steps address potential vignetting as well as the temperature drifting effect observed in other sUAS applications.
Optical Data
Radiometric agreement between different remote sensing platforms is important for further integration. An internal evaluation of the optical data obtained from different sUAS flights was performed by aggregating the high-resolution imagery up to Landsat scale using a point-spread function (PSF). The resulting 30-m pixels were found to agree with Landsat reflectance information. This is due to the use of different sensors than the ones used by Hassan-Esfahani et al. [58].
2.2.2. Eddy Covariance (EC) Fluxes
Surface energy fluxes (LE and H) were calculated from the EC measurements of the sonic temperature, water vapor, and vertical wind speed. In this study, the measurements obtained from the EC were averaged over a 60-min time interval to ensure appropriate averaging time for calculating the H and LE. The sensible heat flux was calculated from the product of the air density, the specific heat of air, and the covariance between the vertical wind speed and sonic temperature. The expression used to calculate H is shown in Equation (18).
where is the air density (kg/m3), is the heat capacity of the air at constant pressure (J/kg/K), is the vertical wind speed (m/s), and is the sonic temperature (Kelvins).
The latent heat flux (LE) was calculated from the product of the latent heat of vaporization () and the covariance between the vertical wind speed () and the water vapor density (). The formula used to calculate the LE is illustrated in Equation (19).
where is the water vapor density (kg/m3).
Table 2 describes the EC towers installed at the different vineyard sites to monitor ET. The EC measurements (April to October) obtained are the surface energy fluxes (Rn, H, and LE) and micrometeorological data. More details about the in situ micrometeorological measurements can be found in the work by Nassar et al. [7].

Table 2.
Description of EC towers in vineyards that were part of this study.
In Sierra Loma, each EC tower monitors grapevines of different ages, while 4 flux towers in Ripperdan 720 measure different water management approaches at 4 different blocks. In this study, the footprint analysis of each EC tower was performed to validate the results obtained from the TSEB model. The Kljun et al. [59] model was used for describing the fetch of the EC contribution area for the hourly period encompassing the sUAS flight times. The shape and orientation of the EC footprint depend on multiple micro-meteorological conditions that are observed by the EC towers installed at the sites, which include the friction velocity, wind speed, wind direction, roughness length, standard deviation of the crosswind velocity, and Monin–Obukhov length as well as the EC tower height. In this study, the authors did not include any energy balance closure to the EC information to minimize biases.
2.3. Goodness-of-Fit Statistics
2.3.1. Quantitative Statistics
The performance indices to evaluate the daily ET approaches in this study involved comparisons of the modeled ET from the five different approaches against daily ET measurements from the EC towers. Computed statistical metrics included the root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), Nash–Sutcliffe efficiency coefficient (NSE), and the coefficient of determination (R2). The NSE coefficient checks the capability of the model to reproduce the following statistical components: correlation coefficient of (r), mean (µ), and variance (s). NSE values range between −∞ and 1, where 1 represents a perfect agreement, while a value of 0 means that the model results are not better than the average of the variable of interest, and values < 0 indicate unacceptable model performance [60].
where denotes the observed value, denotes the modeled value, denotes the mean observed value, denotes the mean modeled value, and N represents the number of observations.
2.3.2. Graphical Representations
Different graphical representations were used to visualize and evaluate the datasets from the EC towers and the performance of the extrapolation techniques. Boxplots were created to describe the variance of surface energy fluxes (Rn, H, LE, and G) at each hour in the dataset. Boxplots were also used to evaluate the performance of the five daily ET extrapolation schemes by presenting the distribution of relative error at each individual hour during the daytime, as shown in the Appendix. Moreover, scatterplots were used to compare the modeled fluxes from TSEB and the measurements from EC systems to evaluate model performance.
3. Results and Discussion
3.1. Diurnal Variation of Energy Fluxes from EC Measurements
An example of the diurnal variation of surface energy fluxes (Rn, H, LE, and G) is shown in Figure 4 for the Sierra Loma vineyard. Diurnal variation plots for the other vineyard study sites (Ripperdan 760, Ripperdan 720, and Barrelli) are shown in Appendix B.1, Appendix C.1 and Appendix D.1 The boxplot at each individual hour represents the seasonal variation (April to October) of surface fluxes due to changes in the irrigation scheduling and variations in weather conditions (wind speed, air temperature, vapor pressure deficit, and soil moisture) [61]. Overall, the behavior of Rn diurnal variation is similar among the different sites, as the solar radiation is relatively consistent. As shown in Figure 4, Rn values are negative in the nighttime and late evening. In the daytime, Rn values vary, with maximum values of nearly 700 W/m2 at solar noon depending on the daily solar radiation. The diurnal pattern of Rn is almost systematic with a peak value appearing during midday, around 1200 standard time. The diurnal distribution of both H and LE exhibits a typical concave-down shape, with minimums in the early morning and late afternoon. The peak value appears near solar noon, between 1030 and 1330. Overnight, the H is almost negative, while the LE is approximately equal to zero, as the incoming solar radiation (Rs) value is 0 at night. Although this is not always the case, the approximation may be acceptable for night [62]. In summertime, the LE value overnight is very small and rarely exceeds 5–10% of the daily total [63]. The study by Shapland et al. [64], which was conducted to estimate the ET over vineyards in California, assumed that the turbulent fluxes are zero during the night to avoid the uncertainty associated with the flux measurement. Another study by Tolk et al. [65], which aimed to quantify the nighttime evapotranspiration ETN-to-24-h ET (ET24) of irrigated and dryland cotton in a semiarid climate, indicated that the ratio of ETN-to-ET24 ranged from an average of 3% for a dryland cotton crop to around 7% for irrigated alfalfa. The contribution of ETN-to-ET24 was the result of a relatively high nighttime vapor pressure deficit (VPD) and wind speed.
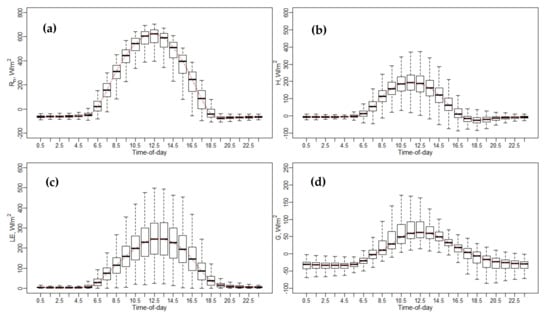
Figure 4.
Diurnal variations of energy fluxes at Sierra Loma Sites 1 and 2 for the years 2014 to 2018, from the April to October irrigation season. (a) Net radiation (Rn), (b) sensible heat flux (H), (c) latent heat flux (LE), (d) soil heat flux (G).
Flux observations indicated that the LE values were higher than the H across the different vineyards, as shown in Figure 4 and Appendix B.1, Appendix C.1 and Appendix D.1. These results stem from the fact that the vineyards are drip irrigated and, during most of the growing season, the cover crop is senescent, so ET is largely controlled by the vine canopy and, hence, mainly affected by the vine leaf stomatal conductance. The diurnal variation of soil heat flux (G) does not follow symmetric behavior, having a right skewness. As demonstrated in Figure 4 and Appendix B.1, Appendix C.1 and Appendix D.1, the G value is much lower than other energy fluxes (Rn, H, and LE), where the peak does not persist across different vineyard sites. For overnight and later evening, G is negative and could yield values around −100 W/m2, as shown in Figure 4d at Sierra Loma vineyard, with similar results obtained at the other vineyard sites included in this study. In the energy balance, usually, the G value is estimated as a portion of Rn (~0.35 Rn) for remote sensing ET models. Meanwhile, the G value is highly affected by the LAI, canopy architecture, row direction, and trellis design, as well as the incoming solar radiation. Reducing the canopy fractional cover results in an increased daytime soil heat flux (G), while increasing the areal coverage of vegetation leads to decreased soil heat flux and greater above-canopy latent heat fluxes, as long as there is ample root zone soil moisture to meet the atmospheric demand.
Figure 5 shows the LE diurnal variation at each individual EC tower included in this study. The boxplot at every hour represents the seasonal variation from April to October due to weather changes and irrigation scheduling. Overall, the general temporal trend of the LE has a shape that resembles solar radiation at different vineyard sites, with a peak value near solar noon, between 1030 and 1330. In early morning and overnight, the LE values were close to zero. Comparing the diurnal variation of LE at different vineyards, the Barrelli site had the lowest LE values. The Barrelli vineyard is located near the Pacific Coast shoreline, which brings cool maritime air that cools the warm interior valleys. The cool and moist air over Barrelli is associated with a decrease in the vapor pressure deficit (VPD) and more cloudiness, which causes a decrease in ET demand. In Sierra Loma and Ripperdan, the VPD and air temperature were higher than Barrelli, as both sites are exposed to a warm Mediterranean climate, which is characterized by abundant sunshine and a large day-to-night temperature difference and, therefore, increases the ET demand [66].
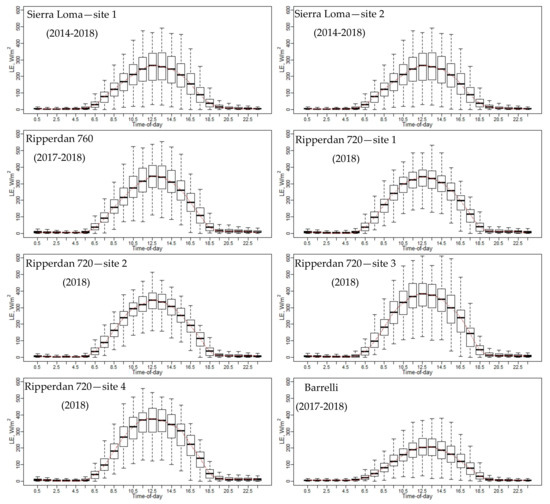
Figure 5.
Diurnal variations of LE for each EC included in this study for the years 2014 to 2018, from the April to October irrigation season.
To compare the contribution of the ET at different hours to the daily ET, additional statistics were included, such as the ratio of hourly ET (ETh)-to-daily ET (ETh/ETd) and the ratio of ETh-to-maximum hourly ET (ETh(max)) (ETh/ETh(max)). An example of the diurnal variation of both ratios (ETh/ETd and ETh/ETh(max)) at different phenological vine stages (bloom, April–May; veraison, June–August; and post-harvest, September–October) is shown in Figure 6 for the Sierra Loma vineyard, while the figures of other sites are shown in Appendix B.2, Appendix B.3, Appendix C.2, Appendix C.3, Appendix D.2 and Appendix D.3. The general trends of ETh/ETd and ETh/ETh(max) resemble a Gaussian behavior, with peak values at solar noon. The results also indicate that the vine phenological stage could affect both ratios in terms of the variation at each individual hour during the daytime. In the veraison stage, low variation was observed in the ETh/ETd and ETh/ETh(max) compared with the bloom and post-harvest stages. In the early growing season (April), the inter-row cover crop was at peak greenness, which was senesced by early June as the vines’ leaves were fully developed (see the phenocam data at different study sites showing the different vine phenological stages: https://hrsl.ba.ars.usda.gov/awhite/CAM/ accessed 10 December 2020). This transition resulted in the main source of transpiration from the inter-rows, where the turbulent exchange was relatively suppressed to the vines with high potential coupled with the atmosphere [67]. On the other hand, the high variability observed in ETh/ETd and ETh/ETh(max) ratios in the time period between September and October were due to vines senescence and stress in the post-harvest stage due to a lack of irrigation and low atmospheric demand, where the daily ET decreased significantly. Moreover, as shown in Figure 6, the results of the ETh/ETd indicate that the major contribution of the daily ET came from the midday time between 1030 to 1530, which represents at least 65% of the daily total. However, in early morning (~0630 to 0930) and evening (~1630 to 1930), the value of ETh/ETd was low, which together represents 25–35% of the daily ET.
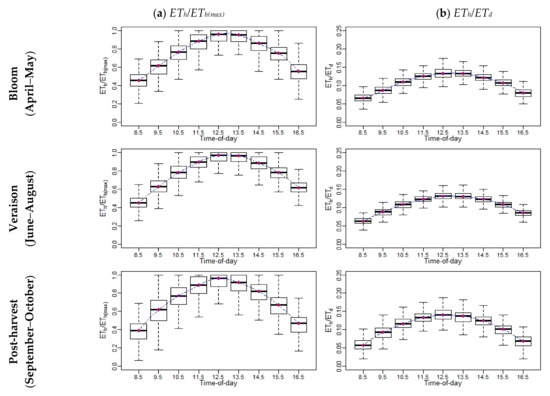
Figure 6.
An example of the diurnal variations of (a) and ETh/ETh(max) and (b) ETh/ETd at different phenological vine stages for Sierra Loma Sites 1 and 2 between 2014 and 2018.
3.2. Comparison between Different ETd Extrapolation Approaches Using the EC Measurements
Table 3 lists the goodness-of-fit statistics comparing the five different extrapolation approaches used to compute daily ET from the hourly EC at two different time windows: near solar noon (1030–1330) and afternoon (1430–1630) PST. The detailed statistics for RMSE and Er at each individual hour at the different vineyard sites are shown in Appendix A.1, Appendix A.2, Appendix B.4, Appendix B.5, Appendix C.4, Appendix C.5, Appendix D.4 and Appendix D.5. The analysis also considered all months segregated into three vine stages/periods (April–May, June–August, and September–October) to investigate how vine phenology could affect the accuracy of estimated daily ET due to the timing of both water uptake and growth. In general, the results indicate that the performance of the methods had different utility in computing an accurate daily ET at different vine canopy development and grapevine phenological stages (bloom, veraison, and post-harvest). As shown in Table 3, the MAPE was lower during the summer months (June–August) compared with the early growing season (April–May) of the vine crop and after harvesting time. Meanwhile, the results indicate that the extrapolated EC-derived ETd could be affected by the time during the day, as a better agreement was observed using instantaneous (hourly) EC ET between 1030 and 1330 PST than within the second time window (1430–1630 PST). Across multiple ETd upscaling approaches during the veraison stage and in the 1030–1330 time window, the MAPE yielded values ranging between 8% and 22%, while in the 1430–1630 time window, the MAPE range increased and yielded values between 15% and 35%.

Table 3.
Goodness-of-fit statistics of daily ET extrapolation methods at two different time windows (1030–1330 and 1430–1630 PST) using only EC tower information in California.
The results indicate that three methods (Rs, GA, and EF) among the five daily ET models have the best performance (low RMSE and MAPE values and a high NSE value). The Rs showed better agreement with the ground measurements among the other extrapolation approaches and was less sensitive to LE variation due to seasonal and climate differences, and particularly when using the one-time-of-day ET in the time window between 1030 and 1330. Using the Rs approach, RMSE values were less than 0.4 mm/day, while the NSE value was higher than 0.9 for all vine stages (season). These results are also supported by a previous study conducted by Cammalleri et al. [29], which compared several upscaling daily ET methods using observations from flux towers within the United States and were evaluated over multiple seasonal cycles. They reported that using solar radiation (Rs) for converting the instantaneous to a daily ET value is more robust. Comparing the less accurate daily ET extrapolation techniques, the Sine method marginally outperformed the Rn/Rs approach in terms of moderate to high error within the time window (1030–1330) in the bloom and veraison stages, while in the post-harvest stage, the Rn/Rs method gave better results than the Sine approach. Using these approaches increased the RMSE, which yielded values above 0.65 mm/day, while the MAPE values were greater than 20% in the time window between 1030 and 1330 for all vine stages (season). This implies that the Sine and Rn/Rs techniques do not work properly for a daily ET estimate in vineyards.
3.3. Assessing the Instantaneous TSEB ET versus EC Measurements
As a first step toward evaluating the performance of the TSEB model, a comparison between the field observations from the EC and modeled fluxes using the TSEB and the sUAS (Table 1) at four different study sites are presented in Figure 7. A more detailed model performance assessment for each energy flux term is shown in Table 4. Surface fluxes were estimated from the sUAS based on the TSEB model, averaged over the EC footprint, and then compared against the measured fluxes. As shown in Figure 7, the estimated fluxes derived from the TSEB model generally align along the 1:1 line at the different vineyard sites, indicating good agreement between the modeled and measured fluxes. Net radiation (Rn) demonstrates a close agreement with the in situ measurement, as indicated by lower RMSE, MAE, and MAPE values, and a high NSE value. The MAE and MAPE for Rn estimates at the different vineyard sites were less than 40 W/m2 and 10%, respectively, while the RMSE ranged between 26 W/m2 and 43 W/m2. The NSE yielded high values at the Sierra Loma and Ripperdan 760 sites, accounting for more than 0.85; however, at the Ripperdan 720 and Barrelli vineyards, the values decreased to less than 0.2 and 0.6, respectively. The results for H agreed well with the EC observations at the Sierra Loma and Ripperdan sites, with the MAE and MAPE values less than 43 W/m2 and 28%, respectively, while the RMSE values were less than 55 W/m2. However, at the Barrelli vineyard, the RMSE and MAE increased to 62 W/m2 and 46 W/m2, respectively, while the MAPE value was 22%. However, this site had only 2 samples to compute the difference statistics, making it difficult to reach any conclusions concerning the model performance in relation to the other sites. The results for LE indicate a slight increase in the RMSE compared to the H, varying between 51 W/m2 and 58 W/m2 at the Sierra Loma and Ripperdan vineyards. However, the Barrelli site results indicate that the RMSE of the LE was less than the H. Overall, the higher values of the RMSE obtained for the LE are attributed mainly to the TSEB method for calculating the LE, which is solved as the residual component of the surface energy balance, LE = Rn-H-G. Therefore, the uncertainties associated with the calculation of energy fluxes (Rn, H, and G) within the TSEB method can adversely affect the estimation of the LE. Another potential uncertainty could be related to the no use of flux closure in the eddy covariance (EC) data. According to previous studies (e.g., Neale et al. 2012) [68], heat fluxes (H and LE) are acceptable when the RMSE ranged between 20 W/m2 and 60 W/m2. This implies that the results of the H and LE obtained from the TSEB model across different vineyards were within an acceptable range and similar to prior studies [50]. The results for G indicate poor performance across the different vineyard sites, except for Ripperdan 720 vineyard, which had a MAPE of less than 25%. Part of these discrepancies between the modeled and observed G can be attributed to the assumption used in this study for calculating G, which is that as a portion of the soil net radiation (Rns), G = 0.35 Rns. This value was obtained based on a proposed method by Nieto et al. [49], which takes into consideration the diurnal variation of the G/Rns and found high scattering/uncertainty in the relationship, with an average value of 0.35 near solar noon. In this study, most of the flights were between 1000 and 1500, and at these time intervals around solar noon, the G/Rns fraction remained rather constant at ~0.35 (see Figure 4 in Nieto et al. (2019)) [49]. Therefore, for the sake of simplicity, and considering that the sinusoidal approach might be site-dependent, the constant fraction at 0.35 was used. This value is also broadly applied over a wide range of crops and environments. Meanwhile, vineyards are characterized by strong heterogeneity, which causes spatial and temporal variability in G values. According to Kustas et al. [69], the simple remote sensing methods for estimating G as a portion of Rn have significant uncertainty due to temporal variability in the G/Rn ratio.
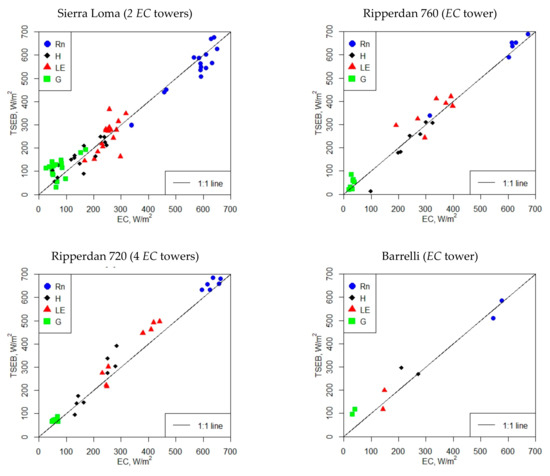
Figure 7.
Comparison of instantaneous TSEB sUAS energy fluxes against EC measurements (without flux closure). The presented subplots include the available sUAS imagery, as described in Table 1.

Table 4.
Goodness-of-fit statistics between the eddy covariance (EC) and the instantaneous TSEB sUAS fluxes at the different vineyard sites of this project.
3.4. Assessment of the Daily ET Extrapolation Approaches Using TSEB sUAS Results
The accuracy of the daily high-resolution ET from the TSEB depends largely on an accurate instantaneous ET estimate at the time of acquisition of the sUAS imagery, as well as the reliability of the approach used to scale up the TSEB-derived ET to a daily value. The five daily ET methods (EF, Rs, Rn/Rs, GA, and Sine) were applied using the modeled energy fluxes derived from the TSEB and compared against the EC-derived daily value, ETd, calculated by integrating the daytime LE fluxes measured by EC towers. Table 5 lists the goodness-of-fit statistics between the modeled daily ET using sUAS data sets and the ground-based EC daily measurements at two time windows during the day: 1030–1330 and 1430–1630. Figure 8 shows the relationship between the modeled and measured fluxes. Overall, the results indicate that the modeled ETd values have better agreement across different upscaling methods using the time window of 1030–1330 PST, while a significant deterioration was observed in the performance of all methods using the 1430–1630 period for upscaling. The RMSE and MAPE statistics yielded values greater than 1.2 mm/day and 25%, respectively, in the 1430–1630 time window; however, these values decreased to less than 1 mm/day and 20% across different methods using the TSEB output in the 1030–1330 timeframe, with one exception. In the case of the Sine approach, the RMSE and MAPE yielded values of 1.32 mm/day and 26%, respectively. These findings align with the results obtained when comparing different ETd methods using measurements from the EC tower (see Section 3.2), where RMSE and MAPE yielded values greater than 0.5 mm/day and 14% in the time window 1430–1630. However, using the time window of 1030–1330, the values of RMSE and MAPE decreased to less than 0.7 mm/day and 23%, respectively. The larger RMSE and MAPE values obtained in the sUAS ETd compared to the EC ETd are due to the bias in the TSEB-derived ET compared to the EC measurements. These results are also supported by previous studies conducted by Jackson et al. [30] and Colaizzi et al. [28], where scaling instantaneous ET to daily values showed better agreement when the measurement was taken within about 1–2 h of solar noon.

Table 5.
Goodness-of-fit statistics comparing multiple daily ET methods at two different time windows (1030–1330 and 1430–1630).
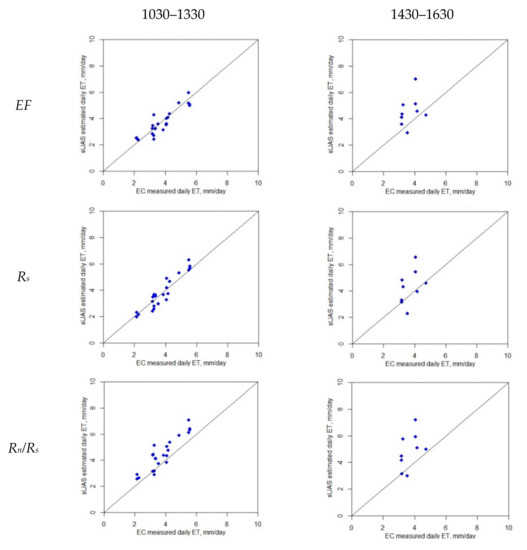
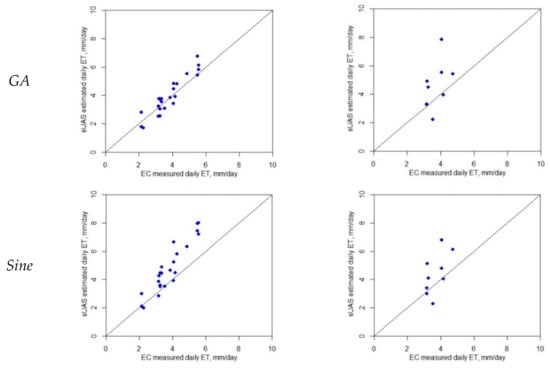
Figure 8.
Comparison between daily ET from TSEB sUAS and EC at two different time windows (1030–1330 and 1430–1630).
Although the results indicate that three (GA, EF, and Rs) out of the five methods for daily ET upscaling agree reasonably well with the ground-based measurements, the Rs technique yielded better agreement at all three sites (Sierra Loma, Ripperdan 720, and Barrelli). This approach generated a robust ETd when a single remote sensing-based ET estimate was taken within 1–2 h of solar noon and provided a close agreement with the ground truth ET measurement. This result also aligns with the EC ETd analysis, which indicates that the Rs approach has better statistical performance (see Table 3). Using the Rs approach for all vineyards, the RMSE values were 0.45 mm/day, and the MAPE was 10%, while the R2 was 0.88 for the time window of 1030–1330 (see Table 5, All Vineyards section).
These results agree with a previous study conducted by Wandera et al. [41], which showed that the Rs-based approach was better for upscaling compared with the EF method. That study was carried out over 41 FLUXNET validation sites for two different times of day, including 1100 and 1330. Furthermore, the found results are also supported by Cammalleri et al. [29], when comparing different daily extrapolation methods. Cammalleri et al. [29] found that the incoming solar radiation (Rs) was the most robust method with the least error when using EC data collected at different flux tower sites within the United States and over multiple seasons. The Rs approach for ET upscaling is highly recommended in situations where obtaining the daily net radiation is not possible [19] or, in some cases, where the modeled Rn is overestimated/underestimated, which will adversely affect the EF ratio. On the other hand, the G is more difficult to estimate than the Rs and Rn, which could limit the accuracy of the EF method. This might explain why the Rs method has a slightly higher agreement than the EF. Comparing the approaches with the lowest performance, the Sine method demonstrated the worst performance, with the largest RMSE and MAPE values and the lowest NSE value in the time window between 1030 and 1330. However, between 1430 and 1630, the results indicate that Sine performed slightly better than Rn/Rs. Still, the RMSE and MAPE values were high and the NSE and R2 values were very low. The hypothesis is that the heterogeneity in the field, due to vine biomass, cover crop, and bare soil, has a larger impact on the Rn/Rs and Sine approaches than other methods.
4. Conclusions
The objective of this study was to assess existing methodologies for upscaling ET from single time-of-day information to daily estimates over commercial vineyards in California’s Central Valley using EC flux measurements and the TSEB model with sUAS imagery. The extrapolation approaches included the evaporative fraction (EF), solar radiation (Rs), net radiation to incoming solar radiation (Rn/Rs), the Gaussian (GA), and Sine technique. First, analysis was performed using flux observations collected at eight EC towers located at three vineyards in California’s Central Valley: Sierra Loma, Ripperdan, and Barrelli. These sites are characterized by different climates, soils, vine variety, and trellis designs. The analysis also considered months of the growing season to coincide with three vine phenological stages (April–May (rapid vine growth, bloom/berry establishment), June–August (berry development/veraison), and September–October (harvest/post-harvest/vine senescence)) to investigate how vine phenology could affect the accuracy of the modeled daily ET due to timing of both water uptake and growth.
The EC analysis results indicate that three daily ET approaches (EF, Rs, and GA) out of five have a reasonable agreement with the EC-based measurements, with the Rs approach being preferred for daytime upscaling of ET across different stages of vine phenology, as it yielded the highest accuracy among the tested methods. Moreover, the results demonstrate that the methods could perform differently at different vine canopy development and grapevine phenology stages and at different time windows during the day. In the time window between 1030 and 1330, MAPE yielded values of 8% when using the Rs approach in the veraison stage, whereas this value increased to 17% between 1430 and 1630 h. In the bloom and post-harvest vine stages, the MAPE yielded values of 10% and 11%, respectively, when using Rs within the 1030–1330 time window, which then increased to 19% and 23%, respectively, between 1430 and 1630.
A similar result was obtained when applying the five ET upscaling methods using instantaneous TSEB-derived ET. The results reported that the Rs, out of the other methods, has better agreement with the ground measurements to extrapolate the instantaneous ET at the time of the sUAS acquisition to daily values, with an RMSE of 0.45 mm/day and an MAPE of 10% in the time window between 1030 and 1330 PST. The EF and GA methods performed relatively well, with a MAPE of 10% and 13%, respectively, in the same time window. However, between 1430 and 1630, the results indicate a significant deterioration in the performance of all methods, with the RMSE and MAPE values greater than 1.2 mm/day and 25%, respectively. The range in climate, vine variety, soils, trellis designs, and times when sUAS imagery was collected support the general results that the Rs extrapolation method can provide reliable daily ET estimates, particularly if the modeled ET is extrapolated from imagery collected 1–2 h before/after solar noon.
Author Contributions
Conceptualization, A.N.; data curation, J.A., L.H., J.P., M.M.A., W.W., L.M. and L.S.; formal analysis, A.N.; methodology, A.N.; project administration, N.D.; resources, C.C.; software, H.N.; supervision, A.T.-R., W.K. and L.H.; validation, A.N.; visualization, A.N.; writing—original draft, A.N.; writing—review and editing, A.T.-R., W.K. and L.H. All authors have read and agreed to the published version of the manuscript.
Funding
Funding provided by E&J Gallo Winery. Utah Water Research Laboratory contributed towards the acquisition and processing of the ground truth and sUAS imagery data collected during GRAPEX IOPs. We would like to acknowledge the financial support for this research from the NASA Applied Sciences Water Resources Program [NNX17AF51G] as well as the USDA Non-Assistance Cooperative Agreement 58-8042-5-092 funding. The USDA is an equal opportunity provider and employer.
Acknowledgments
We would like to thank the Aggieair Service Center team (Ian Gowing, Mark Winkelaar, and Shannon Syrstad) for their extraordinary support in this research, whose cooperation greatly improved the data collection and data processing, and the staff of Viticulture, Chemistry and Enology Division of E&J Gallo Winery for the assistance in the collection and processing of field data during GRAPEX IOPs. This project was partially financially supported by the NASA Applied Sciences Water Resources Program under Award no. 200906 NNX17AF51G, and by the Utah Water Research Laboratory at Utah State University. The authors would like to thank Carri Richards for editing this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Daily ET Analysis at Sierra Loma Vineyard Near Lodi, California
Appendix A.1. Relative Error (Er) at Hourly Scale for EC Measurements
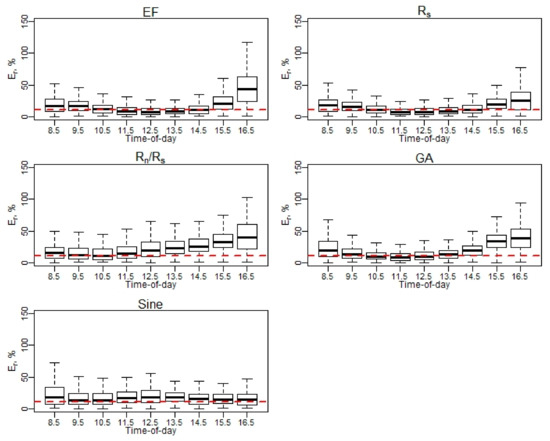
Figure A1.
Er of daily EC ET (April–May).
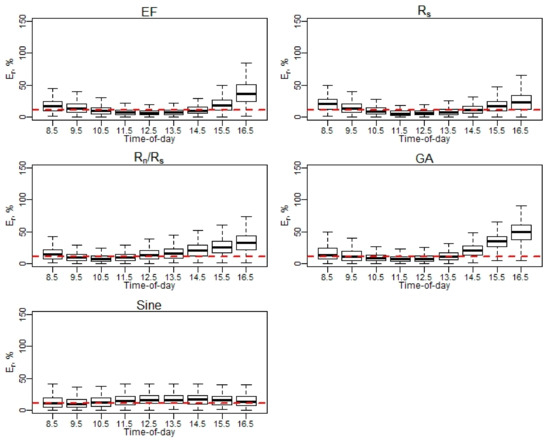
Figure A2.
Er of daily EC ET (June–August).
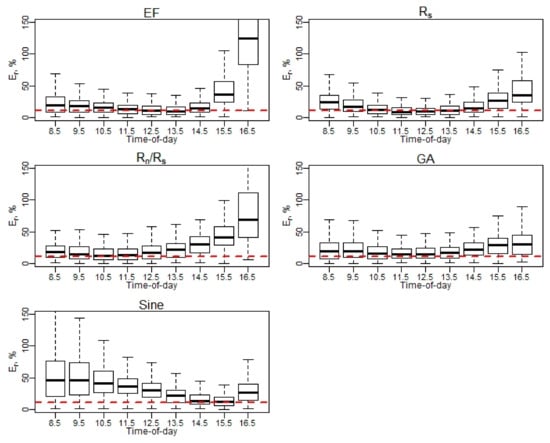
Figure A3.
Er of daily EC ET (September–October). Note: Red dash line represents a 10% relative error (Er).
Appendix A.2. Daily RMSE Performance Using Hourly EC ET Values
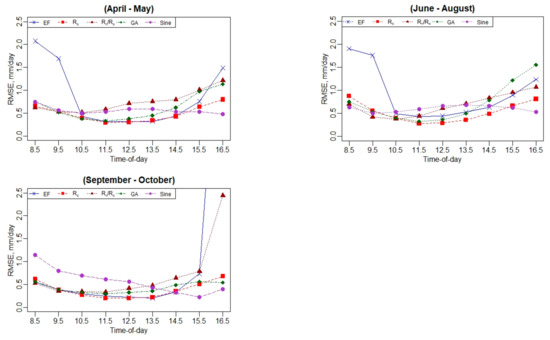
Figure A4.
Daily RMSE performance using hourly EC ET values.
Appendix B. Daily ET Analysis at Ripperdan 760 Vineyard, California
Appendix B.1. Diurnal Variation of Surface Energy Fluxes (Rn, H, LE, and G)
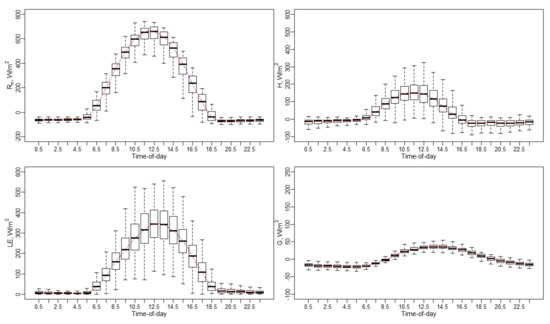
Figure A5.
Diurnal variation of surface energy fluxes (Rn, H, LE, and G).
Appendix B.2. Hourly ET to Maximum Hourly ET Ratio (ETh/ETh(max)) Variation Using EC Measurements
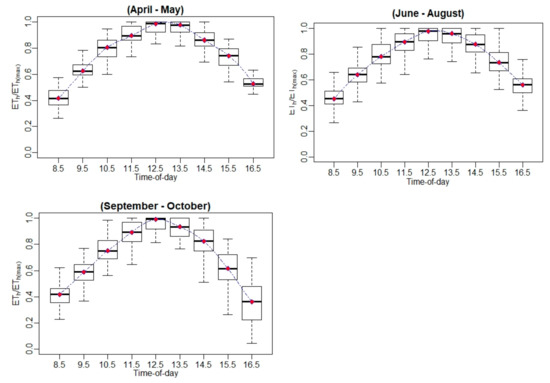
Figure A6.
Hourly ET-to-maximum hourly ET ratio (ETh/ETh(max)) variation using EC measurements.
Appendix B.3. Hourly ET-to-Daily ET Ratio (ETh/ETd) variation Using EC Measurements
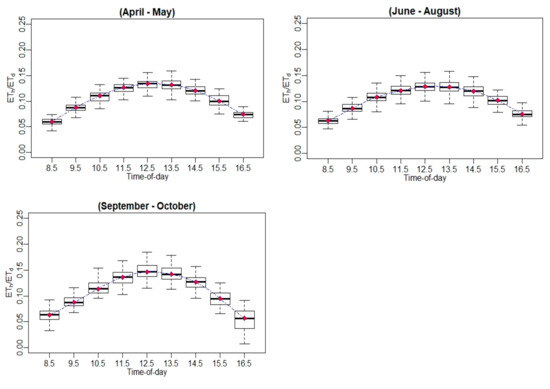
Figure A7.
Hourly ET to daily ET ratio (ETh/ETd) variation using EC measurements.
Appendix B.4. Relative Error (Er) at Hourly Scale for EC Measurements
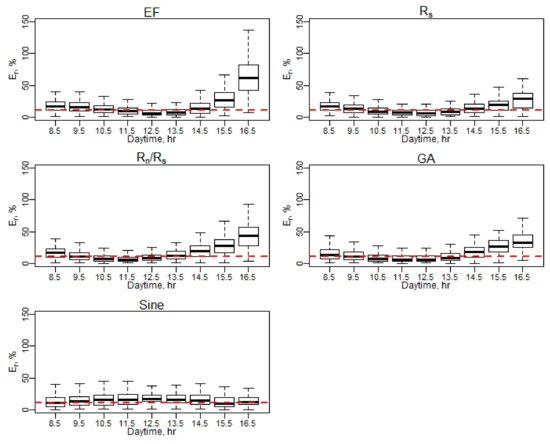
Figure A8.
Er of daily EC ET (April–May).
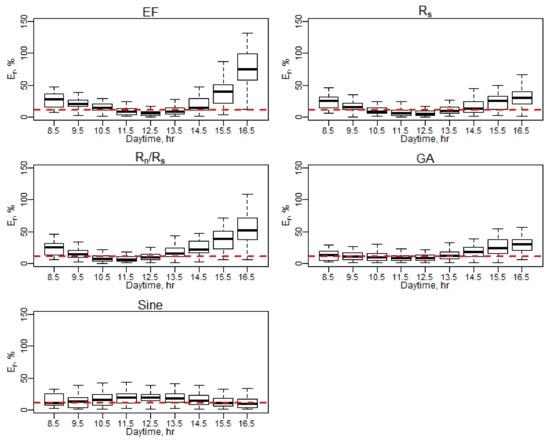
Figure A9.
Er of daily EC ET (June–August).
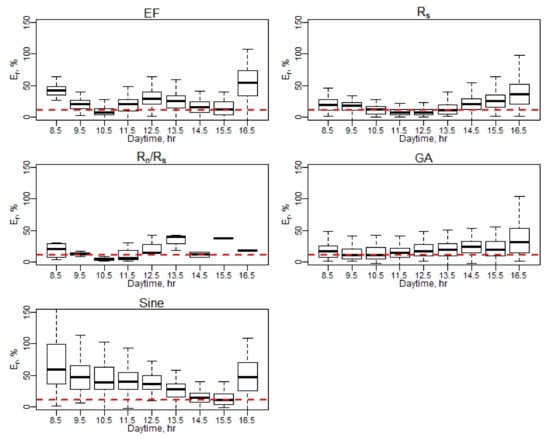
Figure A10.
Er of daily EC ET (September–October). Note: Red dash line represents a 10% relative error (Er).
Appendix B.5. Daily RMSE Performance Using Hourly EC ET Values
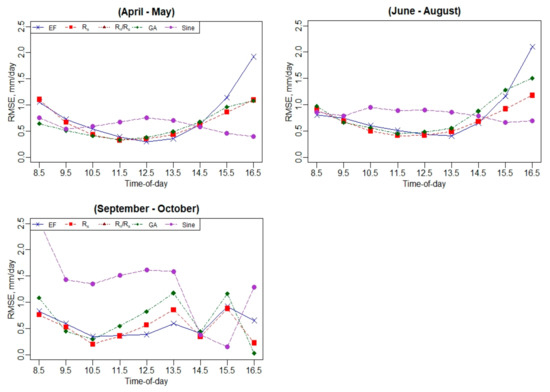
Figure A11.
Daily RMSE performance using hourly EC ET values.
Appendix C. Daily ET Analysis at Ripperdan 720 Vineyard, California
Appendix C.1. Diurnal Variation of Surface Energy Fluxes (Rn, H, LE, and G)
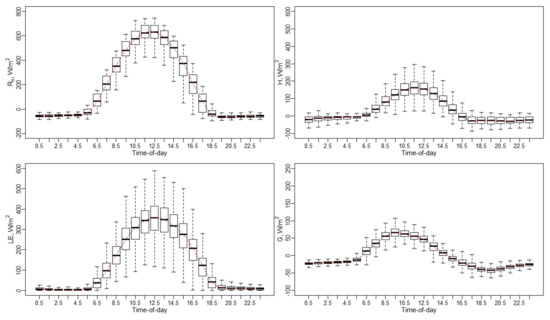
Figure A12.
Diurnal variation of surface energy fluxes (Rn, H, LE, and G).
Appendix C.2. Hourly ET-to-Maximum Hourly ET Ratio (ETh/ETh(max)) Variation Using EC Measurements
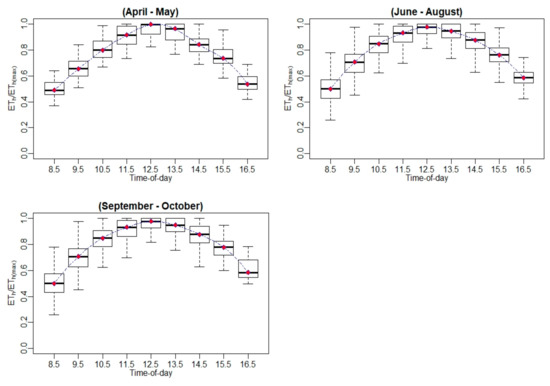
Figure A13.
Hourly ET-to-maximum hourly ET ratio (ETh/ETh(max)) variation using EC measurements.
Appendix C.3. Hourly ET-to-Daily ET Ratio (ETh/ETd) Variation Using EC Measurements
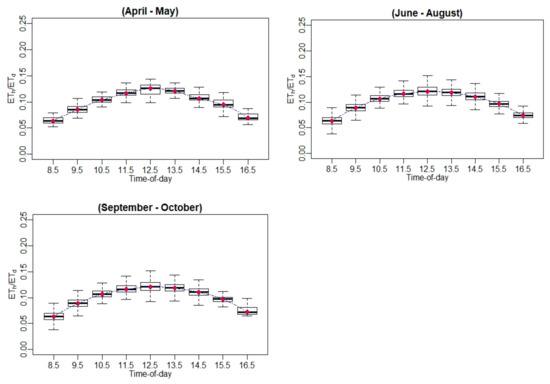
Figure A14.
Hourly ET-to-daily ET ratio (ETh/ETd) variation using EC measurements.
Appendix C.4. Relative Error (Er) at Hourly Scale for EC Measurements
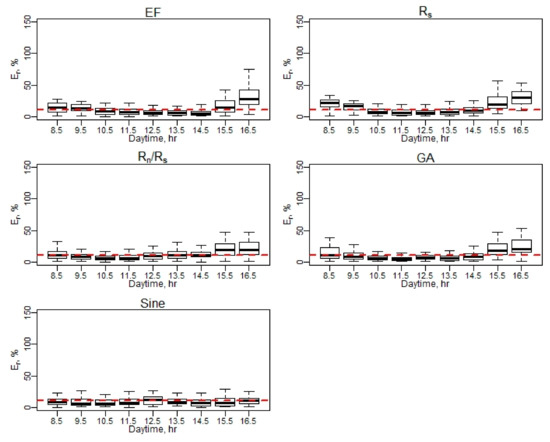
Figure A15.
Er of daily EC ET (April–May).
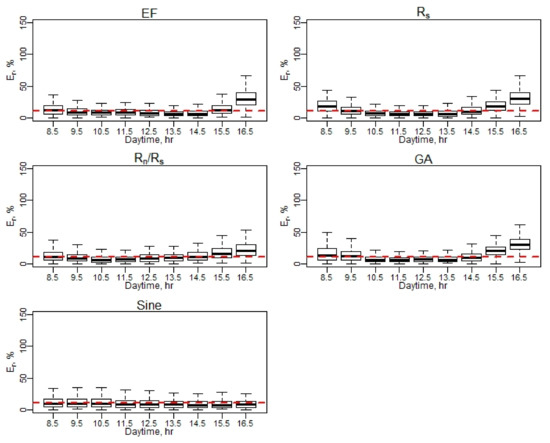
Figure A16.
Er of daily EC ET (June–August).
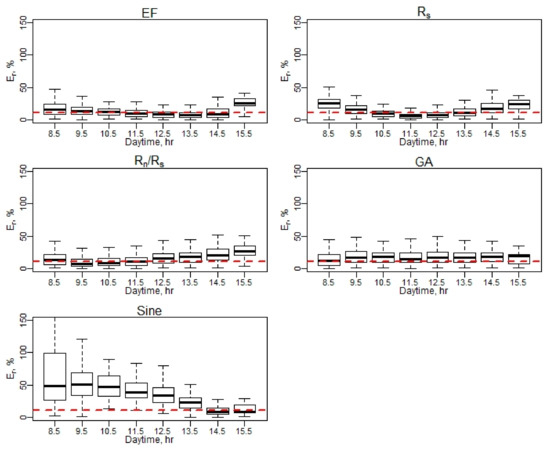
Figure A17.
Er of daily EC ET (September–October). Note: Red dash line represents a 10% relative error (Er).
Appendix C.5. Daily RMSE Performance Using Hourly EC ET Values
Figure A18.
Daily RMSE performance using hourly EC ET values.
Appendix D. Daily ET Analysis at Barrelli Vineyard, California
Appendix D.1. Diurnal Variation of Surface Energy Fluxes (Rn, H, LE, and G)
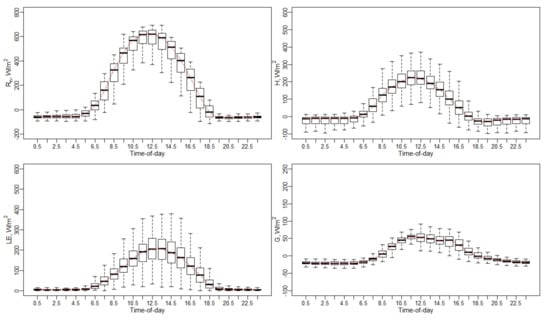
Figure A19.
Diurnal variation of surface energy fluxes (Rn, H, LE, and G).
Appendix D.2. Hourly ET-to-Maximum Hourly ET Ratio (ETh/ETh(max)) Variation Using EC Measurements
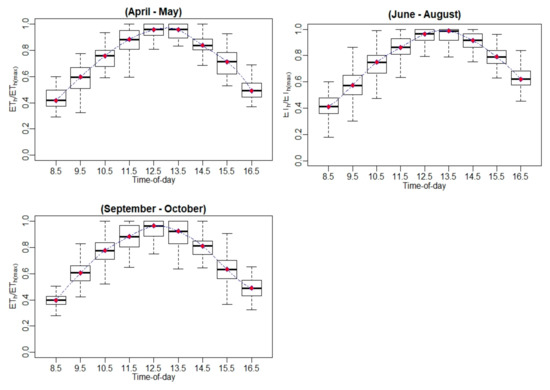
Figure A20.
Hourly ET-to-maximum hourly ET ratio (ETh/ETh(max)) variation using EC measurements.
Appendix D.3. Hourly ET-to-Daily ET Ratio (ETh/ETd) Variation Using EC Measurements
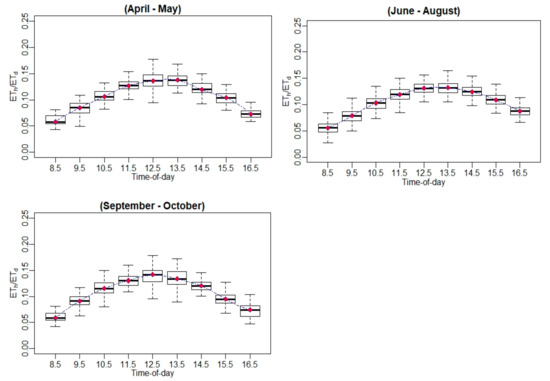
Figure A21.
Hourly ET-to-daily ET ratio (ETh/ETd) variation using EC measurements.
Appendix D.4. Relative Error (Er) at Hourly Scale for EC Measurements
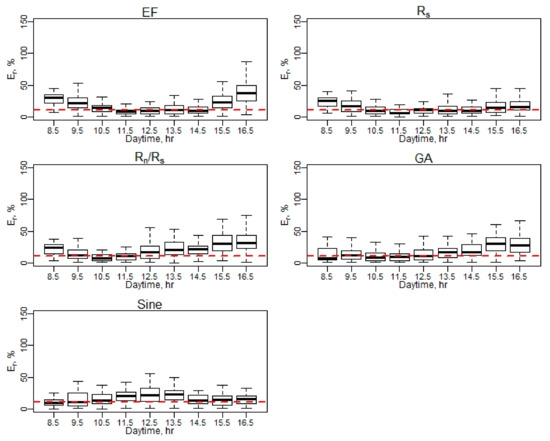
Figure A22.
Er of daily EC ET (April–May).
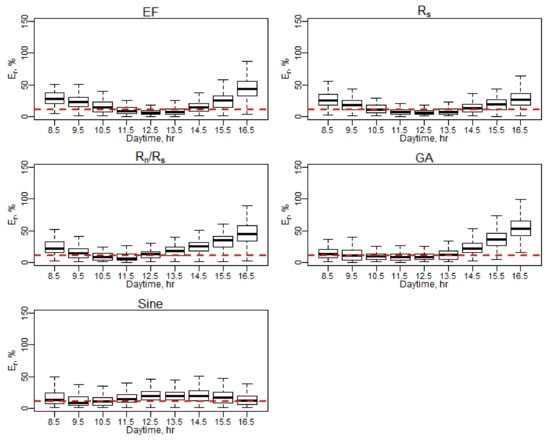
Figure A23.
Er of daily EC ET (June–August).
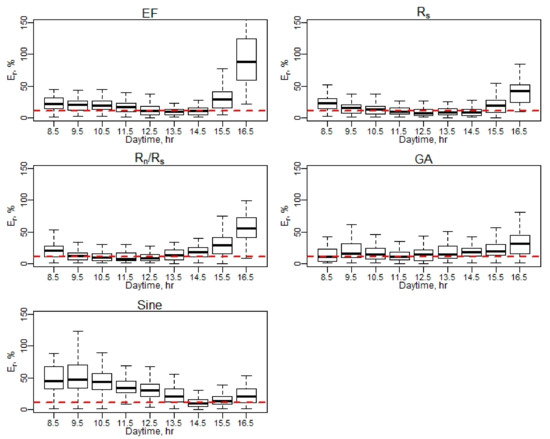
Figure A24.
Er of daily EC ET (September–October). Note: Red dash line represents a 10% relative error (Er).
Appendix D.5. Daily RMSE Performance Using Hourly EC ET Values
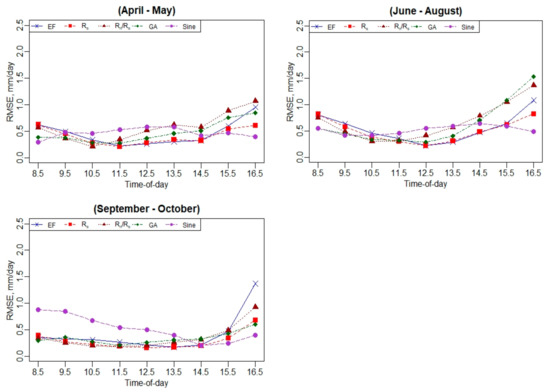
Figure A25.
Daily RMSE performance using hourly EC ET values.
References
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New Analytical Derivation of the Mean Annual Water-Energy Balance Equation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Housh, M.; Cai, X.; Ng, T.L.; McIsaac, G.F.; Ouyang, Y.; Khanna, M.; Sivapalan, M.; Jain, A.K.; Eckhoff, S.; Gasteyer, S.; et al. System of Systems Model for Analysis of Biofuel Development. J. Infrastruct. Syst. 2015, 21, 04014050. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Jiang, X.; Tang, R.; Li, Z.-L.; Zhang, Y.; Huang, C.; Ru, C. Estimation of Daily Evapotranspiration Using Instantaneous Decoupling Coefficient from the MODIS and Field Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1832–1838. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R. A Landsat-Based Energy Balance and Evapotranspiration Model in Western US Water Rights Regulation and Planning. Irrig. Drain. Syst. 2005, 19, 251–268. [Google Scholar] [CrossRef]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, L.; González-Dugo, M.P.; Cammalleri, C.; d’Urso, G.; Pimstein, A.; et al. Mapping Daily Evapotranspiration at Field to Continental Scales Using Geostationary and Polar Orbiting Satellite Imagery. Hydrol. Earth Syst. Sci. 2011, 15, 223–239. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat Thermal Imagery in Monitoring Evapotranspiration and Managing Water Resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Nassar, A.; Torres-Rua, A.; Kustas, W.; Nieto, H.; McKee, M.; Hipps, L.; Stevens, D.; Alfieri, J.; Prueger, J.; Alsina, M.M.; et al. Influence of Model Grid Size on the Estimation of Surface Fluxes Using the Two Source Energy Balance Model and sUAS Imagery in Vineyards. Remote Sens 2020, 12, 342. [Google Scholar] [CrossRef] [Green Version]
- Drexler, J.Z.; Snyder, R.L.; Spano, D.; Paw U, K.T. A Review of Models and Micrometeorological Methods Used to Estimate Wetland Evapotranspiration. Hydrol. Process. 2004, 18, 2071–2101. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Carrasco, M.; Olioso, A.; Acevedo, C.; Poblete, C. Latent Heat Flux over Cabernet Sauvignon Vineyard Using the Shuttleworth and Wallace Model. Irrig. Sci. 2006, 25, 161–170. [Google Scholar] [CrossRef]
- Parry, C.K.; Nieto, H.; Guillevic, P.; Agam, N.; Kustas, W.P.; Alfieri, J.; McKee, L.; McElrone, A.J. An Intercomparison of Radiation Partitioning Models in Vineyard Canopies. Irrig. Sci. 2019, 37, 239–252. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Alfieri, J.G.; Gao, F.; Hipps, L.E.; Los, S.; Prueger, J.H.; McKee, L.G.; Anderson, M.C. Impact of Different within-Canopy Wind Attenuation Formulations on Modelling Sensible Heat Flux Using TSEB. Irrig. Sci. 2019, 37, 315–331. [Google Scholar] [CrossRef]
- University of California Agriculture; the California Garden Web. Available online: http://cagardenweb.ucanr.edu (accessed on 25 December 2020).
- Mitcham, E.J.; Elkins, R.B. Pear Production and Handling Manual; University of California: Oakland, CA, USA, 2007; ISBN 9781879906655. [Google Scholar]
- Prueger, J.H.; Parry, C.K.; Kustas, W.P.; Alfieri, J.G.; Alsina, M.M.; Nieto, H.; Wilson, T.G.; Hipps, L.E.; Anderson, M.C.; Hatfield, J.L.; et al. Crop Water Stress Index of an Irrigated Vineyard in the Central Valley of California. Irrig. Sci. 2019, 37, 297–313. [Google Scholar] [CrossRef] [Green Version]
- USDA—National Agricultural Statistics Service—California. Available online: http://www.nass.usda.gov/ca (accessed on 25 December 2020).
- Alfieri, J.G.; Kustas, W.P.; Nieto, H.; Prueger, J.H.; Hipps, L.E.; McKee, L.G.; Gao, F.; Los, S. Influence of Wind Direction on the Surface Roughness of Vineyards. Irrig. Sci. 2019, 37, 359–373. [Google Scholar] [CrossRef]
- Nassar, A.; Torres-Rua, A.F.; Nieto, H.; Alfieri, J.G.; Hipps, L.E.; Prueger, J.H.; Alsina, M.M.; McKee, L.G.; White, W.; Kustas, W.P.; et al. Implications of Soil and Canopy Temperature Uncertainty in the Estimation of Surface Energy Fluxes Using TSEB2T and High-Resolution Imagery in Commercial Vineyards. In Proceedings of the SPIE, Online, 26 May 2020. [Google Scholar]
- Niu, H.; Zhao, T.; Wang, D.; Chen, Y. Evapotranspiration Estimation with UAVs in Agriculture: A Review. Preprints 2019. [Google Scholar] [CrossRef]
- Chávez, J.L.; Neale, C.M.U.; Prueger, J.H.; Kustas, W.P. Daily Evapotranspiration Estimates from Extrapolating Instantaneous Airborne Remote Sensing ET Values. Irrig. Sci. 2008, 27, 67–81. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. A Data Fusion Approach for Mapping Daily Evapotranspiration at Field Scale. Water Resour. Res. 2013, 49, 4672–4686. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Gao, F.; Hain, C.R.; Kustas, W.P. Mapping Daily Evapotranspiration at Field Scales over Rainfed and Irrigated Agricultural Areas Using Remote Sensing Data Fusion. Agric. For. Meteorol. 2014, 186, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Knipper, K.R.; Kustas, W.P.; Anderson, M.C.; Alsina, M.M.; Hain, C.R.; Alfieri, J.G.; Prueger, J.H.; Gao, F.; McKee, L.G.; Sanchez, L.A. Using High-Spatiotemporal Thermal Satellite ET Retrievals for Operational Water Use and Stress Monitoring in a California Vineyard. Remote Sens. 2019, 11, 2124. [Google Scholar] [CrossRef] [Green Version]
- Tsouros, D.C.; Bibi, S.; Sarigiannidis, P.G. A Review on UAV-Based Applications for Precision Agriculture. Information 2019, 10, 349. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, H.H.M. Evapotranspiration from UAV Images: A New Scale of Measurements; Department of Geosciences and Natural Resource Management, Faculty of Science, University of Copenhagen: Copenhagen, Denmark, 2016. [Google Scholar]
- Nassar, A.; Torres-Rue, A.F.; McKee, M.; Kustas, W.P.; Coopmans, C.; Nieto, H.; Hipps, L. Assessment of UAV Flight Times for Estimation of Daily High Resolution Evapotranspiration in Complex Agricultural Canopy Environments; Universities Council in Water Resources (UCOWR): Snowbird, UT, USA, 2019. [Google Scholar]
- Zhang, C.; Long, D.; Zhang, Y.; Anderson, M.C.; Kustas, W.P.; Yang, Y. A Decadal (2008–2017) Daily Evapotranspiration Data Set of 1 Km Spatial Resolution and Spatial Completeness across the North China Plain Using TSEB and Data Fusion. Remote Sens. Environ. 2021, 262, 112519. [Google Scholar] [CrossRef]
- Allen, G.; Morton, C.; Kamble, B.; Kilic, A.; Huntington, J.; Thau, D.; Gorelick, N.; Erickson, T.; Moore, R.; Trezza, R.; et al. 2015 EEFlux: A Landsat-Based Evapotranspiration Mapping Tool on the Google Earth Engine. In Proceedings of the 2015 ASABE/IA Irrigation Symposium: Emerging Technologies for Sustainable Irrigation—A Tribute to the Career of Terry Howell, Sr. Conference Proceedings, Long Beach, CA, USA, 10–12 November 2015. [Google Scholar]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Comparison of Five Models to Scale Daily Evapotranspiration from One-Time-of-Day Measurements. Trans. ASABE 2006, 49, 1409–1417. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of Evapotranspiration Fluxes from Instantaneous to Daytime Scales for Thermal Remote Sensing Applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Jackson, R.D.; Hatfield, J.L.; Reginato, R.J.; Idso, S.B.; Pinter, P.J. Estimation of Daily Evapotranspiration from One Time-of-Day Measurements. Agric. Water Manag. 1983, 7, 351–362. [Google Scholar] [CrossRef]
- Crago, R.D. Conservation and Variability of the Evaporative Fraction during the Daytime. J. Hydrol. 1996, 180, 173–194. [Google Scholar] [CrossRef]
- Crago, R.D. Comparison of the Evaporative Fraction and the Priestley-Taylor α for Parameterizing Daytime Evaporation. Water Resour. Res. 1996, 32, 1403–1409. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Coudert, B.; Chirouze, J.; Ceschia, E.; Le Dantec, V.; Marloie, O.; Chehbouni, G.; Lagouarde, -P.J. Reconstruction of Temporal Variations of Evapotranspiration Using Instantaneous Estimates at the Time of Satellite Overpass. Hydrol. Earth Syst. Sci. 2012, 16, 2995–3010. [Google Scholar] [CrossRef] [Green Version]
- Suleiman, A.; Crago, R. Hourly and Daytime Evapotranspiration from Grassland Using Radiometric Surface Temperatures. Agron. J. 2004, 96, 384. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Gurney, R.J.; Hsu, A.Y.; Ormsby, J.P. FIFE: The Variation in Energy Partition at Surface Flux Sites. IAHS Publ. 1989, 186, 523–534. [Google Scholar]
- Hoedjes, J.C.B.; Chehbouni, A.; Jacob, F.; Ezzahar, J.; Boulet, G. Deriving Daily Evapotranspiration from Remotely Sensed Instantaneous Evaporative Fraction over Olive Orchard in Semi-Arid Morocco. J. Hydrol. 2008, 354, 53–64. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Kang, S.; Li, F.; Zhang, L.; Zhang, B. Vineyard Evaporative Fraction Based on Eddy Covariance in an Arid Desert Region of Northwest China. Agric. Water Manag. 2008, 95, 937–948. [Google Scholar] [CrossRef]
- Zhang, L.; Lemeur, R. Evaluation of Daily Evapotranspiration Estimates from Instantaneous Measurements. Agric. For. Meteorol. 1995, 74, 139–154. [Google Scholar] [CrossRef]
- Gentine, P.; Entekhabi, D.; Chehbouni, A.; Boulet, G.; Duchemin, B. Analysis of Evaporative Fraction Diurnal Behaviour. Agric. For. Meteorol. 2007, 143, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Van Niel, T.; McVicar, T.; Roderick, M.; Dijk, A.; Beringer, J.; Hutley, L.; Gorsel, E. Upscaling Latent Heat Flux for Thermal Remote Sensing Studies: Comparison of Alternative Approaches and Correction of Bias. J. Hydrol. 2012, 468–469, 35–46. [Google Scholar] [CrossRef]
- Wandera, L.; Mallick, K.; Kiely, G.; Roupsard, O.; Peichl, M.; Magliulo, V. Upscaling Instantaneous to Daily Evapotranspiration Using Modelled Daily Shortwave Radiation for Remote Sensing Applications: An Artificial Neural Network Approach. Hydrol. Earth Syst. Sci. 2017, 21, 197–215. [Google Scholar] [CrossRef] [Green Version]
- French, A.N.; Fitzgerald, G.; Hunsaker, D.; Barnes, E.; Clarke, T.; Lesch, S.; Roth, R.; Pinter, P. Estimating Spatially Distributed Cotton Water Use from Thermal Infrared Aerial Imagery. Impacts Glob. Clim. Chang. 2005. [Google Scholar] [CrossRef]
- Liu, S.; Su, H.; Zhang, R.; Tian, J.; Chen, S.; Wang, W.; Yang, L.; Liang, H. Based on the Gaussian Fitting Method to Derive Daily Evapotranspiration from Remotely Sensed Instantaneous Evapotranspiration. Adv. Meteorol. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source Approach for Estimating Soil and Vegetation Energy Fluxes in Observations of Directional Radiometric Surface Temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Prueger, J.H.; Diak, G.R. Surface Flux Estimation Using Radiometric Temperature: A Dual-Temperature-Difference Method to Minimize Measurement Errors. Water Resour. Res. 2000, 36, 2263–2274. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Alfieri, J.G.; Anderson, M.C.; Colaizzi, P.D.; Prueger, J.H.; Evett, S.R.; Neale, C.M.U.; French, A.N.; Hipps, L.E.; Chávez, J.L.; et al. Evaluating the Two-Source Energy Balance Model Using Local Thermal and Surface Flux Observations in a Strongly Advective Irrigated Agricultural Area. Adv. Water Resour. 2012, 50, 120–133. [Google Scholar] [CrossRef] [Green Version]
- Gao, F.; Kustas, W.; Anderson, M. A Data Mining Approach for Sharpening Thermal Satellite Imagery over Land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef] [Green Version]
- Kustas, W.P.; Norman, J.M. A Two-Source Approach for Estimating Turbulent Fluxes Using Multiple Angle Thermal Infrared Observations. Water Resour. Res. 1997, 33, 1495–1508. [Google Scholar] [CrossRef]
- Nieto, H.; Kustas, W.P.; Torres-Rúa, A.; Alfieri, J.G.; Gao, F.; Anderson, M.C.; White, W.A.; Song, L.; Del Mar Alsina, M.; Prueger, J.H.; et al. Evaluation of TSEB Turbulent Fluxes Using Different Methods for the Retrieval of Soil and Canopy Component Temperatures from UAV Thermal and Multispectral Imagery. Irrig. Sci. 2019, 37, 389–406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xia, T.; Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Gao, F.; McKee, L.; Prueger, J.H.; Geli, H.M.E.; Neale, C.M.U.; Sanchez, L.; et al. Mapping Evapotranspiration with High-Resolution Aircraft Imagery over Vineyards Using One- and Two-Source Modeling Schemes. Hydrol. Earth Syst. Sci. 2016, 20, 1523–1545. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W. Aspects of Bulk Atmospheric Boundary Layer Similarity under Free-Convective Conditions. Rev. Geophys. 1999, 37, 439–451. [Google Scholar] [CrossRef]
- Kustas, W.P.; Nieto, H.; Morillas, L.; Anderson, M.C.; Alfieri, J.G.; Hipps, L.E.; Villagarcía, L.; Domingo, F.; Garcia, M. Revisiting the Paper “Using Radiometric Surface Temperature for Surface Energy Flux Estimation in Mediterranean Drylands from a Two-Source Perspective”. Remote Sens. Environ. 2016, 184, 645–653. [Google Scholar] [CrossRef] [Green Version]
- Kondo, J.; Ishida, S. Sensible Heat Flux from the Earth’s Surface under Natural Convective Conditions. J. Atmos. Sci. 1997, 54, 498–509. [Google Scholar] [CrossRef]
- Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Knipper, K.; Torres-Rua, A.; Parry, C.K.; Nieto, H.; Agam, N.; White, W.A.; Gao, F.; et al. The Grape Remote Sensing Atmospheric Profile and Evapotranspiration Experiment. Bull. Am. Meteorol. Soc. 2018, 99, 1791–1812. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Utah State University AggieAir. Available online: https://uwrl.usu.edu/aggieair/index (accessed on 25 December 2020).
- Torres-Rua, A. Vicarious Calibration of sUAS Microbolometer Temperature Imagery for Estimation of Radiometric Land Surface Temperature. Sensors 2017, 17, 1499. [Google Scholar] [CrossRef] [Green Version]
- Torres-Rua, A.F.; Ticlavilca, A.M.; Aboutalebi, M.; Nieto, H.; Alsina, M.M.; White, A.; Prueger, J.H.; Alfieri, J.G.; Hipps, L.E.; McKee, L.G.; et al. Estimation of Evapotranspiration and Energy Fluxes Using a Deep-Learning-Based High-Resolution Emissivity Model and the Two-Source Energy Balance Model with sUAS Information. In Proceedings of the SPIE, Online, 14 May 2020. [Google Scholar]
- Hassan-Esfahani, L.; Ebtehaj, A.M.; Torres-Rua, A.; McKee, M. Spatial Scale Gap Filling Using an Unmanned Aerial System: A Statistical Downscaling Method for Applications in Precision Agriculture. Sensors 2017, 17, 2106. [Google Scholar] [CrossRef] [Green Version]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Yang, Y.; Wu, R.; Gui, D.; Xue, J.; Liu, Y.; Yan, D. Improving Estimation of Cropland Evapotranspiration by the Bayesian Model Averaging Method with Surface Energy Balance Models. Atmosphere 2019, 10, 188. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Tong, L.; Li, F.; Zhang, L.; Zhang, B.; Kang, S. Variability in Energy Partitioning and Resistance Parameters for a Vineyard in Northwest China. Agric. Water Manag. 2009, 96, 955–962. [Google Scholar] [CrossRef]
- Brutsaert, W.; Chen, D. Diurnal Variation of Surface Fluxes During Thorough Drying (or Severe Drought) of Natural Prairie. Water Resour. Res. 1996, 32, 2013–2019. [Google Scholar] [CrossRef]
- Sugita, M.; Brutsaert, W. Daily Evaporation over a Region from Lower Boundary Layer Profiles Measured with Radiosondes. Water Resour. Res. 1991, 27, 747–752. [Google Scholar] [CrossRef]
- Shapland, T.M.; Snyder, R.L.; Smart, D.R.; Williams, L.E. Estimation of Actual Evapotranspiration in Winegrape Vineyards Located on Hillside Terrain Using Surface Renewal Analysis. Irrig. Sci. 2012, 30, 471–484. [Google Scholar] [CrossRef]
- Tolk, J.A.; Howell, T.A.; Evett, S.R. Nighttime Evapotranspiration from Alfalfa and Cotton in a Semiarid Climate. Agron. J. 2006, 98, 730–736. [Google Scholar] [CrossRef] [Green Version]
- Knipper, K.R.; Kustas, W.P.; Anderson, M.C.; Nieto, H.; Alfieri, J.G.; Prueger, J.H.; Hain, C.R.; Gao, F.; McKee, L.G.; Mar Alsina, M.; et al. Using High-Spatiotemporal Thermal Satellite ET Retrievals to Monitor Water Use over California Vineyards of Different Climate, Vine Variety and Trellis Design. Agric. Water Manag. 2020, 241, 106361. [Google Scholar] [CrossRef]
- Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y.; et al. Monitoring Daily Evapotranspiration over Two California Vineyards Using Landsat 8 in a Multi-Sensor Data Fusion Approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef] [Green Version]
- Neale, C.M.U.; Geli, H.M.E.; Kustas, W.P.; Alfieri, J.G.; Gowda, P.H.; Evett, S.R.; Prueger, J.H.; Hipps, L.E.; Dulaney, W.P.; Chávez, J.L.; et al. Soil Water Content Estimation Using a Remote Sensing Based Hybrid Evapotranspiration Modeling Approach. Adv. Water Resour. 2012, 50, 152–161. [Google Scholar] [CrossRef]
- Kustas, W.P.; Prueger, J.H.; Hatfield, J.L.; Ramalingam, K.; Hipps, L.E. Variability in Soil Heat Flux from a Mesquite Dune Site. Agric. For. Meteorol. 2000, 103, 249–264. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).