Evaluation of Five Deep Learning Models for Crop Type Mapping Using Sentinel-2 Time Series Images with Missing Information
Abstract
:1. Introduction
- What accuracies can different deep learning models achieve for crop type classification by using the Sentinel-2 TSD with missing information (unfilled TSD)?
- Can these models achieve higher accuracies when using the Sentinel-2 TSD after filling in missing information (filled TSD) than when using unfilled TSD?
2. Materials
2.1. Study Site
2.2. Ground Reference Data
2.3. Sentinel-2 Data and Preprocessing
- (1)
- Atmospheric calibration. The Sen2Cor plugin v2.5.5 was employed to process images from top-of-atmosphere Level-1C Sentinel-2 to bottom-of-atmosphere Level-2A (http://www.esa-sen2agri.org/ (accessed on 6 April 2020)).
- (2)
- Masking of clouds. Fmask (Function of mask) 4.0 [33] was utilized to mask clouds and cloud shadows (the parameter of the cloud probability threshold was set as 50%). Fmask 4.0, the most recent version of Fmask [34] can work on Sentinel-2 images in Level-1C. All masks have a 20-m resolution, and both clouds and cloud shadows were marked as missing data. It should be noted that compared with cloud confidence layers in the output of Sen2Cor, most Fmask 4.0 results are more accurate in our study area.
- (3)
- Resampling. The images of the RE1, RE2, RE3, NIR2, SWIR1, and SWIR2 bands from step (1) and the cloud masks from step (2) were resampled to 10 m using the bilinear interpolation method [35].
3. Methodology
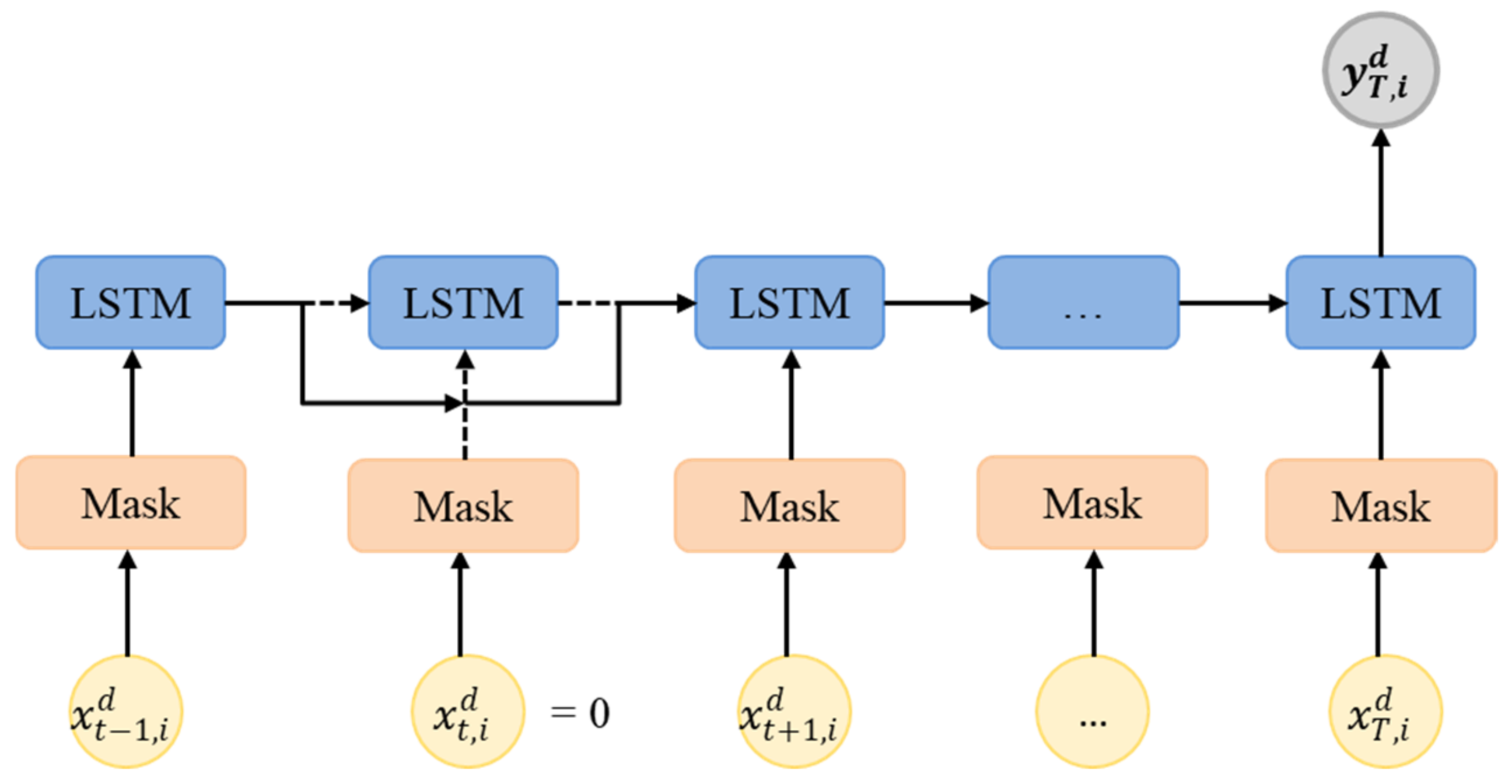
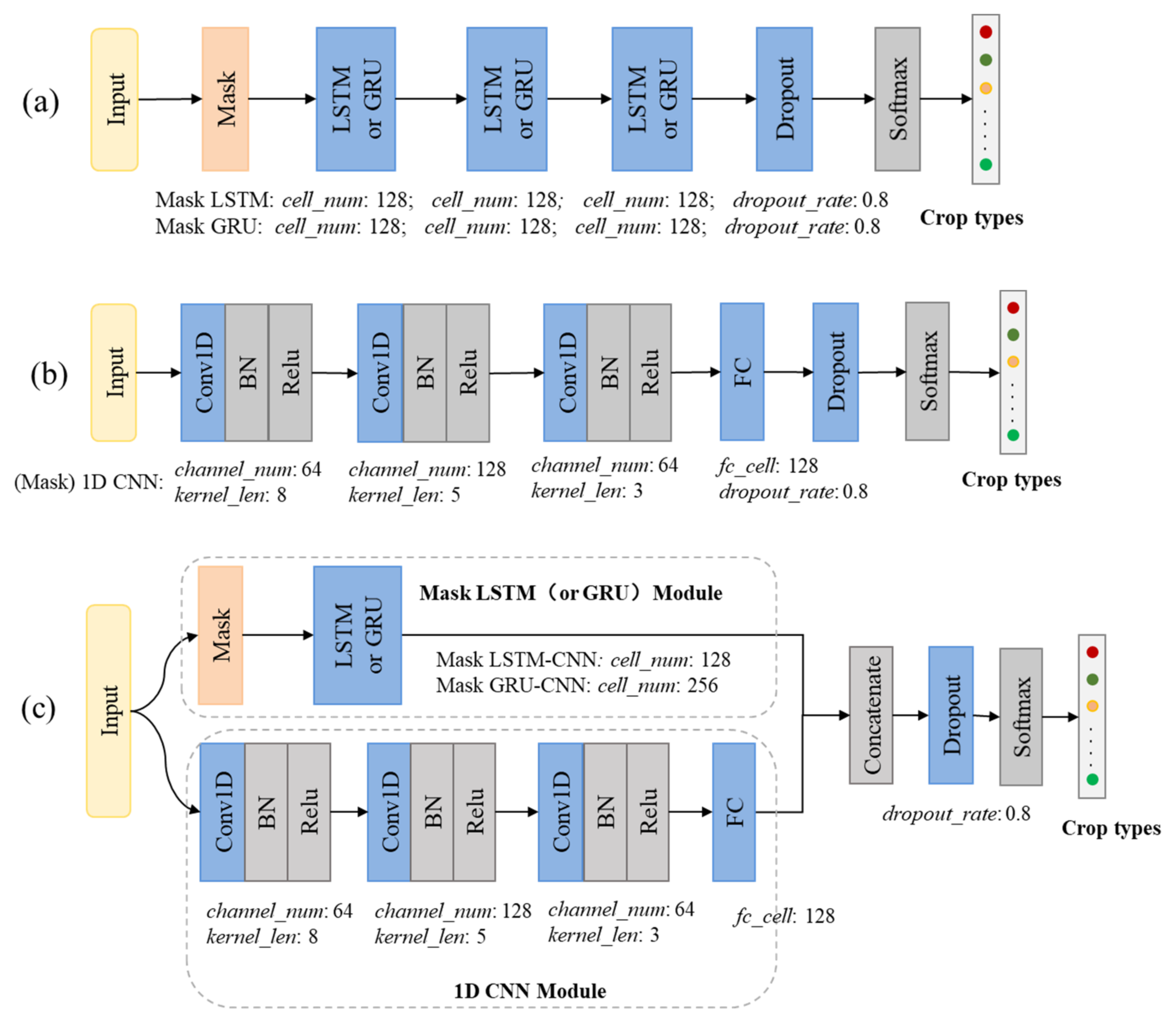
3.1. LSTM and GRU for TSD with Missing Values
3.2. 1D CNN for TSD with Missing Values
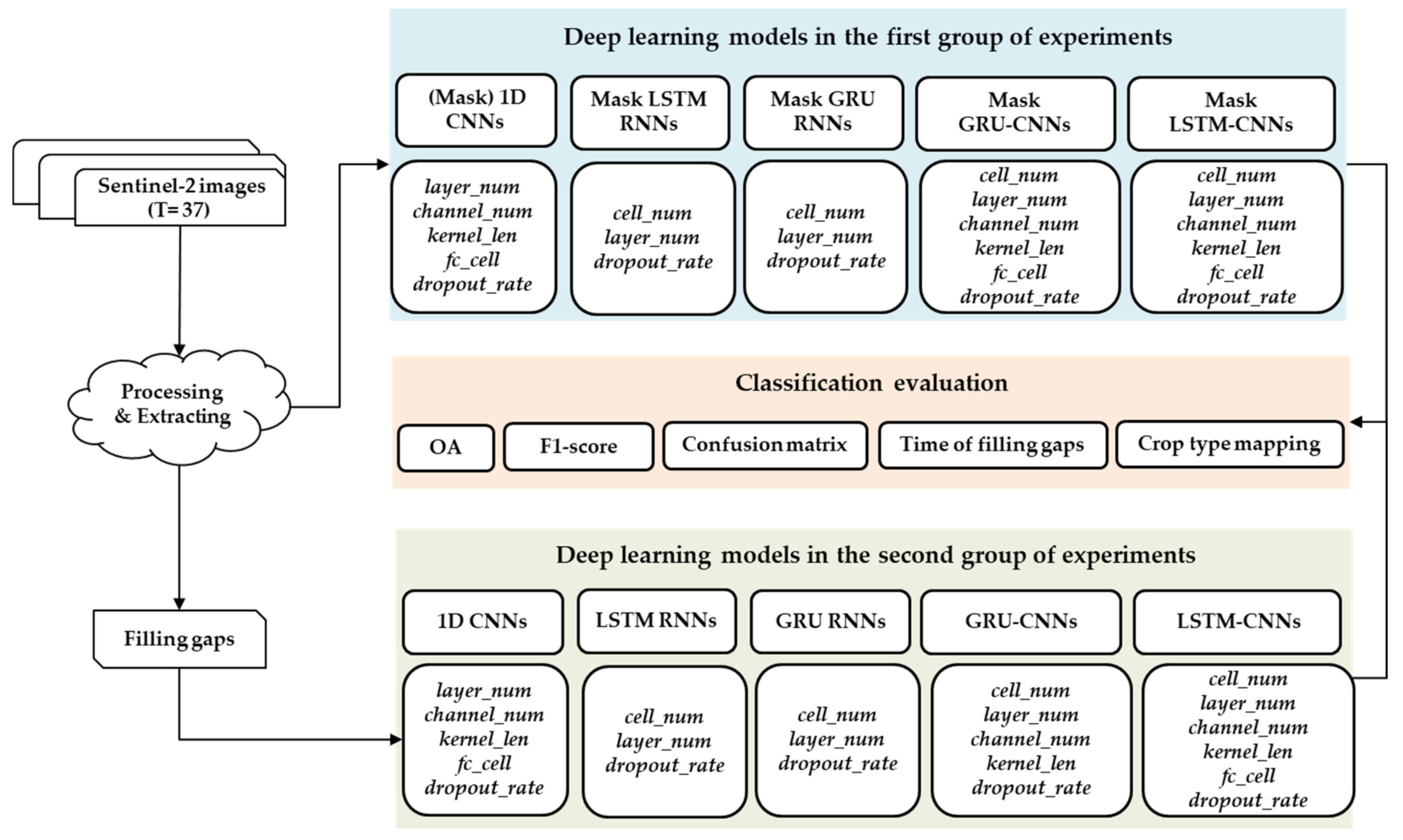
3.3. Experimental Configurations
3.4. Evaluation Methods
4. Results
4.1. Unfilled and Filled Sentinel-2 TSD
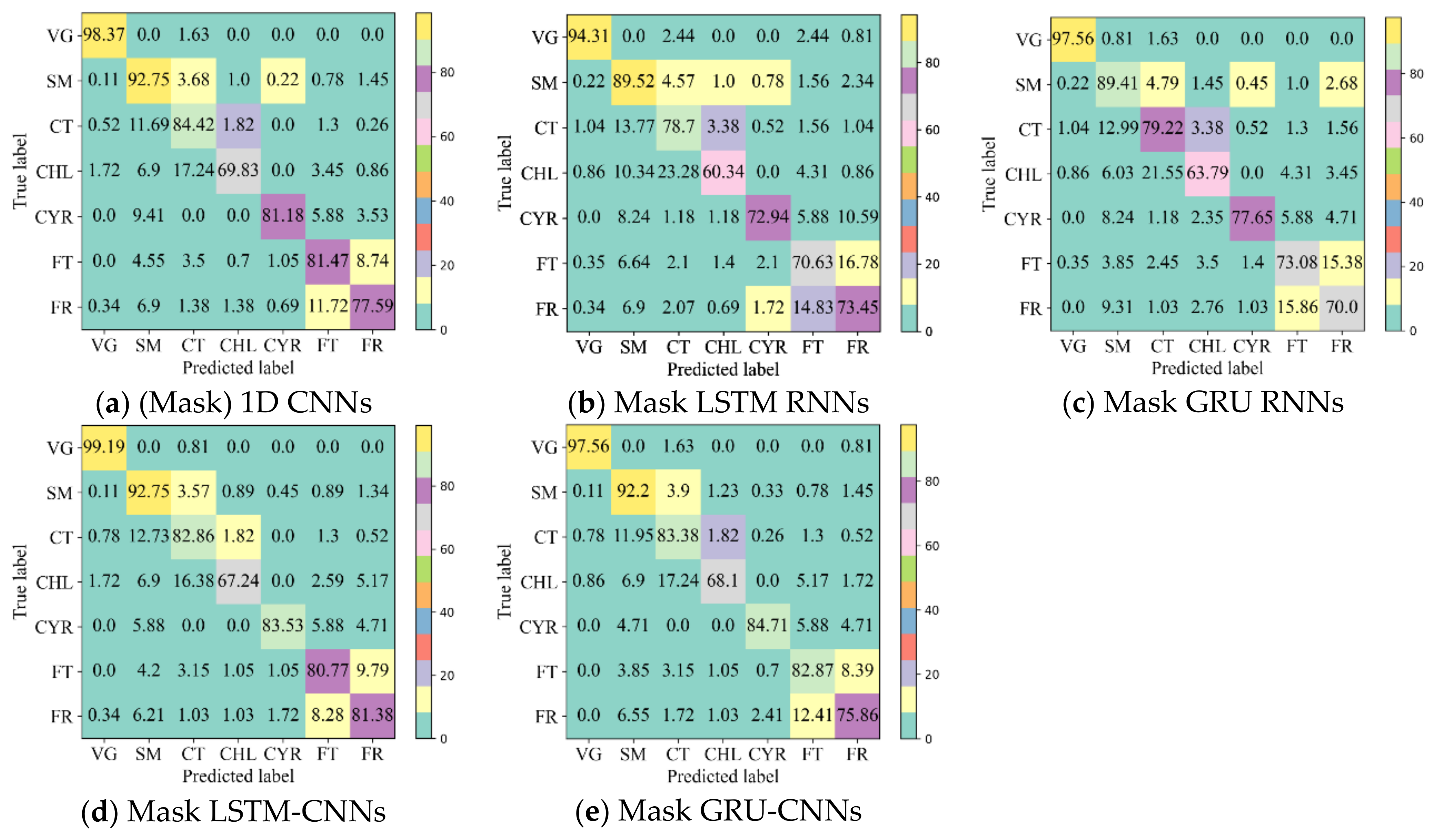
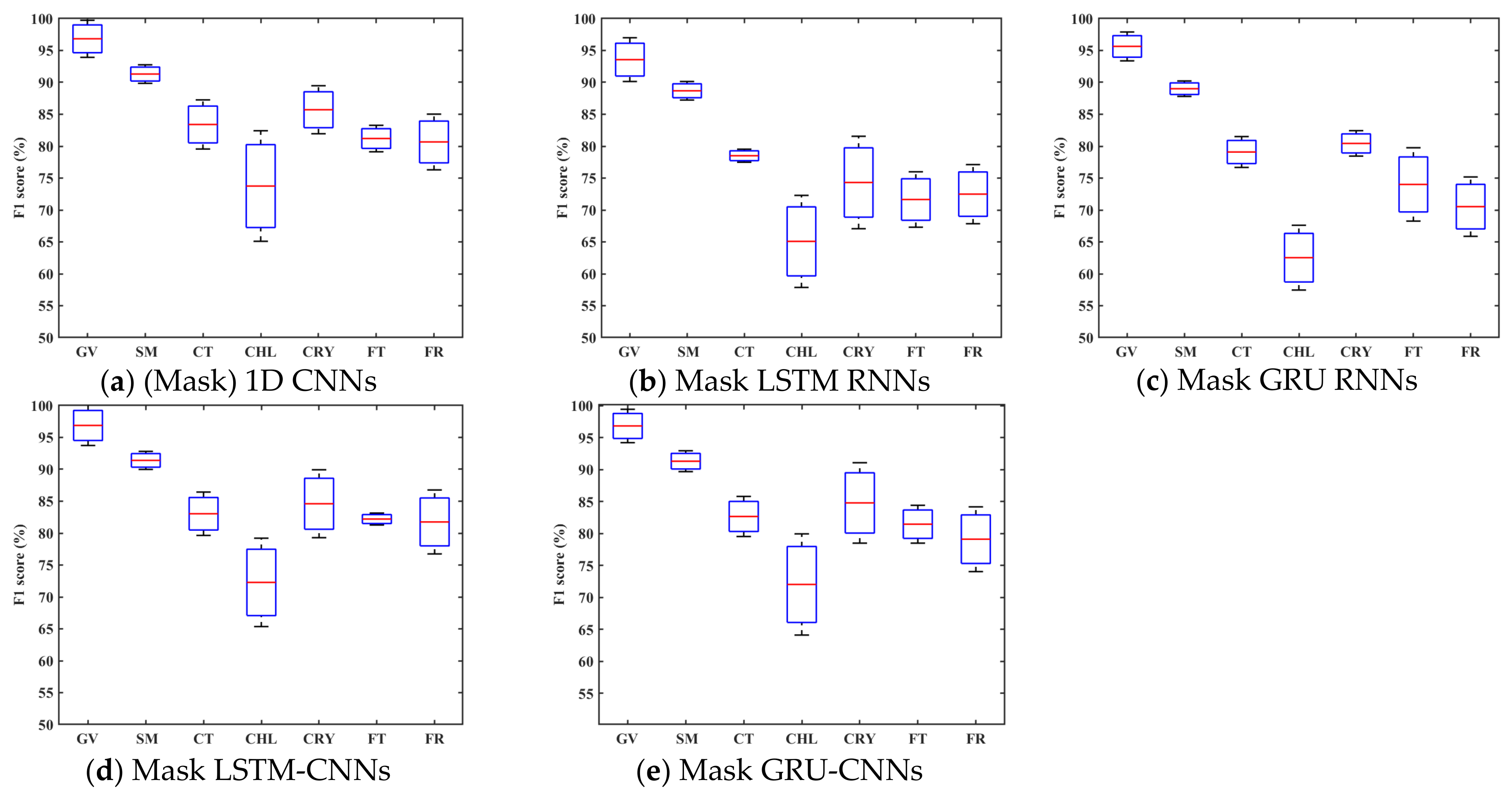
4.2. Classification Accuracy with Unfilled TSD
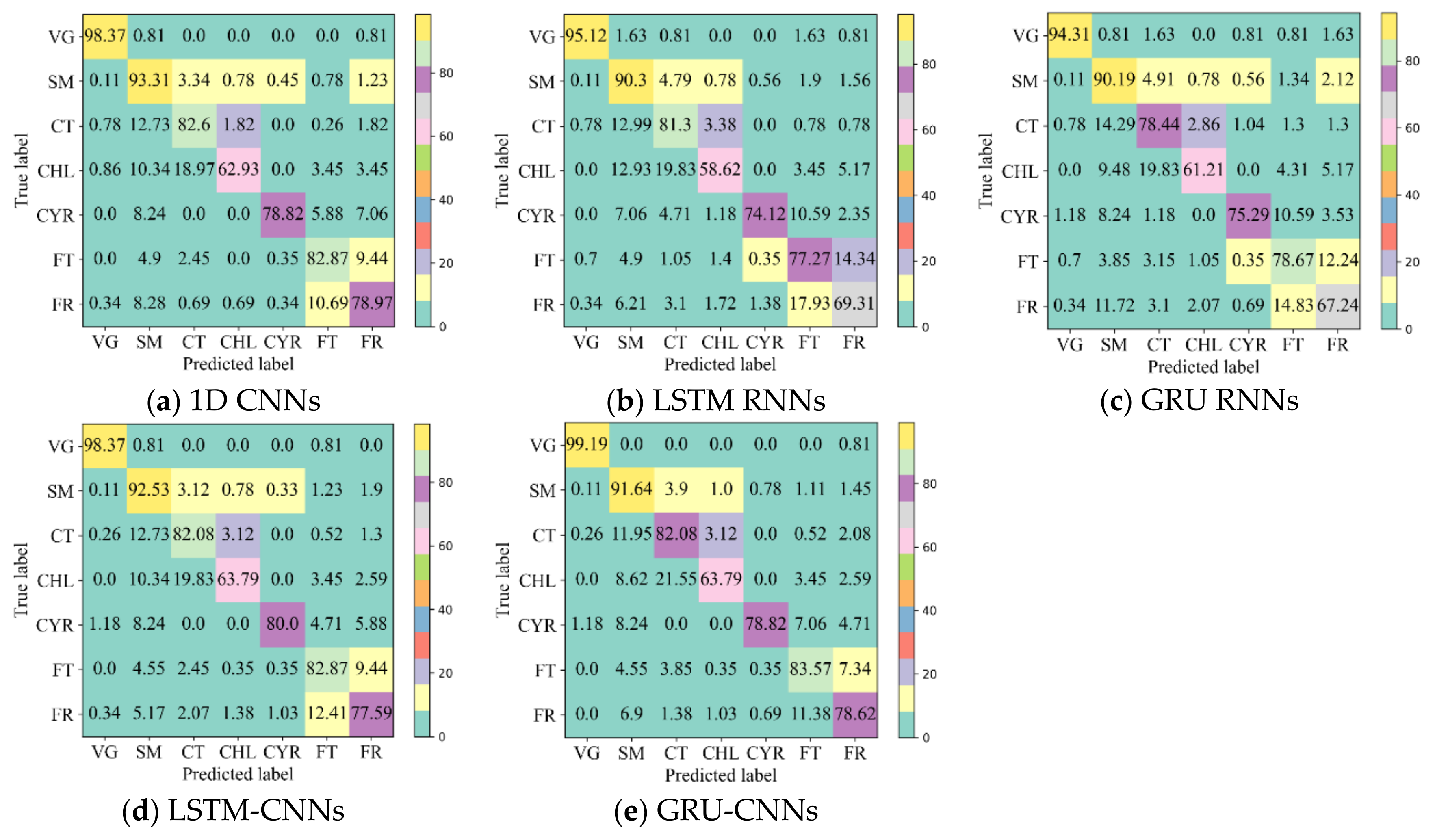
4.3. Comparison of Classification Accuracy with Filled and Unfilled TSD
4.4. Crop Type Mapping
5. Discussion
5.1. Performances of Different Models
- (1)
- The 1D CNN has the potential to learn highly discriminative features for crop type mapping by using TSD with missing information. First, it achieved acceptable accuracy (above 85%) using unfilled TSD; moreover, its OA was higher and performances more stable than those with filled TSD. Second, it attained higher F1s on different crop types when using unfilled TSD than when using filled TSD, especially on cotton, chili, and common yam rhizome, which could easily be inadvertently classified. Third, it had higher recalls on cotton, chili, and common yam rhizome when using unfilled TSD than when using filled TSD (see Figure 11, which illustrates that the interpolated and smoothed TSD may reduce the recalls of crop types with small parcels). Although LSTM and GRU did not attain accuracies as high as 1D CNN using unfilled TSD, their results were almost close to those with filled TSD.
- (2)
- In the two groups of experiments, the performance of LSTM-CNN and GRU-CNN was similar to that of 1D CNN (as discussed in (1)). However, in the mapping results using unfilled TSD, their recall rates of chili and common yam rhizome with small samples and small parcels were higher than that of 1D CNN. This showed that for crop type identification using TSD with missing information, the hybrid model of CNN and RNN (LSTM or GRU) has more advantages than a single model.
- (3)
- When using the networks in the second group for crop type mapping, we first filled in the missing values in the time series images of the mapping area. In this study, there were 329,181 pixels in the mapping area (shown in Figure 11a), and it took 61.3 min to fill in gaps. If we map the crop types of the entire Hengshui City () and use a computer (configured as stated in Section 4.4) to fill in the missing values, it will take about 11.5 days. This is very detrimental to the efficiency of crop monitoring over large areas. Therefore, we believe that this study is of great significance for improving the efficiency of crop monitoring over large areas.
5.2. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kogan, F.; Kussul, N.N.; Adamenko, T.I.; Skakun, S.V.; Kravchenko, A.N.; Krivobok, A.A.; Shelestov, A.Y.; Kolotii, A.V.; Kussul, O.M.; Lavrenyuk, A.N. Winter wheat yield forecasting: A comparative analysis of results of regression and bio-physical models. J. Autom. Inf. Sci. 2013, 45, 68–81. [Google Scholar] [CrossRef]
- Kolotii, A.; Kussul, N.; Shelestov, A.; Skakun, S.; Yailymov, B.; Basarab, R.; Lavreniuk, M.; Oliinyk, T.; Ostapenko, V. Comparison of biophysical and satellite predictors for wheat yield forecasting in Ukraine. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, XL-7/W3, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Wardlow, B.D.; Egbert, S.L.; Kastens, J.H. Analysis of time-series MODIS 250m vegetation index data for crop classification in the U.S. Central Great Plains. Remote Sens. Environ. 2007, 108, 290–310. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Guan, K.; Peng, J.; Wang, S.; Seifert, C.; Wardlow, B.; Li, Z. A high-performance and in-season classification system of field-level crop types using time-series Landsat data and a machine learning approach. Remote Sens. Environ. 2018, 210, 35–47. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.I.; Petitjean, F. Temporal Convolutional Neural Network for the Classification of Satellite Image Time Series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Zhu, Y.; Zhong, R.; Lin, Z.; Lin, T. Deep Crop Mapping: A multi-temporal deep learning approach with improved spa-tial generalizability for dynamic corn and soybean mapping. Remote Sens. Environ. 2020, 247, 111946. [Google Scholar] [CrossRef]
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Ng, M.K.-P.; Yuan, Q.; Yan, L.; Sun, J. An Adaptive Weighted Tensor Completion Method for the Recovery of Remote Sensing Images With Missing Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3367–3381. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Z.; Gao, F.; Anderson, M.; Song, L.; Wang, L.; Hu, B.; Yang, Y. Reconstructing daily clear-sky land surface temperature for cloudy regions from MODIS data. Comput. Geosci. 2017, 105, 10–20. [Google Scholar] [CrossRef]
- Tang, Z.; Adhikari, H.; Pellikka, P.K.; Heiskanen, J. A method for predicting large-area missing observations in Landsat time series using spectral-temporal metrics. Int. J. Appl. Earth Obs. Geoinf. 2021, 99, 102319. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Drusch, M.; Bello, U.D.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Vuolo, F.; Neuwirth, M.; Immitzer, M.; Atzberger, C.; Ng, W.-T. How much does multi-temporal Sentinel-2 data improve crop type classification? Int. J. Appl. Earth Obs. Geoinf. 2018, 72, 122–130. [Google Scholar] [CrossRef]
- Lambert, M.-J.; Traoré, P.C.S.; Blaes, X.; Baret, P.; Defourny, P. Estimating smallholder crops production at village level from Sentinel-2 time series in Mali’s cotton belt. Remote Sens. Environ. 2018, 216, 647–657. [Google Scholar] [CrossRef]
- Ustuner, M.; Sanli, F.B.; Abdikan, S.; Esetlili, M.T.; Kurucu, Y. Crop Type Classification Using Vegetation Indices of RapidEye Imagery. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-7, 195–198. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Xia, X.; Wang, P.; Fei, Y. Do aerosols impact ground observation of total cloud cover over the North China Plain? Glob. Planet. Chang. 2014, 117, 91–95. [Google Scholar] [CrossRef]
- Werbos, P. Backpropagation through Time: What It Does and How to Do It; Institute of Electrical and Electronics Engineers (IEEE): Piscataway Township, NJ, USA, 1990; Volume 78, pp. 1550–1560. [Google Scholar]
- Wang, Z.; Yan, W.; Oates, T. Time series classification from scratch with deep neural networks: A strong baseline. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1578–1585. [Google Scholar]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Liu, Q.; Chen, E.; Ge, Y.; Zhao, J.L. Time Series Classification Using Multi-Channels Deep Convolutional Neural Networks; Li, F., Li, G., Hwang, S., Yao, B., Zhang, Z., Eds.; Web-Age Information Management; Springer: Cham, Switzerland, 2014; pp. 298–310. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder–Decoder Approaches; Association for Computational Linguistics (ACL): Baltimore, MA, USA, 2014. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Parveen, S.; Green, P. Speech Recognition with Missing Data using Recurrent Neural Nets. In Proceedings of the Neural In-formation Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; pp. 1189–1195. [Google Scholar]
- Tian, Y.; Zhang, K.; Li, J.; Lin, X.; Yang, B. LSTM-based traffic flow prediction with missing data. Neurocomputing 2018, 318, 297–305. [Google Scholar] [CrossRef]
- Cao, K.; Kim, H.; Hwang, C.; Jung, H. CNN-LSTM Coupled Model for Prediction of Waterworks Operation Data. J. Inf. Process. Syst. 2018, 14, 1508–1520. [Google Scholar]
- Eitel, A.; Springenberg, J.T.; Spinello, L.; Riedmiller, M.; Burgard, W. Multimodal deep learning for robust RGB-D object recognition. In 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); IEEE: Piscataway Township, NJ, USA, 2015; pp. 681–687. [Google Scholar]
- Mazzia, V.; Khaliq, A.; Chiaberge, M. Improvement in Land Cover and Crop Classification based on Temporal Features Learning from Sentinel-2 Data Using Recurrent-Convolutional Neural Network (R-CNN). Appl. Sci. 2019, 10, 238. [Google Scholar] [CrossRef] [Green Version]
- Rußwurm, M.; Körner, M. Temporal Vegetation Modelling using Long Short-Term Memory Networks for Crop Identification from Medium-Resolution Multi-Spectral Satellite Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1496–1504. [Google Scholar]
- Rußwurm, M.; Körner, M. Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS Int. J. Geo-Inf. 2018, 7, 129. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Liu, X.; Yang, X. Land cover classification from multi-temporal, multi-spectral remotely sensed imagery using patch-based recurrent neural networks. Neural Netw. 2018, 105, 346–355. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, H.; Guo, H.; Yang, L.; Wu, L.; Li, F.; Li, S.; Ni, P.; Liang, X. Occurrence and formation of high fluoride groundwater in the Hengshui area of the North China Plain. Environ. Earth Sci. 2015, 74, 2329–2340. [Google Scholar] [CrossRef]
- Qiu, S.; Zhu, Z.; He, B. Fmask 4.0: Improved cloud and cloud shadow detection in Landsats 4–8 and Sentinel-2 imagery. Remote Sens. Environ. 2019, 231, 111205. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
- Onojeghuo, A.O.; Blackburn, G.A.; Wang, Q.; Atkinson, P.; Kindred, D.; Miao, Y. Mapping paddy rice fields by applying machine learning algorithms to multi-temporal Sentinel-1A and Landsat data. Int. J. Remote Sens. 2018, 39, 1042–1067. [Google Scholar] [CrossRef] [Green Version]
- Dai, Z.; Heckel, R. Channel Normalization in Convolutional Neural Network avoids Vanishing Gradients. arXiv 2020, arXiv:1907.09539. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H.-C. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Improving neural networks by preventing co-adaptation of feature detectors. Neural Evol. Comput. 2012. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Int. Conf. Mach. Learn. 2015, 37, 448–456. [Google Scholar]
- Boureau, Y.L.; Ponce, J.; LeCun, Y. A Theoretical Analysis of Feature Pooling in Visual Recognition. In Proceedings of the 27th international conference on machine learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 111–118. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Stochastic Pooling for Regularization of Deep Convolutional Neural Networks. Learning 2013. [Google Scholar] [CrossRef] [Green Version]
- Kandasamy, S.; Baret, F.; Verger, A.; Neveux, P.; Weiss, M. A comparison of methods for smoothing and gap filling time series of remote sensing observations—Application to MODIS LAI products. Biogeosciences. 2013, 10, 4055–4071. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Jonsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate LSTM-FCNs for time series classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Sabuncu, M. Generalized cross entropy loss for training deep neural networks with noisy labels. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 8778–8788. [Google Scholar]
- Zhao, H.; Chen, Z.; Jiang, H.; Jing, W.; Sun, L.; Feng, M. Evaluation of Three Deep Learning Models for Early Crop Classifi-cation Using Sentinel-1A Imagery Time Series—A Case Study in Zhanjiang, China. Remote Sens. 2019, 11, 2673. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Sasaki, Y. The truth of the F-measure. Teach Tutor Mater 2007, 1, 1–5. [Google Scholar]
- Du, Z.; Yang, J.; Ou, C.; Zhang, T. Smallholder Crop Area Mapped with a Semantic Segmentation Deep Learning Method. Remote Sens. 2019, 11, 888. [Google Scholar] [CrossRef] [Green Version]
- Hao, P.; Tang, H.; Chen, Z.; Liu, Z. Early-season crop mapping using improved artificial immune network (IAIN) and Sentinel data. PeerJ 2018, 6, e5431. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef] [Green Version]
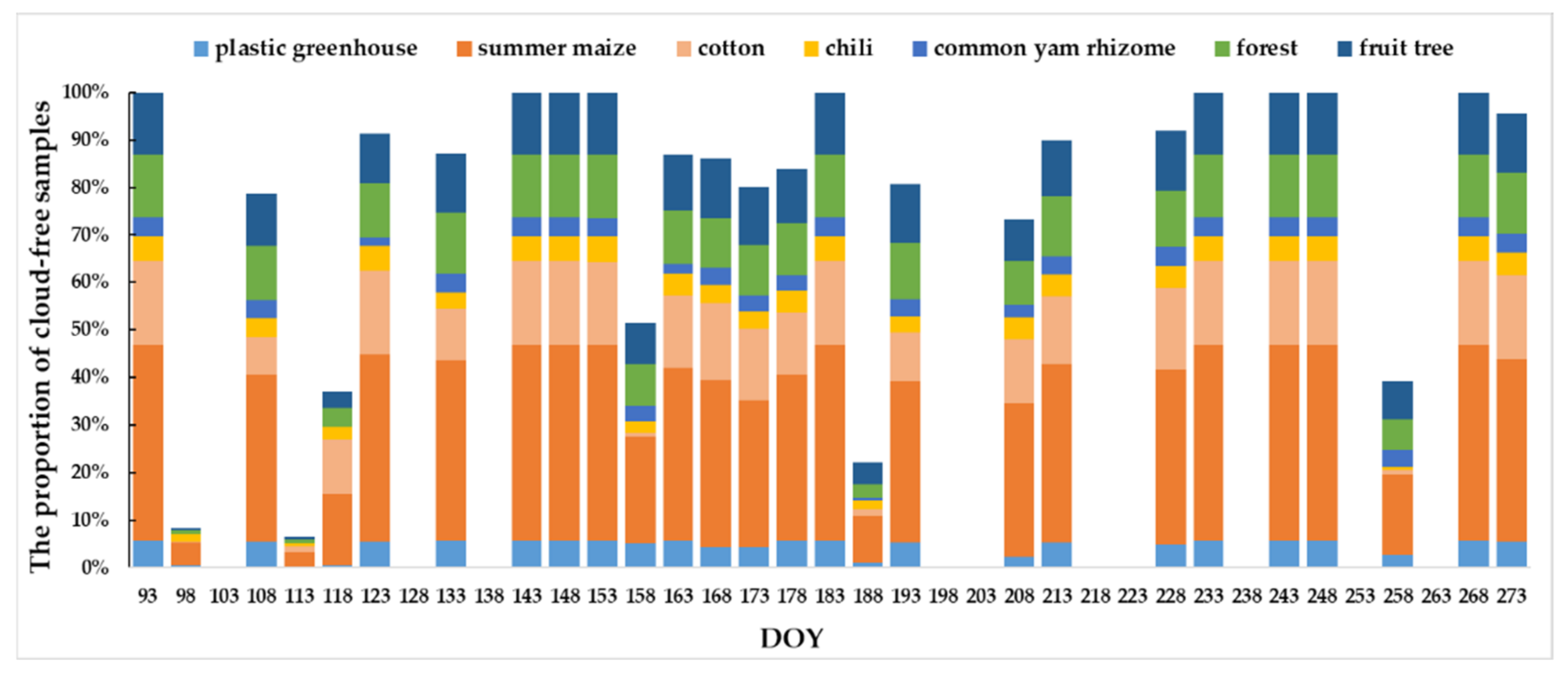
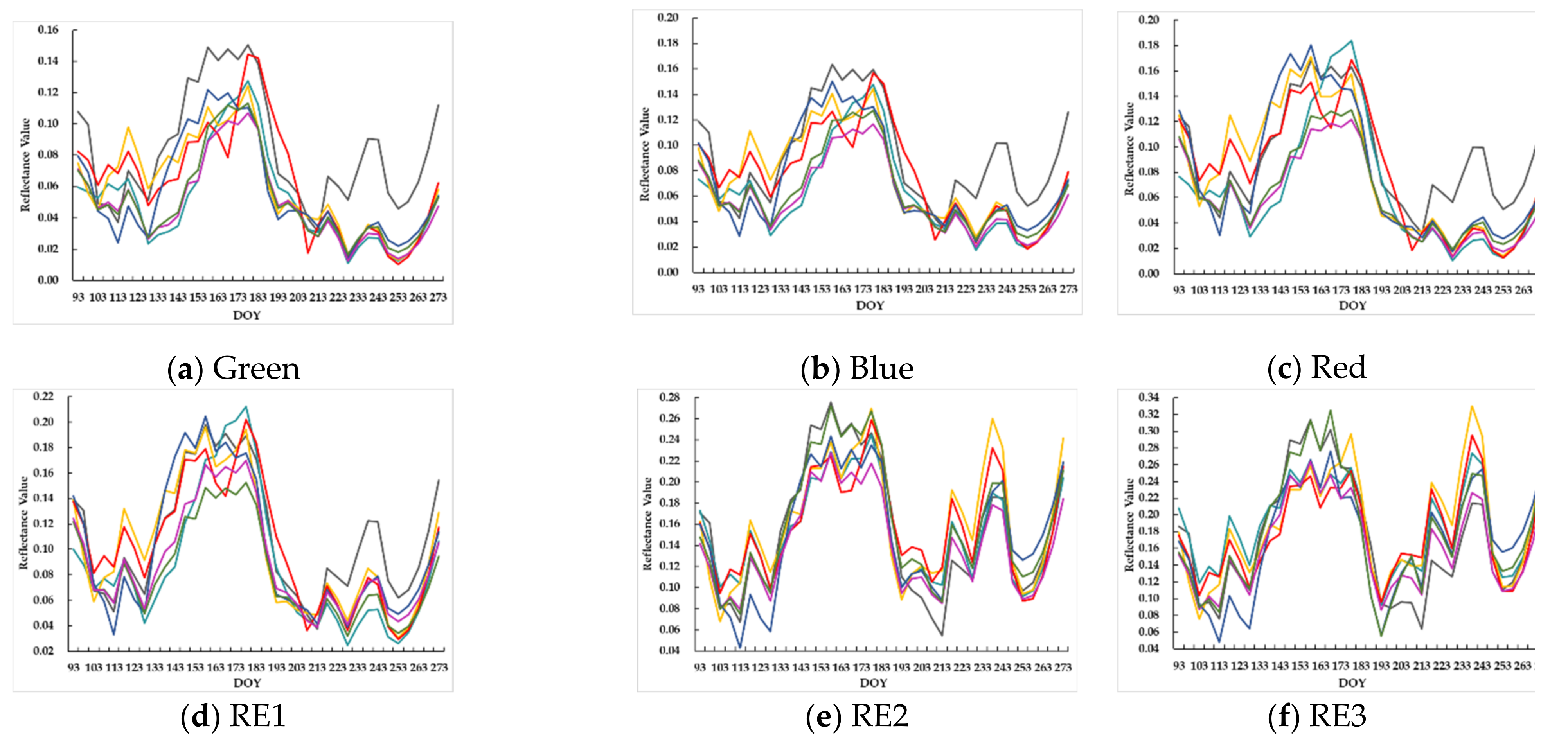
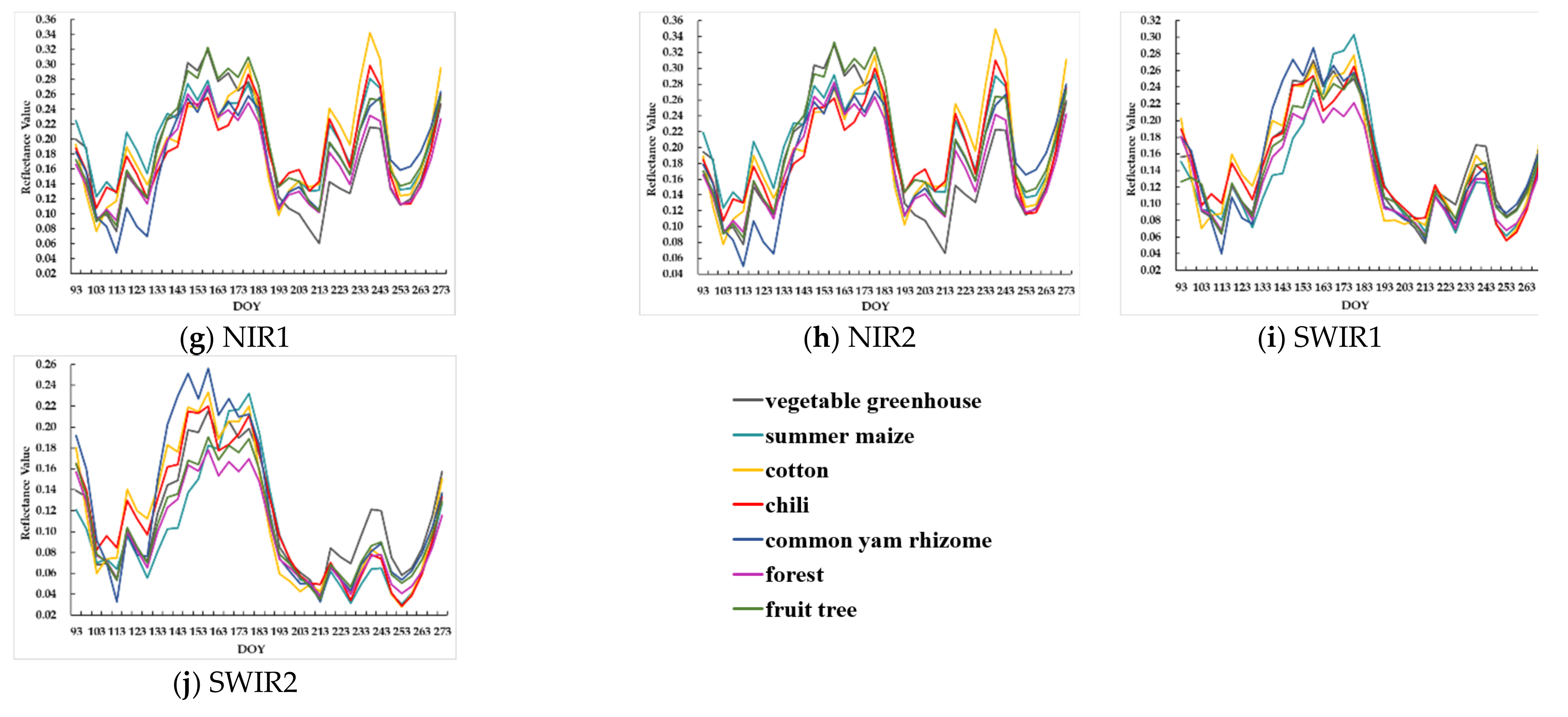
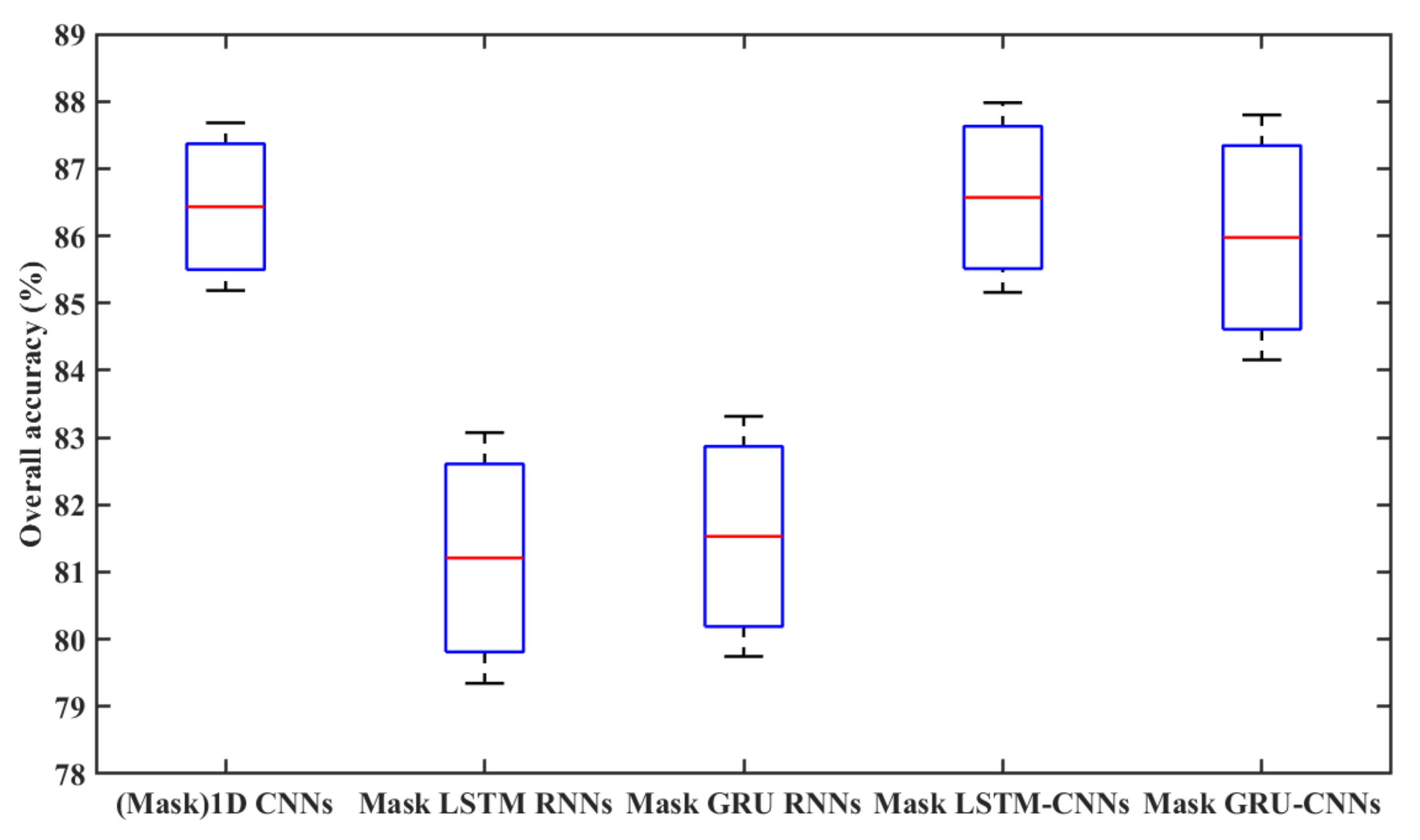

| Class Label | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total |
|---|---|---|---|---|---|---|---|---|
| Class Type | Greenhouse Vegetables | Summer Maize | Cotton | Chili | Common Yam Rhizome | Fruit Trees | Forests | |
| Number | 123 | 897 | 385 | 116 | 85 | 286 | 290 | 2182 |
| Class Type | Sowing | Developing | Maturation | |||
|---|---|---|---|---|---|---|
| Date | DOY | Date | DOY | Date | DOY | |
| Summer maize | June 15–30 | 166–181 | July 1–September 15 | 182–259 | September 16–30 | 260–274 |
| Cotton | April 1–15 | 91–106 | April 16–August 31 | 107–244 | September 1–October 31 | 245–305 |
| Chili | June 15–25 | 166–176 | June 26–August 31 | 177–244 | September 1–30 | 245–274 |
| Common yam rhizome | April 1–15 | 91–106 | April 16–October 10 | 107–284 | October 11–31 | 285–305 |
| Model | 1D CNN | LSTM | GRU | LSTM-LSTM | GRU-CNN | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Networks | (Mask) 1D CNNs | 1D CNNs | Mask LSTM RNNs | LSTM RNNs | Mask GRU RNNs | GRU RNNs | Mask LSTM-CNNs | LSTM -CNNs | Mask GRU-CNNs | GRU-CNNs |
| OA | 86.43 | 86.25 | 80.57 | 82.18 | 81.53 | 81.67 | 86.57 | 85.75 | 85.98 | 85.61 |
| SD | 1.25 | 2.62 | 1.87 | 2.84 | 1.79 | 1.87 | 1.41 | 2.26 | 1.82 | 2.32 |
| Model | 1D CNN | LSTM | GRU | LSTM-CNN | GRU-CNN | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Networks | (Mask) 1D CNNs | 1D CNNs | Mask LSTM RNNs | LSTM RNNs | Mask GRU RNNs | GRU RNNs | Mask LSTM-CNNs | LSTM-CNNs | Mask GRU-CNNs | GRU-CNNs |
| VG | 96.83 ± 2.91 | 96.81 ± 0.94 | 93.57 ± 3.43 | 94.76 ± 3.29 | 95.64 ± 2.26 | 93.92 ± 3.45 | 96.88 ± 3.14 | 97.63 ± 2.27 | 96.81 ± 2.61 | 98.41 ± 1.45 |
| SM | 91.31 ± 1.46 | 90.94 ± 1.39 | 88.68 ± 1.45 | 89.43 ± 1.46 | 89.01 ± 1.21 | 88.68 ± 1.65 | 91.40 ± 1.41 | 91.02 ± 0.70 | 91.29 ± 1.63 | 90.59 ± 1.44 |
| CT | 83.40 ± 3.85 | 83.25 ± 5.46 | 78.51 ± 1.02 | 80.11 ± 5.75 | 79.09 ± 2.42 | 77.90 ± 3.40 | 83.04 ± 3.40 | 82.56 ± 5.64 | 82.65 ± 3.14 | 81.38 ± 5.74 |
| CHL | 73.75 ± 8.66 | 71.28 ± 5.66 | 65.08 ± 7.21 | 63.52 ± 5.81 | 62.53 ± 5.08 | 66.97 ± 7.46 | 72.28 ± 6.93 | 69.13 ± 4.67 | 72.01 ± 7.92 | 68.86 ± 5.05 |
| CYR | 85.71 ± 3.76 | 84.84 ± 3.95 | 74.31 ± 7.24 | 79.67 ± 2.98 | 80.43 ± 1.99 | 79.05 ± 5.15 | 84.60 ± 5.32 | 85.03 ± 3.36 | 84.76 ± 6.29 | 82.73 ± 3.96 |
| FT | 81.20 ± 2.07 | 83.11 ± 5.08 | 71.64 ± 4.34 | 74.53 ± 5.56 | 74.00 ± 5.75 | 76.86 ± 4.44 | 82.21 ± 0.93 | 81.64 ± 4.77 | 81.44 ± 2.96 | 82.46 ± 4.09 |
| FR | 80.66 ± 4.37 | 79.58 ± 6.70 | 72.48 ± 4.63 | 71.80 ± 7.00 | 70.53 ± 4.65 | 69.92 ± 5.70 | 81.75 ± 5.01 | 78.58 ± 6.37 | 79.09 ± 5.06 | 80.31 ± 5.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Duan, S.; Liu, J.; Sun, L.; Reymondin, L. Evaluation of Five Deep Learning Models for Crop Type Mapping Using Sentinel-2 Time Series Images with Missing Information. Remote Sens. 2021, 13, 2790. https://doi.org/10.3390/rs13142790
Zhao H, Duan S, Liu J, Sun L, Reymondin L. Evaluation of Five Deep Learning Models for Crop Type Mapping Using Sentinel-2 Time Series Images with Missing Information. Remote Sensing. 2021; 13(14):2790. https://doi.org/10.3390/rs13142790
Chicago/Turabian StyleZhao, Hongwei, Sibo Duan, Jia Liu, Liang Sun, and Louis Reymondin. 2021. "Evaluation of Five Deep Learning Models for Crop Type Mapping Using Sentinel-2 Time Series Images with Missing Information" Remote Sensing 13, no. 14: 2790. https://doi.org/10.3390/rs13142790
APA StyleZhao, H., Duan, S., Liu, J., Sun, L., & Reymondin, L. (2021). Evaluation of Five Deep Learning Models for Crop Type Mapping Using Sentinel-2 Time Series Images with Missing Information. Remote Sensing, 13(14), 2790. https://doi.org/10.3390/rs13142790








