Modeling the Spectral Properties of Obtrusive Light Incident on a Window: Application to Montréal, Canada
Abstract
:1. Introduction
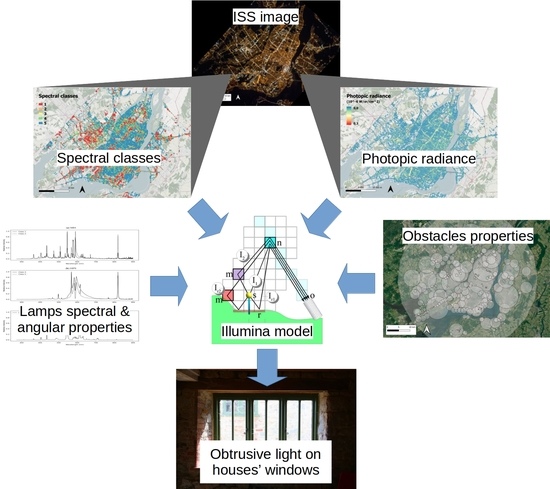
2. Modeling Approaches
3. Modeling Domain and Period
4. Modeling Parameters
4.1. Uniform Parameters
4.2. Gridded Parameters
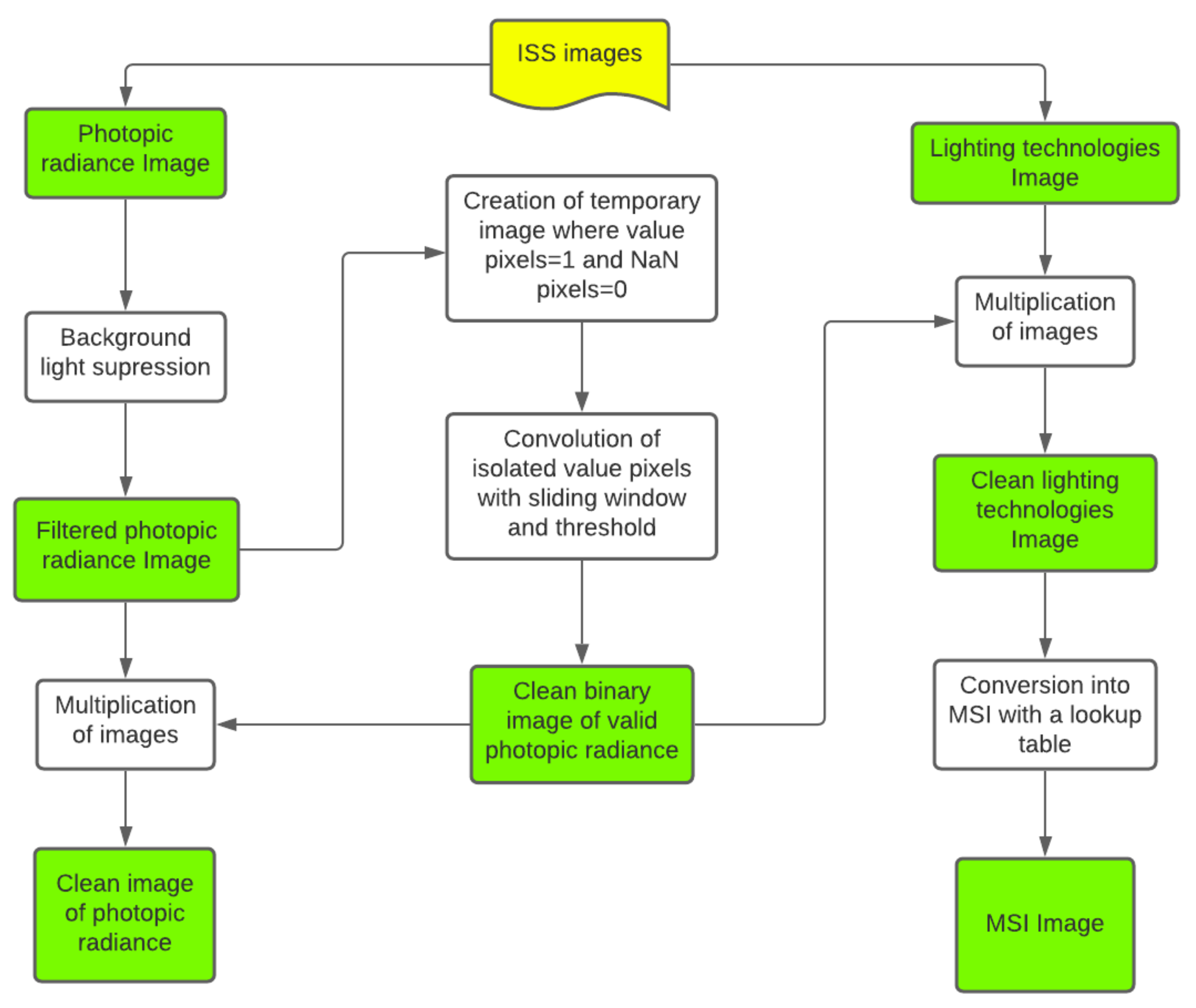
4.3. Lamp Flux and Spectral Type from ISS Images
4.4. Obstacle Properties and Lamps Heights
4.5. Generic Light Output Patterns and Spectra
4.6. Determining the Window Orientation
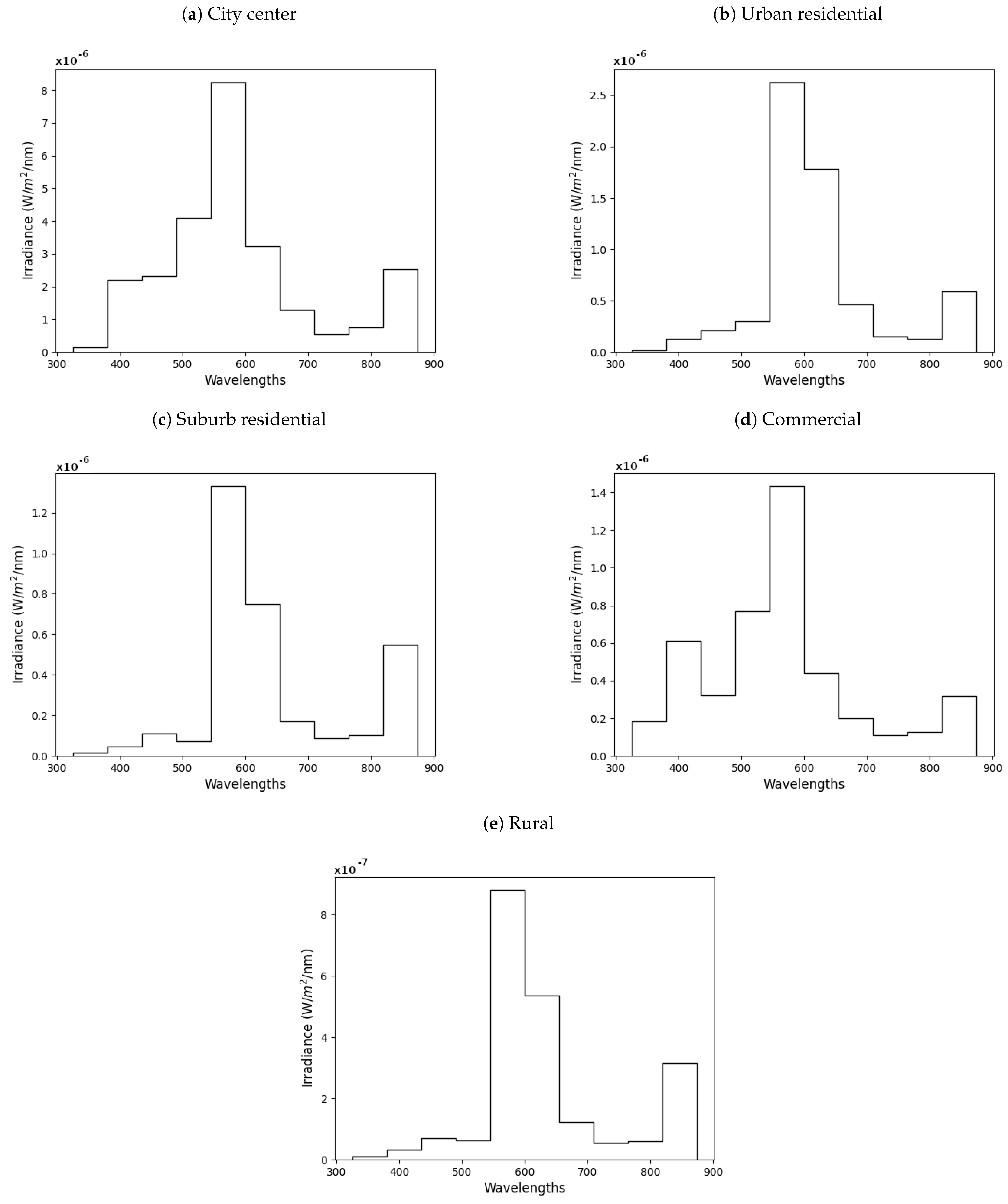
5. Results for Some Montréal Sites in 2013
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
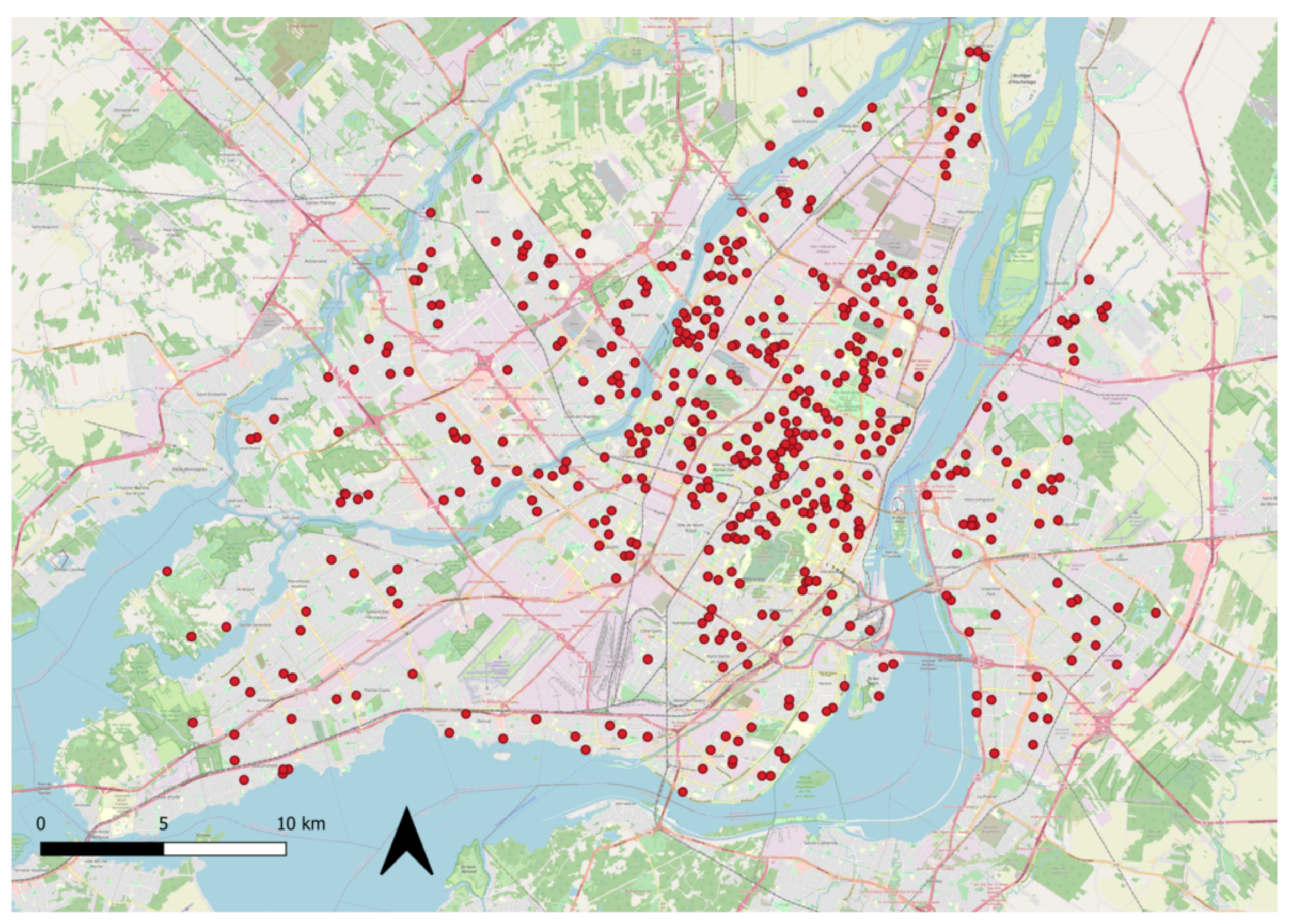
Appendix A. Montréal’s Obstacle and Lamp Height Inventory
| Zone | Latitude | Longitude | Radius | F | |||
|---|---|---|---|---|---|---|---|
| deg | deg | m | m | m | m | ||
| 1 | 45.557810 | −73.672506 | 30,650.92 | 0 | 0 | 0 | 7.5 |
| 2 | 45.494639 | −73.899268 | 4121.07 | 80 | 15 | 1 | 0 |
| 3 | 45.49488 | −73.867339 | 1948.43 | 35 | 11 | 0.93 | 4.5 |
| 4 | 45.508456 | −73.90757 | 1142.83 | 35 | 11 | 0.93 | 4.5 |
| 5 | 45.473517 | −73.886873 | 1048.83 | 35 | 11 | 0.93 | 4.5 |
| 6 | 45.543776 | −73.839687 | 4471.36 | 35 | 10 | 0.93 | 8.5 |
| 7 | 45.558958 | −73.90086 | 4233.07 | 35 | 10 | 0.93 | 8.5 |
| 8 | 45.526015 | −73.929013 | 2172.61 | 35 | 10 | 0.93 | 8.5 |
| 9 | 45.513235 | −73.956225 | 2172.61 | 35 | 10 | 0.93 | 8.5 |
| 10 | 45.499443 | −73.968007 | 2172.32 | 35 | 10 | 0.93 | 8.5 |
| 11 | 45.512158 | −73.964755 | 617.456 | 0 | 15 | 1 | 0 |
| 12 | 45.563189 | −73.983275 | 3804.76 | 0 | 0 | 0 | 7.5 |
| 13 | 45.615289 | −73.900191 | 3798.04 | 0 | 0 | 0 | 7.5 |
| 14 | 45.43119 | −73.957087 | 1550.37 | 43 | 11 | 0.93 | 8 |
| 15 | 45.430829 | −73.953139 | 1035.49 | 0 | 15 | 1 | 0 |
| 16 | 45.553076 | −73.599566 | 5734.21 | 40 | 11 | 0.93 | 8 |
| 17 | 45.600549 | −73.571945 | 5729.25 | 40 | 11 | 0.93 | 8 |
| 18 | 45.638371 | −73.538642 | 4233.28 | 40 | 11 | 0.93 | 8 |
| 19 | 45.487212 | −73.556747 | 1801.99 | 55 | 9 | 0.89 | 9.5 |
| 20 | 45.459964 | −73.548806 | 1943.82 | 45 | 13 | 0.97 | 8 |
| 21 | 45.470838 | −73.541125 | 559.52 | 55 | 9 | 0.89 | 9.5 |
| 22 | 45.493436 | −73.56647 | 2220.89 | 35 | 13 | 0.97 | 9 |
| 23 | 45.496555 | −73.57172 | 1236.33 | 30 | 100 | 0.96 | 9 |
| 24 | 45.477628 | −73.639895 | 6115.16 | 37 | 12 | 0.93 | 8.5 |
| 25 | 45.544292 | −73.764239 | 4334.49 | 40 | 8 | 0.94 | 9 |
| 26 | 45.430243 | −73.95103 | 1567.93 | 0 | 15 | 1 | 0 |
| 27 | 45.420916 | −73.946202 | 538.3 | 0 | 0 | 0 | 7.5 |
| 28 | 45.442709 | −73.603072 | 507.68 | 13 | 15 | 1 | 8 |
| 29 | 45.441032 | −73.609005 | 257.27 | 13 | 15 | 1 | 8 |
| 30 | 45.443038 | −73.596616 | 286.66 | 13 | 15 | 1 | 8 |
| 31 | 45.578561 | −73.711505 | 3574.49 | 40 | 11 | 0.95 | 7.5 |
| 32 | 45.620783 | −73.736125 | 1468.17 | 40 | 9 | 0.92 | 7.8 |
| 33 | 45.567735 | −73.773246 | 469 | 50 | 8 | 0.6 | 11 |
| 34 | 45.573021 | −73.775261 | 573.33 | 50 | 40 | 0.91 | 10 |
| 35 | 45.578094 | −73.726646 | 3343.3 | 75 | 8.5 | 0.8 | 9 |
| 36 | 45.606471 | −73.760197 | 981.7 | 0 | 15 | 1 | 0 |
| 37 | 45.608425 | −73.721034 | 1745.27 | 40 | 9.5 | 0.92 | 7.8 |
| 38 | 45.573973 | −73.732847 | 652.33 | 30 | 10 | 0.85 | 7.5 |
| 39 | 45.58667 | −73.71821 | 475.18 | 30 | 10.5 | 0.85 | 8 |
| 40 | 45.581243 | −73.712424 | 589.31 | 30 | 10.5 | 0.85 | 8 |
| 41 | 45.606794 | −73.678565 | 2757.33 | 40 | 11 | 0.95 | 7.5 |
| 42 | 45.499381 | −73.777284 | 1984.69 | 30 | 8 | 0.93 | 9 |
| 43 | 45.624484 | −73.777209 | 1028.74 | 30 | 8 | 0.93 | 9 |
| 44 | 45.626746 | −73.751446 | 1163.5 | 45 | 10 | 0.79 | 9 |
| 45 | 45.642074 | −73.759972 | 1111.32 | 45 | 10 | 0.79 | 9 |
| 46 | 45.654009 | −73.753926 | 565.21 | 45 | 10 | 0.79 | 9 |
| 47 | 45.628283 | −73.646522 | 864.23 | 100 | 9 | 0.79 | 9 |
| 48 | 45.636819 | −73.644179 | 704.06 | 100 | 9 | 0.79 | 9 |
| 49 | 45.669672 | −73.580719 | 1135.41 | 35 | 10.5 | 0.9 | 9 |
| 50 | 45.655778 | −73.594472 | 756.39 | 35 | 10.5 | 0.9 | 9 |
| 51 | 45.649959 | −73.610008 | 748.64 | 35 | 10.5 | 0.9 | 9 |
| 52 | 45.685863 | −73.593969 | 122.28 | 35 | 10 | 0.9 | 8 |
| 53 | 45.684019 | −73.59329 | 158.31 | 35 | 10 | 0.9 | 8 |
| 54 | 45.687316 | −73.624922 | 397.88 | 40 | 11 | 0.95 | 9 |
| 55 | 45.681938 | −73.626754 | 378.97 | 40 | 11 | 0.95 | 9 |
| 56 | 45.685351 | −73.640389 | 429.63 | 40 | 10.5 | 0.9 | 7.5 |
| 57 | 45.684927 | −73.644576 | 513.06 | 40 | 10.5 | 0.9 | 7.5 |
| 58 | 45.578662 | −73.810779 | 1885.89 | 40 | 9 | 0.92 | 7.5 |
| 59 | 45.669865 | −73.581445 | 1176.66 | 40 | 6 | 0.87 | 7 |
| 60 | 45.658336 | −73.595139 | 486.99 | 40 | 6 | 0.87 | 7 |
| 61 | 45.649695 | −73.607701 | 943.64 | 40 | 6 | 0.87 | 7 |
| 62 | 45.619713 | −73.736748 | 1577.7 | 40 | 9.5 | 0.92 | 7.8 |
| 63 | 45.605547 | −73.802901 | 395.48 | 30 | 8 | 0.93 | 9 |
| 64 | 45.605643 | −73.806192 | 170.05 | 93 | 6.5 | 0.86 | 20 |
| 65 | 45.603383 | −73.805732 | 177.03 | 93 | 6.5 | 0.86 | 20 |
| 66 | 45.601263 | −73.806303 | 138.59 | 93 | 6.5 | 0.86 | 20 |
| 67 | 45.596595 | −73.80829 | 285.24 | 75 | 7 | 0.35 | 5 |
| 68 | 45.589523 | −73.817458 | 598.77 | 40 | 8 | 0.98 | 7.5 |
| 69 | 45.579687 | −73.785752 | 519.3 | 80 | 9 | 0.91 | 10 |
| 70 | 45.566742 | −73.794239 | 956.48 | 95 | 9.5 | 0.86 | 9 |
| 71 | 45.564699 | −73.783424 | 534.76 | 95 | 9.5 | 0.86 | 9 |
| 72 | 45.57769 | −73.809499 | 1685.56 | 40 | 8 | 0.98 | 7.5 |
| 73 | 45.57275 | −73.779812 | 407.35 | 40 | 9 | 0.92 | 6.5 |
| 74 | 45.576025 | −73.769727 | 434.77 | 40 | 9 | 0.92 | 6.5 |
| 75 | 45.577226 | −73.76237 | 277.36 | 40 | 9 | 0.92 | 6.5 |
| 76 | 45.572138 | −73.772153 | 177.08 | 40 | 9 | 0.92 | 6.5 |
| 77 | 45.534093 | −73.788879 | 370.15 | 95 | 7.5 | 0.78 | 8 |
| 78 | 45.530072 | −73.784738 | 373.43 | 95 | 7.5 | 0.78 | 8 |
| 79 | 45.526837 | −73.780306 | 386.65 | 95 | 7.5 | 0.78 | 8 |
| 80 | 45.493572 | −73.824689 | 2915.16 | 43 | 11 | 0.93 | 8 |
| 81 | 45.44632 | −73.841687 | 5030.89 | 43 | 11 | 0.93 | 8 |
| 82 | 45.413312 | −73.900346 | 1294.62 | 43 | 11 | 0.93 | 8 |
| 83 | 45.405117 | −73.920945 | 1287.47 | 43 | 11 | 0.93 | 8 |
| 84 | 45.436933 | −73.92663 | 485.53 | 43 | 11 | 0.93 | 8 |
| 85 | 45.414199 | −73.958716 | 739.01 | 43 | 11 | 0.93 | 8 |
| 86 | 45.447606 | −73.773278 | 1300.58 | 43 | 11 | 0.93 | 8 |
| 87 | 45.437128 | −73.74873 | 1303.57 | 43 | 11 | 0.93 | 8 |
| 88 | 45.437151 | −73.728026 | 1303.57 | 43 | 11 | 0.93 | 8 |
| 89 | 45.436428 | −73.712233 | 1303.57 | 43 | 11 | 0.93 | 8 |
| 90 | 45.435847 | −73.694037 | 1303.57 | 43 | 11 | 0.93 | 8 |
| 91 | 45.461948 | −73.706166 | 1638.72 | 65 | 7 | 0.87 | 9.5 |
| 92 | 45.451977 | −73.735921 | 1365.22 | 65 | 7 | 0.87 | 9.5 |
| 93 | 45.489822 | −73.67055 | 938.96 | 65 | 6 | 0.85 | 9 |
| 94 | 45.489412 | −73.685756 | 580.2 | 65 | 6 | 0.85 | 9 |
| 95 | 45.483317 | −73.699904 | 1126.54 | 65 | 6 | 0.85 | 9 |
| 96 | 45.494602 | −73.713477 | 1121.04 | 65 | 6 | 0.85 | 9 |
| 97 | 45.493228 | −73.727198 | 1016.49 | 65 | 6 | 0.85 | 9 |
| 98 | 45.496296 | −73.747347 | 1345.71 | 65 | 6 | 0.85 | 9 |
| 99 | 45.483364 | −73.771305 | 1218.45 | 65 | 6 | 0.85 | 9 |
| 100 | 45.480148 | −73.787168 | 719.05 | 65 | 6 | 0.85 | 9 |
| 101 | 45.477018 | −73.797811 | 860.89 | 65 | 6 | 0.85 | 9 |
| 102 | 45.472685 | −73.810858 | 737.6 | 65 | 6 | 0.85 | 9 |
| 103 | 45.467943 | −73.820363 | 740.19 | 65 | 6 | 0.85 | 9 |
| 104 | 45.46204 | −73.829461 | 633.07 | 65 | 6 | 0.85 | 9 |
| 105 | 45.455371 | −73.841071 | 587.43 | 65 | 6 | 0.85 | 9 |
| 106 | 45.452773 | −73.853174 | 434.61 | 65 | 6 | 0.85 | 9 |
| 107 | 45.450889 | −73.859754 | 177.03 | 65 | 6 | 0.85 | 9 |
| 108 | 45.449305 | −73.862786 | 177.03 | 65 | 6 | 0.85 | 9 |
| 109 | 45.447943 | −73.866002 | 177.03 | 65 | 6 | 0.85 | 9 |
| 110 | 45.446649 | −73.870508 | 274.22 | 65 | 6 | 0.85 | 9 |
| 111 | 45.444361 | −73.875338 | 273.59 | 65 | 6 | 0.85 | 9 |
| 112 | 45.44284 | −73.880347 | 230.01 | 65 | 6 | 0.85 | 9 |
| 113 | 45.440791 | −73.889868 | 293.27 | 65 | 6 | 0.85 | 9 |
| 114 | 45.458772 | −73.905955 | 488.75 | 43 | 11 | 0.93 | 8 |
| 115 | 45.402525 | −73.946758 | 1367.94 | 43 | 11 | 0.93 | 8 |
| 116 | 45.427927 | −73.905635 | 516.35 | 85 | 11 | 0.82 | 9 |
| 117 | 45.425306 | −73.911214 | 441.22 | 85 | 11 | 0.82 | 9 |
| 118 | 45.421662 | −73.918981 | 407.7 | 85 | 11 | 0.82 | 9 |
| 119 | 45.418576 | −73.927174 | 442.58 | 85 | 11 | 0.82 | 9 |
| 120 | 45.422483 | −73.928008 | 337.96 | 85 | 11 | 0.82 | 9 |
| 121 | 45.430551 | −73.922325 | 339.98 | 85 | 11 | 0.82 | 9 |
| 122 | 45.439212 | −73.67468 | 910.53 | 37 | 8 | 0.92 | 8 |
| 123 | 45.506652 | −73.595021 | 946.73 | 15 | 15 | 1 | 8 |
| 124 | 45.501238 | −73.603776 | 976.3 | 15 | 15 | 1 | 8 |
| 125 | 45.479753 | −73.555974 | 489.03 | 35 | 13 | 0.97 | 9 |
| 126 | 45.477135 | −73.573088 | 1174.82 | 35 | 13 | 0.97 | 9 |
| 127 | 45.469233 | −73.577894 | 1576.84 | 35 | 13 | 0.97 | 9 |
| 128 | 45.455685 | −73.578583 | 1402.7 | 35 | 13 | 0.97 | 9 |
| 129 | 45.455324 | −73.594204 | 1174.42 | 35 | 13 | 0.97 | 9 |
| 130 | 45.441617 | −73.605908 | 1939.18 | 35 | 10 | 0.94 | 9 |
| 131 | 45.430776 | −73.623245 | 2212.91 | 35 | 10 | 0.94 | 9 |
| 132 | 45.430535 | −73.659809 | 1389.83 | 35 | 10 | 0.94 | 9 |
| 133 | 45.443726 | −73.595941 | 241.4 | 2 | 15 | 1 | 0 |
| 134 | 45.442281 | −73.603322 | 544.94 | 2 | 15 | 1 | 0 |
| 135 | 45.441619 | −73.611304 | 119.46 | 2 | 15 | 1 | 0 |
| 136 | 45.440414 | −73.613536 | 112.65 | 2 | 15 | 1 | 0 |
| 137 | 45.439993 | −73.610961 | 112.65 | 2 | 15 | 1 | 0 |
| 138 | 45.511098 | −73.687745 | 1808.9 | 40 | 11 | 0.93 | 8 |
| 139 | 45.516511 | −73.724591 | 1734.61 | 40 | 11 | 0.93 | 8 |
| 140 | 45.531184 | −73.6977 | 1821.15 | 40 | 11 | 0.93 | 8 |
| 141 | 45.537967 | −73.680233 | 1243.1 | 40 | 11 | 0.93 | 8 |
| 142 | 45.540624 | −73.652515 | 763.8 | 65 | 9 | 0.93 | 9 |
| 143 | 45.532847 | −73.657335 | 756.39 | 65 | 9 | 0.93 | 9 |
| 144 | 45.534852 | −73.628654 | 371.56 | 100 | 15 | 0.3 | 17 |
| 145 | 45.532056 | −73.587713 | 178.69 | 10 | 15 | 1 | 17 |
| 146 | 45.526945 | −73.568316 | 297.51 | 10 | 15 | 1 | 17 |
| 147 | 45.524484 | −73.567667 | 193.12 | 10 | 15 | 1 | 17 |
| 148 | 45.525882 | −73.570865 | 192.76 | 10 | 15 | 1 | 17 |
| 149 | 45.538685 | −73.590452 | 142.93 | 100 | 15 | 0.3 | 40 |
| 150 | 45.539332 | −73.5941 | 188.34 | 100 | 15 | 0.3 | 5 |
| 151 | 45.562269 | −73.625156 | 519.59 | 0 | 0 | 0 | 7.5 |
| 152 | 45.564913 | −73.633868 | 483.82 | 0 | 0 | 0 | 7.5 |
| 153 | 45.569832 | −73.613291 | 144.84 | 0 | 0 | 0 | 0 |
| 154 | 45.572223 | −73.615995 | 289.68 | 0 | 0 | 0 | 0 |
| 155 | 45.574607 | −73.61108 | 296.16 | 0 | 0 | 0 | 0 |
| 156 | 45.576691 | −73.623896 | 209.21 | 0 | 0 | 0 | 0 |
| 157 | 45.577986 | −73.626797 | 209.21 | 0 | 0 | 0 | 0 |
| 158 | 45.579337 | −73.630016 | 203.59 | 0 | 0 | 0 | 0 |
| 159 | 45.563097 | −73.562043 | 603.88 | 50 | 15 | 0.5 | 0 |
| 160 | 45.569076 | −73.556293 | 354.04 | 50 | 15 | 0.5 | 0 |
| 161 | 45.56661 | −73.545697 | 628.63 | 150 | 9 | 0.85 | 10 |
| 162 | 45.564507 | −73.531449 | 627.64 | 30 | 9 | 0.85 | 10 |
| 163 | 45.578913 | −73.51808 | 1034.25 | 30 | 9 | 0.85 | 10 |
| 164 | 45.587119 | −73.544519 | 266.44 | 100 | 15 | 0.2 | 0 |
| 165 | 45.588011 | −73.548111 | 241.4 | 100 | 15 | 0.2 | 0 |
| 166 | 45.5889213 | −73.552403 | 241.4 | 100 | 15 | 0.2 | 0 |
| 167 | 45.590504 | −73.55618 | 237.65 | 100 | 15 | 0.2 | 0 |
| 168 | 45.589963 | −73.561347 | 112.65 | 100 | 15 | 0.2 | 0 |
| 169 | 45.590414 | −73.563085 | 109.74 | 100 | 15 | 0.2 | 0 |
| 170 | 45.591149 | −73.565703 | 141.11 | 100 | 15 | 0.2 | 0 |
| 171 | 45.593125 | −73.568101 | 153.25 | 100 | 15 | 0.2 | 0 |
| 172 | 45.617099 | −73.604364 | 370.15 | 75 | 15 | 0.7 | 20 |
| 173 | 45.619891 | −73.607488 | 374.1 | 75 | 15 | 0.7 | 20 |
| 174 | 45.622322 | −73.61063 | 358.69 | 75 | 15 | 0.7 | 12 |
| 175 | 45.425901 | −73.612466 | 261.16 | 75 | 15 | 0.7 | 12 |
| 176 | 45.601307 | −73.610067 | 370.15 | 65 | 8 | 0.95 | 9 |
| 177 | 45.606351 | −73.604574 | 443.68 | 65 | 8 | 0.95 | 9 |
| 178 | 45.601908 | −73.589897 | 403.82 | 65 | 8 | 0.95 | 9 |
| 179 | 45.599265 | −73.583202 | 402.33 | 65 | 8 | 0.95 | 9 |
| 180 | 45.595563 | −73.574813 | 402.33 | 65 | 8 | 0.95 | 9 |
| 181 | 45.599987 | −73.564625 | 402.33 | 65 | 8 | 0.95 | 9 |
| 182 | 45.617505 | −73.573595 | 1384.72 | 65 | 8 | 0.95 | 9 |
| 183 | 45.642984 | −73.564979 | 520.76 | 65 | 8 | 0.95 | 9 |
| 184 | 45.647244 | −73.557512 | 514.99 | 65 | 8 | 0.95 | 9 |
| 185 | 45.650664 | −73.550713 | 514.99 | 65 | 8 | 0.95 | 9 |
| 186 | 45.653797 | −73.544229 | 514.99 | 65 | 8 | 0.95 | 9 |
| 187 | 45.652699 | −73.520683 | 847.72 | 65 | 8 | 0.95 | 9 |
| 188 | 45.645286 | −73.515518 | 245.1 | 65 | 8 | 0.95 | 9 |
| 189 | 45.629559 | −73.565273 | 553.62 | 0 | 15 | 1 | 0 |
| 190 | 45.627203 | −73.560413 | 473.68 | 0 | 0 | 0 | 15 |
| 191 | 45.634786 | −73.540334 | 2026.09 | 110 | 15 | 0.5 | 9 |
| 192 | 45.635317 | −73.511496 | 397.62 | 110 | 15 | 0.5 | 9 |
| 193 | 45.653453 | −73.580984 | 112.65 | 0 | 15 | 1 | 0 |
| 194 | 45.650783 | −73.574353 | 112.65 | 0 | 15 | 1 | 0 |
| 195 | 45.649181 | −73.572868 | 115.85 | 0 | 15 | 1 | 0 |
| 196 | 45.665821 | −73.52684 | 767.75 | 0 | 0 | 0 | 7.5 |
| 197 | 45.669147 | −73.493507 | 979.45 | 40 | 11 | 0.93 | 8 |
| 198 | 45.682365 | −73.496987 | 981.7 | 40 | 11 | 0.93 | 8 |
| 199 | 45.695915 | −73.48791 | 981.7 | 40 | 11 | 0.93 | 8 |
| 200 | 45.680895 | −73.497232 | 340.81 | 0 | 15 | 1 | 0 |
| 201 | 45.670026 | −73.514763 | 291.6 | 0 | 15 | 1 | 0 |
| 202 | 45.676246 | −73.512102 | 418.06 | 0 | 15 | 1 | 0 |
| 203 | 45.680905 | −73.512188 | 292.68 | 0 | 15 | 1 | 0 |
| 204 | 45.431493 | −73.894652 | 572.65 | 0 | 15 | 1 | 0 |
| 205 | 45.439319 | −73.913471 | 728.19 | 0 | 15 | 1 | 0 |
| 206 | 45.443898 | −73.924428 | 415.84 | 0 | 15 | 1 | 0 |
| 207 | 45.450941 | −73.928406 | 545.9 | 0 | 15 | 1 | 0 |
| 208 | 45.46597 | −73.9361 | 1308.31 | 0 | 15 | 1 | 0 |
| 209 | 45.40949 | −73.483236 | 2031.04 | 40 | 11 | 0.93 | 7.5 |
| 210 | 45.460311 | −73.919206 | 462.48 | 43 | 11 | 0.9 | 8 |
| 211 | 45.384537 | −73.567484 | 2654.36 | 40 | 11 | 0.93 | 7.5 |
| 212 | 45.38829 | −73.517825 | 2391.21 | 40 | 11 | 0.93 | 7.5 |
| 213 | 45.365836 | −73.510154 | 497.23 | 40 | 11 | 0.93 | 7.5 |
| 214 | 45.368097 | −73.488407 | 612.36 | 40 | 11 | 0.93 | 7.5 |
| 215 | 45.375095 | −73.490862 | 359.86 | 40 | 11 | 0.93 | 7.5 |
| 216 | 45.383713 | −73.466433 | 528.53 | 40 | 11 | 0.93 | 7.5 |
| 217 | 45.390115 | −73.486617 | 198.1 | 40 | 11 | 0.93 | 7.5 |
| 218 | 45.392521 | −73.482472 | 269.4 | 40 | 11 | 0.93 | 7.5 |
| 219 | 45.401296 | −73.594288 | 1028.76 | 45 | 7 | 0.7 | 13 |
| 220 | 45.39903 | −73.512902 | 1029.98 | 60 | 7 | 0.85 | 13 |
| 221 | 45.398829 | −73.498305 | 620.73 | 60 | 7 | 0.85 | 13 |
| 222 | 45.405579 | −73.487061 | 627.64 | 0 | 0 | 0 | 7.5 |
| 223 | 45.44346 | −73.466336 | 2336.13 | 40 | 11 | 0.93 | 7.5 |
| 224 | 45.491615 | −73.455755 | 5334.41 | 40 | 11 | 0.93 | 7.5 |
| 225 | 45.504905 | −73.380228 | 741.55 | 40 | 11 | 0.93 | 7.5 |
| 226 | 45.526102 | −73.345277 | 2616.82 | 40 | 11 | 0.93 | 7.5 |
| 227 | 45.525959 | −73.501946 | 2114.48 | 40 | 11 | 0.93 | 7.5 |
| 228 | 45.557552 | −73.458245 | 3794.15 | 40 | 11 | 0.93 | 7.5 |
| 229 | 45.592847 | −73.430247 | 3707.6 | 40 | 11 | 0.93 | 7.5 |
| 230 | 45.589204 | −73.345012 | 2024.99 | 40 | 11 | 0.93 | 7.5 |
| 231 | 45.62611 | −73.448933 | 1376.51 | 40 | 11 | 0.93 | 7.5 |
| 232 | 45.661787 | −73.430983 | 1059.7 | 40 | 11 | 0.93 | 7.5 |
| 233 | 45.682631 | −73.42627 | 1757.84 | 40 | 11 | 0.93 | 7.5 |
| 234 | 45.572432 | −73.464773 | 1573.29 | 60 | 9 | 0.96 | 9 |
| 235 | 45.567145 | −73.442114 | 640.6 | 60 | 9 | 0.96 | 9 |
| 236 | 45.562097 | −73.425977 | 1071.75 | 60 | 9 | 0.96 | 9 |
| 237 | 45.548221 | −73.466156 | 532.35 | 0 | 15 | 1 | 0 |
| 238 | 45.55182 | −73.471725 | 501.56 | 0 | 15 | 1 | 0 |
| 239 | 45.544908 | −73.429411 | 1112.15 | 0 | 15 | 1 | 0 |
| 240 | 45.601691 | −73.396831 | 1332.24 | 0 | 15 | 1 | 0 |
| 241 | 45.620184 | −73.411938 | 1952.5 | 0 | 0 | 0 | 7.5 |
| 242 | 45.590527 | −73.430877 | 241.4 | 65 | 11 | 0.9 | 8 |
| 243 | 45.593777 | −73.434972 | 248.7 | 65 | 11 | 0.9 | 8 |
| 244 | 45.53419 | −73.851753 | 537.21 | 80 | 15 | 1 | 0 |
| 245 | 45.531666 | −73.848724 | 531.08 | 80 | 15 | 1 | 0 |
| 246 | 45.525668 | −73.847035 | 236.5 | 80 | 15 | 1 | 0 |
| 247 | 45.530092 | −73.87059 | 609.58 | 80 | 15 | 1 | 0 |
| 248 | 45.583708 | −73.853991 | 819.97 | 35 | 11 | 0.93 | 8.5 |
| 249 | 45.639335 | −73.844072 | 2524.36 | 35 | 10 | 0.93 | 9 |
| 250 | 45.612433 | −73.840306 | 1346.83 | 35 | 11 | 0.93 | 7 |
| 251 | 45.620875 | −73.867936 | 1181.61 | 35 | 10 | 0.93 | 4 |
| 252 | 45.63086 | −73.819304 | 395.32 | 150 | 8 | 0.7 | 12 |
| 253 | 45.626125 | −73.833429 | 294.62 | 65 | 8 | 0.91 | 10 |
| 254 | 45.622643 | −73.828451 | 289.68 | 65 | 8 | 0.91 | 10 |
| 255 | 45.638235 | −73.871145 | 823.41 | 90 | 8.5 | 0.92 | 9.5 |
| 256 | 45.635457 | −73.860373 | 613.65 | 90 | 8.5 | 0.92 | 9.5 |
| 257 | 45.628755 | −73.848429 | 611.55 | 185 | 8.5 | 0.7 | 13 |
| 258 | 45.644005 | −73.839829 | 402.33 | 75 | 15 | 0.85 | 10 |
| 259 | 45.62046 | −73.811862 | 1017.72 | 35 | 11 | 0.93 | 7.5 |
| 260 | 45.650328 | −73.786076 | 1171.49 | 35 | 11 | 0.93 | 4.5 |
| 261 | 45.640103 | −73.796167 | 1351.87 | 35 | 11 | 0.93 | 7.5 |
| 262 | 45.685073 | −73.770836 | 3167.5 | 35 | 10 | 0.93 | 8 |
| 263 | 45.686239 | −73.764711 | 781.05 | 80 | 8 | 0.91 | 9 |
| 264 | 45.693831 | −73.754997 | 454.89 | 80 | 8 | 0.91 | 9 |
| 265 | 45.685292 | −73.781511 | 450.62 | 65 | 8 | 0.91 | 9 |
| 266 | 45.732301 | −73.651759 | 4943.41 | 35 | 10 | 0.93 | 8 |
| 267 | 45.717773 | −73.617568 | 435.69 | 60 | 8 | 0.91 | 8 |
| 268 | 45.711828 | −73.622 | 341.12 | 60 | 8 | 0.91 | 8 |
| 269 | 45.723656 | −73.616404 | 485.45 | 130 | 8 | 0.75 | 13 |
| 270 | 45.728241 | −73.67683 | 310.54 | 65 | 9 | 0.91 | 8.5 |
| 271 | 45.726383 | −73.68301 | 252.41 | 65 | 9 | 0.91 | 8.5 |
| 272 | 45.724885 | −73.689161 | 270.88 | 65 | 9 | 0.91 | 8.5 |
| 273 | 45.72099 | −73.701264 | 500.39 | 100 | 9 | 0.88 | 8.5 |
| 274 | 45.718185 | −73.709356 | 321.87 | 100 | 9 | 0.88 | 8.5 |
| 275 | 45.723627 | −73.69517 | 318.72 | 65 | 9 | 0.91 | 8.5 |
| 276 | 45.715044 | −73.715202 | 386.24 | 100 | 9 | 0.88 | 8.5 |
| 277 | 45.711868 | −73.721554 | 386.24 | 100 | 9 | 0.88 | 8.5 |
| 278 | 45.706062 | −73.719135 | 386.24 | 100 | 9 | 0.88 | 8.5 |
| 279 | 45.702607 | −73.725064 | 391.93 | 100 | 9 | 0.88 | 8.5 |
| 280 | 45.694093 | −73.601574 | 708.11 | 35 | 10 | 0.93 | 8 |
| 281 | 45.701072 | −73.58597 | 1021.75 | 35 | 10 | 0.93 | 8 |
| 282 | 45.704059 | −73.552405 | 460.06 | 35 | 10 | 0.93 | 8 |
| 283 | 45.780634 | −73.629427 | 715.04 | 40 | 7.5 | 0.94 | 7 |
| 284 | 45.717937 | −73.512757 | 1813.91 | 250 | 7.5 | 0.7 | 15 |
| 285 | 45.715355 | −73.499264 | 393.32 | 35 | 10 | 0.93 | 4.5 |
| 286 | 45.709849 | −73.518397 | 708.11 | 35 | 9 | 0.93 | 7 |
| 287 | 45.721475 | −73.517882 | 700.18 | 35 | 9 | 0.93 | 4.5 |
| 288 | 45.725952 | −73.507309 | 491.42 | 150 | 25 | 0.7 | 12 |
| 289 | 45.358039 | −73.736125 | 3138.21 | 35 | 8 | 0.93 | 7 |
| 290 | 45.347865 | −73.686877 | 1096.88 | 70 | 9 | 0.91 | 9 |
| 291 | 45.366609 | −73.710982 | 305.75 | 80 | 8 | 0.75 | 8.5 |
| 292 | 45.363505 | −73.712964 | 110.71 | 80 | 8 | 0.75 | 8.5 |
| 293 | 45.361562 | −73.713524 | 129.44 | 80 | 8 | 0.75 | 8.5 |
| 294 | 45.359212 | −73.715659 | 158.96 | 80 | 8 | 0.75 | 8.5 |
| 295 | 45.358528 | −73.719093 | 110.58 | 150 | 10 | 0.7 | 10 |
| 296 | 45.358851 | −73.722002 | 122.72 | 150 | 10 | 0.7 | 10 |
| 297 | 45.359026 | −73.72511 | 128.75 | 150 | 10 | 0.7 | 10 |
| 298 | 45.359377 | −73.728149 | 111.96 | 150 | 10 | 0.7 | 10 |
| 299 | 45.359779 | −73.731011 | 112.65 | 150 | 10 | 0.7 | 10 |
| 300 | 45.360172 | −73.733924 | 112.65 | 150 | 10 | 0.7 | 10 |
| 301 | 45.356791 | −73.7169 | 144.32 | 80 | 8 | 0.75 | 8.5 |
| 302 | 45.35474 | −73.718359 | 111.27 | 80 | 8 | 0.75 | 8.5 |
| 303 | 45.35275 | −73.719475 | 112.65 | 80 | 8 | 0.75 | 8.5 |
| 304 | 45.351001 | −73.720419 | 112.65 | 80 | 8 | 0.75 | 8.5 |
| 305 | 45.342896 | −73.765213 | 634.29 | 150 | 25 | 0.7 | 12 |
| 306 | 45.356592 | −73.758567 | 144.84 | 40 | 12 | 0.93 | 5.5 |
| 307 | 45.357255 | −73.755048 | 139.51 | 80 | 7 | 0.7 | 11.5 |
| 308 | 45.410403 | −73.671463 | 956.46 | 35 | 7 | 0.93 | 7 |
| 309 | 45.411084 | −73.689762 | 949.51 | 35 | 7 | 0.93 | 7 |
References
- Van Geffen, K.G.; Groot, A.T.; Van Grunsven, R.H.; Donners, M.; Berendse, F.; Veenendaal, E.M. Artificial night lighting disrupts sex pheromone in a noctuid moth. Ecol. Entomol. 2015, 40, 401–408. [Google Scholar] [CrossRef]
- Boldogh, S.; Dobrosi, D.; Samu, P. The effects of the illumination of buildings on house-dwelling bats and its conservation consequences. Acta Chiropterologica 2007, 9, 527–534. [Google Scholar] [CrossRef]
- Kamrowski, R.L.; Limpus, C.; Pendoley, K.; Hamann, M. Influence of industrial light pollution on the sea-finding behaviour of flatback turtle hatchlings. Wildl. Res. 2015, 41, 421–434. [Google Scholar] [CrossRef]
- Brüning, A.; Hölker, F.; Wolter, C. Artificial light at night: Implications for early life stages development in four temperate freshwater fish species. Aquat. Sci. 2011, 73, 143–152. [Google Scholar] [CrossRef]
- Da Silva, A.; Valcu, M.; Kempenaers, B. Light pollution alters the phenology of dawn and dusk singing in common European songbirds. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2015, 370, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Briggs, W.R. Physiology of plant responses to artificial lighting. In Ecological Consequences of Artificial Night Lighting; Island Press: Washington DC, USA, 2016; pp. 281–304. [Google Scholar]
- Ffrench-Constant, R.H.; Somers-Yeates, R.; Bennie, J.; Economou, T.; Hodgson, D.; Spalding, A.; McGregor, P.K. Light pollution is associated with earlier tree budburst across the United Kingdom. Proc. R. Soc. B Biol. Sci. 2016, 283, 20160813. [Google Scholar] [CrossRef] [PubMed]
- Bennie, J.; Davies, T.W.; Cruse, D.; Gaston, K.J. Ecological effects of artificial light at night on wild plants. J. Ecol. 2016, 104, 611–620. [Google Scholar] [CrossRef] [Green Version]
- Škvareninová, J.; Tuhárska, M.; Škvarenina, J.; Babálová, D.; Slobodníková, L.; Slobodník, B.; Středová, H.; Minďaš, J. Effects of light pollution on tree phenology in the urban environment. Morav. Geogr. Rep. 2017, 25, 282–290. [Google Scholar] [CrossRef] [Green Version]
- Bennie, J.; Davies, T.W.; Cruse, D.; Bell, F.; Gaston, K.J. Artificial light at night alters grassland vegetation species composition and phenology. J. Appl. Ecol. 2018, 55, 442–450. [Google Scholar] [CrossRef] [Green Version]
- Kloog, I.; Haim, A.; Stevens, R.G.; Portnov, B.A. Global Co-Distribution of Light at Night (LAN) and Cancers of Prostate, Colon, and Lung in Men. Chronobiol. Int. 2009, 26, 108–125. [Google Scholar] [CrossRef]
- Kloog, I.; Haim, A.; Stevens, R.G.; Barchana, M.; Portnov, B.A. Light at Night Co-distributes with Incident Breast but not Lung Cancer in the Female Population of Israel. Chronobiol. Int. 2008, 25, 65–81. [Google Scholar] [CrossRef] [PubMed]
- Stevens, R.G. Light-at-night, circadian disruption and breast cancer: Assessment of existing evidence. Int. J. Epidemiol. 2009, 38, 963–970. [Google Scholar] [CrossRef] [PubMed]
- Benke, K.E.; Benke, K.K.; Dimitriadis, C. Spectral content of artificial lighting and effects on health. J. Australas. Coll. Nutr. Environ. Med. 2011, 30, 13. [Google Scholar]
- Cajochen, C.; Altanay-Ekici, S.; Münch, M.; Frey, S.; Knoblauch, V.; Wirz-Justice, A. Evidence that the lunar cycle influences human sleep. Curr. Biol. 2013, 23, 1485–1488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garaulet, M.; Ordovas, J.M. Chronobiology and Obesity; Springer: New York, NY, USA, 2013; pp. 133–160. [Google Scholar]
- Aubé, M.; Roby, J.; Kocifaj, M. Evaluating Potential Spectral Impacts of Various Artificial Lights on Melatonin Suppression, Photosynthesis, and Star Visibility. PLoS ONE 2013, 20, e67798. [Google Scholar] [CrossRef] [Green Version]
- Garcia-Saenz, A.; Sánchez de Miguel, A.; Espinosa, A.; Valentin, A.; Aragonés, N.; Llorca, J.; Amiano, P.; Martín Sánchez, V.; Guevara, M.; Capelo, R.; et al. Evaluating the association between artificial light-at-night exposure and breast and prostate cancer risk in Spain (MCC-Spain study). Environ. Health Perspect. 2018, 126, 047011. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Saenz, A.; de Miguel, A.S.; Espinosa, A.; Costas, L.; Aragonés, N.; Tonne, C.; Moreno, V.; Pérez-Gómez, B.; Valentin, A.; Pollán, M.; et al. Association between outdoor light-at-night exposure and colorectal cancer in Spain. Epidemiology 2020, 31, 718–727. [Google Scholar] [CrossRef] [PubMed]
- Garstang, R.H. Model for artificial night-sky illumination. Publ. Astron. Soc. Pac. 1986, 98, 364–375. [Google Scholar] [CrossRef]
- Luginbuhl, C.B.; Duriscoe, D.M.; Moore, C.W.; Richman, A.; Lockwood, W.G.; Davis, D.R. From the ground up II: Sky glow and near-ground artificial light propagation in Flagstaff, Arizona. Publ. Astron. Soc. Pac. 2009, 121, 204–212. [Google Scholar] [CrossRef]
- Cinzano, P.; Falchi, F. The propagation of light pollution in the atmosphere. Mon. Not. R. Astron. Soc. 2012, 427, 3337–3357. [Google Scholar] [CrossRef] [Green Version]
- Aubé, M.; Franchomme-Fossé, L.; Robert-Staehler, P.; Houle, V. Light pollution modelling and detection in a heterogeneous environment: Toward a night-time aerosol optical depth retrieval method. In Optics & Photonics 2005; International Society for Optics and Photonics: Bellingham, WA, USA, 2005; p. 589012. [Google Scholar]
- Kocifaj, M. Light-pollution model for cloudy and cloudless night skies with ground-based light sources. Appl. Opt. 2007, 46, 3013–3022. [Google Scholar] [CrossRef] [PubMed]
- Aubé, M. Light pollution models and detection method take account of heterogeneous environments. SPIE Newsroom 2006. [Google Scholar] [CrossRef]
- Aubé, M.; Simoneau, A. New features to the night sky radiance model illumina: Hyperspectral support, improved obstacles and cloud reflection. J. Quant. Spectrosc. Radiat. Transf. 2018, 211, 25–34. [Google Scholar] [CrossRef]
- Aubé, M.; Simoneau, A.; Muñoz-Tuñón, C.; Díaz-Castro, J.; Serra-Ricart, M. Restoring the night sky darkness at Observatorio del Teide: First application of the model Illumina version 2. Mon. Not. R. Astron. Soc. 2020, 497, 2501–2516. [Google Scholar] [CrossRef]
- Aubé, M.; Simoneau, A. Illumina Webpage. 2021. Available online: https://lx02.cegepsherbrooke.qc.ca/~aubema/index.php/Prof/IllumEn (accessed on 30 May 2021).
- Aubé, M.; Roby, J. Sky brightness levels before and after the creation of the first International Dark Sky Reserve, Mont-Mégantic Observatory, Québec, Canada. J. Quant. Spectrosc. Radiat. Transf. 2014, 139, 52–63. [Google Scholar] [CrossRef]
- Aubé, M. Physical behaviour of anthropogenic light propagation into the nocturnal environment. Phil. Trans. R. Soc. B 2015, 370, 20140117. [Google Scholar] [CrossRef] [Green Version]
- Statistics Canada. Census 2016. Available online: https://www12.statcan.gc.ca/census-recensement/2016/dp-pd/prof/details/page.cfm?lang=E&Geo1=CSD&Code1=2466023&Geo2=PR&Code2=24&SearchText=Montreal&SearchType=Begins&SearchPR=01&B1=All&GeoLevel=PR&GeoCode=2466023&TABID=1&type=0 (accessed on 30 May 2021).
- SkyscraperPage.com. Montreal Skyscraper Diagram. 2017. Available online: https://skyscraperpage.com/diagrams/?cityID=22 (accessed on 30 May 2021).
- Simoneau, A.; Aubé, M.; Bertolo, A. Multispectral analysis of the night sky brightness and its origin for the Asiago Observatory, Italy. Mon. Not. R. Astron. Soc. 2020, 491, 4398–4405. [Google Scholar] [CrossRef]
- Government of Canada. Canadian Climate Normals 1971–2000 Station Data. 2015. Available online: climate.weather.gc.ca/climatenormals/resultse.html?stnID=5415lang=fStationName=montrealSearchType=ContainsstnNameSubmit=godCode=1 (accessed on 30 May 2021).
- AERONET. AERONET Data Display Interface. 2021. Available online: aeronet.gsfc.nasa.gov (accessed on 30 May 2021).
- Shettle, E.P.; Fenn, R.W. Models for the Aerosols of the Lower Atmosphere and the Effects of Humidity Variations on Their Optical Properties. Environ. Res. Pap. 1979, 676, 89. [Google Scholar]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- de Miguel, A.S.; Kyba, C.C.; Aubé, M.; Zamorano, J.; Cardiel, N.; Tapia, C.; Bennie, J.; Gaston, K.J. Colour remote sensing of the impact of artificial light at night (I): The potential of the International Space Station and other DSLR-based platforms. Remote Sens. Environ. 2019, 224, 92–103. [Google Scholar] [CrossRef]
- de Miguel, S. NOKTOsat Website. 2021. Available online: http://noktosat.com (accessed on 30 May 2021).
- Elvidge, C.D.; Baugh, K.; Zhizhin, M.; Hsu, F.C.; Ghosh, T. VIIRS night-time lights. Int. J. Remote Sens. 2017, 38, 5860–5879. [Google Scholar] [CrossRef]
- Roby, J.; Aubé, M.; Morin Paulhus, A. LSPDD: Lamp Spectral Power Distribution Database. 2021. Available online: https://lspdd.org (accessed on 30 May 2021).
- Google Maps. Google Maps. 2021. Available online: https://www.google.ca/maps (accessed on 30 May 2021).
- Google Earth. Google Earth. 2021. Available online: https://www.google.com/earth/ (accessed on 30 May 2021).
- Map Developers. Draw a circle—Create a Circle on a Google Map Using a Point and a Radius. 2021. Available online: https://www.mapdevelopers.com/draw-circle-tool.php (accessed on 30 May 2021).
- Boeing, G. OSMnx: New methods for acquiring, constructing, analyzing, and visualizing complex street networks. Comput. Environ. Urban Syst. 2017, 65, 126–139. [Google Scholar] [CrossRef] [Green Version]
- Aubé, M.; Marseille, C.; Farkouh, A.; Dufour, A.; Simoneau, A.; Zamorano, J.; Roby, J.; Tapia, C. Mapping the Melatonin Suppression, Star Light and Induced Photosynthesis Indices with the LANcube. Remote Sens. 2020, 12, 3954. [Google Scholar] [CrossRef]
- Tscharntke, T.; Hochberg, M.E.; Rand, T.A.; Resh, V.H.; Krauss, J. Author sequence and credit for contributions in multiauthored publications. PLoS Biol. 2007, 5, e18. [Google Scholar] [CrossRef] [PubMed]



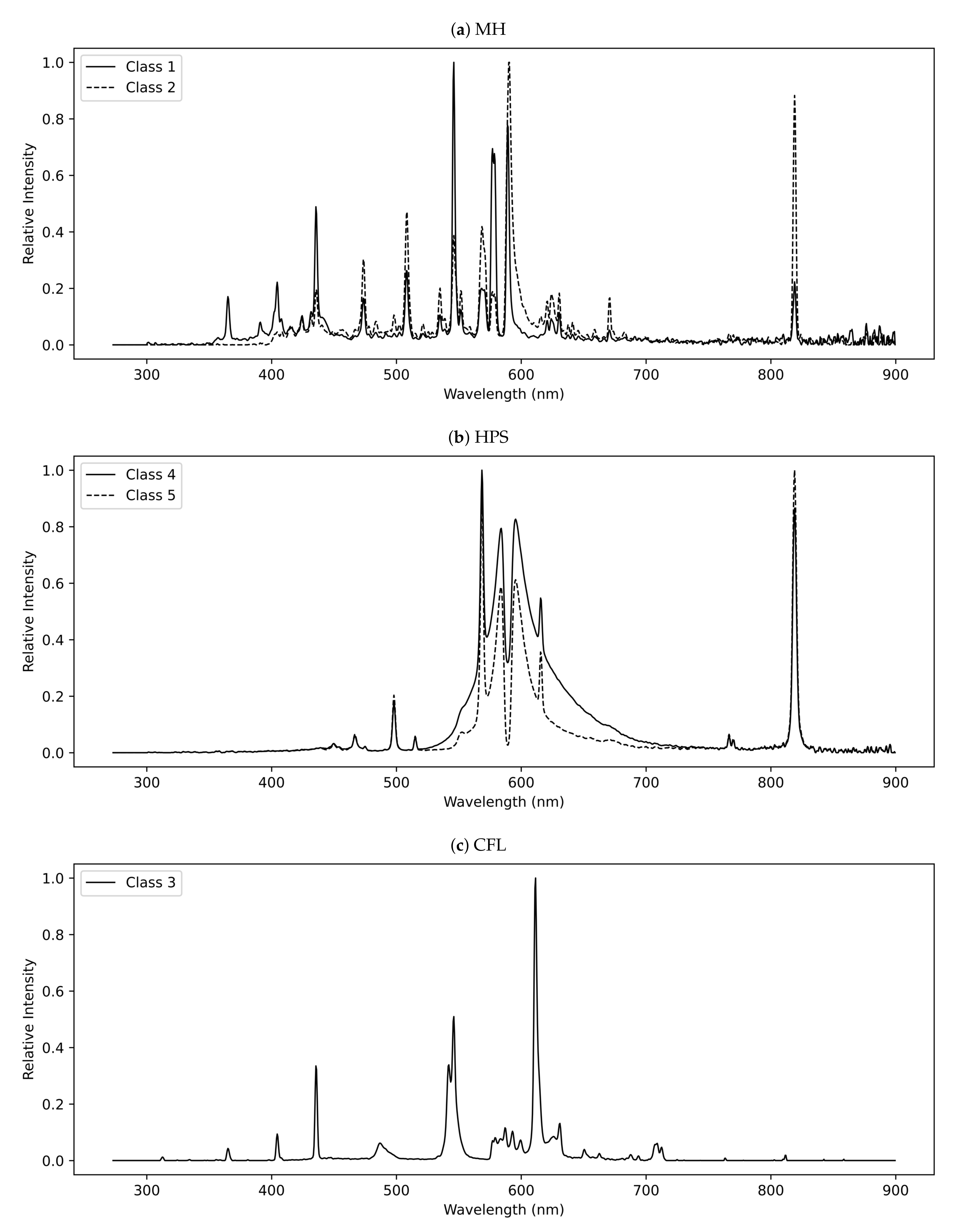

| Class | Technology | ULOR | LOP | CCT | MSI |
|---|---|---|---|---|---|
| % | K | ||||
| 1 | Metal Halide | 5 | Cobrahead | 4700 | 0.58 |
| 2 | Metal Halide | 5 | Cobrahead | 3200 | 0.44 |
| 3 | Compact Fluorescent Lamp | 15 | Farm lantern | 3000 | 0.26 |
| 4 | High-Pressure Sodium | 2 | 0.5 cobrahead + 0.5 helios | 1940 | 0.08 |
| 5 | High-Pressure Sodium | 2 | 0.5 cobrahead + 0.5 helios | 2010 | 0.12 |
| 6 | Low-Pressure Sodium | 0 | Helios | 1750 | 0.02 |
| Parameter | Value(s) | Units | Influence |
|---|---|---|---|
| Relative humidity | 80.0 | % | low |
| Atmospheric pressure | 101.1 | kPa | low |
| Aerosol optical depth | 0.15 | - | low |
| ngstrm coefficient | 1.52 | - | low |
| Aerosol model | urban | - | low |
| Aerosol profile scale height | 2 | km | low |
| Clouds | None | - | low |
| Additional particle layer | None | - | low |
| Surface reflectance | 10% grass & 90% asphalt | % | high |
| Wavelength bins | 10 | moderate | |
| Wavelength bins width | 50 | nm | moderate |
| Starting wavelength | 350 | nm | moderate |
| # | Environment | Window Height | Latitude | Longitude | F | |||
|---|---|---|---|---|---|---|---|---|
| m | deg | deg | ||||||
| 1 | City center | 2, 5, 8 | 45.501171 | −73.565357 | 30 | 100 | 0.96 | 9 |
| 2 | Urban residential | 2, 5 | 45.488376 | −73.596217 | 37 | 12 | 0.93 | 8.5 |
| 3 | Suburb residential | 2 | 45.533026 | −73.703789 | 40 | 11 | 0.93 | 8 |
| 4 | Commercial | 2, 5, 8 | 45.468995 | −73.542072 | 55 | 9 | 0.89 | 9.5 |
| 5 | Rural | 2, 5 | 45.642133 | −73.662191 | 0 | 0 | 0 | 7.5 |
| # | Environment | Illumina | ISS | Illumina | ISS Photopic | Illumina Photopic |
|---|---|---|---|---|---|---|
| Height | MSI | MSI | Radiance | Irradiance | ||
| m | W sr−1 cm−2 | W m−2 | ||||
| 1 | City center | 2 | 0.43 | 0.44 | 0.0442 | 5.91 |
| 5 | 0.44 | 5.47 | ||||
| 8 | 0.44 | 3.18 | ||||
| 2 | Urban residential | 2 | 0.08 | 0.15 | 0.0135 | 1.59 |
| 5 | 0.14 | 1.38 | ||||
| 3 | Suburb residential | 2 | 0.12 | 0.14 | 0.0128 | 7.51 |
| 4 | Commercial | 2 | 0.62 | 0.53 | 0.0511 | 1.03 |
| 5 | 0.53 | 9.52 | ||||
| 8 | 0.53 | 9.14 | ||||
| 5 | Rural | 2 | 0.12 | 0.14 | 0.0037 | 5.08 |
| 5 | 0.14 | 2.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aubé, M.; Houle, J.-P.; Desmarais, J.; Veilleux, N.; Bordeleau, É. Modeling the Spectral Properties of Obtrusive Light Incident on a Window: Application to Montréal, Canada. Remote Sens. 2021, 13, 2767. https://doi.org/10.3390/rs13142767
Aubé M, Houle J-P, Desmarais J, Veilleux N, Bordeleau É. Modeling the Spectral Properties of Obtrusive Light Incident on a Window: Application to Montréal, Canada. Remote Sensing. 2021; 13(14):2767. https://doi.org/10.3390/rs13142767
Chicago/Turabian StyleAubé, Martin, Julien-Pierre Houle, Justine Desmarais, Nikki Veilleux, and Émie Bordeleau. 2021. "Modeling the Spectral Properties of Obtrusive Light Incident on a Window: Application to Montréal, Canada" Remote Sensing 13, no. 14: 2767. https://doi.org/10.3390/rs13142767
APA StyleAubé, M., Houle, J.-P., Desmarais, J., Veilleux, N., & Bordeleau, É. (2021). Modeling the Spectral Properties of Obtrusive Light Incident on a Window: Application to Montréal, Canada. Remote Sensing, 13(14), 2767. https://doi.org/10.3390/rs13142767