Spectral Complexity of Hyperspectral Images: A New Approach for Mangrove Classification
Abstract
:1. Introduction
2. Materials and Methods
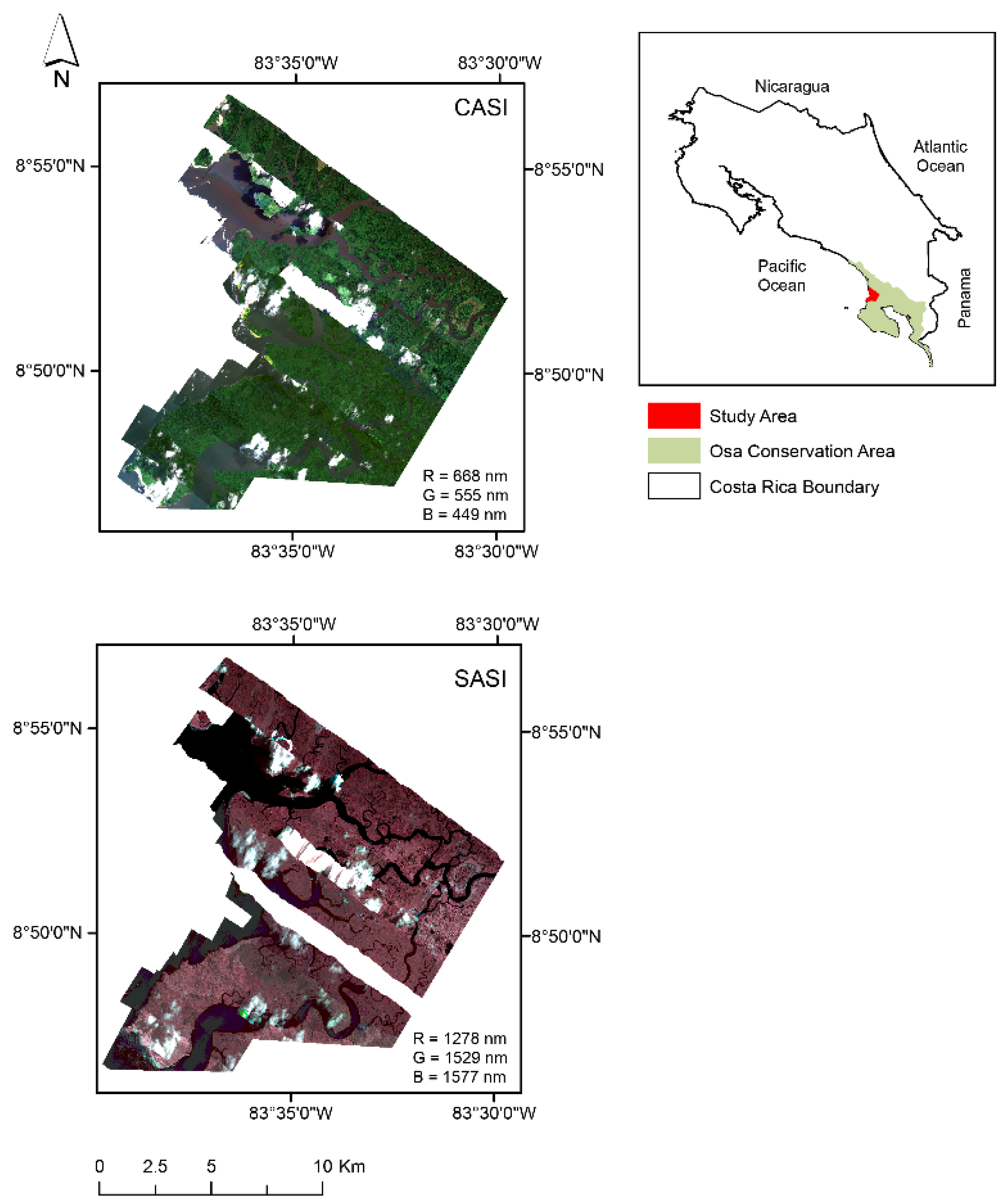
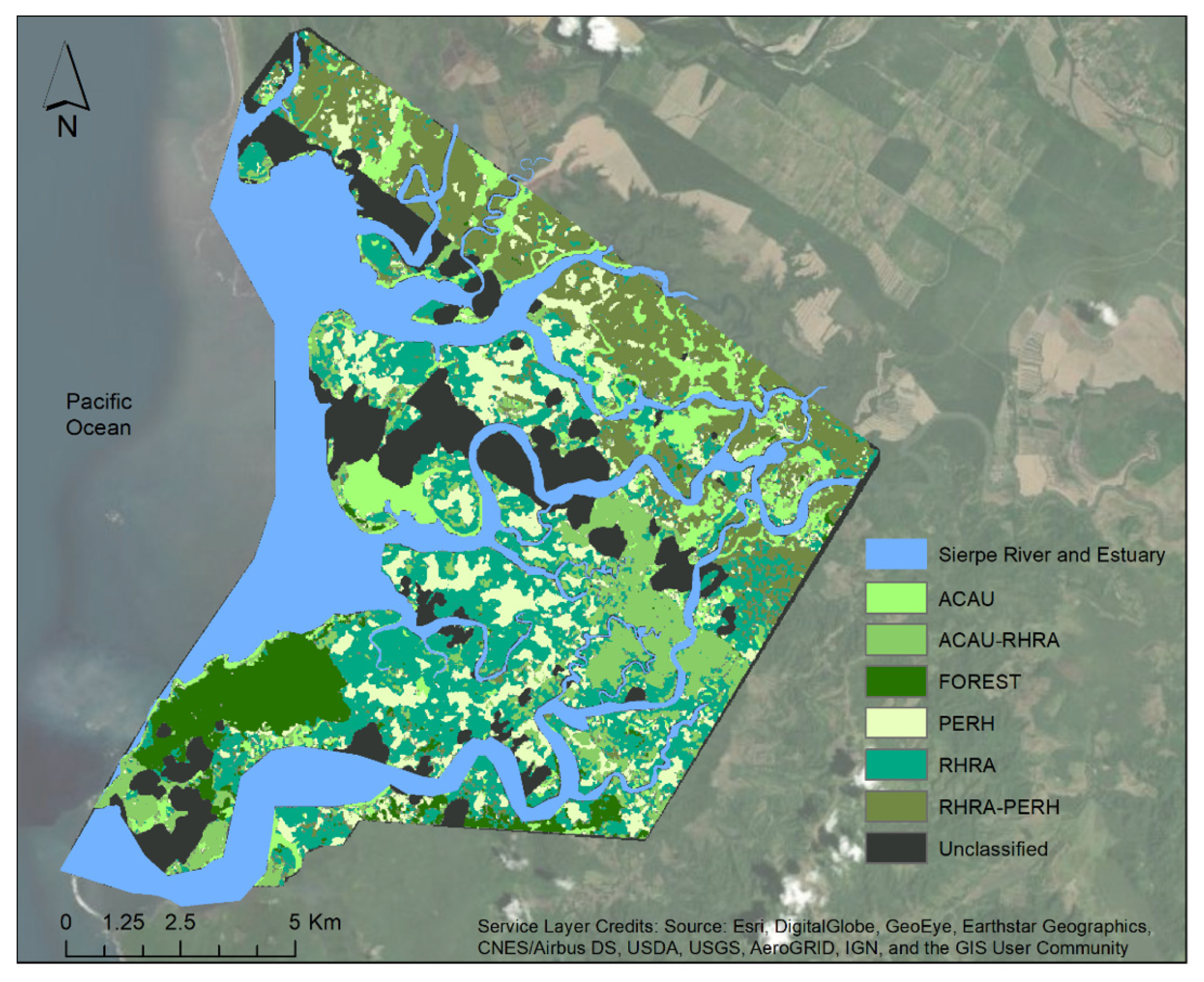
2.1. Study Site
2.2. Airborne Hyperspectral Imagery (HSI)
2.3. Pre-Processing
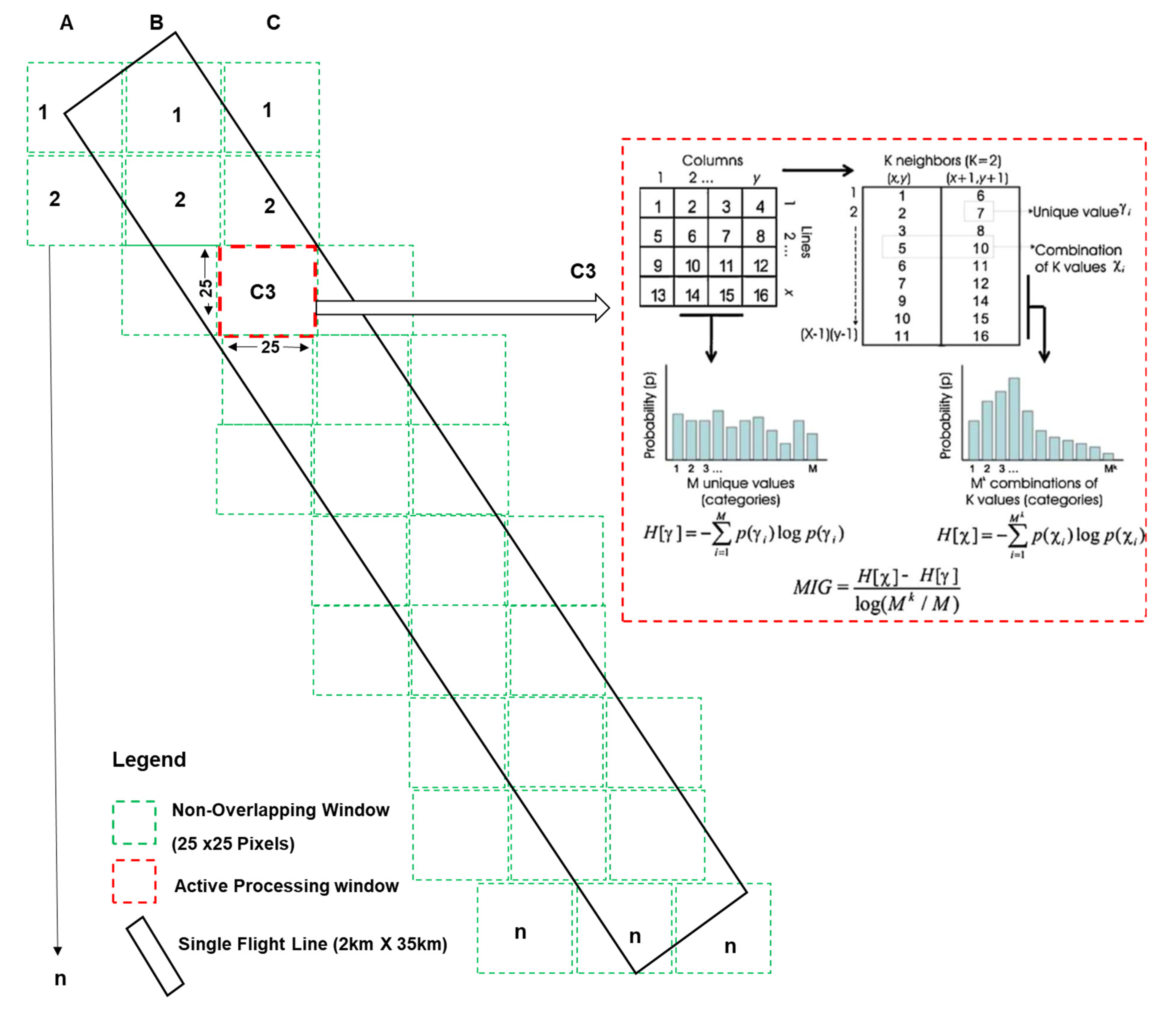
2.4. Non-Overlapping Window Size Determination
Spectral Complexity Metrics (SCM)
- k = 4 (i.e., the observed 2 × 2-pixel neighborhood; when k = 4, it means the combination of positions (x, y), (x + 1, y), (x, y + 1) and (x + 1, y + 1) in the image);
- Nk signifies the maximum number of possible reflectance combinations, given a set number of reflectance values (bins), N;
- log (Nk⁄N) is used to normalize MIG values between 0 and 1;
- p(Xi) is the probability of locating a specific 2 × 2 combination of pixel reflectance; and
- p(Yi) is the relative frequency or probability of locating reflectance value (Yi) in the image irrespective of its location.
2.5. Mangrove-Forest Classification
2.6. Mangrove Species Classification
- B = Upper (α/k) × 100th percentile determined from an χ2 distribution table with 1 degree of freedom
- = Proportion of area occupied by class (i)
- bi = precision for each class (i.e., 0.1)
2.7. Computation of Spectral Beta (β) Diversity
- Skj = Squared deviation of the kth community (ROI) and jth band.
- ŷkj = The mean of m pixels of ROI (k) per class corresponding to the jth band.
- ŷj = The mean of each class (column) and corresponding to the jth band.
3. Results
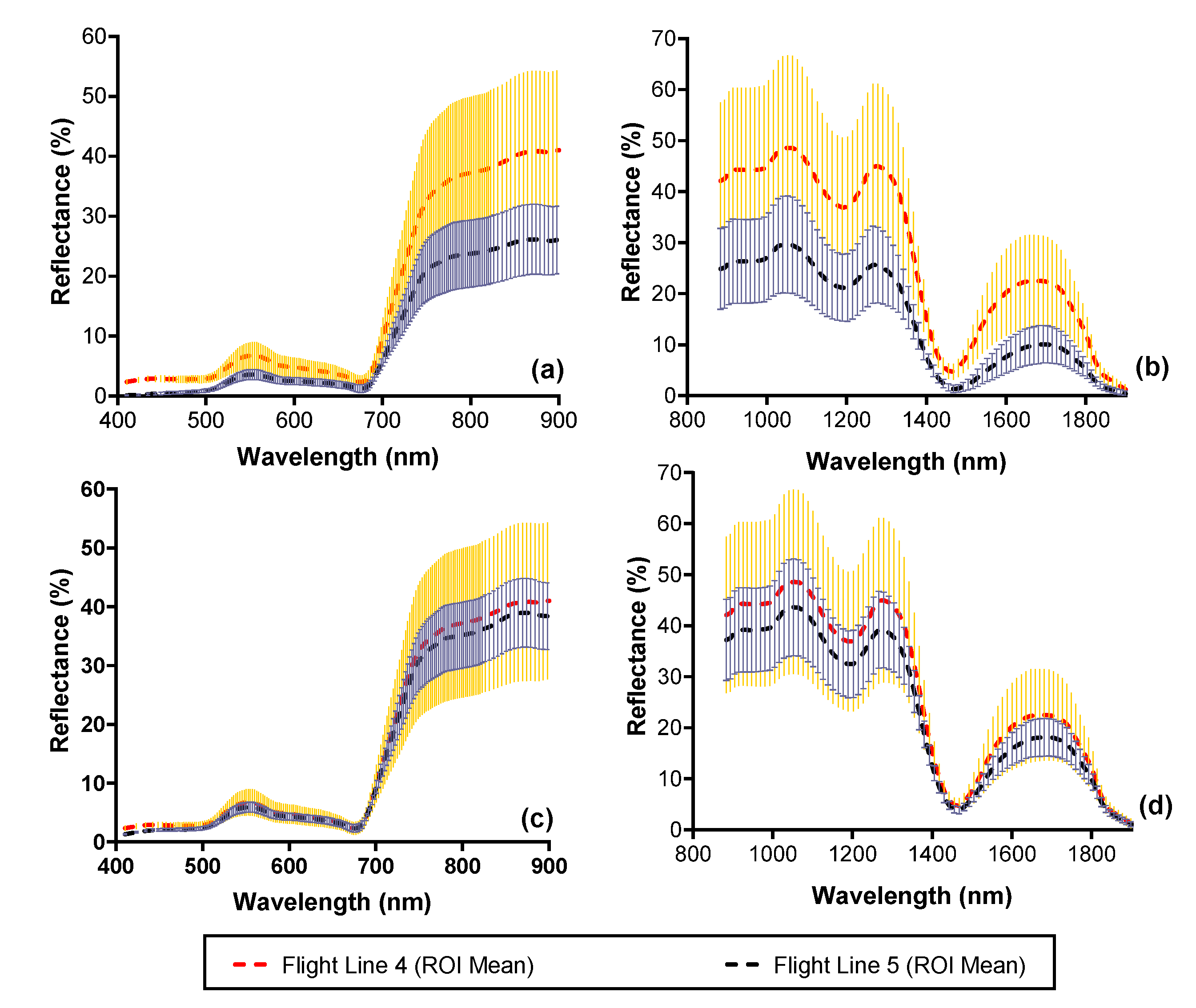
3.1. Spectral Consistency
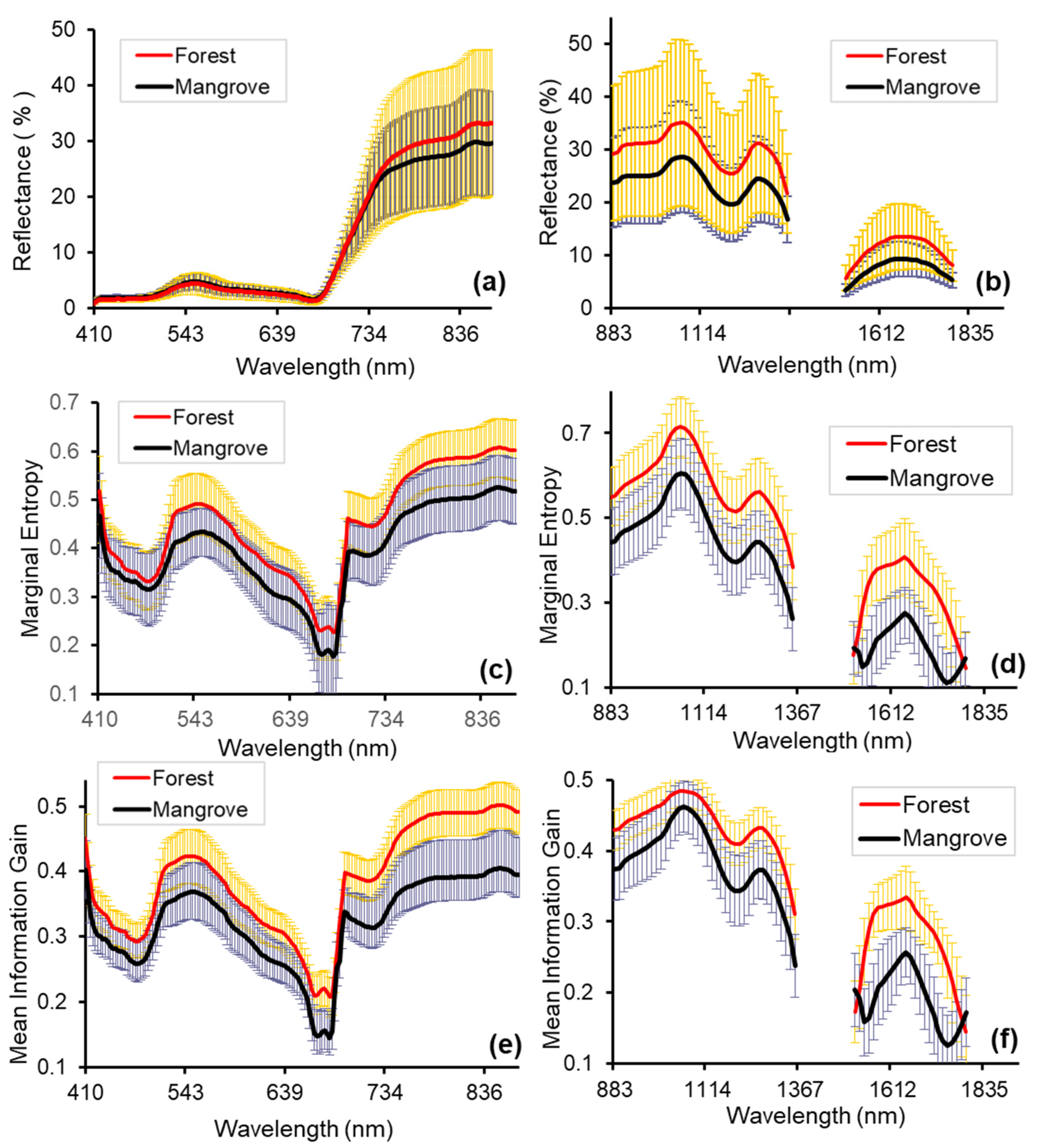
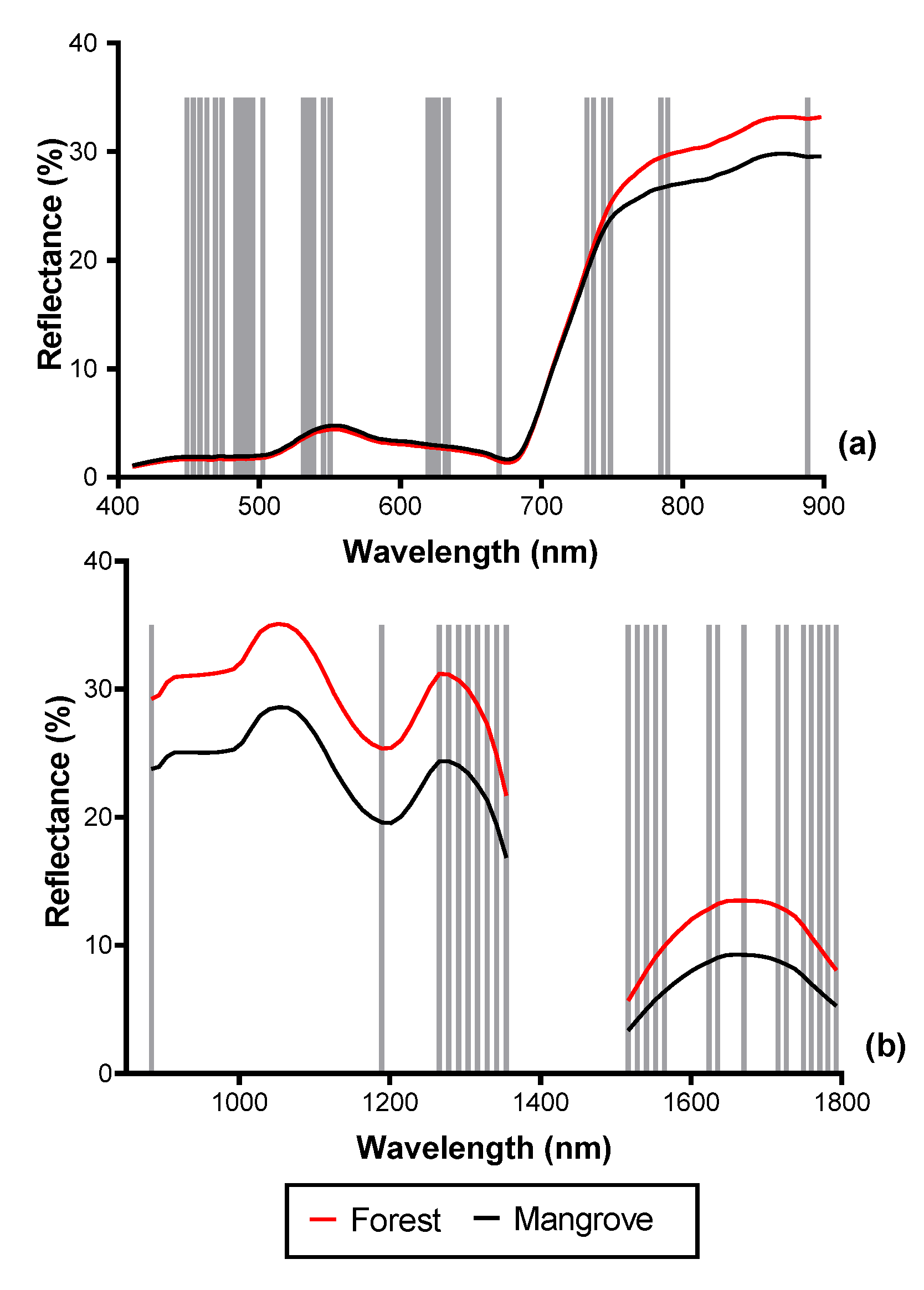
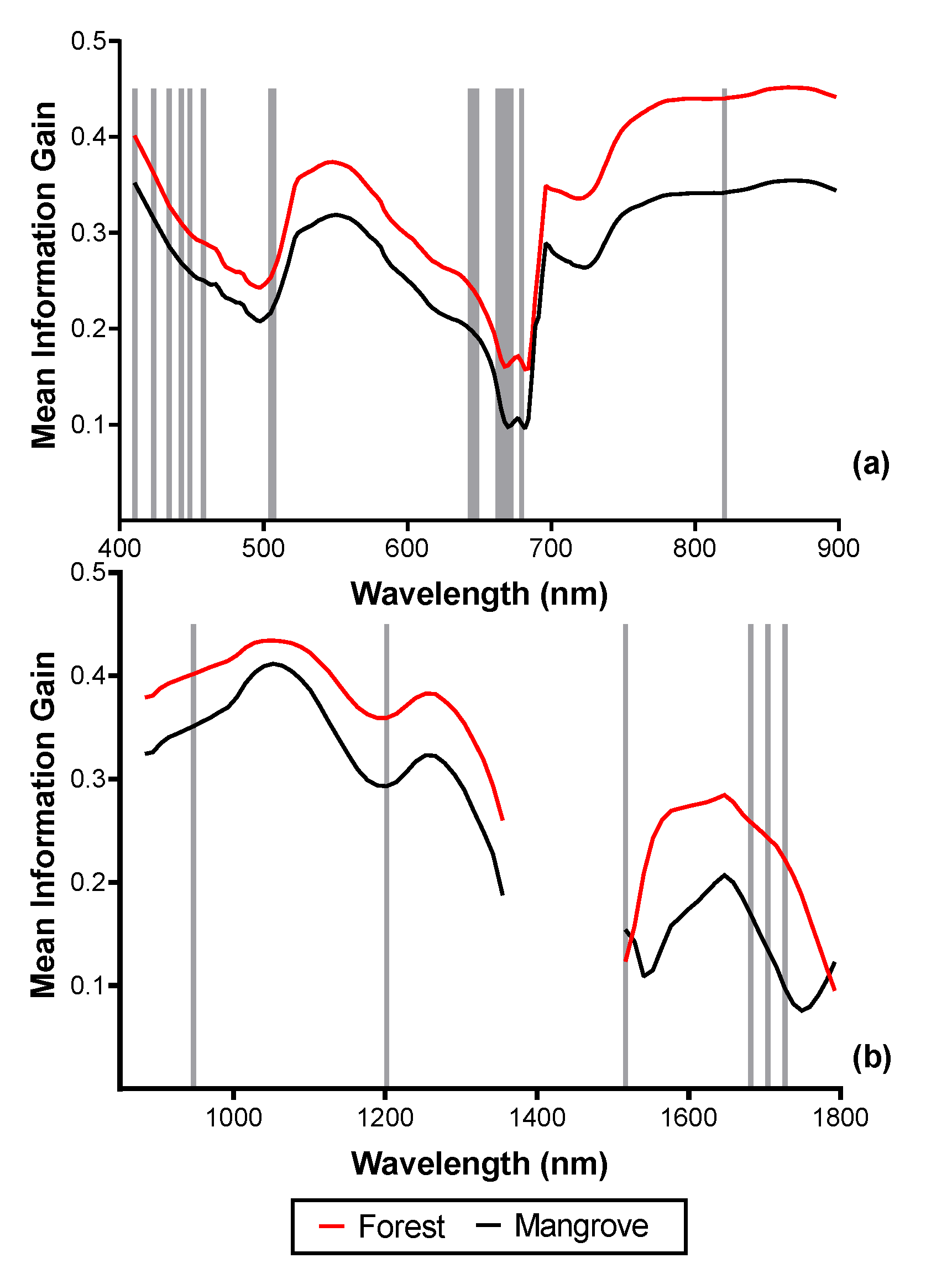
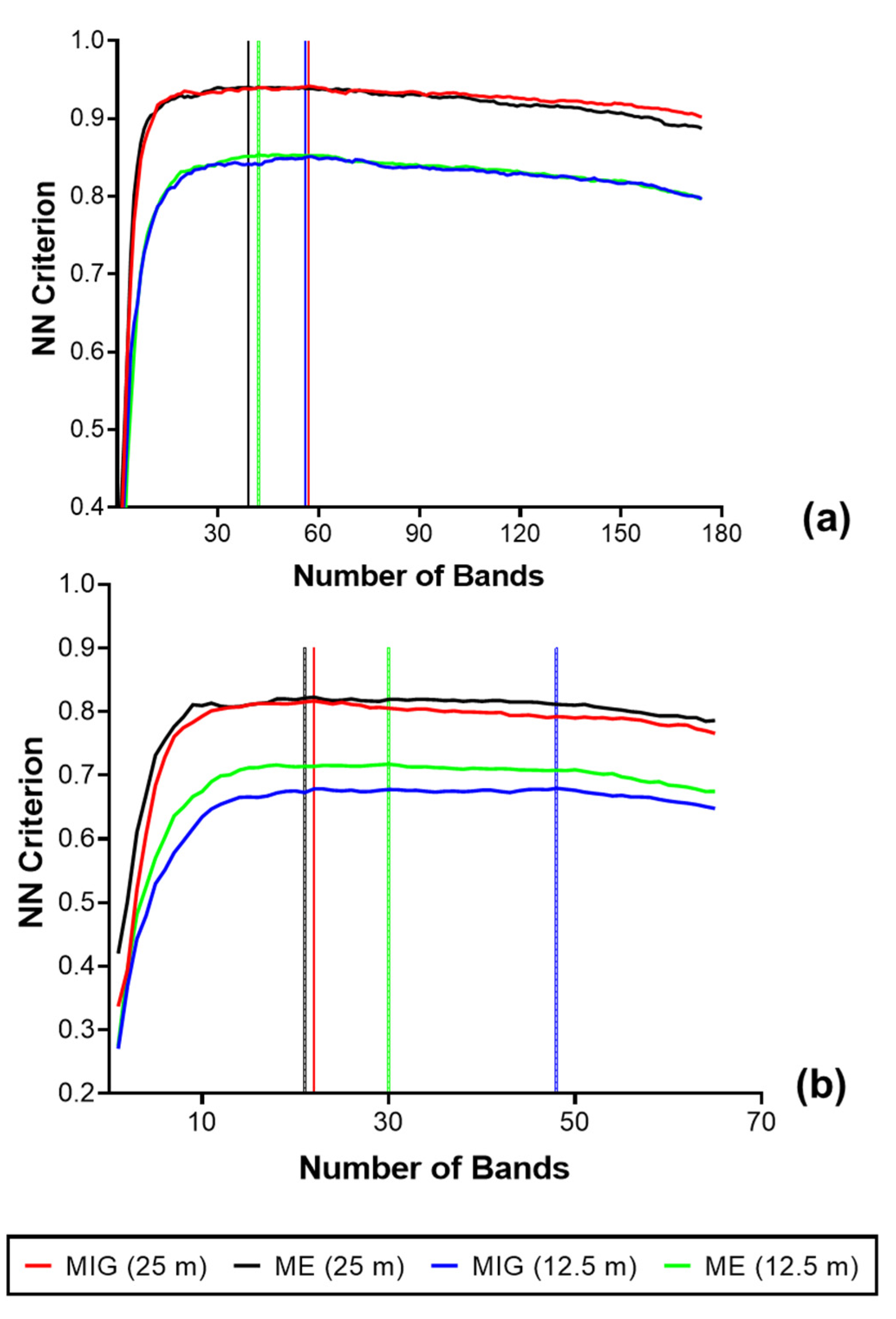
3.2. Spectral Reflectance and Spectral Complexity Metrics
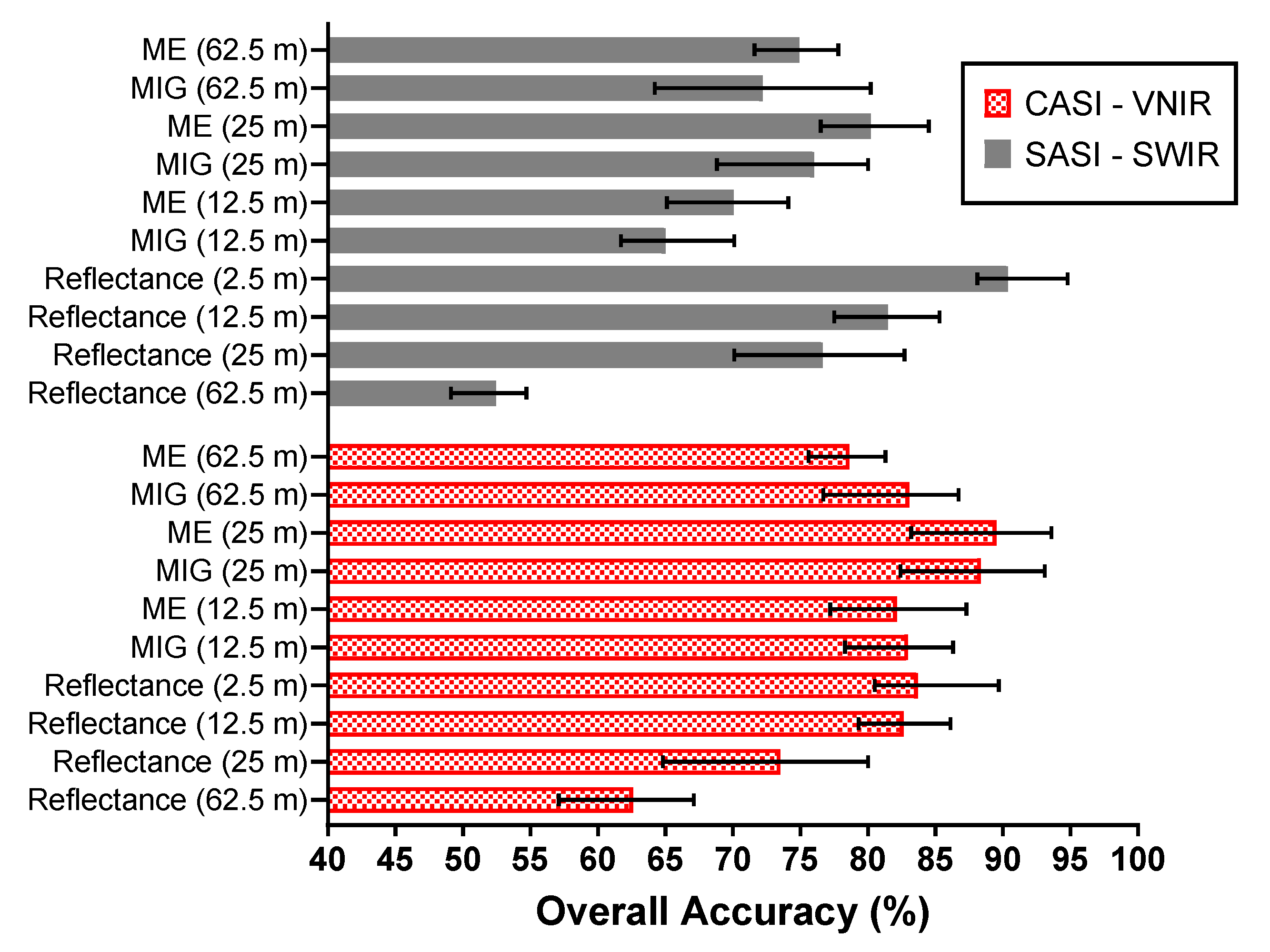
3.3. Mangrove Extent Classification
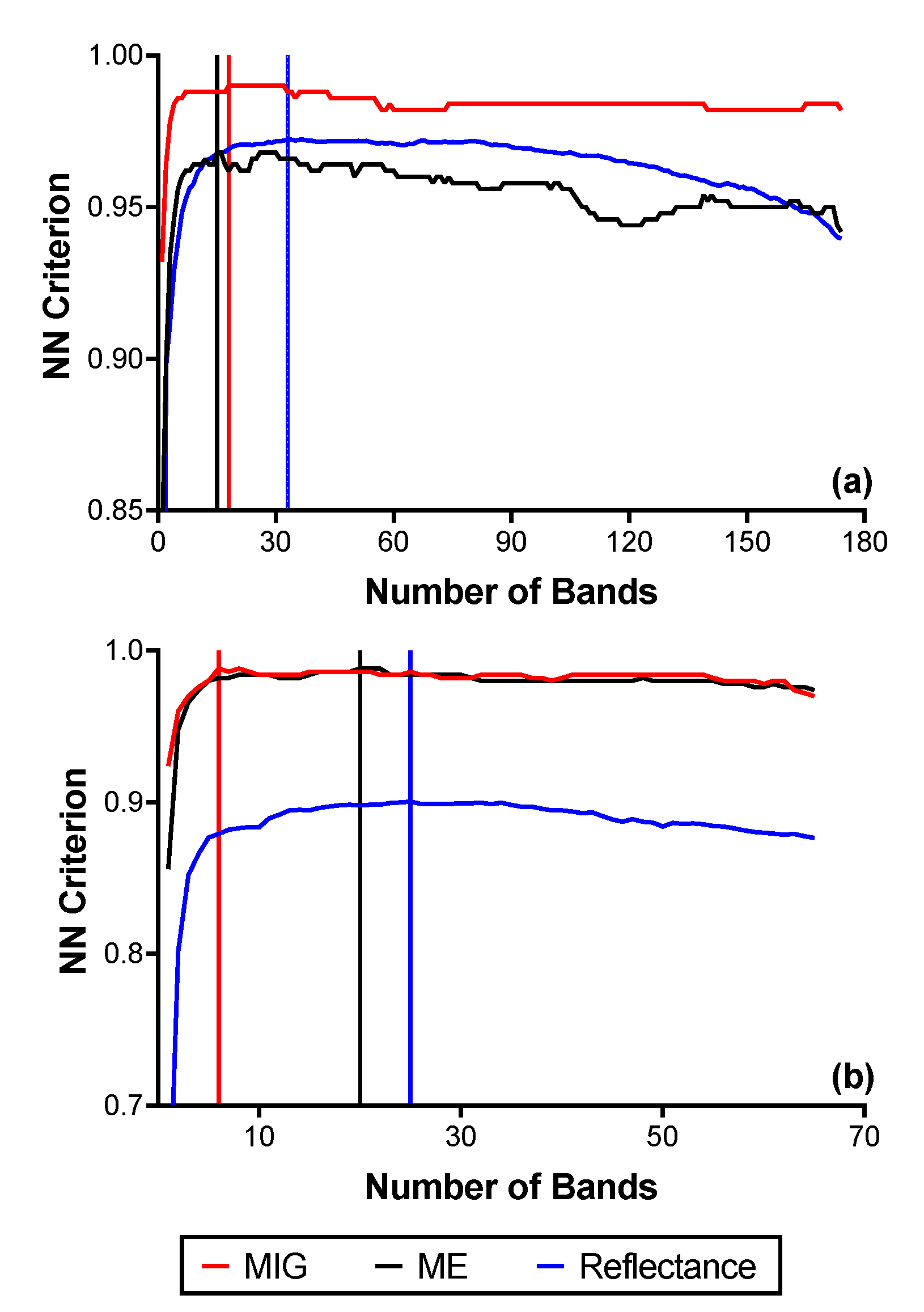
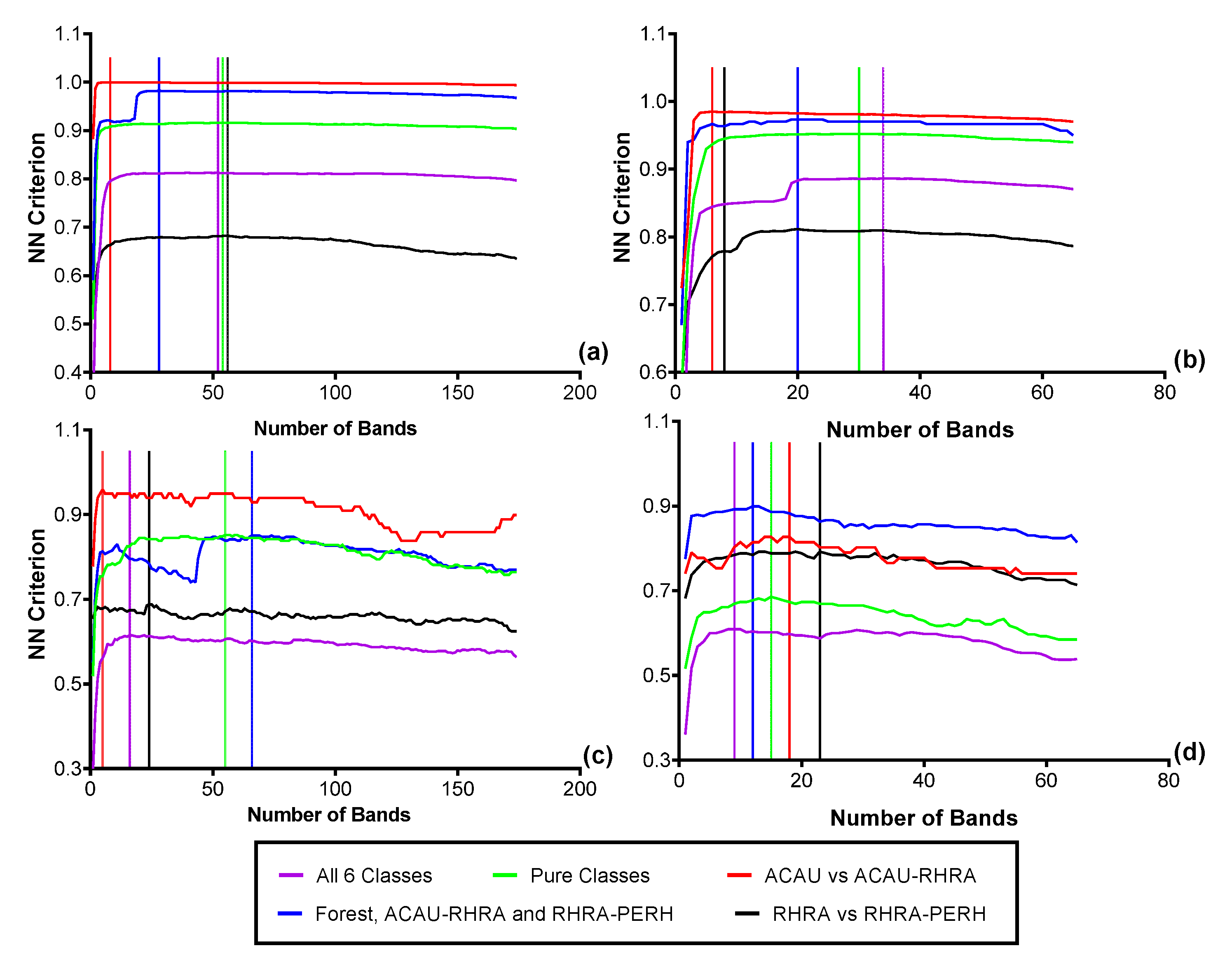
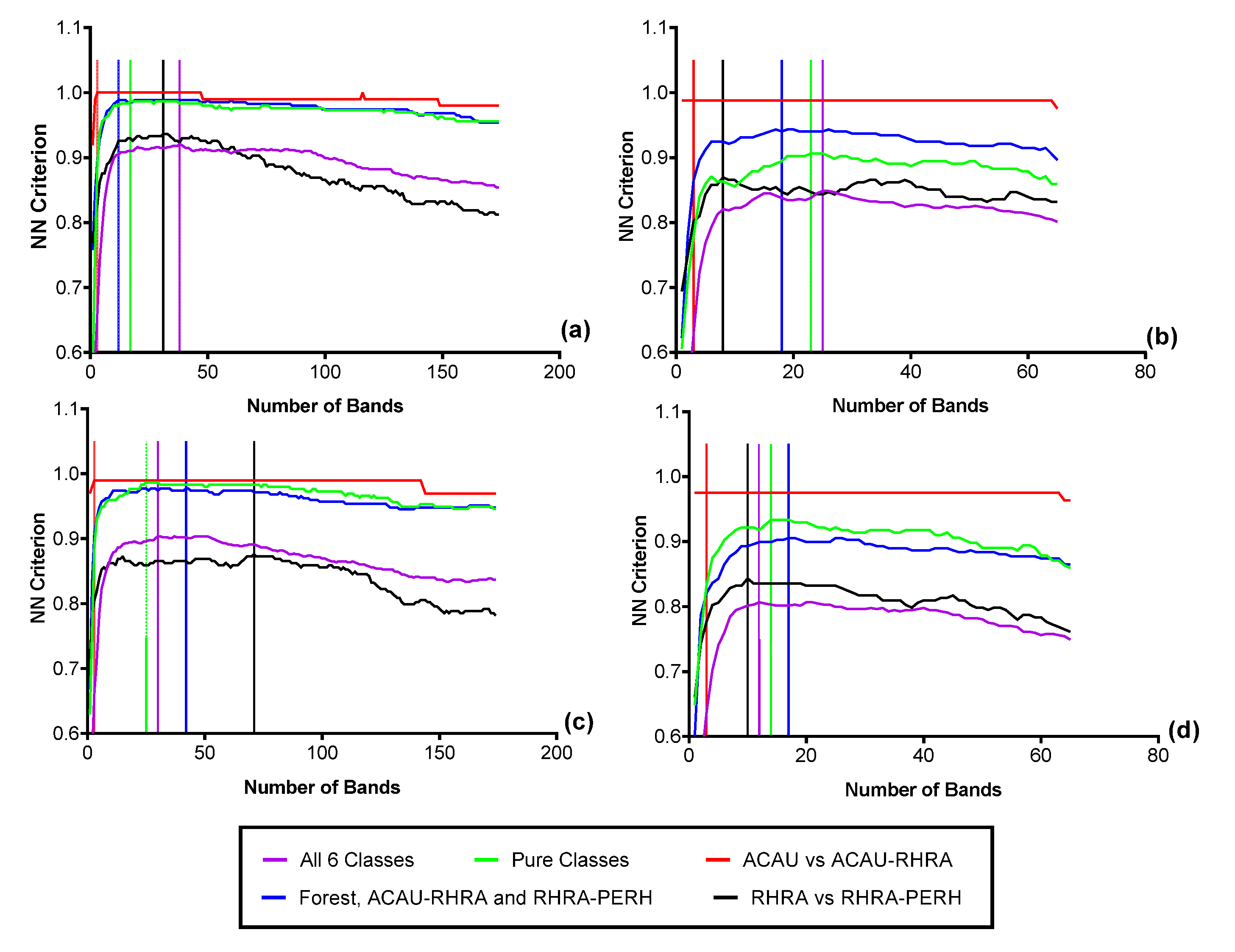
3.4. Feature Selection for Species Discrimination
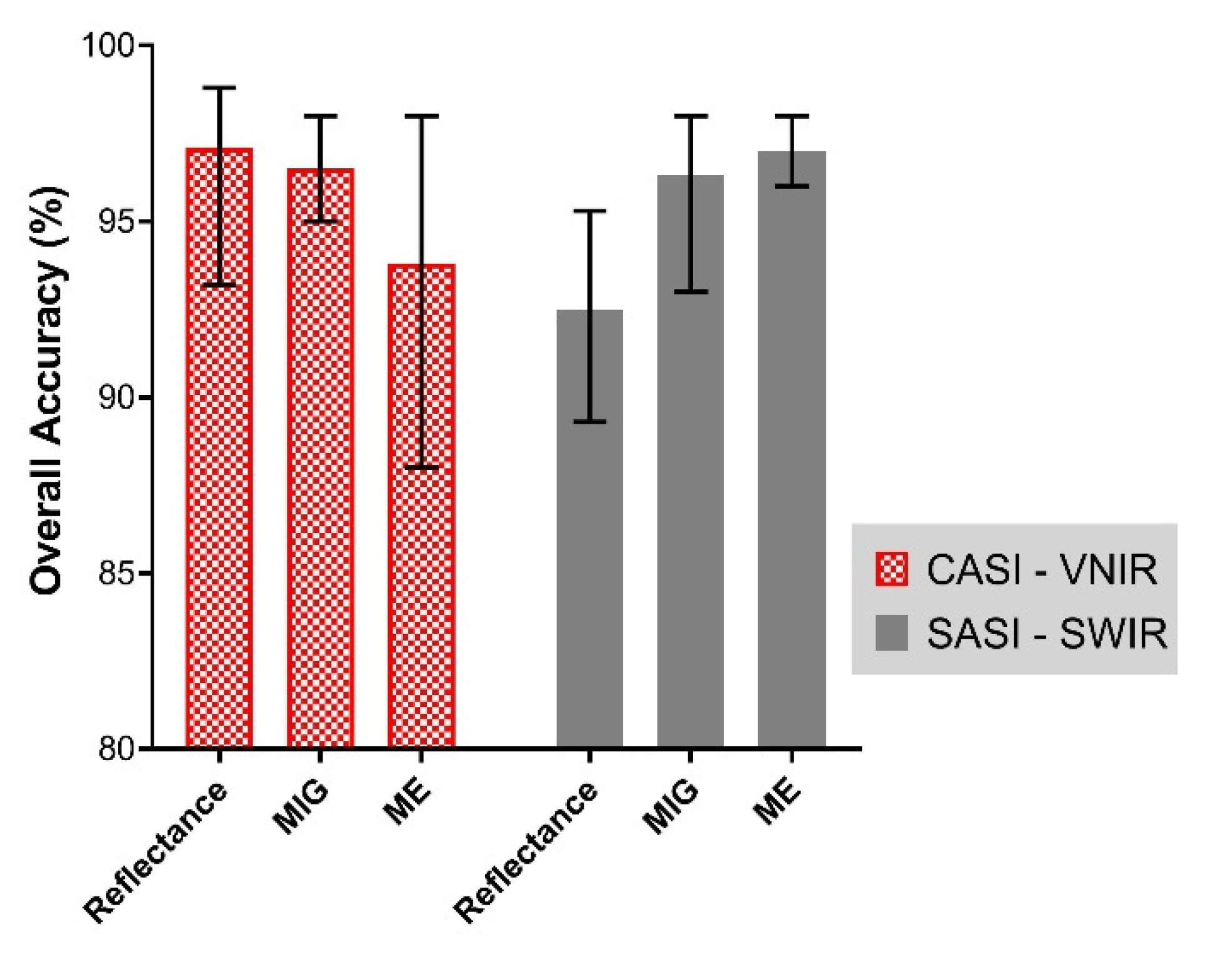
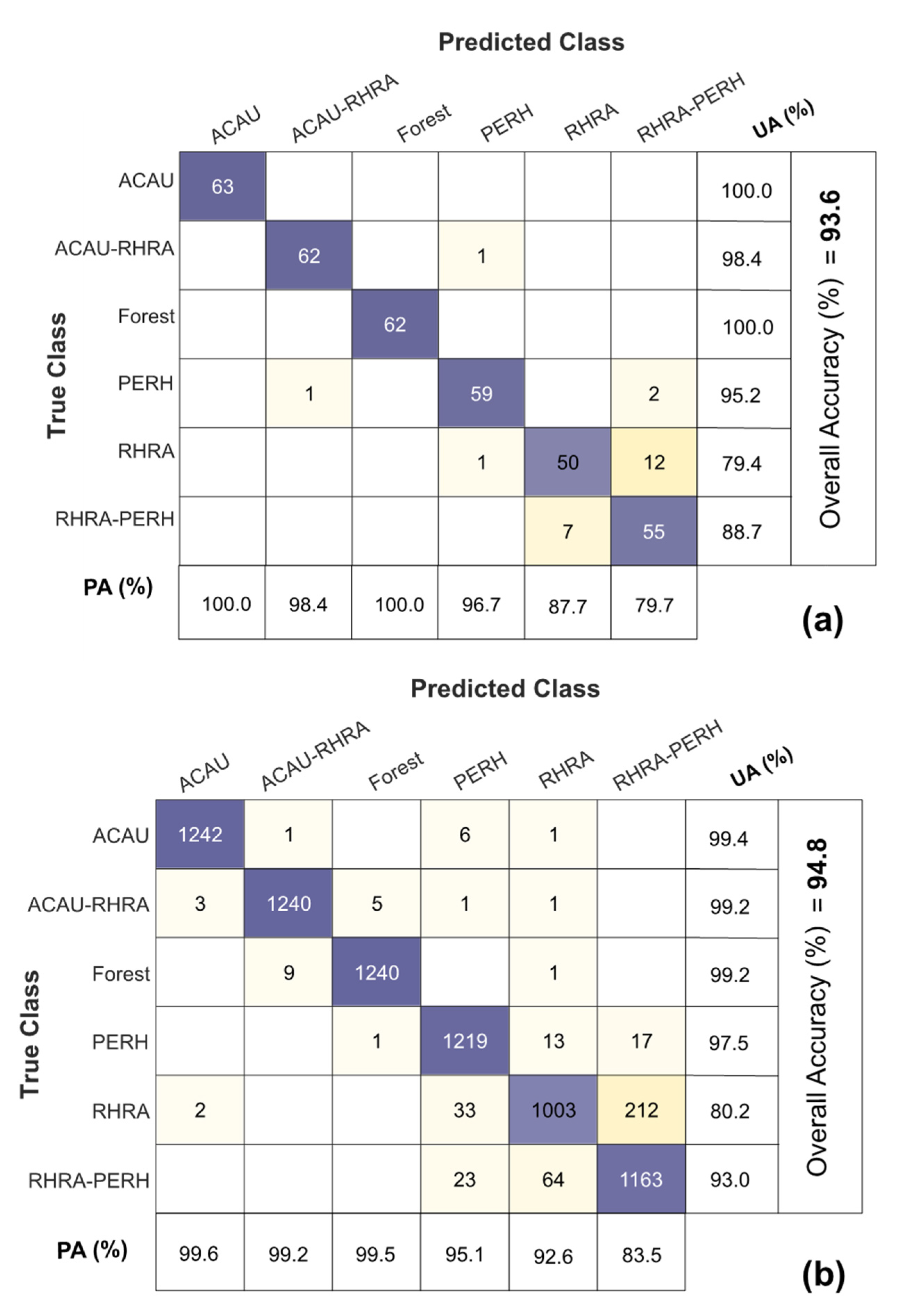
3.5. Species Classification
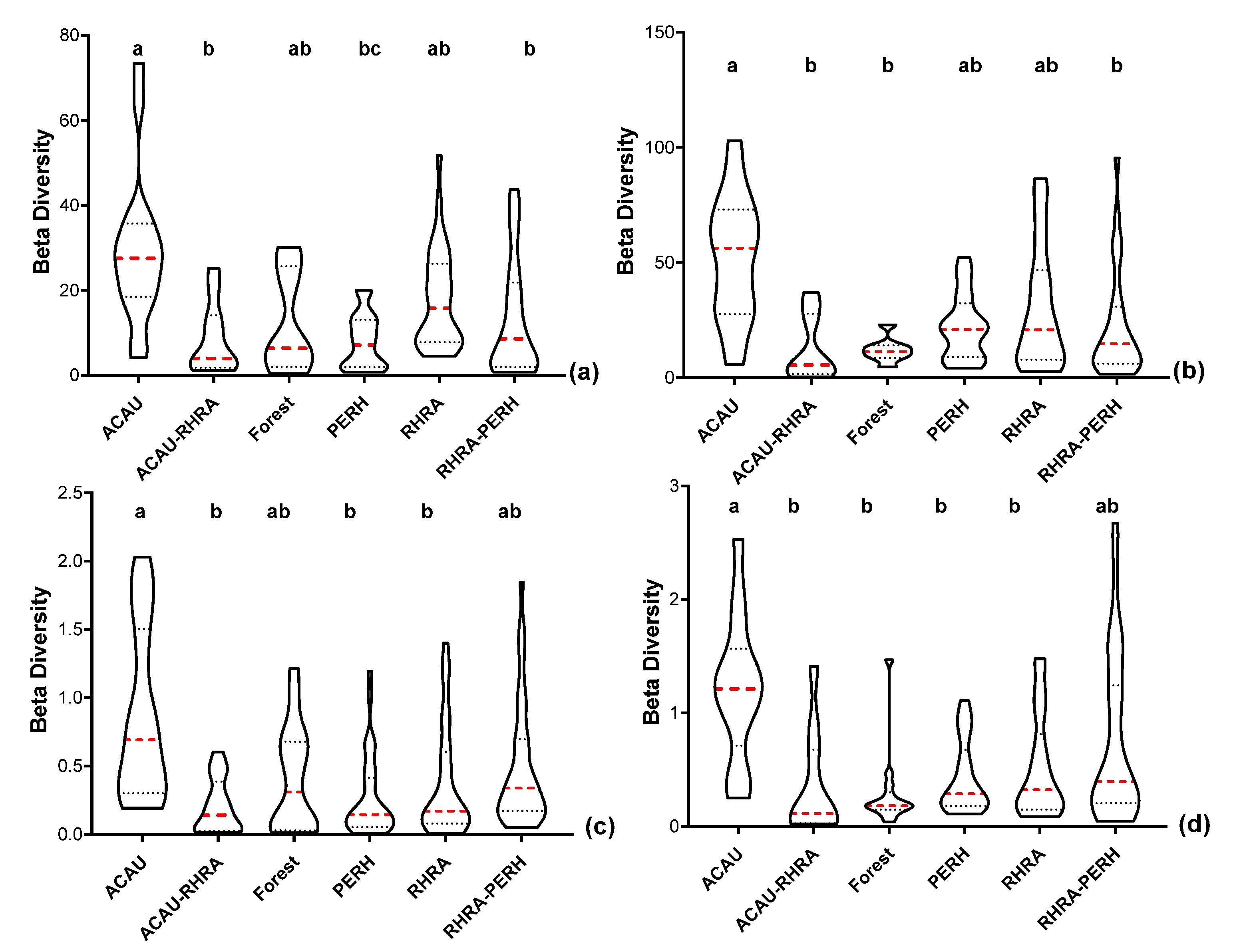
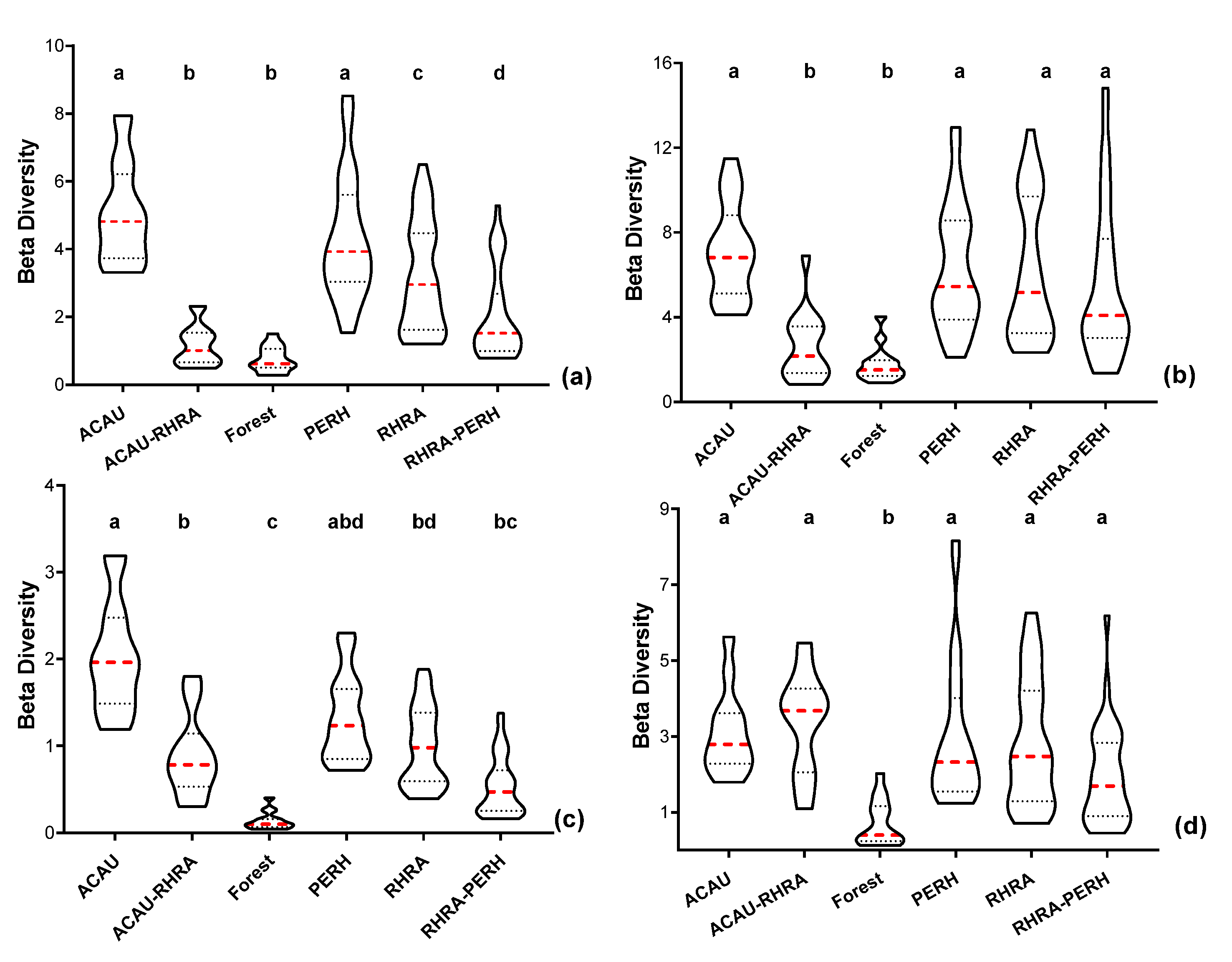
3.6. Spectral Beta (β) Diversity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Valiela, I.; Bowen, J.L.; York, J.K. Mangrove Forests: One of the World’s Threatened Major Tropical Environments: At least 35% of the area of mangrove forests has been lost in the past two decades, losses that exceed those for tropical rain forests and coral reefs, two other well-known threatened environments. Bioscience 2001, 51, 807–815. [Google Scholar]
- Giri, C.; Ochieng, E.; Tieszen, L.L.; Zhu, Z.; Singh, A.; Loveland, T.; Masek, J.; Duke, N. Status and distribution of mangrove forests of the world using earth observation satellite data. Glob. Ecol. Biogeogr. 2011, 20, 154–159. [Google Scholar] [CrossRef]
- Wilkie, M.L.; Fortuna, S. Status and Trends in Mangrove Area Extent Worldwide; FAO: Rome, Italy, 2003. [Google Scholar]
- Alongi, D.M. Present state and future of the world’s mangrove forests. Environ. Conserv. 2002, 29, 331–349. [Google Scholar] [CrossRef] [Green Version]
- Sandilyan, S.; Kathiresan, K. Mangrove conservation: A global perspective. Biodivers. Conserv. 2012, 21, 3523–3542. [Google Scholar] [CrossRef]
- Wang, L.; Jia, M.; Yin, D.; Tian, J. A review of remote sensing for mangrove forests: 1956–2018. Remote Sens. Environ. 2019, 231, 111223. [Google Scholar] [CrossRef]
- Bryan-Brown, D.N.; Connolly, R.M.; Richards, D.R.; Adame, F.; Friess, D.A.; Brown, C.J. Global trends in mangrove forest fragmentation. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Brander, L.M.; Wagtendonk, A.J.; Hussain, S.S.; McVittie, A.; Verburg, P.H.; de Groot, R.S.; van der Ploeg, S. Ecosystem service values for mangroves in Southeast Asia: A meta-analysis and value transfer application. Ecosyst. Serv. 2012, 1, 62–69. [Google Scholar] [CrossRef] [Green Version]
- Kuenzer, C.; Bluemel, A.; Gebhardt, S.; Quoc, T.V.; Dech, S. Remote sensing of mangrove ecosystems: A review. Remote Sens. 2011, 3, 878–928. [Google Scholar] [CrossRef] [Green Version]
- Duke, N.; Nagelkerken, I.; Agardy, T.; Wells, S.; Van Lavieren, H. The Importance of Mangroves to People: A Call to Action; United Nations Environment Programme World Conservation Monitoring Centre: Cambridge, UK, 2014. [Google Scholar]
- Mcleod, E.; Chmura, G.L.; Bouillon, S.; Salm, R.; Björk, M.; Duarte, C.M.; Lovelock, C.E.; Schlesinger, W.H.; Silliman, B.R. A blueprint for blue carbon: Toward an improved understanding of the role of vegetated coastal habitats in sequestering CO2. Front. Ecol. Environ. 2011, 9, 552–560. [Google Scholar] [CrossRef] [Green Version]
- Forestry Economics and Policy Division. The World’s Mangroves 1980–2005; FAO: Rome, Italy, 2007. [Google Scholar]
- Jia, M.; Wang, Z.; Zhang, Y.; Mao, D.; Wang, C. Monitoring loss and recovery of mangrove forests during 42 years: The achievements of mangrove conservation in China. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 535–545. [Google Scholar] [CrossRef]
- Yevugah, L.L.; Osei Jnr, E.M.; Ayer, J.; Osei Nti, J. Spatial Mapping of Carbon Stock in Riverine Mangroves Along Amanzule River in the Ellembelle District of Ghana. Earth Sci. Res. 2017, 6, 120. [Google Scholar] [CrossRef] [Green Version]
- Green, E.P.; Clark, C.D.; Mumby, P.J.; Edwards, A.J.; Ellis, A. Remote sensing techniques for mangrove mapping. Int. J. Remote Sens. 1998, 19, 935–956. [Google Scholar] [CrossRef]
- Cassidy, E. Using Satellites to Measure the Size and Shape of Mangroves; NASA: Washington, DC, USA, 2020. [Google Scholar]
- Zhao, C.; Qin, C.-Z. 10-m-resolution mangrove maps of China derived from multi-source and multi-temporal satellite observations. ISPRS J. Photogramm. Remote Sens. 2020, 169, 389–405. [Google Scholar] [CrossRef]
- Hu, L.; Xu, N.; Liang, J.; Li, Z.; Chen, L.; Zhao, F. Advancing the Mapping of Mangrove Forests at National-Scale Using Sentinel-1 and Sentinel-2 Time-Series Data with Google Earth Engine: A Case Study in China. Remote Sens. 2020, 12, 3120. [Google Scholar] [CrossRef]
- Bunting, P.; Rosenqvist, A.; Lucas, R.M.; Rebelo, L.-M.; Hilarides, L.; Thomas, N.; Hardy, A.; Itoh, T.; Shimada, M.; Finlayson, C.M. The global mangrove watch—A new 2010 global baseline of mangrove extent. Remote Sens. 2018, 10, 1669. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Sousa, W.P.; Gong, P.; Biging, G.S. Comparison of IKONOS and QuickBird images for mapping mangrove species on the Caribbean coast of Panama. Remote Sens. Environ. 2004, 91, 432–440. [Google Scholar] [CrossRef]
- Ramsey, E.W., III; Jensen, J.R. Remote Sensing of Mangrove Wetlands: Relating Canopy Spectra to Site-Specific Data; ASPRS: Bethesda, MA, USA, 1996. [Google Scholar]
- Cao, J.; Leng, W.; Liu, K.; Liu, L.; He, Z.; Zhu, Y. Object-based mangrove species classification using unmanned aerial vehicle hyperspectral images and digital surface models. Remote Sens. 2018, 10, 89. [Google Scholar] [CrossRef] [Green Version]
- Wan, L.; Lin, Y.; Zhang, H.; Wang, F.; Liu, M.; Lin, H. GF-5 Hyperspectral Data for Species Mapping of Mangrove in Mai Po, Hong Kong. Remote Sens. 2020, 12, 656. [Google Scholar] [CrossRef] [Green Version]
- Demuro, M.; Chisholm, L. Assessment of Hyperion for characterizing mangrove communities. In Proceedings of the 12th JPL AVIRIS Airborne Earth Science Workshop, Pasadena, CA, USA, 24–28 February 2003. [Google Scholar]
- Kamal, M.; Phinn, S. Hyperspectral data for mangrove species mapping: A comparison of pixel-based and object-based approach. Remote Sens. 2011, 3, 2222–2242. [Google Scholar] [CrossRef] [Green Version]
- Theiler, J.; Ziemann, A.; Matteoli, S.; Diani, M. Spectral variability of remotely sensed target materials: Causes, models, and strategies for mitigation and robust exploitation. IEEE Geosci. Remote Sens. Mag. 2019, 7, 8–30. [Google Scholar] [CrossRef]
- Tanner, J.E.; Mellin, C.; Parrott, L.; Bradshaw, C.J. Fine-scale benthic biodiversity patterns inferred from image processing. Ecol. Complex. 2015, 22, 76–85. [Google Scholar] [CrossRef]
- Parrott, L. Measuring ecological complexity. Ecol. Indic. 2010, 10, 1069–1076. [Google Scholar] [CrossRef]
- Kovalenko, K.E.; Thomaz, S.M.; Warfe, D.M. Habitat complexity: Approaches and future directions. Hydrobiologia 2012, 685, 1–17. [Google Scholar] [CrossRef]
- Proulx, R.; Parrott, L. Structural complexity in digital images as an ecological indicator for monitoring forest dynamics across scale, space and time. Ecol. Indic. 2009, 9, 1248–1256. [Google Scholar] [CrossRef]
- Mellin, C.; Parrott, L.; Andréfouët, S.; Bradshaw, C.J.; MacNeil, M.A.; Caley, M.J. Multi-scale marine biodiversity patterns inferred efficiently from habitat image processing. Ecol. Appl. 2012, 22, 792–803. [Google Scholar] [CrossRef] [Green Version]
- Proulx, R.; Parrott, L. Measures of structural complexity in digital images for monitoring the ecological signature of an old-growth forest ecosystem. Ecol. Indic. 2008, 8, 270–284. [Google Scholar] [CrossRef]
- Kalacska, M.; Lalonde, M.; Moore, T. Estimation of foliar chlorophyll and nitrogen content in an ombrotrophic bog from hyperspectral data: Scaling from leaf to image. Remote Sens. Environ. 2015, 169, 270–279. [Google Scholar] [CrossRef]
- Lahmann, E. The mangrove forests of Sierpe, Costa Rica. Towards Wise Use Wetl. 1993, 82–88. [Google Scholar]
- Sanchez-Azofeifa, G.A.; Rivard, B.; Calvo, J.; Moorthy, I. Dynamics of tropical deforestation around national parks: Remote sensing of forest change on the Osa Peninsula of Costa Rica. Mt. Res. Dev. 2002, 22, 352–358. [Google Scholar] [CrossRef]
- Cornejo, X.; Mori, S.A.; Aguilar, R.; Stevens, H.; Douwes, F. Phytogeography of the trees of the Osa Peninsula, Costa Rica. Brittonia 2012, 64, 76–101. [Google Scholar] [CrossRef]
- Wehrtmann, I.S.; Cortés, J. Marine Biodiversity of Costa Rica, Central America; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 86. [Google Scholar]
- Thomas, N.; Bunting, P.; Lucas, R.; Hardy, A.; Rosenqvist, A.; Fatoyinbo, T. Mapping mangrove extent and change: A globally applicable approach. Remote Sens. 2018, 10, 1466. [Google Scholar] [CrossRef] [Green Version]
- Lizano, O.; Amador, J.; Soto, R. Caracterización de Manglares de Centroamérica Con Sensores Remotos. Rev. De Biol. Trop. 2001, 49, 331–340. [Google Scholar]
- Acuña-Piedra, J.F.; Quesada-Román, A.; Vargas-Bolaños, C. Cobertura y Distribución de las Especies de Mangle en el Humedal Nacional Térraba-Sierpe, Costa Rica. Anuário Do Inst. De Geociências 2019, 41, 120–129. [Google Scholar] [CrossRef]
- Barrantes Leiva, R.M.; Cerdas Salas, A. Spatial distribution of mangrove species and their association with the substrate sediment types, estuarine sector Térraba-Sierpe National Wetlands, Costa Rica. Rev. De Biol. Trop. 2015, 63, 47–60. [Google Scholar]
- Kalacska, M.; Arroyo-Mora, J.P.; Soffer, R.; Leblanc, G. Quality control assessment of the mission airborne carbon 13 (mac-13) hyperspectral imagery from Costa Rica. Can. J. Remote Sens. 2016, 42, 85–105. [Google Scholar] [CrossRef]
- Inamdar, D.; Kalacska, M.; Leblanc, G.; Arroyo-Mora, J.P. Characterizing and Mitigating Sensor Generated Spatial Correlations in Airborne Hyperspectral Imaging Data. Remote Sens. 2020, 12, 641. [Google Scholar] [CrossRef] [Green Version]
- Soffer, R.J.; Ifimov, G.; Arroyo-Mora, J.P.; Kalacska, M. Validation of Airborne Hyperspectral Imagery from Laboratory Panel Characterization to Image Quality Assessment: Implications for an Arctic Peatland Surrogate Simulation Site. Can. J. Remote Sens. 2019, 45, 476–508. [Google Scholar] [CrossRef]
- Manley, M.; McGoverin, C.M.; Engelbrecht, P.; Geladi, P. Influence of grain topography on near infrared hyperspectral images. Talanta 2012, 89, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Richter, R.; Schläpfer, D. Atmospheric and Topographic Correction (ATCOR Theoretical Background Document). DLR IB 2019, 564-03. [Google Scholar]
- Schläpfer, D.; Richter, R. Spectral polishing of high resolution imaging spectroscopy data. In Proceedings of the 7th SIG-IS Workshop on Imaging Spectroscopy, Edinburgh, UK, 11–13 April 2011; pp. 11–13. [Google Scholar]
- Crippen, R.; Buckley, S.; Agram, P.; Belz, E.; Gurrola, E.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.; Neumann, M.; et al. Nasadem Global Elevation Model: Methods and Progress. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B4, 125–128. [Google Scholar] [CrossRef] [Green Version]
- Vega-García, C.; Chuvieco, E. Applying local measures of spatial heterogeneity to Landsat-TM images for predicting wildfire occurrence in Mediterranean landscapes. Landsc. Ecol. 2006, 21, 595–605. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.P.; Kalacska, M.; Caraballo, B.; Trujillo, J.; Vargas, O. Assessing Recovery Following Selective Logging of Lowland Tropical Forests Based on Hyperspectral Imagery; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Van Der Heijden, F.; Duin, R.P.; De Ridder, D.; Tax, D. Classification, parameter estimation and state estimation. In An Engineering Approach using Matlab; Wiley Online Library: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lei, B.; Xu, G.; Feng, M.; Zou, Y.; Van der Heijden, F.; De Ridder, D.; Tax, D. Classification, Parameter Estimation and State Estimation; Wiley Online Library: Hoboken, NJ, USA, 2017. [Google Scholar]
- Defernez, M.; Kemsley, E.K. The use and misuse of chemometrics for treating classification problems. TrAC Trends Anal. Chem. 1997, 16, 216–221. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Laliberté, E.; Schweiger, A.K.; Legendre, P. Partitioning plant spectral diversity into alpha and beta components. Ecol. Lett. 2020, 23, 370–380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pastor-Guzman, J.; Atkinson, P.M.; Dash, J.; Rioja-Nieto, R. Spatiotemporal variation in mangrove chlorophyll concentration using Landsat 8. Remote Sens. 2015, 7, 14530–14558. [Google Scholar] [CrossRef] [Green Version]
- Kumar, T.; Mandal, A.; Dutta, D.; Nagaraja, R.; Dadhwal, V.K. Discrimination and classification of mangrove forests using EO-1 Hyperion data: A case study of Indian Sundarbans. Geocarto Int. 2019, 34, 415–442. [Google Scholar] [CrossRef]
- Kumar, L.; Schmidt, K.; Dury, S.; Skidmore, A. Imaging spectrometry and vegetation science. In Imaging spectrometry; Springer: Berlin/Heidelberg, Germany, 2002; pp. 111–155. [Google Scholar]
- Eismann, M. Hyperspectral Remote Sensing; SPIE: Bellingham, WA, USA, 2012. [Google Scholar]
- Mitsch, W.J.; Gosselink, J.G.; Zhang, L.; Anderson, C.J. Wetland Ecosystems; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Vaiphasa, C.; Ongsomwang, S.; Vaiphasa, T.; Skidmore, A.K. Tropical mangrove species discrimination using hyperspectral data: A laboratory study. Estuar. Coast. Shelf Sci. 2005, 65, 371–379. [Google Scholar] [CrossRef]
- Dangan-Galon, F.; Dolorosa, R.G.; Sespeñe, J.S.; Mendoza, N.I. Diversity and structural complexity of mangrove forest along Puerto Princesa Bay, Palawan Island, Philippines. J. Mar. Isl. Cult. 2016, 5, 118–125. [Google Scholar] [CrossRef] [Green Version]
- Feller, I.C.; Lovelock, C.E.; Berger, U.; McKee, K.L.; Joye, S.B.; Ball, M. Biocomplexity in mangrove ecosystems. Annu. Rev. Mar. Sci. 2010, 2, 395–417. [Google Scholar] [CrossRef] [Green Version]
- Nageswara-Rao, M.; Soneji, J.R.; Sudarshana, P. Structure, diversity, threats and conservation of Tropical Forests. Trop. For. 2012, 3–18. [Google Scholar]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M. Remotely sensed spectral heterogeneity as a proxy of species diversity: Recent advances and open challenges. Ecol. Inform. 2010, 5, 318–329. [Google Scholar] [CrossRef]
- Shi, T.; Liu, J.; Hu, Z.; Liu, H.; Wang, J.; Wu, G. New spectral metrics for mangrove forest identification. Remote Sens. Lett. 2016, 7, 885–894. [Google Scholar] [CrossRef]
- Gupta, K.; Mukhopadhyay, A.; Giri, S.; Chanda, A.; Majumdar, S.D.; Samanta, S.; Mitra, D.; Samal, R.N.; Pattnaik, A.K.; Hazra, S. An index for discrimination of mangroves from non-mangroves using LANDSAT 8 OLI imagery. MethodsX 2018, 5, 1129–1139. [Google Scholar] [CrossRef] [PubMed]
- Schneider, F.D.; Morsdorf, F.; Schmid, B.; Petchey, O.L.; Hueni, A.; Schimel, D.S.; Schaepman, M.E. Mapping functional diversity from remotely sensed morphological and physiological forest traits. Nat. Commun. 2017, 8, 1–12. [Google Scholar] [CrossRef] [Green Version]
- White, J.C.; Gómez, C.; Wulder, M.A.; Coops, N.C. Characterizing temperate forest structural and spectral diversity with Hyperion EO-1 data. Remote Sens. Environ. 2010, 114, 1576–1589. [Google Scholar] [CrossRef]
- Kamal, M.; Phinn, S.; Johansen, K. Characterizing the spatial structure of mangrove features for optimizing image-based mangrove mapping. Remote Sens. 2014, 6, 984–1006. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Wan, B.; Qiu, P.; Su, Y.; Guo, Q.; Wang, R.; Sun, F.; Wu, X. Evaluating the performance of sentinel-2, landsat 8 and pléiades-1 in mapping mangrove extent and species. Remote Sens. 2018, 10, 1468. [Google Scholar] [CrossRef] [Green Version]
- Hati, J.P.; Samanta, S.; Chaube, N.R.; Misra, A.; Giri, S.; Pramanick, N.; Gupta, K.; Majumdar, S.D.; Chanda, A.; Mukhopadhyay, A. Mangrove classification using airborne hyperspectral AVIRIS-NG and comparing with other spaceborne hyperspectral and multispectral data. Egypt. J. Remote Sens. Space Sci. 2020, 24, 273–281. [Google Scholar]
- Li, Q.; Wong, F.K.K.; Fung, T. Mapping multi-layered mangroves from multispectral, hyperspectral, and LiDAR data. Remote Sens. Environ. 2021, 258, 112403. [Google Scholar] [CrossRef]
- Hoa, P.; Giang, N.; Binh, N.; Hieu, N.; Trang, N.; Toan, L.; Long, V.; Ai, T.; Hong, P.; Hai, L. Mangrove Species Discrimination in Southern Vietnam Based on in-situ Measured Hyperspectral Reflectance. Int. J. Geoinformatics 2017, 13. [Google Scholar]
- Kaufmann, H.; Segl, K.; Foerster, S.; Kuester, T.; Rogass, C.; Chabrillat, S.; Scheffler, D.; Mielke, C.; Bösche, N.; Hostert, P.; et al. The Environmental Mapping and Analysis Program (EnMAP)—Current Status and Science Activities. In Proceedings of the 5th EARSeL Land Use and Land Cover, Berlin, Germany, 17–18 March 2014. [Google Scholar]
- Kaufmann, H.; Segl, K.; Chabrillat, S.; Hofer, S.; Stuffler, T.; Mueller, A.; Richter, R.; Schreier, G.; Haydn, R.; Bach, H. EnMAP a hyperspectral sensor for environmental mapping and analysis. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 1617–1619. [Google Scholar]
- Matsunaga, T.; Iwasaki, A.; Tsuchida, S.; Iwao, K.; Tanii, J.; Kashimura, O.; Nakamura, R.; Yamamoto, H.; Kato, S.; Obata, K. Current status of hyperspectral imager suite (HISUI) onboard International Space Station (ISS). In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 443–446. [Google Scholar]
- Labate, D.; Ceccherini, M.; Cisbani, A.; De Cosmo, V.; Galeazzi, C. The PRISMA payload optomechanical design, a high performance instrument for a new hyperspectral mission. Acta Astronaut. 2009, 65, 1429–1436. [Google Scholar] [CrossRef]
- Planet Labs Inc. Reaching New Scales of Sight, -Monitoring the Earth in Hyperspectral. Available online: https://learn.planet.com/reaching-new-scales-datasheet.html?utm_source=website&utm_medium=carbon-mapper-page&utm_campaign=carbon-mapper-datasheet&utm_content=carbon-mapper-datasheet (accessed on 30 May 2021).
- Arroyo-Mora, J.P.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.S.; Ifimov, G.; Elmer, K. Implementation of a UAV–Hyperspectral Pushbroom Imager for Ecological Monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.K.; Rivard, B.; Sanchez-Azofeifa, A.; Castro-Esau, K. Intra and inter-class spectral variability of tropical tree species at La Selva, Costa Rica: Implications for species identification using HYDICE imagery. Remote Sens. Environ. 2006, 105, 129–141. [Google Scholar] [CrossRef]
- Ajithkumar, T.; Thangaradjou, T.; Kannan, L. Spectral reflectance properties of mangrove species of the Muthupettai mangrove environment, Tamil Nadu. J. Environ. Biol. 2008, 29, 785–788. [Google Scholar] [PubMed]
- Botha, E.J.; Brando, V.E.; Dekker, A.G. Effects of per-pixel variability on uncertainties in bathymetric retrievals from high-resolution satellite images. Remote Sens. 2016, 8, 459. [Google Scholar] [CrossRef] [Green Version]
- Gross, J.; Flores, E.E.; Schwendenmann, L. Stand structure and aboveground biomass of a Pelliciera rhizophorae mangrove forest, Gulf of Monitjo Ramsar site, Pacific Coast, Panama. Wetlands 2014, 34, 55–65. [Google Scholar] [CrossRef]
- Robadue, D., Jr.; Twilley, R.; Bodero, A. Mangrove Ecosystem Biodiversity and Conservation in Ecuador; AAAS Press: Washington, DC, USA, 1993. [Google Scholar]
- Blanco, J.F.; Estrada, E.; Ortiz, L.F.; Urrego, L.E. Ecosystem-wide impacts of deforestation in mangroves: The Urabá Gulf (Colombian Caribbean) case study. Int. Sch. Res. Not. 2012, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Luis, C.S. Restoring Mangroves & Managing the Mangrove Fern. Available online: https://osaconservation.org/restoring-mangroves-managing-the-mangrove-fern/ (accessed on 6 June 2021).
- Luis, C.S. Mangrove Restoration Actions in the Térraba Sierpe National Wetland. Available online: https://osaconservation.org/mangrove-restoration-actions-terraba-sierpe-national-wetland/ (accessed on 6 June 2021).
- Abelardo, C. SINAC Will Start Process of Restoration of Térraba Sierpe Wetland. Available online: https://thecostaricanews.com/sinac-will-start-process-of-restoration-of-terraba-sierpe-wetland/ (accessed on 6 June 2021).


| Sensor Characteristic | CASI-1500 | SASI-644 |
|---|---|---|
| Field of view (FOV) (°) | 39.9° | 39.7° |
| No. across-track pixels (image) | 1493 | 640 |
| Maximum number of spectral channels | 288 (programmable) | 160 (nonprogrammable) |
| Spectral range (nm) | 375–1050 | 883–2523 |
| Spectral resolution (nm) | 3.2 | 16 nm @ 883 nm |
| 12 nm @ 2523 nm |
| ACOSA Mission | Parameter | CASI | SASI |
|---|---|---|---|
| Flight Planning Parameter | Ground Speed (kn) | 120 | 120 |
| Flight line side overlap | 15% | 15% | |
| Planned maximum roll (°) | 5 | 5 | |
| Avg. flight line length (km) | 28.1 | 28.1 | |
| Number of flight lines | 16 | 16 | |
| Integration time (ms) | 32 | 2.88–5.06 | |
| Calculated Parameter | Altitude (m AGL) | 2570 | 2570 |
| Flight line spacing (m) | 1350 | 1350 | |
| Across-track pixel resolution (m) * | 1.5 | 3.4 | |
| Along-track pixel resolution (m) * | 2.0 | 3.5 | |
| Average coverage per flight line (km2) | 45.2 | 45.0 |
| Metric | Spatial Resolution | No. of Training Pixels |
|---|---|---|
| SCM/Reflectance | 62.5 m | 700 |
| SCM/Reflectance | 25 m | 1500 |
| SCM/Reflectance | 12.5 m | 3000 |
| Reflectance | 2.5 m | 5000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osei Darko, P.; Kalacska, M.; Arroyo-Mora, J.P.; Fagan, M.E. Spectral Complexity of Hyperspectral Images: A New Approach for Mangrove Classification. Remote Sens. 2021, 13, 2604. https://doi.org/10.3390/rs13132604
Osei Darko P, Kalacska M, Arroyo-Mora JP, Fagan ME. Spectral Complexity of Hyperspectral Images: A New Approach for Mangrove Classification. Remote Sensing. 2021; 13(13):2604. https://doi.org/10.3390/rs13132604
Chicago/Turabian StyleOsei Darko, Patrick, Margaret Kalacska, J. Pablo Arroyo-Mora, and Matthew E. Fagan. 2021. "Spectral Complexity of Hyperspectral Images: A New Approach for Mangrove Classification" Remote Sensing 13, no. 13: 2604. https://doi.org/10.3390/rs13132604
APA StyleOsei Darko, P., Kalacska, M., Arroyo-Mora, J. P., & Fagan, M. E. (2021). Spectral Complexity of Hyperspectral Images: A New Approach for Mangrove Classification. Remote Sensing, 13(13), 2604. https://doi.org/10.3390/rs13132604







