Automated Simulation Framework for Urban Wind Environments Based on Aerial Point Clouds and Deep Learning
Abstract
1. Introduction
2. Automated Simulation Framework for Urban Wind Environments
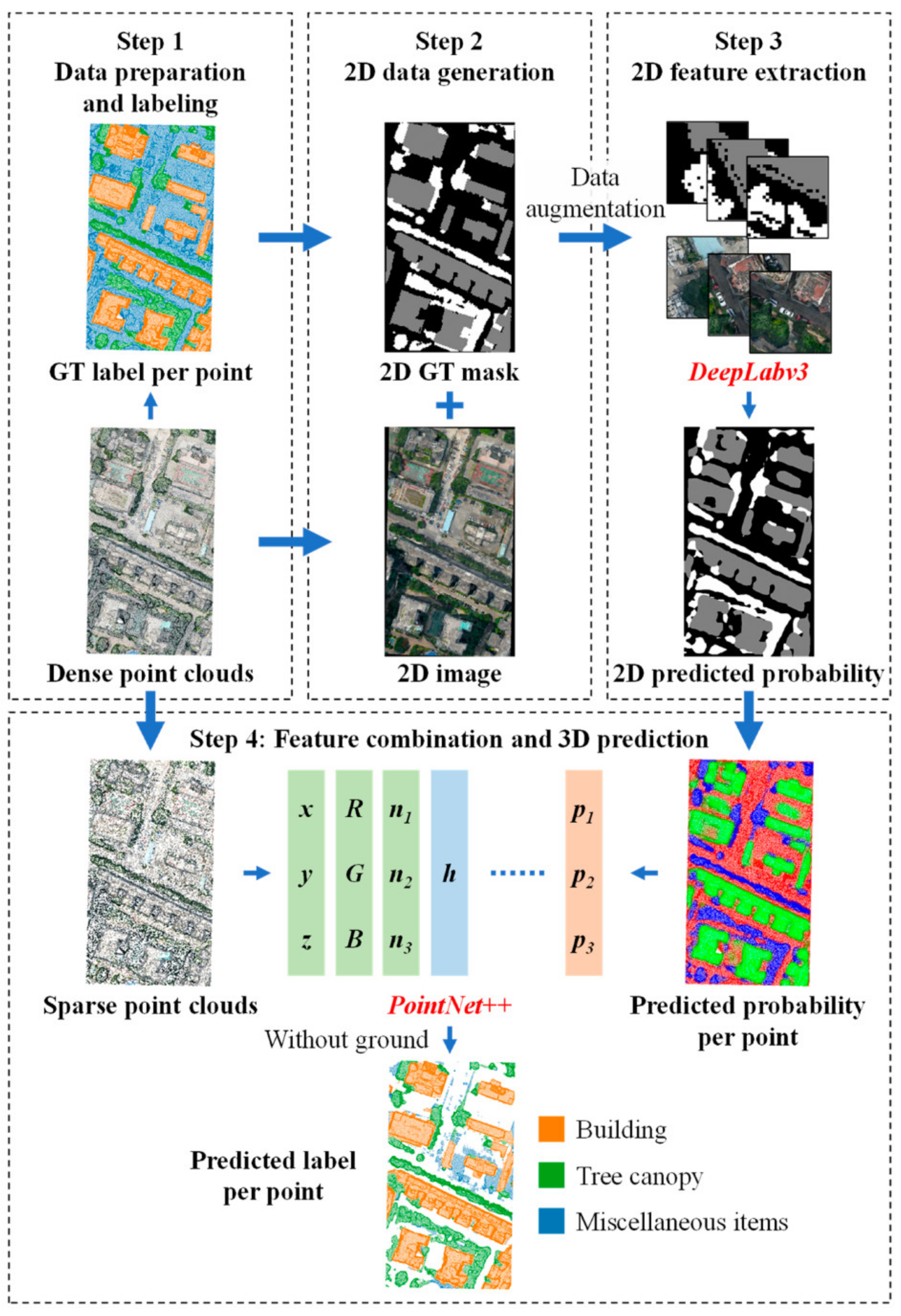
3. Point Clouds Separation Based on Deep Learning
3.1. Terrain Filtering
3.2. Segmentation of Buildings and Tree Canopies
- (1)
- The 2D prediction of DeepLabv3 is combined with the 3D input features of PointNet++, which allows fully utilizing the advantages of the 2D data containing dense texture features and overcomes the shortcoming of the 3D network of losing the local characteristics when the point clouds are sparsified owing to device capacity.
- (2)
- The coordinates and the relative heights entailed in PointNet++ strengthen the importance of the vertical information and improve the accuracy at the edges of objects compared to that of the single 2D network.
- (3)
- The input images of the 2D network are not oblique photos captured by a UAV but are the images rasterized from the projected point clouds. No extra efforts are needed to determine the mapping relationship between the oblique photos and the 3D point clouds. Labeling for training is required only once for the point clouds, which avoids the burden of labeling on 2D images.
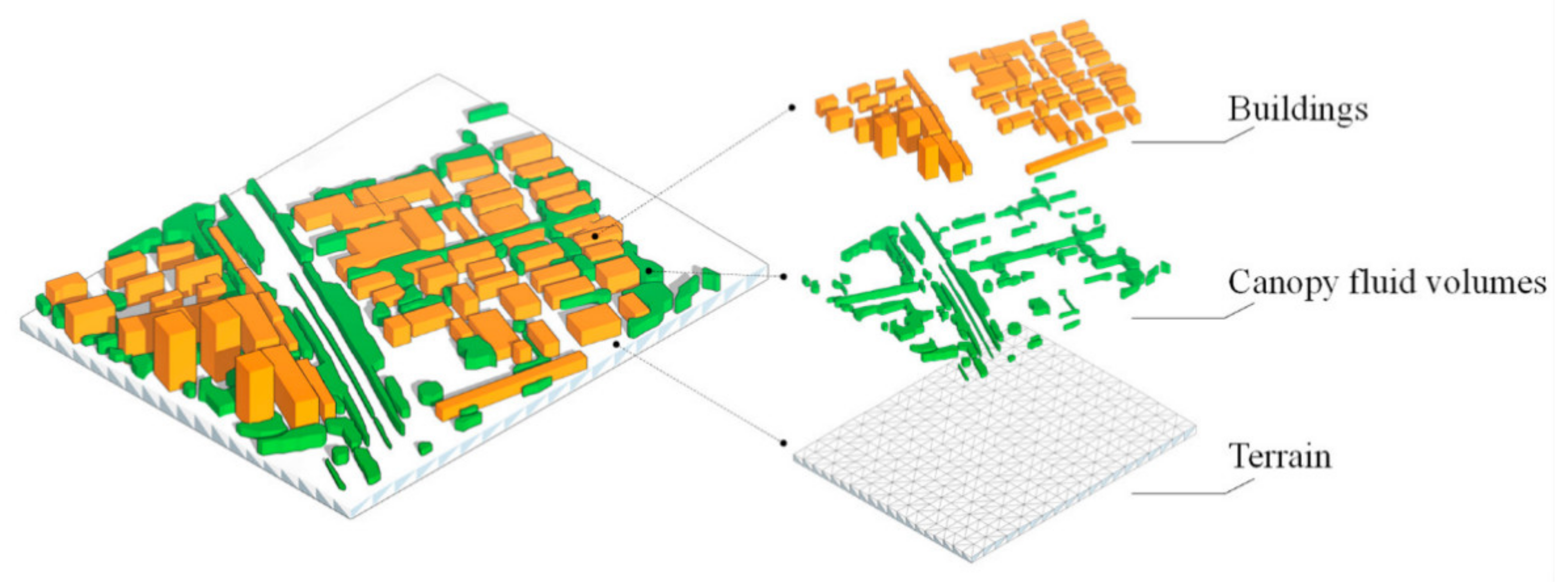
4. Geometric 3D Reconstruction
4.1. Terrain Generation
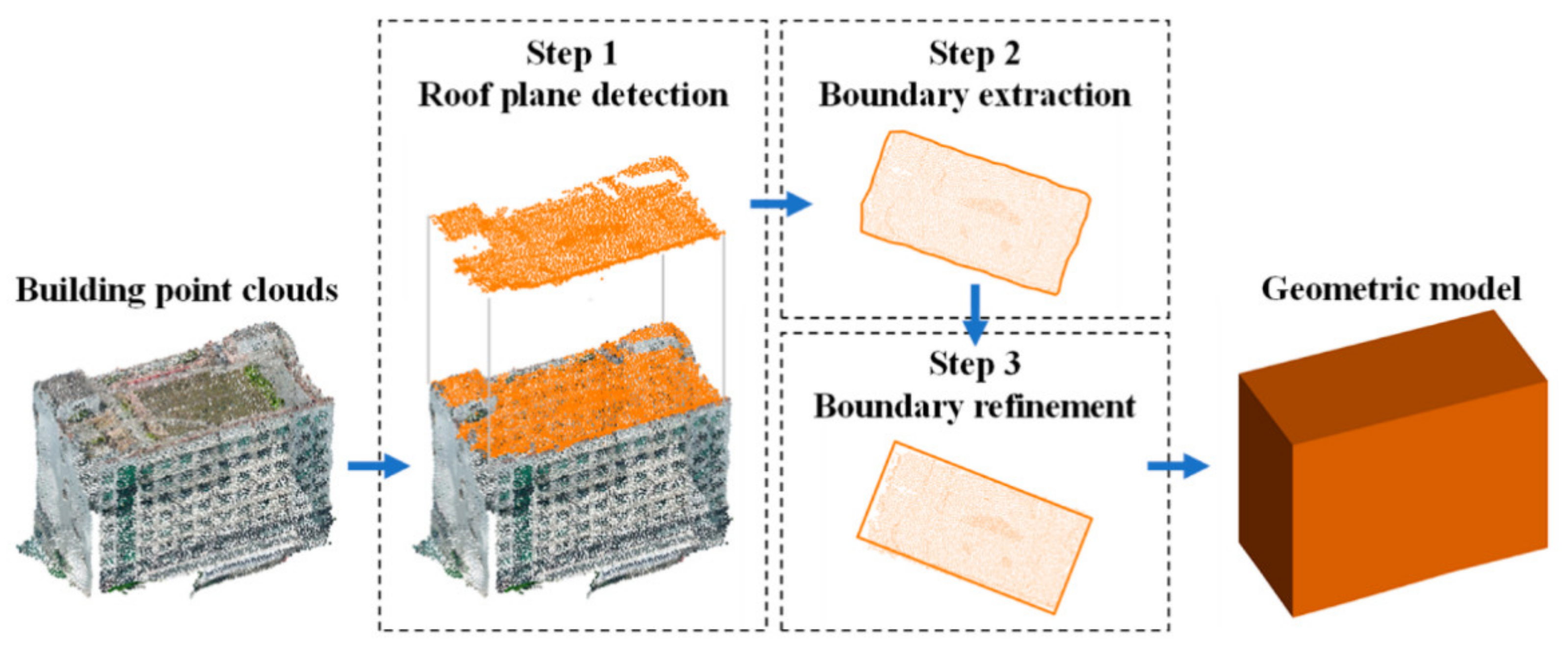
4.2. Building Reconstruction
- (1)
- To address the zig-zag problem, the method proposed by Poullis [52] is adopted, which detects principal directions and regularizes building boundaries based on Gaussian mixture models and energy minimization. The energy minimization problem is equivalent to a minimum cut problem and is solved using gco-v3.0 [53,54,55,56] in this study.
- (2)
- (3)
- All boundary line segments in the target area are searched for the segment pairs whose two segments have a distance and an angle within certain thresholds. Subsequently, each segment pair is combined to make both segments in the pair collinear in the horizontal plane.
- (4)
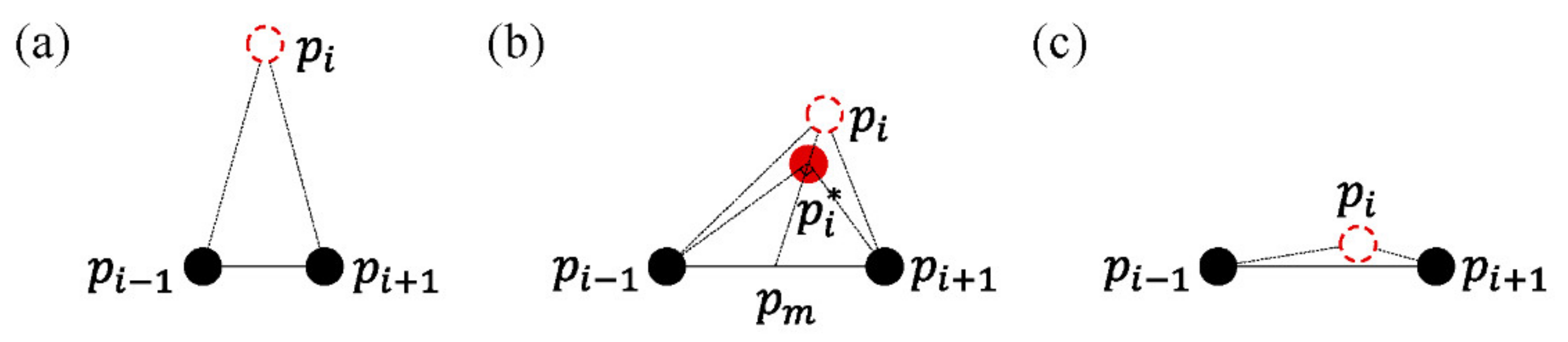
- The angle between each adjacent boundary line segment pair of a building is further revised. As shown in Figure 4, for the point set of a building boundary, , and its sequential points , , and , based on the threshold, the revision is as follows:
- (a)
- The extreme acute angles caused by outliers are eliminated. The new point set of the building boundary, , becomes
- (b)
- is moved along the median of the triangle to when the angle is approximately a right angle. Coordinates of in are revised as follows:
- (c)
- The obtuse angles that are approximately 180° are eliminated to further smoothen the boundary. is modified as in Equation (4).
4.3. Canopy Fluid Volumes
- (1)
- The outliers with average distances to neighboring points remarkably larger than the average level in the entire area are removed.
- (2)
- The point clouds need to be clustered into groups for modeling. Different clustering algorithms have been developed in existing studies [59,60,61]. For the grouping task based on the Euclidean distance, k-means-based algorithms require a pre-specified number of clusters and assume the clusters are convex. Thus, the DBSCAN algorithm [59] is adopted due to its robustness to outliers, explicit control over density via parameters, and variable cluster shapes. The minPoints and eps of DBSCAN are set to 1 and 3.0, respectively, in this study. The groups with a point number less than the threshold are ignored and removed.
- (3)
| Algorithm 1. Generation of boundaries of tree canopy volumes |
| Input: point clouds of tree canopies |
| Output: set of boundaries of tree canopy volumes |
| fortodo |
| //Set of n-nearest neighbors of |
| //Average distance in |
| end |
| //Set of clustered point clouds |
| foreachofdo |
| //Boundary points of tree canopy |
| end |
4.4. Postprocessing
5. Case Study
5.1. Case Description
5.2. Results and Analysis
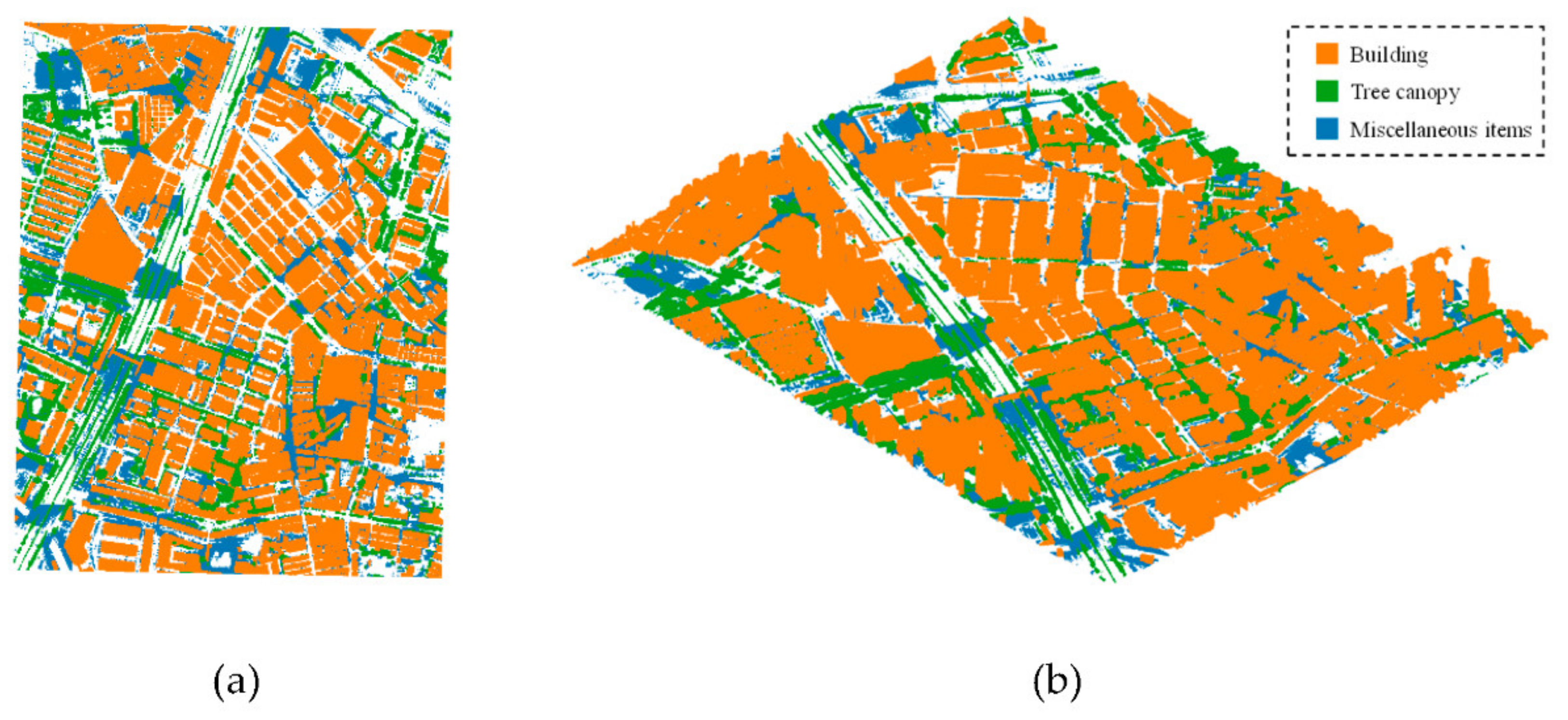
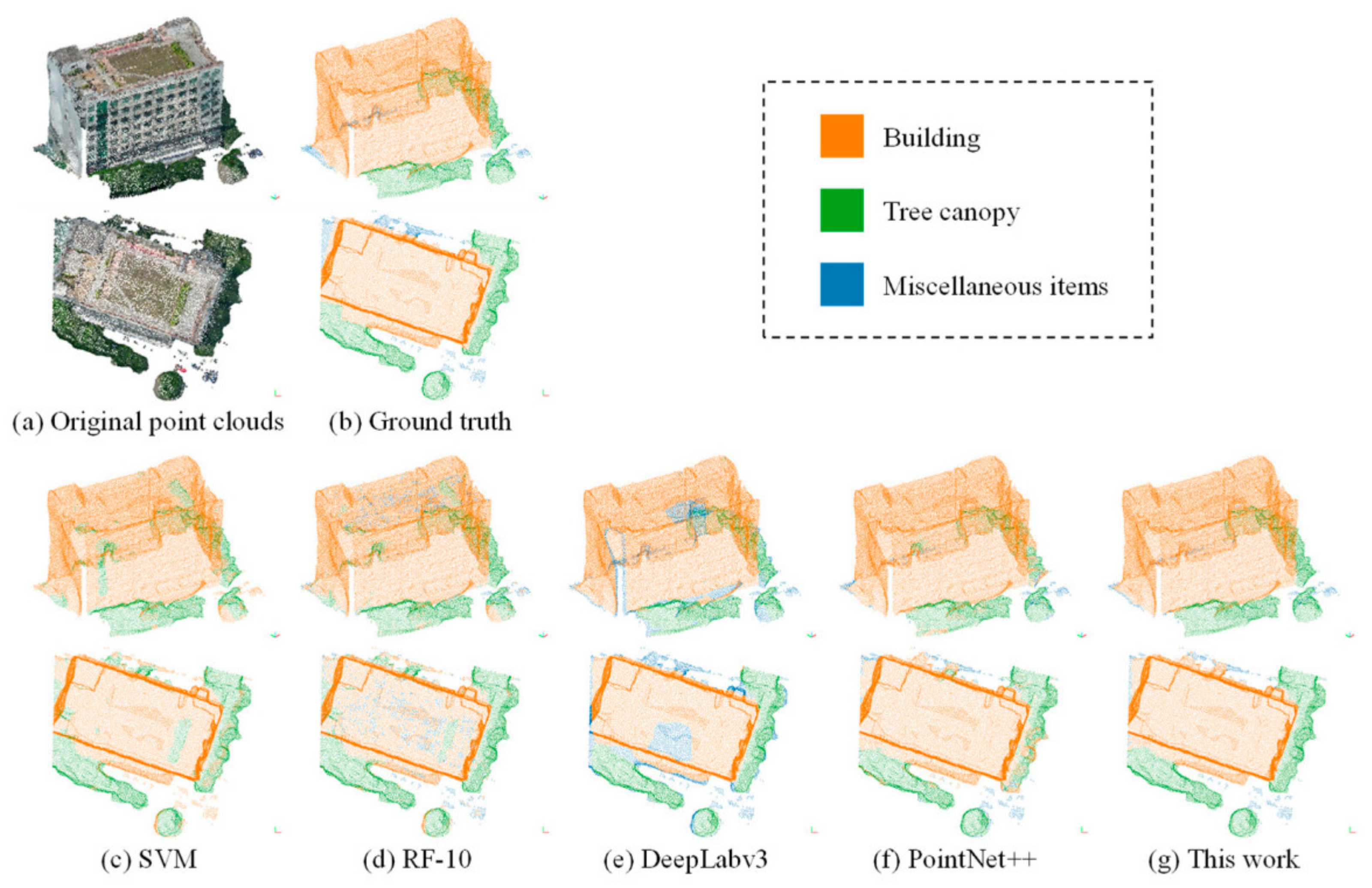
5.2.1. Point Cloud Separation
- (1)
- The SVM fails to differentiate between buildings and tree canopies, leading to a misprediction of miscellaneous items (Figure 8c) and relatively low precision for buildings and canopies.
- (2)
- The RF hardly improves its performance when the number of trees increases but has a slightly higher performance than the SVM; however, there are many outliers mixed in the true classes, which is disadvantageous for the subsequent modeling process.
- (3)
- Because DeepLabv3 does not have height information, it has a low accuracy at the edges of objects and tends to predict the edge points as miscellaneous items (blue points at the edges of the buildings and the canopies in Figure 8e). This makes the recall higher for miscellaneous items and significantly lower for buildings and canopies compared to their respective precision.
- (4)
- Although PointNet++ has a satisfying result for buildings, the precision for canopies is low because the normal vector distribution of the canopy areas is irregular. As shown in Figure 8f, the canopy points on the right side of the building have a high probability of being predicted as building points. This may lead to unexpected building point clouds and incomplete canopy point clouds in the modeling step.
- (5)
- The method proposed in this paper combining DeepLabv3 and PointNet++ improves the accuracy at the edges of objects as well as addresses the problems caused by the complexity of point cloud characteristics and the low generation quality due to occlusion. The accuracy for miscellaneous items is remarkably improved, and the precision and recall of buildings and canopies are balanced well, which can provide accurate point clouds for 3D modeling.
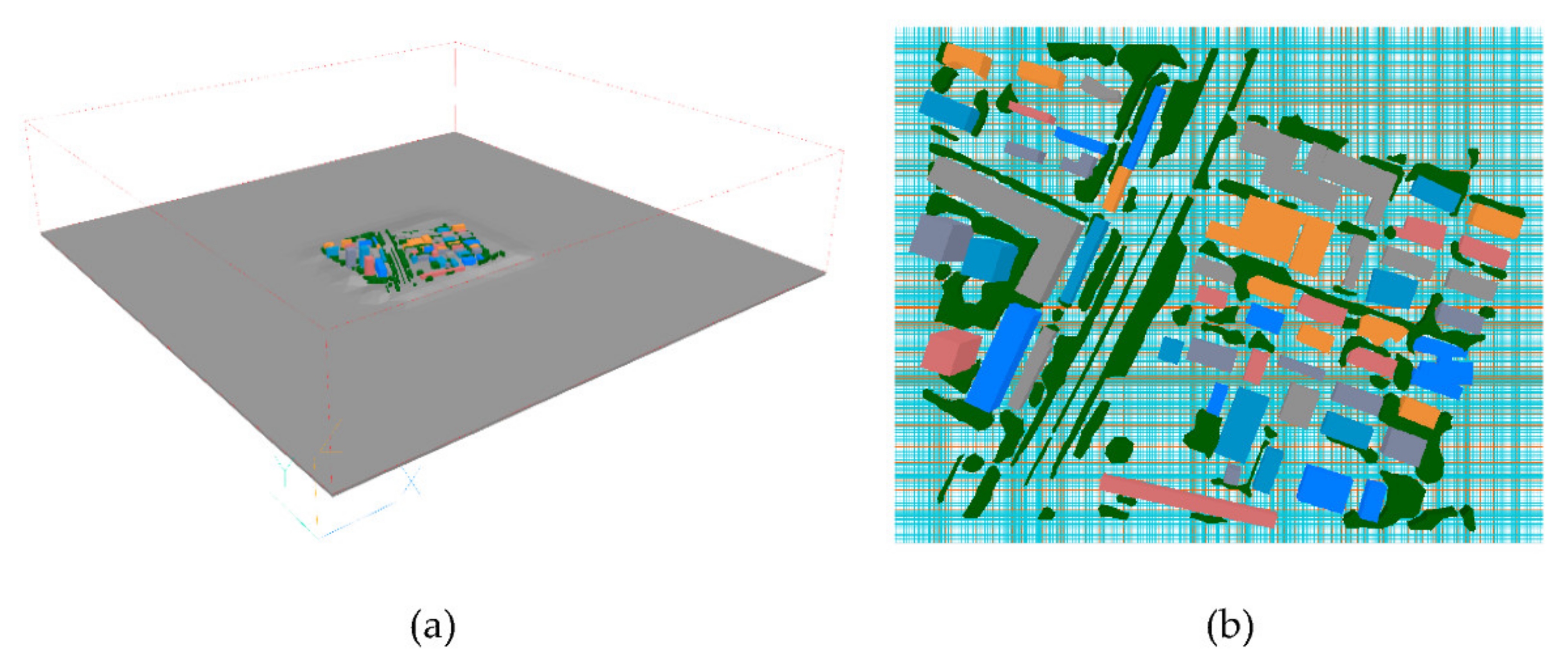
5.2.2. Three-Dimensional Reconstruction
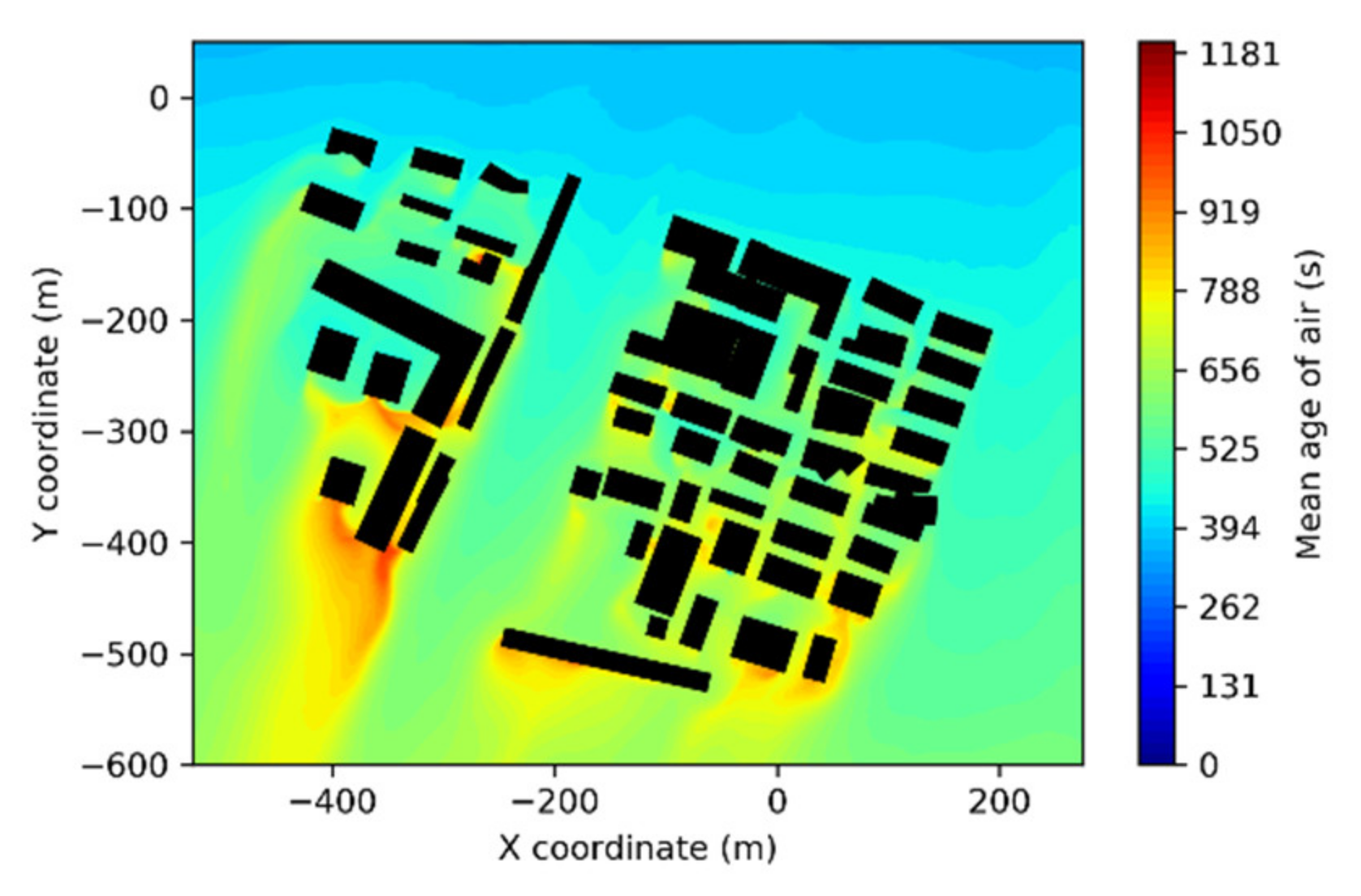
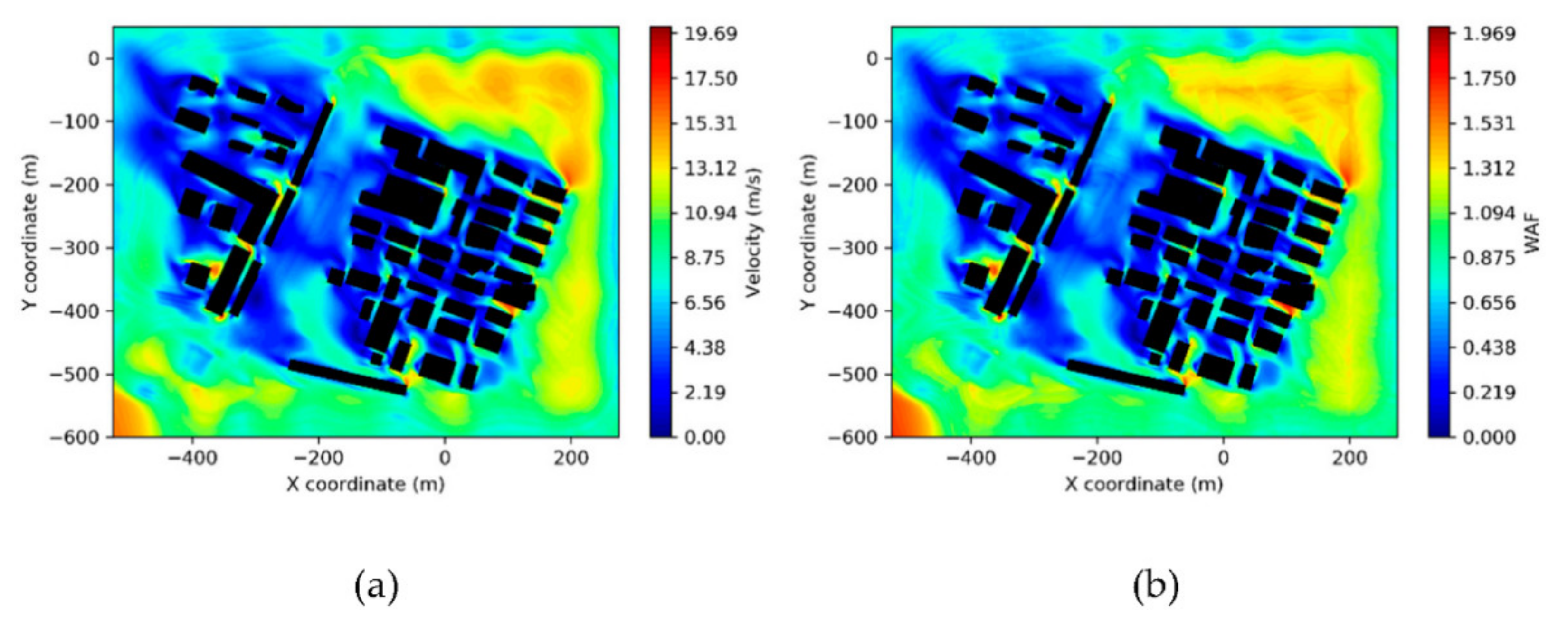
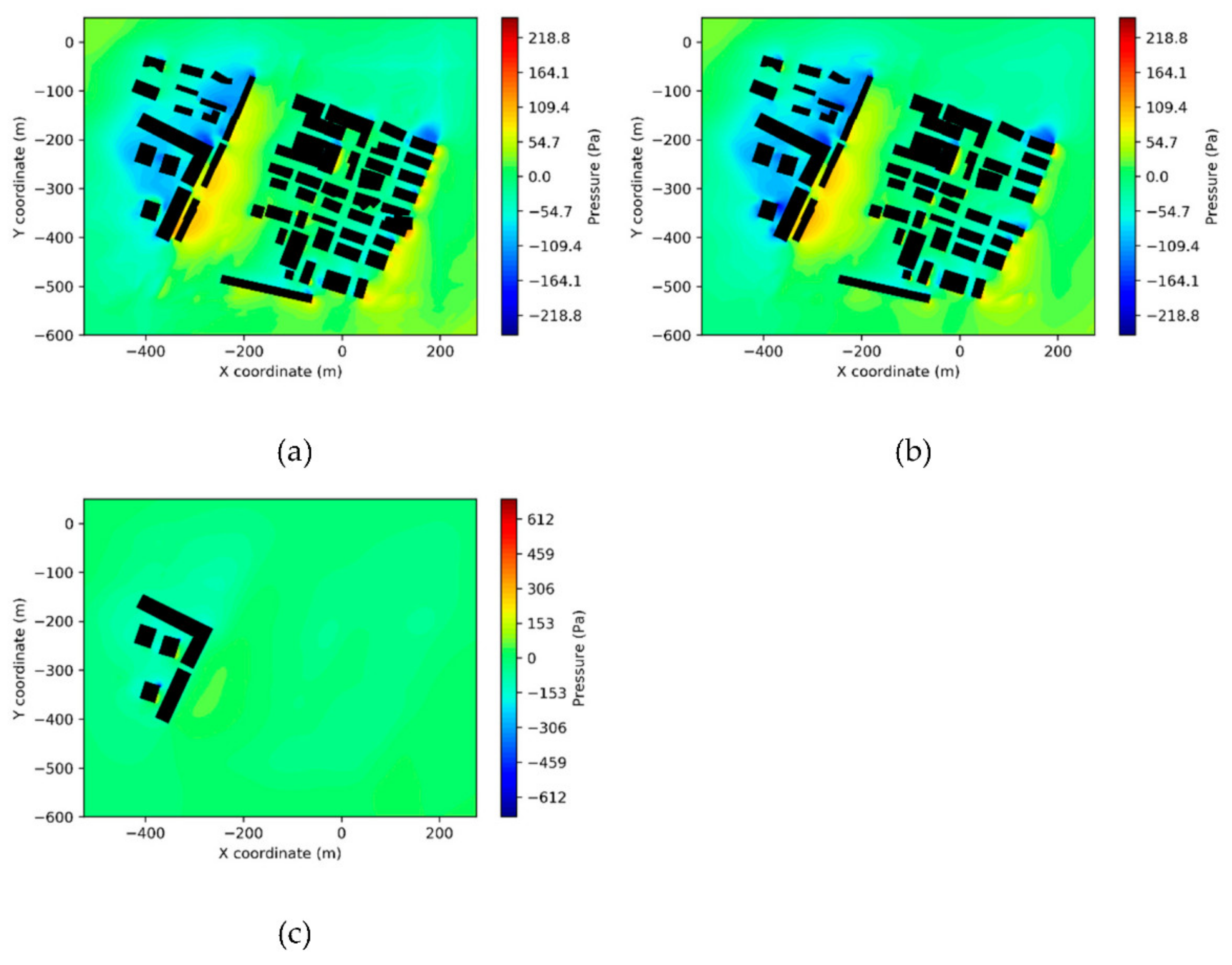
5.2.3. CFD Simulation
6. Discussion
6.1. Data Acquisition and Errors
6.2. Efficiency
6.3. Geometric Quality
7. Conclusions
- (1)
- Compared with the traditional CFD modeling methods based on GISs, the automated method based on oblique photography point clouds can reflect the current environment of the target area and drastically reduce the labor cost.
- (2)
- Compared to the point cloud semantic segmentation methods based on SVM, RF, or a single deep learning network, the proposed method combining 2D and 3D deep learning techniques achieves a higher accuracy, which provides more accurate classification results for the modeling process.
- (3)
- The modeling method of the terrain, buildings, and canopy fluid volumes can retain general geometric characteristics of the objects while reducing the model complexity, which meets the requirements of CFD simulations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 0.09 | 0.75 | 1.15 | 1.15 | 1.9 | 0.25 | 1.50 | 1.50 | 1.00 | 4.00 | 0.20 | 4.00 |
References
- Blocken, B. Computational Fluid Dynamics for Urban Physics: Importance, Scales, Possibilities, Limitations and Ten Tips and Tricks towards Accurate and Reliable Simulations. Build. Environ. 2015, 91, 219–245. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, K.; Shen, Z.; Bai, X.; Lu, X.; Soares, C.G. Economic Impact of Typhoon-Induced Wind Disasters on Port Operations: A Case Study of Ports in China. Int. J. Disaster Risk Reduct. 2020, 50, 101719. [Google Scholar] [CrossRef]
- Song, B.; Galasso, C.; Garciano, L. Wind-Uplift Fragility Analysis of Roof Sheathing for Cultural Heritage Assets in the Philippines. Int. J. Disaster Risk Reduct. 2020, 51, 101753. [Google Scholar] [CrossRef]
- Schulman, L.L.; DesAutels, C.G. Computational Fluid Dynamics Simulations to Predict Wind-Induced Damage to a Steel Building during Hurricane Katrina. In Forensic Engineering 2012; American Society of Civil Engineers: San Francisco, CA, USA, 2012; pp. 793–800. [Google Scholar] [CrossRef]
- Blocken, B.; Janssen, W.D.; van Hooff, T. CFD Simulation for Pedestrian Wind Comfort and Wind Safety in Urban Areas: General Decision Framework and Case Study for the Eindhoven University Campus. Environ. Model. Softw. 2012, 30, 15–34. [Google Scholar] [CrossRef]
- Gu, D.; Zhao, P.; Chen, W.; Huang, Y.; Lu, X. Near Real-Time Prediction of Wind-Induced Tree Damage at a City Scale: Simulation Framework and Case Study for Tsinghua University Campus. Int. J. Disaster Risk Reduct. 2021, 53, 102003. [Google Scholar] [CrossRef]
- Amorim, J.H.; Rodrigues, V.; Tavares, R.; Valente, J.; Borrego, C. CFD Modelling of the Aerodynamic Effect of Trees on Urban Air Pollution Dispersion. Sci. Total. Environ. 2013, 461, 541–551. [Google Scholar] [CrossRef] [PubMed]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Standard for Green Performance Calculation of Civil. Buildings (JGJ/T 449-2018); China Architecture & Building Press: Beijing, China, 2018.
- Gu, D.; Zheng, Z.; Zhao, P.; Xie, L.; Xu, Z.; Lu, X. High-Efficiency Simulation Framework to Analyze the Impact of Exhaust Air from COVID-19 Temporary Hospitals and Its Typical Applications. Appl. Sci. 2020, 10, 3949. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Prasad, S.; Pacifici, F.; Gamba, P.; Chanussot, J.; Benediktsson, J.A. Challenges and Opportunities of Multimodality and Data Fusion in Remote Sensing. Proc. IEEE 2015, 103, 1585–1601. [Google Scholar] [CrossRef]
- Jochem, W.C.; Bird, T.J.; Tatem, A.J. Identifying Residential Neighbourhood Types from Settlement Points in a Machine Learning Approach. Comput. Environ. Urban. Syst. 2018, 69, 104–113. [Google Scholar] [CrossRef]
- Hecht, R.; Meinel, G.; Buchroithner, M. Automatic Identification of Building Types Based on Topographic Databases—A Comparison of Different Data Sources. Int. J. Cartogr. 2015, 1, 18–31. [Google Scholar] [CrossRef]
- Shirowzhan, S.; Sepasgozar, S.M.E.; Li, H.; Trinder, J.; Tang, P. Comparative Analysis of Machine Learning and Point-Based Algorithms for Detecting 3D Changes in Buildings over Time Using Bi-Temporal Lidar Data. Autom. Constr. 2019, 105, 102841. [Google Scholar] [CrossRef]
- Chen, J.; Tang, P.; Rakstad, T.; Patrick, M.; Zhou, X. Augmenting a Deep-Learning Algorithm with Canal Inspection Knowledge for Reliable Water Leak Detection from Multispectral Satellite Images. Adv. Eng. Inform. 2020, 46, 101161. [Google Scholar] [CrossRef]
- Cooner, A.J.; Shao, Y.; Campbell, J.B. Detection of Urban Damage Using Remote Sensing and Machine Learning Algorithms: Revisiting the 2010 Haiti Earthquake. Remote. Sens. 2016, 8, 868. [Google Scholar] [CrossRef]
- Gomez, C.; Purdie, H. UAV-Based Photogrammetry and Geocomputing for Hazards and Disaster Risk Monitoring—A Review. Geoenviron. Disasters 2016, 3, 23. [Google Scholar] [CrossRef]
- Xiong, C.; Li, Q.; Lu, X. Automated Regional Seismic Damage Assessment of Buildings Using an Unmanned Aerial Vehicle and a Convolutional Neural Network. Autom. Constr. 2020, 109, 102994. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, L.; Love, P.E.D.; Ding, L.; Zhou, C. Three-Dimensional (3D) Reconstruction of Structures and Landscapes: A New Point-and-Line Fusion Method. Adv. Eng. Inform. 2019, 42, 100961. [Google Scholar] [CrossRef]
- Sun, X.; Shen, S.; Hu, Z. Automatic Building Extraction from Oblique Aerial Images. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 663–668. [Google Scholar] [CrossRef]
- Tomljenovic, I.; Tiede, D.; Blaschke, T. A Building ExSegmentation of Airborne Point Cloud Data for Autcanner Data Utilizing the Object Based Image Analysis Paradigm. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 137–148. [Google Scholar] [CrossRef]
- Gilani, S.A.N.; Awrangjeb, M.; Lu, G. Segmentation of Airborne Point Cloud Data for Automatic Building Roof Extraction. GISci. Remote. Sens. 2018, 55, 63–89. [Google Scholar] [CrossRef]
- Verma, V.; Kumar, R.; Hsu, S. 3D Building Detection and Modeling from Aerial LIDAR Data. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 2, pp. 2213–2220. [Google Scholar] [CrossRef]
- Anuar, S.F.K.; Nasir, A.A.M.; Azri, S.; Ujang, U.; Majid, Z.; González Cuétara, M.; de Miguel Retortillo, G. 3D Geometric Extraction Using Segmentation for Asset Management. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Göttingen, Germany, 2020; Volume XLIV-4-W3-2020, pp. 61–69. [Google Scholar] [CrossRef]
- Zhou, Q. 3D Urban Modeling from City-Scale Aerial LiDAR Data. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2012. [Google Scholar]
- Rida, I.; Almaadeed, N.; Almaadeed, S. Robust Gait Recognition: A Comprehensive Survey. IET Biom. 2019, 8, 14–28. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs. arXiv 2016, arXiv:1412.7062. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for Real-Time Object Recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar] [CrossRef]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5105–5114. [Google Scholar]
- Zhang, Y.; Huo, K.; Liu, Z.; Zang, Y.; Liu, Y.; Li, X.; Zhang, Q.; Wang, C. PGNet: A Part-Based Generative Network for 3D Object Reconstruction. Knowl. Based Syst. 2020, 194, 105574. [Google Scholar] [CrossRef]
- Kim, H.; Yoon, J.; Sim, S.-H. Automated Bridge Component Recognition from Point Clouds Using Deep Learning. Struct. Control. Health Monit. 2020, 27, e2591. [Google Scholar] [CrossRef]
- Lowphansirikul, C.; Kim, K.; Vinayaraj, P.; Tuarob, S. 3D Semantic Segmentation of Large-Scale Point-Clouds in Urban Areas Using Deep Learning. In Proceedings of the 2019 11th International Conference on Knowledge and Smart Technology (KST), Phuket, Thailand, 23–26 January 2019; pp. 238–243. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the Shape of a Set of Points in the Plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Bernardini, F.; Mittleman, J.; Rushmeier, H.; Silva, C.; Taubin, G. The Ball-Pivoting Algorithm for Surface Reconstruction. IEEE Trans. Vis. Comput. Graph. 1999, 5, 349–359. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson Surface Reconstruction. In Proceedings of the 4th Eurographics Symposium on Geometry Processing, Sardinia, Italy, 26–28 June 2006; Eurographics Association: Goslar, Germany, 2006; pp. 61–70. [Google Scholar]
- Xu, Z.; Wu, Y.; Lu, X.; Jin, X. Photo-Realistic Visualization of Seismic Dynamic Responses of Urban Building Clusters Based on Oblique Aerial Photography. Adv. Eng. Inform. 2020, 43, 101025. [Google Scholar] [CrossRef]
- Hågbo, T.-O.; Giljarhus, K.E.T.; Hjertager, B.H. Influence of Geometry Acquisition Method on Pedestrian Wind Simulations. arXiv 2020, arXiv:2010.12371. [Google Scholar]
- Chen, L.; Teo, T.; Rau, J.; Liu, J.; Hsu, W. Building Reconstruction from LIDAR Data and Aerial Imagery. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, 2005. (IGARSS ’05), Seoul, Korea, 29–29 July 2005; Volume 4, pp. 2846–2849. [Google Scholar] [CrossRef]
- Wang, X.; Chan, T.O.; Liu, K.; Pan, J.; Luo, M.; Li, W.; Wei, C. A Robust Segmentation Framework for Closely Packed Buildings from Airborne LiDAR Point Clouds. Int. J. Remote. Sens. 2020, 41, 5147–5165. [Google Scholar] [CrossRef]
- Lu, X.; Guo, Q.; Li, W.; Flanagan, J. A Bottom-up Approach to Segment Individual Deciduous Trees Using Leaf-off Lidar Point Cloud Data. ISPRS J. Photogramm. Remote. Sens. 2014, 94, 1–12. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, M.; Yao, Y.; Zhang, L.; Lin, J. Use of UAV Oblique Imaging for the Detection of Individual Trees in Residential Environments. Urban. For. Urban. Green. 2015, 14, 404–412. [Google Scholar] [CrossRef]
- Wang, Y.; Weinacker, H.; Koch, B. A Lidar Point Cloud Based Procedure for Vertical Canopy Structure Analysis and 3D Single Tree Modelling in Forest. Sensors 2008, 8, 3938–3951. [Google Scholar] [CrossRef] [PubMed]
- Phoenics. Available online: http://www.cham.co.uk/phoenics.php (accessed on 5 January 2021).
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote. Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- CloudCompare: 3D Point Cloud and Mesh Processing Software, Open Source Project. Available online: https://www.danielgm.net/cc/ (accessed on 30 November 2020).
- Vasudevan, S.; Ramos, F.; Nettleton, E.; Durrant-Whyte, H.; Blair, A. Gaussian Process Modeling of Large Scale Terrain. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1047–1053. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for Point-Cloud Shape Detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Poullis, C. A Framework for Automatic Modeling from Point Cloud Data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2563–2575. [Google Scholar] [CrossRef] [PubMed]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast Approximate Energy Minimization via Graph Cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Kolmogorov, V.; Zabin, R. What Energy Functions Can Be Minimized via Graph Cuts? IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 147–159. [Google Scholar] [CrossRef]
- Boykov, Y.; Kolmogorov, V. An Experimental Comparison of Min-Cut/Max- Flow Algorithms for Energy Minimization in Vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef]
- Delong, A.; Osokin, A.; Isack, H.N.; Boykov, Y. Fast Approximate Energy Minimization with Label Costs. Int. J. Comput. Vis. 2012, 96, 1–27. [Google Scholar] [CrossRef]
- Ramer, U. An Iterative Procedure for the Polygonal Approximation of Plane Curves. Comput. Graph. Image Process. 1972, 1, 244–256. [Google Scholar] [CrossRef]
- Douglas, D.; Peucker, T. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature. Cartogr. Int. J. Geogr. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; AAAI Press: Portland, OR, USA, 1996; pp. 226–231. [Google Scholar]
- Pio, G.; Ceci, M.; Loglisci, C.; D’Elia, D.; Malerba, D. Hierarchical and Overlapping Co-Clustering of mRNA: MiRNA Interactions. In Proceedings of the 20th European Conference on Artificial Intelligence, Montpellier, France, 27–31 August 2012; IOS Press: Amsterdam, The Netherlands, 2012; pp. 654–659. [Google Scholar]
- Slonim, N.; Aharoni, E.; Crammer, K. Hartigan’s K-Means versus Lloyd’s K-Means: Is It Time for a Change? In Proceedings of the 23rd International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; AAAI Press: Beijing, China, 2013; pp. 1677–1684. [Google Scholar]
- 3ds Max: 3D Modeling, Animation & Rendering Software. Available online: https://www.autodesk.com/products/3ds-max/overview (accessed on 5 January 2021).
- Bentley Systems, Create 3D Models from Simple Photographs. Available online: https://www.bentley.com/en/products/brands/contextcapture (accessed on 30 November 2020).
- Scikit-Learn: Machine Learning in Python. Available online: https://scikit-learn.org/stable/ (accessed on 7 January 2021).
- PyTorch: An Open Source Machine Learning Framework that Accelerates the Path from Research Prototyping to Production Deployment. Available online: https://www.pytorch.org (accessed on 30 November 2020).
- Guo, F.; Zhu, P.; Wang, S.; Duan, D.; Jin, Y. Improving Natural Ventilation Performance in a High-Density Urban District: A Building Morphology Method. Proced. Eng. 2017, 205, 952–958. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Eftekhari, M.; Qi, Q.; Jiang, D.; Song, Y.; Tian, P. Improvement Strategies Study for Outdoor Wind Environment in a University in Beijing Based on CFD Simulation. Adv. Civ. Eng. 2020, 2020, e8850254. [Google Scholar] [CrossRef]
- Alhasan, W.; Yuning, C. Environmental Analysis of Nanjing Mosque Courtyard Layout Based on CFD Simulation Technology. E3S Web Conf. 2019, 136, 04040. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ Guidelines for Practical Applications of CFD to Pedestrian Wind Environment around Buildings. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Meteorological Bureau of Shenzhen Municipality. Shenzhen Climate Bulletin 2019; Meteorological Bureau of Shenzhen Municipality: Shenzhen, China, 2019. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Assessment Standard for Green Building (GB/T 50378-2019); China Architecture & Building Press: Beijing, China, 2019.
- White, J.C.; Wulder, M.A.; Vastaranta, M.; Coops, N.C.; Pitt, D.; Woods, M. The Utility of Image-Based Point Clouds for Forest Inventory: A Comparison with Airborne Laser Scanning. Forests 2013, 4, 518–536. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, S.; Hu, H.; Zhong, R.; Wu, B.; Xie, L. Multiple Point Clouds Data Fusion Method for 3D City Modeling. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 1962–1971. (In Chinese) [Google Scholar]
- Despotović, I.; Jelača, V.; Vansteenkiste, E.; Philips, W. Noise-Robust Method for Image Segmentation. In Advanced Concepts for Intelligent Vision Systems; Lecture Notes in Computer Science; Blanc-Talon, J., Bone, D., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 153–162. [Google Scholar] [CrossRef]
- Corizzo, R.; Ceci, M.; Japkowicz, N. Anomaly Detection and Repair for Accurate Predictions in Geo-Distributed Big Data. Big Data Res. 2019, 16, 18–35. [Google Scholar] [CrossRef]
- Gopalakrishnan, R.; Ali-Sisto, D.; Kukkonen, M.; Savolainen, P.; Packalen, P. Using ALS Data to Improve Co-Registration of Photogrammetry-Based Point Cloud Data in Urban Areas. Remote. Sens. 2020, 12, 1943. [Google Scholar] [CrossRef]
- Chen, Y.-S.; Kim, S.-W. Computation of Turbulent Flows Using an Extended K-Epsilon Turbulence Closure Model. NASA STI/Recon Tech. Rep. N 1987, 88, 11969. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Green, R.S. Modelling Turbulent Air Flow in a Stand of Widely-Spaced Trees. Phoenics J. 1992, 5, 294–312. [Google Scholar]
- Liu, J.; Chen, J.M.; Black, T.A.; Novak, M.D. E-ε Modelling of Turbulent Air Flow Downwind of a Model Forest Edge. Bound. Layer Meteorol. 1996, 77, 21–44. [Google Scholar] [CrossRef]
- Svensson, U.; Häggkvist, K. A Two-Equation Turbulence Model for Canopy Flows. J. Wind. Eng. Ind. Aerodyn. 1990, 35, 201–211. [Google Scholar] [CrossRef]
- Sanz, C. A Note on k-ε Modelling of Vegetation Canopy Air-Flows. Bound. Layer Meteorol. 2003, 108, 191–197. [Google Scholar] [CrossRef]
- Huang, J.; Cassiani, M.; Albertson, J.D. The Effects of Vegetation Density on Coherent Turbulent Structures within the Canopy Sublayer: A Large-Eddy Simulation Study. Bound. Layer Meteorol. 2009, 133, 253–275. [Google Scholar] [CrossRef]





| Classes | Building | Tree Canopy | Miscellaneous Items | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Metrics | Precision | Recall | F1 | Precision | Recall | F1 | Precision | Recall | F1 |
| SVM | 0.88 | 0.96 | 0.92 | 0.72 | 0.81 | 0.76 | 0.00 | 0.00 | 0.00 |
| RF-10 | 0.89 | 0.94 | 0.91 | 0.76 | 0.82 | 0.79 | 0.34 | 0.16 | 0.22 |
| RF-50 | 0.89 | 0.95 | 0.92 | 0.76 | 0.84 | 0.80 | 0.42 | 0.12 | 0.19 |
| RF-100 | 0.89 | 0.96 | 0.92 | 0.76 | 0.84 | 0.80 | 0.43 | 0.12 | 0.18 |
| DeepLabv3 | 0.97 | 0.85 | 0.90 | 0.90 | 0.80 | 0.85 | 0.36 | 0.79 | 0.49 |
| PointNet++ | 0.93 | 0.94 | 0.93 | 0.76 | 0.82 | 0.79 | 0.59 | 0.45 | 0.51 |
| This work | 0.96 | 0.96 | 0.96 | 0.86 | 0.92 | 0.89 | 0.68 | 0.62 | 0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Zhang, F.; Zhao, P.; Zhao, X.; Huang, Y.; Lu, X. Automated Simulation Framework for Urban Wind Environments Based on Aerial Point Clouds and Deep Learning. Remote Sens. 2021, 13, 2383. https://doi.org/10.3390/rs13122383
Sun C, Zhang F, Zhao P, Zhao X, Huang Y, Lu X. Automated Simulation Framework for Urban Wind Environments Based on Aerial Point Clouds and Deep Learning. Remote Sensing. 2021; 13(12):2383. https://doi.org/10.3390/rs13122383
Chicago/Turabian StyleSun, Chujin, Fan Zhang, Pengju Zhao, Xinyi Zhao, Yuli Huang, and Xinzheng Lu. 2021. "Automated Simulation Framework for Urban Wind Environments Based on Aerial Point Clouds and Deep Learning" Remote Sensing 13, no. 12: 2383. https://doi.org/10.3390/rs13122383
APA StyleSun, C., Zhang, F., Zhao, P., Zhao, X., Huang, Y., & Lu, X. (2021). Automated Simulation Framework for Urban Wind Environments Based on Aerial Point Clouds and Deep Learning. Remote Sensing, 13(12), 2383. https://doi.org/10.3390/rs13122383






