Coarse-to-Fine Loosely-Coupled LiDAR-Inertial Odometry for Urban Positioning and Mapping
Abstract
1. Introduction
- Development of a coarse-to-fine LC-LIO pipeline based on window optimization. Meanwhile, the adaptive covariance estimation of the LiDAR scan-to-map registration is proposed for further LiDAR/Inertial integration.
- Theoretical analysis of performance upper bound of LC and TC LiDAR-inertial fusion considering the error propagation from LiDAR and inertial measurements.
- Validation of the proposed method with challenging datasets collected in urban canyons of Hong Kong. The convergence results of both the LC-LIO and TC-LIO are presented to experimentally verify the theoretical analysis in the second aspect.
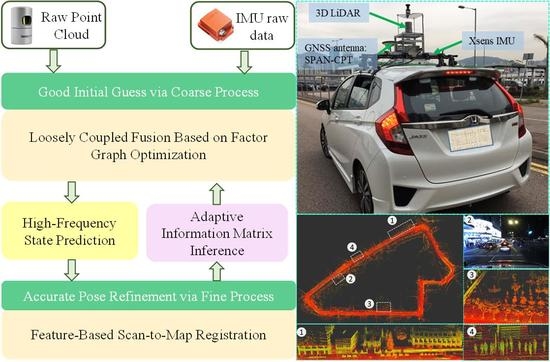
2. Overview of the Proposed LC-LIO
- The LiDAR body frame is represented as , which is fixed at the center of the LiDAR sensor.
- The IMU body frame is represented as , which is fixed at the center of the IMU sensor.
- The world frame is represented as , which is originated at the initial position of the vehicle. It is assumed to coincide with the initial LiDAR frame.
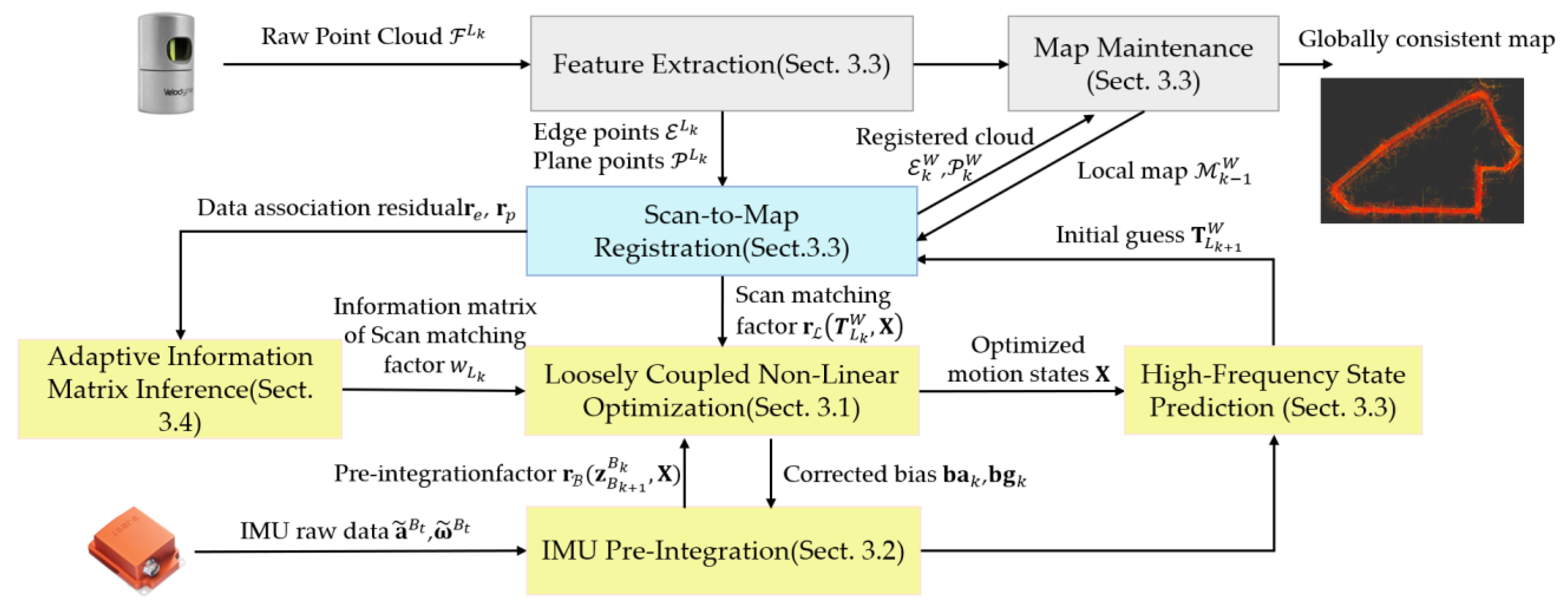
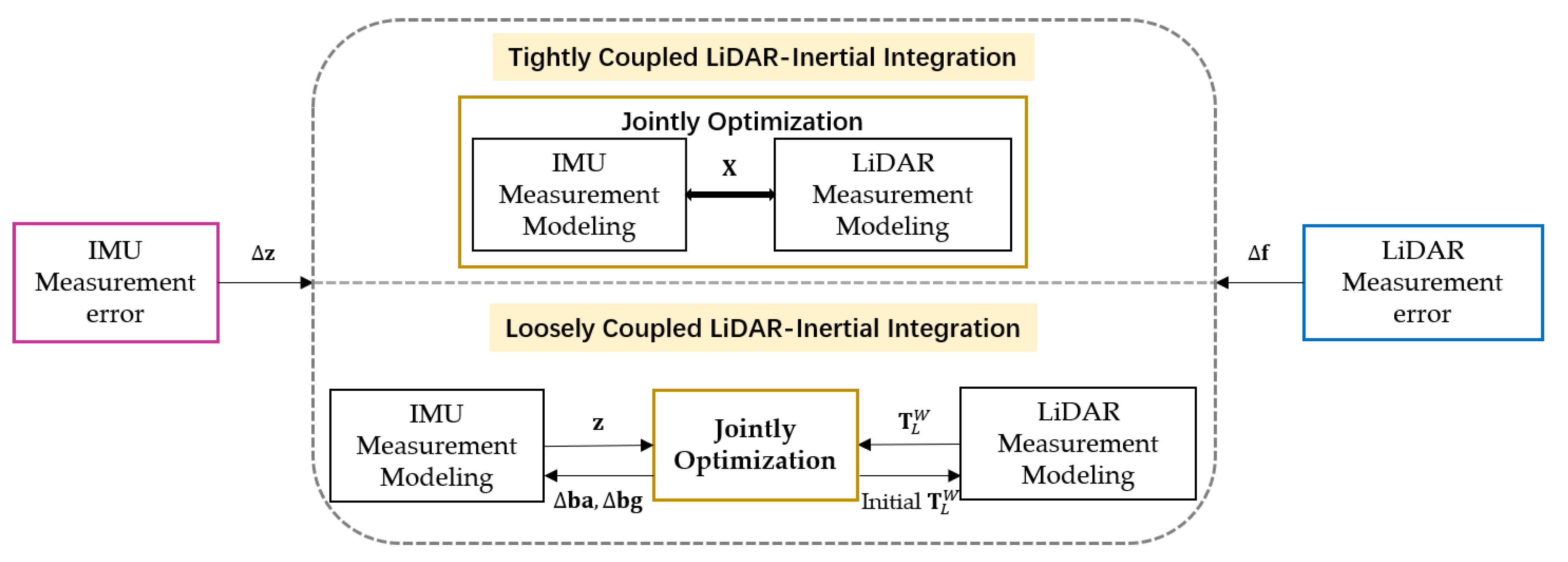
3. Coarse-to-Fine Loosely-Coupled LiDAR-Inertial Integration
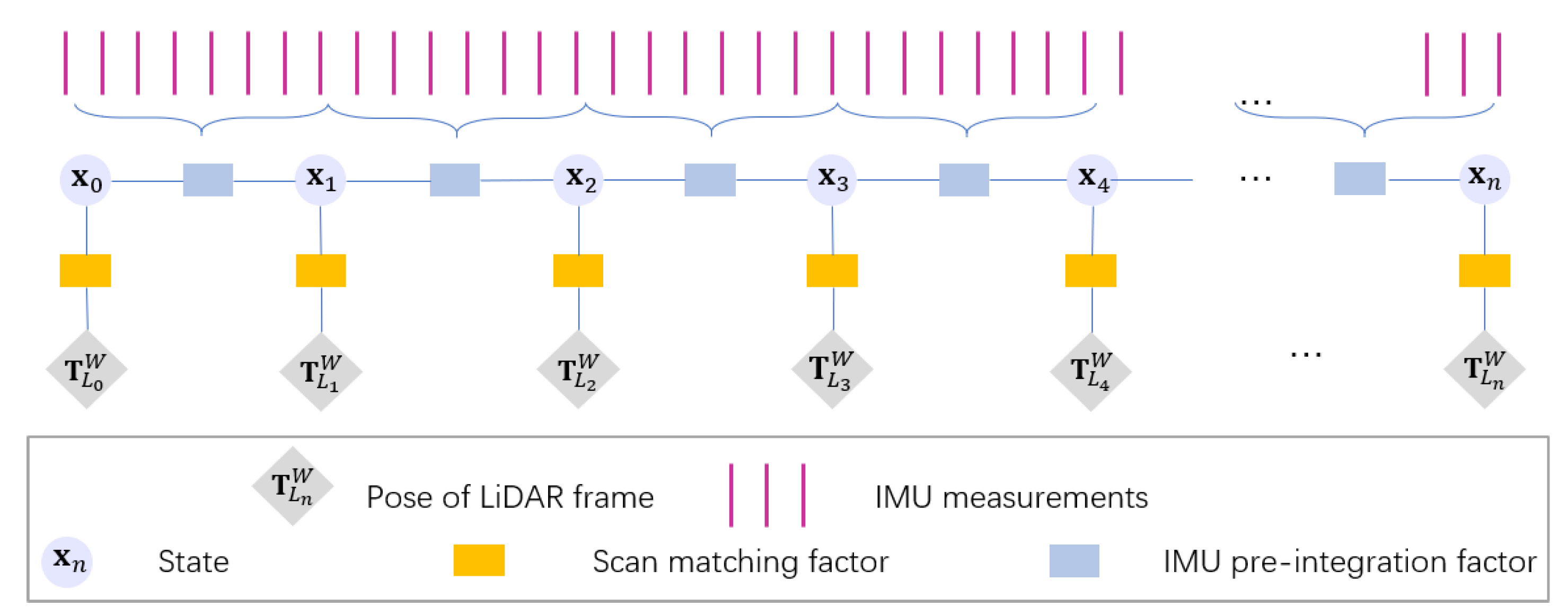
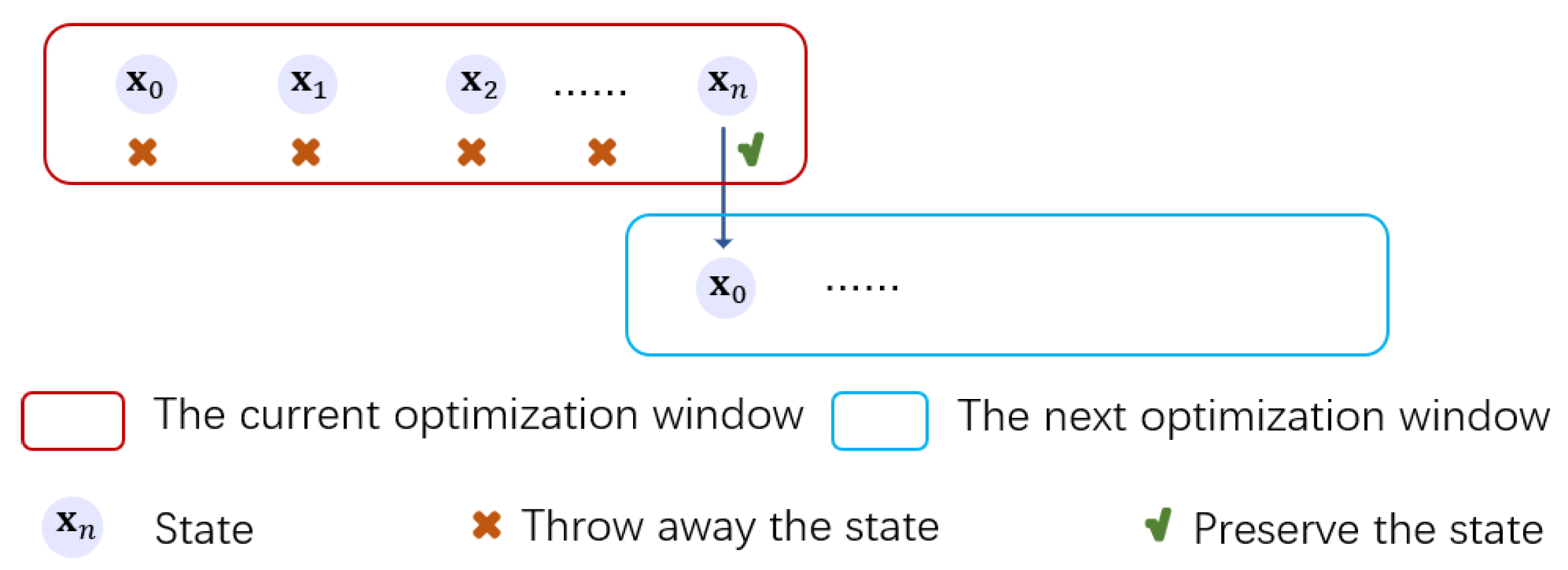
3.1. LC-LIO Factor Graph
3.2. IMU Measurement Modeling
3.3. LiDAR Scan Matching Modeling
3.4. Adaptively Weighted LiDAR-Inertial Fusion
- A monotonically decreasing function of ;
- A positive function of ;
- Decreasing rate and ranges concerning can be regulated by the control parameters and thus be employed in general scenarios.
4. Performance Upper Bound Analysis of Tightly Coupled and Loosely Coupled LiDAR-Inertial Integration
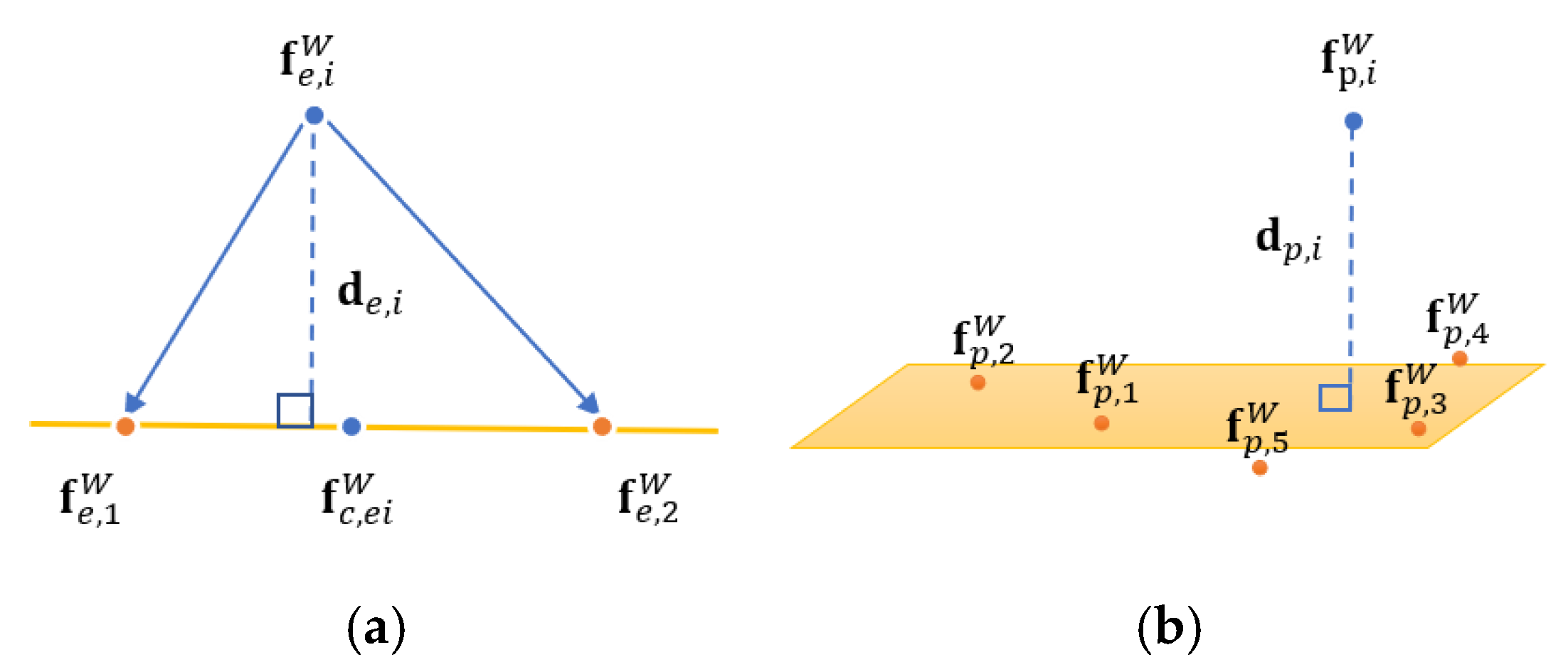
4.1. Error Propagation of LiDAR Measurement in TC-LIO
4.2. Error Propagation in LiDAR Measurement Modeling of LC-LIO
4.3. Performance Upper Bound Analysis
5. Experimental Results
5.1. Experiment Setup
5.1.1. Sensor Setups
5.1.2. Evaluation Metrics
- (1)
- LiLi-OM [16]: Tightly-coupled integration of LiDAR/inertial method.
- (2)
- LC-LIO-FC: The proposed coarse-to-fine loosely-coupled integration of LiDAR/inertial with fixed covariance.
- (3)
- LC-LIO-AC: The proposed coarse-to-fine loosely-coupled integration of LiDAR/inertial with adaptive covariance based on Equation (28).
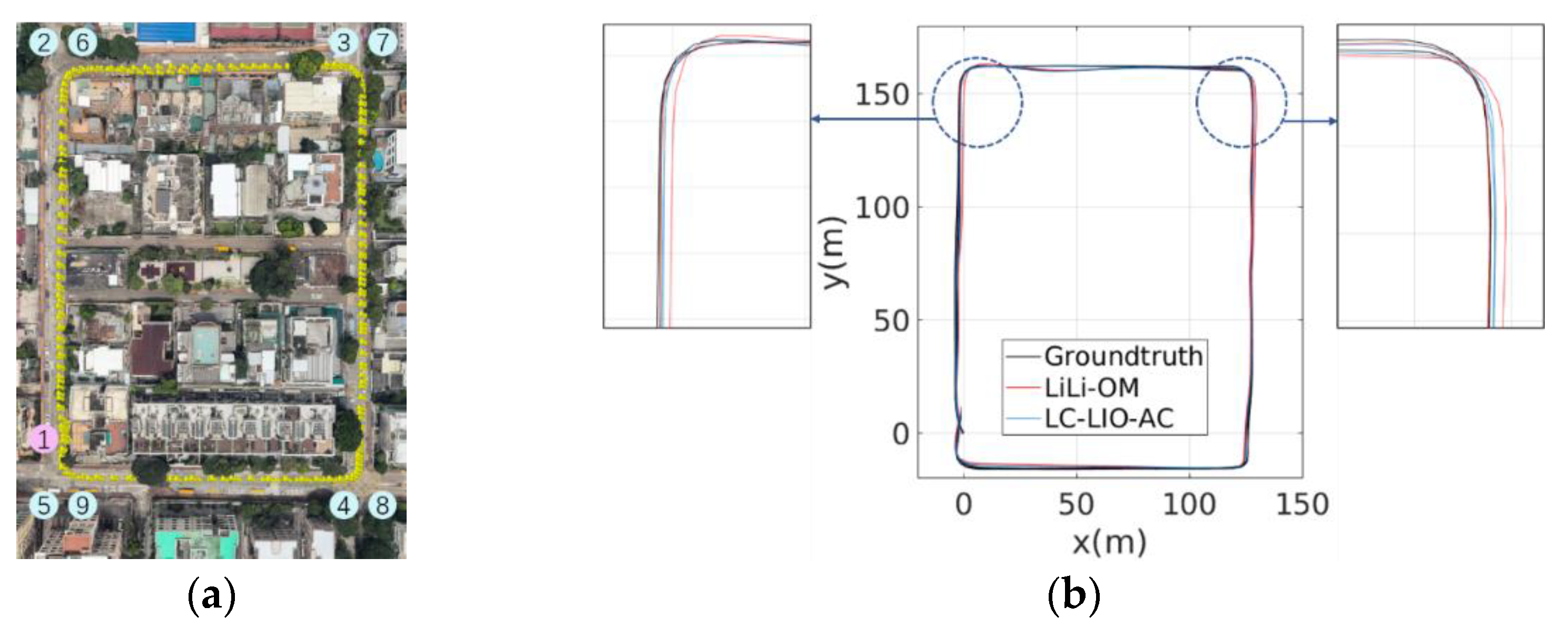
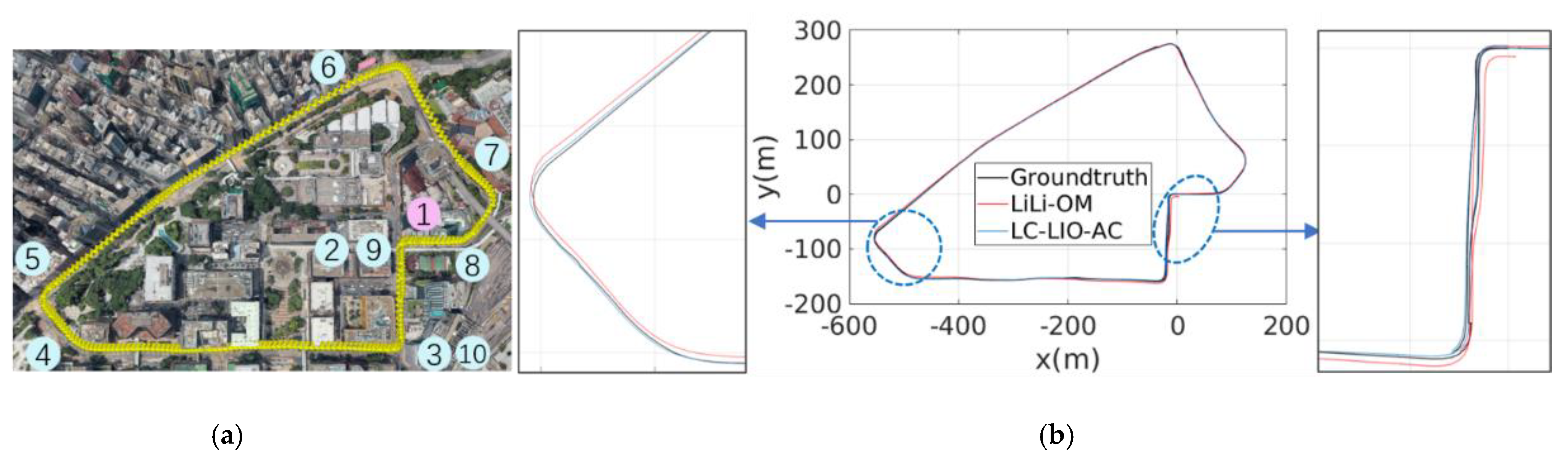
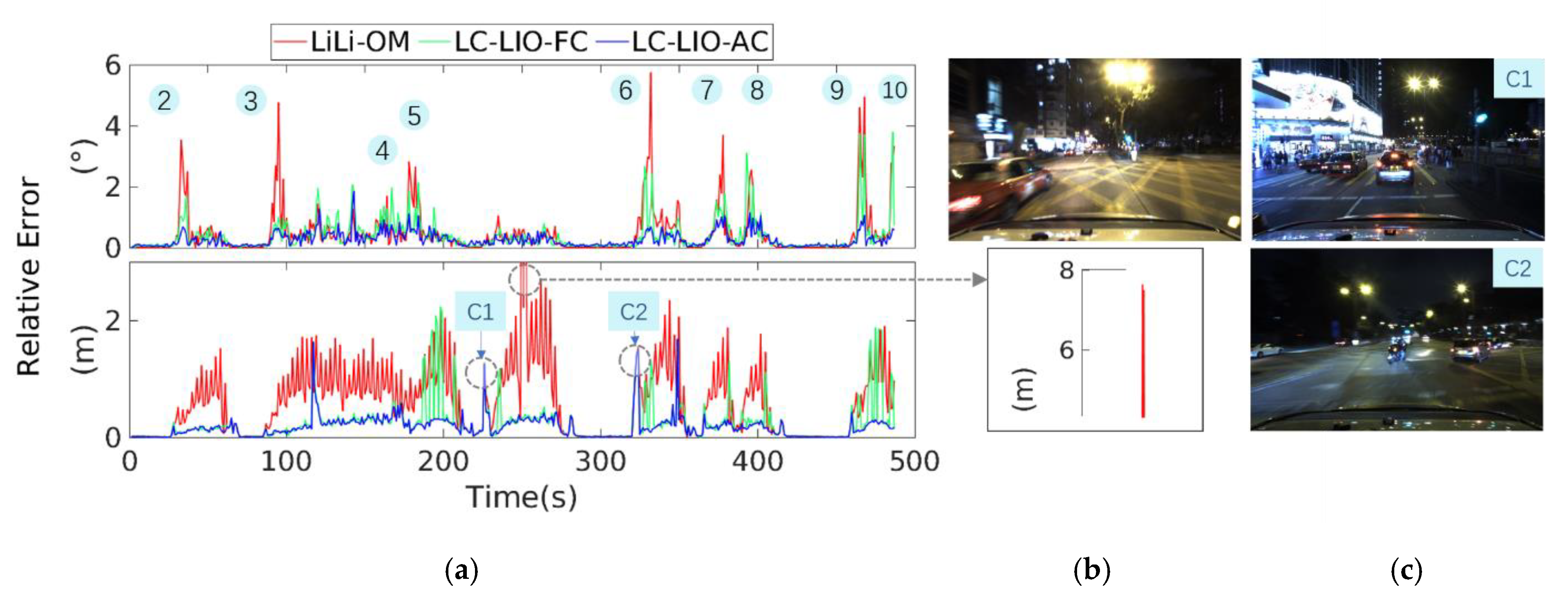
5.2. Experiments in Urban Canyon 1: The HK-Data20200314 Dataset
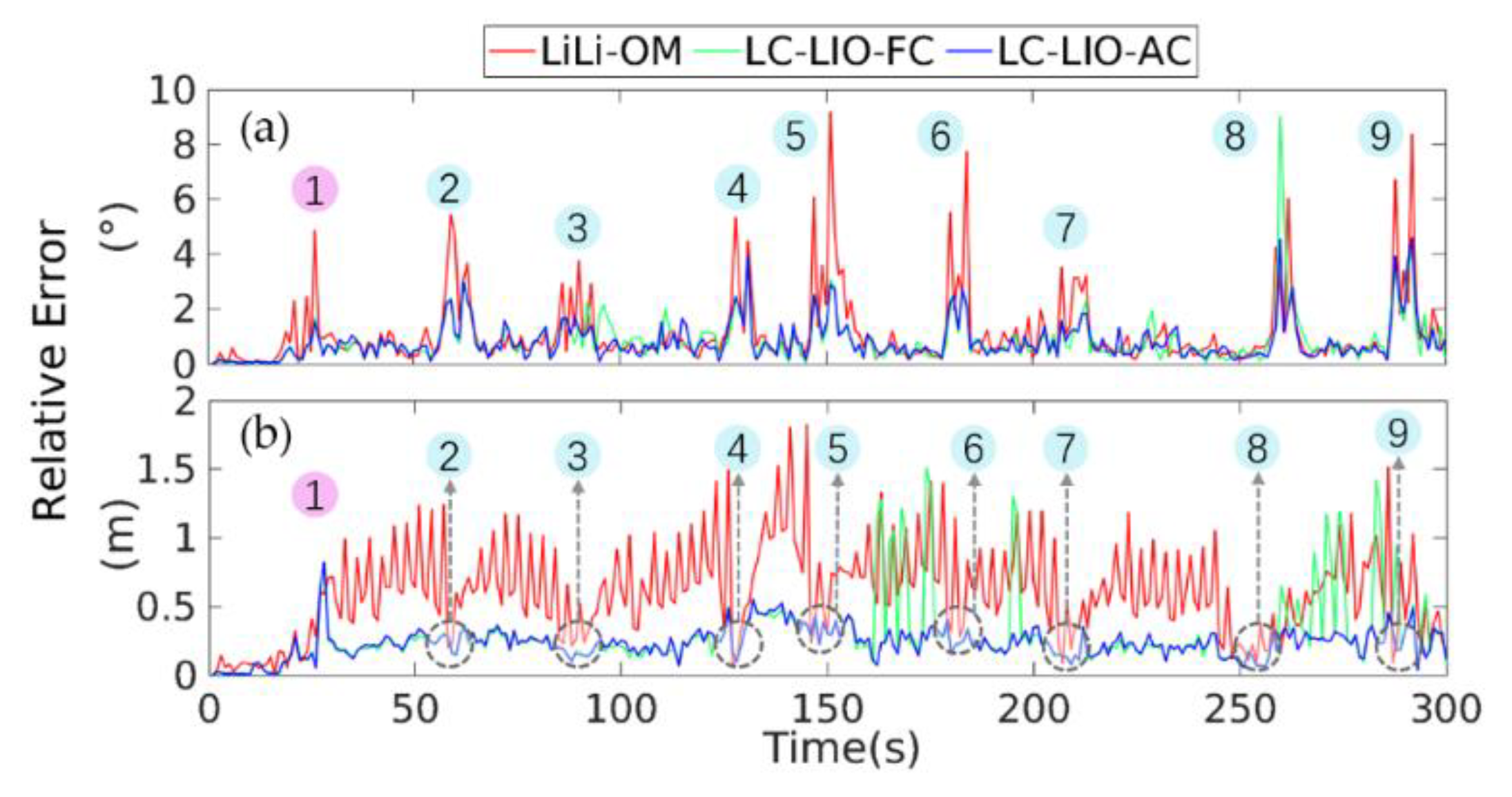
5.2.1. Performance Analysis
5.2.2. Quantitative Analysis of the Performance Upper Bound in TC-LIO and LC-LIO
5.2.3. Mapping Result
5.3. Experiments in the Urban Canyon 2: The HK-Data20190428 Dataset
5.3.1. Performance Analysis
5.3.2. Quantitative Analysis of the Performance Upper Bound in TC-LIO and LC-LIO
5.3.3. Mapping Result of the Proposed LC-LIO
6. Conclusions and Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wen, W.; Zhang, G.; Hsu, L.-T. GNSS NLOS exclusion based on dynamic object detection using LiDAR point cloud. IEEE Trans. Intell. Transp. Syst. 2019, 22, 853–862. [Google Scholar] [CrossRef]
- Breßler, J.; Reisdorf, P.; Obst, M.; Wanielik, G. GNSS positioning in non-line-of-sight context—A survey. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1147–1154. [Google Scholar]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2017, 41, 401–416. [Google Scholar] [CrossRef]
- Wen, W.; Zhou, Y.; Zhang, G.; Fahandezh-Saadi, S.; Bai, X.; Zhan, W.; Tomizuka, M.; Hsu, L.-T. Urbanloco: A full sensor suite dataset for mapping and localization in urban scenes. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 2310–2316. [Google Scholar]
- Merriaux, P.; Dupuis, Y.; Boutteau, R.; Vasseur, P.; Savatier, X. LiDAR point clouds correction acquired from a moving car based on CAN-bus data. arXiv 2017, arXiv:1706.05886. [Google Scholar]
- Wen, W.; Hsu, L.-T.; Zhang, G. Performance analysis of NDT-based graph SLAM for autonomous vehicle in diverse typical driving scenarios of Hong Kong. Sensors 2018, 18, 3928. [Google Scholar] [CrossRef]
- Thrun, S. Probabilistic robotics. Commun. ACM 2002, 45, 52–57. [Google Scholar] [CrossRef]
- Dellaert, F.; Kaess, M. Factor graphs for robot perception. Found. Trends Robot. 2017, 6, 1–139. [Google Scholar] [CrossRef]
- Qin, C.; Ye, H.; Pranata, C.E.; Han, J.; Zhang, S.; Liu, M. LINS: A Lidar-Inertial State Estimator for Robust and Efficient Navigation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8899–8906. [Google Scholar]
- Wen, W.; Pfeifer, T.; Bai, X.; Hsu, L.T. Factor Graph Optimization for GNSS/INS Integration: A Comparison with the Extended Kalman Filter. Navigation 2020, 68, 315–331, accepted. [Google Scholar]
- Ye, H.; Chen, Y.; Liu, M. Tightly coupled 3d lidar inertial odometry and mapping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 3144–3150. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. Vins-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24–30 October 2020; pp. 5135–5142. [Google Scholar]
- Kaess, M.; Ranganathan, A.; Dellaert, F. iSAM: Incremental smoothing and mapping. IEEE Trans. Robot. 2008, 24, 1365–1378. [Google Scholar] [CrossRef]
- Balsa-Barreiro, J.; Fritsch, D. Generation of visually aesthetic and detailed 3D models of historical cities by using laser scanning and digital photogrammetry. Digit. Appl. Archaeol. Cult. Herit. 2018, 8, 57–64. [Google Scholar] [CrossRef]
- Li, K.; Li, M.; Hanebeck, U.D. Towards high-performance solid-state-lidar-inertial odometry and mapping. IEEE Robot. Autom. Lett. 2021, 6, 5167–5174. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Shan, T.; Englot, B. Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 4758–4765. [Google Scholar]
- Demir, M.; Fujimura, K. Robust localization with low-mounted multiple LiDARs in urban environments. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 3288–3293. [Google Scholar]
- Tang, J.; Chen, Y.; Niu, X.; Wang, L.; Chen, L.; Liu, J.; Shi, C.; Hyyppä, J. LiDAR scan matching aided inertial navigation system in GNSS-denied environments. Sensors 2015, 15, 16710–16728. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Zhang, T.; Liu, Y.; Yan, Q. 14 Lectures on Visual SLAM: From Theory to Practice; Publishing House of Electronics Industry: Beijing, China, 2017; pp. 236–241. [Google Scholar]
- Huai, Z.; Huang, G. Robocentric visual-inertial odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 6319–6326. [Google Scholar]
- Barfoot, T.D. State Estimation for Robotics; Cambridge University Press: Cambridge, UK, 2017; pp. 205–284. [Google Scholar] [CrossRef]
- Sola, J. Quaternion kinematics for the error-state Kalman filter. arXiv 2017, arXiv:1711.02508. [Google Scholar]
- Qin, T.; Cao, S.; Pan, J.; Shen, S. A general optimization-based framework for global pose estimation with multiple sensors. arXiv 2019, arXiv:1901.03642. [Google Scholar]
- Zhang, Z. Parameter estimation techniques: A tutorial with application to conic fitting. Image Vis. Comput. 1997, 15, 59–76. [Google Scholar] [CrossRef]
- Hu, G.; Khosoussi, K.; Huang, S. Towards a reliable SLAM back-end. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 37–43. [Google Scholar]
- Agarwal, S.; Mierle, K. Ceres Solver. Available online: http://ceres-solver.org (accessed on 6 January 2021).
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual—Inertial Odometry. IEEE Trans. Robot. 2016, 33, 1–21. [Google Scholar] [CrossRef]
- Lupton, T.; Sukkarieh, S. Visual-inertial-aided navigation for high-dynamic motion in built environments without initial conditions. IEEE Trans. Robot. 2011, 28, 61–76. [Google Scholar] [CrossRef]
- Balsa Barreiro, J.; Avariento Vicent, J.P.; Lerma García, J.L. Airborne light detection and ranging (LiDAR) point density analysis. Sci. Res. Essays 2012, 7, 3010–3019. [Google Scholar] [CrossRef]
- Balsa-Barreiro, J.; Lerma, J.L. Empirical study of variation in lidar point density over different land covers. Int. J. Remote Sens. 2014, 35, 3372–3383. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, F. Loam livox: A fast, robust, high-precision LiDAR odometry and mapping package for LiDARs of small FoV. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 3126–3131. [Google Scholar]
- Zhang, J.; Singh, S. Laser–visual–inertial odometry and mapping with high robustness and low drift. J. Field Robot. 2018, 35, 1242–1264. [Google Scholar] [CrossRef]
- Zhang, J.; Kaess, M.; Singh, S. On degeneracy of optimization-based state estimation problems. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 809–816. [Google Scholar]
- Zhang, J.; Singh, S. Visual-lidar odometry and mapping: Low-drift, robust, and fast. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2174–2181. [Google Scholar]
- Hsu, L.-T.; Kubo, N.; Chen, W.; Liu, Z.; Suzuki, T.; Meguro, J. UrbanNav:An open-sourced multisensory dataset for benchmarking positioning algorithms designed for urban areas (Accepted). In Proceedings of the ION GNSS+ 2021, Miami, FL, USA, 20–24 September 2021. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. ICRA Workshop Open Source Softw. 2009, 3, 5. [Google Scholar]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and SLAM. Available online: https://github.com/MichaelGrupp/evo (accessed on 1 March 2021).
- Zhang, Z.; Scaramuzza, D. A tutorial on quantitative trajectory evaluation for visual (-inertial) odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7244–7251. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1991; pp. 586–606. [Google Scholar]
- Wen, W.; Hsu, L.-T. 3D LiDAR Aided GNSS and Its Tightly Coupled Integration with INS Via Factor Graph Optimization. In Proceedings of the ION GNSS+ 2020, Richmond Heights, MO, USA, 22–25 September 2020. [Google Scholar]
- Wen, W.; Zhang, G.; Hsu, L.-T. Exclusion of GNSS NLOS receptions caused by dynamic objects in heavy traffic urban scenarios using real-time 3D point cloud: An approach without 3D maps. In Proceedings of the Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 158–165. [Google Scholar]
- Wen, W.; Zhang, G.; Hsu, L.T. Correcting NLOS by 3D LiDAR and building height to improve GNSS single point positioning. Navigation 2019, 66, 705–718. [Google Scholar] [CrossRef]







| Dataset | Method | Relative Rotation Error (°) | Relative Translation Error (m) | ||
|---|---|---|---|---|---|
| Mean Value | RMSE | Mean Value | RMSE | ||
| Urban Canyon 1 (HK-Data20200314) | LiLI-OM | 1.133 | 1.762 | 0.605 | 0.693 |
| LC-LIO-FC | 0.885 | 1.249 | 0.271 | 0.348 | |
| LC-LIO-AC | 0.800 | 1.115 | 0.233 | 0.262 | |
| Dataset | Method | Relative Rotation Error (°) | Relative Translation Error (m) | ||
|---|---|---|---|---|---|
| Mean Value | RMSE | Mean Value | RMSE | ||
| Urban Canyon 2 (HK-Data20190428) | LiLi-OM | 0.458 | 0.878 | 0.609 | 0.891 |
| LC-LIO-FC | 0.421 | 0.671 | 0.249 | 0.431 | |
| LC-LIO-AC | 0.331 | 0.478 | 0.182 | 0.267 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wen, W.; Huang, F.; Chen, X.; Hsu, L.-T. Coarse-to-Fine Loosely-Coupled LiDAR-Inertial Odometry for Urban Positioning and Mapping. Remote Sens. 2021, 13, 2371. https://doi.org/10.3390/rs13122371
Zhang J, Wen W, Huang F, Chen X, Hsu L-T. Coarse-to-Fine Loosely-Coupled LiDAR-Inertial Odometry for Urban Positioning and Mapping. Remote Sensing. 2021; 13(12):2371. https://doi.org/10.3390/rs13122371
Chicago/Turabian StyleZhang, Jiachen, Weisong Wen, Feng Huang, Xiaodong Chen, and Li-Ta Hsu. 2021. "Coarse-to-Fine Loosely-Coupled LiDAR-Inertial Odometry for Urban Positioning and Mapping" Remote Sensing 13, no. 12: 2371. https://doi.org/10.3390/rs13122371
APA StyleZhang, J., Wen, W., Huang, F., Chen, X., & Hsu, L.-T. (2021). Coarse-to-Fine Loosely-Coupled LiDAR-Inertial Odometry for Urban Positioning and Mapping. Remote Sensing, 13(12), 2371. https://doi.org/10.3390/rs13122371