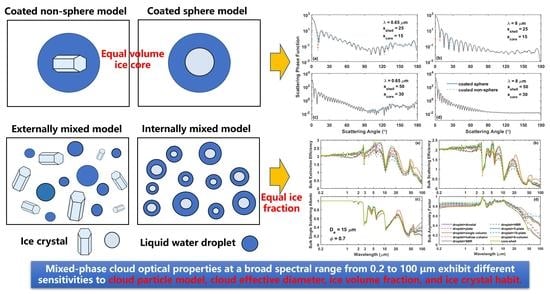
Sensitivity of Mixed-Phase Cloud Optical Properties to Cloud Particle Model and Microphysical Factors at Wavelengths from 0.2 to 100 µm
Abstract
1. Introduction
2. Models and Methods
2.1. Particle Size Distributions
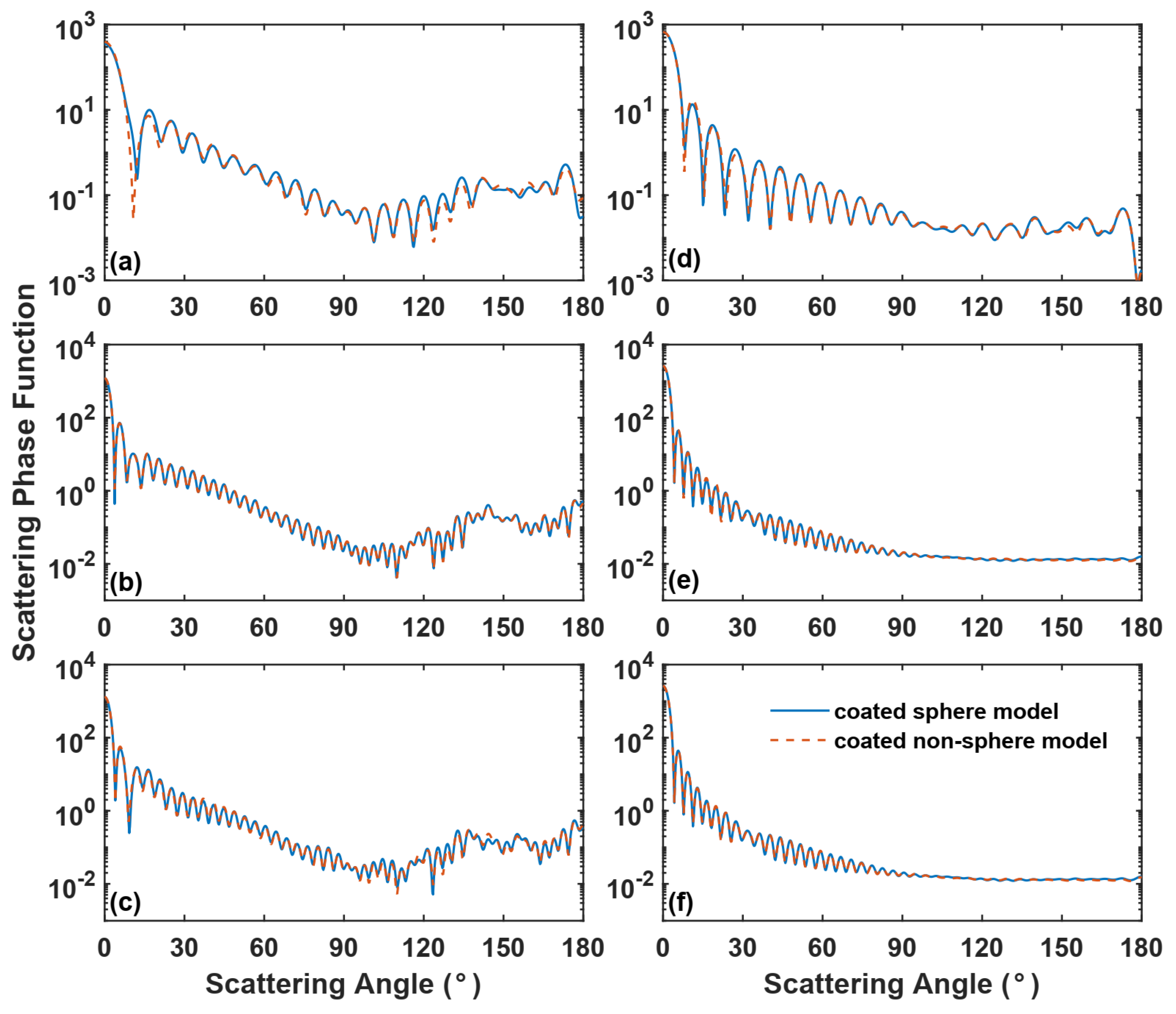
2.2. Mixed-Phase Cloud Particle Models
2.3. Formulation of Optical Properties
3. Results and Discussions
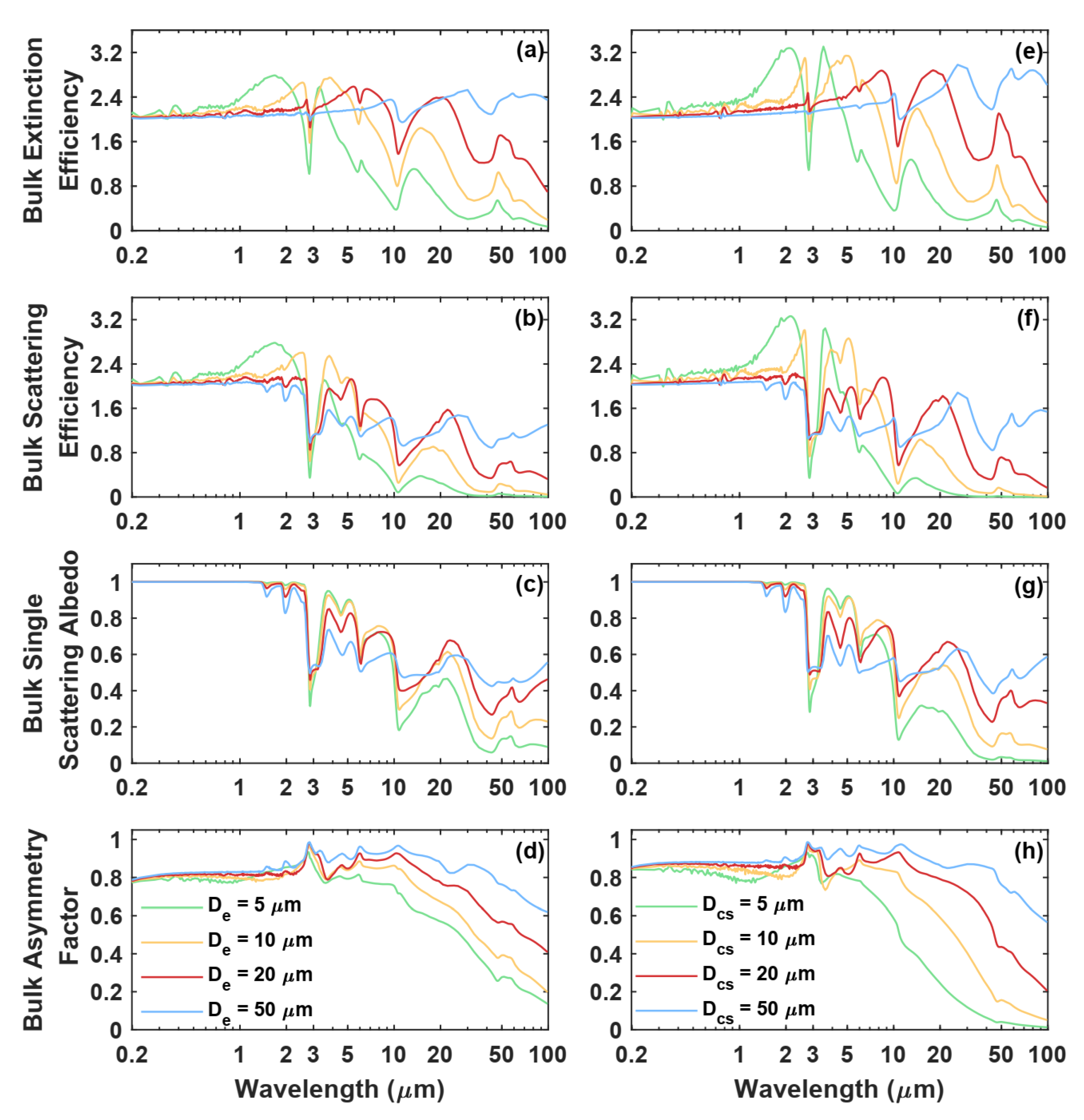
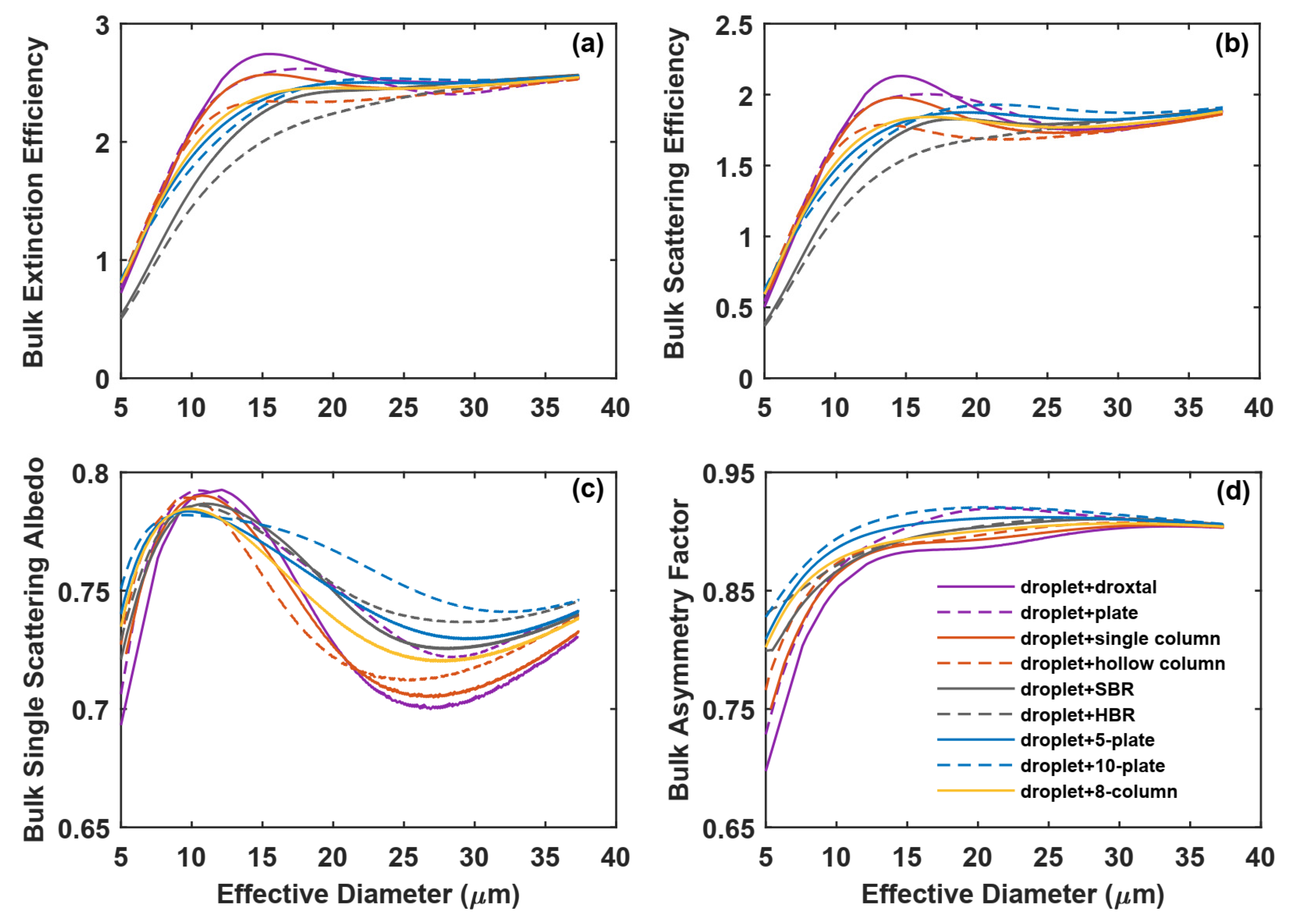
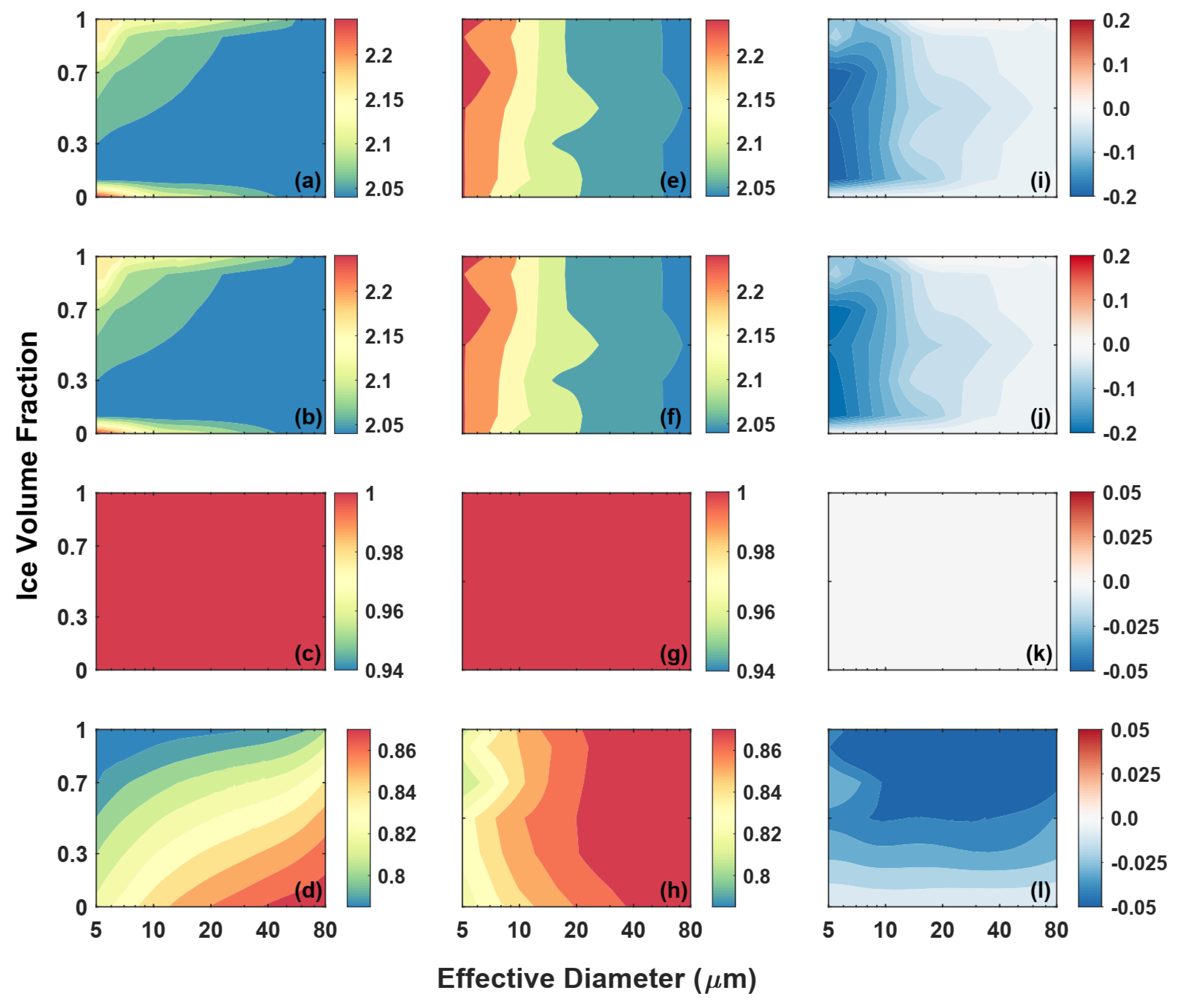
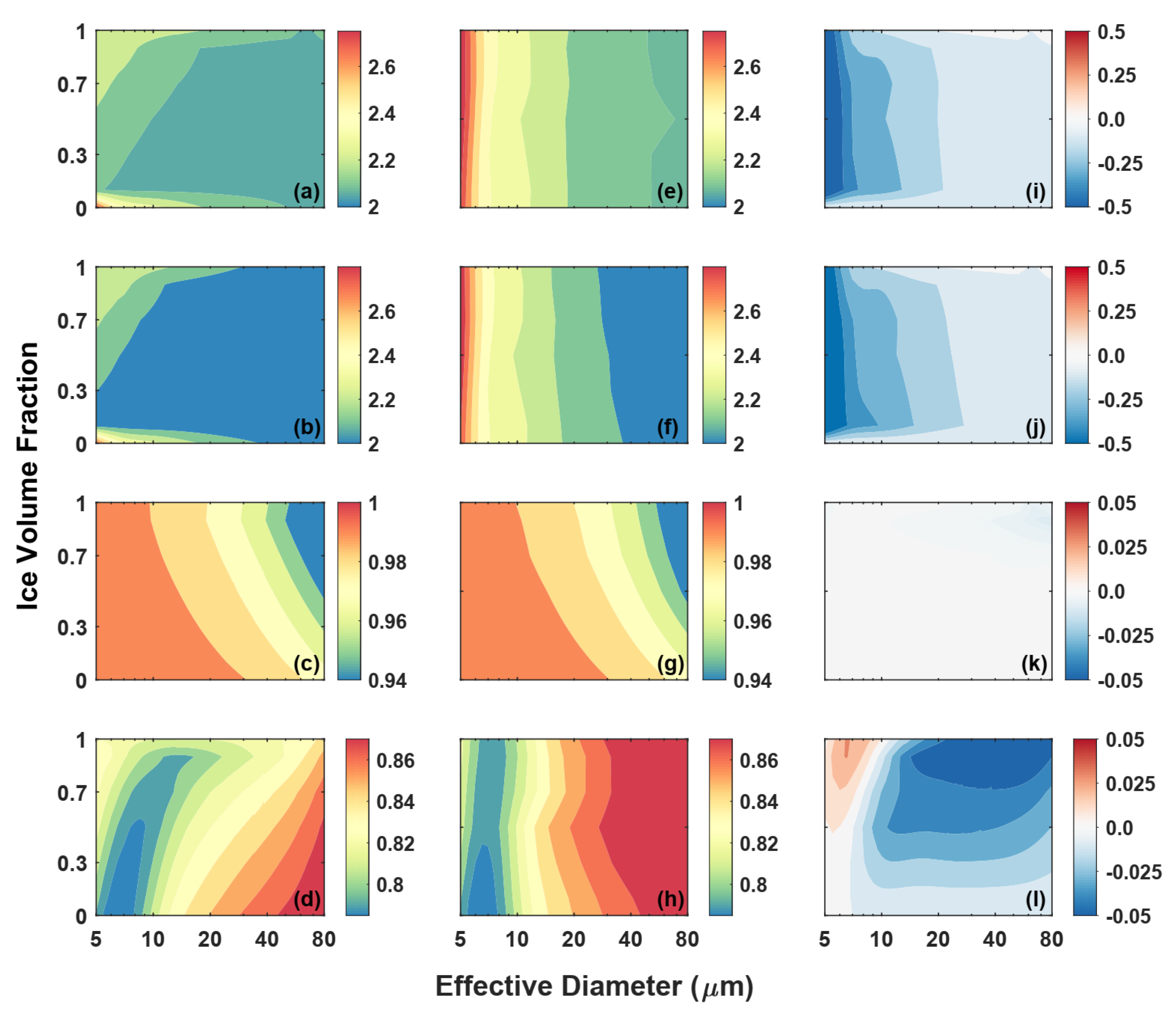
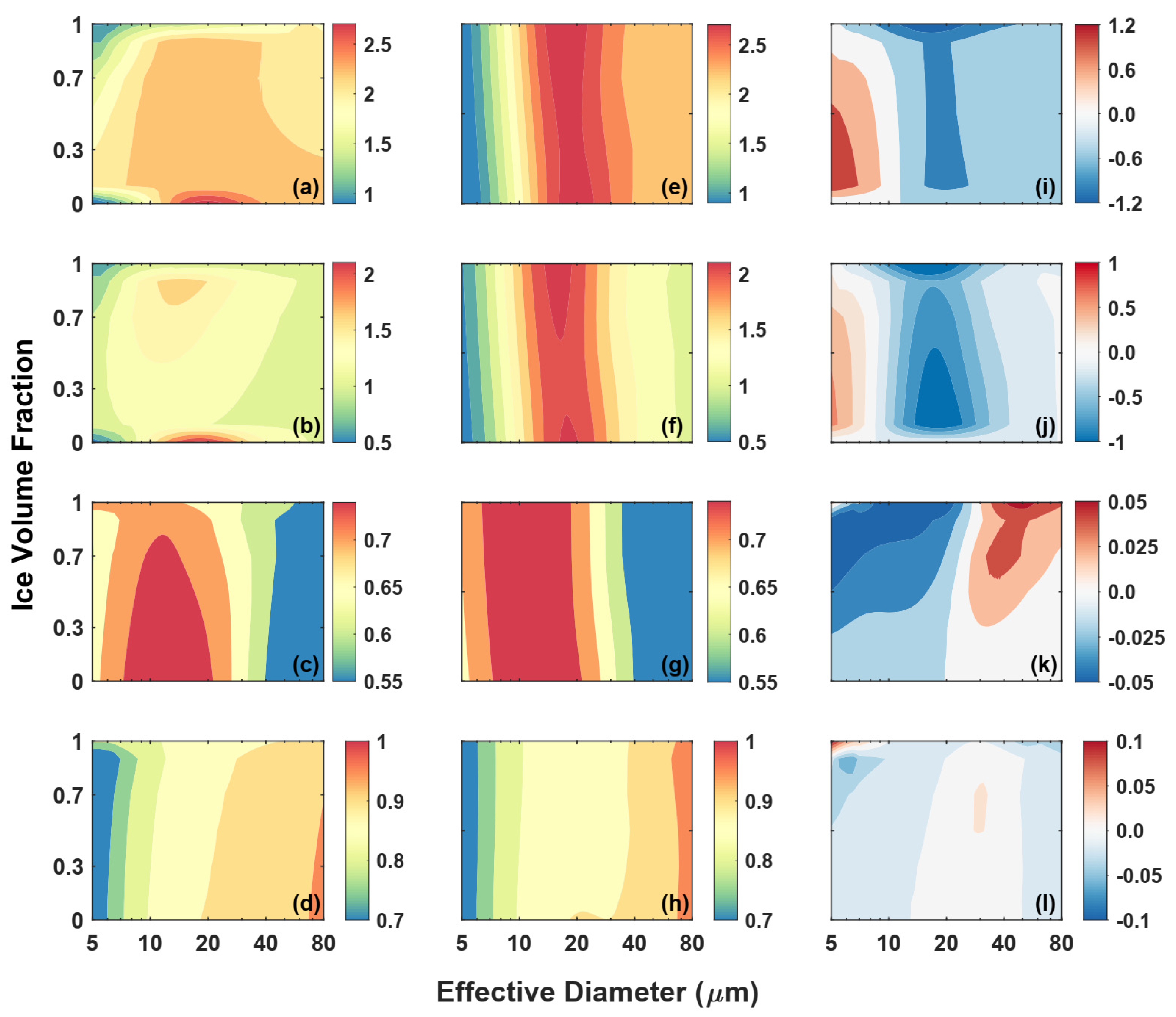
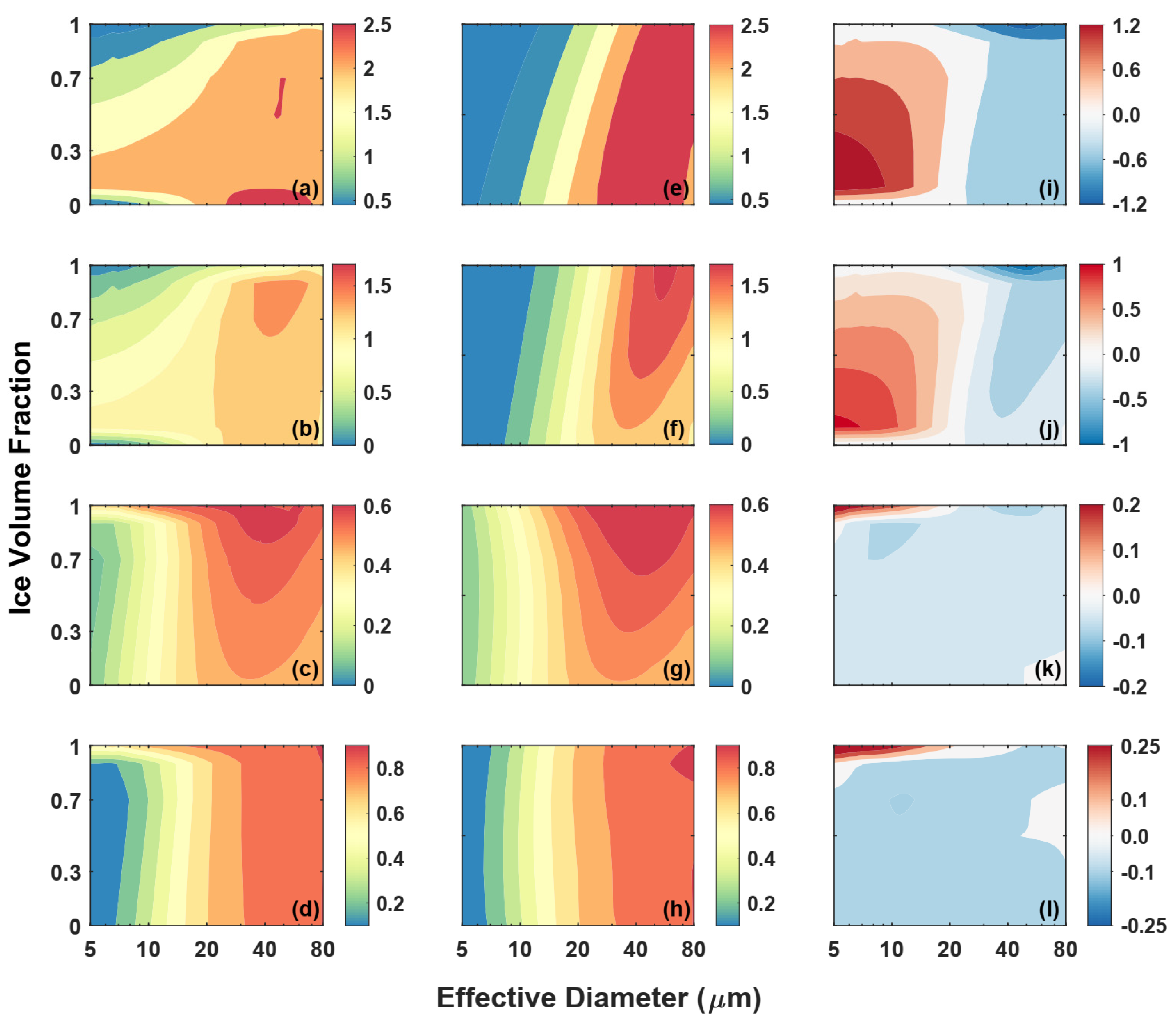
3.1. Effective Diameter
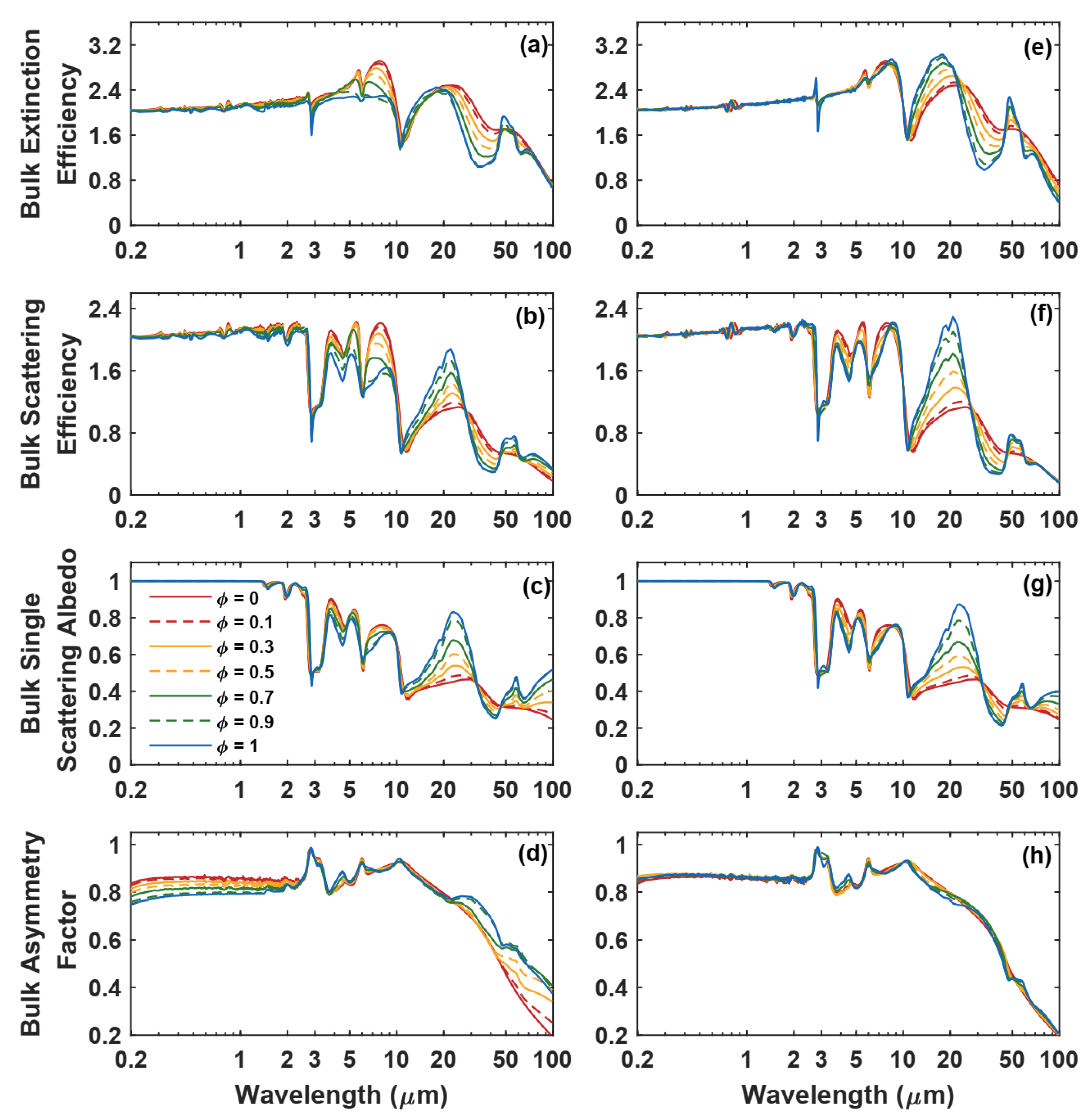
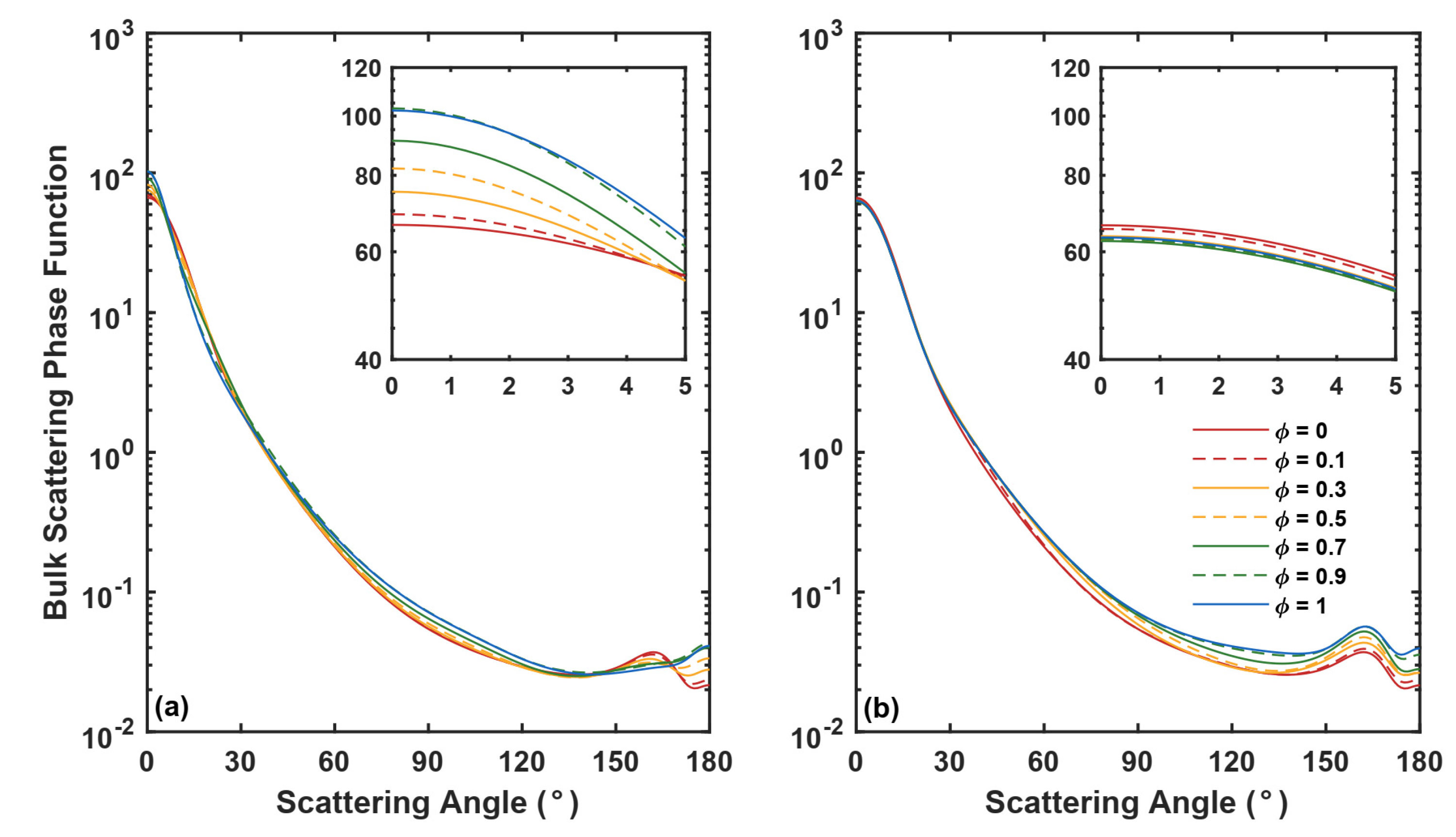
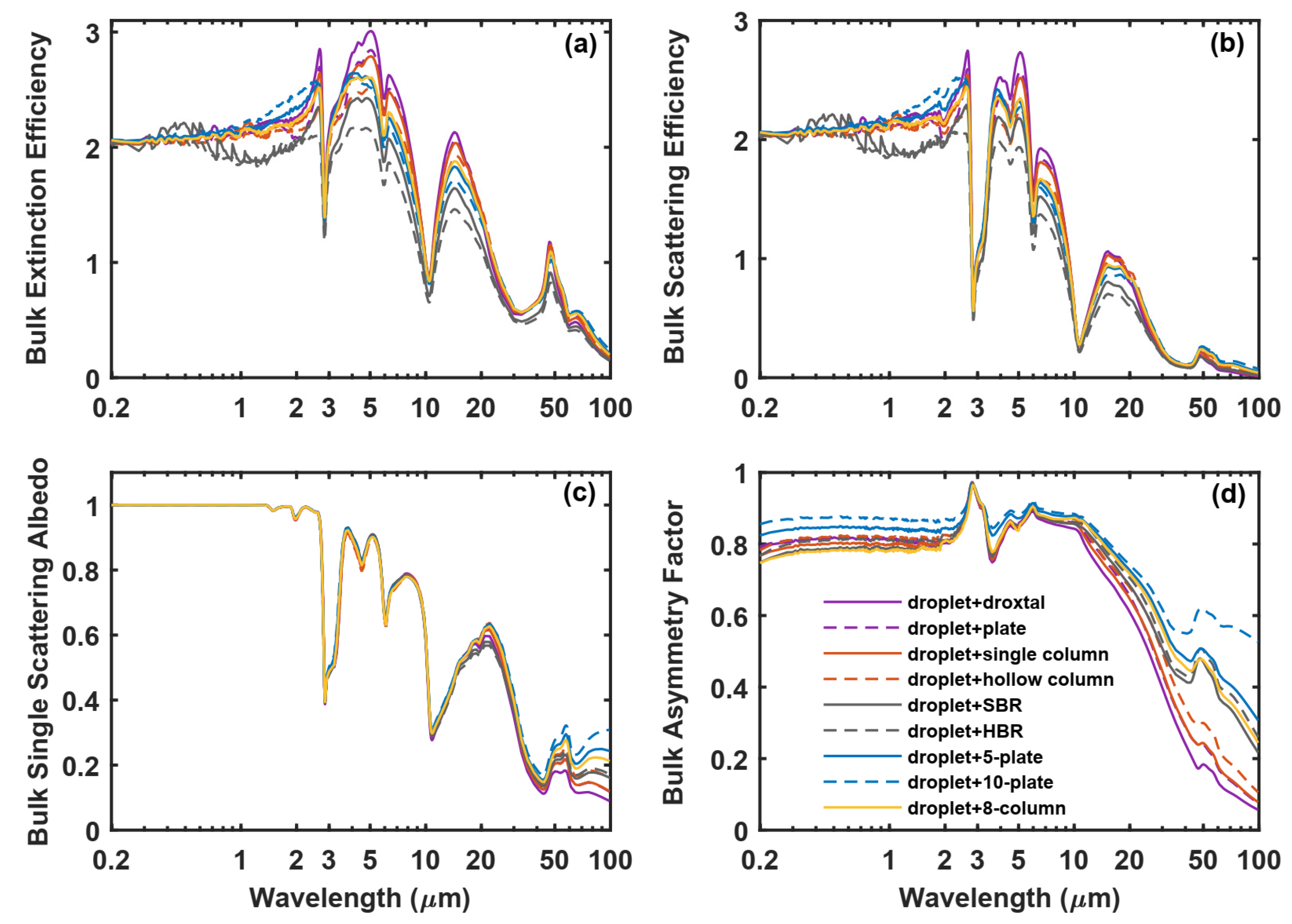
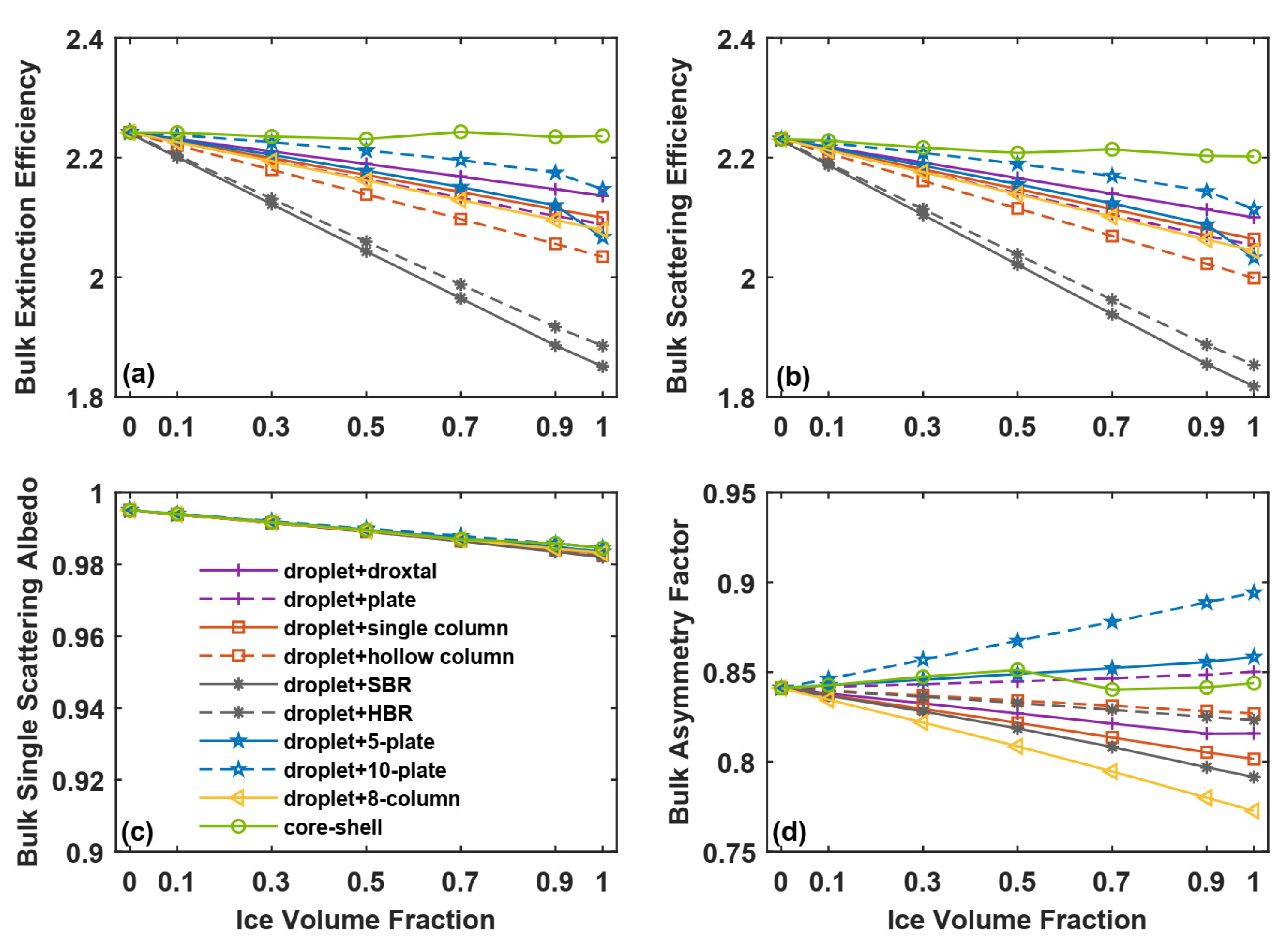
3.2. Ice Volume Fraction
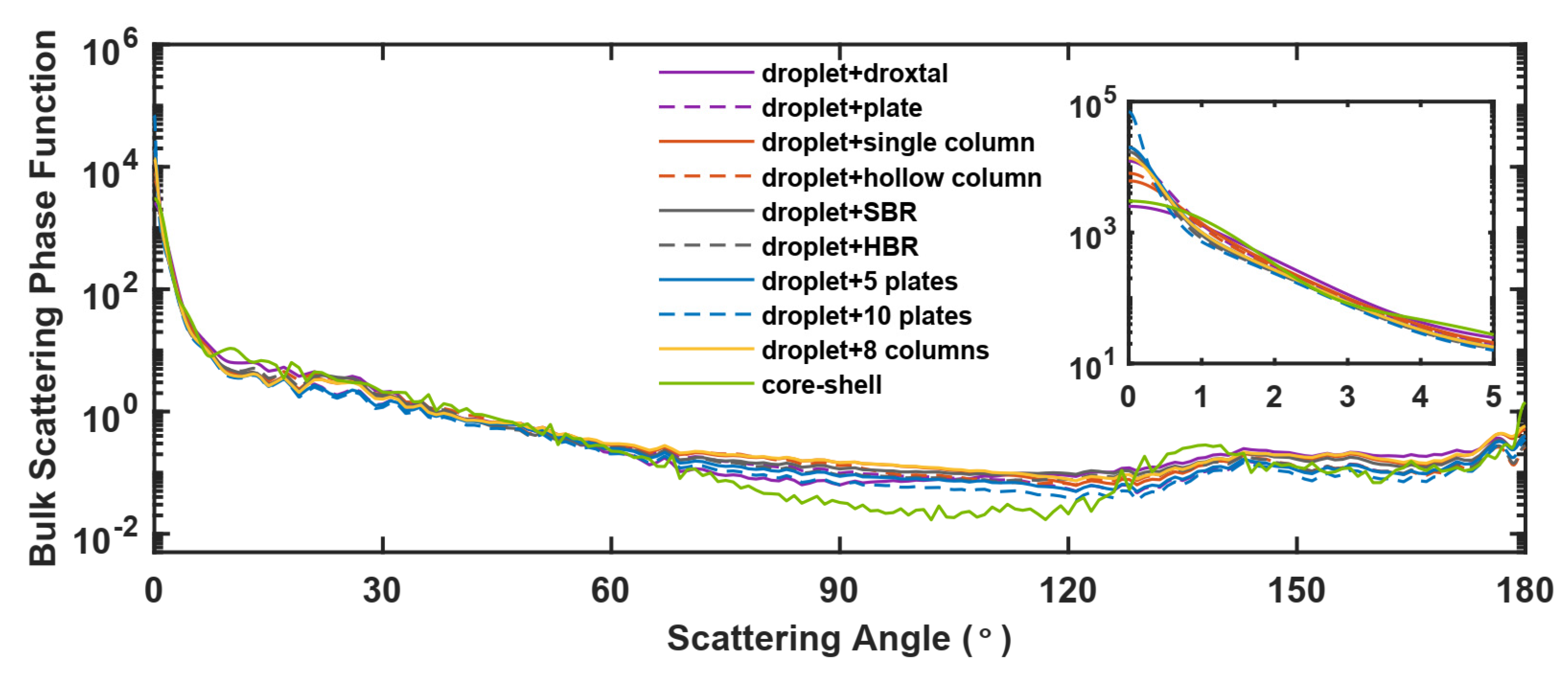
3.3. Shapes of Ice Crystals
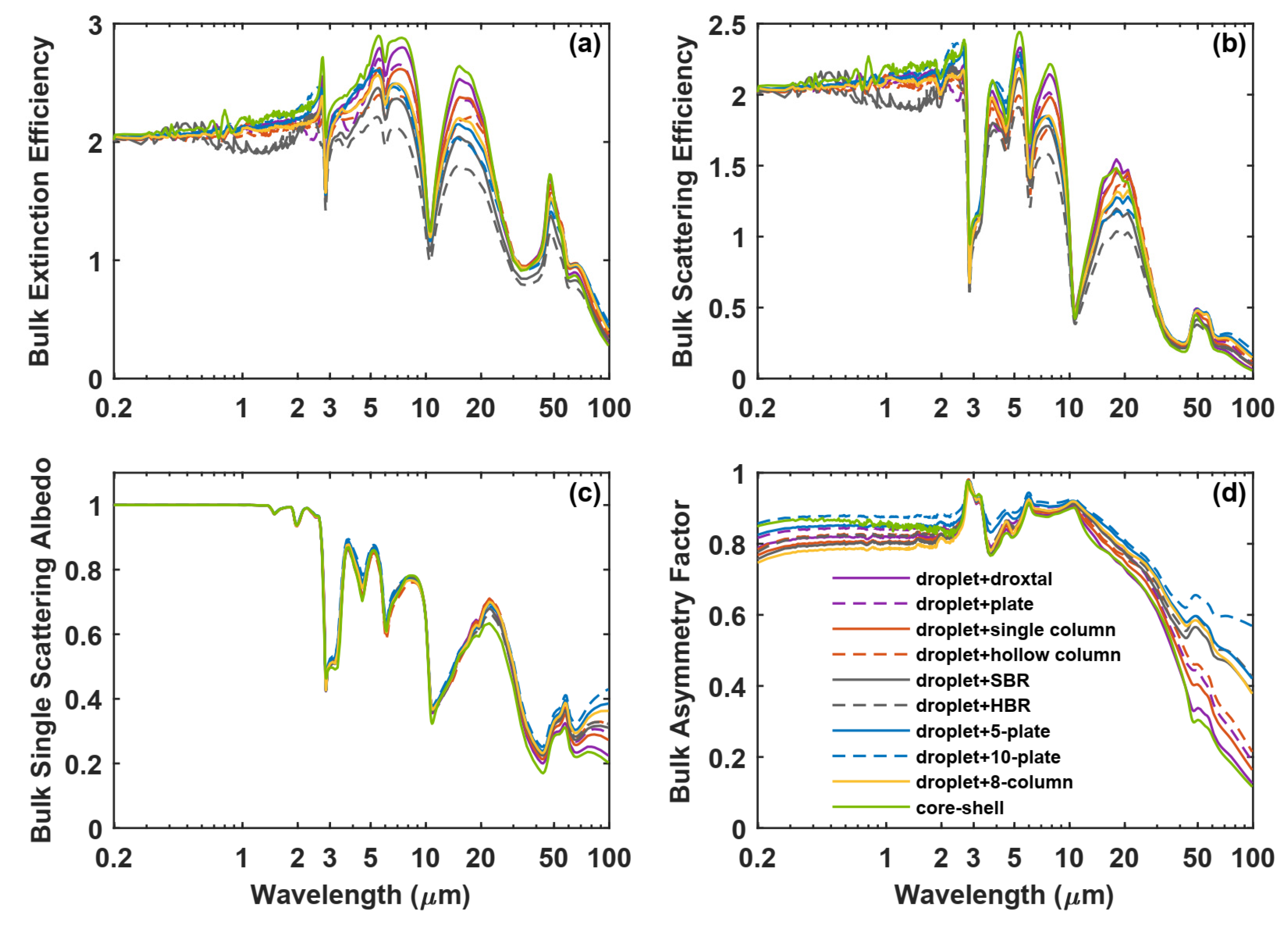
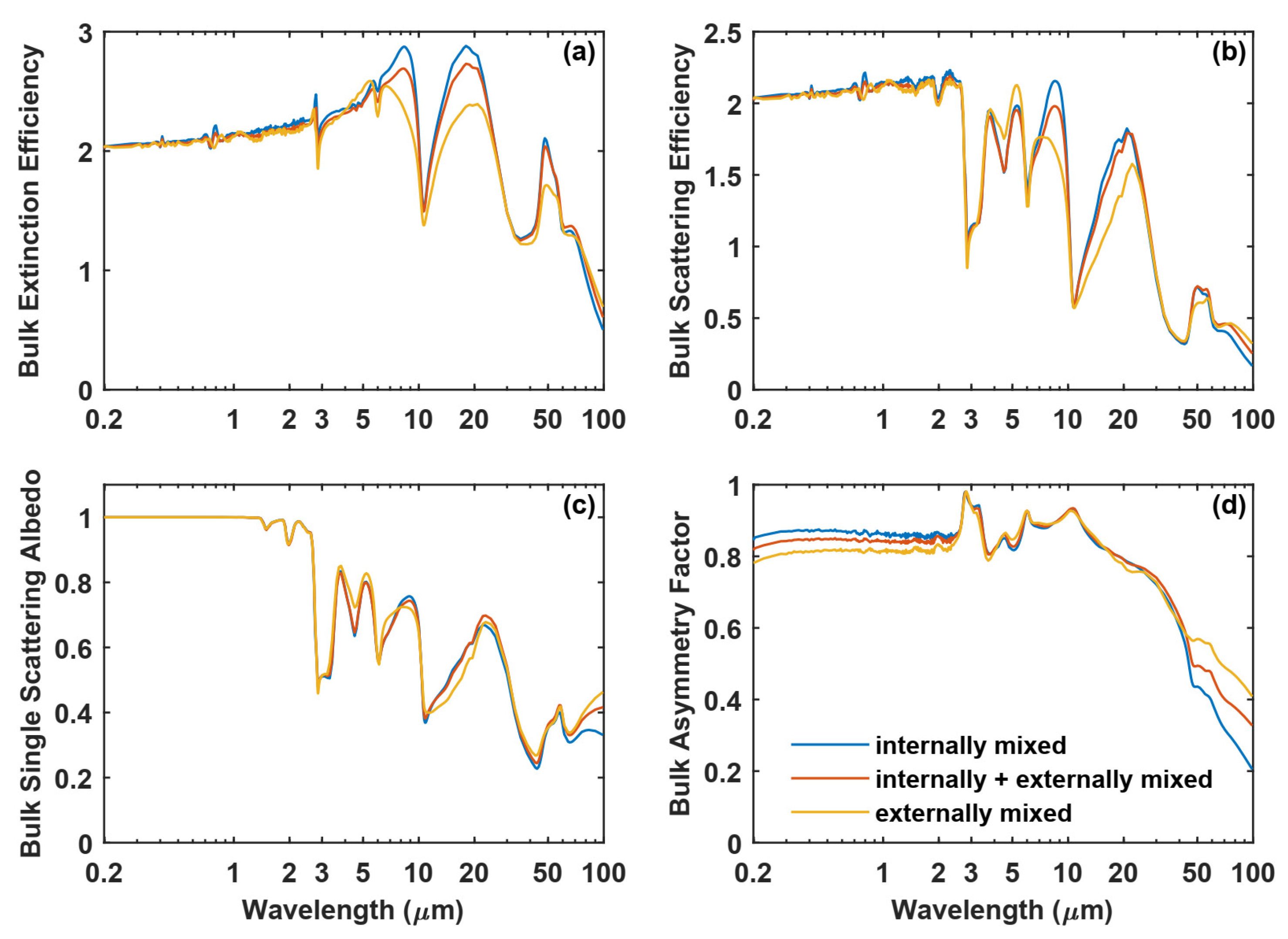
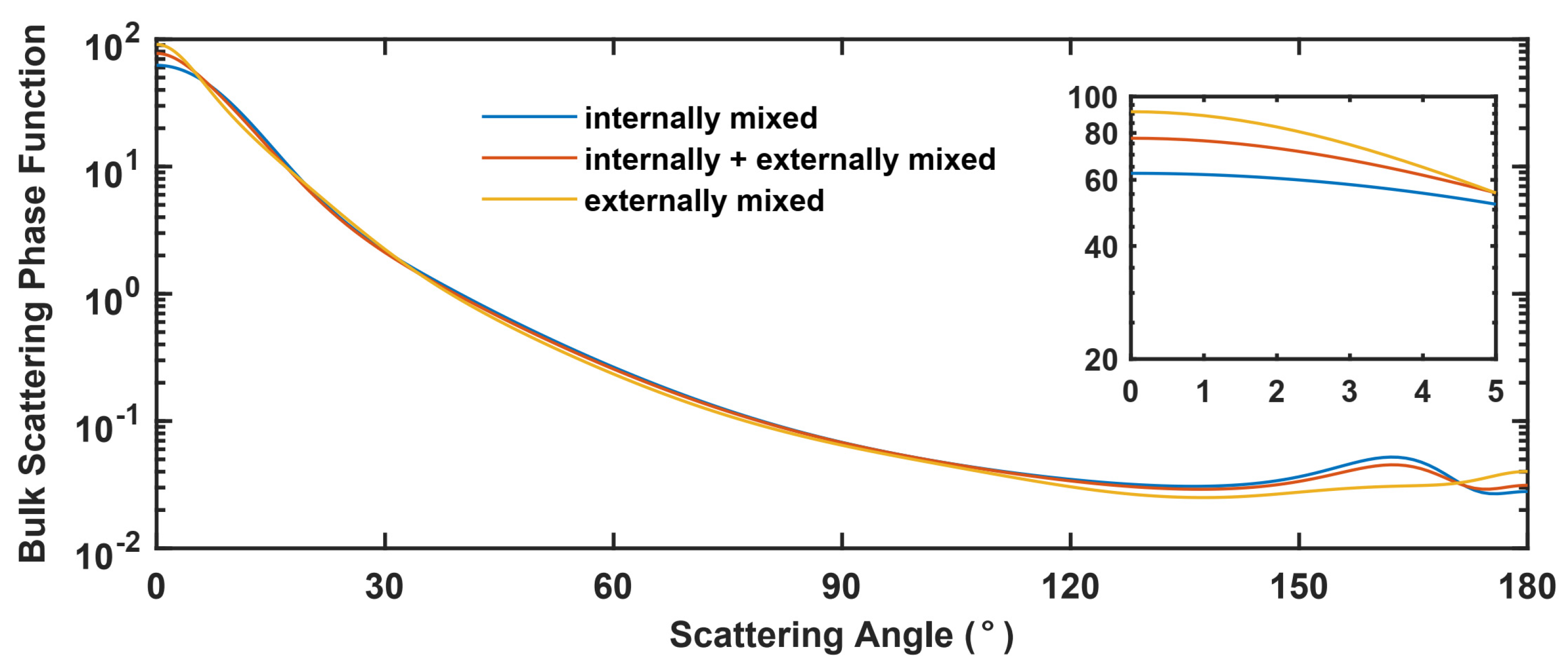
3.4. Mixture Models
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Ramanathan, V.; Cess, R.D.; Harrison, E.F.; Minnis, P.; Barkstrom, B.R.; Ahmad, E.; Hartmann, D. Cloud-Radiative Forcing and Climate: Results from the Earth Radiation Budget Experiment. Science 1989, 243, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J.F.B.; Senior, C.A.; Ingram, W.J. CO2 and Climate: A Missing Feedback? Nature 1989, 341, 132–134. [Google Scholar] [CrossRef]
- Ebert, E.E.; Curry, J.A. A Parameterization of Ice Cloud Optical Properties for Climate Models. J. Geophys. Res. Atmos. 1992, 97, 3831–3836. [Google Scholar] [CrossRef]
- McCoy, D.T.; Hartmann, D.L.; Grosvenor, D.P. Observed Southern Ocean Cloud Properties and Shortwave Reflection. Part I: Calculation of SW Flux from Observed Cloud Properties. J. Clim. 2014, 27, 8836–8857. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, X.; Liu, Y.; Lu, J. Comparison of Mixed-phase Clouds over the Arctic and the Tibetan Plateau: Seasonality and Vertical Structure of Cloud Radiative Effects. Clim. Dyn. 2020, 54, 4811–4822. [Google Scholar] [CrossRef]
- Morrison, H.; Pinto, J. Intercomparison of Bulk Cloud Microphysics Schemes in Mesoscale Simulations of Springtime Arctic Mixed-Phase Stratiform Clouds. Mon. Wea. Rev. 2006, 134, 1880–1900. [Google Scholar] [CrossRef]
- Barrett, A.I.; Hogan, R.J.; Forbes, R.M. Why are Mixed-phase Altocumulus Clouds Poorly Predicted by Large-scale Models? Part 1. Physical processes. J. Geophys. Res. Atmos. 2017, 122, 9903–9926. [Google Scholar] [CrossRef]
- Korolev, A.; McFarquhar, G.; Field, P.R.; Franklin, C.; Lawson, P.; Wang, Z.; Borrmann, S. Mixed-phase Clouds: Progress and Challenges. Herpetol. Monographs 2017, 58, 5. [Google Scholar] [CrossRef]
- Sun, Z.; Shine, K.P. Studies of the Radiative Properties of Ice and Mixed-Phase Clouds. Q. J. R. Meteorol. Soc. 1994, 120, 111–137. [Google Scholar] [CrossRef]
- McFarquhar, G.M.; Cober, S.G. Single-Scattering Properties of Mixed-Phase Arctic Clouds at Solar Wavelengths: Impacts on Radiative Transfer. J. Clim. 2004, 17, 3799–3813. [Google Scholar] [CrossRef]
- Korolev, A.V.; Isaac, G.A.; Cober, S.G.; Strapp, J.W.; Hallett, J. Microphysical Characterization of Mixed-phase Clouds. Q. J. R. Meteorol. Soc. 2003, 129, 39–65. [Google Scholar] [CrossRef]
- Shupe, M.D.; Daniel, J.S.; De Boer, G.; Eloranta, E.W.; Kollias, P.; Long, C.N.; Luke, E.P.; Turner, D.D.; Verlinde, J. A Focus on Mixed-Phase Clouds: The Status of Ground-Based Observational Methods. Bull. Am. Meteorol. Soc. 2008, 89, 1549–1562. [Google Scholar] [CrossRef]
- de Boer, G.; Eloranta, E.W.; Shupe, M.D. Arctic Mixed-Phase Stratiform Cloud Properties from Multiple Years of Surface-Based Measurements at Two High-Latitude Locations. J. Atmos. Sci. 2009, 66, 2874–2887. [Google Scholar] [CrossRef]
- D’Alessandro, J.J.; Diao, M.; Wu, C.; Liu, X.; Jensen, J.B.; Stephens, B.B. Cloud Phase and Relative Humidity Distributions over the Southern Ocean in Austral Summer Based on In Situ Observations and CAM5 Simulations. J. Clim. 2019, 32, 2781–2805. [Google Scholar] [CrossRef]
- Sassen, K. Evidence for Liquid-Phase Cirrus Cloud Formation from Volcanic Aerosols: Climatic Implications. Science 1992, 257, 516–519. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Shine, K.P. Parameterization of Ice Cloud Radiative Properties and Its Application to the Potential Climatic Importance of Mixed-Phase Clouds. J. Clim. 1995, 8, 1874–1888. [Google Scholar] [CrossRef]
- Cober, S.G.; Isaac, G.A.; Korolev, A.V.; Strapp, J.W. Assessing Cloud-Phase Conditions. J. Appl. Meteorol. Climatol. 2001, 40, 1967–1983. [Google Scholar] [CrossRef]
- Vidaurre, G.; Hallett, J. Ice and Water Content of Stratiform Mixed-phase Cloud. Q. J. R. Meteorol. Soc. 2010, 135, 1292–1306. [Google Scholar] [CrossRef]
- Shupe, M.D.; Uttal, T.; Matrosov, S.Y.; Frisch, A.S. Cloud water contents and hydrometeor sizes during the FIRE Arctic Clouds Experiment. J. Geophys. Res. Atmos. 2001, 106, 15015–15028. [Google Scholar] [CrossRef]
- Lee, J.; Yang, P.; Dessler, A.E.; Baum, B.A.; Platnick, S. The Influence of Thermodynamic Phase on the Retrieval of Mixed-Phase Cloud Microphysical and Optical Properties in the Visible and near-Infrared Region. IEEE Geosci. Remote. Sens. Lett. 2006, 3, 287–291. [Google Scholar] [CrossRef]
- Sassen, K.; Khvorostyanov, V.I. Microphysical and Radiative Properties of Mixed-Phase Altocumulus: A Model Evaluation of Glaciation Effects. Atmos. Res. 2007, 84, 390–398. [Google Scholar] [CrossRef]
- Tan, I.; Storelvmo, T.; Zelinka, M.D. Observational Constraints on Mixed-Phase Clouds Imply Higher Climate Sensitivity. Science 2016, 352, 224–227. [Google Scholar] [CrossRef]
- Yang, P.; Wei, H.L.; Baum, B.A.; Huang, H.L.; Heymsfield, A.J.; Hu, Y.X.; Turner, D.D. The Spectral Signature of Mixed-Phase Clouds Composed of Non-Spherical Ice Crystals and Spherical Liquid Droplets in the Terrestrial Window Region. J. Quant. Spectrosc. Radiat. Transf. 2003, 79, 1171–1188. [Google Scholar] [CrossRef]
- Sikand, M.; Koskulics, J.; Stamnes, K.; Hamre, B.; Stamnes, J.J.; Lawson, R.P. Estimation of Mixed-Phase Cloud Optical Depth and Position Using In Situ Radiation and Cloud Microphysical Measurements Obtained from a Tethered-Balloon Platform. J. Atmos. Sci. 2013, 70, 317–329. [Google Scholar] [CrossRef]
- Ehrlich, A.; Wendisch, M.; Bierwirth, E.; Herber, A.; Schwarzenböck, A. Ice crystal shape effects on solar radiative properties of Arctic mixed-phase clouds—Dependence on microphysical properties. Atmos. Res. 2008, 88, 266–276. [Google Scholar] [CrossRef]
- Harrington, J.Y.; Olsson, P.Q. A Method for the Parameterization of Cloud Optical Properties in Bulk and Bin Microphysical Models. Implications for Arctic Cloudy Boundary Layers. Atmos. Res. 2001, 57, 51–80. [Google Scholar] [CrossRef]
- Ramaswamy, V.; Detwiler, A. Interdependence of Radiation and Microphysics in Cirrus Clouds. J. Atmos. Sci. 1986, 43, 2289–2301. [Google Scholar] [CrossRef]
- Liou, K.-N. Electromagnetic Scattering by Arbitrarily Oriented Ice Cylinders. Appl. Opt. 1972, 11, 667–674. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Liou, K.N. Parameterization of the Radiative Properties of Cirrus Clouds. J. Atmos. Sci. 1993, 50, 2008–2025. [Google Scholar] [CrossRef]
- Lawson, R.P.; Baker, B.A.; Schmitt, C.G.; Jensen, T.L. An Overview of Microphysical Properties of Arctic Clouds Observed in May and July 1998 during FIRE ACE. J. Geophys. Res. 2001, 106, 14989–15014. [Google Scholar] [CrossRef]
- Fleishauer, R.P.; Larson, V.E.; Haar, T.H.V. Observed Microphysical Structure of Midlevel, Mixed-Phase Clouds. J. Atmos. Sci. 2002, 59, 1779–1804. [Google Scholar] [CrossRef]
- Baker, B.A.; Lawson, R.P. In Situ Observations of the Microphysical Properties of Wave, Cirrus, and Anvil Clouds. Part II: Cirrus Clouds. J. Atmos. Sci. 2006, 63, 3160–3185. [Google Scholar] [CrossRef]
- Bailey, M.P.; Hallett, J. A Comprehensive Habit Diagram for Atmospheric Ice Crystals: Confirmation from the Laboratory, AIRS II, and Other Field Studies. J. Atmos. Sci. 2009, 66, 2888–2899. [Google Scholar] [CrossRef]
- Key, J.R.; Yang, P.; Baum, B.A.; Nasiri, S.L. Parameterization of Shortwave Ice Cloud Optical Properties for Various Particle Habits. J. Geophys. Res. 2002, 107, 4181. [Google Scholar] [CrossRef]
- Yang, P.; Wei, H.; Huang, H.-L.; Baum, B.A.; Hu, Y.X.; Kattawar, G.W.; Fu, Q. Scattering and Absorption Property Database for Nonspherical Ice Particles in the near- through Far-Infrared Spectral Region. Appl. Opt. 2005, 44, 5512–5523. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Bi, L.; Baum, B.A.; Liou, K.-N.; Kattawar, G.W.; Mishchenko, M.I.; Cole, B. Spectrally Consistent Scattering, Absorption, and Polarization Properties of Atmospheric Ice Crystals at Wavelengths from 0.2 to 100 μm. J. Atmos. Sci. 2013, 70, 330–347. [Google Scholar] [CrossRef]
- Letu, H.; Ishimoto, H.; Riedi, J.; Nakajima, T.Y.; Sekiguchi, M. Investigation of Ice Particle Habits to Be Used for Ice Cloud Remote Sensing for the GCOM-C Satellite Mission. Atmos. Chem. Phys. 2015, 15, 31665–31703. [Google Scholar] [CrossRef]
- Saito, M.; Yang, P. Oriented Ice Crystals: A Single-Scattering Property Database for Applications to Lidar and Optical Phenomenon Simulations. J. Atmos. Sci. 2019, 76, 2635–2652. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, H. Effects of ice crystal habit weight on ice cloud optical properties and radiation. Acta Meteorol. Sin. 2018, 76, 279–288. [Google Scholar] [CrossRef]
- Miles, N.L.; Verlinde, J.; Clothiaux, E.E. Cloud Droplet Size Distributions in Low-Level Stratiform Clouds. J. Atmos. Sci. 2000, 57, 295–311. [Google Scholar] [CrossRef]
- Hansen, J.E. Multiple Scattering of Polarized Light in Planetary Atmospheres Part II. Sunlight Reflected by Terrestrial Water Clouds. J. Atmos. Sci. 1971, 28, 1400–1426. [Google Scholar] [CrossRef]
- Ulbrich, C.W. Natural Variations in the Analytical Form of the Raindrop Size Distribution. J. Appl. Meteorol. 1983, 22, 1764–1775. [Google Scholar] [CrossRef]
- Morrison, H.; Curry, J.A.; Khvorostyanov, V.I. A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models. Part I: Description. J. Atmos. Sci. 2005, 62, 1665–1677. [Google Scholar] [CrossRef]
- Sekhon, R.S.; Srivastava, R.C. Snow Size Spectra and Radar Reflectivity. J. Atmos. Sci. 1970, 27, 299–307. [Google Scholar] [CrossRef]
- Jacobson, M.Z. Strong Radiative Heating Due to the Mixing State of Black Carbon in Atmospheric Aerosols. Nature 2001, 409, 695–697. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Whitehead, J.; Alfarra, M.R.; Reyes-Villegas, E.; Spracklen, D.V.; Reddington, C.L.; Haslett, S. Black-Carbon Absorption Enhancement in the Atmosphere Determined by Particle Mixing State. Nat. Geosci. 2017, 10, 184–188. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, H.; Zhao, S.; Li, J. On Effective Radiative Forcing of Partial Internally and Externally Mixed Aerosols and Their Effects on Global Climate. J. Geophys. Res. 2018, 123, 401–423. [Google Scholar] [CrossRef]
- Wang, Z.; Bi, L.; Yi, B.; Zhang, X. How the Inhomogeneity of Wet Sea Salt Aerosols Affects Direct Radiative Forcing. Geophys. Res. Lett. 2019, 46, 1805–1813. [Google Scholar] [CrossRef]
- Bi, L.; Yang, P.; Kattawar, G.W.; Mishchenko, M.I. Efficient Implementation of the Invariant Imbedding T-Matrix Method and the Separation of Variables Method Applied to Large Nonspherical Inhomogeneous Particles. J. Quant. Spectrosc. Radiat. Transf. 2013, 116, 169–183. [Google Scholar] [CrossRef]
- Bi, L.; Yang, P.; Kattawar, G.W.; Mishchenko, M.I. A Numerical Combination of Extended Boundary Condition Method and Invariant Imbedding Method Applied to Light Scattering by Large Spheroids and Cylinders. J. Quant. Spectrosc. Radiat. Transf. 2013, 123, 17–22. [Google Scholar] [CrossRef]
- Bi, L.; Yang, P. Accurate Simulation of the Optical Properties of Atmospheric Ice Crystals with the Invariant Imbedding T-Matrix Method. J. Quant. Spectrosc. Radiat. Transf. 2014, 138, 17–35. [Google Scholar] [CrossRef]
- Bi, L.; Lin, W.; Wang, Z.; Tang, X.; Zhang, X.; Yi, B. Optical Modeling of Sea Salt Aerosols: The Effects of Nonsphericity and Inhomogeneity. J. Geophys. Res. 2018, 123, 543–558. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 1998; Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9783527618156 (accessed on 11 June 2021).
- Bi, L.; Yang, P. Improved Ice Particle Optical Property Simulations in the Ultraviolet to Far-Infrared Regime. J. Quant. Spectrosc. Radiat. Transf. 2017, 189, 228–237. [Google Scholar] [CrossRef]
- Warren, S.G.; Brandt, R.E. Optical Constants of Ice from the Ultraviolet to the Microwave: A Revised Compilation. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Hale, G.M.; Querry, M.R. Optical Constants of Water in the 200-nm to 200-μm Wavelength Region. Appl. Opt. 1973, 12, 555–563. [Google Scholar] [CrossRef] [PubMed]
- Palmer, K.F.; Williams, D. Optical Properties of Water in the near Infrared. J. Opt. Soc. Amer. 1974, 64, 1107–1110. [Google Scholar] [CrossRef]
- Downing, H.D.; Williams, D. Optical Constants of Water in the Infrared. J. Geophys. Res. 1975, 80, 1656–1661. [Google Scholar] [CrossRef]
- Baum, B.A.; Yang, P.; Heymsfield, A.J.; Schmitt, C.G.; Xie, Y.; Bansemer, A.; Zhang, Z. Improvements in Shortwave Bulk Scattering and Absorption Models for the Remote Sensing of Ice Clouds. J. Appl. Meteorol. Climatol. 2011, 50, 1037–1056. [Google Scholar] [CrossRef]
- Arnott, W.P.; Dong, Y.Y.; Hallett, J. Extinction Efficiency in the Infrared (2–18 μm) of Laboratory Ice Clouds: Observations of Scattering Minima in the Christiansen Bands of Ice. Appl. Opt. 1995, 34, 541–551. [Google Scholar] [CrossRef] [PubMed]
- Avery, M.A.; Ryan, R.A.; Getzewich, B.J.; Vaughan, M.A.; Winker, D.M.; Hu, Y.; Garnier, A.; Pelon, J.; Verhappen, C.A. CALIOP V4 cloud thermodynamic phase assignment and the impact of near-nadir viewing angles. Atmos. Meas. Tech. 2020, 13, 4539–4563. [Google Scholar] [CrossRef]
- Liu, D.; Liu, Q.; Qi, L.; Fu, Y. Oceanic single-layer warm clouds missed by the Cloud Profiling Radar as inferred from MODIS and CALIOP measurements. J. Geophys. Res. Atmos. 2016, 121, 12947–12965. [Google Scholar] [CrossRef]
- Luo, T.; Wang, Z.; Li, X.; Deng, S.; Huang, Y.; Wang, Y. Retrieving the polar mixed-phase cloud liquid water path by combining CALIOP and IIR measurements. J. Geophys. Res. Atmos. 2018, 123, 1755–1770. [Google Scholar] [CrossRef]
- Bréon, F.-M.; Dubrulle, B. Horizontally oriented plates in clouds. J. Atmos. Sci. 2004, 61, 2888–2898. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, P.; Dessler, A.E.; Hu, Y.; Baum, B.A. Study of horizontally oriented ice crystals with CALIPSO observations and comparison with Monte Carlo radiative transfer simulations. J. Appl. Meteor. Climatol. 2012, 51, 1426–1439. [Google Scholar] [CrossRef]

| Coated Sphere Model | Coated Non-Sphere Model | |||||||
|---|---|---|---|---|---|---|---|---|
| λ (μm) | xcore | Qext | Qsca | g | xcore | Qext | Qsca | g |
| 0.65 | 5 | 2.5071 | 2.5040 | 0.8584 | 5.9 | 2.5040 | 2.5040 | 0.8589 |
| 15 | 2.2612 | 2.3267 | 0.8535 | 17.7 | 2.3267 | 2.3267 | 0.7798 | |
| 1.6 | 5 | 2.1252 | 2.1291 | 0.8468 | 5.9 | 2.1291 | 2.1291 | 0.8473 |
| 15 | 1.8730 | 1.8998 | 0.8317 | 17.7 | 1.8998 | 1.8998 | 0.8330 | |
| 8 | 5 | 1.1306 | 1.1291 | 0.9584 | 5.9 | 1.1291 | 1.1291 | 0.9526 |
| 15 | 1.1190 | 1.1330 | 0.9573 | 17.7 | 1.1330 | 1.1330 | 0.9581 | |
| 30 | 5 | 1.1695 | 1.1689 | 0.9324 | 5.9 | 1.1689 | 1.1689 | 0.9328 |
| 10 | 1.1695 | 1.1689 | 0.9324 | 12.6 | 1.1689 | 1.1689 | 0.9328 | |
| Coated Sphere Model | Coated Non-Sphere Model | |||||||
|---|---|---|---|---|---|---|---|---|
| λ (μm) | xcore | Qext | Qsca | g | xcore | Qext | Qsca | g |
| 0.65 | 15 | 1.9072 | 1.9072 | 0.8470 | 17.7 | 1.9119 | 1.9119 | 0.8477 |
| 30 | 2.0378 | 2.0378 | 0.8620 | 35.4 | 2.0621 | 2.0621 | 0.8626 | |
| 1.6 | 15 | 2.2958 | 2.2773 | 0.8808 | 17.7 | 2.2695 | 2.2511 | 0.8789 |
| 30 | 2.3068 | 2.2805 | 0.8846 | 35.4 | 2.2890 | 2.2645 | 0.8824 | |
| 8 | 15 | 2.1452 | 1.1021 | 0.9749 | 17.7 | 2.1438 | 1.1005 | 0.9750 |
| 30 | 2.1454 | 1.1018 | 0.9749 | 35.4 | 2.1455 | 1.1018 | 0.9750 | |
| 30 | 15 | 2.1378 | 1.1609 | 0.9361 | 23.2 | 2.1379 | 1.1603 | 0.9365 |
| 20 | 2.1378 | 1.1609 | 0.9361 | 35.7 | 2.1379 | 1.1603 | 0.9365 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Q.; Yi, B.; Bi, L. Sensitivity of Mixed-Phase Cloud Optical Properties to Cloud Particle Model and Microphysical Factors at Wavelengths from 0.2 to 100 µm. Remote Sens. 2021, 13, 2330. https://doi.org/10.3390/rs13122330
Luo Q, Yi B, Bi L. Sensitivity of Mixed-Phase Cloud Optical Properties to Cloud Particle Model and Microphysical Factors at Wavelengths from 0.2 to 100 µm. Remote Sensing. 2021; 13(12):2330. https://doi.org/10.3390/rs13122330
Chicago/Turabian StyleLuo, Qing, Bingqi Yi, and Lei Bi. 2021. "Sensitivity of Mixed-Phase Cloud Optical Properties to Cloud Particle Model and Microphysical Factors at Wavelengths from 0.2 to 100 µm" Remote Sensing 13, no. 12: 2330. https://doi.org/10.3390/rs13122330
APA StyleLuo, Q., Yi, B., & Bi, L. (2021). Sensitivity of Mixed-Phase Cloud Optical Properties to Cloud Particle Model and Microphysical Factors at Wavelengths from 0.2 to 100 µm. Remote Sensing, 13(12), 2330. https://doi.org/10.3390/rs13122330