Fengyun-3D/MERSI-II Cloud Thermodynamic Phase Determination Using a Machine-Learning Approach
Abstract
1. Introduction
2. Methodology
2.1. The Optimal Machine-Learning Algorithm
- Training parameters were selected. BT data from the six FY-3D/MERSI-II IR bands (bands 20—3.8 μm, 21—4.05 μm, 22—7.2 μm, 23—8.55 μm, 24—10.8 μm, and 25—12.0 μm), Airmass (1/cos (satellite zenith angle)), and CP products from MODIS (MYD06; July 2018 to June 2019) were collocated as original features (training samples). To reduce errors caused by rapid changes in cloud properties, only data from two sensors within 5 min difference were collocated;
- The ratio between training data and validation data was set. Note that for selecting the algorithm, only 1% of samples were randomly selected for training and testing with a ratio of 7:3 to reduce the memory occupation and time consumption;
- The performances of five ML algorithms were compared in training the sample set, namely, KNN [28,29], Stacking [30], RF [31], AdaBoost [32], and GBDT [33]. Adjustment parameters and dynamic ranges of the five algorithms are shown in Table 1 [19,34,35]. Through these comparisons, the GridSearchCV module in Sklearn, with relatively high accuracy and the shortest running time, was selected to adjust the parameters automatically and iteratively (Table 2).
2.2. Training Scheme and Model Configuration
3. Data
3.1. Reference Pixel Label
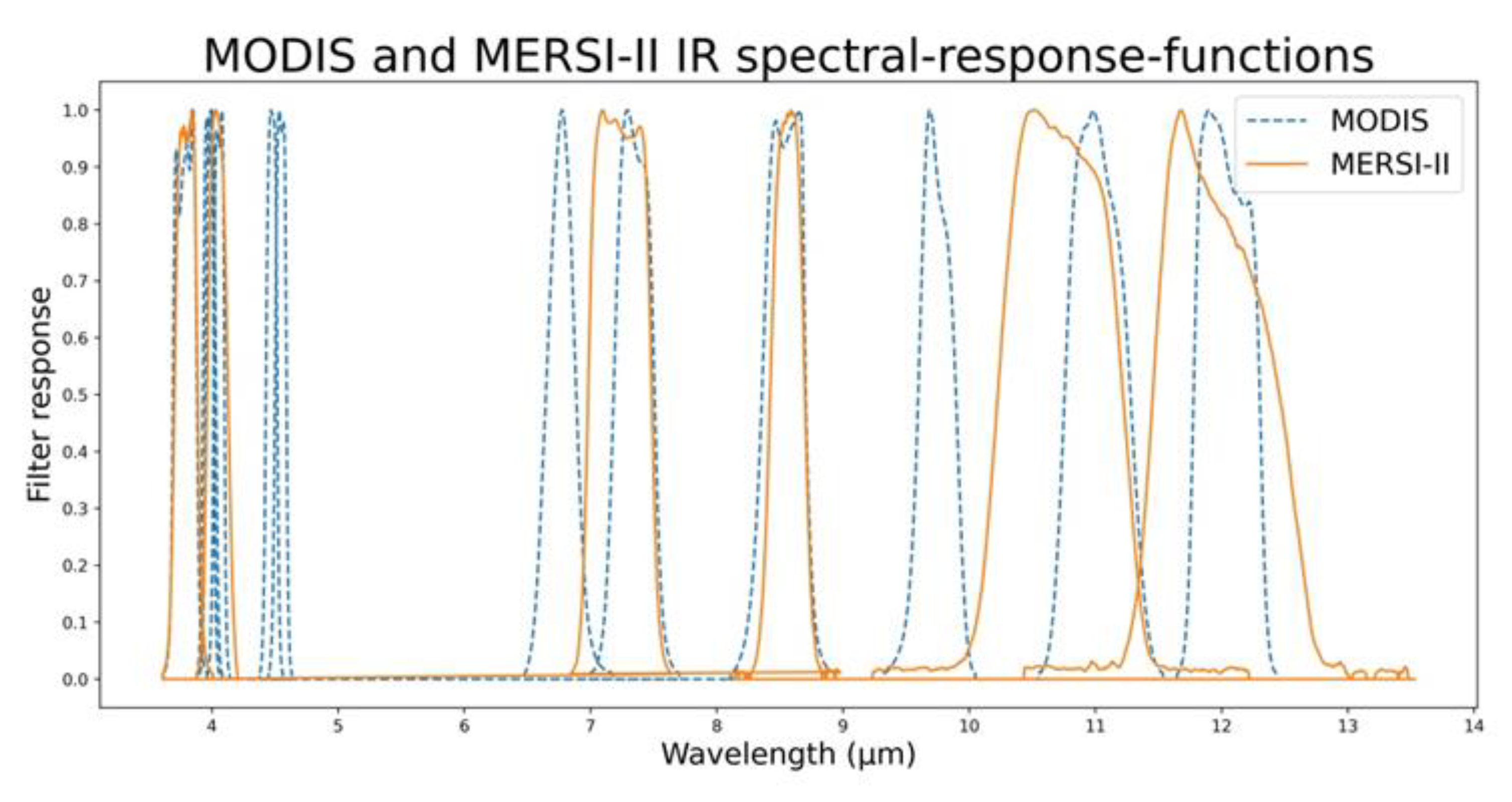
3.2. FY-3D/MERSI-II
3.3. CALIOP Cloud Products
4. Validation and Discussion
4.1. Validation Using Independent MODIS CP Product
4.2. Comparison of Spatial Distributions
4.3. Comparison with Active CALIOP CP Data
5. Summary
- The RF CP product is spatially consistent with MODIS CP product, and its accuracy is comparable with that of MODIS CP product when compared with CALIPSO cloud products.
- The RF-based CP algorithm has the highest accuracy at high latitudes and the lowest accuracy at mid-latitude winter compared with the MODIS CP product.
- The RF product developed here may supplement the lack of data from existing MERSI-II CP products at night; it also indicates an improvement in accuracy over the operational FY-3D/MERSI-II CP product.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kerr, R.A. Darker clouds promise brighter future for climate models. Science 1995, 267, 454. [Google Scholar] [CrossRef] [PubMed]
- King, M.D.; Nakajima, T.; Spinhirne, J.D.; Radke, L.F. Cloud microphysical properties from multispectral reflectance measurements. Proc. SPIE 1990, 1299, 139–153. [Google Scholar] [CrossRef]
- Menzel, W.; Frey, R. Cloud Top Properties and Cloud Phase Algorithm Theoretical Basis Document. 2015. Available online: https://atmosphere-imager.gsfc.nasa.gov/sites/default/files/ModAtmo/MOD06-ATBD_2015_05_01_1.pdf (accessed on 12 April 2021).
- Pavolonis, M.J. Advances in Extracting Cloud Composition Information from Spaceborne Infrared Radiances—A Robust Alternative to Brightness Temperatures. Part I: Theory. J. Appl. Meteorol. Climatol. 2010, 49, 1992–2012. [Google Scholar] [CrossRef]
- Toshiro, I. A cloud type classification with NOAA 7 split-window measurements. J. Geophys. Res. 1987. [Google Scholar] [CrossRef]
- Strabala, K.I.; Ackerman, S.A.; Menzel, W.P. Cloud properties inferred from 8–12 m data. J. Appl. Meteorol. 1994, 33, 212–229. [Google Scholar] [CrossRef]
- Baum, B.A.; Menzel, W.P.; Frey, R.A.; Tobin, D.C.; Yang, P. MODIS Cloud-Top Property Refinements for Collection 6. J. Appl. Meteorol. Climatol. 2012, 51, 1145–1163. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Pavolonis, M.J. Gazing at Cirrus Clouds for 25 Years through a Split Window. Part I: Methodology. J. Appl. Meteorol. Climatol. 2009, 48. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Pavolonis, M.J.; Holz, R.E.; Baum, B.A.; Berthier, S. Using CALIPSO to explore the sensitivity to cirrus height in the infrared observations from NPOESS/VIIRS and GOES-R/ABI. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Arking, A.; Childs, J.D. Retrieval of Cloud Cover Parameters from Multispectral Satellite Images. J. Appl. Meteorol. 2003, 24. [Google Scholar] [CrossRef]
- Pilewskie, P.; Twomey, S. Cloud Phase Discrimination by Reflectance Measurements near 1.6 and 2.2 μm. J. Atmos. Sci. 1987, 44, 3419–3420. [Google Scholar] [CrossRef]
- Baum, B.A.; Spinhirne, J.D. Remote sensing of cloud properties using MODIS airborne simulator imagery during SUCCESS: 3. Cloud Overlap. J. Geophys. Res. Atmos. 2000, 105. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Jourdan, O.; Burrows, J.P. The Cloud Phase Discrimination from a Satellite. IEEE Geosci. Remote. Sens. Lett. 2006, 3, 103–106. [Google Scholar] [CrossRef]
- Yang, P.; Nasiri, S.L.; Cho, H.-M. Application of CALIOP Measurements to the Evaluation of Cloud Phase Derived from MODIS Infrared Channels. J. Appl. Meteorol. Climatol. 2009, 48, 2169–2180. [Google Scholar] [CrossRef]
- Yinghui, L.; Ackerman, S.A.; Maddux, B.C.; Key, J. Errors in Cloud Detection over the Arctic Using a Satellite Imager and Implications for Observing Feedback Mechanisms. J. Clim. 2010, 23, 1894–1907. [Google Scholar] [CrossRef]
- Wang, C.; Platnick, S.; Meyer, K.; Zhang, Z.; Zhou, Y. A machine-learning-based cloud detection and thermodynamic-phase classification algorithm using passive spectral observations. Atmos. Meas. Tech. 2020, 13, 2257–2277. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, Z.; Songyan, G.; Xiuqin, H.; Shihao, T.; Leiku, Y.; Na, X.; Zhaojun, Z.; Ling, W.; Qiong, W.; et al. Capability of Fengyun-3D Satellite in Earth System Observation. J. Meteorol. Res. 2019, 33, 1113–1130. [Google Scholar] [CrossRef]
- Bo, L.; Lui, R.; Tang, S. Inversion and Preliminary Validation for Cloud Classification and Cloud Phase Products of Fengyun-3D in CMA-NSMC. In Proceedings of the International Conference on Meteorology Observations (ICMO), Chengdu, China, 28–31 December 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Min, M.; Bai, C.; Guo, J.; Sun, F.; Liu, C.; Wang, F.; Xu, H.; Tang, S.; Li, B.; Di, D.; et al. Estimating Summertime Precipitation from Himawari-8 and Global Forecast System Based on Machine Learning. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2557–2570. [Google Scholar] [CrossRef]
- Tan, Z.; Huo, J.; Ma, S.; Han, D.; Wang, X.; Hu, S.; Yan, W. Estimating cloud base height from Himawari-8 based on a random forest algorithm. Int. J. Remote Sens. 2021, 42, 2485–2501. [Google Scholar] [CrossRef]
- Yan, W.; Ren, J.-Q.; Lu, W.; Wu, X. Cloud phase discrimination technology based on spaceborne millimeter wave radar and lidar data. J. Infrared Millim. Waves 2011, 30, 68–73. [Google Scholar] [CrossRef]
- Zeng, S.; Omar, A.; Vaughan, M.; Ortiz, M.; Trepte, C.; Tackett, J.; Yagle, J.; Lucker, P.; Hu, Y.; Winker, D.; et al. Identifying Aerosol Subtypes from CALIPSO Lidar Profiles Using Deep Machine Learning. Atmosphere 2021, 12, 10. [Google Scholar] [CrossRef]
- Zhang, T.; He, W.; Zheng, H.; Cui, Y.; Song, H.; Fu, S. Satellite-based ground PM2.5 estimation using a gradient boosting decision tree. Chemosphere 2021, 268, 128801. [Google Scholar] [CrossRef] [PubMed]
- Winker, D.M.; Hunt, W.H.; Mcgill, M.J. Initial performance assessment of CALIOP. Geophys. Res. Lett. 2007, 34, 228–262. [Google Scholar] [CrossRef]
- Stephens, G.L.; Vane, D.G.; Boain, R.J.; Mace, G.G.; Sassen, K.; Wang, Z.; Illingworth, A.J.; O’Connor, E.J.; Rossow, W.B.; Durden, S.L. THE Cloudsat Mission and the A-train. Bull. Am. Meteorol. Soc. 2002, 83, 1771–1790. [Google Scholar] [CrossRef]
- Seemann, S.W.; Borbas, E.; Knuteson, R.O.; Stephenson, G.R.; Huang, H.L. Development of a Global Infrared Land Surface Emissivity Database for Application to Clear Sky Sounding Retrievals from Multispectral Satellite Radiance Measurements. J. Appl. Meteorol. Climatol. 2008, 47, 108–123. [Google Scholar] [CrossRef]
- Zhu, W.; Zhu, L.; Li, J.; Sun, H. Retrieving Volcanic Ash Top Height through Combined Polar Orbit Active and Geostationary Passive Remote Sensing Data. Remote Sens. 2020, 12, 953. [Google Scholar] [CrossRef]
- Coomans, D.; Massart, D.L. Alternative k-nearest neighbour rules in supervised pattern recognition: Part 1. k-Nearest neighbour classification by using alternative voting rules. Analytica Chimica Acta 1982. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 2017, 5, 241–259. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhu, J.; Arbor, A.; Hastie, T. Multi-class AdaBoost. Stat. Interface 2006, 2, 349–360. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Liu, Z.; Min, M.; Li, J.; Sun, F.; Zhang, X. Local Severe Storm Tracking and Warning in Pre-Convection Stage from the New Generation Geostationary Weather Satellite Measurements. Remote Sens. 2019, 11, 383. [Google Scholar] [CrossRef]
- Min, M.; Li, J.; Wang, F.; Liu, Z.; Menzel, W.P. Retrieval of cloud top properties from advanced geostationary satellite imager measurements based on machine learning algorithms. Remote Sens. Environ. 2020, 239. [Google Scholar] [CrossRef]
- Holz, R.E.; Ackerman, S.; Nagle, F.W.; Frey, R.; Dutcher, S.; Kuehn, R.E.V.; Aughan, M.A.; Baum, B. Global Moderate Resolution Imaging Spectroradiometer (MODIS) cloud detection and height evaluation using CALIOP. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauß, T. Precipitation Estimates from MSG SEVIRI Daytime, Nighttime, and Twilight Data with Random Forests. J. Appl. Meteorol. Climatol. 2014, 53, 2457–2480. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Minnett, P.J.; Le Borgne, P.; Merchant, C.J. Multi-satellite measurements of large diurnal warming events. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, X.; Gu, S.; Yang, L.; Min, M.; Chen, L.; Xu, N.; Sun, L.; Bai, W.; Ma, G.; et al. Latest Progress of the Chinese Meteorological Satellite Program and Core Data Processing Technologies. Adv. Atmos. Sci. 2019, 36, 1027–1045. [Google Scholar] [CrossRef]
- Hu, X.; Na, X.; Rw, A.; Lin, C. Performance assessment of FY-3C/MERSI on early orbit. Proc. SPIE 2014, 9264, 92640Y. [Google Scholar]
- Lu, X.-M.; Jiang, Y.-S. Statistical properties of clouds over Beijing derived from CALIPSO lidar measurements. Chin. J. Geophys. Chin. Ed. 2011, 54, 2487–2494. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Liu, Z.; Vaughan, M.; Winker, D.; Kittaka, C.; Getzewich, B.; Kuehn, R.; Omar, A.; Powell, K.; Trepte, C.; Hostetler, C. The CALIPSO Lidar Cloud and Aerosol Discrimination: Version 2 Algorithm and Initial Assessment of Performance. J. Atmos. Ocean. Technol. 2009, 26, 1198–1213. [Google Scholar] [CrossRef]
- Avery, M.A.; Ryan, R.A.; Getzewich, B.J.; Vaughan, M.A.; Verhappen, C.A. CALIOP V4 Cloud Thermodynamic Phase Assignment and the Impact of Near-Nadir Viewing Angles. Atmos. Meas. Tech. 2020, 13, 4539–4563. [Google Scholar] [CrossRef]
- Wang, C.; Platnick, S.; Zhang, Z.; Meyer, K.; Wind, G.; Yang, P. Retrieval of ice cloud properties using an optimal estimation algorithm and MODIS infrared observations: 2. Retrieval evaluation. J. Geophys. Res. 2016, 121, 5827–5845. [Google Scholar] [CrossRef]
- Wang, C.; Platnick, S.; Zhang, Z.; Meyer, K.; Yang, P. Retrieval of ice cloud properties using an optimal estimation algorithm and MODIS infrared observations: 1. Forward model, error analysis, and information content. J. Geophys. Res. 2016, 121. [Google Scholar] [CrossRef] [PubMed]

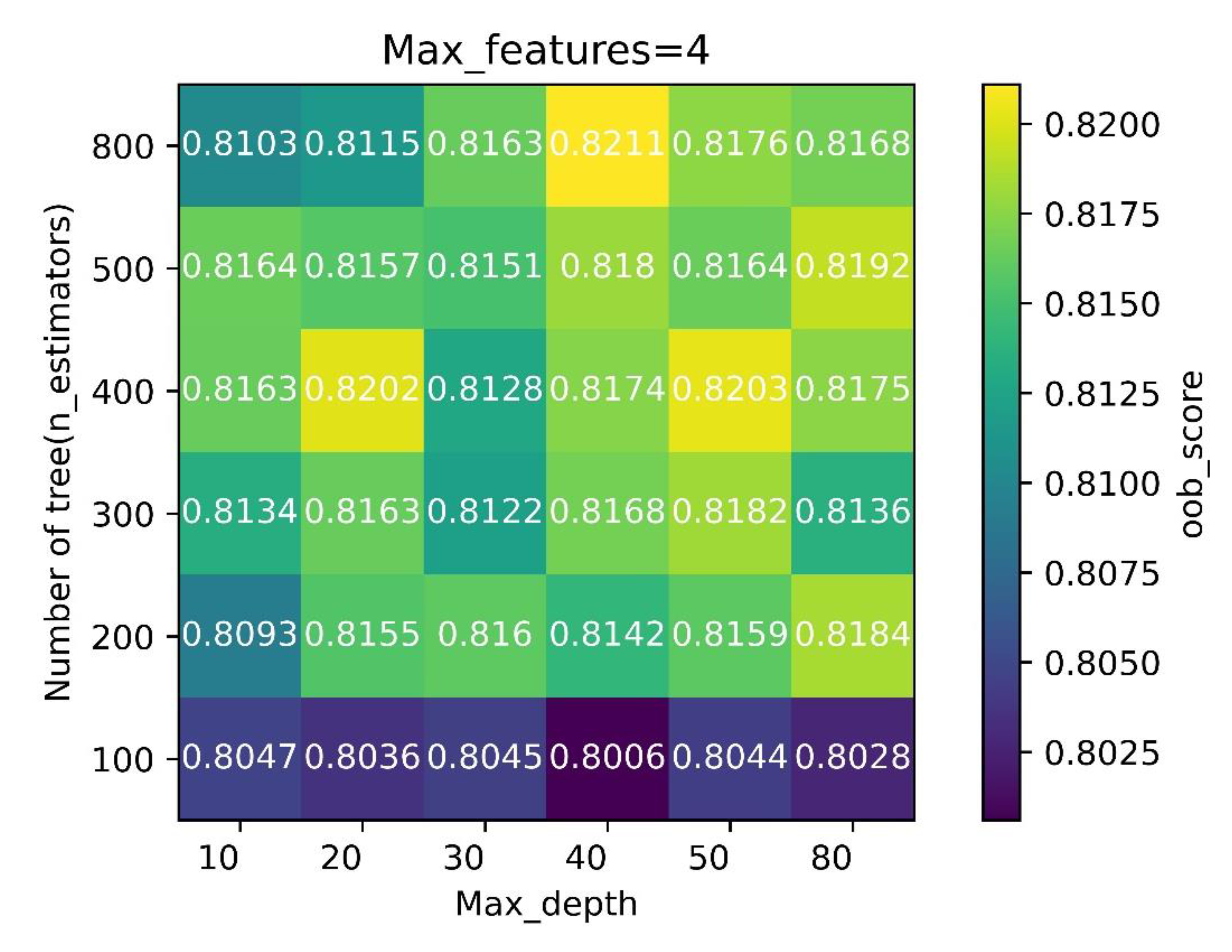


| Algorithm (Dimension) | Parameters and Range of Variation | |||||||
|---|---|---|---|---|---|---|---|---|
| Random forest (5 × 5 × 5 × 5 = 625) | The number of trees in the forest (n_estimators): [100, 200, 300, 400, 500] | maximum depth of the tree(max_depth): [10, 20, 30, 40, 50] | minimum number of samples required to split an internal node (min_samples_split): [2, 4, 6, 8, 10] | minimum number of samples required to be at a leaf node (min_samples_leaf): [1, 3, 5, 7, 9] | ||||
| AdaBoost (5 × 10 = 50) | maximum number of estimators (n_estimators): [100, 200, 300, 400, 500] | Learning rate (learning_rate): [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1] | ||||||
| K-nearest-neighbor (5 × 2 = 10) | Number of neighbors to use by default for k neighbors queries(n_neighbors): [5, 10, 15, 20, 25] | weight function used in prediction (weight S): ‘uniform’ or ‘distance’ | ||||||
| Gradient Boosting Decision Tree (5 × 10 × 5 × 5 × 5 = 6250) | maximum number of estimators (n_estimators): [100, 200, 300, 400, 500] | Learning rate (learning_rate): [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1] | maximum depth of the tree (max_depth): [10, 20, 30, 40, 50] | minimum number of samples required to split an internal node (min_samples_split): [2, 4, 6, 8, 10] | minimum number of samples required to be at a leaf node (min_samples_leaf): [1, 3, 5, 7, 9] | |||
| Stacking | Integration of the above four optimal algorithms | |||||||
| Algorithm | Parameter | HR | POD | FAR | Time (s) |
|---|---|---|---|---|---|
| RF | n_estimators = 300; max_depth = 30; min_samples_split = 2; min_samples_leaf = 7 | 0.91 | 0.91 | 0.10 | 101 |
| GBDT | n_estimators = 400; max_depth = 30; min_samples_split = 2; min_samples_leaf = 7; learning_rate = 0.4 | 0.91 | 0.92 | 0.10 | 258 |
| AdaBoost | n_estimators = 400; learning_rate = 0.8 | 0.88 | 0.89 | 0.11 | 125 |
| KNN | n_neighbors = 10; weight S = ‘uniform’ | 0.84 | 0.88 | 0.19 | 179 |
| Stacking | Integration of the above four optimal algorithms | 0.91 | 0.91 | 0.10 | 648 |
| Variable | Importance Score for Variable | Ranking | Physical Characteristics |
|---|---|---|---|
| BTD (8.6–10.8 μm) | 0.2015 | 1 | 8–10 µm is the weak absorption region of particles. |
| BTD (10.8–12.0 μm) | 0.1080 | 2 | Stronger increases in the absorption of ice particles can be found at 10–11 μm than that at 11–12 μm, while the effect on water particles is the opposite. This allows distinguishing between ice and water particles. |
| BT (7.2μm) | 0.1070 | 3 | The water vapor absorption channel is very sensitive to the amount of water vapor |
| BTD (3.8–10.8 μm) | 0.0891 | 4 | Difference between split–window channel |
| BTD (4.1–10.8 μm) | 0.0800 | 5 | Difference between split–window channel |
| BT (12.0 μm) | 0.0769 | 6 | Total water and sea surface temperature |
| BTD (7.2–10.8 μm) | 0.0618 | 7 | Difference between split–window channel |
| BT (10.8 μm) | 0.0613 | 8 | Split–window channel |
| BT (8.6 μm) | 0.0575 | 9 | Surface temperature, cloud phase, and cirrus cloud detection |
| BT (3.8 μm) | 0.0571 | 10 | Cloud effective particle radius, clouds, and underlying surface temperature |
| BT (4.1 μm) | 0.0508 | 11 | Clouds and underlying surface temperature |
| Airmass (1/cos(satellite zenith angle)) | 0.0490 | 12 | Reduces the inversion error caused by the path of light in the atmosphere |
| Classification | POD | FAR | CSI | HR | HSS |
|---|---|---|---|---|---|
| Mid-latitude spring and autumn | 0.91 | 0.13 | 0.76 | 0.86 | 0.72 |
| Mid-latitude winter | 0.80 | 0.08 | 0.74 | 0.82 | 0.61 |
| Mid-latitude summer | 0.90 | 0.08 | 0.84 | 0.87 | 0.63 |
| Low latitude all year | 0.91 | 0.13 | 0.77 | 0.84 | 0.68 |
| High latitude all year | 0.94 | 0.11 | 0.84 | 0.90 | 0.8 |
| All year | 0.85 | 0.06 | 0.80 | 0.84 | 0.60 |
| Time | Picture | CP Product | POD | FAR | CSI | HR | HSS |
|---|---|---|---|---|---|---|---|
| 11 October 2020 14:10 | Mid-latitude spring and autumn | RF | 0.90 | 0.17 | 0.76 | 0.84 | 0.67 |
| FY-3D/MERSI-II | 0.82 | 0.17 | 0.70 | 0.80 | 0.60 | ||
| 12 July 2020 12:25 | Mid-latitude winter | RF | 0.95 | 0.06 | 0.95 | 1.00 | 0.97 |
| FY-3D/MERSI-II | 0.99 | 0.06 | 0.99 | 1.00 | 0.99 | ||
| 12 July 2020 9:30 | Mid-latitude summer | RF | 0.60 | 0.35 | 0.45 | 0.84 | 0.53 |
| FY-3D/MERSI-II | 1.00 | 0.60 | 0.40 | 0.67 | 0.38 | ||
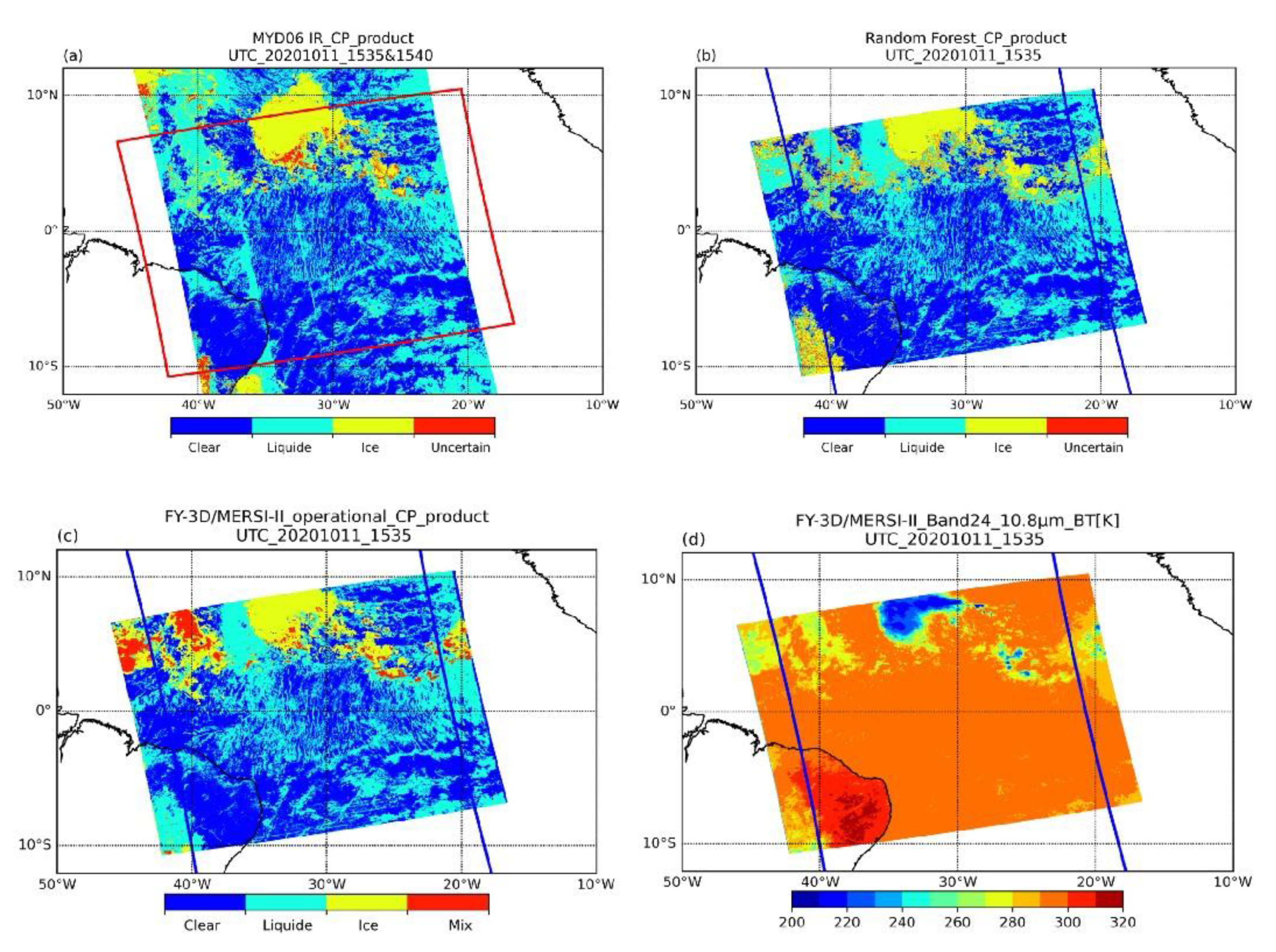
| 11 October 2020 15:35 | Low latitude | RF | 0.90 | 0.07 | 0.85 | 0.90 | 0.80 |
| FY-3D/MERSI-II | 0.91 | 0.09 | 0.79 | 0.90 | 0.80 | ||
| 11 October 2020 20:20 | High latitude | RF | 0.61 | 0.19 | 0.54 | 0.86 | 0.61 |
| FY-3D/MERSI-II | 0.03 | 0.11 | 0.03 | 0.74 | 0.04 |
| CALIOP Phase | MODIS IR Phase | RF Phase | FY-3D Phase | ||||
|---|---|---|---|---|---|---|---|
| Liquid | Ice | Liquid | Ice | Liquid | Ice | ||
| mid-latitude spring and autumn | Liquid | 75.0% | 25.0% | 88.3% | 11.7% | 56.1% | 43.9% |
| Ice | 6.6% | 93.4% | 6.6% | 93.4% | 5.4% | 94.6% | |
| Mid-latitude Winter | Liquid | 96.4% | 3.6% | 87.6% | 12.4% | 69.8% | 30.2% |
| Ice | 18.7% | 81.3% | 50.0% | 50.0% | 7.8% | 92.2% | |
| Mid-latitude Summer | Liquid | 75.2% | 24.9% | 77.12% | 22.8% | 87.6% | 12.4% |
| Ice | 19.4% | 80.6% | 13.4% | 83.6% | 18.7% | 81.3% | |
| Low latitude | Liquid | 65.1% | 34.9% | 61.9% | 38.1% | 73.5% | 26.5% |
| Ice | 6.0% | 94.0% | 12.6% | 87.4% | 31.0% | 69% | |
| High latitude | Liquid | 72.1% | 27.9% | 75.9% | 24.1% | 16.2% | 83.8% |
| Ice | 5.9% | 94.1% | 6.3% | 93.7% | 2.5% | 97.5% | |
| Oriented ice crystal | 0 | 100% | 0 | 100% | 0 | 100.0% | |
| All | Liquid | 76.8% | 23.2% | 78.2% | 21.8% | 60.6% | 39.4% |
| Ice | 11.3% | 88.7% | 18.4% | 81.6% | 13.1% | 86.9% | |
| Oriented ice crystal | 0 | 100% | 0 | 100% | 0 | 100% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Zhu, L.; Sun, H.; Li, J.; Wang, W. Fengyun-3D/MERSI-II Cloud Thermodynamic Phase Determination Using a Machine-Learning Approach. Remote Sens. 2021, 13, 2251. https://doi.org/10.3390/rs13122251
Zhao D, Zhu L, Sun H, Li J, Wang W. Fengyun-3D/MERSI-II Cloud Thermodynamic Phase Determination Using a Machine-Learning Approach. Remote Sensing. 2021; 13(12):2251. https://doi.org/10.3390/rs13122251
Chicago/Turabian StyleZhao, Dexin, Lin Zhu, Hongfu Sun, Jun Li, and Weishi Wang. 2021. "Fengyun-3D/MERSI-II Cloud Thermodynamic Phase Determination Using a Machine-Learning Approach" Remote Sensing 13, no. 12: 2251. https://doi.org/10.3390/rs13122251
APA StyleZhao, D., Zhu, L., Sun, H., Li, J., & Wang, W. (2021). Fengyun-3D/MERSI-II Cloud Thermodynamic Phase Determination Using a Machine-Learning Approach. Remote Sensing, 13(12), 2251. https://doi.org/10.3390/rs13122251





