Abstract
After 30 years since the beginning of the Global Positioning System (GPS), or, more generally, Global Navigation Satellite System (GNSS) meteorology, this technique has proven to be a reliable method for retrieving atmospheric water vapor; it is low-cost, weather independent, with high temporal resolution and is highly accurate and precise. GNSS ground-based networks are becoming denser, and the first stations installed have now quite long time-series that allow the study of the temporal features of water vapor and its relevant role inside the climate system. In this review, the different GNSS methodologies to retrieve atmospheric water vapor content re-examined, such as tomography, conversion of GNSS tropospheric delay to water vapor estimates, analyses of errors, and combinations of GNSS with other sources to enhance water vapor information. Moreover, the use of these data in different kinds of studies is discussed. For instance, the GNSS technique is commonly used as a reference tool for validating other water vapor products (e.g., radiosounding, radiometers onboard satellite platforms or ground-based instruments). Additionally, GNSS retrievals are largely used in order to determine the high spatio-temporal variability and long-term trends of atmospheric water vapor or in models with the goal of determining its notable influence on the climate system (e.g., assimilation in numerical prediction, as input to radiative transfer models, study of circulation patterns, etc.).
Keywords:
GNSS; GPS; water vapor; ground-based; methodology; validation; spatio-temporal; time-series; meteorology; climate 1. Introduction
Water vapor is a trace gas of the Earth’s atmosphere. Despite its relatively low concentration, it is of paramount importance to the Earth’s climate. Firstly, water vapor is the major contributor to the natural greenhouse effect and, therefore, in global warming, presents positive climate feedback [1,2]. It also has an obvious role in the hydrological cycle, and plays a key role in energy transport. Water is evaporated at low latitudes, and its vapor is transported to higher latitudes where, by condensation, it releases high amounts of heat [3].
Water vapor can be quantified using different methods. One of the most common is the integrated water vapor (IWV), which is also known by other names in the literature, such as precipitable water vapor (PWV), precipitable water (PW), integrated precipitable water vapor (IPWV), and so forth. This quantity represents the integral of the concentration of water vapor along the vertical path, and can also be pictured as the height that, in a vessel of a unit cross-section, the water vapor in a column of the same cross-section would reach if all of it condensed to liquid water. The density of liquid water allows the establishment of the equivalence between the superficial concentration (in ) and the height in the vessel (in ).
Another interesting measurement of water vapor is its distribution with height. This distribution can be given as a mixing ratio (grams of water per gram of dry air), as relative humidity, or other measurements of concentration.
Global Navigation Satellite Systems (GNSS) allow the retrieval of information about atmospheric water vapor, with different techniques. In this article, we will focus on the ground-based techniques, since GNSS radio-occultation techniques have already been discussed elsewhere [4,5,6].
Global Positioning System (GPS) meteorology started when Bevis et al. [7] suggested this approach to remotely sensing water vapor, in a time when even GPS, the first GNSS constellation, was not still completed. In that paper, the methodology to derive IWV from tropospheric delay is thoroughly explained. Moreover, some possible applications are depicted. One of them is the obvious use of GNSS-receiver networks to monitor IWV, but also the idea of water vapor tomography by using dense networks is shown.
The main idea behind remote sensing of the water vapor through GNSS is that the GNSS signal between satellite and ground-based receiver is delayed by the troposphere, along with other effects. The GNSS processing for obtaining the position of the receiver needs to account for this, which is called slant tropospheric delay (STD). This is usually given in terms of the zenith tropospheric delay (ZTD), since it is not satellite-dependent and, to convert STD to ZTD, a mapping function is needed. Once ZTD is obtained, meteorological data (typically surface atmospheric pressure) are used to compute the non-dipolar component of this ZTD, known as the zenith hydrostatic delay (ZHD). By subtracting the ZHD from the ZTD, only the dipolar component remains, which is exclusively due to the presence of water vapor (because it is the only atmospheric component with permanent dipolar moment). This component is called the zenith wet delay (ZWD). It can be converted to IWV using a factor usually represented by (sometimes by Q). The factor has been calculated by many methods in the literature (see Section 2.1). The most accurate methods model as a function of the weighted mean temperature of the atmosphere, also known as Davis temperature ().
One simple way to estimate is through linear regression with surface temperature (). Bevis et al. [8] performed a linear regression of and surface temperature () using radiosonde data in the United States, which is currently known as the Bevis Formula (). This work also included a more detailed explanation of the method for ground-based GNSS water vapor monitoring, providing specific figures for all the constants involved, and discussing their uncertainty in depth. The refractivity constants were obtained by statistical treatment of values from other studies, while the computation of values was also carried out using numerical weather prediction models (NWP), yielding a root mean square error (RMSE) of (as compared to the RMSE of from using the so called “Bevis formula”).
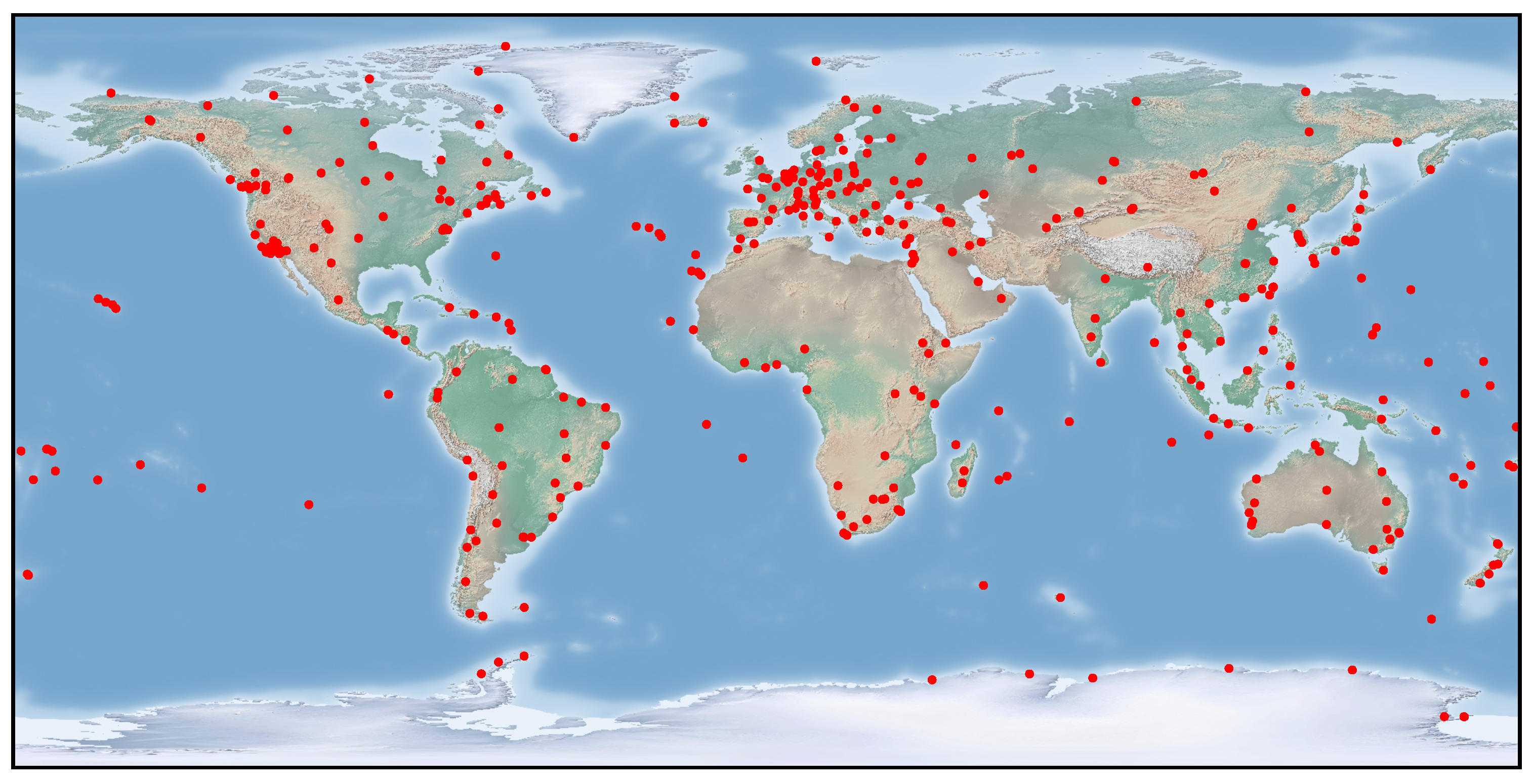
After these studies, the importance of water vapor and the need of improving its spatial and temporal resolution and coverage was acknowledged in some studies, such as [9]. Moreover, GNSS meteorology was found to be suitable for this task, as most of the infrastructure was already there (for navigation and geodetic applications, mainly). Therefore, it was a unique opportunity to obtain more meteorological information at a very low cost. However, these efforts would be useless without the information provided by services like the International GNSS Service IGS [10], operating since 1994 and providing necessary information for the processing of GNSS data, such as precise and real-time orbits, clock corrections, tropospheric products, and so on. The IGS counts with a global network of ground-based receivers and a set of Analysis Centers to process their data. This global network is depicted in Figure 1.
Figure 1.
Current network of 506 stations belonging to IGS. Color and shape are related to the last data available date. Source: https://www.igs.org/maps/#station-map (accessed on 19 May 2021).
It must be noted that the processing of tropospheric delays must be finely tuned for meteorological purposes. For navigation techniques, the estimation of the different delays do not need to be very precise, as long as their combination adds up to the total delay suffered by the satellite-receiver signals. However, for meteorological purposes, the other delays need to be obtained with high precision to avoid that part of the error can be transferred to the tropospheric delay estimate. For instance, the ocean tide loading can induce errors of up to in ZTD if it is not properly modeled [11].
GFZ-Potsdam started the development of one of the first systematic near real-time water vapor products based on a German network and in association with other research centers. This was the so-called GNSS Atmosphere Sounding Project (GASP). It was partly dedicated to space-based GNSS observations but also to ground-based measurements [12]. The STD started to be assimilated in analysis experiments for dense GNSS networks, developing ways of estimating the 3D structure of water vapor [13]. The use of ground-based GNSS networks for tomography of the troposphere, obtaining 4D maps of water vapor, was first discussed by Flores et al. [14]. They proposed a methodology (software LOTTOS) to retrieve these maps from STD measurements and concluded that the technique could be used for monitoring the troposphere.
Later, Morland et al. [15] presented the STARTWAVE (STudies in Atmospheric Radiative Transfer and Water Vapour Effects) project, whose objective was to obtain a database of different water vapor products (including ground-based GNSS ones) that allowed the study of the role of water vapor in the climate. At the same time, the idea of using GNSS networks for water vapor tomography was still in the air, and Bender and Raabe [16] considered the idea of different network geometries. They concluded that the spatial resolution would be given by the mean inter-station distance. It was also reported that the quality and quantity of measurements depend on the distribution of the satellite constellation and, therefore, on time, they would improve as more satellites (including other constellations such as GLONASS or Galileo) became available. Multi-GNSS processing became operational for near real-time applications a few years later, when Li et al. [17] first compared this kind of measurement with single-GNSS ones. The processing was possible thanks to the efforts of the IGS Multi-GNSS Experiment MGEX [18].
This article reviews different methodologies used to retrieve water vapor information from GNSS processing in Section 2. The vast applications of these processing techniques are discussed in the following sections, namely the inter-comparisons with other techniques (Section 3), the spatio-temporal analysis of water vapor distribution (Section 4), and the impact of water vapor variability on meteorology and climate (Section 5). Finally, conclusions are drawn in Section 6.
2. GNSS Methodologies
2.1. Conversion of Tropospheric Delays to Water Vapor
The conversion of ZWD to IWV is performed through the factor . Typically, its value is estimated by the relation described by Equation (1),
where is the density of liquid water, the specific gas constant for water vapor, and are refractivity constants and is the weighted mean temperature of the atmosphere, defined as Equation (2):
is typically obtained by using a linear regression between surface temperature () and (obtained from radiosondes). The relationship given by Bevis et al. [7] was obtained using radiosondes in the United States. Logically, some efforts have been made to improve it for application to other locations. Emardson and Derks [19] considered two models for in Europe: (1) series expansion of the deviation from mean surface temperature, and (2) a combination of the former with a seasonal variation based on decimal day of year and latitude. Both models presented RMSE values between and , fitting the coefficients to all Europe, by regions or by site. Slight increases in RMSE values were found as the fitting involved wider regions. In more equatorial regions, such as southern India, has been reported to be less dependent on variations, allowing to set it to a fixed value without relevant precision loss [20]. Another work addressed the model to calculate in tropical regions, finding that the Bevis formula is shown to be less adequate with high temperatures and low variability. In fact, the definition of assumes that temperatures are not so high, and Bevis et al. [7] indicates a larger dispersion for high values. Therefore, it is suggested that the redefinition of should be addressed for tropical regions.
NWP, as with the reanalysis from European Centre for Medium-Range Weather Forecasts (ECMWF), have been widely used to retrieve surface pressure and since 2009 approximately. Heise et al. [21] obtained a global 5-min data-set from the IGS GNSS network using this approach. The ECMWF reanalysis version used (ERA-Interim) had 6-h resolution, and the estimated uncertainty due to time interpolation was less than . Later, Wang et al. [22] compared the GNSS IWV product using the new ECMWF reanalysis (ERA5) for pressure and , on the one hand, and using the legacy version (ERA-Interim), on the other hand, against a reference GNSS IWV product using data from meteorological stations. The biases and RMSE of both products were of a few tenths of a millimeter. Against radiosondes, the RMSE was of about 2–4 . ERA5 interpolation data-set was found to be more stable than ERA-Interim one. Zhang et al. [23] showed that ERA5 GNSS IWV improved ERA-Interim GNSS IWV in China, thanks to ERA5’s pressure enhancement, and with a similar performance on . The contribution of ERA5 to the IWV error was estimated to be less than , and diurnal variations were better caught by ERA5 GNSS IWV than by ERA-Interim GNSS IWV.
Moreover, there have been some approaches to use NWP data for retrieving mapping function parameters, pressure and temperature [24,25]. These approaches can be useful when there are not any meteorological stations available nearby the GNSS station or when access to NWP data is difficult.
Another possible approach is to use local models of temperature and pressure to convert ZTD to IWV, using local meteorological stations over a long time series. Charoenphon and Satirapod [26] followed this methodology in Thailand, finding that RMSE was below , therefore it was considered suitable for weather nowcasting.
All of these different methodologies to convert ZTD to IWV have advantages and disadvantages. The most precise approach is to use measurements of temperature and pressure at the station location, but sometimes this is not possible or not fast enough for some applications. In addition, it is important to apply the necessary corrections when the meteorological station and the GNSS receiver are not at the same height. Moreover, the use of models can be very helpful for some applications or to retrieve data from receivers that are far away from meteorological stations or to extend the time series of stations that have a meteorological station nearby in the present but not in the past.
2.2. Error Analysis
Since GNSS meteorology is a rather indirect technique, there can be sources of error in each step of the process. For instance, the presence of patterns of water vapor gradients can induce errors in GNSS-derived IWV to the point that methodologies have been developed to correct for this [27]. Another important feature when computing ZTD from GNSS measurements is the satellite Antenna Phase Center (APC) variations. The APC model changed with the addition of new satellites to the GNSS constellation. Jarlemark et al. [28] studied the influence of not applying proper modeling for APC, obtaining spurious, additional trends in IWV of up . On 6 November 2006, IGS changed their processing strategy from using relative antenna phase center calibrations to absolute ones. Ortiz de Galisteo et al. [29] showed the impact of this change in GNSS IWV products, using data in four locations in Spain from two years before and after this change. With relative calibrations, a 2–3 bias of GNSS with respect to other instruments (radiosonde, sun-photometer) was found. However, GNSS IWV after the change to absolute calibrations exhibited a practically zero bias. In addition, RMSE reduced to half and correlations slightly increased.
Satellite positions and clock corrections are fundamental to the retrieval of tropospheric GNSS products. However, precise data can only be obtained after a few days, so they cannot be used for near real-time applications. A comparison of near real-time water vapor product with final products to compare the effect of rapid/final satellite orbit estimation obtained negligible bias and RMSE below [30].
The mapping functions that transform slant delays into zenith delays are also error-prone. Labib et al. [31] compared GNSS IWV computed with Global Mapping Function (GMT) and Vienna Mapping Functions 1 (VMF1) on a global scale. Both products were compared against radiosonde observations. The authors concluded that there was not a better option. However, both mapping functions must be revisited for climate zones other than mid-latitude regions.
Another feature in ZTD processing that can affect IWV measurements is cutoff in elevation angle. Ning and Elgered [32] computed IWV trend using data-sets obtained with 8 different cutoff elevation angles at seven sites in Finland and Sweden for 14 years (1997–2010). In comparison with radiosonde trends, best RMSE was found for angles of and . However, the best correlation () was found for cutoff angles of . Therefore, it was shown that GNSS data contained information about trends, but these were too small to be uniquely detected.
It is important to notice that, specially when dealing with trend estimation, GNSS-IWV time series data must be retrieved with the same parameters to avoid inhomogeneities in the series.
2.3. Tomography
Although there have been some experiments with single-station retrievals of the vertical structure of water vapor [33,34], profiles are generally obtained from network solutions. Otherwise, a distribution has to be decided a priori (typically a decreasing exponential with height). One of the first efforts to water vapor tomography was made by Bi et al. [35], who developed a method for obtaining slant water vapor (water vapor integrated along the slant path) and compared it to water vapor radiometer (WVR), with RMSE less than .
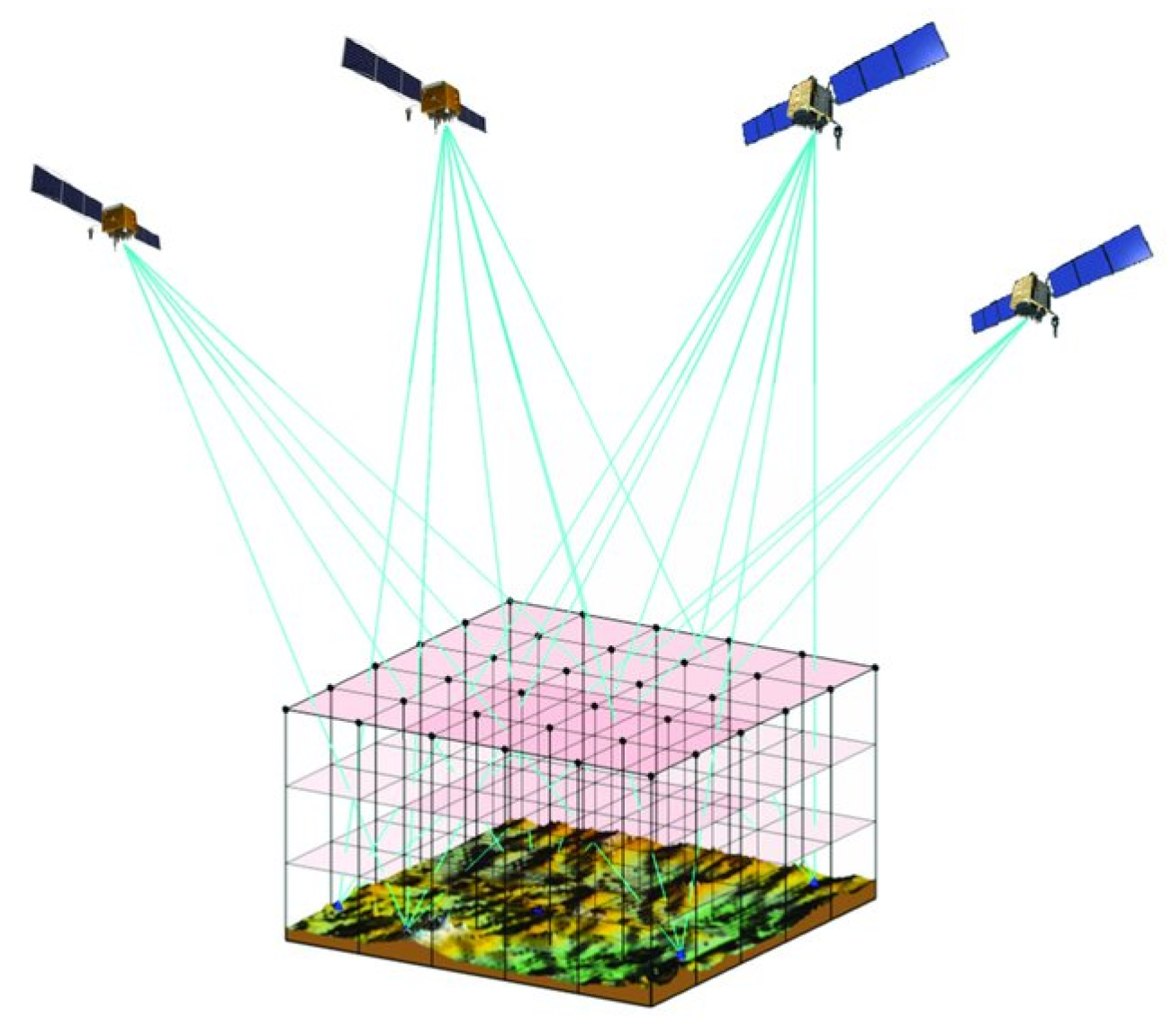
Voxel approaches, however, discretize the space in cubes (voxels) and try to obtain the concentration of water vapor in each of these voxels. This way, they provide a 3D (or 4D, if time is also considered) representation of water vapor. There are, however, many different approaches to accomplish this and none of them are trivial. One way to optimize the process was provided by Yao and Zhao [36]. They proposed the use of a long-term mean radiosonde water vapor profile in the location of the GNSS network. The horizontal voxel definition was optimized using a non-uniform symmetrical division, based on the geometry of the network. Figure 2 shows a representation of the voxel tomography, with rays crossing the voxels. At a specific time, one voxel can be crossed by many rays, while other by very few rays. This fact and other complexities of the tomography problem make it need regularization and optimization. Haji-Aghajany and Amerian [37] showed a method to solve some of these issues, obtaining tomography values of water vapor density with high spatio-temporal resolution, resulting in RMSE of . The method was to use a ray-tracing technique in which rays are allowed to move in the 3D space with a hybrid regularization method, which mixed direct and iterative methods. The main idea was to project the large-scale problem into a small-scale one that can be regularized by a direct method, and then transform back to large-scale. The technique, apart from being more efficient computationally, improved the results in some cases with respect to other methods. A different method by Yang et al. [38] tried to maximize the number of rays by considering water vapor density in the upper region outside the boundaries as four (one per direction) new parameters to obtain. This addition to the traditional method allowed the use of rays that do not come from the top boundary of the study region, but from the sides. An experiment in Hong Kong was carried out to test this method, showing better results than traditional tomography. Yang et al. [38] also showed that, to improve tomography, it is more relevant to increase the number of voxels crossed by rays than than increasing the number of rays. However, the number of possible approaches is large and, therefore, Brenot et al. [39] compared several variations of approaches to tomographic techniques with radiosonde and ECMWF reanalysis. This study recommended using stacked data over a 30 min window (increasing the number of available rays) and pseudo-slant observations in case studies and nowcasting. Regarding parametrization, another study compared some methods using the European Cooperation in Science and Technology (COST) data-set (central Europe) [40]. Among them, ray-tracing was found to be more adequate than straight-line methods. In an effort to increase the number of observations with respect to the number of unknowns, Zhang et al. [41] proposed another method, which consisted on modeling the height factor for both the isotropic and anisotropic part of slant wet delay (SWD). This would allow signals that do not cross the tomography top boundary to be included in the calculations, increasing the number of valid observations.
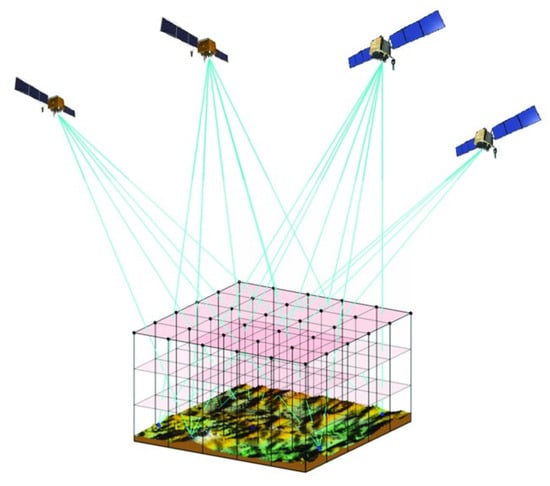
Figure 2.
Voxel-based representation of tomography, with signal rays crossing the voxels. Source: Dong and Jin [42].
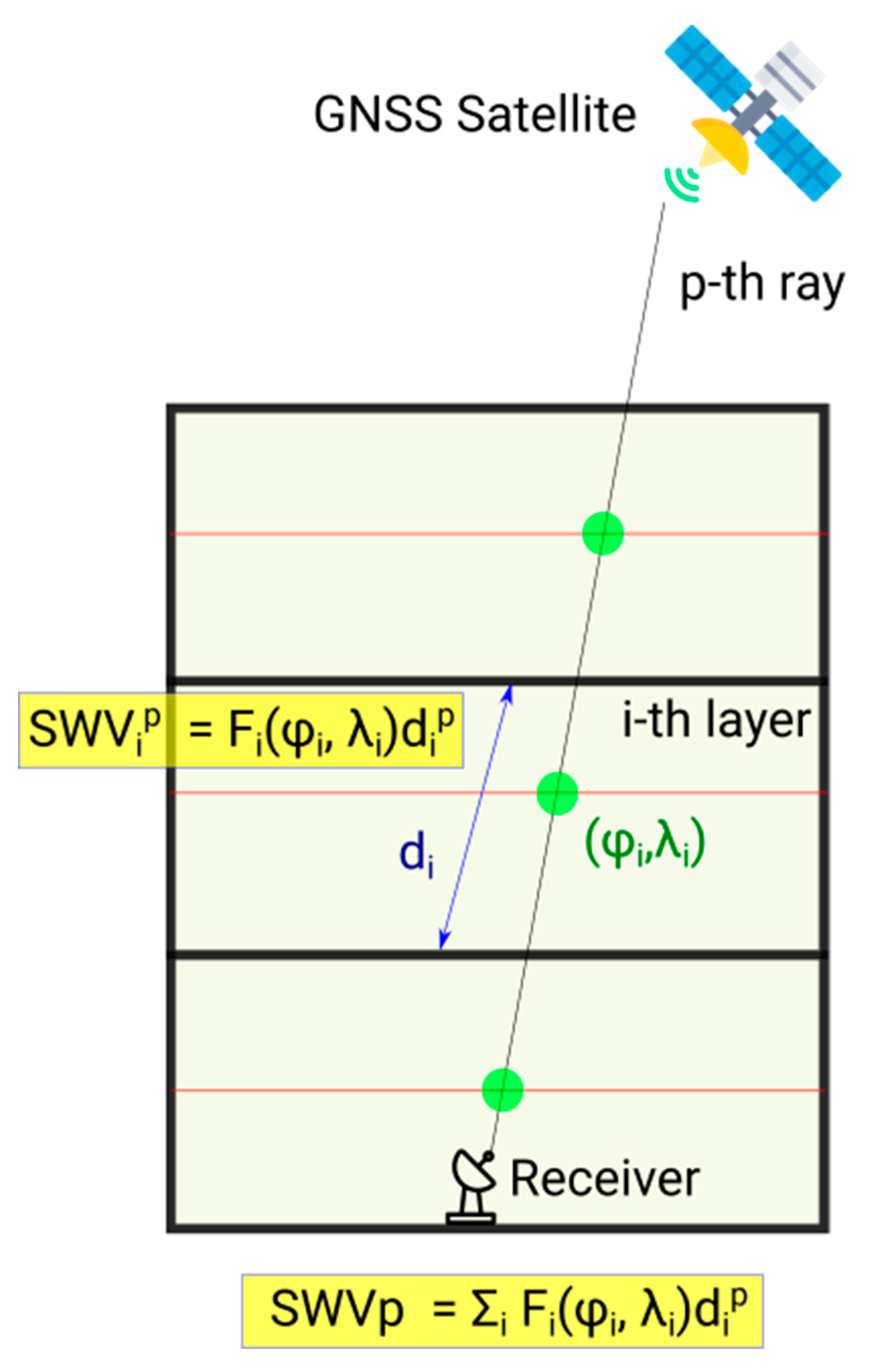
Voxel-based methodologies, despite being quite popular, have some drawbacks: (1) the rank deficiency in the coefficient matrix, leading to the need of applying constraints; (2) the assumption that water vapor is constant in the space inside each voxel; and (3) the number of unknown parameters is high compared to the number of observations. In order to avoid these drawbacks, some methodologies avoiding the use of voxels have been developed. One of then considered a function-based tomography, as Figure 3 shows. This approach uses B-spline functions and a distribution of the atmosphere in layers as the base to build the system of equations. A prior constraint of the 3D structure of the water vapor needs to be applied in this vector, based on radiosonde data. A test [43] with a 17-station network in California was carried out, comparing the conventional, voxel-based method, and this new B-spline function method, both validated against radiosonde observations. RMSE was reported to reduce by about . Instead of B-spline functions, Zhang et al. [44] proposed another method based on nodes rather than in voxels, with the aim of reducing the discretization effects. Also, a piece-wise linear fitting was used, instead of the standard (one-time) one. In an experiment to compare the standard method and this node-based method against reference radiosonde profiles, RMSE was found to decrease from to . The improvement was stronger in rainy days.
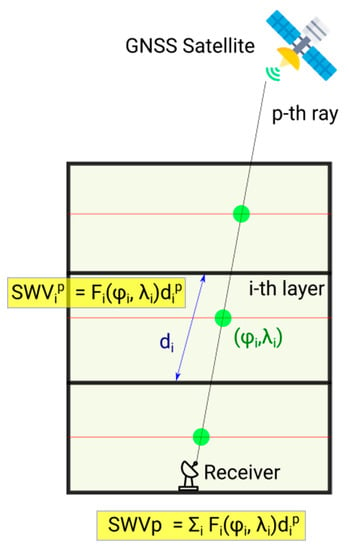
Figure 3.
Schematics of the function-based tomography [43]. The satellite and receiver images are originaly made by Freepik (https://www.freepik.com) and Flaticon (https://www.flaticon.com/) (accessed on 10 June 2021).
Whatever the tomography method proposed, another way to increase the number of observations is to include several GNSS [42]. The multi-GNSS tomography approach was validated using the Continuously Operating Reference Stations (CORS) network in Wuhan, China, against radiosonde and ERA5, improving in a GPS-only tomography. The comparison of GPS-only, GPS+GLONASS (Globalnaya navigatsionnaya sputnikovaya sistema, Russian GNSS) and GPS+GLONASS+BDS (BeiDou Navigation Satellite System, Chinese GNSS), showed that BDS did not improve much the tomography. The improvements were associated to the increase of signals available for tomography ( times more for 2-GNSS, and for the three GNSS).
Tomography of water vapor using GNSS networks is an emerging field that, although it has room for improvement, will provide very useful information about the 3D water vapor distribution. The use of multi-GNSS approaches and the densification of station networks will help improving tomography. This will improve NWP analysis and forecasts, and the general knowledge of atmospheric water vapor.
2.4. Combining with Other Measurements
Being the atmospheric water vapor highly varying in space and time, the combination of different data-sets with different characteristics can enhance the knowledge of its spatial and temporal distribution. For example, Furumoto et al. [45] proposed an algorithm to use GNSS-derived water vapor measurements to improve humidity profiles estimated from middle and upper atmosphere radar with the radio acoustic sounding technique.
The use of satellite measurements with GNSS data is an interesting idea, since satellite instruments have opposed characteristics to GNSS: high spatial, but low temporal resolution. They are also generally not available for all weather situations, but GNSS data are available for all weather situations without important quality loss. One example of this approach [46] used MEdium Resolution Imaging Spectrometer (MERIS) satellite observations combined with GNSS measurements to estimate IWV by means of a kriging methodology. Thus, IWV was retrieved at a time and point in space by means of (1) a kriging combination of GNSS IWV from several locations at that same time; and (2) MERIS IWV from that point in space at the closest time available. Another example of combination of satellite and GNSS IWV was provided by Leontiev and Reuveni [47]. This approach used Meteosat-10 data to identify cloud features, and then using this information in the GNSS IWV interpolation (Delaunay triangulation or kriging interpolation) process. Using this approach in the Israel area, and validating against radiosonde, the obtained bias and RMSE were and to and , respectively.
Other works combine GNSS data with models. An experiment ingested GNSS and Interferometric synthetic-aperture radar (InSAR) IWV and the Weather Research and Forcasting (WRF) model to cover areas that are underrepresented by GNSS/InSAR stations, using a fixed-rank kriging approach [48]. The results were compared to MERIS imagery, and uncertainties of less than were found. One of the strengths of this technique is that more data sources can be used, improving further the quality of the generated IWV maps. Another hybrid data-fusion model has been proposed, using GPT2 model as base, and correcting it with polynomial fitting and spherical harmonics functions obtained from GNSS and radiosonde IWV, also considering correction for height differences associated to each station [49].
Data fusion approaches allow increasing even more the benefits of the continuously operating GNSS networks, which have the potential to enhance weather forecasts and analysis. When applying them, it is important to correct the IWV for height differences, since IWV decrease with increasing height.
3. Inter-Comparisons with Other Techniques
3.1. Validations of GNSS Water Vapor with Other Techniques as Reference
Table 1 presents a summary of the main findings of the works used to develop this subsection. One of the first GNSS IWV validations as an emerging system for water vapor monitoring was performed by Duan et al. [50]. They applied an approach that incorporated GNSS stations that were far away (long baselines) to estimate the absolute ZTD, while previous methodologies used WVR for calibration of the relative ZTD path. This could lead to errors, since WVR overestimate IWV during rainfall. Then, they compared IWV at a few stations in Oklahoma and Kansas with nearby WVR stations, obtaining negligible bias and RMSE in the interval 1.0–1.5 . It was proved that GNSS could, by itself, provide accurate ZTD values without the need of auxiliary instruments, which was specially important for all-weather IWV retrieval, since WVR typically fails under intense rainfall. Another work analyzed the usefulness of GNSS for IWV monitoring, and compared the estimates against NWP. It was found that, although GNSS IWV showed the potential to become a powerful tool for improving forecasts, the products still needed to be refined, as biases were found in the 2–4 and RMSE of [51]. In this work, it must be noted that the meteorological data used for converting ZTD to IWV was obtained from the NWP itself, and therefore not as accurate as a meteorological station, specially for near real-time applications. There were also validations against radiosonde stations, which are usually a reference for water vapor sensing. For instance, Basili et al. [52] studied the comparison of GNSS and WVR against radiosondes during 1999 in non-precipitating conditions, using the Cagliari (Italy) GNSS station and nearby radiosonde and WVR sites. The bias between GNSS and radiosondes was and the standard deviation , which already showed better results than Iwabuchi et al. [51].

Table 1.
Summary of studies on validation of GNSS measurements. Column Year is the publication year. N is the number of stations. Instr. is the instruments (besides ground-based GNSS) used in the study. Start and End mark the period considered in the study, in year-month format. Bias is the bias in mm, and DEV is the RMSE or SD also in mm. Corr is the correlation coefficient (R).
It is useful to test the slant-IWV, as it can be used in some applications (for instance, tomography) and it is also an interesting exercise to evaluate GNSS observations without the possible errors from mapping functions. Braun et al. [53] compared line-of-sight integrals of water vapor from GNSS using WVR as a reference in Oklahoma. They found very good agreement between both techniques (correlation , RMSE ). This work concluded that GNSS data provided an all-weather alternative that is especially useful under rainfall or sever weather events, situations in which other instruments (such as WVR itself) fail.
The potential of GNSS IWV for model verification was assessed by Guerova et al. [60]. GNSS was starting to be acknowledged as a reliable technique for validating models and other instruments. Particularly, this work includes some validation of GNSS IWV against radiosondes and MWR in Switzerland between 2001 and June 2003. During daytime, GNSS showed a positive bias against radiosonde (), while at night, the bias became negative (). However, against MWR, both night and daytime GNSS IWV showed positive bias (). Therefore, in general terms, it was concluded that GNSS IWV was an accurate technique, and it was used to evaluate Alpine Model analysis and forecast [60]. The model showed a seasonal dependence with an increased dry bias in summer 2002. The main conclusion was that GNSS provide information accurate enough for model verification and assimilation. Another work [54] compared the Fifth-Generation Penn State/NCAR Mesoscale Model (MM5) forecast IWV against GNSS, radiosonde and microwave radiometer (MWR), showing that summer had worse performance (higher errors, smaller correlation) than other seasons. In this work, summer also had a higher bias (wet in this case) but this is associated to the fact that IWV values are higher in summer. The diurnal cycle is also reported to be an aspect to improve, and errors are mainly associated to errors in the temperature daily cycle by MM5. Therefore, in this work, GNSS IWV was successfully used as a reference to find deficiencies in models.
However, one of the best tests for GNSS IWV products is to compare them against radiosonde measurements, a direct method usually considered a reference despite known bias issues, see [61]. Glowacki et al. [55] compared GNSS IWV from eight stations in Australia against collocated or nearby radiosonde stations, obtaining standard deviations of , except for Antarctic stations, which increased to 18–21%. It must be noticed that GNSS is considered less sensitive to small amounts of water vapor and, therefore, in regions with small IWV, GNSS technique can perform worse. This was assessed by a cross-validation including, FTIR, sun-photometer, multifilter rotating shadowband radiometer (MFRSR), radiosonde, and GNSS in the Izaña Observatory (Canary Islands, Spain) during years 2005–2009, showed similar biases with respect to GNSS ( to ), and standard deviations (between and ), which is consistent with other works. GNSS accuracy was found to be better than for values over . However, for values under this limit, the accuracy is worse (∼20%) and a systematic dry bias appears [62].
Other comparisons against radiosondes, like the one set in four stations of the Malaysian Peninsula by Musa et al. [57] during the year 2008, or the one with four collocated reference GRUAN radiosonde stations [59], assessed the high quality of GNSS to monitor water vapor. RMSE values were in the range 3.5–4.3 in the former, while standard deviations were 0.61–1.10 in the latter, and correlations were of 0.80–0.88, reaching in the second work. Both works presented dry biases, varying between and in the first cases, and 0.49–0.87 in the second. The different biases are mainly associated to dry bias in the radiosonde measurements, while the better results in the second work could be due to the use of GRUAN stations, with high quality standards, and also to the fact that both radiosondes and GNSS stations were exactly collocated. These works show that GNSS data are high quality but, in any case, the presence of redundant measurements help assess the quality of products. Radiosonde dry bias was also assessed by Bock et al. [63]. This work inter-compared GNSS, radiosonde, Special Sensor Microwave/Imager (SSM/I) satellite instrument (in coastal stations only) and NWP (ERA-40 and National Centers for Environmental Prediction 2, NCEP2) for stations in Africa. The standard deviations were of , , , and , respectively, while the biases (GNSS - instrument) were , , , and , respectively. The results confirmed the high potential of GNSS for water vapor monitoring. Another work found a cause for dry bias in tropical regions [64]: the Integrated Global Radiosonde Archive (IGRA) product only integrates water vapor up to a pressure level of . While this is usually a fair approximation, in tropical regions it induces a dry bias in the radiosonde product; in the case of Tahiti, of 9%.
Another interesting region for validation is Antarctica. It is a region with relatively scarce water vapor observation data; yet its water vapor spatial distribution and temporal variability influences precipitation patterns and, therefore, ice accumulation. Hence, a GNSS-derived data set for Antarctica, with proven accuracy and stability, could be very useful for modeling and obtaining trends [58]. A work used homogeneously reprocessed GNSS data for the year 2004 in 12 stations [58] in this region. These data had three important improvements compared to previous GNSS IWV products: first, it used absolute antenna phase center variations. Second, it used VMF1 mapping functions. And third, an accurate a priori model for ZHD. For comparison, radiosonde measurements were used as reference, finding a GNSS bias of , very adequate even for a region with low IWV that could affect GNSS sensitivity to water vapor. Atmospheric Infrared sounder (AIRS) and Moderate Resolution Imaging Spectroradiometer (MODIS) IWV products were also compared to GNSS in this work, with low bias ( and , respectively) and RMSE ( and ). This concluded that the newly analyzed GNSS IWV product had enhanced capabilities for assimilation in NWP.
Multi-comparisons can help attribute errors to one or another instrument, making easier to analyze deeper the possible causes of error. As an example, a work that compared radiosonde, GNSS, Fourier-transform infrared spectroscopy (FTIR), MWR, Advanced Microwave Sounding Unit (AMSU-B) satellite based microwave radiometer, and ERA-Interim NWP in the location of Kiruna (Sweden) [65] found systematic differences in the range of , consistent with other mentioned works. Although the overall comparison shows a good agreement among the different techniques, they aimed to characterize the slope and offset of the different techniques, combining their study with others, but no consistent pattern emerged (the only pattern was that systematic differences were in the 1–2 range). This work also presented a method to compare values of IWV with different heights (that is, where the lower limit of the integral starts a different heights), based on a correction factor linearly dependent with height. The factor was obtained with radiosonde data. The representativeness error was also addressed, presenting a method to estimate it and, finding that it can dominate the differences among techniques, what could make it so that observed differences do not contain much information about the true precision of the techniques. This must be taken into account in future works to make validations more statistically significant. Another interesting inter-comparison [66] involved radiosondes, GNSS, sun-photometers, a combination of GOME, GOME-2 and SCIAMACHY products, and AIRS IWV product. The study was carried out in 28 sites in Northern Hemisphere. It was found that biases were in the to interval, with larger standard deviation (SD) values (0.96–3.96 ) specially for satellite instruments. Correlations with GNSS IWV were larger for ground-based instruments () while slightly smaller for satellite instruments (). Sun-photometers and satellite retrievals were shown to need low cloud fractions to perform properly, being this more important than proximity between GNSS station and satellite pixel center or sun-photometer station. All instruments showed worse performance with respect to GNSS as cloud fraction increases, which in the case of satellite instruments can be explained for the so-called screening effect. As cloudy skies typically have larger IWV, the instruments show stronger dry bias for high IWV. Radiosonde and AIRS measure both in daytime and nighttime, and both showed a wet bias during nighttime, being reduced (radiosonde) or changed to dry bias (AIRS) during daytime. In any case, inter-comparisons are reported to be site- and instrument-dependent, as Buehler et al. [65] indicated.
Not only IWV has been tested, but also profiles obtained through tomography. Ha et al. [56] validated GNSS water vapor profiles with collocated MWR and radiosonde observations, using MWR as a reference in Ulleungdo (Korea) for a few days in July 2009. It was found that GNSS tomography could even improve radiosonde’s RMSE values, but in some cases GNSS profiles were degraded, which was associated with the fact that only two GNSS stations were used in the tomography. Under severe weather, GNSS showed very good agreement with MWR, in comparison with radiosonde. This work concluded that another important issue for improving GNSS tomography was the satellite geometry, which is expected to improve with multi-GNSS approaches.
The different validations show that GNSS has great potential as a tool for IWV monitoring. It is important to put an effort into homogenizing the series, especially when calculating trends and, when performing comparisons, taking into account possible height differences and other deficiencies in the instruments considered. These efforts help reduce spurious biases and variability. The GNSS technique has the advantage of being relatively cheap, weather-independent and with high temporal resolution, and for these reasons this technique is preferred to others in many cases.
3.2. Validations of NWP with GNSS Water Vapor as Reference
Table 2 presents a summary of the main findings of the works used to develop this subsection. GNSS ground-based stations have been widely used for testing NWP. One of the first works of this kind validated High Resolution Limited Area Model (HIRLAM) against GNSS IWV in Spanish (Madrid Sierra) station [67], obtaining a bias of and RMSE of during two short periods in December 1996. Another work by Köpken [68] compared the Baltic Sea Experiment (BALTEX) model and the Europa model against 25 GNSS stations in Finland and Sweden. They found relatively high biases (2.5–3.0 ), and adequate standard deviations ( on average) and correlations ( on average), but with worse results than HIRLAM. Testing against radiosondes yielded smaller biases, what suggested GNSS could have a slight dry bias in that region. SSM/I was also analyzed in this work and showed a good correlation with the GNSS product, assessing the use of both independent instruments for validation and ingestion in analysis. NCEP reanalysis was deeply validated at a global scale against GNSS by Vey et al. [69], for a ten-year period (1994–2004) at daily resolution. The study considered 11 clusters of stations for regional analysis. The clusters were based on humidity regimes and geographical information. Also, homogeneity of time-series from GNSS stations was analyzed to select only homogeneous time-series or to correct those which had jumps in the series. The validation of NCEP covered several aspects: correlation, bias, seasonal signal, anomalies and variability. Correlation was shown to be very close to the unit, in the range 0.89–0.99, except in some regions of South America and the Antarctic Peninsula, which are regions that have a small number of observations available to be assimilated by the model and, therefore, worse performance is expected. Regarding bias, most stations were in the range, and the biases were associated to differences between the model height and the GNSS station height (which causes errors due to the assumption of temperature lapse rate). The biases were also associated with stations with high elevation, where the reduction of pressure to station level could also be error prone. Biases in stations that did not fit with these two problems (i.e., large elevation differences or large elevations) are associated with NCEP problems, such as inconsistencies in assimilated observations and inability of the model to resolve local changes. Regarding the seasonal signal, it is found to be strongly underestimated in Antarctica, while having a good agreement in Europe and most of North America. The computation of anomalies suggest sub-millimeter accuracy in GNSS, assessing its suitability for climate studies, providing that the processing strategy remains unchanged and modifications of hardware or number of GNSS observations were considered in the analysis. The study also concluded that the Southern Hemisphere needs more observations for reanalysis assimilation, suggesting the use of GNSS IWV to accomplish this.

Table 2.
Summary of studies on validation of NWP data. Column Year is the publication year. N is the number of stations. Instr. is the instruments (besides ground-based GNSS) used in the study. Start and End mark the period considered in the study, in year-month format. Bias is the bias in mm, and DEV is the RMSE or SD also in mm. Corr is the correlation coefficient (R).
However, not only direct comparisons are performed, but also other aspects, like the effect of different spatial resolution in NWP, are studied. Yang et al. [70] evaluated HIRLAM against GNSS network in Northern Europe, along with some forecasts. It was found that relatively coarse resolution () runs had a similar performance to finer resolution () ones. Therefore, a finer resolution did not mean better agreement with observations. It was also found that NWP are useful for detecting erroneous data in GNSS series.
Other studies have focused on the causes of discrepancies between NWP and GNSS. The height difference between the orography of the model and the GNSS station can induce systematic differences, since the integrals are not measured from the same base level. This issue was studied by Matsuyama et al. [71], who compared Japanese 55-year Reanalysis (JRA-55) and GNSS in 26 Japanese stations in the period July 2010 to December 2012. After JRA-55 was corrected to account for the height difference between the GNSS station and the JRA-55 integral base level of geopotential, some dry bias in JRA-55 IWV still remained. This suggested that not all of the discrepancy in IWV could be attributed to the height difference and, therefore, the hydrological cycle of this reanalysis needed deeper analysis. Moreover, NWP can provide inaccurate data when the observations assimilated have erroneous or biased data. For example, some radiosonde models have a well-known issue that caused a dry bias. To study this problem, Bock and Nuret [72] compared radiosondes and NWP (ECMWF Integrated Forecasting System, and NCEP reanalysis I and II) against GNSS IWV in western Africa over 2005–2008. In this case, the Vaisala RS80-A radiosonde had a dry bias leading to errors in NWP through assimilation, causing a dry bias of NWP with respect to GNSS. Other two radiosonde models (Vaisala RS92 and MODEM) seemed to cause a wet bias in NWP models. Another issue is how a pixel from NWP is representative of a point (i.e., a GNSS station) in the area it covers. Bock and Parracho [73] addressed the representativeness error that ERA-Interim can have with respect to GNSS in stations distributed globally. A “representativeness error statistic” was developed, showing a correlation of with standard deviation of IWV differences between ERA-Interim and GNSS. This statistic is based on the information contained in the ERA-Interim data-set for the four surrounding pixels for the GNSS station. To reduce the representativeness error, it was recommended to bilinearly interpolate data to the position of the GNSS station, as well as time-averaging. Some problematic cases (stations whose data do not fit as well as the rest) were discussed.
Nevertheless, not only is IWV tested in NWP, but also its trends. Trends of IWV are very important for discussing how climate is evolving over the years. For this reason, Bengtsson [74] discussed whether reanalysis data can provide valid trends for IWV and other variables. Particularly, IWV and its trends, computed with the ERA40 and NOSAT experiment (reanalysis without satellite data assimilation to mimic the pre-satellite era), were compared globally against GNSS data. ERA40 trends were corrected to avoid spurious trends due to changes in the observation system. In any case, the trends could not be properly reproduced when compared to GNSS data. Later, Parracho et al. [75] studied trends from ERA-Interim and Modern-Era Retrospective analysis for Research and Applications, Version 2 (MERRA-2) IWV data-sets for the period 1980–2016, as well as for 104 GNSS sites globally from 1995 to 2010. It was found that ERA-Interim was generally consistent with GNSS trends, while MERRA-2 tended globally to more moistening trends. Inconsistent trends between both reanalyses were found in Antarctica and most of the Southern Hemisphere, as well as central and Northern Africa. These regions have a high uncertainty in both reanalysis, due to the low number of in-situ observations, and the dispersion between one model and the other is generally high. Arid regions are found to have an important dependence of water vapor on circulation patterns, and therefore, in those regions the Clausius-Clapeyron scaling ratio is not a good proxy to infer IWV inter-annual variability and decadal trends.
GNSS IWV products have proven to be a reliable source of data for testing NWP performance. However, some issues must be addressed, like the homogenization of time-series (specially when dealing with trend estimation) and possible height differences between GNSS station and pixel in the orography of the NWP.
3.3. Validation of Satellite Measurements with GNSS as Reference
Table 3 presents a summary of the main findings of the works used to develop this subsection. GNSS IWV data have been widely used as a reference to validate satellite IWV products. Satellite radiometers use different regions of the electromagnetic spectrum in which water vapor have absorption bands. One of the most common is the infra-red (IR) or near infra-red (NIR), in which water vapor is the main absorbent when compared to the rest of atmospheric species. However, liquid water masses, like clouds, can disrupt the signal. This is the so-called screening effect: water vapor below the cloud remains “hidden” to the satellite radiometer, resulting in a dry bias. This is not always reflected in the comparisons, probably due to corrections in the retrieval algorithms.

Table 3.
Summary of studies on validation of satellite measurements. Column Year is the publication year. N is the number of stations. Instr. is the instruments (besides ground-based GNSS) used in the study. Start and End mark the period considered in the study, in year-month format. Bias is the bias in mm, and DEV is the RMSE or SD also in mm. Corr is the correlation coefficient (R).
Another common region for water vapor sensing is the visible, typically red or blue bands. In this case, we have the same problem as with infra-red: clouds are opaque to visible light. In addition, water vapor bands are not so strong in this region, and therefore the sensitivity will not be as high as in the IR case. However, this can be an advantage in some situations. When there is a high amount of IWV, the infra-red absorption can saturate and therefore we would not be able to sense water vapor over a certain threshold. Nevertheless, in that case, the visible bands would not saturate.
The microwave, which GNSS also use, is another common region for extracting information about water vapor. This region has the advantage of being more independent of clouds. However, passive systems (that is to say, radiometers that just receive the electromagnetic radiation reflected by the Earth’s surface and atmosphere) receive very small amounts of microwave energy. This makes it difficult to properly sense water vapor with this kind of instrument.
As we show in the following lines, different works provide very different values depending mostly on three parameters: the region studied, the specific satellite product and the quality control applied. Other sources of differences can be the use of averaged data (daily or monthly means, for example) and the period involved.
One of the first validations of satellite IWV products using GNSS as a reference was carried out by Raja et al. [76]. They compared AIRS IWV retrieval against GNSS data from a network in the United States (375 stations) during April–October 2004. Bias (AIRS-GNSS) were in the range 0.5–1.2 , while RMSE values were between and . Correlations (0.91–0.98) were calculated monthly. The biases were found to have a seasonal behavior (from negative in April, to peak positive in July and then decreasing). It was concluded that GNSS data are an excellent tool for satellite validation, because they allow all-weather verification, with a high number of pairs thanks to their high temporal resolution (30 min in this work), and their accuracy. The quality of AIRS retrievals was assessed.
The Iberian Peninsula has been widely tested, in part because of two main reasons: first, it is a region that gives home to different climate regimes in a relatively small area and, second, it is a region with a relatively dense network of GNSS stations and collocated (or nearby) meteorological stations. Bennouna et al. [77] studied the performance of MODIS-IR and NIR IWV annual cycle against ground-based techniques, mainly GNSS, in 18 locations in the Iberian Peninsula. The comparison is very detailed by zones of this region and by season, finding high differences in MODIS performance between coastal and interior stations. Representativeness error is also studied, finding that using only time-coincident data for monthly means improves the agreement between MODIS and GNSS. RMSE were found to be between and , biases of 0.1–0.4 , and correlations of 0.83–0.88. Global Ozone Monitoring Experiment 2 (GOME-2) satellite instrument was later evaluated by Román et al. [78] in this region, using 21 stations during the years 2007–2012. Bias was found to be on average, and standard deviation . They also analyzed some factors that can influence GOME-2 retrieval performance. It was found that increasing solar zenith angle also increases both bias and standard deviation, that cloud presence increases bias but does not have an effect on standard deviation, and that, under cloudless conditions, GOME-2 errors are within its nominal error. Other studies followed in the Iberian Peninsula, like those by Vaquero-Martínez et al. [82,83,84], who compared Ozone Monitoring Instrument (OMI), MODIS and a set of satellite instruments, respectively, against reference GNSS data. We will focus on the last article, as it includes OMI and MODIS (both NIR and IR products), and also other products like GOME-2, SCanning Imaging Absorption SpectroMeter for Atmospheric CHartographY (SCIAMACHY), AIRS, and Spinning Enhanced Visible and Infrared Imager (SEVIRI). They studied the pseudomedian (rather than mean bias) and the inter-quartile range (rather than standard deviation) of relative differences between satellite products and reference GNSS product in nine stations the interior Iberian Peninsula during the period 2007–2013. It was found that all satellite products tended to smooth IWV values (low IWV values tended to be overestimated, while high IWV ones tended to be underestimated). was in the range , pseudomedians between and , and inter-quartile ranges between and . Dependencies on some variables were also studied, namely, solar zenith angle, IWV, season and cloudiness, which highlighted the differences among the different satellite remote sensing approaches.
A similar multi-comparison including AIRS, GOME-2, MODIS (NIR and IR), OMI, POLarization and Directionality of the Earth’s Reflectances (POLDER) and SCIAMCHY against GNSS data in the Ny-Alesund station (European Arctic) during the period 2010–2017 was performed in another work [89]. It was found that NIR had a very low performance in this region, and that some external source for filtering out cloudy scenes is needed. OMI version 4.0 product showed high bias and variability as compared with the other products. The biases were in the range –5.9 , RMSE 2.4–5.2 and between and .
OMI IWV product has also been validated in successive versions of its algorithm retrieval [81,87]. We will only discuss the latest version (4.0) of the algorithm, which was tested against GNSS IWV globally distributed network for land and SSMI/S over the oceans. The influence of cloud scenes is studied, recommending filtering data with cloud fraction less than 0.05–0.25 and cloud top pressure more than , apart from quality flag. In the comparison, cloud fraction limit is set to , with bias of , standard deviation of and correlation with respect to GNSS. They also demonstrate the usefulness of OMI data for assimilation with WRF. However, on a more local scale, Vaquero-Martínez et al. [89] showed that, in the Arctic, OMI-GNSS bias can be very high. Therefore, although OMI product has a good performance globally, it is important to study local performance when using it for specific regions.
Ningombam et al. [80] validated MODIS-NIR IWV against a GNSS station in the Trans-Himalayan region. Bias was and RMSE , while correlation was for daily data. The comparison was also performed in a monthly/seasonal basis, finding that summer values were worse than in other seasons, which is expected because IWV increases in summer. These values were better than others reported in the literature for this product, probably because of the use of daily data.
Orbiting Carbon Observatory-2 IWV was compared against the SuomiNet global network and other instruments (IGRA’s radiosondes and AERONET sun-photometers) as references [79]. RMSE value reported against SuomiNet is and correlation of .
Gong et al. [85] analyzed the Fengyun-3A Medium resolution spectral imager (FY-3A/MERSI) IWV product against GNSS and sun-photometer measurements in the Tibetan Plateau in 2009–2013. RMSE was in the range 1.87–2.75 and bias –0.64 . He and Liu [86] compared FY-3A/MERSI, Terra/MODIS and Envisat/MERIS (all NIR satellite instruments) against GNSS in US. It was found that NIR instruments tend to underestimate IWV under cloudy conditions, as NIR cannot penetrate clouds. RMSE was of , and . RMSE was found to increase under moist conditions. Under clear-sky conditions, was of and for MERIS and MODIS, and for MERSI.
Carbajal Henken et al. [88] validated the satellite instruments, Infrared Atmospheric Sounding Interferometer (IASI), MIRS, MODIS, and MODIS-FUB, against the GNSS network in Germany. The biases were , , , and , respectively, while RMSE were in the range 2.11–3.77 and correlations 0.88–0.96. Monthly means showed similar differences, and no impact was found on time-averaging or low temporal sampling from satellite instruments. Therefore, sampling of IWV seemed to affect the mean values only marginally, but it could have an effect on frequency distribution. Nevertheless, in more challenging regions, satellite estimates of water vapor can improve greatly when averaged in time, as shown by Alraddawi et al. [90]. In this work, monthly IWV products from GOME-2, MODIS and SCIAMACHY were compared against GNSS in three Arctic stations (in the period 2001–2014). The Arctic is known to be a challenging region for satellite retrieval, as high solar zenith angle, high frequency of cloudy skies and presence of snow are problematic conditions for retrieval and remote sensing algorithms. Generally, seasonal biases were less than for AIRS, for SCIAMACHY, and for MODIS. Moreover, the increase in cloud fraction was related to increasing dry bias. Therefore, authors suggested that more robust information about clouds must be included in the retrievals to reduce the aforementioned biases.
The wide variety of satellite products using different instruments and algorithms, together with different quality criteria and the use of different regions for testing, makes it very difficult to extract common conclusions to different works. Even the most used statistical parameters can largely change with different methodological approaches, especially different quality controls. For that reason, we conclude that the scientific community should establish a series of common practices to perform validations in order to make different works comparable. Moreover, it can be concluded that satellite measurements can have very good quality if the right conditions are met. There is a general agreement that cloudy and/or high moisture situations tend to cause worse values of accuracy and precision metrics (i.e., MBE or SD).
4. Spatio-Temporal Analysis
Table 4 summarizes some of the findings of each paper from this section.
4.1. Asia
China. Jin et al. [91] investigated the spatial, seasonal and diurnal distribution of water vapor for three years (2004–2007). The region with the highest IWV was the South-East, with a strong annual cycle (amplitude of ∼), while the lowest IWV was found in the North-West region, with a smaller annual cycle (amplitude of ∼). Mean diurnal cycle amplitude was found to be . The spatial distribution was dependent on latitude, topography, season and monsoon. Wu et al. [92] studied midsummer diurnal variations over 18 stations around the Poyang Lake during three year period (2015–2018). Diurnal IWV typically peaks at 1200–2000 Local Solar Time (LST). Air temperature diurnal cycle was reported to be likely behind the IWV diurnal cycle. The semi-diurnal cycle was found to account for about of variance contribution. Tibetan Plateau is a region of high interest in China, specially because of its role in the summer monsoon. Takagi et al. [93] studied the premonsoon and monsoon diurnal variability at the station of Lhasa in this region. Premonsoon minima and maxima occurred at 1800 and 0400 LST, respectively, while, in the monsoon period, these were displaced to 1500 and 2300 LST. This result shows that water vapor is affected by local circulation. It also indicates the usefulness of GNSS for studying the IWV daily cycle and recommends the addition of more stations to the Plateau in order to study moisture transport in the region.
Japan. Iwasaki and Miki [94] studied the diurnal variability in 5 GNSS stations and the other three radiosonde stations. The maximum was found around 1800–2000 LST, some hours later than in China. Li et al. [95] also analyzed the diurnal variations in central Japan during August 2000, which found the maximum at the same hours. The moisture transport was found to cause the differences in phase of the diurnal cycle of IWV among different locations.
Sumatra. Wu et al. [96] presented the diurnal variation in the island of Sumatra, and found a distinct diurnal cycle. Torri et al. [97] used data from the Sumatran GNSS array to study the diurnal cycle of water vapor. The Madden–Julian oscillation (MJO) was found to impact on the diurnal cycle, appearing smaller in both the daily mean and the amplitude of the diurnal cycle during the suppressed phase relative to the developing/active MJO phase. The evening/nighttime peaks of IWV offshore appeared later during the suppressed phase of the MJO compared to its active phase (from 1900 LST in the active phase to 2200 LST in the suppressed phase).
South Korea. Sohn and Cho [98] estimated the trend over 5 stations of South Korea (2000–2009) as year. They also calculated seasonal trends for summer ( year), winter ( year), spring ( year), and autumn ( year).

Table 4.
Summary of spatio-temporal studies. Unless indicated otherwise, times are given in local solar time and trends in .
Table 4.
Summary of spatio-temporal studies. Unless indicated otherwise, times are given in local solar time and trends in .
| Work | Year | N | Start | End | Region | Type | Value |
|---|---|---|---|---|---|---|---|
| [94] | 2001 | 5 | 1999-07 | 1999-08 | Japan | Diurnal | max: 1900 |
| [99] | 2002 | 54 | 1996-01 | 2000-12 | North America (US) | Diurnal | max: 1000–1400 (winter) and midafternoon-midnight (summer) |
| [100] | 17 | 1993-08 | Scandinavia (Sweden) | Trends | 0.15 | ||
| [101] | 2007 | 2 | 1998-01 | 2006-12 | Africa (South Africa) | Trends | non-significant |
| [95] | 2008 | 6 | 2000-08 | 2000-08 | Japan | Diurnal | max: 1900, min: noon |
| [102] | 2009 | 32 | 1996-01 | 2005-12 | Baltic (Finland, Latvia, Sweden) | Diurnal | - |
| [103] | 9 | 2003-01 | Antarctic | Seasonal | |||
| Diurnal | max: 0600–0900 UTC, min: 1800–2100 UT | ||||||
| [98] | 2010 | 5 | 2000-01 | 2009-12 | SouthKorea | Trends | 0.11 |
| [104] | 2011 | 10 | 2002-01 | 2011-12 | Iberian P. (Spain) | Diurnal | min: 0430–0530 UTC, Afternoon |
| [105] | 2015 | 4 | 2009-01 | 2012-12 | Europe | Seasonal | |
| Diurnal | - | ||||||
| [106] | 2017 | 113 | 1996-01 | 2015-12 | Europe (Germany) | Trends | −0.15–0.23 |
| [107] | 5 | 2004-01 | 2012-12 | Northeast India (India) | Seasonal | max: summer, min: winter | |
| Northeast India (India) | Diurnal | max: 1000–1300 UTC | |||||
| [108] | 2018 | 2 | 2006-01 | 2018-01 | Central France (France) | Diurnal | - |
| Central France (France) | Trends | non-significant | |||||
| [97] | 2019 | 24 | 2005-01 | 2008-12 | Sumatra | Diurnal | max: 1900 (land); 1300 and 0100 (offshore) |
| [109] | 192 | 2004-01 | 2017-12 | Global | Seasonal | ||
| Trends | - | ||||||
| [110] | 2020 | 35 | 2000-01 | 2018-12 | Europe (Switzerland) | Trends | 0.001–0.109 |
| [111] | 8 | 2018-06 | 2020-03 | SW Indian Ocean | Diurnal | - | |
| [112] | 12 | 2009-01 | 2019-12 | Indian Ocean | Seasonal | max: austral summer | |
| Diurnal | max: late afternoon/evening (land); night (ocean); early morning (coastal), min: morning (land); mid-day (ocean); late afternoon (coastal) | ||||||
| [113] | 11 | 2007-01 | 2015-12 | Thailand | Seasonal | max: mid-May–end-October | |
| Trends | - | ||||||
| [92] | 18 | 2015-01 | 2018-12 | Poyang Lake (China) | Diurnal | max: 1600 |
India. Barman et al. [107] analyzed GNSS IWV from five stations in India during the period 2004–2012. They found that high altitude sites had weaker annual variability than low altitude ones. However, seasonal variability was similar in the five sites. Seasonal IWV was strongly linked to the monsoon, with maximum in summer and minimum in winter. The diurnal cycle was marked in high altitude sites, while weak in low altitude ones. Bousquet et al. [111] presented a new GNSS network in the Southwest Indian Ocean in the frame of the Indian Ocean GNSS Application for Meteorology Project, which is being deployed since November 2017. They analyzed the period from 2018 to 2020 and found that minimum seasonal values decrease away from the equator. Diurnal cycle was found to differ at both sides of Madagascar. This study was extended by Lees et al. [112], where the seasonal time-scale was studied. The annual amplitude of IWV was reported to vary in the interval 10–15 near the equator and in the interval 20–30 in the subtropics. The strongest daily IWV amplitudes were found in the mountainous islands. The reanalysis ERA5 was found to reproduce the main features of IWV time series.
Thailand. Trakolkul and Satirapod [113] studied GNSS IWV series of 11 CORS stations in Thailand to analyze seasonal features and trends. The annual variation amplitude was reported to be in the range 6–19 .
4.2. Europe
General. Sharifi and Souri [105] used a hybrid approach to time series modeling of GNSS IWV series over four sites in Europe (years 2009–2012, 5-min sampling), combining least squares harmonic estimation (for modeling harmonic characteristics) with least squares support vector machine optimized by cross-validation strategy (for modeling non-harmonic features). Inter-seasonal variability was found to be greater than inter-annual variability. Diurnal cycles were strong in summer with maxima between 1200 and 1800 LST. The peaks were related to solar flux and the phase to other features, such as location or wind/temperature patterns.
Northern Europe. Gradinarsky et al. [100] studied trends of water vapor in the region of Scandinavia during the years 1993 and 2000. They found that the GNSS station radome can affect measurements to an extent between and . Trends were positive, 0.1–0.2 . These GNSS-calculated trends were found to be consistent with other measurements (i.e., radiosondes and MWR), assessing the potential of GNSS IWV in climate monitoring. Jakobson et al. [102] analyzed the diurnal variability of water vapor in 32 sites in the Baltic region, during 1996–2005. Peak to peak difference was of 0.5–0.6 in spring/summer, while winter and autumn lacked a clear pattern. The high variability (mainly with synoptic situation, or substitution of air masses) makes that the diurnal cycle can only be observed when averaging over many years.
France. Hadad et al. [108] combined different types of water vapor measurements to study two sites in France. The work presented a non-significant trend at the site of Cézeaux of . Both stations presented almost no diurnal cycle and the authors concluded that variability of surface water vapor was influenced by sporadic circulation patterns rather than by regular diurnal variations.
Switzerland. Bernet et al. [110] studied trends of water vapor over Switzerland using different instruments, including 31 GNSS sites in the period 1995 to 2018. Jumps caused by instrumentation changes were corrected. IWV was found to increase with a rate of 2–5% . From the comparison among different instruments, it was concluded that GNSS data are reliable for the detection of trends, but a few stations need quality control and harmonization.
Spain. Ortiz de Galisteo et al. [104] analyzed the diurnal cycle of IWV in 10 GNSS Spanish stations for the years 2002–2011, finding that it explained 3–7% of sub-daily annual variability. IWV was found to peak at 0430–0530 UTC, and the diurnal cycle was found to be more important in the Mediterranean sites than in the inland or Atlantic ones. The summer diurnal cycle is also more variable among sites. The first two harmonics (diurnal and semidiurnal cycles) explained of the variance. Another work analyzed the annual cycle in the same period and stations [114], finding that the 12-month harmonic explained of variance, with a maximum in summer and minimum in the winter months. Southwestern sites, however, showed a local minimum in July, which can be explained by the presence of dry air masses. The Mediterranean sites had larger amplitudes than inland sites. The July local minimum had been already reported by Torres et al. [115], who characterized the IWV in the Gulf of Cadiz region, in southern Iberian Peninsula using GNSS, radiosondes and a sun-photometer.
Germany. Alshawaf et al. [106] studied the IWV time series over 113 GNSS stations in Germany, with 10–19 years of temporal coverage, together with meteorological data from automatic stations and ERA-Interim reanalysis. GNSS IWV trend ranged between and . However, longer time-series from ERA-Interim (∼) revealed positive trends in all sites, which also had a gradient from southwest to northeast. Trends obtained from dew-point temperature were comparable with the other estimates, and therefore can be used when observations are not available.
4.3. Africa
Combrink et al. [101] studied times-series of GNSS-derived IWV in South Africa, with the aim of detecting trends in the period. They used the autoregressive–moving-average (ARMA)(1,1) model, concluding that this model represents better the real trend, provided that more than five years of data are used. They also concluded that none of the two stations used had statistically significant trends.
4.4. America
Dai et al. [99] studied GNSS IWV from 54 stations over North America. Diurnal variations were significant, explaining over the of the subdaily variance, specially in summer, with weaker diurnal cycles in the rest of the seasons. Peaks are found around 1000–1400 LST in winter, and from midafternoon to to midnight in summer. The semidiurnal cycle is rather weak.
Yu et al. [116] proposed a model to spatially interpolate GNSS ZTD and used interpolated values from meteorological stations for pressure and in California. The interpolation method is iterative and tries to decouple turbulent- and elevation-dependent ZTD components. Validation with MODIS as a reference yielded RMSE of .
Bordi et al. [117] studied temporal series of six GNSS stations in Eastern US, where it was found that the variability of IWV is dominated by the annual cycle, with a missing daily cycle, while RH from weather stations is more characterized by the daily cycle, without an annual cycle.
4.5. Antarctic Region
Suparta et al. [103] studied the GNSS IWV over 9 sites in Antarctic during two years (2003–2005). The diurnal variation was remarkable in summer, but not in winter. IWV was higher in summer than in winter. Moreover, it was found that the presence of strong winds can cause a decrease in monthly IWV.
4.6. Global
Jin and Luo [118] analyzed 13 years (1995–2007) of data from 155 GNSS stations globally and distributed and studied the seasonal variation of IWV. Globally, seasonal maxima were found in summer and minima in winter. Annual cycle amplitude was 10–20 in mid-latitudes and in high latitudes and equatorial areas. Semiannual variation amplitudes were less important, at about . The diurnal cycle was also studied and it was found to have an amplitude of 0.2–1.2 , and the maximum and minimum occurred around noon and midnight, respectively. The semidiurnal cycle was reported to have a weaker amplitude below . Zhao et al. [109] agreed with this, finding that annual variability was the more important component in IWV variation. This last work used 192 IGS stations distributed globally to interpolate and analyze IWV at a global scale during the period 2004–2017. Despite the different periods with very few years in common, both works show similar results.
Regarding trends, Chen and Liu [119] presented a global analysis of the trends of IWV using different products, including reanalysis ERA-Interim and NCEP, SSM/I microwave satellite, radiosondes and GNSS. Particularly, 100 GNSS stations were used in the study, with a time-span of 15 years. The other products had longer time-series, reaching 36 years of reanalysis and radiosondes. Therefore, the trends were calculated at different timescales to allow comparisons. The 15 year period 2000–2014 was concluded to have stronger upward trends than longer periods. The trends were not homogeneous, being negative in Asia, the United States or North Africa, while large positive trends were found in the North and West Pacific, Europe, the eastern Indian Ocean, and southern Asia. The polar region is the one with a larger increase in IWV. Another interesting issue discussed in this work is the relationship between surface temperature and IWV. According to Clausius-Clapeyron equation, the increase rate of water vapor should be 6–13%. However, some regions depart greatly from this range, reaching negative values in this rate. Such large departures were associated to regional moisture divergence/convergence. At a global scale, the Clausius-Clapeyron estimate remains valid. This issue was also studied by Wang et al. [120], who found that using night surface temperature had better correlation with IWV, and therefore it was suggested to use it for studies on water vapor feedback.
5. Impact of Water Vapor Variability on Meteorology and Climate
5.1. Assimilation
NWP models need to ingest real data in the process known as assimilation to be able to perform predictions. Therefore, GNSS data can be an interesting source for NWP assimilation, especially in regions where other sources of atmospheric water vapor information are missing. Gutman and Benjamin [121] showed that GNSS data improved forecasts from NWP models. Particularly they used the Rapid Update Cycle in the US, and assimilated data from 18 and 55 stations. They found improvements in relative humidity (RH) of up to for the 55-station experiment and up to for the 18-station experiment. Despite being a modest improvement, it must be taken into account that the US had already good knowledge of the moisture from other kinds of measurements already assimilated by the model. Therefore, in other regions this could be enhanced, and even in the US, the improvement was evident, especially in the 3-h forecast. They also developed techniques to retrieve GNSS IWV measurements every 30 min to be available for forecasters and modelers, improving IGS service in latency. Other works from the 2000s found moderated improvements in models as well: Guerova et al. [122], who assimilated GNSS IWV from COST Action 716 into the MeteoSwiss NWP model; Yuan et al. [123], who assimilated IWV data from 11 GNSS stations in China into the MM5 model; Gendt et al. [124], who presented a near real-time GNSS IWV product in the context of the project GASP and assimilated it into the local model from German Weather Service; and Zhang et al. [125], who tested the GNSS assimilation in a severe weather event in Beijing.
All these works considered the assimilation of the IWV GNSS data. However, it is possible to use more direct data, such as SWD. Ha et al. [126] compared the assimilation of SWD and IWV from the GNSS network and found SWD to be more appropriate for correctly retrieving temperature and moisture profiles. They used a hypothetical GNSS network of 64 stations in the US, using the MM5 4-dimensional variational data assimilation system. Liu and Xue [127] used a similar approach, but assimilated slant water vapor (SWV) into the 3D-variational (3DVAR). The tests included hypothetical GNSS stations as well and sensitivity analysis, concluding that GNSS SWV assimilation is positive even with the inclusion of typical errors in measurements.
The introduction of multi-GNSS processing can improve near real-time measurements in several ways. First, it can provide more accurate data by increasing the number of frequencies used, as new GNSS satellites introduce a third frequency (better combinations of signals). Second, having more satellites available makes possible to increase temporal resolution (below 30 min) and spatial resolution through networks and tomography techniques. Karabatić et al. [128] performed an experiment in Austria with the use of multi-GNSS (GNSS and GLONASS) network, finding the assimilation of multi-GNSS data very positive and concluding that Galileo constellation inclusion could improve analysis even more.
In addition to this, it must be noted that regions lacking dense networks of ground-based GNSS stations can also benefit from GNSS data assimilation. Kumar et al. [129] showed that assimilating GNSS data from a single station was enough to locally improve (∼) the short-term forecasts in an experiment over southern India during the monsoon. Of course, it will be better if there is moisture information from more GNSS stations, but regions lacking moisture information from other sources can benefit from GNSS data even with a single station in the region of interest. If two-frequency stations are not available, it may be possible to use single-frequency receivers for assimilation. This issue is still under study and more research could be useful, as the use of single-frequency receivers can provide very dense networks as compared to dual-frequency ones. One experiment was performed using the Regional Atmospheric Modeling System (RAMS) 3D variational data assimilation system to assimilate GNSS-ZTD from single-frequency receivers. It was concluded that, although results are preliminary and some issues must be addressed, the assimilation was very positive for both ZTD and IWV fields [130].
5.2. Circulation
As pointed out in Section 3, water vapor is greatly affected by circulation patterns, which can transport moisture or dry air to different regions. For this reason, GNSS can provide information about these circulation patterns in certain regions. Graham et al. [131] used GNSS IWV data to show that important differences in IWV can occur between the Swiss plains and nearby Alps during some thunderstorms events, attributable to regional airflow convergence. They presented a method to acquire information about the amount and change of total IWV over time for the mesoscale in the Bernese Oberland area using the GNSS IWV data. An anti-correlation pattern was found between Payerne and Saanen, which suggested a mountain-plain circulation pattern. Moreover, Kingsmill et al. [132] and Neiman et al. [133] used GNSS IWV products among other remote-sensing information about the state of the atmosphere to study the northern California Valley, which has sierra barrier jets and land-falling atmospheric rivers (ARs), modulators of the rainfall in this region. The study links these two phenomena with the orographic configuration of the Valley, and the concurrence of both phenomena at the same time, or just one of them, affects the spatio-temporal rainfall pattern.
GNSS has been used to study water vapor during El Niño events in the coast of the South China Sea [134]. During these events, IWV drops, reaching a minimum about 10 weeks later, while the opposite happens during La Niña events. Therefore, GNSS IWV is suggested to be a useful instrument for studying ENSO activity.
5.3. Radiative Transfer Studies
There has been recent interest in the role of water vapor in radiative balance, enhanced by the increase in water vapor data availability, with higher spatial and temporal resolution. Vaquero-Martínez et al. [135] studied the short-wave effects of water vapor using 20 GNSS stations in the Iberian Peninsula as input to Santa Barbara’s dissort radiative transfer model (SBDART). They found that the effect for cloudless skies followed an empirical power relation of the short-wave effect with IWV and the cosine of the solar zenith angle. An extended study [136], including short- and long-wave in seven selected stations, found that positive trends for long-wave (and total) water vapor effects could partially explain the well-known increase of surface air temperatures in the Iberian Peninsula, while the negative trend in the short-wave effect represented about a quarter of the contribution of aerosols to the so-called brightening effect.
In a more practical fashion, GNSS data are also used for the modeling of atmospheric transmission. The PWV_KPNO python package [137] uses GNSS IWV data from the SuomiNet network for modeling atmospheric transmission function due to water vapor. The package interpolates IWV data from the GNSS stations to the desired position and then applies the MODTRAN model to obtain the atmospheric transmission.
6. Conclusions
GNSS sensing of atmospheric water vapor is already a well established technique that allows for the monitoring of this trace gas with wide (yet land-only) coverage, with high temporal resolution and without weather restrictions. These features make this technique very suitable for testing other techniques, especially when weather is adverse. In comparison with other products, GNSS water vapor data are high quality, being considered a reference for the validation of other ground-based and satellite-based water vapor measurements and model estimates. However, we consider that special care must be taken with some issues. First, IWV is dependent on height and therefore when comparing data related to different heights (i.e., ground-based stations and different heights, satellite or NWP pixels at a mean height of the area, different from the real height of the GNSS station) it is important to apply the corresponding correction to account for this height difference. Second, the homogeneity of the series must be checked (especially if there are changes in antenna or processing strategy). Third, it is considered a rule of thumb that GNSS retrieve water vapor information of about radius, which can be used to set a condition on distance to GNSS station when performing validations.
Nowadays, time-series of GNSS data products are starting to be long enough to study water vapor in long term studies, such as its trends and variability across different time scales. Additionally, the increasing amplitude of the ground-based GNSS networks allows for a detailed analysis of its spatial distribution. It is observed that, despite the average behavior based mainly on temperature (according to the Clausius-Clapeyron equation), local circulation is more important. Although there are clear cycles in daily and annual regimes, situations with relevant local circulation can disrupt these. Therefore, it is fundamental to use long-term data to study daily and annual cycles, especially in regions where strong circulation patterns can modify air moisture.
GNSS water vapor has been widely used for several meteorological and climate applications such as assimilation, circulation of the atmosphere and radiative effects. It is shown that assimilation can be improved with GNSS data, especially in regions where there may be a lack of moisture information. It must be noted that GNSS are relatively cheap and easy to maintain, and provide continuous measurements for all-weather conditions. This means they can be used in regions with fewer resources or those where human access is difficult.
Despite being a well established technique, it must be noted that many other GNSS-based techniques, such as tomography or data fusion approaches, can make the best out of the information that GNSS meteorology has to offer. The use of multi-GNSS techniques, especially, have the potential to improve the quality of these approaches. The use of low-cost devices (i.e., single frequency receivers) can be interesting in terms of retrieving moisture information cost-effectively.
In summary, the GNSS technique allows the retrieval of accurate atmospheric water vapor data. This method exhibits great potential to be extraordinarily useful in the monitoring of the weather and climate.
Author Contributions
Conceptualization, M.A.; Data curation, J.V.-M.; writing—original draft preparation, J.V.-M.; writing—review and editing, M.A.; supervision, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partly supported by the Ministerio de Economia y Competitividad of the Spanish Government (CGL2017-87917-P), and by Junta de Extremadura and European Regional Development Fund (IB18092). Javier Vaquero-Martinez was supported by a predoctoral fellowship (PD18029) from Junta de Extremadura and European Social Fund.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AIRS | Atmospheric Infrared sounder |
| AMSU-B | Advanced Microwave Sounding Unit |
| APC | Antenna Phase Center |
| AR | atmospheric river |
| BALTEX | Baltic Sea Experiment |
| BDS | BeiDou Navigation Satellite System (Chinese GNSS) |
| CORS | Continuously Operating Reference Stations |
| COST | Cooperation in Science and Technology |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| FTIR | Fourier-transform infrared spectroscopy |
| FY-3A/MERSI | Fengyun-3A Medium resolution spectral imager |
| GASP | Atmosphere Sounding Project |
| GLONASS | Globalnaya navigatsionnaya sputnikovaya sistema (Russian GNSS) |
| GNSS | Global Navigation Satellite Systems |
| GOME-2 | Global Ozone Monitoring Experiment 2 |
| GPS | Global Positioning System |
| GPT | Global Pressure and Temperature |
| HIRLAM | High Resolution Limited Area Model |
| IGS | International GNSS Service |
| InSAR | Interferometric synthetic-aperture radar |
| IPWV | Integrated precipitable water vapor |
| ITU-R | International Telecommunication Union - Radiocommunications |
| IWV | Integrated water vapor |
| JRA-55 | Japanese 55-year Reanalysis |
| MERIS | MEdium Resolution Imaging Spectrometer |
| MERRA-2 | Modern-Era Retrospective analysis for Research and Applications Version 2 |
| MFRSR | Multifilter rotating shadowband radiometer |
| MGEX | Multi-GNSS Experiment |
| MJO | Madden–Julian oscillation |
| MM5 | Fifth-Generation Penn State/NCAR Mesoscale Model |
| NWP | Numerical weather models |
| OMI | Ozone Monitoring Instrument |
| POLDER | POLarization and Directionality of the Earth’s Reflectances |
| PW | Precipitable water |
| PWV | Precipitable water vapor |
| RAMS | Regional Atmospheric Modeling System |
| RH | Relative humidity |
| RMSE | Root mean square error |
| SBDART | Santa Barbara’s dissort radiative transfer model |
| SCIAMACHY | SCanning Imaging Absorption SpectroMeter for Atmospheric CHartographY |
| SD | Standard deviation |
| SEVIRI | Spinning Enhanced Visible and Infrared Imager |
| SSM/I | Special Sensor Microwave/Imager |
| SSMI/S | Special Sensor Microwave Imager/Sounder |
| STD | Slant tropospheric delay |
| SWD | Slant wet delay |
| Tm | Weighted mean temperature of the atmosphere |
| Ts | Surface temperature |
| VMF1 | Vienna Mapping Functions 1 |
| WVR | Water vapor radiometer |
| ZHD | Zenith hydrostatic delay |
| ZTD | Zenith tropospheric delay |
| ZWD | Zenith wet delay |
References
- Colman, R. A Comparison of Climate Feedbacks in General Circulation Models. Clim. Dyn. 2003, 20, 865–873. [Google Scholar] [CrossRef]
- Colman, R.A. Climate Radiative Feedbacks and Adjustments at the Earth’s Surface. J. Geophys. Res. Atmos. 2015, 120, 3173–3182. [Google Scholar] [CrossRef]
- Myhre, G.; Shindell, D.; Bréon, F.M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambrdige University Press: Cambridge, UK, 2013; pp. 659–740. [Google Scholar]
- Bonafoni, S.; Biondi, R.; Brenot, H.; Anthes, R. Radio Occultation and Ground-Based GNSS Products for Observing, Understanding and Predicting Extreme Events: A Review. Atmos. Res. 2019, 230, 104624. [Google Scholar] [CrossRef]
- Liu, C.; Kirchengast, G.; Syndergaard, S.; Kursinski, E.; Sun, Y.; Bai, W.; Du, Q. A Review of Low Earth Orbit Occultation Using Microwave and Infrared-Laser Signals for Monitoring the Atmosphere and Climate. Adv. Space Res. 2017, 60, 2776–2811. [Google Scholar] [CrossRef]
- Wickert, J.; Michalak, G.; Schmidt, T.; Beyerle, G.; Cheng, C.Z.; Healy, S.B.; Heise, S.; Huang, C.Y.; Jakowski, N.; Köhler, W.; et al. GPS Radio Occultation: Results from CHAMP, GRACE and FORMOSAT-3/COSMIC. Terr. Atmos. Ocean. Sci. 2009, 20, 35. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. Climatol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Dabberdt, W.F.; Schlatter, T.W. Research Opportunities from Emerging Atmospheric Observing and Modeling Capabilities. Bull. Am. Meteorol. Soc. 1996, 77, 305–323. [Google Scholar] [CrossRef]
- Dow, J.; Neilan, R.; Gendt, G. The International GPS Service: Celebrating the 10th Anniversary and Looking to the next Decade. Adv. Space Res. 2005, 36, 320–326. [Google Scholar] [CrossRef]
- Dach, R.; Dietrich, R. Influence of the Ocean Loading Effect on GPS Derived Precipitable Water Vapor. Geophys. Res. Lett. 2000, 27, 2953–2956. [Google Scholar] [CrossRef]
- Dick, G.; Gendt, G.; Reigber, C. First Experience with near Real-Time Water Vapor Estimation in a German GPS Network. J. Atmos. Sol. Terr. Phys. 2001, 63, 1295–1304. [Google Scholar] [CrossRef]
- MacDonald, A.E.; Xie, Y.; Ware, R.H. Diagnosis of Three-Dimensional Water Vapor Using a GPS Network. Mon. Weather Rev. 2002, 130, 386–397. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D Tropospheric Tomography Using GPS Slant Wet Delays. Ann. Geophys. 2000, 18, 0223–0234. [Google Scholar] [CrossRef]
- Morland, J.; Deuber, B.; Feist, D.G.; Martin, L.; Nyeki, S.; Kämpfer, N.; Mätzler, C.; Jeannet, P.; Vuilleumier, L. The STARTWAVE Atmospheric Water Database. Atmos. Chem. Phys. 2006, 6, 2039–2056. [Google Scholar] [CrossRef]
- Bender, M.; Raabe, A. Preconditions to Ground Based GPS Water Vapour Tomography. Ann. Geophys. 2007, 25, 1727–1734. [Google Scholar] [CrossRef]
- Li, X.; Dick, G.; Lu, C.; Ge, M.; Nilsson, T.; Ning, T.; Wickert, J.; Schuh, H. Multi-GNSS Meteorology: Real-Time Retrieving of Atmospheric Water Vapor From BeiDou, Galileo, GLONASS, and GPS Observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6385–6393. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, Prospects and Challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Emardson, T.; Derks, H. On the Relation between the Wet Delay and the Integrated Precipitable Water Vapour in the European Atmosphere. Meteorol. Appl. 2000, 7, 61–68. [Google Scholar] [CrossRef]
- Suresh Raju, C.; Saha, K.; Thampi, B.V.; Parameswaran, K. Empirical Model for Mean Temperature for Indian Zone and Estimation of Precipitable Water Vapor from Ground Based GPS Measurements. Ann. Geophys. 2007, 25, 1935–1948. [Google Scholar] [CrossRef]
- Heise, S.; Dick, G.; Gendt, G.; Schmidt, T.; Wickert, J. Integrated Water Vapor from IGS Ground-Based GPS Observations: Initial Results from a Global 5-Min Data Set. Ann. Geophys. 2009, 27, 2851–2859. [Google Scholar] [CrossRef][Green Version]
- Wang, Z.; Xing, Z.; Zhou, X.; Tang, Q.; Zhou, D.; Sun, W. GPS-Based Precipitable Water Vapour Retrieval and Variability Using Measured and Global Reanalysis Data in the Coastal Regions of China. Int. J. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Liang, H.; Lou, Y.; Cai, Y.; Cao, Y.; Zhou, Y.; Liu, W. On the Suitability of ERA5 in Hourly GPS Precipitable Water Vapor Retrieval over China. J. Geod. 2019, 93, 1897–1909. [Google Scholar] [CrossRef]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an Improved Empirical Model for Slant Delays in the Troposphere (GPT2w). GPS Solut. 2015, 19, 433–441. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Charoenphon, C.; Satirapod, C. Improving the Accuracy of Real-Time Precipitable Water Vapour Using Country-Wide Meteorological Model with Precise Point Positioning in Thailand. J. Spat. Sci. 2020, 1–17. [Google Scholar] [CrossRef]
- Iwasaki, H.; Kimura, F.; Nakagawa, K.; Miki, T.; Kimata, F.; Shimada, S.; Nakao, S. The Influence of the Moisture Gradient on the Accuracy of Precipitable Water Derived from GPS Data. J. Meteorol. Soc. Jpn. Ser. II 2000, 78, 223–231. [Google Scholar] [CrossRef]
- Jarlemark, P.; Emardson, R.; Johansson, J.; Elgered, G. Ground-Based GPS for Validation of Climate Models: The Impact of Satellite Antenna Phase Center Variations. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3847–3854. [Google Scholar] [CrossRef]
- Ortiz de Galisteo, J.P.; Toledano, C.; Cachorro, V.; Torres, B. Improvement in PWV Estimation from GPS Due to the Absolute Calibration of Antenna Phase Center Variations. GPS Solut. 2010, 14, 389–395. [Google Scholar] [CrossRef]
- Yadav, J.; Giri, R.; Malik, D. Effect of Broadcast and Precise Satellite Orbits in the Estimation of Zenith Tropospheric Delay and Integrated Precipitable Water Vapour from GPS. MAUSAM 2010, 61, 197–202. [Google Scholar]
- Labib, B.; Yan, J.; Barriot, J.P.; Zhang, F.; Feng, P. Monitoring Zenithal Total Delays over the Three Different Climatic Zones from IGS GPS Final Products: A Comparison between the Use of the VMF1 and GMF Mapping Functions. Geod. Geodyn. 2019, 10, 93–99. [Google Scholar] [CrossRef]
- Ning, T.; Elgered, G. Trends in the Atmospheric Water Vapor Content From Ground-Based GPS: The Impact of the Elevation Cutoff Angle. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 744–751. [Google Scholar] [CrossRef]
- Caputo, M.; Ruggiero, V.; Sutera, A.; Zirilli, F. On the Retrieval of Water Vapour Profiles from a Single GPS Station. Nuovo C Della Soc. Ital. Fis. C 2000, 23, 611–620. [Google Scholar]
- Iassamen, A.; Sauvageot, H.; Jeannin, N.; Ameur, S. Distribution of Tropospheric Water Vapor in Clear and Cloudy Conditions from Microwave Radiometric Profiling. J. Appl. Meteorol. Climatol. 2009, 48, 600–615. [Google Scholar] [CrossRef]
- Bi, Y.M.; Mao, J.T.; Liu, X.Y.; Fu, Y.; Li, C.C. Remote Sensing of the Amount of Water Vapor along the Slant Path Using the Ground-Base GPS. Chin. J. Geophys. 2006, 49, 282–290. [Google Scholar] [CrossRef]
- Yao, Y.; Zhao, Q. A Novel, Optimized Approach of Voxel Division for Water Vapor Tomography. Meteorol. Atmos. Phys. 2017, 129, 57–70. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y. Hybrid Regularized GPS Tropospheric Sensing Using 3-D Ray Tracing Technique. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1475–1479. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Shi, J.; Zhao, Y.; Zhou, L.; Song, S. A New Method of GPS Water Vapor Tomography for Maximizing the Use of Signal Rays. Appl. Sci. 2019, 9, 1446. [Google Scholar] [CrossRef]
- Brenot, H.; Rohm, W.; Kačmařík, M.; Möller, G.; Sá, A.; Tondaś, D.; Rapant, L.; Biondi, R.; Manning, T.; Champollion, C. Cross-Comparison and Methodological Improvement in GPS Tomography. Remote Sens. 2019, 12, 30. [Google Scholar] [CrossRef]
- Adavi, Z.; Rohm, W.; Weber, R. Analyzing Different Parameterization Methods in GNSS Tomography Using the COST Benchmark Dataset. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 6155–6163. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Ding, N.; Zhao, Q. A Tropospheric Tomography Method with a Novel Height Factor Model Including Two Parts: Isotropic and Anisotropic Height Factors. Remote Sens. 2020, 12, 1848. [Google Scholar] [CrossRef]
- Dong, Z.; Jin, S. 3-D Water Vapor Tomography in Wuhan from GPS, BDS and GLONASS Observations. Remote Sens. 2018, 10, 62. [Google Scholar] [CrossRef]
- Haji-Aghajany, S.; Amerian, Y.; Verhagen, S. B-Spline Function-Based Approach for GPS Tropospheric Tomography. GPS Solut. 2020, 24, 88. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, S.; Ding, N.; Ma, P. An Improved Tropospheric Tomography Method Based on the Dynamic Node Parametrized Algorithm. Acta Geodyn. Geomater. 2020, 17, 191–206. [Google Scholar] [CrossRef]
- Furumoto, J.; Kurimoto, K.; Tsuda, T. Continuous Observations of Humidity Profiles with the MU Radar-RASS Combined with GPS and Radiosonde Measurements. J. Atmos. Ocean. Technol. 2003, 20, 23–41. [Google Scholar] [CrossRef]
- Lindenbergh, R.; Keshin, M.; van der Marel, H.; Hanssen, R. High Resolution Spatio-temporal Water Vapour Mapping Using GPS and MERIS Observations. Int. J. Remote Sens. 2008, 29, 2393–2409. [Google Scholar] [CrossRef]
- Leontiev, A.; Reuveni, Y. Augmenting GPS IWV Estimations Using Spatio-Temporal Cloud Distribution Extracted from Satellite Data. Sci. Rep. 2018, 8, 14785. [Google Scholar] [CrossRef]
- Alshawaf, F.; Fersch, B.; Hinz, S.; Kunstmann, H.; Mayer, M.; Meyer, F.J. Water Vapor Mapping by Fusing InSAR and GNSS Remote Sensing Data and Atmospheric Simulations. Hydrol. Earth Syst. Sci. 2015, 19, 4747–4764. [Google Scholar] [CrossRef]
- Zhao, Q.; Du, Z.; Yao, W.; Yao, Y. Hybrid Precipitable Water Vapor Fusion Model in China. J. Atmos. Sol. Terr. Phys. 2020, 208, 105387. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rocken, C.; Solheim, F.; van Hove, T.; Ware, R.; et al. GPS Meteorology: Direct Estimation of the Absolute Value of Precipitable Water. J. Appl. Meteorol. 1996, 35, 830–838. [Google Scholar] [CrossRef]
- Iwabuchi, T.; Naito, I.; Mannoji, N. A Comparison of Global Positioning System Retrieved Precipitable Water Vapor with the Numerical Weather Prediction Analysis Data over the Japanese Islands. J. Geophys. Res. Atmos. 2000, 105, 4573–4585. [Google Scholar] [CrossRef]
- Basili, P.; Bonafoni, S.; Ferrara, R.; Ciotti, P.; Fionda, E.; Arnbrosini, R. Atmospheric Water Vapor Retrieval by Means of Both a GPS Network and a Microwave Radiometer during an Experimental Campaign in Cagliari, Italy, in 1999. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2436–2443. [Google Scholar] [CrossRef]
- Braun, J.; Rocken, C.; Liljegren, J. Comparisons of Line-of-Sight Water Vapor Observations Using the Global Positioning System and a Pointing Microwave Radiometer. J. Atmos. Ocean. Technol. 2003, 20, 606–612. [Google Scholar] [CrossRef]
- Memmo, A.; Fionda, E.; Paolucci, T.; Cimini, D.; Ferretti, R.; Bonafoni, S.; Ciotti, P. Comparison of MM5 Integrated Water Vapor with Microwave Radiometer, GPS, and Radiosonde Measurements. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1050–1058. [Google Scholar] [CrossRef]
- Glowacki, T.; Penna, N.; Bourke, W. Validation of GPS-Based Estimates of Integrated Water Vapour for the Australian Region and Identification of Diurnal Variability. Aust. Meteorol. Mag. 2006, 55, 131–148. [Google Scholar]
- Ha, J.; Park, K.D.; Kim, K.; Kim, Y.H. Comparison of Atmospheric Water Vapor Profiles Obtained by GPS, MWR, and Radiosonde. Asia-Pac. J. Atmos. Sci. 2010, 46, 233–241. [Google Scholar] [CrossRef]
- Musa, T.; Amir, S.; Othman, R.; Ses, S.; Omar, K.; Abdullah, K.; Lim, S.; Rizos, C. GPS Meteorology in a Low-Latitude Region: Remote Sensing of Atmospheric Water Vapor over the Malaysian Peninsula. J. Atmos. Sol. Terr. Phys. 2011, 73, 2410–2422. [Google Scholar] [CrossRef]
- Thomas, I.D.; King, M.A.; Clarke, P.J.; Penna, N.T. Precipitable Water Vapor Estimates from Homogeneously Reprocessed GPS Data: An Intertechnique Comparison in Antarctica. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.P.; Román, R.; Cachorro, V.E.; Mateos, D. Comparison of Integrated Water Vapor from GNSS and Radiosounding at Four GRUAN Stations. Sci. Total Environ. 2019, 648, 1639–1648. [Google Scholar] [CrossRef]
- Guerova, G.; Brockmann, E.; Schubiger, F.; Morland, J.; Mätzler, C. An Integrated Assessment of Measured and Modeled Integrated Water Vapor in Switzerland for the Period 2001-03. J. Appl. Meteorol. 2005, 44, 1033–1044. [Google Scholar] [CrossRef]
- Dirksen, R.J.; Sommer, M.; Immler, F.J.; Hurst, D.F.; Kivi, R.; Vömel, H. Reference Quality Upper-Air Measurements: GRUAN Data Processing for the Vaisala RS92 Radiosonde. Atmos. Meas. Tech. 2014, 7, 4463–4490. [Google Scholar] [CrossRef]
- Schneider, M.; Romero, P.M.; Hase, F.; Blumenstock, T.; Cuevas, E.; Ramos, R. Continuous Quality Assessment of Atmospheric Water Vapour Measurement Techniques: FTIR, Cimel, MFRSR, GPS, and Vaisala RS92. Atmos. Meas. Tech. 2010, 3, 323–338. [Google Scholar] [CrossRef]
- Bock, O.; Bouin, M.N.; Walpersdorf, A.; Lafore, J.P.; Janicot, S.; Guichard, F.; Agusti-Panareda, A. Comparison of Ground-Based GPS Precipitable Water Vapour to Independent Observations and NWP Model Reanalyses over Africa: PRECIPITABLE WATER VAPOUR DATA OVER AFRICA. Q. J. R. Meteorol. Soc. 2007, 133, 2011–2027. [Google Scholar] [CrossRef]
- Zhang, F.; Barriot, J.P.; Xu, G.; Yeh, T.K. Metrology Assessment of the Accuracy of Precipitable Water Vapor Estimates from GPS Data Acquisition in Tropical Areas: The Tahiti Case. Remote Sens. 2018, 10, 758. [Google Scholar] [CrossRef]
- Buehler, S.A.; Östman, S.; Melsheimer, C.; Holl, G.; Eliasson, S.; John, V.O.; Blumenstock, T.; Hase, F.; Elgered, G.; Raffalski, U.; et al. A Multi-Instrument Comparison of Integrated Water Vapour Measurements at a High Latitude Site. Atmos. Chem. Phys. 2012, 12, 10925–10943. [Google Scholar] [CrossRef]
- Van Malderen, R.; Brenot, H.; Pottiaux, E.; Beirle, S.; Hermans, C.; De Mazière, M.; Wagner, T.; De Backer, H.; Bruyninx, C. A Multi-Site Intercomparison of Integrated Water Vapour Observations for Climate Change Analysis. Atmos. Meas. Tech. 2014, 7, 2487–2512. [Google Scholar] [CrossRef]
- Cucurull, L.; Navascues, B.; Ruffini, G.; Elósegui, P.; Rius, A.; Vilà, J. The Use of GPS to Validate NWP Systems: The HIRLAM Model. J. Atmos. Ocean. Technol. 2000, 17, 773–787. [Google Scholar] [CrossRef]
- Köpken, C. Validation of Integrated Water Vapor from Numerical Models Using Ground-Based GPS, SSM/I, and Water Vapor Radiometer Measurements. J. Appl. Meteorol. 2001, 40, 1105–1117. [Google Scholar] [CrossRef]
- Vey, S.; Dietrich, R.; Rülke, A.; Fritsche, M.; Steigenberger, P.; Rothacher, M. Validation of Precipitable Water Vapor within the NCEP/DOE Reanalysis Using Global GPS Observations from One Decade. J. Clim. 2010, 23, 1675–1695. [Google Scholar] [CrossRef]
- Yang, X.; Sass, B.H.; Elgered, G.; Johansson, J.M.; Emardson, T.R. A Comparison of Precipitable Water Vapor Estimates by an NWP Simulation and GPS Observations. J. Appl. Meteorol. Climatol. 1999, 38, 941–956. [Google Scholar] [CrossRef]
- Matsuyama, H.; Flores, J.; Oikawa, K.; Miyaoka, K. Comparison of Precipitable Water via JRA-55 and GPS in Japan Considering Different Elevations. Hydrol. Res. Lett. 2020, 14, 9–16. [Google Scholar] [CrossRef]
- Bock, O.; Nuret, M. Verification of NWP Model Analyses and Radiosonde Humidity Data with GPS Precipitable Water Vapor Estimates during AMMA. Weather Forecast. 2009, 24, 1085–1101. [Google Scholar] [CrossRef]
- Bock, O.; Parracho, A.C. Consistency and Representativeness of Integrated Water Vapour from Ground-Based GPS Observations and ERA-Interim Reanalysis. Atmos. Chem. Phys. 2019, 19, 9453–9468. [Google Scholar] [CrossRef]
- Bengtsson, L. Can Climate Trends Be Calculated from Reanalysis Data? J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Parracho, A.C.; Bock, O.; Bastin, S. Global IWV Trends and Variability in Atmospheric Reanalyses and GPS Observations. Atmos. Chem. Phys. 2018, 18, 16213–16237. [Google Scholar] [CrossRef]
- Raja, M.K.R.V.; Gutman, S.I.; Yoe, J.G.; McMillin, L.M.; Zhao, J. The Validation of AIRS Retrievals of Integrated Precipitable Water Vapor Using Measurements from a Network of Ground-Based GPS Receivers over the Contiguous United States. J. Atmos. Ocean. Technol. 2008, 25, 416–428. [Google Scholar] [CrossRef]
- Bennouna, Y.S.; Torres, B.; Cachorro, V.E.; de Galisteo, J.P.O.; Toledano, C. The Evaluation of the Integrated Water Vapour Annual Cycle over the Iberian Peninsula from EOS-MODIS against Different Ground-Based Techniques. Q. J. R. Meteorol. Soc. 2013, 139, 1935–1956. [Google Scholar] [CrossRef]
- Román, R.; Antón, M.; Cachorro, V.; Loyola, D.; Ortiz de Galisteo, J.; de Frutos, A.; Romero-Campos, P. Comparison of Total Water Vapor Column from GOME-2 on MetOp-A against Ground-Based GPS Measurements at the Iberian Peninsula. Sci. Total Environ. 2015, 533, 317–328. [Google Scholar] [CrossRef] [PubMed]
- Nelson, R.R.; Crisp, D.; Ott, L.E.; O’Dell, C.W. High-Accuracy Measurements of Total Column Water Vapor from the Orbiting Carbon Observatory-2: Total column water vapor from OCO-2. Geophys. Res. Lett. 2016, 43, 12,261–12,269. [Google Scholar] [CrossRef]
- Ningombam, S.S.; Jade, S.; Shrungeshwara, T.; Song, H.J. Validation of Water Vapor Retrieval from Moderate Resolution Imaging Spectro-Radiometer (MODIS) in near Infrared Channels Using GPS Data over IAO-Hanle, in the Trans-Himalayan Region. J. Atmos. Sol. Terr. Phys. 2016, 137, 76–85. [Google Scholar] [CrossRef]
- Wang, H.; Gonzalez Abad, G.; Liu, X.; Chance, K. Validation and Update of OMI Total Column Water Vapor Product. Atmos. Chem. Phys. 2016, 16, 11379–11393. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.P.; Cachorro, V.E.; Wang, H.; González Abad, G.; Román, R.; Costa, M.J. Validation of Integrated Water Vapor from OMI Satellite Instrument against Reference GPS Data at the Iberian Peninsula. Sci. Total Environ. 2017, 580, 857–864. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.P.; Cachorro, V.E.; Costa, M.J.; Román, R.; Bennouna, Y.S. Validation of MODIS Integrated Water Vapor Product against Reference GPS Data at the Iberian Peninsula. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 214–221. [Google Scholar] [CrossRef][Green Version]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.P.; Cachorro, V.E.; Álvarez-Zapatero, P.; Román, R.; Loyola, D.; Costa, M.J.; Wang, H.; Abad, G.G.; et al. Inter-Comparison of Integrated Water Vapor from Satellite Instruments Using Reference GPS Data at the Iberian Peninsula. Remote Sens. Environ. 2018, 204, 729–740. [Google Scholar] [CrossRef]
- Gong, S.; Hagan, D.F.T.; Zhang, C. Analysis on Precipitable Water Vapor over the Tibetan Plateau Using FengYun-3A Medium Resolution Spectral Imager Products. J. Sens. 2019, 2019, 1–12. [Google Scholar] [CrossRef]
- He, J.; Liu, Z. Comparison of Satellite-Derived Precipitable Water Vapor Through Near-Infrared Remote Sensing Channels. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10252–10262. [Google Scholar] [CrossRef]
- Wang, H.; Souri, A.H.; González Abad, G.; Liu, X.; Chance, K. Ozone Monitoring Instrument (OMI) Total Column Water Vapor Version 4 Validation and Applications. Atmos. Meas. Tech. 2019, 12, 5183–5199. [Google Scholar] [CrossRef]
- Carbajal Henken, C.; Dirks, L.; Steinke, S.; Diedrich, H.; August, T.; Crewell, S. Assessment of Sampling Effects on Various Satellite-Derived Integrated Water Vapor Datasets Using GPS Measurements in Germany as Reference. Remote Sens. 2020, 12, 1170. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Román, R.; Cachorro, V.E.; Wang, H.; González Abad, G.; Ritter, C. Water Vapor Satellite Products in the European Arctic: An Inter-Comparison against GNSS Data. Sci. Total Environ. 2020, 741, 140335. [Google Scholar] [CrossRef]
- Alraddawi, D.; Sarkissian, A.; Keckhut, P.; Bock, O.; Noël, S.; Bekki, S.; Irbah, A.; Meftah, M.; Claud, C. Comparison of Total Water Vapour Content in the Arctic Derived from GNSS, AIRS, MODIS and SCIAMACHY. Atmos. Meas. Tech. 2018, 11, 2949–2965. [Google Scholar] [CrossRef]
- Jin, S.; Li, Z.; Cho, J. Integrated Water Vapor Field and Multiscale Variations over China from GPS Measurements. J. Appl. Meteorol. Climatol. 2008, 47, 3008–3015. [Google Scholar] [CrossRef]
- Wu, S.; Zou, H.; Wu, J. The Diurnal Variations of GPS PWV near Poyang Lake in China during Midsummer. Adv. Meteorol. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Takagi, T.; Kimura, F.; Kono, S. Diurnal Variation of GPS Precipitable Water at Lhasa in Premonsoon and Monsoon Periods. J. Meteorol. Soc. Jpn. 2000, 78, 175–180. [Google Scholar] [CrossRef]
- Iwasaki, H.; Miki, T. Observational Study on the Diurnal Variation in Precipitable Water Associated with the Thermally Induced Local Circulation over the “Semi-Basin” around Maebashi Using GPS Data. J. Meteorol. Soc. Jpn. 2001, 79, 1077–1091. [Google Scholar] [CrossRef]
- Li, G.; Kimura, F.; Sato, T.; Huang, D. A Composite Analysis of Diurnal Cycle of GPS Precipitable Water Vapor in Central Japan during Calm Summer Days. Theor. Appl. Climatol. 2008, 92, 15–29. [Google Scholar] [CrossRef]
- Wu, P.; Hamada, J.I.; Mori, S.; Tauhid, Y.I.; Yamanaka, M.D.; Kimura, F. Diurnal Variation of Precipitable Water over a Mountainous Area of Sumatra Island. J. Appl. Meteorol. 2003, 42, 1107–1115. [Google Scholar] [CrossRef]
- Torri, G.; Adams, D.K.; Wang, H.; Kuang, Z. On the Diurnal Cycle of GPS-Derived Precipitable Water Vapor over Sumatra. J. Atmos. Sci. 2019, 76, 3529–3552. [Google Scholar] [CrossRef]
- Sohn, D.H.; Cho, J.H. Trend Analysis of GPS Precipitable Water Vapor Above South Korea Over the Last 10 Years. J. Astron. Space Sci. 2010, 27, 231–238. [Google Scholar] [CrossRef]
- Dai, A.; Wang, J.; Ware, R.H.; Van Hove, T. Diurnal Variation in Water Vapor over North America and Its Implications for Sampling Errors in Radiosonde Humidity: Water vapor Diurnal variation over north america. J. Geophys. Res. Atmos. 2002, 107, ACL 11-1–ACL 11-14. [Google Scholar] [CrossRef]
- Gradinarsky, L.; Johansson, J.; Bouma, H.; Scherneck, H.G.; Elgered, G. Climate Monitoring Using GPS. Phys. Chem. Earth Parts A/B/C 2002, 27, 335–340. [Google Scholar] [CrossRef]
- Combrink, A.Z.; Bos, M.S.; Fernandes, R.M.; Combrinck, W.L.; Merry, C.L. On the Importance of Proper Noise Modelling for Long-Term Precipitable Water Vapour Trend Estimations. S. Afr. J. Geol. 2007, 110, 211–218. [Google Scholar] [CrossRef]
- Jakobson, E.; Ohvril, H.; Elgered, G. Diurnal Variability of Precipitable Water in the Baltic Region, Impact on Transmittance of the Direct Solar Radiation. Boreal Environ. Res. 2009, 14, 45–55. [Google Scholar]
- Suparta, W.; Ali, M.A.M.; Yatim, B.; Fraser, G.J. Analysis of GPS-Sensed Atmospheric Water Vapour Variability and Its Response to the Terrestrial Winds over Antarctica. Phys. Chem. Earth Parts A/B/C 2009, 34, 72–87. [Google Scholar] [CrossRef]
- Ortiz de Galisteo, J.P.; Cachorro, V.; Toledano, C.; Torres, B.; Laulainen, N.; Bennouna, Y.; de Frutos, A. Diurnal Cycle of Precipitable Water Vapor over Spain. Q. J. R. Meteorol. Soc. 2011, 137, 948–958. [Google Scholar] [CrossRef]
- Sharifi, M.A.; Souri, A.H. A Hybrid LS-HE and LS-SVM Model to Predict Time Series of Precipitable Water Vapor Derived from GPS Measurements. Arab. J. Geosci. 2015, 8, 7257–7272. [Google Scholar] [CrossRef]
- Alshawaf, F.; Balidakis, K.; Dick, G.; Heise, S.; Wickert, J. Estimating Trends in Atmospheric Water Vapor and Temperature Time Series over Germany. Atmos. Meas. Tech. 2017, 10, 3117–3132. [Google Scholar] [CrossRef]
- Barman, P.; Jade, S.; Kumar, A.; Jamir, W. Inter Annual, Spatial, Seasonal, and Diurnal Variability of Precipitable Water Vapour over Northeast India Using GPS Time Series. Int. J. Remote Sens. 2017, 38, 391–411. [Google Scholar] [CrossRef]
- Hadad, D.; Baray, J.L.; Montoux, N.; Van Baelen, J.; Fréville, P.; Pichon, J.M.; Bosser, P.; Ramonet, M.; Yver Kwok, C.; Bègue, N.; et al. Surface and Tropospheric Water Vapor Variability and Decadal Trends at Two Supersites of CO-PDD (Cézeaux and Puy de Dôme) in Central France. Atmosphere 2018, 9, 302. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. Studies of Precipitable Water Vapour Characteristics on a Global Scale. Int. J. Remote Sens. 2019, 40, 72–88. [Google Scholar] [CrossRef]
- Bernet, L.; Brockmann, E.; von Clarmann, T.; Kämpfer, N.; Mahieu, E.; Mätzler, C.; Stober, G.; Hocke, K. Trends of Atmospheric Water Vapour in Switzerland from Ground-Based Radiometry, FTIR and GNSS Data. Atmos. Chem. Phys. 2020, 20, 11223–11244. [Google Scholar] [CrossRef]
- Bousquet, O.; Lees, E.; Durand, J.; Peltier, A.; Duret, A.; Mekies, D.; Boissier, P.; Donal, T.; Fleischer-Dogley, F.; Zakariasy, L. Densification of the Ground-Based GNSS Observation Network in the Southwest Indian Ocean: Current Status, Perspectives, and Examples of Applications in Meteorology and Geodesy. Front. Earth Sci. 2020, 8. [Google Scholar] [CrossRef]
- Lees, E.; Bousquet, O.; Roy, D.; de Bellevue, J.L. Analysis of Diurnal to Seasonal Variability of Integrated Water Vapour in the South Indian Ocean Basin Using Ground-based GNSS and Fifth-generation ECMWF Reanalysis (ERA5) Data. Q. J. R. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Trakolkul, C.; Satirapod, C. Variations of Precipitable Water Vapor Using GNSS CORS in Thailand. Surv. Rev. 2020, 1–7. [Google Scholar] [CrossRef]
- Ortiz de Galisteo, J.P.; Bennouna, Y.; Toledano, C.; Cachorro, V.; Romero, P.; Andrés, M.I.; Torres, B. Analysis of the Annual Cycle of the Precipitable Water Vapour over Spain from 10-Year Homogenized Series of GPS Data: Annual Cycle of the Precipitable Water Vapour over Spain. Q. J. R. Meteorol. Soc. 2014, 140, 397–406. [Google Scholar] [CrossRef]
- Torres, B.; Cachorro, V.E.; Toledano, C.; Ortiz de Galisteo, J.P.; Berjón, A.; de Frutos, A.M.; Bennouna, Y.; Laulainen, N. Precipitable Water Vapor Characterization in the Gulf of Cadiz Region (Southwestern Spain) Based on Sun Photometer, GPS, and Radiosonde Data. J. Geophys. Res. 2010, 115, 1–11. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of Real-time Mode High-resolution Water Vapor Fields from GPS Observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Bordi, I.; Fraedrich, K.; Sutera, A.; Zhu, X. Ground-Based GPS Measurements: Time Behavior from Half-Hour to Years. Theor. Appl. Climatol. 2014, 115, 615–625. [Google Scholar] [CrossRef]
- Jin, S.; Luo, O. Variability and Climatology of PWV From Global 13-Year GPS Observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1918–1924. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z. Global Water Vapor Variability and Trend from the Latest 36 Year (1979 to 2014) Data of ECMWF and NCEP Reanalyses, Radiosonde, GPS, and Microwave Satellite: Global water vapor variability and trend. J. Geophys. Res. Atmos. 2016, 121, 11442–11462. [Google Scholar] [CrossRef]
- Wang, J.; Dai, A.; Mears, C. Global Water Vapor Trend from 1988 to 2011 and Its Diurnal Asymmetry Based on GPS, Radiosonde, and Microwave Satellite Measurements. J. Clim. 2016, 29, 5205–5222. [Google Scholar] [CrossRef]
- Gutman, S.I.; Benjamin, S.G. The Role of Ground-Based GPS Meteorological Observations in Numerical Weather Prediction. GPS Solut. 2001, 4, 16–24. [Google Scholar] [CrossRef]
- Guerova, G.; Bettems, J.M.; Brockmann, E.; Matzler, C. Assimilation of the GPS-Derived Integrated Water Vapour (IWV) in the MeteoSwiss Numerical Weather Prediction Model—A First Experiment. Phys. Chem. Earth Parts A/B/C 2004, 29, 177–186. [Google Scholar] [CrossRef]
- Yuan, Z.; Ding, J.; Chen, M. Preliminary Study on the Application of GPS Observations to a Mesoscale Numerical Model. Acta Meteorol. Sin. 2005, 19, 332–344. [Google Scholar]
- Gendt, G.; Dick, G.; Reigber, C.; Tomassini, M.; Liu, Y.; Ramatschi, M. Near Real Time GPS Water Vapor Monitoring for Numerical Weather Prediction in Germany. J. Meteorol. Soc. Jpn. 2004, 82, 361–370. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, M.; Kuo, Y.H.; Fan, S.; Zhong, J. Numerical Assessing Experiments on the Individual Component Impact of the Meteorological Observation Network on the “July 2000” Torrential Rain in Beijing. Acta Meteorol. Sin. 2006, 20, 389–401. [Google Scholar]
- Ha, S.Y.; Kuo, Y.H.; Guo, Y.R.; Lim, G.H. Variational Assimilation of Slant-Path Wet Delay Measurements from a Hypothetical Ground-Based GPS Network. Part I: Comparison with Precipitable Water Assimilation. Mon. Weather Rev. 2003, 131, 2635–2655. [Google Scholar] [CrossRef]
- Liu, H.; Xue, M. Retrieval of Moisture from Slant-Path Water Vapor Observations of a Hypothetical GPS Network Using a Three-Dimensional Variational Scheme with Anisotropic Background Error. Mon. Weather Rev. 2006, 134, 933–949. [Google Scholar] [CrossRef][Green Version]
- Karabatić, A.; Weber, R.; Haiden, T. Near Real-Time Estimation of Tropospheric Water Vapour Content from Ground Based GNSS Data and Its Potential Contribution to Weather Now-Casting in Austria. Adv. Space Res. 2011, 47, 1691–1703. [Google Scholar] [CrossRef]
- Kumar, P.; Gopalan, K.; Shukla, B.P.; Shyam, A. Impact of Single-Point GPS Integrated Water Vapor Estimates on Short-Range WRF Model Forecasts over Southern India. Theor. Appl. Climatol. 2017, 130, 755–760. [Google Scholar] [CrossRef]
- Mascitelli, A.; Federico, S.; Fortunato, M.; Avolio, E.; Torcasio, R.C.; Realini, E.; Mazzoni, A.; Transerici, C.; Crespi, M.; Dietrich, S. Data Assimilation of GPS-ZTD into the RAMS Model through 3D-Var: Preliminary Results at the Regional Scale. Meas. Sci. Technol. 2019, 30, 055801. [Google Scholar] [CrossRef]
- Graham, E.; Koffi, E.N.; Mätzler, C. An Observational Study of Air and Water Vapour Convergence over the Bernese Alps, Switzerland, during Summertime and the Development of Isolated Thunderstorms. Meteorol. Z. 2012, 21, 561–574. [Google Scholar] [CrossRef]
- Kingsmill, D.E.; Neiman, P.J.; Moore, B.J.; Hughes, M.; Yuter, S.E.; Ralph, F.M. Kinematic and Thermodynamic Structures of Sierra Barrier Jets and Overrunning Atmospheric Rivers during a Landfalling Winter Storm in Northern California. Mon. Weather Rev. 2013, 141, 2015–2036. [Google Scholar] [CrossRef]
- Neiman, P.J.; Hughes, M.; Moore, B.J.; Ralph, F.M.; Sukovich, E.M. Sierra Barrier Jets, Atmospheric Rivers, and Precipitation Characteristics in Northern California: A Composite Perspective Based on a Network of Wind Profilers. Mon. Weather Rev. 2013, 141, 4211–4233. [Google Scholar] [CrossRef][Green Version]
- Suparta, W. Observations of Precipitable Water Vapor along the Maritime Continent Associated with El Niño-Southern Oscillation Activity. Ann. Geophys. 2018, 61. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Ortiz de Galisteo, J.P.; Román, R.; Cachorro, V.E. Water Vapor Radiative Effects on Short-Wave Radiation in Spain. Atmos. Res. 2018, 205, 18–25. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; Sanchez-Lorenzo, A.; Cachorro, V.E. Evaluation of Water Vapor Radiative Effects Using GPS Data Series over Southwestern Europe. Remote Sens. 2020, 12, 1307. [Google Scholar] [CrossRef]
- Perrefort, D.; Wood-Vasey, W.M.; Bostroem, K.A.; Gilmore, K.; Joyce, R.; Matheson, T.; Corson, C. Pwv_kpno: A Python Package for Modeling the Atmospheric Transmission Function Due to Precipitable Water Vapor. Publ. Astron. Soc. Pac. 2019, 131, 025002. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).