Development of a Shoreline Detection Method Using an Artificial Neural Network Based on Satellite SAR Imagery
Abstract
1. Introduction
2. Preprocessing of SAR Data for NN-Based Land–Sea Classification
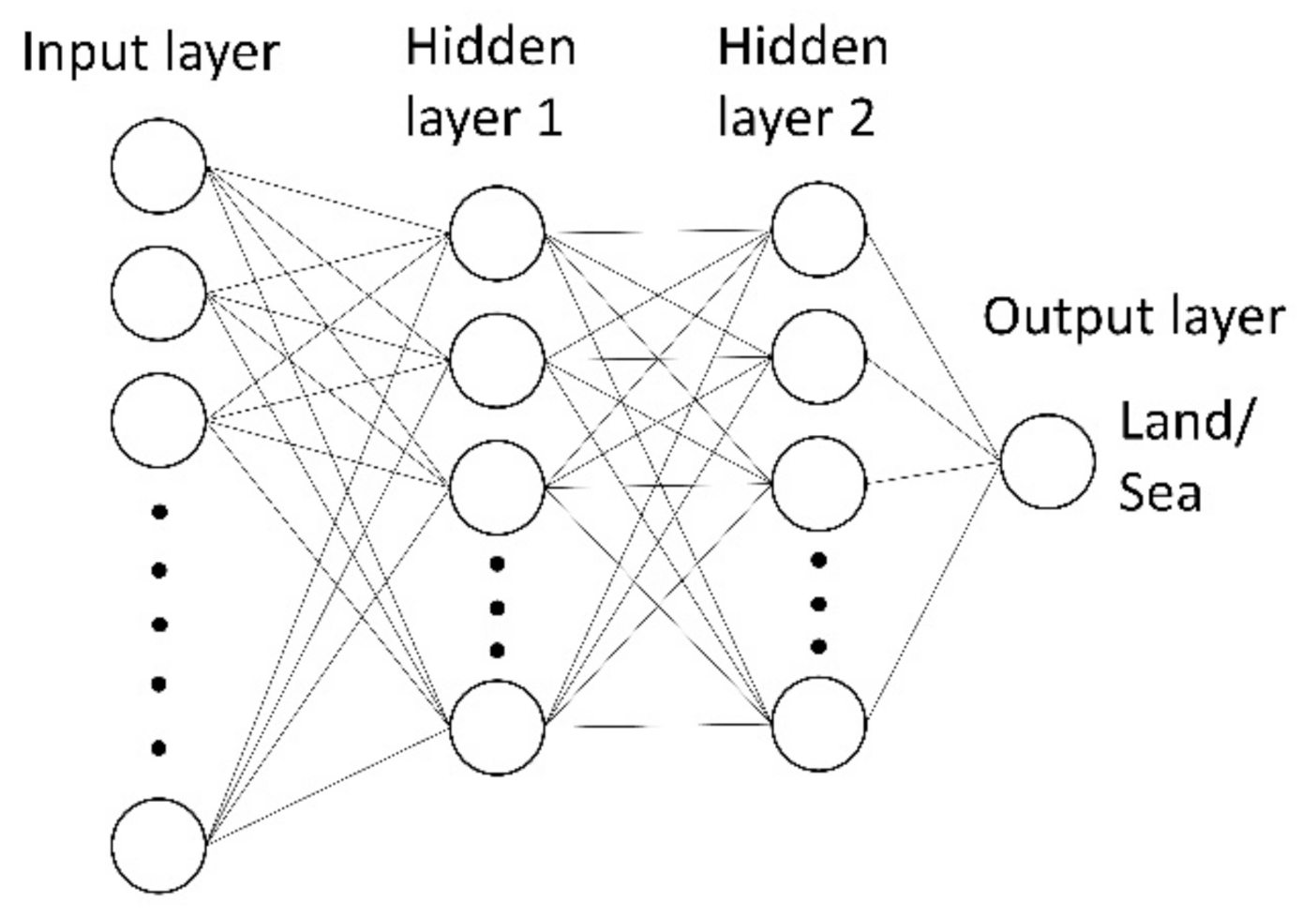
3. Development of the NN-Based Land–Sea Classification Method
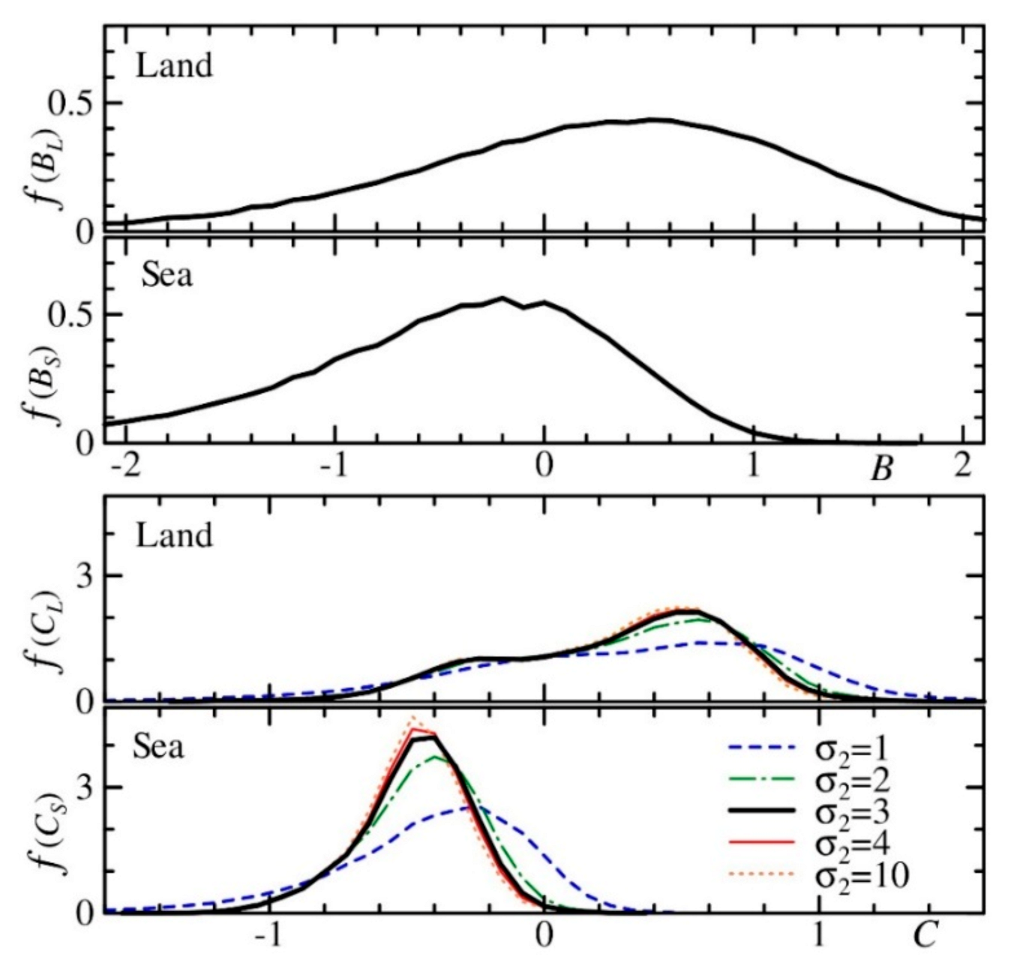
3.1. Input Layer
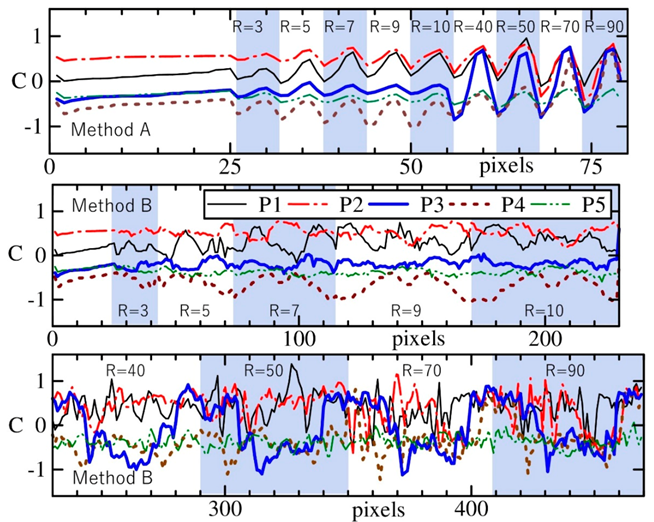
- Extract 60 C values of pixels in equal intervals along the circumference of the largest circle with the radius of R = 90 pixels, Ck, with k = 1,2, …60.
- Determine 〈Ck〉 as a moving average of Ck with a weight of a Gaussian kernel along the circumference of the circle.
- Find the point k, where the obtained 〈Ck〉 yields the maximum value along the circumference of the circle.
- Determine the initial angle as the angle between the northward direction and the direction from the center of the circle to the above-mentioned point.
- Use this initial angle to determine the initial point along each circle with different R.
- Extract the C values of the pixel along the circumference of each circle starting from the initial point in the clockwise direction in constant intervals.
- Place groups of these C values of each circle in ascending order of R.
3.2. Training Samples
3.3. Training Procedures
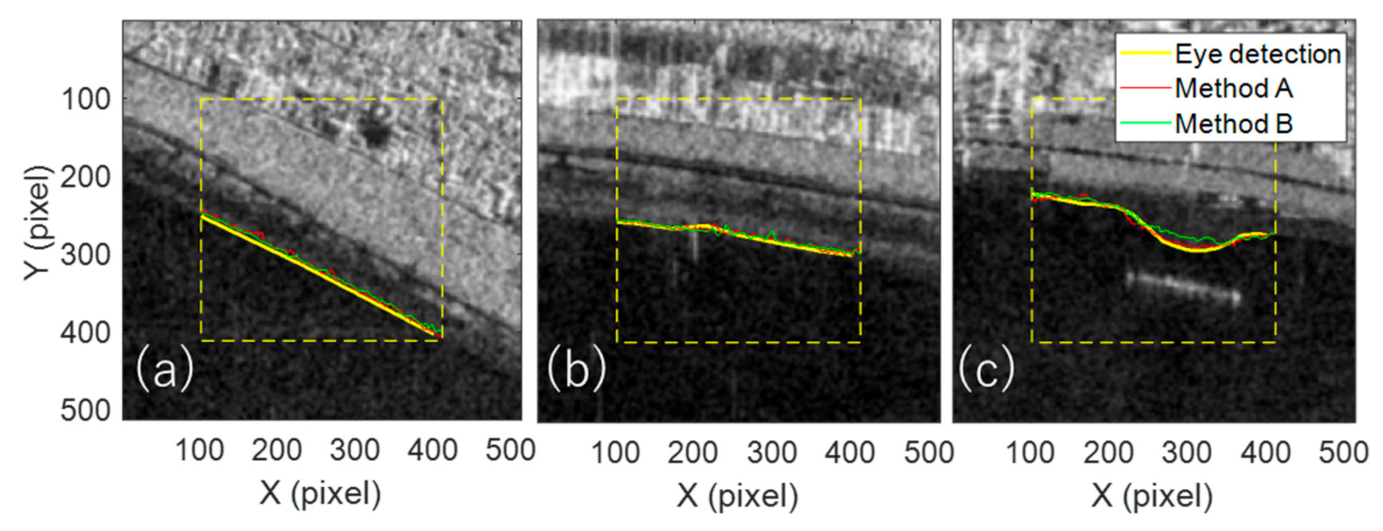
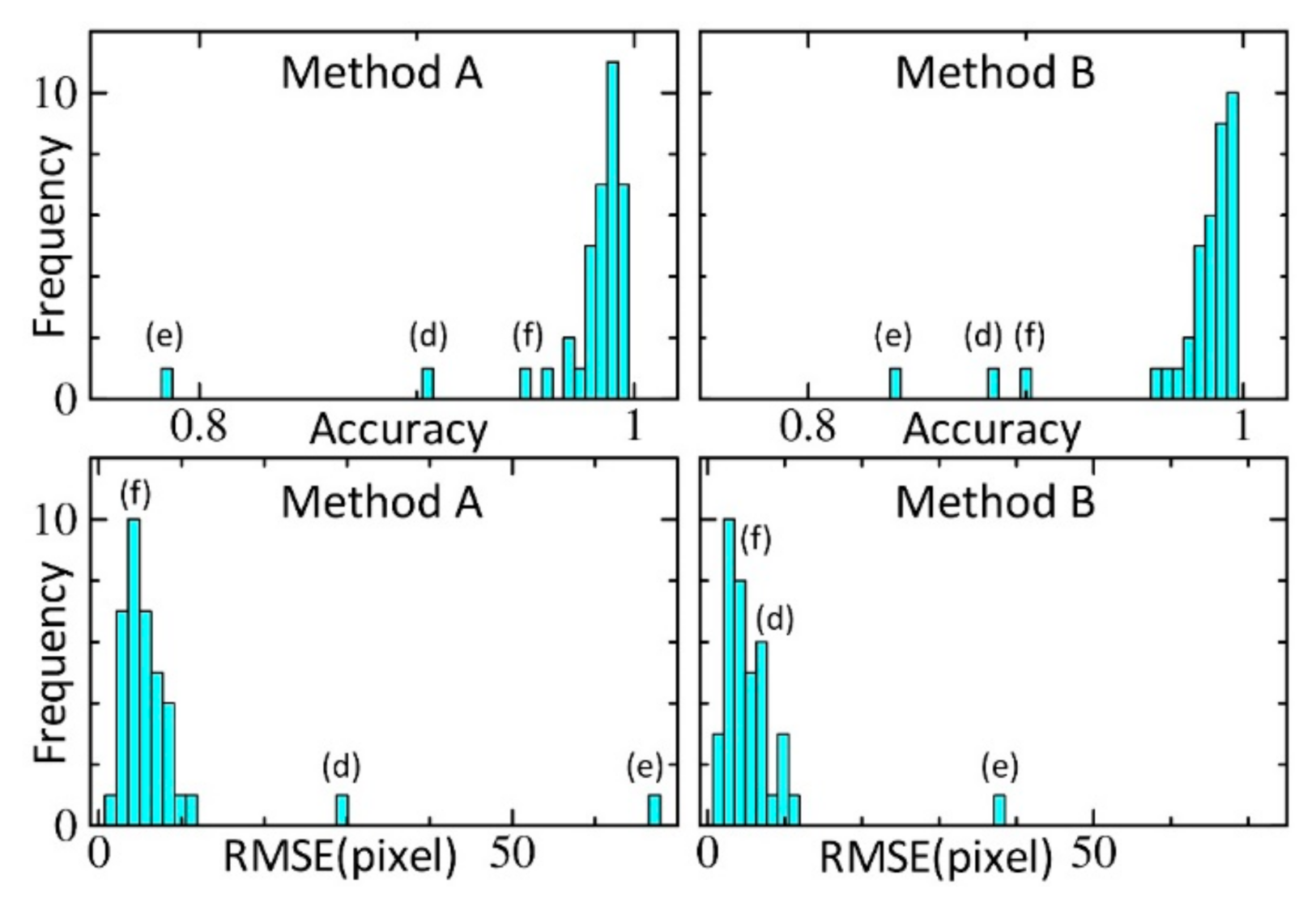
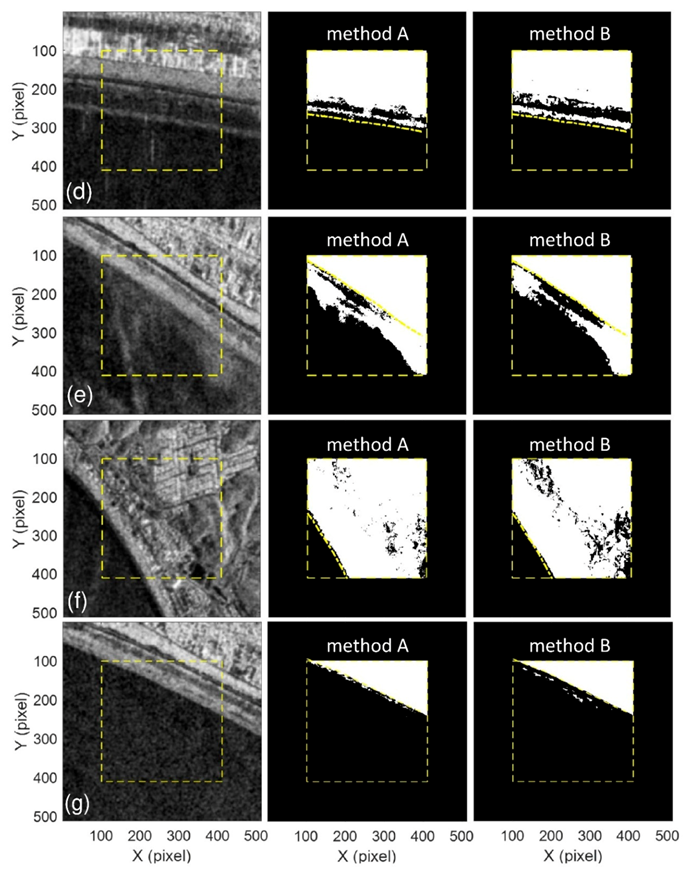
3.4. Testing Results
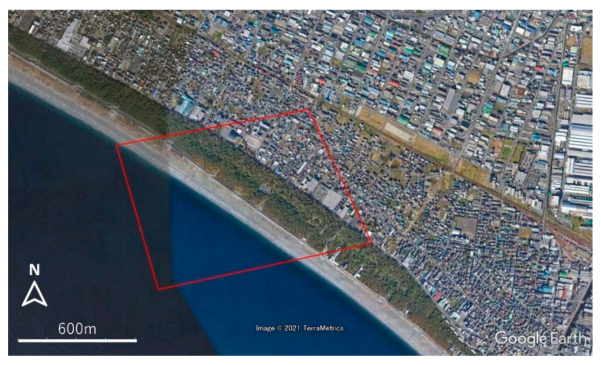
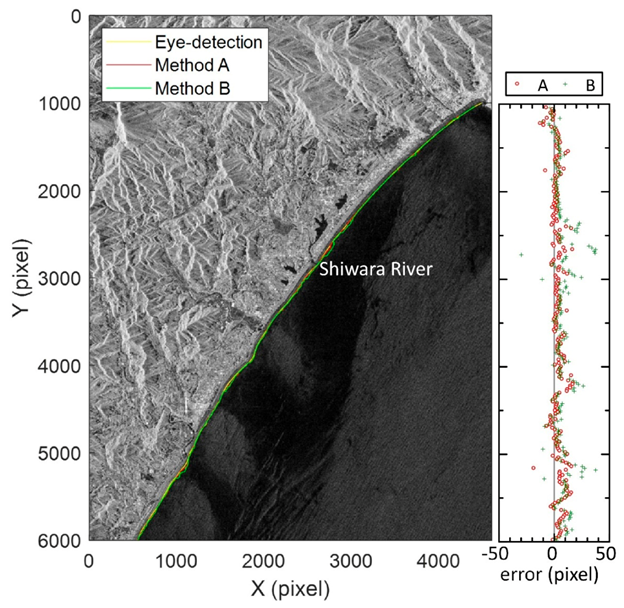
4. Application of the Present System to the Other Coasts
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boak, E.H.; Turner, I.L. Shoreline definition and detection: A review. J. Coast. Res. 2005, 21, 688–703. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.-F.; Voukouvalas, E.; Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Hussain, M.A.; Tajima, Y.; Gunasekara, K.; Rana, S.; Hasan, R. Recent coastline changes at the eastern part of the Meghna Estuary using PALSAR and Landsat images. IOP Conf. Ser. Earth Environ. Sci. 2014, 20, 012047. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; de Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar] [CrossRef]
- Mason, D.C.; Davenport, I.J. Accurate and efficient determination of the shoreline in ERS-1 SAR images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1243–1253. [Google Scholar] [CrossRef]
- Wu, L.H.; Tajima, Y.; Yamanaka, Y.; Shimozono, T.; Sato, S. Study on characteristics of synthetic aperture radar (SAR) imagery around the coast for shoreline detection. Coast. Eng. J. 2019, 61, 152–170. [Google Scholar] [CrossRef]
- Tajima, Y.; Wu, L.H.; Fuse, T.; Shimozono, T.; Sato, S. Study on shoreline monitoring system based on satellite SAR imagery. Coast. Eng. J. 2019, 61, 401–421. [Google Scholar] [CrossRef]
- Liu, H.; Jezek, K.C. Automated extraction of coastline from satellite imagery by integrating canny edge detection and locally adaptive thresholding methods. Int. J. Remote Sens. 2004, 25, 937–958. [Google Scholar] [CrossRef]
- Wang, Y.; Allen, T.R. Estuarine shoreline change detection using Japanese ALOS PALSAR HH and JERS-1 L-HH SAR data in the Albemarle-Pamlico sounds, North Carolina, USA. Int. J. Remote Sens. 2008, 29, 4429–4442. [Google Scholar] [CrossRef]
- Buono, A.; Nunziata, F.; Mascolo, L.; Migliaccio, M. A multipolarization analysis of coastline extraction using X-band COSMO-SkyMed SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2811–2820. [Google Scholar] [CrossRef]
- Al Fugura, A.; Billa, L.; Pradhan, B. Semi-automated procedures for shoreline extraction using single RADARSAT-1 SAR image. Estuar. Coast. Shelf Sci. 2011, 95, 395–400. [Google Scholar] [CrossRef]
- Sheng, G.F.; Yang, W.; Deng, X.P.; He, C.; Cao, Y.F.; Sun, H. Coastline detection in synthetic aperture radar (SAR) images by integrating watershed transformation and controllable Gradient Vector Flow (GVF) snake model. IEEE J. Ocean. Eng. 2012, 37, 375–383. [Google Scholar] [CrossRef]
- Zhang, D.; Vangool, L.; Oosterlinck, A. Coastline detection for SAR images. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Pasadena, CA, USA, 8–12 August 1994; IEEE: New York, NY, USA, 1994; Volumes 1–4, pp. 2134–2136. [Google Scholar]
- Ding, X.W.; Li, X.F. Coastalline detection in SAR images using multiscale normalized cut segmentation. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Nunziata, F.; Buono, A.; Migliaccio, M.; Benassai, G. Dual-polarimetric C- and X-Band SAR data for coastline extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4921–4928. [Google Scholar] [CrossRef]
- Vandebroek, E.; Lindenbergh, R.; van Leijen, F.; de Schipper, M.; de Vries, S.; Hanssen, R. Semi-automated monitoring of a mega-scale beach nourishment using high-resolution TerraSAR-X satellite data. Remote Sens. 2017, 9, 653. [Google Scholar] [CrossRef]
- Fuse, T.; Ohkura, T. Development of shoreline extraction method based on spatial pattern analysis of satellite SAR images. Remote Sens. 2018, 10, 1361. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the 6th International Conference on Computer Vision, Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tajima, Y.; Wu, L.; Watanabe, K. Development of a Shoreline Detection Method Using an Artificial Neural Network Based on Satellite SAR Imagery. Remote Sens. 2021, 13, 2254. https://doi.org/10.3390/rs13122254
Tajima Y, Wu L, Watanabe K. Development of a Shoreline Detection Method Using an Artificial Neural Network Based on Satellite SAR Imagery. Remote Sensing. 2021; 13(12):2254. https://doi.org/10.3390/rs13122254
Chicago/Turabian StyleTajima, Yoshimitsu, Lianhui Wu, and Kunihiro Watanabe. 2021. "Development of a Shoreline Detection Method Using an Artificial Neural Network Based on Satellite SAR Imagery" Remote Sensing 13, no. 12: 2254. https://doi.org/10.3390/rs13122254
APA StyleTajima, Y., Wu, L., & Watanabe, K. (2021). Development of a Shoreline Detection Method Using an Artificial Neural Network Based on Satellite SAR Imagery. Remote Sensing, 13(12), 2254. https://doi.org/10.3390/rs13122254






