Injection of Traditional Hand-Crafted Features into Modern CNN-Based Models for SAR Ship Classification: What, Why, Where, and How
Abstract
1. Introduction
- Illustrate what this technique is, including the definition of injection, and the introductions of traditional features and CNN-based models studied in this paper.
- Explain why this technique is needed, including the motivation of this paper, and the meaningfulness of our work.
- Discuss where this technique should be applied, including where traditional features should be injected into CNN-based models.
- Describe how this technique is implemented, including how to make it more effective.
- The possibility of injection of traditional hand-crafted features into modern CNN-based models to further improve SAR ship classification accuracy is explored.
- What this technique is, why it is needed, where it should be applied, and how it is implemented are introduced in this paper.
- The proposed injection technique can improve SAR ship classification accuracy greatly, and the maximum improvement can reach 6.75%.
2. Methodology
2.1. What
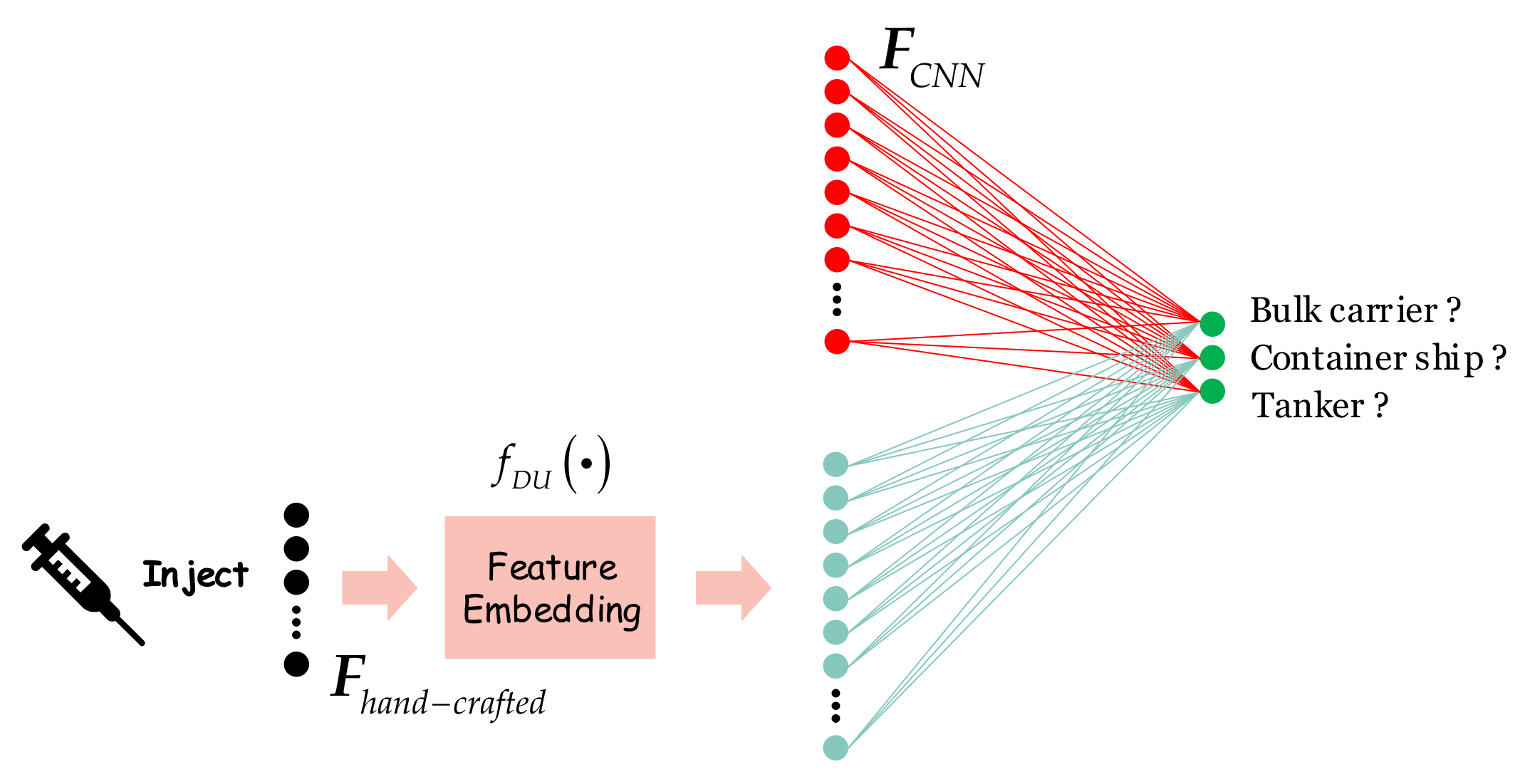
2.1.1. Injection
- The first is that the direct injection is easier to implement than the pipeline structure that might involve some tedious interface designs.
- The second is that the direct injection does not lose the original input image information. However, for the pipeline structure in Figure 2, although some interference can be suppressed after images are pre-processed via traditional means, the amount of information in the original image will be reduced. In other words, it is to obtain interference suppression at the expense of a certain amount of ship information. This practice will potentially have a negative impact on the final classification of ships.
- The third is that the direct injection does not propagate error from the previous phase. However, for the pipeline structure in Figure 2, if there are some deviations in the traditional pre-processing techniques, then such deviations will be propagated to the follow-up steps, and even become bigger and bigger, which seriously reduces the final classification accuracy.
- The fourth is that the direct injection can ensure the end-to-end training-test as long as the stimulants are prepared, more concisely, efficiently, and automatically. However, for the pipeline structure in Figure 2, if the traditional post-processing tools are adopted, e.g., the Fisher or support vector machine (SVM) discrimination, one has to train both the CNN-based model and the post-processing discriminator, respectively, which not only decreases the algorithm efficiency but also adds redundant interface designs. Particularly, it is a common consensus that the end-to-end training-test is one of CNN-based models’ advantages. If this advantage is lost, the design of classifiers will become rather troublesome.
2.1.2. Traditional Hand-Crafted Features
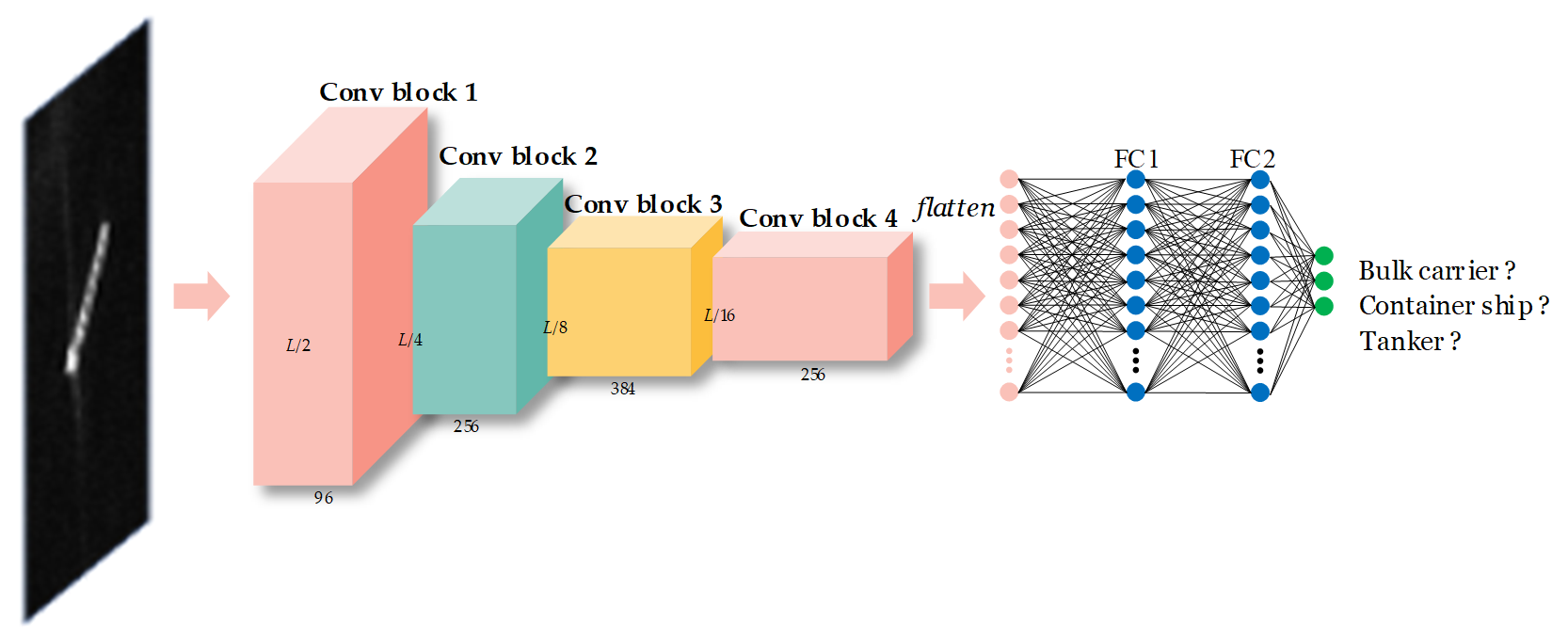
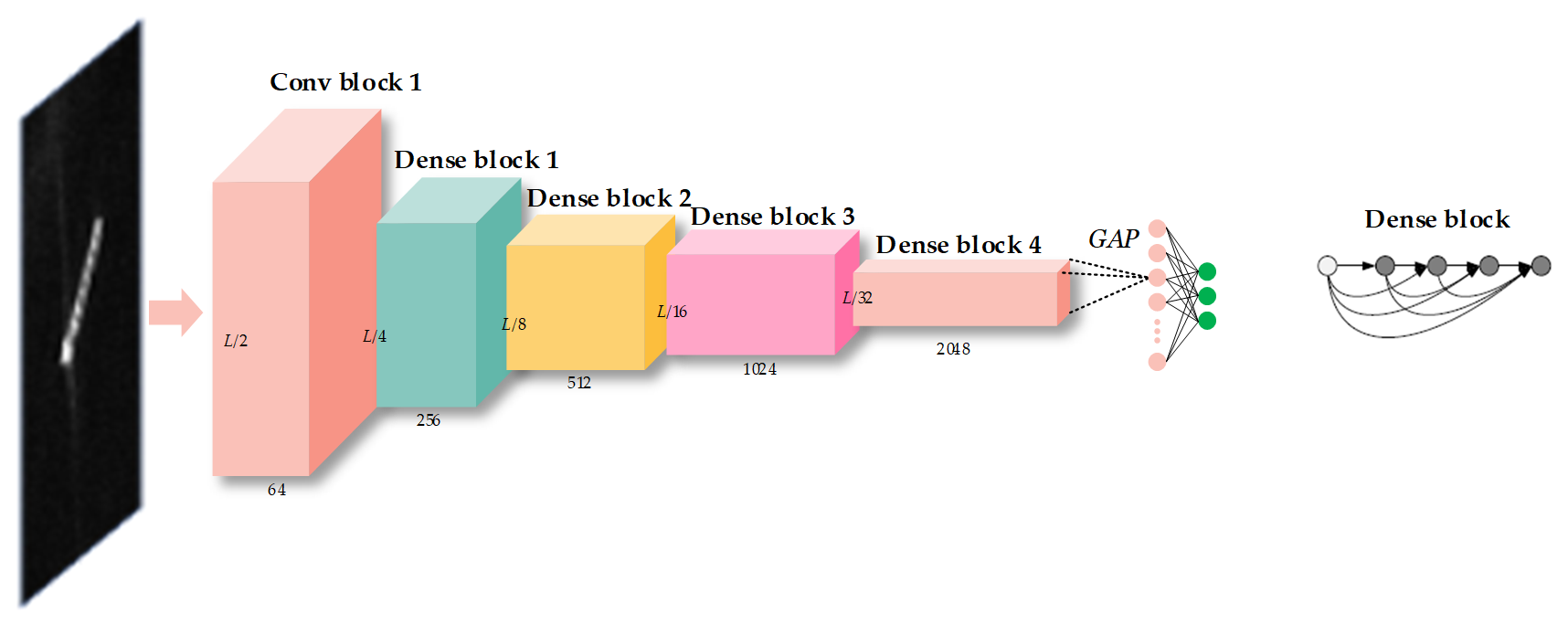
2.1.3. CNN-Based Models
2.2. Why
2.2.1. Valuable Traditional Hand-Crafted Features
2.2.2. Inexplicable CNN-Based Abstract Features
2.2.3. Limited Labeled Data
2.2.4. Improve Classification Performance Further
- If a kind of traditional hand-crafted features achieves a 70% classification accuracy, and a CNN-based model also achieves a 70% classification accuracy, it will very likely to produce a superposition effect to further improve accuracy, i.e., 70% + 70% > 70%, although it must be unlikely to obtain an accuracy of 140%. At least, this phenomenon has a higher probability to occur, from the intuitive understanding.
- In the computer vision community, the model ensemble can integrate the learning ability of each model to improve the generalization ability of the final model. To some extent, such injection process might be regarded as the model ensemble.
- When traditional hand-crafted features are injected into CNN-based models, it may alleviate the adverse effects of over-fitting from limited data. The over-fitting usually refers that the performance on training data is far better than on test data. When the network is about to overfit during training, traditional features might correct the original wrong optimization direction effectively.
- When traditional hand-crafted features are injected, the previous decision-making results of the raw CNN-based models seem to be further screened by experienced experts, which can effectively correct errors.
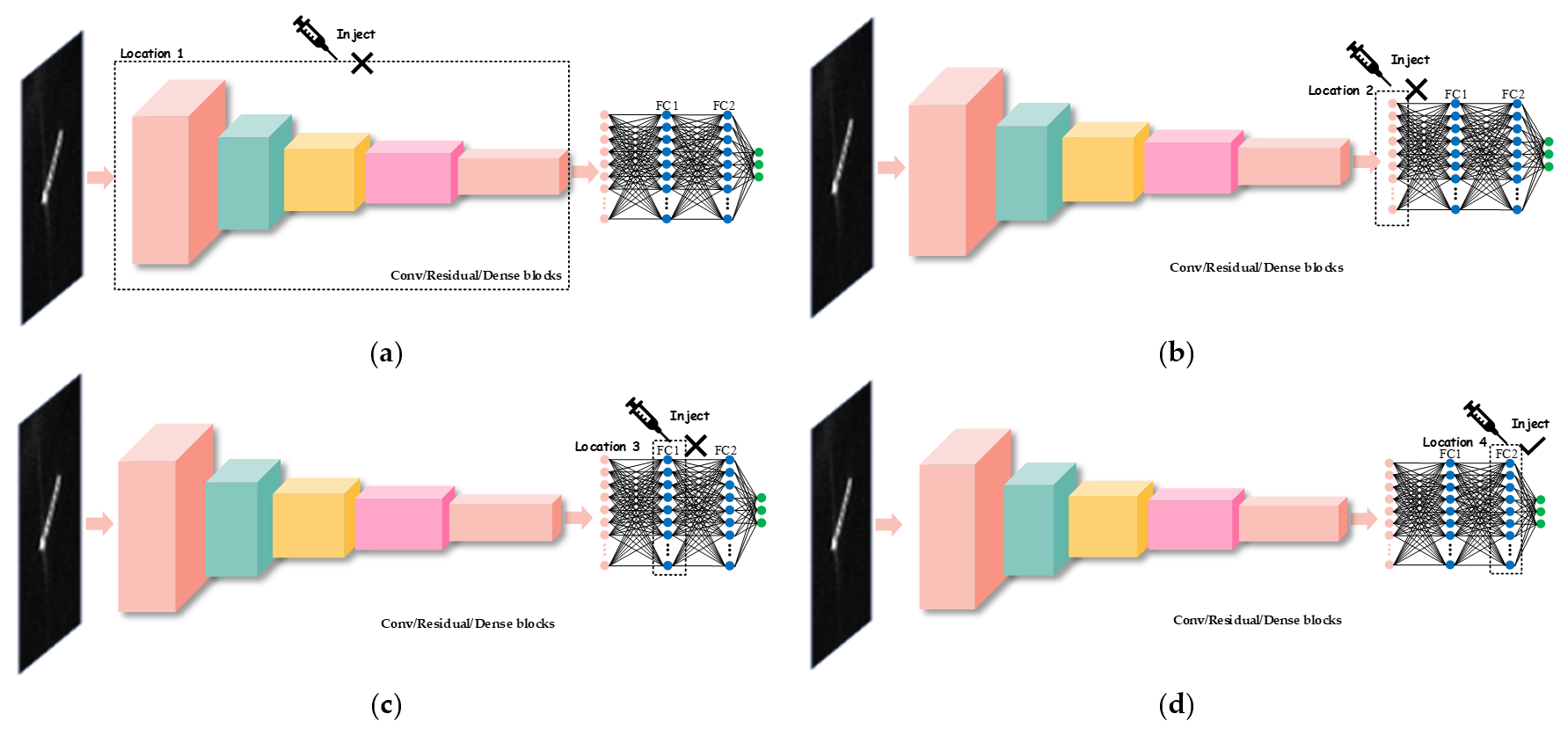
2.3. Where
2.3.1. Location 1: Conv, Residual, or Dense Blocks
2.3.2. Location 2: 1D Reshaped CNN-Based Features
2.3.3. Location 3: Internal FC Layer
2.3.4. Location 4: Terminal FC Layer
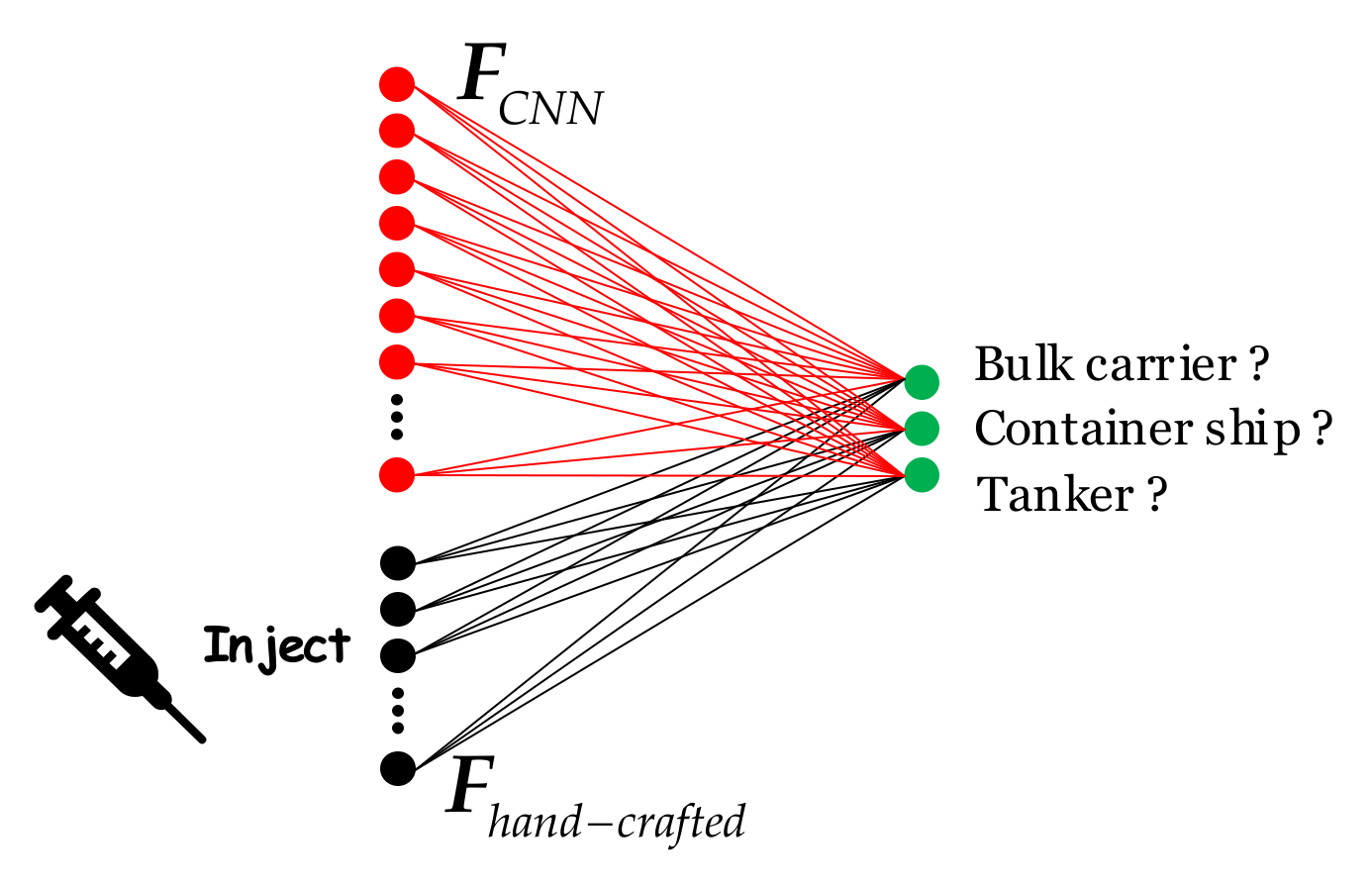
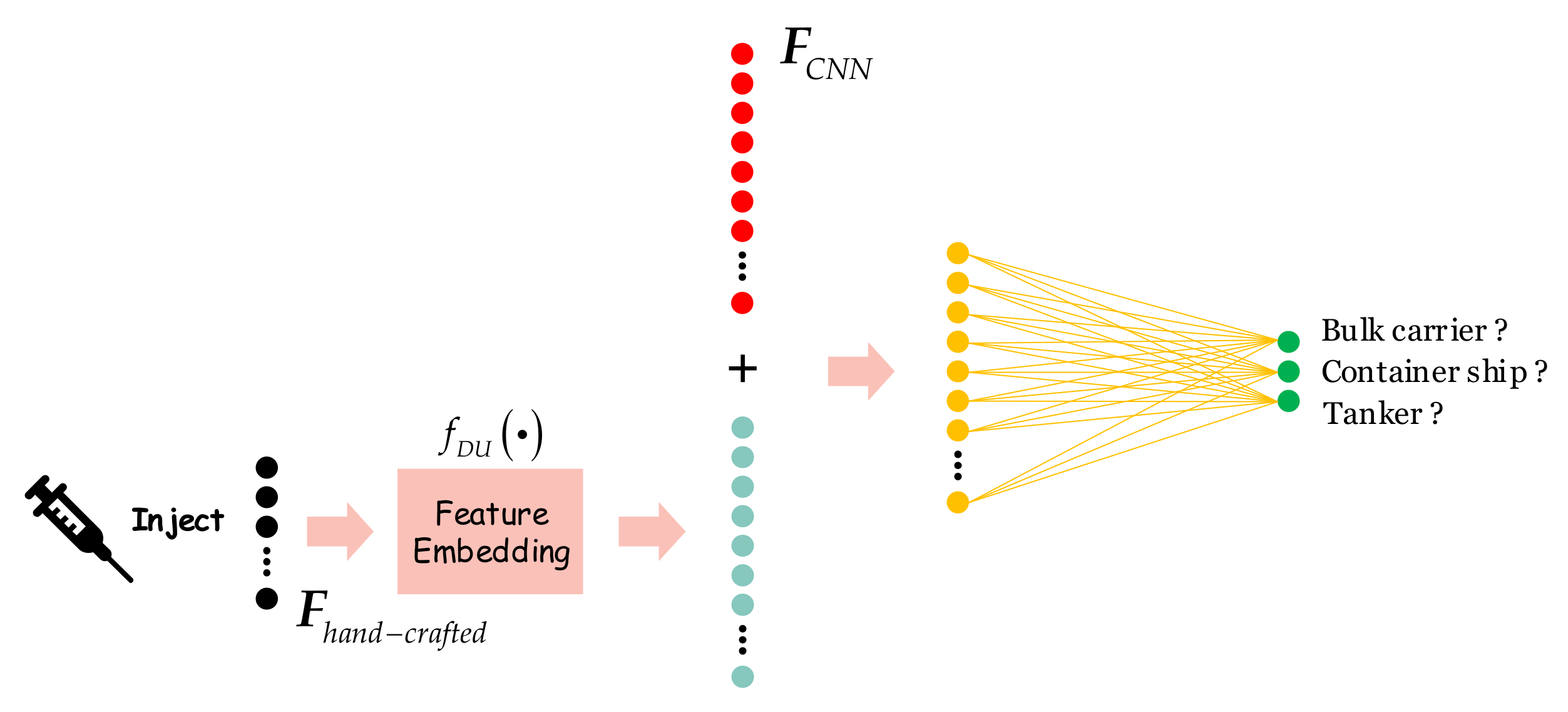
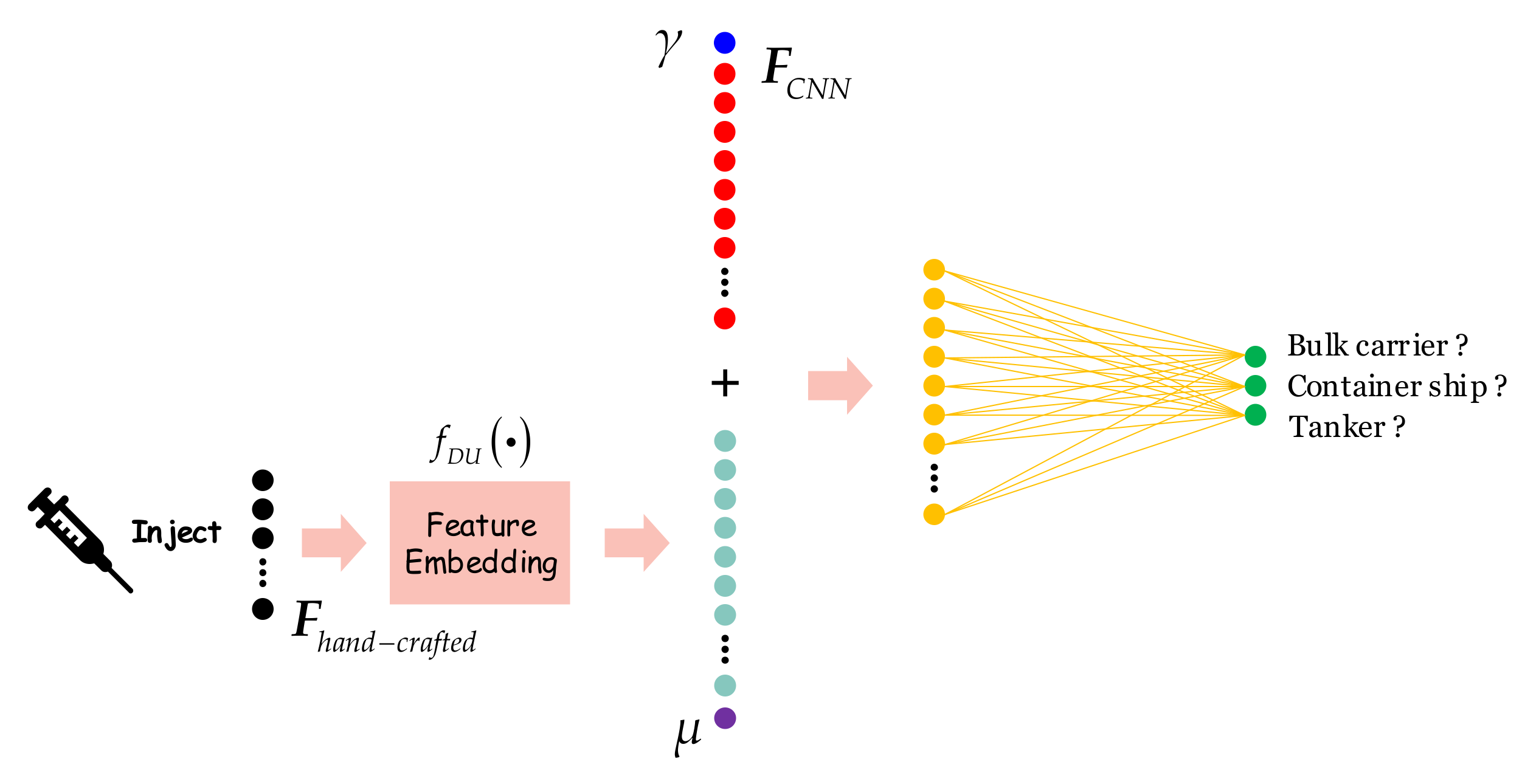
2.4. How
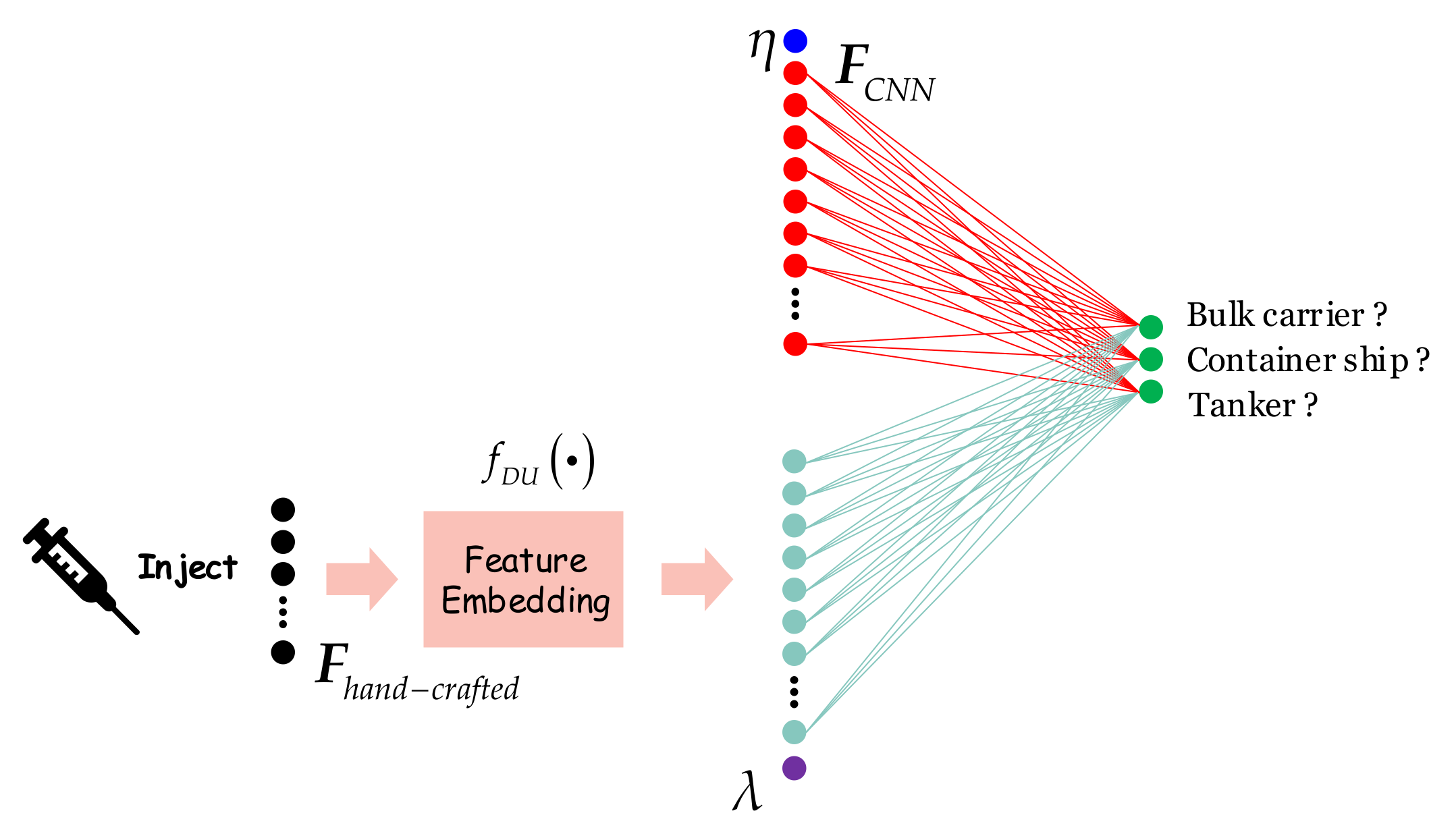
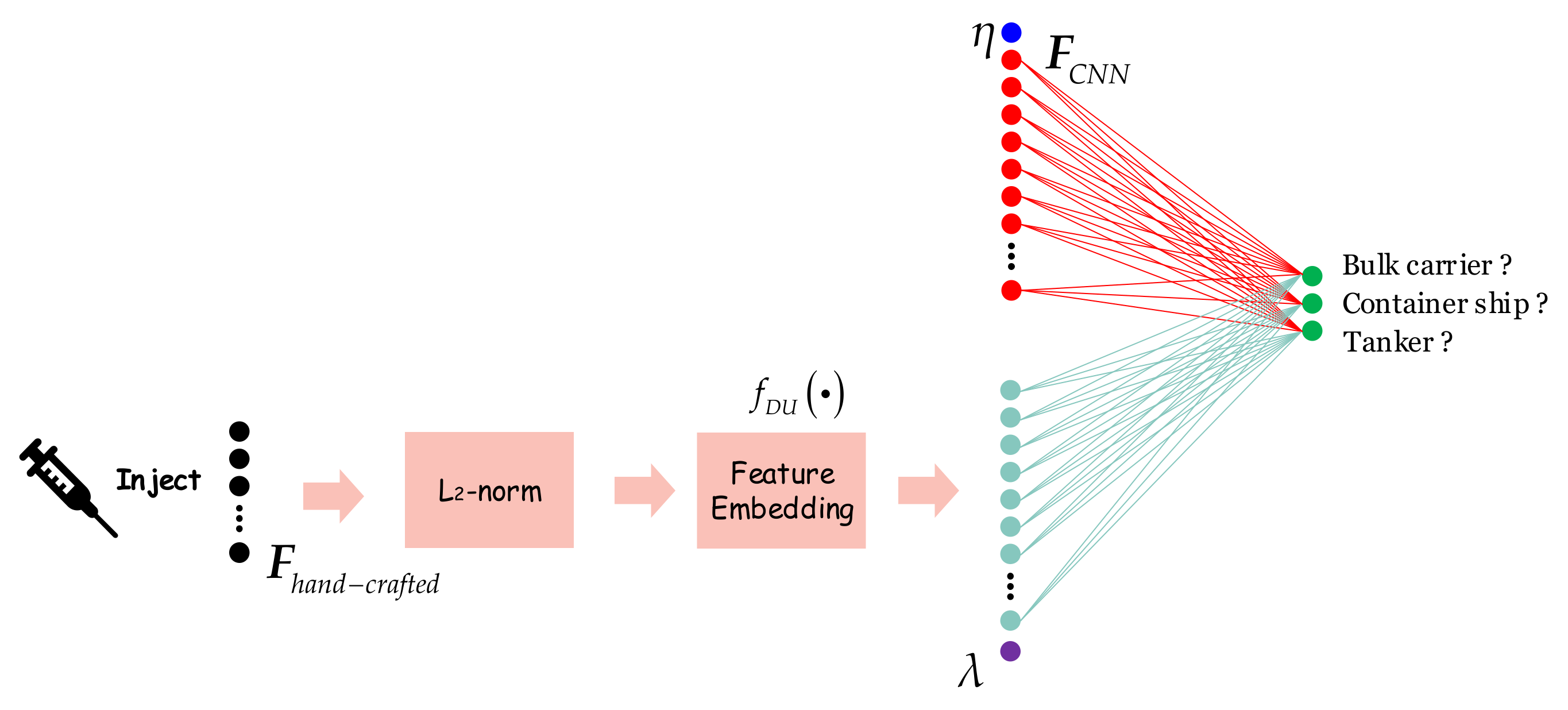
2.4.1. Mode 1: Cat
2.4.2. Mode 2: W-Cat
2.4.3. Mode 3: DU-Add
2.4.4. Mode 4: DUW-Add
2.4.5. Mode 5: DU-Cat
2.4.6. Mode 6: DUW-Cat
2.4.7. Mode 7: DUW-Cat-FN
3. Experiments
3.1. Datasets
3.1.1. Dataset 1: OpenSARShip-1.0
3.1.2. Dataset 2: FUSAR-Ship
3.2. Training Details
3.3. Loss Function
3.4. Evaluation Indices
4. Results
4.1. Accuracy
- Injection of any type of traditional hand-crafted features into any type of CNN-based models all can improve the classification accuracy, effectively. The smallest accuracy improvement reaches 1.41% from DenseNet + PAFs. Notably, the largest accuracy improvement reaches 6.25% from VGGNet + HOG. The above confirm powerfully the effectiveness of our proposed injection technique. Therefore, our proposed injection technique can improve the accuracy without using gorgeous network structure designs, easily and significantly. Certainly, it is obvious that our hypothesis in Section 2.2.4 is also reasonable. The motivation of our research has been well verified, experimentally.
- Different CNN-based models have different sensitivities to different traditional features. Specifically, when AlexNet receives LRCS, the accuracy reaches the best (75.51%). For VGGNet, the best injection feature is HOG (76.76%); for ResNet, that is PAFs (76.52%); for DenseNet, that is LRCS (78.00%). The internal mechanism of this phenomenon may need to be further researched in the future. In other words, how to select the most suitable traditional hand-crafted features for injection into the most suitable CNN-based model is a meaningful work, which is worthy of further study in the future.
- The sensitivity differences of different models to different traditional features are all different, but seem to be not rather significant, universally around or even lower than 2%. Specifically, for AlexNet, the optimal LRCS injection is better than the worst NGFs one by 2.11%; for VGGNet, the optimal HOG injection is better than the worst NGFs one by 1.56%; for ResNet, the optimal PAFs injection is better than the worst HOG one by 1.09%; for DenseNet, the optimal LRCS injection is better than the worst PAFs one by 1.63%. The internal mechanism of this phenomenon needs to be further researched in the future.
- For the original model with relatively poor performance, the accuracy improvement is more significant. For example, the original AlexNet model has a 70.05% classification accuracy, and its improvement with injection is 4.29% on average; but, the original DenseNet model has a 74.96% classification accuracy, and its improvement with injection is only 2.09% on average. The internal mechanism of this phenomenon may also need further research in the future.
4.2. Accuracy Comparison with Pure Traditional Hand-Crafted Features
- On the OpenSARShip-1.0 dataset, NGFs offers the best classification accuracy, i.e., 69.81%. This accuracy value is very close to that of the CNN-based model AlexNet in Table 4, i.e., 69.81% vs 70.05%. Therefore, traditional hand-crafted features can offer comparative accuracies with modern CNN-based models. This reveals the true importance of traditional hand-crafted features, which should not be abandoned completely.
- On the FUSAR-Ship dataset, NGFs also offers the best classification accuracy, i.e., 78.62%. Even, this accuracy value is slightly better than that of the CNN-based model AlexNet in Table 5, i.e., 78.62% vs 77.42%. One possible reason for this may be that the performance of CNN-based models is really constrained by limited training data, which hinders them to play their maximum advantages. Therefore, under the condition of limited training data, traditional hand-crafted features will become more valuable if they are injected into CNN-based models. The above also reveals the true importance of traditional hand-crafted features, which should not be abandoned completely.
4.3. Confusion Matrix
5. Discussion
5.1. Discussion on Where
5.2. Discussion on How
- Most modes can improve the classification accuracy, except the mode 3 and 4. Therefore, the five concatenation modes (i.e., Cat, W-Cat, DU-Cat, DUW-Cat, and DUW-Cat-FN) can achieve the approving combination of traditional features and CNN-based features, effectively. However, the two adding modes (i.e., DU-Add and DUW-Add) might make learning confusing during training, leading to the poor classification performance. We think that it seems unreasonable to blindly add the abstract and the concrete directly; because, essentially, the physical meanings to which they belong are completely inconsistent.
- The weighted (W) modes outperform the non-weighted ones, e.g., 74.65% of W-Cat > 74.18% of Cat, and 75.90% of DUW-Cat > 75.12% of DU-Cat. In this way, the weighted coefficients via learning adaptively in training can better reflect the importance of different types of features. This reasonable allocation of decision-makings can potentially further improve accuracy.
- The dimension-unification (DU) modes outperform the non-dimension-unification ones, e.g., 75.12% of DU-Cat > 74.18% of Cat. In this way, the feature dimension between the traditional hand-crafted features and the CNN-based ones is balanced, which potentially not only reduces the benefits of network learning, but also reduces the risk of the network falling into the over-fitting of a certain type of features, as shown in Figure 15.
- The feature normalization (FN) can further improve classification performance, i.e., 76.76% of DUW-Cat-FN > 75.90% of DUW-Cat. In this way, the range of values of traditional hand-crafted features is constrained to the same level as the CNN-based ones, bringing more stable training and enhancing learning benefits.
6. Conclusions
- Study how to select the most suitable traditional hand-crafted features for injection.
- Rethink and analyze the deep-seated internal mechanisms of this injection technique.
- Study hybrid/multi feature injection forms, which may improve classification accuracy further.
- Strive to improve the accuracy of each category, e.g., the “fishing” and “other” categories in the FUSAR-Ship.
- Apply this injection technique to classify more types of ships, e.g., war ships.
- Optimize the extraction process of the minimum bounding rectangle of a ship. Moreover, study simpler and faster ways to calculate ship length, width and orientation.
- Explore CNNs’ potentials of exploiting sidelobes for classifying large reflective ships.
- Perform experiments on the OpenSARShip-2.0 dataset.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, L.; Liu, B.; Li, B.; Guo, W.; Yu, W.; Zhang, Z.; Yu, W. OpenSARShip: A Dataset Dedicated to Sentinel-1 Ship Interpretation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 195–208. [Google Scholar] [CrossRef]
- Lang, H.; Wu, S. Ship Classification in Moderate-Resolution SAR Image by Naive Geometric Features-Combined Multiple Kernel Learning. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1765–1769. [Google Scholar] [CrossRef]
- Lang, H.; Zhang, J.; Zhang, X.; Meng, J. Ship Classification in SAR Image by Joint Feature and Classifier Selection. IEEE Geosci. Remote Sens. Lett. 2016, 13, 212–216. [Google Scholar] [CrossRef]
- Xu, Y.; Lang, H. Ship Classification in SAR Images with Geometric Transfer Metric Learning. IEEE Trans. Geosci. Remote Sens. 2020, 1–15. [Google Scholar] [CrossRef]
- Wu, F.; Wang, C.; Jiang, S.; Zhang, H.; Zhang, B. Classification of Vessels in Single-Pol COSMO-SkyMed Images Based on Statistical and Structural Features. Remote Sens. 2015, 7, 5511–5533. [Google Scholar] [CrossRef]
- Lin, H.; Song, S.; Yang, J. Ship Classification Based on MSHOG Feature and Task-Driven Dictionary Learning with Structured Incoherent Constraints in SAR Images. Remote Sens. 2018, 10, 190. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, H.; Wang, C.; Wang, Y. Fine-grained ship classification based on deep residual learning for high-resolution SAR images. Remote Sens. Lett. 2019, 10, 1095–1104. [Google Scholar] [CrossRef]
- Huang, G.; Liu, X.; Hui, J.; Wang, Z.; Zhang, Z. A novel group squeeze excitation sparsely connected convolutional networks for SAR target classification. Int. J. Remote Sens. 2019, 40, 4346–4360. [Google Scholar] [CrossRef]
- Hou, X.; Ao, W.; Song, Q.; Lai, J.; Wang, H.; Xu, F. FUSAR-Ship: Building a high-resolution SAR-AIS matchup dataset of Gaofen-3 for ship detection and recognition. Sci. China Inf. Sci. 2020, 63, 140303. [Google Scholar] [CrossRef]
- He, J.; Wang, Y.; Liu, H. Ship Classification in Medium-Resolution SAR Images via Densely Connected Triplet CNNs Integrating Fisher Discrimination Regularized Metric Learning. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1–18. [Google Scholar] [CrossRef]
- Zeng, L.; Zhu, Q.; Lu, D.; Zhang, T.; Wang, H.; Yin, J.; Yang, J. Dual-Polarized SAR Ship Grained Classification Based on CNN With Hybrid Channel Feature Loss. IEEE Geosci. Remote Sens. Lett. 2021, 1–5. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. High-Speed Ship Detection in SAR Images Based on a Grid Convolutional Neural Network. Remote Sens. 2019, 11, 1206. [Google Scholar] [CrossRef]
- Li, J.; Qu, C.; Peng, S. A ship detection method based on cascade CNN in SAR images. Control Decis. 2019, 34, 2191–2197. [Google Scholar]
- Yang, R.; Wang, G.; Pan, Z.; Lu, H.; Zhang, H.; Jia, X. A Novel False Alarm Suppression Method for CNN-Based SAR Ship Detector. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Song, S.; Xu, B.; Yang, J. SAR Target Recognition via Supervised Discriminative Dictionary Learning and Sparse Representation of the SAR-HOG Feature. Remote Sens. 2016, 8, 683. [Google Scholar] [CrossRef]
- Leng, X.; Ji, K.; Zhou, S.; Xing, X.; Zou, H. 2D comb feature for analysis of ship classification in high-resolution SAR imagery. Electronics Lett. 2017, 53, 500–502. [Google Scholar] [CrossRef]
- Chen, W.T.; Ji, K.F.; Xing, X.W.; Zou, H.X.; Sun, H. Ship recognition in high resolution SAR imagery based on feature selection. In Proceedings of the International Conference on Computer Vision in Remote Sensing, Xiamen, China, 16–18 December 2012; pp. 301–305. [Google Scholar]
- Jiang, M.; Yang, X.; Dong, Z.; Fang, S.; Meng, J. Ship Classification Based on Superstructure Scattering Features in SAR Images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 616–620. [Google Scholar] [CrossRef]
- Huang, S.; Cheng, F.; Chiu, Y. Efficient Contrast Enhancement Using Adaptive Gamma Correction with Weighting Distribution. IEEE Trans. Image Process. 2013, 22, 1032–1041. [Google Scholar] [CrossRef] [PubMed]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 886–893. [Google Scholar]
- Zhang, T.; Zhang, X.; Ke, X.; Liu, C.; Xu, X.; Zhan, X.; Wang, C.; Ahmad, I.; Zhou, Y.; Pan, D.; et al. HOG-ShipCLSNet: A Novel Deep Learning Network with HOG Feature Fusion for SAR Ship Classification. IEEE Trans. Geosci. Remote. Sens. 2021, 1–21. [Google Scholar] [CrossRef]
- Lang, H.; Wu, S.; Xu, Y. Ship Classification in SAR Images Improved by AIS Knowledge Transfer. IEEE Geosci. Remote Sens. Lett. 2018, 15, 439–443. [Google Scholar] [CrossRef]
- Xing, X.; Ji, K.; Zou, H.; Chen, W.; Sun, J. Ship Classification in TerraSAR-X Images with Feature Space Based Sparse Representation. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1562–1566. [Google Scholar] [CrossRef]
- Margarit, G.; Tabasco, A. Ship Classification in Single-Pol SAR Images Based on Fuzzy Logic. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3129–3138. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS), Curran Associates Inc., Lake Tahoe, NV, USA, 3–6 December 2012; pp. 1097–1105. [Google Scholar]
- Wang, C.; Shi, J.; Zhou, Y.; Yang, X.; Zhou, Z.; Wei, S.; Zhang, X. Semisupervised Learning-Based SAR ATR via Self-Consistent Augmentation. IEEE Trans. Geosci. Remote Sens. 2020, 1–12. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. arXiv 2013, arXiv:1312.4400. [Google Scholar]
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar]
- Hu, M.-K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Zhang, X.; Shi, J.; Wei, S. Depthwise Separable Convolution Neural Network for High-Speed SAR Ship Detection. Remote Sens. 2019, 11, 2483. [Google Scholar] [CrossRef]
- Yang, R.; Wang, R.; Deng, Y.; Jia, X.; Zhang, H. Rethinking the Random Cropping Data Augmentation Method Used in the Training of CNN-based SAR Image Ship Detector. Remote Sens. 2021, 13, 14. [Google Scholar]
- Tang, G.; Zhuge, Y.; Claramunt, C.; Men, S. N-YOLO: A SAR Ship Detection Using Noise-Classifying and Complete-Target Extraction. Remote Sens. 2021, 13, 871. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Shi, J.; Wei, S.; Wang, J.; Li, J.; Su, H.; Zhou, Y. Balance Scene Learning Mechanism for Offshore and Inshore Ship Detection in SAR Images. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Pelich, R.; Chini, M.; Hostache, R.; Lopez-Martinez, C.; Matgen, P.; Nuevo, M.; Ries, P.; Eiden, G. Large-Scale Automatic Vessel Monitoring Based on Dual-Polarization Sentinel-1 and AIS Data. Remote Sens. 2019, 11, 1078. [Google Scholar] [CrossRef]
- Song, J.; Kim, D.-J.; Kan, K.-M. Automated Procurement of Training Data for Machine Learning Algorithm on Ship Detection Using AIS Information. Remote Sens. 2020, 12, 1443. [Google Scholar] [CrossRef]
- Kurekin, A.; Loveday, B.; Clements, O.; Quartly, G.; Miller, P.; Wiafe, G.; Adu Agyekum, K. Operational Monitoring of Illegal Fishing in Ghana through Exploitation of Satellite Earth Observation and AIS Data. Remote Sens. 2019, 11, 293. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X. ShipDeNet-20: An Only 20 Convolution Layers and <1-MB Lightweight SAR Ship Detector. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Gao, F.; He, Y.; Wang, J.; Hussain, A.; Zhou, H. Anchor-free Convolutional Network with Dense Attention Feature Aggregation for Ship Detection in SAR Images. Remote Sens. 2020, 12, 2619. [Google Scholar] [CrossRef]
- Fan, W.; Zhou, F.; Bai, X.; Tao, M.; Tian, T. Ship Detection Using Deep Convolutional Neural Networks for PolSAR Images. Remote Sens. 2019, 11, 2862. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Shi, J.; Wei, S. HyperLi-Net: A hyper-light deep learning network for high-accurate and high-speed ship detection from synthetic aperture radar imagery. ISPRS J. Photogramm. Remote Sens. 2020, 167, 123–153. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, T.; Lei, P.; Bai, X. A Hierarchical Convolution Neural Network (CNN)-Based Ship Target Detection Method in Spaceborne SAR Imagery. Remote Sens. 2019, 11, 620. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, Z.; Yu, W.; Sun, X. Perspective on explainable SAR target recognition. J. Radars 2020, 9, 462–476. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.-J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Li, J.; Qu, C.; Shao, J. Ship detection in SAR images based on an improved faster R-CNN. In Proceedings of the SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA), Beijing, China, 13–14 November 2017; pp. 1–6. [Google Scholar]
- Wang, Y.; Wang, C.; Zhang, H.; Dong, Y.; Wei, S. A SAR Dataset of Ship Detection for Deep Learning under Complex Backgrounds. Remote Sens. 2019, 11, 765. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Z.; Sun, Y.; Diao, W.; Zhang, Y.; Fu, K. AIR-SARShip-1.0: High-resolution SAR Ship Detection Dataset. J. Radars 2019, 8, 852. [Google Scholar]
- Wei, S.; Zeng, X.; Qu, Q.; Wang, M.; Su, H.; Shi, J. HRSID: A High-Resolution SAR Images Dataset for Ship Detection and Instance Segmentation. IEEE Access 2020, 8, 120234–120254. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, X.; Ke, X.; Zhan, X.; Shi, J.; Wei, S.; Pan, D.; Li, J.; Su, H.; Zhou, Y.; et al. LS-SSDD-v1.0: A Deep Learning Dataset Dedicated to Small Ship Detection from Large-Scale Sentinel-1 SAR Images. Remote Sens. 2020, 12, 2997. [Google Scholar] [CrossRef]
- Kang, M.; Ji, K.; Leng, X.; Lin, Z. Contextual Region-Based Convolutional Neural Network with Multilayer Fusion for SAR Ship Detection. Remote Sens. 2017, 9, 860. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, ICML, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Zhang, H.; Tian, X.; Wang, C.; Wu, F.; Zhang, B. Merchant Vessel Classification Based on Scattering Component Analysis for COSMO-SkyMed SAR Images. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1275–1279. [Google Scholar] [CrossRef]
- Huang, Z.; Pan, Z.; Lei, B. What, Where, and How to Transfer in SAR Target Recognition Based on Deep CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2324–2336. [Google Scholar] [CrossRef]
- Marine-Traffic, Ship List with Details and Photos. 2007. Available online: http://www.marinetraffic.com/en/ais/index/ships/all (accessed on 6 April 2021).
- Li, B.; Liu, B.; Huang, L.; Guo, W.; Zhang, Z.; Yu, W. OpenSARShip 2.0: A large-volume dataset for deeper interpretation of ship targets in Sentinel-1 imagery. In Proceedings of the 2017 SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA), Beijing, China, 13–14 November 2017; pp. 1–5. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar]


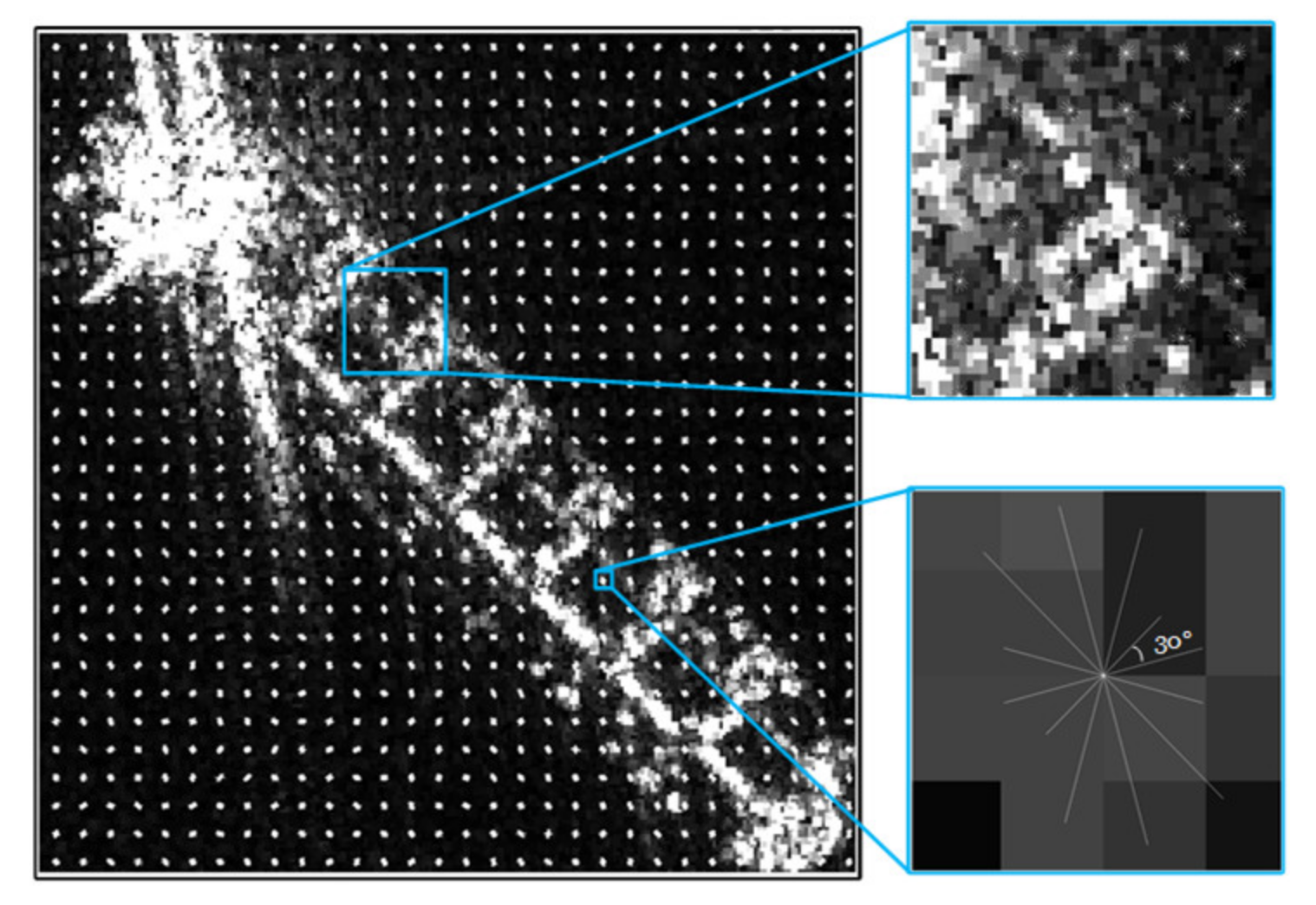








| NGFs | Definition | Description |
|---|---|---|
| L | Length | |
| W | Width | |
| 2 × (L + W) | Naive perimeter | |
| L × W | Naive area | |
| L/W | Aspect ratio (a) | |
| W/L | Aspect ratio (b) | |
| (L + W)2/(L × W) | Shape complex | |
| W2/(L2 + W2) | / | |
| (L − W)/(L + W) | / | |
| L/(L + W) | / | |
| W/(L + W) | / |
| Category | Training | Test | All |
|---|---|---|---|
| Bulk carrier | 338 | 328 | 666 |
| Container ship | 338 | 808 | 1146 |
| Tanker | 338 | 146 | 484 |
| Category | Training | Test | All |
|---|---|---|---|
| Bulk carrier | 1150 | 494 | 1644 |
| Container ship | 1219 | 523 | 1742 |
| Fishing | 1101 | 473 | 1574 |
| Tanker | 1215 | 521 | 1736 |
| General cargo | 1205 | 517 | 1722 |
| Other cargo | 1214 | 521 | 1735 |
| Other | 1211 | 520 | 1731 |
| CNN Model | Injection Feature Type | Acc (%) | Improvement (%) | Improvement Remarks |
|---|---|---|---|---|
| AlexNet | ✗ | 70.05 | - | - |
| HOG | 74.02 | 3.97 | Avg = 4.29% Max − Min = 2.11% | |
| NGFs | 73.40 | 3.35 | ||
| LRCS | 75.51 | 5.46 | ||
| PAFs | 74.41 | 4.36 | ||
| VGGNet | ✗ | 70.51 | - | - |
| HOG | 76.76 | 6.25 1 | Avg = 5.55% Max − Min = 1.56% | |
| NGFs | 75.20 | 4.69 | ||
| LRCS | 76.44 | 5.93 | ||
| PAFs | 75.83 | 5.32 | ||
| ResNet | ✗ | 72.54 | - | - |
| HOG | 75.43 | 2.89 | Avg = 3.46% Max − Min = 1.09% | |
| NGFs | 76.13 | 3.59 | ||
| LRCS | 75.90 | 3.36 | ||
| PAFs | 76.52 | 3.98 | ||
| DenseNet | ✗ | 74.96 | - | - |
| HOG | 76.83 | 1.87 | Avg = 2.09% Max − Min = 1.63% | |
| NGFs | 76.99 | 2.03 | ||
| LRCS | 78.00 | 3.04 | ||
| PAFs | 76.37 | 1.41 |
| CNN Model | Injection Feature Type | Acc (%) | Improvement (%) | Improvement Remarks |
|---|---|---|---|---|
| AlexNet | ✗ | 77.42 | - | - |
| HOG | 82.38 | 4.96 | Avg = 5.44% Max − Min = 1.79% | |
| NGFs | 82.46 | 5.04 | ||
| LRCS | 84.17 | 6.75 1 | ||
| PAFs | 82.43 | 5.01 | ||
| VGGNet | ✗ | 80.75 | - | - |
| HOG | 84.79 | 4.04 | Avg = 3.95% Max − Min = 2.53% | |
| NGFs | 84.70 | 3.95 | ||
| LRCS | 83.38 | 2.63 | ||
| PAFs | 85.91 | 5.16 | ||
| ResNet | ✗ | 81.20 | - | - |
| HOG | 85.57 | 4.37 | Avg = 4.20% Max − Min = 1.76% | |
| NGFs | 86.21 | 5.01 | ||
| LRCS | 85.35 | 4.15 | ||
| PAFs | 84.45 | 3.25 | ||
| DenseNet | ✗ | 84.14 | - | - |
| HOG | 86.21 | 2.07 | Avg = 1.87% Max − Min = 1.54% | |
| NGFs | 85.32 | 1.18 | ||
| LRCS | 86.86 | 2.72 | ||
| PAFs | 85.65 | 1.51 |
| Dataset | Feature Type | Acc (%) |
|---|---|---|
| OpenSARShip-1.0 | HOG | 66.07 |
| NGFs | 69.81 | |
| LRCS | 67.47 | |
| PAFs | 59.91 | |
| FUSAR-Ship | HOG | 73.05 |
| NGFs | 78.62 | |
| LRCS | 71.36 | |
| PAFs | 69.74 |
| Predicte | Bulk Carrier | Container Ship | Tanker | Acc (%) | |
|---|---|---|---|---|---|
| True | |||||
| Bulk carrier | 202 | 93 | 33 | 61.59 | |
| Container ship | 150 | 613 | 45 | 75.87 | |
| Tanker | 17 | 14 | 115 | 78.77 | |
| Predicte | Bulk Carrier | Container Ship | Tanker | Acc (%) | |
|---|---|---|---|---|---|
| True | |||||
| Bulk carrier | 204 | 88 | 36 | 62.20 | |
| Container ship | 122 | 643 | 43 | 79.58 | |
| Tanker | 12 | 14 | 120 | 82.19 | |
| Predicte | Bulk Carrier | Container Ship | Fishing | General Cargo | Other | Other Cargo | Tanker | Acc (%) | |
|---|---|---|---|---|---|---|---|---|---|
| True | |||||||||
| Bulk carrier | 451 | 19 | 0 | 10 | 10 | 4 | 0 | 91.30 | |
| Container ship | 16 | 463 | 6 | 14 | 8 | 3 | 13 | 88.53 | |
| Fishing | 8 | 2 | 391 | 0 | 32 | 34 | 6 | 82.66 | |
| General cargo | 28 | 21 | 0 | 437 | 4 | 3 | 24 | 84.53 | |
| Other | 14 | 3 | 69 | 1 | 331 | 78 | 25 | 63.53 | |
| Other cargo | 5 | 3 | 44 | 0 | 50 | 382 | 36 | 73.46 | |
| Tanker | 2 | 11 | 9 | 8 | 14 | 34 | 443 | 85.03 | |
| Predicte | Bulk Carrier | Container Ship | Fishing | General Cargo | Other | Other Cargo | Tanker | Acc (%) | |
|---|---|---|---|---|---|---|---|---|---|
| True | |||||||||
| Bulk carrier | 453 | 8 | 5 | 7 | 2 | 1 | 18 | 91.70 | |
| Container ship | 9 | 501 | 4 | 1 | 2 | 5 | 1 | 95.79 | |
| Fishing | 2 | 3 | 358 | 0 | 61 | 35 | 14 | 75.69 | |
| General cargo | 6 | 0 | 0 | 499 | 8 | 1 | 3 | 96.52 | |
| Other | 19 | 0 | 81 | 0 | 314 | 66 | 41 | 60.27 | |
| Other cargo | 3 | 0 | 36 | 0 | 21 | 452 | 8 | 86.92 | |
| Tanker | 19 | 6 | 4 | 4 | 9 | 2 | 477 | 91.55 | |
| Where | Name | Acc (%) | Improve? |
|---|---|---|---|
| Baseline | - | 70.51 | - |
| Location 1 | Conv, Residual, or Dense Blocks | - | - |
| Location 2 | 1D Reshaped CNN-based Features | 69.19 | ✗ |
| Location 3 | Internal FC layer | 68.56 | ✗ |
| Location 4 | Terminal FC layer | 76.76 | ✓ |
| How | Name | Acc (%) | Improve? |
|---|---|---|---|
| Baseline | - | 70.51 | - |
| Mode 1 | Cat | 74.18 | ✓ |
| Mode 2 | W-Cat | 74.65 | ✓ |
| Mode 3 | DU-Add | 69.66 | ✗ |
| Mode 4 | DUW-Add | 70.44 | ✗ |
| Mode 5 | DU-Cat | 75.12 | ✓ |
| Mode 6 | DUW-Cat | 75.90 | ✓ |
| Mode 7 | DUW-Cat-FN | 76.76 | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Zhang, X. Injection of Traditional Hand-Crafted Features into Modern CNN-Based Models for SAR Ship Classification: What, Why, Where, and How. Remote Sens. 2021, 13, 2091. https://doi.org/10.3390/rs13112091
Zhang T, Zhang X. Injection of Traditional Hand-Crafted Features into Modern CNN-Based Models for SAR Ship Classification: What, Why, Where, and How. Remote Sensing. 2021; 13(11):2091. https://doi.org/10.3390/rs13112091
Chicago/Turabian StyleZhang, Tianwen, and Xiaoling Zhang. 2021. "Injection of Traditional Hand-Crafted Features into Modern CNN-Based Models for SAR Ship Classification: What, Why, Where, and How" Remote Sensing 13, no. 11: 2091. https://doi.org/10.3390/rs13112091
APA StyleZhang, T., & Zhang, X. (2021). Injection of Traditional Hand-Crafted Features into Modern CNN-Based Models for SAR Ship Classification: What, Why, Where, and How. Remote Sensing, 13(11), 2091. https://doi.org/10.3390/rs13112091







