On the Relationship between Low Latitude Scintillation Onset and Sunset Terminator over Africa

Abstract

The solar terminator is a moving boundary between day-side and night-side regions on the Earth, which is a substantial source of perturbations in the ionosphere. In the vicinity of the solar terminator, essential parameters like ${\mathrm{S}}_4$ index measurements are widely analyzed in order to monitor and predict perturbations in the ionosphere. The utilization of the scintillation index ${\mathrm{S}}_4$ is a well-accepted approach to describe the amplitude/intensity fluctuation of a received signal, predominantly caused by small-scale irregularities of the ionospheric plasma. We report on the longitudinal daily and seasonal occurrence of GNSS signal scintillations, using the data derived from the GNSS stations in Bahir Dar, Ethiopia, Lomé, Togo and Dakar, Senegal. The observed seasonal climatology of GNSS signal scintillations in equatorial Africa is adequately explained by the alignment of the solar terminator and local geomagnetic declination line. It should be pointed out that the strongest scintillations are most frequently observed during the time when the solar terminator is best aligned with the geomagnetic declination line. At all three stations, the comparison of computational and observational results indicated that the scintillation activity culminated around equinoxes in the years 2014, 2015 and 2016. Comparatively, the western equatorial Africa sector has the most intense, longest-lasting, and highest scintillation occurrence rate in equinoctial seasons in all three years. For the first time, we show that the seasonal variation of the scintillation peaks changes systematically from west to east at equatorial GNSS stations over Africa. A detailed analysis of the solar day–night terminator azimuth at ionospheric heights including the time equation shows that the scintillation intensity has a maximum if the azimuth of the terminator coincides with the declination line of the geomagnetic field. Due to the remarkable change of the declination by about 10° at the considered GNSS stations, the distance between scintillation peaks increases by 46 days when moving westward from the Bahir Dar to the Dakar GNSS station. The observations agree quite well with the computational results, thus confirming Tsunoda’s theory.

1. Introduction

The solar terminator is a regular and effective source of perturbations in the ionosphere, which substantially affects the trans-ionospheric propagation of radio waves [1]. The degree of perturbations in the ionosphere due to small-scale irregularities and plasma bubbles can be largely responsible for the fluctuations in the amplitude and phase of GNSS signals, referred to as scintillations. Ionospheric scintillations can cause severe degradation and disruption of the GNSS-based positioning and navigation applications. Strong fading depths of up to 25 dB were observed on GPS signals in the equatorial anomaly region [2]. Even though there are ample studies spanning more than five decades about the various effects of the ionosphere on the propagation of GNSS signals, many open questions still remain, for example, regarding the possible driving mechanisms for the appearance of deeper and wedge-shaped structures of plasma depletion in the African sector and their impact levels on GNSS signals. Obtaining a better understanding of their dynamics and climatology is therefore an active research goal in ionospheric and radio physics. To avoid problems related to navigation safety and increase positioning accuracy, our knowledge of the physical processes behind radio scintillations must be improved in order to develop appropriate mitigation techniques and forecast tools. It is believed that the linear growth rate variations of generalized Rayleigh–Taylor instability [3] and the presence of seed perturbation [4] primarily account for the occurrence phenomenology of GNSS signal scintillations between different regions in equatorial Africa. Furthermore, authors in [5] reported that the uplift of the equatorial F-layer enhances the gravity-driven eastward current that plays an important role in the development of post-midnight equatorial plasma bubbles (EPBs). As described in [6,7], the redistribution of electron-density irregularities by a fountain-like effect can form a double-humped structure of ionization crests near $\pm$15° geomagnetic latitude and a trough at the geomagnetic equator, commonly referred to as equatorial ionization anomaly (EIA). Surprisingly, Africa shares the largest portion of the global EIA with a deficiency of diverse ground-based ionospheric monitoring instruments. However, many reasonable studies have been conducted to understand the possible driving mechanisms for the occurrence of GNSS signal scintillations in Africa (e.g., [8,9,10,11]). One key to studying the generation mechanism of ionospheric irregularities is geometric-orientation arguments. As reported in [12,13], the ionosphere over Africa shows some peculiarities concerning ionospheric irregularities. These peculiar behaviors of ionospheric irregularities require detailed studies of relationships between various geophysical observables. Here, we focus on carefully studying the relationship between the solar day–night terminator and the geomagnetic declination regarding the occurrence of small-scale irregularities in the equatorial ionosphere over the west-to-east extension of Africa. Because the declination of the geomagnetic field varies by more than 10° from East to West Africa, here we evaluate the related impact on the occurrence of irregularities as expected by Tsunoda’s theory.

2. Database and Processing

The German Aerospace Center (DLR) and its partners have installed high-rate GNSS stations near the geomagnetic equator to monitor perturbations of the ionosphere and their effects on the space-based and ground-based systems (e.g., [14]). We used three observational sites over equatorial Africa to obtain essential evidence for the unique relationship between scintillation onset and geomagnetic declination that is associated with the azimuth of the day–night terminator at different altitudes of the ionosphere. So, this study has been carried out by using the data derived from the GNSS stations in Bahir Dar, Ethiopia, Lomé, Togo and Dakar, Senegal, with the station positions summarized in

Table 1. GNSS observation sites in the east–west African ionosphere.

Station Name	Geographic Latitude	Geographic Longitude	Geomagnetic Latitude	Geomagnetic Longitude	Geomagnetic Declination
Bahir Dar	11.6°N	37.4°E	2.8°N	109.2°E	3.3°
Lomé	6.2°S	1.2°E	8.1°S	73.5°E	−1.9°
Dakar	14.7°N	17.5°W	2.1°N	1.0°E	−6.7°

. The geomagnetic declination difference between stations on the east and west coasts of Africa such as Bahir Dar and Dakar in particular is about 10°, with geographic longitudinal of about 55°. The geomagnetic separation of the stations is about 5°, sufficiently high to study declination-related effects over Africa. This geomagnetic declination was computed by using the data source in “Natural Resources Canada” (https://www.nrcan.gc.ca/home), accessed on 11 March 2020. The stations are equipped with a 50 Hz scintillation receiver like the JAVAD Delta 3G GNSS in combination with an external Temex LPFRS rubidium clock (at Bahir Dar) and Sceptentrio PolaRxS or Novatel FlexPack 6 (at Lomé and Dakar). These receivers are sensors capable of recording data from different constellations with different frequencies like GPS (L1, L2 and L5), Glonass (L1, L2), Galileo (E1, E5a), Beidou (B1, B2 and B3), and space-based augmentation systems from geostationary satellites such as the Wide Area Augmentation System (WAAS) and the European Geostationary Navigation Overlay Service (EGNOS) with a sampling rate up to 50 Hz. Tracking signals from more satellite systems with different frequencies play a significant role in improving the accuracy of positioning, monitoring, detecting and recording the trans-ionospheric propagation of GNSS signals. At all stations, an elevation cut off of ≥20° was implemented to reduce multi-paths, used to allow clear detection of scintillation events. Furthermore, the discrimination of the artificial scintillations caused by multi-path effects was mitigated by analyzing the scintillation versus the azimuth angle for the whole three years. Note that the embedded processing software of the stations can calculate the observed scintillation indices for every individual GNSS link. Cycle slips were removed from the datasets before analyzing the longitudinal-seasonal (spatio-temporal) variations of small-scale irregularities by using parameters like ${\mathrm{S}}_4$ and/or ${\sigma }_{\phi }$ indices. Near the geomagnetic equator, plasma density irregularities at the size of the first Fresnel radius cause fluctuations in amplitude of GNSS signals. These can be characterized by a statistical quantifier tool called amplitude scintillation, defined as the ratio of the standard deviation of the signal power to the mean signal power computed by a period of one minute [15]:

$${\mathrm{S}}_4=\sqrt{\frac{〈I^2〉-{〈I〉}^2}{{〈I〉}^2}},$$

(1)

where ${\mathrm{S}}_4$ is the amplitude scintillation index, $I=A^2$ is the signal intensity and 〈〉 refers to the averaging of I within a period of one minute. A is the signal amplitude, which is directly obtained from the scintillation-processing software, and is computed using:

$$A^2=i^2+q^2,$$

(2)

where i is the high-rate in-phase ($i=A·cos\Phi$) and q is quadrature ($q=A·sin\Phi$). Both components are provided by the GNSS receiver (e.g., the JAVAD receiver). A detailed discussion is available at (https://gssc.esa.int/navipedia/GNSS_Book/ESA_GNSS-Book_TM-23_Vol_I.pdf, accessed on 11 March 2020). By rearranging various terms and neglecting the amount of TEC derived from ray path bending as well as higher-order terms such as magnetic field and collision, the expression for dual-frequency relative TEC over the equator region can for example be derived using Equation (3) by author [16]:

$$\mathrm{TEC}=\frac{{\mathrm{f}}_1^2{\mathrm{f}}_2^2}{\mathrm{K}({\mathrm{f}}_1^2-{\mathrm{f}}_2^2)}({\lambda }_1{\Phi }_1-{\lambda }_2{\Phi }_2),$$

(3)

where ${\mathrm{f}}_{1,2}$ and ${\lambda }_{1,2}$ are the carrier frequencies and their corresponding wavelengths, ${\Phi }_1$ and ${\Phi }_2$ are the carrier phase measurements and K is a numerical quantity that amounts to 40.3 m${}^3 {\mathrm{s}}^{-2}$. Comprehensive studies by [17,18] report that the occurrence rate as well as the wedge-shaped structure of small-scale irregularities and plasma bubbles are more prevalent, stronger, deeper and active all year in the African ionospheric sector. This peculiar behavior of ionospheric irregularities over Africa requires detailed studies of potential relationships with various geophysical observables. Here, we focus on studying the relationship between the solar day–night terminator and the geomagnetic declination regarding the occurrence of small-scale irregularities in the equatorial ionosphere over the west-to-east extension of Africa.

3. Observations

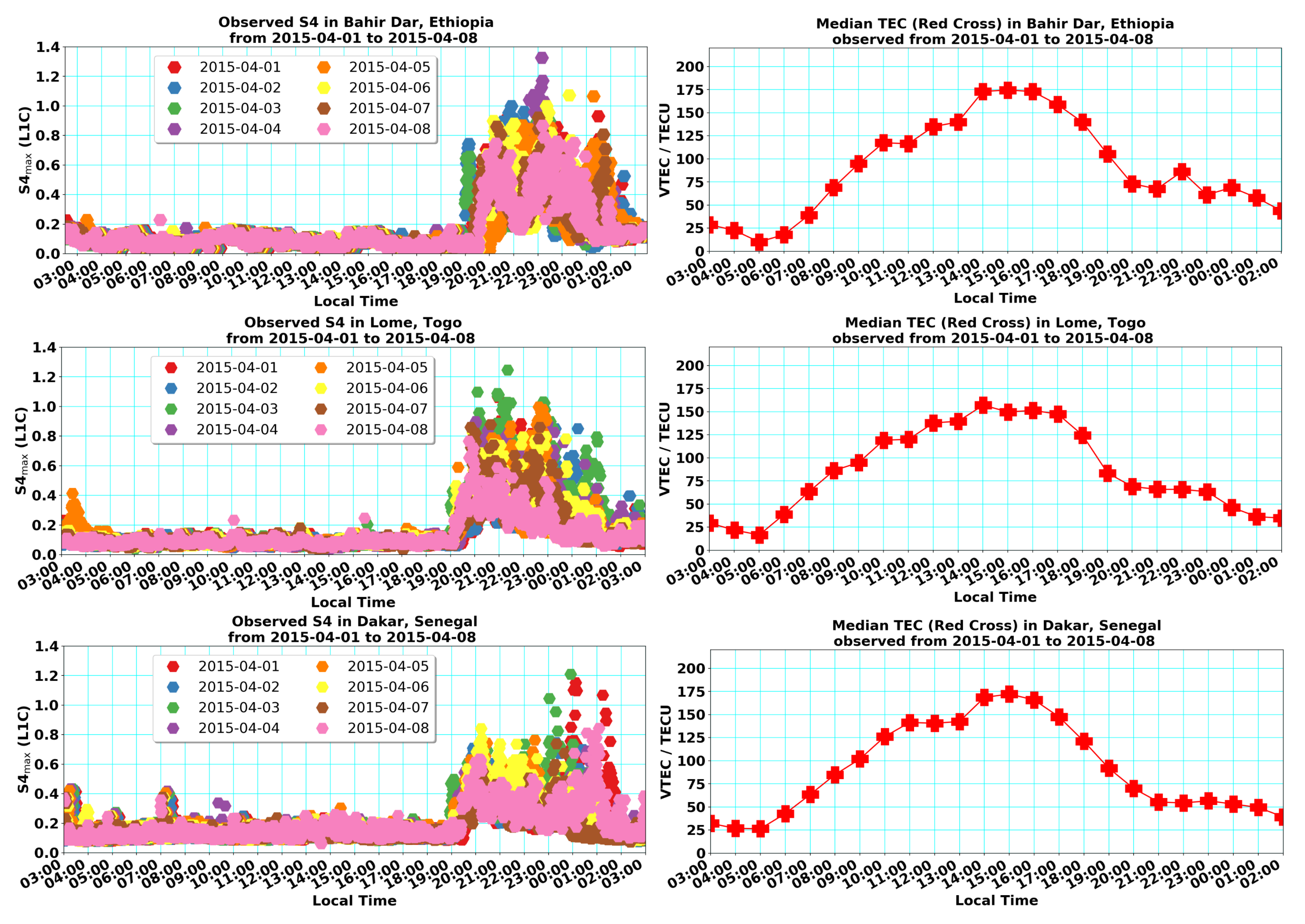
Referring to [19,20], strong prereversal enhancement (PRE) generates equatorial spread F (ESF) and equatorial plasma bubbles (EPBs) around the sunset terminator, in turn playing a dominant role in the onset of amplitude scintillations. The left panels of Figure 1 show the ${\mathrm{S}}_4$ scintillation activity as a function of local time observed in Bahir Dar, Lomé and Dakar, during the period 1–8 April 2015.

At the three GNSS stations, the observed scintillation values, such as moderate ($0.3\le {\mathrm{S}}_4<0.6$), strong ($0.6\le {\mathrm{S}}_4<0.9$) and extreme ($0.9\le {\mathrm{S}}_4<1.4$), are clearly indicated. It is important to note that much stronger ${\mathrm{S}}_4$ values were mainly confined within the time interval between 19:00 and 02:00 LT at all three stations over the eight days. These observations could be attributed to the fact that the trans-ionospheric propagation of GNSS signal fluctuations in amplitude ${\mathrm{S}}_4$ (L1C) are caused by the plasma density irregularities associated with EPBs in the early evening and post-midnight local times. Authors in [21] indicated that the plasma irregularities generated by the Rayleigh–Taylor instability mechanism can extend 1 or 2 h after midnight, commonly called the post-midnight scintillations. This term refers to the latter occurrence of plasma density irregularities, caused by different mechanisms in some specified season and solar cycle conditions (still under discussion). For comparison with the scintillation activity, we plotted the corresponding TEC behavior averaged over eight successive days from 1 to 8 April 2015 in Bahir Dar, Lomé and Dakar (cf. right panels of Figure 1). The TEC plots show a plateau of the vertical TEC at about 50–75 TECU simultaneous to enhanced scintillation activity at night at all three stations. It is assumed that VTEC is maintained by an upward-directed E × B drift of plasma associated with the generation of plasma irregularities. 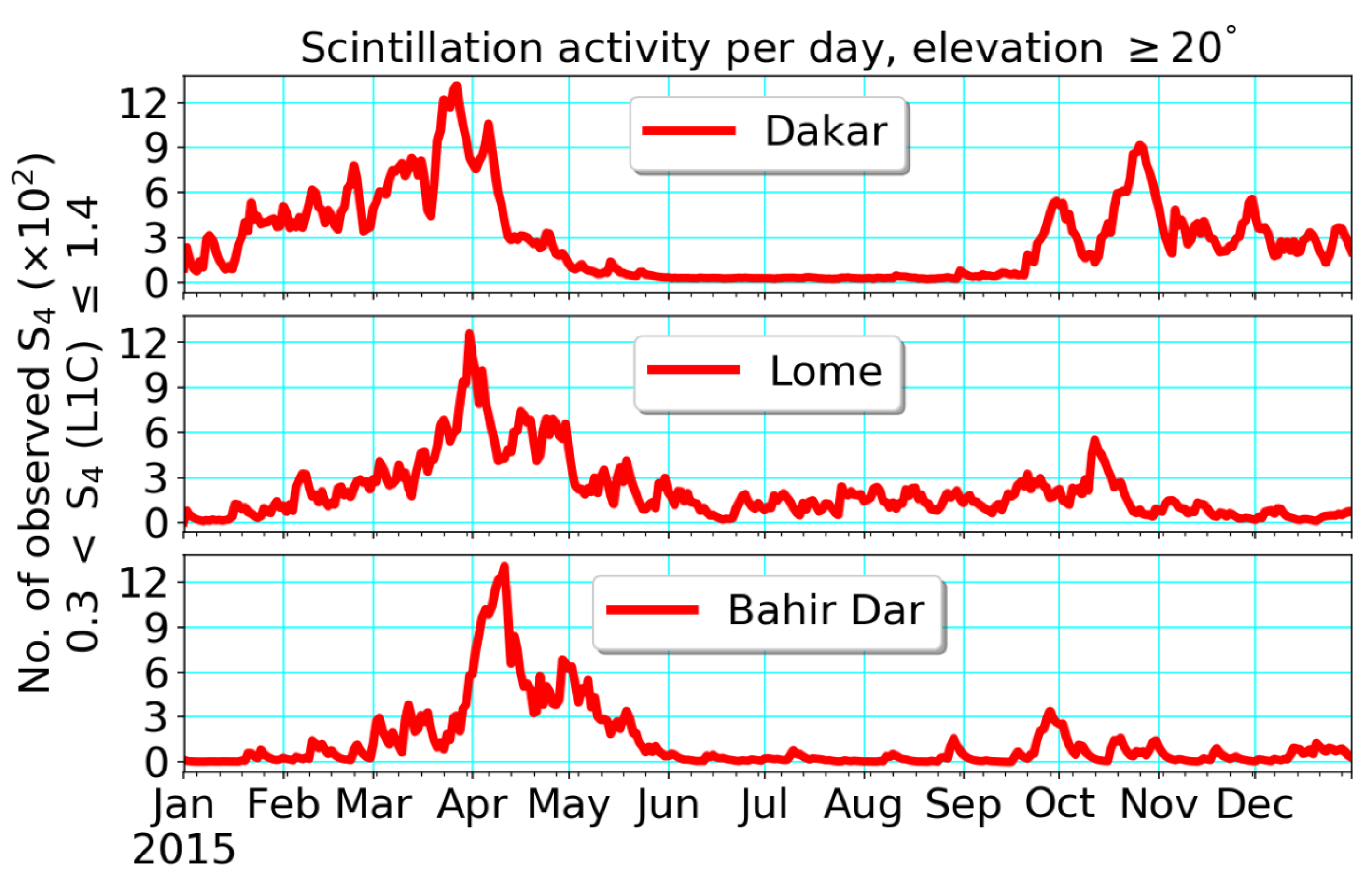Figure 2 shows the number of scintillation events recorded with a 50 Hz receiver for the year 2015 at three equatorial stations: Bahir Dar, Lomé and Dakar, which represents the East–West (Bahir Dar–Dakar) and African-Atlantic (Lomé–Dakar) sectors, respectively. In all three stations, it is common to observe a high number of scintillation events during the equinoctial seasons. However, during the equinoctial seasons in 2015, the highest number and the longest period of scintillation events were only observed in the African-Atlantic sector. Interestingly, the scintillation events observed at Lomé were much more frequent and longer lasting than those at the Bahir Dar GNSS station. The overall observations can probably be attributed to the difference in the geomagnetic declination between the east and west coasts of African regions. For example, a series of studies [22,23] suggest that the possible physical mechanisms responsible for the seasonal-longitudinal variability of plasma density irregularity is the strength of the geomagnetic field. 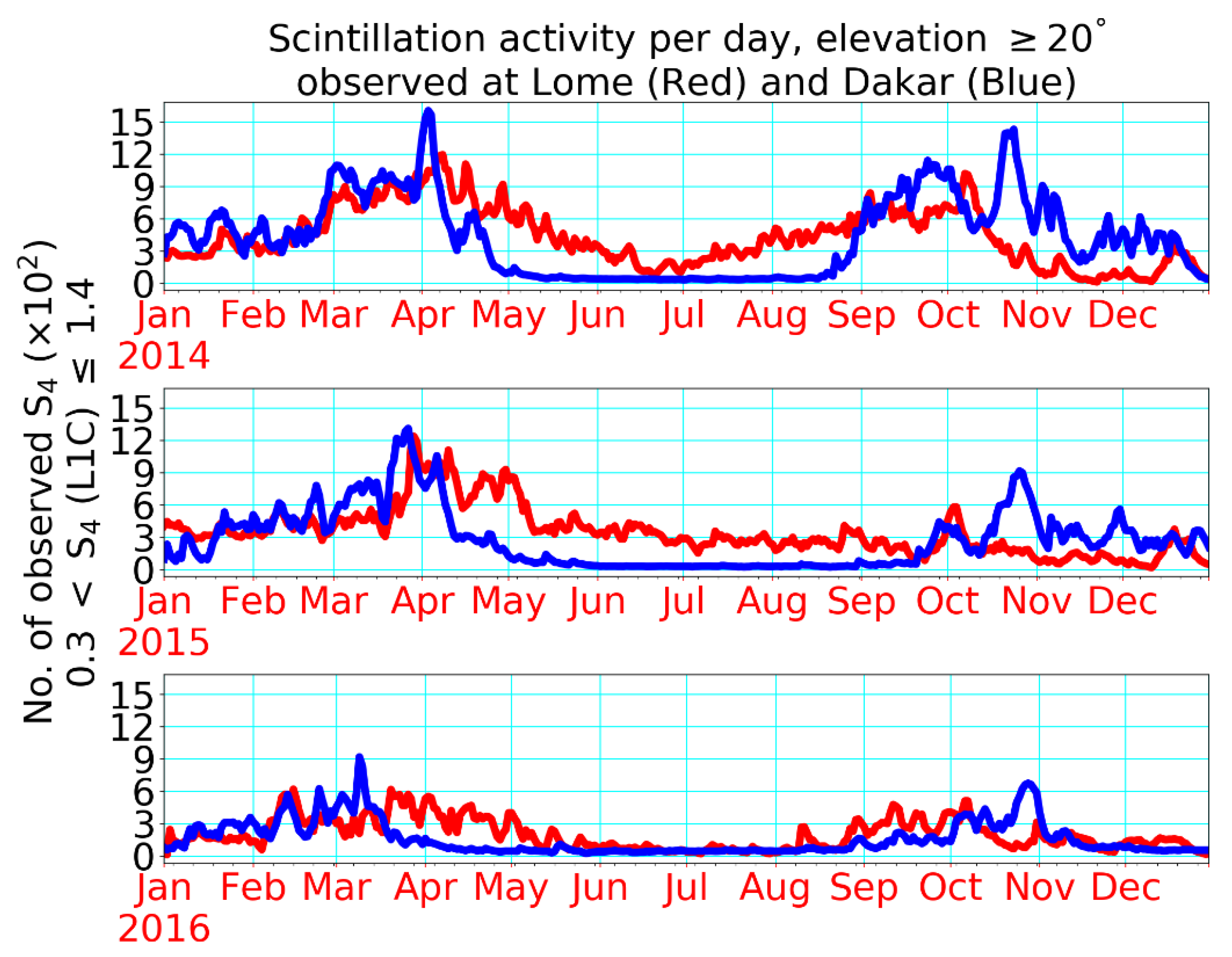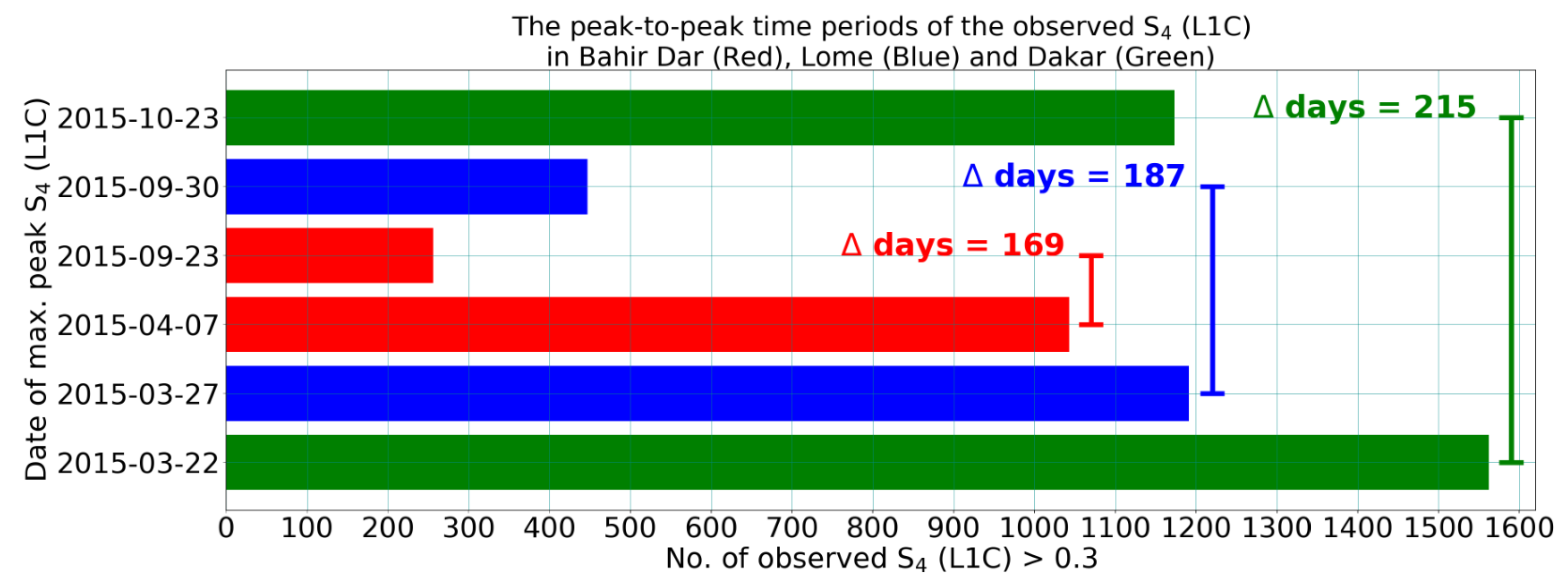Figure 3 displays a detailed climatological pattern of scintillation events observed at Lomé (red) and Dakar (blue) for the years 2014, 2015 and 2016, respectively. In order to provide essential evidence, comparisons need to be made in order to monitor the climatology of the GNSS scintillations from 2014 to 2016 in a timely manner and with high accuracy. Comparatively, the most maximal and most frequent ${\mathrm{S}}_4$ indices were detected during equinoctial seasons in 2014, more than in 2015, while they were very minimal and least frequent in the year 2016. A few studies [24,25,26] noted that the occurrence rate of plasma bubbles and radio wave scintillations are well correlated in the African ionosphere.

As seen in Figure 2 and Figure 3, the behavior of ${\mathrm{S}}_4$ peaks around equinoxes indicate three apparent features of observations over Africa: (a) There was an asymmetry between spring and autumn with higher values in spring; (b) The asymmetry grew from west to east, with stronger scintillation intensity at West Africa; and (c) The time interval between ${\mathrm{S}}_4$ peaks increased from west to east. The asymmetry between equinoctial maxima is a matter of its own that has been addressed in several papers. Authors in [8] also observed an asymmetry at Bahir Dar in 2013. To explain this phenomenon, several assumptions have been considered in the literature. Thus, the studies [27,28] assume that thermospheric winds could play an important role in the equinoctial asymmetry in the occurrence of ionospheric irregularities. An investigation in [29] describes differences of the vertical E × B drift between spring and autumn equinoxes that even change with longitude. The systematic increase of the asymmetry from west to east agrees with observations of [30] who have shown that the equinoctial asymmetry is different in the West and East African sectors assumed to be related to geomagnetic field strength changes. Due to this complexity, the investigation of the equinoctial asymmetry is also a matter of its own and requires detailed systematic studies. In the subsequent discussion, we will focus on the explanation of the growing time interval between ${\mathrm{S}}_4$ peaks when moving from Dakar via Lomé to Bahir Dar (cf. see above case (c)).

4. Discussion

Of particular interest are the sunrise and sunset terminators when rapid irregularities and inhomogeneities occur in the ionospheric plasma compositions and their dynamics. This issue is often overlooked and not fairly well handled due to the complexities associated with the calculation of the exact temporal-spatial effects of the solar terminator. Following [31], mathematical formulae were deduced and an algorithm was developed for calculating the temporal-spatial variations of the solar terminator as a function of the geographic latitude–longitude and day of the year. The solar zenith angle $\chi$ in the ionosphere during sunset can be described according to:

$$\chi \approx 90°+1.01\times \sqrt{{\mathrm{h}}_{\mathrm{I}}-\mathrm{S}}.$$

(4)

This gives $\chi$ in degrees when ${\mathrm{h}}_{\mathrm{I}}$ and S are expressed in kilometers. Here ${\mathrm{h}}_{\mathrm{I}}$ stands for the height of the ionosphere and S means the screening height measured from the ground to a specified location in the ionosphere. Here we assume a screening height of 90 km or higher, which is to be taken due to strong absorption and radiation used for the ionization at lower heights. Mitra [32] applied the law of cosine to the spherical triangles whose vertices are the North Pole, the sun, and solar zenith angle, used to calculate the local hour angle (LHA) at sunset and sunrise:

$$\mathrm{LHA}=arccos\left(\frac{cos\chi -sin{\phi }_D\times sin\delta }{cos{\phi }_D\times cos\delta }\right),$$

(5)

where ${\phi }_D$ is the latitude of the point on Earth and $\delta$ is the declination of the sun. Keep in mind that the algebraic sign of LHA is chosen to be either the sunrise (–) or sunset (+) terminator. Equation of time (EoT) is a formula used in the process of converting between solar time and clock time to compensate for Earth’s elliptical orbit around the sun and its axial tilt. Noticeably, the Earth does not move perfectly in a circular orbit. It is necessary to include EoT in our calculation, used to determine the Greenwich Mean Time (or Universal Time) for sunrise and sunset, which is possibly approximated by the following formula [33]:

$$\mathrm{EoT}=9.87\times sin\left(2B\right)-7.53\times cos\left(B\right)-1.50\times sin\left(B\right),$$

(6)

where $B=\left(\frac{360.0}{365.0}\right)\times (N-81.0)$. Here N is the day number (e.g., 1 January= day 1). The Universal Time of sunrise (UTR) and sunset (UTS) in hours can be calculated from the value of the Greenwich hour angle of the sun at Greenwich mean noon. Thus, they are given by:

$$\left.\begin{array}{cc}\mathrm{UTS}\hfill & \\ \mathrm{UTR}\hfill & \end{array}\right\}=12+\mathrm{EoT}-{\theta }_D\pm \mathrm{LHA},$$

(7)

where ${\theta }_D$ is the geographic longitude of the point on Earth expressed in hours. The LHAs at sunrise and sunset are also expressed in hours. Furthermore, the geographic longitude ${\theta }_D$ is also used to calculate an approximated local time of sunrise (LTR) and sunset (LTS) as follows:

$$\mathrm{LTS}=\left\{\begin{array}{cc}\mathrm{UTS}+{\theta }_D/15,\mathrm{if}0°\le {\theta }_D\le 180°\hfill & \\ \mathrm{UTS}-{\theta }_D/15,\mathrm{if}180°\le {\theta }_D\le 360°.\hfill & \end{array}\right.$$

(8)

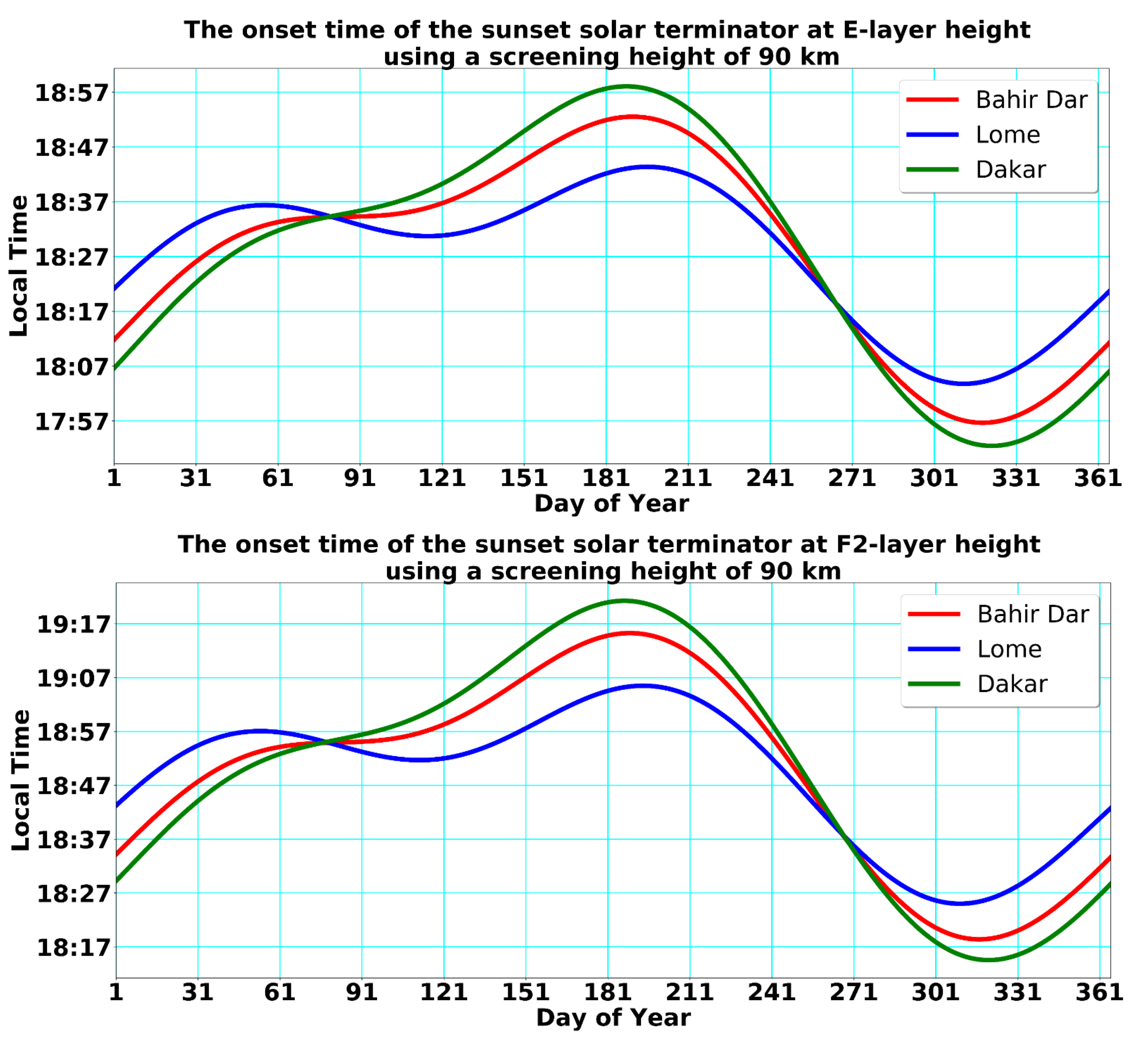
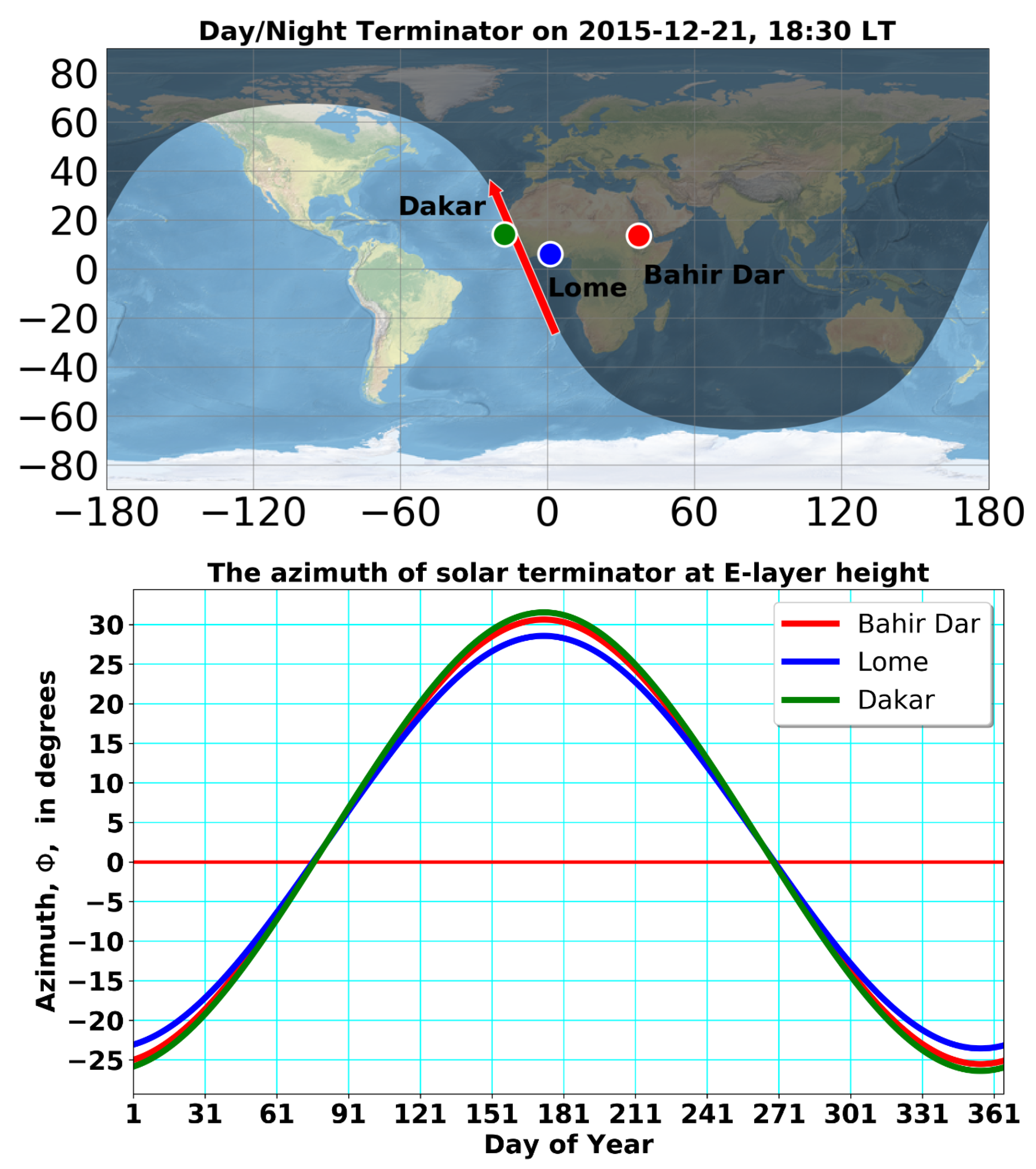
Analogously, one can calculate the LTR with a similar method by taking east to be positive and west to be negative. Figure 4 shows the onset time of the sunset terminator in the E-layer at a height of 120 km (top panel) and in the F2-layer at a height of 250 km (bottom panel) with a screening height of 90 km, computed for selected geographic locations in the equatorial ionosphere such as Bahir Dar, Lomé and Dakar, which are given in the red, blue and green modulated curves, respectively.

The performance of the developed algorithm was tested by considering the onset time of the sunset terminator at different heights of the ionosphere as well as at different seasons of the year. As expected, the sunset terminator has more recently occurred at ionospheric heights than in lower ionospheric heights. Moreover, our computation shows the geometrical orientation of the sunset terminator line, which can easily be related to the geomagnetic declination line. Note that Figure 1 (left panels) and Figure 4 (both panels) indicate the key relationship between the onset time of scintillation activity and sunset terminator over the African equatorial ionosphere. In other words, they clearly indicate that scintillation onset starts immediately around sunset times with high intensity at the Bahir Dar, Lomé and Dakar stations, respectively. An investigation found that plasma density irregularities as well as plasma bubbles can be continuously generated near the sunset terminator over the longitudinal range of Asia, Africa and the Atlantic region [34]. Essential constituents of ionosphere particles are in a non-equilibrium state under the solar terminator region as a result of non-linear processes (R–T instability), leading to the generation of small-scale irregularities. The modulation of sunset curves, following mainly the solar declination over the year, is due to the equation of time to correct the true solar time in civil local time. Because the scintillation culminates around equinoxes at all three stations considered here, we could not identify a significant time difference between sunset times at these stations, as illustrated in Figure 4. The upper panel of Figure 5 demonstrates the geometrical orientation of the terminator line that passes at the ground through the Dakar station. As illustrated in Figure 5 (upper panel), the azimuth of the solar terminator, indicated by a red arrow, changes with the season. At ionospheric altitudes where the ionized gas component becomes significant (cf. lower panel of Figure 5), the azimuth of the terminator line is nearly the same at all three stations over the year. Due to its permanent change, the solar terminator is in line with the geomagnetic declination line twice a year, providing optimal conditions for rapid changes in the electromagnetic coupling processes, mainly in the E-layer ionosphere.

Near the terminator region, the ionospheric plasma density initially rises in response to an enhanced eastward electric field, used to ensure current continuity across the steep conductivity gradient during E-region sunset in different seasons of the year, e.g., [35,36]. Small-to-medium-scale plasma irregularities are intensively originated and stretched along the solar terminator line in the equatorial region [37,38]. In effect, a relative longer-time blackout of radio-communication happens when a radio wave propagates near the solar terminator line in the equatorial latitude [39]. 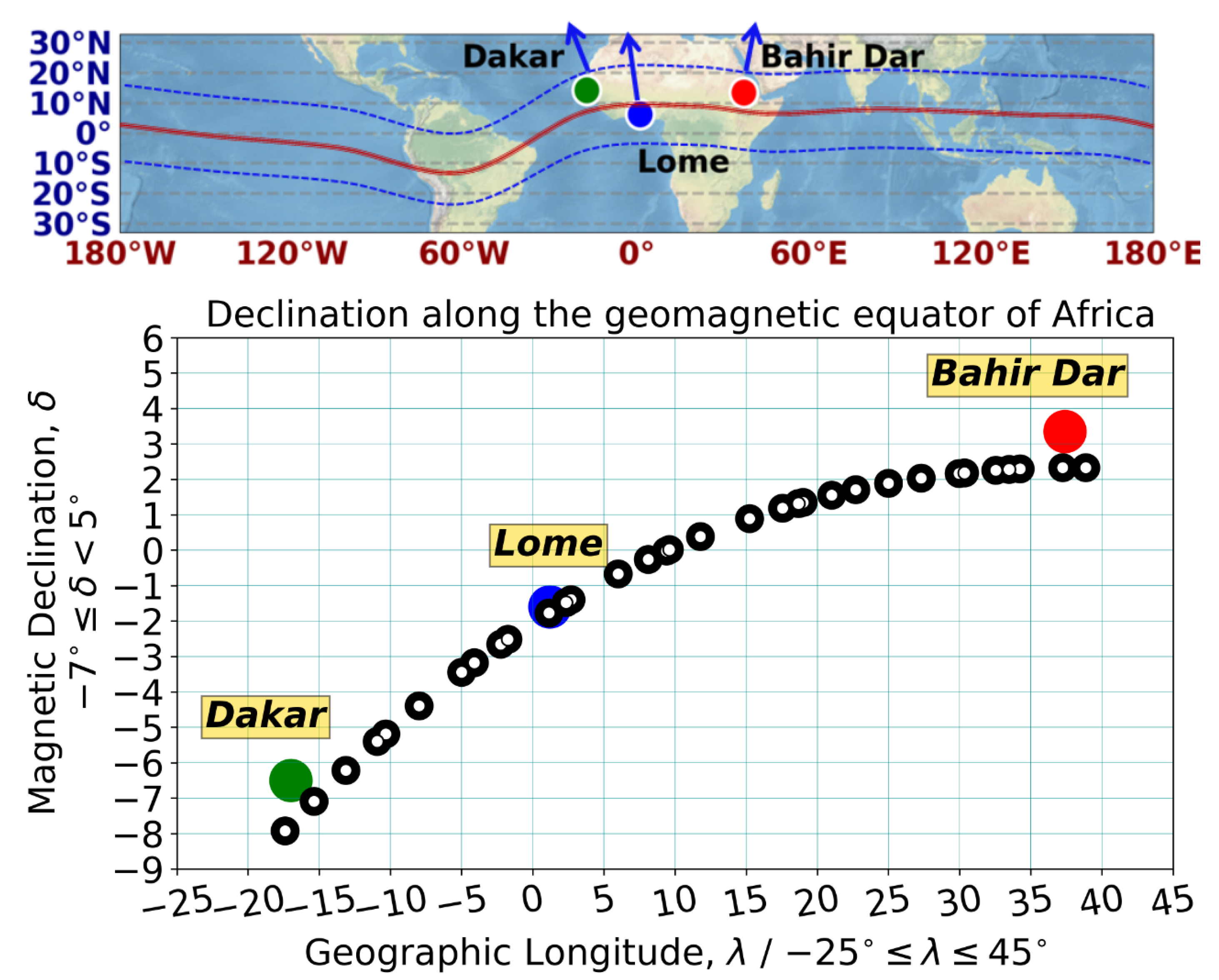Figure 6 (upper panel) approximates the contours of the geomagnetic equator (red line) guided by the location of both crests (dashed blue lines) and illustration of the quite different geomagnetic declinations at the selected stations (Dakar, Lomé and Bahir Dar). By convention, the blue arrows represent the B-field declinations; for example, Bahir Dar’s declination tilts to the east of true north (≈3.3°), Lomé’s declination tilts to the west of true north (≈−1.9°) and Dakar’s declination also tilts to the west of true north (≈−6.7°), respectively.

It is well-known that the geomagnetic declination ($\delta$) varies with geographic longitude, particularly in the vicinity of the South Atlantic Magnetic Anomaly (SAMA) of the geomagnetic field. In this context, it is interesting to note that the B-field declination changes continuously with longitude over Africa, as can be seen in the lower panel of Figure 6. The curve made by black circles is merely present as a reference to support the orientation of declination along the geomagnetic equator of Africa, indicated by the blue arrows in the upper panel of Figure 6. So, the declination changes by about 10° between Bahir Dar and Dakar. It is evident that this change has consequences with respect to the coincidences with the azimuth of the day–night terminator at these three stations. A graphical analysis is required in order to provide a concrete analysis of the variations of the azimuth of the solar terminator line, and depends on a few key parameters, such as different solar declinations, zeniths and local hour angles, corresponding to different dates throughout the year. 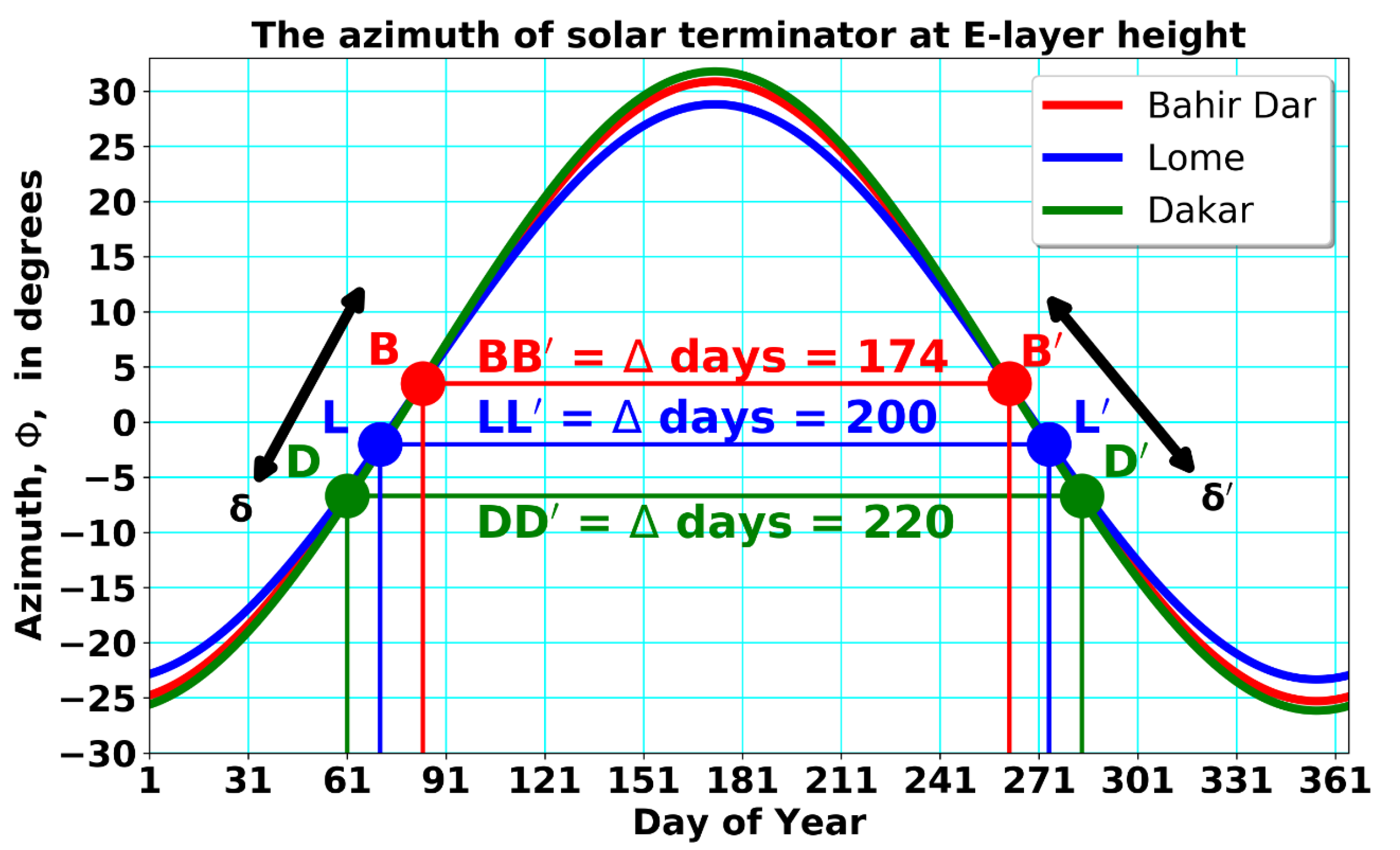Figure 7 primarily demonstrates the azimuth of the day–night terminator ($\Phi$) as a function of the day of the year, computed by considering the E-layer height of the ionosphere (Bahir Dar, red bell curve; Lomé, blue bell curve; Dakar, green bell curve).

The colored pairs of dots connected by the horizontal lines are the days of coincidences between the azimuth of the day–night terminator and geomagnetic declination at Bahir Dar represented by B and ${\mathrm{B}}^{\prime }$ (red dots), Lomé represented by L and ${\mathrm{L}}^{\prime }$ (blue dots) and Dakar represented by D and ${\mathrm{D}}^{\prime }$ (green dots) during vernal and autumnal equinoxes, respectively. Substantially accurate coincidences between $\Phi$ and $\delta$ were revealed by indicating the marked dots in Figure 7. The greater emphasis on these three marked dots, namely B, L and D, represents $\delta$ during vernal equinoxes, while ${\mathrm{B}}^{\prime }$, ${\mathrm{L}}^{\prime }$ and ${\mathrm{D}}^{\prime }$ represent ${\delta }^{\prime }$ during autumn equinoxes, respectively. Thus, the coincidences occur at quite different days of the year. This is clearly demonstrated in Figure 8, where the days of coincidences between geomagnetic declination and the azimuth of the terminator are indicated at different stations. It is interesting to note that the periodical interval between days of coincidences is denoted by $\Delta$ days and they change significantly at the selected stations (cf. Figure 7 and

Table 2. Comparison of coincidences between the sunset terminator and geomagnetic declination by the observed scintillation of peak-to-peak distances.

Station Name	Computed Time Periods between Coincidences/Days	Observations of Peak-to-Peak Distance in the Year 2015/Days
Bahir Dar	174	169
Lomé	200	187
Dakar	220	215

). So, it changes from 220 days at Dakar ($\mathrm{D}{\mathrm{D}}^{\prime }$) to 200 days at Lomé ($\mathrm{L}{\mathrm{L}}^{\prime }$) to 174 at Bahir Dar ($\mathrm{B}{\mathrm{B}}^{\prime }$), respectively. Assuming that the coincidences of geomagnetic declination with the azimuth of the sunset terminator line provide optimal conditions for the generation of ionospheric irregularities that are obviously causing radio scintillations, we should see this in a shift of scintillation peaks according to the day of coincidences at the GNSS stations seen in Figure 7 and Figure 8 and in Table 2.

Overall, our computational-observational results support Tsunoda’s hypothesis of [40,41] to a greater extent, in that ionospheric responses exhibited seasonal-longitudinal dependencies. The occurrence rate of radio signal scintillations and equatorial plasma bubbles peaked near the times of year when $\alpha$, the angle between the magnetic declination ($\delta$) and the azimuth of the solar terminator ($\Phi$), approached zero. Furthermore, the seasonal climatology of GNSS signal scintillations was in a good agreement with Tsunoda’s solar terminator and local geomagnetic field declination hypothesis, that is, the scintillations were most frequently observed during the time when the alignment of the solar terminator with the geomagnetic declination was best. At the equatorial ionosphere, the rapid decay of the E-layer electron density and conductivity coupled with the zonal neutral wind play a significant role in the development of an enhanced eastward electric field on the day-side of the terminator and westward electric field on the night-side of the terminator, largely responsible for the variability of plasma density irregularities in the F-layer. Especially, the maximum plasma density irregularities occurred close to the time of reversal drift velocity in the night-side terminator when the F-layer reaches its highest altitude and the growth rate of the R–T instability is maximum. In order to provide sufficient evidence for the solar terminator’s role in the directional-seasonal occurrence of scintillation activity, ${\mathrm{S}}_4$ index measurements need to be made in the eastward- and westward-looking satellite-receiver links at a specified station.

We separated the station datasets for east and west directions by an algorithm that can automatically screening the satellite-receiver links with an elevation angle ≥ 20° and an azimuth angle in the eastward (45° ≤ azimuth ≤ 135°) and the westward (225° ≤ azimuth ≤ 315°). Taking into consideration the azimuth of solar terminator at the F2-layer, an altitude of 250 km was mostly taken as the thin-shell altitude of the ionosphere. 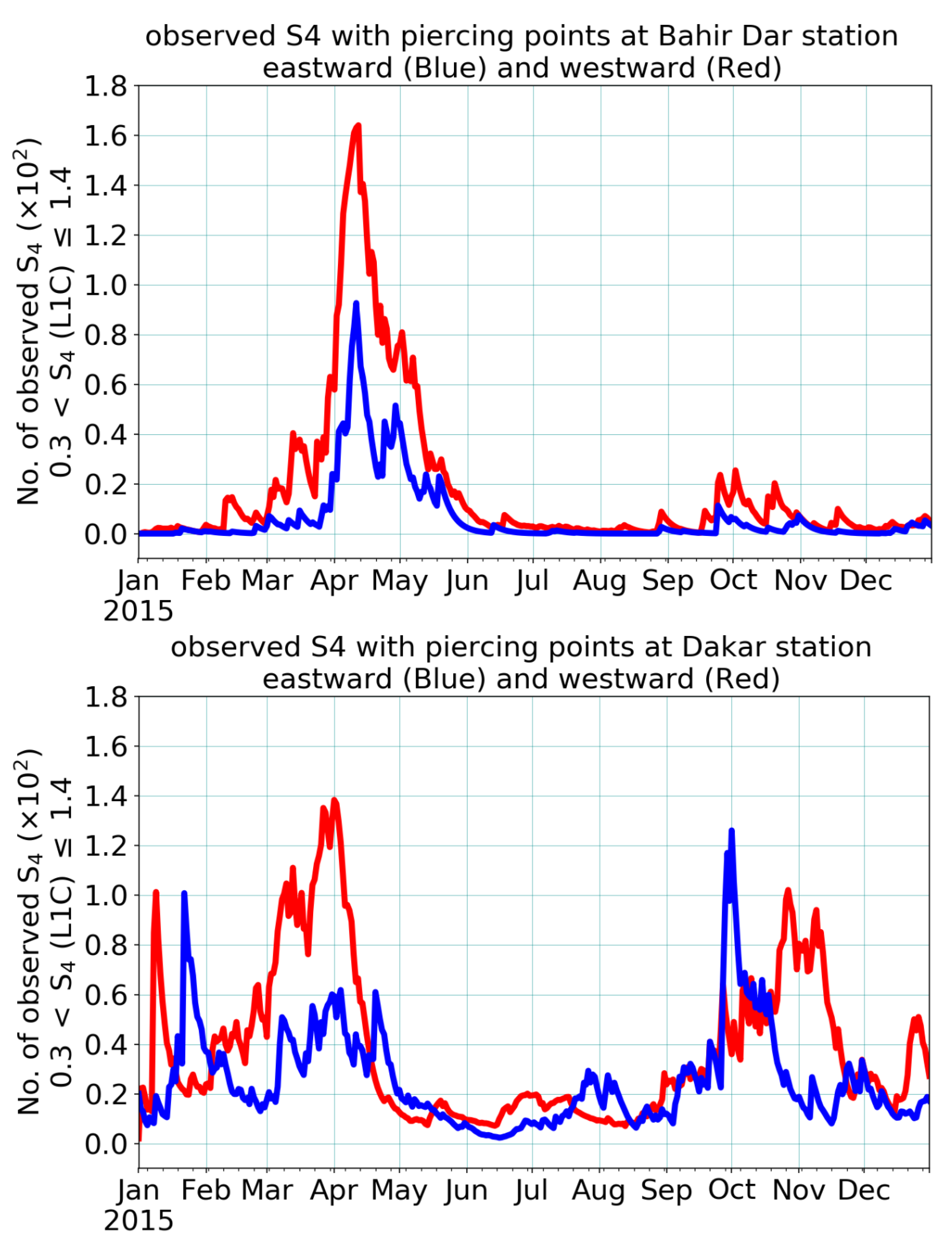Figure 9 shows that the directional-seasonal occurrence of scintillation activity was observed from eastward- (blue) and westward-looking (red) satellite-receiver links at Bahir Dar’s (upper panel) and Dakar’s (lower panel) GNSS stations in 2015.

These observations demonstrate that the solar terminator was an effective source of perturbations in the ionosphere, which can be described by applying the well-accepted ${\mathrm{S}}_4$ index measurements. Most of the time, the peak of scintillation events in the westward direction was higher than that in the eastward direction observed during 2015 at Bahir Dar and Dakar. Our observations indicate that some satellite-receiver links present in the passage of the solar terminator were affected by the local ionosphere irregularities and inhomogeneities, causing much more scintillation activity observed in the westward than in eastward satellite-receiver links. 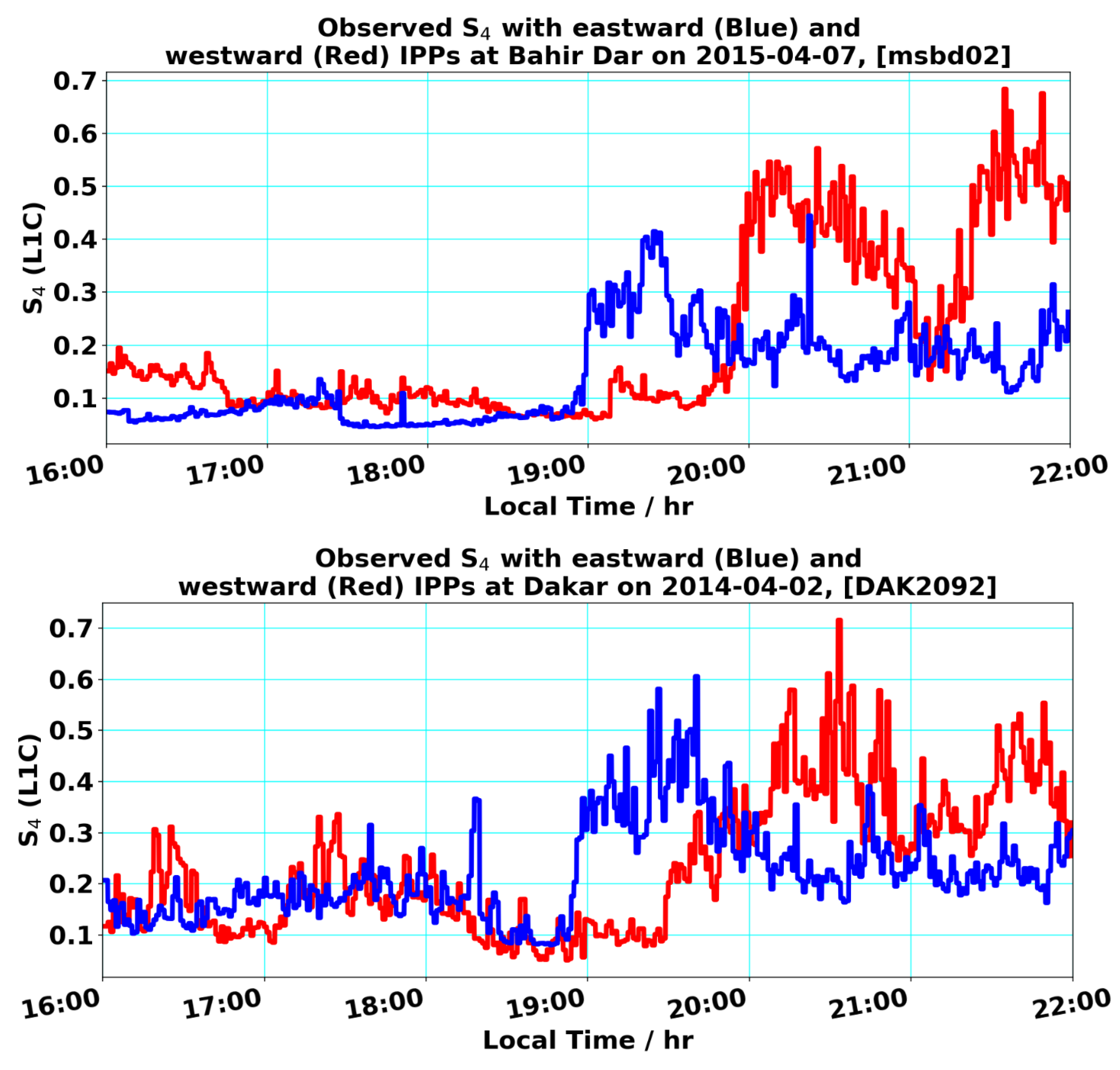Figure 10 is a preliminary and rather satisfactory result showing that ${\mathrm{S}}_4$ index measurements can be a manifestation of the different degree of perturbations in the ionosphere, especially during the time interval between 19:00 and 22:00 LT. All observations were recorded from eastward- (blue) to westward-looking (red) satellite-receiver links at Bahir Dar’s and Dakar’s GNSS stations, respectively.

A set of interrelated ionospheric key features like upward plasma drifts and eastward electric fields developed near the sunset of the solar terminator, referred to as the prereversal enhancement (PRE). It is widely known that this PRE is a polarization effect required to maintain current continuity near the sunset terminator, which is important for the formation of ${\mathrm{S}}_4$ indices and EPBs. In both panels of Figure 10, clear enhanced ${\mathrm{S}}_4$ values can be observed around 19:00–20:00 LT in eastward-looking (blue) satellite-receiver links at two stations. This equatorial feature is directly associated with a strengthening of the vertical upward plasma drift. Since the polarity of the vertical drifts usually reverses after sunset (≈after 20:00 LT), this results in a stabilization of the bottom side of the F-layer against further irregularity growth (low ${\mathrm{S}}_4$ indices observed in eastward-looking satellite-receiver links of the stations). On the other hand, the observed ${\mathrm{S}}_4$ index measurements from the westward-looking (red) satellite-receiver links were enhanced between 20:00 and 22:00 LT, with a minor depression around 21:00 LT. This is due to the quick decrease of the vertical upward plasma drift and the reversal of the eastward electric field, which provides favorable conditions for the generation and propagation of plasma density irregularities via the Rayleigh–Taylor gradient instability in the region of the geomagnetic equator. As with Figure 10 (both panels), this also clearly indicates that there was no enhanced scintillation activity at around 21:00 LT. This observation can be interpreted as the vertical upward plasma drift of the eastward electric field, which quickly dropped down to zero and continued to move downwards, finally being responsible for the breakdown of the equatorial anomaly. Again, the enhanced scintillation activities (moderate and/or strong ${\mathrm{S}}_4$ values) observed between 21:00 and 22:00 LT at both GNSS station were signatures of small-scale ionospheric irregularities for the time-cumulative nature of the resultant ionospheric features in the trough region of the equatorial anomaly. On the night side, dynamo-driven electric fields tend to be westward, resulting in the penetration of electric fields, used as an agent of a stabilizer against the non-linear growth of generalized R–T instability. Perhaps due to the absence of the normal night-side westward zonal electric field, ever-present gravitational currents driven by $m_i$ g × B, can attain enough time in order to derive bottom-side R–T instability into the non-linear regime [42]. This equatorial feature is responsible for a number of electrodynamic processes, often leading to the formation of small-to-medium-scale irregularities and equatorial plasma bubbles (EPBs). Generally speaking, ionospheric irregularities are characterized by the depletions in the plasma generated by spatial large-scale density perturbations that serve as a seeding source for the development of EPBs. A better understanding of the physics behind ionospheric irregularities can be associated with a few possible triggering mechanisms, such as the vertical rise of the F-layer, atmospheric gravity waves, and gravity wave manifestation as large-scale wave structures.

5. Summary

A high degree of perturbations in the low-latitude ionosphere due to small-scale irregularities and plasma bubbles is an intrinsic regular phenomenon and can cause fluctuations in the amplitude and phase of GNSS signals, consequently leading to a severe degradation of the quality in different applications of GNSS-based services. It is necessary to better understand the physical mechanisms that drive the unique phenomenological occurrence of small-scale irregularities and plasma bubbles with specified seasonal-longitudinal conditions and magnetic-field variations in Africa. The ${\mathrm{S}}_4$ index measurements are well described by geometric-orientation arguments in solar terminator alignment along the local geomagnetic field declination. Our key results demonstrate a noticeable change of the seasonal behavior in the occurrence of ionospheric irregularities over Africa as a function of longitude, which was closely related to the alignment of the solar day–night terminator with the geomagnetic declination line. Effective regular perturbations in the ionosphere exhibited seasonal-longitudinal dependency on the culmination of radio signal scintillations and equatorial plasma bubbles (EPBs) near the times of year when $\alpha$, the angle between the geomagnetic declination $\delta$ and the azimuth of day–night solar terminator $\Phi$ approach zero—that is, the scintillations were most frequently observed during the time when the alignment of the solar terminator with the geomagnetic meridian was closest. Due to its permanent change, the solar terminator is in line with the geomagnetic declination line twice a year, providing optimal conditions for rapid changes in the electromagnetic coupling processes, especially in the E-region ionosphere. Overall, the geomagnetic declination varied with geographic longitude in equatorial Africa and had major consequences for the coincidences with the azimuth of the day–night terminator for the three equatorial stations. These geometric coincidences occurred at quite different days of the year with a periodic interval of 220 for Dakar, 200 for Lomé and 174 for Bahir Dar, respectively. This paper is mainly focused on the occurrence, phenomenology and morphology of GNSS signal scintillations that are inherently associated with the solar terminator and the magnetic meridian of the equatorial station, by taking into consideration the spatio-temporal, seasonal and daily specific features for different geographic longitudes in the equatorial African sector. The findings of this work could be helpful in the development of future GNSS signal scintillation models and robust GNSS-based positioning and navigation applications in Africa.