Abstract
Regular automatic recordings of the time series of the magnetic field, together with routine manual absolute measurements for establishing dynamic baselines at Lampedusa Island—south of Sicily—Italy (geographic coordinates 35°31′N; 12°32′E, altitude 33 m a.s.l.), show a signature of very low electromagnetic noise. The observatory (provisional IAGA code: LMP) lays inside a restricted and remote wildlife reserve, far away from the built-up and active areas of the island, which at present is the southernmost location of the European territory for such observations. The availability of high-quality data from such site, whose survey started in 2005, is valuable for filling the spatial gap due to the lack of observatories in the whole south Mediterranean and North African sectors. We compare observations at Lampedusa, in both time and frequency domains, with those at the other Italian observatories (Castello Tesino and Duronia-L’Aquila), operating since the 1960s of last century, allowing us to report even the secular variation. Using data recorded in the last few years, we investigate higher frequency variations (from diurnal to Pc3-4 pulsations) in order to magnetically characterize the Italian territory and the local response to external forcing. In particular, we present a characterization in terms of diurnal variation and its seasonal dependence for the three observatories. This latter feature is in good agreement with a geomagnetic Sq-model, leading us to speculate about the position of the north Sq-current system vortex and its seasonal displacement with respect to the geographic positions of the observatories. We also study the geomagnetic individual response to intense space weather events by performing Superposed Epoch Analysis (SEA), with an ad-hoc significance test. Magnetic responses in the Ultra Low Frequency range (ULF) from spectral, local Signal-to-Noise Ratio (SNR) analyses under different local time, and polarization rates are computed. These latter studies lead us to search for possible signatures of magnetic field line resonances during intense space weather events, using cross-phase multi-observatory analysis, revealing the promising detection capability of such technique even at low latitudes. The geomagnetic observatories prove to be important points of observation for space weather events occurring at different spatial and time scales, originating in both upstream and ionospheric regions, here analyzed by several well-established methodologies and techniques. The quiet environmental site of LMP, providing high-quality geomagnetic data, allows us such investigations even at inner Earth’s magnetospheric shell.
1. Introduction
It is well known that any ground measurement of geomagnetic field results in a superposition of magnetic field of internal and external origins. The field of internal origin, which is the main contributor to the main field, shows changes with time scale greater than 1 year in magnetic intensity, declination, and inclination angles. Such variations reflect the complex dynamic of electric currents flowing in the Earth’s external fluid core, as well as the westward drift of non-dipole field [1] and migrating magnetic poles [2,3] linked to electric currents flowing at the core–mantle boundary [4]: these slow and irregular variations are usually indicated as secular variation of the main magnetic field (see [5] for a review).
At shorter time scales, the Earth’s magnetic field is subject to the interaction with the solar wind (SW) and the interplanetary magnetic field (IMF): the strong variability of both SW and IMF leads to the generation of several phenomena ranging from the magnetospheric and geomagnetic storms and substorms, which represent the most intense events, the ionospheric storms and traveling ionospheric disturbances, the magnetospheric and geomagnetic micropulsations, and many others. Geomagnetic storms mainly consist in a sudden decrease in the northward component of the geomagnetic field H due to the reinforcement of the ring current intensity observed at ground from low to mid latitudes. At high latitudes, the main geomagnetic activity enhancement is generally represented by the superposition of SW-related directly driven and the tail-related (substorm) unloading components (see [6] for a review). During geomagnetic storms the modification and intensification of Field-Aligned Currents (FACs) also occur, causing a sudden increase in the Joule heating effect in the upper atmosphere, which drives traveling atmospheric disturbances (TADs), possibly leading to the formation of traveling ionospheric disturbances (TIDs) ([7] and references therein). Both of these represent the powerful manifestations of the SW–magnetosphere interaction, which could potentially affect the performance of space and ground infrastructures by disrupting operations and communications in multiple sectors of society. Extreme events could involve economic consequences with potential costs for disruptions and damages estimated in tens or even hundreds of billion of Euros [8,9].
It is well known that magnetic field fluctuations, due to the Sun–Earth interaction, also occurring in the Ultra Low Frequency range (ULF, 1 mHz–5 Hz), are even observed at low latitudes: they are commonly divided by their morphology into irregular (Pi) and continuous (Pc) pulsations and by their frequency band (see [10,11] for their extensive theoretical and experimental treatise). More specifically, regarding the ULF waves in the Pc5 (1–7 mHz), Pc4 (7–22 mHz), and Pc3 (22–100 mHz) frequency ranges, their spectral characteristics are well known to be linked with their circum-terrestrial source [12,13,14,15], while the Pc2-1 (100 mHz–5 Hz) waves are generally believed to be generated by electromagnetic ion cyclotron (EMIC) resonance in the near-equatorial magnetospheric regions, for example, during the storm-time [11] when cold and hot plasma, related with plasmasphere and enhanced ring current, may be superimposed. EMIC waves are mainly observed at high latitudes where they are injected as Alfvén waves and propagate, after conversion into compressional waves [16], in the ionospheric wave guide [17,18].
The above-mentioned Sun–Earth interactions, and many other related phenomena, are nowadays grouped under the name of space weather events. The awareness that damages to infrastructures and malfunctions or loss of communication systems should be avoided or at least mitigated through a constant monitoring of geomagnetic and ionospheric conditions pushed the INGV to become partner of PECASUS consortium, one of the three global centers providing space weather advisories for civil aviation according to ICAO regulations (http://www.pecasus.eu/, accessed on 4 August 2021). These advisories are generated by the continuous monitoring of parameters derived from ionospheric and geomagnetic observations in Italy (http://www.eswua.ingv.it/, http://geomag.rm.ingv.it/index.php, accessed on 4 August 2021).
Finally, we would like to point out that space weather and space climate events also affect the atmosphere at high latitudes through both polar cap electrodynamics and energetic particle precipitation. The atmospheric parameters are influenced at different time-scales, ranging from weeks [19] to days [20,21], with consequences at mid and low latitudes, which are not yet completely understood.
A constant monitoring of the geomagnetic field variations, both at regional and global scales, is necessary for understanding the complex dynamics of the Earth’s core, the core–mantle boundary interaction and the solar wind–magnetosphere interaction and their effects on the terrestrial environment. It is also important to achieve a homogeneous monitoring in space, in particular, regarding the Mediterranean region (see Figure 1); a great gap in geomagnetic observations is evident in the North African sector, so the INGV geomagnetic observatory at Lampedusa represents a strategic site. In the following sections, secular and diurnal variations, as well as geomagnetic field variations at shorter time scales from transient phenomena such as ULF waves and geomagnetic storms, observed at Lampedusa are presented and compared with the two other Italian observatories at Castello Tesino and Duronia. In particular, two geomagnetic storms that occurred during September 2017 and August 2018 recently studied in different geographic sectors [22,23] are studied here for the first time in the Mediterranean region for providing evidence of Field Line Resonance (FLR) events on Duronia–Lampedusa intermediate field line. FLRs are a useful tool to remotely sense the plasma mass density in the inner magnetosphere, a key parameters in the space weather context. Indeed, ULF hydromagnetic and ion cyclotron waves propagation is strongly influenced by the ambient ion plasma. In this framework, the Italian observatory at LMP is a potential extension towards lower latitudes of magnetometer networks currently operating in the European sector.
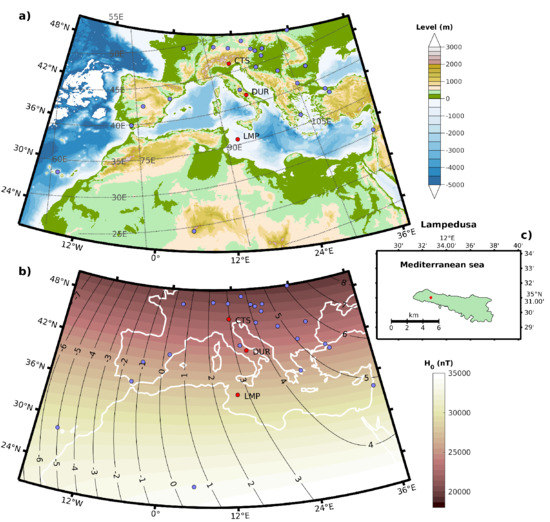
Figure 1.
The location of geomagnetic observatories used in this work (red filled circles): (panel a) the bathymetry of Mediterranean region, where gray dotted lines indicate the magnetic coordinates referred to geomagnetic dipole reference system (north geomagnetic dipole pole coordinate: latitude = 80.4°N, longitude = 287.36°E); (panel b) the total horizontal magnetic field (of internal origin) and isogonic lines (constant declinations) map obtained by IGRF13 model for the Mediterranean region in 2017; (panel c) the Lampedusa island details. In both panels (a,b), the positions of INTERMAGNET observatories (blue filled circles; among them, in central Italy, AQU is also indicated), and the Italian observatories of CTS, DUR and LMP are indicated. The maps are produced by M_Map software [24]. The bathymetry data are provided by NOAA high resolution topographic dataset [25].
2. Materials
Besides the covering of the northern and central part of Italy where two historical geomagnetic observatories are in operation, i.e., Castello Tesino (CTS) and Duronia (DUR), which replaced L’Aquila observatory (AQU, ∼100 km from DUR), partially damaged by the 2009 earthquake, the prospect to extend the observation of the Earth’s magnetic field towards the south led us to establish in 2005 a new observatory in the southernmost region of the Italian territory, the island of Lampedusa. Moreover, the geomagnetic observatory of Lampedusa (LMP) is, at present, the southernmost observatory of the European territory. A complete list of geographic and altitude-adjusted corrected geomagnetic (AACGM) coordinates of the observatories is reported in Table 1, together with the McIlwain L parameter [26] and the magnetic local time (MLT), where L represents the geocentric distance of the equatorial magnetic field line crossing point in the Earth’s radii. Both AACGM coordinates and MLT are estimated by using the Shepherd [27] algorithm at 120 km above the observatory for the year 2017, while L is derived by the IGRF13 model (https://www.ngdc.noaa.gov/IAGA/vmod/coeffs/igrf13coeffs.txt, accessed on 4 August 2021).

Table 1.
Geomagnetic observatories used in this study, geographic coordinates, AACGM coordinates, L parameter, and MLT at 00:00 UT. Italian local time LT = UT + 1.
About 200 km south of Sicily and about 150 km east of Tunisia, in the middle of the Sicily Channel of the Mediterranean sea, the island, with its east–west elongated form, lays at the southern sector of the Plio-Quaternary foreland rift zone. The area is characterized by a moderate seismicity, as attested by the INGV seismic database during 1981–2020 (see Mappa della sismicità 1981–2020, [28,29]). Lampedusa also represents an important point of observation since the northern part of Africa is lacking of observation points (see Figure 1).
The geomagnetic observatory is located inside a restricted natural area (Riserva Integrale dell’Isola di Lampedusa), characterized by a very low electromagnetic noise level due to the distance from the small village, from transport infrastructures (port and airport), and to the absence of electrified railways (a rarity for the Italian territory). It has been continuously upgraded since 2005 and has been completely operating since 2017, satisfying high standards with the aim of becoming a member of the INTERMAGNET consortium (https://www.intermagnet.org/, accessed on 4 August 2021).
As recommended by IAGA, each of the three observatories is equipped by two identical instrumental systems (main and back-up system) with magnetically oriented vector fluxgate and scalar magnetometers. Magnetic inclination and declination angles (the so-called absolute measurements) are measured by a local trained operator, for providing base lines for the automatic magnetic field dataset. Magnetic field vector components are stored at 1 Hz and filtered according to the INTERMAGNET requirement to gather 1 min data, after being coupled and synchronized to the scalar component through GPS timing. Raw 1 min data are then treated by automatic de-spiking procedure, supervised by trained staff, plotted and double checked before their release. Definitive 1 min magnetic field data are freely available from INGV data portal at the following URL: http://geomag.rm.ingv.it/ (accessed on 4 August 2021).
It is well known that fluxgate magnetometers are affected by thermal drift; our high quality instruments are within nominal rate 0.1 nT/°C. Instruments are partially thermal stabilized, being installed underground, inside suitable wells. This condition allows the range of variation introduced by the fluxgate magnetometers to be kept well below the INTERMAGNET requirements (max 5 nT/year).
In this paper we analyzed both 1 min and 1 sec data from LMP, DUR, and CTS for the years 2017–2020. For a comparison with global magnetospheric and interplanetary conditions, we analyzed also SymH [30] and Kp [31] indices (data from https://cdaweb.gsfc.nasa.gov/, accessed on 4 August 2021) as well as the local K index at Italian observatories derived by KAsm algorithm [32] through the appropriately selected L9 level for each observatory (see [33] for further details). We applied several different data analysis procedures since various aspects and characteristics of geomagnetic field variations were investigated. We prefer to briefly describe each method in the following section, instead of describing all of them here.
3. Methods and Results
3.1. Secular Variation
Secular variation has an internal origin and a characteristic time scale greater than decades. We investigated the secular variation observed in the Italian territory using the complete time series of the geomagnetic field annual mean values at the three observatories; for increasing the time coverage in the central Italy, we used both AQU and DUR datasets. We show in Figure 2a the yearly average values of declination D, inclination I, and total field intensity F, together with the corresponding values from IGRF13 model. It is evident that there is good agreement between experimental and model data, confirming the reliability of the 13th generation of magnetic field model. The relationships between geomagnetic elements are drawn in Figure 2b.
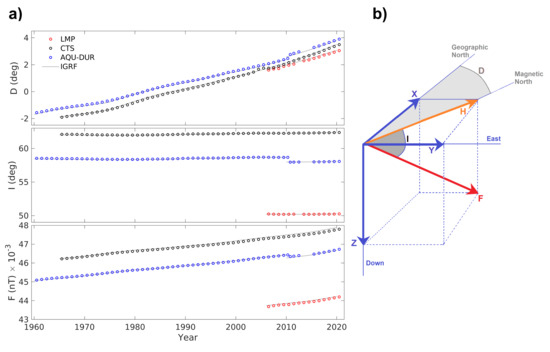
Figure 2.
(a) Yearly average values of declination (D, top), inclination (I, mid), and intensity (F, bottom) of geomagnetic field measured at Italian observatories of LMP (red circles), AQU/DUR (blues circles), and CTS (black circles), together with the corresponding values estimated by IGRF13 model (gray lines). The measurements at AQU terminated in 2010 when those at DUR observatory started. (b) Sketch of the magnetic elements which are interrelated by the following formulas: , , , , .
It can be seen that both D and F increase following a linear dependence throughout the years in the whole Italian territory, with a rate of , ∼, and ∼0.133 (deg/year), and , ∼40 and ∼ (nT/year) at LMP, DUR and CTS, respectively: more specifically, we performed a linear regression analysis by using the least squared method, and we considered the time interval 2010–2020 for all observatories; conversely, I seems to be almost constant at each observatory during the considered time interval, although the linear regression analysis indicates a slightly increasing value with a rate of one tenth with respect to the rate of D at each observatory.
3.2. Diurnal Variation and Its Seasonal Dependence
Diurnal variation is mainly due to the current system flowing in the ionosphere that appears mainly fixed in the Sun–Earth reference frame. It exhibits an astronomical dependence, which gives a seasonal modulation.
Diurnal variation can be conveniently isolated from longer period variations by using the appropriate filter procedure. In our case, we used the moving average, which represents a simple and efficient method for identifying long trends (e.g., [22,23,34,35]). In this regard, since diurnal variations have a periodicity of 24 h (and its sub-harmonics, 12, 8, 6, 4 h, and so on), we computed the moving average over 3 days: this value is sufficient to efficiently suppress the daily variations and not too large to include sub-harmonics of 27-day Sun’s synodic rotation period (see in particular [36,37]). We then subtracted the 3-day moving averaged time series from the original ones.
The whitening procedure described above allows us to study diurnal variation. In this regard, we performed a Superposed Epoch Analysis (SEA), firstly introduced in 1913 by Chree [38], computing both composites mean and standard error of the mean (SEM) on 24 h long time series segments, by using geomagnetic data collected at LMP, DUR, and CTS from 2017 to 2019.
Figure 3 shows diurnal variations in H (northward), D (eastward), and Z (downward) geomagnetic field components in the geomagnetic reference frame at three observatories during Lloyd seasons, together with their confidence intervals, indicated here by colored strip and computed as SEM [34,36]. The coefficient was chosen in order to define confidence intervals at 1% confidence level on almost Gaussian distributed variables. The pattern of diurnal variation of the D component is very regular and very similar at the three observatories and over different seasons; in particular, it exhibits a bipolar variation, with a maximum in the morning and a minimum in the afternoon. The hour at which it maximizes progressively shifts during the year, being about 7:00, 8:00, and 9:00 UT in the summer, equinoctial, and winter months, respectively. Conversely, the hour of the postnoon minimum is less variable, being at 12:30 UT during summer and equinoxes and at about 12 UT during winter. Regarding its amplitude, the D component diurnal variation is definitely greater during summer, progressively decreasing during equinoxes, and minimum during the winter.
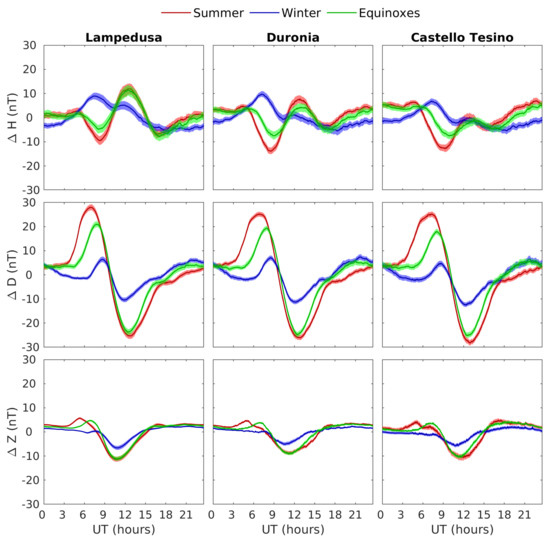
Figure 3.
Composites (mean) diurnal variation, derived from SEA, at LMP (left), DUR (mid) and CTS (right) in the H (top) and D (middle) and Z (bottom) geomagnetic field components during equinoctial (green), summer (red), and winter (blue) months, together with 1% confidence intervals (same color strips).
In addition, the pattern of the H component diurnal variation is quite similar at the three observatories, but it is more complex, being different during winter with respect to the rest of the year: during equinoctial and summer months it minimizes at about 8:30 UT (slightly earlier in summer), maximizes at about 13:00 UT, and exhibits a smaller minimum, more evident at the lowest latitude observatory LMP, around 17:00 UT; conversely, during winter, two positive peaks are observed at about 7:30 UT and at 12:00 UT, the second one being definitely smaller than the first one and progressively less evident for increasing latitude.
For a comparison, we computed the diurnal variation in the two horizontal components from Campbell [39] Sq model (available at https://www.ngdc.noaa.gov/geomag/geom_util/sq1.shtml, accessed on 4 August 2021); in particular, we computed its UT pattern (with a step of 20 min) setting the model at the longitude of LMP and at different latitudes, from 20° to 60° with a step of 2°. For each considered UT and each latitude, the amplitude of the and variation was converted into an equivalent current vector with direction and intensity obtained by a simple 90° clockwise rotation of horizontal magnetic field variations, i.e., . The resulting pattern of the equivalent currents is shown in Figure 4, for the dates 21 December, 21 June, and 22 September 2005, corresponding to equinoxes and solstices (2005 is the last year allowed by the model).
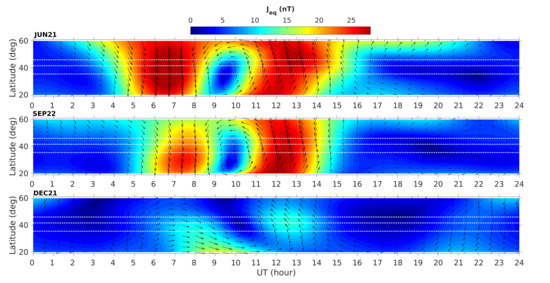
Figure 4.
Equivalent current system vectors derived from geomagnetic Sq-model [39] in correspondence of solstices and equinoxes days in the northern hemisphere for 2005. The time and latitude resolutions are 20 min and 2 deg for the intensity (in color scheme), while the vectors are superimposed with a resolution of 40 min and 4 deg. Horizontal white dotted lines mark observatories latitudes.
We can see that the equivalent current system consists of a current vortex flowing in the counterclockwise direction; its intensity is maximum in summer and minimum in winter, according with the observed amplitude of the diurnal variation, especially at the D component.
The most intense currents in the morning, as well as the focus of the current vortex, are shifted to earlier hours in summer with respect to equinoxes and winter; such maximum currents, which are predominantly directed southward, correspond to the morning maximum of the D component diurnal variation, while the focus corresponds to its inflection point. The hour when the currents maximize in the afternoon is less dependent on season, accordingly with the observed minimum of the D component variation. The different behavior of the H component diurnal variation during winter is well in accordance with the corresponding equivalent current system at the latitude of the three observatories (white horizontal lines in Figure 4): the winter currents for both prenoon and postnoon maxima show a relevant azimuthal component, differently from summer and equinoxes when the currents are prevailingly meridional. Moreover, the focus of the currents shifts to higher latitude in winter, resulting in a different position with respect to the sites: as a result, LMP is at lower latitude with respect to the focus, and the currents at its latitude do not reverse their azimuthal component until noon, and this well explains the persistent positive values of the H component diurnal variation. Conversely, the winter currents at CTS latitude around noon almost vanish (being near the focus), and this corresponds to almost null values of the H component variation.
3.3. Geomagnetic Field Variations at Italian Observatories during Intense Space Weather Events
In the context of space weather, it is important to know the response of the Earth’s magnetosphere to SW and IMF variations. In this regard, the extreme case is represented by geomagnetic storms. A geomagnetic storm occurs when an interplanetary disturbance, for example a traveling plasma cloud originating from the so-called Coronal Mass Ejection (CME), or a Corotating Interaction Region (CIR), intercepts the magnetosphere with a strong and prolonged southward orientation of the IMF component [40].
In this section, we present the geomagnetic field variations observed at Italian observatories during selected time intervals when an intense SW–magnetosphere interaction occurs. We consider two different typologies of ground events: the sudden storm commencements (SSC) and forward sudden impulses (SI), due to fast magnetospheric compressions, and the main phase of geomagnetic storms, due to ring-current enhancements. To extend these space weather events, we also used the SymH geomagnetic activity index, , and solar wind dynamic pressure . Although SW and IMF parameters used in this sections are time-shifted to the bow shock nose, additional time of flight should be considered for propagating disturbances from the bow shock to the magnetopause. It can be done following Lockwood et al. [41] and by using both magnetopause [42] and bow shock [43] dynamics models.
During SSC/SI events, the magnetosphere retreats as a consequence of the new hydrodynamic balance that is established by SW and magnetospheric pressures: it follows an increased Chapman–Ferraro magnetopause currents, in particular the subsolar dawn–dusk currents, which in turn induce positive variations in the H component of magnetic field at any site. The other manifestation of intense space weather events consists in a intensification of the magnetospheric ring current due to the increased number of magnetically trapped ions and electrons at ∼4 Earth radii, which in turn manifests as a depression of the northward H magnetic field component at any site. In the nighttime magnetosphere, magnetotail currents and Field Aligned Currents are also present, making difficult to discriminate their effects from those of the ring current.
We selected the events related to ring current enhancements using the geomagnetic activity index SymH [44] at 5 min time resolution; we chose significant geomagnetic storm events for years 2017, 2018, and 2019 imposing a maximum threshold value of SymH (−50 nT) and including only events for which the minimum SymH value occurs during daytime interval at our observatories (i.e., 6–18 LT). Regarding the SSC/SI events, we analyzed the ones published by Ebre Observatory (http://www.obsebre.es/en/rapid, accessed on 4 August 2021), entrusted by IAGA, selecting the SSCs and forward SIs for years 2017, 2018, and 2019.
The SEA method was applied for each selected space weather event to several variables, namely , , SymH, and the geomagnetic field variations , , and . For each variable X we computed composite mean and , identifying the epochs, a sort of zero-time or starting temporal point, at the minimum of SymH for the ring current maximum intensification events or at the time of the event for SSC/SIs provided by Ebro observatory. The composite means and SEM for , , and SymH are computed as average of selected sub-intervals, while the geomagnetic field variations are treated as follows before computing their composites.
- For consistency with OMNI data, the geomagnetic field variations are resampled at 5 min time resolution;
- The linear trends of geomagnetic field variations are computed over the years 2017–2019 considering only the time intervals 1–4 LT, which represent the nominal minimum of geomagnetic activity, and subtracted the entire time series of magnetic field measurements, obtaining a detrended time series;
- The diurnal variation, as well as any shorter period variation, is removed by subtracting the moving average computed over 3 days from the time series.
For each event, we finally removed from SymH and geomagnetic field data their average computed over the time interval that represents the pre-event or reference conditions. For each geomagnetic storm event, the reference value is computed considering the time interval 3–12 h before the epoch, while for each SSC/SI-related event, the average is computed considering one hour before the epoch of the event.
To identify statistically significant composite means, we also applied the SEA method to all variables by selecting as test epochs and their related time intervals, the complementary conditions adopted for recognizing the events, i.e., any sub-intervals that do not contain SymH < −50 nT and do not contain SSC/SI events; they are uniformly selected in the same time intervals of epochs (6-18 LT) for the SymH-related events and in the whole day for the SSC/SI events. Finally, only time intervals that were not superimposed are considered, in order to obtain stochastically independent sub-intervals. This method can be considered an alternative to the Monte Carlo test, based on surrogates of synthetically generated signals. Indeed, although we carefully removed long trends and diurnal variations, residual fluctuations (both regular and random) could survive: the difficulty in simulating surrogates can be easily overcome by this newly proposed method.
The above procedure allows, for any given parameter X, to compare the composite corresponding to space weather events with the one corresponding to reference conditions: this means that variations in X are statistically significant (significantly related to space weather events) if its confidence bound is not largely superimposed with . In this sense, statistically significant composites of ground geomagnetic field variations indicate time intervals significantly related to space weather events. As in previous sections, we computed the confidence bound at 1% confidence level by assuming . The estimated confidence intervals of almost quiet conditions are represented in each panels of two following figures by gray strips.
Figure 5 shows the results of the SEA method on 23 selected events (minimum SymH). Panels (a) and (b) report and (blue lines and strips) and their correspondence with the geomagnetic storm evidenced by the SymH composite (orange line and strip in panel (c)), whose minimum is marked by the vertical dashed lines. It can be seen that ∼3 h before the minimum of SymH (dotted vertical lines), attains significantly negative values, far from the confidence reference interval; conversely, emerges from its confidence bounds at least ∼6 h before ∼1–2 h after the epoch. At ground, the composites of geomagnetic field variations in H (panel d), D (panel e) and Z (panel f) components show very similar behaviors at all observatories. The major variations are revealed in the H component, with minimum levels of approximately , , and nT at LMP, DUR, and CTS, respectively, according to the expected decreasing response at increasing latitude with a factor of [45], where represent the magnetic dipole latitude. The H components remain well outside its corresponding reference interval up to ∼9 h after the epoch. Conversely, the D component at all sites does not reveal any significant variations in correspondence to the geomagnetic storms, except for a weak negative deviation during the main phase.
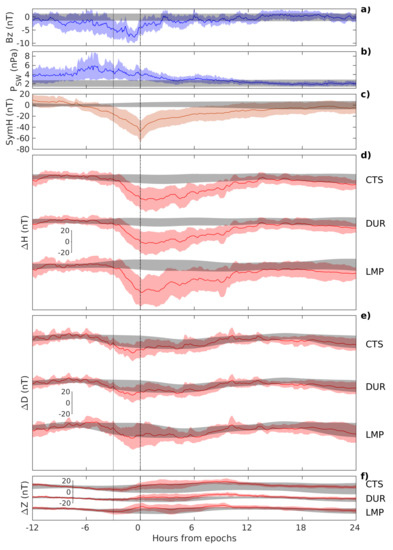
Figure 5.
The results of SEA method around the minimum values of SymH of 23 selected geomagnetic storms occurring during 2017–2019. From top to bottom: the composites of (panel a), SW pressure (panel b), geomagnetic activity index SymH (panel c) and geomagnetic field variations (panel d), (panel e) and (panel f) at LMP, DUR, and CTS. In panels (d–f), reference vertical bars are reported. In all panels, the composites and their corresponding SEMs are marked with red lines and strips, respectively. The corresponding reference values are represented by gray strips (see text for details).
Interestingly, in the Z component, we observe a significant, although low, enhancement at LMP, in correspondence and just after the epoch, probably attributable to electric currents system developing in the ground and surrounding sea salt water during these events: however, the deviation from the quiet confidence bound (gray strip) is small, probably due to the typical low level of geomagnetic storms occurring during 2017–2019: no remarkable CME-driven geomagnetic storms are observed because the whole time interval corresponds to the minimum of solar cycle 24. At CTS and DUR no significant Z component deviations are observed in correspondence to the geomagnetic storms.
Figure 6 shows the results of SEA on 36 selected SSC and SI events. In each panel, the epoch is marked with vertical dashed lines and represents the rising phase SSC/SI. As for the previous analysis, the H component manifests the greater deviation (∼20 nT) from the reference interval (gray strip) at all observatories. The D component shows small negative deviations, emerging at DUR and CTS for just a few nT from the reference interval. Finally, the Z component shows sudden minor variations at all sites, positive at CTS and DUR and negative at LMP; only at LMP the composite mean is slightly outside from the reference interval, probably as an enhanced response to the presence of sea salt water surrounding LMP.
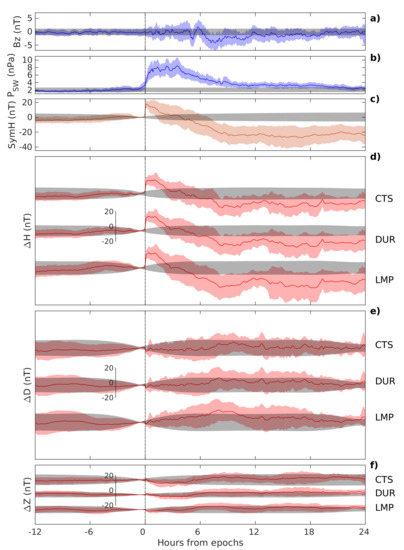
Figure 6.
The same as Figure 5, but referring to 36 selected SSC/SI events (see text for details).
3.4. Spectral Characteristics
In this section, we present a characterization and a comparison of the three observatories through a spectral analysis. For this purpose, the whole detrended time series of geomagnetic field at 1 s sampling period was divided into 3 h time intervals, each one time-shifted by 1 h (nominal time resolutions of spectral analysis); following Welch’s method, we computed, for each 3 h time interval, power spectral density (hereafter indicated for simplicity with S) of H, D, and Z components, as well as the cross-power spectral density between H and D, by using 1 h time window (frequency resolution of ∼0.28 mHz) with step size of 30 min (50% overlap). Each 3 h spectrum is smoothed by using a triangular window over nine frequency bands (final frequency resolution of ∼1.1 mHz), increasing the reliability of each spectrum: note that the final frequency resolution represents the true resolvable spectral peaks in terms of frequency bands [46,47]. The use of the triangular shape instead of a rectangular one has the advantage of reducing random fluctuations at the edge of the window, enhancing the confidence level of the peaks, while maintaining a reasonable spectral resolution.
Previous analysis, not shown here, confirmed a time dependence of spectra characteristics with a general increased power level in the daytime hours with respect to the nighttime hours. We restricted the analysis to the most quiet periods, considering only 3 h time intervals characterized by . Figure 7 shows the averages of selected spectra S in the time intervals, with a duration of 12 h, centered at 00 LT and 12 LT at Italian observatories. The power level is generally higher during diurnal hours, when the magnetospheric field lines approach the source regions, magnetopause flanks, and upstream regions, where the Sun–Earth interactions take place. It is clear that power level increases with increasing latitude, as expected, since the corresponding magnetospheric field lines are closer to the magnetopause. This aspect is more evident during the diurnal time interval. A power law dependence of the spectra S is recognizable in the H and D components of the kind , which corresponds in the log–log scale (as shown in Figure 7) to the linear law usually called red noise due to the negative spectral index p. The spectra of Z component show a similar power law dependence of the H and D spectra except for Lampedusa where it manifests a steeper decrease in the lower frequency band ( mHz, especially during diurnal hours) and then a slower decrease for higher frequencies, with respect to DUR and CTS; this different behavior is possibly attributable to the large difference in the subsoil and surrounding regions of the LMP observatory.
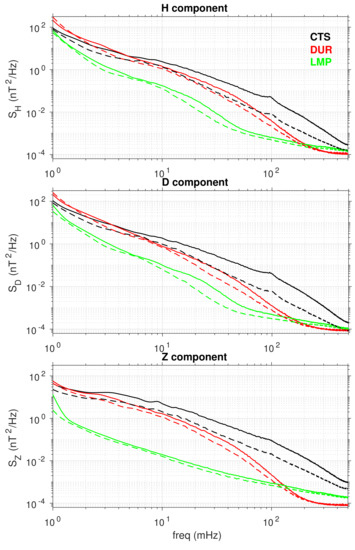
Figure 7.
Average of selected spectra with around 12 LT (filled lines) and 00 LT (dashed lines) at Italian observatories of CTS (black lines), DUR (red lines) and LMP (green lines) during the year 2018 for the H (, top panel), D (, mid panel), and Z (, bottom panel) components.
The Pc5 (1–7 mHz) ULF magnetic field fluctuations are mainly observable at high latitudes, where the corresponding magnetic field lines are closer to the magnetopause region: ULF waves at these frequencies are attributed to several source phenomena such as the the Kelvin–Helmholtz instability occurring on the magnetopause flanks [12,48] and the compressive ULF waves generated in the leading edge of the Corotating Interaction Regions (CIR) [13,49] and by SW fluctuations at discrete frequencies [50]. These waves can penetrate in the magnetosphere with decreasing amplitude with a decreasing latitude and can be observed also at Italian latitudes [51].
The observed well-known noise behavior in the Pc3-4 (7–100 mHz) frequency range allows us to study the Signal-to-Noise Ratio (SNR) at Italian observatories as it follows: . Here, S represents the sum of signal and noise N (i.e., the experimental spectra ) where the noise N was estimated by the linear fit of points of the power spectrum at the extremes of Pc3-4 frequency range, where the spectra change their slopes, as [52,53]. We want to remark that N represents also the sum of noise of natural and anthropogenic origin and that these two contributions are difficult to discriminate.
It can be noted that in the 10–100 mHz frequency range the S level is higher with respect to the corresponding noise N during daytime hours. To investigate this aspect, we computed the SNR on hourly averaged power spectra of both horizontal components . The time dependence of resulting hourly SNR, spectral index p, and power noise or level in the 10–100 mHz frequency range are shown in Figure 8 for the three observatories. Our analysis shows that the signal emerges mainly during morning hours, since intense Pc3-4 are mainly generated upstream of the morning flank region of the bow shock, where the IMF, mainly oriented with a cone angle of ∼45°, makes a small angle with respect to the bow shock normal direction [15,46,53,54,55]. We observed a greater amplitude at DUR, suggesting that at CTS, there is an higher level of local noise while at LMP there is a greater attenuation of external origin waves.
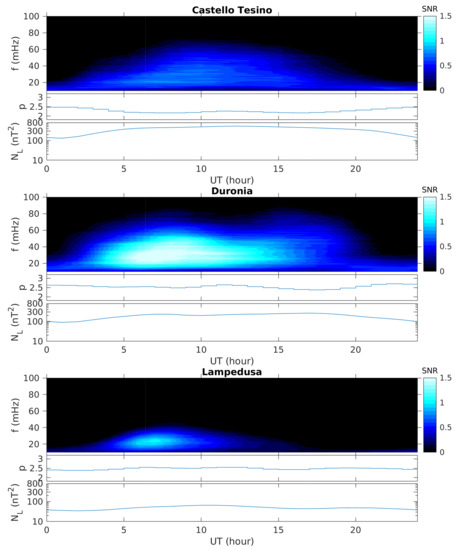
Figure 8.
Signal-to-Noise ratio at CTS (top panel), DUR (middle panel), and LMP (bottom panel) in the frequency range 10–100 mHz during the year 2018, together with their spectral index p and noise level .
At LMP, the SNR is very low and clearly confined around morning hours; in these hours, the magnetic field line mapping to LMP approaches the magnetopause regions preferentially impacted by upstream waves. The transmitted ULF signals propagate more efficiently along the corresponding magnetic field line, possibly emerging as power enhancement above the local noise at ground. Conversely, at DUR (and less clearly at CTS), the SNR also extends to early afternoon hours in agreement with the finding at AQU by De Lauretis et al. [53], possibly indicating the important contribution of FLR in the H component at these latitudes. The observed FLR phenomena will be discussed in the next section. Figure 8 also shows p and : p attains values of ∼ in agreement with the value found by De Lauretis et al. [53] at AQU; regarding the , it is clearly higher at CTS, and it attains, at all observatories, minimum values around ∼2 UT, while the maximum values are observed around noon, with the higher broad peak at CTS in the larger time interval ∼6–19 UT. The SNR is a useful tool for distinguishing Pc3-4 events from a signal as long as the noise is well recognized by a model function.
The polarization ratio of fluctuating geomagnetic field along H and D components is also useful to distinguish signal from noise; its values are in the range between 0 (completely not polarized waves) and 1 (fully polarized waves). We computed in the Pc3-4 frequency range by following the procedure by Fowler et al. [56]. In the examined frequency range, we also studied the occurrence rate of polarized signals (). Figure 9 shows the dependence of this occurrence rate on frequency , with a frequency resolution of ∼0.28 mHz. The highest () is found at DUR (red) around 50–80 mHz which probably represents the expected FLR frequency range at this site. At LMP (red), is lower, reaching values higher than 40% in the frequency range 3–30 mHz. At CTS (black), there is not a clear peak in the occurrence rate of polarized signal, except for the narrow peak around 100 mHz; this frequency is also coincident with the spectral relative peak observed in Figure 7, and it is probably due to local artificial contamination. The results shown here are in agreement with those shown by SNR just examined. Indeed, the polarized signals at DUR and LMP are in the same frequency range of the observed SNR enhancement; the same could be tentatively observed for CTS, although the noise level is probably higher at this site.
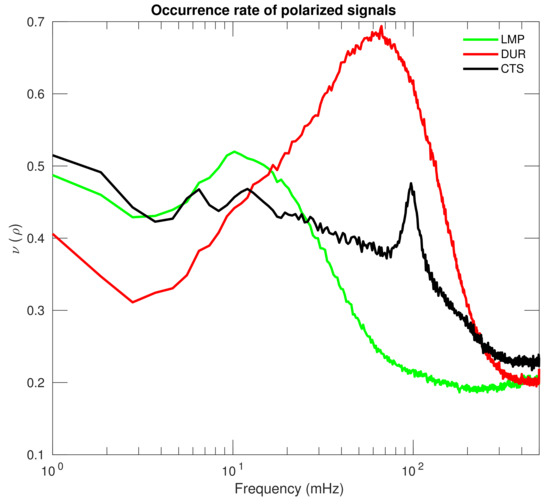
Figure 9.
Occurrence rates of polarized horizontal components () for each frequency band at LMP (green line), DUR (red line), and CTS (black line) during 2018.
3.5. Observation of Field Line Resonances
Magnetohydrodynamic (MHD) waves naturally occur in the magnetosphere and are one of the processes responsible for the energy transfer through magnetospheric plasma. Whatever the source, traveling MHD compressive waves can produce resonances of the geomagnetic field lines whenever the frequency of the forcing wave matches with the eigenfrequency of a given field line [57]. In this description, the geomagnetic field lines are considered as vibrating strings with fixed footprints at ionospheric heights. This assumption is justified by the high ionospheric conductivity, which allows perfect reflection and thus the formation of standing Alfvèn waves. In fact, this condition is generally satisfied only during daytime, when both footprints are sunlit. After sunset, the conductivity decreases and in particular, situations one or both ends of the field line should be theoretically considered free [58]. However, a recent study by Takahashi et al. [59] interpreted resonances observed in the midnight sector as fix-end modes, suggesting that even during nighttime, the ionospheric condition could sustain normal modes.
FLRs can be used to remotely sense the equatorial plasma mass density in the inner magnetosphere and led the scientific community to set up large meridional arrays of magnetometers such as the Mid-continent MAgnetoseismic Chain (McMAC, [60]) and the Canadian Array for Realtime InvestigationS of Magnetic Activity (CARISMA, [61]) in North America, which, when combined, provide magnetic field data from to 11 at the same local time (≈UT − 6.5 h). Similarly, the European quasi-Meridional Magnetometer Array (EMMA, [62]) provides data from to 6.5 at an average local time of UT + 2 h. Starting from the FLR frequencies simultaneously observed by several station pairs of a network, the equatorial radial profile of the plasma mass density can be inferred by solving the governing MHD wave equation [63], making assumptions of the magnetic field topology and on the plasma distribution along the field lines.
FLR frequencies can be estimated using the gradient method [64,65], a technique based on the cross-spectral analysis of magnetic signals along the H component recorded by latitude separated station pairs aligned along the same magnetic meridian. The basic idea is that the spectral features of the H component recorded by the two stations are very similar but slightly shifted in frequency. As a consequence, the amplitude ratio between poleward (p) and equatorward (e) sites should cross the unity with positive slope at the FLR frequency of the field line whose footprint is the midpoint of the stations. At the same frequency, the cross-phase spectrum between the two signals shows a maximum.
The FLR frequency generally decreases with increasing latitude, except for those field lines mapping into the plasmaphere boundary layer, for which the frequency increases. This implies a reversed behavior of the spectral features described above; that is, the FLR frequency is identified by a minimum in the spectra and by a negative slope in the amplitude ratio [66]. A cross-phase reversal can also occur at very low latitude (), for which the FLR frequency can increase with increasing latitude, reflecting the mass loading of ionospheric heavy ions [67,68].
Usually, the gradient method is applied to observatory pairs with a latitude separation of 1–3 degrees. This separation is required to ensure a sufficient difference between the resonance frequencies of the two points of observation but at the same time ensure enough coherency between the observed signals. As pointed out by statistical works [69,70], the occurrence of FLRs depends on the latitude and local time. In particular, at very low latitudes (), the power of the signal decreases, and it is often impossible to detect resonances. It is worth nothing, however, that a larger latitude separation could counteract this effect, because the cross-phase peaks arise more prominently from the baseline.
In this work, we applied the semi-automated procedure developed by Del Corpo et al. [70] to the pair DUR–LMP to determine FLRs during two geomagnetic storms: 5–11 September 2017 [22] and 23–29 August 2018 [23]. The procedure basically searches for a maximum in the spectra and then checks if at the same frequency the typical amplitude ratio pattern is matched. The uncertainty of the selected frequency is the half width of the peak at 80% of its height. The DUR–LMP pair has a latitude separation (≈6 degree) that is usually considered too large for the gradient method. However, Chi and Russell [71] showed that gradient method could work for distances as long as 800 km. Chi et al. [69] tested the efficency of the gradient method with McMAC stations in the L-range 1.46–2.58, using pair separations ranging from 318 to 1842 km. They found that the detection rate is still significant for points separation greater than 1000 km, although it drops by 60% with respect to a separation of 300 km. They also suggested that large separations work well for station pairs at low latitudes. DUR–LMP has a separation of ∼700 km, which corresponds to a relatively small L-shell variation of (see Table 1).
Figure 10 shows from top to bottom the SymH index, the Kp index, the local K index at LMP, DUR and CTS, and the FLR frequency observed for the storm of September 2017.
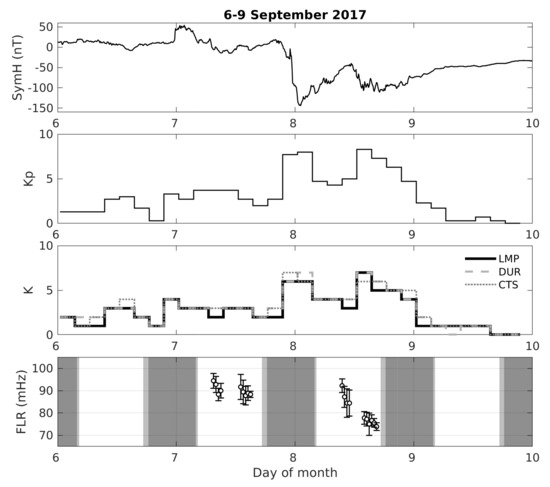
Figure 10.
Some geomagnetic activity indices and FLRs frequencies dected at DUR-LMP on 6–9 September 2017. From top to bottom are reported the SymH, the Kp, the local K evaluated at the three geomagnetic observatories, and the FLR frequencies. Light and dark shadowed areas represent periods with one or both field line footprints not lighted by the sun.
The frequencies detected during nighttime are generally not reliable [70]; thus we added shadowed areas to highlight intervals in which the frequency cannot be trusted. As suggested by Del Corpo et al. [72], the sunrise and sunset time of the pair and of the conjugate point are evaluated at the height of 120 km and the intervals in which one or both the field line footprints are in darkness are represented in Figure 10 as light or dark shadowed areas, respectively. In both the events analyzed no frequencies where found in those critical periods.
The first day of the interval was characterized by quiet geomagnetic conditions, that is, low Kp and K values and stable, almost null, SymH values. At the end of the day, a sudden impulse due to an interplanetary shock [22] is recognizable as a positive variation in the SymH and is followed by a slight increase in the geomagnetic activity (see Kp index). The main phase of the storm started on 7 September at about 21:30, as evidenced by the steep decrease in SymH and the simultaneous increase in the Kp and K indices. The recovery phase began after only three hours and was interrupted around noon of 8 September by a second perturbation. The following day, the recovery proceeded under very quiet geomagnetic conditions.
We are able to confidently identify FLR frequencies for only two days. This is not surprising since, as stated before, during quiet days, the energy of the waves penetrating the inner magnetosphere is very low. For this event, there is enough power after the sudden impulse and after the main phase. The average FLR frequency on 7 September was around 90 mHz, while on 8 September it decrease from 90 to 75 mHz. This behavior is compatible with an increase in the plasma mass density in the flux tube previously depleted as an effect of the disturbed geomagnetic conditions.
Figure 11 shows the same parameters of Figure 10 for the storm of August 2018. In this event, the storm was preceded by a prolonged quiet period that lasted for several days. The main phase started at the end of 25 August and ended at about 7:00 UT of the following day when the SymH reached a value of ≈−200 nT and the Kp a maximum value of . During the recovery phase, the geomagnetic conditions remained disturbed until the end of 28 August, when a new quiet phase began. Similarly to the first event, we were able to identify FLR frequencies only for the most disturbed days, the ones following the main phase. The general quality of the cross-spectra for this event is very low, making the selected frequencies somewhat questionable, in particular the ones detected on 28 August. A possible explanation for such degradation could be the presence of the maximum in the latitudinal profile of the FLR frequency between LMP and DUR latitudes. However, the general behavior of the frequency is compatible with a flux tube recovery that roughly follows the decrease in the disturbance level. Indeed, as the activity decreases, the daily average frequency value passes from 74 to 72 to 60 mHz, respectively.
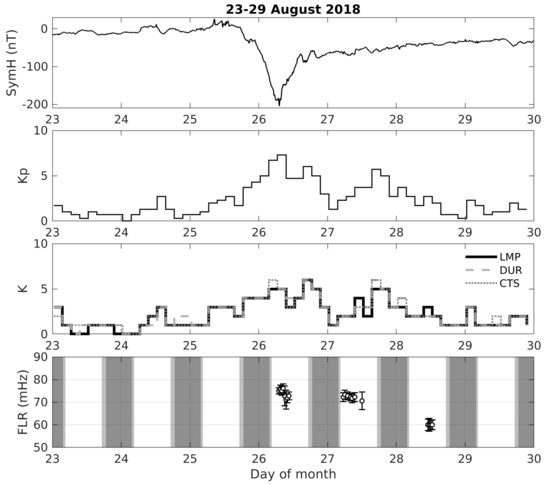
Figure 11.
The same as Figure 10 but for the interval 23–29 August 2018.
4. Discussion
Long trends of the magnetic declination, inclination, and scalar intensity F are reported for the last decades, for each of the three Italian geomagnetic observatories, whose site locations cover in latitude the entire length of the territory, from the northernmost (Castello Tesino, CTS) to the southernmost (Lampedusa, LMP), passing to the center (Duronia, DUR) part of Italy. LMP is the latest to be established, in 2005, and its position in the middle of the Mediterranean Sea is particularly valuable since a large strip of the North African continent, as well as the southern part of the Euro-Mediterranean sector, is lacking of geomagnetic observatories.
Geomagnetic diurnal variations at the three observatories are reported by analysing the last four years (2017–2020) of the 1 min based dataset. The comparison of their seasonal variations allows us to speculate about the latitudinal displacements of the vortex’s focus of the ionospheric Sq electric current systems, as consistently estimated by the geomagnetic empirical model from Campbell [39]. The position of the three Italian observatories, being very close to the latitude of the current vortex focus, well identified by the model [39], is favorable to detect possible latitudinal displacements of the focus itself [73].
We statistically investigate the geomagnetic individual response to intense space weather events, such as SSCs and forward SIs, which correspond to sudden magnetospheric compressions, and significant minima of SymH (<−50 nT), which mark the manifestation of geomagnetic storms. In this regard, we performed the SEA method with an ad hoc significance test based on experimental data: it mitigates any complication due to the usage of artificial or surrogate dataset, such as those derived by Monte Carlo tests. Results show that the most remarkable variations emerge in the H component; in particular, for the minima of SymH, LMP has the greatest significant deviation due to its lower latitude [45]. Moreover, the vertical component at LMP exhibits a low enhancement in correspondence and just after the events, suggesting a link with an inductive effect due to electric currents system developing in the ground and in the surrounding conductive sea salt water [37,74,75]. At Italian latitudes, in correspondence to stronger events, such inductive effects could generate the so-called ground induced currents (GICs) (see [76,77]), which typically occur and attain higher intensity at higher latitudes. The Z-component deviations that we observe at three observatories hardly emerge with respect to the confidence bound, probably due to the typical low intensity of space weather events occurring in the last few years, in coincidence with the minimum of solar cycle of 24. With the rising phase of the next solar cycle 25 we may hopefully face major CME-driven events, which could allow us to better investigate these features.
Comparison of the spectral content of each magnetic component at each observatory allows recognizing that LMP has the lowest-power spectral density amplitude in the frequency range 1–100 mHz, both during diurnal and nocturnal hours, as expected because of power level of the magnetic field increases with increasing latitude, i.e., with decreasing distance of magnetospheric field line from the magnetopause. At the LMP site, at frequencies lower than 2 mHz, the spectral amplitude of the vertical component shows a rise of almost 1 order of magnitude during diurnal hours, possibly linked to inductive effects because of the peculiarity of the local subsoil and surrounding (higher conductive) regions, when the environmental noise of anthropic origin is slightly enhanced.
In this regard, as disclosed by aeromagnetic surveys carried out in Italy, including the sector over Lampedusa [78], crustal magnetic anomalies (magnetic highs) located in the northwest and northeast areas surrounding the island may play a role.
A further characterization of the magnetic signal recorded at the three observatories comes from the analysis of the Signal-to-Noise ratio and noise level applied to the hourly averaged power spectra of H and D components. These analyses show that the signal, for frequencies up to 100 mHz, emerges mainly during morning hours, when the corresponding geomagnetic field line approaches the magnetopause region preferentially hit by upstream waves. The highest Signal-to-Noise ratio amplitude is reached at DUR, while the noise level progressively decreases from CTS to LMP, suggesting that CTS is affected by the highest level of local noise and that LMP shows the greatest attenuation of external origin waves. The behavior of Signal-to-Noise ratio in relation with both latitude and local time is well reported in literature by means of statistical [53] and case studies [46].
The most evident signature of Pc3-4 events emerges at DUR. An additional tool for characterizing the signal content is given by the computation of the polarization ratio over fluctuations in the magnetic field, between the two horizontal components H and D. This further analysis shows the major occurrence of polarized signal at DUR in the 50–80 mHz frequency range, a lower occurrence at LMP at 3–30 mHz, while at CTS, no clear peak in the occurrence of polarized signals emerges.
A possible application of the continuous monitoring of the geomagnetic field variations observed at ground is the individuation of field-line resonance events. We applied the procedure by Del Corpo et al. [70] to the H component of LMP and DUR for two geomagnetic storms. The technique is suitable to estimate the resonance frequency of the the field line, whose footprint lies midway between the observatories, and was able to detect field line resonances only during the most disturbed periods, i.e, in the main and recovery phases of the two studied storms. The frequency generally decreases during the recovery phase, a behavior compatible with a flux tube recovery that roughly follows the decrease in the disturbance level. The observed field line resonance frequencies vary between 60 and 90 mHz, in agreement with previous works. Indeed, field line resonance frequencies in the L-range 1.3–1.6 are reported in literature to vary between 60 and 100 mHz depending on several factors including the geomagnetic activity, the season and the solar cycle phase [67,68,69,79,80].
Starting from the field line resonance frequencies detected, one could infer the corresponding equatorial plasma mass density modeling the plasma mass density distribution along the field line () with a power law , where r is the geocentric distance and m is the power law coefficient. In previous investigation [81,82], Del Corpo et al. [70] assumed for each latitude and geomagnetic condition. As pointed out by Vellante and Förster [82], at very low latitudes, the field lines are for the most part inside the ionosphere, and a value of m significantly higher than 1 could be necessary. A thorough investigation of the best value for m should be carried out before using the DUR–LMP pair to infer plasma mass density. The pair could be useful to describe the plasma mass density profile in extreme space weather conditions when the plasmasphere boundary layer can move earthward below , and even a few points could make the difference in interpreting the plasmasphere dynamic. These results possibly indicate that LMP is a potential extension of the EMMA network (presently extending down to ) towards lower latitudes, although the installation of new observational sites between LMP and DUR could provide further information on the latitudinal frequency variation.
5. Conclusions
The geomagnetic observatory at Lampedusa (LMP), a small island in the southern part of Italy, is the latest Italian monitoring point setup for recording the earth’s magnetic field variations, according to the IAGA recommendations. Differently from the other two Italian observatories (Castello Tesino and Duronia), which are located in the continental territory, LMP lies in the middle of the Mediterranean Sea. The availability of data from this site, surrounded by sea water, is a novelty for the interested scientific community, since the whole northern African sector and the south Mediterranean basin are lacking such kinds of observation. For this reason, the release of geomagnetic data from LMP represents both a motivation and an incentive to sustain the effort for gaining high quality observations (data download at geomag.rm.ingv.it, accessed on 4 August 2021). From a magnetic point of view, data comparison in both time and frequency domains with the other Italian observatories reveals the electromagnetic quiet character of the site, being also the observatory located in the inner part of a wild park with limited access. Variations at different frequency ranges are examined for the three observatories, allowing us to characterize diurnal variation and its seasonal dependence in the larger frame of the secular variation for the older observatories. The combined features are in good agreement with the geomagnetic Sq-model used in this study, confirming the seasonal displacement of the north Sq-current system vortex, indicating that the focus of the currents shifts to higher latitude during local winters in the Mediterranean region. With the application of the Superposed Epoch Analysis (SEA) to geomagnetic data from each of the three observatories, individual responses to intense space weather events are shown, indicating a weak anomalous response at LMP with respect to the other observatories occurring in correspondence with rapid external forcing, probably attributable to the surrounding sea salt water. Magnetic responses in the Ultra-Low-Frequency (ULF) range from spectral, local Signal-to-Noise Ratio (SNR) analyses under different local time and polarization rates are computed, showing that even at middle/low latitudes signatures of magnetic field line, resonances are detected. As confirmed by an in-depth analysis for two selected storms, field line resonances at those latitude can contribute to understanding the plasmasphere dynamic during highly disturbed geomagnetic conditions, improving the picture derived by already present magnetometer arrays. Even in the modern satellite era, the valuable support from ground-based observations remains an opportunity for integrating and calibrating the in situ satellite observations. Results from data gained by geomagnetic observatories, whose long lasting data archives are of primary importance, demonstrate an important contribution in sensing, retrieving and characterizing the response to space weather events even from ground level, both at single-site level and, as a collective action, at global scale, and from solid Earth’s induction to remote magnetospheric phenomena.
Author Contributions
Infrastructures management, D.D.M. and L.C.; methodology, M.R., S.L., A.D.C. and D.D.M.; software and data analysis, M.R. and A.D.C.; instruments maintenance, G.D., P.B. and G.B.; data validation P.B. and G.D.; writing—original draft preparation, M.R., D.D.M., S.L. and A.D.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Datasets used in this study are freely accessible from each owner’s websites (referenced in the text) as cited in Section 2, Section 3.1, Section 3.2 and Section 3.3. All datasets suppliers are also acknowledged. One second data from Italian geomagnetic observatories are available upon request, addressed to the corresponding author.
Acknowledgments
The high resolution maps are realized by using ETOPO1 1 Arc-Minute Global Relief Model (https://www.ngdc.noaa.gov/mgg/global/relief/ETOPO1/data/ice_surface/grid_registered/binary/, accessed on 4 August 2021) and Global Self-consistent, Hierarchical, High-resolution Geography Database (GSHHG) (http://www.ngdc.noaa.gov/mgg/shorelines/data/gshhs/, accessed on 4 August 2021) both provided by National Oceanic and Atmospheric Administration (NOAA), and by using M_Map tools available online at https://www.eoas.ubc.ca/~rich/map.html, (accessed on 4 August 2021). The authors also thank the members of IAGA Working Group V-MOD for computing the IGRF coefficients, freely available at https://www.ngdc.noaa.gov/IAGA/vmod/igrf.html, (accessed on 4 August 2021). We also thank OMNI web (https://cdaweb.gsfc.nasa.gov/, accessed on 4 August 2021) for providing interplanetary magnetic field and solar wind data, as well as the geomagnetic activity indices Kp and SymH. This work is supported by INGV-MUR Project Pianeta Dinamico—The Working Earth (CUP D53J19000170001), theme 3 SERENA, https://progetti.ingv.it/it/pianeta-dinamico, accessed on 4 August 2021.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AACGM | Altitude-Adjusted Corrected Geomagnetic (coordinates) |
| AQU | L’Aquila observatory |
| CME | Coronal Mass Ejection |
| CTS | Castello Tesino observatory |
| DUR | Duronia observatory |
| EMIC | Electromagnetic Ion Cyclotron (waves) |
| EMMA | European quasi-Meridional Magnetometer Array |
| FAC | Field Aligned Current |
| FLR | Field Line Resonance |
| GNSS | Global Navigation Satellite System |
| IGRF | International Geomagnetic Reference Field model |
| IMF | Interplanetary Magnetic Field |
| LMP | Lampedusa observatory |
| MHD | Magnetohydrodynamic |
| MLT | Magnetic Local Time |
| Pc | Continuous Pulsation |
| Pi | Irregular Pulsation |
| SEA | Superposed Epoch Analysis |
| SEM | Standard Error of the Mean |
| SNR | Signal-to-Noise Ratio |
| SSC | Sudden Storm Commencement |
| SI | Sudden Impulse |
| SW | Solar Wind |
| TAD | Traveling Atmospheric Disturbance |
| TID | Traveling Ionospheric Disturbance |
| ULF | Ultra Low Frequency |
References
- Bullard, E.C.; Freedman, C.; Gellman, H.; Nixon, J. The westward drift of the Earth’s magnetic field. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Sci. 1950, 243, 67–92. [Google Scholar] [CrossRef]
- Newitt, L.R.; Chulliat, A.; Orgeval, J.J. Location of the North Magnetic Pole in April 2007. Earth Planets Space 2009, 61, 703–710. [Google Scholar] [CrossRef] [Green Version]
- Regi, M.; Di Mauro, D.; Lepidi, S. The Location of the Earth’s Magnetic Poles From Circum-Terrestrial Observations. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028513:1–e2020JA028513:19. [Google Scholar] [CrossRef]
- Gubbins, D. Convection in the Earth’s Core and Mantle—Harold Jeffreys Lecture 1990. Q. J. R. Astron. Soc. 1991, 32, 69. [Google Scholar]
- Lanza, R.; Meloni, A. The Earth’s Magnetism: An Introduction for Geologists; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Akasofu, S.I. A Review of Studies of Geomagnetic Storms and Auroral/Magnetospheric Substorms Based on the Electric Current Approach. Front. Astron. Space Sci. 2021, 7, 604750:1–604750:20. [Google Scholar] [CrossRef]
- Zakharenkova, I.; Astafyeva, E.; Cherniak, I. GPS and in situ Swarm observations of the equatorial plasma density irregularities in the topside ionosphere. Earth Planets Space 2016, 68, 120:1–120:11. [Google Scholar] [CrossRef] [Green Version]
- National Research Council. Severe Space Weather Events: Understanding Societal and Economic Impacts: A Workshop Report; The National Academies Press: Washington, DC, USA, 2008. [CrossRef]
- MacAlester, M.H.; Murtagh, W. Extreme Space Weather Impact: An Emergency Management Perspective. Space Weather 2014, 12, 530–537. [Google Scholar] [CrossRef]
- Jacobs, J.A. Geomagnetic Micropulsations; Physics and Chemistry in Space; Springer: Berlin/Heidelberg, Germany, 1970. [Google Scholar] [CrossRef]
- Menk, F.W. Magnetospheric ULF Waves: A Review. In The Dynamic Magnetosphere; Liu, W., Fujimoto, M., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 223–256. [Google Scholar] [CrossRef]
- Kivelson, M.G.; Zu-Yin, P. The Kelvin-Helmholtz instability on the magnetopause. Planet. Space Sci. 1984, 32, 1335–1341. [Google Scholar] [CrossRef]
- Takahashi, K.; Ukhorskiy, A.Y. Timing analysis of the relationship between solar wind parameters and geosynchronous Pc5 amplitude. J. Geophys. Res. Space Phys. 2008, 113, A12204:1–A12204:13. [Google Scholar] [CrossRef] [Green Version]
- De Lauretis, M.; Regi, M.; Francia, P.; Marcucci, M.F.; Amata, E.; Pallocchia, G. Solar wind-driven Pc5 waves observed at a polar cap station and in the near cusp ionosphere. J. Geophys. Res. Space Phys. 2016, 121, 11145–11156. [Google Scholar] [CrossRef]
- Regi, M.; De Lauretis, M.; Francia, P. The occurrence of upstream waves in relation with the solar wind parameters: A statistical approach to estimate the size of the foreshock region. Planet. Space Sci. 2014, 90, 100–105. [Google Scholar] [CrossRef]
- Altman, C.; Fijalkow, E. Mechanism of Transmission of Hydromagnetic Waves through the Earth’s Lower Ionosphere. Nature 1968, 220, 53–55. [Google Scholar] [CrossRef]
- Kim, H.; Lessard, M.R.; Engebretson, M.J.; Young, M.A. Statistical study of Pc1–2 wave propagation characteristics in the high-latitude ionospheric waveguide. J. Geophys. Res. Space Phys. 2011, 116, A07227:1–A07227:20. [Google Scholar] [CrossRef] [Green Version]
- Regi, M.; Marzocchetti, M.; Francia, P.; De Lauretis, M. A statistical analysis of Pc1–2 waves at a near-cusp station in Antarctica. Earth Planets Space 2017, 69, 152:1–152:16. [Google Scholar] [CrossRef] [Green Version]
- Seppälä, A.; Matthes, K.; Randall, C.E.; Mironova, I.A. What is the solar influence on climate? Overview of activities during CAWSES-II. Prog. Earth Planet. Sci. 2014, 1, 24:1–24:12. [Google Scholar] [CrossRef] [Green Version]
- Tinsley, B.A. The global atmospheric electric circuit and its effects on cloud microphysics. Rep. Prog. Phys. 2008, 71, 066801:1–066801:31. [Google Scholar] [CrossRef]
- Lam, M.M.; Tinsley, B.A. Solar wind-atmospheric electricity-cloud microphysics connections to weather and climate. J. Atmos. Sol. Terr. Phys. 2016, 149, 277–290. [Google Scholar] [CrossRef] [Green Version]
- Alfonsi, L.; Cesaroni, C.; Spogli, L.; Regi, M.; Paul, A.; Ray, S.; Lepidi, S.; Di Mauro, D.; Haralambous, H.; Oikonomou, C.; et al. Ionospheric disturbances over the Indian sector during 8 September 2017 geomagnetic storm: Plasma structuring and propagation. Space Weather 2021, 19, e2020SW002607:1–e2020SW002607:16. [Google Scholar] [CrossRef]
- Spogli, L.; Sabbagh, D.; Regi, M.; Cesaroni, C.; Perrone, L.; Alfonsi, L.; Di Mauro, D.; Lepidi, S.; Campuzano, S.A.; Marchetti, D.; et al. Ionospheric Response Over Brazil to the August 2018 Geomagnetic Storm as Probed by CSES-01 and Swarm Satellites and by Local Ground-Based Observations. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028368:1–e2020JA028368:16. [Google Scholar] [CrossRef]
- Pawlowicz, R. M_Map: A mapping Package for MATLAB, Computer Software. 2020. Available online: http://www.eoas.ubc.ca/~rich/map.html (accessed on 4 August 2021).
- US National Geophysical Data Center (NGDC); National Environmental Satellite, Data, and Information Service (NESDIS); National Oceanic and Atmospheric Administration (NOAA); U.S. Department of Commerce. TerrainBase, Global 5 Arc-minute Ocean Depth and Land Elevation from the US National Geophysical Data Center (NGDC); National Center for Atmospheric Research: Boulder, CO, USA, 1995.
- McIlwain, C.E. Coordinates for mapping the distribution of magnetically trapped particles. J. Geophys. Res. 1961, 66, 3681–3691. [Google Scholar] [CrossRef]
- Shepherd, S.G. Altitude-adjusted corrected geomagnetic coordinates: Definition and functional approximations. J. Geophys. Res. (Space Phys.) 2014, 119, 7501–7521. [Google Scholar] [CrossRef]
- Civile, D.; Lodolo, E.; Tortorici, L.; Lanzafame, G.; Brancolini, G. Relationships between magmatism and tectonics in a continental rift: The Pantelleria Island region (Sicily Channel, Italy). Mar. Geol. 2008, 251, 32–46. [Google Scholar] [CrossRef]
- Civile, D.; Lodolo, E.; Alp, H.; Ben-Avraham, Z.; Cova, A.; Baradello, L.; Accettella, D.; Burca, M.; Centonze, J. Seismic stratigraphy and structural setting of the Adventure Plateau (Sicily Channel). Mar. Geophys. Res. 2014, 35, 37–53. [Google Scholar] [CrossRef]
- Iyemori, T.; Takeda, M.; Nose, M.; Odagi, Y.; Toh, H. Mid-latitude Geomagnetic Indices ASY and SYM for 2009 (Provisional): Internal Report of Data Analysis Center for Geomagnetism and Space Magnetism; Kyoto University: Kyoto, Japan, 2010. [Google Scholar]
- Bartels, J. The geomagnetic measures for the time-variations of solar corpuscular radiation, described for use in correlation studies in other geophysical fields. Ann. Intern. Geophys. 2010, 4, 227–236. [Google Scholar]
- Nowozyński, K.; Ernst, T.; Jankowski, J. Adaptive smoothing method for computer derivation of K-indices. Geophys. J. Int. 1991, 104, 85–93. [Google Scholar] [CrossRef] [Green Version]
- Regi, M.; Bagiacchi, P.; Di Mauro, D.; Lepidi, S.; Cafarella, L. On the validation of K-index values at Italian geomagnetic observatories. Geosci. Instrum. Methods Data Syst. 2020, 9, 105–115. [Google Scholar] [CrossRef] [Green Version]
- Laken, B.A.; Čalogović, J. Composite analysis with Monte Carlo methods: An example with cosmic rays and clouds. J. Space Weather Space Clim. 2013, 3, A29:1–A29:13. [Google Scholar] [CrossRef]
- Regi, M.; Del Corpo, A.; De Lauretis, M. The use of the empirical mode decomposition for the identification of mean field aligned reference frames. Ann. Geophys. 2016, 59, G0651:1–G0651:16. [Google Scholar] [CrossRef]
- Regi, M.; Redaelli, G.; Francia, P.; De Lauretis, M. ULF geomagnetic activity effects on tropospheric temperature, specific humidity, and cloud cover in Antarctica, during 2003–2010. J. Geophys. Res. Atmos. 2017, 122, 6488–6501. [Google Scholar] [CrossRef]
- Regi, M.; De Lauretis, M.; Francia, P.; Lepidi, L.; Piancatelli, A.; Urbini, S. The geomagnetic coast effect at two 80°S stations in Antarctica, observed in the ULF range. Ann. Geophys. 2018, 36, 193–203. [Google Scholar] [CrossRef] [Green Version]
- Chree, C. Some Phenomena of Sunspots and of Terrestrial Magnetism at Kew Observatory. Philos. Trans. R. Soc. Lond. Ser. 1913, 212, 75–116. [Google Scholar] [CrossRef]
- Campbell, W.H. Introduction to Geomagnetic Fields, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kivelson, M.G.; Russell, C.T. Introduction to Space Physics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Lockwood, M.; Sandholt, P.E.; Cowley, S.W.H.; Oguti, T. Interplanetary magnetic field control of dayside auroral activity and the transfer of momentum across the dayside magnetopause. Planet. Space Sci. 1989, 37, 1347–1365. [Google Scholar] [CrossRef]
- Shue, J.H.; Song, P.; Russell, C.T.; Steinberg, J.T.; Chao, J.K.; Zastenker, G.; Vaisberg, O.L.; Kokubun, S.; Singer, H.J.; Detman, T.R.; et al. Magnetopause location under extreme solar wind conditions. J. Geophys. Res. Space Phys. 1998, 103, 17691–17700. [Google Scholar] [CrossRef]
- Peredo, M.; Slavin, J.A.; Mazur, E.; Curtis, S.A. Three-dimensional position and shape of the bow shock and their variation with Alfvénic, sonic and magnetosonic Mach numbers and interplanetary magnetic field orientation. J. Geophys. Res. Space Phys. 1995, 100, 7907–7916. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Kan, J.R. Contribution of the partial ring current to the SYMH index during magnetic storms. J. Geophys. Res. Space Phys. 2011, 116, A11222:1–A11222:12. [Google Scholar] [CrossRef] [Green Version]
- Sugiura, M.; Kamei, T. Equatorial Dst Index 1957–1986; Number 40 in IAGA Bulletin; ISGI Publications Office: Paris, Italy, 1991. [Google Scholar]
- Francia, P.; Regi, M.; De Lauretis, M.; Villante, U.; Pilipenko, V.A. A case study of upstream wave transmission to the ground at polar and low latitudes. J. Geophys. Res. Space Phys. 2012, 117, A01210:1–A01210:14. [Google Scholar] [CrossRef]
- Regi, M.; Francia, P.; De Lauretis, M.; Glassmeier, K.H.; Villante, U. Coherent transmission of upstream waves to polar latitudes through magnetotail lobes. J. Geophys. Res. Space Phys. 2013, 118, 6955–6963. [Google Scholar] [CrossRef]
- Southwood, D.J. The hydromagnetic stability of the magnetospheric boundary. Planet. Space Sci. 1968, 16, 587–605. [Google Scholar] [CrossRef]
- Regi, M.; De Lauretis, M.; Francia, P. Pc5 geomagnetic fluctuations in response to solar wind excitation and their relationship with relativistic electron fluxes in the outer radiation belt. Earth Planets Space 2015, 67, 9:1–9:9. [Google Scholar] [CrossRef] [Green Version]
- Kepko, L. Observations of discrete, global magnetospheric oscillations directly driven by solar wind density variations. J. Geophys. Res. Space Phys. 2003, 108, 1257:1–1257:13. [Google Scholar] [CrossRef] [Green Version]
- Villante, U.; Francia, P.; Lepidi, S.; De Lauretis, M.; Pietropaolo, E.; Cafarella, L.; Meloni, A.; Lazarus, A.J.; Lepping, R.P.; Mariani, F. Geomagnetic field variations at low and high latitude during the 10–11 January 1997 magnetic cloud. Geophys. Res. Lett. 1998, 25, 2593–2596. [Google Scholar] [CrossRef] [Green Version]
- Ponomarenko, P.V.; Fraser, B.J.; Menk, F.W.; Ables, S.T.; Morris, R.J. Cusp-latitude Pc3 spectra: Band-limited and power-law components. Ann. Geophys. 2002, 20, 1539–1551. [Google Scholar] [CrossRef] [Green Version]
- De Lauretis, M.; Francia, P.; Regi, M.; Villante, U.; Piancatelli, A. Pc3 pulsations in the polar cap and at low latitude. J. Geophys. Res. Space Phys. 2010, 115, A11223:1–A11223:10. [Google Scholar] [CrossRef] [Green Version]
- Greenstadt, E.W.; McPherron, R.L.; Takahashi, K. Solar Wind Control of Daytime, Midperiod Geomagnetic Pulsations. J. Geomagn. Geoelectr. 1980, 32, SII89–SII110. [Google Scholar] [CrossRef] [Green Version]
- Russell, C.T.; Luhmann, J.G.; Odera, T.J.; Stuart, W.F. The rate of occurrence of dayside Pc 3,4 pulsations: The L-value dependence of the IMF cone angle effect. Geophys. Res. Lett. 1983, 10, 663–666. [Google Scholar] [CrossRef]
- Fowler, R.A.; Kotick, B.J.; Elliott, R.D. Polarization analysis of natural and artificially induced geomagnetic micropulsations. J. Geophys. Res. 1967, 72, 2871–2883. [Google Scholar] [CrossRef]
- Southwood, D. Some features of field line resonances in the magnetosphere. Planet. Space Sci. 1974, 22, 483–491. [Google Scholar] [CrossRef]
- Allan, W.; Knox, F. A dipole field model for axisymmetric alfvén waves with finite ionosphere conductivities. Planet. Space Sci. 1979, 27, 79–85. [Google Scholar] [CrossRef]
- Takahashi, K.; Vellante, M.; Del Corpo, A.; Claudepierre, S.G.; Kletzing, C.; Wygant, J.; Koga, K. Multiharmonic Toroidal Standing Alfvén Waves in the Midnight Sector Observed During a Geomagnetically Quiet Period. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027370:1–e2019JA027370:20. [Google Scholar] [CrossRef]
- Chi, P.J.; Engebretson, M.J.; Moldwin, M.B.; Russell, C.T.; Mann, I.R.; Samson, J.C.; López Cruz-Abeyro, J.A.; Yumoto, K.; Lee, D.H. Mid-continent Magnetoseismic Chain (McMAC): A Meridional Magnetometer Chain for Magnetospheric Sounding. In Proceedings of the Enviroment Modeling Workshop, Monterey, CA, USA, 1–3 June 2005; pp. 17–22. [Google Scholar]
- Mann, I.; Milling, D.; Rae, I.J.; Ozeke, L.; Kale, A.; Kale, Z.; Murphy, K.; Parent, A.; Usanova, M.; Pahud, D.; et al. The upgraded CARISMA magnetometer array in the THEMIS era. Space Sci. Rev. 2008, 141, 413–451. [Google Scholar] [CrossRef]
- Lichtenberger, J.; Clilverd, M.A.; Heilig, B.; Vellante, M.; Manninen, J.; Rodger, C.J.; Collier, A.B.; Jørgensen, A.M.; Reda, J.; Holzworth, R.H.; et al. The plasmasphere during a space weather event: First results from the PLASMON project. J. Space Weather Space Clim. 2013, 3, A23:1–A23:13. [Google Scholar] [CrossRef] [Green Version]
- Singer, H.; Southwood, D.; Walker, R.; Kivelson, M. Alfvén wave resonances in a realistic magnetospheric magnetic field geometry. J. Geophys. Res. Space Phys. 1981, 86, 4589–4596. [Google Scholar] [CrossRef] [Green Version]
- Baransky, L.; Borovkov, J.; Gokhberg, M.; Krylov, S.; Troitskaya, V. High resolution method of direct measurement of the magnetic field lines’ eigen frequencies. Planet. Space Sci. 1985, 33, 1369–1374. [Google Scholar] [CrossRef]
- Waters, C.L.; Menk, F.W.; Fraser, B.J. The resonance structure of low latitude Pc3 geomagnetic pulsations. Geophys. Res. Lett. 1991, 18, 2293–2296. [Google Scholar] [CrossRef] [Green Version]
- Kale, Z.C.; Mann, I.R.; Waters, C.L.; Goldstein, J.; Menk, F.W.; Ozeke, L.G. Ground magnetometer observation of a cross-phase reversal at a steep plasmapause. J. Geophys. Res. Space Phys. 2007, 112, A10222:1–A10222:9. [Google Scholar] [CrossRef] [Green Version]
- Menk, F.W.; Waters, C.L.; Fraser, B.J. Field line resonances and waveguide modes at low latitudes: 1. Observations. J. Geophys. Res. Space Phys. 2000, 105, 7747–7761. [Google Scholar] [CrossRef]
- Kawano, H.; Yumoto, K.; Pilipenko, V.A.; Tanaka, Y.M.; Takasaki, S.; Iizima, M.; Seto, M. Using two ground stations to identify magnetospheric field line eigenfrequency as a continuous function of ground latitude. J. Geophys. Res. Space Phys. 2002, 107, SMP25-1–SMP25-12. [Google Scholar] [CrossRef]
- Chi, P.J.; Engebretson, M.J.; Moldwin, M.B.; Russell, C.T.; Mann, I.R.; Hairston, M.R.; Reno, M.; Goldstein, J.; Winkler, L.I.; Cruz-Abeyro, J.L.; et al. Sounding of the plasmasphere by Mid-continent MAgnetoseismic Chain (McMAC) magnetometers. J. Geophys. Res. Space Phys. 2013, 118, 3077–3086. [Google Scholar] [CrossRef]
- Del Corpo, A.; Vellante, M.; Heilig, B.; Pietropaolo, E.; Reda, J.; Lichtenberger, J. Observing the cold plasma in the Earth’s magnetosphere with the EMMA network. Ann. Geophys. 2019, 62, GM447:1–GM447:19. [Google Scholar] [CrossRef]
- Chi, P.J.; Russell, C.T. An interpretation of the cross-phase spectrum of geomagnetic pulsations by the field line resonance theory. Geophys. Res. Lett. 1998, 25, 4445–4448. [Google Scholar] [CrossRef]
- Del Corpo, A.; Vellante, M.; Heilig, B.; Pietropaolo, E.; Reda, J.; Lichtenberger, J. An Empirical Model for the Dayside Magnetospheric Plasma Mass Density Derived From EMMA Magnetometer Network Observations. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027381:1–e2019JA027381:19. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Maute, A. Sq and EEJ—A review on the daily variation of the geomagnetic field caused by ionospheric dynamo currents. Space Sci. Rev. 2017, 206, 299–405. [Google Scholar] [CrossRef] [Green Version]
- Parkinson, W.D.; Jones, F.W. The geomagnetic coast effect. Rev. Geophys. 1979, 17, 1999–2015. [Google Scholar] [CrossRef]
- Hitchman, A.P.; Milligan, P.R.; Lilley, F.T.; White, A.; Heinson, G.S. The total-field geomagnetic coast effect: The CICADA97 line from deep Tasman Sea to inland New South Wales. Explor. Geophys. 2000, 31, 52–57. [Google Scholar] [CrossRef] [Green Version]
- Borovsky, J.E.; Denton, M.H. Differences between CME-driven storms and CIR-driven storms. J. Geophys. Res. 2006, 111, A07S08:1–A07S08:17. [Google Scholar] [CrossRef] [Green Version]
- Pulkkinen, A.; Lindahl, S.; Viljanen, A.; Pirjola, R. Geomagnetic storm of 29–31 October 2003: Geomagnetically induced currents and their relation to problems in the Swedish high-voltage power transmission system. Space Weather 2005, 3, S08C03:1–S08C03:19. [Google Scholar] [CrossRef]
- Tontini, F.C.; Stefanelli, P.; Giori, I.; Faggioni, O.; Carmisciano, C. The revised aeromagnetic anomaly map of Italy. Ann. Geophys. 2009, 47. [Google Scholar] [CrossRef]
- Green, A.W.; Worthington, E.W.; Baransky, L.N.; Fedorov, E.N.; Kurneva, N.A.; Pilipenko, V.A.; Shvetzov, D.N.; Bektemirov, A.A.; Philipov, G.V. Alfven field line resonances at low latitudes (L = 1.5). J. Geophys. Res. Space Phys. 1993, 98, 15693–15699. [Google Scholar] [CrossRef]
- Vellante, M.; Förster, M.; Villante, U.; Zhang, T.L.; Magnes, W. Solar activity dependence of geomagnetic field line resonance frequencies at low latitudes. J. Geophys. Res. Space Phys. 2007, 112, A02205:1–A02205:14. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, K.; Denton, R.E.; Anderson, R.R.; Hughes, W.J. Frequencies of standing Alfvén wave harmonics and their implication for plasma mass distribution along geomagnetic field lines: Statistical analysis of CRRES data. J. Geophys. Res. Space Phys. 2004, 109, A08202:1–A08202:15. [Google Scholar] [CrossRef] [Green Version]
- Vellante, M.; Förster, M. Inference of the magnetospheric plasma mass density from field line resonances: A test using a plasmasphere model. J. Geophys. Res. Space Phys. 2006, 111, A11204:1–A11204:13. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).