Joint Geoeffectiveness and Arrival Time Prediction of CMEs by a Unified Deep Learning Framework
Abstract
1. Introduction
- (1)
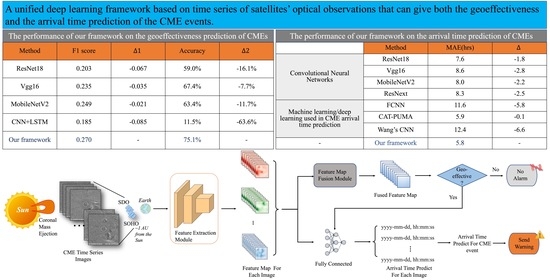
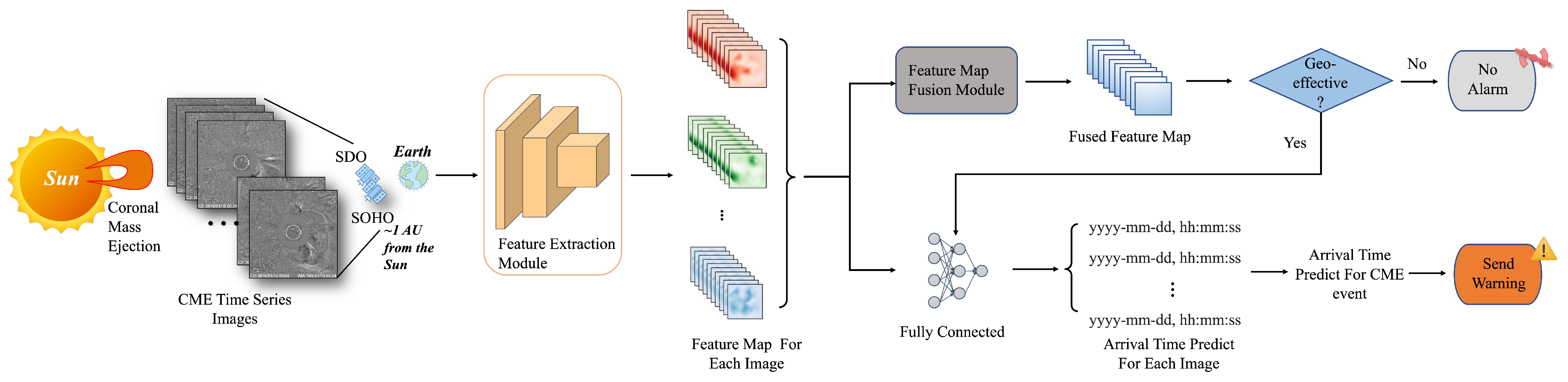
- It is the first time that making geoeffectiveness and arrival time predictions of CMEs in a unified deep learning framework and forming an end-to-end prediction. Once we get the observation images, we can immediately get the prediction result without selecting features manually or professional knowledge.
- (2)
- For the geoeffectiveness prediction of CMEs, we propose a deep residual network embedded with the attention mechanism and the feature map fusion module. Based on those, we can effectively extract key regional features and fuse the feature from each image.
- (3)
- For the arrival time prediction of geoeffective CMEs, we propose a data expansion method to increase the scale of data and deep residual regression network to capture the feature of the observation image. Meanwhile, the cost-sensitive regression loss function is proposed to allow the network focus more attention on hard predicting samples.
2. Methods
2.1. Geoeffectiveness Prediction of CMEs
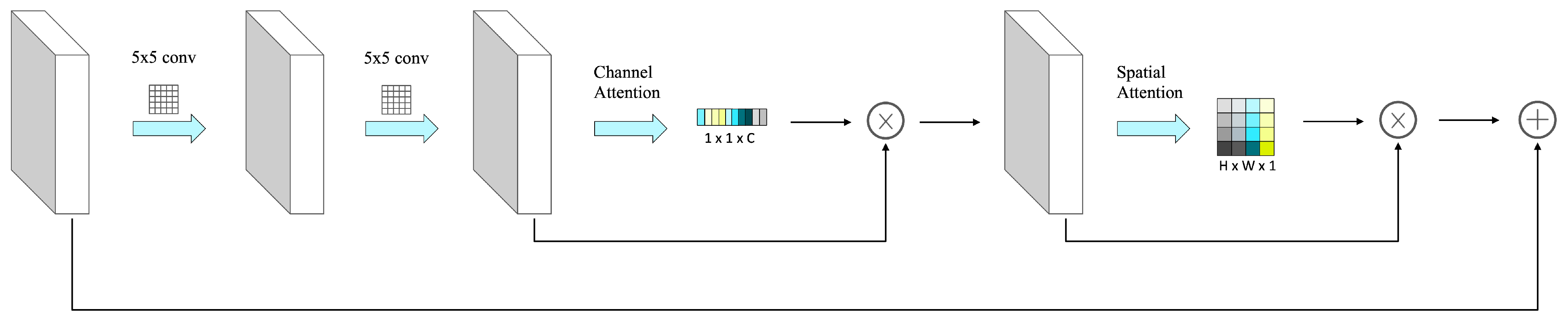
2.1.1. Deep Residual Network Embedded with the Attention Mechanism
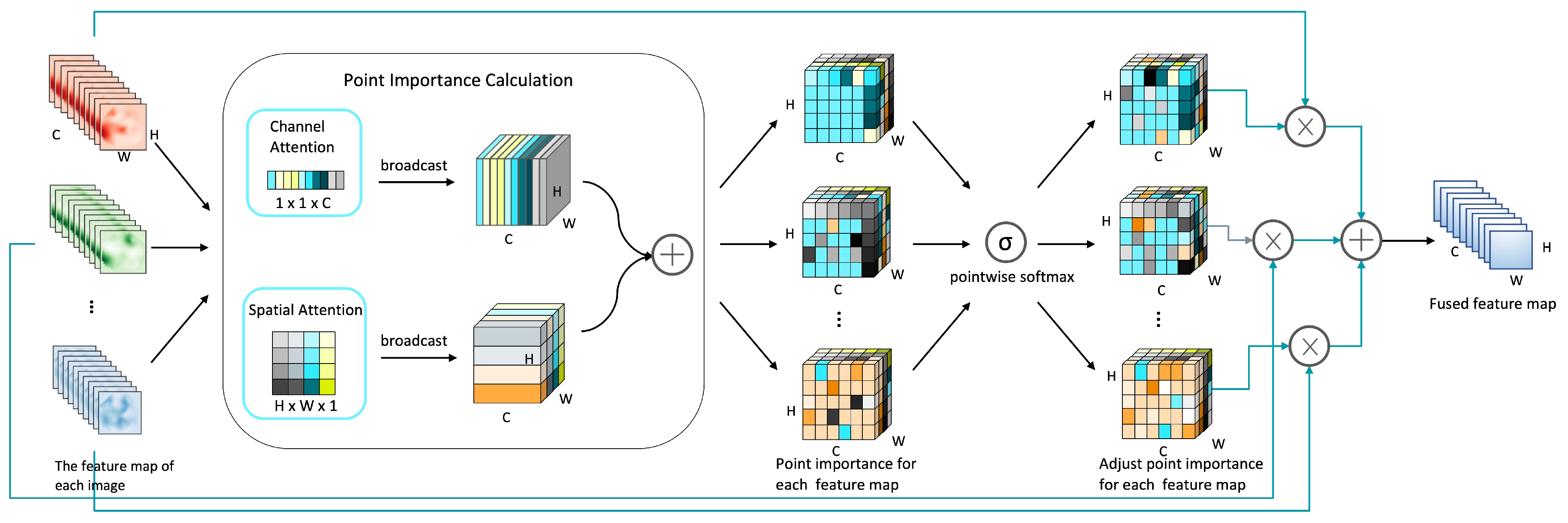
2.1.2. Feature Map Fusion Module
- Calculate the importance of each point in the feature map based on the attention mechanism. The module attention mechanism can focus limited attention on important regions. Through the above-mentioned channel attention module and spatial attention module, the feature map attention weights of the different channels axes and spatial axes are obtained, then the two attention weights are combined by adding to obtain the each point importance of the feature map.
- Adjust the point importance of each feature map in combination with the mutual influence between the time series feature maps. If there are N feature maps, for each point coordinate of the ith feature map, it will adjust its weight through the weight of the same position in other feature maps as follows:where represents the importance of the point whose coordinates of the j feature map is . Here, assuming that the shape of the feature map is , then , , .
- Fuse all feature map weights and point importances into one feature map. We multiply the point importance of each feature map with the original feature map weights to obtain the contribution of each feature map in the final fused feature map, and add the contribution of each feature map to get a fused feature map.
2.2. Arrival Time Prediction for Geoeffective CMEs
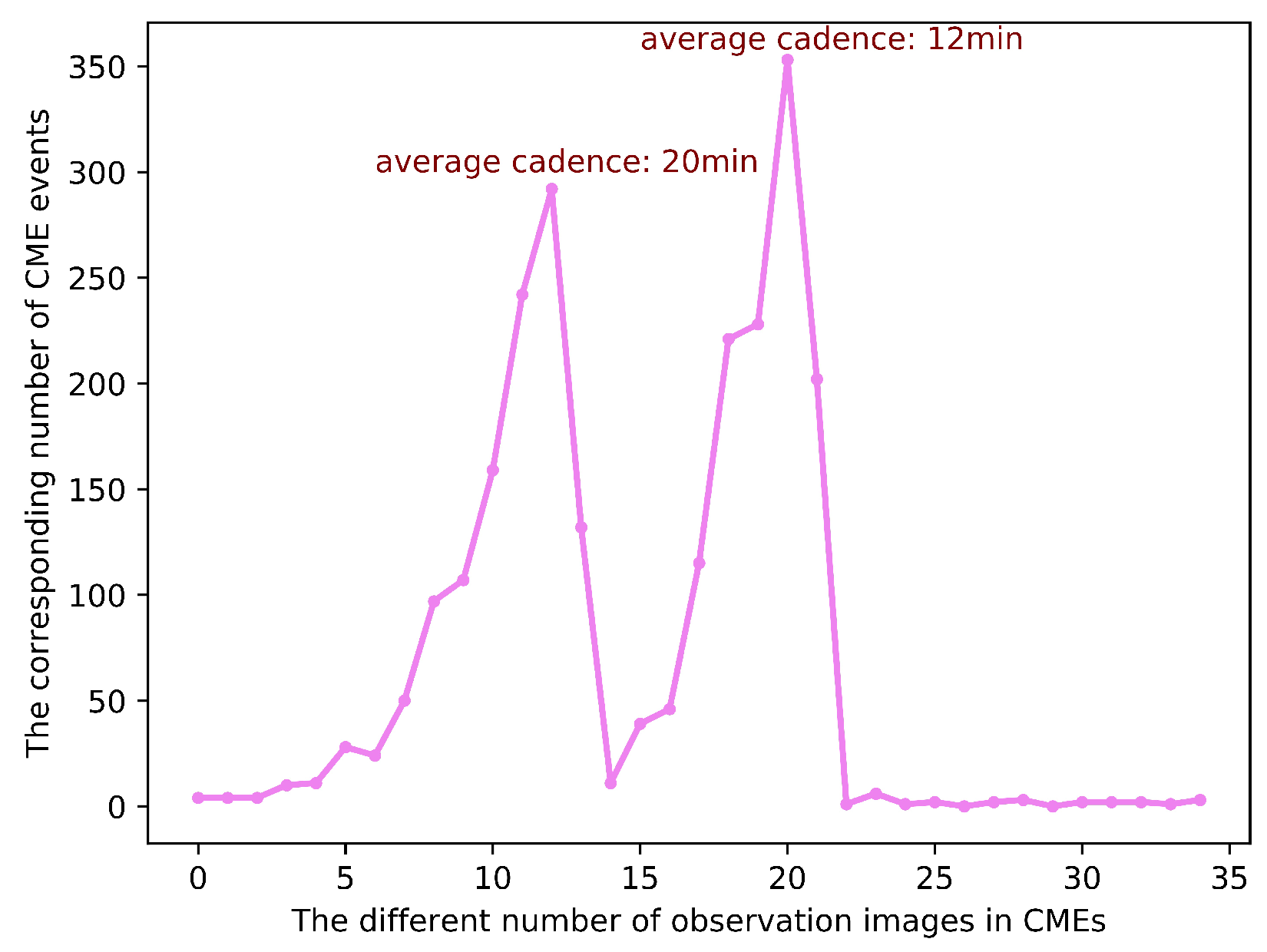
2.2.1. Data Expansion Based on Sample Split
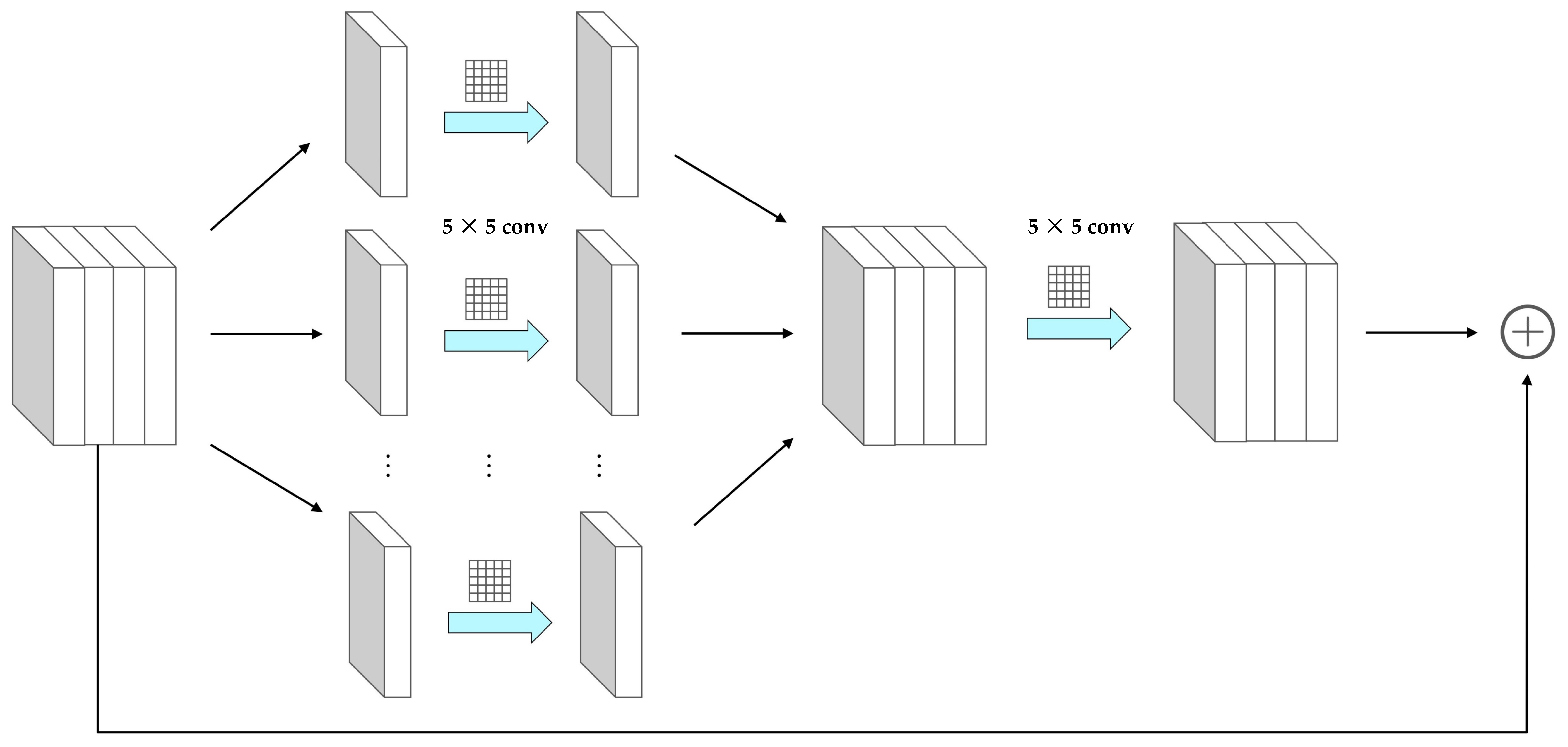
2.2.2. Deep Residual Regression Network Based on Group Convolution
2.2.3. Cost-Sensitive Regression Loss Function
3. Experiments
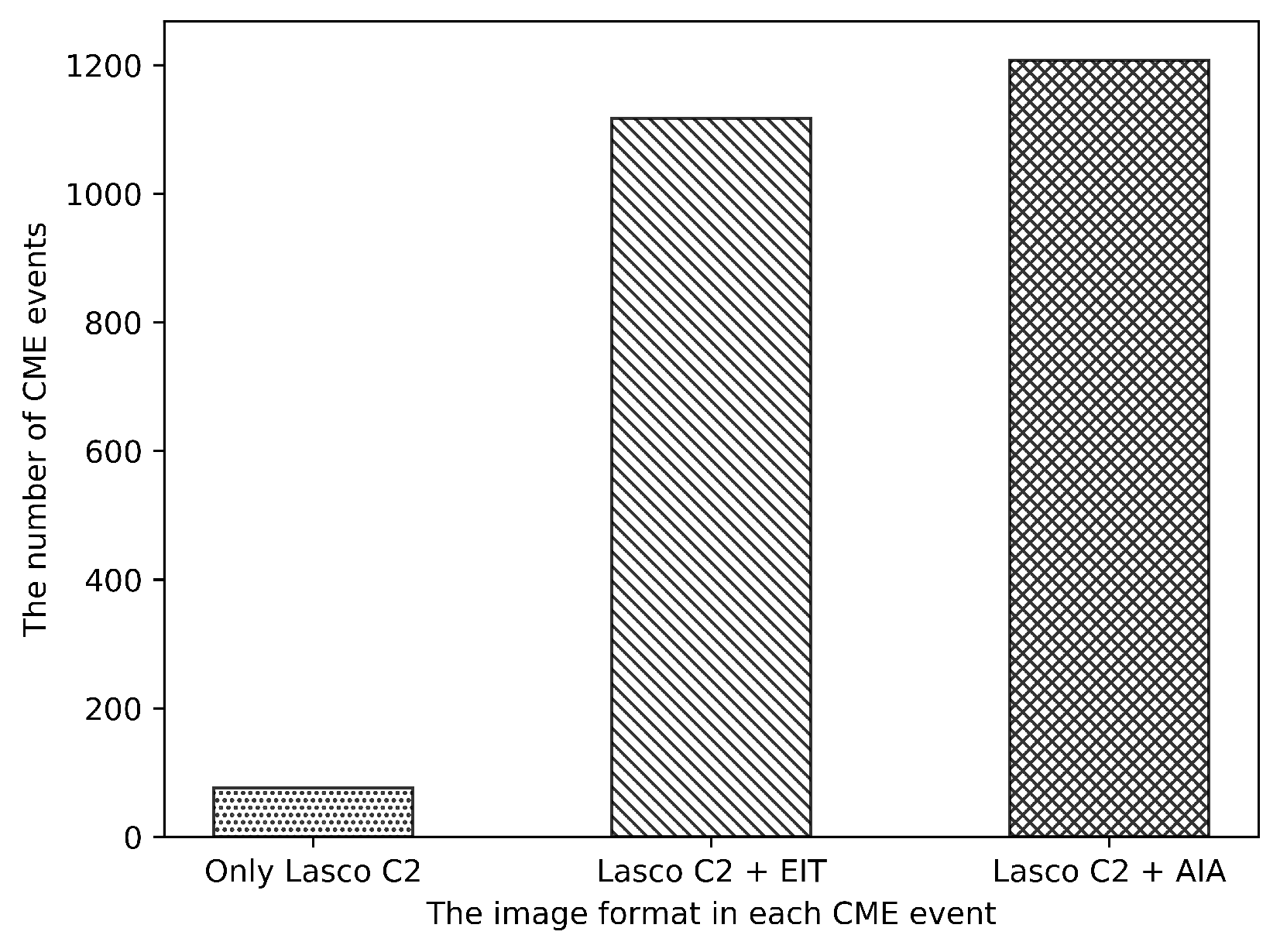
3.1. Dataset
3.2. Experimental Setting
4. Results
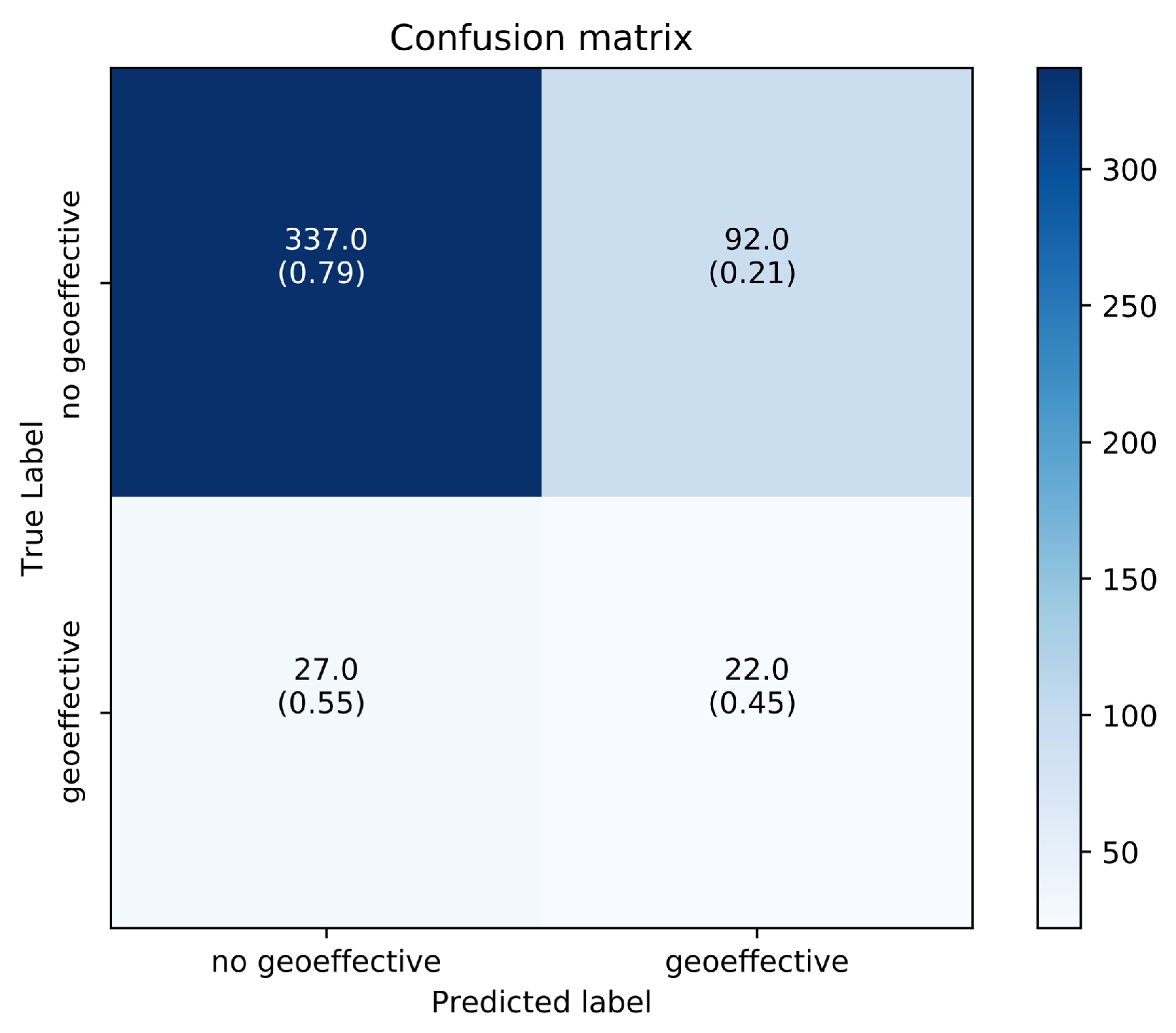
4.1. Results on the Geoeffectiveness Prediction of CMEs
4.2. Results on the Arrival Time Prediction for Geoeffective CMEs
5. Discussion
- This is the first time that making geoeffectiveness and arrival time prediction of CMEs in a unified deep learning framework.
- This is the first time that the CNN method is applied to geoeffectiveness prediction of CMEs.
- The only input of the deep learning framework is the time series images from synchronized solar white-light and EUV observation images that are directly observed.
- Once we get the observation images, we can immediately get the prediction result with no requirement of manually feature selection and professional knowledge.
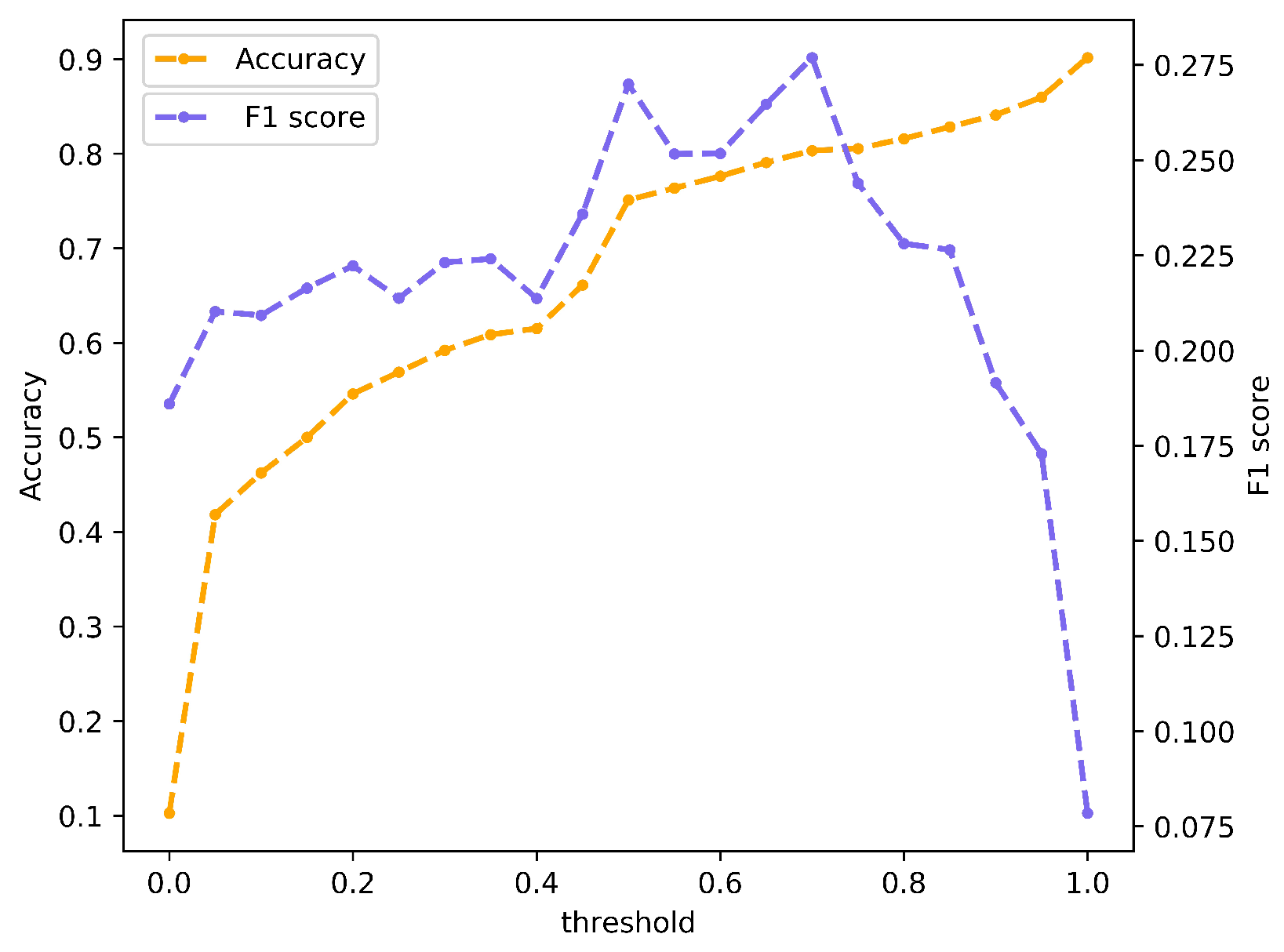
5.1. Discussion on the Prediction of Geoeffectiveness
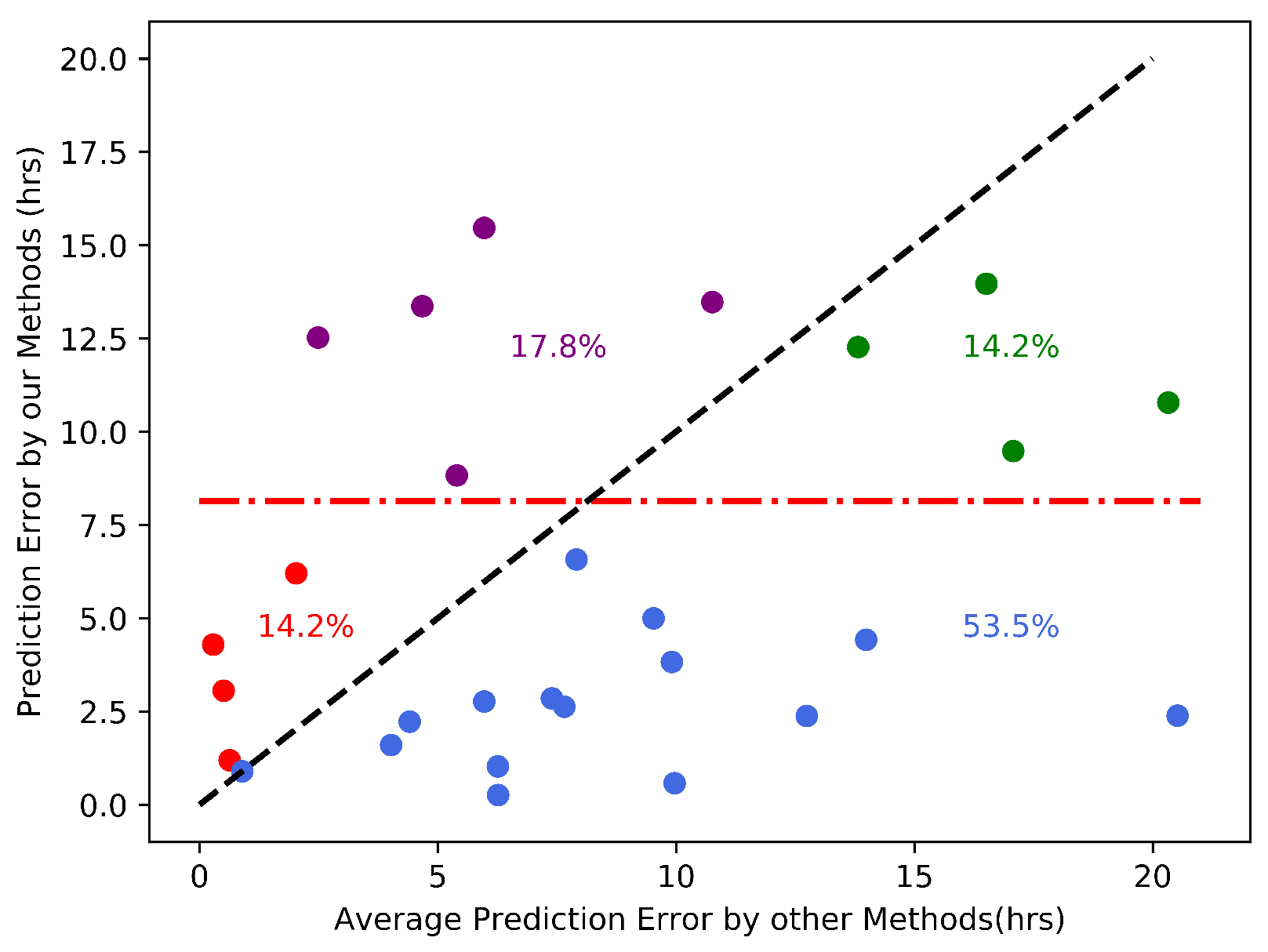
5.2. Discussion on the Arrival Time Prediction for Geoeffective CMEs
5.3. Applicability of the Proposed Framework in the Feature
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kataoka, R. Probability of occurrence of extreme magnetic storms. Space Weather 2013, 11, 214–218. [Google Scholar] [CrossRef]
- Gonzalez, W.D.; Tsurutani, B.T.; De Gonzalez, A.L.C. Interplanetary origin of geomagnetic storms. Space Sci. Rev. 1999, 88, 529–562. [Google Scholar] [CrossRef]
- Eastwood, J.; Biffis, E.; Hapgood, M.; Green, L.; Bisi, M.; Bentley, R.; Wicks, R.; McKinnell, L.A.; Gibbs, M.; Burnett, C. The economic impact of space weather: Where do we stand? Risk Anal. 2017, 37, 206–218. [Google Scholar] [CrossRef] [PubMed]
- Domingo, V.; Fleck, B.; Poland, A. SOHO: The solar and heliospheric observatory. Space Sci. Rev. 1995, 72, 81–84. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Mäkelä, P.; Xie, H.; Yashiro, S. Testing the empirical shock arrival model using quadrature observations. Space Weather 2013, 11, 661–669. [Google Scholar] [CrossRef]
- Xie, H.; Ofman, L.; Lawrence, G. Cone model for halo CMEs: Application to space weather forecasting. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- Davies, J.; Harrison, R.; Perry, C.; Möstl, C.; Lugaz, N.; Rollett, T.; Davis, C.; Crothers, S.; Temmer, M.; Eyles, C.; et al. A self-similar expansion model for use in solar wind transient propagation studies. Astrophys. J. 2012, 750, 23. [Google Scholar] [CrossRef]
- Howard, T.; Nandy, D.; Koepke, A. Kinematic properties of solar coronal mass ejections: Correction for projection effects in spacecraft coronagraph measurements. J. Geophys. Res. Space Phys. 2008, 113, A01104. [Google Scholar] [CrossRef]
- Kaiser, M.L.; Kucera, T.; Davila, J.; Cyr, O.S.; Guhathakurta, M.; Christian, E. The STEREO mission: An introduction. Space Sci. Rev. 2008, 136, 5–16. [Google Scholar] [CrossRef]
- Howard, R.A.; Moses, J.; Vourlidas, A.; Newmark, J.; Socker, D.G.; Plunkett, S.P.; Korendyke, C.M.; Cook, J.; Hurley, A.; Davila, J.; et al. Sun Earth connection coronal and heliospheric investigation (SECCHI). Space Sci. Rev. 2008, 136, 67–115. [Google Scholar] [CrossRef]
- Möstl, C.; Isavnin, A.; Boakes, P.; Kilpua, E.; Davies, J.; Harrison, R.; Barnes, D.; Krupar, V.; Eastwood, J.; Good, S.; et al. Modeling observations of solar coronal mass ejections with heliospheric imagers verified with the Heliophysics System Observatory. Space Weather 2017, 15, 955–970. [Google Scholar] [CrossRef]
- Vršnak, B.; Žic, T.; Vrbanec, D.; Temmer, M.; Rollett, T.; Möstl, C.; Veronig, A.; Čalogović, J.; Dumbović, M.; Lulić, S.; et al. Propagation of interplanetary coronal mass ejections: The drag-based model. Sol. Phys. 2013, 285, 295–315. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, X. A new prediction method for the arrival time of interplanetary shocks. Sol. Phys. 2006, 238, 167–186. [Google Scholar] [CrossRef]
- Corona-Romero, P.; Gonzalez-Esparza, J.; Aguilar-Rodriguez, E.; De-la Luz, V.; Mejia-Ambriz, J. Kinematics of ICMEs/shocks: Blast wave reconstruction using type-II emissions. Sol. Phys. 2015, 290, 2439–2454. [Google Scholar] [CrossRef][Green Version]
- Feng, X.; Zhou, Y.; Wu, S. A novel numerical implementation for solar wind modeling by the modified conservation element/solution element method. Astrophys. J. 2007, 655, 1110. [Google Scholar] [CrossRef]
- Shen, F.; Feng, X.; Wu, S.; Xiang, C. Three-dimensional MHD simulation of CMEs in three-dimensional background solar wind with the self-consistent structure on the source surface as input: Numerical simulation of the January 1997 Sun-Earth connection event. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Wold, A.M.; Mays, M.L.; Taktakishvili, A.; Jian, L.K.; Odstrcil, D.; MacNeice, P. Verification of real-time WSA- ENLIL+ Cone simulations of CME arrival-time at the CCMC from 2010 to 2016. J. Space Weather. Space Clim. 2018, 8, A17. [Google Scholar] [CrossRef]
- Tóth, G.; Sokolov, I.V.; Gombosi, T.I.; Chesney, D.R.; Clauer, C.R.; De Zeeuw, D.L.; Hansen, K.C.; Kane, K.J.; Manchester, W.B.; Oehmke, R.C.; et al. Space Weather Modeling Framework: A new tool for the space science community. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]
- Besliu-Ionescu, D.; Talpeanu, D.C.; Mierla, M.; Muntean, G.M. On the prediction of geoeffectiveness of CMEs during the ascending phase of SC24 using a logistic regression method. J. Atmos. Sol. Terr. Phys. 2019, 193, 105036. [Google Scholar] [CrossRef]
- Sudar, D.; Vršnak, B.; Dumbović, M. Predicting coronal mass ejections transit times to Earth with neural network. Mon. Not. R. Astron. Soc. 2015, 456, 1542–1548. [Google Scholar] [CrossRef]
- Liu, J.; Ye, Y.; Shen, C.; Wang, Y.; Erdélyi, R. A new tool for CME arrival time prediction using machine learning algorithms: CAT-PUMA. Astrophys. J. 2018, 855, 109. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Jiang, Y.; Erdélyi, R. CME Arrival Time Prediction Using Convolutional Neural Network. Astrophys. J. 2019, 881, 15. [Google Scholar] [CrossRef]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft coco: Common objects in context. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2014; pp. 740–755. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50× fewer parameters and <0.5 MB model size. arXiv 2016, arXiv:1602.07360. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. Mobilenets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 15–20 June 2019; pp. 6105–6114. [Google Scholar]
- Balduzzi, D.; Frean, M.; Leary, L.; Lewis, J.; Ma, K.W.D.; McWilliams, B. The shattered gradients problem: If resnets are the answer, then what is the question? In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 342–350. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted boltzmann machines. In Proceedings of the International Conference on Machine Learning, PMLR, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Roy, A.G.; Navab, N.; Wachinger, C. Concurrent spatial and channel ‘squeeze & excitation’ in fully convolutional networks. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 421–429. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Li, X.; Wang, W.; Hu, X.; Yang, J. Selective kernel networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 510–519. [Google Scholar]
- Yang, Q.L.Z.Y.B. SA-Net: Shuffle Attention for Deep Convolutional Neural Networks. arXiv 2021, arXiv:2102.00240. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Yashiro, S.; Michalek, G.; Stenborg, G.; Vourlidas, A.; Freeland, S.; Howard, R. The soho/lasco cme catalog. Earth Moon Planets 2009, 104, 295–313. [Google Scholar] [CrossRef]
- Richardson, I.G.; Cane, H.V. Near-Earth interplanetary coronal mass ejections during solar cycle 23 (1996–2009): Catalog and summary of properties. Sol. Phys. 2010, 264, 189–237. [Google Scholar] [CrossRef]
- Shen, C.; Wang, Y.; Pan, Z.; Zhang, M.; Ye, P.; Wang, S. Full halo coronal mass ejections: Do we need to correct the projection effect in terms of velocity? J. Geophys. Res. Space Phys. 2013, 118, 6858–6865. [Google Scholar] [CrossRef]
- Hess, P.; Zhang, J. A study of the Earth-affecting CMEs of Solar Cycle 24. Sol. Phys. 2017, 292, 1–20. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Jeni, L.A.; Cohn, J.F.; De La Torre, F. Facing imbalanced data–recommendations for the use of performance metrics. In Proceedings of the 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction, Geneva, Switzerland, 2–5 September 2013; pp. 245–251. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Qu, M.; Shih, F.Y.; Jing, J.; Wang, H. Automatic detection and classification of coronal mass ejections. Sol. Phys. 2006, 237, 419–431. [Google Scholar] [CrossRef]

| Layer Name | Layer | Output Size |
|---|---|---|
| Conv1 | , 64, stride 1 | |
| Max Pool | , max pool, stride 2 | |
| Conv2_x | ||
| Conv3_x | ||
| Conv4_x |
| Layer Name | Layer | Output Size |
|---|---|---|
| Conv1 | , 64, stride 1 | |
| Max Pool | , max pool, stride 2 | |
| Conv2_x | ||
| Conv3_x | ||
| Conv4_x | ||
| FC1 | FC, Dropout | |
| FC2 | FC |
| Method | F1 Score | Accuracy | ||
|---|---|---|---|---|
| ResNet18 | 0.203 | 59.0% | % | |
| Vgg16 | 0.235 | 67.4% | % | |
| MobileNetv2 | 0.249 | 63.4% | % | |
| CNN+LSTM | 0.185 | 11.5% | % | |
| Ours | 0.270 | - | 75.1% | - |
| Method | MAE (Hours) | ||
|---|---|---|---|
| Convolutional Neural Networks | ResNet18 | 7.6 | |
| Vgg16 | 8.6 | ||
| MobilenetV2 | 8.0 | ||
| ResNext | 8.3 | ||
| Machine learning/deep learning used in CME arrival time prediction | FCNN | 11.6 | |
| CAT-PUMA | 5.9 | ||
| Wang’s CNN | 12.4 | ||
| - | Ours | 5.8 | - |
| Loss | MAE (Hours) |
|---|---|
| L2 Loss | 6.4 |
| cost-sensitive regression loss with = 2 | 6.1 |
| cost-sensitive regression loss with = 3 | 5.8 |
| cost-sensitive regression loss with = 4 | 6.2 |
| cost-sensitive regression loss with = 4.5 | 6.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, H.; Zheng, Y.; Ye, Y.; Feng, X.; Liu, C.; Ma, H. Joint Geoeffectiveness and Arrival Time Prediction of CMEs by a Unified Deep Learning Framework. Remote Sens. 2021, 13, 1738. https://doi.org/10.3390/rs13091738
Fu H, Zheng Y, Ye Y, Feng X, Liu C, Ma H. Joint Geoeffectiveness and Arrival Time Prediction of CMEs by a Unified Deep Learning Framework. Remote Sensing. 2021; 13(9):1738. https://doi.org/10.3390/rs13091738
Chicago/Turabian StyleFu, Huiyuan, Yuchao Zheng, Yudong Ye, Xueshang Feng, Chaoxu Liu, and Huadong Ma. 2021. "Joint Geoeffectiveness and Arrival Time Prediction of CMEs by a Unified Deep Learning Framework" Remote Sensing 13, no. 9: 1738. https://doi.org/10.3390/rs13091738
APA StyleFu, H., Zheng, Y., Ye, Y., Feng, X., Liu, C., & Ma, H. (2021). Joint Geoeffectiveness and Arrival Time Prediction of CMEs by a Unified Deep Learning Framework. Remote Sensing, 13(9), 1738. https://doi.org/10.3390/rs13091738