Computation Approach for Quantitative Dielectric Constant from Time Sequential Data Observed by CYGNSS Satellites
Abstract
1. Introduction
2. Site Study and Database
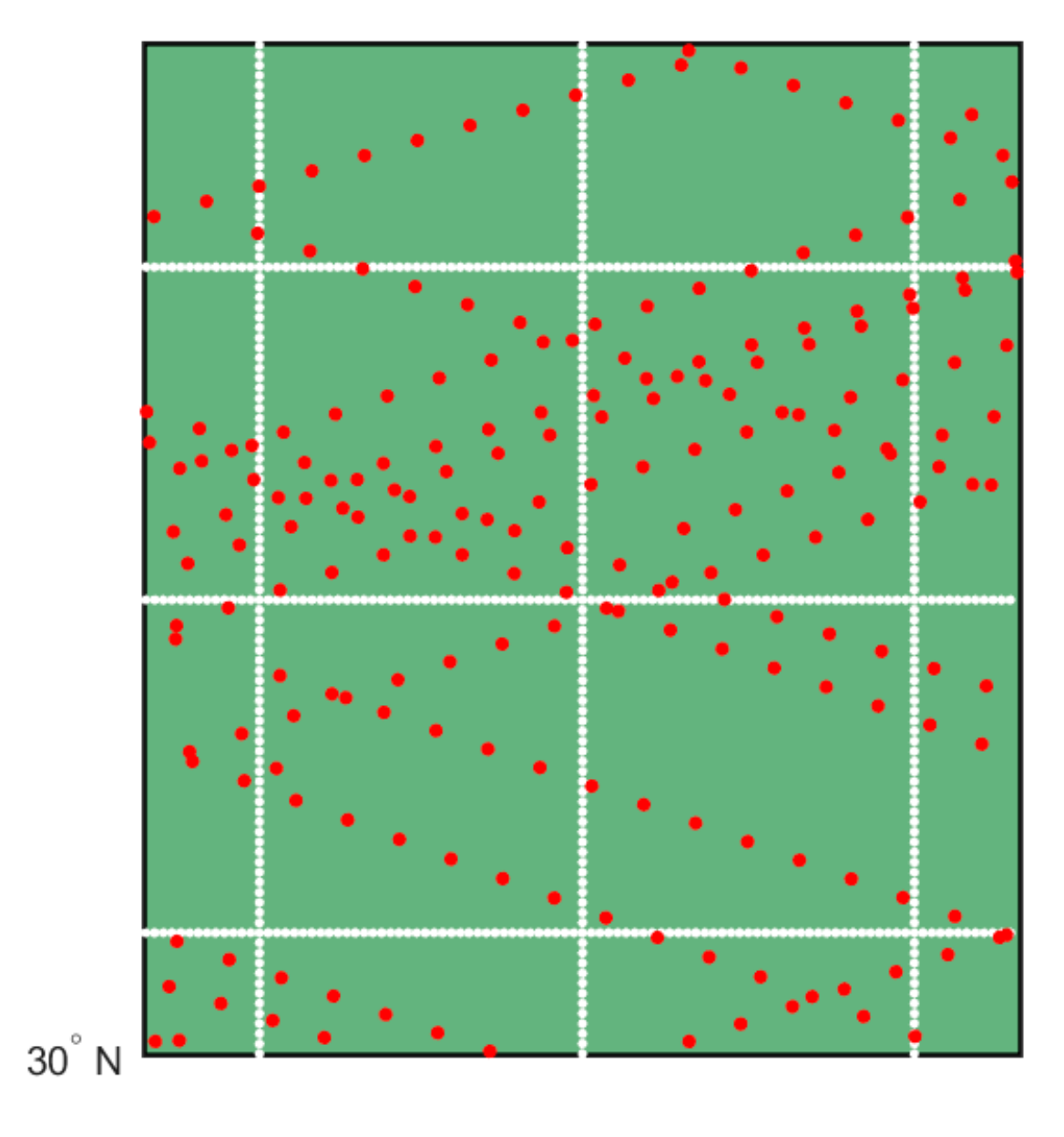
2.1. Site Study
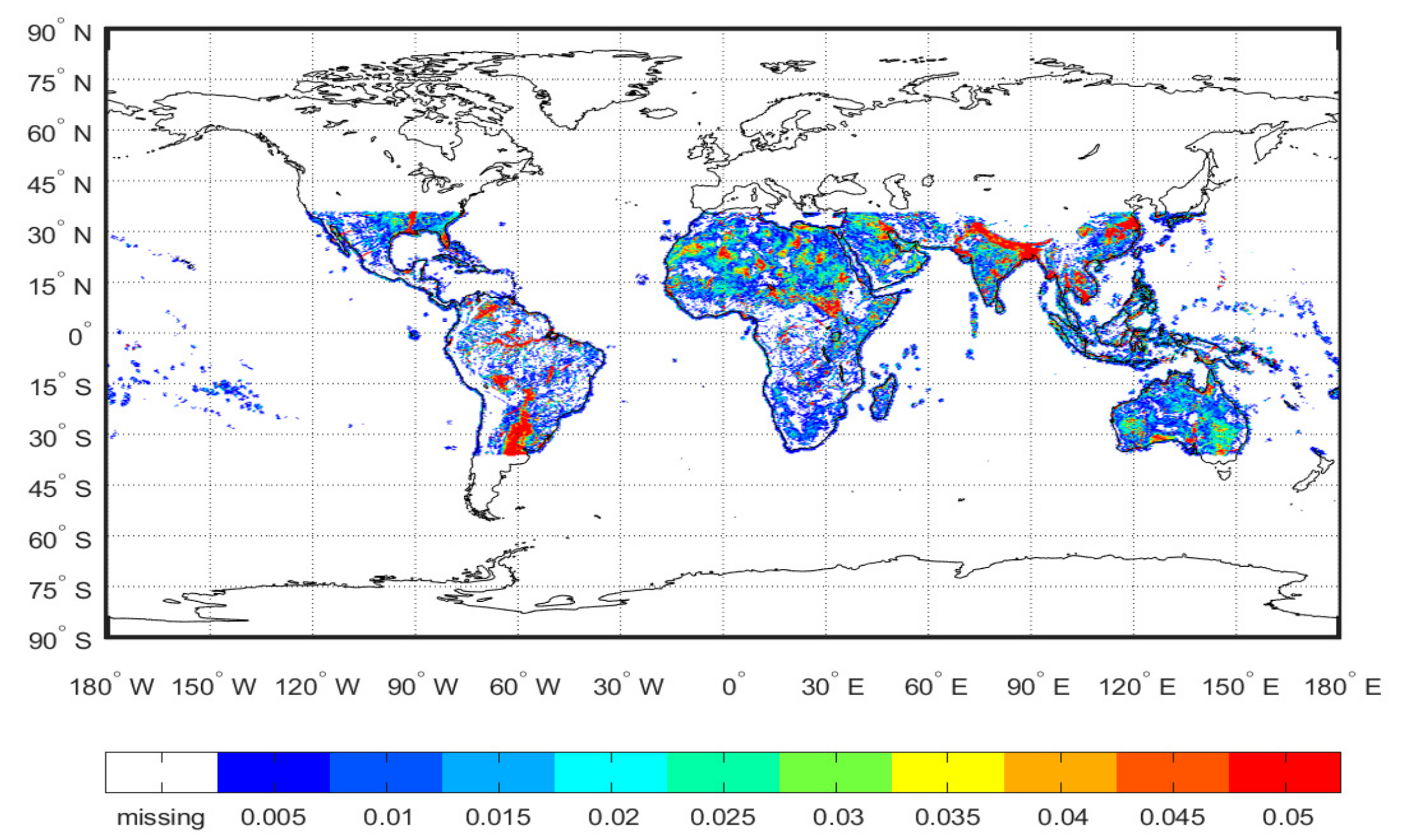
2.2. Data
3. Methodology
3.1. Analysis Method
3.2. EASE Grid 2.0
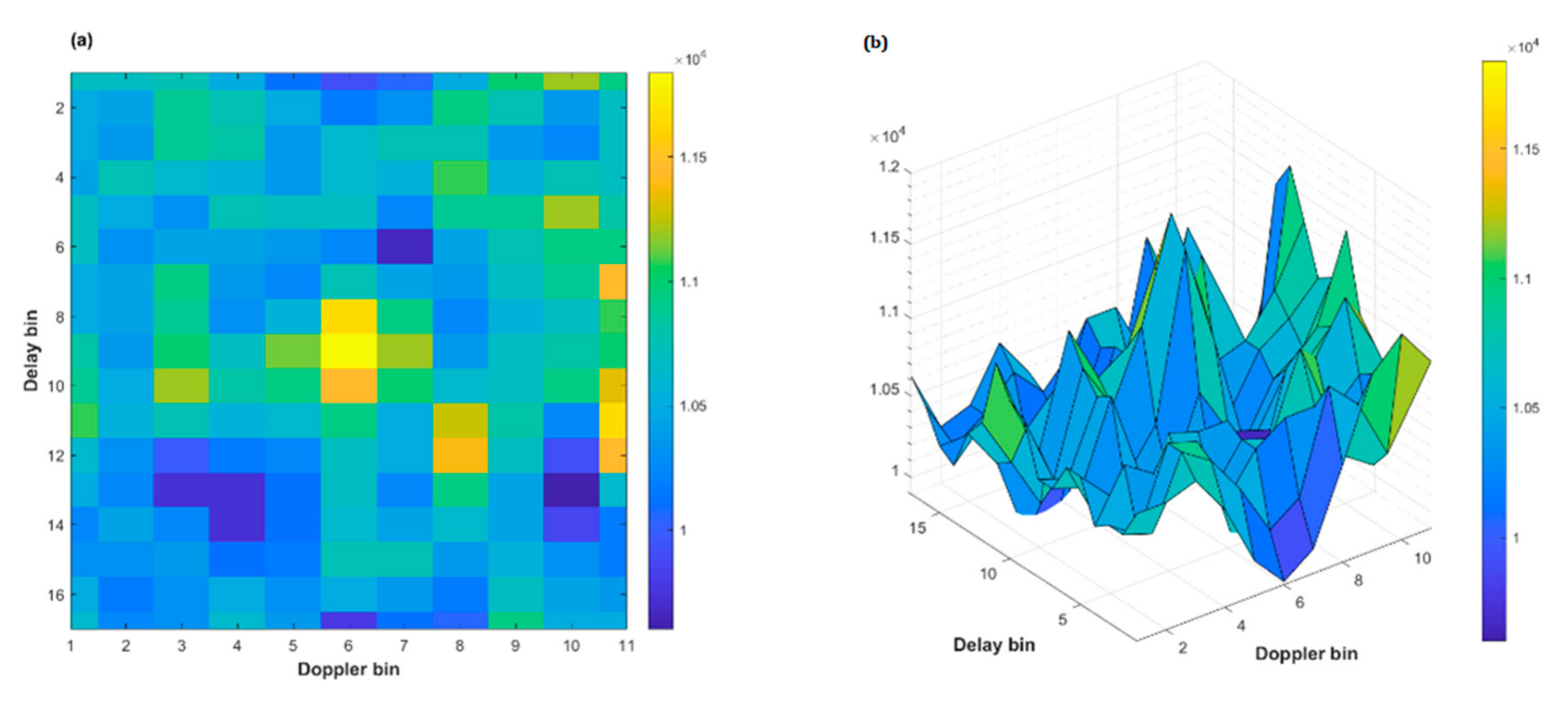
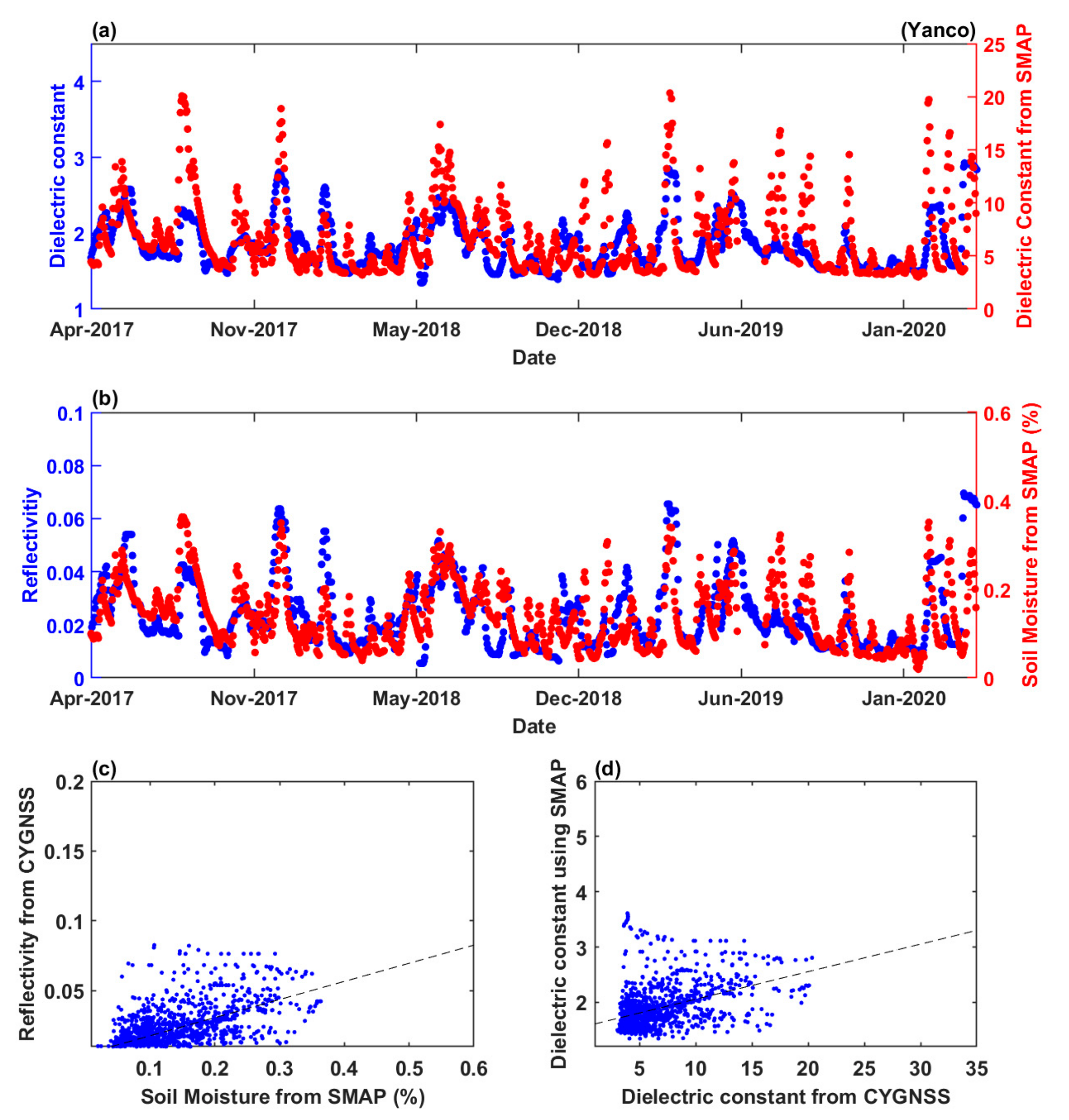
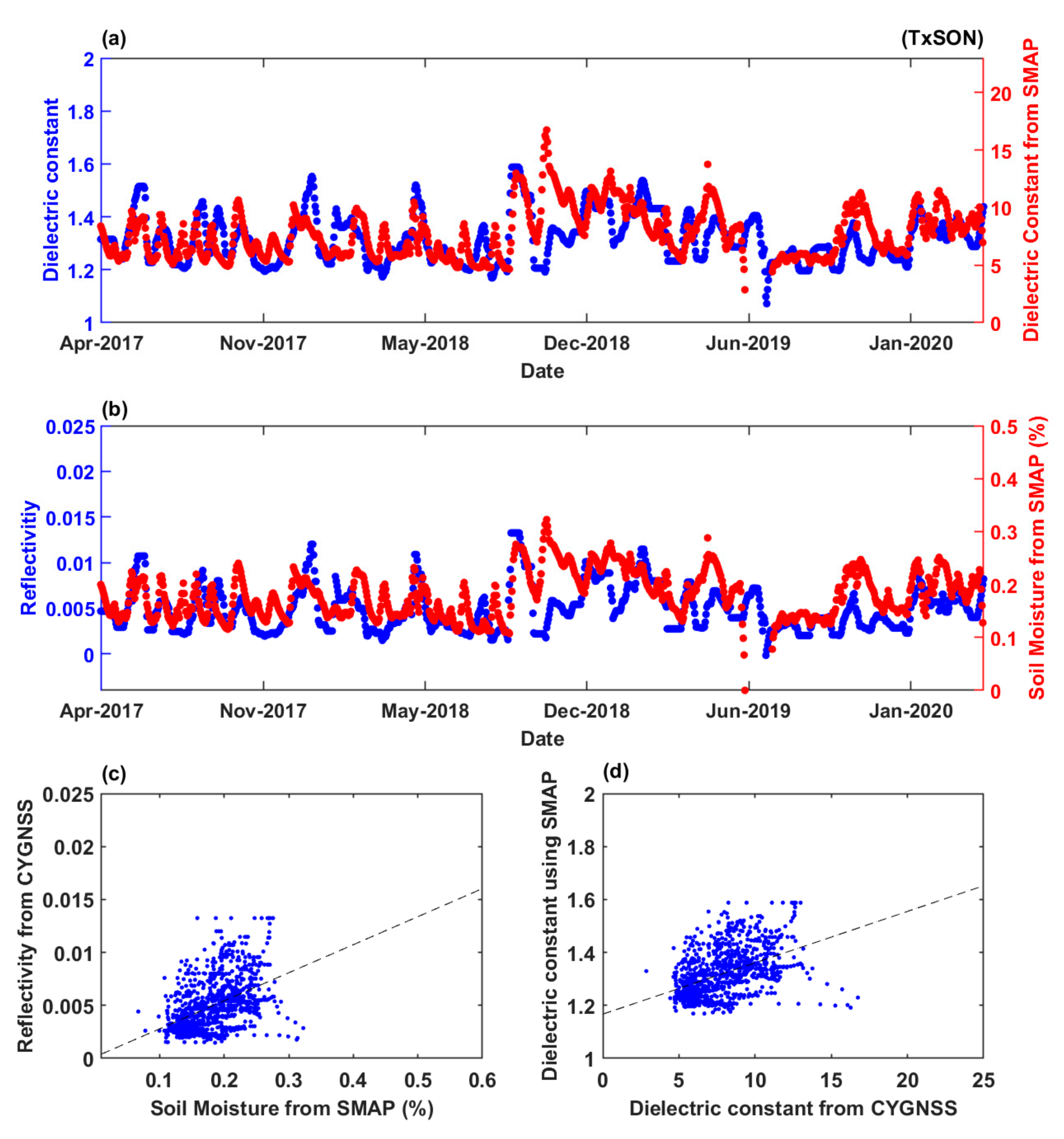
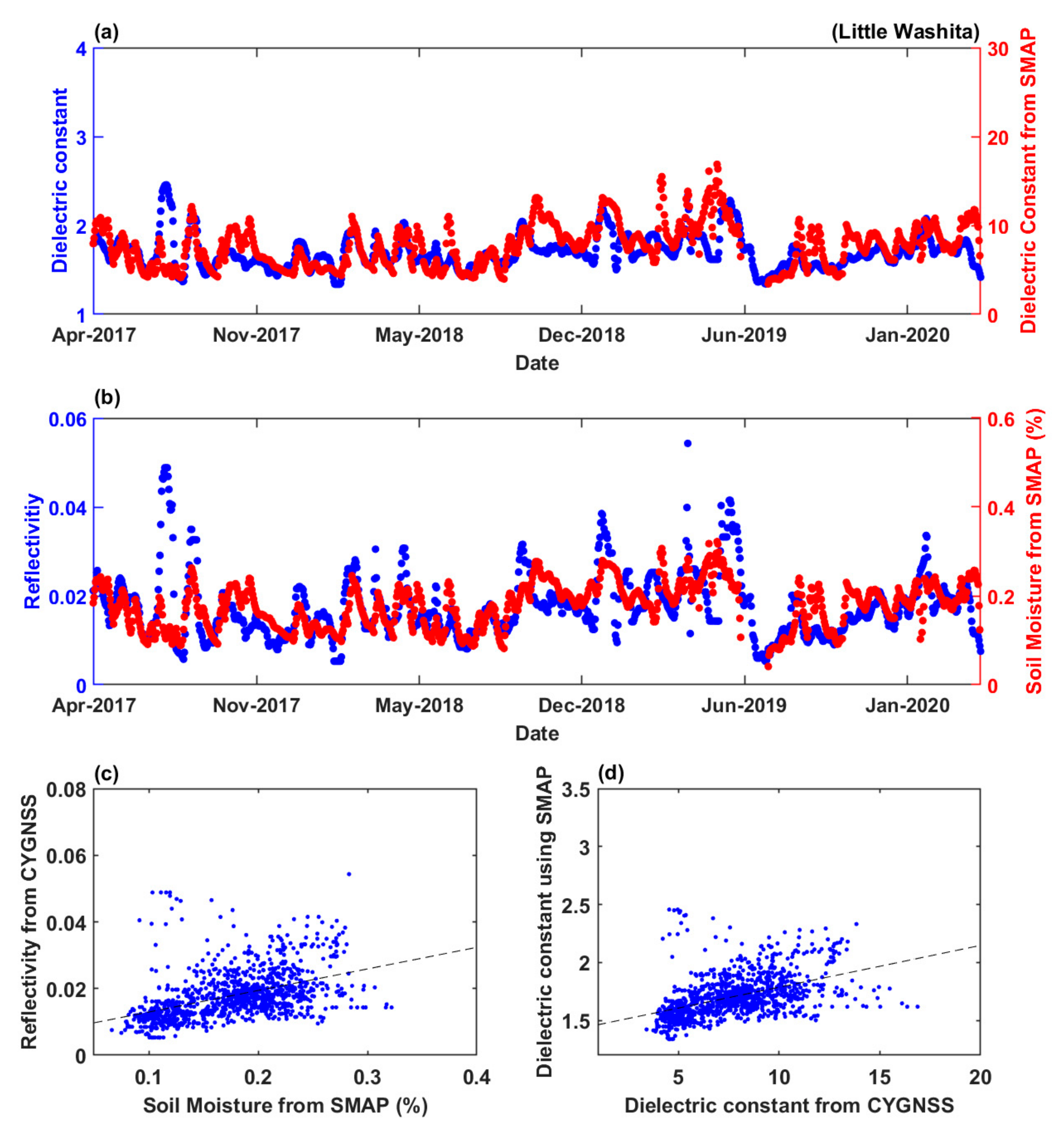
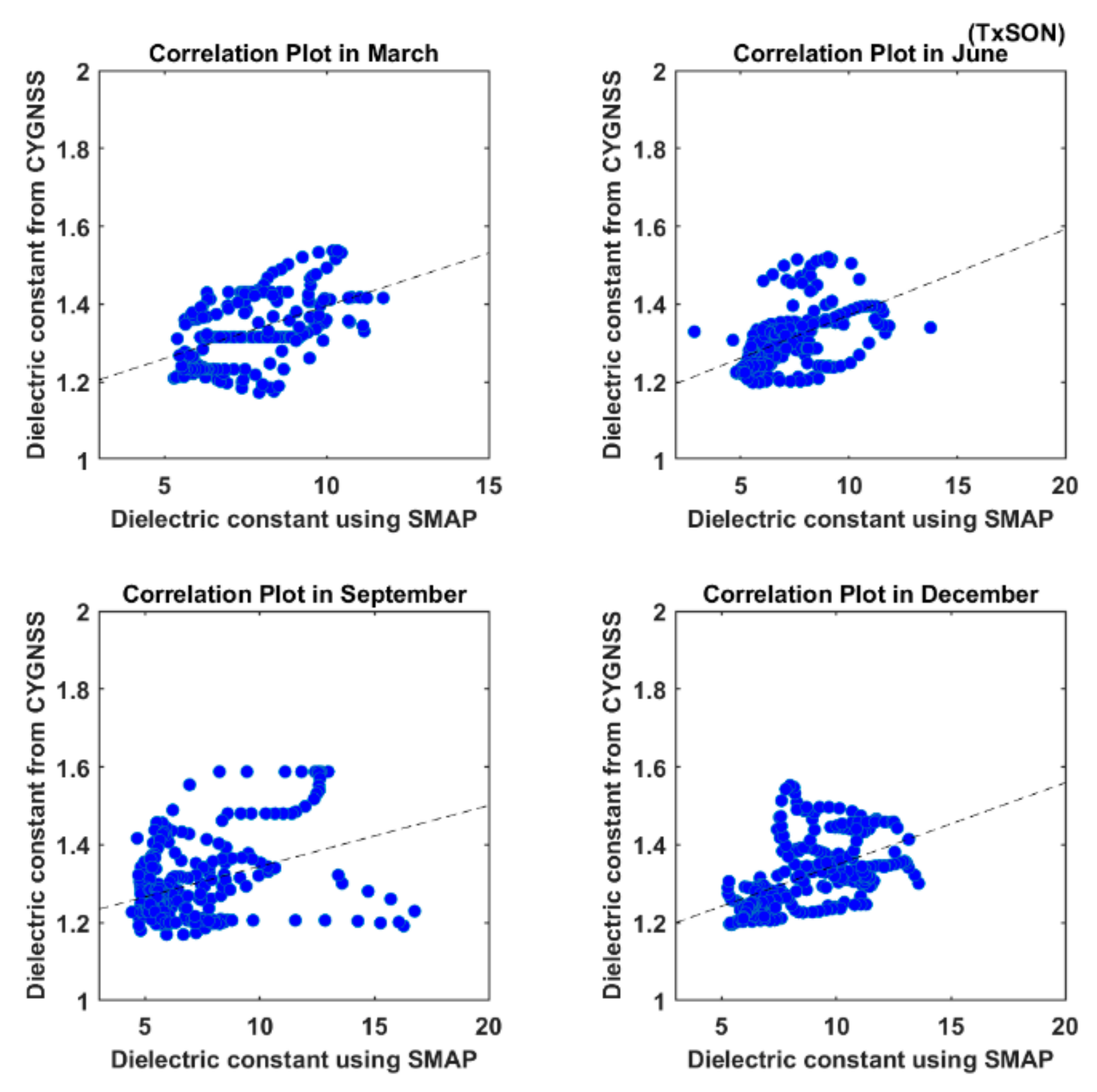
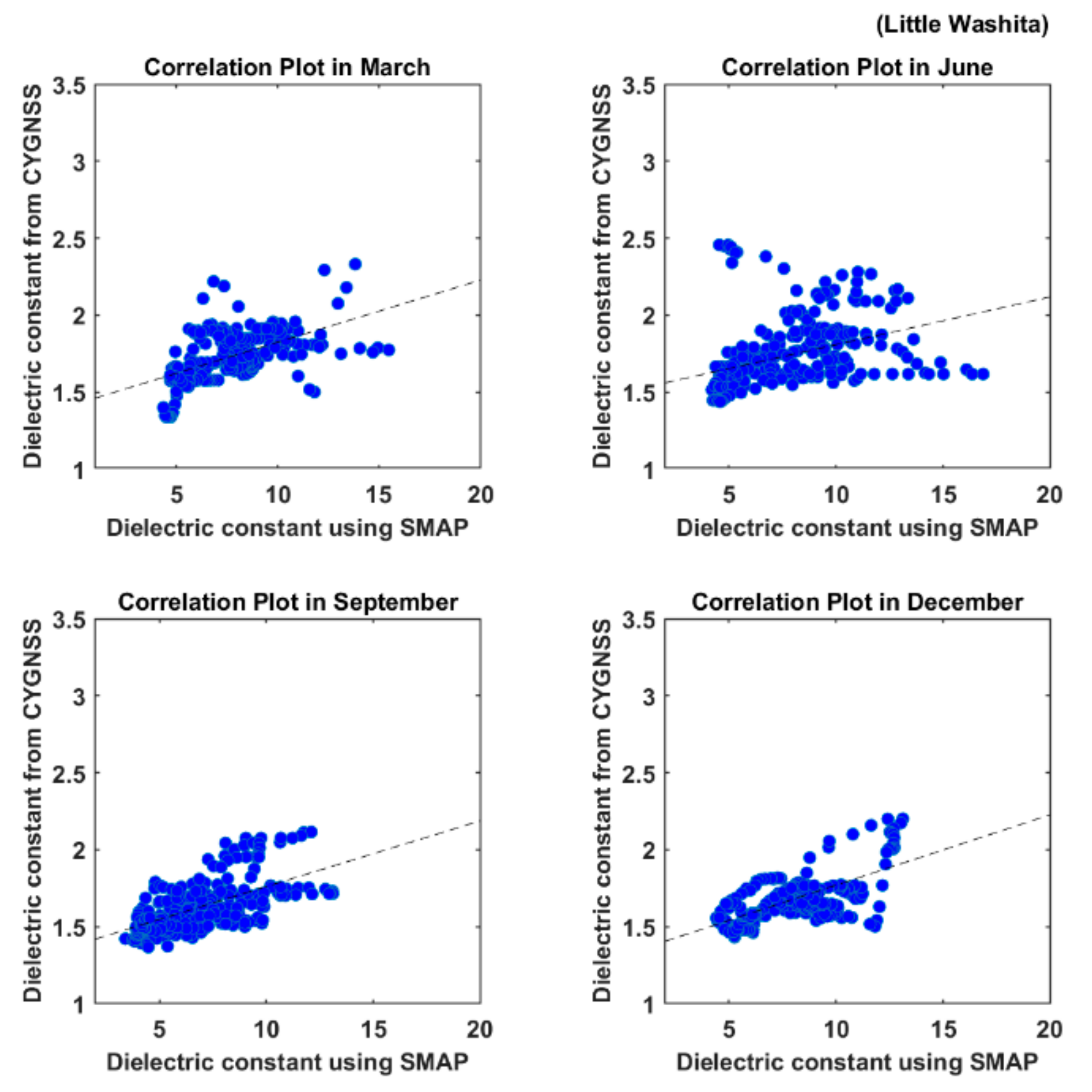
4. Results
4.1. Daily Time Variation of Dielectric Constant
4.2. Seasonal Variation at Various Locations
5. Discussion
- Vegetation type or land classification: the classification of land can be of concern due to the parameters that affect the calculation of dielectric constant when the reflectivity is transformed to the Fresnel reflection coefficient (Equation (3)). Therefore, an investigation, including vegetation type, is essential for improving the qualities of soil moisture or dielectric constant retrieval. Over the past few decades, there has been an attempt to classify land type by observing topography using satellite instruments, such as the International Geosphere–Biosphere Programme (IGBP) Land Classification. With comprehensive analysis regarding reflections over distinct land classifications, the results from GNSS-R will be similar to the reference instrument. NDVI or Freeze/thaw state will also be related to the dielectric constant, as referred to in [52]. Elaborated analysis for figuring out the characteristics of derived dielectric constant will be done in future research.
- Spatial resolution: in this research, the EASE grid v2.0 with 36 km × 36 km of resolution is applied to build two-dimensional images and to acquire information from assigned pixels according to specified locations. From the perspective of global images, the 36 km resolution is good enough to produce usable imagery. The land surface and other classifications, such as urban, cropland, or grassland, were included in the designated pixel. In other words, two specular points in the same pixel are possible for experiencing the reflection on different land classifications. Because the averaging of data over the same pixel has been implemented, the resulting dielectric constant estimates must contain an error. Increasing spatial resolution and investigating land classification is required to remove errors. However, the specific approach is demanding, because high spatial resolution can cause statistical errors for short periods of observations.
- Soil moisture model: a soil moisture model was applied to convert soil moisture from SMAP to the dielectric constant. In this conversion, the semi-empirical model is used [29]; although, the semi-empirical model was developed based on the in-situ measurements of microwave frequency waves rather than a remote sensing technique. Because the semi-empirical soil moisture model is not specialized to GNSS-R, it consistently contains unexpected errors in conversion. Even though it was established to deal with remote sensing observation results, it still required particular soil moisture to produce coincident results while using GNSS-R.
6. Conclusions
7. Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lakshmi, V. Remote Sensing of Soil Moisture. ISRN Soil. Sci. 2013, 2013, 1–33. [Google Scholar] [CrossRef]
- Hollinger, J.P.; Peirce, J.L.; Poe, G.A. SSM/I Instrument Evaluation. IEEE Trans. Geosci. Remote Sens. 1990, 28, 781–790. [Google Scholar] [CrossRef]
- Paloscia, S.; Macelloni, G.; Santi, E.; Koike, T. A Multifrequency Algorithm for the Retrieval of Soil Moisture on a Large Scale Using Microwave Data from SMMR and SSM/I Satellites. IEEE Trans. Geosci. Remote Sens. 2019, 39, 1655–1661. [Google Scholar] [CrossRef]
- Guha, A.; Lakshmi, V. Sensitivity, Spatial Heterogeneity, and Scaling of C-Band Microwave Brightness Temperatures for Land Hydrology Studies. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2626–2635. [Google Scholar] [CrossRef]
- Guha, A.; Lakshmi, V. Use of the Scanning Multichannel Microwave Radiometer (SMMR) to Retrieve Soil Moisture and Surface Temperature over the Central United States. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1482–1494. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Dubois, P.C.; van Zyl, J. Radar Mapping of Surface Soil Moisture. J. Hydrol. 1996, 184, 57–84. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Kustas, W.P.; Ritchie, J.C.; Jackson, T.J.; Rango, A. Remote Sensing in Hydrology. Adv. Water Resour. 2002, 25, 1367–1385. [Google Scholar] [CrossRef]
- Martin-Neira, M. A Passive Reflectometry and Interferometry System (PARIS): Applications to Ocean Altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Garrison, J.L.; Komjathy, A.; Zavorotny, V.U.; Katzberg, S.J. Wind Speed Measurement Using Forward Scattered GPS Signals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 50–65. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS Signals from the Ocean with Wind Remote Sensing Application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef]
- Cardellach, E.; Fabra, F.; Rius, A.; Pettinato, S.; D’Addio, S. Characterization of Dry-Snow Sub-Structure Using GNSS Reflected Signals. Remote Sens. Environ. 2012, 124, 122–134. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Soil Moisture Sensing Using Spaceborne GNSS Reflections: Comparison of CYGNSS Reflectivity to SMAP Soil Moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef]
- Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating Soil Moisture Remote Sensing with Observations from the UK TechDemoSat-1 Satellite Mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.-W.; Judge, J. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation. IEEE J. Sel. Top. Appl. 2016, 9, 4730–4742. [Google Scholar] [CrossRef]
- Egido, A.; Paloscia, S.; Motte, E.; Guerriero, L.; Pierdicca, N.; Caparrini, M.; Santi, E.; Fontanelli, G.; Floury, N. Airborne GNSS-R Polarimetric Measurements for Soil Moisture and Above-Ground Biomass Estimation. IEEE J. Sel. Top. Appl. 2014, 7, 1522–1532. [Google Scholar] [CrossRef]
- Katzberg, S.J.; Torres, O.; Grant, M.S.; Masters, D. Utilizing Calibrated GPS Reflected Signals to Estimate Soil Reflectivity and Dielectric Constant: Results from SMEX02. Remote Sens. Environ. 2006, 100, 17–28. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Vall-llossera, M.; Valencia, E.; Marchan-Hernandez, J.F.; Ramos-Perez, I. Soil Moisture Retrieval Using GNSS-R Techniques: Experimental Results Over a Bare Soil Field. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Chew, C.C.; Dong, J.; Ochsner, T.E. Validation of GPS-IR Soil Moisture Retrievals: Comparison of Different Algorithms to Remove Vegetation Effects. IEEE J. Sel. Top. Appl. 2016, 9, 4759–4770. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. On the Spatial Resolution of GNSS Reflectometry. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1064–1068. [Google Scholar] [CrossRef]
- Cardellach, E.; Rius, A.; Martin-Neira, M.; Fabra, F.; Nogues-Correig, O.; Ribo, S.; Kainulainen, J.; Camps, A.; D’Addio, S. Consolidating the Precision of Interferometric GNSS-R Ocean Altimetry Using Airborne Experimental Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4992–5004. [Google Scholar] [CrossRef]
- Cardellach, E.; Li, W.; Rius, A.; Semmling, M.; Wickert, J.; Zus, F.; Ruf, C.S.; Buontempo, C. First Precise Spaceborne Sea Surface Altimetry with GNSS Reflected Signals. IEEE J. Sel. Top. Appl. 2019, 13, 102–112. [Google Scholar] [CrossRef]
- Zavorotny, V.U.; Voronovich, A.G. Bistatic GPS Signal Reflections at Various Polarizations from Rough Land Surface with Moisture Content. In Proceedings of the IEEE 2000 International Geoscience and Remote Sensing Symposium—Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Honolulu, HI, USA, 24–28 July 2000; Volume 7, pp. 2852–2854. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-Llossera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Perez, I.; Valencia, E.; Marchan-Hernandez, J.F.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; et al. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 71–84. [Google Scholar] [CrossRef]
- Ruf, C.S.; Atlas, R.; Chang, P.S.; Clarizia, M.P.; Garrison, J.L.; Gleason, S.; Katzberg, S.J.; Jelenak, Z.; Johnson, J.T.; Majumdar, S.J.; et al. New Ocean Winds Satellite Mission to Probe Hurricanes and Tropical Convection. Bull. Am. Meteorol. Soc. 2016, 97, 385–395. [Google Scholar] [CrossRef]
- Kim, H.; Lakshmi, V. Use of Cyclone Global Navigation Satellite System (CyGNSS) Observations for Estimation of Soil Moisture. Geophys. Res. Lett. 2018, 45, 8272–8282. [Google Scholar] [CrossRef]
- Guo, P.; Shi, J.; Gao, B.; Wan, H. Evaluation of Errors Induced by Soil Dielectric Models for Soil Moisture Retrieval at L-Band. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1679–1682. [Google Scholar] [CrossRef]
- Yang, T.; Wan, W.; Sun, Z.; Liu, B.; Li, S.; Chen, X. Comprehensive Evaluation of Using TechDemoSat-1 and CYGNSS Data to Estimate Soil Moisture over Mainland China. Remote Sens. 2020, 12, 1699. [Google Scholar] [CrossRef]
- Hallikainen, M.; Ulaby, F.; Dobson, M.; El-rayes, M.; Wu, L. Microwave Dielectric Behavior of Wet Soil-Part 1: Empirical Models and Experimental Observations. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 25–34. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Hallikainen, M.T.; El-Rayes, M.A. Microwave Dielectric Behavior of Wet Soil-Part II: Dielectric Mixing Models. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 35–46. [Google Scholar] [CrossRef]
- Jia, Y.; Savi, P.; Canone, D.; Notarpietro, R. Estimation of Surface Characteristics Using GNSS LH-Reflected Signals: Land Versus Water. IEEE J. Sel. Top. Appl. 2016, 9, 4752–4758. [Google Scholar] [CrossRef]
- Egido, A.; Ruffini, G.; Caparrini, M.; Martin, C.; Farres, E.; Banque, X. Soil moisture monitorization using gnss reflected signals. arXiv 2008, arXiv:0805.1881. [Google Scholar]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.B.; Cosh, M.H.; Dunbar, R.S.; Dang, L.; Pashaian, L.; et al. Validation of SMAP Surface Soil Moisture Products with Core Validation Sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Pierdicca, N.; Guerriero, L.; Giusto, R.; Brogioni, M.; Egido, A. SAVERS: A Simulator of GNSS Reflections from Bare and Vegetated Soils. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6542–6554. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Braun, J.J. Sensing Vegetation Growth with Reflected GPS Signals. Geophys. Res. Lett. 2010, 37, L12401. [Google Scholar] [CrossRef]
- Hu, C.; Benson, C.; Park, H.; Camps, A.; Qiao, L.; Rizos, C. Detecting Targets above the Earth’s Surface Using GNSS-R Delay Doppler Maps: Results from TDS-1. Remote Sens. 2019, 11, 2327. [Google Scholar] [CrossRef]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance Metrics for Soil Moisture Retrievals and Application Requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- SMAP L3 Radiometer Global Daily 36 Km EASE-Grid Soil Moisture, Version 6. Available online: https://nsidc.org/data/SPL3SMP/versions/6 (accessed on 15 May 2021).
- O’Neill, P.E.; Chan, S.; Njoku, E.G.; Jackson, T.; Bindlish, R.; Chaubell, J. SMAP L3 Radiometer Global Daily 36 Km EASE-Grid Soil Moisture, Version 6. Available online: https://doi.org/10.5067/EVYDQ32FNWTH (accessed on 15 August 2019).
- PO.DAAC. Available online: https://podaac.jpl.nasa.gov/ (accessed on 14 May 2018).
- Ruf, C.; Chang, P.S.; Clarizia, M.-P.; Gleason, S.; Jelenak, Z.; Majumdar, S.; Morris, M.; Murray, J.; Musko, S.; Posselt, D.; et al. CYGNSS Handbook Cyclone Global Navigation Satellite System: Deriving Surface Wind Speeds in Tropical Cyclones; National Aeronautics and Space Administration: Ann Arbor, MI, USA, 2016; ISBN 978-1-60785-380-0.
- Chew, C.; Lowe, S.; Parazoo, N.; Esterhuizen, S.; Oveisgharan, S.; Podest, E.; Zuffada, C.; Freedman, A. SMAP Radar Receiver Measures Land Surface Freeze/Thaw State through Capture of Forward-Scattered L-Band Signals. Remote Sens. Environ. 2017, 198, 333–344. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-Series Retrieval of Soil Moisture Using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Calabia, A.; Molina, I.; Jin, S. Soil Moisture Content from GNSS Reflectometry Using Dielectric Permittivity from Fresnel Reflection Coefficients. Remote Sens. 2020, 12, 122. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS Data for Soil Moisture Retrieval. IEEE J. Sel. Top. Appl. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled Seamless SRTM Data V4. Available online: http://srtm.csi.cgiar.org/ (accessed on 5 May 2021).
- Stutzman, W.L. Polarization in Electromagnetic Systems; Artech House: Norwood, MA, USA, 1993. [Google Scholar]
- Griffiths, D.J. Introduction to Electrodynamics; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Jackson, T.J.; Hurkmans, R.; Hsu, A.; Cosh, M.H. Soil Moisture Algorithm Validation Using Data from the Advanced Microwave Scanning Radiometer (AMSR-E) in Mongolia. Ital. J. Remote Sens. 2004, 30, 23–32. [Google Scholar]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. Geo-inf. 2012, 1, 32–45. [Google Scholar] [CrossRef]
- Dente, L.; Guerriero, L.; Comite, D.; Pierdicca, N. Space-Borne GNSS-R Signal Over a Complex Topography: Modeling and Validation. IEEE J. Sel. Top. Appl. 2019, 13, 1218–1233. [Google Scholar] [CrossRef]
- National Snow & Ice Data Center. Update: SMAP in Safe Mode. Available online: https://nsidc.org/the-drift/data-update/update-smap-in-safe-mode/ (accessed on 27 June 2019).
- Comite, D.; Cenci, L.; Colliander, A.; Pierdicca, N. Monitoring Freeze-Thaw State by Means of GNSS Reflectometry: An Analysis of TechDemoSat-1 Data. IEEE J. Sel. Top. Appl. 2019, 13, 2996–3005. [Google Scholar] [CrossRef]


| Yanco | TxSON | L.W. | |
|---|---|---|---|
| RMSE (a) | 5.73 | 6.74 | 6.40 |
| RMSE (b) | 0.13 | 0.18 | 0.17 |
| ubRMSE (a) ubRMSE (b) | 3.31 0.07 | 2.08 0.04 | 2.32 0.05 |
| C.C. (a) | 0.4495 | 0.4680 | 0.4714 |
| C.C. (b) | 0.4116 | 0.4687 | 0.4494 |
| RMSE Yanco | RMSE TxSON | RMSE L.W. | |
|---|---|---|---|
| March | 4.32 | 6.43 | 6.23 |
| June | 6.33 | 6.17 | 6.78 |
| September | 6.57 | 6.20 | 5.72 |
| December | 4.65 | 7.69 | 6.56 |
| ubRMSE Yanco | ubRMSE TxSON | ubRMSE L.W. | |
| March | 2.82 | 1.52 | 2.23 |
| June | 2.77 | 1.75 | 2.69 |
| September | 3.29 | 2.16 | 2.44 |
| December | 2.77 | 2.12 | 2.02 |
| C.C. Yanco | C.C. TxSON | C.C. L.W. | |
| March | 0.4904 | 0.5010 | 0.5538 |
| June | 0.5944 | 0.4955 | 0.5759 |
| September | 0.6465 | 0.3875 | 0.6279 |
| December | 0.5492 | 0.5217 | 0.6738 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Bisnath, S.; Lee, R.S.K.; Kilane, N.G. Computation Approach for Quantitative Dielectric Constant from Time Sequential Data Observed by CYGNSS Satellites. Remote Sens. 2021, 13, 2032. https://doi.org/10.3390/rs13112032
Lee J, Bisnath S, Lee RSK, Kilane NG. Computation Approach for Quantitative Dielectric Constant from Time Sequential Data Observed by CYGNSS Satellites. Remote Sensing. 2021; 13(11):2032. https://doi.org/10.3390/rs13112032
Chicago/Turabian StyleLee, Junchan, Sunil Bisnath, Regina S.K. Lee, and Narin Gavili Kilane. 2021. "Computation Approach for Quantitative Dielectric Constant from Time Sequential Data Observed by CYGNSS Satellites" Remote Sensing 13, no. 11: 2032. https://doi.org/10.3390/rs13112032
APA StyleLee, J., Bisnath, S., Lee, R. S. K., & Kilane, N. G. (2021). Computation Approach for Quantitative Dielectric Constant from Time Sequential Data Observed by CYGNSS Satellites. Remote Sensing, 13(11), 2032. https://doi.org/10.3390/rs13112032






