Towards a Topographically-Accurate Reflection Point Prediction Algorithm for Operational Spaceborne GNSS Reflectometry—Development and Verification †
Abstract
1. Introduction
2. Motivation and Requirements
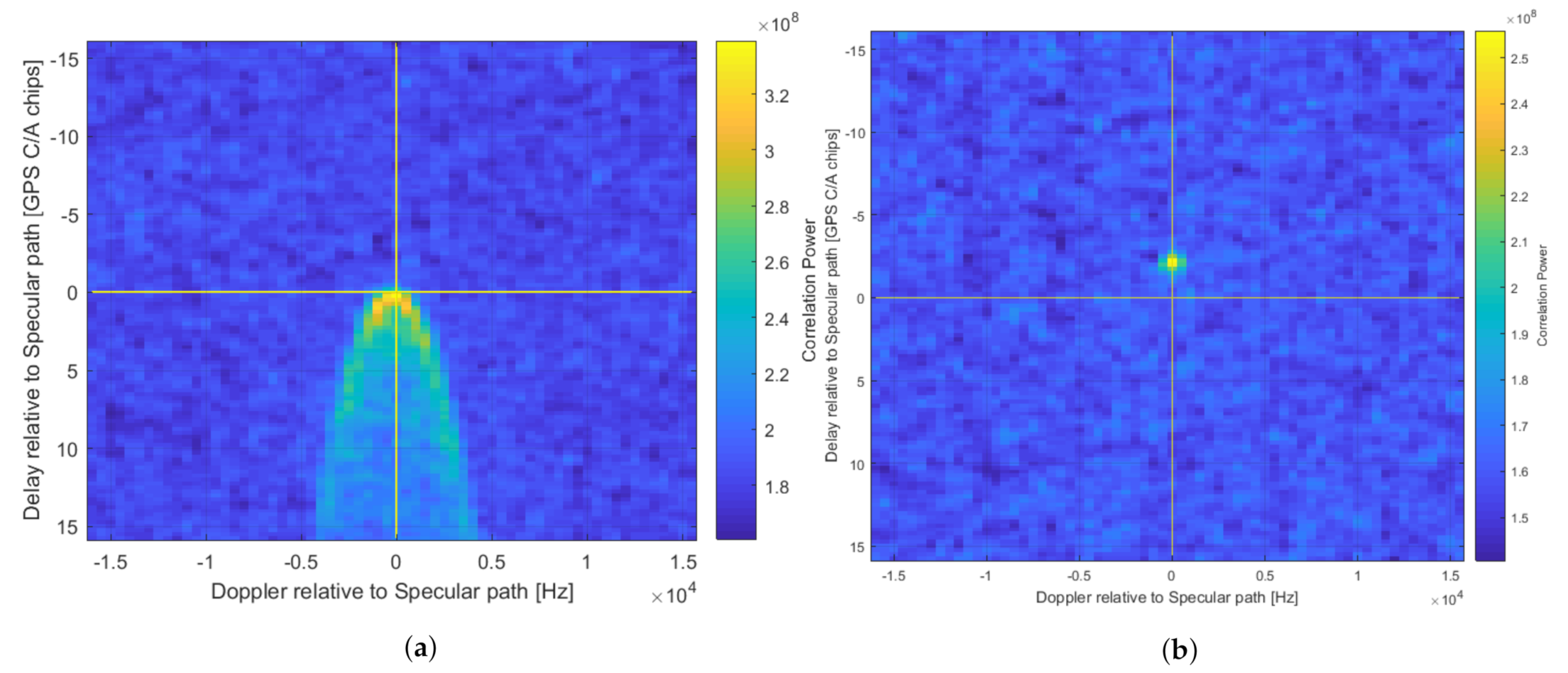
- The DDM is built up through correlation of the received reflected signals with a clean replica that is systematically shifted through the various combinations of delay and Doppler to calculate the received power at every pixel. If the prediction of of the specular reflection is correct, this reflected power will be present at the centre of the DDM. However, if the prediction is wrong, this power can appear at other positions in the DDM or sometimes may not appear at all (see Equation (3)). An example of the latter can be seen in Figure 1b, where the peak reflected power is offset from the centre due to topography. If the reflected power is not captured within the DDM at all then that measurement is lost.
- For forward-scattered DDMs, the centring of the reflected power allows the definition of a “Noise Box” in the null space at the top of the DDM, which corresponds to delays shorter than the predicted specular point (SP) delay—over the ocean such delays are typically not physically possible and so any power in this region can be assumed to be noise. This Noise Box is used to help measure noise power and thus calculate absolute received signal power from measured Signal-to-Noise Ratio (SNR). Reflections from unaccounted-for topography can contaminate the area resulting in inaccurate measurements or an inability to use the method at all [21].
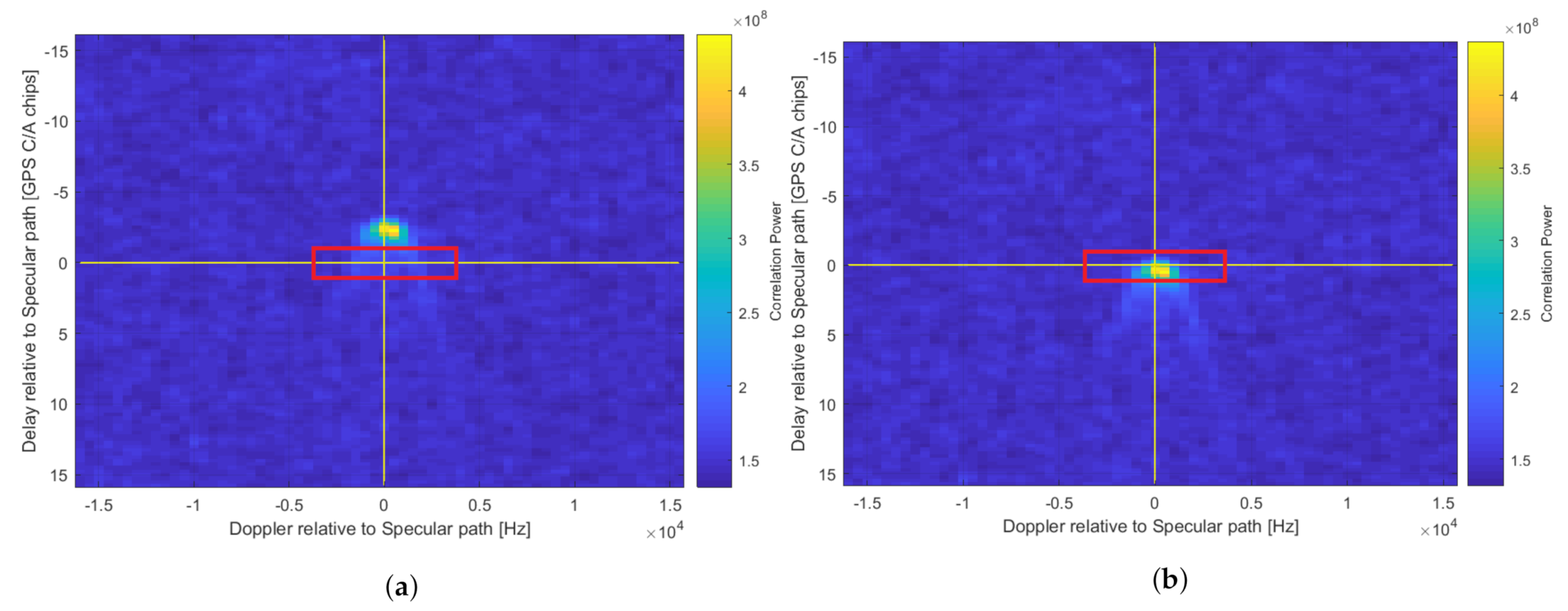
- The minimum requirement for successful recording of reflected power on the spacecraft is that the peak is located somewhere within the DDM (the effect on the Noise Box and thus calibration notwithstanding). If necessary, users can perform more accurate geo-location on the ground through re-processing. However, a stronger requirement is for the peak reflected power to be recorded as close to the centre of the DDM (delay offset = Doppler offset = 0) as possible at the on-board processing stage. This allows more efficient methods of data compression (i.e., windowing the DDM) to be used, which can be an enabler for usable data to be disseminated to users on the ground faster. This is key for soil moisture in particular. For certain missions e.g., those using very low power platforms, significant compression may be essential to close the data downlink budget. In general, regardless of the application or size of the platform, enabling better data compression is desirable for more efficient operation. For example, to enable 24/7 Level 1b DDM downlink operations on DoT-1 (an SSTL spacecraft on which this algorithm will be tested) it has been calculated that DDMs should be reduced to a window with 64 pixels in area. An 8 × 8 box has been chosen for initial testing (over e.g., 16 × 4) as this places a stronger test on the path length prediction requirement, and will also capture more of the DDM width, which may help to record multiple peaks if they should occur in e.g., mountainous terrain. Figure 3 demonstrates the impact of this desired windowing on DDMs generated with and without a topographically accurate algorithm.
- Some mission concepts that have recently been developed have proposed a so-called “coherent channel” to track the peak reflected power with longer coherent integration times, which allows carrier phase information to be preserved. As this results in twice as much data (both I and Q components are stored), the channel should ideally monitor one pixel of the DDM only, and therefore the peak reflected power must be located accurately in this coherent pixel. An accurate topography algorithm is part of the process for achieving this.
3. Algorithm
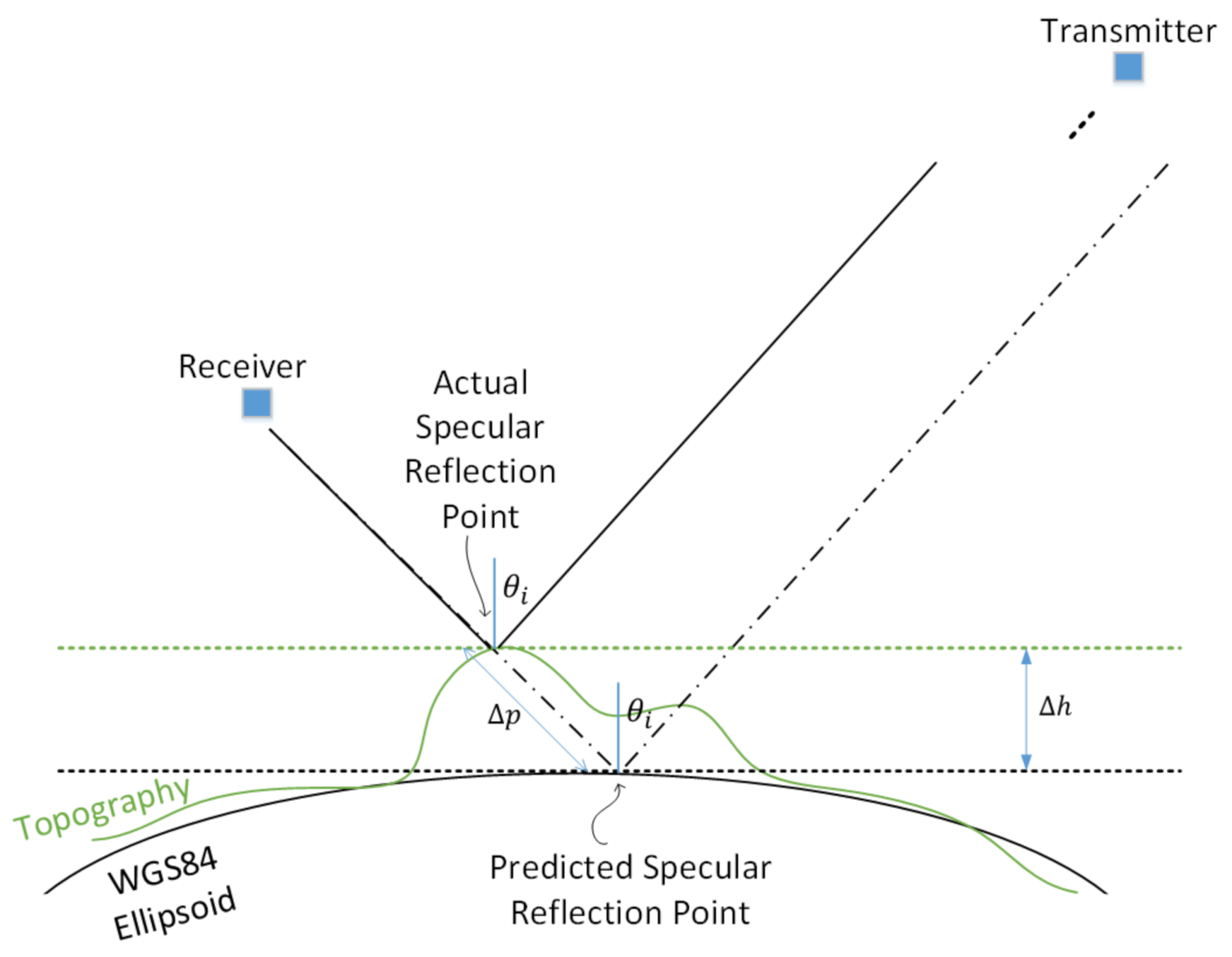
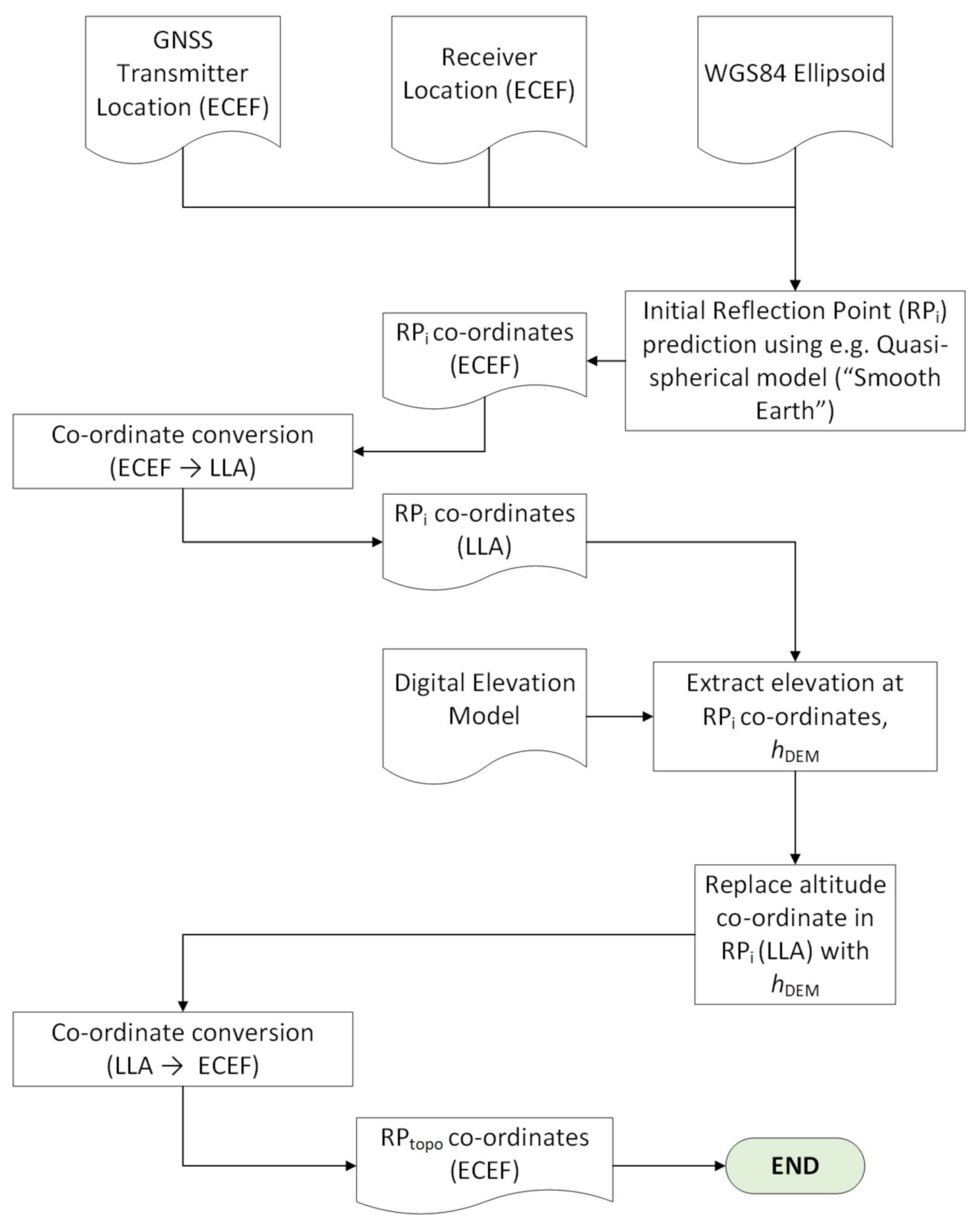
3.1. Baseline Algorithm (Elevation Only)—TARPP v1
3.2. Digital Elevation Models and On-Board Constraints
- Uplink rate, affecting file size.
- On-board storage, also affecting file size.
- Processing requirements for unpacking and using on-board.
4. Test Procedure
4.1. Datasets
4.2. Method—MATLAB Testing
4.3. Analysis 1a—Peak Power Offset Graphs
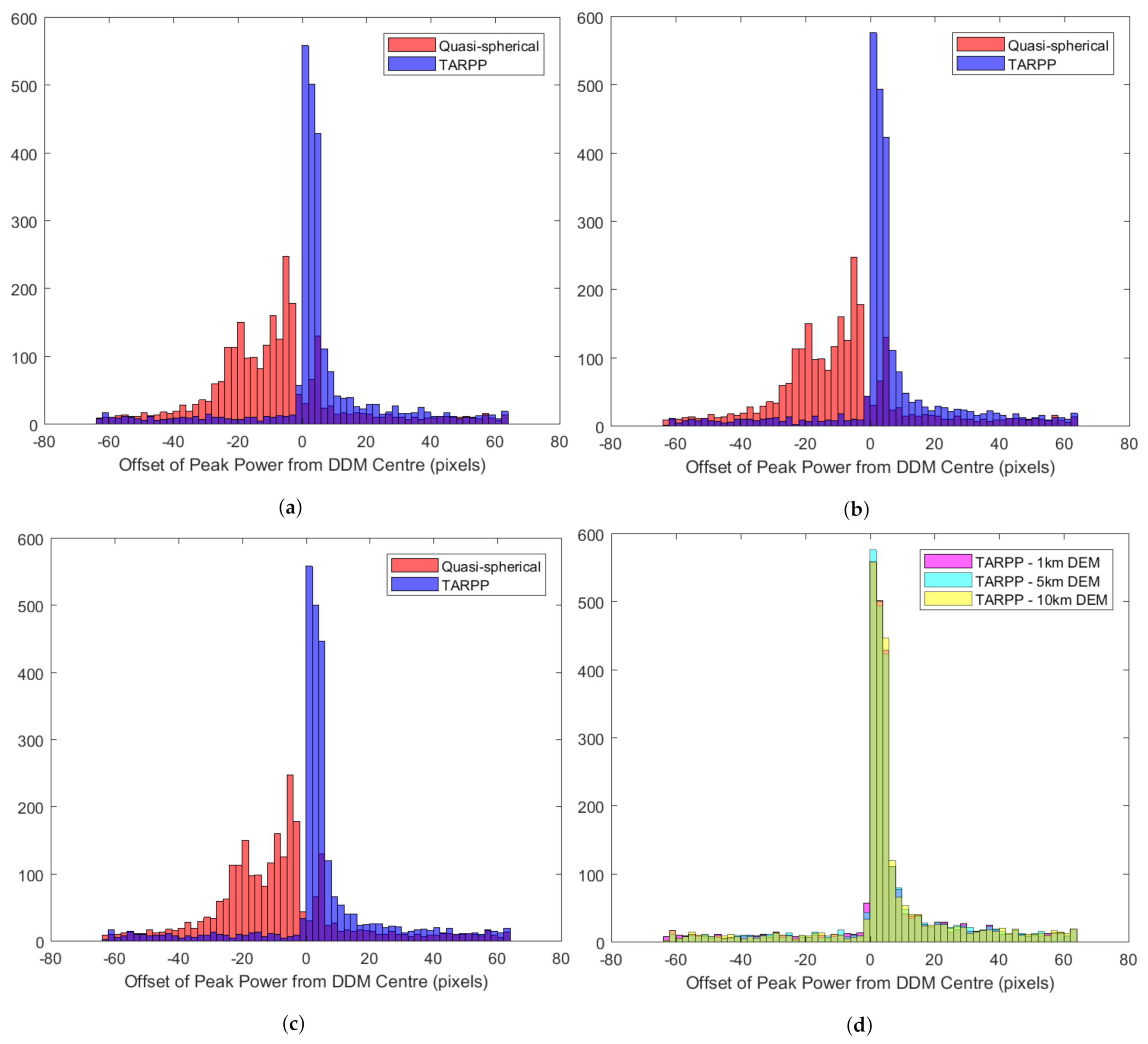
4.4. Analysis 1b—Peak Power Offset Histograms
4.5. Analysis 2—Compression Boxes
5. Results and Discussion
5.1. Analysis 1a
5.2. Analysis 1b
5.3. Analysis 2
6. Future Work
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foti, G.; Gommenginger, C.; Jales, P.; Unwin, M.; Shaw, A.; Robertson, C.; Rosellõ, J. Spaceborne GNSS reflectometry for ocean winds: First results from the UK TechDemoSat-1 mission. Geophys. Res. Lett. 2015, 42, 5435–5441. [Google Scholar] [CrossRef]
- Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.W.; Judge, J. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Soil Moisture Sensing Using Spaceborne GNSS Reflections: Comparison of CYGNSS Reflectivity to SMAP Soil Moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef]
- Jales, P. Spaceborne Receiver Design for Scatterometric GNSS Reflectometry. Ph.D. Thesis, University of Surrey, Guildford, UK, 2012. [Google Scholar]
- Unwin, M.; Jales, P.; Tye, J.; Gommenginger, C.; Foti, G.; Rosello, J. Spaceborne GNSS-Reflectometry on TechDemoSat-1: Early Mission Operations and Exploitation. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2016, 9, 4525–4539. [Google Scholar] [CrossRef]
- DMA WGS84 Development Committee. Department of Defense World Geodetic System 1984, Its Definition and Relationships with Local Geodetic Systems, 2nd ed.; Technical Report 8350.2; Department of Defense: Fort Lee, VA, USA, 1991.
- Martin-Neira, M. PARIS: Application to Ocean Altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Fraczek, W. Mean Sea Level, GPS, and the Geoid; ArcUser: Redlands, CA, USA, 2003. [Google Scholar]
- Grieco, G.; Stoffelen, A.; Portabella, M.; Belmonte Rivas, M.; Lin, W.; Fabra, F. Quality Control of Delay-Doppler Maps for Stare Processing. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 2990–3000. [Google Scholar] [CrossRef]
- King, L.; Unwin, M.; Rawlinson, J.; Guida, R.; Underwood, C. A Topographically-Accurate GNSS-R Reflection Point Predictor For On-Board Operational Processing. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 Septmber–2 October 2020; pp. 6194–6197. [Google Scholar] [CrossRef]
- Gleason, S. A Real-Time On-Orbit Signal Tracking Algorithm for GNSS Surface Observations. Remote. Sens. 2019, 11, 1858. [Google Scholar] [CrossRef]
- Campbell, J.D.; Melebari, A.; Moghaddam, M. Modeling the Effects of Topography on Delay-Doppler Maps. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 1740–1751. [Google Scholar] [CrossRef]
- Gleason, S.; O’Brien, A.; Russel, A.; Al-Khaldi, M.M.; Johnson, J.T. Geolocation, Calibration and Surface Resolution of CYGNSS GNSS-R Land Observations. Remote. Sens. 2020, 12, 1317. [Google Scholar] [CrossRef]
- Global Climate Observing System (GCOS). Essential Climate Variables; GCOS: Geneva, Switzerland, 2010. [Google Scholar]
- Global Climate Observing System (GCOS). The GCOS Story; GCOS: Geneva, Switzerland, 2010. [Google Scholar]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil moisture for hydrological applications: Open questions and new opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Global Climate Observing System (GCOS). GCOS Monitoring Principles; GCOS: Geneva, Switzerland, 2003. [Google Scholar]
- Camps, A.; Vall·Llossera, M.; Park, H.; Portal, G.; Rossato, L. Sensitivity of TDS-1 GNSS-R Reflectivity to Soil Moisture: Global and Regional Differences and Impact of Different Spatial Scales. Remote. Sens. 2018, 11, 1856. [Google Scholar] [CrossRef]
- Pierdicca, N.; Mollfulleda, A.; Costantini, F.; Guerriero, L.; Dente, L.; Paloscia, S.; Santi, E.; Zribi, M. Spaceborne GNSS Reflectometry Data For Land Applications: An Analysis Of TechDemoSat Data. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3343–3346. [Google Scholar]
- Comite, D.; Cenci, L.; Colliander, A.; Pierdicca, N. Monitoring Freeze-Thaw State by Means of GNSS Reflectometry: An Analysis of TechDemoSat-1 Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2020, 13, 2996–3005. [Google Scholar] [CrossRef]
- Surrey Satellite Technology Ltd. MERRByS Product Manual—GNSS Reflectometry on TDS-1 with the SGR-ReSI, 7th ed.; Surrey Satellite Technology Ltd.: Guildford, UK, 2019. [Google Scholar]
- Eakins, B.W.; Sharman, G.F. Hypsographic Curve of Earth’s Surface from ETOPO1; NOAA National Geophysical Data Center: Boulder, CO, USA, 2012.
- Wu, G.; Liu, Y. Impacts of the Tibetan Plateau on Asian Climate. Meteorol. Monogr. 2016, 56, 7.1–7.29. [Google Scholar] [CrossRef]
- Gleason, S. Algorithm Theoretical Basis Document—Level 1B DDM Calibration, CYGNSS, rev 2 ed.; NASA: Washington, DC, USA, 2018.
- Amatulli, G.; Domisch, S.; Tuanmu, M.N.; Parmentier, B.; Ranipeta, A.; Malczyk, J.; Jetz, W. A suite of global, cross-scale topographic variables for environmental and biodiversity modeling. Sci. Data 2018, 5, 1–15. [Google Scholar] [CrossRef]
- Danielson, J.; Gesch, D. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); U.S. Geological Survey Open-File Report 2011-1073; US Geological Survey: Sunrise Valley, VA, USA, 2011.
- Jarvis, A.; Reuter, H.; Nelson, A. Hole-Filled Seamless SRTM Data V4; International Centre for Tropical Agriculture (CIAT): Cali, Colombia, 2008. [Google Scholar]
- O’Loughlin, F.; Paiva, R.; Durand, M.; Alsdorf, D.; Bates, P. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote. Sens. Environ. 2016, 182, 49–59. [Google Scholar] [CrossRef]
- Loria, E.; O’Brien, A.; Zavorotny, V.; Downs, B.; Zuffada, C. Analysis of scattering characteristics from inland bodies of water observed by CYGNSS. Remote. Sens. Environ. 2020, 245, 111825. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; Gleason, S.; Loria, E.; O’Brien, A.J.; Yi, Y. An Algorithm for Detecting Coherence in Cyclone Global Navigation Satellite System Mission Level-1 Delay-Doppler Maps. IEEE Trans. Geosci. Remote. Sens. 2020, 1–10. [Google Scholar] [CrossRef]
- SSTL; NOC. Measurement of Earth Reflected Radio-Navigation Signals By Satellite; SSTL: Guildford, UK, 2015. [Google Scholar]
- De Vos Van Steenwijk, R.; Unwin, M.; Jales, P. Introducing the SGR-ReSI: A next generation spaceborne GNSS receiver for navigation and remote-sensing. In Proceedings of the Programme and Abstract Book—5th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, NAVITEC 2010, Noordwijk, The Netherlands, 8–10 December 2010. [Google Scholar] [CrossRef]
- Kwan, P. NAVSTAR GPS Space Segment/User Segment Interfaces; IS-GPS-200; GPS Directorate, Space & Missile Systems Center (SMC): Los Angeles, CA, USA, 2019. [Google Scholar]
- Rius, A.; Cardellach, E.; Martin-Neira, M. Altimetric Analysis of the Sea-Surface GPS-Reflected Signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2119–2127. [Google Scholar] [CrossRef]

| Algorithm Outcome | Land Sensing Enabled over Whole Globe | Noise Box Preserved | Data Compression Enabled (Windowing) | Coherent Pixel Tracking |
|---|---|---|---|---|
| Baseline Outcome Requirement: SP power captured within 128 × 20 pixel window | ✓ | Not guaranteed | × | × |
| Good Outcome Requirement: SP power captured within 8 × 8 pixel window | ✓ | ✓ | ✓ | × |
| Best Outcome—“Stretch Objective” Requirement: Location of SP power in DDM window known to 1 pixel. | ✓ | ✓ | ✓ | ✓ |
| Dataset Test ID | Collection Date and Timeslot | No. of DDMs | Approx. Location | Land Cover | PRN | Track Start | Track End | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Co-Ordinate | Elevation (m) | El. angle at SP (°) | Co-Ordinate | Elevation (m) | El. angle at SP (°) | ||||||
| TT1 | 2015-01-11, H18 | 126 | Texas, USA | Open shrubland and grassland. Some mountainous regions. | 15 | 35.585, −97.421 | 316 | 65.3 | 30.627, −98.897 | 385 | 61.1 |
| 18 | 35.650, −103.721 | 1259 | 59.7 | 30.596, −104.891 | 994 | 59.1 | |||||
| 21 | 36.702, −101.193 | 861 | 69.3 | 31.637, −102.525 | 849 | 64.3 | |||||
| TT2 | 2015-06-05, H12 | 129 | Sahara Desert (Algeria to Mali) | Desert | 12 | 25.665, −2.526 | 298 | 66.1 | 18.709, −4.045 | 284 | 66.7 |
| 15 | 24.408, 0.665 | 332 | 74.0 | 17.309, −1.029 | 288 | 79.0 | |||||
| 24 | 29.132, −0.741 | 342 | 56.0 | 22.345, −2.368 | 352 | 48.3 | |||||
| TT3 | 2015-11-04, H06 | 130 | Far Eastern China (Taklamakan Desert) to N. India. | Desert and mountains | 5 | 41.255, 81.677 | 985 | 61.2 | 34.417, 79.510 | 5504 | 52.9 |
| 20 | 37.967, 76.976 | 1522 | 67.3 | 30.982, 75.161 | 216 | 75.9 | |||||
| 29 | 40.964, 76.881 | 3910 | 69.0 | 33.818, 74.953 | 1631 | 64.1 | |||||
| TT4 | 2015-11-19, H18 | 130 | Arizona to Californian coast, USA | Desert and shrubland, mountains (Sierra Nevada). Some tracks cross the ocean. | 15 | 36.069, −110.878 | 1713 | 53.1 | 29.163, −113.060 | 0 | 49.9 |
| 18 | 35.530, −117.960 | 948 | 67.9 | 28.472, −119.648 | 0 | 70.9 | |||||
| 20 | 38.840, −111.737 | 2050 | 50.9 | 32.107, −113.652 | 388 | 42.9 | |||||
| 21 | 38.055, −116.500 | 2060 | 67.5 | 31.018, −118.364 | 0 | 60.0 | |||||
| TT5 | 2018-10-06, H12 | 128 | South Sudan to DR Congo | Savanna and forests. Some rivers. | 8 | 1.589, 27.740 | 682 | 46.6 | −5.211, 26.360 | 584 | 54.2 |
| 11 | 6.872, 27.991 | 466 | 75.9 | −0.195, 26.493 | 585 | 71.4 | |||||
| 18 | 7.140, 30.227 | 414 | 73.4 | 0.097, 28.772 | 1166 | 66.2 | |||||
| 23 | 6.338, 25.489 | 649 | 54.9 | −0.560, 24.021 | 458 | 55.0 | |||||
| TT6 | 2018-10-11, H12 | 129 | DR Congo | Forest, some mountainous regions, savanna. Some lakes. | 8 | −7.152, 27.347 | 639 | 49.3 | −14.058, 25.878 | 1115 | 57.2 |
| 11 | −2.067, 27.266 | 939 | 77.4 | −9.205, 25.726 | 795 | 71.7 | |||||
| 18 | −1.813, 29.517 | 2158 | 70.9 | −8.937, 28.073 | 1452 | 64.0 | |||||
| Dataset and PRN | No. of DDMs | Box Size (Pixels) | Score (% Success Rate of Placing Pixel in Box) | |||
|---|---|---|---|---|---|---|
| Quasi-Spherical | TARRP—1 km | TARPP—5 km | TARPP—10 km | |||
| TT1, 15 | 126 | 4 × 4 | 1.6 | 4.8 | 4.8 | 4.8 |
| 8 × 8 | 23.8 | 68.3 | 72.2 | 74.6 | ||
| 20 × 20 | 88.9 | 85.7 | 85.7 | 85.7 | ||
| TT1, 18 | 126 | 4 × 4 | 0 | 5.6 | 11.9 | 8.7 |
| 8 × 8 | 1.6 | 55.6 | 54.0 | 51.6 | ||
| 20 × 20 | 4.8 | 81.7 | 81.0 | 79.4 | ||
| TT1, 21 | 126 | 4 × 4 | 0 | 1.6 | 0.8 | 0.8 |
| 8 × 8 | 2.4 | 77.0 | 72.2 | 72.2 | ||
| 20 × 20 | 4.8 | 92.9 | 92.9 | 92.9 | ||
| Box Size (Pixels) | Weighted Average Score (% Success Rate of Placing Pixel in Box) | |||
|---|---|---|---|---|
| Quasi-Spherical | TARRP—1 km | TARPP—5 km | TARPP—10 km | |
| 4 × 4 | 1.05 | 30.18 | 30.77 | 30.36 |
| 8 × 8 | 10.35 | 55.52 | 55.09 | 54.46 |
| 20 × 20 | 35.20 | 67.72 | 67.76 | 67.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
King, L.; Unwin, M.; Rawlinson, J.; Guida, R.; Underwood, C. Towards a Topographically-Accurate Reflection Point Prediction Algorithm for Operational Spaceborne GNSS Reflectometry—Development and Verification. Remote Sens. 2021, 13, 1031. https://doi.org/10.3390/rs13051031
King L, Unwin M, Rawlinson J, Guida R, Underwood C. Towards a Topographically-Accurate Reflection Point Prediction Algorithm for Operational Spaceborne GNSS Reflectometry—Development and Verification. Remote Sensing. 2021; 13(5):1031. https://doi.org/10.3390/rs13051031
Chicago/Turabian StyleKing, Lucinda, Martin Unwin, Jonathan Rawlinson, Raffaella Guida, and Craig Underwood. 2021. "Towards a Topographically-Accurate Reflection Point Prediction Algorithm for Operational Spaceborne GNSS Reflectometry—Development and Verification" Remote Sensing 13, no. 5: 1031. https://doi.org/10.3390/rs13051031
APA StyleKing, L., Unwin, M., Rawlinson, J., Guida, R., & Underwood, C. (2021). Towards a Topographically-Accurate Reflection Point Prediction Algorithm for Operational Spaceborne GNSS Reflectometry—Development and Verification. Remote Sensing, 13(5), 1031. https://doi.org/10.3390/rs13051031







