Abstract
Time series analysis has gained popularity in forest disturbance monitoring thanks to the availability of satellite and airborne remote sensing images and the development of different time series methods for change detection. Previous research has focused on time series data noise reduction, the magnitude of breakpoints, and accuracy assessment; however, few have looked in detail at how the trend and seasonal model components contribute to disturbance detection in different forest types. Here, we use Landsat time series images spanning 1994–2018 to map forest disturbance in a western Pacific area of Mexico, where both temperate and tropical dry forests have been subject to severe deforestation and forest degradation processes. Since these two forest types have distinct seasonal characteristics, we investigate how trend and seasonal model components, such as the goodness-of-fit (R2), magnitude of change, amplitude, and model length in a stable historical period, affect forest disturbance detection. We applied the Breaks For Additive Season and Trend Monitor (BFAST) algorithm and after accuracy assessment by stratified random sample points, and we obtained 68% and 86% of user accuracy and 75.6% and 86% of producer’s accuracy in disturbance detection, in tropical dry forests and temperate forests, respectively. We extracted the noncorrelated trend and seasonal model components R2, magnitude, amplitude, length of the stable historical period, and percentage of pixels with NA and tested their effects on disturbance detection employing forest-type specific logistic regression. Our results showed that, for all forests combined, the amplitude and stable historical period length contributed to disturbance detection. While for tropical dry forest alone, amplitude was the main predictor, and for the temperate forest alone, the stable historical period length contributed most to the prediction, although it was not statistically significant. These findings provide insights for improving the results of forest disturbance detection in different forest types.
Keywords:
Landsat; NDVI; deforestation; forest degradation; magnitude of change; goodness-of-fit; amplitude 1. Introduction
Forests play a vital role in ecosystem goods and services to humanity, by providing energy, shelter, and livelihoods []. Human-induced land use and management practices, such as deforestation for agriculture, logging, plantation, or transitional subsistence farming, such as shifting cultivation, have led to forest cover loss []. Reliable information on forest cover and its changes is crucial for policymakers to design effective plans in forest conservation.
Forest disturbances have been detected and quantified using multitemporal spaceborne optical remote sensing, such as Landsat, which has been providing images for over three decades and is being used for characterizing forest extent and change [,,]. The normalized difference vegetation index (NDVI), computed using near infrared and red channel [], is related to vegetation photosynthetic activity and measures vegetation greenness and productivity [,,]. It has the advantage of being robust and easily interpretable [] and is sensitive to forest change when used in a time series (TS) context [,,,,,,,,,,]. A change in NDVI signals in TS can be related to change in green vegetation biomass, cover, and structure [,].
Both annual or biennial time-steps [,,,,,,,,,,] and dense intra-annual temporal frequency [,,,,,,,,,,] have been used, with the former minimizing vegetation seasonality and seeking deviations from stable conditions, and the latter integrating seasonality and trend analysis to describe complete TS trajectories []. It was found that a seasonal trend model shows better performance than methods that remove the seasonal cycle of the TS [].
Trend and seasonal model estimation, such as the Breaks For Additive Seasonal Trend (BFAST), allows the detection of changes in the long-term NDVI trend and in the phenological cycle []. It decomposes the TS into trend, seasonal, and residual components. Major shifts in trends are identified as breakpoints by statistical tests, and the differences between the observed and modeled NDVI correspond to the magnitudes of breakpoints. Since not all the interannual variability detected by breakpoints represents disturbance, different approaches [,,,,] have been applied to identify a suitable magnitude for disturbance detection, including a simple empirical threshold value [,], a more sophisticated random forest machine learning algorithm [,,], or a hybrid of these two approaches combined with field-based TS fusion []. It was found that by adding seasonality and trend information, especially magnitude, amplitude, and slope, the BFAST performance improved compared to using breakpoints alone [].
Goodness-of-fit is one of the tools to assess the ability of a model to simulate reality []. Often measured by coefficient of determination (R2), a higher R2 indicates a higher degree of collinearity between the observed and model-simulated variables []. To ensure a good performance of a model, R2 is often tested as a threshold to accept or reject a fitted model []. Other statistical measures, such as F-statistic [,] and chi-square statistics [], have also been adopted for the same purpose. To the knowledge of the authors, no previous studies have been found to associate the goodness-of-fit with the performance of a model for change detection.
Amplitude, as one of the seasonal components in the trend analysis, is related to vegetation phenology change detection []. The trend and seasonal model are capable of phenological change detection with data of different ranges of low, medium, and high amplitude []. However, the signal-to-noise ratio in TS affects phenological change detection; changes can be detected in a large range of land covers, including grassland and forests with different seasonal amplitudes, provided that their seasonal amplitude is larger than the noise level []. A minimum seasonal amplitude is required, for example, to use MODIS NDVI TS; a seasonal amplitude of 0.1 NDVI is necessary to detect phenological change [].
In addition, the performance of a trend and seasonal model is affected by the amount of interannual variability; for example, spectral changes caused by variability in illumination, seasonality, or atmospheric scattering in the NDVI TS other than disturbances [,]. A stable historical period is a time period when the components of the NDVI TS remain stable and without any disturbance []. It has been recommended that the stable historical period length should be at least two years, so that the BFAST model is capable of properly fitting its parameters []. Neither amplitude nor stable historical period has been assessed in previous studies for their effects on forest disturbance detection.
Given the importance of the trend and the seasonal model components in TS model prediction, and the fact that little previous research has been carried out on how these components affect forest disturbance detection in different forest types, we report on a study that focuses on disturbance detection in both tropical dry forests (TDF) and temperate forests (TF), encompassing four research questions:
- (1)
- Do TDF and TF differ in accuracy in forest disturbance detection by BFAST trend and seasonal model?
- (2)
- Is the difference in accuracy related to the BFAST components, such as the magnitude, goodness-of-fit, amplitude, and length of the stable historical period?
- (3)
- Within the same type of forest, do the BFAST trend and seasonal model components affect the correct detection of forest disturbance?
- (4)
- How does the percentage of pixels with no data values in a TS, caused by clouds and shadow removals in those pixels, affect forest disturbance detection?
We aim to answer these questions by exploring the potential of Landsat NDVI TS from 1994 to 2018 with the BFAST model for forest disturbance detection in both TF and TDF. These two types of forest in the Ayuquila River Basin have been subject to severe disturbances, with agriculture conversion and shifting cultivation in the TDF and selective logging in the TF. We compare the disturbance detection in these two types of forest by examining components in their trend and seasonal model, such as goodness-of-fit, magnitude, amplitude, length of stable period, and percentage of no data value in the TS, and associate these factors to the difference in disturbance detection.
2. Materials and Methods
Figure 1 presents the overall data and data processing flow.
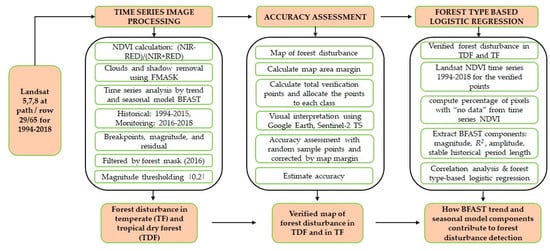
Figure 1.
Flowchart of the data and data processing methods applied in this study.
2.1. Forest in Ayuquila River Basin and Main Drivers of Forest Disturbances
The study area, the watershed of the Ayuquila River, is located in the western Pacific area of Mexico (Figure 2). It is characterized by large topographic variations, with the elevation ranging from 260 to 2500 m above mean sea level; the average annual precipitation is 800–1200 mm and occurs mostly between June and October; the average monthly temperature ranges from 18 to 22 °C []. There are both temperate forests (TF) and tropical dry forests (TDF) in this area. TF is distributed in the higher elevation of the watershed, occupying about 12% of the watershed, including pine (Pinus spp.), fir (Abies spp.), and oak forests (Quercus spp.). TDF is distributed in the lower topographic areas, occupying about 24% of the watershed and composed of deciduous and semideciduous woodlands with much lower biomass density, canopy cover, and height than the TF. While TDF is used mainly for shifting cultivation, fuelwood extraction, cattle grazing, poles extraction for constructing fences, and harvesting mushrooms and medicinal plants [], TF is exploited mainly for timber, although recently, avocado (Persea americana) plantations have been established in areas of TF.
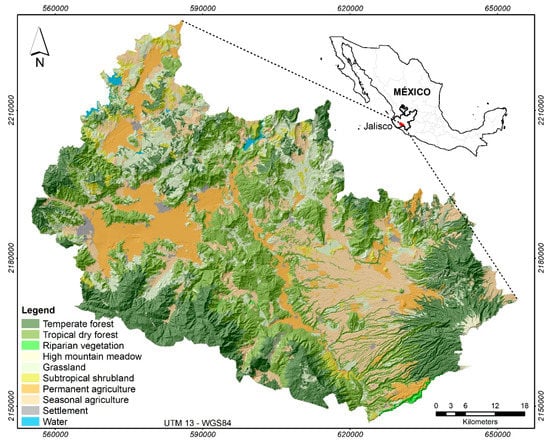
Figure 2.
The study area, the Ayuquila River Basin (ARB), is in the Jalisco state, central western Mexico. Forests, especially the temperate forest, are distributed in the higher elevation of the watershed.
2.2. Data Collection and Preprocessing
We employed Landsat-5 TM, Landsat-7 ETM+, and Landsat-8 OLI level-1 terrain-corrected (L1T) surface reflectance scenes at path/row (29/65) from 1994 to 2018 available from Google Earth Engine (GEE, []). We applied cloud-and-shadow masks, with the FMASK algorithm [] built into the GEE to mask out clouds and cloud shadows. Intercalibration of the different Landsat sensors has been recommended to reduce the sensor effects on the radiometry of the scenes []. In our case, we considered using uncalibrated scenes that would have minor effects on the change detection, since the selected historical period (1994–2015) includes at least two complete years where Landsat-7 ETM and Landsat-8 OLI were operational. Therefore, we assume that the BFAST algorithm can fit a stable model, considering the NDVI variations between the two different sensors.
We computed the NDVI from the near infrared (NIR) and red (RED) bands []:
where the RED and NIR are band 3 (0.626–0.693 ) and band 4 (0.776–0.904 ), respectively, of Landsat TM and ETM+, and the band 4 (0.630–0.680 ) and band 5 (0.845–0.885 ), respectively, of Landsat 8 OLI. The compiled NDVI TS images have data values ranging from −1 to 1. Figure 3 shows an NDVI TS for TDF and TF from January 2013 to June 2018. TDF demonstrates a more pronounced seasonal pattern than TF.
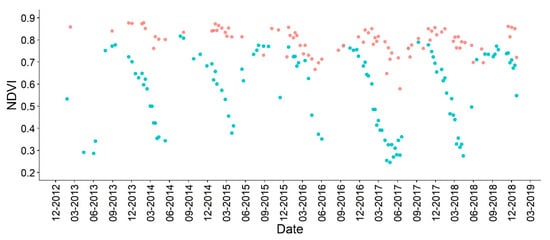
Figure 3.
Monthly time series NDVI profile for temperate forest, represented by the red points and tropical dry forest, represented by the blue points, from January 2013 to June 2018. Comparatively, few data were available from January to July 2013, since only Landsat-7 ETM+ was available during this period. More observations became available after the launch of Landsat-8 OLI.
In the Landsat TS, the pixels with clouds and cloud shadows removed have values of “no data” (NA). Pixels with NA also include those in the data gap in Landsat-7 ETM+ and those with missing values, due to the difference in acquisition swath extent in different dates. The monthly distribution of the NA observations for the forest area is shown in Table 1. The percentage of NA observations is lower in the dry season from January to May and from November to December, and higher in the rainy season from June to October.

Table 1.
Monthly average percentage of NA observations in forested areas in ARB. The months of the rainy season are marked in gray. This information was derived from the time series data of verified disturbances (see Section 2.4).
2.3. Forest Disturbance Detection
To monitor forest disturbances, we applied the BFAST Monitor algorithm []. In this study, we define “forest disturbance” as negative changes that occur in the forest canopy induced by human activities, such as logging and shifting cultivation, or natural events such as fires and hurricanes. A detailed description of the algorithm can be found in [,]. Briefly, this algorithm works by first defining a stable historical period using a reverse-ordered CUSUM test (ROC) []. Afterward, it derives a first-order harmonic seasonal model from data in the stable historical period (Equation (2)) and projects it into the monitoring period:
where the intercept , slope , amplitude , and phases are the unknown parameters to describe the trend and seasonal patterns, which can be estimated and tested using ordinary least squares (OLS) techniques. The frequency that describes the number of annual observations is and represents the harmonic terms, and we adopt = 1.
We define 1994–2015 as the historical period and January 2016–June 2018 as the monitoring period, considering that a disturbance would probably still be recognizable in the field verification (October 2018), within two and a half years after the disturbance occurred. The data in the monitoring period are checked for consistency with the model built in the stable historical period by way of moving sums (MOSUM) of the residuals []. The definition for each time point (t) in a monitoring period is expressed in Equation (3):
where is the predicted variance from the trend in the historical period, is the number of observations in the sample, and and are the observed and predicted values at time point (), respectively; are the residuals in the MOSUM window, and is the MOSUM bandwidth, defined as a fraction of the number of observations in the sample, often assigned as for the disturbance detection [,,]. When the null hypothesis of the stability of the seasonality pattern is rejected, a breakpoint is registered. The decision to reject this null hypothesis is based on a boundary condition; more detail is provided in [].
If the TS pattern in the monitoring period is stable compared to the data in the stable historical period, all of the residuals and their MOSUM values should be near zero. Otherwise, a breakpoint is registered in the monitoring period. In addition, the residual ) is calculated as a magnitude of change. Disturbances are often indicated by negative magnitudes; however, not all the breakpoints indicate disturbances because of interannual variability []. Therefore, a magnitude threshold can be applied to reduce false positive detections [,,].
We chose the magnitude threshold by field verification carried out in 15–24 October 2018. We verified 12 breakpoints with a magnitude of change ranging from () to () and identified false detection corresponding to magnitude < (). Note that, for forest disturbance detection, the magnitude value was negative, but we used its absolute value to facilitate interpretation of the results. We eliminated all breakpoints with magnitudes < and took the earliest remaining breakpoint for each pixel as the “final” forest disturbance. During the field campaign, anthropogenic causes of forest disturbances including deforestation for Agave spp. plantations and fire-induced forest damage were identified. Since only forest pixels were analyzed, the changes detected are very likely the result of forest clearing for cattle ranching, shifting cultivation, or permanent agriculture such as avocado plantations.
The BFAST Monitor approach requires a historical period from which a stable TS can be modeled to detect the forest disturbance in the monitoring period []. We applied the BFAST algorithm to all the pixels in the watershed and applied a forest mask to keep only the forest disturbances detected in the forest area. For this, we visually updated a land cover map from 2011 to January 2016 to make certain the existing forests before the beginning of the monitoring period was being analyzed. We merged the non-forest categories, including agriculture, grassland, human settlements, riparian vegetation, and water bodies, into one non-forest category, and merged all forest types, including evergreen, deciduous, and shrubland, into a single category of forest. Landsat NDVI TS images were compiled in GEE []. The BFAST Monitor algorithm was applied through the bfastspatial package [] (https://github.com/loicdtx/bfastSpatial, accessed on 20 May 2021) using R []. It is worth mentioning that BFAST implementation in GEE is now available, which might be of interest for future users [].
2.4. Accuracy Assessment
We evaluated the accuracy of forest disturbances detection by adopting the protocol described in [,]. The protocol includes a sampling and response design that defines a representative set of samples and uses it to initially form a traditional confusion matrix [], which was then corrected by a mapped area to estimate the unbiased area for each class. This procedure also had the purpose of generating variables of the seasonal model components from the correctly and falsely identified disturbances for the analysis of logistic regression; more details can be found in Section 2.5. We calculated the total number of samples by applying the equation for stratified random sampling (Equation (4)):
where is the standard error of the estimated overall accuracy, and we adopt 0.01 as suggested by []. is the mapped proportion of area of class and is the standard deviation of class , and . The variables are listed in Table 2.

Table 2.
The parameters for the computation of the total number of stratified random sampling points and the number of random points allocated for each class. TDF: tropical dry forest, TF: temperate forest.
We distributed the total sampling points in the four classes as follows: 50 points each to the two disturbance classes, TDF–disturbance and TF–disturbance, with the rest of the points distributed proportionally to the forest classes with no disturbance detected, TDF–no change and TF–no change. For the response design, we visually interpreted the points employing TS Sentinel-2 images available in GEE and high spatial resolution Google Earth images, considering both spatial and temporal accuracy. During the interpretation process, we deleted 25 points from the 327 points of TDF–no change, and 12 points from the 235 points of TF–no change because of the errors in the mask, which correspond to non-forest areas at the beginning of the monitoring period (2016).
We summarized the results of accuracy assessment in a confusion matrix using both the number of points and the proportion of the categories [,,]. Using the area-weighted confusion matrix, we calculated the estimated accuracy indices, including overall accuracy and user’s and producer’s accuracies. We also estimated the areas of disturbance and permanent forests with 95% confidence intervals. The estimation assumes that the reference validation data used for the computation of the confusion matrix can represent a proportion of the whole area [].
2.5. Logistic Regression with BFAST Model Components
We assume that certain BFAST model components, such as the magnitude of change, goodness-of-fit measured by coefficient of determination (R2), the amplitude and the length of the stable historical period, and the percentage of NA in a TS play a role in the performance of change detection in TDF and TF. Therefore, we used the verified random points for correct and false detection to extract the NDVI TS and calculated the former mentioned BFAST model components.
We incorporated these components as independent variables in a logistic regression to test their importance in labeling the disturbance as correct or false (Equation (5)).
where is the intercept, ….. are the expected change in the logarithm odds of the dependent variable according to changes in each independent variable, … are the independent variables (predictors), and is the dependent variable (correct or false positive detected disturbance). The forest type variable was encoded as binary, defining TF as 0 and TDF as 1, while all the other variables were numerical variables. The dependent variable was also encoded as binary, defining 0 as incorrect detection and 1 as correct detection. As we are interested in the role of forest type in disturbance detection, we applied three logistic regressions, each with a different focus of forest type: all forests, only TDF, and only TF.
From a statistical point of view, it is important to carry out the analysis on pixels with the same length of data availability. This is to exclude the possibility that the analysis is affected by the uneven data distribution within the sampled pixels. In satellite data, especially from the tropics, the contamination from clouds and cloud shadows cause invalid observations in a TS (Table 1) and possibly uneven distributions of the observations. However, in our case, since the pixels are from the same study area with a relatively small size, and the TS data include a long historical period (1994–2015), we assume that the difference in the distribution of observations in the TS data will be relatively insignificant. Nevertheless, the percentage of NA was included among the analyzed variables, as an indicator of the ratio of invalid/valid observations.
Prior to fitting the logistic regression model, we conducted a variance inflation factor (VIF) statistical analysis to assess the degree of collinearity among the variables. According to [], the VIF can be derived from the multiple correlation coefficient (Equation (6)).
where is the multiple correlation coefficient of independent variable regressed on the remaining independent variables. For example, a variable with a coefficient of 0.6 would result in a VIF of 2.5, and a higher coefficient corresponds to higher VIF. Following the recommendations from [], we excluded highly redundant variables that have VIF > 2.5.
3. Results
3.1. Change Detection with BFAST
In total, 496.7 ha were detected as forest disturbances in a period of two and a half years, January 2016–June 2018, with about 329.22 ha in TDF and 167.5 ha in TF. The definition of disturbance categories and areas of detected disturbances and forest covers with no change are summarized in Table 3.

Table 3.
The definitions for disturbance categories and forests with no changes and their corresponding areas. The last row shows the total area, including detected forest disturbances and forest area with no change.
Figure 4 presents the forest disturbance detection with BFAST in NDVI TS of both TF and TDF. The yellow vertical line indicates the breakpoint that was registered as disturbance with a magnitude of change equal or lower than . In Figure 4A, a disturbance was detected on 02 December 2016 in a TF, and in Figure 4B, a disturbance was detected on 10 December 2016 in a TDF.
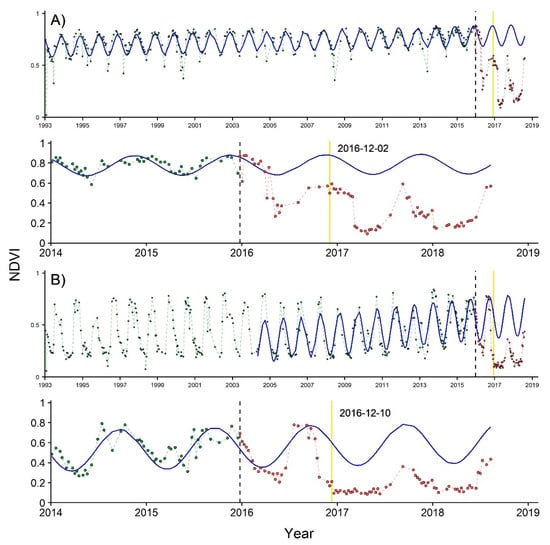
Figure 4.
NDVI time series from 1993 to 2018 with detected disturbances in two types of forest. (A) The first row shows the complete profile of a pixel in temperate forest, while the second row shows the same time series, but amplified to the 2014–2019 interval. (B) The same as (A) but for a pixel in tropical dry forest. The dashed vertical black line separates the observations of the historical period, represented by green points, from the ones of the monitoring period, represented by red points. The blue solid line indicates the modeled trend that is fitted in the historical period and projected into the monitoring period. Note that the start of the blue line also indicates the beginning of the stable historical period. The yellow vertical line indicates the date when a breakpoint was registered.
3.2. Accuracy Assessment of Detected Changes in TDF and in TF
Based on the independent reference sample, the labeled points were used to quantify the accuracy of the map of forest disturbances using confusion metrics weighted by area []. Table 4 presents the confusion matrices in both the number of samples and the area weighted probabilities. The change detection obtained a 96.52% overall accuracy estimated by the area weighted confusion matrix, and 68% and 86% of user’s accuracy for disturbances in TDF and in TF, respectively. Because each of the two disturbance classes occupied a small proportion of the map area, 0.13% and 0.07% for disturbances in tropical dry forest and in temperate forest, respectively, omissions in these classes had a large negative impact on the precision of the two forest disturbance classes. In the case of TDF–disturbance, the confusion matrix with number of samples shows that 11 points that were selected in the TDF–no change stratum but were identified as disturbances (TDF–disturbance). This omission error for TDF–disturbance has a large impact on the producer’s accuracy, since it occurs in a large TDF–no change stratum with 58% of the total map area. Because of this impact, the producer’s accuracy for TDF–disturbance decreased from 68% in a sample-based error matrix to barely 4% in an area-weighted matrix. Similarly, the producer’s accuracy of TF disturbances decreased from 86% to 4.1%. The results of accuracy assessment show that TF–disturbance had higher accuracy in both user’s and producer’s accuracies than TDF–disturbance.

Table 4.
Confusion matrix for accuracy assessment. The upper half of the confusion matrix was built with counts of samples and the lower half was based on the sample counts, but weighted by area proportions of the change detection map with categories of disturbances in tropical dry forest (TDF) and temperate forest (TF) and categories of no change in both forests.
3.3. Logistic Regression
3.3.1. Statistical Description of the BFAST Model Components
We extracted the BFAST trend and seasonal model components from the 100 verified pixels of disturbances (Table 4), including the amplitude, stable historical period length, magnitude, NA percentage, and R2. Since we are interested in the role of forest type in disturbance detection, we applied three models of logistic regressions, including all forests, only TDF and only TF.
We balanced the number of observations. In the forest model, we have 46 observations, 23 in each category (i.e., correct, or false). In the TDF–only model, we have 32 observations, 16 in each category, and in the TF–only model, we have 14 observations, 7 in each category. The statistics of the variables are presented in Table 5.

Table 5.
Statistics of BFAST model components in correct and false disturbance detections as explanatory variables in the logistic regression model. The statistics include the mean and standard deviations of each variable.
In the TDF–only dataset, the correct detections correspond to higher R2, slightly higher NA percentage, same magnitude, higher stable historical period length, and higher amplitude value. This seems to suggest that within the same TDF, the correct detections correspond to the BFAST model, with high values in R2, stable historical period length and amplitude, and perhaps slightly higher NA percentage. In the TF–only dataset, the correct detections correspond to higher R2, lower NA percentage, higher magnitude, higher stable historical period length, and similar but slightly lower amplitude. This seems to suggest that within the same TF, the correct detections correspond to BFAST model, with high values in R2 and stable historical period length. For both TDF and TF, when measured separately, higher values in R2, and stable historical period length are important for correct detection, while NA percentage does not seem to affect the correct or false detections.
3.3.2. Detection of Multi-Collinearity among the Variables
The VIF was calculated for each dataset (Table 6). For all forests, three variables showed a VIF > 2.5: forest type, amplitude and R2. We removed forest type and R2 from the dataset for the logistic regression model (LRM). Although amplitude also has VIF higher than 2.5, after removing forest type, the value of VIF for amplitude was lowered, and therefore, we included amplitude in the regression. In the case of TDF, the only two redundant variables were amplitude and NA percentage, so we eliminated NA percentage, as all forest models included amplitude as a significant variable (Section 3.3.3). Finally, for TF, the redundant variables were amplitude and R2 and we opted to include amplitude for the same reason as the case of TDF.

Table 6.
The Variance Inflation Factor of each BFAST component in the three logistic regression models (LRM) using all forests, TDF and TF as datasets. The components with underlined VIF values were included in the LRM.
3.3.3. Logistic Regression Models
The three fitted logistic regression models are presented in Table 7. The first model with all forests has the amplitude and stable historical period length as independent variables to predict forest disturbance. Both are statistically significant (p < 0.05) for the correct disturbance detection. The TDF–only model has amplitude as a significant predictor, and the TF–only model has stable historical period length as a predictor, however, it was not statistically significant.

Table 7.
The coefficients and significance of three logistic regression models: all forest, TDF–only, and TF–only. The significant independent variables (p < 0.05) in each logistic regression model are in bold font.
The odds ratio is calculated as the Euler’s constant (e) raised to the power of the estimate (β), and it represents the change in the odds of correctly identifying a disturbance depending on the independent variables. The odds ratio ranges from 0 to infinite. When its value is between 0 and 1, the independent variable decreases the odds of a correct detection; when it is larger than 1, the independent variable increases the odds of correct detection. All the independent variables have an odds ratio larger than 1, therefore all the independent variables in the regression model increases the odds of correct detection.
4. Discussion
4.1. Forest Disturbances in TDF and TF
The disturbance detection in TF obtained a higher accuracy than in TDF. This is in line with the finding from [] showing that the trend and seasonal model such as BFAST tends to yield higher accuracy in forests with less seasonality, such as those dominated by conifers, because this facilitates the discrimination between phenological changes and disturbances. Indeed, in our study area, the TDF has a very pronounced seasonality controlled mainly by humidity, with a rapid response to the onset of the rainy season, reflected in the drastic changes in NDVI. The variation in the precipitation from year to year might cause BFAST flags breakpoints that are triggered by interannual variations in the TDF phenology rather than disturbances [].
Additionally, in ARB, disturbances in TF are caused mainly by selective logging, forest fires, and recently by permanent conversion to avocado plantations. These activities happen on a larger scale and cause more severe damage to the forest than the subtle changes, such as those caused by shifting cultivation, which is the main type of forest disturbance in TDF. In our experiment, most detected disturbances had led to complete forest clearing instead of vegetation thinning.
4.2. Logistic Regression with All Forests
The logistic regression for all forests shows that amplitude and stable historical period length are significant variables with positive coefficient. Although the odds ratio of amplitude (342.09) is much higher than that of stable historical period length (1.17), since amplitude has a small value range (i.e., 0–1), the effect of its high odds ratio is balanced out. In fact, stable historical period length has higher significance value (p = 0.003) in the regression than amplitude (p = 0.029).
Since amplitude often acts as an indicator of forest type: higher amplitude usually corresponds to more seasonal forest such as TDF (see Figure 3). At a first glance, the positive relation between amplitude and correct disturbance detection seems contradictory knowing that TDF has lower accuracy than TF. Nevertheless, a closer look at our data shows two key aspects: (1) the false disturbances in TDF demonstrate a similar value and variation as TF false and correct; and (2) correctly identified disturbances had higher amplitude values, especially in TDF (see Table 5). Therefore, the significant effect of amplitude corresponds to the effect of TDF. This topic will be further discussed in the next section.
4.3. Forest-Type Specific Logistic Regression
The forest-type specific logistic regression shows that for TDF, the single most important predictor of correct or false detection is amplitude. As typical areas covered by TDF correspond to very pronounced seasonal NDVI patterns (i.e., high amplitude values, see Figure 3); low amplitude values could be used as an indicator of models that were fitted rather inaccurately, and therefore, are more prone to false detections. We consider that a main reason for this inaccurate fit is related to the presence of artifacts in the TS, which is not reflected in the NA percentage.
In the case of TF, stable historical period length was the most important variable, however, it was not statistically significant with p = 0.057. Since we have a low number of observations in the false disturbance category (n = 7), the effect of stable historical period length on correct/false disturbance identification might be obscured. Although it would be desirable to follow a sampling procedure to increase the number of false disturbances, it is difficult to identify these areas prior to the verification procedure.
4.4. General Considerations
The other two BFAST components, NA percentage and magnitude, did not show as significant variables in the disturbance detection. NA percentage was used as an indicator of the data quality in the entire TS; however, it does not necessarily represent the data quality in the modelled period (covered by the stable historical period length). We believe that a more relevant variable would be an indicator for the data quality in the stable historical period length, that will ultimately affect the BFAST model fit and disturbance detection. Additionally, other data quality indicators, such as those related to the presence of artifacts, might be of greater importance to the fit of the BFAST model and therefore affects the disturbance detection.
Magnitude is the variable that is often used in previous studies for eliminating false disturbances. Our study adopted the magnitude threshold of , which resulted from field verification. The lack of explanatory power of magnitude in the logistic regression is related to the fact that a threshold was already applied, and therefore, magnitude values higher than did not gave more information for discriminating between false and correct disturbances.
Previous studies [] showed that integrating components such as magnitude, slope, and amplitude for forest-type specific models improved disturbance detection. Based on our results, we found that, in addition, stable historic period length is an important factor as well in refining the results of forest disturbance detection with BFAST model.
5. Conclusions
This study evaluated the contribution of the components of BFAST model and the percentage of NAs in a time series to forest disturbance detection. Time series NDVI from Landsat spanning 1994–2018 was applied, employing BFAST model in both temperate forest and tropical dry forest and its accuracy was evaluated by 624 random sample points. Afterwards, BFAST model components, including goodness-of-fit (R2), magnitude, amplitude, length of the stable historical period, and the percentage of NA, were extracted from the time series data of the verified disturbances. The main findings are the following:
- (1)
- The disturbance detection yielded higher accuracy in the temperate forest than in the tropical dry forest.
- (2)
- The difference in accuracy is associated with the BFAST model components, especially the amplitude and stable historical period length.
- (3)
- Within the same forest type, the components affect disturbance detection. For TDF, the amplitude was the statistically significant factor, and for TF, the stable historical period length contributed most to the detection, however, with no statistical significance.
- (4)
- The percentage of NAs in a time series was not an important factor in disturbance detection.
This study confirmed that BFAST model components, though varying with forest type, play an important role in forest disturbance detection. To explore the full potential of these methods to map and quantify forest disturbances, future studies should evaluate different BFAST model components in combination with techniques that help reduce the signal-to-noise ratio. For example, variables that represent data quality in the stable historical period might be more relevant as a data quality indicator in the BFAST model fitting, and therefore, help distinguish between correct and false detected disturbances.
Author Contributions
Conceptualization and methodology, Y.G., J.V.S. and A.Q.; software J.V.S. and A.Q.; validation, Y.G., J.V.S. and J.O.L.-C.; writing—original draft preparation, Y.G.; writing—review and editing, Y.G. and J.V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Consejo Nacional de Ciencia y Tecnologia (CONACyT) grant number “Ciencia Basica” SEP-285349.
Data Availability Statement
The time series Landsat-5 TM, Landsat-7 ETM+, and Landsat-8 OLI data compilation and preprocessing were carried out in GEE. The scripts in R for disturbance detection by BFAST monitor are available through the link https://github.com/alequech/Change-forest-cover (accessed on 20 May 2021). The extraction of the trend and seasonal model components is available through the link https://github.com/JonathanVSV/BFAST_params_extr (accessed on 20 May 2021).
Acknowledgments
The authors acknowledge José Antonio Navarrete Pacheco for elaborating Figure 2 for the study area.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, Y.; Birdsey, R.A.; Phillips, O.L.; Jackson, R.B. The Structure, Distribution, and Biomass of the World’s Forests. Annu. Rev. Ecol. Evol. Syst. 2013, 44, 593–622. [Google Scholar] [CrossRef]
- Curtis, P.G.; Slay, C.M.; Harris, N.; Tyukavina, A.; Hansen, M.C. Classifying drivers of global forest loss. Science 2018, 361, 1108–1111. [Google Scholar] [CrossRef] [PubMed]
- Frolking, S.; Palace, M.W.; Clark, D.B.; Chambers, J.Q.; Shugart, H.H.; Hurtt, G.C. Forest disturbance and recovery: A general review in the context of spaceborne remote sensing of impacts on aboveground biomass and canopy structure. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W. An integrated Landsat time series protocol for change detection and generation of annual gap-free surface reflectance composites. Remote Sens. Environ. 2015, 158, 220–234. [Google Scholar] [CrossRef]
- Hansen, M.C.; Krylov, A.; Tyukavina, A.; Potapov, P.V.; Turubanova, S.; Zutta, B.; Ifo, S.; Margono, B.; Stolle, F.; Moore, R. Humid tropical forest disturbance alerts using Landsat data. Environ. Res. Lett. 2016, 11, 034008. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D. Atmospherically Resistant Vegetation Index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships Between NDVI, Canopy Structure, and Photosynthesis in Three Californian Vegetation Types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S. Evaluation of MODIS LAI, fAPAR and the relation between fAPAR and NDVI in a semi-arid environment using in situ measurements. Remote Sens. Environ. 2004, 91, 490–507. [Google Scholar] [CrossRef]
- Jackson, R.D.; Huete, A.R. Interpreting vegetation indices. Prev. Veter-Med. 1991, 11, 185–200. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. MODIS time-series imagery for forest disturbance detection and quantification of patch size effects. Remote Sens. Environ. 2005, 99, 462–470. [Google Scholar] [CrossRef]
- Neigh, C.S.; Bolton, D.K.; Diabate, M.; Williams, J.J.; Carvalhais, N. An Automated Approach to Map the History of Forest Disturbance from Insect Mortality and Harvest with Landsat Time-Series Data. Remote Sens. 2014, 6, 2782–2808. [Google Scholar] [CrossRef]
- Eckert, S.; Hüsler, F.; Liniger, H.; Hodel, E. Trend analysis of MODIS NDVI time series for detecting land degradation and regeneration in Mongolia. J. Arid Environ. 2015, 113, 16–28. [Google Scholar] [CrossRef]
- Lambert, J.; Denux, J.-P.; Verbesselt, J.; Balent, G.; Cheret, V. Detecting Clear-Cuts and Decreases in Forest Vitality Using MODIS NDVI Time Series. Remote Sens. 2015, 7, 3588–3612. [Google Scholar] [CrossRef]
- Fensholt, R.; Horion, S.; Tagesson, T.; Ehammer, A.; Ivits, E.; Rasmussen, K. Global-scale mapping of changes in ecosystem functioning from earth observation-based trends in total and recurrent vegetation. Glob. Ecol. Biogeogr. 2015, 24, 1003–1017. [Google Scholar] [CrossRef]
- Jamali, S.; Jönsson, P.; Eklundh, L.; Ardö, J.; Seaquist, J. Detecting changes in vegetation trends using time series segmentation. Remote Sens. Environ. 2015, 156, 182–195. [Google Scholar] [CrossRef]
- Reiche, J.; De Bruin, S.; Hoekman, D.; Verbesselt, J.; Herold, M. A Bayesian Approach to Combine Landsat and ALOS PALSAR Time Series for Near Real-Time Deforestation Detection. Remote Sens. 2015, 7, 4973–4996. [Google Scholar] [CrossRef]
- Gärtner, P.; Förster, M.; Kleinschmit, B. The benefit of synthetically generated RapidEye and Landsat 8 data fusion time series for riparian forest disturbance monitoring. Remote Sens. Environ. 2016, 177, 237–247. [Google Scholar] [CrossRef]
- Ghazaryan, G.; Dubovyk, O.; Kussul, N.; Menz, G. Towards an Improved Environmental Understanding of Land Surface Dynamics in Ukraine Based on Multi-Source Remote Sensing Time-Series Datasets from 1982 to 2013. Remote Sens. 2016, 8, 617. [Google Scholar] [CrossRef]
- Murillo-Sandoval, P.J.; Hilker, T.; Krawchuk, M.A.; Hoek, J.V.D. Detecting and Attributing Drivers of Forest Disturbance in the Colombian Andes Using Landsat Time-Series. Forests 2018, 9, 269. [Google Scholar] [CrossRef]
- Prada, M.; Cabo, C.; Hernández-Clemente, R.; Hornero, A.; Majada, J.; Martínez-Alonso, C. Assessing canopy responses to thinnings for sweet chestnut coppice with time-series vegetation indices derived from landsat-8 and sentinel-2 imagery. Remote Sens. 2020, 12, 3068. [Google Scholar] [CrossRef]
- Hamunyela, E.; Verbesselt, J.; Herold, M. Using spatial context to improve early detection of deforestation from Landsat time series. Remote Sens. Environ. 2016, 172, 126–138. [Google Scholar] [CrossRef]
- Vogeler, J.C.; Braaten, J.D.; Slesak, R.A.; Falkowski, M.J. Extracting the full value of the Landsat archive: Inter-sensor harmonization for the mapping of Minnesota forest canopy cover (1973–2015). Remote Sens. Environ. 2018, 209, 363–374. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Cohen, W.B.; Schroeder, T.A. Trajectory-based change detection for automated characterization of forest disturbance dynamics. Remote Sens. Environ. 2007, 110, 370–386. [Google Scholar] [CrossRef]
- Masek, J.G.; Goward, S.N.; Kennedy, R.E.; Cohen, W.B.; Moisen, G.G.; Schleeweis, K.; Huang, C. United States Forest Disturbance Trends Observed Using Landsat Time Series. Ecosystems 2013, 16, 1087–1104. [Google Scholar] [CrossRef]
- Huang, C.; Goward, S.N.; Masek, J.G.; Thomas, N.; Zhu, Z.; Vogelmann, J.E. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Environ. 2010, 114, 183–198. [Google Scholar] [CrossRef]
- Hirschmugl, M.; Steinegger, M.; Gallaun, H.; Schardt, M. Mapping Forest Degradation due to Selective Logging by Means of Time Series Analysis: Case Studies in Central Africa. Remote Sens. 2014, 6, 756–775. [Google Scholar] [CrossRef]
- Grogan, K.; Pflugmacher, D.; Hostert, P.; Kennedy, R.; Fensholt, R. Cross-border forest disturbance and the role of natural rubber in mainland Southeast Asia using annual Landsat time series. Remote Sens. Environ. 2015, 169, 438–453. [Google Scholar] [CrossRef]
- Schneibel, A.; Frantz, D.; Röder, A.; Stellmes, M.; Fischer, K.; Hill, J. Using Annual Landsat Time Series for the Detection of Dry Forest Degradation Processes in South-Central Angola. Remote Sens. 2017, 9, 905. [Google Scholar] [CrossRef]
- White, J.C.; Wulder, M.A.; Hermosilla, T.; Coops, N.C.; Hobart, G.W. A nationwide annual characterization of 25 years of forest disturbance and recovery for Canada using Landsat time series. Remote Sens. Environ. 2017, 194, 303–321. [Google Scholar] [CrossRef]
- Cohen, W.B.; Yang, Z.; Healey, S.P.; Kennedy, R.E.; Gorelick, N. A LandTrendr multispectral ensemble for forest disturbance detection. Remote Sens. Environ. 2018, 205, 131–140. [Google Scholar] [CrossRef]
- Frazier, R.J.; Coops, N.C.; Wulder, M.A.; Hermosilla, T.; White, J.C. Analyzing spatial and temporal variability in short-term rates of post-fire vegetation return from Landsat time series. Remote Sens. Environ. 2018, 205, 32–45. [Google Scholar] [CrossRef]
- Hislop, S.; Jones, S.; Soto-Berelov, M.; Skidmore, A.; Haywood, A.; Nguyen, T.H. A fusion approach to forest disturbance mapping using time series ensemble techniques. Remote Sens. Environ. 2019, 221, 188–197. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Schmidt, M.; Lucas, R.; Bunting, P.; Verbesselt, J.; Armston, J. Multi-resolution time series imagery for forest disturbance and regrowth monitoring in Queensland, Australia. Remote Sens. Environ. 2015, 158, 156–168. [Google Scholar] [CrossRef]
- Schultz, M.; Clevers, J.G.; Carter, S.; Verbesselt, J.; Avitabile, V.; Quang, H.V.; Herold, M. Performance of vegetation indices from Landsat time series in deforestation monitoring. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 318–327. [Google Scholar] [CrossRef]
- Dutrieux, L.P.; Verbesselt, J.; Kooistra, L.; Herold, M. Monitoring forest cover loss using multiple data streams, a case study of a tropical dry forest in Bolivia. ISPRS J. Photogramm. Remote Sens. 2015, 107, 112–125. [Google Scholar] [CrossRef]
- Grogan, K.; Pflugmacher, D.; Hostert, P.; Verbesselt, J.; Fensholt, R. Mapping Clearances in Tropical Dry Forests Using Breakpoints, Trend, and Seasonal Components from MODIS Time Series: Does Forest Type Matter? Remote Sens. 2016, 8, 657. [Google Scholar] [CrossRef]
- Platt, R.V.; Ogra, M.V.; Badola, R.; Hussain, S.A. Conservation-induced resettlement as a driver of land cover change in India: An object-based trend analysis. Appl. Geogr. 2016, 69, 75–86. [Google Scholar] [CrossRef]
- Jakovac, C.C.; Dutrieux, L.P.; Siti, L.; Peña-Claros, M.; Bongers, F. Spatial and temporal dynamics of shifting cultivation in the middle-Amazonas river: Expansion and intensification. PLoS ONE 2017, 12, e0181092. [Google Scholar] [CrossRef]
- Romero-Sanchez, M.E.; Ponce-Hernandez, R. Assessing and Monitoring Forest Degradation in a Deciduous Tropical Forest in Mexico via Remote Sensing Indicators. Forests 2017, 8, 302. [Google Scholar] [CrossRef]
- Smith, V.; Portillo-Quintero, C.; Sanchez-Azofeifa, A.; Hernandez-Stefanoni, J.L. Assessing the accuracy of detected breaks in Landsat time series as predictors of small scale deforestation in tropical dry forests of Mexico and Costa Rica. Remote Sens. Environ. 2019, 221, 707–721. [Google Scholar] [CrossRef]
- Tang, X.; Bullock, E.L.; Olofsson, P.; Estel, S.; Woodcock, C.E. Near real-time monitoring of tropical forest disturbance: New algorithms and assessment framework. Remote Sens. Environ. 2019, 224, 202–218. [Google Scholar] [CrossRef]
- Bullock, E.L.; Woodcock, C.E.; Olofsson, P. Monitoring tropical forest degradation using spectral unmixing and Landsat time series analysis. Remote Sens. Environ. 2020, 238, 110968. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.; Reichstein, M. Trend Change Detection in NDVI Time Series: Effects of Inter-Annual Variability and Methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- DeVries, B.; Verbesselt, J.; Kooistra, L.; Herold, M. Robust monitoring of small-scale forest disturbances in a tropical montane forest using Landsat time series. Remote Sens. Environ. 2015, 161, 107–121. [Google Scholar] [CrossRef]
- Gao, Y.; Quevedo, A.; Szantoi, Z.; Skutsch, M. Monitoring forest disturbance using time-series MODIS NDVI in Michoacán, Mexico. Geocarto Int. 2019, 1–17. [Google Scholar] [CrossRef]
- Pratihast, A.K.; Devries, B.; Avitabile, V.; De Bruin, S.; Kooistra, L.; Tekle, M.; Herold, M. Combining Satellite Data and Community-Based Observations for Forest Monitoring. Forests 2014, 5, 2464–2489. [Google Scholar] [CrossRef]
- Schultz, M.; Shapiro, A.; Clevers, J.G.P.W.; Beech, C.; Herold, M. Forest Cover and Vegetation Degradation Detection in the Kavango Zambezi Transfrontier Conservation Area Using BFAST Monitor. Remote Sens. 2018, 10, 1850. [Google Scholar] [CrossRef]
- Reiche, J.; Hamunyela, E.; Verbesselt, J.; Hoekman, D.; Herold, M. Improving near-real time deforestation monitoring in tropical dry forests by combining dense Sentinel-1 time series with Landsat and ALOS-2 PALSAR-2. Remote Sens. Environ. 2018, 204, 147–161. [Google Scholar] [CrossRef]
- LeGates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Chen, J.; Liu, H.; Chen, J.; Peng, S. Trend forecast based approach for cropland change detection using Lansat-derived time-series metrics. Int. J. Remote Sens. 2018, 39, 7587–7606. [Google Scholar] [CrossRef]
- Kennedy, R.E.; Yang, Z.G.; Cohen, W.B. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Saxena, R.; Watson, L.T.; Wynne, R.H.; Brooks, E.B.; Thomas, V.A.; Zhiqiang, Y.; Kennedy, R.E. Towards a polyalgorithm for land use change detection. ISPRS J. Photogramm. Remote Sens. 2018, 144, 217–234. [Google Scholar] [CrossRef]
- Naill, P.E.; Momani, M. Time Series Analysis Model for Rainfall Data in Jordan: Case Study for Using Time Series Analysis. Am. J. Environ. Sci. 2009, 5, 599–604. [Google Scholar]
- Ghaderpour, E.; Vujadinovic, T. The Potential of the Least-Squares Spectral and Cross-Wavelet Analyses for Near-Real-Time Disturbance Detection within Unequally Spaced Satellite Image Time Series. Remote Sens. 2020, 12, 2446. [Google Scholar] [CrossRef]
- Cuevas, R.; Núñez, N.; Guzmán, H.L. El Bosque Tropical Caducifolio En La Reserva de La BiosferaSierra Manantlan, Jalisco-Colima, Mexico. Bol. IBUG 1998, 5, 445–491. [Google Scholar]
- Borrego, A.; Skutsch, M. How Socio-Economic Differences Between Farmers Affect Forest Degradation in Western Mexico. Forests 2019, 10, 893. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Automated cloud, cloud shadow, and snow detection in multitemporal Landsat data: An algorithm designed specifically for monitoring land cover change. Remote Sens. Environ. 2014, 152, 217–234. [Google Scholar] [CrossRef]
- Roy, D.; Kovalskyy, V.; Zhang, H.; Vermote, E.; Yan, L.; Kumar, S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef] [PubMed]
- Devries, B.; Decuyper, M.; Verbesselt, J.; Zeileis, A.; Herold, M.; Joseph, S. Tracking disturbance-regrowth dynamics in tropical forests using structural change detection and Landsat time series. Remote Sens. Environ. 2015, 169, 320–334. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Hamunyela, E.; Roşca, S.; Mirt, A.; Engle, E.; Herold, M.; Gieseke, F.; Verbesselt, J. Implementation of BFAST monitor algorithm on Google Earth engine to support large-area and sub-annual change monitoring using Earth observation data. Remote Sens. 2020, 12, 2953. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data—Principles and Practices, 3rd ed.; CPC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Card, D.H. Using Known Map Category Marginal Frequencies to Improve Estimates of Thematic Map Accuracy. Photogramm. Eng. Remote Sens. 1982, 48, 431–439. [Google Scholar]
- Belsley, D.A.; Kuh, E.; Welsch, R.E. Regression Diagnostics—Identifying Influential Data and Sources of Collinearity; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1980. [Google Scholar]
- Johnston, R.; Jones, K.; Manley, D. Confounding and collinearity in regression analysis: A cautionary tale and an alternative procedure, illustrated by studies of British voting behaviour. Qual. Quant. 2018, 52, 1957–1976. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).