A Novel MIMO Radar Orthogonal Waveform Design Algorithm Based on Intelligent Ions Motion

Abstract

Orthogonal waveform design is one of the key technologies that affects the detection performance of MIMO radars. Most of the existing methods indirectly tackle this problem as an intractable nonconvex optimization and an NP-hard problem. In this work, we propose a novel waveform design algorithm based on intelligent ions motion optimization (IMO) to directly obtain a set of polyphase codes with good orthogonality. The autocorrelation sidelobe and cross-correlation sidelobe are first derived and subsequently integrated into evaluation functions for evaluating the orthogonality of polyphase codes. In order to effectively cope with the aforementioned problem, we present a strengthened IMO that is highly robust and converges rapidly. In the liquid state, an optimal guiding principle of same-charge ions is suggested to enhance global search ability and avoid falling into local optima. An ion updating strategy based on fitness ranking is presented to improve the search efficiency in the crystal state. Finally, the improved algorithm is employed to optimize the polyphase codes. The experimental results, compared with other state-of-the-art algorithms, show that the polyphase codes obtained by the proposed algorithm have better orthogonality.

1. Introduction

Recently, the great potential of multiple-input multiple-output (MIMO) radars [1,2,3] has attracted considerable attention in terms of waveform design and diversity [4,5,6,7,8,9]. Unlike traditional phased-array radars, MIMO radars transmit multiple orthogonal signals via several transmitters. The resulting waveforms enable the MIMO radars to perform more efficiently compared with other types of radar systems. The target detection capability of MIMO radars is significantly enhanced by design optimization of detector signals and treatment methods [10,11,12]. These improvements are gained by using the diversity of transmitting waveforms [13,14,15]. Currently, there are three main types of waveform designs and diversity methods, which are used to improve the signal-to-interference-plus-noise ratio (SINR) [4,5,8,16,17,18], beampattern shaping [6,11,19,20,21], and the correlation property [3,10,11,12,13,14,15,22,23,24,25]. The waveform design and diversity provide a distinctive ability that enable MIMO radars to be used widely in various fields [26,27,28], such as remote sensing, missile seekers, and resource exploration.

A number research activities have concerned the design of MIMO radar transmission waveforms by maximizing the SINR of the transmission code [16,17,18], or considering the transmission beampattern [19,20,21]. In [8], the authors present a constant envelope waveform design method in correlated MIMO radars, which achieves higher SINR and interference suppression ability compared with the covariance matrix approaches of the same type. Similarly, an efficient method with robust interference suppression and high SINR is proposed in [16] to generate the transmission waveform covariance matrix. The resulting optimization problem is solved in a short period of time. Additionally, the waveform covariance matrix design problem is transformed into a convex optimization problem in [17], and a min-max approach is used to maximize the worst-case SINR of the waveform covariance matrix. In [18], the authors present a coordinate descent algorithm used to obtain a set of phase sequences for improving SINR of the MIMO radar. In [6], the authors derive a retraction update strategy that allows monotonic cost function improvement while maintaining feasibility over the circle manifold. For quadratic cost functions (as is the case with beampattern deviation), the authors guarantee monotonic cost function improvement along with the proof of convergence to a local optimum. In [11], the authors considered the design of wideband MIMO radar waveforms for approximating the desired beampattern. A general design involving modulus, power, and energy constraints on the probing waveforms is introduced. In order to deal with the resulting non-convex design, a novel iterative algorithm with low computational complexity is proposed. Zhang et al. [19] considered the waveform design of MIMO radars to approximate a desired beam pattern while minimizing the cross-correlation sidelobes. In order to tackle this high-dimensional nonlinear problem, a residual neural network is used. A weighted objective function is developed to design the dual-functional waveform for the MIMO radar communication system in [20]. In [21], the researchers propose a novel technique to design the transmission waveforms for wideband MIMO radar systems. This technique is based on the optimization of the cross-spectral density matrix and achieves a low peak-to-average power ratio as desired in practical radar systems.

Waveform design for improving the correlation property has been a focus of the research community [22,23,24]. Alaie et al. [3] proposed a second-order cone programming algorithm to design a waveform for time division multiplexing MIMO radar systems. The optimization of sidelobe peaks is non-convex and NP-hard. In order to obtain the optimal set of sequences, it is converted into a convex optimization problem based majorization-minimization algorithm. In Ref. [10], a new approach is presented based on maximizing the mutual information between the random target impulse response and the received echoes with respect to the transmitted waveform. In [11], the authors present a technique for MIMO radar waveform design in the space-time domain, rendering the MIMO radar capable of satisfying the transmission beamforming constraint in the space-domain as well as the waveform orthogonality requirement in the time domain. In Ref. [12], a waveform design for MIMO radars in the presence of clutter is considered in two scenarios. In the first case, the robust waveforms are computed by minimizing the estimation error of the worst-case target realization. In the second case, the target estimation error of the scaled least square estimator is minimized. In Ref. [14], a greedy code, i.e., a search-based memetic algorithm, is proposed to design polyphase code sets with low autocorrelation sidelobe peaks and low cross-correlation peaks. In [22], the authors express the waveform autocorrelation in the frequency domain and use the proximal method of multipliers to tackle the resultant non-convex and non-smooth constrained optimization. Unlike existing methods, this method indirectly solves the weighted integrated sidelobe minimization involving a fourth-order objective function and constant modulus constraint. A nonlinear alternating direction method of multipliers is presented in [23] to directly deal with the bi-quadratic problem.

In this work, we focus on the minimization of the cross-correlation information of the transmission waveform under a nonconvex constant modulus constraint. This is modeled as a high-dimensional and nonconvex optimization problem (also known as an NP-hard problem), and it is difficult to solve this problem using conventional algorithms. As a nonlinear system, the intelligent optimization algorithm [29,30,31] is suitable for directly solving the high-dimensional nonconvex optimization problems. Therefore, we introduce a strengthened ion motion optimization with high robustness and fast convergence to optimize the polyphase codes under an evaluation function. The contributions of this work are listed below:

• We derive the autocorrelation and cross-correlation functions of polyphase codes.
• We design an evaluation function to evaluate the orthogonal performance of the polyphase codes.
• The improved ions motion algorithm (IIMO) is presented along with an optimal guiding principle of the same charge ions in the liquid state and an ion updating strategy based on the fitness ranking in the crystal state.
• The improved algorithm is employed to optimize the polyphase codes.

2. Orthogonal Waveform Design for MIMO Radar

In order to avoid interference between different signal channels, a MIMO radar is usually required to transmit the orthogonal signals. In general, good orthogonality refers to low autocorrelation and cross-correlation sidelobes of the transmitted waveforms. These properties ensure that a waveform is almost uncorrelated with its own time-shifted versions and any time-shifted waveforms of other transmission signals. This ensures that the transmission waveforms can be separated easily. As a result, the orthogonality of transmission waveforms directly affects the detection performance. In this work, a polyphase coding method with constant modulus is used to encode the MIMO radar waveform.

Suppose that a MIMO radar system comprises L transmitting signals and the length of each signal is N. Then, the transmitted signals are expressed as follows:

$$\begin{array}{c}{s}_l=\left[s_l\left(1\right),\cdots ,s_l\left(n\right),\cdots ,s_l\left(N\right)\right], l=1,2,\cdots ,L\hfill \\ s_l\left(n\right)=e^{j{\delta }_l\left(n\right)}, n=1,2,\cdots ,N\hfill \end{array}$$

(1)

where ${\delta }_l\left(n\right)$ represents the phase of the nth sub-pulse of the lth signal. Note that if the polyphase codes have M optional discrete phases, then the phase must be selected from Equation (2).

$${\delta }_l\left(n\right)=i\frac{2\pi }{M}, i=0,1,\cdots ,M-1$$

(2)

For a polyphase code set S, where the number of signals is L and the length of the signal is N, S is expressed by the L × N polyphase matrix as presented in (3):

$$S\left(L,N,M\right)=\left[\begin{array}{cccc}{\delta }_1\left(1\right)& {\delta }_1\left(2\right)& \cdots & {\delta }_1\left(N\right)\\ {\delta }_2\left(1\right)& {\delta }_2\left(2\right)& \cdots & {\delta }_2\left(N\right)\\ ⋮& ⋮& \cdots & ⋮\\ {\delta }_L\left(1\right)& {\delta }_L\left(2\right)& \cdots & {\delta }_L\left(N\right)\end{array}\right]$$

(3)

where the ith row of S represents the N phase of the ith signal, the number of rows of S represents the number of signals, and the number of columns of S represents the length of the signals.

According to the relevant properties, autocorrelation and cross-correlation functions of transmission signals are expressed as follows:

$$A\left(s_p,k\right)=\{\begin{array}{c}\frac{1}{N}{\displaystyle {\displaystyle \sum }_{n=1}^{N-k}}{e}^{j\left[{\delta }_p\left(n\right)-{\delta }_p\left(n+k\right)\right]},0\le k<N,p=1,2,\cdots ,L\hfill \\ \frac{1}{N}{\displaystyle {\displaystyle \sum }_{n=-k+1}^N}{e}^{j\left[{\delta }_p\left(n\right)-{\delta }_p\left(n+k\right)\right]},-N<k<0,p=1,2,\cdots ,L\hfill \end{array}$$

(4)

$$C\left(s_p,s_q,k\right)=\{\begin{array}{c}\frac{1}{N}{\displaystyle {\displaystyle \sum }_{n=1}^{N-k}}{e}^{j\left[{\delta }_p\left(n\right)-{\delta }_q\left(n+k\right)\right]},0\le k<N,p,q=1,2,\cdots ,L\hfill \\ \frac{1}{N}{\displaystyle {\displaystyle \sum }_{n=-k+1}^N}{e}^{j\left[{\delta }_p\left(n\right)-{\delta }_q\left(n+k\right)\right]},-N<k<0, p,q=1,2,\cdots ,L\hfill \end{array}$$

(5)

where A (s_p, k) denotes an aperiodic autocorrelation function; C (s_p, s_q, k) denotes an aperiodic cross-correlation function; k represents the discrete time; s_p and s_q represent the pth and the qth signals, respectively; and δ_p (n) denotes the phase of the nth sub pulse in s_p.

The autocorrelation function of an ideal orthogonal signal is an impulse and the cross-correlation function is zero, as presented in (6) and (7).

$$A(s_p,k)=\{\begin{array}{l}1, k=0\\ 0, k\ne 0\end{array}\begin{array}{c}, -N<k<N\end{array}$$

(6)

$$C(s_p,s_q,k)=0, -N<k<N$$

(7)

Notably, the ideal orthogonal signals do not exist in the real world. Thus, the signals partially satisfy the conditions presented in (6) and (7). Therefore, we consider minimizing the autocorrelation sidelobe peak energy and cross-correlation peak energy. The minimization of the total autocorrelation side lobe energy and cross-correlation energy using the fitness function for evaluating orthogonality is mathematically expressed as:

$$E=w_1{\displaystyle \sum }_{p=1}^L{\displaystyle \sum }_{k=-N+1}^{N-1}|A\left(s_p,k\right){|}^2+w_2{\displaystyle \sum }_{p=1}^{L-1}{\displaystyle \sum }_{q=p+1}^L{\displaystyle \sum }_{k=-N+1}^{N-1}|C\left(s_p,s_q,k\right){|}^2$$

(8)

When E is small, the orthogonality of the transmission signals is better. Thus, the minimization of (8) is almost equivalent to the design of a set of orthogonal transmission signals. The swarm intelligence optimization algorithms are a promising solution to effectively tackle this non-convex and NP-hard problem [29,30,31].

3. Improved Ions Motion Algorithm for Orthogonal Waveform Design

3.1. Ions Motion Algorithm

The swarm intelligence optimization algorithms do not depend on the analytic properties of the objective function. In addition, these optimization algorithms have a strong search ability, high robustness, and good adaptability. Therefore, they are able to achieve excellent performance in multimodal optimization and nonconvex optimization. The IMO is a novel intelligence optimization algorithm based on the idea of same-charge repulsion and attraction between anions and cations in physical phenomena. The candidate solutions for a given optimization problem in the IMO algorithm are divided into two groups, i.e., anions and cations. Moreover, each group of ions goes through the liquid phase and crystal phase. An ion moves under the action of other ions, and then searches for the optimal solution. The key steps of IMO mainly include the liquid phase and the crystal phase.

3.1.1. Liquid State

In the liquid phase, the forces of attraction among ions of opposite charge are greater than the forces of repulsion among ions of similar charge. This allows the ions to move freely. The IMO ignores the repulsion forces in this phase in order to explore the search space. The only factor for computing forces of attraction is the distance between the ions. This is equivalent to the exploration strategy in other optimization algorithms.

$$A_i\left(t+1\right)=A_i\left(t\right)+A{F}_i^t\left(C_{best}\left(t\right)-A_i\left(t\right)\right)$$

(9)

$$C_i\left(t+1\right)=C_i\left(t\right)+C{F}_i^t\left(A_{best}\left(t\right)-C_i\left(t\right)\right)$$

(10)

$$A{F}_i^t=\frac{1}{1+e^{-0.1/A{D}_i^t}}$$

(11)

$$C{F}_i^t=\frac{1}{1+e^{-0.1/C{D}_i^t}}$$

(12)

$$A{D}_i^t=\left|A_i\left(t\right)-C_{best}\left(t\right)\right|$$

(13)

$$C{D}_i^t=\left|C_i\left(t\right)-A_{best}\left(t\right)\right|$$

(14)

where t denotes the number of iterations, A_i (t) denotes the position of the ith anion, C_i (t) denotes the position of the ith cation, C_best (t) denotes the best cation in the tth iteration, and A_best (t) represents the best anion in the tth iteration.

3.1.2. Crystal State

The speed of ions increases rapidly in the crystal phase, i.e., the ions eventually converge to a solution in the search space. This is similar to the convergence in optimization problems. In order to resolve the local optima, the IMO model representing this phenomenon is provided as follows:

$$A_i\left(t+1\right)=\{\begin{array}{c}{A}_i\left(t\right)+{\varphi }_1\times \left(C_{best}\left(t\right)-1\right),r\le 0.5\hfill \\ A_i\left(t\right)+{\varphi }_1\times C_{best}\left(t\right),r>0.5\hfill \end{array}$$

(15)

$$C_i\left(t+1\right)=\{\begin{array}{c}{C}_i\left(t\right)+{\varphi }_2\times \left(A_{best}\left(t\right)-1\right),r\le 0.5\hfill \\ C_i\left(t\right)+{\varphi }_2\times A_{best}\left(t\right),r>0.5\hfill \end{array}$$

(16)

where ${\varphi }_1$, ${\varphi }_2$ denote the random numbers in [−1, 1] and r denotes a random number between 0 and 1.

3.2. Improved Ions Motion Algorithm

3.2.1. Same-Sex Optimal Guidance in Liquid State

In the liquid phase, the IMO algorithm focuses on the forces of attraction among opposite ions, i.e., the movement of the cations (anions) is only related to the attraction of the anions (cations). Note that the repulsive forces of the same-charge ions are ignored. In this case, the motion of ions is mainly affected by the optimal opposite-charge ions. Subsequently, the exploration ability of ions decreases, which means that the algorithm may fall into a local optimum during the process of optimization. In order to improve the exploration ability and maintain the diversity of anion (cation) populations in the liquid phase, we propose a same-charge optimal guidance strategy based on the mutual repulsion of the same-charge ions. By introducing the optimal feedback mechanism in the same-charge ions population, a same-charge optimal guidance in the liquid state is proposed, as shown as (17) and (18), for reducing the cohesiveness between the same-charge ion populations as well as enhancing the diversity of the ion population.

$$\begin{array}{cc}{A}_i\left(t+1\right)=\hfill & A_i\left(t\right)+r\times A{F}_i^t\times \left(C_{best}\left(t\right)-A_i\left(t\right)\right)+\left(1-r\right)\times A{F}_i^t\times (A_{best}\left(t\right)\hfill \\ & \hspace{1em}-A_i\left(t\right))\hfill \end{array}$$

(17)

$$\begin{array}{cc}{C}_i\left(t+1\right)=\hfill & C_i\left(t\right)+r\times C{F}_i^t\times \left(A_{best}\left(t\right)-C_i\left(t\right)\right)+\left(1-r\right)\times C{F}_i^t\times (C_{best}\left(t\right)\hfill \\ & \hspace{1em}-C_i\left(t\right))\hfill \end{array}$$

(18)

where t represents the number of iterations, A_i (t) represents the position of the ith anion, AF_i^t represents the attraction coefficient of the anion, C_i (t) represents the position of the ith cation, CF_i^t represents the attraction coefficient of the cation, and r denotes a random number between 0 and 1.

The main difference between (9) ((10)) and (17) ((18)) is that the repulsion of the optimal same-charge ions is added, as shown in the third term on the right of (17) ((18)). On one hand, the above process maintains the attraction of the optimal oppositely charge ions, which makes the population approach the optimal solution. On the other hand, the repulsive forces between the optimal same-charge ions are added to enable the ions to explore a wider search space to maintain the population diversity and avoid falling into local optima. Therefore, the same-charge optimal guidance effectively balances the relationship between convergence and diversity.

3.2.2. Crystal State Updating Based on Ranking Mechanism

The IMO algorithm is updated in the crystal state if two conditions are met, namely the optimal cation fitness value is greater than or equal to half of the worst cation fitness value and the optimal anion fitness value is greater than or equal to half of the worst anion fitness value. However, in some cases, the aforementioned conditions are difficult to meet, resulting in the decline in the development ability of the IMO algorithm and the lack of convergence. Therefore, in this work, we propose a crystal-updating method based on the ranking mechanism. The cations and anions are sorted in descending order according to their fitness values as shown in (19) and (20), respectively. Then, they are divided into three levels: excellent level, medium level, or poor level. We adopt different updating methods for different levels of ions.

$$Fit{C}_i\left(t\right)=\frac{E{C}_i\left(t\right)+1}{P+1}$$

(19)

$$Fit{A}_i\left(t\right)=\frac{E{A}_i\left(t\right)+1}{P+1}$$

(20)

where P denotes the number of ions, EC_i (t) denotes the fitness value of the ith cation calculated using (8), and EA_i (t) denotes the fitness value of the ith anion calculated using (8).

The ions in the excellent level adopt the following updating methods:

$$A_i\left(t+1\right)=rand\left(\left[A_{best}\left(t\right)-\frac{1}{t^4},A_{best}\left(t\right)+\frac{1}{t^4}\right]\right)$$

(21)

$$C_i\left(t+1\right)=rand\left(\left[C_{best}\left(t\right)-\frac{1}{t^4},C_{best}\left(t\right)+\frac{1}{t^4}\right]\right)$$

(22)

where t denotes the number of iterations and rand ([a, b]) represents a random number between a and b.

The ions in the medium level use the following updating methods:

$$A_i\left(t+1\right)=A_i\left(t\right)+rand()\times \left(A_{best}\left(t\right)-A_i\left(t\right)\right)+rand()\times \left(A_{best}-A_i\left(t\right)\right)$$

(23)

$$C_i\left(t+1\right)=C_i\left(t\right)+rand()\times \left(C_{best}\left(t\right)-C_i\left(t\right)\right)+rand()\times \left(C_{best}-C_i\left(t\right)\right)$$

(24)

where t denotes the number of iterations, rand ( ) represents a random number between 0 and 1, C_best denotes the best cation, and A_best denotes the best anion.

The ions in the poor level apply the following updating methods:

$$A_i\left(t+1\right)=C_i\left(t+1\right)=floor\left[rand\left(L,N\right)\right]\times \left(M-1\right)\times \frac{2\pi }{M}$$

(25)

3.3. Orthogonal Waveform Optimization

3.3.1. Ions Initialization

In order to meet the requirements of the polyphase code, the initial population of anions and cations is transformed into a matrix. The anions and cations are randomly generated, and each ion is composed of sub-pulse phases.

$$C=\left[\begin{array}{cccc}{c}_{11}& c_{12}& \cdots & c_{1N}\\ c_{21}& c_{22}& \cdots & c_{2N}\\ ⋮& ⋮& \cdots & ⋮\\ c_{L1}& c_{L2}& \cdots & c_{LN}\end{array}\right]$$

(26)

$$A=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1N}\\ a_{21}& a_{22}& \cdots & a_{2N}\\ ⋮& ⋮& \cdots & ⋮\\ a_{L1}& a_{L2}& \cdots & a_{LN}\end{array}\right]$$

(27)

For the sub-pulses a_ij and c_ij, the value is in the range $\left\{0,\frac{2\pi }{M},\frac{4\pi }{M},\cdots ,\left(M-1\right)\frac{2\pi }{M}\right\}$, $i=1,2,\cdots ,L$, $j=1,2,\cdots ,N$. The ions are initialized using (25).

3.3.2. Implementation Process

Step 1: Initialize parameters L, N, and the maximum number of iterations T.

Step 2: Generate the initial population including P/2 anions and P/2 cations. The anions and cations are randomly generated according to (26) and (27).

Step 3: Calculate the fitness value. The fitness value of each anion and cation is calculated according to (8). Afterward, the optimal value and the positions of anion and cation are recorded.

Step 4: Liquid state. The ions are updated in the liquid state according to (17) and (18).

Step 5: Solid state. The rankings of cation and anion are calculated according to (19) and (20). Note that different types of ions are updated according to (21)–(25).

Step 6: Analyze if the maximum number of iterations has been reached. If yes, output the best ion. Otherwise, return to Step 3.

3.4. Computational Complexity

Assuming that in each generation, the population size is P, the dimension of the decision variable is L × N, and the dimension of the objective function is m, then the complexity of IIMO is as follows: the liquid state requires O (PLN/2) computations; the solid state requires O (PLN/2) computations; calculating the fitness value requires O (PLNm) computations; updating ions population requires O (PLN + PLNm) computations. Thus, the overall complexity of one generation in IIMO is O (PLNm).

In addition, the complexity of IMO [29] is O (PLNm), the complexity of particle swarm optimization (PSO) [30] is O (PLNm), and the complexity of enhanced ions motion optimization (EIMO) [32] is O (PLNm).

To summarize, the complexity of our algorithm is similar to other algorithms.

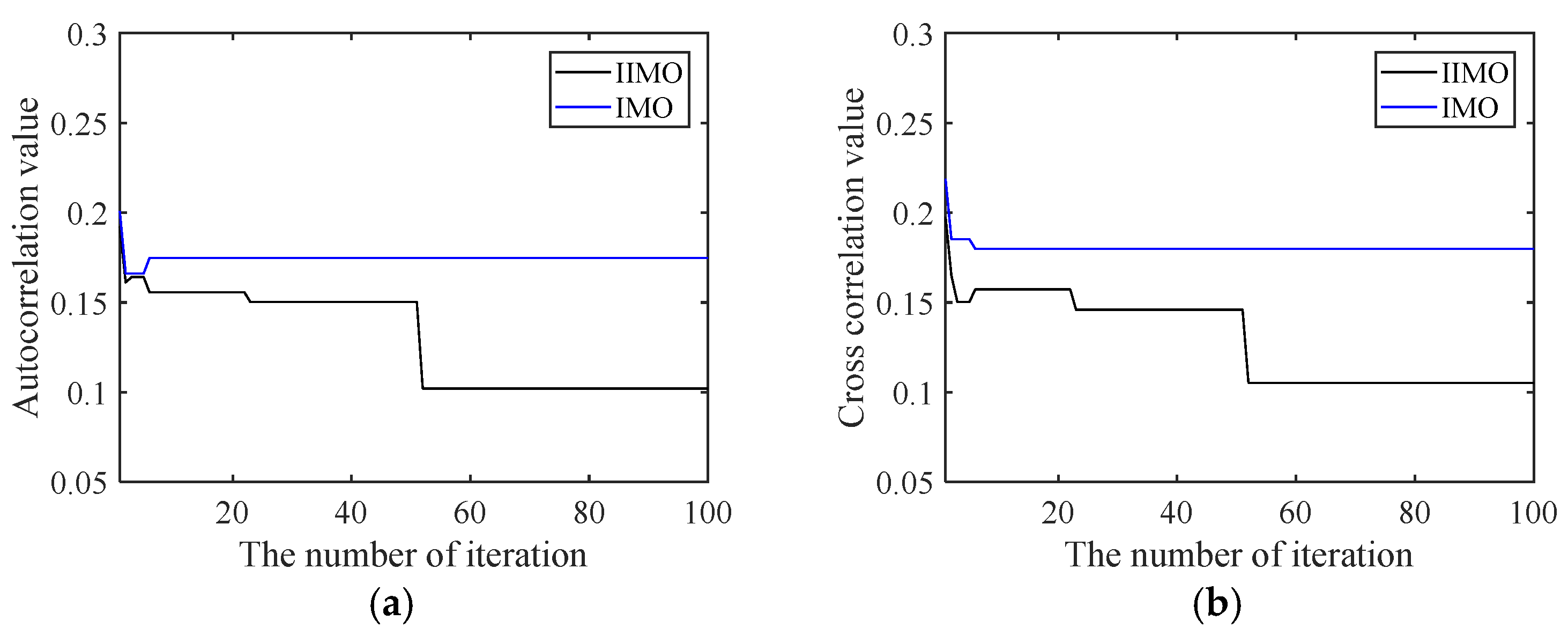
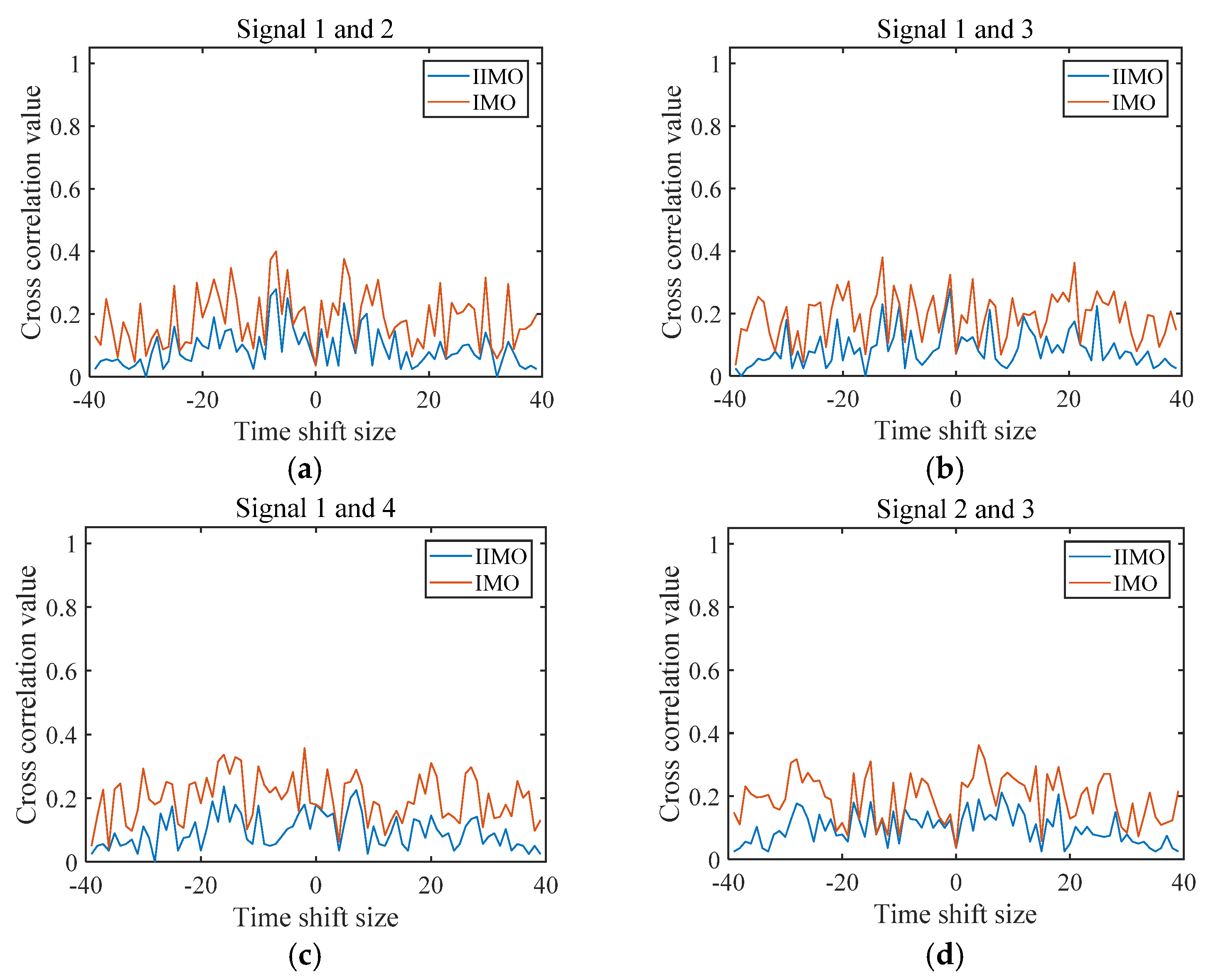
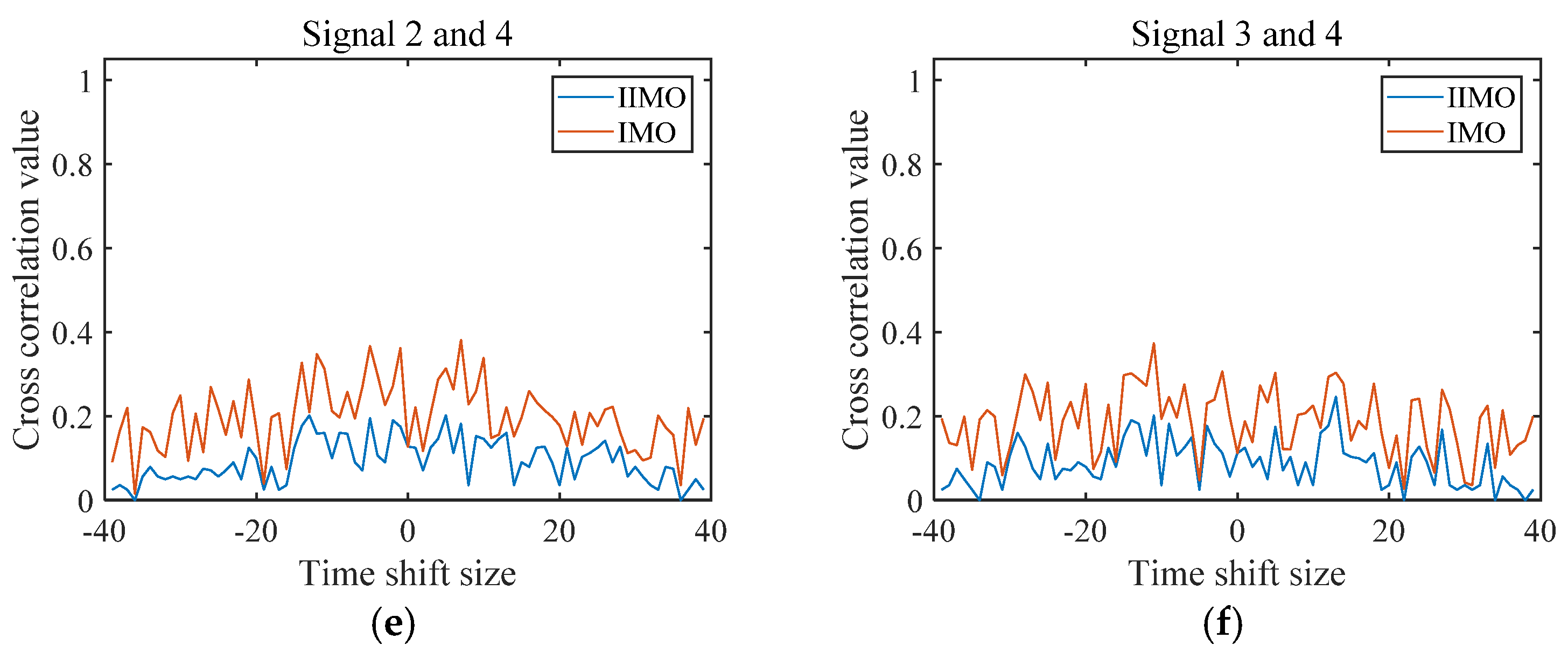
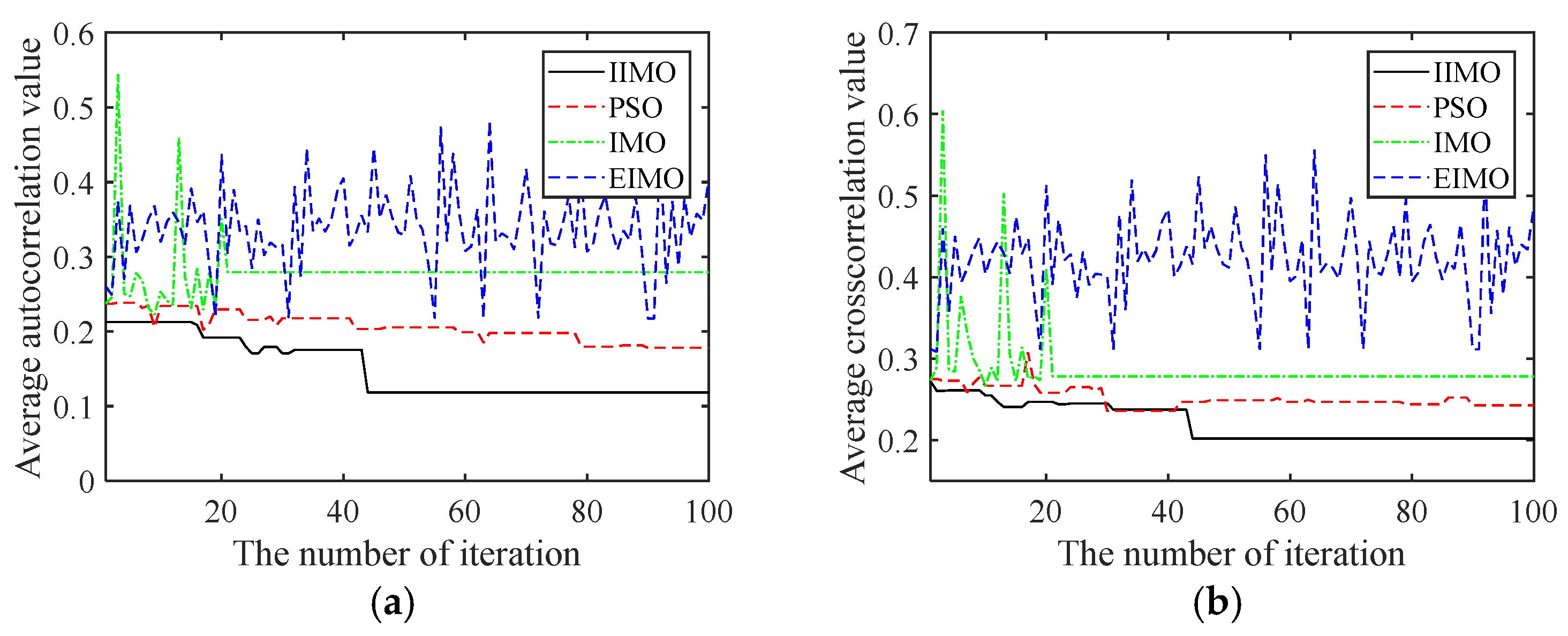
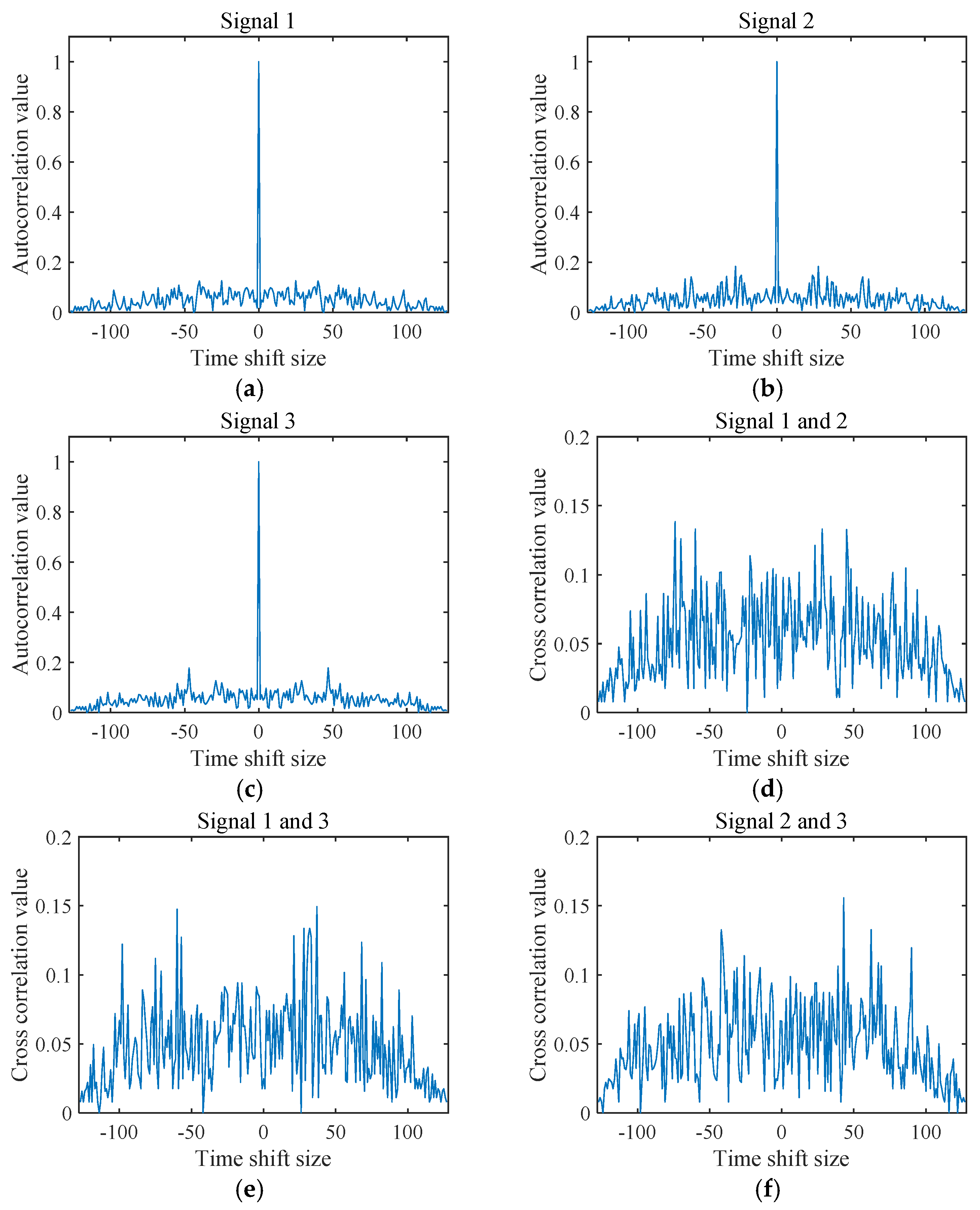
4. Experimental Results and Analysis

All experiments were implemented on a computer with an Intel (R) Core (TM) i5-8265u [email protected] with memory of 8.00 GB. The development environment was MATLAB R2018b. In order to evaluate the performance of our algorithms (IIMO), we carried out simulation experiments and compared them with particle swarm optimization (PSO) [30], IMO [29], and enhanced ions motion optimization (EIMO) [32]. The comparative criteria were the average and standard deviation of the best solutions obtained over 50 independent runs. The experimental parameters were set as follows: the number of signals L = 4, the signal length N = 40, the number of signals L = 3, the signal length N = 128, the maximum number of iterations T = 100, and the number of initial population P = 100.

In order to verify the effectiveness of the improved algorithm presented in Section 3.2, we compared IMO and IIMO. The experimental results are presented in Figure 1 and Figure 2. As presented in Figure 1, it is evident that in the early stage of evolution, the IMO is unstable and the curve oscillates. Finally, it converges to the local optimum. At the same time, the IIMO finds substantially better average autocorrelation and cross-correlation values. This means that the IIMO has a better capability to perform a global search. In Figure 2, the IIMO obtains better average auto-correlation values as well as the cross-correlation values compared with IMO. Therefore, the improved evolutionary strategy in the liquid phase of IIMO enhances the diversity of the population and avoids local convergence.

Figure 3 and Figure 4 present the autocorrelation and the cross-correlation of the optimal polyphase codes obtained by IMO and IIMO under L = 4 and N = 40, respectively. As presented in Figure 3 and Figure 4, the polyphase codes obtained by the IIMO in this work achieved lower autocorrelation side lobe values and cross-correlation side lobe values than IMO in all cases. These showed that the proposed algorithm IIMO has a much better convergence accuracy, improves the orthogonal performance of the transmitting signal set, as well as effectively reduces the interference between the diverse signals. These results further verify the effectiveness of the proposed algorithm.

According to the convergence curves presented in Figure 5, we concluded that the proposed IIMO always achieves lower average autocorrelation and cross-correlation values compared with IMO, PSO, and EIMO for same number of iterations. At the end of the iterations, the global optimal average autocorrelation and cross-correlation values obtained by the IIMO algorithm were significantly lower compared with the values obtained by the other three algorithms. The curve of IIMO tended to be stable when the number of iterations is 45. Note that although the IMO is unstable until the number of iterations reaches 20, the accuracy is low. Therefore, we proved that the convergence accuracy and convergence speed of IIMO are significantly better compared with IMO. Notably, the PSO curve tended to be stable when the number of iterations reached 90, while the curve of EIMO was consistently unstable and the algorithm did not converge. In short, the proposed algorithm IIMO not only avoids falling into local optima, but also has a higher convergence accuracy and faster convergence speed.

In order to further verify the performance of IIMO, we performed experiments with different numbers and lengths of signals. Figure 6 depicts the autocorrelation curve and the cross-correlation curve of the optimal polyphase codes obtained by using the IIMO for L = 3 and N = 128. It is evident from Figure 6 that the signal set optimized by the proposed algorithm performed well in terms of autocorrelation and cross-correlation.

5. Conclusions

In this work, we constructed a novel waveform design algorithm based on intelligent ions motion optimization called IIMO to obtain the orthogonal polyphase codes. First, we derived the autocorrelation sidelobe function and cross-correlation sidelobe function and then integrated them into the evaluation functions. This was accomplished to evaluate the orthogonality of the polyphase codes. From the perspective of the poor diversity maintenance and convergence performance of IMO in dealing with nonconvex optimization and NP-hard problems, an optimal guiding principle of the same-charge ions was suggested to enhance the global search ability and avoid falling into local optima in the liquid state. In addition, an ion-updating strategy based on fitness ranking was proposed to improve the search efficiency in the crystal state. Finally, to validate the competitiveness of the proposed method, we conducted a comprehensive experimental comparison with three state-of-the-art algorithms, IMO, PSO, and EIMO. The experimental results showed that the polyphase codes obtained by the proposed algorithm satisfy orthogonality.