Abstract
As a special micro-motion feature of rotor target, rotational angular velocity can provide a discriminant basis for target classification and recognition. In this paper, the authors focus on an efficient rotational angular velocity estimation method of the rotor target is based on the combination of the time–frequency analysis algorithm and Hough transform. In order to avoid the problems of low time–frequency resolution and cross-term interference in short-time Fourier transform and Wigner–Ville distribution algorithm, a modified short-time fractional Fourier transform (M-STFRFT) is proposed to obtain the time-FRFT domain (FRFD)-frequency spectrum with the highest time–FRFD–frequency resolution. In particular, an orthogonal matching pursuit (OMP)-based algorithm is proposed to reduce the computational complexity when estimating the matched transform order in the proposed M-STFRFT algorithm. Firstly, partial transform order candidates are selected randomly from the complete candidates. Then, a partial entropy vector corresponding to partial transform order candidates is calculated from the FRFT results and utilized to reconstruct the complete entropy vector via the OMP algorithm, and the matched transform order can be estimated by searching minimum entropy. Based on the estimated matched transform order, STFRFT is performed to obtain the time–FRFD–frequency spectrum. Moreover, Hough transform is employed to obtain the energy accumulation spectrum, and the micro-Doppler parameter of rotational angular velocity can be estimated by searching the peak value from the energy accumulation spectrum. Both simulated data and measured data collected by frequency modulated continuous wave radar validate the effectiveness of the proposed algorithm.
1. Introduction
The micro-Doppler (m-D) effect is a frequency modulation (FM) induced by the micro-motion [1,2,3], including rotation, vibration, precession, and nutation, which widely exists in many objects or their structures, such as rotors of a helicopter, warhead in mid-phase, running vehicle engines, and so on. As the m-D effect can provide abundant information about a target’s motion, it has attracted extensive application in target imaging, detection, recognition, and classification. The m-D effect of radar echo signals usually behaves as the nonlinear and time-varying frequency in a narrow frequency band, which is related to the target structure, micro-motion property, and the carrier frequency of the transmitting signal [4,5]. This valuable relationship may help realize micro-motion parameter estimation based on m-D distribution signatures in the time–frequency domain.
By contrast with the Fourier transform (FT), the time–frequency analysis class transforms not only provide joint distribution information in the time domain and frequency domain, but also clearly describe the relationship between signal frequency and time. Therefore, they are widely employed in micro-motion parameter estimation [6,7]. Generally, time-frequency analysis class transforms can be divided into two categories: (1) linear time–frequency transform, such as short-time Fourier transform (STFT) and continuous wavelet transform (CWT) [8]; (2) nonlinear time–frequency transform, including Wigner–Ville distribution (WVD) and Cohen class distribution [9].
As a typical algorithm of linear time–frequency transform, STFT has received wide attention and been applied in several fields, such as the instantaneous frequency estimation [10] and the enhancing of spectral resolution [11]. Although these methods have achieved effective performance in parameter estimation and low computational complexity, respectively, the STFT algorithm still suffers from poor concentration [12]. WVD, as the most basic Cohen class bilinear time–frequency distribution, was first proposed by Wigner in quantum mechanics, and then was first applied to signal analysis by Ville [13]. It not only essentially distributes the signal energy in the time–frequency plane, but also has a good time–frequency resolution. However, the existence of cross-term makes it have false information when analyzing multicomponent signals [14,15]. In view of this problem, several studies have been in-depth conducted by many scholars, such as pseudo Wigner–Ville distribution (PWVD) [16] and reassigned smoothed pseudo Wigner–Ville distribution (RSPWVD) [17]. Since Hough transform can map the time–frequency distribution on the parameter space through achieving energy accumulation along the Doppler frequency change rule of the signal, it is usually used to estimate the micro-Doppler parameters from the time–frequency domain spectrum. The Hough transform was combined with STFT, WVD, PWVD, and RSPWVD for parameter estimation in the Hough–STFT algorithm [18], Hough–WVD algorithm [15], Hough–PWVD algorithm [6], and Hough–RSPWVD algorithm [19], respectively. In these algorithms, the correct micro-Doppler parameters can be estimated from parameter candidate sets by finding the location of the maximal Hough integration in these algorithms. Although the time–frequency analysis algorithms mentioned above can realize the estimation of micro-Doppler parameters, they are still plagued by low time–frequency resolution and cross-term interference.
The fractional Fourier transform (FRFT) [20,21] is a generalization of the Fourier transform with an additional transform order parameter and was first proposed by Victor Namias in 1980 [22]. Because of the best energy concentration in the FRFT domain (FRFD) with a certain order in terms of the chirp signal, several implementations and fast computational algorithms of FRFT have been derived in recent years; also, they are widely applied in radar signal processing. Inspired by sparse Fourier transform (SFT) [23] and Pei’s discrete FRFT [24], a novel sparse discrete FRFT (SDFRFT) was proposed by Liu et al. to reduce the computational complexity when dealing with large data sets, which are sparsely represented in the FRFD [25]. Chen et al. proposed adaptive sparse fractional Fourier transform algorithm and used it in fast and refined processing of radar maneuvering target [26]. These algorithms implement FRFT and improve the effectiveness of FRFT through sparse representation. However, in the essential stage of the matched transform order estimation, these algorithms still use the traditional search method or the combination of polynomial phase transform and accurate search method, which are more time-consuming and will increase the computational complexity. However, the FRFT only reveals the signal energy distribution in FRFD under the matched transform order and fails to show the changes of FRFD-frequency with time. In order to introduce the FRFT to the traditional time–frequency representation, the short-time fractional Fourier transform (STFRFT) was proposed [27,28], which draws the process of windowing in STFT into FRFT, to clarify the instantaneous FRFD-frequency and display the time and FRFD information jointly in the time-FRFD plane. With higher concentration and no interference of cross-term, the STFRFT could provide tight support for the signals and eliminate the interference [29,30]. An effective algorithm based on STFRFT is proposed for target detection and m-D signal extraction, in which the radar echoes of sea target with transaction and rotation movement can be approximated as the sum of linear frequency modulated signals within a short time [31]. The concept of SFT was also introduced to STFRFT to achieve high time–FRFD–frequency resolution and low complexity of time–frequency distribution [32]. However, these STFRFT-based algorithms do not give an effective solution to the estimation of the matched transform order. It is common knowledge that the transform order is important and essential in FRFT, where FRFT or STFRFT will achieve the best performance while choosing the optimal transform order related to the chirp rate [33,34]. Therefore, it is of great significance to study an effective and fast matched transform order estimation algorithm for the application of FRFT or STFRFT. Serbes and Aldimashki [35] proposed a fast and accurate matched transform order estimation method using the golden section search (GSS)-based FRFT algorithm. Guan et al. [36] proposed a grading iterative search method to increase the estimation accuracy and calculation speed of the matched transform order. Both the golden section search method and the grading iterative search method require that the amplitude spectrum of FRFT must be unimodal. However, these methods are no longer applicable for the FRFT amplitude spectrum with Doppler frequency of quasi-linear frequency modulation signal, which is multimodal. The main reason is that the multimodal amplitude spectrum will make the method fall into local iterative convergence, resulting in a large error of matched transform order estimation.
In this paper, we propose a novel modified short-time fractional Fourier transform (M-STFRFT) algorithm to estimate the micro-Doppler parameter of rotational angular velocity. The contributions of this paper can be summarized as: (1) Interested in the framework of rotational angular velocity estimation based on the time–frequency analysis algorithm and Hough transform, instead of the STFT and WVD algorithm, we combine the STFRFT algorithm and Hough transform to realize the rotational angular velocity estimation. The rotational angular velocity can be estimated by searching the peak value from the energy accumulation spectrum obtained by Hough transform in the micro-Doppler parameter space. (2) In order to avoid the local iterative convergence in the GSS-based algorithm and solve the heavy computational complexity in the traditional search method, we propose a novel orthogonal matching pursuit (OMP)-based matched transform order estimation method in the M-STFRFT algorithm. Several comparative experimental results based on both simulated data and measured data are implemented to verify the effectiveness of the proposed algorithm in solving the contradiction between the estimation accuracy and the efficiency and avoiding the problem of local iterative convergence in the matched transform order estimation. From the results, we can conclude that the proposed algorithm is more effective and stable in rotational angular velocity estimation than GSS-based FRFT method proposed in [35] and other mentioned time–frequency analysis estimation algorithms.
The rest of this paper is organized as follows. The echo model and time–frequency analysis of FRFT are reviewed in Section 2. The proposed estimation algorithm of rotational angular velocity based on modified short-time fractional Fourier transform is summarized in Section 3. Section 4 verifies the effectiveness of the proposed algorithm by simulated experiments. Conclusions are presented in Section 5.
2. Fundamental Knowledge
2.1. Echo Model
When an aircraft target is observed by ground-based radar, the received signal is composed of echoes reflected by multiple scatterers. For targets with rotors, such as a helicopter or propeller aircraft, the echo contains not only the translation movement of scatterers on the fuselage but also the fretting characteristics of the scatterers on the rotor blades. In the following discussion, we take the helicopter as an example; the special geometry between radar and a helicopter is shown in Figure 1a, in which the distance between the radar and rotor target center is denoted as RC, and the angle of pitch is denoted as β. Considering the 2-D slant-range plane, the simplified geometry is shown in Figure 1b. A radar coordinate system XOY and target coordinate system X′O′Y′ are set up, in which the rotor center is denoted as O′. The rotation radius of scatterer F on the rotor blade is assumed to be r—i.e., the distance from F to O′ is r—and the distance from F to the radar is denoted as RF. The scatterer F rotates around the target coordinate system center O′ with a rotational angular velocity ω, and the rotation angle at the initial time is denoted as θ0. It is assumed that the radial velocity of the helicopter’s translational motion is v.
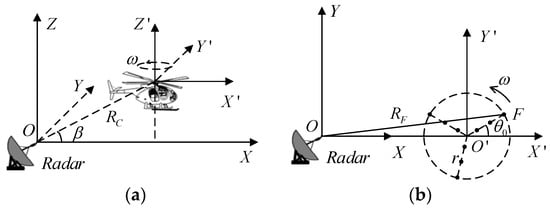
Figure 1.
Geometry between radar and rotor target: (a) space geometry; (b) 2-D plane geometry.
Considering the far field condition, the instantaneous distance between the scatterer F and the radar can be written as:
where tm = mTr is the slow time, m is the m-th echo pulse, and Tr is the pulse repetition interval.
In this paper, we take the linear frequency modulation (LFM) as the transmitted signal, which can be expressed as:
where is the rectangular window, is the fast time, Tp is the pulse width, fc is the signal carrier frequency, μ is the chirp rate, and is the total time. There are two different time variables and t in the transmitted signal described in Equation (2). The reason is that the signal carrier frequency fc exists on the whole pulse transmission time axis, while the chirp rate μ is used to adjust the change of Doppler frequency within a pulse. The echo signal of scatterer F can be expressed as:
where σ is the scattering coefficient of the scatterer F, Ta is the observation time, and c is the speed of light. The target echo signal after pulse compression can be expressed as:
where B is the signal bandwidth, λ is the wavelength, and denotes the white Gaussian noise signal. By taking the derivative of the phase, the micro-Doppler frequency can be obtained as:
It can be seen from Equation (5) that the Doppler frequency of the scatterer echo on the rotor blade is related not only to the radial velocity v of the translational movement but also to the rotational angular velocity ω of the rotating component and the rotor blade length r. In a short observation time, the change of rotation angle ωtm is quite small, the trigonometric function is expanded and can be approximated by Taylor series expansion, that is, sin ωtm ≈ ωtm and cos ωtm ≈ 1. We can rewrite Equation (5) as:
As we can see from Equation (6) that the Doppler frequency of the scatterer echo on rotor blades after translation movement compensation is a linear function of time tm, which indicates that the scatterer echo on rotor blades can be expressed as an LFM signal.
2.2. Time-Frequency Analysis
FRFT can be interpreted as a rotation of Fourier transform with the transform angle α in the time–frequency plane, it is defined by means of the transform kernel Kp (tm, u), and can be expressed as:
where FRFTp(u) is the result of FRFT of signal sF(tm) corresponding to the transform order p, Fp is the operator of FRFT, and Kp(tm,u) is indicated by:
where k is an integer, α is the transform angle, and α = pπ/2, is the impulse function.
As we can see from Equation (7) that the definition of FRFT implies that it is the decomposition into the chirp bases Kp (tm,u), so the result of FRFT under a proper transform order, which is called the matched transform order, of the chirp signal is an impulse. In other words, the result of the FRFT of the signal is the most concentrated in the matched transform order. As a matter of fact, if the chirp rate of the signal sF(tm) is μ0, the matched transform order is p0 = 2α0/π, where α0 is the matched transform angle and can be expressed as [26,31]:
where S is the scale factor introduced in Reference [37], and , fr is the pulse sample frequency, that is the pulse repetition frequency.
In Equation (7), the variable u represents a new physical quantity extended from the frequency concept and is termed the FRFD-frequency, so the FRFT can also be interpreted as the FRFD-spectrum, which is the chirp-multiplied and scaled Fourier domain spectrum that consists of the initial frequencies of the chirp signal. However, FRFT is not a strict time–frequency analysis algorithm, because it cannot provide the instantaneous frequency modulation at any specified moment during the observation duration. It is well known that as an improvement of FT, the STFT can represent the energy of a signal in the time–frequency domain with a sliding window, where the time–frequency spectrum can be obtained by intercepting each short signal to do FT and arranging the obtained spectrum along the time axis. Similarly, by multiplying the signal with a window before taking the FRFT, another time–frequency analysis method of STFRFT can be obtained as:
where STFRFTp(tm,u) is the time–FRFD–frequency spectrum, and g(tm) is the window function. In this paper, the commonly used Gaussian window is regarded as the window function, which is the optimal window [30] and can be expressed as:
where σ is the standard deviation.
In order to distinguish the results of STFRFT from those with the same window function but different transform order, it is usually called the p-th order STFRFT in some cases. The window with short time support is capturing a portion of the signal around the window center, and the FRFT of this portion is viewed as the instantaneous FRFD-spectrum of the chirp signal. By moving the window along the time axis, the STFRFT can be realized, and the time–FRFD–frequency spectrum is obtained, which can provide not only the FRFD-frequency contents, but also how they change by time.
3. The Proposed Rotational Angular Velocity Estimation Algorithm
One can see from Equation (10) that the result of STFRFT is not only a time–FRFD–frequency spectrum, but also related to the transform order p, and there is an optimal time-FRFD- frequency spectrum with the highest time–FRFD–frequency resolution in the case of the matched transform order p0 or the matched transform angle α0. In practice, the matched transform order p0, which is an unknown variable, should be estimated from the FRFT result and used in STFRFT to obtain the optimal time–FRFD–frequency spectrum. As a parameter space transform algorithm, Hough transform can realize the energy accumulation from the time–FRFD–frequency spectrum of the target echo. The rotational angular velocity can be estimated according to the peak value of the energy accumulation. The flowchart of the rotational angular velocity estimation method based on STFRFT and Hough transform is shown in Figure 2.
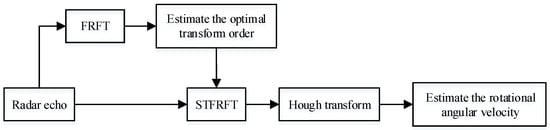
Figure 2.
Estimation method of rotational angular velocity based on STFRFT and Hough transform.
As we can see from Figure 2, in order to obtain the time–FRFD–frequency spectrum with the highest time–FRFD–frequency resolution and accurately estimate the rotational angular velocity, the transform order p used in STFRFT should be estimated and as close as possible to the matched transform order p0.
3.1. The Traditional Search Method of Estimating the Matched Transform Order
In the traditional search method, the estimation of the matched transform order is to take p as a variable with a search step size of Δp and calculate FRFT of the signal in a two-dimensional energy distribution on the (p,u) plane. All the discretization values of the transform order are regarded as the candidate values. Then we can search the maximum amplitude, which is the highest energy accumulation, and the corresponding transform order candidate is the estimated matched transform order, which we called the optimal transform order. The flowchart of the traditional search method to estimate the matched transform order is shown in Figure 3.
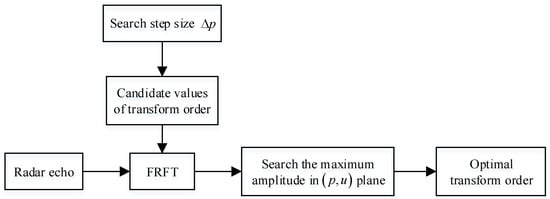
Figure 3.
The traditional search method of estimating the optimal transform order.
As we can see from Figure 3, each candidate value of the transform order will be used in FRFT. When a candidate value is equal to or close to the matched transform order, the energy of the signal in the FRFT result is the most concentrated. However, there will be a contradiction between the estimation accuracy and the computational complexity in the estimation of optimal transform order using the traditional search method. On the one hand, the higher the estimation accuracy, the smaller the search step size of transform order. At the same time, more FRFT times will be implemented, which will lead to greater computational complexity. On the other hand, the computational complexity of the traditional search method can be reduced by increasing the search step size of the transform order or by reducing the number of operations of the FRFT. However, with the increase of the search step size, the estimation accuracy of the optimal transform order will be reduced, resulting in the reduction of the time–FRFD–frequency resolution of the STFRFT, which is not conducive to the estimation of the micro-Doppler parameter of rotational angular velocity. In order to solve this problem, a novel modified short-time fractional Fourier transform algorithm is proposed in this paper, where the problem of searching the maximum amplitude or the maximum energy accumulation in FRFT is converted into the entropy minimization problem and an OMP-based algorithm is proposed to reduce the computational complexity in the estimation of the matched transform order.
3.2. The Proposed OMP-Based Algorithm of Estimating the Matched Transform Order
Different transform orders correspond to different maximum amplitude values of FRFT results. When the candidate value of transform order is equal to the matched transform order, the maximum amplitude value of FRFT results reaches the maximum. Although we can estimate the matched transform order by searching the maximum amplitude value of the FRFT result, it is easy to be affected by noise, which leads to inaccurate estimation of the matched transform order. As we all know, entropy can effectively measure the focusing of signal energy [38], and the more concentrated the signal energy is, the smaller the corresponding entropy is. When the candidate value of the transform order is equal to the matched transform order, the energy accumulation in FRFT result is the strongest, and the corresponding entropy is the smallest. Therefore, the matched transform order can be effectively estimated by calculating the entropy of the FRFT result and searching the minimum entropy.
The transform order of FRFT is related to the rotation angle of time–frequency axis, so FRFT has the characteristics of periodicity and symmetry with transform order as an independent variable [39], where the period is 4 and the axis of symmetry within a period [0, 4] is p = 2. Therefore, it only needs to consider the FRFT results with the transform order in the range of [0, 2] in the traditional search method. It is assumed that the variable p is discretized by the search step size Δp in the range of [0, 2] to P = [p1,…pi,…,pN]T, which we called the candidate values of the transform order. The total number of candidate values is , where represents the rounding down operation. The discrete form of the echo signal sF(tm) of the range unit where the target is located can be expressed as:
where M is the number of echo pulses in one observation time. According to Equation (7), the FRFT result of the echo signal with the candidate value of the transform order pi is:
The entropy of the FRFT result can be calculated as:
where represents the 2-norm. All the candidate values of transform order P are used in FRFT and the corresponding complete entropy vector can be expressed as:
The minimum entropy value can be found from the entropy vector, and the corresponding candidate value of transform order is the optimal transform order where we call this method the minimum entropy criterion-based optimal transform order estimation method, and the flowchart of this method is summarized and shown in Figure 4.
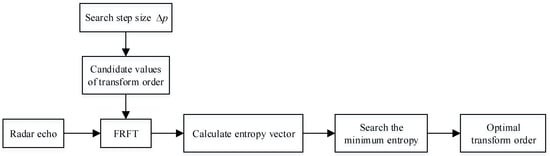
Figure 4.
Minimum entropy criterion-based optimal transform order estimation method.
In order to reduce the computational complexity of the optimal transform order estimation in the traditional search method, partial candidate values of the transform order Pη are selected randomly with a ratio η (0 ≤ η ≤ 1), which we called the reconstruction data ratio, from the complete candidate values of the transform order P. Then, a partial entropy vector Eη corresponding to the selected candidate values of the transform order is calculated. Finally, the OMP algorithm is utilized to reconstruct the complete entropy vector E, and the optimal transform order can be estimated by searching the minimum entropy from the reconstructed entropy vector .
Partial candidate values of the transform order Pη can be expressed as:
where is the total number of the partial candidate values of the transform order and Pη is selected randomly from P, that is, Pη ⊆ P. The random selection process can be described by a matrix multiplication as:
where Φ is a partial unit matrix of size Nη × N, which is called dictionary matrix, and it can be obtained according to the position of the transform order selected from the complete candidate values P in advance. The elements in the dictionary matrix Φ take values from . Only one element in each row is 1, and the rest are 0. Taking 1 means that the samples at the corresponding position in P are selected in Pη. Each candidate value of Pη is carried into Equations (13) and (14), and the partial entropy vector can be expressed as:
where Eη is a measurement vector of size Nη × 1, and is the sparse entropy vector to be reconstructed and solved.
According to the theory of compressed sensing, the OMP-based sparse optimization algorithm can be used to solve Equation (18) to get sparse solution , which can be expressed as:
where denotes L0 norm, and ε0 denotes the error threshold in the sparse recovery processing. The optimal transform order can be estimated by searching the minimum entropy from the reconstructed entropy vector, which can be expressed as:
To sum up, the flowchart of the proposed OMP-based algorithm of estimating the matched transform order is summarized in Figure 5, and the main steps of the OMP algorithm to reconstruct the complete entropy vector are shown in Algorithm 1.
| Algorithm 1 Main steps of the OMP algorithm to reconstruct the complete entropy vector. |
| Input: measurement vector , dictionary matrix , error threshold ε0. |
| Initialization: let the iterative counter k = 1, residual matrix γ0 = Eη, the index set . |
| Iteration: at the k-th iteration |
| (1) Update the index set , where , φi is the i-th column of Φ. |
| (2) Update the support set , and calculate the signal . |
| (3) Update the residual matrix . |
| (4) Increment k, and return to Step (1) until the stopping criterion is met. The selection of the error threshold ε0 is related to the precision requirement. |
| Output: Reconstructed entropy vector . |
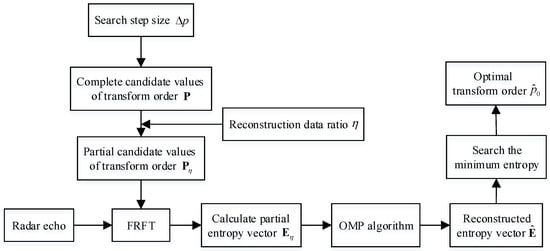
Figure 5.
The flowchart of the proposed OMP-based algorithm of estimating the optimal transform order.
3.3. Rotational Angular Velocity Estimation via Modified Short-Time Fractional Fourier Transform
In this paper, the estimated matched transform order is used in STFRFT to obtain the time–FRFD–frequency spectrum that has the highest time–FRFD–frequency resolution compared to other spectra corresponding to other candidate values of the transform order. After the time FRFD-frequency domain is characterized by the STFRFT, the Hough transform is employed to map the time FRFD-frequency domain on the micro-Doppler parameter space {ω,r,θ}, where ω, r, and θ denote the rotational angular velocity, the length, and initial phase of the rotor blades, respectively. The Hough transform for parameter estimation of sinusoidal frequency modulated signals is defined as:
where denotes the absolute value symbol, is the STFRFT result obtained by Equation (10) with the optimal transform order and is the time–FRFD–frequency spectrum with the Doppler frequency change rule .
As we can see from Equation (21), the result of the Hough transform is not only related to the length and initial phase of the rotor blades, but also to the rotational angular velocity of the rotor target. We can also say that these three variables determine the trajectory of Hough transform to accumulate energy and should be discretized into multiple candidate values before Hough transform, i.e., , and , where Nω, Nr and Nθ represent the number of discrete values of three variables ω, r, and θ, respectively. For each candidate value of the rotational angular velocity ωi, there will be an energy accumulation spectrum in the two-dimensional parameter space {r,θ}. When a rotational angular velocity candidate value is equal to or close to the real rotational angular velocity of the rotor target, the energy accumulation spectrum in two-dimensional parameter space {r,θ} has the highest energy accumulation peak. Therefore, we can search the peak value from the energy accumulation spectrum in two-dimensional parameter space {r,θ} to estimate the rotational angular velocity of the rotor target. This estimation process of rotational angular velocity can be expressed as:
where Hv(ω,v) denotes the peak value of energy accumulation corresponding to different candidate values of the rotational angular velocity, denotes the estimated rotational angular velocity.
By accurately estimating the optimal transform order, the rotational angular velocity of the rotor target can be estimated by searching the peak value from the energy accumulation spectrum obtained by Hough transform. To summarize, the complete procedure of the proposed method for rotational angular velocity estimation of rotor target is shown in Figure 6, in which the process in the blue dotted box is the matched transform order estimation based on the OMP algorithm and the process in the red dashed box is the rotational angular velocity estimation based on the combination of the M-STFRFT algorithm and Hough transform.
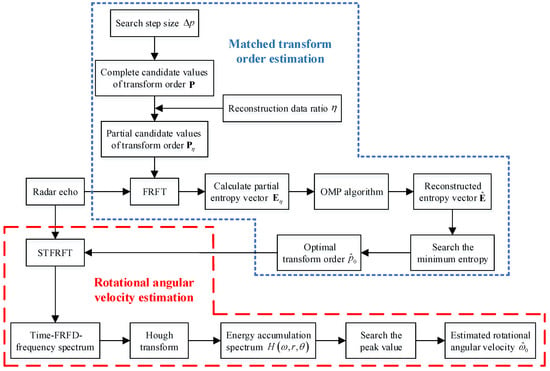
Figure 6.
The flowchart of the proposed method for rotational angular velocity estimation.
3.4. Computational Complexity Analysis
Compared with the traditional search method where 100% transform order candidates are selected, the proposed sparse-based method only selects partial transform order candidates and realizes the estimation of matched transform order through OMP reconstruction algorithm, so it is computationally efficient, because fractional Fourier transform and entropy operation corresponding to several transform order candidates are avoided. The following is a comparative analysis of the computational complexity between the traditional search method and the proposed sparse-based method, in which we take an addition, multiplication, and logarithm operation as a calculating unit.
In the traditional search method where 100% transform order candidates are selected, the computational complexity depends on the discrete FRFT and entropy operation. The digital computation of FRFT requires only a sequence of FFTs with the computational complexity O(Mlog2M), the entropy operation of Equation (14) requires the computational complexity of O(4M). Therefore, the total computational complexity of the traditional search method where 100% transform order candidates are selected can be expressed as:
Suppose that the data ratio of selected transform order candidates is η in the proposed sparse-based method. The computational complexity of the OMP reconstruction algorithm is O(NηN). The whole process of the proposed sparse-based method consists of Nη FRFTs, Nη entropy operations, and one OMP reconstruction operation, so the total computational complexity can be given by:
As we can see from Equations (24) and (25), the computational complexity of the traditional search method and the proposed sparse-based method are related to the search step size Δp and reconstruction data ratio η. The comparison between Equations (24) and (25) implies that the computational complexity of the proposed sparse-based method is much less than that of the traditional search method where 100% transform order candidates are selected, which will be validated through the simulation of computation time in Section 4.3.
4. Experimental Results
In this section, several comparative experiments of simulated data are conducted, and simulation results based on measured data collected by frequency modulated continuous wave radar are presented to validate the performance and effectiveness of the proposed algorithm. We consider that a monostatic early warning radar and the micro-Doppler signals are simulated by rotation of the rotor blades in a helicopter, the main rotor part consists of two blades, and the blade length is 6 m. Suppose that there is a scatterer at the outermost end of each blade, so the echo signal contains two micro-Doppler components that we call rotor echo with the same rotational angular velocity and different initial phases. In this experiment, the main parameters of the transmitted signal and the rotor part are summarized in Table 1.

Table 1.
Main parameters of the transmitted signal and the rotor part.
The simulation experiments are composed of five parts: (1) simulations to analyze the influence of the transform order on parameter estimation; (2) simulations to select the parameters of the OMP reconstruction algorithm in the estimation of matched transform order; (3) simulations to validate the effectiveness of the proposed algorithm; (4) comparative experiments of parameter estimation among time–frequency analysis algorithms; (5) verification experiment based on measured data.
4.1. Influence Analysis of the Transform Order on Parameter Estimation
In the experiment, we consider the noise-free case and investigate the influence of the transform order used in STFRFT on the estimation of the rotational angular velocity. The rotating part consists of two blades with the same rotational angular velocity ω = 25 rad/s and different initial phase π/2 and 3π/2. Therefore, two different micro-Doppler components caused by them in the echo signal have different chirp rates, corresponding to different matched transform orders. According to the parameters of radar transmitting signal and Equation (9), we can calculate that the matched transform orders of echo components with initial phases of π/2 and 3π/2 are p01 = 0.9535 and p02 = 1.0465, respectively. We take the transform order as a variable, which is ranged from 0.91 to 0.99 with a step size of 0.05, and each transform order is used as the optimal transform order in STFRFT. Therefore, multiple time–FRFD–frequency spectra corresponding to different transform orders can be obtained, and then the rotational angular velocity of the rotor target can be estimated by Hough transform and energy peak search. The simulation result of the estimation error of rotational angular velocity is shown in Figure 7, from which one can see that the estimation error of rotational angular velocity is the smallest when the transform order is 0.955, which is close to the matched transform order p01. We can also see that the farther the transform order is away from the matched transform order, the greater the estimation error of the rotational angular velocity is. Therefore, it can be concluded that: (1) the matched transform order is the optimal transform order because of the smallest estimation error of the rotational angular velocity; (2) when STFRFT is used in parameter estimation, it is not only necessary to estimate the matched transform order to improve the estimation accuracy of the rotational angular velocity but also to reduce the computational complexity of the algorithm, that is, to solve the contradiction between the estimation accuracy and the calculation speed.
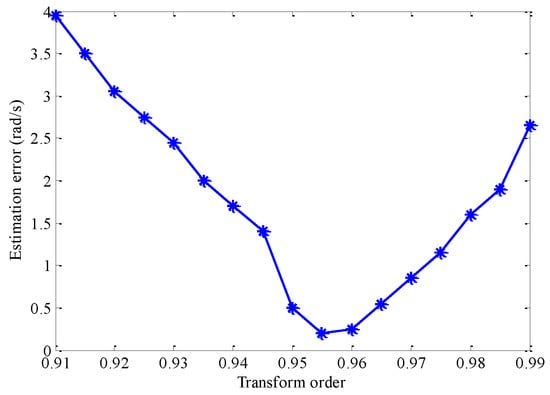
Figure 7.
Estimation error of the rotational angular velocity.
Figure 8 shows the results of the time–FRFD–frequency spectrum of target echo signal under different transform orders. For the echo signal with multiple micro-Doppler components, each matched transform order can only ensure that the time–FRFD–frequency spectrum of the corresponding echo component has a higher time–FRFD–frequency resolution, while the other echo components cannot be effectively accumulated due to the mismatch of the rotation angle. Figure 8a is the result of STFRFT with the transform order of 0.955, since the transform order 0.955 is closer to the matched transform order of the echo component with the initial phase π/2, the time–FRFD–frequency resolution of this component is higher, while that of the echo component with initial phase 3π/2 is lower. However, this result does not degrade the estimation accuracy of the rotational angular velocity, because these echo components are from different blades of the same rotating part with the same rotational angular velocity. As long as one echo component has the highest time–FRFD–frequency resolution, it can accurately estimate the rotational angular velocity through the signal energy peak accumulated by the Hough transform. In Figure 7, the estimation error of the rotational angular velocity is the smallest with the transform order of 0.955, which can also be confirmed from Figure 8a. Compared with the time–FRFD–frequency spectrum with the transform order of 0.91 in Figure 8b, the closer the transform order is to the matched transform order, the higher the time–FRFD–frequency resolution, and the more concentrated the echo signal energy accumulated by the Hough transform.
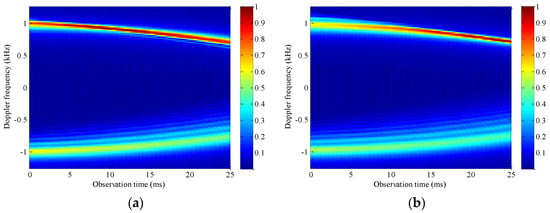
Figure 8.
Normalized time–FRFD–frequency spectrum of target echo signal under different transform orders. (a) Transform order p = 0.955; (b) transform order p = 0.91.
4.2. Parameters Selection of OMP Reconstruction Algorithm in the Estimation of Matched Transform Order
In order to solve the contradiction between the estimation accuracy and the computational complexity, an OMP-based matched transform order estimation algorithm is presented in the proposed M-STFRFT algorithm, in which transform order candidate values with a certain ratio are randomly selected from the search range from 0 to 2, and the entropy value of each searched transform order’s FRFT result is calculated. Then, based on the compression sensing theory, the OMP algorithm is used to reconstruct the complete entropy vector, and the matched transform order is estimated according to the position of the minimum entropy. There is no doubt that the reconstruction data radio and the search step size of the transform order are the key factors that directly affect the estimation accuracy and the computational complexity.
In this experiment, we first investigate the influence of the reconstruction data ratio of transform order on the estimation accuracy of the rotational angular velocity in a noise environment. It is assumed that the search step size of the transform order is a constant value of 0.001, and the received signal is added with white Gaussian noise and the signal-to-noise (SNR) is defined as , where is the echo signal without pulse compression in Equation (3) and is the variance of the noise. Figure 9 plots the estimation error, such as root-mean-square error (RMSE) and standard deviation (SD), of rotational angular velocity varying different reconstruction data ratio of the transform order. The calculation formulas of RMSE and SD are and , where , , and ω denote estimated value, mean of the estimated value, and true value of the rotational angular velocity, respectively. N = 1000 is the number of estimated values, that is, each value of RMSE and SD is obtained and averaged by 1000 Monte-Carlo trials.
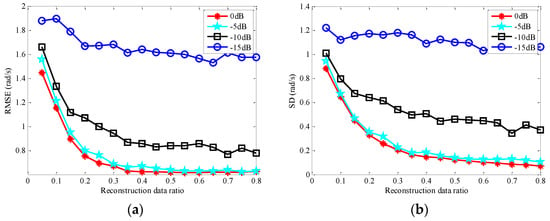
Figure 9.
Estimation error of rotational angular velocity varying different reconstruction data ratios and SNR. (a) RMSE; (b) SD.
As we can see from Figure 9, on the one hand, with the increase of reconstruction data ratio of transform order from 0.05 to 0.8, the estimated RMSE and SD of rotational angular velocity decrease gradually under the same SNR. We can also see that the smaller the reconstruction data ratio, the larger the estimation error of rotational angular velocity, the more unstable the estimation, and the greater the change of estimated RMSE and SD. In addition, when the reconstruction data ratio of transform order exceeds 0.5, the change of estimated RMSE and SD is very small. On the other hand, under the same reconstruction data ratio of transform order, the lower the SNR of the target echo, the greater the change of the estimated RMSE and SD. Moreover, one can see that the estimated RMSE and SD of the rotational angular velocity with the contrastive SNR of 0 dB and −5 dB are similar. However, for the same SNR variation of 5 dB, the estimated RMSE and SD corresponding to the SNR of −10 dB and −15 dB change greatly, which shows that the effect of the SNR on estimated RMSE and SD of rotational angular velocity changes nonlinearly.
In order to investigate the influence of both the search step size and reconstruction data radio of the transform order on the estimation of rotational angular velocity, we do this experiment in a noise environment with an SNR of 0 dB. The results of the estimated RMSE and SD of the rotational angular velocity are shown in Figure 10, which varies both reconstruction data ratio and search step size of the transform order. As we can see from Figure 10, with the increase of the reconstruction data ratio of transform order, the estimated RMSE and SD of rotational angular velocity decrease gradually and change more slowly under the same search step size of transform order. When a lower reconstruction data ratio is adopted to estimate the optimal transform order, there will be a larger deviation between the estimated optimal transform order and the real matched transform order, and a larger estimation error of rotational angular velocity. Additionally, it is easily found that when the search step size of transform order is 0.001, the trend and value of the estimation error of rotational angular velocity in Figure 10 are the same as that in Figure 9. Moreover, with the same reconstruction data ratio, the larger search step size of the transform order can lead to the larger estimation error of the rotational angular velocity. It can be concluded from this experiment that (1) the larger the reconstruction data ratio and the smaller the search step size of the transform order, the more accurate and stable the estimation of the rotational angular velocity, but it will lead to a large amount of computational complexity. (2) When the reconstruction data ratio and the search step size of transform order are 0.5 and 0.001, respectively, the estimated RMSE and SD are not only small but also stable, which shows that the rotational angular velocity estimation is more efficient under this parameters selection.
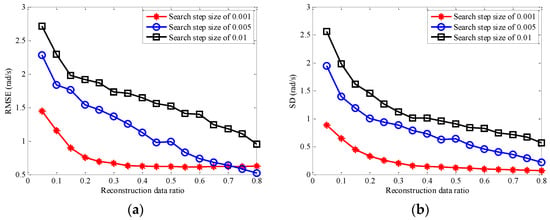
Figure 10.
Estimation error of rotational angular velocity varying different reconstruction data ratios and search step sizes of transform order. (a) RMSE; (b) SD.
4.3. Effectiveness Validation of the Proposed Algorithm
In this experiment, two aspects of comparative simulation experiments are implemented to verify the effectiveness of the proposed OMP-based algorithm in estimating the matched transform order. They are the computation time of the algorithm and the estimation error of rotational angular velocity. Firstly, we consider the noise-free case and compare the computation time between the proposed OMP-based method and the traditional search method in the estimation of the matched transform order. The experiments are implemented by using MATLAB 2014a on a PC (Intel Celeron CPU 1007U 1.5 GHz and a 4096-MB memory capacity), and results are shown in Figure 11. Figure 11a plots the comparison of the computation time among the proposed OMP-based algorithm with different reconstruction data ratios of 10%, 50%, and 90%, and Figure 11b plots the comparison of the computation time between the proposed OMP-based algorithm and the traditional search method. It should be pointed out that the difference among the comparative experiments in Figure 11b is the solution of the matched transform order, which can be described as follows: (1) the proposed OMP-based algorithm with the reconstruction data ratio of 50% is utilized to estimate the matched transform order; (2) 50% of transform order candidate values are selected randomly and used to search for the matched transform order in the traditional search method; (3) 100% of transform order candidate values are used for estimating the matched transform order in the traditional search method.
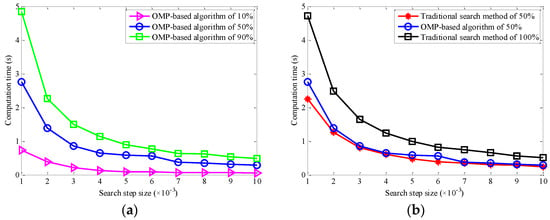
Figure 11.
Comparison of computation time among different methods in estimating the matched transform order. (a) Different reconstruction data ratios; (b) different estimation methods.
As we can see from Figure 11a, different reconstruction data ratios of 10%, 50%, and 90% are adopted in the proposed OMP-based algorithm in estimating the matched transform order, and the computation time varies with the different reconstruction data ratios and search step sizes. For the same reconstruction data ratio, with the increase of the search step size, the computation time decreases gradually, because the increase of the search step size leads to the decrease of the number of the transform order candidates. We can also see that for the same search step size, the larger the reconstruction data ratio of the selected transform order candidate values, the more FRFT times need to be calculated, so the computation time will be increased. From Figure 11b, we can see that in accordance with the OMP-based algorithm proposed in this paper, no matter whether 50% or 100% of the transform order candidate values are selected in the traditional search method, with the increase of the search step size, the computation time is also gradually reduced. Moreover, under the same search step size, the computation time of the proposed OMP-based algorithm with the reconstruction data ratio of 50% is slightly higher than that of the traditional search method where 50% transform order candidate values are selected, but it is significantly lower than that of the traditional search method where 100% transform order candidate values are utilized, which shows that in order to reduce the computational complexity or computation time in estimating the matched transform order, the OMP-based algorithm proposed in this paper is effective to estimate the matched transform order.
Secondly, we compare the estimation error of the rotational angular velocity between the proposed OMP-based algorithm and the traditional search method. In this comparative experiment, the candidate values of the transform order are from 0 to 2 with a step size of 0.001, and the three estimation methods are the same as mentioned in Figure 11b and are implemented to estimate the matched transform order. Then, the estimated matched transform orders obtained from the above three methods are used in the STFRFT algorithm for obtaining the time–FRFD–frequency spectrum, and the Hough transform is adopted to estimate the rotational angular velocity. The results of the estimation error of rotational angular velocity are shown in Figure 12.
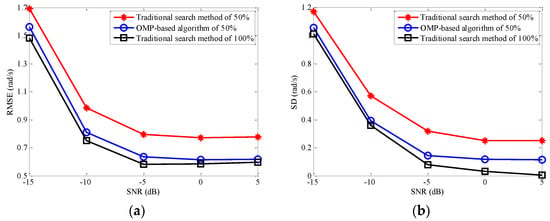
Figure 12.
Estimation error of rotational angular velocity among different methods. (a) RMSE; (b) SD.
As we can see from Figure 12, with the increase of SNR, the estimation error of rotational angular velocity obtained by any method mentioned above decreases. The reason is that the higher the SNR, the higher the estimation accuracy of the matched transform order whether 50% or 100% of the candidate values are selected in the traditional search method. We can also conclude from Figure 12 that the higher the SNR is, the slower the change of estimation error of RMSE or SD is. Compared with the traditional search method where 100% transform order candidate values are utilized, the traditional search method where 50% transform order candidate values are selected reduces the computational complexity or the computation time displayed in Figure 11b by reducing the number of solutions of optimal transform order. It is actually a kind of increasing the search step size of transform order candidate values in a disguised way, which will lead to the increase of the estimation error between the estimated optimal transform order and the real matched transform order. Then, the resolution of the time–FRFD–frequency spectrum and the estimation accuracy of rotational angular velocity are both reduced, which are confirmed in the results of Figure 12.
Although the OMP-based algorithm proposed in this paper only uses 50% of the transform order candidate values to estimate the optimal transform order in this experiment, it is different from the traditional search method for which 50% transform order candidate values are selected. This proposed OMP-based algorithm combines the compressed sensing theory and estimates the optimal transform order through the OMP reconstruction algorithm, which not only reduces the computational complexity of the algorithm but also can get the optimal transform order more accurately than the traditional search method for which 50% transform order candidate values are selected. It can be seen from Figure 12 that the estimation error of the rotational angular velocity obtained by the proposed OMP-based algorithm in this paper is significantly lower than that of the traditional search method where 50% transform order candidate values are selected but slightly higher than that of the traditional search method with 100% of transform order candidate values are utilized to estimate the optimal transform order. The reason why the estimation accuracy of the rotational angular velocity of the proposed OMP-based algorithm is not up to that of the traditional search method where 100% transform order candidate values are utilized lies in the existence of reconstruction error. It can be concluded from the experimental results that the OMP-based algorithm proposed in this paper is better than the traditional search method using the same data ratio of transform order candidate values in estimating the rotational angular velocity, which indicates that the proposed algorithm can estimate the rotational angular velocity quickly and effectively while ensuring the estimation accuracy.
4.4. Comparative Experiments of Parameter Estimation among Time-Frequency Analysis Algorithms
In this experiment, we first consider the noise-free case and compare the results obtained by the Hough–STFT, the Hough–WVD, the Hough–PWVD, the Hough–RSPWVD, and the proposed algorithm, and then evaluate the estimation error of rotational angular velocity among the aforementioned algorithms in a noise environment. It is assumed that there are two scatterers at the end of the rotor blade on a rotor target with the rotational angular velocity ω = 25 rad/s and the initial phases of each blade at the beginning of the observation are π/2 and 3π/2, respectively, and the blade length is 6 m. Additionally, it is assumed that the translational compensation is carried out to the target echo, so it can be calculated that the maximal Doppler frequency of each rotor echo is 1000 Hz. In the proposed algorithm, the candidate values of the transform order are from 0 to 2 with a search step size of 0.001, and the reconstruction data ratio is set as 50%.
The results obtained by the Hough–STFT, the Hough–WVD, the Hough–PWVD, the Hough–RSPWVD, and the proposed algorithm are provided in Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17, respectively. Figure 13a, Figure 14a, Figure 15a, Figure 16a and Figure 17a show the time–frequency characteristics of the received rotor echo obtained by the STFT, WVD, PWVD, RSPWVD, and the proposed M-STFRFT algorithm, respectively, where the two micro-Doppler components can be seen clearly and the maximal micro-Doppler frequency of each micro-Doppler components is close to the theoretical value 1000Hz. However, as we can see from the figures, STFT and WVD have the problems of low time–frequency resolution and cross-term interference, respectively. To some extent, PWVD and RSPWVD reduce the cross-term interference, but at the same time, the time–frequency resolution is reduced, which is not conducive to the estimation of micro-Doppler parameters. As we can see from Figure 17a, although the resolution of the time–frequency characteristics of a micro-Doppler component is low due to the mismatch with the estimated optimal transform order, the time–FRFD–frequency resolution of another micro-Doppler component corresponding to the estimated optimal transform order is higher than the STFT, PWVD, and RSPWVD algorithm, and there is no cross-term interference in the result obtained by the proposed M-STFRFT algorithm. Therefore, we can estimate the rotational angular velocity effectively by using the high-resolution micro-Doppler component. Compared with the Hough accumulation results in Figure 13b, Figure 14b, Figure 15b and Figure 16b, which display the energy distribution in parameter space {r,θ} and are obtained by Hough transform, the energy of the micro-Doppler component with the highest time–frequency resolution of the proposed algorithm in Figure 17b is more concentrated in the coordinate of the correct value of {r,θ}. Although the energy concentration of the micro-Doppler component with low time–frequency resolution is relatively low, this does not affect the estimation performance of the rotational angular velocity. According to the above simulation results, it can be concluded that the aforementioned time–frequency algorithms are effective for the micro-Doppler parameter of rotational angular velocity estimation and the proposed M-STFRFT algorithm performs more efficiently than the other four algorithms.
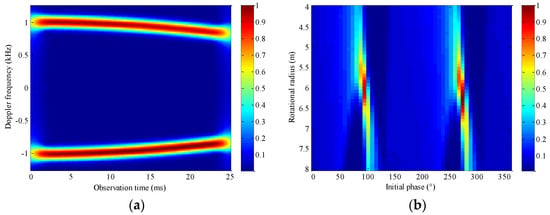
Figure 13.
Results obtained by Hough–STFT algorithm. (a) Normalized time–frequency spectrum obtained by STFT; (b) parameter space {r,θ} obtained by Hough transform.
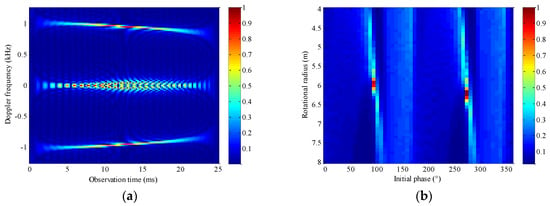
Figure 14.
Results obtained by Hough–WVD algorithm. (a) Normalized time–frequency spectrum obtained by WVD; (b) parameter space {r,θ} obtained by Hough transform.
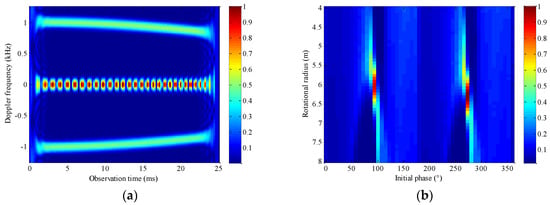
Figure 15.
Results obtained by Hough–PWVD algorithm. (a) Normalized time–frequency spectrum obtained by PWVD; (b) parameter space {r,θ} obtained by Hough transform.
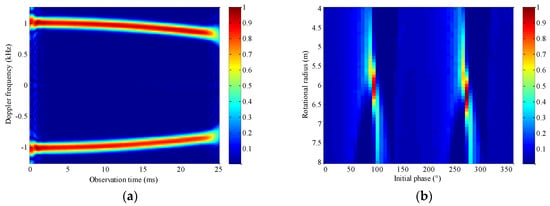
Figure 16.
Results obtained by Hough–RSPWVD algorithm. (a) Normalized time–frequency spectrum obtained by RSPWVD; (b) parameter space {r,θ} obtained by Hough transform.
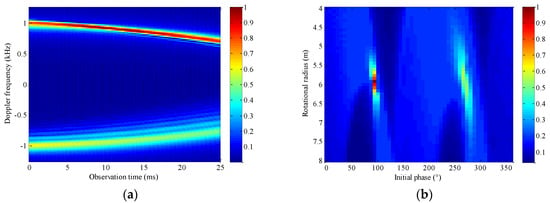
Figure 17.
Results obtained by the proposed algorithm. (a) Normalized time–frequency spectrum obtained by M-STFRFT; (b) parameter space {r,θ} obtained by Hough transform.
Figure 18 shows the estimated RMSE and SD of rotational angular velocity among the proposed algorithm, the Hough–GSS-based STFRFT algorithm, and other time–frequency analysis algorithms, where the received signal is added with white Gaussian noise, and each value of RMSE and SD are obtained and averaged by 1000 Monte-Carlo trails. It should be pointed out that the rotational angular velocity estimation process of the Hough–GSS-based STFRFT algorithm is the same as that of the algorithm proposed in this paper, except that the Hough–GSS-based STFRFT algorithm adopts the GSS-based FRFT method proposed in [35] when estimating the matched transform order. As a comparison, we give the rotational angular velocity estimation results of the method described in Section 3.1, in which the matched transform order is estimated by searching the maximum amplitude value of FRFT in the traditional method, which is labeled as Hough–Max-STFRFT in Figure 18.
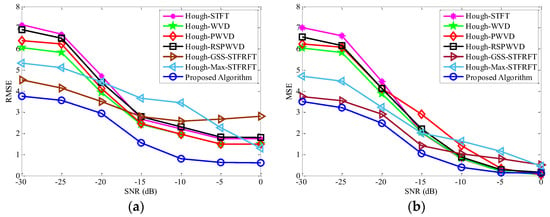
Figure 18.
Estimation error of rotational angular velocity among different parameter estimation methods. (a) RMSE; (b) SD.
As we can see from Figure 18a,b that with the increase of SNR, the accuracy and stability of the aforementioned estimation algorithms and the proposed algorithm are improved, and finally tend to be stable. We can also see that the Hough–WVD algorithm is more accurate in rotational angular velocity estimation than Hough–STFT, Hough–PWVD, and Hough–RSPWVD algorithms because of the higher time–frequency resolution, while the Hough–STFT algorithm is the least. However, there exists cross-term interference in the WVD algorithm, and the resolution of the WVD algorithm is obviously reduced at the beginning and ending of the observation time, which will lead to the incorrect estimation of the rotational angular velocity and will increase the estimation error of RMSE and SD. By comparing and observing the results of Hough–Max-STFRFT method, we find that the matched transform order estimation method of searching the maximum of FRFT results is easily affected by noise, which leads to inaccurate and unstable estimation of matched transformation order and is not conducive to the estimation of rotational angular velocity. Compared with other time–frequency analysis algorithms, the Hough–GSS-based STFRFT algorithm has a smaller and more stable estimation error under the condition of a low SNR, but it is larger when the SNR is high. Moreover, the estimated RMSE and SD of the Hough–GSS-based STFRFT algorithm in the range of SNR from −30 dB to 0 dB are significantly larger than those of the proposed algorithm. The main reason for this result is that the GSS-based matched transform order estimation algorithm used in the Hough–GSS-based STFRFT algorithm has a local iterative convergence problem.
In the algorithm proposed in this paper, although one micro-Doppler component does not match the estimated optimal transform order, another micro-Doppler component matching the optimal transform order has the highest time–FRFD–frequency resolution, and there is no cross-term interference. Therefore, the proposed algorithm has a higher estimation accuracy of rotational angular velocity than other aforementioned algorithms, which can be reflected in Figure 18a. We can also see that compared with the Hough–GSS-based STFRFT algorithm and other time–frequency analysis algorithms mentioned in this paper, the algorithm proposed in this paper also has better rotational angular velocity estimation performance in the case of low SNR. In summary, we can conclude that the proposed modified short-time fractional Fourier transform has a good performance on rotational angular velocity estimation, which can verify the effectiveness and stability of the algorithm proposed in this paper.
4.5. Verification Experiment based on Measured Data
We now present the experimental results based on measured data collected by frequency modulated continuous wave radar, where the carrier frequency is 24 GHz and the pulse repetition interval is 600 μs. The experimental target is a corner reflector with the circular motion. The schematic diagram of experimental scene is shown in Figure 19, where ABCDEF denotes the corner reflector with a circular motion around point O under the action of human factors and traction rope AH, and it moves to A′B′C′D′E′F′ after half a cycle; G is the center of the scatterer; ω denotes the rotational angular velocity.
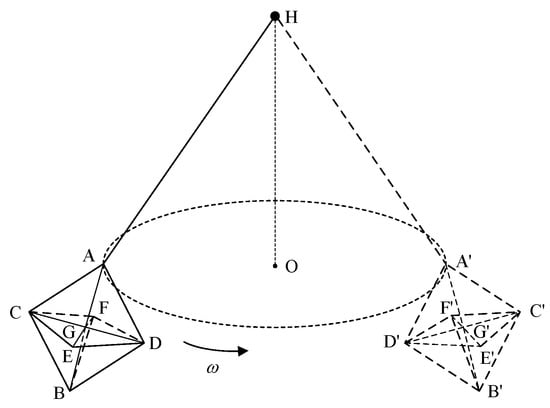
Figure 19.
The schematic diagram of experimental scene.
Figure 20a shows the time–frequency spectrum of the target echo. It can be seen from Figure 20 that the echo Doppler frequency of the corner reflector is approximately sinusoidal signal, which is consistent with the echo Doppler frequency of the scatterer in the theoretical derivation in this paper, which also verifies the accuracy of using this scene to simulate the real radar observation process of the rotor target. However, we can also see from the figure that the echo of the corner reflector has strong fixed ground clutter near the zero frequency, and there is translational radial motion, because the center of the sinusoidal signal is not at the zero frequency, which are all not conducive to the estimation of rotational angular velocity.
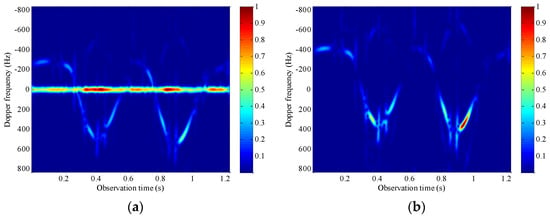
Figure 20.
Normalized time–frequency spectrum of the target echo. (a) Original target echo; (b) target echo after preprocessing.
In this experiment, moving target indication processing is used to filter the clutter near zero frequency in the echo, and translational compensation is utilized to remove the influence of translational motion on the Doppler frequency of the echo, that is, the echo signal is multiplied by the translational compensation term , where v denotes the translational radial velocity. After these two steps of preprocessing, the time–frequency spectrum of the echo is shown in Figure 20b. Comparing Figure 20a,b, it can be found that the clutter of fixed ground objects and translational motion are basically eliminated.
It should be pointed out that the measured data is collected on the frequency modulated continuous wave radar platform, which can realize the continuous observation of the corner reflector. However, in the actual observation process of the narrowband early warning radar on the rotor target, due to the limitation of antenna rotation and target distance, the continuous observation of the target cannot be realized. In order to simulate the real scene, we extract four effective segments from the measured data echo to verify the effectiveness of the proposed algorithm, which are shown in Figure 21 of the time–frequency spectrum marked with a red box.
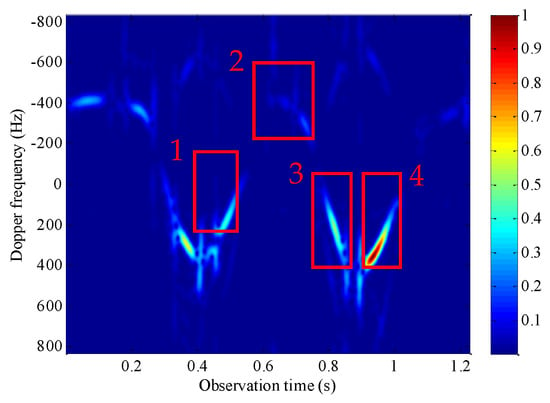
Figure 21.
Extracted segments from the measured data.
Four echo segments marked with a red box in the time–frequency spectrum of Figure 21 are intercepted from the original target echo, and the rotational angular velocity of the corner reflector is estimated according to the algorithm proposed in this paper. The results are shown in Table 2. As a comparison, the experimental results of other time–frequency analysis algorithms mentioned in Section 4.4 are given.

Table 2.
Main steps of the OMP algorithm to reconstruct the complete entropy vector.
From the simulation results in Table 2, it can be seen that compared with other time–frequency analysis algorithms, the algorithm based on M-STFRFT proposed in this paper is more stable for the estimation of the rotational angular velocity of the echoes in four segments. In order to verify the correctness of the estimation results, we fit a sinusoidal Doppler frequency curve , where the amplitude is A = 494, the rotational angular velocity is ω = 13.2 rad/s, and the initial phase angle is . The fitting result of Doppler frequency of the corner reflector is shown in Figure 22, in which the black scattered points represent the real Doppler frequency of the corner reflector estimated from the time–frequency spectrum, the red scattered points represent that the Doppler frequency value is zero, and the blue scattered points represent the fitting Doppler frequency value of the corner reflector.
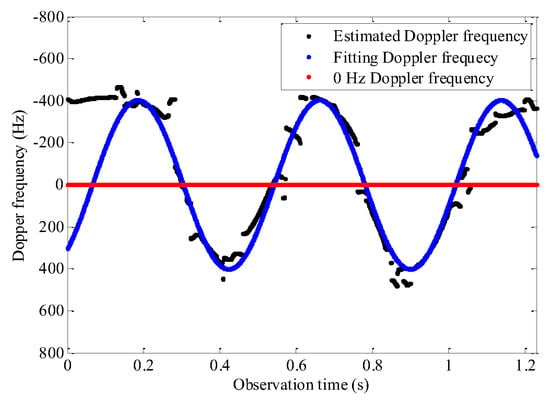
Figure 22.
Comparing of the estimated Doppler frequency and the fitting Doppler frequency.
According to our verification, under the Doppler frequency fitting of this group of parameters, the coincidence degree of blue scattered points and black scattered points is the highest, especially in the four segments marked in Figure 21. Therefore, it can be concluded that the rotational angular velocity of the corner reflector in the measured data is about 13.2 rad/s, which can demonstrate the correctness of the estimation results in Table 2, thus verifying the effectiveness of the algorithm proposed in this paper.
5. Conclusions
In this paper, we have presented a novel modified short-time fractional Fourier transform algorithm for efficient rotational angular velocity estimation of the rotor target. The OMP-based algorithm is used to estimate the matched transform order in the proposed M-STFRFT algorithm, and the problem of searching the maximum amplitude in FRFT is converted into the entropy minimization problem. Compared with the traditional search method, the proposed method is computationally efficient, because partial transform order candidate values are selected randomly to estimate the matched transform order through the OMP-based algorithm. The estimated matched transform order and STFRFT are applied to obtain the time–FRFD–frequency spectrum with the highest time–FRFD–frequency resolution, and the rotational angular velocity can be estimated through searching the peak value from the energy accumulation spectrum obtained by Hough transform. Simulations results demonstrate that the proposed algorithm yields better time–FRFD–frequency resolution in comparison with other mentioned time–frequency analysis algorithms, faster estimation of matched transform order than the traditional search method and more accurate rotational angular velocity estimation than the Hough–GSS-based STFRFT algorithm and other time–frequency analysis algorithms mentioned in this paper. Moreover, experimental results based on measured data collected by frequency modulated continuous wave radar validate the effectiveness of the proposed algorithm.
Although our proposed algorithm is effective in rotational angular velocity estimation, it can still be improved further. In the future, we will not only focus on the more effective estimation of the matched transform order but also verify the effectiveness of the proposed algorithm in the actual radar equipment by experimenting with measured data.
Author Contributions
Writing—original draft preparation, W.W.; methodology, W.W., Z.T., and Y.C.; writing—review and editing, W.W. and Y.C.; validation, W.W. and Z.Z.; data curation, Y.S., Y.Z., and C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 61901514, and in part by Young Talent Program of Early Warning Academy under Grant TJRC425311G11.
Acknowledgments
The authors would like to thanks to the editor and anonymous reviewers for processing our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
Abbreviations of nouns and algorithms mentioned in this paper are as follows.
| Abbreviations | Full Name |
| M-STFRFT | Modified Short-Time Fractional Fourier Transform |
| FRFT | Fractional Fourier Transform |
| STFRFT | Short-Time FRFT |
| FRFD | FRFT Domain |
| OMP | Orthogonal Matching Pursuit |
| m-D | micro-Doppler |
| FT | Fourier Transform |
| CWT | Continuous Wavelet Transform |
| STFT | Short-Time Fourier Transform |
| WVD | Wigner–Ville Distribution |
| PWVD | Pseudo Wigner–Ville Distribution |
| RSPWVD | Reassigned Smoothed Pseudo Wigner–Ville Distribution |
| Hough-STFT | Combination of Hough Transform and STFT |
| Hough-WVD | Combination of Hough Transform and WVD |
| Hough-PWVD | Combination of Hough Transform and PWVD |
| Hough-RSPWVD | Combination of Hough Transform and RSPWVD |
| SFT | Sparse Fourier Transform |
| SDFRFT | Sparse Discrete FRFT |
| GSS | Golden Section Search |
| SNR | Signal-to-Noise |
| RMSE | Root-Mean-Square Error |
| SD | Standard Deviation |
References
- Chen, V.C.; Li, F.; Ho, S.S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model and simulation study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Karabacak, C.; Gurbuz, S.Z.; Gurbuz, A.C.; Guldogan, M.B.; Hendeby, G.; Gustafsson, F. Knowledge exploitation for human micro-Doppler classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2125–2129. [Google Scholar] [CrossRef]
- Biondi, F.; Addabbo, P.; Orlando, D.; Clemente, C. Micro-motion estimation of maritime targets using pixel tracking in Cosmo-Skymed synthetic aperture radar data—An operative assessment. Remote Sens. 2019, 11, 1637. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Q.; Qiu, C.W.; Liang, X.J.; Li, K.M. Micro-Doppler effect analysis and feature extraction in SAR imaging with stepped-frequency chirp signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2087–2098. [Google Scholar]
- Singh, A.K.; Kim, Y.H. Automatic measurement of blade length and rotation rate of drone using W-band micro-Doppler radar. IEEE Sens. J. 2018, 18, 1895–1902. [Google Scholar] [CrossRef]
- Cirillo, L.; Zoubir, A.; Amin, M. Parameter estimation for locally linear FM signals using a time-frequency Hough transform. IEEE Trans. Signal Process. 2008, 56, 4162–4175. [Google Scholar] [CrossRef]
- Wang, J.; Lei, P.; Sun, J.P.; Hong, W. Spectral characteristics of mixed micro-Doppler time-frequency data sequences in micro-motion and inertial parameter estimation of radar targets. IET Radar Sonar Navig. 2014, 8, 275–281. [Google Scholar] [CrossRef]
- Bian, Z.; Li, J.T.; Guo, L.X. Simulation and feature extraction of the dynamic electromagnetic scattering of a hypersonic vehicle covered with plasma sheath. Remote Sens. 2020, 12, 2740. [Google Scholar] [CrossRef]
- Orović, I.; Stanković, S.; Jokanović, B. A suitable hardware realization for the Cohen class distributions. IEEE Trans. Circuits Syst. II Express Briefs 2013, 60, 607–611. [Google Scholar] [CrossRef]
- Djurović, I.; Popović-Bugarin, V.; Simeunović, M. The STFT-based estimator of micro-Doppler parameters. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1273–1283. [Google Scholar] [CrossRef]
- Kim, B.H.; Kong, S.H.; Kim, S. Low computational enhancement of STFT-based parameter estimation. IEEE J. Sel. Top. Signal Process. 2015, 9, 1610–1619. [Google Scholar] [CrossRef]
- Millioz, F.; Martin, N. Circularity of the STFT and spectral kurtosis for time-frequency segmentation in Gaussian environment. IEEE Trans. Signal Process. 2011, 59, 515–524. [Google Scholar] [CrossRef]
- Boashash, B.; Black, P. An efficient real-time implement of the Wigner-Ville distribution. IEEE Trans. Acoust. Speechand Signal Process. 1987, 35, 1611–1618. [Google Scholar] [CrossRef]
- Malnar, D.; Sucic, V.; O’Toole, J.M. Automatic quality assessment and optimization of quadratic time-frequency representations. Electron. Lett. 2015, 51, 1029–1031. [Google Scholar] [CrossRef]
- Bouchikhi, A.; Boudraa, A.O.; Cexus, J.C.; Chonavel, T. Analysis of multicomponent LFM signals by Teager Huang-Hough transform. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1222–1233. [Google Scholar] [CrossRef]
- Lerga, J.; Sucic, V. Nonlinear IF estimation based on the pseudo WVD adapted using the improved sliding pairwise ICI rule. IEEE Signal Process. Lett. 2009, 16, 953–956. [Google Scholar] [CrossRef]
- Chen, T.C. Joint signal parameter estimation of frequency-hopping communications. IET Commun. 2012, 6, 381–389. [Google Scholar] [CrossRef]
- Ding, Y.P.; Sun, Y.H.; Huang, G.W.; Liu, R.J.; Yu, X.L.; Xu, X.M. Human Target Localization Using Doppler Through-Wall Radar Based on Micro-Doppler Frequency Estimation. IEEE Sens. J. 2020, 20, 8778–8788. [Google Scholar] [CrossRef]
- Barbarossa, S.; Lemoine, O. Analysis of nonlinear FM signals by pattern recognition of their time-frequency representation. IEEE Signal Process. Lett. 1996, 3, 112–115. [Google Scholar] [CrossRef]
- Suresh, P.; Thayaparan, T.; Obulesu, T.; Venkataramaniah, K. Extracting micro-Doppler radar signatures from rotating targets using Fourier-Bessel transform and time-frequency analysis. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3204–3210. [Google Scholar] [CrossRef]
- Su, X.H.; Tao, R.; Kang, X.J. Analysis and comparison of discrete fractional Fourier transform. Signal Process. 2019, 160, 284–298. [Google Scholar] [CrossRef]
- Victor, N. The fractional order Fourier transform and its application to quantum mechanics. IMA J. Appl. Math. 1980, 25, 241–265. [Google Scholar]
- Chen, X.L.; Guan, J.; Chen, W.S.; Zhang, L.; Yu, X.H. Sparse long-time coherent integration–based detection method for radar low-observable maneuvering target. IET Radar Sonar Navig. 2020, 14, 538–546. [Google Scholar] [CrossRef]
- Pei, S.C.; Ding, J.J. Closed-form discrete fractional and affine Fourier transforms. IEEE Trans. Signal Process. 2000, 48, 1338–1353. [Google Scholar]
- Liu, S.H.; Shan, T.; Tao, R.; Zhang, Y.D.; Zhang, G.; Zhang, F. Sparse discrete fractional Fourier transform and its applications. IEEE Trans. Signal Process. 2014, 62, 6582–6595. [Google Scholar] [CrossRef]
- Chen, X.L.; Guan, J.; Wang, G.Q.; Ding, H.; Huang, Y. Fast and refined processing of radar maneuvering target based on hierarchical detection via sparse fractional representation. IEEE Access 2019, 7, 149878–149889. [Google Scholar] [CrossRef]
- Capus, C.; Brown, K. Short-time fractional Fourier methods for the time-frequency representation of chirp signals. J. Acoust. Soc. Am. 2003, 113, 3253–3263. [Google Scholar] [CrossRef]
- Lu, G.K.; Xiao, M.L.; Wei, P. Adaptive short time fractional Fourier transform for time-frequency segmentation. Electron. Lett. 2016, 52, 615–617. [Google Scholar] [CrossRef]
- Qiao, X.S.; Shan, T.; Tao, R.; Bai, X.; Zhao, J. Separation of human micro-Doppler signals based on short-time fractional Fourier transform. IEEE Sens. J. 2019, 19, 12205–12216. [Google Scholar] [CrossRef]
- Tao, R.; Li, Y.L.; Wang, Y. Short-time fractional Fourier transform and its applications. IEEE Trans. Signal Process. 2010, 58, 2568–2580. [Google Scholar] [CrossRef]
- Chen, X.L.; Guan, J.; Bao, Z.H.; He, Y. Detection and extraction of target with micro-motion in spiky sea clutter via short-time fractional Fourier transform. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1002–1017. [Google Scholar] [CrossRef]
- Chen, X.L.; Yu, X.H.; Huang, Y.; Guan, J. Adaptive clutter suppression and detection algorithm for radar maneuvering target with high-order motions via sparse fractional ambiguity function. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1515–1526. [Google Scholar] [CrossRef]
- Dida, M.A.; Huan, H.; Tao, R.; Wang, T.; Urynbassariva, D. Constant envelope FrFT OFDM: Spectral and energy efficiency analysis. J. Syst. Eng. Electron. 2019, 30, 467–473. [Google Scholar] [CrossRef]
- Singh, K.; Saxena, R.; Kumar, S. Caputo-based fractional derivative in fractional Fourier transform. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 330–337. [Google Scholar] [CrossRef]
- Serbes, A.; Aldimashki, O. A Fast and Accurate Chirp Rate Estimation Algorithm Based on the Fractional Fourier Transform. In Proceeding of the 25th European Signal Processing Conference, Kos, Greece, 28 August–2 September 2017. [Google Scholar]
- Guan, J.; Chen, X.L.; Huang, Y.; He, Y. Adaptive fractional Fourier transform-based detection algorithm for moving target in heavy sea clutter. IET Radarsonar Navig. 2012, 6, 389–401. [Google Scholar] [CrossRef]
- Zhou, Q.; Zheng, H.; Wu, X.B.; Yue, X.C.; Chen, Z.Y.; Wang, Q.X. Fractional Fourier transform-based radio frequency interference suppression for high-frequency surface wave radar. Remote Sens. 2019, 12, 75. [Google Scholar] [CrossRef]
- Chen, Y.C.; Li, G.; Zhang, Q. Iterative minimum entropy algorithm for refocusing of moving targets in SAR images. IET Radar Sonar Navig. 2019, 13, 1279–1286. [Google Scholar] [CrossRef]
- Ma, J.M.; Miao, H.X.; Su, X.H.; Gao, C.; Kang, X.J.; Tao, R. Research progress in theories and applications of the fractional Fourier transform. Opto-Electron. Eng. 2018, 45, 5–28. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).