Fast Target Localization Method for FMCW MIMO Radar via VDSR Neural Network
Abstract
1. Introduction
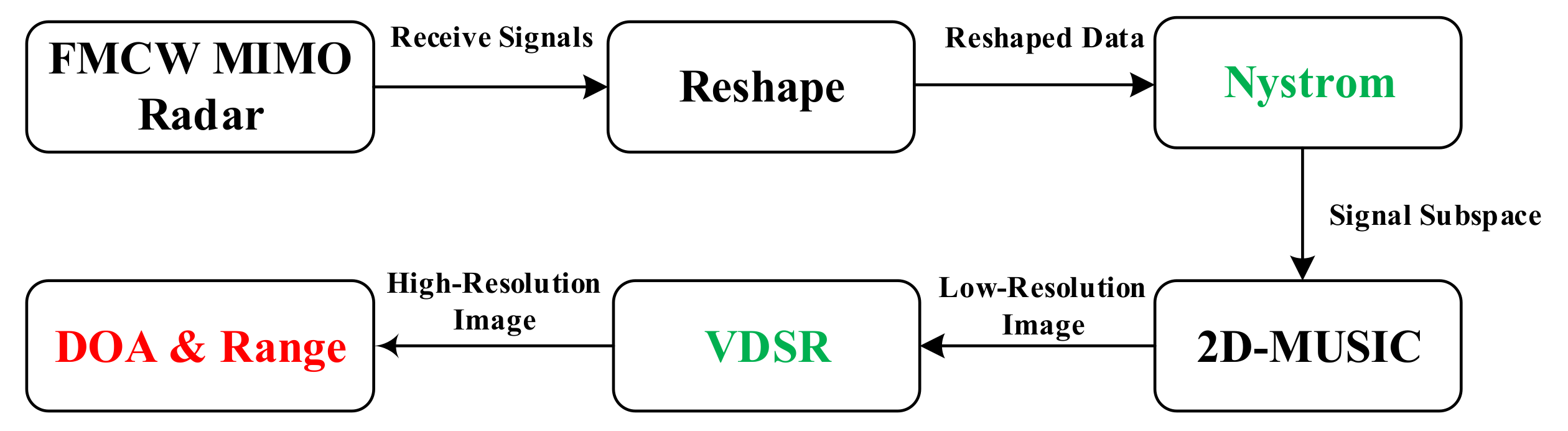
2. Data Model
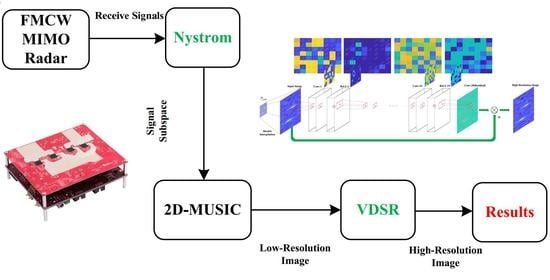
3. Fast Joint DOA and Range Estimation
3.1. Nystrom-Based Low-Resolution Imaging
3.2. VDSR-Based High-Resolution Imaging
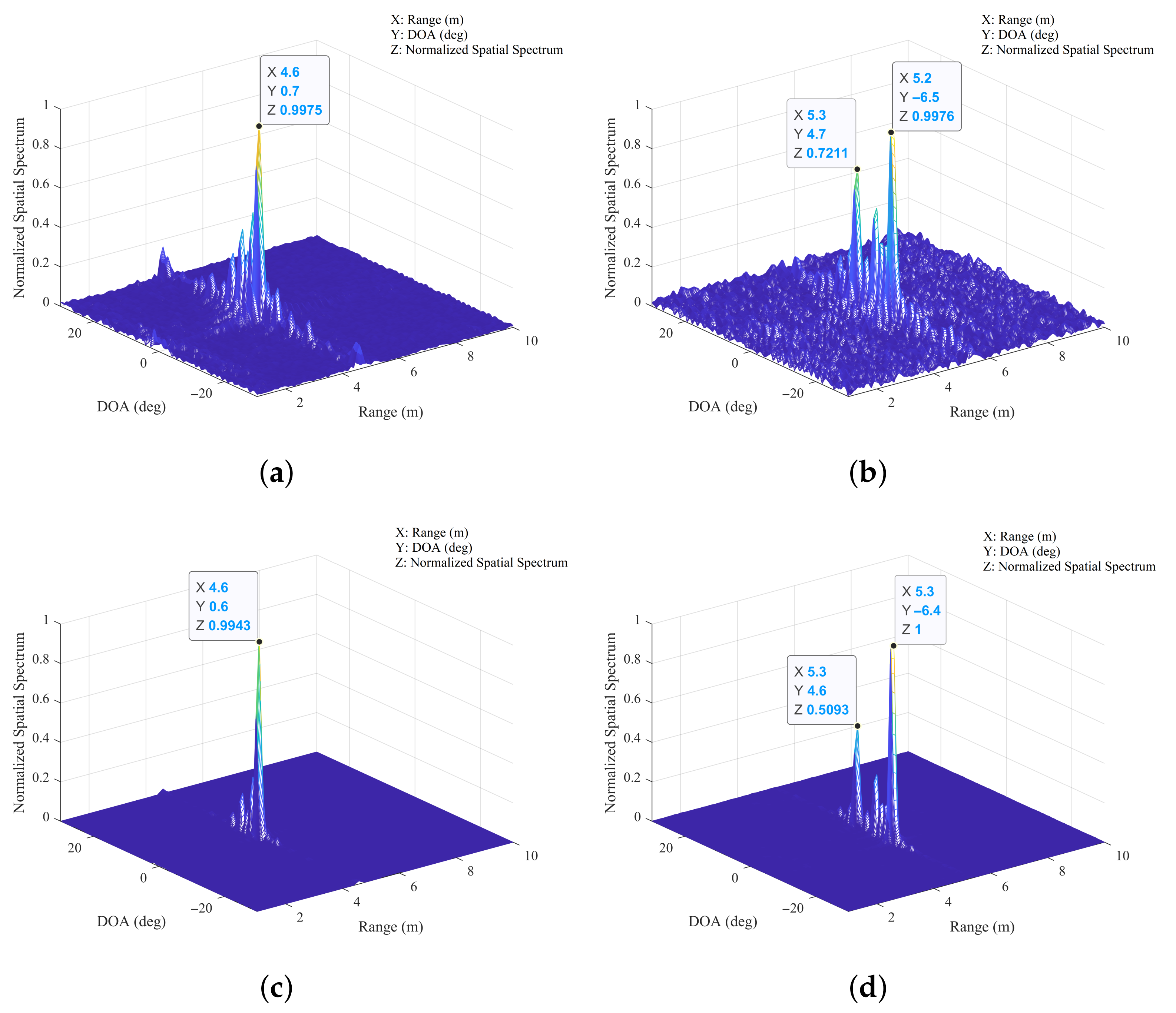
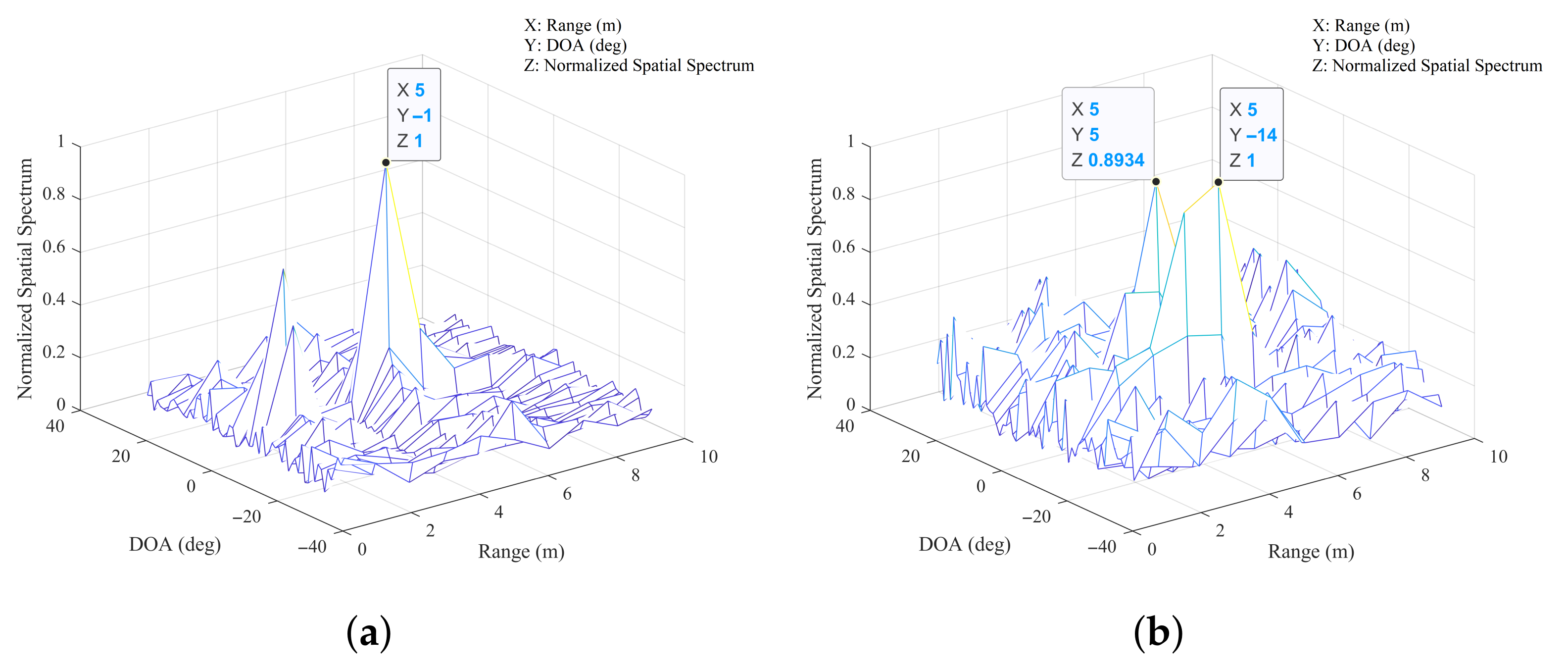
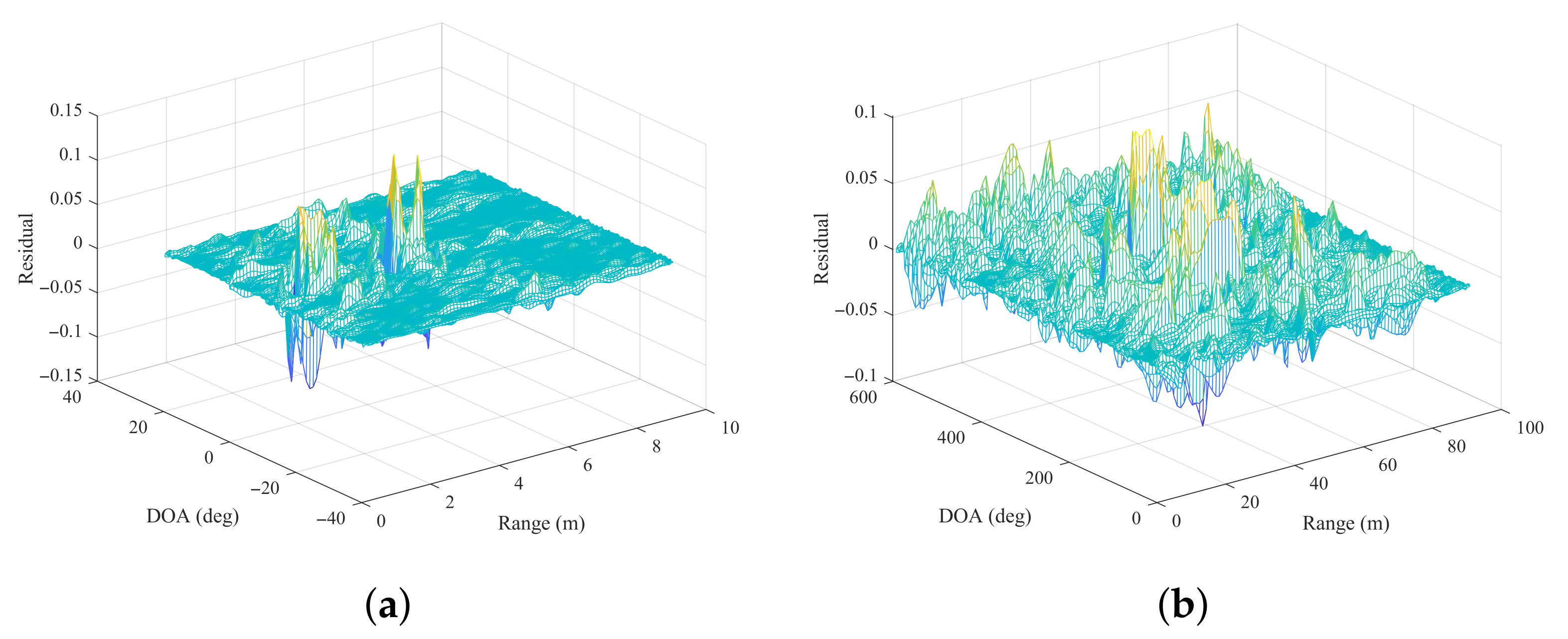
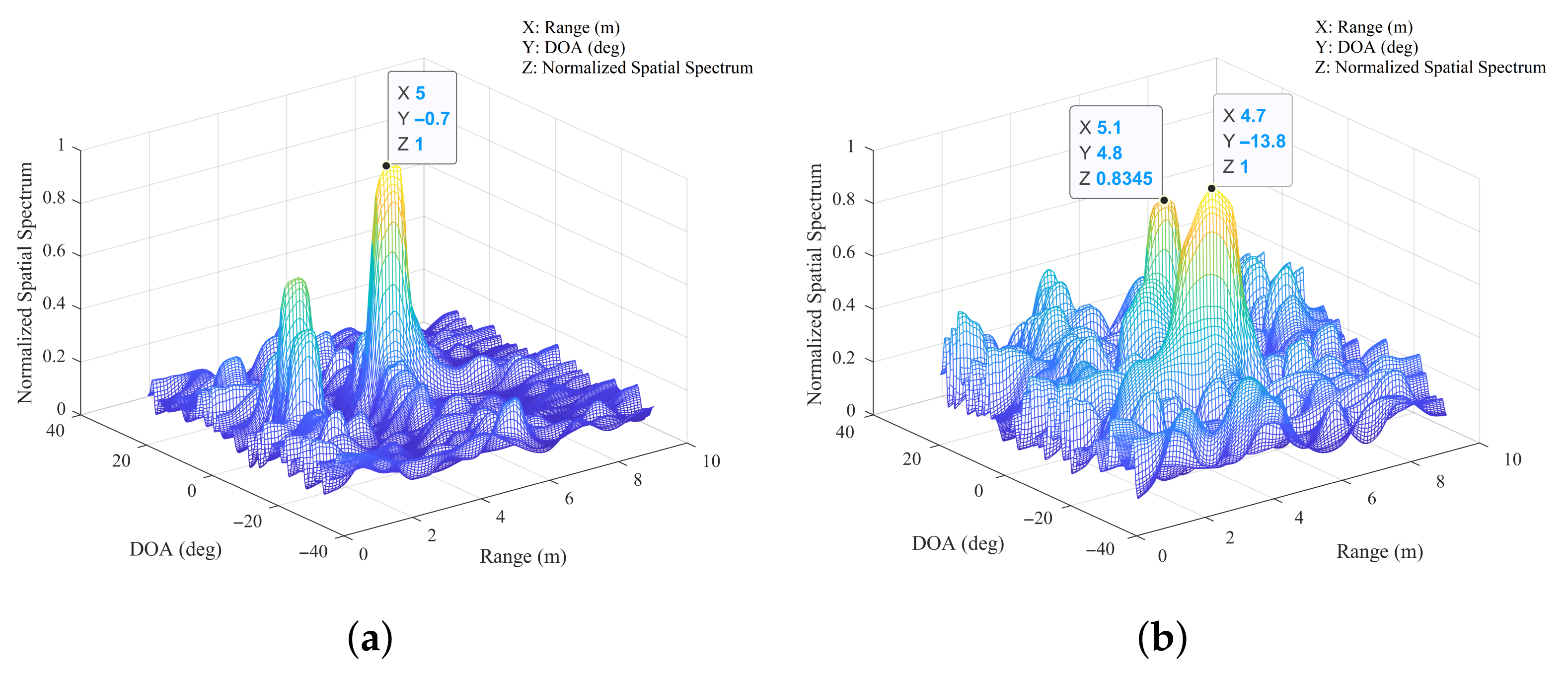
4. Simulations and Experiments
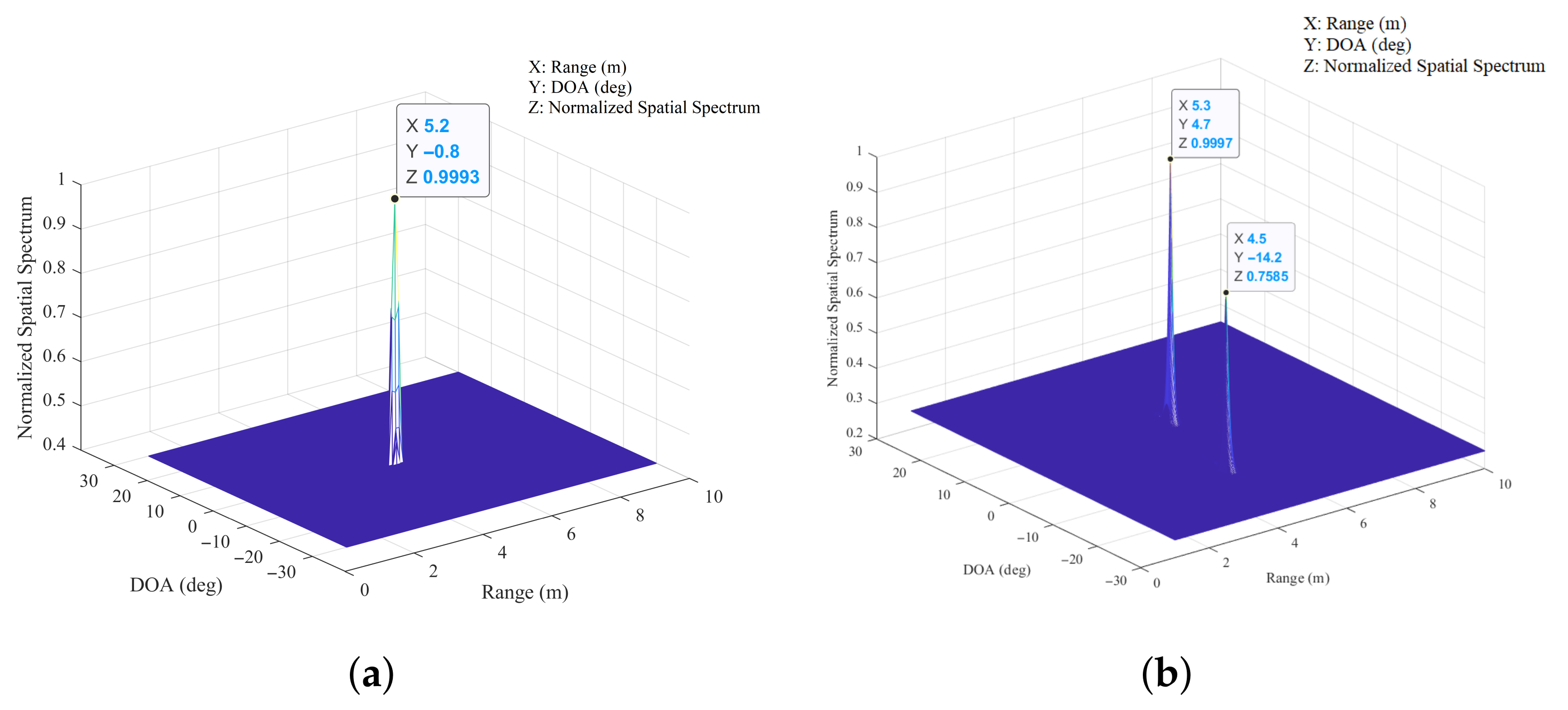
4.1. Simulations
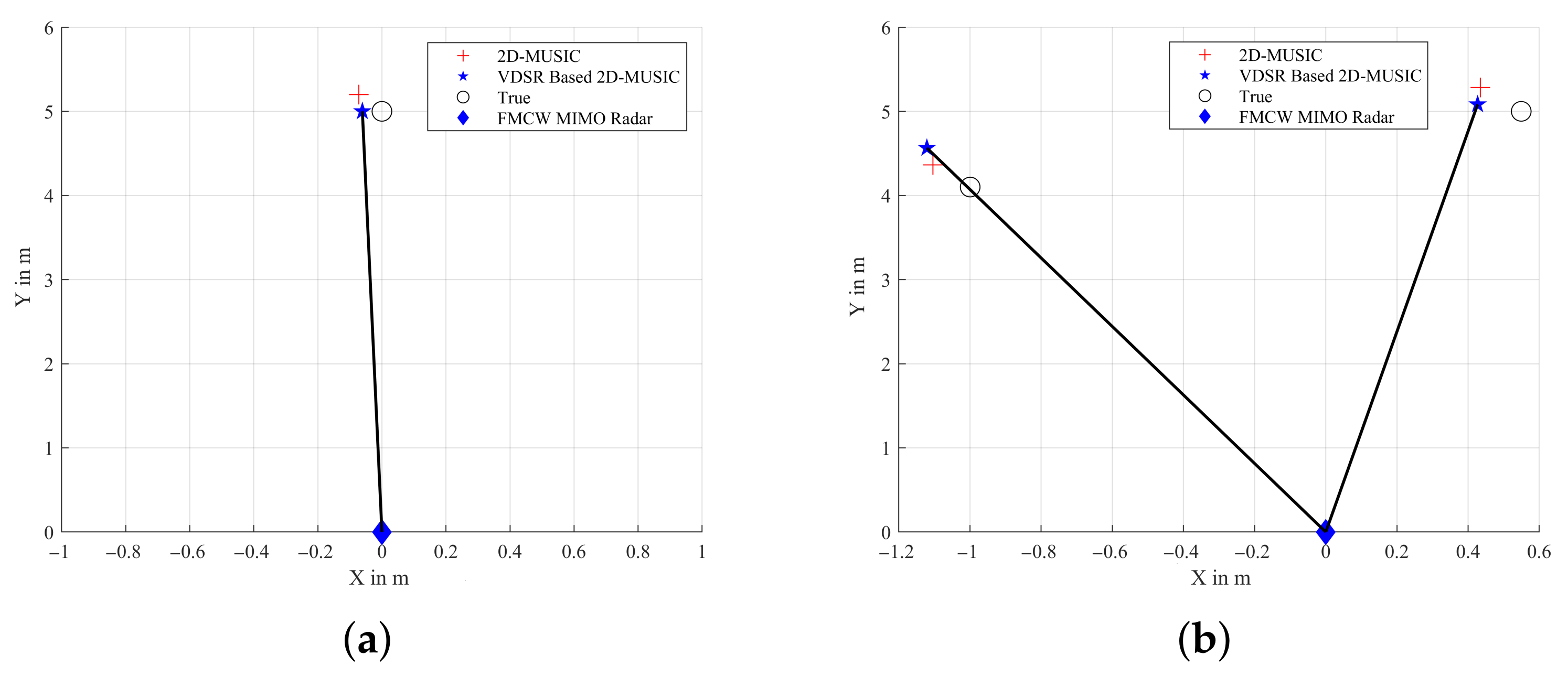
4.2. Experiments
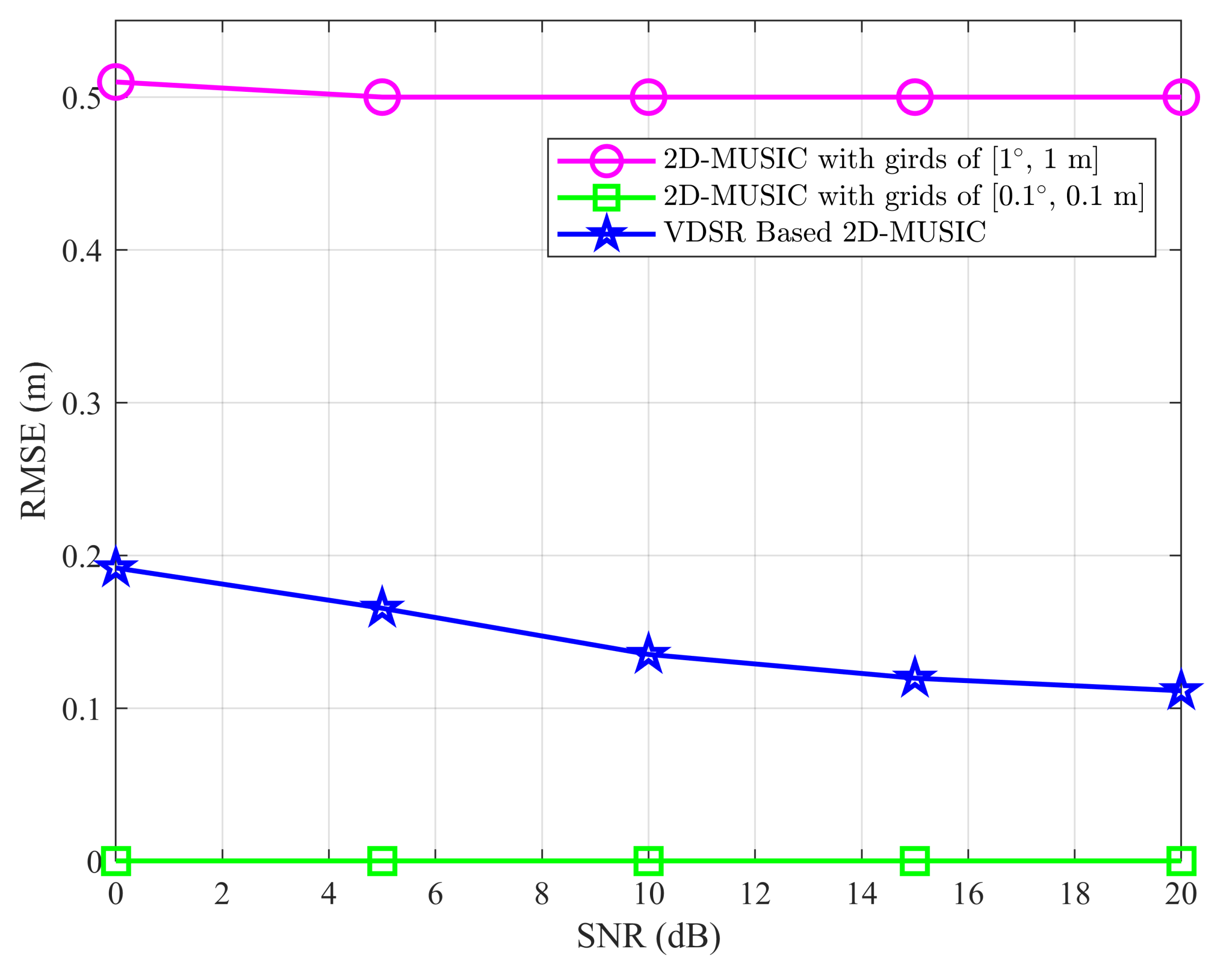
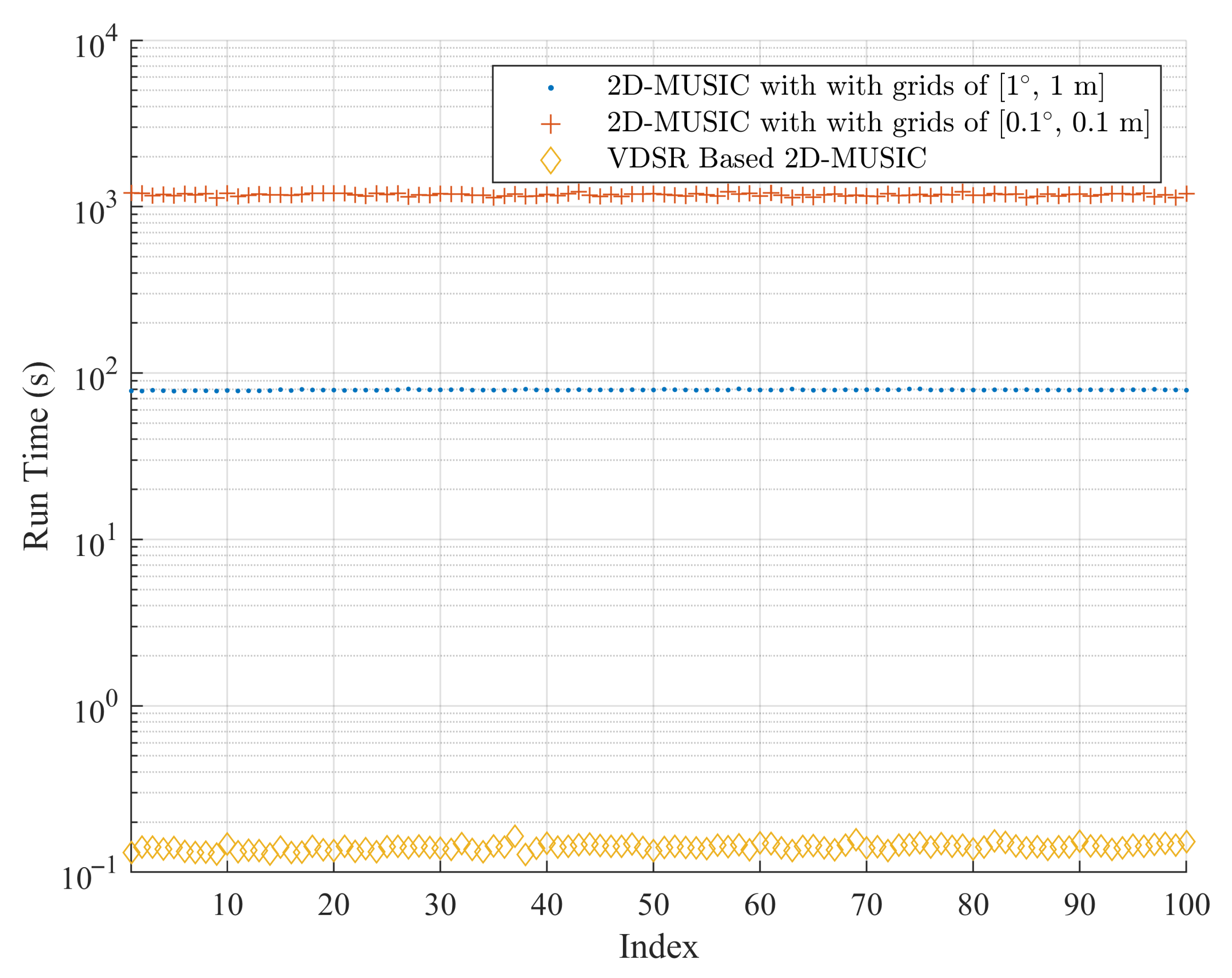
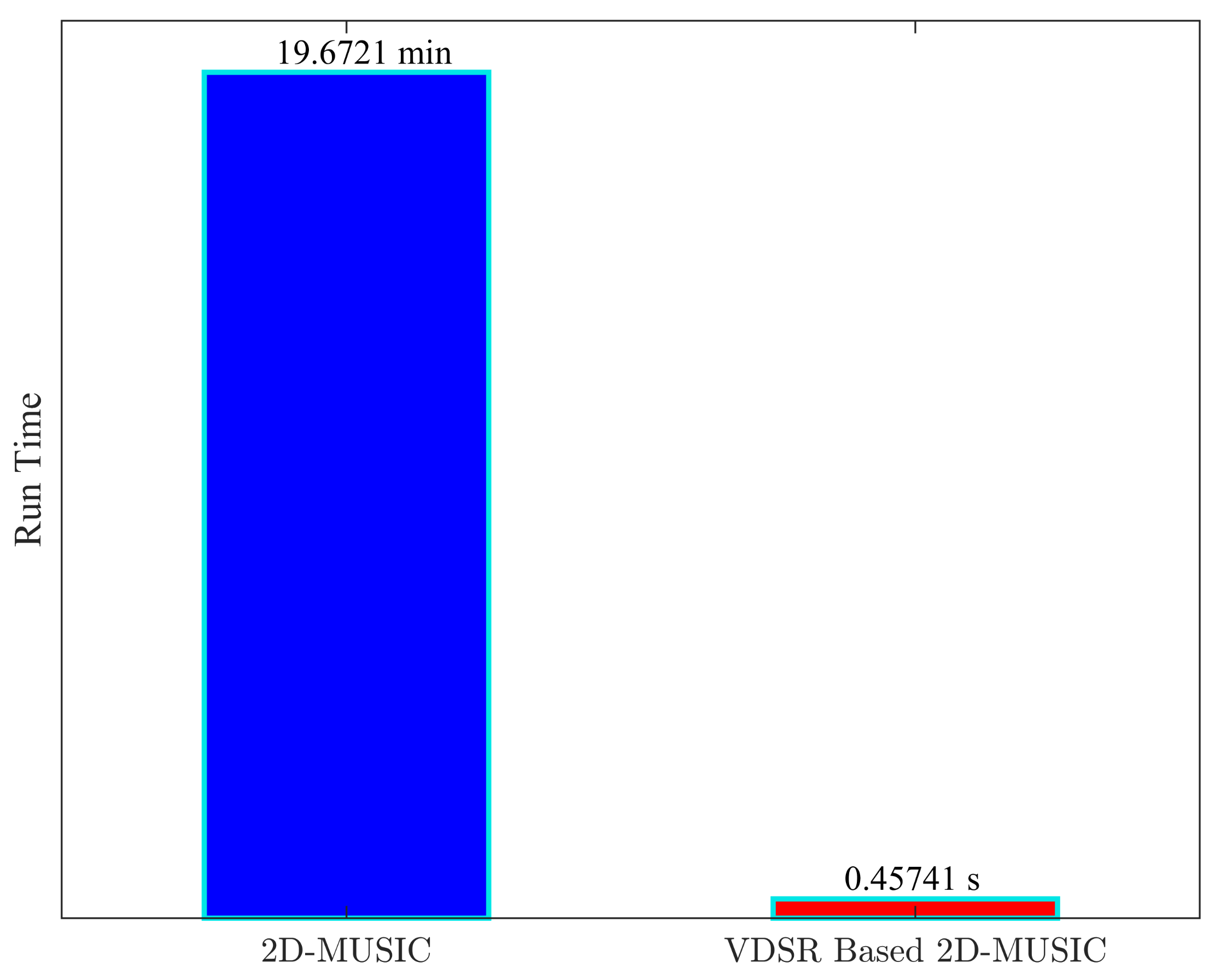
4.2.1. Comparisons of the 2D-MUSIC Algorithm and the Nystrom-Based 2D-MUSIC Algorithm
4.2.2. Comparisons of the 2D-MUSIC Algorithm and the VDSR-Based 2D-MUSIC Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Skolnik, M. Introduction to radar. In Radar Handbook; McGraw-Hill Book Co: New York, NY, USA, 1962; p. 22. [Google Scholar]
- Hasch, J.; Topak, E.; Schnabel, R.; Zwick, T.; Weigel, R.; Waldschmidt, C. Millimeter-Wave Technology for Automotive Radar Sensors in the 77 GHz Frequency Band. IEEE Trans. Microw. Theory Tech. 2012, 60, 845–860. [Google Scholar] [CrossRef]
- Rohling, H.; Meinecke, M. Waveform design principles for automotive radar systems. In Proceedings of the 2001 CIE International Conference on Radar Proceedings (Cat No.01TH8559), Beijing, China, 15–18 October 2001; pp. 1–4. [Google Scholar]
- Schneider, M. Automotive radar-status and trends. In Proceedings of the German Microwave Conference, Munich, Germany, 5–7 April 2005; pp. 144–147. [Google Scholar]
- Esposito, C.; Berardino, P.; Natale, A.; Perna, S. On the Frequency Sweep Rate Estimation in Airborne FMCW SAR Systems. Remote Sens. 2020, 12, 3448. [Google Scholar] [CrossRef]
- Esposito, C.; Natale, A.; Palmese, G.; Berardino, P.; Lanari, R.; Perna, S. On the Capabilities of the Italian Airborne FMCW AXIS InSAR System. Remote Sens. 2020, 12, 539. [Google Scholar] [CrossRef]
- Wang, R.; Loffeld, O.; Nies, H.; Knedlik, S.; Hagelen, M.; Essen, H. Focus FMCW SAR Data Using the Wavenumber Domain Algorithm. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2109–2118. [Google Scholar] [CrossRef]
- Giusti, E.; Martorella, M. Range Doppler and Image Autofocusing for FMCW Inverse Synthetic Aperture Radar. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2807–2823. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, Y.K.; Wang, R.; Loffeld, O. Bistatic FMCW SAR Signal Model and Imaging Approach. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 2017–2028. [Google Scholar] [CrossRef]
- Stove, A. Linear FMCW radar techniques. IEE Proc. F (Radar Signal Process.) 1992, 139, 343–350. [Google Scholar] [CrossRef]
- Brennan, P.; Huang, Y.; Ash, M.; Chetty, K. Determination of Sweep Linearity Requirements in FMCW Radar Systems Based on Simple Voltage-Controlled Oscillator Sources. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1594–1604. [Google Scholar] [CrossRef]
- Wang, X.; Wan, L.; Huang, M.; Shen, C.; Han, Z.; Zhu, T. Low-complexity channel estimation for circular and noncircular signals in virtual MIMO vehicle communication systems. IEEE Trans. Veh. Technol. 2021, 69, 3916–3928. [Google Scholar] [CrossRef]
- Feger, R.; Wagner, C.; Schuster, S.; Scheiblhofer, S.; Jager, H.; Stelzer, A. A 77-GHz FMCW MIMO Radar Based on an SiGe Single-Chip Transceiver. IEEE Trans. Microw. Theory Tech. 2009, 57, 1020–1035. [Google Scholar] [CrossRef]
- Wang, X.; Huang, M.; Wan, L. Joint 2D-DOD and 2D-DOA Estimation for Coprime EMVS–MIMO Radar. Circuits Syst. Signal Process. 2021. [Google Scholar] [CrossRef]
- Belfiori, F.; van Rossum, W.; Hoogeboom, P. 2D-MUSIC technique applied to a coherent FMCW MIMO radar. In Proceedings of the IET International Conference on Radar Systems (Radar 2012), Glasgow, UK, 22–25 October 2012; pp. 1–6. [Google Scholar]
- Hamidi, S.; Nezhad-Ahmadi, M.; Safavi-Naeini, S. TDM based Virtual FMCW MIMO Radar Imaging at 79GHz. In Proceedings of the 2018 18th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Waterloo, ON, Canada, 19–22 August 2018; pp. 1–2. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Timofte, R.; Smet, V.; Gool, H. A+: Adjusted anchored neighborhood regression for fast super-resolution. In Proceedings of the Asian Conference on Computer Vision, Singapore, 1–5 November 2014; Springer: Cham, Switzerland, 2014; pp. 111–126. [Google Scholar]
- Schulter, S.; Leistner, C.; Bischof, H. Fast and accurate image upscaling with super-resolution forests. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3791–3799. [Google Scholar]
- Huang, J.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Dong, C.; Loy, C.; He, K.; Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 295–307. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Huang, M.; Cao, C.; Li, H. Angle Estimation of Noncircular Source in MIMO Radar via Unitary Nystrom Method. In Proceedings of the International Conference in Communications, Signal Processing, and Systems, Harbin, China, 14–16 July 2017; Springer: Singapore, 2017. [Google Scholar]
- Grubinger, M.; Clough, P.; Müller, H.; Deselaers, T. The IAPR TC12 Benchmark: A New Evaluation Resource for Visual Information Systems. In Proceedings of the OntoImage 2006 Language Resources for Content-Based Image Retrieval, Genoa, Italy, 22 May 2006; Volume 5, p. 10. [Google Scholar]
- Cong, J.; Wang, X.; Huang, M.; Wan, L. Robust DOA Estimation Method for MIMO Radar via Deep Neural Networks. IEEE Sensors J. 2021, 21, 7498–7507. [Google Scholar] [CrossRef]
- Wang, X.; Yang, L.T.; Meng, D.; Dong, M.; Ota, K.; Wang, H. Multi-UAV Cooperative Localization for Marine Targets Based on Weighted Subspace Fitting in SAGIN Environment. IEEE Internet Things J. 2021. [Google Scholar] [CrossRef]
- Winoto, A.S.; Kristianus, M.; Premachandra, C. Small and Slim Deep Convolutional Neural Network for Mobile Device. IEEE Access 2020, 8, 125210–125222. [Google Scholar] [CrossRef]
- Baozhou, Z.; Al-Ars, Z.; Hofstee, H.P. REAF: Reducing Approximation of Channels by Reducing Feature Reuse within Convolution. IEEE Access 2020, 8, 169957–169965. [Google Scholar] [CrossRef]










| Notations | Definitions |
|---|---|
| capital bold italic letters | matrices |
| lowercase bold italic letters | vectors |
| j | imaginary unit |
| e | Euler number |
| t | time |
| conjugate transpose operator | |
| transpose operator | |
| vectorization operator | |
| dimensional complex matrix set | |
| 2-norm operator | |
| mathematical expectation | |
| ⊗ | Kronecker product |
| ⊙ | Khatri-Rao product |
| Moore-Penrose Inverse | |
| expansion space operator | |
| minimum value | |
| maximum value | |
| Identity matrix of order M | |
| Rectified Linear Units |
| Name | Type | Activations | Learnables |
|---|---|---|---|
| Input Image | Image Input | - | |
| Image Size: | |||
| Conv.1 | Convolution | Weights | |
| Number of Filters: 64, Filter Size: | |||
| with stride [1 1] and padding [1 1 1 1] | Bias | ||
| ReLU.1 | ReLU | - | |
| Conv.2 | Convolution | Weights | |
| Number of Filters: 64, Filter Size: | |||
| with stride [1 1] and padding [1 1 1 1] | Bias | ||
| ReLU.2 | ReLU | - | |
| Conv.3 | Convolution | Weights | |
| Number of Filters: 64, Filter Size: | |||
| with stride [1 1] and padding [1 1 1 1] | Bias | ||
| ReLU.3 | ReLU | - | |
| … | … | … | … |
| Conv.19 | Convolution | Weights | |
| Number of Filters: 64, Filter Size: | |||
| with stride [1 1] and padding [1 1 1 1] | Bias | ||
| ReLU.19 | ReLU | - | |
| Conv.20 | Convolution | Weights | |
| Number of Filters: 1, Filter Size: | |||
| with stride [1 1] and padding [1 1 1 1] | Bias | ||
| Residual Output | Regression Output | - | - |
| mean-squared-error | |||
| with response “ResponseImage” |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| c | |||
| d | M | 86 | |
| L | 75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cong, J.; Wang, X.; Lan, X.; Huang, M.; Wan, L. Fast Target Localization Method for FMCW MIMO Radar via VDSR Neural Network. Remote Sens. 2021, 13, 1956. https://doi.org/10.3390/rs13101956
Cong J, Wang X, Lan X, Huang M, Wan L. Fast Target Localization Method for FMCW MIMO Radar via VDSR Neural Network. Remote Sensing. 2021; 13(10):1956. https://doi.org/10.3390/rs13101956
Chicago/Turabian StyleCong, Jingyu, Xianpeng Wang, Xiang Lan, Mengxing Huang, and Liangtian Wan. 2021. "Fast Target Localization Method for FMCW MIMO Radar via VDSR Neural Network" Remote Sensing 13, no. 10: 1956. https://doi.org/10.3390/rs13101956
APA StyleCong, J., Wang, X., Lan, X., Huang, M., & Wan, L. (2021). Fast Target Localization Method for FMCW MIMO Radar via VDSR Neural Network. Remote Sensing, 13(10), 1956. https://doi.org/10.3390/rs13101956