Abstract
This paper presents a new group target tracking method based on the standard multi-sensor multi-target multi-Bernoulli (MS-MeMBer) filter. In the prediction step, the group structure is used to constrain the movement of the constituent members within the respective groups. Specifically, the group of members is considered as an undirected random graph. Combined with the virtual leader-follower model, the motion equation of the members within groups is formulated. In the update step, the partitioning problem of multiple sensors is transformed into a multi-dimensional assignment (MDA) problem. Compared with the original two-step greedy partitioning mechanism, the MDA algorithm achieves better measurement partitions in group target tracking scenarios. To evaluate the performance of the proposed method, a simulation scenario including group splitting and merging is established. Results show that, compared with the standard MS-MeMBer filter, our method can effectively estimate the cardinality of members and groups at the cost of increasing computational load. The filtering accuracy of the proposed method outperforms that of the MS-MeMBer filter.
1. Introduction
Group targets [1] can be considered as the formation of cooperative members whose locations obey special structures, such as unmanned aerial vehicle (UAV) formations, vehicle convoys, and flocks of birds, which are densely distributed and maintain certain patterns of movement. For tracking such targets, if a standard point target tracking method e.g., [2] was adopted, performance degradation would occur. On the one hand, the high density of measurement may lead to complex computations by standard tracking methods. On the other hand, the interaction between the members within the group is ignored, which is not conducive for improving the tracking accuracy and stability. In general, there are mainly two methods for tracking group targets: The “holistic” tracking method based on the group shape and centroid [3,4,5,6], and the “internal” tracking method based on group structures [7,8,9].
It is difficult to establish a stable trajectory for densely clustered targets with poor measurement resolution and severe echo crossing. A “holistic” tracking strategy [3] has been proposed to handle such targets, which focuses on the group shape and centroid state instead of focusing on targets within the group. Similar to the extended target tracking method [10,11,12,13,14], this strategy models the group shape, such as the elliptical model [15], the random hypersurface model (RHM) [16], and the star-convex model [17].
Tracking members within the group is of great significance in certain cases. For instance, by estimating the members’ states, one can distinguish friendly objects from enemies or predict the intention of the groups. In a high-resolution sensor system, the measurements of different members within the group are located in different resolution units and maintain a special distribution structure. Modelling the group structure is the basis for tracking internal members. By combining the group structure with the member’s state, the integrity and stability of target tracking can be improved. Several models of group structures have been proposed and widely used, such as the virtual leader-follower model [7], the Markov random field (MRF) model [8], and the evolving network model [9].
The filter based on random finite set (RFS) [18] avoids the complicated data association process and introduces a complete theoretical framework for target tracking. In the single-sensor field, the probability hypothesis density (PHD) [19], multi-target multi-Bernoulli (MeMBer) [20], generalized labelled multi-Bernoulli (GLMB) filters [21], and their variants [22,23,24] for group target tracking have been proposed. Moreover, the multi-sensor PHD (MS-PHD) [25], multi-sensor MeMBer (MS-MeMBer) [26], and multi-sensor GLMB (MS-GLMB) filters [27] have shown promising performance in handling multi-sensor measurements. Besides, several particle filters [28,29,30] have been proposed to improve the accuracy of the target state estimation. However, very few “internal” tracking methods have been considered in the literature for multi-sensor RFS filtering.
The MS-MeMBer filter inherits the advantages of the multi-Bernoulli filters with straightforward particle implementations and state estimation [20]. Although it cannot obtain target trajectories, it has a lower computational cost than that of the labelled versions [27]. Inspired by the idea of [23], we propose a group target tracking method using the virtual leader–follower model and the MS-MeMBer filter. Specifically, in the prediction step of the MS-MeMBer filter, we consider the group of individuals as an undirected random graph. Furthermore, the motion equation of targets within groups is introduced, combined with the virtual leader–follower model. Then, in the update step, the partition of multi-sensor measurements is transformed into a multi-dimensional assignment (MDA) problem. Using the MDA algorithm proposed in [31], better measurement partitions can be achieved in conditions for tracking targets within groups.
2. Background
2.1. The Random Finite Set
In the random finite set (RFS), the number of elements is random and finite, and the elements themselves are random and unordered. Thus, in the multi-target tracking field, the multi-target state and the measurements of targets can be intuitively represented by the RFS. Some examples of RFSs with special distributions are given next.
A Bernoulli RFS has a probability of being empty, and a probability of being a singleton whose element is distributed with a function . The probability density of a Bernoulli RFS is given by
which can be simplified to .
A Multi-Bernoulli RFS is a union of a fixed number of independent Bernoulli RFSs, i.e., . is the number of Bernoulli RFSs in , and the probability density of a multi-Bernoulli RFS is given by
which can be further simplified to .
2.2. The MS-MeMBer Filter
In the established MS-MeMBer filter [26], the multi-target state at time is modelled as a multi-Bernoulli RFS and characterized by a posterior density . The target is observed by S sensors, which generate independent measurements. The MS-MeMBer filter aims to estimate the density of the RFS given the set of all the measurements up to time k. The measurement partition is finished in the update step. Therefore, the multi-target state can be obtained in a Bayesian recursion [32] via prediction and update:
We summarize each step in the following sections.
2.2.1. The Prediction Step
Consider a multi-Bernoulli RFS composed of independent Bernoulli RFSs. The density of is
where each represents the independent Bernoulli density with probability and distribution function . Intuitively, indicates how likely the i-th Bernoulli RFS in is generated by a true target and describes the estimated current state of the target [33]. Therefore, we can obtain the multi-target state estimation by calculating the corresponding multi-Bernoulli density.
Given the birth multi-Bernoulli RFS with density , the predicted density is also a multi-Bernoulli with
where is the number of birth Bernoulli RFSs.
Additionally, the survival Bernoulli density follows
where represents the probability that a target with state x can survive to the next moment and is the inner product function. is the state transfer function at time k, given previous state .
2.2.2. Multi-Sensor Measurement Partition
In the update step of the MS-MeMBer filter, multi-sensor measurement partitions need to be produced. Measurement partition aims to divide the multi-sensor measurement set into target-originated subsets, which can be employed to associate the predicted Bernoulli RFSs.
Given a multi-sensor measurement set , each contains all measurements from sensor j at time k. For a number of predicted Bernoulli RFSs, we define a partition of set as , where
In partition , each denotes the measurement set of target i generated by all S sensors and is the clutter measurement set. Each in (8) contains the measurement of target i generated by sensor j. is the collection of all clutter measurements on sensor j.
is defined as the collection of all possible measurement partitions P. Finally, we define the mapping function , where j is the sensor number and is the l-th measurement in set .
It is difficult to obtain the exact implementation of the MS-MeMBer filter because of the complexity of obtaining all the measurement partitions. Partitions with low scores can be ignored because they have little effect on the update step. For this, a two-step greedy partitioning mechanism is proposed in [25], which can obtain several high-scoring measurement partitions.
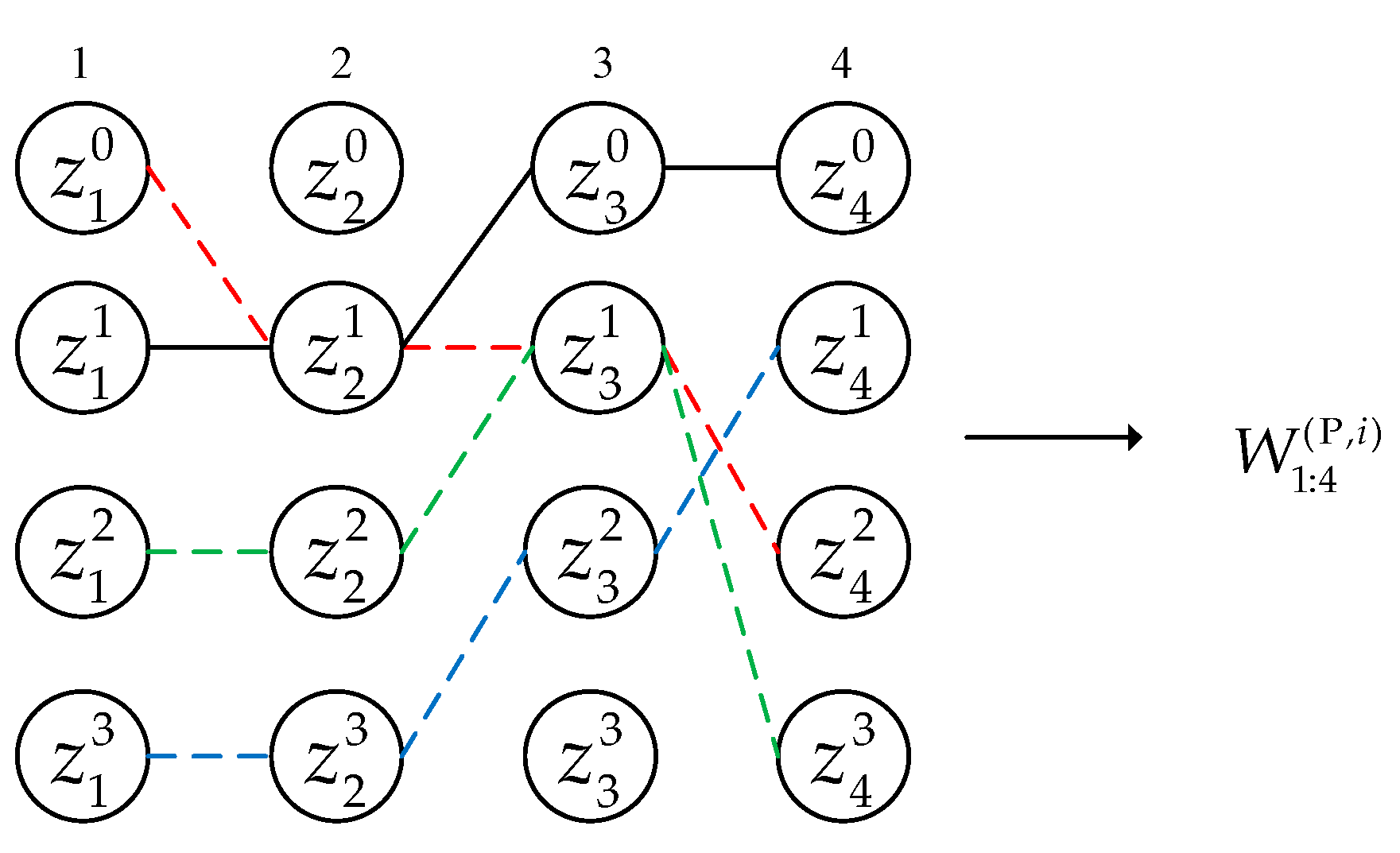
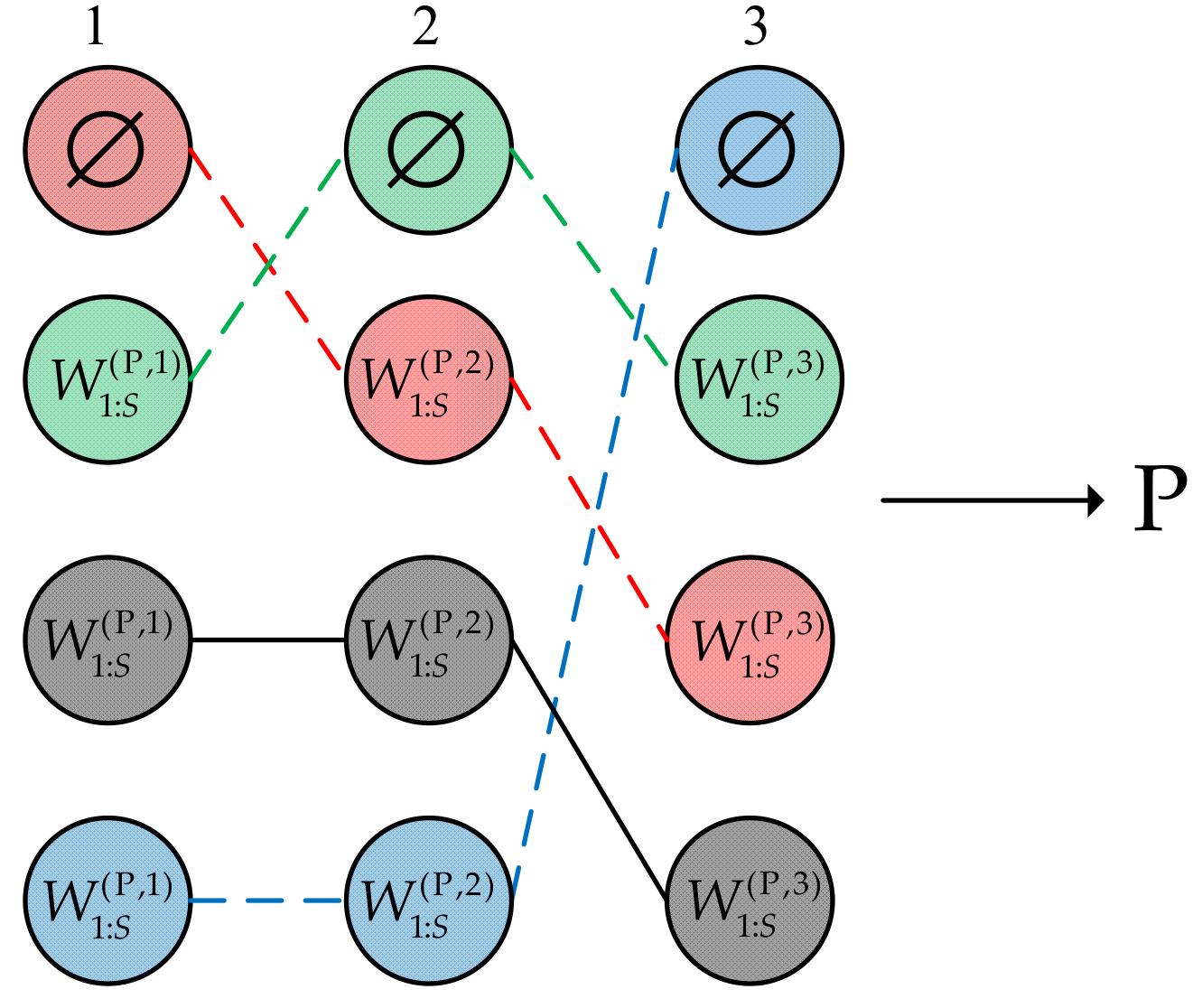
In the two-step greedy partitioning mechanism, the global problem to obtain is decomposed into independent sub-problems. We consider a measurement partitioning process with four sensors and three predicted Bernoulli components. First, local optimal solutions are achieved for each Bernoulli component, as shown in Figure 1. indicates that there is no measurement of sensor j associated with the Bernoulli component. Second, local optimal solutions of each Bernoulli component are combined to obtain several high-scoring partitions, as seen in Figure 2. The empty set means that all the measurements of S sensors are not associated with the Bernoulli component.
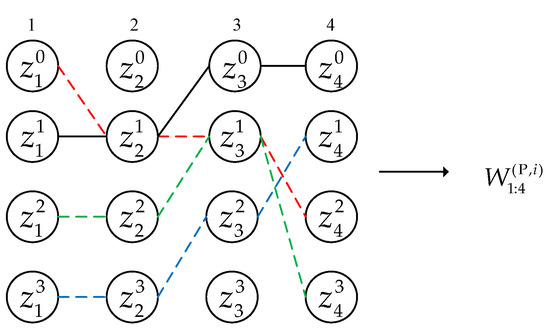
Figure 1.
Illustration of the first step. Given a Bernoulli RFS of target i, we can generate the corresponding set according to the sensor order, where the measurements in the same column are generated from the same sensor. The solid line represents the current best combination, and the dotted line represents other better alternatives.
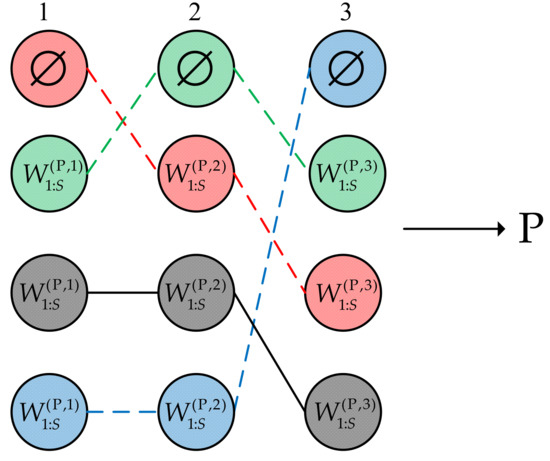
Figure 2.
Illustration of the second step. Partitions are formed by sequentially processing the set . In the i-th column, differently colored represent different results from the first step of the two-step greedy partitioning mechanism.
2.2.3. The Update Step
Given the predicted multi-target density with
and the updated multi-target density can be approximately expressed as
where . For a given partition in set , we can get the updated Bernoulli density with
As can be seen from (12) and (13), each updated Bernoulli component is obtained only by the corresponding set . is the probability that a target is detected by no sensor. is the target detection probability of sensor j. is the single-target multi-sensor likelihood function under clutter conditions, and follows
and are the measurement likelihood and the clutter density of sensor j, respectively.
The coefficient is given by
where
In (15), represents the value of function evaluated at . Intuitively, scores the association of the measurement set with the i-th Bernoulli component , while represents a score of the partition . represents the weight of in collection , which can be calculated by dividing the score of by the sum of all the partitioning scores in . denotes the constraint of the clutter set, where is the cardinality of set , and is the n-th derivative of the clutter probability generating function.
3. The Group Target Tracking
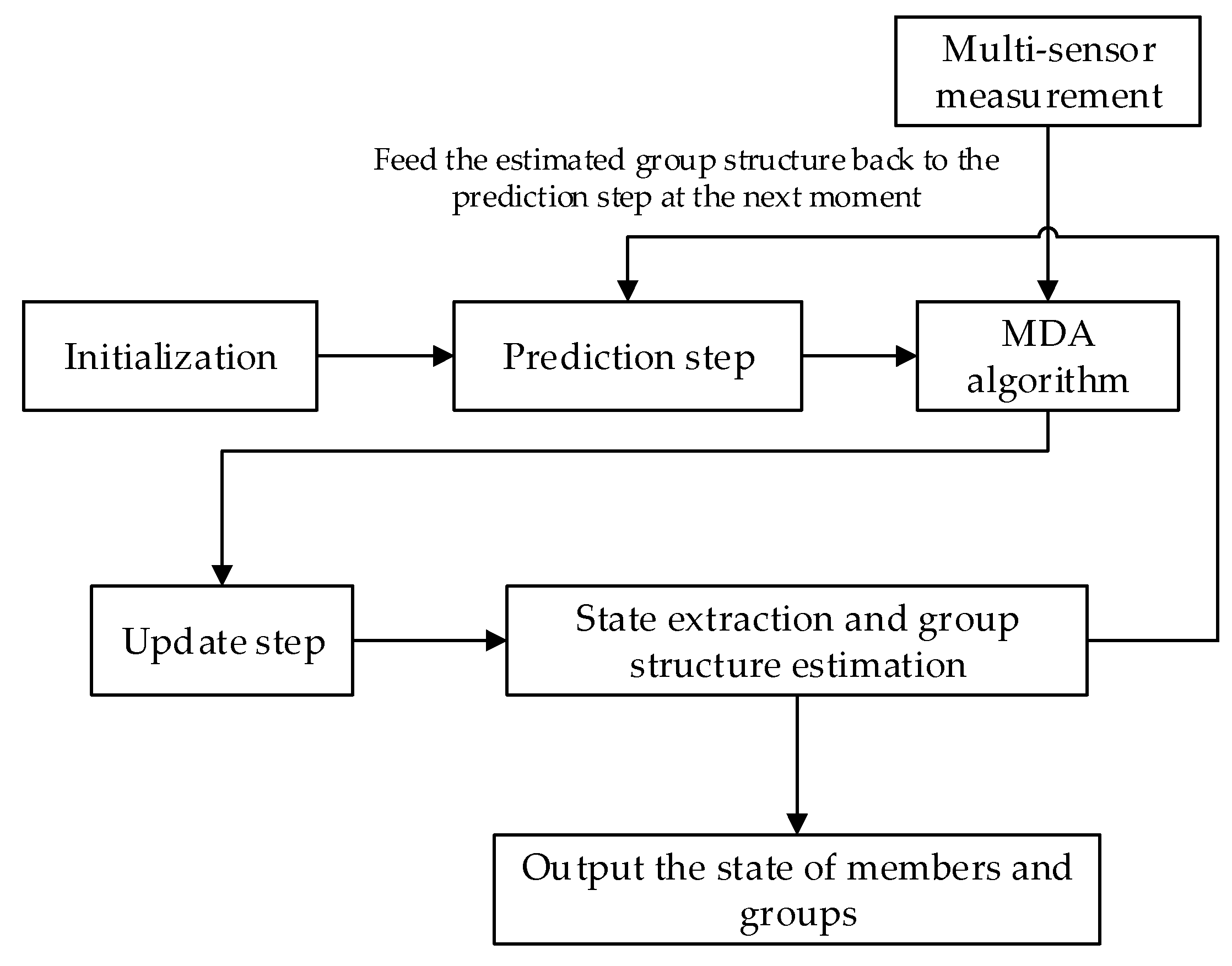
Based on the MS-MeMBer filter, a new group target tracking method is proposed. First, the filter parameters and the group structure are initialized according to the initial state of members. Then, in the prediction step, the movement of the members within a group is constrained by the group structure. Furthermore, in the update step, the partition of multi-sensor measurements is transformed into a multi-dimensional assignment (MDA) problem. Compared with the original two-step greedy partitioning mechanism [26], the MDA algorithm [31] can obtain better measurement partitions in group target tracking scenarios. Finally, the group structure is estimated through the current state of internal members and is fed back to the prediction step at the next moment. Also, the current state of members and groups is output. The flowchart of the proposed method is shown in Figure 3.
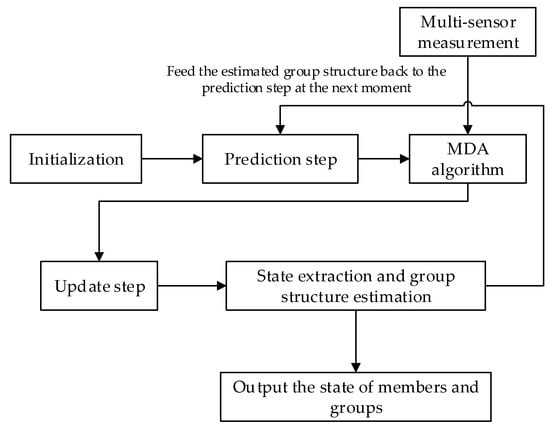
Figure 3.
The filtering flowchart of the proposed method.
3.1. Graphical Representation of the Group
Graph theory [22] provides a convenient tool for describing groups, in which the relations between members are reflected by the edges between the related graph vertices. In this section, we consider the group of members as an undirected graph.
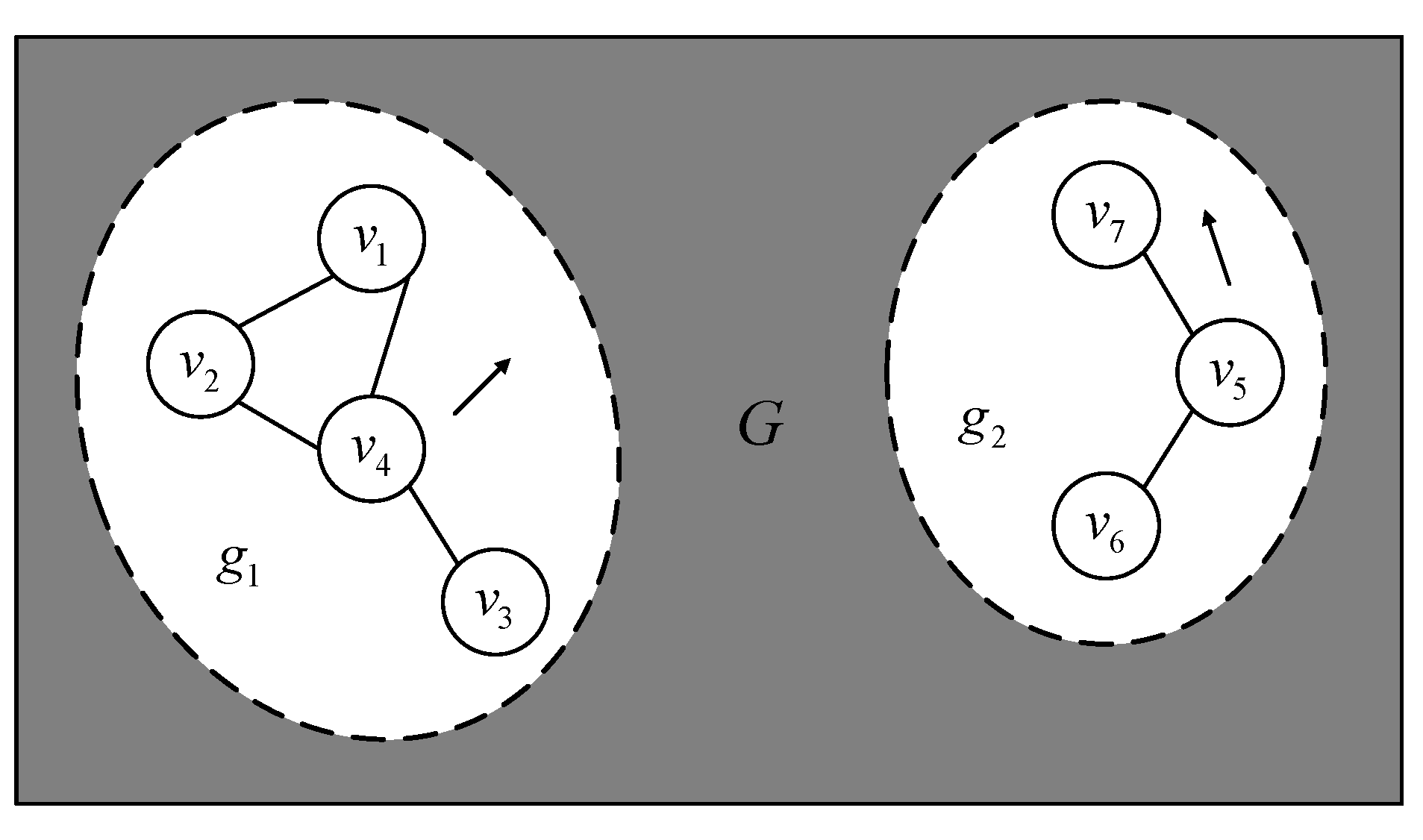
Given an undirected graph, of group m at time . is the vertex set composed of n individuals within group m, and each vertex contains the state and covariance of target i. For two different vertices and , if the Mahalanobis distance is less than the threshold , it is determined that there is an edge connection between them. In other words, targets i and j are in the same group. is the collection of all edges between vertices in . is a mapping function that points to other members in the same group with target i. represents a set of undirected graphs for each group. Figure 4 is a graphical representation of group targets, which shows seven moving targets belonging to two groups.

Figure 4.
Graphical representation of groups. Seven moving targets belong to two groups. The arrow shows the direction of movement of the group. Note that there is no edge between and . However, they are in the same group because of the common connection with .
3.2. The System Model of Group Movement
The virtual leader–follower model [7] assumes that the state of any member is the translational offset of the group centroid. Consider a group with members at time . We represent the member state as . and are the target positions. and represent the target velocities along respective axes. According to the leader–follower model, the motion equation of the i-th member is given by
where
and are the unit matrix and zero matrix of size d, respectively. The process noise is considered as the zero-mean white Gaussian noise with variance . We can see from (17) that the movement of the members is not only related to its own state at the previous moment, but also restricted by other members in the same group. If is an empty set, then (17) can be simplified to the standard motion equation [2].
The observation equation of group members is given by
where is the observation of , and is the measurement noise, which is usually assumed to be the zero-mean white Gaussian noise with variance . is the observation matrix at time k.
3.3. Multi-Sensor Measurement Partition and MDA
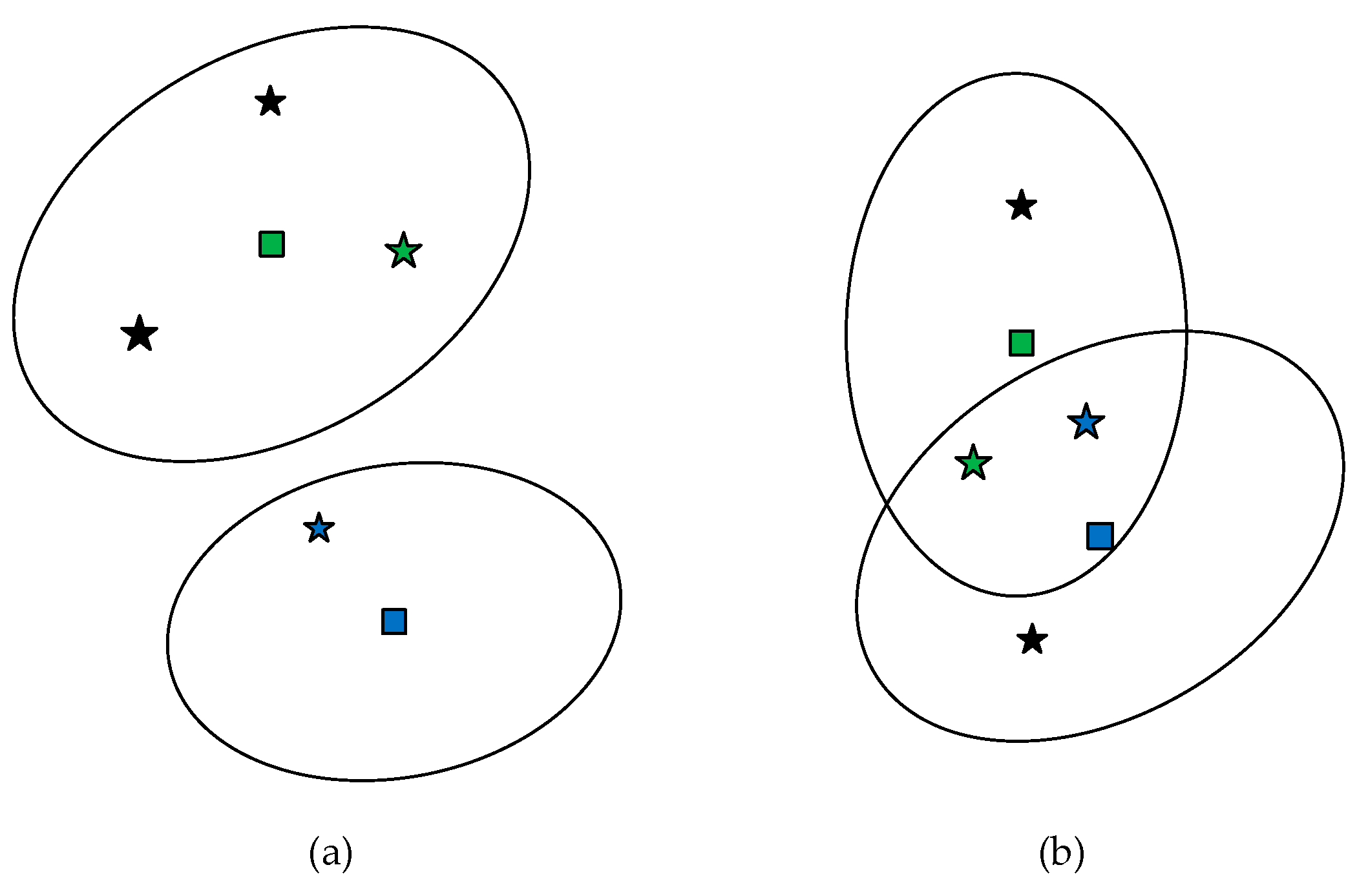
In the two-step greedy partitioning algorithm, each Bernoulli RFS (target) is assumed to be independent. Then, the target measurement set of each Bernoulli RFS can be obtained separately. Also, the clutter measurement set is assumed to be independent of the target. Therefore, measurement partitions can be formed by combining each independent measurement set. As a divide-and-conquer strategy, this algorithm breaks the partitioning problem up into several independent sub-problems, which improves the efficiency of measurement partition. However, due to the dense distribution of individuals within groups, the association between measurements and targets is more complex. As can be seen from Figure 5, the measurement of a member would fall within the correlation threshold of other members in the same group. In this case, it is hard to maintain independence between the sub-problems in the two-step greedy partitioning mechanism. If the divide-and-conquer strategy is still adopted in group target tracking scenarios, the quality of the measurement partitions would deteriorate.
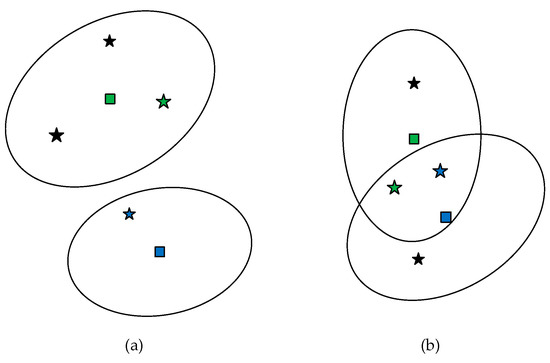
Figure 5.
Examples of associations between targets and measurements for (a) standard point target tracking case and (b) group target tracking case. The square represents the target, distinguished by different colors. Measurements include clutter (black hexagrams) and target measurements (hexagrams in other colors). The ellipse is the correlation threshold. Note that a target is only associated with measurements fall within its threshold.
In this section, by eliminating the constraint of the clutter measurement set, the multi-sensor measurement partition can be interpreted as a multi-dimensional allocation problem, which can be solved by the MDA algorithm [27]. Compared with the two-step greedy partitioning mechanism, the MDA algorithm is implemented from the whole perspective, which improves the quality of multi-sensor measurement partitions. The derivation detail is given as follows.
From [25], the n-th derivative of function obeys
where is the clutter intensity of sensor j.
Then the coefficient in (15) can be written as
where
We employ as a ratio of the likelihood that is generated by target i to the likelihood that is the clutter set. As can be seen from (22), the constraint of the clutter set is eliminated. Therefore, we can obtain the partition by associating Bernoulli RFSs with the measurements of S sensors.
In order to get the best association between multi-sensor measurements and Bernoulli components, the maximum score of is required:
The maximization problem shown in (25) is equivalent to the negative logarithmic minimization problem:
where
In (27), the decision variable denotes that the measurement set is associated with the i-th Bernoulli RFS. The number of predicted Bernoulli RFSs is given by and the number of measurements from sensor j at time k is . The constraint condition can be expressed as
which guarantees that two different Bernoulli RFSs cannot share the same real measurement, and that a Bernoulli RFS can be associated with an empty set .
The minimization problem shown in (26) can be solved by the MDA algorithm [27]. Also, multiple high-scoring partitions are needed in the update step. Therefore, a list can be created that ranks feasible solutions in the order of cost factors.
3.4. Gaussian Mixture Implementation
It is very intractable to calculate multiple integrals in the prediction step and update step of the MS-MeMBer filter. Therefore, a Gaussian mixture (GM) implementation is adopted, in which the distribution function of each Bernoulli component is assumed to follow a GM form.
3.4.1. Prediction Step
Assume that at time , the distribution function of each Bernoulli component has the following GM form:
where is a Gaussian function with mean and variance . is the number of the Gaussian components. is the weight of the corresponding component.
Using (17), the transfer function follows
Define the target survival probability as , and the distribution function of newborn targets as a GM form with .Then the distribution function of each survival Bernoulli component also has a GM form:
where
Furthermore, the probability of each survival Bernoulli follows
3.4.2. Update Step
Assume that the distribution of each predicted Bernoulli component has the following GM form:
Given the measurement likelihood function of each sensor , and the detection probability of each sensor , the distribution function of each updated Bernoulli component also has a GM form:
where
and
The updated probability satisfies
3.5. The State Extraction and Group Structure Estimation
The state extraction [25] is adopted to calculate the movement of all the targets, where the mean value is obtained from the densities of the updated Bernoulli RFSs with the exiting probabilities exceeding a given threshold. Consider the multi-target movement at time k, where and are the kinematic state and covariance matrix of member i, respectively.
Suppose that at time k, the adjacency matrix is given by
where
The structure and number of groups can be obtained by the adjacency matrix [23]. If the Mahalanobis distance between two targets is less than the threshold , the two targets can be determined to be in the same group, and the corresponding value in the adjacency matrix is equal to one. For instance, the adjacency matrix of group 1 in Figure 4 can be denoted by
Furthermore, the estimated group structure can be fed to the next step to update the state of members within the group.
4. Simulation Results
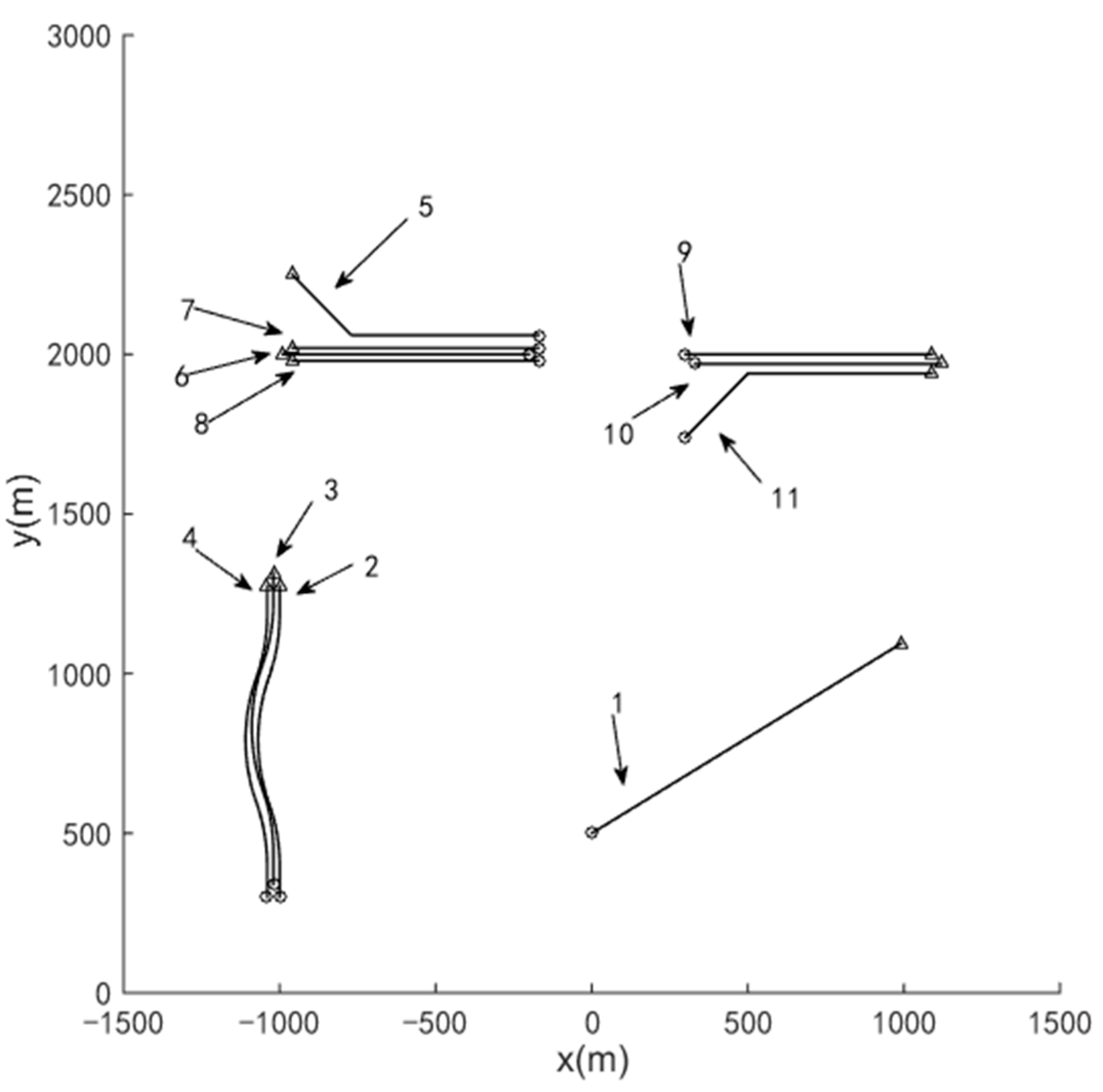
In this section, a two-dimensional area with size [−1500 m, 1500 m] × [0 m, 3000 m] is considered. Suppose that group targets that involve three subgroups moving in x-y plane. To verify the capability of the proposed method for tracking standard point targets, a single target in consistent velocity (CV) style is also considered. As shown in Figure 6, 11 moving targets are simulated. Among them, target 1 moves independently; target 2, target 3, and target 4 constitute group 1; target 5, target 6, target 7, and target 8 constitute group 2. Besides, target 5 separates from group 2 at about 65 s; target 9 and target 10 constitute group 3, and target 11 merges with this group at about 40 s. The kinematic parameters of targets are shown in Table 1.
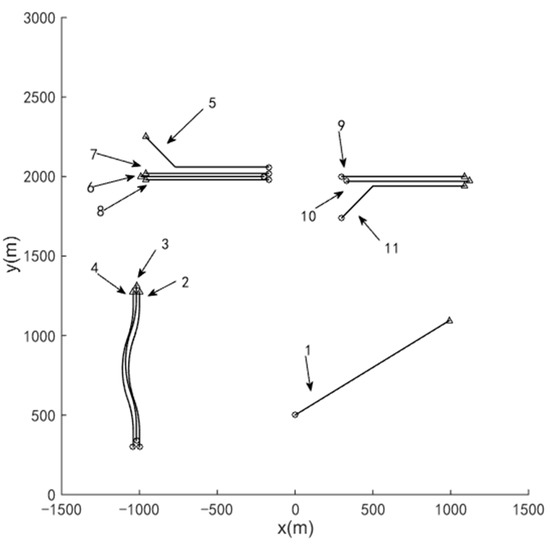
Figure 6.
True trajectories of targets. Born/Death positions for each target are marked with ○/△.

Table 1.
The true movement of targets.
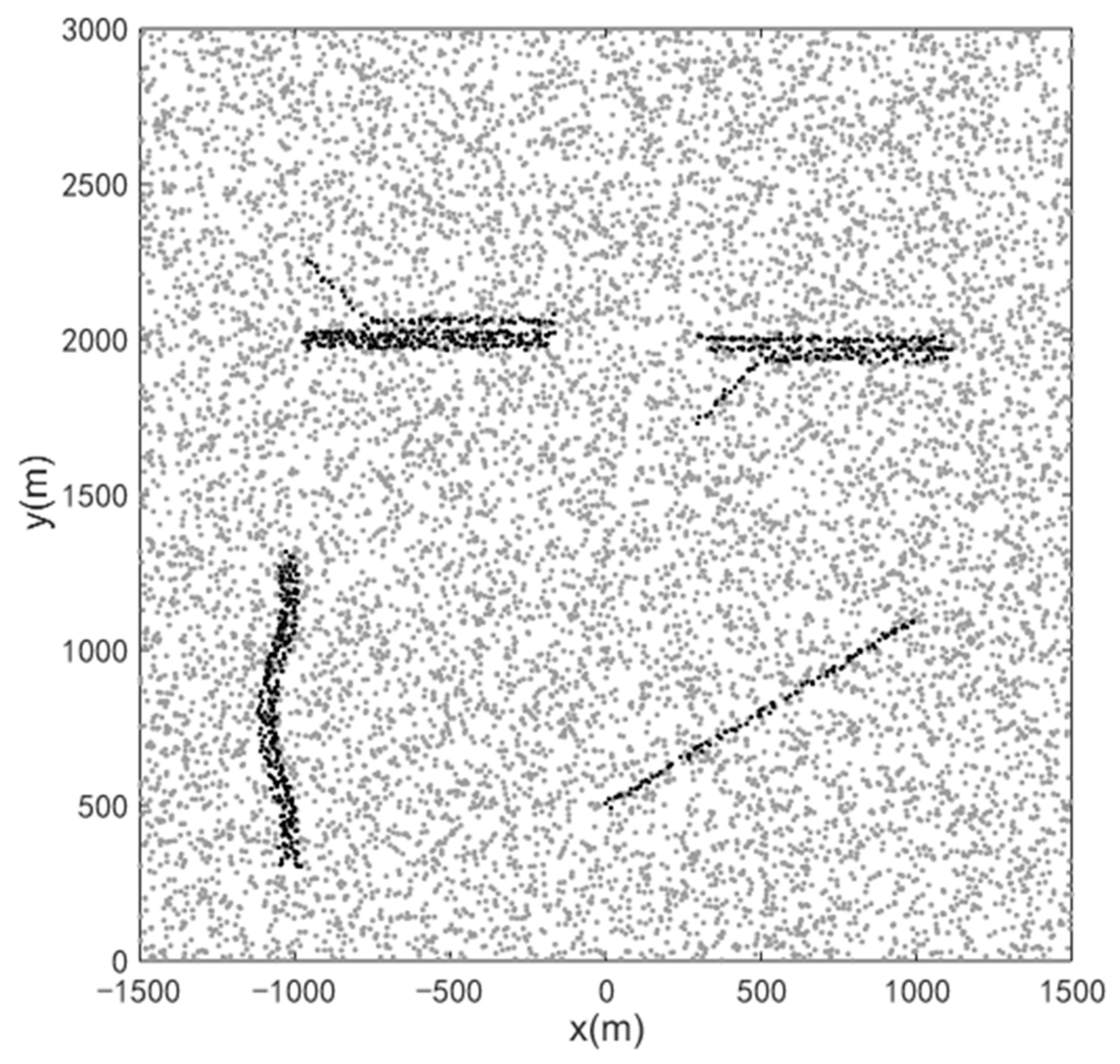
The duration time is 100 s, and the sampling period . There are three sensors in the observation area. Figure 7 shows the measurements collected from sensor 1. The detection probability of each sensor is , and the clutter intensity is . The birth model is set according to the initial state of the targets. The target survival probability is set as . The process noise covariance matrix , and the observation noise covariance matrix are respectively:
where and .
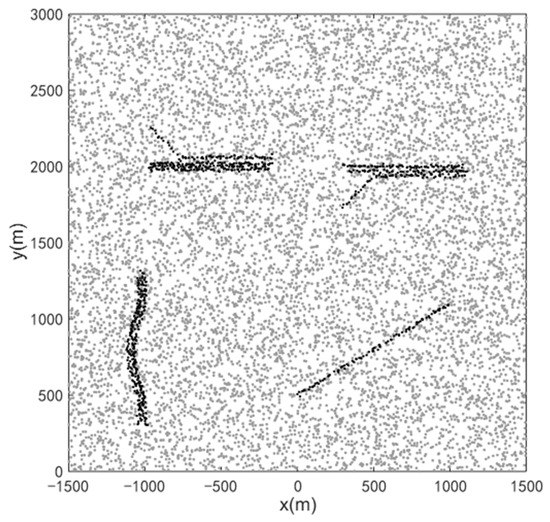
Figure 7.
The measurements of sensor 1. The black dot represents the target measurement, and the gray dot represents the clutter.
In the simulation, the number of the Bernoulli components is not more than , the number of the Gaussian components per target is not more than . The pruning threshold is set as . There are at most four measurement partitioning hypotheses in the set , and the number of the measurement subsets in each hypothesis is up to . In addition, the Mahalanobis distance threshold is . The simulation is performed using algorithms implemented in MATLAB on computers with one Intel Core i7-6700 CPU and 16 GB RAM. The average result is obtained through 50 Monte Carlo runs. The filtering performance is measured by the optimal sub-pattern assignment (OSPA) distance [34]. The OSPA distance accounts for both errors in estimation of target states and errors in estimation of target cardinality, where we set order and the penalty factor .
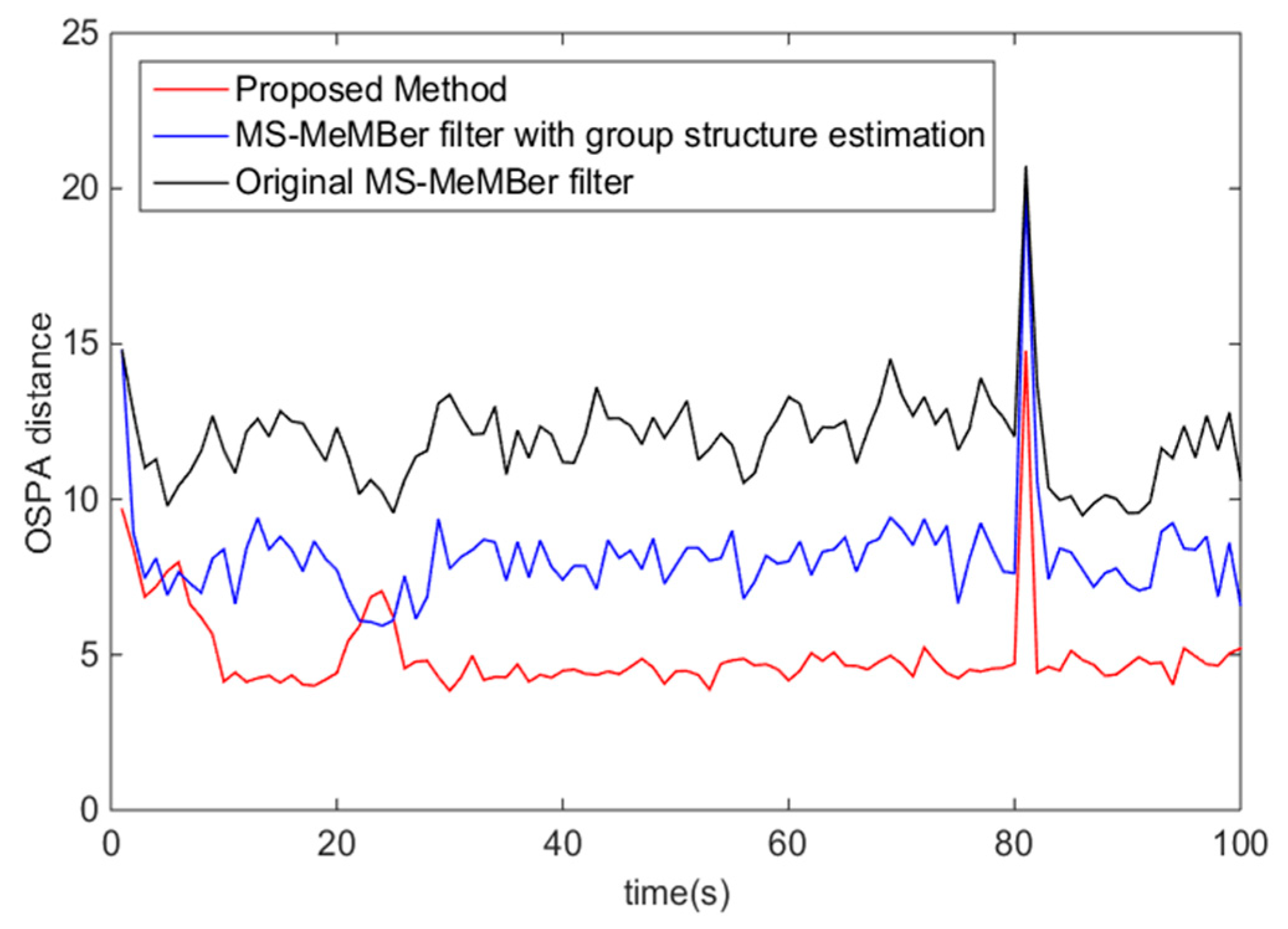
As can be seen from Figure 8, in the group target tracking scenario, the OPSA error of the MS-MeMBer filter with group structure estimation is significantly smaller than that of the original MS-MeMBer filter. This means that the filtering accuracy is improved by using the group structure. In addition, compared with the above two methods, the proposed method with both the MDA algorithm and group structure estimation has the optimal filtering performance. Note that there is a peak of the OSPA error at about 80 s. This is because the filters mentioned above react slower to the death of the members.
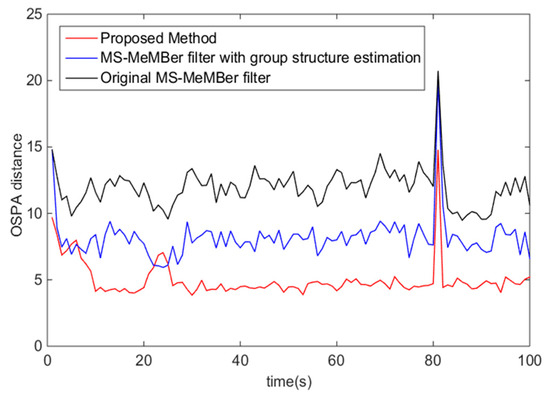
Figure 8.
The OSPA distance error for the original MS-MeMBer filter, the MS-MeMBer filter with group structure estimation, and the proposed method with sensors each having .
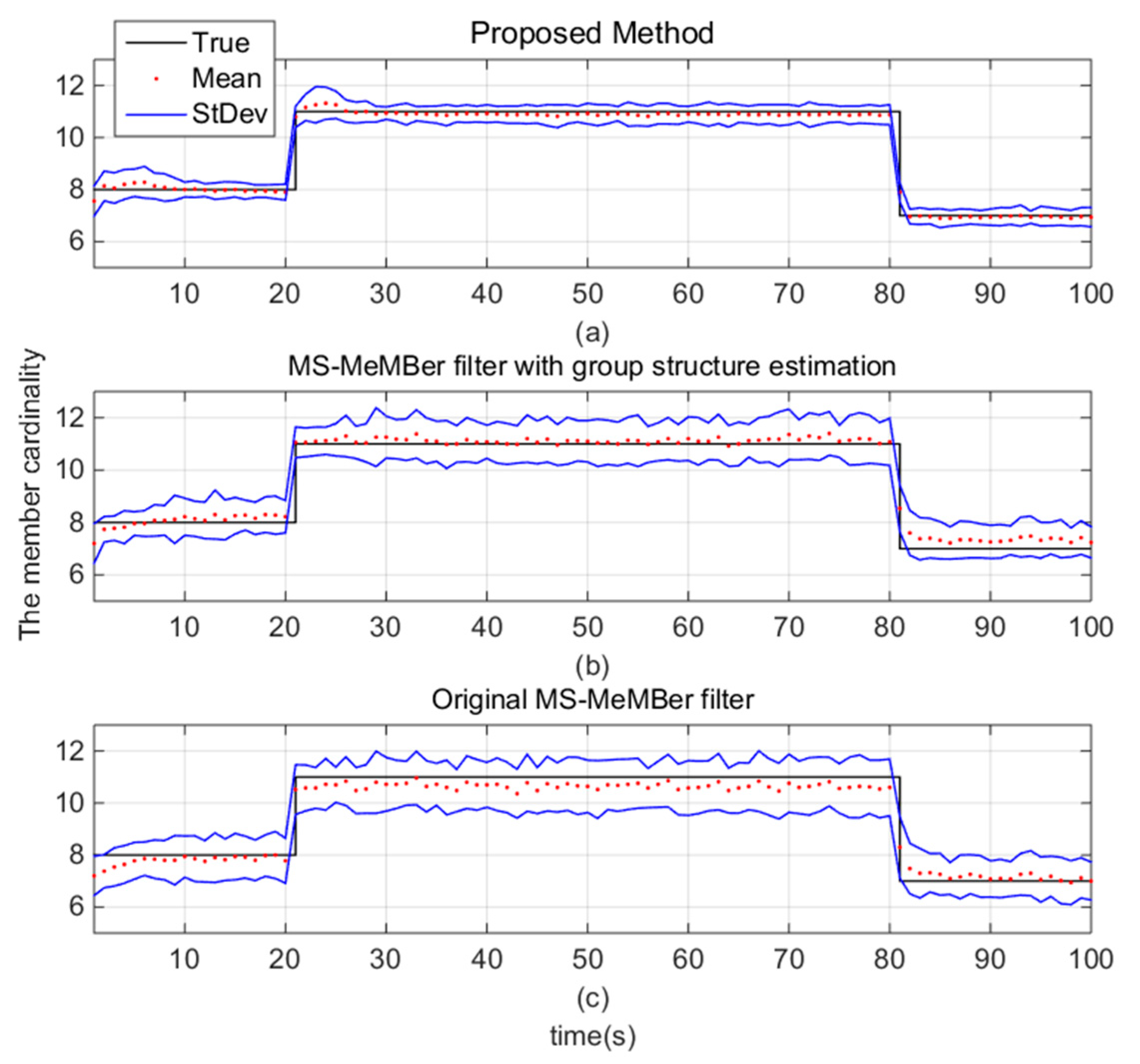
Figure 9 shows the members’ cardinality estimation of the above methods. The black line is the true cardinality of the members, the red dot is the estimated cardinality at the corresponding time, and the blue line represents the standard deviation of the estimated cardinality. We can see that for group target tracking, a cardinality estimation bias occurs in the original MS-MeMBer filter, which can be eliminated by using the group structure. Moreover, the standard deviation of cardinality estimation is further reduced by the MDA algorithm.
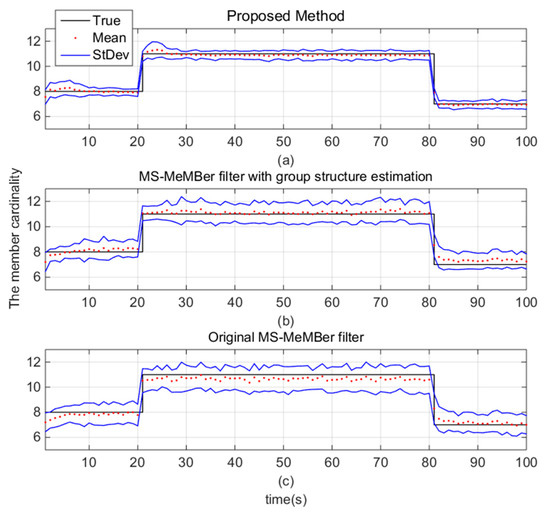
Figure 9.
The estimated cardinality of members for the (a) proposed method, (b) MS-MeMBer filter with group structure estimation, and (c) original MS-MeMBer filter.
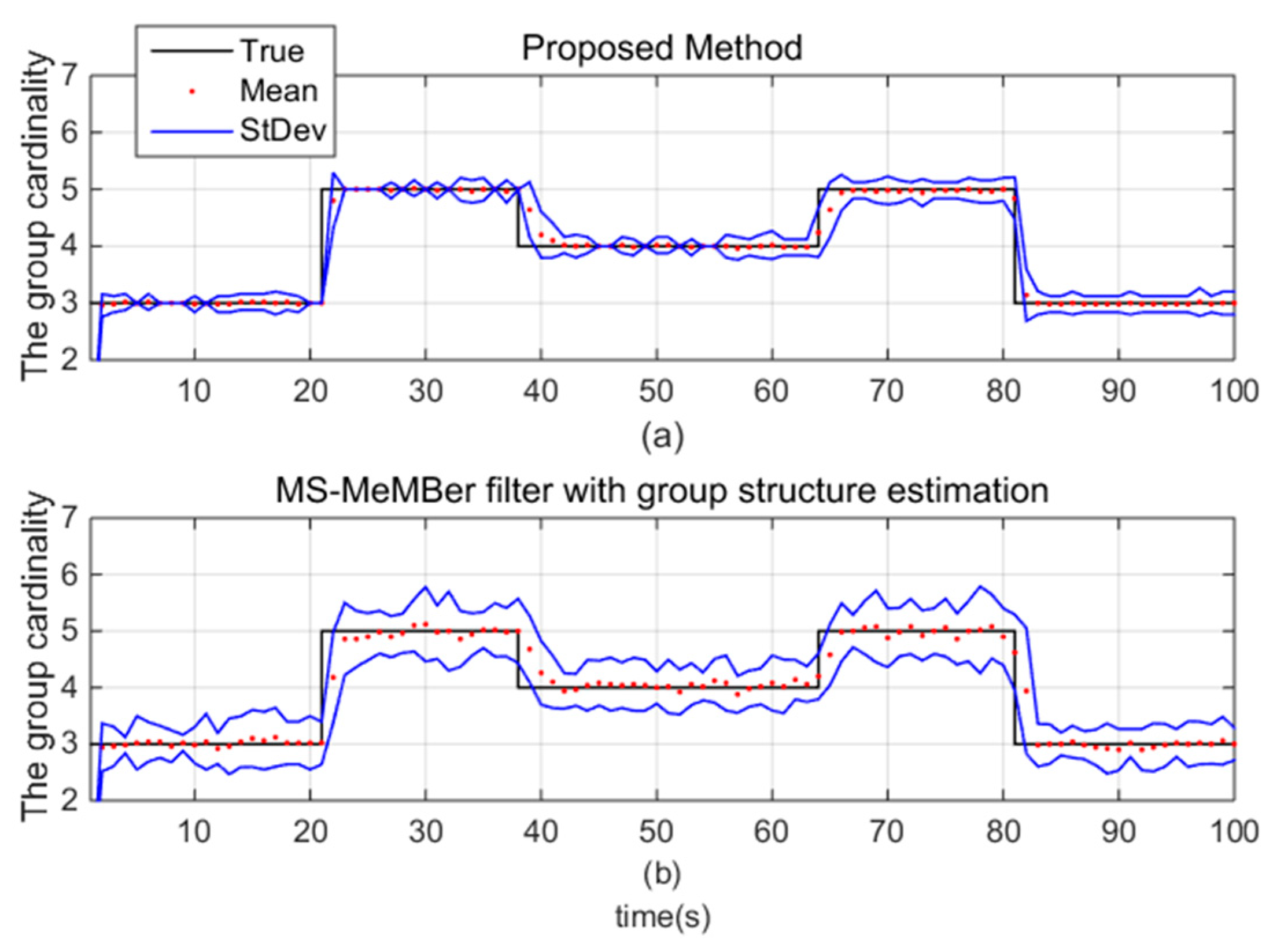
Figure 10 shows the estimated group cardinality of the proposed method. It can be seen that the proposed method obtains smaller standard deviations of the estimated group cardinality. We can conclude that compared with the MS-MeMBer filter, which only contains the group structure estimation, the proposed method with both group structure estimation and MDA algorithm obtains better estimation of the group cardinality.
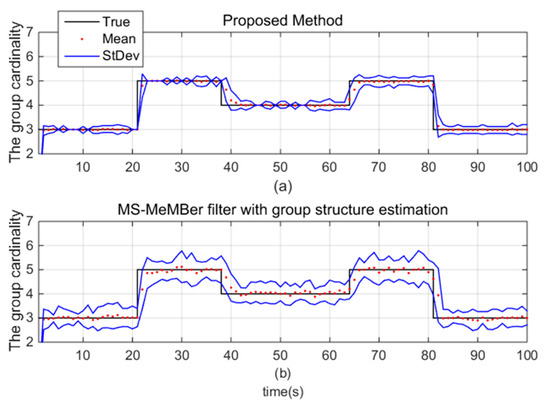
Figure 10.
The estimated group cardinality for (a) the proposed method and (b) the MS-MeMBer filter with group structure estimation.
Table 2 shows the average running time of the MS-MeMBer filter and the proposed method in scenarios with different number of sensors. The number of the sensors is varied in the range {3, 4, 5}. By comparison, they have similar time consumptions when the number of the sensors is small. However, the computational complexity of the MDA algorithm increases exponentially with the increasing number of the sensors, leading to a significant increase in the time consumption of the proposed method.

Table 2.
Average running time.
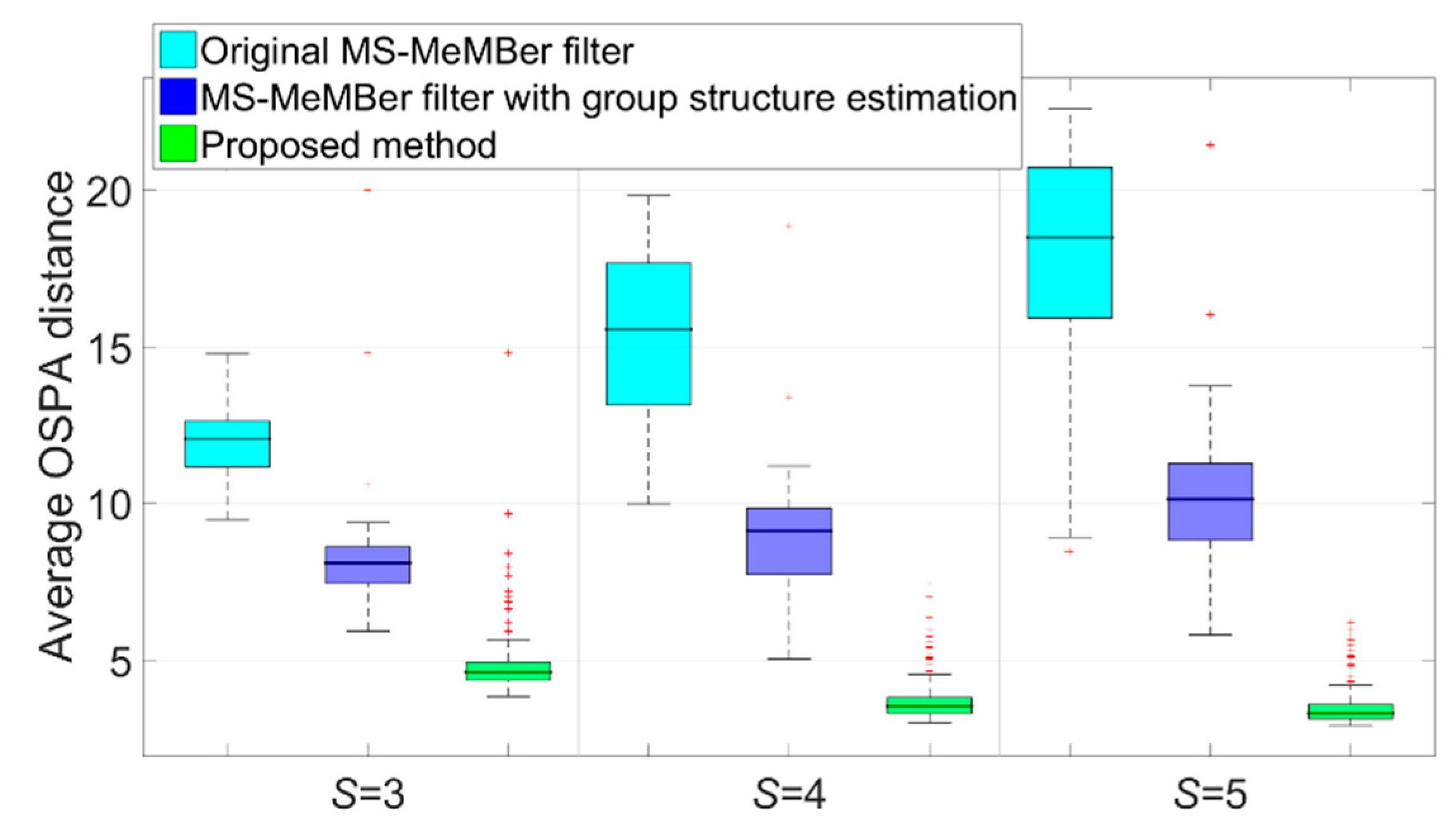
The time-averaged OSPA errors (via 50 MC runs) of the above methods in scenarios with different sensor numbers are displayed in Figure 11. It can be seen that as the number of the sensors increases, the time-average OSPA error of the two methods without MDA algorithm increases. The reason is that as S increases, the association between the measurements and Bernoulli components is more complicated because of the densely clustered members within the group. On the contrary, as the number of the sensors increases, the proposed method combined with the MDA algorithm and group structure estimation together can obtain better filtering results.
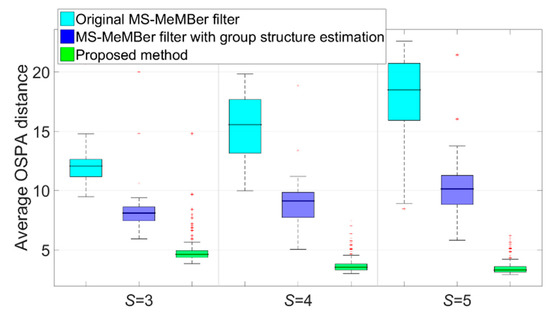
Figure 11.
Box plot of time-average OSPA distance errors with different sensor numbers (50 MC runs).
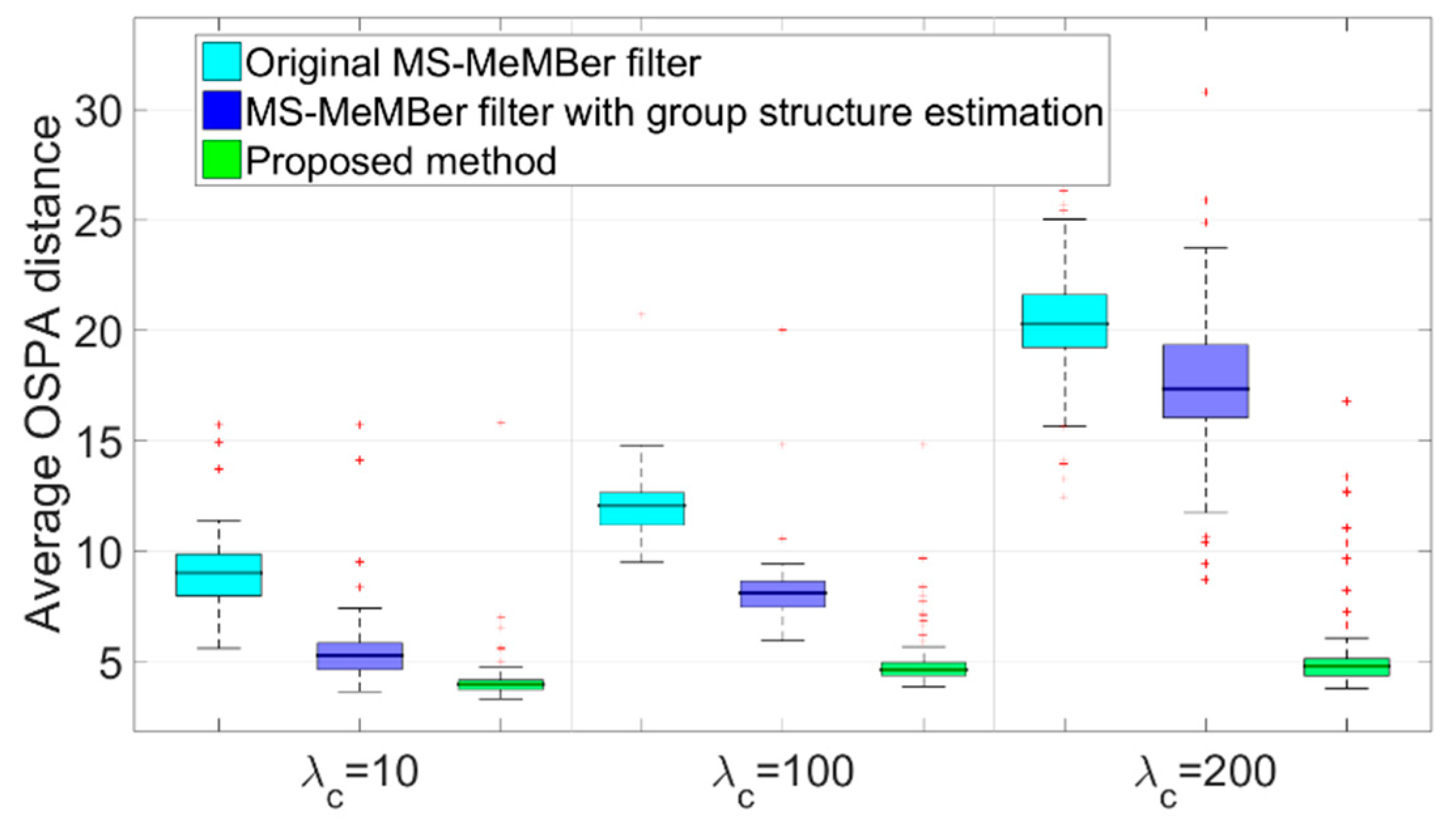
Figure 12 shows the performance of the original MS-MeMBer filter, the MS-MeMBer filter with group structure estimation, and the proposed method under different clutter intensities. The clutter intensity is varied in the range {10, 100, 200}. It can be concluded that the performance of the first two methods decreases significantly with the increase of clutter intensity. However, by using the MDA algorithm, the proposed method can still obtain better filtering results in clutter-intensive scenes.
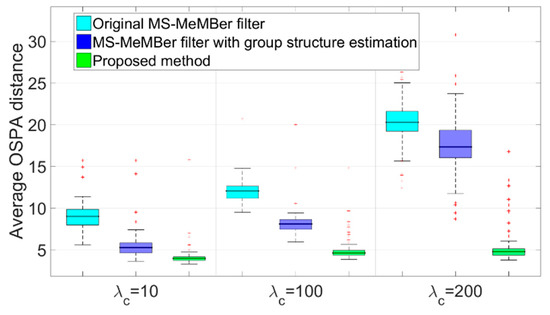
Figure 12.
Box plot of time-average OSPA distance errors with different clutter intensities (50 MC runs).
5. Discussion
In this paper, we proposed a group target tracking method based on the MS-MeMBer filter. We used the group structure to constrain the movement of members within the group. We also improved the multi-sensor measurement partition through the MDA algorithm. Finally, we established a simulation scenario with splitting and merging of groups. Simulation results showed that compared with the original MS-MeMBer filter, the proposed method has achieved better robustness and accuracy in group target tracking scenarios, at the cost of an acceptable increasing computational load.
However, the MS-MeMBer filter is not strictly a tracker, because it can only get the target state, not the target trajectory. To obtain multi-target trajectories, the filter based on the labeled RFS or additional track maintenance operation can be considered. Furthermore, the proposed method ignores the dynamic evolution of the group structure. Future work will explore the multi-sensor multi-target filter, which can accommodate the evolution of group structures and can estimate target trajectories.
Author Contributions
Conceptualization, Z.Z. and J.S.; methodology, Z.Z.; writing—original draft, Z.Z. and J.S.; writing—review and editing, J.S., H.Z., and C.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 62073334), and the Royal Society-Newton Advanced Fellowship (No. NA160342).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, X.; Song, L.; Zou, Z. Multiple group target tracking with evolving networks and labeled box particle PHD filter. In Proceedings of the Chinese Control and Decision Conference, Shenyang, China, 9–11 June 2018; pp. 4046–4051. [Google Scholar]
- Zhang, Y.; Zhang, J.; Wang, S.; Li, Z. Research on Target tracking Based on Improved KCF Algorithm. In Proceedings of the IEEE International Conference on Power Electronics, Computer Applications, Shenyang, China, 22–24 January 2021; pp. 507–512. [Google Scholar]
- Peng, C.; Ye, W. An Improved Adaptive ET-PHD Algorithm for Newborn Target Intensity. In Proceedings of the IEEE 3rd Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 12–14 October 2018; pp. 2137–2142. [Google Scholar]
- Daniyan, A.; Lambotharan, S.; Deligiannis, A.; Gong, Y.; Chen, W. Bayesian Multiple Extended Target Tracking Using Labeled Random Finite Sets and Splines. IEEE Trans. Signal Process. 2018, 66, 6076–6091. [Google Scholar] [CrossRef]
- Xia, Y.; Granström, K.; Svensson, L.; García-Fernández, A.F.; Williams, J.L. Extended target Poisson multi-Bernoulli mixture trackers based on sets of trajectories. In Proceedings of the 22th International Conference on Information Fusion, Ottawa, ON, Canada, 2–5 July 2019; pp. 1–8. [Google Scholar]
- Li, Y.; Xiao, H.; Hao, W.; Qiang, F. Labeled particle unresolved target PHD filter for multiple group target tracking. In Proceedings of the IET International Radar Conference, Hangzhou, China, 14–16 October 2015; pp. 1–5. [Google Scholar]
- Pang, S.; Li, J.; Godsill, S. Models and Algorithms for Detection and Tracking of Coordinated Groups. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 1–8 March 2008; pp. 1–17. [Google Scholar]
- Khan, Z.; Balch, T.; Dellaert, F. MCMC-based particle filtering for tracking a variable number of interacting targets. IEEE Trans. Pattern Anal. 2005, 27, 1805–1819. [Google Scholar] [CrossRef] [PubMed]
- Gning, A.; Mihaylova, L.; Maskell, S.; Pang, S.; Godsill, S. Group Object Structure and State Estimation With Evolving Networks and Monte Carlo Methods. IEEE Trans. Signal Process. 2011, 59, 1383–1396. [Google Scholar] [CrossRef]
- Zou, Z.B.; Song, L.P.; Cheng, X. Labeled box-particle CPHD filter for multiple extended targets tracking. Syst. Eng. Electron. 2019, 30, 57–67. [Google Scholar]
- Granstrom, K.; Fatemi, M.; Svensson, L. Poisson Multi-Bernoulli Mixture Conjugate Prior for Multiple Extended Target Filtering. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 208–225. [Google Scholar] [CrossRef]
- Tuncer, B.; Özkan, E. Random Matrix Based Extended Target Tracking with Orientation: A New Model and Inference. IEEE Trans. Signal Process. 2021, 69, 1910–1923. [Google Scholar] [CrossRef]
- Magnant, C.; Kemkemian, S.; Zimmer, L. Joint tracking and classification for extended targets in maritime surveillance. In Proceedings of the IEEE Radar Conference, Oklahoma City, OK, USA, 23–27 April 2018; pp. 1117–1122. [Google Scholar]
- Li, Q.; Song, L. Axisymmetric extended target tracking using Gaussian process. In Proceedings of the IEEE 3rd International Conference on Information Communication and Signal Processing, Shanghai, China, 12–15 September 2020; pp. 306–311. [Google Scholar]
- Alqaderi, H.; Govaers, F.; Schulz, R. Spacial Elliptical Model for Extended Target Tracking Using Laser Measurements. In Proceedings of the Sensor Data Fusion: Trends, Solutions, Bonn, Germany, 15–17 October 2019; pp. 1–6. [Google Scholar]
- Baum, M.; Hanebeck, U. Random Hypersurface Models for extended object tracking. In Proceedings of the IEEE International Symposium on Signal Processing and Information, Ajman, United Arab Emirates, 14–17 December 2009; pp. 178–183. [Google Scholar]
- Baum, M.; Hanebeck, U. Shape tracking of extended objects and group targets with star-convex RHMs. In Proceedings of the 14th International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 1–8. [Google Scholar]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House, Inc.: Norwood, MA, USA, 2007. [Google Scholar]
- Wang, Z.; Han, B. A Multi-Target Detection and Tracking Technology Based on Labeled PHD Filtering. In Proceedings of the IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference, Chongqing, China, 12–14 March 2021; pp. 766–775. [Google Scholar]
- Vo, B.T.; Vo, B.N.; Cantoni, A. On multi-Bernoulli approximations to the Bayes multi-target filter. In Proceedings of the IEEE International Symposium on Signal Processing and Information, Xi’an, China; 2007; pp. 1–8. [Google Scholar]
- Vo, B.N.; Vo, B.T.; Hoang, H. An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 1975–1987. [Google Scholar] [CrossRef]
- Clark, D.; Simon, G. Group Target Tracking with the Gaussian Mixture Probability Hypothesis Density Filter. In Proceedings of the 3rd International Conference on Intelligent Sensors, Sensor Networks and Information, Melbourne, VIC, Australia, 3–6 December 2007; pp. 149–154. [Google Scholar]
- Liu, W.; Zhu, S.; Wen, C. Structure modeling and estimation of multiple resolvable group targets via graph theory and multi-Bernoulli filter. Automatica 2018, 89, 274–289. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, W.; Weng, C.; Cui, H. Multiple group targets tracking using the Generalized Labeled Multi-Bernoulli Filter. In Proceedings of the 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 4871–4876. [Google Scholar]
- Nannuru, S.; Blouin, S.; Coates, M.; Rabbat, M. Multisensor CPHD filter. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1834–1854. [Google Scholar] [CrossRef]
- Saucan, A.; Coates, M.; Rabbat, M. Multisensor Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 5495–5509. [Google Scholar] [CrossRef]
- Vo, B.N.; Vo, B.T.; Beard, M. Multi-Sensor Multi-Object Tracking with the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2019, 67, 5952–5967. [Google Scholar] [CrossRef]
- Martino, L.; Read, J.; Elvira, V.; Louzada, F. Cooperative Parallel Particle Filters for on-Line Model Selection and Applications to Urban Mobility. Digit. Signal Process. 2017, 60, 172–185. [Google Scholar] [CrossRef]
- Dan, C.; Miguez, J. Nested particle filters for online parameter estimation in discrete-time state-space Markov models. Bernoulli 2013, 24, 1–35. [Google Scholar]
- Carvalho, C.M.; Johannes, M.S.; Lopes, H.F.; Hedibert, F.; Polson, N. Particle Learning and Smoothing. Soc. Sci. Electron. 2010, 25, 88–106. [Google Scholar] [CrossRef]
- Deb, S.; Yeddanapudi, M.; Pattipati, K. A generalized S-D assignment algorithm for multisensor-multitarget state estimation. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 523–538. [Google Scholar]
- Dehghannasiri, R.; Esfahani, M.S.; Qian, X.; Dougherty, E.R. Optimal Bayesian Kalman Filtering with Prior Update. IEEE Trans. Signal Process. 2018, 66, 1982–1996. [Google Scholar] [CrossRef]
- García-Fernández, A.F.; Xia, Y.; Granström, K.; Svensson, L.; Williams, J.L. Gaussian implementation of the multi-Bernoulli mixture filter. In Proceedings of the 22th International Conference on Information Fusion, Ottawa, ON, Canada, 2–5 July 2019; pp. 1–8. [Google Scholar]
- Schuhmacher, D.; Vo, B.T.; Vo, B.N. A consistent metric for performance evaluation of multi-object filters. IEEE Trans. Signal Process. 2008, 56, 3447–3457. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).