Abstract
Phytoplankton plays a key role in the carbon cycle and supports the oceanic food web. While its seasonal and interannual cycles are rather well characterized owing to the modern satellite ocean color era, its longer time variability remains largely unknown due to the short time-period covered by observations on a global scale. With the aim of reconstructing this longer-term phytoplankton variability, a support vector regression (SVR) approach was recently considered to derive surface Chlorophyll-a concentration (Chl, a proxy of phytoplankton biomass) from physical oceanic model outputs and atmospheric reanalysis. However, those early efforts relied on one particular algorithm, putting aside the question of whether different algorithms may have specific behaviors. Here, we show that this approach can also be applied on satellite observations and can even be further improved by testing performances of different machine learning algorithms, the SVR and a neural network with dense layers (a multi-layer perceptron, MLP). The MLP, thanks to its ability to capture complex non-linear relationships, outperforms the SVR to capture satellite Chl spatial patterns (correlation of 0.75 vs. 0.65 on a global scale, respectively) along with its interannual variability and trend, despite an underestimated amplitude. Among deep learning algorithms, neural network such as MLP models appear to be promising tools to investigate phytoplankton long-term time-series.
1. Introduction
Phytoplankton—the microalgae that populates the upper sunlit layers of the ocean—fuels the oceanic food web and regulates oceanic and atmospheric carbon dioxide levels through photosynthetic carbon fixation ([,]). Seasonal and inter-annual cycles of phytoplankton biomass are now relatively well characterized, thanks to the large amount of studies based on radiometric satellite observations (e.g., [,]). Since the launch of the Sea-viewing Wide Field-of-View Sensor (SeaWiFS) in late 1997, satellite radiometric observations are continuous. However, 20 years of observations is still too short to thoroughly investigate decadal Chlorophyll-a concentration (Chl, a proxy of phytoplankton biomass) variations. The unavailability of global scale observations over a continuous time-series longer than two decades led the scientific community to rely on coupled physical–biogeochemical ocean modeling to investigate phytoplankton biomass decadal variability. While models are able to resolve seasonal to interannual biogeochemical variability to an ever-improving degree (e.g., [,]), they diverge in reproducing decadal observations, in particular phytoplankton regime shifts [,,]. Consequently, it is still not possible on a global scale to clearly separate the phytoplankton long-term response to climate change from natural variability.
However, well-characterized decadal cycles of phytoplankton (in terms of biomass, community composition, and carbon fluxes) are crucial as (1) They can accentuate, weaken, or even mask the climate-related trends (the recent debate about the observed North Atlantic regional cooling in the context of climate change illustrates the crucial need for better understanding decadal variability []; (2) The observed changes in phytoplankton during decadal cycle warm phases may provide insights into how future climate warming-induced changes will alter carbon cycle and the marine food web.
The distribution of phytoplankton is strongly controlled by physical processes over a large part of the global ocean (e.g., [,,,]). Consequently, past Chl variations may be reconstructed from past physical environmental factors. To our knowledge only two studies have been performed to reconstruct surface Chl in order to investigate its decadal variability. The first one allowed the derivation of spatio-temporal surface Chl variations over the 1958–2008 period in the tropical Pacific []. This reconstruction used a linear canonical correlation analysis on sea surface temperature (SST) and sea surface height to improve the description of the Chl response to the diversity of observed El Niño events and decadal climate variations in the tropical Pacific. The second one investigated the ability of a non-linear statistical approach based on support vector regression (SVR) to reconstruct historical Chl variations on a global scale using selected surface oceanic and atmospheric physical variables from a numerical model as predictors []. The SVR method was able to reproduce trends as well as the main modes of the interannual Chl variability depicted by satellite observations in most regions. Changes observed by satellite Chl between the 1980s and 2000s were also qualitatively captured by the SVR. The main bias of this approach was to underestimate the amplitude of the Chl variations by a factor of two.
Here, we investigate how a multi-layer perceptron (MLP) may be more skillful than this SVR approach to reconstruct satellite Chl on a global scale. While, in [], we used physical outputs from an ocean forced model to train the SVR and reconstruct surface Chl, here we choose to only use physical predictors from satellite observations and numerical atmospheric reanalysis. This choice is motivated by (i) our ultimate objective, which is to reconstruct Chl from physical observations (i.e., not relying on biogeochemical numerical models); and (ii) the use of the most realistic environmental conditions that those observations allow. However, those observations are mainly available through remotely sensed surface data (oceanic observations below the surface are indeed usually not accessible at large spatial-scales or interannual time-scales) and predictors are then limited to surface variables. With such limited 2D sampling, we are aiming at building a statistical model that may challenge more complex numerical models which simulate complex three-dimensional processes. Indeed, such models may not only strongly diverge in capturing Chl variations at a timescale of a decade but they are also not straightforward to run and require large computing resources.
2. Materials and Methods
2.1. Oceanic and Atmospheric Datasets
Phytoplankton needs light and nutrients to grow. Physical processes strongly control spatial distribution and time-variability of nutrient inputs in the upper-sunlit layer, and thus of phytoplankton over a large part of the global ocean. Thus, we make use of this physical (bottom-up) control to derive statistical models that relate several physical variables (predictors) to satellite Chl (output) as detailed in Table 1.

Table 1.
Physical predictors, their relevance to Chl variability, the products used, and their resolution.
Chl was retrieved from the Ocean Colour–Climate Change Initiative (OC-CCI) from the European Space Agency (ESA, []). This product has generated global, ocean-colour products for climate research by merging observations from different sensors while attempting to reduce inter-sensor biases []. The V4.2 product was extracted on a 1° grid and with a monthly temporal resolution over 1998–2015. It is referred hereafter to as ChlOC-CCI.
Predictors have been extracted over the same time period than ChlOC-CCI. Those with a higher resolution than 1° and a month have been averaged to match the Chl grid. The 2° × 2° bins of the short-wave radiation product have been divided to match the Chl grid.
The Multivariate El Niño Southern Oscillation Index (MEI) has been provided by the National Oceanic and Atmospheric Administration (NOAA) website [].
2.2. Machine Learning Models
2.2.1. Support Vector Regression (SVR)
Support vector machine is a kernel-based supervised learning method [] developed for classification purposes in the early 1990s and then extended for regression by []. The basic idea behind SVR is to map the variables into a new space, possibly in a non-linear way using the so-called kernel function, so that the regression task hopefully becomes linear in this space. Because SVR can efficiently capture complex non-linear relationships, it has been used in a variety of fields, and more specifically for oceanographic, meteorological and climate impact studies [,,], as well as in marine bio-optics [,,]. Considering a Gaussian kernel, SVR only involves the selection of two hyperparameters: the penalty parameter C of the error term and the kernel band with gamma. Following [], (i) these two parameters have been set to 2 and 0.3, respectively; and (ii) the SVR was trained on only 9% of the database (randomly selected) due to computational limitations. The SVR is set up with python and the Scikit-learn library. Reconstructed Chl is hereafter referred to as ChlSVR.
2.2.2. Neural Networks
Deep learning models and neural networks (NNs) are at the core of the state-of-the-art in machine learning and artificial intelligence for a large range of applications []. NNs are particularly appealing due to their capacity to learn complex relationships from raw data better than other models, when data are abundant. Though the concept of NNs has been around for a long time, these state-of-the-art approaches recently obtained impressive results for many supervised or unsupervised learning problems thanks to the availability of very large datasets, and the increase in computational power in the last few decades []. NNs learn complex patterns through the composition of simple elementary operations forming a global highly-nonlinear input/output relationships, whose parameters can be efficiently trained using the back-propagation algorithm. These recent advances motivate an increasing number of applications in spatial oceanography, (e.g., [,]). In this context, physics-informed and theory-guided NNs [] are of key interest as new means to exploit the computational and learning efficiency of NNs, while exploiting prior knowledge and making easier model interpretation. Here, we follow such an approach with a MLP architecture, which uses the same physical features and geospatial information as inputs as the SVR.
NN frameworks exploit mini-batch gradient descent schemes during the training phase. This can allow us to exploit the entire dataset contrary to the SVR model. Indeed, SVR is known not to scale up well with large training datasets. The considered MLP architecture exploits LeakyReLU activation functions after each dense layer (Figure S1). Dropout layers [] are added to the last 3 layers to reduce overfitting. Since we are dealing with a regression task, the last layer is linear. Thanks to its benefit of penalizing large errors, MSE is used as the loss function for the MLP. The MLP is set up with python and the Keras library. Configurations details are provided in Table S1.
As for the SVR, we first train a MLP on 9% of the training dataset, randomly selected. The reconstructed Chl is hereafter referred to as ChlMLP-9%. The aim is to provide a first consistent comparison with ChlSVR using the same training setting. Then, we take advantage of the MLP ability to be trained on larger database and a second MLP is trained on 80% of the dataset. Reconstructed Chl is referred to as ChlMLP. The two learning curves are provided in Figure S2.
2.2.3. Data Preprocessing and Procedure
Predictors and log(Chl) are normalized by removing their respective average and dividing them by their standard deviations. The SVR and the two MLP are trained from 1998 (the first complete year of the satellite ChlOC-CCI time-series) to 2015 between 50° S and 50° N (Step 1 in Figure 1). Thus, the resulting SVR and NN schemes are applied on the physical predictors over 1998–2015, and the annual means and standard deviations initially removed are applied to perform the back transformation and reconstruct Chl values, namely either ChlSVR, ChlMLP-9% and ChlMLP outputs (Step 2 in Figure 1). These three Chl reconstructed whole datasets are then compared to ChlOC-CCI to evaluate their skills in reconstructing satellite observations (Step 3 in Figure 1).
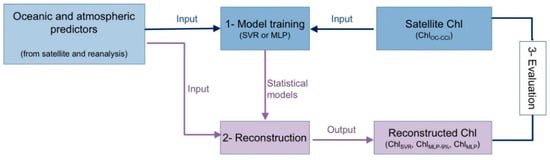
Figure 1.
Three-step procedure to train the machine learning models, reconstruct surface Chlorophyll-a concentration (Chl) and evaluate the statistical model skills over 1998–2015.
2.3. Statistical Diagnostics and Empirical Orthogonal Functions
First, scatter plots are performed to compare satellite vs. reconstructed Chl for the Atlantic, Pacific and Indian Oceans between 50° S and 50° N. Root mean square error (RMSE) is derived at basin-scale as , with N the sample number. Pearson correlation and normalized RMSE (NRMSE) are also derived, with NRMSE = and the mean ChlOC-CCI value.
Empirical orthogonal function (EOF) analysis is performed to investigate the model’s ability to reconstruct Chl seasonal and interannual variability. First, centered seasonal and interannual ChlOC-CCI are obtained by removing their annual and monthly means over 1998–2015, respectively, and by dividing them by their standard deviations. Then, the so-called reference EOF analysis is performed on these centered seasonal and interannual ChlOC-CCI anomalies to avoid an overly dominant contribution of high values on the analysis []. Thus, ChlSVR and ChlMLP outputs are projected onto the seasonal and interannual ChlOC-CCI spatial patterns to obtain their associated time components (i.e., principal component-PC). Seasonal and interannual PCs for each dataset are then compared.
3. Results
3.1. Statistical Performances
A first evaluation of the ChlSVR vs. ChlOC-CCI is provided during 1998–2015 at basin scales and for the whole dataset (Figure 2, upper row). Determination coefficients between both datasets are below 0.88, while RMSE is above 0.25 in the three basins. The MLP trained on the same amount of data than the SVR is more skillful than the SVR at reconstructing ChlOC-CCI (Figure 2, middle row). Determination coefficients between the log of ChlMLP-9% vs. ChlOC-CCI increase higher than 0.9 in the Atlantic and Pacific oceans, and RMSE are slightly improved. Increasing from 9% to the usual 80%, the MLP training dataset further increases the skills of the NN approach to reconstruct ChlOC-CCI with a relative gain of 9% to 16% in RMSE and regression lines between the log of ChlMLP vs. ChlOC-CCI closer to the 1:1 line for each oceanic basin (Figure 2, lower row). Nevertheless, ChlMLP still underestimates ChlOC-CCI, more specifically in the Pacific. Some of these differences may be related to changes in Chl, which may due for instance to photo acclimation (e.g., [,]) or by other components that are not Chl such as suspended particulate matter (SPM) or colored dissolved organic matter (CDOM; []). Interestingly, the use of a MLP not only removes computational restrictions imposed by the SVR (i.e., size of the training samples), but it also appears to be more efficient in reconstructing surface Chl from oceanic and atmospheric variables. Thereafter, ChlOC-CCI and ChlSVR are compared to the best NN product, ChlMLP (i.e., trained on 80% of the dataset).
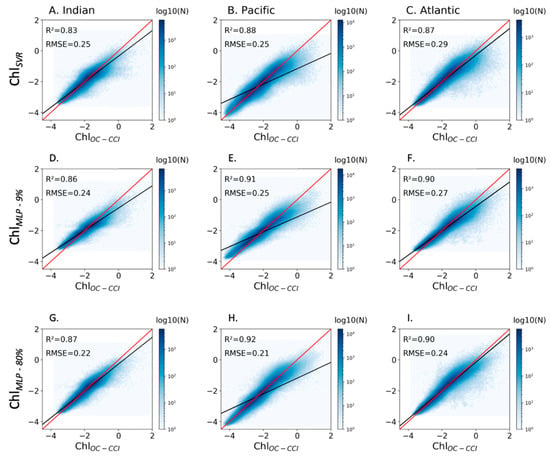
Figure 2.
Scatter plots of log of ChlOC-CCI vs. (A–C) ChlSVR, (D–F) ChlMLP-9% and (G–I) ChlMLP trained on 80% of the dataset, for each oceanic basin between 50° S and 50° N and over 1998–2015. The ChlOC-CCI vs. reconstructed Chl regression lines are plotted in black and the 1:1 regression lines are plotted in red. The figure is color-coded according to the density of observations.
Consistent with the scatterplots, ChlOC-CCI temporal correlations with ChlSVR are significantly lower than with ChlMLP (Figure 3A,C; r = 0.65 vs. 0.75 and NRMSE = 0.31 vs. 0.26 on a global scale, respectively). ChlOC-CCI-ChlSVR correlations are higher than 0.8 (p < 0.001) over limited regions such as the Atlantic, Indian, and Pacific subtropical areas (Figure 3A). The MLP allows for a significant improvement in the correlation with ChlOC-CCI with values higher than 0.75 over most of the global ocean (Figure 3C). Areas of high and low NRMSE are similarly distributed for ChlSVR and ChlMLP (Figure 3B,D). For instance, in both cases, NRMSE is higher at the highest latitudes and along the Amazon plume in the Atlantic Ocean. Although the MLP slightly reduces NRMSE compared to the SVR, biases in reference to ChlOC-CCI still remain in these regions. High NRMSE can reflect the influence of other components than phytoplankton biomass on the Chl signal as mentioned above, or/and the impact of other predictors not considered to train the neural network models. This is, for instance, suggested from the Amazon plume where the Chl signal is known to be influenced by river flow and may thus rather be associated with CDOM or SPM than phytoplankton biomass [].
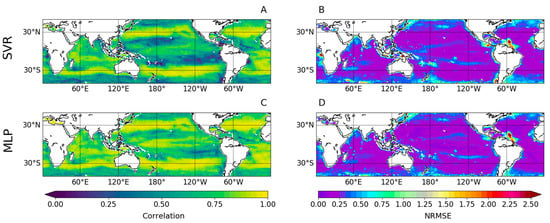
Figure 3.
(A,C) Correlation and (B,D) NRMSE of ChlOC-CCI vs. (up) ChlSVR and (bottom) ChlMLP over 1998–2015.
3.2. Seasonal to Interannual Variability and Trends
EOF analysis provides complementary insights into the MLP and SVR ability in reconstructing Chl spatio-temporal variability. Seasonal and interannual ChlOC-CCI spatial variability are illustrated through their respective EOF first modes with a total variance of 27.6% and 12.6%, respectively (Figure 4A,C). The well-known Chl seasonal patterns are highlighted with a variability out of phase between the northern vs. southern hemisphere due to the reversal of the season order (Figure 4A,B). It is also out of phase between high latitudes (light limited) vs. low and mid-latitudes (rather nutrient limited). ChlMLP and ChlSVR are then projected on this reference ChlOC-CCI spatial seasonal pattern. The seasonal variability of ChlOC-CCI is well reproduced by both the SVR and MLP (correlations between ChlOC-CCI and ChlSVR or ChlMLP PCs are both of 0.99; Figure 4B).
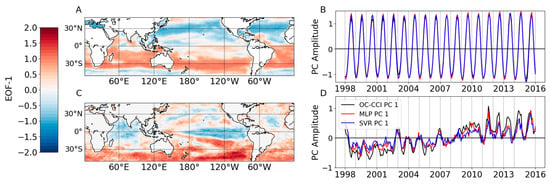
Figure 4.
First mode of the ChlOC-CCI (A) seasonal and (C) interannual EOFs over 1998–2015, and their associated principal components (B,D), respectively. ChlMLP and ChlSVR PCs obtained from the ChlOC-CCI EOF projections are reported in (B,D).
The first EOF mode performed on interannual ChlOC-CCI illustrates the largely reported impact of El Nino Southern Oscillation (ENSO) [,,,,] (Figure 4C).
Here, the MLP results in an improvement compared with the SVR to reconstruct ChlOC-CCI inter annual variability, with its first PC correlation with ChlOC-CCI of 0.95 vs. 0.91 for ChlSVR and amplitude closer to ChlOC-CCI (Figure 4D).
Over the last 18 years, observed ChlOC-CCI trends have increased over most of the global ocean (Figure 5A). Regionally, some decreases are observed such as in the Indian Ocean, the equatorial Pacific and the Atlantic and Pacific oligotrophic subtropical gyres. While most of these trends are captured by ChlSVR, inverse trends occur in the South Indian and Atlantic Oceans (Figure 5B). In addition, the trend estimation for ChlSVR reveals an unrealistic high-frequency pattern, which may relate to the support of the Gaussian kernels implemented by the SVR model. On its side, ChlMLP better reproduces ChlOC-CCI trends in terms of spatial distribution, although their amplitude remain underestimated, especially in the Indian Ocean (Figure 5C).
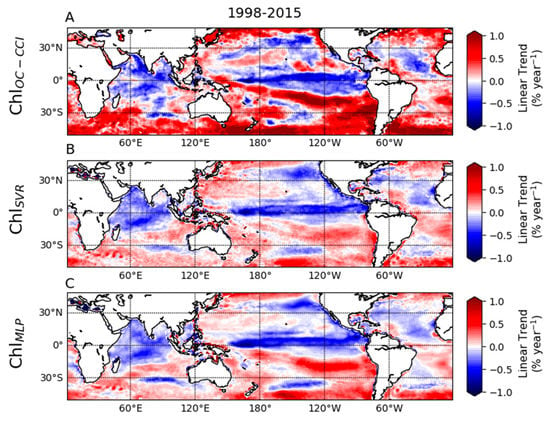
Figure 5.
Linear log of (Chl) trend (in % year−1) calculated over 1998–2015 from the monthly (A) ChlOC-CCI, (B) ChlSVR, (C) ChlMLP.
A similar conclusion can be done when considering Chl trends in oligotrophic gyres (with surface Chl < 0.07 mg.m−3 as in []) over the last 15 years. Such trends can be weak and not sufficiently well resolved by the MLP (nor the SVR) in terms of sign or amplitude (Figure 6). While it is crucial to improve the reconstruction of the signal amplitude on a global scale, it is particularly appealing in those oceanic deserts which would tend to expand in the context of climate warming and increasing stratification [,,]. As expected, the spread of these oligotrophic areas is different here from ChlOC-CCI than those observed by [] based on a single-sensor Chl product over 1998–2006 []. Thus, training deep learning schemes on Chl products from both single and multi-sensors could provide a more synoptic view on the impact and interpretation of reconstructed Chl long time-series.
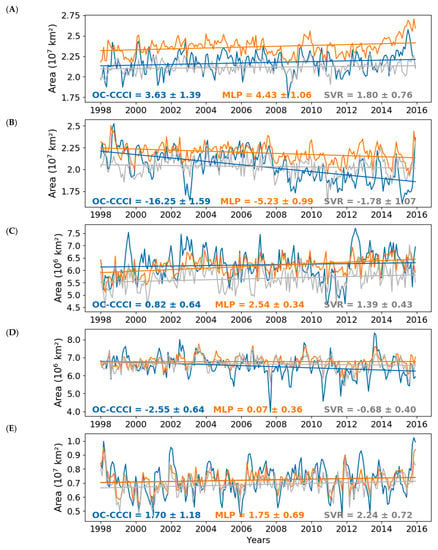
Figure 6.
Time series of the monthly mean area (km2) with surface Chl less than or equal to 0.07 mg.m−3 between 5° and 45° N/° S latitude with the seasonal cycle removed in the (A) North Pacific, (B) South Pacific, (C) North Atlantic, (D) South Atlantic and (E) Indian Oceans. ChlOC-CCI is in blue, ChlSVR in grey and ChlMLP in orange. Straight lines are the linear trends calculated as in Figure 5. The average trends and standard deviation are also indicated.
Finally, a first attempt to investigate predictors’ relative importance is performed with the MLP approach and a perturbation-based method []. Besides latitudes, and as expected, the SST and short-wave radiations are the two most important physical predictors (Table 2). Interestingly, among the physical predictors, the surface wind components seem slightly more important than the sea level anomaly, while this is a common variable used to infer regression between Chl and ocean dynamics []. Indeed, redundant indirect information about the ocean circulation can be derived from those predictors, with potentially more information “embedded” within the wind stress that may also be linked to a meaningful parameter for phytoplankton growth: the mixed layer depth. Spatial coordinates, and more specifically the latitude, remain important for the reconstructions, although part of this information is embedded in the spatial patterns of the physical predictors. Indeed, removing spatial information from the MLP training still allows us to reconstruct realistic Chl, unlike the SVR, which produces unrealistic concentrations, suggesting that the MLP can extract geospatially dependent features from other predictors than the coordinates themselves. The impact of the different predictors on Chl reconstruction according to the oceanic regions and/or the climate cycles should, therefore, be specifically considered and investigated in a dedicated study, once a deep learning scheme will have been considered as sufficiently satisfying.

Table 2.
Multi-layer perceptron (MLP) predictor’s relative importance.
4. Discussion
To our knowledge, the only study that has been performed to reconstruct satellite surface Chl on a global scale used a SVR approach []. In this former study, we also used ChlOC-CCI and the same physical predictors than in the present study, but the predictors were originating from a numerical model (vs. satellite observations and numerical atmospheric reanalysis here). The SVR accurately reproduced most aspects of the satellite Chl variability (although underestimated by half) and spatial patterns. Here, we show that the SVR, trained on satellite data and atmospheric reanalysis, also encounters difficulties to well reproduce the Chl signal. The MLP demonstrates the ability of deep learning schemes to reproduce satellite Chl with better skill than the SVR, not only to capture the general spatial patterns of Chl but also their interannual signal and trends. Neither the training of the MLP nor that of the SVR involve time information through the training loss which only involves a grid point-wise reconstruction error criterion. Thus, our results support the greater ability of the MLP to generalize time patterns than the SVR and the relevance of neural network approaches compared with kernel methods.
However, further efforts still remain to alleviate the issue of Chl underestimation. One plausible hypothesis would be that complementary predictors may provide additional insights to this issue. For instance, precipitation is among a key driver of coastal run-off and river discharge could be considered. Thus, applying similar learning-based schemes to CDOM and SPM, especially jointly to Chl, would be note-worthy. Such combined approaches could help improving both reconstruction and interpretation of Chl in regions where satellite Chl products from case 1 waters may reflect changes from other components than phytoplankton biomass. Particulate backscattering (as a proxy of the Particulate Organic Carbon) retrieved from satellite also deserves to be considered in addition to Chl in the training/reconstruction process. Indeed, it would allow us to investigate the extent to which the Chl variability reflects changes in phytoplankton biomass vs. cellular changes in response to light [,,], which is of particular importance in oligotrophic gyres.
If, in this study, we demonstrate the better potential of NNs to accurately represent Chl spatial distribution as well as the interannual and trend signals, compared to the SVR, so far, only an MLP was used. MLP is known to not explicitly consider the spatial and temporal correlations in the dataset. Specific architectures to handle spatially or temporally structured data, i.e., convolutional neural networks and recurrent neural networks (such as long short-term memory networks), are currently under investigation and are expected to further improve the Chl reconstruction performance, in particular for the Chl amplitude. Interestingly, such NN architectures would provide additional insights on the physical variables of interest through sensitivity tests, which could drive the reconstruction of Chl beyond the set of predictors considered in this study. Recent advances in deep learning for irregularly-sampled datasets also suggest that future work could learn such NN representations from datasets involving missing data patterns, which may be of key interest for Chl patterns in some regions [,].
5. Conclusions
The present study investigates two statistical approaches to derive from satellite observations the Chl seasonal to interannual variability and trends, as well as their potential in reconstructing biological past long-term time-series. The MLP is more skillful than the SVR to capture both the spatio-temporal patterns and amplitude of ChlOC-CCI on a global scale over 1998–2015. ChlMLP and ChlOC-CCI seasonal and interannual first mode of variability are highly correlated (r-PCs = 0.99 and 0.95, p < 0.001), suggesting that the MLP is reliable to reproduce ChlOC-CCI, at least over the last 18 years. However, some underestimation in ChlMLP amplitudes as well as regional bias need to be fixed in future studies and the predictors’ importance in Chl reconstruction deserve to be more deeply investigated.
Supplementary Materials
The following are available online at https://www.mdpi.com/2072-4292/12/24/4156/s1, Figure S1: MLP architecture. Table S1: MLP configuration. Figure S2: Learning curves of ChlMLP-9% and ChlMLP.
Author Contributions
Conceptualization, E.M., A.B., T.G., L.D., J.R., P.T., G.M. and R.F.; data creation, A.B. and J.R.; methodology, A.B., L.D., R.F., P.T., E.M., T.G. and G.M.; formal analysis, A.B. and J.R.; writing—original draft preparation, E.M.; writing—review and editing, T.G., L.D., R.F., P.T., J.R., A.B. and G.M.; supervision, E.M., T.G., L.D. and R.F.; funding acquisition, E.M. All authors have read and agreed to the published version of the manuscript.
Funding
Funding for the internship of A. Brini and GPU was provided by the CNES/TOSCA call (Grant n°160515/00) PhytoDeV project. The J. Roussillon PhD grant was funded by the ISblue project, Interdisciplinary graduate school for the blue planet (ANR-17-EURE-0015) and co-funded by a grant from the French government under the program “Investissements d’Avenir”.
Acknowledgments
We would like to thank the three anonymous reviewers whose comments have helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sabine, C.L.; Feely, R.A.; Gruber, N.; Key, R.M.; Lee, K.; Bullister, J.L.; Wanninkhof, R.; Wong, C.S.; Wallace, D.W.R.; Tilbrook, B.; et al. The oceanic sink for anthropogenic CO2. Science 2004, 305, 367–371. [Google Scholar] [CrossRef]
- Falkowski, P. Ocean science: The power of plankton. Nature 2012, 483, S17–S20. [Google Scholar] [CrossRef]
- Longhurst, A.; Sathyendranath, S.; Platt, T.; Caverhill, C. An estimate of global primary production in the ocean from satellite radiometer data. J. Plankton Res. 1995, 17, 1245–1271. [Google Scholar] [CrossRef]
- Messié, M.; Chavez, F.P. A global analysis of ENSO synchrony: The oceans’ biological response to physical forcing. J. Geophys. Res. Oceans 2012, 117, C09001. [Google Scholar] [CrossRef]
- Dutkiewicz, S.; Follows, M.; Marshall, J.; Gregg, W.W. Interannual variability of phytoplankton abundances in the North Atlantic. Deep Sea Res. II Top. Stud. Oceanogr. 2001, 48, 2323–2344. [Google Scholar] [CrossRef]
- Aumont, O.; Ethé, C.; Tagliabue, A.; Bopp, L.; Gehlen, M. PISCESv2: An ocean biogeochemical model for carbon and ecosystem studies. Geosci. Model Dev. 2015, 8, 2465–2513. [Google Scholar] [CrossRef]
- Henson, S.A.; Dunne, J.P.; Sarmiento, J.L. Decadal variability in North Atlantic phytoplankton blooms. J. Geophys. Res. Ocean. 2009, 114, C04013. [Google Scholar] [CrossRef]
- Henson, S.A.; Raitsos, D.; Dunne, J.P.; McQuatters-Gollop, A. Decadal variability in biogeochemical models: Comparison with a 50-year ocean colour dataset. Geophys. Res. Lett. 2009, 36, L21061. [Google Scholar] [CrossRef]
- Patara, L.; Visbeck, M.; Masina, S.; Krahmann, G.; Vichi, M. Marine biogeochemical responses to the North Atlantic Oscillation in a coupled climate model. J. Geophys. Res. Ocean. 2011, 116, C07023. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T. An apparent hiatus in global warming? Earth’s Future 2013, 1, 19–32. [Google Scholar] [CrossRef]
- Wilson, C.; Adamec, D. A global view of bio-physical coupling from SeaWiFS and TOPEX satellite data, 1997–2001. Geophys. Res. Lett. 2002, 29, 1257. [Google Scholar] [CrossRef]
- Wilson, C.; Coles, V.J. Global climatological relationships between satellite biological and physical observations and upper ocean properties. J. Geophys. Res. Ocean. 2005, 110, C10001. [Google Scholar] [CrossRef]
- Kahru, M.; Gille, S.T.; Murtugudde, R.; Strutton, P.G.; Manzano-Sarabia, M.; Wang, H.; Mitchell, B.G. Global correlations between winds and ocean chlorophyll. J. Geophys. Res. Ocean. 2010, 115, C12040. [Google Scholar] [CrossRef]
- Messié, M.; Chavez, F.P. Seasonal regulation of primary production in eastern boundary upwelling systems. Prog. Oceanogr. 2015, 134, 1–18. [Google Scholar] [CrossRef]
- Uz, S.S.; Busalacchi, A.J.; Smith, T.M.; Evans, M.N.; Brown, C.W.; Hackert, E. Interannual and decadal variability in tropical pacific chlorophyll from a statistical reconstruction: 1958–2008. J. Clim. 2017, 30, 7293–7315. [Google Scholar] [CrossRef]
- Martinez, E.; Gorgues, T.; Lengaigne, M.; Fontana, C.; Sauzède, R.; Menkes, C.; Uitz, J.; Di Lorenzo, E.; Fablet, R. Reconstructing Global Chlorophyll-a Variations Using a Non-linear Statistical Approach. Front. Mar. Sci. 2020, 7, 464. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; O’Malley, R.T.; Siegel, D.A.; McClain, C.R.; Sarmiento, J.L.; Feldman, G.C.; Milligan, A.J.; Falkowski, P.G.; Letelier, R.M.; Boss, E.S. Climate-driven trends in contemporary ocean productivity. Nature 2006, 444, 752–755. [Google Scholar] [CrossRef]
- Polovina, J.J.; Howell, E.A.; Abecassis, M. Ocean’s leastproductive waters are expanding. Geophys. Res. Lett. 2008, 35, L03618. [Google Scholar] [CrossRef]
- Martinez, E.; Antoine, D.; D’Ortenzio, F.; Gentili, B. Climate-driven basin-scale decadal oscillations of oceanic phytoplankton. Science 2009, 36, 1253–1256. [Google Scholar] [CrossRef]
- Thomas, A.C.; Strub, P.T.; Weatherbee, R.A.; James, C. Satellite views of Pacific chlorophyll variability: Comparisons to physical variability, local versus nonlocal influences and links to climate indices. Deep-Sea Res. II Top. Stud. Oceanogr. 2012, 77, 99–116. [Google Scholar] [CrossRef]
- Lewandowska, A.M.; Hillebrand, H.; Lengfellner, K.; Sommer, U. Temperature effects on phytoplankton diversity—The zooplankton link. J. Sea Res. 2014, 85, 359–364. [Google Scholar] [CrossRef]
- Available online: http://iridl.ldeo.columbia.edu/ (accessed on 18 December 2020).
- Wilson, C.; Adamec, D. Correlations between surface chlorophyll and sea surface height in the tropical Pacific during the 1997-1999 El Nino-Southern event. J. Geophys. Res. Ocean. 2001, 106, 31175–31188. [Google Scholar] [CrossRef]
- Radenac, M.H.; Léger, F.; Singh, A.; Delcroix, T. Sea surface chlorophyll signature in the tropical Pacific during eastern and central Pacific ENSO events. J. Geophys. Res. Ocean. 2012, 117, C04007. [Google Scholar] [CrossRef]
- Available online: https://resources.marine.copernicus.eu/?option=com_csw&task=results (accessed on 18 December 2020).
- Martinez, E.; Antoine, D.; D’Ortenzio, F.; de Boyer Montégut, C. Phytoplankton spring and fall blooms in the North Atlantic in the 1980s and 2000s. J. Geophys. Res. Ocean. 2011, 116, C11029. [Google Scholar] [CrossRef]
- Available online: https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim (accessed on 18 December 2020).
- Radenac, M.H.; Messié, M.; Léger, F.; Bosc, C. A very oligotrophic zone observed from space in the equatorial Pacific warm pool. Remote Sens. Environ. 2013, 134, 224–233. [Google Scholar] [CrossRef]
- Available online: https://podaac.jpl.nasa.gov/dataset/OSCAR_L4_OC_third-deg (accessed on 18 December 2020).
- Available online: https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.surfaceflux.html (accessed on 18 December 2020).
- Sauzède, R.; Claustre, H.; Jamet, C.; Uitz, J.; Ras, J.; Mignot, A.; D’Ortenzio, F. Retrieving the vertical distribution of chlorophyll a concentration and phytoplankton community composition from in situ fluorescence profiles: A method based on a neural network with potential for global-scale applications. J. Geophys. Res. Ocean. 2015, 120, 451–470. [Google Scholar] [CrossRef]
- Available online: https://www.oceancolour.org (accessed on 18 December 2020).
- Belo Couto, A.; Brotas, V.; Mélin, F.; Groom, S.; Sathyendranath, S. Inter-comparison of OC-CCI chlorophyll—A estimates with precursor data sets. Int. J. Remote Sens. 2016, 37, 4337–4355. [Google Scholar] [CrossRef]
- Available online: www.esrl.noaa.gov/psd (accessed on 18 December 2020).
- Vapnik, V. Statistics for engineering and information science. In The Nature of Statistical Learning Theory; Jordan, M.J., Lawless, J.F., Lauritzen, S.L., Nair, V., Eds.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Descloux, E.; Mangeas, M.; Menkes, C.E.; Lengaigne, M.; Leroy, A.; Tehei, T.; Guillaumot, L.; Teurlai, M.; Gourinat, A.-C.; Benzler, J.; et al. Climate-based models for understanding and forecasting dengue epidemics. PLoS Negl. Trop. Dis. 2012, 6, e1470. [Google Scholar] [CrossRef]
- Elbisy, M.S. Sea wave parameters prediction by support vector machine using a genetic algorithm. J. Coast. Res. 2015, 31, 892–899. [Google Scholar] [CrossRef]
- Neetu, S.; Lengaigne, M.; Vialard, J.; Mangeas, M.; Menkes, C.; Suresh, I.; Leloup, J.; Knaff, J. Quantifying the benefits of non-linear methods for global statistical hindcasts of tropical cyclones intensity. Mon. Weather Rev. 2020, 35, 807–820. [Google Scholar] [CrossRef]
- Kim, Y.H.; Im, J.; Ha, H.K.; Choi, J.K.; Ha, S. Machine learning approaches to coastal water quality monitoring using GOCI satellite data. Gisci. Remote Sens. 2014, 51, 158–174. [Google Scholar] [CrossRef]
- Hu, S.; Liu, H.; Zhao, W.; Shi, T.; Hu, Z.; Li, Q.; Wu, G. Comparison of machine learning techniques in inferring phytoplankton size classes. Remote Sens. 2018, 10, 191. [Google Scholar] [CrossRef]
- Blix, K.; Eltoft, T. Machine learning automatic model selection algorithm for oceanic chlorophyll-a content retrieval. Remote Sens. 2018, 10, 775. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Ahmad, H. Machine learning applications in oceanography. Aquat. Res. 2019, 2, 161–169. [Google Scholar] [CrossRef]
- Sammartino, M.; Marullo, S.; Santoleri, R.; Scardi, M. Modelling the vertical distribution of phytoplankton biomass in the Mediterranean Sea from satellite data: A neural network approach. Remote Sens. 2018, 10, 1666. [Google Scholar] [CrossRef]
- Wang, C.; Tandeo, P.; Mouche, A.; Stopa, J.E.; Gressani, V.; Longepe, N.; VanDeMark, D.; Foster, R.C.; Chapron, B. Classification of the global Sentinel-1 SAR vignettes for ocean surface process studies. Remote Sens. Environ. 2019, 234, 111457. [Google Scholar] [CrossRef]
- Karpatne, A.; Atluri, G.; Faghmous, J.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery. arXiv 2016, arXiv:1612.08544. [Google Scholar] [CrossRef]
- Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Srivastva, N. System and Method for Addressing Overfitting in a Neural Network. US Patent 9,406,017, 2 August 2016. [Google Scholar]
- Emery, W.; Thomson, R. Data Analysis in Physical Oceanography; Pergamon: New York, NY, USA, 1997; p. 634. [Google Scholar]
- Laws, E.A.; Bannister, T.T. Nutrient-and light-limited growth of Thalassiosira fluviatilis in continuous culture, with implications for phytoplankton growth in the ocean. Limnol. Oceanogr. 1980, 25, 457–473. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; O’Malley, R.T.; Boss, E.S.; Westberry, T.K.; Graff, J.R.; Halsey, K.H.; Milligan, A.J.; Siegel, D.A.; Brown, M.B. Revaluating ocean warming impacts on global phytoplankton. Nat. Clim. Chang. 2015, 6, 323–330. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B. The dissolved yellow substance and the shades of blue in the Mediterranean Sea. Biogeosciences 2009, 6, 2625–2636. [Google Scholar] [CrossRef]
- Del Vecchio, R.; Subramaniam, A. Influence of the Amazon River on the surface optical properties of the western tropical North Atlantic Ocean. J. Geophys. Res. Ocean. 2004, 109, C11. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Randerson, J.T.; McClain, C.R.; Feldman, G.C.; Los, S.O.; Tucker, C.J.; Falkowski, P.G.; Field, C.B.; Frouin, R.; Esaias, W.E.; et al. Biospheric primary production during an ENSO transition. Science 2001, 291, 2594–2597. [Google Scholar] [CrossRef] [PubMed]
- Yoder, J.A.; Kennelly, M.A. Seasonal and ENSO variability in global ocean phytoplankton chlorophyll derived from 4 years of SeaWiFS measurements. Glob. Biogeochem. Cycles 2003, 17, 1112. [Google Scholar] [CrossRef]
- Chavez, F.P.; Messié, M.; Pennington, J.T. Marine primary production in relation to climate variability and change. Annu. Rev. Mar. Sci. 2011, 3, 227–260. [Google Scholar] [CrossRef] [PubMed]
- Doney, S.C. Plankton in a warmer world. Nature 2006, 444, 695–696. [Google Scholar] [CrossRef] [PubMed]
- Irwin, A.J.; Oliver, M.J. Are ocean deserts getting larger? Geophys. Res. Lett. 2009, 36, L18609. [Google Scholar] [CrossRef]
- Mélin, F.; Vantrepotte, V.; Chuprin, A.; Grant, M.; Jackson, T.; Sathyendranath, S. Assessing the fitness-for-purpose of satellite multi-mission ocean color climate data records: A protocol applied to OC-CCI chlorophyll-a data. Remote Sens. Environ. 2017, 203, 139–151. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, H.C.; Han, D.; Lee, S.; Im, J. Prediction of monthly Arctic sea ice concentrations using satellite and reanalysis data based on convolutional neural networks. Cryosphere 2020, 14, 1083–1104. [Google Scholar]
- Siegel, D.A.; Maritorena, S.; Nelson, N.B.; Behrenfeld, M.J. Independence and interdependencies among global ocean color properties: Reassessing the bio-optical assumption. J. Geophys. Res. Ocean. 2005, 110, C07011. [Google Scholar] [CrossRef]
- Westberry, T.; Behrenfeld, M.J.; Siegel, D.A.; Boss, E. Carbon-based primary productivity modeling with vertically resolved photoacclimation. Glob. Biogeochem. Cycles 2008, 22, GB2024. [Google Scholar] [CrossRef]
- Beauchamp, M.; Fablet, R.; Ubelmann, C.; Ballarotta, M.; Chapron, B. Intercomparison of data-driven and learning-based interpolations of along-track Nadir and wide-swath Swot altimetry observations. Remote Sens. 2020, 12, 3806. [Google Scholar] [CrossRef]
- Nguyen, D.; Ouala, S.; Drumetz, L.; Fablet, R. Variational Deep Learning for the Identification and Reconstruction of Chaotic and Stochastic Dynamical Systems from Noisy and Partial Observations. arXiv 2020, arXiv:2009.02296. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).