Development of an Improved Model for Prediction of Short-Term Heavy Precipitation Based on GNSS-Derived PWV
Abstract
1. Introduction
2. Data and Methodologies
2.1. Selection of Data
2.1.1. Selection of Location and Data Period
2.1.2. Selection of Experimental Data
2.2. GNSS Data
2.2.1. Retrieval of GNSS-PWV
2.2.2. Evaluation of GNSS-PWV
- To ensure the density of pressure levels in each profile, if the difference in the pressure levels of any two adjacent layers exceeded 200 hPa, then the profile was excluded.
- If the pressure levels in each profile missed any of the following levels:
- (a)
- The mandatory levels specified by WMO;
- (b)
- The significant levels suggested by the US National Weather Service (NWS); then the profile was excluded [82].
2.3. Methods for Determining Thresholds and Evaluating Prediction Results
2.3.1. Criteria for Determining Thresholds and Evaluating of Prediction Results
2.3.2. Threshold Determination Based on CSI
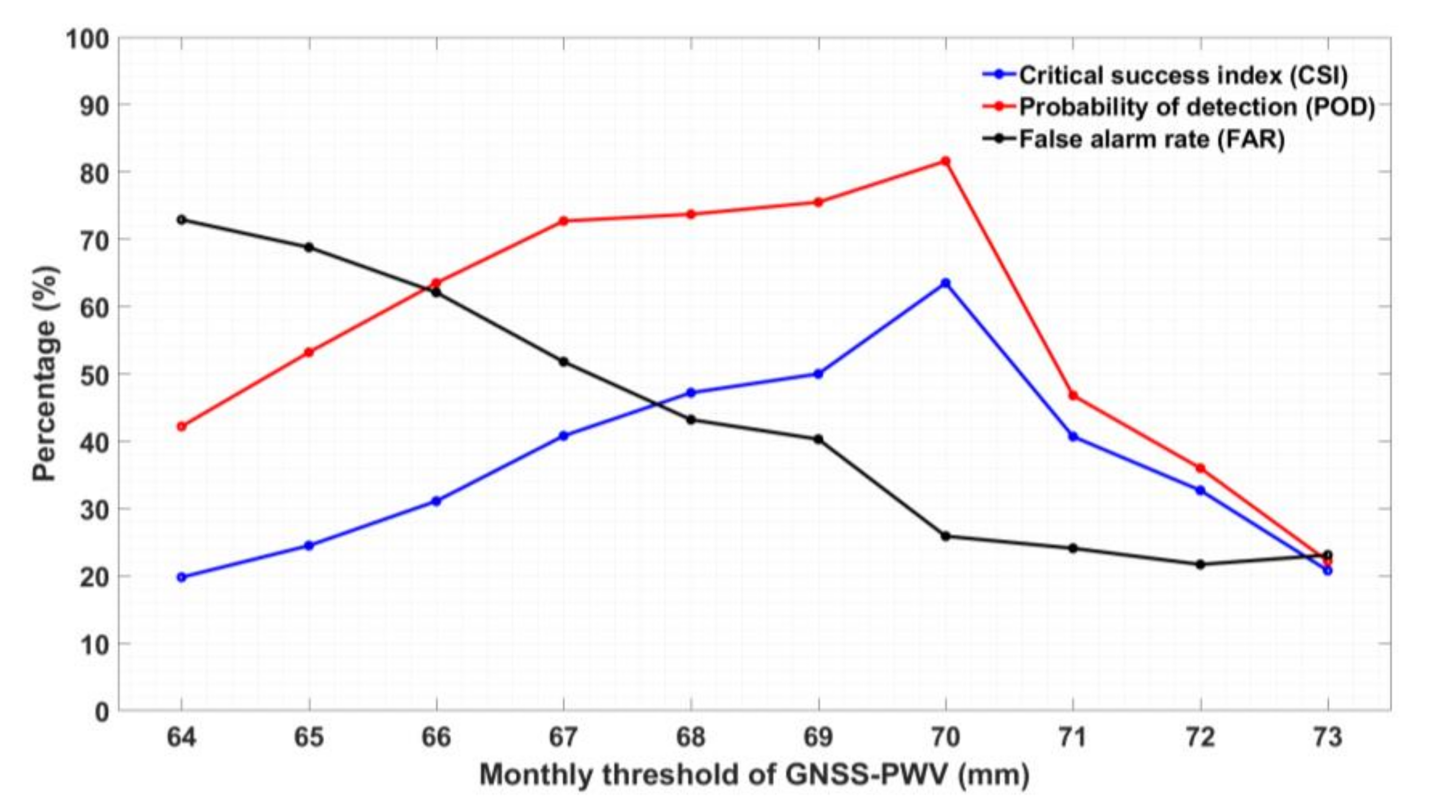
- A set of candidate threshold values were selected by examining the sample PWV values and the hourly precipitation records in each of the summer months. For example, for the month of June at the HKSC-KP stations, all the GNSS-PWV values (in June from 2010 to 2017) were found in the range 64–73 mm; thus, a set of integer values from this range were taken as candidate threshold values (see the left column in Table 4).
- Based on the above candidate values and the sample data in the month, n11, n12 and n21 (in Table 3) were counted; then, the candidate’s CSI score was calculated using Equation (12). Table 4 lists the prediction results, including the CSI, POD and FAR scores, resulting from each candidate threshold, and Figure 3 shows the same results, merely for easy comparisons.
- The candidate that led to the highest CSI score was determined as the optimal threshold. Since the highest CSI score was resulting from the threshold value of 70, 70 was determined as the optimal threshold for the month of June.
2.3.3. Impact of Different-Length Samples on Determined Thresholds
3. Relationship between PWV Variation and Heavy Precipitation
3.1. Overview
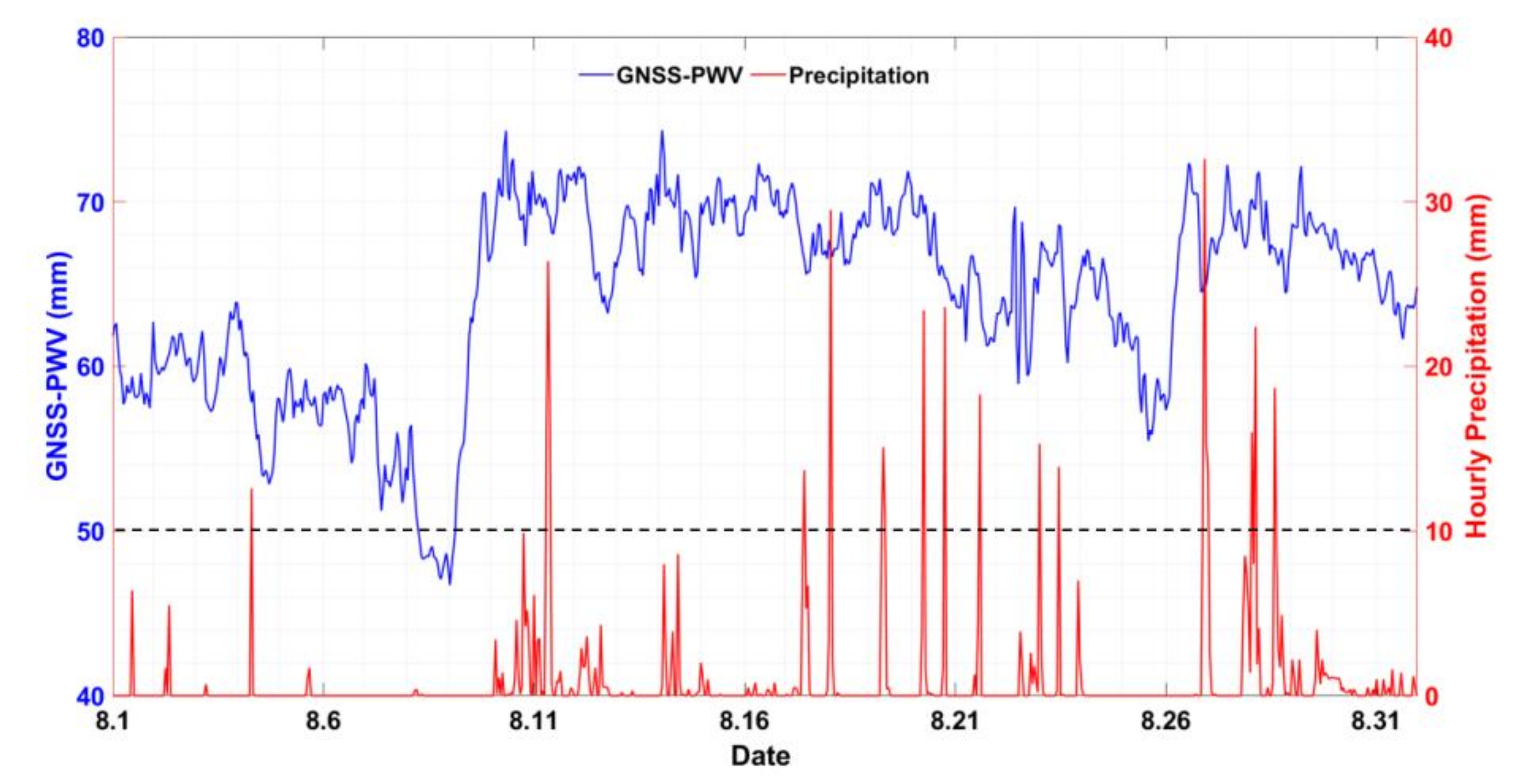
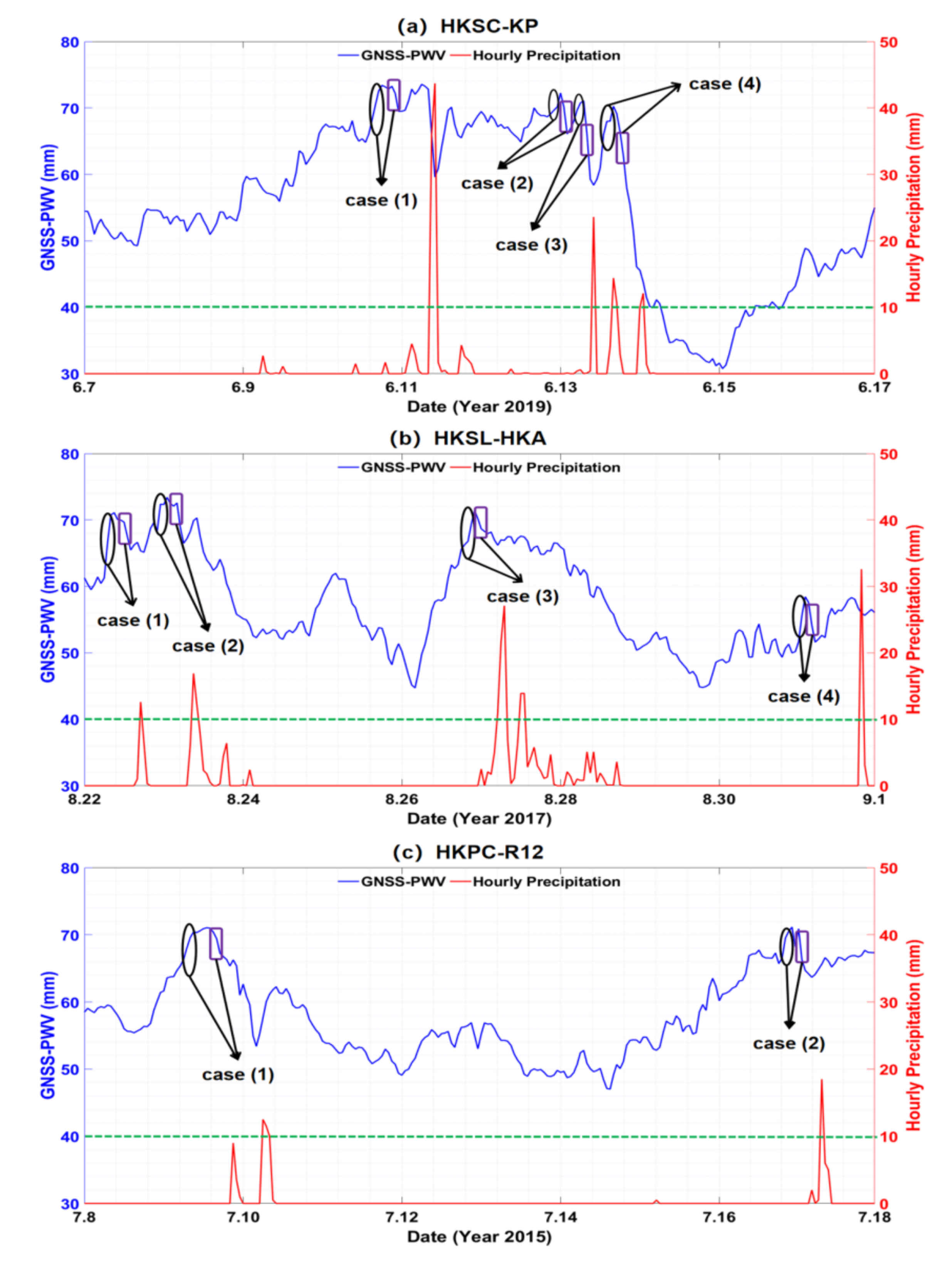
3.2. PWV Variation before the Onset of Heavy Precipitation
3.2.1. Formation of Heavy Precipitation
3.2.2. PWV Variation Prior to Heavy Precipitation
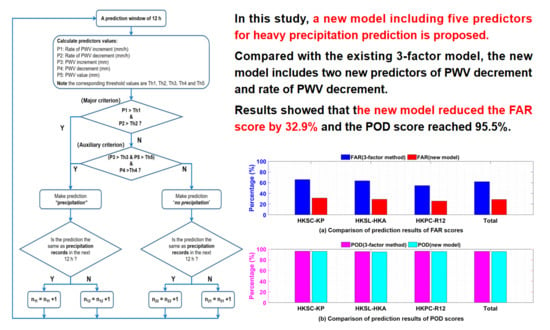
4. Determination and Testing of Five Thresholds for New Model
4.1. Determination of Optimal Set of Thresholds
4.2. Testing of New Model
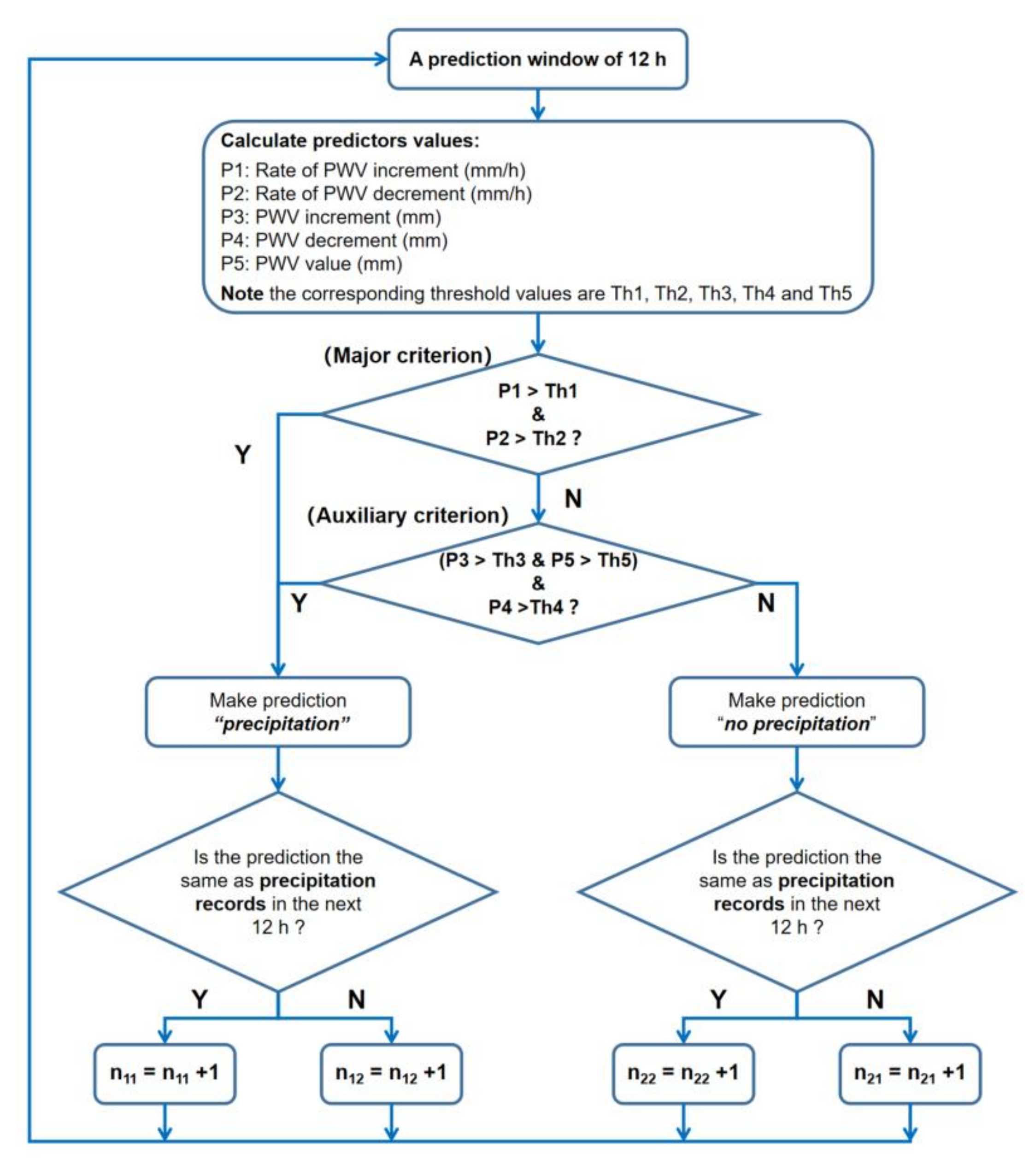
4.2.1. Criteria Determined for Heavy Precipitation Prediction
4.2.2. Procedure for New Model Testing
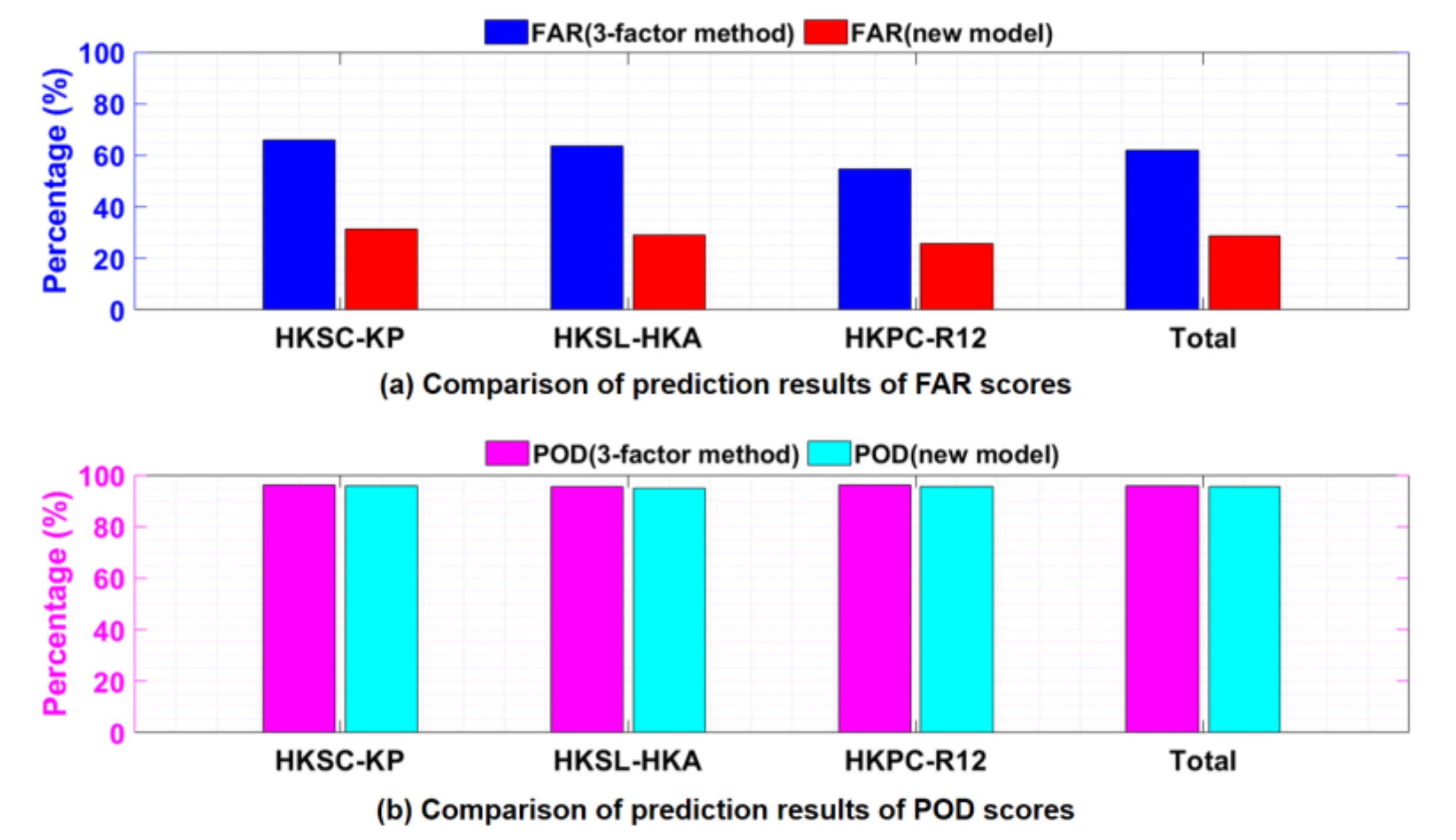
4.2.3. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, P.W.; Wong, W.K.; Cheung, P.; Yeung, H.Y. An overview of nowcasting development, applications, and services in the Hong Kong Observatory. J. Meteorol. Res. 2014, 28, 859–876. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Z.; Wong, W.K.; Woo, W.C. Detecting water vapor variability during heavy precipitation events in Hong Kong using the GPS tomographic technique. J. Atmos. Ocean. Tech. 2017, 34, 1001–1019. [Google Scholar] [CrossRef]
- Foster, J.; Bevis, M.; Chen, Y.L.; Businger, S.; Zhang, Y. The Ka ’u storm (November 2000): Imaging precipitable water using GPS. J. Geophys. Res. 2003, 108, 4585. [Google Scholar] [CrossRef]
- Seko, H.; Nakamura, H.; Shoji, Y.; Iwabuchi, T. The Meso-γ scale Water Vapor Distribution Associated with a Thunderstorm Calculated from a Dense Network of GPS Receivers. J. Meteorol. Soc. Jpn. 2004, 82, 569–586. [Google Scholar] [CrossRef]
- Chiang, K.W.; Peng, W.C.; Yeh, Y.H.; Chen, K.H. Study of alternative GPS network meteorological sensors in Taiwan: Case studies of the plum rains and typhoon Sinlaku. Sensors 2009, 9, 5001–5021. [Google Scholar] [CrossRef]
- Moore, A.W.; Small, I.J.; Gutman, S.I.; Bock, Y.; Dumas, J.L.; Fang, P.; Laber, J.L. National weather service forecasters use GPS precipitable water vapor for enhanced situational awareness during the southern California summer monsoon. Bull. Am. Meteorol. Soc. 2015, 96, 1867–1877. [Google Scholar] [CrossRef]
- Muller, C.J.; Back, L.E.; O’Gorman, P.A.; Emanuel, K.A. A model for the relationship between tropical precipitation and column water vapor. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Van Baelen, J.; Reverdy, M.; Tridon, F.; Labbouz, L.; Dick, G.; Bender, M.; Hagen, M. On the relationship between water vapour field evolution and the life cycle of precipitation systems. Q. J. R. Meteorol. Soc. 2011, 137, 204–223. [Google Scholar] [CrossRef]
- Brettle, M.; Galvin, J. Back to basics: Radiosondes: Part 1—The instrument. Weather 2006, 58, 336–341. [Google Scholar] [CrossRef]
- England, M.; Schmidlin, F.J.; Johansson, J. Atmospheric Moisture Measurements: A Microwave Radiometer-Radiosonde Comparison. IEEE Trans. Geosci. Remote Sens. 1993, 31, 389–398. [Google Scholar] [CrossRef]
- Buehler, S.A.; Kuvatov, M.; John, V.O.; Milz, M.; Soden, B.J.; Jackson, D.L.; Notholt, J. An upper tropospheric humidity data set from operational satellite microwave data. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Niell, A.E.; Coster, A.; Solheim, F.; Mendes, V.; Toor, P.; Langley, R.; Upham, C.A. Comparison of Measurements of Atmospheric Wet Delay by Radiosonde, Water Vapor Radiometer, GPS, and VLBI. J. Atmos. Ocean. Technol. 2001, 18, 830–850. [Google Scholar] [CrossRef]
- Liu, Z.; Wong, M.; Nichol, J.; Chan, P.W. A multi-sensor study of water vapour from radiosonde, MODIS and AERONET: A case study of Hong Kong. Int. J. Clim. 2013, 33, 109–120. [Google Scholar] [CrossRef]
- Elliott, W.P. On detecting long-term changes in atmospheric moisture. Clim. Chang. 1995, 31, 349–367. [Google Scholar] [CrossRef]
- Wang, H.; He, J.; Wei, M.; Zhang, Z. Synthesis analysis of one severe convection precipitation event in Jiangsu using ground-based GPS technology. Atmosphere 2015, 6, 908–927. [Google Scholar] [CrossRef]
- Gui, K.; Che, H.; Chen, Q.; Zeng, Z.; Liu, H.; Wang, Y.; Zhang, X. Evaluation of radiosonde, MODIS-NIR-Clear, and AERONET precipitable water vapor using IGS ground-based GPS measurements over China. Atmos. Res. 2017, 197, 461–473. [Google Scholar] [CrossRef]
- Baker, H.C.; Dodson, A.H.; Penna, N.T.; Higgins, M.; Offiler, D. Ground-based GPS water vapour estimation: Potential for meteorological forecasting. J. Atmos. Sol.-Terr. Phys. 2001, 63, 1305–1314. [Google Scholar] [CrossRef]
- Brenot, H.; Neméghaire, J.; Delobbe, L.; Clerbaux, N.; De Meutter, P.; Deckmyn, A.; Van Roozendael, M. Preliminary signs of the initiation of deep convection by GNSS. Atmos. Chem. Phys. 2013, 13, 5425–5449. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of Tropospheric Delay for Microwaves from Surface Weather Data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Elgered, G.; Davis, J.; Herring, T.; Shapiro, I. Geodesy by radio interferometry: Water vapor radiometry for estimation of the wet delay. J. Geophys. Res. Atmos. 1991, 96, 6541–6555. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.; Rocken, C.; Anthes, R.; Ware, R. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.; Anthes, R.; Rocken, C.; Ware, R. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Rocken, C.; Hove, T.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Chiswell, S.; Businger, S. GPS/STORM-GPS sensing of atmospheric water vapour for meteorology. J. Atmos. Ocean. Technol. 1995, 12, 468–478. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rocken, C.; Solheim, F.; Hove, T.; Ware, R.; et al. GPS Meteorology: Direct Estimation of the Absolute Value of Precipitable Water. J. Appl. Meteorol. 1996, 35, 830–838. [Google Scholar] [CrossRef]
- Yuan, L.; Anthes, R.; Ware, R.; Rocken, C.; Bonner, W.; Bevis, M.; Businger, S. Sensing climate change using the global positioning system. J. Geophys. Res. 1993, 981, 14925–14938. [Google Scholar] [CrossRef]
- Rocken, C.; Ware, R.; Hove, T.; Solheim, F.; Alber, C.; Johnson, J.; Bevis, M.; Businger, S. Sensing atmospheric water vapor with the Global Positioning System. Geophys. Res. Lett. 1993, 20, 2631–2634. [Google Scholar] [CrossRef]
- Jin, S.; Li, Z.; Cho, J. Integrated water vapor field and multiscale variations over China from GPS measurements. J. Appl. Meteorol. Clim. 2008, 47, 3008–3015. [Google Scholar] [CrossRef]
- Nilsson, T.; Elgered, G. Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data. J. Geophys. Res. 2008, 113, D19101. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; He, C.; Cheng, Y.; Li, X. Determination of zenith hydrostatic delay and its impact on GNSS-derived integrated water vapor. Atmos. Meas. Tech. 2017, 10, 2807–2820. [Google Scholar] [CrossRef]
- Vedel, H.; Huang, X.Y.; Haase, J.; Ge, M.; Calais, E. Impact of GPS zenith tropospheric delay data on precipitation forecasts in Mediterranean France and Spain. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Wu, S.; Li, Z.; Cheng, Y.; Li, L.; Yuan, H. The correlation between GNSS-derived precipitable water vapor and sea surface temperature and its responses to El Niño–Southern Oscillation. Remote Sens. Environ. 2018, 216, 1–12. [Google Scholar] [CrossRef]
- Le Marshall, J.; Norman, R.; Howard, D.; Rennie, S.; Moore, M.; Kaplon, J.; Lehmann, P. Using global navigation satellite system data for real-time moisture analysis and forecasting over the Australianregion I. The system. J. South. Hemisph. Earth 2019, 69, 161–171. [Google Scholar] [CrossRef]
- Gradinarsky, L.P.; Johansson, J.; Bouma, H.; Scherneck, H.-G.; Elgered, G. Climate monitoring using GPS. Phys. Chem. Earth 2002, 27, 335–340. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.; Cho, J.-H.; Park, P.-H. Seasonal variability of GPS-derived zenith tropospheric delay (1994–2006) and climate implications. J. Geophys. Res. 2007, 112, D09110. [Google Scholar] [CrossRef]
- Rohm, W.; Yuan, Y.; Biadeglgne, B.; Zhang, K.; Le Marshall, J. Ground-based GNSS ZTD/IWV estimation system for numerical weather prediction in challenging weather conditions. Atmos. Res. 2013, 138, 414–426. [Google Scholar] [CrossRef]
- Choy, S.; Zhang, K.; Wang, C.S.; Li, Y.; Kuleshov, Y. Remote Sensing of the Earth’s Lower Atmosphere during Severe Weather Events using GPS Technology: A Study in Victoria, Australia. In Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011), Oregon Convention Center, Portland, OR, USA, 20–23 September 2011; Volume 1, pp. 559–571. [Google Scholar]
- Suparta, W.; Zulkeple, S.K.; Putro, W.S. Estimation of thunderstorm activity in tawau, sabah using GPS data. Adv. Sci. Lett. 2017, 23, 1370–1373. [Google Scholar] [CrossRef]
- Jones, J.; Guerova, G.; Douša, J.; Dick, G.; de Haan, S.; Pottiaux, E.; van Malderen, R. Advanced GNSS Tropospheric Products for Monitoring Severe Weather Events and Climate; COST Action ES1206 Final Action Dissemination Report; Springer: Berlin/Heidelberg, Germany, 2019; p. 563. [Google Scholar] [CrossRef]
- Singh, R.P.; Mishra, N.C.; Verma, A.; Ramaprasad, J. Total precipitable water over the Arabian Ocean and the Bay of Bengal using SSM/I data. Int. J. Remote Sens. 2000, 21, 2497–2503. [Google Scholar] [CrossRef]
- Singh, R.P.; Dey, S.; Sahoo, A.K.; Kafatos, M. Retrieval of water vapor using SSM/I and its relation with the onset of monsoon. Ann. Geophys. 2004, 22, 3079–3083. [Google Scholar] [CrossRef]
- Champollion, C.; Masson, F.; Van Baelen, J.; Walpersdorf, A.; Chéry, J.; Doerflinger, E. GPS monitoring of the tropospheric water vapor distribution and variation during the 9 September 2002 torrential precipitation episode in the Cévennes (southern France). J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Kedem, B.; Chiu, L.S.; Karni, Z. An analysis of the threshold method for measuring area-average rainfall. J. Appl. Meteorol. 1990, 29, 3–20. [Google Scholar] [CrossRef][Green Version]
- Cheng, M.; Brown, R. Estimation of area-average rainfall for frontal rain using the threshold method. Quart. J. R. Meteorol. Soc. 1993, 119, 825–844. [Google Scholar] [CrossRef]
- Kanda, M. Correlation between convective heavy rainfalls and GPS precipitable water. In Proceedings of the International Workshop on GPS Meteorology, Tsukuba, Japan, 14–17 January 2003; pp. 3–12. [Google Scholar]
- Shoji, Y. Retrieval of Water Vapor Inhomogeneity Using the Japanese Nationwide GPS Array and its Potential for Prediction of Convective Precipitation. J. Meteorol. Soc. Jpn. 2013, 91, 43–62. [Google Scholar] [CrossRef]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Real-time GPS precise point positioning-based precipitable water vapor estimation for rainfall monitoring and forecasting. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3452–3459. [Google Scholar]
- Yeh, T.K.; Shih, H.C.; Wang, C.S.; Choy, S.; Chen, C.H.; Hong, J.S. Determining the precipitable water vapor thresholds under different rainfall strengths in Taiwan. Adv. Space Res. 2018, 61, 941–950. [Google Scholar] [CrossRef]
- Benevides, P.; Catalao, J.; Miranda, P. On the inclusion of GPS precipitable water vapour in the nowcasting of rainfall. Nat. Hazard. Earth Syst. 2015, 15, 2605–2616. [Google Scholar] [CrossRef]
- Yao, Y.; Shan, L.; Zhao, Q. Establishing a method of short-term rainfall forecasting based on GNSS-derived PWV and its application. Sci. Rep. 2017, 7, 1–11. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Y.; Ma, X.; Yao, W.; Yao, Y.; Li, X. An Improved Rainfall Forecasting Model Based on GNSS Observations. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Brenot, H.; Wautelet, G.; Warnant, R.; Nemeghaire, J.; Van Roozendael, M.; Theys, N.; Hurtmans, D. A GPS network for tropospheric tomography in the framework of the Mediterranean hydrometeorological observatory Cévennes-Vivarais (southeastern France). Nat. Hazards Earth Syst. Sci. 2014, 14, 1099–1123. [Google Scholar] [CrossRef]
- Manning, T.; Zhang, K.; Rohm, W.; Choy, S.; Hurter, F. Detecting Severe Weather using GPS Tomography: An Australian Case Study. J. Glob. Position. Syst. 2012, 11, 58–70. [Google Scholar] [CrossRef]
- Seco, A.; Ramírez, F.; Serna, E.; Prieto, E.; García, R.; Moreno, A.; Cantera, J.; Miqueleiz, L.; Priego, J. Rain pattern analysis and forecast model based on GPS estimated atmospheric water vapor content. Atmos. Environ. 2012, 49, 85–93. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S. GPS-PWV Based Improved Long-Term Rainfall Prediction Algorithm for Tropical Regions. Remote Sens. 2019, 11, 2643. [Google Scholar] [CrossRef]
- Manandhar, S.; Lee, Y.H.; Meng, Y.S.; Yuan, F.; Ong, J. GPS-Derived PWV for Rainfall Nowcasting in Tropical Region. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4835–4844. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmos. Sol.-Terr. Phy. 2018, 167, 124–133. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, Y. Preliminary result of capturing the signature of heavy rainfall events using the 2-d-/4-d water vapour information derived from GNSS measurement in Hong Kong. Adv. Space Res. 2020, 66, 1537–1550. [Google Scholar] [CrossRef]
- Łoś, M.; Smolak, K.; Guerova, G.; Rohm, W. GNSS-Based Machine Learning Storm Nowcasting. Remote Sens. 2020, 12, 2536. [Google Scholar] [CrossRef]
- Boniface, K.; Ducrocq, V.; Jaubert, G.; Yan, X.; Brousseau, P.; Masson, F.; Champollion, C.; Chery, J.; Doerflinger, E. Impact of high-resolution data assimilation of GPS zenith delay on Mediterranean heavy rainfall forecasting. Ann. Geophys. 2009, 27, 2739–2753. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, Q.; Yao, W.; Ma, X.; Yao, Y.; Liu, L. Short-term rainfall forecast model based on the improved Bp–nn algorithm. Sci. Rep. 2019, 9, 1–12. [Google Scholar] [CrossRef]
- Manandhar, S.; Dev, S.; Lee, Y.H.; Meng, Y.S.; Winkler, S. A data-driven approach for accurate rainfall prediction. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9323–9331. [Google Scholar] [CrossRef]
- Bonafoni, S.; Biondi, R.; Brenot, H.; Anthes, R. Radio occultation and ground-based GNSS products for observing, understanding and predicting extreme events: A review. Atmos. Res. 2019, 230, 104624. [Google Scholar] [CrossRef]
- Pruppacher, H.R.; Klett, J.D. Diffusion Growth and Evaporation of Water Drops and Snow Crystals. In Microphysics of Clouds and Precipitation; Springer: Dordrecht, The Netherlands, 2010; pp. 502–567. [Google Scholar]
- Wang, P.K. Physics and Dynamics of Clouds and Precipitation; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Madhulatha, A.; Rajeevan, M.; Venkat Ratnam, M.; Bhate, J.; Naidu, C.V. Nowcasting severe convective activity over southeast India using ground-based microwave radiometer observations. J. Geophys. Res. Atmos. 2013, 118, 1–13. [Google Scholar] [CrossRef]
- Barindelli, S.; Realini, E.; Venuti, G.; Fermi, A.; Gatti, A. Detection of water vapor time variations associated with heavy rain in northern Italy by geodetic and low-cost GNSS receivers. Earth Planets Space 2018, 70, 28. [Google Scholar] [CrossRef]
- Zhang, K.; Manning, T.; Wu, S.; Rohm, W.; Silcock, D.; Choy, S. Capturing the Signature of Severe Weather Events in Australia Using GPS Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sen. 2015, 8, 1839–1847. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, B.; Chan, S.-T.; Yunchang, C.; Gao, Y.; Zhang, K.; Nichol, J. Analysis and modelling of water vapour and temperature changes in Hong Kong using a 40-year radiosonde record: 1973–2012. Int. J. Clim. 2014, 35, 462–474. [Google Scholar] [CrossRef]
- Zhao, P.; Zhou, Z.; Liu, J. Variability of Tibetan spring snow and its associations with the hemispheric extratropical circulation and East Asian summer monsoon rainfall: An observational investigation. J. Clim. 2007, 20, 3942–3955. [Google Scholar] [CrossRef]
- Chow, K.C.; Tong, H.W.; Chan, J.C. Water vapor sources associated with the early summer precipitation over China. Clim. Dyn. 2008, 30, 497–517. [Google Scholar] [CrossRef]
- Hong Kong Observatory. Observed Climate Change in Hong Kong: Extreme Weather Events. 2016. Available online: http://www.weather.gov.hk/climate_change/obs_hk_extreme_weather_e.htm (accessed on 18 July 2020).
- WMO. Guide to Instruments and Methods of Observation, Volume I—Measurement of Meteorological Variables; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Tietze, W.; Domrös, M. The climate of China. GeoJournal. 1987, 14, 265–266. [Google Scholar] [CrossRef]
- Hong Kong Observatory. Number of Days with Rainfall Observed at the Hong Kong Observatory Since 1885, Exclude 1940–1946. 2019. Available online: https://www.hko.gov.hk/en/cis/statistic/rf_days.htm (accessed on 29 August 2020).
- Rocken, C.; Hove, T.; Ware, R. Near Real-Time GPS Sensing of Atmospheric Water Vapour. Geophys. Res. Lett. 1997, 24, 3221–3224. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software; Version 5.2; Astronomical Institute, University of Bern: Berne, Switzerland, 2015. [Google Scholar]
- Böhm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and the Stratosphere in Radio Ranging of Satellites. Geophys. Monogr. 1972, 15, 247–251. [Google Scholar]
- Chen, Y. Inversing the content of vapor in atmosphere by GPS observations. Mod. Surv. Mapp. 2005, 28, 3–6. [Google Scholar]
- Durre, I.; Vose, R.; Wuertz, D. Overview of the Integrated Global Radiosonde Archive. J. Clim. 2006, 19, 53–68. [Google Scholar] [CrossRef]
- Wright, J.M., Jr. Federal Meteorological Handbook No. 3: Rawinsonde and Pibal Obervations; Office of the Federal Coordinator for Meteorology, National Oceanic and Atmospheric Administration: Washington, DC, USA, May 1997. Available online: https://www.ofcm.gov/publications/fmh/FMH3/00-entire-FMH3.pdf (accessed on 31 August 2020).
- Offiler, D.; Jones, J.; Bennit, G.; Vedel, H. EIG EUMETNET GNSS Water Vapour Programme (E-GVAP-II). Prod. Requir. Doc. MetOffice. 2010. Available online: http://egvap.dmi.dk/support/formats/egvap_prd_v10.pdf (accessed on 19 July 2020).
- Chen, B.; Dai, W.; Liu, Z.; Wu, L.; Xia, P. Assessments of GMI-Derived Precipitable Water Vapor Products over the South and East China Seas Using Radiosonde and GNSS. Adv. Meteorol. 2018. [Google Scholar] [CrossRef]
- Doswell Iii, C.; Flueck, J. Forecasting and Verifying in a Field Research Project: DOPLIGHT’87. Weather 1989, 4, 97–109. [Google Scholar] [CrossRef]
- Donaldson, R.; Dyer, R.; Kraus, M. Objective evaluator of techniques for predicting severe weather events. Bull. Amer. Meteorol. Soc. 1975, 56, 755. [Google Scholar]
- Ding, J. Review of Weather Prediction Verifying Techniques. J. Nanjing Inst. Meteorol. 1995, 18, 143–150. [Google Scholar]
- Gilleland, E.; Ahijevch, D.; Brown, B.; Casati, B.; Ebert, E. Intercomparison of Spatial Forecast Verification Methods. Weather 2009, 24, 1416–1430. [Google Scholar] [CrossRef]
- Doswell, C., III; Davies-Jones, R.; Keller, D. On Summary Measures of Skill in Rare Event Forecasting Based on Contingency Tables. Weather 1990, 5, 576–585. [Google Scholar] [CrossRef]
- Li, L.; Kuang, C.L.; Zhu, J.J.; Chen, W.; Chen, Y.Q.; Long, S.C.; Li, H.Y. Rainstorm nowcasting based on GPS real-time precise point positioning technology. Diqiu Wuli Xuebao 2012, 55, 1129–1136. [Google Scholar]
- Liu, X.C.; Wang, Y.Q.; Zhang, Z.L. Analysis of Harbin Area Atmosphere Precipitable Water Vapor by Using GPS Technology. Bull. Surv. Mapp. 2006, 4, 10–16. [Google Scholar]
- Sapucci, L.F.; Machado, L.A.; Menezes de Souza, E.; Campos, T.B. GPS-PWV jumps before intense rain events. Atmos. Meas. Tech. Discuss. 2016, 1–27. [Google Scholar] [CrossRef]
- Holton, J.R. An introduction to dynamic meteorology. Am. J. Phys. 1973, 41, 752. [Google Scholar] [CrossRef]
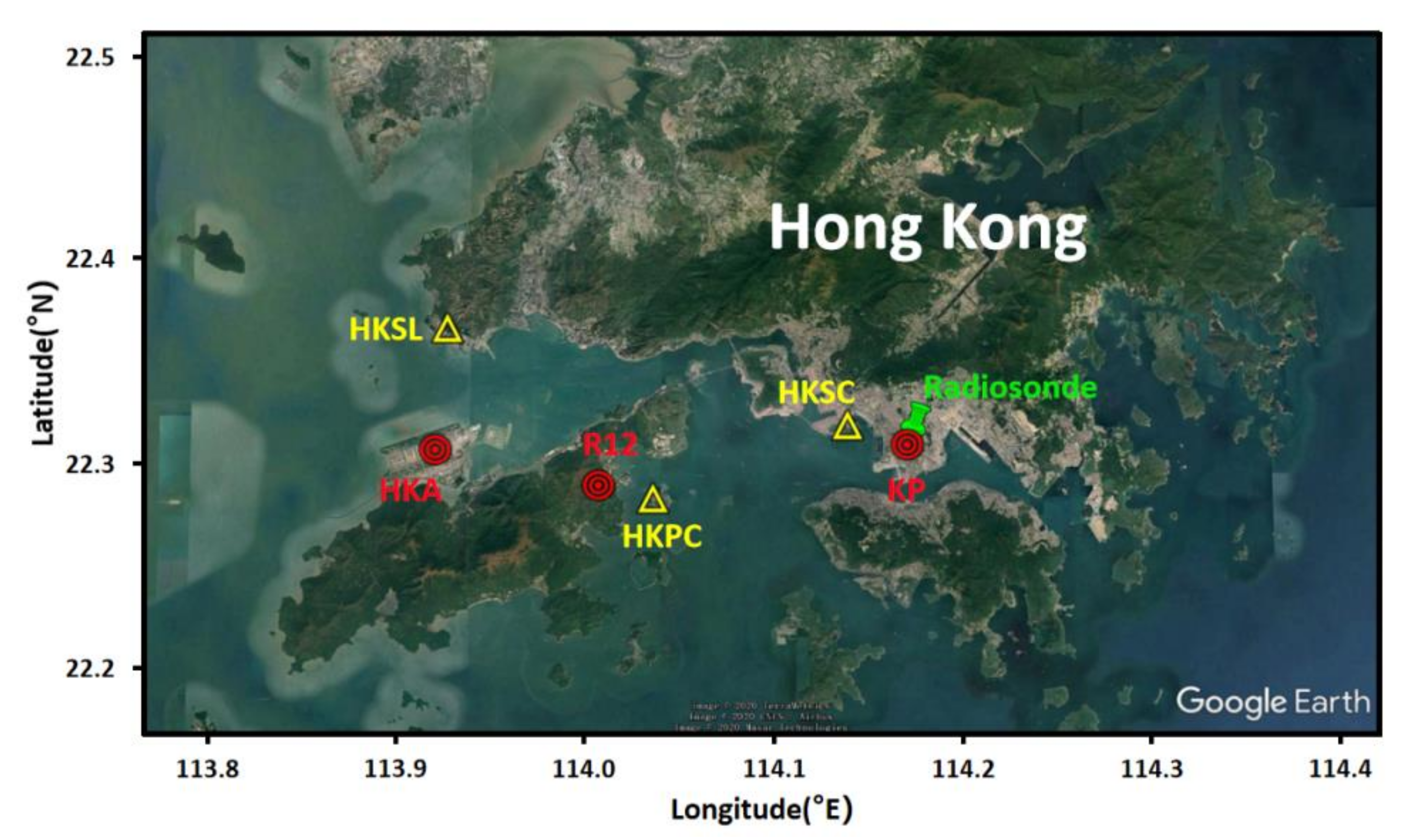

| Station ID | Latitude (°) | Longitude (°) | Distance (km) | |
|---|---|---|---|---|
| 1 | HKSC | 22.32 | 114.14 | 3.29 |
| KP | 22.31 | 114.17 | ||
| 2 | HKSL | 22.37 | 113.93 | 2.63 |
| HKA | 22.31 | 113.92 | ||
| 3 | HKPC | 22.28 | 114.04 | 2.96 |
| R12 | 22.29 | 114.01 | ||
| Station | Number of Samples | Bias (mm) | RMS Error (mm) | Correlation Coefficient |
|---|---|---|---|---|
| HKSC | 1406 | 1.23 | 2.18 | 0.995 |
| Truth | Prediction | Total | ||
|---|---|---|---|---|
| Yes | No | |||
| Precipitation | Yes | n11 | n21 | n11 + n21 |
| No | n12 | n22 | n12 + n22 | |
| Total | n11 + n12 | n21 + n22 | n11 + n12 + n21 + n22 | |
| Candidate Threshold (mm) | Number of Real Heavy Precipitation Events | n11 | n12 | n21 | CSI (%) | POD (%) | FAR (%) |
|---|---|---|---|---|---|---|---|
| 64 | 45 | 19 | 51 | 26 | 19.8 | 42.2 | 72.9 |
| 65 | 47 | 25 | 55 | 22 | 24.5 | 53.2 | 68.8 |
| 66 | 52 | 33 | 54 | 19 | 31.1 | 63.5 | 62.1 |
| 67 | 55 | 40 | 43 | 15 | 40.8 | 72.7 | 51.8 |
| 68 | 57 | 42 | 32 | 15 | 47.2 | 73.7 | 43.2 |
| 69 | 53 | 40 | 27 | 13 | 50.0 | 75.5 | 40.3 |
| 70 | 49 | 40 | 14 | 9 | 63.5 | 81.6 | 25.9 |
| 71 | 47 | 22 | 7 | 25 | 40.7 | 46.8 | 24.1 |
| 72 | 50 | 18 | 5 | 32 | 32.7 | 36.0 | 21.7 |
| 73 | 45 | 10 | 3 | 35 | 20.8 | 22.2 | 23.1 |
| Threshold Candidate | Length of Time | |||
|---|---|---|---|---|
| 2-Year | 4-Year | 6-Year | 8-Year | |
| 64 | 14.8 | 18.8 | 19.7 | 19.8 |
| 65 | 20.0 | 21.3 | 21.4 | 24.5 |
| 66 | 25.0 | 31.7 | 25.0 | 31.1 |
| 67 | 31.8 | 36.6 | 34.9 | 40.8 |
| 68 | 25.0 | 30.8 | 39.7 | 47.2 |
| 69 | 41.2 | 41.2 | 42.4 | 50 |
| 70 | 47.6 | 50.0 | 51 | 63.5 |
| 71 | 50.0 | 46.7 | 43.2 | 40.7 |
| 72 | 37.5 | 32.0 | 32.4 | 32.7 |
| 73 | 23.1 | 18.2 | 18.8 | 20.8 |
| Predictor | Definition | Remark | |
|---|---|---|---|
| 1 | PWV value | Hourly GNSS-PWV value | Proposed by Yao et al. [49] |
| 2 | PWV increment | the maximum PWV before precipitation—the minimum PWV before the adjacent maximum PWV | |
| 3 | Rate of PWV increment | PWV increment/interval epoch within the ascending trend | |
| 4 | PWV decrement | the previous maximum PWV (PWV value at the beginning of the descending trend)—the PWV at the current epoch (in the descending trend) | Proposed in this study |
| 5 | Rate of PWV decrement | PWV decrement/interval epoch within the descending trend | |
| Additional parameters used in the calculation process: Interval epoch within the ascending trend = time1 (corresponding to the maximum PWV)—time2 (corresponding to the minimum PWV). Interval epoch within the descending trend = time3 (corresponding to the current epoch in the descending trend)—time4 (corresponding to the previous maximum PWV). | |||
| Heavy Precipitation Event | PWV Increment (mm) | Rate of PWV Increment (mm/h) | Max. PWV Decrement (mm) | Max. Rate of PWV Decrement (mm/h) | |
|---|---|---|---|---|---|
| HKSC-KP | case 1 | 8.58 | 1.72 | 4.91 | 2.46 |
| case 2 | 3.58 | 0.87 | 6.17 | 3.09 | |
| case 3 | 4.97 | 0.99 | 12.68 | 5.85 | |
| case 4 | 11.87 | 1.98 | 24.6 | 3.44 | |
| HKSL-HKA | case 1 | 10.65 | 2.66 | 5.63 | 1.13 |
| case 2 | 5.06 | 1.69 | 6.07 | 3.70 | |
| case 3 | 8.74 | 1.46 | 3.50 | 1.38 | |
| case 4 | 8.45 | 2.11 | 6.83 | 2.28 | |
| HKPC-R12 | case 1 | 14.72 | 0.82 | 10.04 | 2.62 |
| case 2 | 5.43 | 1.36 | 7.23 | 4.64 | |
| Month | Rate of PWV Increment (mm/h) | Rate of PWV Decrement (mm/h) | PWV Increment (mm) | PWV Decrement (mm) | PWV Value (mm) | |
|---|---|---|---|---|---|---|
| HKSC-KP | Jun | 1.30 | 2.10 | 5.3 | 6.3 | 70 |
| Jul | 1.20 | 1.95 | 3.7 | 2.8 | 68 | |
| Aug | 1.10 | 1.25 | 3.6 | 2.0 | 70 | |
| HKSL-HKA | Jun | 1.70 | 2.30 | 5.3 | 5.1 | 68 |
| Jul | 1.70 | 1.95 | 4.1 | 3.3 | 66 | |
| Aug | 1.40 | 1.80 | 2.3 | 3.0 | 68 | |
| HKPC-R12 | Jun | 1.45 | 2.15 | 4.5 | 5.9 | 69 |
| Jul | 1.30 | 1.50 | 4.0 | 3.0 | 66 | |
| Aug | 1.10 | 1.50 | 3.3 | 2.3 | 70 | |
| Month | No. of Correct Predictions (n11) | No. of Misdiagnosis Predictions (n12) | No. of Omissive Predictions (n21) | POD (%) | FAR (%) | |
|---|---|---|---|---|---|---|
| HKSC-KP | Jun | 20 | 6 | 2 | 90.9 | 23.1 |
| Jul | 18 | 10 | 0 | 100 | 35.7 | |
| Aug | 32 | 16 | 1 | 97.0 | 33.3 | |
| Summer | 70 | 32 | 3 | 95.9 | 31.4 | |
| HKSL-HKA | Jun | 21 | 5 | 1 | 95.5 | 19.2 |
| Jul | 15 | 7 | 1 | 93.8 | 31.8 | |
| Aug | 20 | 11 | 1 | 95.2 | 35.5 | |
| Summer | 56 | 23 | 3 | 94.9 | 29.1 | |
| HKPC-R12 | Jun | 20 | 4 | 3 | 87.0 | 16.7 |
| Jul | 14 | 5 | 0 | 100 | 26.3 | |
| Aug | 29 | 13 | 0 | 100 | 31.0 | |
| Summer | 63 | 22 | 3 | 95.5 | 25.9 | |
| Total | 189 | 77 | 9 | 95.5 | 28.9 | |
| Month | No. of Correct Predictions (n11) | No. of Misdiagnosis Predictions (n12) | No. of Omissive Predictions (n21) | POD (%) | FAR (%) | |
|---|---|---|---|---|---|---|
| HKSC-KP | Jun | 20 | 34 | 2 | 90.9 | 63.0 |
| Jul | 21 | 54 | 0 | 100 | 72.0 | |
| Aug | 35 | 58 | 1 | 97.2 | 62.4 | |
| Summer | 76 | 146 | 3 | 96.2 | 65.8 | |
| HKSL-HKA | Jun | 22 | 28 | 1 | 95.7 | 56.0 |
| Jul | 17 | 27 | 1 | 94.4 | 61.4 | |
| Aug | 23 | 54 | 1 | 95.8 | 70.1 | |
| Summer | 62 | 109 | 3 | 95.4 | 63.7 | |
| HKPC-R12 | Jun | 28 | 20 | 3 | 90.3 | 41.7 |
| Jul | 19 | 34 | 0 | 100 | 64.2 | |
| Aug | 29 | 37 | 0 | 100 | 56.1 | |
| Summer | 76 | 91 | 3 | 96.2 | 54.5 | |
| Total | 214 | 346 | 9 | 96.0 | 61.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Wang, X.; Wu, S.; Zhang, K.; Chen, X.; Qiu, C.; Zhang, S.; Zhang, J.; Xie, M.; Li, L. Development of an Improved Model for Prediction of Short-Term Heavy Precipitation Based on GNSS-Derived PWV. Remote Sens. 2020, 12, 4101. https://doi.org/10.3390/rs12244101
Li H, Wang X, Wu S, Zhang K, Chen X, Qiu C, Zhang S, Zhang J, Xie M, Li L. Development of an Improved Model for Prediction of Short-Term Heavy Precipitation Based on GNSS-Derived PWV. Remote Sensing. 2020; 12(24):4101. https://doi.org/10.3390/rs12244101
Chicago/Turabian StyleLi, Haobo, Xiaoming Wang, Suqin Wu, Kefei Zhang, Xialan Chen, Cong Qiu, Shaotian Zhang, Jinglei Zhang, Mingqiang Xie, and Li Li. 2020. "Development of an Improved Model for Prediction of Short-Term Heavy Precipitation Based on GNSS-Derived PWV" Remote Sensing 12, no. 24: 4101. https://doi.org/10.3390/rs12244101
APA StyleLi, H., Wang, X., Wu, S., Zhang, K., Chen, X., Qiu, C., Zhang, S., Zhang, J., Xie, M., & Li, L. (2020). Development of an Improved Model for Prediction of Short-Term Heavy Precipitation Based on GNSS-Derived PWV. Remote Sensing, 12(24), 4101. https://doi.org/10.3390/rs12244101