Abstract
The retrieval of sun-induced chlorophyll fluorescence is greatly beneficial to studies of marine phytoplankton biomass, physiology, and composition, and is required for user applications and services. Customarily phytoplankton chlorophyll fluorescence is determined from satellite measurements through a fluorescence line-height algorithm using three bands around 680 nm. We propose here a modified retrieval, making use of all available bands in the relevant wavelength range, with the goal to improve the effectiveness of the algorithm in optically complex waters. For the Ocean and Land Colour Instrument (OLCI), we quantify a Fluorescence Peak Height by fitting a Gaussian function and related terms to the top-of-atmosphere reflectance bands between 650 and 750 nm. This algorithm retrieves, what we call Fluorescence Peak Height by fitting a Gaussian function upon other terms to top-of-atmosphere reflectance bands between 650 and 750 nm. This approach is applicable to Level-1 and Level-2 data. We find a good correlation of the retrieved fluorescence product to global in-situ chlorophyll measurements, as well as a consistent relation between chlorophyll concentration and fluorescence from radiative transfer modelling and OLCI/in-situ comparison. Evidence suggests, the algorithm is applicable to complex waters without needing an atmospheric correction and vicarious calibration, and features an inherent correction of small spectral shifts, as required for OLCI measurements.
1. Introduction
Chlorophyll fluorescence is light re-emitted by chlorophyll molecules when returning from excited to non-excited states [1]. Quantification of solar-induced phytoplankton fluorescence has two main advantages in marine bio-geochemistry applications [2,3]. These are: (1) the improvement of the chlorophyll retrieval, and (2) additional information on phytoplankton physiological state, biomass and maximum layer depth. The chlorophyll retrieval is customarily based on the detection of the chlorophyll absorption signal [4,5,6] which can be gained through the ratio of the chlorophyll fluorescence to the absorption signal [7]. Remotely sensed Fluorescence Line Height (FLH, see also Equation (1)) can better reveal blooms in coastal areas than chlorophyll retrievals based on the ratios of water-leaving radiances in the blue and green spectral range (440–560 nm) by allowing better differentiation of phytoplankton chlorophyll-a concentrations from suspended sediments and colored dissolved organic matter (CDOM) [8]. Therefore, a fluorescence retrieval could be of particular value in optically complex waters, which are independently influenced by CDOM, phytoplankton, and suspended sediments.
The pure fluorescence signal not only varies with variation in the chlorophyll-a pigment concentration, but is also affected by photoinhibition, phytoplankton species, and physiological states [9,10], and layering of phytoplankton. Lin et al. [11] reports a strong diel cycle in in-situ measured fluorescence lifetimes (which has a strong positive correlation to fluorescence efficiency), where the lifetimes are higher at night than during daytime.
One of the major design goals of the Medium Resolution Imaging Spectrometer (MERIS) was the capability to measure the signal of the chlorophyll fluorescence stimulated by ambient sunlight to improve the phytoplankton observation. The use of chlorophyll fluorescence was considered to be especially useful in coastal waters. Based on a variety of studies, the three spectral channels centred at 665, 681.25 and 708.5 nm were included in the design of MERIS for retrieving the fluorescence signal.
Using Radiative Transfer Modelling (RTM), Fischer and Kronfeld [12] show that sun-stimulated natural fluorescence of chlorophyll-a is a good predictor for phytoplankton, even in optically complex waters with varying suspended matter and yellow substance concentrations. They found an increase in fluorescence of about 0.05 mWmsrnm caused by an increase in chlorophyll concentration of 1 mg/m, when a fluorescence efficiency factor of 0.3% was assumed. They also quantified the effect of vertical stratification.
As of now, the most established fluorescence product, which is operationally available is the Fluorescence Line Height (FLH) [13,14,15]. Here, a baseline is first formed by a linear interpolation of two baseline bands, and then subtracted from the radiance of the fluorescence band to obtain the FLH, as follows:
where , , are the center wavelengths of the fluorescence band and the two baseline bands, respectively. , , are the radiances of the fluorescence band and the two baseline bands, respectively. For MERIS, the common band combination is = 681 nm, = 665 nm, = 709 nm. For MODIS, it is = 678 nm, = 667 nm, = 748 nm. For MODIS, the standard algorithm returns the normalized Fluorescence Line Height (nFLH) in mW cm−2m−1 sr−1, which is based on the normalized water-leaving radiance (). Here, normalization implies the application of a Bidirectional Reflectance Distribution Function (BRDF) correction.
Alternative algorithms use a simple reflectance ratio of the reflectance peak around 685 nm, for example, reflectance at 670 and 560 nm [5]. Fluorescence products are customarily given in the unit of the processed quantity, because they measure the height or amplitude of the fluorescence peak in the measured spectrum.
A number of studies investigated the performance of FLH compared to chlorophyll absorption approaches in different regions. Hoge et al. [16] conducted a validation of Terra-MODIS FLH using airborne laser-induced phytoplankton chlorophyll fluorescence data retrievals within Gulf Stream, continental slope, shelf, and coastal waters of the western North Atlantic Ocean. They derived a correlation coefficient of r = 0.85 and conclude that the FLH is equally valid within similar oceanic provinces of the global oceans. Huot et al. [17] discussed important sources of variability in sun-induced chlorophyll fluorescence, such as incident radiance, species composition and nutritional status, and examined difficulties in deriving fluorescence data products from satellite imagery. According to their findings, MODIS FLH can be related to the total flux being emitted by fluorescence. Moreno-Madrinán and Fischer [18] investigated the performance of the MODIS FLH algorithm in estuarine waters and derived no overall relationship between in-situ chlorophyll-a and the FLH product (r = 0.20, n = 507). Nevertheless, the weak relationship obtained was still eight times stronger than that between in-situ chlorophyll-a and the standard product OC3M [19] traditionally used to estimate chlorophyll-a in ocean waters.
Gower and King [15] validated FLH from MERIS on the west coast of Canada. They presented an average relation between FLH and surface chlorophyll concentration from research cruises and from the blue to green ratio observed by MERIS based on a simple model accounting for absorption of stimulating and emitted radiation by chlorophyll pigments, which gives a good fit to the observations. Their results show a difference between the FLH-chlorophyll-relation for offshore waters and those in coastal straits and inlets, which is in agreement with the findings of Gons et al. [20], who documented the effective use of the MERIS FLH product in oligotrophic waters of the Laurentian Great Lakes, but how the MERIS FLH product fails (with FLH diminishing and becoming negative) in mesotrophic and eutrophic waters.
Overall, we can conclude that operational FLH algorithms that are based on the measurements of reflectance at three wavelengths in and around the fluorescence band, are sufficient for fluorescence retrieval in the open ocean where atmospheric correction algorithms work well and elastic reflectance in the fluorescence band is well approximated by the baseline curve due to the relatively weak elastic scattering signal which depends on chlorophyll alone [21]. However, this is not the case in coastal areas. FLH products in coastal waters are significantly affected by a peak in the underlying elastic reflectance which spectrally overlaps and disturbs any fluorescence retrieval (see Figure 1 for visualization). The shape and magnitude of this near-infrared peak is the result of a modulation of the particulate elastic spectrum (from both algal and non algal particles) by the combined phytoplankton and water absorption spectra. The confluence of the decreasing phytoplankton absorption and the increasing absorption of water with wavelength results in a local absorption minimum. This absorption minimum leads to the maximum in the reflectance spectra which is inversely related to the total absorption [5,22].
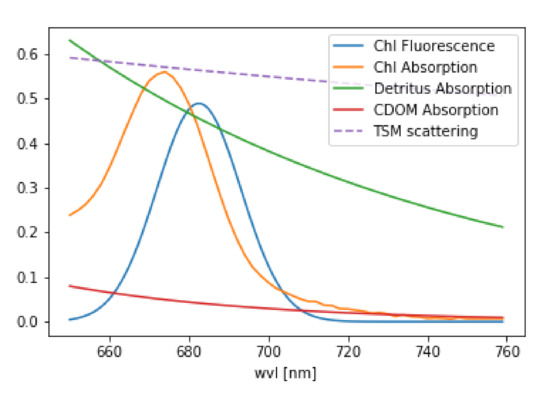
Figure 1.
Optical properties of water constituents considered in the retrieval. Note, that this is only an example of the magnitude of the different properties.
Binding et al. [23] even reported a moderate negative relationship (R = 0.57) between FLH and in-situ chlorophyll at Lake of the Woods with chlorophyll concentration ranging between 2–70 mg/m. As a reason, they suggest that at this intensity of a bloom the absorption signal of chlorophyll dominates in the 681 nm band leading to a negative FLH. Consequently, Ioannou et al. [24] conclude that in order to improve the operational FLH algorithms for coastal waters and compensate for the effects of the overlap of fluorescence, absorption and scattering, suitable models must be developed. Such models can take the larger impact of the spectral variation of the underlying elastic reflectance peak into account and relate the ratio of the elastic reflectance components at 667 and 678 nm to that at 488 and 547 nm. In that way, the new algorithms would improve the performance in the quantification of chlorophyll in coastal waters compared to the standard FLH algorithms.
The variability in fluorescence quantum yield caused by taxonomic differences, phytoplankton physiology and light exposure history [21,25] results in an additional complexity of the relationship between chlorophyll-a and FLH. Nonetheless, Hu et al. [26] established a robust relationship between MODIS FLH and in-situ chlorophyll-a in the west Florida Shelf waters, that yields superior estimates of chlorophyll-a compared with standard SeaWiFS or MODIS band-ratio chlorophyll-a. They were able to use FLH to differentiate between dark features on enhanced RGB images produced by high chlorophyll-a and those produced by high CDOM.
Recently, methods were developed to detect chlorophyll fluorescence in water from hyperspectral satellite measurements. Wolanin et al. [27] uses the filling-in of Fraunhofer lines in order to detect fluorescence from SCIAMACHY measurements. Erickson et al. [28] on the contrary, use the shape of the fluorescence peak for the retrieval of a fluorescence efficiency profile from TROPOMI. Reference [29] published a global retrieval of fluorescence from TROPOMI measurements and found a good correlation to MODIS nflh. However, existing hyper-spectral satellite data generally suffers from poor spatial resolution and signal-to-noise ratio.
The Earth observation satellites Sentinel-3A and Sentinel 3B, which both carry the Ocean and Land Colour Instrument (OLCI) on board, were launched in February 2016 and April 2018, respectively. The key mission driver for the SENTINEL-3 OLCI instrument is continuity of the ENVISAT MERIS instrument capability, with its primary mission to observe the spectral distribution of the water-leaving reflectance, which is then used to estimate geophysical parameters through the application of bio-optical algorithms. Atmospheric correction for ocean colour data is challenging (International Ocean Colour Coordinating Group—IOCCG, 2010) as only about 4% of the radiation measured by a satellite instrument originates from the water surface and sensors require a high signal to noise ratio (SNR), which is around 10% for the red spectral range in the case of OLCI. The water-leaving reflectance is an operational Level-2 product, which delivers, after atmospheric correction, the Surface directional reflectance, corrected for atmospheric attenuation, the Sun illumination geometry, and the mean Earth-Sun distance. In comparison to MERIS, the OLCI swath is not centred at nadir but the whole field-of-view is shifted across track by 12.6 away from the sun to minimise the impact of sun glint. OLCI products are available at two spatial resolutions, Full Resolution (FR) at approximately 300 m and Reduced Resolution (RR) at approximately 1.2 km. OLCI data is acquired in Full Resolution over Land and Ocean, but processing in FR mode is undertaken only if any charted land is present within 300 km of the nominal swath. OLCI spectral bands are optimised to measure ocean colour over the open ocean and coastal zones. A band at 673 nm has been added in comparison to MERIS to better capture the chlorophyll fluorescence peak. However, no algorithm takes full advantage of the improved spectral capacities of OLCI for the detection of fluorescence.
The aim of this paper is the introduction of a new fluorescence algorithm (OC-Fluo), that makes use of OLCI’s enhanced spectral capabilities in order to allow the retrieval of fluorescence even in optically complex waters. The physical principles are presented as well as the technical implementation. Finally, the product is evaluated by comparing the algorithm results with in-situ measured chlorophyll concentration, OLCI’s standard chlorophyll concentration, FLH from MODIS and using Radiative Transfer Modelling (RTM).
Table 1 compares OLCI and MODIS spectral bands and properties, that are used for the respective fluorescence respective products.

Table 1.
Comparison of Ocean and Land Colour Instrument (OLCI) and MODIS spectral bands and properties that are used for the respective fluorescence retrievals and products.
2. The OC-Fluo Algorithm
In-water chlorophyll fluorescence is unique in its spectral shape and restricted to a distinct and narrow wavelength range. Most other inherent optical properties (IOP’s) in the water have comparably flat spectral features. In addition, the predominant fraction of the atmospheric influence is spectrally flat (for the influence of ozone and water vapour see Section 2.5). Chlorophyll absorption alone induces another narrow spectral feature in the vicinity of the fluorescence peak. Our algorithm utilizes the fact that chlorophyll causes the only spectrally high varying features in the 650–750 nm spectral range which allows us to be independent of absolute values and therefore, of atmospheric correction. We limit the analysis to this spectral range and apply a simple curve fit to the measurements. Two Gaussian functions of defined width and spectral position capture chlorophyll absorption and fluorescence, while all other optical influences are covered by an offset and a slope.
Consequently, both, Level-1B and Level-2 data can be processed by the OC-Fluo algorithm. It is specifically developed for OLCI measurements, but the methodology can be adapted to different sensors that measure in sufficient spectral resolution in the spectral region around the fluorescence peak. At least four bands are required, covering the chlorophyll absorption dip and the fluorescence peak between 650 and 750 nm.
Due to the uniqueness of the spectral appearance of fluorescence, the algorithm should improve the retrieval in optically complex waters, where current algorithms often fail [18,20]. This failure is in many cases initiated by a failure of the atmospheric correction, where for example, an erroneous black pixel assumption leads to an overestimation of the aerosol reflectance and an underestimated or negative water reflectance values in the blue bands [30]. There are some algorithms dealing with these problems [31], but these still result in retrieval errors of around 20–40%. For those cases, the Level-1 fluorescence product may be still reliable. For OLCI Level-2 reflectances, the following Water Quality Science Flags (WQSF) are applied: INVALID, LAND, CLOUD [32]. The algorithm does not flag negative values of , since the algorithm can give reasonable results also with negative , when the spectral shape of the data is preserved. Here, we apply the OC-FLuo algorithm to OLCI Level-1B top of atmosphere (TOA) radiances and Level-2 water remote sensing reflectance () at bands 8–12 (see Section 3).
2.1. Theoretical Description
The physical basis of the presented algorithm is the Lambert-Beer law, which describes the extinction of electromagnetic radiation by matter.
Here, and I are incoming and outgoing intensity, respectively. is the attenuation cross section of the attenuating species i in the material sample; is the number density of the attenuating species i in the material sample; L is the path length of the beam of light through the material sample. The equation can also be written as
In atmospheric remote sensing, it is common to use the DOAS (Differential Optical Absorption Spectroscopy, Reference [33]) approach, where the individual absorption cross sections of trace gases are fitted to the logarithm of . Since each atmospheric trace gas has its own unique spectral finger print, it is possible to mathematically separate them. The same is valid for chlorophyll fluorescence with its unique spectral shape. The IOPs of the major water constituents, as they are implemented in the RTM MOMO ([34], see also Section 3.4) are shown in Figure 1. These are: chlorophyll fluorescence, which is an elastic process and can be modelled by a Gaussian curved source of radiation in radiative transfer, chlorophyll absorption, described by a measured absorption spectrum [35], detritus and CDOM absorption, both represented by an exponential decay with different slopes [36] and scattering on particles, which is assumed as an spectrally inverse function [35]. For the fluorescence retrieval, we use a simplified version of Equation (3), because the light path of the photons throughout the complete wavelength range of interest is similar. We use either radiance (~I) or reflectance (~). This is done under the assumption that the spectral features, which are extracted by the retrieval, are induced only by the water body.
The nomenclature we are using here for the retrieval follows the conventions given in Rodgers [37]. In short:
- expresses the state vector, which includes the parameters to be retrieved.
- expresses the measurement vector, which includes the measurements.
- is the forward model, which describes as a function of
The measured radiance or reflectance (the equation only expresses radiance for clarity) is described as:
which is a function of 4 unknown (state) parameters:
- O = offset, accounting for atmospheric and oceanic scattering processes.
- S = slope gradient, accounting for atmospheric and oceanic scattering processes and absorption.
- = amplitude of Gaussian function at (absorption minimum of chlorophyll).
- = amplitude of Gaussian function at (chlorophyll fluorescence peak).
(For the components see Figure 2):
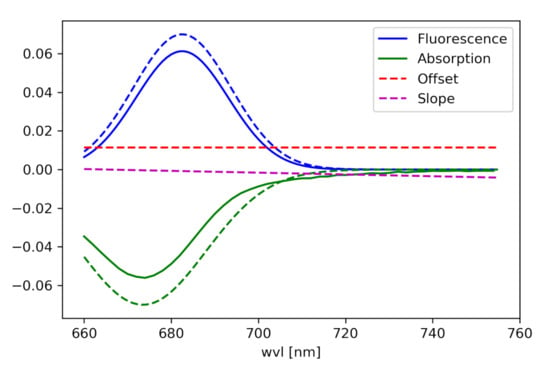
Figure 2.
Components of the curve, which is fitted to the radiance spectrum.
And 4 fixed model parameters:
- = center wavelength of the Gaussian absorption maximum of chlorophyll in the red = 673.5 nm (from fitting to a measured chlorophyll absorption spectrum published in Reference [35]).
- = center wavelength of the Gaussian fluorescence maximum of chlorophyll = 682.5 nm (compromise between the values from different publications for example, References [12,38,39,40] and a measured chlorophyll fluorescence spectrum (R. Röttgers, pers. communication, 2019).
- w = 2c = 250 nm, with c being the standard deviation of the Gaussian fluorescence of chlorophyll [38,40].
- w = 2c = 416 nm, with c being the standard deviation of the Gaussian absorption of chlorophyll (from fitting to a measured chlorophyll absorption spectrum published in Reference [35]).
The unknown parameter in Equation (5) defines the fluorescence product.
2.2. Technical Description
Given the definitions above, the measurement vector y is given by OLCI data band 8–12 and the state x is defined by the factor for fluorescence (FPH), absorption (APD), a slope (S) and an offset (O).
The Jacobian is the derivative matrix of the measurement to the state. Each line of this matrix is the derivative of the forward function to the corresponding state parameter.
and therefore:
Inserting Equation (5) gives:
For the application of this algorithm to OLCI measurements, are given by the nominal wavelength of band Oa8–12 (665.0 nm, 673.75 nm, 681.25 nm, 708.75 nm, 753.75 nm). In order to keep computation time low, we assume these values to be constant (for the correction of small spectral shifts see Section 2.4). Inserting the values for , , w and w gives:
is a rectangle matrix with full row rank and thus features a right inverse , so that the state vector can be derived from:
In principle, the number of channels that are included in the measurement vector is flexible and can be adapted according to the sensor. The number of measurements (bands) must be equal or larger than the number of state parameters to be retrieved in order to get a K-matrix that is invertable. However, including , , w, w (see Equation (5)) as additional parameters, makes the problem non-linear. A non-linear inversion problem can be solved by defining it locally linear, but then a number of iterations has to be performed, with an iteratively changing K, which is also different for each pixel.
The approach could also be expanded to an optimal estimation approach, which includes a priori knowledge about the state. Here, measurement and a priori knowledge are weighted by their particular covariance matrices.
where is the measurement covariance matrix, the a priori covariance matrix and the a priori state. The approach we are presenting here is the simplest special case of the possibilities given above and most promising at this stage for OLCI measurements. In future, with either more knowledge about fluorescence in water (a priori knowledge) or with hyper-spectral measurements (more possible retrieval parameters), the above mentioned equation could be applied.
L-FPH is the amplitude of the Gaussian function, which is related to the fluorescence peak (centered at 682.5 nm) that is fitted to Level-1 radiance (L). It is therefore a measure of the fluorescence signal in the TOA radiance spectrum without any normalization. L-FPH is given in units of mWmsrnm. -FPH is the amplitude of the Gaussian function, which is related to the fluorescence peak (centered at 682.5 nm) that is fitted to Level-2 water-leaving reflectance (). It is therefore a measure of the fluorescence signal in the water-leaving reflectance which is normalized by irradiance. Operational OLCI Level-2 products are defined as the directional water surface reflectance, -FPH, which is dimensionless. The OLCI Level-2 products include the corrections to the water reflectance value with the Sun at zenith, the mean Earth-Sun distance, and non-attenuating atmosphere. They do not include the BRDF corrections for viewing geometry, water optical properties, and the sky radiance distribution. For an overview of OC-Fluo input and output parameters see Table 1.
2.3. Spectral Solar Irradiance () Weighting for L-FPH
The spectral distribution of the solar irradiance is known and the seasonally corrected in-band solar irradiance () is delivered with Level-1 OLCI data. In order to compensate for spectral structures introduced by F that could interfere with optical properties of chlorophyll, the preprocessing for the retrieval of L-FPH includes a rectification with a normalised . In practice, L are divided by and multiplied by in band 682 nm.
2.4. The Correction of Small Spectral Shifts (Smile) for L-FPH
OLCI consists of five optical cameras, each of which exhibits a variation of the relative spectral response of the bands across the field of view called a smile effect. This variation is further different for each module [41]. The camera to camera variations in the central spectral wavelength as well as additional small variations in each detector array are visible as stripes across the swath. Variations up to 1.5 nm are hardly visible when looking at the whole spectral range, but they can be important when spectrally narrow features are measured with spectrally narrow channels. Accordingly, the stripes can be visible in the results from algorithms assuming measurements at nominal wavelength, as is the case for our algorithm. Level-1 data is delivered including the central wavelength for each pixel. Operationally, Level-2 data is smile corrected assuming a linear relationship between Rayleigh corrected reflectances in neighbouring bands [32]. With this assumption, the water reflectances are corrected to the values as if they were measured at nominal wavelengths. We developed and implemented a smile correction for Level-1b data for band Oa08–Oa12. The internal OC-Fluo smile correction is based on the relationship between neighbouring bands defined by Equation (5), therefore, it begins technically with the application of the retrieval (Equation (12)) on Level-1b data () measured at (the subscript denotes the shifted measures),
with the resulting state . Assuming that the forward modelled spectrum based on represents the slope from measured to nominal wavelength, the change in radiance units can be calculated from the shift in wavelength through :
This is then added to the measured .
is now input to the retrieval. As an example for the effectiveness of this smile correction, Figure 3 shows a detail of the Barents Sea scene (also used for evaluation (see Section 3.2) with L-FPH), which was smile corrected by our retrieval (Figure 3a) and -FPH (Figure 3b), where the boundary of two cameras is still visible despite of the Level-2 smile correction.
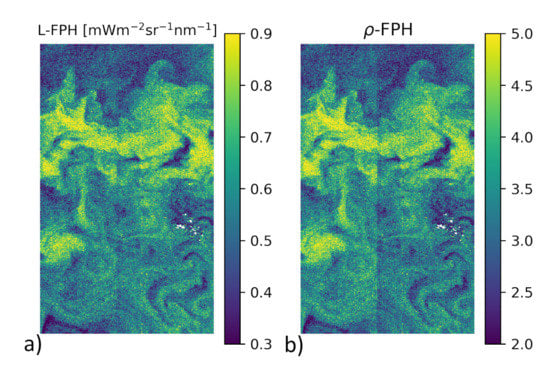
Figure 3.
Comparison of the internal smile correction on Level-1b data and the standard smile correction of OLCI Level-2 data, through the comparison of the two different products in a detail of the Barents Sea scene on the 7 May 2018 with (a) L-FPH and (b) -FPH. Note how the boundary of two cameras is visible in the -FPH but not in the L-FPH.
2.5. Uncertainty with Respect to Trace Gas Absorption in L-FPH
The assumption of a spectrally flat atmospheric influence in the respective wavelength range is not valid when considering trace gases. Water vapour, ozone and nitrogen dioxide are absorbing trace gases with a non-flat spectral signature. A trace gas absorption correction is complex due to the dependency on and interaction between the trace gas vertical profile and the light path of the measured radiance. This is not yet implemented in the OC-Fluo algorithm. In order to quantify the uncertainty in the L-FPH product caused by the neglect of this absorption, we calculate the transmission of the respective gases based on Reference [42]. For this example, total column NO is set to 2.5 molec/cm, ozone to 300 DU and water vapor ranges between 0 to 4 g/cm. After multiplying the transmission on synthetic spectra (for RTM see Section 3.4), the L-FPH without and with transmission correction at an upper limit is retrieved. The difference between both (ΔL-FPH) is mainly driven by the concentration of water vapour and ranges from −0.2 in high latitudes to up to 0.4 L-FPH in the tropics (Figure 4). In mid-latitudes, the difference is only around 0.02 L-FPH. The spatial variation of water vapor is very low above open ocean and higher in coastal regions, but generally lower compared to the spatial variation of chlorophyll. Hence, neglecting trace gas absorption will cause a regional offset in most cases and not modify the spatial structures in the retrieved L-FPH. Nevertheless, time series and global assessments will be influenced by a varying water vapor, therefore, a further development of the algorithm will include a correction for water vapor (and ozone).
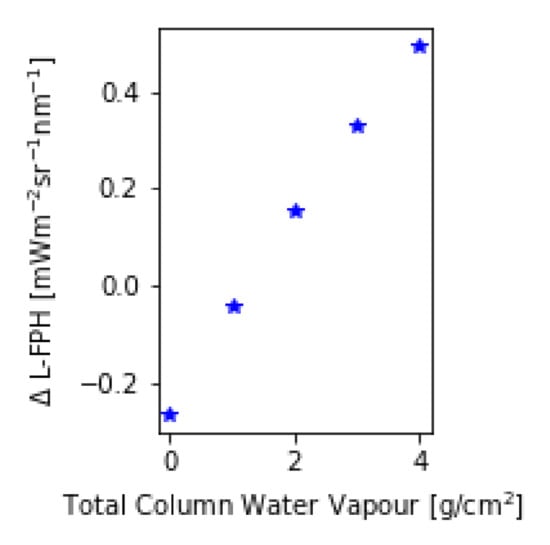
Figure 4.
Difference in L-FPH without and with transmission correction over a global range of total column water vapor applied on synthetic spectra.
Retrieval Noise
The retrieval noise is the uncertainty of the result caused by measurement noise and can be calculated by propagating measurement noise through the retrieval. Following a Gaussian error retrieval, we calculate the error covariance as follows
with the diagonal elements of being the absolute noise of the measurement. Assuming a SNR of 63 for full resolution images, this results in around 10% uncertainty for both L-FPH and -FPH. Since we are using a linear forward model, is a constant and therefore is a constant as well.
2.6. Forward Model Parameter Uncertainty
The forward model parameter uncertainty is the uncertainty that is introduced through an uncertainty in the parameters in the forward model. The forward model for the OC-Fluo algorithm comprises four parameters: Pa = [, w, , w] (Equation (9) and description below). The parameters are taken from different publications or the result of fitting already published data. In order to get a first estimation of resulting uncertainties, we assume a plausible uncertainty range for each parameter: Pa-Pa (see Table 2). Inserting the lower and upper limit in Equation (10), a corresponding (Pa) and (Pa) is calculated and following Equation (12), a corresponding FPH(Pa) and FPH(Pa).

Table 2.
Uncertainties in FPH due to the different forward model parameter.
The resulting FPH is calculated by the weighted difference of FPH with the respective parameter at its lower (FPH(Pa)) and its upper (FPH(Pa)) limit:
Table 2 summarizes forward model parameters, assumed uncertainty ranges and resulting uncertainties.
This is an estimation of an upper limit of uncertainty, which is caused by not knowing the forward model parameter exactly. It is not the error which is made in each measurement and therefore, not include in the presentation of the results.
2.7. Evaluation Method of the Algorithm
Fluorescence is a complex measure because it is not a property of the water body alone (an Inherent Optical Property, like for example, chlorophyll absorption), but is also a property of current and historical illumination. We cannot rely on a fluorescence ground truth for the evaluation, since in-situ fluorescence measurements are governed by active light pulses and therefore, not comparable to sun-induced fluorescence. The comparison to chlorophyll is state-of-the-art for the evaluation of fluorescence algorithms (see Section 1). The fluorescence is expected, to first order, to be correlated to chlorophyll concentration [12]. Following these consideration, we investigate the value of our processor by the comparison to: (1) in-situ chlorophyll measurements, (2) standard OLCI chlorophyll products OC4me [43] and NN [44], (3) the MODIS nFLH product and (4) results from RTM (Figure 5).
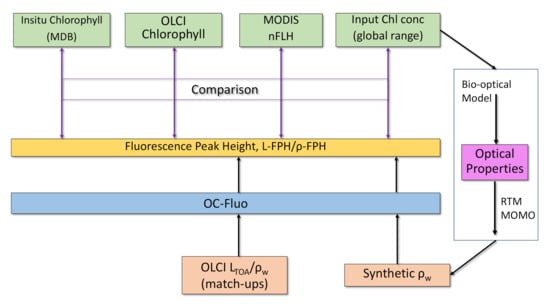
Figure 5.
Evaluation of the OC-Fluo algorithm based on in-situ chlorophyll measurements, standard OLCI chlorophyll products, the MODIS nFLH product and an end-to-end simulation including Radiative Transfer Modelling (RTM).
3. Results
3.1. FPH against In-Situ Chlorophyll
As it is a common practice for the evaluation of remote sensing products, the main part is performed through the comparison to in-situ measurements of the same quantity. In this case, the most closely related quantity, that is measured in-situ, is the chlorophyll concentration. For this in-situ matchup comparison, the chlorophyll concentration is the result of HPLC measurements. The data is extracted from the HPLC Matchup Database which includes global HPLC data from NASA SeaBASS [45] with OLCI matchups and is available at https://ocdb.eumetsat.int/ [46]. The HPLC Matchups DataBase is distributed as a netCDF file, providing both OLCI data (25 × 25 pixel centred over in-situ coordinates) and in-situ data. All variables are included as they are in the original OLCI Level-2 products. HPLC measurements are optically weighted to provide a unique value when multiple casts are provided within a radius of 150 m within 1 h from the first measurement below the surface. A ±3 h window is assigned around the satellite overpass as the condition for coincidence. Only in-situ measurements which have at least one measurement available in the top layer are included. For the satellite matchups, we follow the OLCI matchup protocol [47]. A box of 5 × 5 pixels is defined, centered on the location of the in-situ measurement. This box allows the generation of simple statistics, such as the mean and standard deviation, to assist in the evaluation of spatial stability, or homogeneity, at the evaluation point. On a pixel basis, we applied the suggested Level-2 WQSF flags: CLOUD, CLOUDAMBIGUOUS, CLOUDMARGIN, INVALID, COSMETIC, SATURATED, SUSPECT, HISOLZEN, HIGHGLINT, SNOWICE, ACFAIL, WHITECAPS, ANNOTABSOD, ANNOTMIXR1, ANNOTTAU06, RWNEGO2, RWNEGO3, RWNEGO4, RWNEGO5, RWNEGO6, RWNEGO7, RWNEGO8, OC4MeFAIL. Only measurements where the sensor zenith is lower than 60 and the sun zenith is lower than 70 are included. After applying this selective criteria, most of the remaining matchups are located in Santa Barbara Gulf in California. Thus, they are not representative of all kinds of waters, but they are very well distributed throughout seasons providing examples of different levels of chlorophyll-a concentration (green triangles in Figure 6).
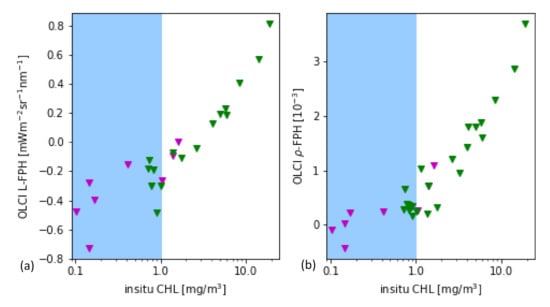
Figure 6.
(a) L-FPH and (b) -FPH from OLCI matchups over in-situ chlorophyll concentration from HPLC measurements from global measurements. The white background shows the proposed sensitivity range.
Figure 6 shows the retrieved -FPH and L-FPH from OLCI matchups over in-situ chlorophyll concentration from global measurements. As well as L-FPH, -FPH from OLCI matchups show a good correlation to global in-situ measured chlorophyll, when the chlorophyll concentration is higher than 1 mg/m. L-FPH obtains negative values for low chlorophyll concentration, which is most probably a negative offset due to atmospheric spectral influence. Because of the large scatter and negative values in FPH for a chlorophyll concentration roughly lower than 1 mg/m, we define the sensitivity range of the algorithm above this limit, shown in white in Figure 6.
3.2. FPH against OLCI Level-2 Chlorophyll
Additionally, L-FPH and -FPH are correlated to chlorophyll from the two standard operational Level-2 chlorophyll processors for OLCI, Neural Network (NN) and OC4me. In this section, we compare L-FPH and -FPH to chlorophyll retrieved from the Neural Network and OC4me processor by means of two example scenes with different water types. The NN chlorophyll is estimated through an Inverse Radiative Transfer Model-Neural Network approach. Here, the normalised water-leaving reflectance at OLCI bands and among others the log10 of the absorption coefficient of algal pigment is estimated, from which Chl NN is derived [44]. OC4Me is a Maximum Band Ratio semi-analytical algorithm, developed by Reference [43]. For the comparison, it is important to note that OC4Me is only appropriate in open ocean waters. Both measures are part of the operational OLCI Level-2 products.
The Barents Sea is a marginal sea of the Arctic Ocean, located off the northern coasts of Norway and Russia and is divided between Norwegian and Russian Exclusive Economic Zones. It is a rather shallow shelf sea, with an average depth of 230 m, and is an important site for both fishing and hydrocarbon exploration. Despite being part of the Arctic Ocean, the Barents Sea has been characterised as “turning into the Atlantic” because of its status as “the Arctic warming hot spot”. Hydrologic changes due to global warming have led to a reduction in sea ice and in stratification of the water column, which could lead to major changes in weather in Eurasia. Due to the North Atlantic drift, the Barents Sea has high biological production compared to other oceans of similar latitude. The spring bloom of phytoplankton can start quite early close to the ice edge, because the fresh water from the melting ice makes up a stable water layer on top of the sea water. Figure 7 shows the L-FPH in the Barents Sea on the 7 May 2018, with only the processors default flags (see Section 2) applied, clearly revealing nice swirling and filamentary patterns of ocean chlorophyll.
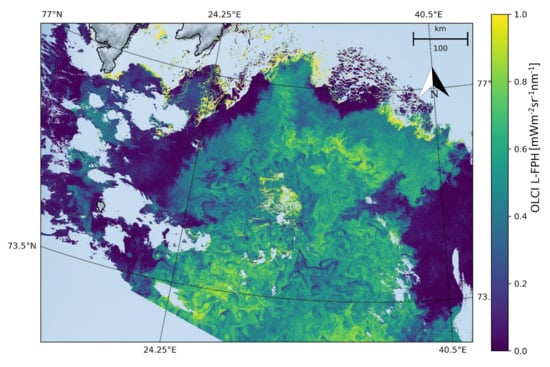
Figure 7.
L-FPH from OLCI on the 7 May 2018 in the Barents Sea.
The comparison of L-FPH and -FPH to chlorophyll from OC4Me and NN in the Barents Sea is shown in Figure 8. For this pixel-wise comparison the OLCI matchup protocol [47] is applied. There is a clear correlation between both fluorescence and chlorophyll concentration measures. For chlorophyll > 1 mg/m, the correlation becomes stronger in both cases
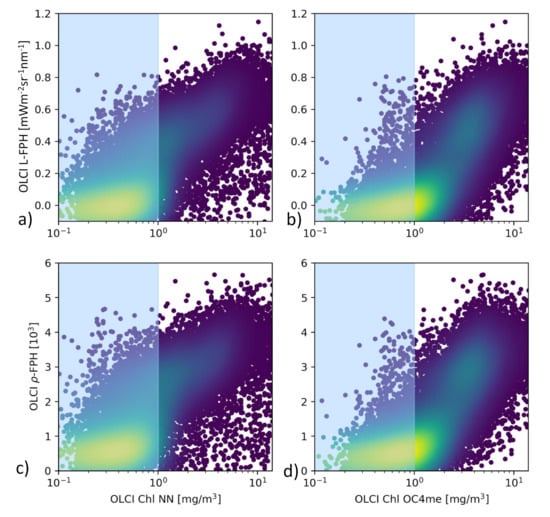
Figure 8.
(a) L-FPH against chlorophyll from NN and (b) against chlorophyll from OC4me, (c) -FPH against chlorophyll from NN and (d) against chlorophyll from OC4me in the Barents Sea, on the 7 May 2018.
As an example of extreme complex water, we examine the Rio de la Plata Estuary. The South Atlantic Ocean near the Rio de la Plata Estuary is a highly dynamic and complex region that encompasses both Case 1 and Case 2 water types. The head of the estuary is characterized by a well-developed turbidity front. High turbidity constrains photosynthesis. Immediately offshore of the turbidity front, water becomes less turbid and phytoplankton peaks [48].
Figure 9 shows the L-FPH retrieved in this region on the 26 November 2017. There is a strong gradient from the delta to the open ocean and the fluorescence peaks along a front, at the location of the reported turbidity front.
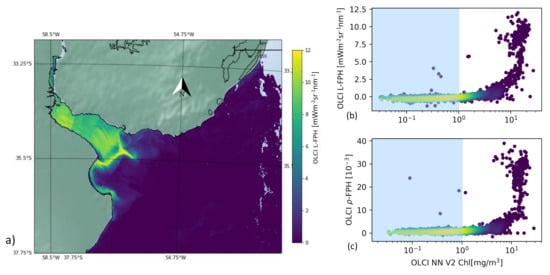
Figure 9.
(a) OLCI L-FPH, (b) OLCI L-FPH and (c) OLCI -FPH against chlorophyll from NN V2 on the 26 November 2017 in the Rio de la Plata Estuary.
For the pixel-wise comparison of FPH and chlorophyll in the Rio de la Plata delta, we apply the C2RCC alternate net processor (NN V2) [44,49], which has been amended by a set of additional neural networks that have been trained to cover extreme ranges of scattering and absorption. This scene is characterized by extremely high, but also very low values of chlorophyll. The concentration estimated by the C2RCC processor reaches from 0.02 mg/m in the open ocean to 25 mg/m in the estuary. We can see a clear correlation, which is flat for low and becoming steep for high chlorophyll values.
3.3. OLCI FPH against MODIS nFLH
Only in the comparison of L-FPH, -FPH and MODIS nFLH, are two fluorescence measures compared to each other. nFLH from MODIS is a well-established remote sensing product and independent of our OLCI FPH products in terms of instrumental issues as well as in terms of retrieval algorithm issues. The retrieval of MODIS nFLH is described in detail in Reference [13]. In the following, we show three examples of a matchup comparison between OLCI and MODIS along a wide range of latitudes. The results are collocated by projecting OLCI on MODIS pixels through nearest neighbour sampling. For this comparison, we follow the OLCI matchup protocol [47]. The quantitative comparison is shown in a scatter plot in Figure 10. Both, MODIS nFLH and OLCI L-FPH are based on the physical radiances (the MODIS one has undergone atmospheric correction), where the spectral peak around 682 nm is expected to originate from the ocean. Accordingly, both measures are expected to be very similar in absolute values. However, MODIS nFLH algorithm is based on the fully normalized water-leaving radiances, including BRDF correction, as described in Reference [50] and both our OLCI products still include BRDF effects (see Section 1). Also, MODIS nFLH characterizes the line-height of the measured spectrum at 678 nm and OLCI FPH characterizes a peak height of a peak centered at 682.5 nm, taking into account the overlaying absorption dip centered at 673.5 nm. Table 1 compares OLCI and MODIS spectral bands and properties that are used for the respective fluorescence products.
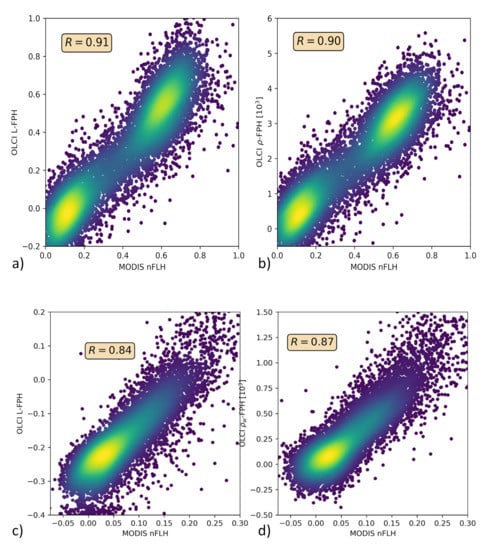
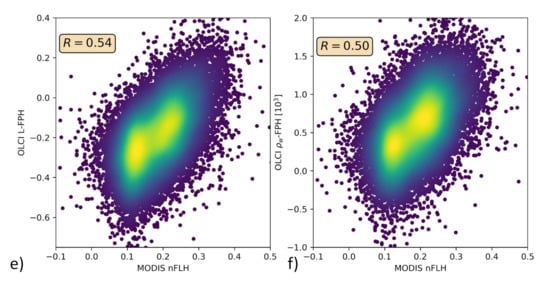
Figure 10.
(a,c,e) OLCI L-FPH against MODIS nFLH and (b,d,f) OLCI -FPH against MODIS nFLH, (a,b) in the Barents Sea, (c,d) the German Bight and (e,f) the Namibian coast.
The overall patterns of OLCI L-FPH and -FPH are so alike that the correlation coefficient to MODIS is in both cases nearly the same. Due to the physical units, absolute values of L-FPH are more comparable to MODIS, than the ones of -FPH, while the negative offset of -FPH is more comparable to MODIS, than the one from L-FPH. This is most likely due to the atmospheric correction, which is applied as well to MODIS as to OLCI . The correlation is very good for the Barents Sea and the German Bight example and less good for the Namibian coast, where the time gap of 4 h is probably too large.
3.4. FPH from Simulated Data
Finally, L-FPH and -FPH are compared to the input chlorophyll from RTM simulations. Radiative transfer simulations of synthetic L and spectra were performed for the development and evaluation of the OC-Fluo algorithm. As described before, the emitted fluorescence quantum in nature depends on many factors, like the quantum yield, the chlorophyll concentration, illumination, and so forth, which are not known, or at least not accurately known. A synthetic approach, like the one described here, is the only way to control all influences on the fluorescence signal. In the RTM, fluorescence is a strictly increasing function of the chlorophyll concentration. For the mathematical function to capture the fluorescence peak from OLCI spectrally convoluted reflectances, the retrieved FPH should be a strictly increasing function to input chlorophyll.
The simulations are performed using the vector version of MOMO [51,52]. In this model, a horizontal homogeneous atmosphere and ocean consisting of layers with vertically uniform optical properties are assumed. The upward and downward directed light field is calculated at all inter-layer boundaries and for all solar positions. The azimuthal dependence of the light field is internally expressed as Fourier series and reconstructed at equidistant distributed azimuth angles.
For this particular set of simulations, a water body was implemented with 20 layers, each 1 m thick, and assumed to have a homogeneous distribution of constituents (phytoplankton and CDOM) in each layer. A bio-optical model is applied, where chlorophyll concentration governs chlorophyll absorption, CDOM absorption and scattering by particles. The coupling between chlorophyll concentration and chlorophyll absorption represents an average behaviour of phytoplankton absorption with pigment packaging [53], and is again coupled to chlorophyll fluorescence with a quantum yield of 0.03. The chlorophyll-a extinction coefficient and the corresponding single scattering albedo control the amplitude and spectral signature of phytoplankton. A normalized chlorophyll-a absorption spectrum [35] is scaled at 440 nm in order to calculate the absorption spectrum () for different phytoplankton amounts [53]. The single scattering albedo at 440 nm is set to 0.68 to calculate spectral phytoplankton scattering () with
Phytoplankton scattering is constrained by a phase function measured by Petzold [54] which can be mathematically expressed with the Fournier-Forand function with a backscattering ratio of 0.01986. The simulated data cover a large range of chlorophyll concentrations (see Table 3), which are governed by the absorption coefficients at 440 nm from 0.04 m to 7 m. The simulations are performed in 1 nm resolution from 390 nm to 740 nm.

Table 3.
Input chlorophyll for the simulations.
Technically, the fluorescence is simulated in two subsequent model runs. In the first run, the energy that is absorbed by chlorophyll (photosynthetically active radiation, PAR) is calculated and in the second model run, this energy is multiplied by the quantum efficiency of 0.03 and implemented as a Gaussian shaped peak source, centered at 682.5 nm and half-width of 25 nm.
L is a direct model output, namely the upward radiance () at the uppermost atmospheric layer. The is not a direct model output, but is derived from up- and downward radiances (, ) and irradiances (, ) just above water surface:
where the water-leaving radiance is calculated from
and is from only the ocean surface. This is realised in the model, by implementing a very thin water body with a black surface below.
L and are convoluted using the spectral response functions of OLCI. is shown in Figure 11 in 1 nm resolution and in OLCI’s spectral resolution within the spectral domain of the OLCI bands Oa8 to Oa12. The MERIS band setting, which is a subset of OLCI’s bands, is included.
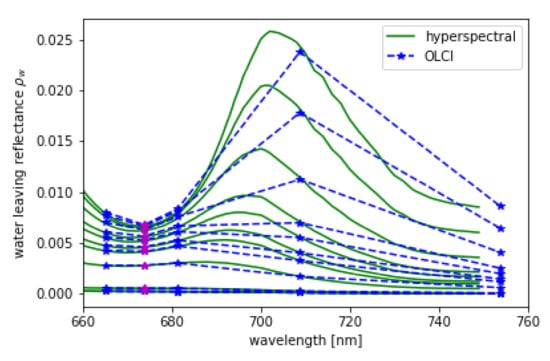
Figure 11.
Hyper-spectral (green) from RTM and its convolution to OLCI (blue) spectral resolution for = 48, = 34, = 90 and chlorophyll concentrations given in Table 3, while the lowest spectrum is the one with the lowest chlorophyll concentration. Band Oa09 from OLCI which is additional to MERIS bands is shown in magenta.
From the synthetic L and , L-FPH and -FPH are retrieved and compared to the input chlorophyll-a concentration. This is shown in Figure 12 for OLCI and MERIS band setting, while the MERIS results are produced by just excluding band Oa9 from the retrieval. Both band settings give an unambiguous and very similar relationship. Up to 40 mg/m chlorophyll, the difference is less than 4% and even for very high concentrations up to 140 mg/m, it does not exceed 10%. In order to investigate the reasons for the similarity of OLCI and MERIS results, we show a retrieval fit, which illustrates the extracted spectral components. The division into the spectral components is shown in Figure 13 for OLCI and for only MERIS bands applied to a -spectrum with low and with high chlorophyll. For low chlorophyll concentrations, the spectral model seems to reproduce the simulated spectrum perfectly well for both MERIS and OLCI band settings. For higher concentrations, the additional band Oa9 pulls the reproduced spectrum a bit down, which leads to a slightly lower FPH. The fact that the reproduced spectrum is slightly off the measured bands indicates that, for extremely high chlorophyll concentrations, the model could be adjusted to an even more spectrally complex behaviour.
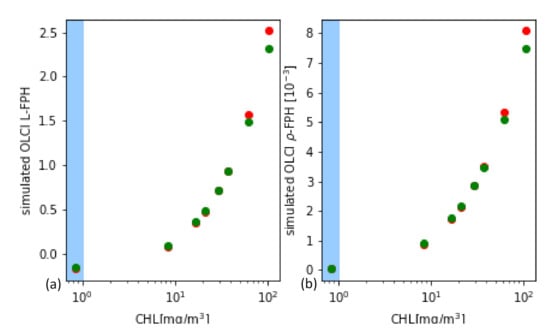
Figure 12.
(a) L-FPH and (b) -FPH retrieved from synthetic spectra over chlorophyll, which was input for the RTM for OLCI (green) and for MERIS (red) band setting.
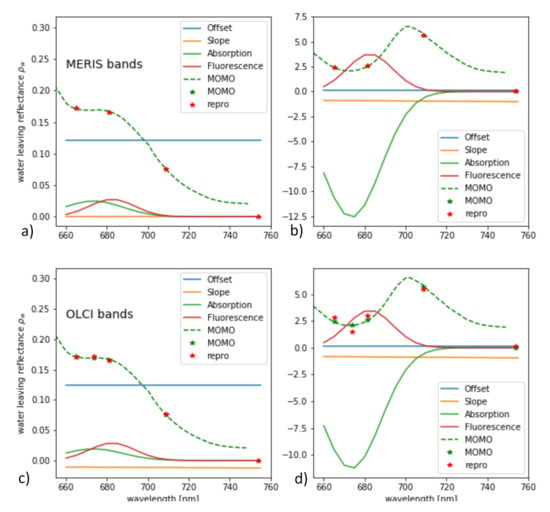
Figure 13.
Spectral components found by the retrieval of -FPH applied to a -spectrum with (a,c) low and (b,d) high chlorophyll for (a,b) MERIS and (c,d) OLCI band setting.
In order to test this with real measurements, we performed the retrieval of the Barents Sea scene (see Section 3.2) also without band Oa9. Figure 14 shows L-FPH retrieved from OLCI measurements over L-FPH retrieved from MERIS-like measurements and the same for -FPH. The correlation is very high and shows that the algorithm could be directly transferred to MERIS data.
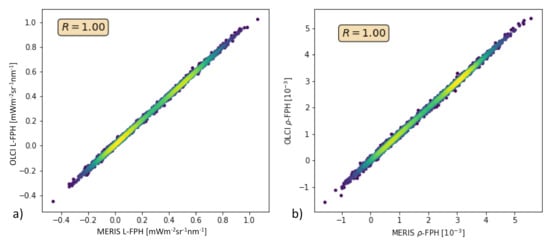
Figure 14.
(a) L-FPH retrieved from OLCI measurements over L-FPH retrieved from MERIS-like measurements, (b) -FPH retrieved from OLCI measurements over -FPH retrieved from MERIS-like measurements.
Finally, the results of the RTM exercise, which are shown in Figure 12 are overlaid with the results from the in-situ comparison in Section 3.1 (see Figure 15). Absolute values and slope of the FPH—chlorophyll comparison are very consistent.
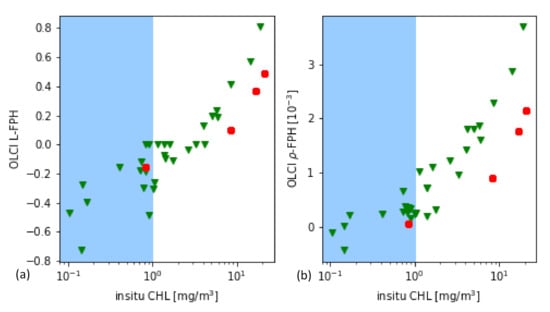
Figure 15.
(a) L-FPH and (b) -FPH retrieved from OLCI measurements and simulated spectra over chlorophyll.
4. Discussion
4.1. FPH against In-Situ Chlorophyll
The comparison of FPH to in-situ chlorophyll implies that the relation of fluorescence to chlorophyll concentration is non-linear, but both measures are in principle highly correlated, with a saturating fluorescence for high chlorophyll concentration values. Considering all factors, that have an additional impact on this relation, this result is very convincing for the FPH product. Certainly, the limited geographical extend of the contributing stations lowers the significance of this conclusion and calls for further quantitative global in-situ satellite matchup based comparisons.
4.2. FPH against OLCI Level-2 Chlorophyll
The implication regarding the relation of fluorescence to chlorophyll concentration, is confirmed by the comparison of FPH to OLCI Level-2 Chlorophyll. However, absolute values of L-FPH and -FPH do not correspond to quite the same absolute values of both measures of OLCI Level-2 Chlorophyll, as in the in-situ comparison, which is most probably due to BRDF effects. Even though the comparison includes only two scenes, this exercise, in addition to the comparison to in-situ chlorophyll, includes a high number of individual samples: 2 × 10 in the Barents Sea and 3 × 10 in the Rio de la Plata Delta. A global time series of this kind of comparison could give more confidence in the product and insight into biological factors influencing this relation.
4.3. OLCI FPH against MODIS nFLH
The comparison OLCI FPH against MODIS nFLH relates two fluorescence measures and shows a clear linear correlation, in spite of some inherent differences like a different footprint, different overpass time and the BRDF correction in case of MODIS. The linear correlation coefficient decreases with increasing time gap (see Table 4). This implies that OLCI FPH and MODIS nFLH measure a highly correlated quantity, and moreover, OLCI L-FPH and MODIS nFLH are also equal in Unit and absolute quantity. The next step should be a global matchup comparison on the basis of monthly means.

Table 4.
Overpass times and time gap for MODIS and OLCI matchups.
4.4. General L-FPH and -FPH from OLCI
The particular slopes of L-FPH and -FPH for all above mentioned studies are so similar that we can conclude that in those particular cases, there is no issue with atmospheric correction in the Level-2 product and in addition, we can extract the same signal from Level-1 without performing an atmospheric correction.
4.5. FPH from Simulated Data
The evaluation on the basis of RTM proves the plausibility and consistency of the approach. The observed relation of chlorophyll fluorescence and concentration can be reproduced through a coupling between chlorophyll concentration and chlorophyll absorption in the model, which represents an average behaviour of phytoplankton absorption with pigment packaging. This relation fits well to the FPH against the in-situ chlorophyll comparison. This implies that at least for our in-situ satellite evaluation, pigment packaging is the predominant process causing the non-linearity of the two measures. For future studies, RTM with independently varying packaging, scattering, CDOM absorption and the height of the chlorophyll layer, will help to differentiate the various effects on the retrieved FPH.
The application of the OC-Fluo algorithm to real and synthetic measurements with MERIS band setting implies a direct transferability of the algorithm to MERIS measurements. This could be proved with MERIS in-situ matchups in future.
The application of the algorithm to hyperspectral in situ data from inland waters could be of great value. We are expecting the L-FPH to be not as influenced by adjacency effects as rho-FPH and we have already observed, that L-FPH is able to retrieve sensible values closer to cloud edges compared to the standard chlorophyll algorithms.
The additional retrieved chlorophyll absorption at 673.5 nm (APD) is another parameter of high interest, since chlorophyll absorption is also a good proxy for phytoplankton biomass. This is valid for the maximum absorption in the green spectral range as well as for the weaker absorption peak in the red. The APD, which is evaluated in the red, is affected in the same way by the specific layering of the phytoplankton as the FPH. But it is not affected in the same way, or not as intensively by phytoplankton species, physiological state or photoinhibition. The combination of APD and FPH can give new insights into the biology, the layering and physiological states of phytoplankton. The algorithm as it is, assumes a fixed position of the fluorescence peak. However, in reality, this position can change with phytoplankton species and functional type. For hyper-spectral measurements, the retrieval may be extended to include more retrieval parameters, for example, .
5. Conclusions
We have presented an algorithm that derives the Fluorescence Peak Height (L-FPH and -FPH) from spectral radiance satellite data. The algorithm is based on a simple physical model of spectral absorption and emission in water. The algorithm is applicable to Level-1 data, and therefore, does not depend on atmospheric correction, which is often problematic above open ocean and even more in complex waters. The technical implementation allows for a very fast and stable retrieval.
An theoretical uncertainty estimation reveals uncertainties of 10% retrieval noise as a random error. The resulting L-FPH and -FPH might be biased up to 20% due to the uncertain position of the fluorescence peak. Trace gas absorption in the atmosphere, which will be corrected in future versions can cause a bias of −0.2 mWmsrnm in high latitudes up to 0.4 mWmsrnm L-FPH in the tropics.
The new fluorescence algorithm is applied to OLCI Level-1 and Level-2 data and evaluated by a comparison of the retrieved L-FPH and -FPH to chlorophyll concentration from various other sources. First, the comparison to in-situ HPLC measurements from a global OLCI matchup database gives a good correlation. Due to more scatter and estimated negative FPH values, we define a sensitivity threshold for the algorithm above a concentration of around 1 mg/m chlorophyll. Secondly, the direct comparison to other OLCI standard products like NN and OC4me chlorophyll shows an overall good correlation. Even in complex waters like the Rio de la Plata estuary, the correlation between the retrieved L-FPH and -FPH to chlorophyll from an NN version for complex waters [44,49] is good. The third part of the evaluation is based on the correlation to MODIS FLH evaluated by means of a matchup comparison in the Barents Sea, the Namibian coast and the German Bight, which gives a nearly linear correlation. The nearly identical slope in L-FPH and -FPH to chlorophyll in the presented examples suggests, on one hand, a working atmospheric correction for the Level-2 product, and on the other, the ability of the presented fluorescence algorithm to skip the step of atmospheric correction. A fourth part of the evaluation is based on RTM. Here, synthetic data is processed and the resulting L-FPH and -FPH are compared to the used chlorophyll concentration. The resulting relationship between FPH and chlorophyll from the RTM exercise and the in-situ matchup comparison are consistent. The algorithm is applicable to measurements of spectral radiance or reflectance with at least 4 bands in the range between 650 and 750 nm. From RTM we can conclude, that the band setting of OLCIs predecessor MERIS band setting is sufficient to be input to the presented algorithm. This is also tested with real measurements. The consistent application on MERIS data is of special interest in the scope of Ocean Colour (OC), which is recognised as an Essential Climate Variable (ECV) by the Global Climate Observing System (GCOS). With both, MERIS and OLCI observations, a global time series of nearly twenty years of FPH could be generated and analysed. The algorithm is implemented and available through SNAP [55] as the plugin “OLCI Fluorescence Processor”.
Author Contributions
Conceptualization, L.K., R.P. and J.F.; methodology, L.K. and R.P.; software, L.K. and R.P.; validation, L.K., R.P. and J.F.; formal analysis, L.K.; investigation, L.K., R.P. and J.F.; resources, L.K.; data curation, L.K. and R.P.; writing—original draft preparation, L.K.; writing—review and editing, L.K., R.P. and J.F.; visualization, L.K. and R.P.; supervision, L.K., R.P. and J.F.; project administration, L.K., R.P. and J.F.; funding acquisition, L.K., R.P. and J.F. All authors have read and agreed to the published version of the manuscript.
Funding
We thank the European Commission for founding from the Copernicus Programme in contract EUM/OPS-COPER/SOW/17/954797. We acknowledge support from the Open Access Publication Initiative of Freie Universität Berlin.
Acknowledgments
We acknowledge EUMETSAT for founding and especially Ewa Kwiatkowska for her substantial support. We thank David Siegel, Toby Westberry, Michael Behrenfeld, Emmanuel Boss, Lynne Talley, Curt Davis, Ajit Subramaniam, Antonio Mannino, Aimee Neeley and Javier Concha for their effort in collecting the data used in this investigation and for making them available for publication. We also thank the EC Copernicus Programme and EUMETSAT for establishing and maintaining the OCDB. We thank the reviewers for their constructive comments. We thank Bronwyn Cahill for extensive proofreading and editing.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Krause, G.H.; Weis, E. Chlorophyll Fluorescence and Photosynthesis: The Basics. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1991, 42, 313–349. [Google Scholar] [CrossRef]
- Donlon, C. Estec Sentinel-3 Mission Requirements Traceability Document (MRTD)—PDF; Technical Report; European Space Research and Technology Centre: Noordwijk, The Netherlands, 2011. [Google Scholar]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Odermatt, D.; Gitelson, A.; Brando, V.E.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef]
- Xing, X.G.; Zhao, D.Z.; Liu, Y.G.; Yang, J.H.; Xiu, P.; Wang, L. An overview of remote sensing of chlorophyll fluorescence. Ocean. Sci. J. 2007, 42, 49–59. [Google Scholar] [CrossRef]
- Neville, R.A.; Gower, J.F.R. Passive remote sensing of phytoplankton via chlorophyll α fluorescence. J. Geophys. Res. 2008, 82, 3487–3493. [Google Scholar] [CrossRef]
- Babin, M.; Morel, A.; Gentili, B. Remote sensing of sea surface Sun-induced chlorophyll fluorescence: Consequences of natural variations in the optical characteristics of phytoplankton and the quantum yield of chlorophyll a fluorescence. Int. J. Remote Sens. 1996, 17, 2417–2448. [Google Scholar] [CrossRef]
- Gower, J.; King, S. Use of satellite images of chlorophyll fluorescence to monitor the spring bloom in coastal waters. Int. J. Remote Sens. 2012, 33, 7469–7481. [Google Scholar] [CrossRef]
- Falkowski, P.; Kiefer, D.A. Chlorophyll-a fluorescence in phytoplankton: Relationship to photosynthesis and biomass. J. Plankton Res. 1985, 7, 715–731. [Google Scholar] [CrossRef]
- Mazeran, C.; Brockmann, C.B.; Ruddick, K.; Voss, K.; Zagolski, F. Requirements for Copernicus Ocean Colour Vicarious Calibration Infrastructure; Eumetsat: Darmstadt, Germany, 2017. [Google Scholar]
- Lin, H.; Kuzminov, F.I.; Park, J.; Lee, S.; Falkowski, P.G.; Gorbunov, M.Y. Phytoplankton. The fate of photons absorbed by phytoplankton in the global ocean. Science 2016, 351, 264–267. [Google Scholar] [CrossRef]
- Fischer, J.; Kronfeld, U. Sun-stimulated chlorophyll fluorescence 1: Influence of oceanic properties. Int. J. Remote Sens. 1990, 11, 2125–2147. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Westberry, T.K.; Boss, E.S.; O’Malley, R.T.; Siegel, D.A.; Wiggert, J.D.; Franz, B.A.; McClain, C.R.; Feldman, G.C.; Doney, S.C.; et al. Satellite-detected fluorescence reveals global physiology of ocean phytoplankton. Biogeosciences 2009, 6, 779–794. [Google Scholar] [CrossRef]
- Gower, J.F.R.; Borstad, G.A. On the potential of MODIS and MERIS for imaging chlorophyll fluorescence from space. Int. J. Remote Sens. 2004, 25, 1459–1464. [Google Scholar] [CrossRef]
- Gower, J.; King, S. Validation of chlorophyll fluorescence derived from MERIS on the west coast of Canada. Int. J. Remote Sens. 2007, 28, 625–635. [Google Scholar] [CrossRef]
- Hoge, F.E.; Lyon, P.E.; Swift, R.N.; Yungel, J.K.; Abbott, M.R.; Letelier, R.M.; Esaias, W.E. Validation of Terra-MODIS phytoplankton chlorophyll fluorescence line height I Initial airborne lidar results. Appl. Opt. 2003, 42, 2767. [Google Scholar] [CrossRef]
- Huot, Y.; Brown, C.A.; Cullen, J.J. New algorithms for MODIS sun-induced chlorophyll fluorescence and a comparison with present data products. Limnol. Oceanogr. Methods 2005, 3, 108–130. [Google Scholar] [CrossRef]
- Moreno-Madriñán, M.J.; Fischer, A.M. Performance of the MODIS FLH algorithm in estuarine waters: A multi-year (2003–2010) analysis from Tampa Bay, Florida (USA). Int. J. Remote Sens. 2013, 34, 6467–6483. [Google Scholar] [CrossRef]
- Carder, K.L.; Chen, F.R.; Lee, Z.; Hawes, S.K.; Cannizzaro, J.P. ATBD 19, Case 2 Chlorophyll a; Technical Report; University of South Florida, College of Marine Science: Tampa, FL, USA, 2003. [Google Scholar]
- Gons, H.; Auer, M.; Effler, S.W. MERIS satellite chlorophyll mapping of oligotrophic and eutrophic waters in the Laurentian Great Lakes. Remote Sens. Environ. 2008, 112, 4098–4106. [Google Scholar] [CrossRef]
- Letelier, R. An analysis of chlorophyll fluorescence algorithms for the moderate resolution imaging spectrometer (MODIS). Remote Sens. Environ. 1996, 58, 215–223. [Google Scholar] [CrossRef]
- Gower, J.F.R.; Doerffer, R.; Borstad, G.A. Interpretation of the 685nm peak in water-leaving radiance spectra in terms of fluorescence, absorption and scattering, and its observation by MERIS. Int. J. Remote Sens. 1999, 20, 1771–1786. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Jerome, J.H.; Bukata, R.P.; Letourneau, G. An assessment of MERIS algal products during an intense bloom in Lake of the Woods. J. Plankton Res. 2011, 33, 793–806. [Google Scholar] [CrossRef]
- Ioannou, I.; Zhou, J.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. New algorithm for MODIS chlorophyll fluorescence height retrieval: Performance and comparison with the current product. In Remote Sensing of the Ocean, Sea Ice, and Large Water Regions 2009; International Society for Optics and Photonics: Berlin, Germany, 2009; p. 747309. [Google Scholar] [CrossRef]
- Kiefer, D.A. Fluorescence properties of natural phytoplankton populations. Mar. Biol. 1973, 22, 263–269. [Google Scholar] [CrossRef]
- Hu, C.; Muller-Karger, F.E.; Taylor, C.J.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
- Wolanin, A.; Rozanov, V.; Dinter, T.; Noël, S.; Vountas, M.; Burrows, J.; Bracher, A. Global retrieval of marine and terrestrial chlorophyll fluorescence at its red peak using hyperspectral top of atmosphere radiance measurements: Feasibility study and first results. Remote Sens. Environ. 2015, 166, 243–261. [Google Scholar] [CrossRef]
- Erickson, Z.K.; Frankenberg, C.; Thompson, D.R.; Thompson, A.F.; Gierach, M. Remote Sensing of Chlorophyll Fluorescence in the Ocean Using Imaging Spectrometry: Toward a Vertical Profile of Fluorescence. Geophys. Res. Lett. 2019, 46, 1571–1579. [Google Scholar] [CrossRef]
- Köhler, P.; Behrenfeld, M.J.; Landgraf, J.; Joiner, J.; Magney, T.S.; Frankenberg, C. Global Retrievals of Solar-Induced Chlorophyll Fluorescence at Red Wavelengths with TROPOMI. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Ovidio, F.; Rijkeboer, M. Atmospheric correction of Sea WiFS imagery for turbid coastal and inland waters. Appl. Opt. 2000, 39, 897–912. [Google Scholar] [CrossRef]
- Mograne, M.; Jamet, C.; Loisel, H.; Vantrepotte, V.; Mériaux, X.; Cauvin, A. Evaluation of Five Atmospheric Correction Algorithms over French Optically-Complex Waters for the Sentinel-3A OLCI Ocean Color Sensor. Remote Sens. 2019, 11, 668. [Google Scholar] [CrossRef]
- Bourg, L.; Vincent, E.; Muguet, I. OLCI Level 2 Algorithm Theoretical Basis Document. Available online: https://sentinel.esa.int/documents/247904/349589/OLCI_L2_ATBD_Instrumental_Correction.pdf (accessed on 23 March 2020).
- Platt, U.; Perner, D. Measurements of Atmospheric Trace Gases by Long Path Differential UV/Visible Absorption Spectroscopy. Opt. Laser Remote Sens. 1983, 39, 97–105. [Google Scholar] [CrossRef]
- Fischer, J.; Preusker, R.; Lindstrot, R. Correction of the Impact of the Absorption of Atmospheric Gases—OLCI Level 2 Algorithm Theoretical Basis Document. Available online: https://sentinel.esa.int/documents/247904/349589/OLCI_L2_ATBD_Gaseous_Correction.pdf (accessed on 22 March 2020).
- Doerffer, R.; Schiller, H. The MERIS Case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Prieur, L.; Sathyendranath, S. An optical classification of coastal and oceanic waters based on the specific spectral absorption curves of phytoplankton pigments, dissolved organic matter, and other particulate materials. Limnol. Oceanogr. 1981, 26, 671–689. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar]
- Gordon, H.R. Diffuse reflectance of the ocean: The theory of its augmentation by chlorophyll a fluorescence at 685 nm. Appl. Opt. 1979, 18, 1161. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Qiu, Z.; Pang, H.; Liu, Y.; Chen, Y.; Jiang, L. Chlorophyll fluorescence extraction from water-leaving radiance of algae-containing water through polarization. J. Ocean. Univ. China 2017, 16, 1003–1008. [Google Scholar] [CrossRef]
- Pedrós, R.; Moya, I.; Goulas, Y.; Jacquemoud, S. Chlorophyll fluorescence emission spectrum inside a leaf. Photochem. Photobiol. Sci. 2008, 7, 498–502. [Google Scholar] [CrossRef] [PubMed]
- Vincent, E.; Muguet, I. Level 2 Algorithm Theoretical Basis Document Instrumental Corrections OLCI; Technical Report; ACRI-ST: Biot, France, 2010. [Google Scholar]
- Doppler, L.; Preusker, R.; Bennartz, R.; Fischer, J. K-bin and k-IR: K-distribution methods without correlation approximation for non-fixed instrument response function and extension to the thermal infrared-Applications to satellite remote sensing. J. Quant. Spectrosc. Radiat. Transf. 2014, 133, 382–395. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B.; Claustre, H.; Babin, M.; Bricaud, A.; Ras, J.; Tièche, F. Optical properties of the “clearest” natural waters. Limnol. Oceanogr. 2007, 52, 217–229. [Google Scholar] [CrossRef]
- Brockmann, C.; Doerffer, R.; Marco, P.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC Neural Network For Sentinel 2 and 3 for the Retrieval of Ocean. In Proceedings of the ‘Living Planet Symposium 2016’, Prague, Czech Republic, 9–13 May 2016; pp. 9–13. [Google Scholar]
- Werdell, P.J.; Bailey, S.; Fargion, G.; Pietras, C.; Knobelspiesse, K.; Feidman, G.; Mcclain, C. Unique data repository facilitates ocean color satellite validation. Eos 2003, 84, 2002–2004. [Google Scholar] [CrossRef]
- Eumetsat. Ocean Colour In-Situ Database; Eumetsat: Darmstadt, Germany, 2019. [Google Scholar]
- Eumetsat. Recommendations for Sentinel-3 OLCI Ocean Colour Product Validations in Comparison with In Situ Measurements—Matchup Protocols; Technical Report; Eumetsat: Darmstadt, Germany, 2019. [Google Scholar]
- Marcelo Acha, E.; Mianzan, H.; Guerrero, R.; Carreto, J.; Giberto, D.; Montoya, N.; Carignan, M. An overview of physical and ecological processes in the Rio de la Plata Estuary. Cont. Shelf Res. 2008, 28, 1579–1588. [Google Scholar] [CrossRef]
- Doerffer, R. MERIS Case 2 Water ATBD 4th Reproc Algorithm Theoretical Bases Document (ATBD) for L2 Processing of MERIS Data of Case 2 Waters, 4th Reprocessing; Technical Report; Brockmann Consult: Hamburg, Germany, 2015. [Google Scholar]
- Feldman, G.C. NASA’s OceanColor Web. Available online: http://step.esa.int (accessed on 12 May 2020).
- Fell, F.; Fischer, J. Numerical simulation of the light field in the atmosphere-ocean system using the matrix-operator method. J. Quant. Spectrosc. Radiat. Transf. 2001, 69, 351–388. [Google Scholar] [CrossRef]
- Hollstein, A.; Fischer, J. Radiative transfer solutions for coupled atmosphere ocean systems using the matrix operator technique. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 536–548. [Google Scholar] [CrossRef]
- Bricaud, A.; Babin, M.; Claustre, H.; Ras, J.; Tièche, F. Light absorption properties and absorption budget of Southeast Pacific waters. J. Geophys. Res. Ocean. 2010, 115, 1–19. [Google Scholar] [CrossRef]
- Petzold, T. Volume Scattering Functions for Selected Ocean Waters. Scripps Inst. Oceanogr. 1972, 72–78. [Google Scholar] [CrossRef]
- SNAP—ESA Sentinel Application Platform v7.0.3. Available online: http://step.esa.int (accessed on 6 August 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).