Next Article in Journal
How Does Peri-Urbanization Trigger Climate Change Vulnerabilities? An Investigation of the Dhaka Megacity in Bangladesh
Next Article in Special Issue
Comparison of Thermal Infrared-Derived Maps of Irrigated and Non-Irrigated Vegetation in Urban and Non-Urban Areas of Southern California
Previous Article in Journal
Radar Remote Sensing to Supplement Pipeline Surveillance Programs through Measurements of Surface Deformations and Identification of Geohazard Risks
Previous Article in Special Issue
Detection of Irrigated and Rainfed Crops in Temperate Areas Using Sentinel-1 and Sentinel-2 Time Series
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 23
10.3390/rs12233937
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Semantic Segmentation of Sentinel-2 Imagery for Mapping Irrigation Center Pivots

by
Lukas Graf
1,2,*,
Heike Bach
2 and
Dirk Tiede
1
1
Department of Geoinformatics—Z_GIS, University of Salzburg, 5020 Salzburg, Austria
2
Vista Remote Sensing in Geosciences GmbH, 80333 Munich, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(23), 3937; https://doi.org/10.3390/rs12233937
Submission received: 4 November 2020 / Revised: 23 November 2020 / Accepted: 30 November 2020 / Published: 1 December 2020
(This article belongs to the Special Issue Irrigation Mapping Using Satellite Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Estimating the number and size of irrigation center pivot systems (CPS) from remotely sensed data, using artificial intelligence (AI), is a potential information source for assessing agricultural water use. In this study, we identified two technical challenges in the neural-network-based classification: Firstly, an effective reduction of the feature space of the remote sensing data to shorten training times and increase classification accuracy is required. Secondly, the geographical transferability of the AI algorithms is a pressing issue if AI is to replace human mapping efforts one day. Therefore, we trained the semantic image segmentation algorithm U-NET on four spectral channels (U-NET SPECS) and the first three principal components (U-NET principal component analysis (PCA)) of ESA/Copernicus Sentinel-2 images on a study area in Texas, USA, and assessed the geographic transferability of the trained models to two other sites: the Duero basin, in Spain, and South Africa. U-NET SPECS outperformed U-NET PCA at all three study areas, with the highest f1-score at Texas (0.87, U-NET PCA: 0.83), and a value of 0.68 (U-NET PCA: 0.43) in South Africa. At the Duero, both models showed poor classification accuracy (f1-score U-NET PCA: 0.08; U-NET SPECS: 0.16) and segmentation quality, which was particularly evident in the incomplete representation of the center pivot geometries. In South Africa and at the Duero site, a high rate of false positive and false negative was observed, which made the model less useful, especially at the Duero test site. Thus, geographical invariance is not an inherent model property and seems to be mainly driven by the complexity of land-use pattern. We do not consider PCA a suited spectral dimensionality reduction measure in this. However, shorter training times and a more stable training process indicate promising prospects for reducing computational burdens. We therefore conclude that effective dimensionality reduction and geographic transferability are important prospects for further research towards the operational usage of deep learning algorithms, not only regarding the mapping of CPS.

Graphical Abstract

1. Introduction

Agriculture is the largest consumer of fresh water at the global scale. In 2008, Wisser et al. [1] reported that 70% of the surface and ground water resources were used for agricultural purposes. While this figure was confirmed in more recent studies [2,3] the number is set to increase further due to global population growth and an increasing demand for food and biomass [4,5]. At the same time, an intensified competition for the allocation of water resources due to anthropogenic climate change, increased water withdrawal from industry and urban consumers, and the uninterrupted growth of urban areas is projected [6]. Agricultural water demand is mainly driven by irrigation [5]. Here, we define irrigation as the temporary or continuous supply of water to crops. Such water supply can either compensate for fluctuations in precipitation and thus reduce inter-annual yield variations [7,8] or increase yields in arid areas where crop growth is hardly possible without irrigation [9]. Irrigation is therefore considered a central asset for closing yield gaps and expanding agricultural activities in space and time [10].
While there are manifold irrigation techniques, irrigation center pivot systems (CPSs) can be found in many parts of the world, including Northern America [11], Saudi-Arabia [12], South Africa [13], China [14], and Brazil [15,16]. In Europe, CPSs are mainly applied in Mediterranean countries, including Spain, France, and Italy [17]. CPSs are characterized by an overhead sprinkler mounted on a moveable arm that allows for irrigating crops in a circular pattern. Low costs of acquisition and maintenance, as well as the high degree of flexibility regarding sector-wise variable irrigation rates, have made CPSs particularly attractive [18,19]. The latter is also important regarding improved water-use efficiency by means of site-specific farming measures [20].
Due to their circular or circle-like shapes, CPSs can be mapped by using high-resolution optical remotely sensed imagery (spatial resolution smaller than or equal to 30 m). A prominent example is the so-called “Nebraska Centre-Pivot Inventory” [21], which covers more than 50,000 CPSs in the state of Nebraska, USA, in its latest version (2005). The CPSs were mapped by using Landsat-TM and aerial imagery by human experts. With the advent of freely available optical remotely sensed imagery (e.g., the Sentinel-2 mission by the European Space Agency) and advances in the power of graphic card processing units (GPUs), deep learning (DL) models have gained more attention for detecting and mapping CPSs in an automated and reasonable fast manner: Zhang et al. [22] applied three different convolutional neural networks (CNN) to Landsat-5 TM data covering 20,000 km2 in Colorado, USA, using the three TM channels in the visible part of the electro-magnetic spectrum. The authors reported successful detection of CPSs, with precision (i.e., compliance of class assignments for positive labels) of about 95.85% and recall (i.e., effectiveness of a classifier in identifying positive labels) of about 93.33%. Their approach, however, was restricted to the detection of CPSs and did not allow for mapping the exact size and shape of the CPS. This limitation was overcome by a more recent approach by Saraiva et al. [16], who used a semantic segmentation algorithm—namely U-NET—trained on high-resolution (3.0 to 3.7 m) planet imagery on a study area in Brazil. U-NET [23] is a state-of-the-art DL build upon the “fully convolutional network” proposed by Shelhamer et al. [24].U-NET has a down- and an upsampling branch of convolutional layers to preserve spatial context. In detail, the spatial (i.e., contextual) and spectral information is passed from the down- to the upsampling branch in the form of feature maps that describe the activation of the individual neural layers. Thus, the localization information can be passed on from input to output, and spatial relationships can be explicitly considered. For instance, using the three visible and the near-infrared bands, Saraiva et al. [16] archived a remarkable precision of 99% and a recall of 88% for center pivot segmentation, making U-NET a promising tool for mapping CPS.
While these studies highlight the potentials of DL-based approaches and particularly U-NET for mapping CPS, some open points remain: Firstly, given that U-NET shall one day replace human experts, it has to be capable to deal with contrasting geographic locations and provide constantly high segmentation and classification accuracy. Research on the geographic transferability of DL approaches, however, is still at its infancy. In a comprehensive review on deep learning methods in remote sensing, Zhu et al. [25] conclude that the transferability of models trained on geographically limited datasets to the global scale is an ongoing challenge. Since CPSs can be found in many parts of the world, the question arises as to how well a model trained on a single study area performs when transferred to geographically contrasting areas. Arguably, this aspect is crucial for the applicability of U-NET to wider areas and will be decisive when attempting to replace human experts. Secondly, most deep learning implementations in remote sensing only use a small amount of the available spectral information (see, e.g., References [26,27]). The visible bands of remotely sensed imagery obtained from sensors like Sentinel-2 MSI are spectrally highly correlated [28] and only provide limited information about vegetation characteristics but are often used in DL studies. Since the usage of a higher number of spectral bands would significantly increase computational requirements, we investigated the effects of using the wide-spread principal component analysis (PCA) approach for spectral dimensionality reduction [29], on U-NET CPS classification and segmentation accuracy.
Consequently, the objectives of this work were twofold: Firstly, we compared the classification and segmentation accuracy of U-NET trained on four spectral Sentinel-2 bands to U-NET trained on the first three principal components of Sentinel-2, using a CPS dataset from Northern Texas, USA. Secondly, we assessed how well these two models performed when transferred to geographically contrasting areas: South Africa and the Duero basin in Spain. Based on these objectives we aligned the structure of the paper. Following a description of the study areas and the CPS datasets, we explain the processing of the Sentinel-2 imagery and outline the training data generation and model training process in Section 2. In Section 3, we present the results of the semantic segmentation approach and compare the performance of the two U-NET implementations and assess their geographic transferability, which is discussed in Section 4.

2. Materials and Methods

2.1. Materials

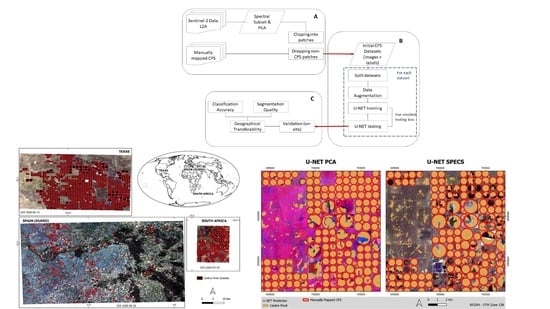
2.1.1. Study Areas

We chose three different study areas where CPSs can be found. In all study areas, CPSs represent a substantial part of the irrigated area. The areas differ in terms of climatic conditions, land-use systems, and natural vegetation, but, in each of the areas, water resources are either non-renewable or scarce, or will probably become in the future. The three areas and the mapped CPSs are shown in Figure 1, as well as their position on the world map.
The Texas study area (Figure 1A) encompasses 1714.54 km2 and is part of the High Plains region which is characterized by a climatic water deficit, i.e., potential evaporation exceeds actual evaporation [30]. Since the amount of rainfall (mainly during the summer months) would only allow for extensive dryland agriculture, the region experienced a rapid expansion of irrigated agricultural land that replaced the natural prairie grassland vegetation [31]. The water is mostly (>80%) withdrawn from the High Plains Aquifer for which a median relative decrease in recharge of −10% for 2050 relative to 1990 conditions is reported under climate change projections [32]. At the same time, the aquifer is subject to intensive depletion resulting in a decline in the saturated layer of the ground water table [33] and reduced water quality due to pollutants from intensive agricultural activities [34]. Mapping the extent of irrigated agriculture is particularly important to implement and monitor groundwater policies [35].
In the Spanish study area (Figure 1B) groundwater resources play less of a role, since the water is mostly taken from the Duero River: The Duero and its tributaries form the largest catchment on the Iberian Peninsula. Precipitation rates (1961–1990 reference period) are around 625 mm/yr on multi-annual average [36] which are mostly recorded during the winter months due to the Mediterranean climate. 70 to 75% of the available water resources in the Duero catchment are used for growing crops (mostly wheat and maize), with between 6476 and 7646 m3 of water per hectare and year needed for irrigation [37,38]. Around 45% of the entire study area (4129.57 km2) are permanently irrigated according to latest (2018) CORINE land-use/cover data. This is in line with findings by Lopez-Gunn et al. [39] who reported that up to 60% of the agricultural production in Spain is due to irrigation. CPSs account for parts of these numbers but are intertwined with other land-use patterns, such as roads, water courses, or smaller built-up areas which makes this area the most complex one. Since Ceballos et al. [40] observed an increase in the inter-annual variability of rainfall pattern and prolonged dry spells, the Duero region is at an increased risk of drought. Furthermore, drought risks are likely to increase under current climate change projections [41]. To respond to the risk of droughts and to ensure a minimum discharge in the river as required by the European Union Water Framework Directive (2000/60/EC) mapping the extent of irrigated agricultural is essential.
While droughts and water scarcity are considered future scenarios for the Texas and Duero study areas, the debate about water scarcity and “day-zero” scenarios for urban areas are an ongoing issue in South Africa [42] where the third study area is located (Figure 1, lower right). The area (270.55 km2) is characterized by a semi-arid climate causing evaporation to exceed precipitation rates [43]. Although water resources are scarce, the expansion of irrigated agriculture was favored by water policies to support the development of rural areas [44]. The aforementioned expansion of agricultural production, the growth of urban areas, and increased rainfall variabilities due to climate change will most likely intensify water shortages until 2050 and increase conflicts about the allocation of water resources [45]. Moreover, it is estimated that agriculture employs up to 70% of South Africa’s labor force [46], making it essential to safeguard agricultural production from a socio-economic perspective. The development of sustainable water use scenarios is therefore of great importance and requires accurate data.

2.1.2. Center Pivot Datasets

Using the available Sentinel-2 imagery (see Section 2.2.1.), human experts mapped the CPSs in the three study areas (see also Figure 1). In total, 2219 CPSs were mapped. Descriptive statistics denoting the main characteristics of the CPSs were calculated and are summarized in Table 1. Besides the area of the CPS, we calculated the Compactness Index (CI) [47] of the individual CPS’s geometries. The CI is defined as the ratio of the area of a geometry, A G , to the area, A C , of a circle with the same perimeter:
CI   =   A G / A C
The index takes values between 0 and 1, with values close to one indicating an almost perfect circularity of the geometry under consideration.
As Table 1 shows, most CPSs are in the Texas study area (1208), which is why it was selected for training the U-NET algorithm. The CPSs there are by far the largest (average size 541,675.9 m2), and most of them are perfectly circular (average CI is 0.99). The second largest number of CPSs is found in the Duero site (615), but they only occupy a small part of the rather large study area (124.4 of 4129.6 km2) and are spatially sparsely scattered (see Figure 1). The CPSs there are smallest on average (202,323.7 m2) and more often show non-perfect circularity, resulting in a mean CI of 0.91 and a standard deviation of CI of 0.12. This is three times higher than in the other two regions. In the South African test site, only 396 CPSs were mapped, since it is also the smallest site (270.6 km2), but their shape is comparable to the CPSs in Texas. Although they are, on average, smaller than the CPSs in Texas (314,949.2 m2), they have a similarly high CI (on average 0.98) and the same low standard deviation (0.04).

2.2. Methods

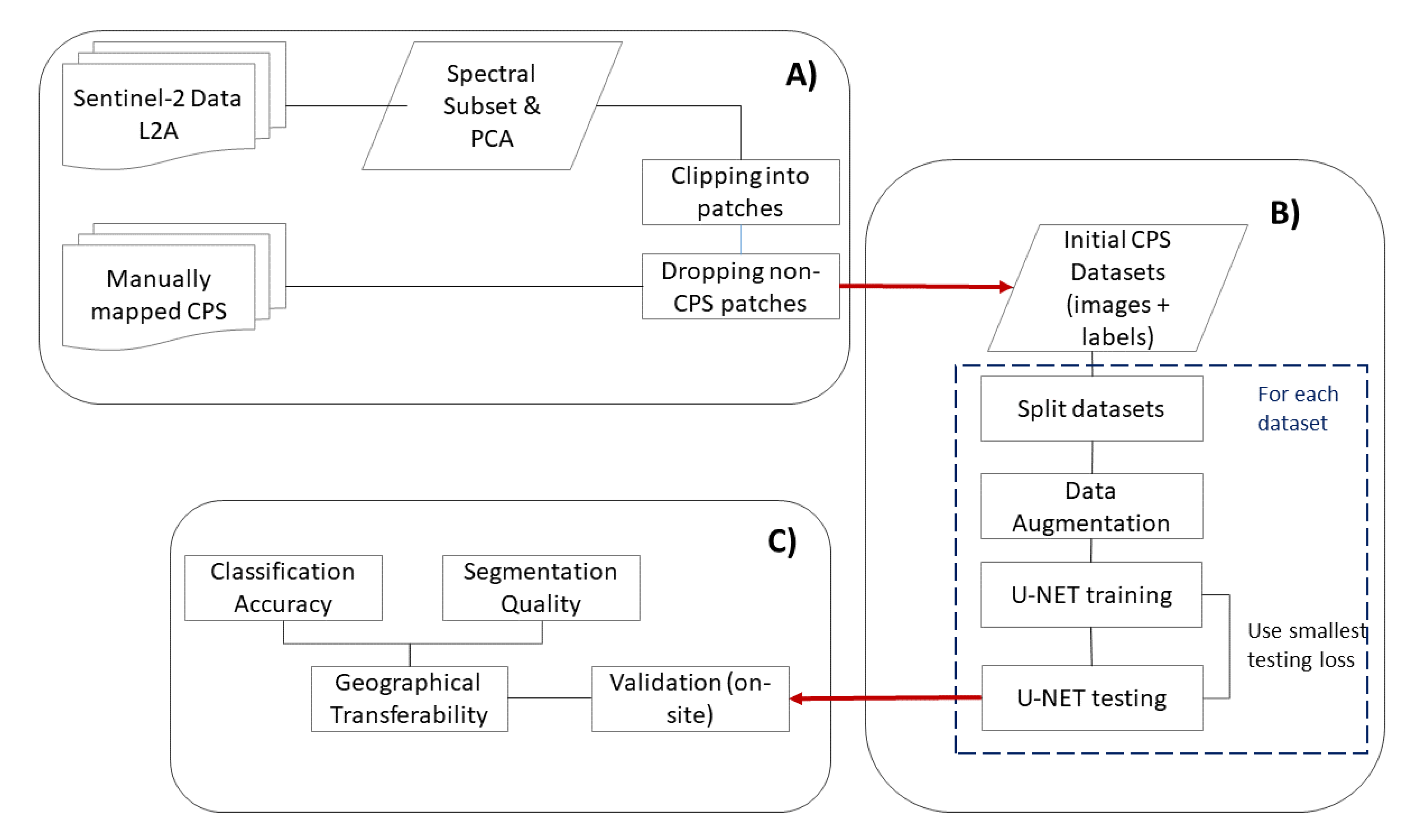
2.2.1. Sentinel-2 Data Preparation

We acquired three cloud-free (cloud cover < 5%) Sentinel-2 scenes in L1C processing level from Copernicus Open Access Hub (https://scihub.copernicus.eu/dhus/#/home) covering each of the three study areas (see Section 2.1.1). The Sentinel-2 mission comprises two identical satellites (Sentinel-2A and 2B), which are equipped with an optical multispectral sensor comprising 13 channels from visible (440 nm) to near infrared (2200 nm). The spatial resolution is 10, 20, or 60 m depending on the channel [48]. Due to the 180° offset orbits, the Sentinel-2 Mission provides an average of one image of a point on Earth every five days, making it very suitable for agricultural applications [49]. The L1C processing level implies that the data were already geometrically rectified and projected into a planar coordinate system, but does not yet contain bottom-of-atmosphere reflectance values, which are required for assessing crop growth conditions.
Table 2 shows the main properties of the scenes including the platform, Sentinel-2 granule, and the acquisition date. In case of the Spanish Duero site it was necessary to mosaic two Sentinel-2 granules (30TUM and 30TUL).
The Sentinel-2 scenes listed in Table 2 were converted to surface reflectance images (L2A processing level) using the atmospheric radiative transfer model MODTRAN [50] applying an interrogation technique developed by Verhoef and Bach [51]. Only the Sentinel-2 bands 2, 3, 4, 5, 6, 7, 8A, 11, and 12 were retained since these bands provide relevant information about land surface properties [52]. Band 8 was not used because of its coarser spectral resolution (compared to band 8A). The spatial resolution of all these spectral bands was resampled to 10 m. For each scene listed in Table 2, we created two datasets:
  • One dataset containing the Sentinel-2 spectral bands 2 (blue), 3 (green), 4 (red), and 5 (NIR1) in accordance to a study undertaken by Saraiva et al. [14], who also used this spectral combination;
  • One dataset containing the first three principal components calculated from the nine Sentinel-2 bands available.
The principal component analysis (PCA) [53] is a widely-used tool for dimensionality reduction [54,55,56]. Mathematically, PCA corresponds to a linear base transformation, whereby the original coordinate system spanned by the Sentinel-2 spectral bands is rotated towards the direction of the largest variance [57]. In detail, the original spectral bands which are partly linearly correlated are transformed into a set of orthogonal base vectors with the first base vector (first principal component) denoting the largest variance.

2.2.2. Training Data Generation

We used the Texas study area (see Figure 1 and Table 1) due to its large number of CPSs for the generation of two training datasets for U-NET as outlined in the previous paragraph. The workflow for generating the training data closely follows the approach proposed by Saraiva et al. [16] and is shown in Figure 2: First, we clipped the input imagery into patches of 128 by 128 pixels (1.28 by 1.28 km), using a moving window that was shifted 64 pixels in x and y direction to obtain overlapping image chips. The same procedure was applied to the rasterized representations of the CPS data (using 10 m spatial resolution) that served as labels. This allowed for enlarging the number of training samples and produced different representations of CPSs, to enhance the generalization capacity of the U-NET models. We retained only those image patches that had at least a single pixel corresponding to the manually mapped CPSs (Figure 2A). Second, we split the data into a training, testing, and validation dataset. Two-thirds of the study area were assigned as training area and all image patches located within this spatial subset were used for training U-NET. The testing area, covering one sixth of the entire study area, was selected to test the generalization performance of the U-NET network after each training epoch (see Section 2.2.3), whereas the samples located in the validation area were used to assess the classification accuracy and segmentation quality of the network after the training was finished.
In the case of the dataset consisting of the four spectral channels, the patches were normalized using z standardization. The z-standardization uses the mean reflection, µ, in band i   , and its standard deviation, σ, to obtain normalized reflectance values, Z i , with µ = 0 and σ = 1 from the original pixel values,   x i :
Z i =   x i − µ σ ,
We employed data augmentation to further increase the number of training samples available: All training samples were flipped vertically and horizontally, as well as rotated by 90, 180, and 270 degrees. Not only was the number of training samples increased by factor of six but also the rotation and flipping invariance was improved as networks based on convolution kernels by default are not invariant to flipping and rotation operations [58,59].
Overall, 10896 samples (Sentinel-2 patches plus labels) were available for training, 309 for testing and 472 for validation purposes from the Texas study area for each of the two datasets (Sentinel-2 bands 2 to 5 and first three principal components). We validated the two trained models on the Texas site, and then assessed the geographic transferability of the U-NET instances based on classification accuracy and segmentation quality (see Section 2.2.4 and Figure 2C). In South Africa, 51 samples, and in the Duero study area, 303 samples were available for performing these tasks.

2.2.3. U-NET Architecture and Training

A U-NET network was trained for both datasets, which for simplicity are referred to as U-NET SPECS for U-NET trained on the Sentinel 2 channels 2 to 5 and as U-NET PCA for U-NET trained on the first three principal components. The only difference in architecture between the two networks is the number of input channels, which is 4 (U-NET SPECS) and 3 (U-NET PCA). We implemented the network using a Tensorflow based version of the U-NET algorithm [60] coded in Python (Version 3.7).
The architecture used is summarized in Table 3 and builds upon the network architecture proposed by Ronneberger et al. [23] and the modifications made by Saraiva et al. [16]. U-NET has two branches: In the downsampling branch, as with almost all CNNs, convolution and max pooling operations are performed [61]. This branch—also called contracting path—records the spectral and spatial context in the form of feature maps. The upsampling path uses up-convolutions, which are combined with the feature maps from the contracting path. Pooling operators are replaced by upsampling functions. This allows the localization information to be carried along from input to output and retains the contextual information. However, only those pixels from input to output that have full spatial context are retained. This means that the segmentation map is always smaller than the input image.
For the down- and the upsampling branch of U-NET 4 layers per branch were used. In the contracting (downsampling) branch two subsequent convolutions with a 3-by-3 pixel kernel size were performed first in each layer. The kernel size of 3 was chosen as a compromise between sufficient filtering of data on the one hand and sufficient network depth on the other. The output of each convolution was passed on using the Rectified Linear Unit (ReLU) activation function, which is widely recognized for image processing tasks [62]. The output of the two convolutions was pooled in a second step, using the max pooling operator with a kernel size of 2 by 2 pixels and a stride of 2 pixels. In the upsampling branch, the pooling operations were replaced by up-convolution operators. In the last layer 1 by 1 convolution was used to map the network output to class assignment probabilities. The number of feature channels, which allow to preserve contextual information, was set to 32 (Table 3).
The network weights and biases were iteratively adjusted during the training using error backpropagation. The parameters used for training are shown in Table 4. In particular, we set the training and verification batch size to 32 and trained the network in total 150 times (epochs). In each epoch, 200 training iterations (steps) were conducted. A GPU optimized version of Tensorflow on an NVIDIA GEFORCE ® GT630 graphics card under Linux Ubuntu 18.04 LTS was used for the training. To calculate the network error for updating the network weights after each batch the cross-entropy loss (CE) cost function was used. CE, not only considers the class assignment but also the probability scores.
For the optimization problem of minimizing the value of cost function, the Adam (adaptive moment estimation) [63] solver was employed with an initial learning rate of 0.001. The learning rate is adapted for each network independently, using an exponential moving average of the gradient and its squared representation. To prevent overfitting, we used a dropout probability of 25%, which is the chance of randomly dropping (i.e., ignoring) network connections during training stages [64].
To determine the epoch after which the network generalized best, we calculated the value of the CE function on the testing dataset after each training epoch. We then used the network weights obtained at the epoch with the overall lowest testing data loss.

2.2.4. Validation Strategies

Since U-NET performs both segmentation and classification, accuracy metrics are required to evaluate the capacity of the trained model to reproduce reference data not shown to the network during training. While segmentation quality is qualitatively examined by visual inspection of U-NET results against CPS reference geometries, pixel-by-pixel classification accuracy is checked by using widely accepted metrics of binary classification evaluation. These are listed in Table 5 together with the formula behind them and the meaning of the metric.
In addition, the receiver operator characteristic (ROC) curve was used, which graphically represents the capability of a binary classifier using different discrimination probabilities for class assignment [67]. For drawing the curve, the true positive rate on the ordinate axis is compared to the false positive rate on the abscissa. The steeper the ROC curve rises (i.e., high true positive rate and low false positive rate for low discrimination thresholds), the better a classifier is. For quantifying the characteristics of the U-NET models, the integral of the area under the ROC curve—often referred to as “Area Under the Curve” (AUC) [68]—which is equal to one in case of a perfect classifier was provided as an additional measure. We selected these metrics because they are often used in the evaluation of binary classifiers [69,70] and give a quick overview of the predictive capacity of the classifier.

3. Results

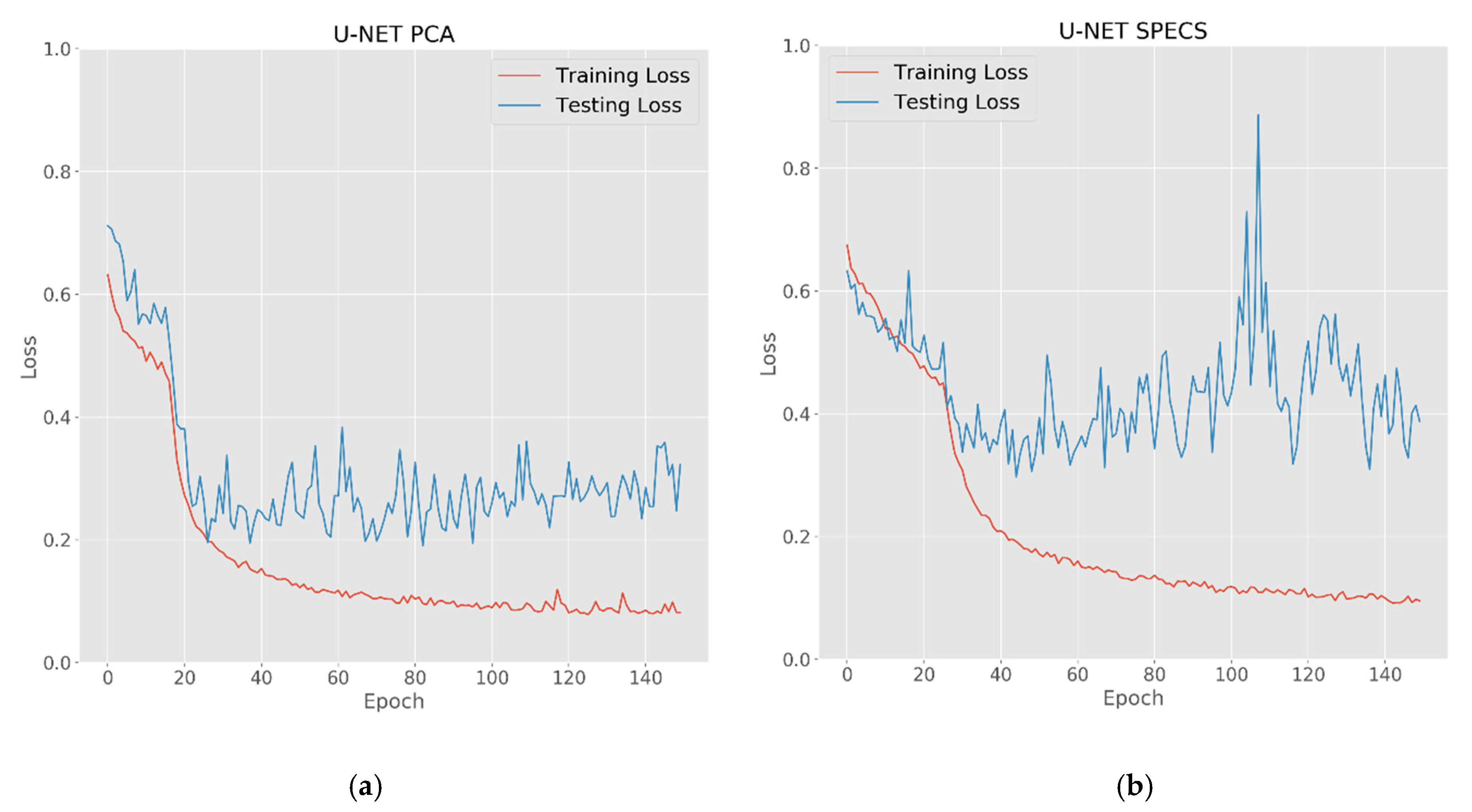
3.1. U-NET Training

The results of training the two models over a total of 150 epochs on the Texas study area are shown in Figure 3. The orange line represents the average training loss per epoch, and the blue line denotes the value of the CE cost function applied to the testing data after each epoch. U-NET PCA (Figure 3a) shows a clear convergence of training and testing loss values in the last two thirds of the training time. The testing loss fluctuates around 0.3, while the training loss approaches the 0.1 line. For U-NET SPECS (Figure 3b), a similar picture for the training loss, but the testing loss is significantly higher from epoch 50 onwards, and increases significantly at epoch 110. The training of U-NET-PCA took about 1779 min (1 d, 5 h, 39 min, and 30 s) and was therefore faster than U-NET-SPECS, which after 2052 min (1 d, 10 h, 12 min, and 36 s) had passed through all 150 epochs.
Based on the value of the training loss, the network weights for the final U-NET were determined. In the case of U-NET PCA, a global minimum training loss was reached after 83 epochs, so the network weights were used as they were after this epoch. In the case of U-NET SPECS, this minimum was reached after 45 epochs.

3.2. Pixel-Based Error Metrics

The pixel-based metrics (see Table 5) are listed in Table 6 for both U-NET models and all three study areas. The better performing model per study area is marked in green; red indicates worse performance. Orange cells highlight that both models achieve the same score. Both U-NET models showed the highest values for precision, recall, f1-score, and AUC in Texas, where the model training was conducted (see Section 3.1). The results of the other two study areas used for assessing the geographical transferability of the approach indicate a lower classification accuracy of the two models, with the Duero study area clearly revealing the lowest values in relation to the f1-score (0.08 for U-NET PCA and 0.16 for U-NET SPECS). The South African study area occupies a medium position, in relative terms. The transfer to other geographical areas thus shows a decrease in classification quality, but with differences between the models.
In detail, the predictions made by the U-NET models in Texas are of high precision for U-NET PCA (0.91) and U-NET SPECS (0.85). The recall for U-NET SPECS is also high, at 0.89, but lower for U-NET PCA (0.76). Accordingly, U-NET SPECS has the higher f1-score (0.87 to 0.83). The AUC value is also slightly higher for U-NET SPECS (0.88 to 0.84). The same applies to the accuracy score (0.88 to 0.83).
In the Duero Study area, U-NET SPECS also has a higher accuracy score than U-NET PCA (0.94 to 0.64, respectively). The precision score is very low for both models (U-NET PCA: 0.04, U-NET SPECS: 0.16). While the recall is also very low for U-NET SPECS (0.17), it is much higher for U-NET PCA (0.50). As a result, the f1-score is low for both models, and it is lowest with U-NET PCA at 0.08 (U-NET SPECS: 0.16). As the AUC value of 0.57 for both models indicates, the U-NET models performed only slightly better than a random classifier.
In the South African study area, where the overall model performance was higher than in the Duero area, but lower than in Texas, all metrics indicate a higher performance of U-NET SPECS. U-NET SPECS has the higher accuracy score (0.73 to 0.57), precision (0.77 to 0.58), recall (0.61 to 0.35), and consequently f1-score (0.68 to 0.43). The same applies to the AUC (0.72 to 0.56). The AUC value of 0.56 in the case of U-NET PCA also represents the lowest value among all three study areas.

3.3. Segmentation Results

In addition to the pixel-based metrics, the segmentation quality was determined by visual comparison with the CPS reference geometries. Segmentation quality refers to the capacity of the model to reproduce the manually mapped center pivot geometries. As with the quantitative evaluation of the classification quality (see Section 3.2.), the qualitative, visual examination of the results shows a decrease in the segmentation quality from Texas, over South Africa to the Duero region, where the results revealed an extremely low performance of both models.

3.3.1. Texas Study Area

Figure 4 displays the results of the semantic segmentation for the part of the Texas study area used for validation. The results from U-NET PCA are shown on the left side of Figure 4 and the results from U-NET SPECS on the right side. U-NET PCA reproduced the smaller CPSs, in particular, with high quality, and it had only occasional omissions. However, the larger CPSs, which are located central in the map, were only fragmentarily mapped by U-NET. In the western part of the area, which has no CPSs, some false positives can be found.
In case of U-NET SPECS, the misclassifications in the western area appear more spatially distributed, i.e., speckle-like and not organized into larger spatial clusters (Figure 4b). In addition, not all CPSs were reproduced in their circular form, and a few CPSs were not detected by the algorithm. The larger CPSs also reveal classification and segmentation problems (e.g., larger parts of the center pivots were not assigned to the center pivot class by the model), but at least individual segments of the circle were correctly recognized.

3.3.2. Duero Study Area

For a part of the Duero area, the results of the two models are shown in Figure 5, analogous to Figure 4. The poor segmentation quality of U-NET PCA is clearly visible in Figure 5a, which shows pixels assigned as CPSs in large, contiguous areas. This is especially the case in the northern part of the area, but not limited to it. Some of these areas correspond to CPSs in the reference, but the geometries resulting from the segmentation have little in common with the actual CPS geometries.
A completely different picture emerges from the results of U-NET SPECS (Figure 5b): The number of pixels classified as CPSs is significantly smaller than in U-NET PCA. The areas segmented are spatially more separated from each other, but often do not correspond to the actual CPS geometries. Only a very small part of the CPS (in the north-western part) was successfully segmented.

3.3.3. South Africa Study Area

Finally, the results for the South African study area can be found in Figure 6, where again, as in the Duero study area (Figure 5), U-NET PCA tends to misclassify large, connected areas. Only a small part of the reference CPS is reproduced with high segmentation quality; many CPSs remain undetected or are covered by only a few pixels, which take up a very small part of the actual area of the reference geometries (small intersection over union).
U-NET SPECS (Figure 6b) did not provide completely accurate segmentation and classification results, since neither all CPSs were found nor are all objects completely segmented. Nevertheless, many segments correspond to the reference geometries and the number of large-area misclassifications is lower and less dominant in visual inspection than with U-NET PCA (Figure 6a).

4. Discussion

4.1. Center Pivot Classification and Segmentation

In terms of classification accuracy (Table 6) and segmentation quality (Figure 4, Figure 5 and Figure 6), U-NET SPECS mostly outperformed U-NET PCA. The segmentation and classification accuracy obtained in Texas is comparable to the results achieved by Saraiva et al. [16] in Brazil when considering both models. Although the quality in South Africa is higher than in the Duero area, in both areas the two models do not reach the accuracy and quality as in Texas.
Both models have the same receptive field and neural architecture, so the differences can likely be explained by the spectral information used. U-NET SPECS uses only a relatively small portion of the spectral information actually available from Sentinel-2 (VIS and NIR), whereas the first three principal components in U-NET PCA have significantly reduced the Sentinel-2 spectral feature space. We suppose that the contextual information resulting from the principal components is less suitable than the original Sentinel-2 channels used in U-NET SPECS, to separate CPSs from other structures. The principal components likely tend to show spectral differences in local neighborhoods, which are less indicative of the presence of CPSs than, e.g., differences in cultivation practices (especially irrigation in all forms). Moreover, PCA might emphasize site-specific characteristics such as differences in soil type and plant physiology. The spectral feature space reduction performed may therefore have highlighted non-discriminatory differences that are of secondary importance for the segmentation of CPSs. We speculate that while feature space reduction by PCA has reduced spectral redundancies, it has not necessarily contributed to complexity reduction. From this we conclude that, in addition to the integration of spectral attributes, spatial information should be included in the feature space reduction to archive an effective complexity reduction to boost classification accuracy and segmentation quality. Mathematical concepts like the "core tensor" proposed by López et al. [71] could therefore be a promising approach for effective feature space and complexity reduction. Nevertheless, we argue that such reductions are necessary due to reduced computing times and the more stable training behavior of U-NET PCA compared to U-NET SPECS (see Figure 3). However, it should be noted that the experiments could not be repeated more often due to time constraints, so the results should be interpreted with caution.
It is noticeable that smaller CPSs are generally delimited with higher accuracy. Since local texture and neighborhood information within the receptive field are crucial for pixel-by-pixel classification, the information processing by U-NET differs from the approach of human experts, which might explain why smaller CPSs are easier to detect for U-NET. Human experts tend to orient themselves more towards the "Gestalt" principles [72] in the evaluation (i.e., perception) of visual information and use these concepts intuitively in the delimitation of objects [73]. Here, larger spatial relationships in the form of edges and color differences are more important than texture in relatively small foci. Human experts tend to perform object extraction rather than wall-to-wall classification, as is the case with U-NET. Since the receptive field of U-NET in this study is relatively small (128 by 128 pixels; i.e., 1.28 by 1.28 km) this may not be large enough to segment larger CPSs with sufficient quality. For smaller CPS, which are also less likely to show internal heterogeneities (e.g. due to sectoral differences in crop types or irrigation management), the limited neighborhood information seems to be sufficient. The importance of local texture and neighborhood can also explain why larger, contiguous areas are misclassified, as is the case with U-NET PCA, since edges and spatial arrangement of objects are less decisive.
This point coincides with an observation by Li et al. [74]: Using the example of land–sea classification tasks, the authors showed that U-NET had problems to capture complex connectivity patterns and produce coherent, accurate segmentation results. In particular, the authors found that the number of convolution layers was too low to capture the inherent complexity of land-sea arrangements. This could also be the case in the study presented here. However, to make the network deeper, the input patches have to become larger, since the current size of 128 to 128 pixels does not allow for more layers than the one currently in use. A recent study by Yang et al. [75] seems to confirm this finding, as a deeper network architecture and a larger receptive field outperformed conventional U-NET segmentation. A deeper network architecture, however, increases the training times significantly, since more free parameters have to be determined. Whether the additional effort results in a significant increase in segmentation quality and classification accuracy in the CPS is a prospect for further research.

4.2. Geographic Transferability

The best results in terms of classification accuracy and segmentation quality were achieved in Texas, which is to be expected since the models were trained in this region. At the Spanish Duero and the South African test site, the models showed very different results, with both models providing hardly any useful results in Spain. U-NET SPECS almost exclusively performed better than U-NET PCA (see Section 4.1). It follows that geographical transferability of the models is not an inherent characteristic. Partly, the lack of geographical invariance results from the properties of convolution networks, which are shift and conditionally scale invariant, but cannot deal a-priori with geometric distortions and illumination differences [58,76].
Since the CPSs in the three study areas are not homogeneous in terms of size and compactness (see Table 1), and differences in land-use and vegetation patterns exist, part of this lack of invariance can be explained by the characteristics of CNNs. In addition, only a single Sentinel-2 scene was used per study area (Table 2). Thus, multi-temporal parameters (such as median reflectance covering, e.g., two vegetation periods) as proposed by Saraiva et al. [16] were not used. This also results in different illumination geometries and bi-directional reflection properties of the surfaces [77] per study area. Further research could tie in at this point and use multi-temporal variables instead of mono-temporal Sentinel-2 images.
Furthermore, the CPS density differs in each area: In Texas, almost 38% of the study area is covered by CPS, and in South Africa, even 45%, whereas, in the Duero, it is only 3% of the area (see Table 1). This therefore increases the chance of false positives, especially in Spain. Spain also has the most complex patterns in terms of land-use types, as agricultural land is often intersected by roads and settlements. Furthermore, only a small part of the agricultural land on the Duero belongs to the CPS. In Texas and South Africa, in contrast, agriculture concentrates exclusively on the CPS, so that the other areas are largely non-arable land, which reduces the classification problem of CPSs to the recognition of the arable land.
Although the performance of the two models was lower in South Africa than in Texas, the results of U-NET SPECS in particular showed comparatively high classification accuracy (Table 6). This can be explained by the relatively similar structure of the CPS, their spatial arrangement and comparable land-use patterns. We therefore postulate a conditional geographical transferability of at least the U-NET SPECS model. The transferability is restricted to areas with similar natural features and land-use patterns. Operationally, we propose to express such similarity through global image metrics such as the Shannon Entropy [78]. The Shannon Entropy—originating from information theory—is a measure of the disorder of an image. The greater the degree of complexity, the higher the degree of disorder. In detail, both the Texas and the South-Africa study area have a low entropy (~1.92), whereas the Duero region revealed a much higher value (15.99). Further research efforts are necessary to test whether image entropy alone is an indicator of the geographical transferability of the models, and whether thresholds can be defined above which transferability is not given.
Of course, it would be possible to simply compensate for the missing invariances by extending the training dataset to all three study areas. However, this only shifts the problem of lacking geographical transferability, since, more or less, all areas with CPSs at the global level would then presumably have to be included, which in turn would mean a great deal of manual mapping effort. Since this is clearly contrary to the goal of keeping manual invention to a minimum, we propose to train a minimum number of networks, each applicable to specific, similar regions in terms of land-use pattern and CPS characteristics. These could be expressed by land-use clusters. For example, in this study, two clusters could be defined: (i) CPSs located in dry climates (Texas and South Africa) and (ii) CPSs located in semi-arid regions embedded into complex agricultural patterns (Duero). Thus, a separate network would have to be trained for Spain; the network from Texas, on the other hand, could also be used operationally in South Africa. By using the Shannon Entropy and comparing other geographical factors (e.g., vegetation patterns, crop types, and rotation, average field size, number of land uses) similarity between geographic regions could be expressed. The number of different networks required for global coverage would only have to be as large as the number of identified clusters. However, this clearly requires further research beyond the scope of this work.

5. Conclusions

We trained two U-NET models for semantic segmentation of CPSs in Texas and applied the two resulting networks to other geographic areas with CPSs: the Spanish Duero Basin and South Africa. We were able to show that the reduction of the spectral feature space by means of principal component analysis shortens computation time and stabilizes the training process, but does not increase the quality of classification and segmentation. We assume that effective dimensionality reduction should include spatial (i.e., contextual) properties, in addition to spectral attributes. Since algorithms such as U-NET are supposed to increasingly automate manual mapping, we investigated the generalizability of both U-NET models with respect to their geographical transferability. The results clearly showed that geographical invariance is not an inherent property of U-NET and the complexity of land-use patterns should not be neglected. At this point, we cannot make a proposal for a globally applicable model for segmenting CPS, but we have used the Shannon Entropy as an indication of the transferability of a model to other geographical regions. However, this clearly requires further research.
We assume that the difficulties and approaches for further research presented here are not only relevant for the mapping of CPSs from Sentinel-2 data, but also for many other applications of deep learning algorithms in remote sensing.

Author Contributions

Conceptualization, L.G., D.T., and H.B.; methodology, L.G., H.B., and D.T.; software, L.G.; validation, L.G.; formal analysis, L.G.; investigation, L.G.; resources, H.B.; data curation, L.G.; writing—original draft preparation, L.G.; writing—review and editing, H.B. and D.T.; visualization, L.G.; supervision, H.B. and D.T.; project administration, H.B.; funding acquisition, H.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by European Union’s Horizon 2020 research and innovation programme within the project “ExtremeEarth—From Copernicus Big Data to Extreme Earth Analytics”, grant number 825258.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wisser, D.; Frolking, S.; Douglas, E.M.; Fekete, B.M.; Vörösmarty, C.J.; Schumann, A.H. Global irrigation water demand: Variability and uncertainties arising from agricultural and climate data sets. Geophys. Res. Lett. 2008, 35, 35. [Google Scholar] [CrossRef] [Green Version]
  2. Hedley, C.; Knox, J.; Raine, S.; Smith, R. Water: Advanced irrigation technologies. In Encyclopedia of Agriculture and Food Systems; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
  3. Gilbert, N. Water under pressure: A UN analysis sets out global water-management concerns ahead of Earth Summit. Nature 2012, 483, 256–258. [Google Scholar] [CrossRef] [Green Version]
  4. De Fraiture, C.; Wichelns, D. Satisfying future water demands for agriculture. Agric. Water Manag. 2010, 97, 502–511. [Google Scholar] [CrossRef]
  5. Chaturvedi, V.; Hejazi, M.; Edmonds, J.; Clarke, L.; Kyle, P.; Davies, E.; Wise, M. Climate mitigation policy implications for global irrigation water demand. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 389–407. [Google Scholar] [CrossRef]
  6. Flörke, M.; Schneider, C.; McDonald, R.I. Water competition between cities and agriculture driven by climate change and urban growth. Nat. Sustain. 2018, 1, 51–58. [Google Scholar] [CrossRef]
  7. Geerts, S.; Raes, D. Deficit irrigation as an on-farm strategy to maximize crop water productivity in dry areas. Agric. Water Manag. 2009, 96, 1275–1284. [Google Scholar] [CrossRef] [Green Version]
  8. Oweis, T.; Pala, M.; Ryan, J. Stabilizing rainfed wheat yields with supplemental irrigation and nitrogen in a Mediterranean climate. Agron. J. 1998, 90, 672–681. [Google Scholar] [CrossRef]
  9. Kresović, B.; Tapanarova, A.; Tomić, Z.; Životić, L.; Vujović, D.; Sredojević, Z.; Gajić, B. Grain yield and water use efficiency of maize as influenced by different irrigation regimes through sprinkler irrigation under temperate climate. Agric. Water Manag. 2016, 169, 34–43. [Google Scholar] [CrossRef]
  10. Mueller, N.D.; Gerber, J.S.; Johnston, M.; Ray, D.K.; Ramankutty, N.; Foley, J.A. Closing yield gaps through nutrient and water management. Nature 2012, 490, 254–257. [Google Scholar] [CrossRef] [PubMed]
  11. McKnight, T.L. Center pivot irrigation in California. Geogr. Rev. 1983, 73, 1–14. [Google Scholar] [CrossRef]
  12. Abo-Ghobar, H.M. Losses from low-pressure center-pivot irrigation systems in a desert climate as affected by nozzle height. Agric. Water Manag. 1992, 21, 23–32. [Google Scholar] [CrossRef]
  13. Olivier, F.; Singels, A. Survey of Irrigation Scheduling Practices in the South African Sugar Industry; South African Sugar Technologists’ Association: Durban, South Africa, 2004; Volume 78, pp. 239–244. [Google Scholar]
  14. Li, J. Increasing crop productivity in an eco-friendly manner by improving sprinkler and micro-irrigation design and management: A review of 20 years’ research at the Iwhr, China. Irrig. Drain. 2018, 67, 97–112. [Google Scholar] [CrossRef]
  15. Lobo, M., Jr.; Lopes, C.; Silva, W.L.C. Sclerotinia rot losses in processing tomatoes grown under centre pivot irrigation in central Brazil. Plant Pathol. 2000, 49, 51–56. [Google Scholar] [CrossRef]
  16. Saraiva, M.; Protas, É.; Salgado, M.; Souza, C. Automatic mapping of center pivot irrigation systems from satellite images using deep learning. Remote Sens. 2020, 12, 558. [Google Scholar] [CrossRef] [Green Version]
  17. Monaghan, J.M.; Daccache, A.; Vickers, L.H.; Hess, T.M.; Weatherhead, E.K.; Grove, I.G.; Knox, J.W. More ‘crop per drop’: Constraints and opportunities for precision irrigation in European agriculture. J. Sci. Food Agric. 2013, 93, 977–980. [Google Scholar] [CrossRef] [PubMed]
  18. Evans, R.G.; Han, S.; Kroeger, M.; Schneider, S.M. Precision center pivot irrigation for efficient use of water and nitrogen. Precis. Agric. 1996, 75–84. [Google Scholar] [CrossRef]
  19. Montero, J.; Martínez, A.; Valiente, M.; Moreno, M.A.; Tarjuelo, J.M. Analysis of water application costs with a centre pivot system for irrigation of crops in Spain. Irrig. Sci. 2013, 31, 507–521. [Google Scholar] [CrossRef]
  20. Dukes, M.D.; Perry, C. Uniformity testing of variable-rate center pivot irrigation control systems. Precis. Agric. 2006, 7, 205. [Google Scholar] [CrossRef]
  21. Carlson, M.P. The Nebraska Center-Pivot Inventory: An example of operational satellite remote sensing on a long-term basis. Photogramm. Eng. Remote Sens. 1989, 55, 587–590. [Google Scholar]
  22. Zhang, C.; Yue, P.; Di, L.; Wu, Z. automatic identification of center pivot irrigation systems from landsat images using convolutional neural networks. Agriculture 2018, 8, 147. [Google Scholar] [CrossRef] [Green Version]
  23. Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional networks for biomedical image segmentation. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
  24. Shelhamer, E.; Long, J.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
  25. Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
  26. Ghosh, A.; Ehrlich, M.; Shah, S.; Davis, L.; Chellappa, R. Stacked U-Nets for ground material segmentation in remote sensing imagery. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 252–2524. [Google Scholar]
  27. Zhao, X.; Yuan, Y.; Song, M.; Ding, Y.; Lin, F.; Liang, D.; Zhang, D. Use of unmanned aerial vehicle imagery and deep learning unet to extract rice lodging. Sensors 2019, 19, 3859. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  28. Frampton, W.J.; Dash, J.; Watmough, G.; Milton, E.J. Evaluating the capabilities of Sentinel-2 for quantitative estimation of biophysical variables in vegetation. ISPRS J. Photogramm. Remote Sens. 2013, 82, 83–92. [Google Scholar] [CrossRef] [Green Version]
  29. Singh, A.; Harrison, A. Standardized principal components. Int. J. Remote Sens. 1985, 6, 883–896. [Google Scholar] [CrossRef]
  30. Stephenson, N. Actual evapotranspiration and deficit: Biologically meaningful correlates of vegetation distribution across spatial scales. J. Biogeogr. 1998, 25, 855–870. [Google Scholar] [CrossRef]
  31. Johnston, C.A. Agricultural expansion: Land use shell game in the U.S. Northern Plains. Landsc. Ecol. 2014, 29, 81–95. [Google Scholar] [CrossRef]
  32. Crosbie, R.S.; Scanlon, B.R.; Mpelasoka, F.S.; Reedy, R.C.; Gates, J.B.; Zhang, L. Potential climate change effects on groundwater recharge in the High Plains Aquifer, USA. Water Resour. Res. 2013, 49, 3936–3951. [Google Scholar] [CrossRef] [Green Version]
  33. Terrell, B.L.; Johnson, P.N.; Segarra, E. Ogallala aquifer depletion: Economic impact on the Texas high plains. Water Policy 2002, 4, 33–46. [Google Scholar] [CrossRef]
  34. Nativ, R.; Smith, D.A. Hydrogeology and geochemistry of the Ogallala aquifer, Southern High Plains. J. Hydrol. 1987, 91, 217–253. [Google Scholar] [CrossRef]
  35. Johnson, J.; Johnson, P.N.; Segarra, E.; Willis, D. Water conservation policy alternatives for the Ogallala Aquifer in Texas. Water Policy 2009, 11, 537–552. [Google Scholar] [CrossRef]
  36. Mayor, B.; López-Gunn, E.; Villarroya, F.I.; Montero, E. Application of a water–energy–food nexus framework for the Duero river basin in Spain. Water Int. 2015, 40, 791–808. [Google Scholar] [CrossRef]
  37. Segovia-Cardozo, D.A.; Rodriguez-Sinobas, L.; Zubelzu, S. Water use efficiency of corn among the irrigation districts across the Duero river basin (Spain): Estimation of local crop coefficients by satellite images. Agric. Water Manag. 2019, 212, 241–251. [Google Scholar] [CrossRef]
  38. Miguel, Á.D.; Kallache, M.; García-Calvo, E. The water footprint of agriculture in Duero river basin. Sustainability 2015, 7, 6759–6780. [Google Scholar] [CrossRef]
  39. Lopez-Gunn, E.; Zorrilla, P.; Prieto, F.; Llamas, M.R. Lost in translation? Water efficiency in Spanish agriculture. Agric. Water Manag. 2012, 108, 83–95. [Google Scholar] [CrossRef]
  40. Ceballos, A.; Martinez-Fernandez, J.; Luengo-Ugidos, M.A. Analysis of rainfall trends and dry periods on a pluviometric gradient representative of Mediterranean climate in the Duero Basin, Spain. J. Arid Environ. 2004, 58, 215–233. [Google Scholar] [CrossRef]
  41. Gil, M.; Garrido, A.; Gómez-Ramos, A. Economic analysis of drought risk: An application for irrigated agriculture in Spain. Agric. Water Manag. 2011, 98, 823–833. [Google Scholar] [CrossRef] [Green Version]
  42. Bischoff-Mattson, Z.; Maree, G.; Vogel, C.; Lynch, A.; Olivier, D.; Terblanche, D. Shape of a water crisis: Practitioner perspectives on urban water scarcity and ‘Day Zero’ in South Africa. Water Policy 2020, 22, 193–210. [Google Scholar] [CrossRef]
  43. Rusere, F.; Crespo, O.; Dicks, L.; Mkuhlani, S.; Francis, J.; Zhou, L. Enabling acceptance and use of ecological intensification options through engaging smallholder farmers in semi-arid rural Limpopo and Eastern Cape, South Africa. Agroecol. Sustain. Food Syst. 2020, 44, 696–725. [Google Scholar] [CrossRef]
  44. Perret, S.R. Water policies and smallholding irrigation schemes in South Africa: A history and new institutional challenges. Water Policy 2002, 4, 283–300. [Google Scholar] [CrossRef] [Green Version]
  45. Du Plessis, A. Water scarcity and other significant challenges for South Africa. In Freshwater Challenges of South Africa and its Upper Vaal River: Current State and Outlook; du Plessis, A., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 119–125. ISBN 978-3-319-49502-6. [Google Scholar]
  46. Elum, Z.A.; Modise, D.M.; Marr, A. Farmer’s perception of climate change and responsive strategies in three selected provinces of South Africa. Clim. Risk Manag. 2017, 16, 246–257. [Google Scholar] [CrossRef]
  47. MacEachren, A.M. Compactness of geographic shape: Comparison and evaluation of measures. Geogr. Ann. Ser. B Hum. Geogr. 1985, 67, 53–67. [Google Scholar] [CrossRef]
  48. Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
  49. Richter, K.; Hank, T.B.; Vuolo, F.; Mauser, W.; D’Urso, G. Optimal exploitation of the Sentinel-2 spectral capabilities for crop leaf area index mapping. Remote Sens. 2012, 4, 561–582. [Google Scholar] [CrossRef] [Green Version]
  50. Berk, A.; Anderson, G.P.; Bernstein, L.S.; Acharya, P.K.; Dothe, H.; Matthew, M.W.; Adler-Golden, S.M.; Chetwynd, J.H.; Richtsmeier, S.C.; Pukall, B.; et al. MODTRAN4 radiative transfer modeling for atmospheric correction. In Proceedings of the SPIE’s International Symposium on Optical Science, Engineering, and Instrumentation, Denver, CO, USA, 20 October 1999; Volume 3756, pp. 348–353. [Google Scholar] [CrossRef]
  51. Verhoef, W.; Bach, H. Simulation of hyperspectral and directional radiance images using coupled biophysical and atmospheric radiative transfer models. Remote Sens. Environ. 2003, 87, 23–41. [Google Scholar] [CrossRef]
  52. Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and-3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
  53. Pearson, K. Principal components analysis. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 6, 559. [Google Scholar] [CrossRef] [Green Version]
  54. Byrne, G.; Crapper, P.; Mayo, K. Monitoring land-cover change by principal component analysis of multitemporal Landsat data. Remote Sens. Environ. 1980, 10, 175–184. [Google Scholar] [CrossRef]
  55. Cablk, M.; Minor, T. Detecting and discriminating impervious cover with high-resolution IKONOS data using principal component analysis and morphological operators. Int. J. Remote Sens. 2003, 24, 4627–4645. [Google Scholar] [CrossRef]
  56. Celik, T. Unsupervised change detection in satellite images using principal component analysis and k-means clustering. IEEE Geosci. Remote Sens. Lett. 2009, 6, 772–776. [Google Scholar] [CrossRef]
  57. Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417. [Google Scholar] [CrossRef]
  58. Xu, Y.; Xiao, T.; Zhang, J.; Yang, K.; Zhang, Z. Scale-invariant convolutional neural networks. arXiv 2014, arXiv:1411.6369. [Google Scholar]
  59. Marcos, D.; Volpi, M.; Tuia, D. Learning rotation invariant convolutional filters for texture classification. In Proceedings of the 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2012–2017. [Google Scholar]
  60. Akeret, J.; Chang, C.; Lucchi, A.; Refregier, A. Radio frequency interference mitigation using deep convolutional neural networks. Astron. Comput. 2017, 18, 35–39. [Google Scholar] [CrossRef] [Green Version]
  61. LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef] [Green Version]
  62. Dahl, G.E.; Sainath, T.N.; Hinton, G.E. Improving deep neural networks for LVCSR using rectified linear units and dropout. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8609–8613. [Google Scholar]
  63. Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
  64. Wu, H.; Gu, X. Towards dropout training for convolutional neural networks. Neural Netw. 2015, 71, 1–10. [Google Scholar] [CrossRef] [Green Version]
  65. Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
  66. Kohl, M. Performance measures in binary classification. Int. J. Stat. Med. Res. 2012, 1, 79–81. [Google Scholar] [CrossRef]
  67. Decker, L.R.; Pollack, I. Confidence ratings, message-reception, and the receiver operator characteristic. J. Acoust. Soc Am. 1957, 29, 1263. [Google Scholar] [CrossRef]
  68. Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [Green Version]
  69. Hossin, M.; Sulaiman, M. A review on evaluation metrics for data classification evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1. [Google Scholar]
  70. Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2020. [Google Scholar] [CrossRef]
  71. López, J.; Torres, D.; Santos, S.; Atzberger, C. Spectral imagery tensor decomposition for semantic segmentation of remote sensing data through fully convolutional networks. Remote Sens. 2020, 12, 517. [Google Scholar] [CrossRef] [Green Version]
  72. Wertheimer, M. A brief introduction to gestalt, identifying key theories and principles. Psychol. Forsch. 1923, 4, 301–350. [Google Scholar] [CrossRef]
  73. Lang, S. Object-based image analysis for remote sensing applications: Modeling reality—Dealing with complexity. In Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Blaschke, T., Lang, S., Hay, G.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–27. ISBN 978-3-540-77058-9. [Google Scholar]
  74. Li, R.; Liu, W.; Yang, L.; Sun, S.; Hu, W.; Zhang, F.; Li, W. Deepunet: A deep fully convolutional network for pixel-level sea-land segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3954–3962. [Google Scholar] [CrossRef] [Green Version]
  75. Yang, T.; Jiang, S.; Hong, Z.; Zhang, Y.; Han, Y.; Zhou, R.; Wang, J.; Yang, S.; Tong, X.; Kuc, T. Sea-land segmentation using deep learning techniques for landsat-8 OLI imagery. Mar. Geod. 2020, 43, 105–133. [Google Scholar] [CrossRef]
  76. Long, Y.; Gong, Y.; Xiao, Z.; Liu, Q. Accurate object localization in remote sensing images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2486–2498. [Google Scholar] [CrossRef]
  77. Liang, S.; Strahler, A.H. Retrieval of surface BRDF from multiangle remotely sensed data. Remote Sens. Environ. 1994, 50, 18–30. [Google Scholar] [CrossRef]
  78. Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 12 03937 g001 550
Figure 1. Maps showing the three selected study areas ((A) Texas, (B) the Spanish Duero Basin, and (C) South Africa) and their geographic location on the globe (D). For each study area, the manually mapped center pivot systems (CPSs) are displayed in red, and the corresponding Sentinel-2 scene used for U-NET semantic segmentation is shown as an RGB true-color composite. Coordinates are projected in WGS-84.
Figure 1. Maps showing the three selected study areas ((A) Texas, (B) the Spanish Duero Basin, and (C) South Africa) and their geographic location on the globe (D). For each study area, the manually mapped center pivot systems (CPSs) are displayed in red, and the corresponding Sentinel-2 scene used for U-NET semantic segmentation is shown as an RGB true-color composite. Coordinates are projected in WGS-84.
Remotesensing 12 03937 g001
Remotesensing 12 03937 g002 550
Figure 2. Workflow used for setting up, training and validation of the two U-NET models (SPECS and principal component analysis (PCA)). In (A), the Sentinel-2 data preprocessing is shown, whereas (B) accounts for the generation of training data and the model training process. The best performing model in terms of smallest testing loss is used to assess the geographic transferability in terms of classification accuracy and segmentation quality (C) for each of the two U-NET instances.
Figure 2. Workflow used for setting up, training and validation of the two U-NET models (SPECS and principal component analysis (PCA)). In (A), the Sentinel-2 data preprocessing is shown, whereas (B) accounts for the generation of training data and the model training process. The best performing model in terms of smallest testing loss is used to assess the geographic transferability in terms of classification accuracy and segmentation quality (C) for each of the two U-NET instances.
Remotesensing 12 03937 g002
Remotesensing 12 03937 g003 550
Figure 3. U-NET training (orange) and testing (blue) loss per epoch for both U-NET configurations, showing U-NET PCA (a) and U-NET SPECS (b).
Figure 3. U-NET training (orange) and testing (blue) loss per epoch for both U-NET configurations, showing U-NET PCA (a) and U-NET SPECS (b).
Remotesensing 12 03937 g003
Remotesensing 12 03937 g004 550
Figure 4. Semantic segmentation results (orange) of U-NET PCA (a) and U-NET SPECS (b) for the validation area part of the Texas site. The manually mapped CPSs are displayed in red. In addition, the first three principal components are shown for U-NET PCA and the Sentinel-2 bands 2, 3, and 4 for U-NET SPECS in the background.
Figure 4. Semantic segmentation results (orange) of U-NET PCA (a) and U-NET SPECS (b) for the validation area part of the Texas site. The manually mapped CPSs are displayed in red. In addition, the first three principal components are shown for U-NET PCA and the Sentinel-2 bands 2, 3, and 4 for U-NET SPECS in the background.
Remotesensing 12 03937 g004
Remotesensing 12 03937 g005 550
Figure 5. Semantic segmentation results (orange) of U-NET PCA (a) and U-NET SPECS (b) for the Duero study area. The manually mapped CPSs are displayed in red. In addition, the first three principal components are shown for U-NET PCA and the Sentinel-2 bands 2, 3, and 4 for U-NET SPECS in the background.
Figure 5. Semantic segmentation results (orange) of U-NET PCA (a) and U-NET SPECS (b) for the Duero study area. The manually mapped CPSs are displayed in red. In addition, the first three principal components are shown for U-NET PCA and the Sentinel-2 bands 2, 3, and 4 for U-NET SPECS in the background.
Remotesensing 12 03937 g005
Remotesensing 12 03937 g006 550
Figure 6. Semantic segmentation results (orange) of U-NET PCA (a) and U-NET SPECS (b) for the South African study area. The manually mapped CPSs are displayed in red. In addition, the first three principal components are shown for U-NET PCA and the Sentinel-2 bands 2, 3, and 4 for U-NET SPECS in the background.
Figure 6. Semantic segmentation results (orange) of U-NET PCA (a) and U-NET SPECS (b) for the South African study area. The manually mapped CPSs are displayed in red. In addition, the first three principal components are shown for U-NET PCA and the Sentinel-2 bands 2, 3, and 4 for U-NET SPECS in the background.
Remotesensing 12 03937 g006
Table
Table 1. Descriptive statistics of CPSs found in the three study areas, including the number of CPS; their total area and size; and their Compactness Index (CI) distributions in terms of average, minimum, maximum, and standard deviation (SD) of size and CI values found for the single CPS.
Table 1. Descriptive statistics of CPSs found in the three study areas, including the number of CPS; their total area and size; and their Compactness Index (CI) distributions in terms of average, minimum, maximum, and standard deviation (SD) of size and CI values found for the single CPS.
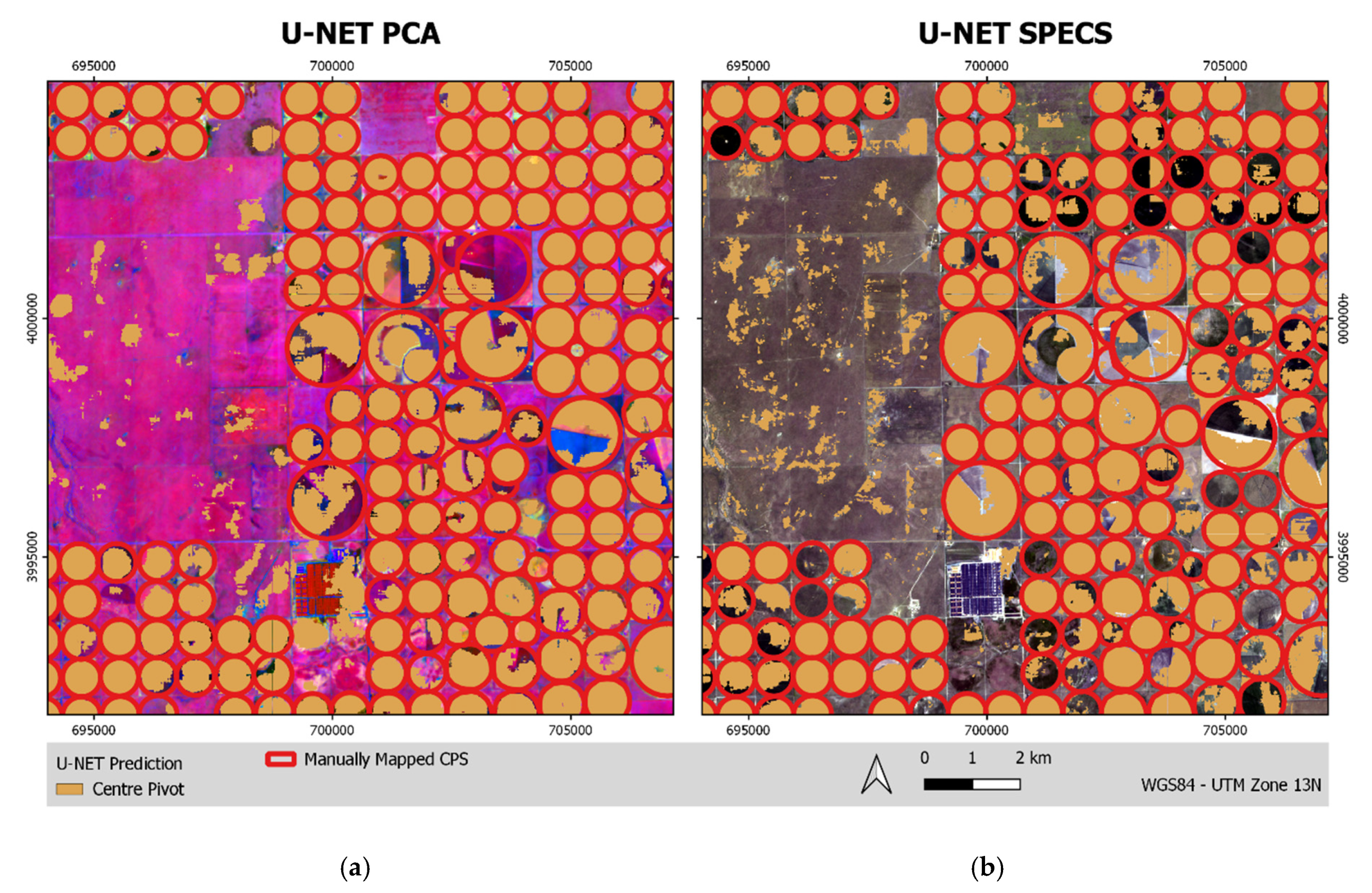
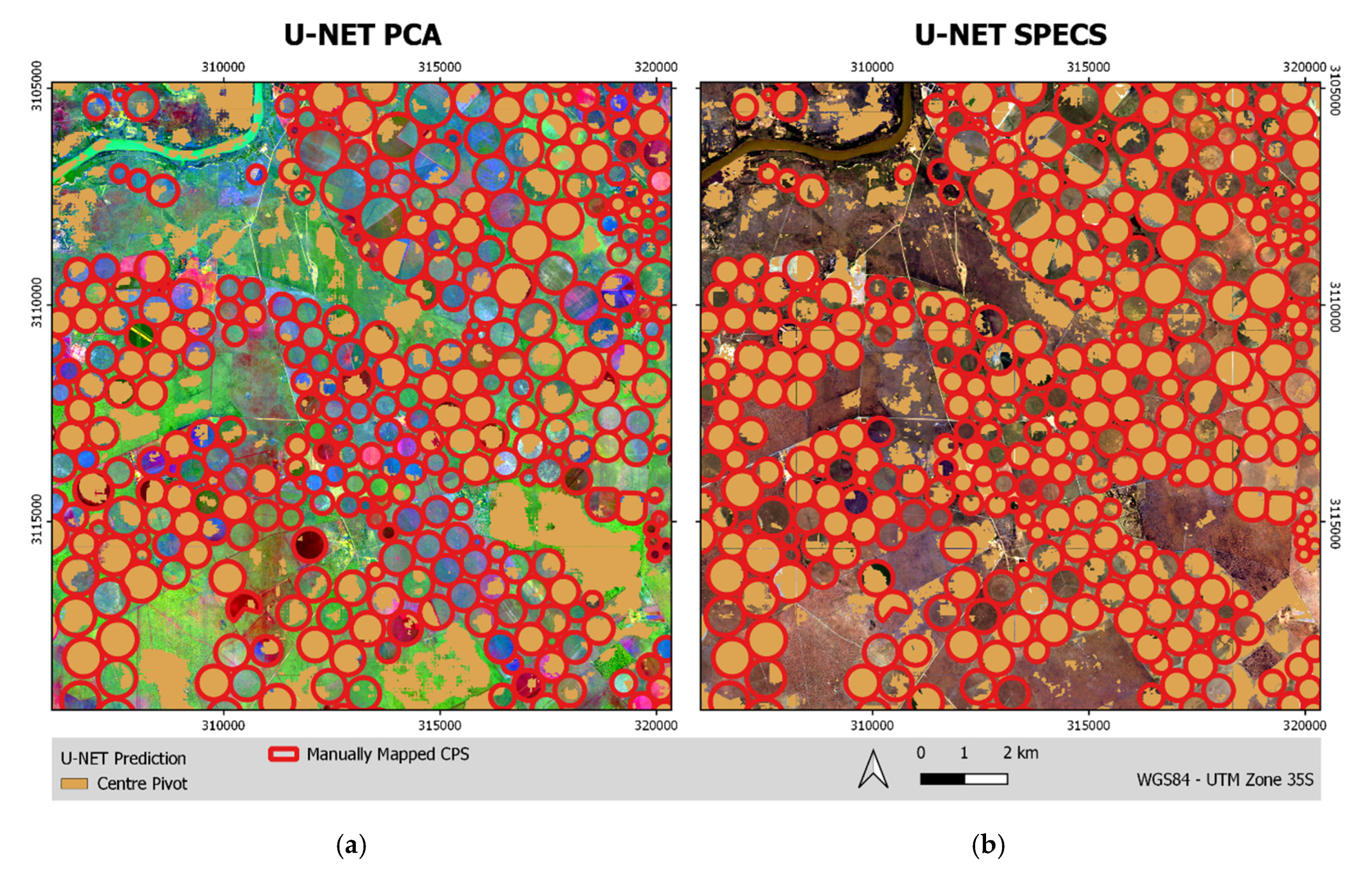
ParameterTexasDuero (Spain)South Africa
Number of CPS1208615396
Study Area Size (km2)1714.54129.6270.6
CPS Total Area (km2)648.9124.4122.2
Average CPS Size (m2)541,675.9202,323.7314,949.2
Minimum CPS Size (m2)71,842.119,110.224,612.6
Maximum CPS Size (m2)2,048,315.61,268,512.11,013,469.7
SD CPS Size (m2)275,031.5141,025.2186,157.8
Average CI (-)0.990.910.98
Minimum CI (-)0.600.590.64
Maximum CI (-)1.001.001.00
SD CI (-)0.040.120.04
Table
Table 2. List of Sentinel-2 scenes used in this study. For each entry, the platform (Sentinel-2A or Sentinel-2B), granule, and the sensing time are shown. In case of the Duero site, it was necessary to mosaic two Sentinel-2 granules.
Table 2. List of Sentinel-2 scenes used in this study. For each entry, the platform (Sentinel-2A or Sentinel-2B), granule, and the sensing time are shown. In case of the Duero site, it was necessary to mosaic two Sentinel-2 granules.
Test SitePlatformGranule(s)Acquisition Date
TexasSentinel-2B13SFA15 June 2018
Duero (Spain)Sentinel-2A30TUM, 30TUL26 June 2018
South AfricaSentinel-2A35JLJ10 March 2020
Table
Table 3. U-NET architecture used in this study for U-NET SPECS and U-NET PCA.
Table 3. U-NET architecture used in this study for U-NET SPECS and U-NET PCA.
ParameterValue
Input patch size (pixels)128 by 128
Output prediction size (pixels)36 by 36
Number of input channels (-)3, 4 *
Number of feature channels (-)32
Convolution filter size (pixels)3 by 3
Pool size (pixels)2 by 2
Layers per branch (-)4
Activation functionReLU
* 3 channels for U-NET PCA, 4 channels for U-NET SPECS.
Table
Table 4. Hyper-parameters used for training the two U-NET models.
Table 4. Hyper-parameters used for training the two U-NET models.
ParameterValue
Training batch size (samples)32
Verification batch size (samples)32
Epochs (-)150
Training iteration per epoch (-)200
Initial learning rate (-)0.001
Dropout probability (%)25
OptimizerAdam
Cost functionCross Entropy
Table
Table 5. Pixel-based measures of binary classification accuracy, compiled from Sokolova and Lapalme [65] and Kohl [66], used for assessing U-NET classification performance. TP denotes the number of true positive; FP, false positives; TN, true negatives; and FN, false negative class assignments.
Table 5. Pixel-based measures of binary classification accuracy, compiled from Sokolova and Lapalme [65] and Kohl [66], used for assessing U-NET classification performance. TP denotes the number of true positive; FP, false positives; TN, true negatives; and FN, false negative class assignments.
MetricFormulaMeaning
Accuracy Score T P + T N T P + T N + F P + F N Metric how effectively a classifier detects or excludes a condition
Precision T P T P + F P Compliance of class assignments for positive labels
Recall T P T P + F N Effectiveness of a classifier in identifying positive samples
F1-score 2 × p r e c i s i o n × r e c a l l p r e c i s i o n + r e c a l l Harmonic mean of precision and recall as alternative overall accuracy measure
AUC-“Area under the Curve”: the integral of the receiver operator characteristic curve (ROC)
Table
Table 6. Pixel-based metrics of classification accuracy for the CPS class, including the accuracy score, precision, recall, f1-score, and the area under the curve (AUC). For each study area, the results of the two U-NET implementations are shown.
Table 6. Pixel-based metrics of classification accuracy for the CPS class, including the accuracy score, precision, recall, f1-score, and the area under the curve (AUC). For each study area, the results of the two U-NET implementations are shown.
TexasDuero (Spain)South Africa
U-NET PCAU-NET SPECSU-NET PCAU-NET SPECSU-NET PCAU-NET SPECS
Accuracy Score (-)0.830.880.640.940.570.73
Precision (-)0.910.850.040.160.580.77
Recall (-)0.760.890.500.170.350.61
F1-Score (-)0.830.870.080.160.430.68
AUC (-)0.840.880.570.570.560.72
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Graf, L.; Bach, H.; Tiede, D. Semantic Segmentation of Sentinel-2 Imagery for Mapping Irrigation Center Pivots. Remote Sens. 2020, 12, 3937. https://doi.org/10.3390/rs12233937

AMA Style

Graf L, Bach H, Tiede D. Semantic Segmentation of Sentinel-2 Imagery for Mapping Irrigation Center Pivots. Remote Sensing. 2020; 12(23):3937. https://doi.org/10.3390/rs12233937

Chicago/Turabian Style

Graf, Lukas, Heike Bach, and Dirk Tiede. 2020. "Semantic Segmentation of Sentinel-2 Imagery for Mapping Irrigation Center Pivots" Remote Sensing 12, no. 23: 3937. https://doi.org/10.3390/rs12233937

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop