A Method of Marine Moving Targets Detection in Multi-Channel ScanSAR System
Abstract
1. Introduction
2. Problem Formulation
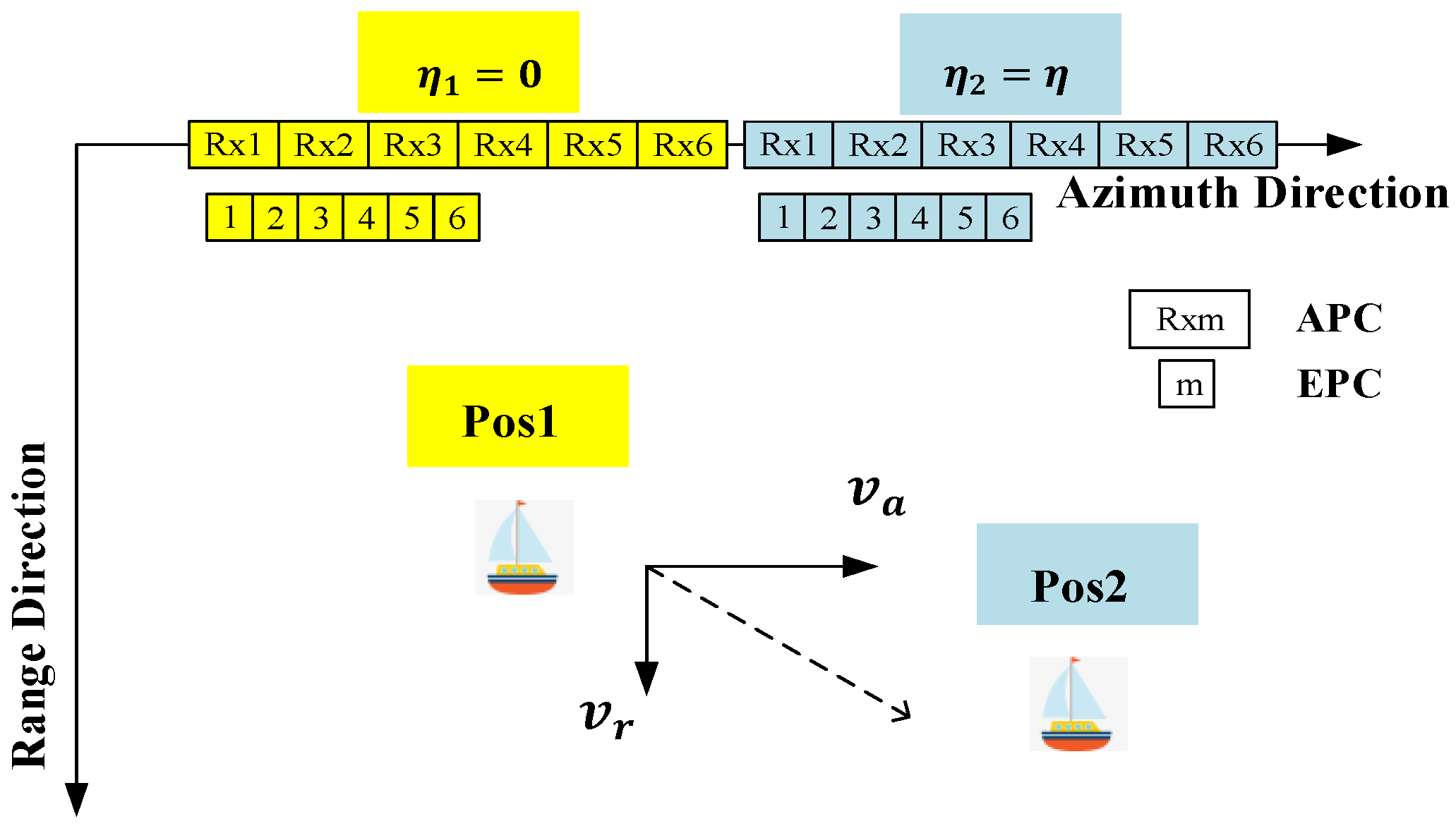
2.1. Geometry Model
2.2. Mathematical Model
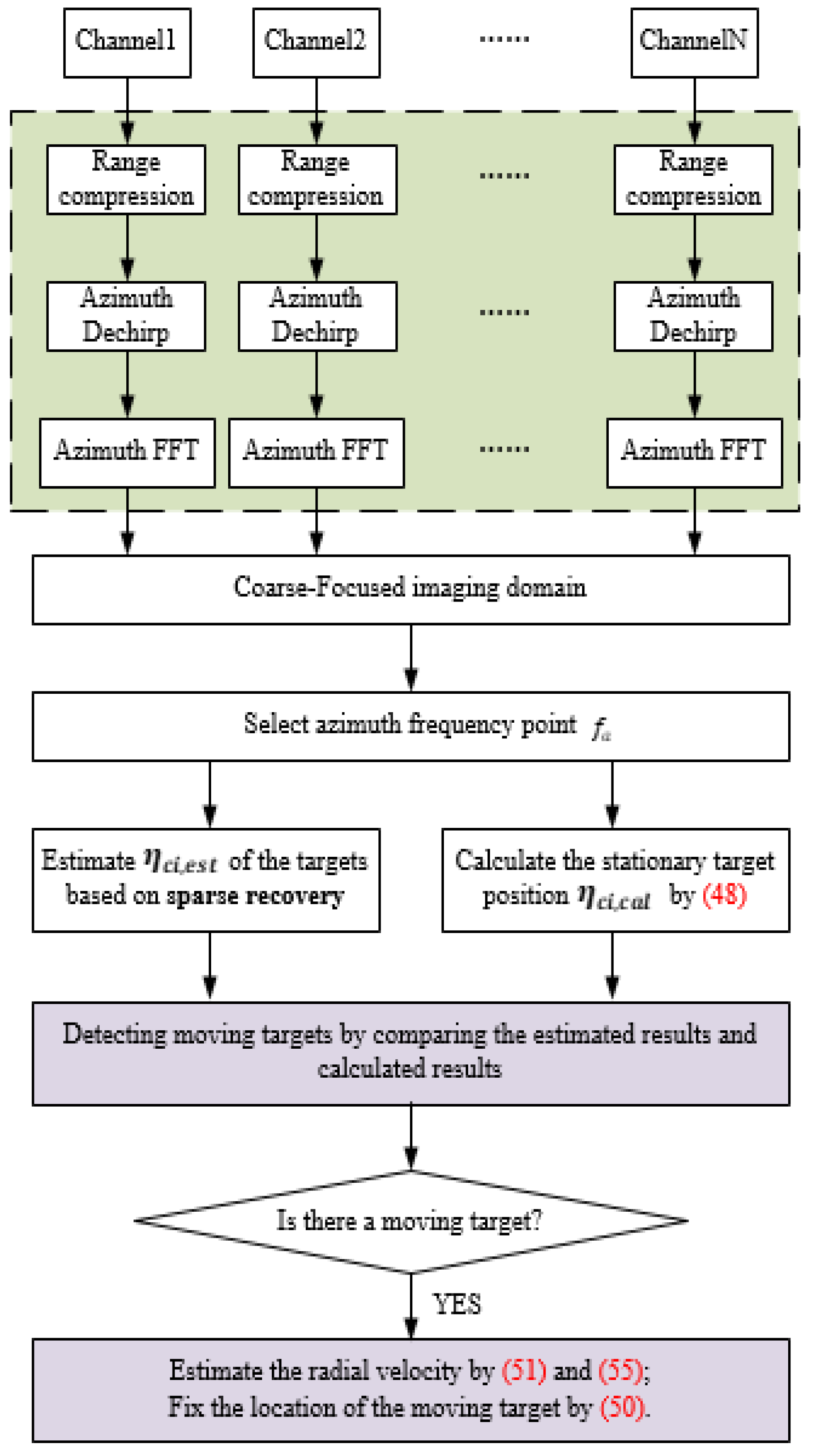
3. Moving Target Detection
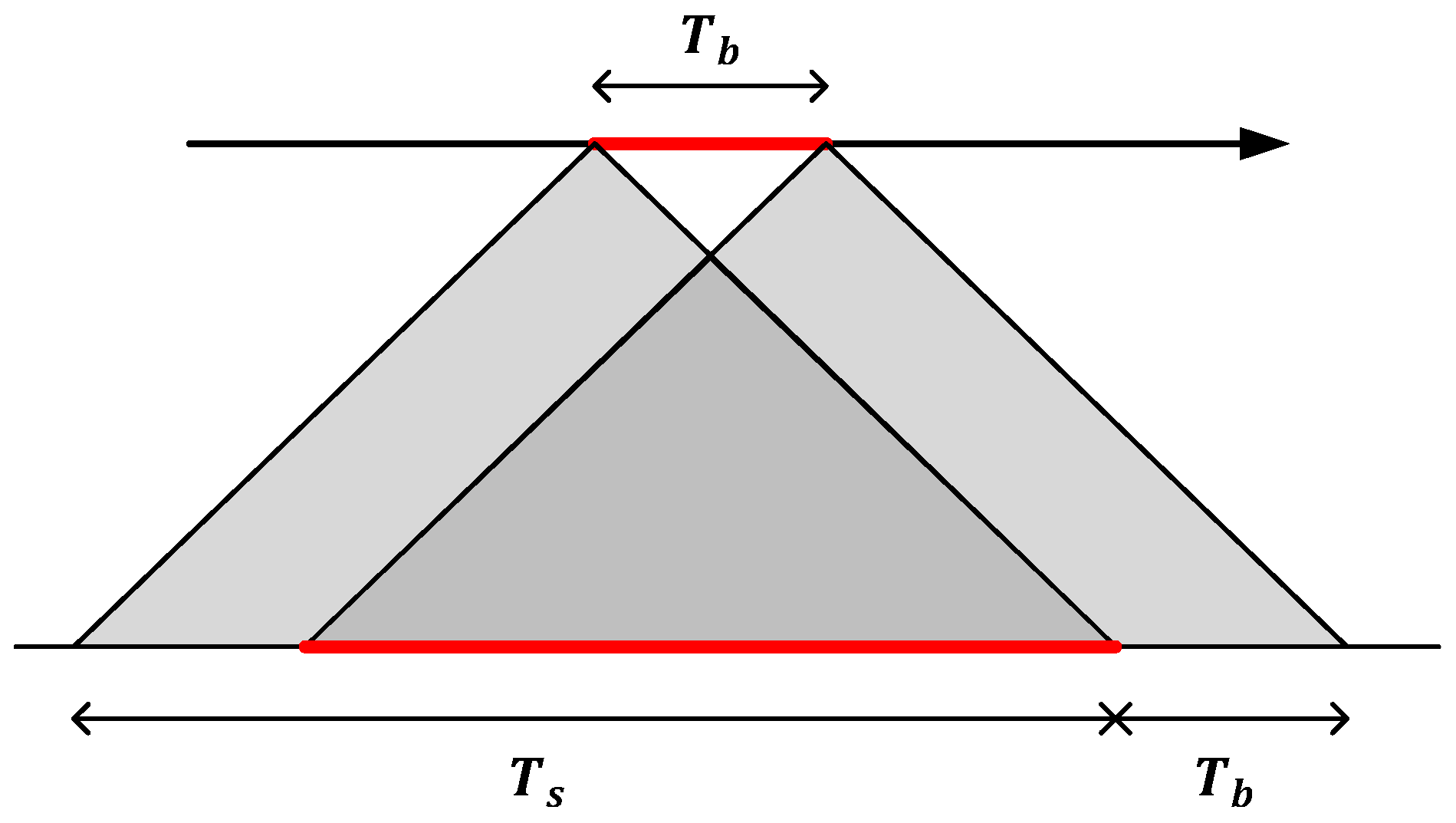
3.1. Coarse-Focused Image Domain
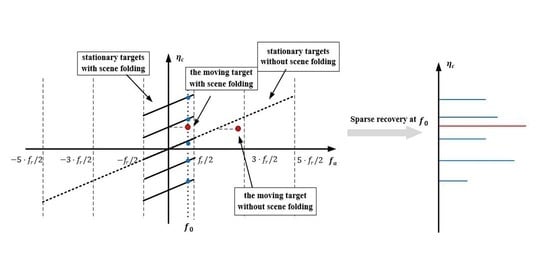
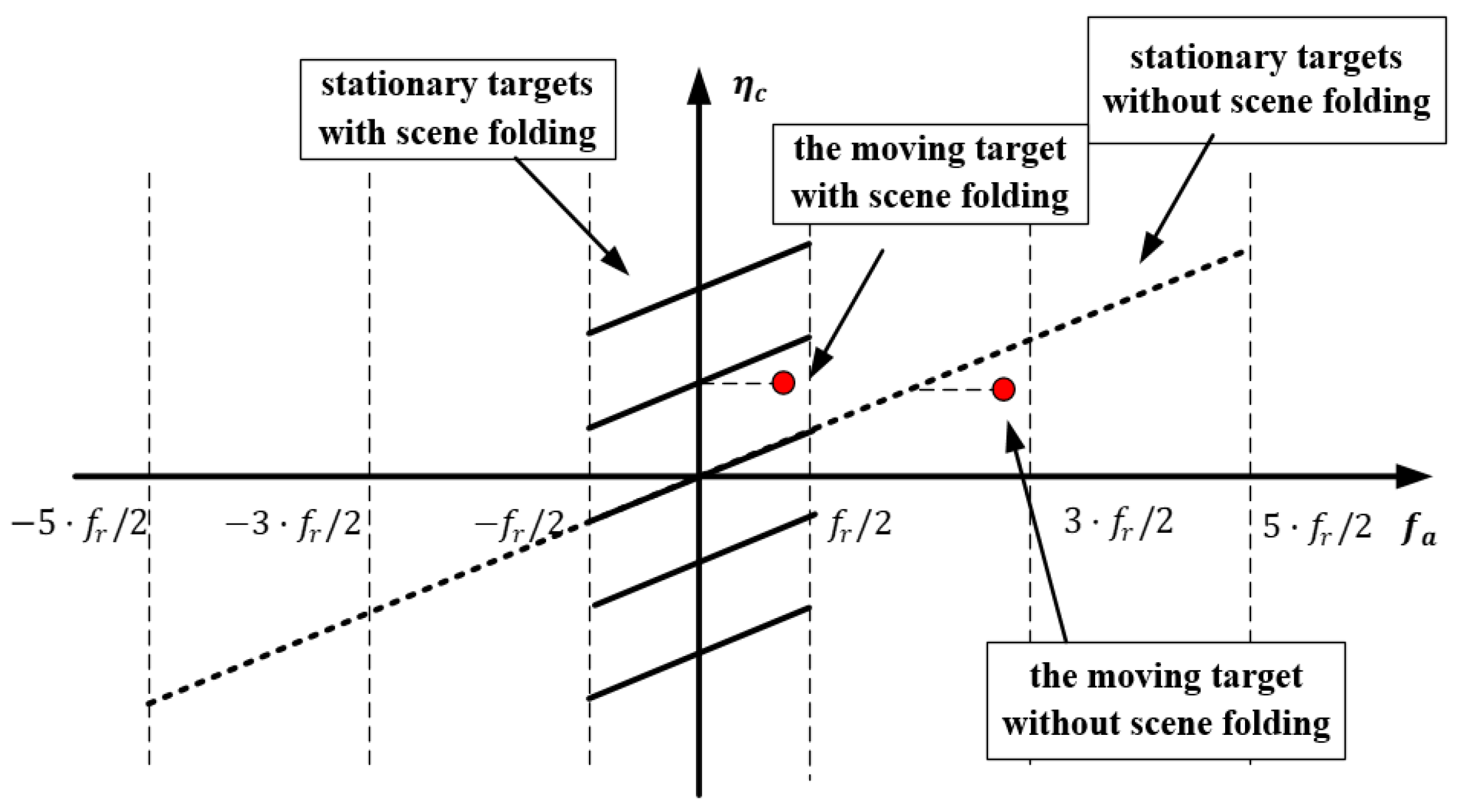
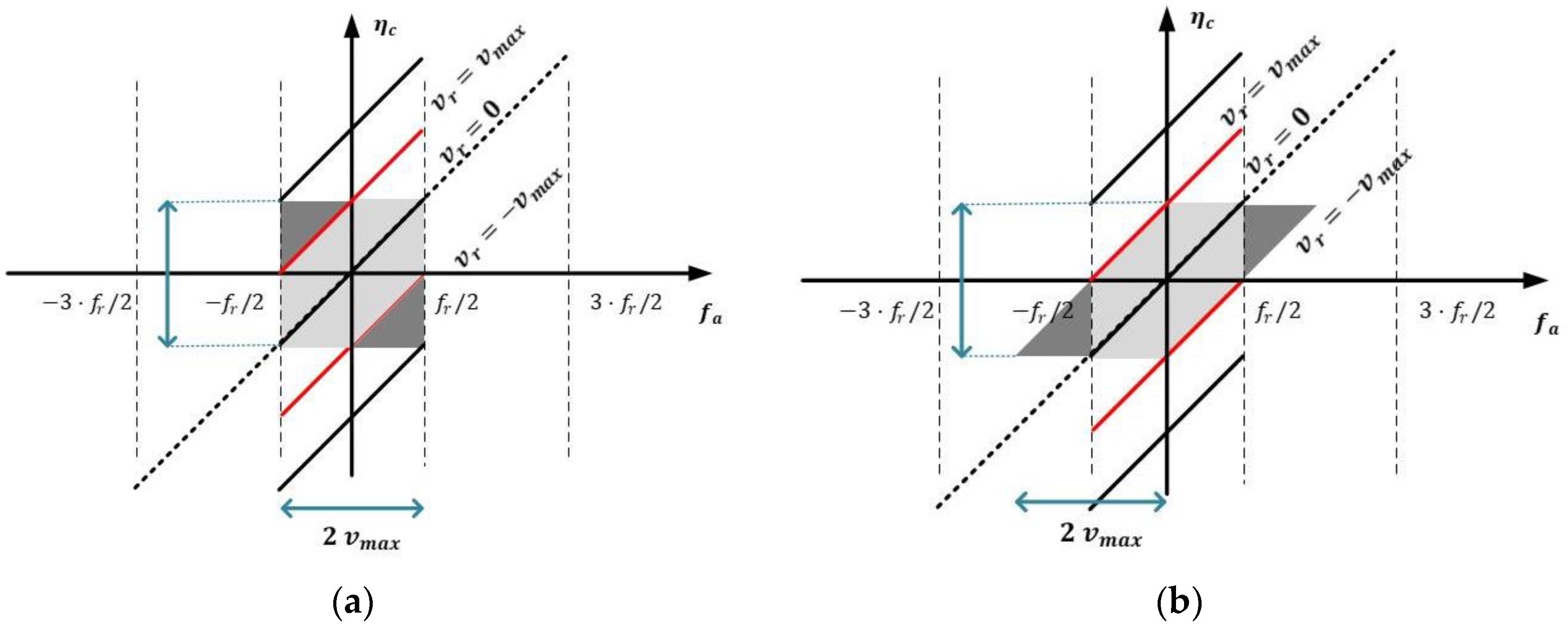
3.2. Scene Folding Times
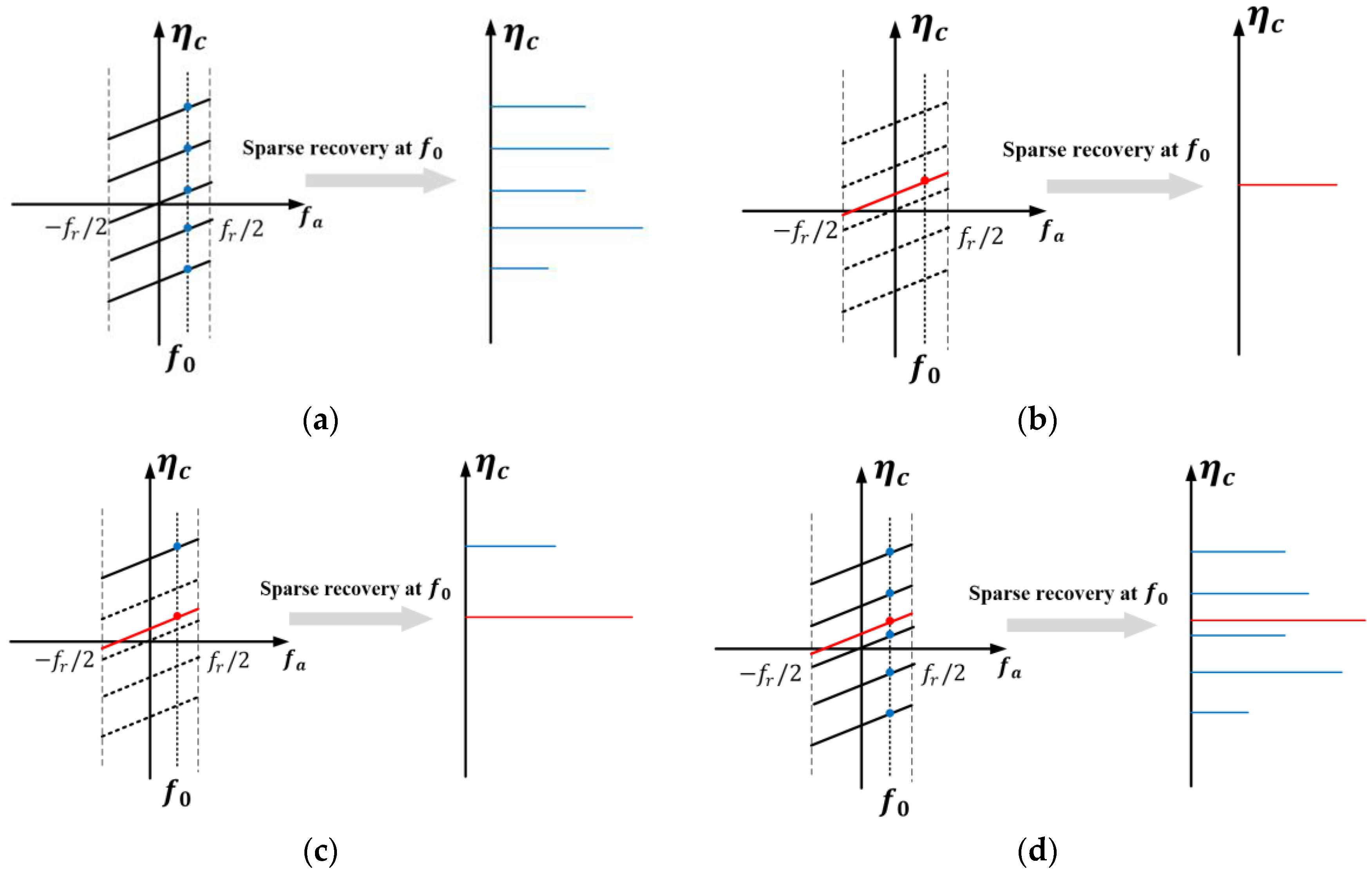
3.3. MTD Based on Sparse Recovery
3.4. Radial Velocity Estimation and Positioning
4. Simulation Results
4.1. Different Scenes
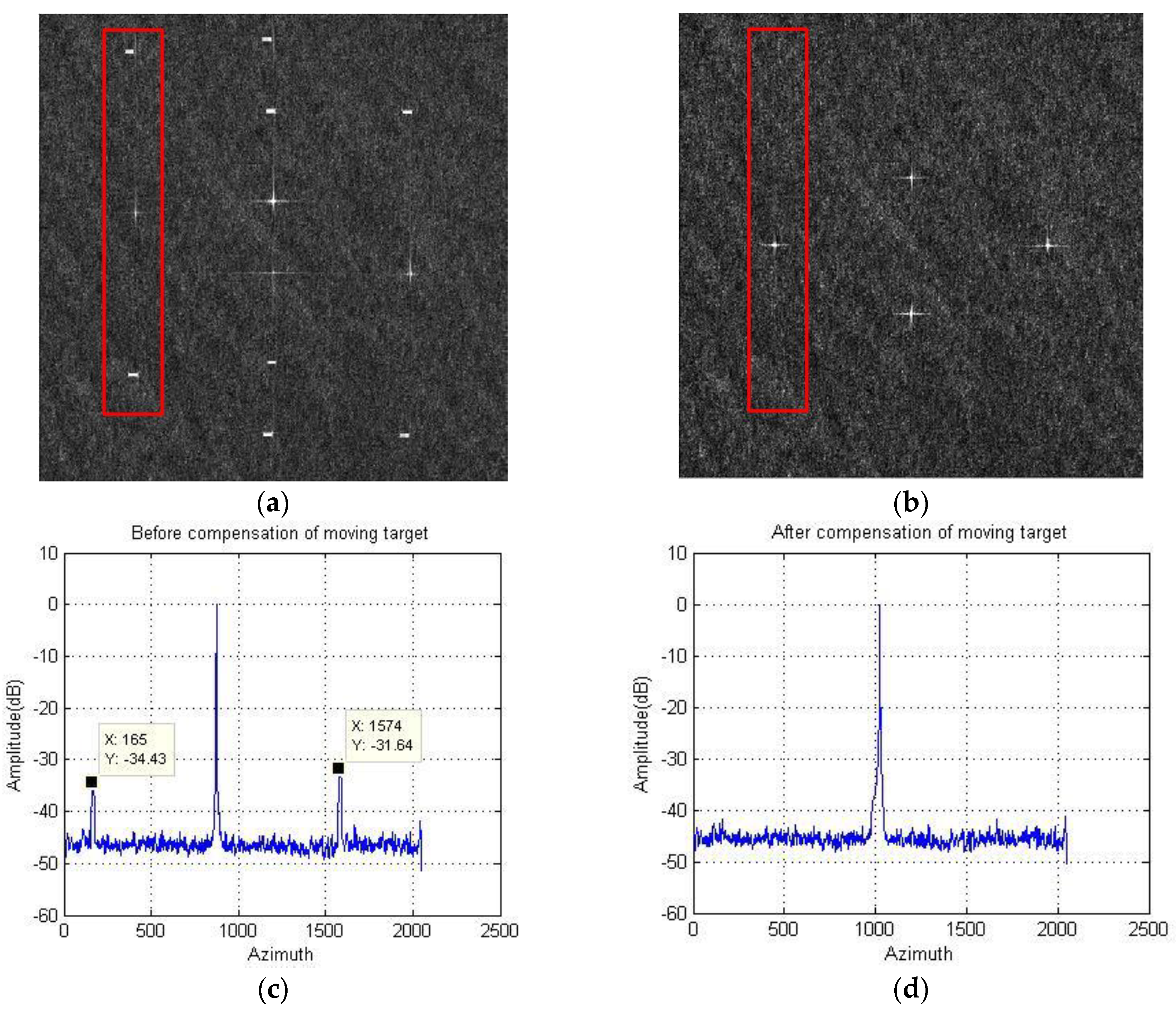
4.2. MTD Effect Demonstration
4.3. Unambiguous Imaging of Moving Targets
5. Performance Analysis
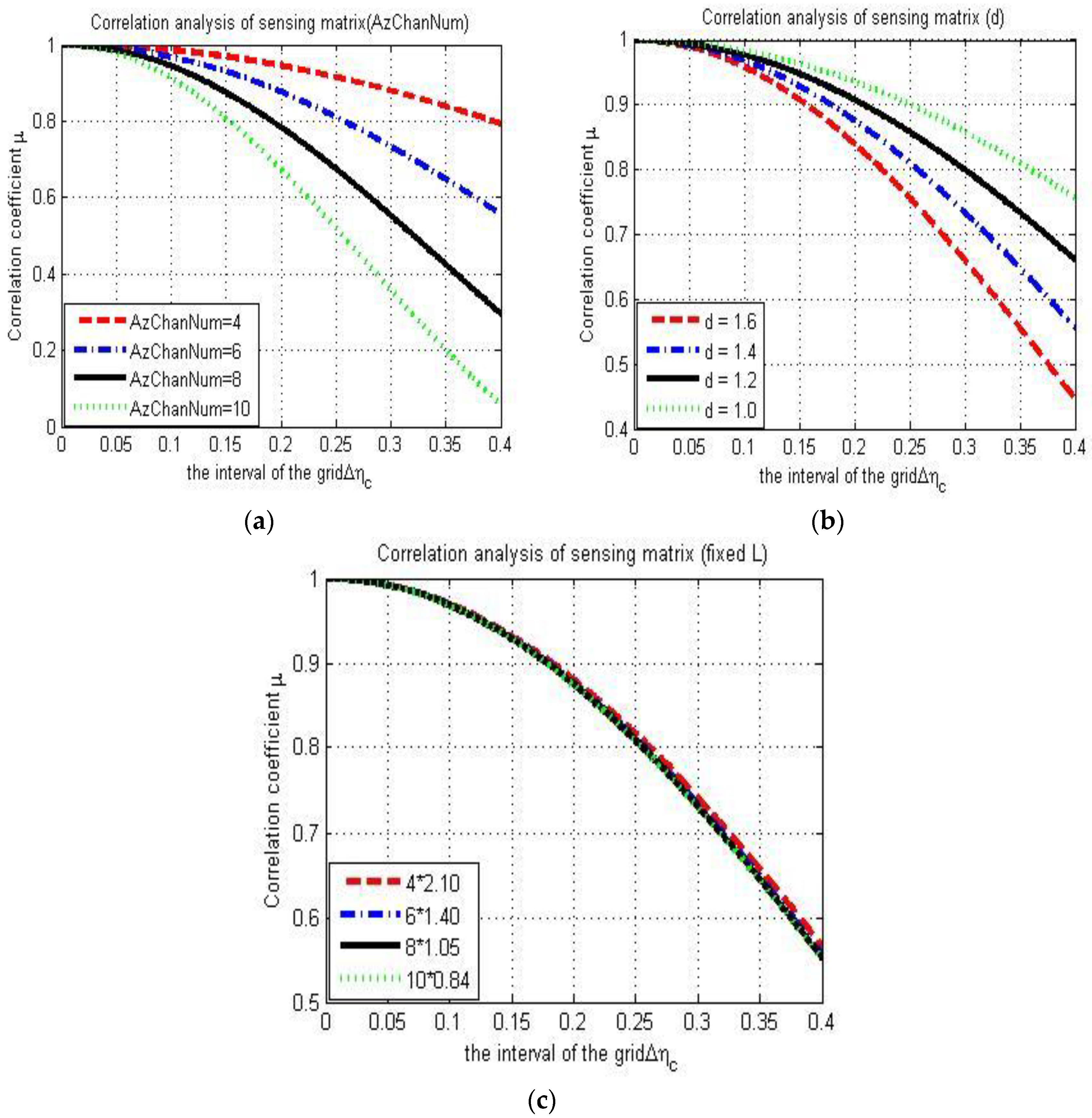
5.1. Rationality Analysis
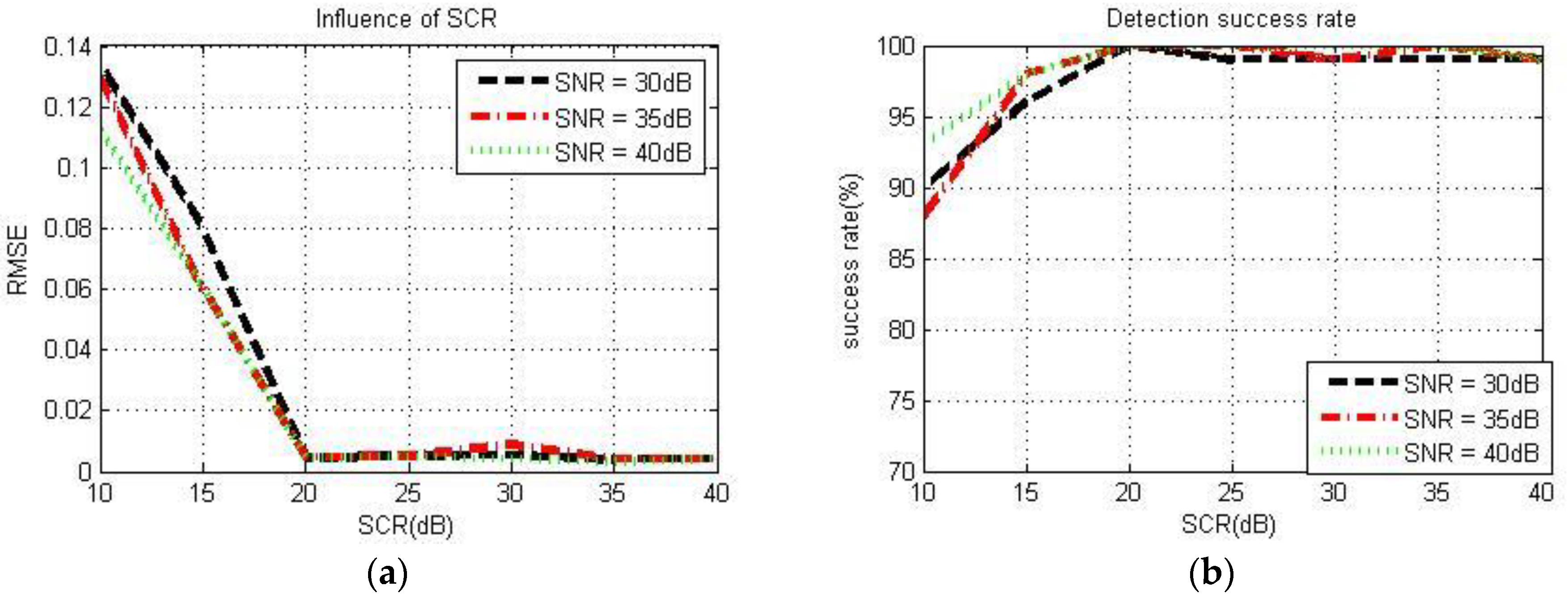
5.2. Influence of SCR in Coarse-Focused Imaging Domain
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tomiyasu, K. Tutorial review of synthetic-aperture radar (SAR) with applications to imaging of the ocean surface. Proc. IEEE 1978, 66, 563–583. [Google Scholar] [CrossRef]
- Tomiyasu, K. Image processing of synthetic aperture radar range ambiguous signals. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1114–1117. [Google Scholar] [CrossRef]
- Freeman, A.; Johnson, W.T.K.; Huneycutt, B.; Jordan, R.; Hensley, S.; Siqueira, P.; Curlander, J. The “Myth” of the minimum SAR antenna area constraint. IEEE Trans. Geosci. Remote Sens. 2000, 38, 320–324. [Google Scholar] [CrossRef]
- Currie, A.; Brown, M.A. Wide-swath SAR. IEE Proc. F Radar Signal Process. 1992, 139, 125–135. [Google Scholar] [CrossRef]
- Gebert, N.; Krieger, G.; Moreira, A. Digital Beamforming on Receive: Techniques and Optimization Strategies for High-Resolution Wide-Swath SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 564–592. [Google Scholar] [CrossRef]
- Yang, T.; Li, Z.; Suo, Z.; Bao, Z. Performance Analysis for Multichannel HRWS SAR Systems Based on STAP Approach. IEEE Trans. Geosci. Remote Sens. 2013, 10, 1409–1413. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling. IEEE. Geosci. Remote Sens. Lett. 2004, 1, 260–264. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Multichannel Azimuth Processing in ScanSAR and TOPS Mode Operation. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2994–3008. [Google Scholar]
- Yang, W.; Li, C.; Wang, P.; Chen, J. Performance analysis and data processing of space-borne multi-channel ScanSAR Mode for high-resolution wide-swath. In Proceedings of the IET International Radar Conference 2009, Guilin, China, 20–22 April 2019. [Google Scholar]
- Krieger, G.; Younis, M.; Gebert, N.; Huber, S.; Bordoni, F.; Patyuchenko, A.; Moreira, A. Advanced concepts for high-resolution wide-swath SAR imaging. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 524–527. [Google Scholar]
- Gebert, N.; Krieger, G.; Younis, M.; Bordoni, F.; Moreira, A. Ultra wide swath imaging with multi-channel ScanSAR. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. 21–24. [Google Scholar]
- Rousseau, L.; Gierull, C.; Chouinard, J. First Results from an Experimental ScanSAR-GMTI Mode on RADARSAT-2. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5068–5080. [Google Scholar] [CrossRef]
- Gierull, C.H.; Sikaneta, I.C. Raw data based two-aperture SAR ground moving target indication. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 1032–1034. [Google Scholar]
- Lightstone, L.; Faubert, D.; Rempel, G. Multiple phase centre DPCA for airborne radar. In Proceedings of the IEEE National Radar Conference, Los Angeles, CA, USA, 12–13 March 1991; pp. 36–40. [Google Scholar]
- Zebker, H.A.; Goldstein, R.M. Topographic mapping from interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 1986, 91, 4993–4999. [Google Scholar] [CrossRef]
- Breit, H.; Eineder, M.; Holzner, J.; Runge, H.; Bamler, R. Traffic monitoring using SRTM along-track interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 1187–1189. [Google Scholar]
- Ender, J.H.G. Space-time processing for multichannel synthetic aperture radar. Electron. Commun. Eng. J. 1999, 11, 29–38. [Google Scholar] [CrossRef]
- Ward, J. Space-time adaptive processing for airborne radar. In Proceedings of the IEE Colloquium on Space-Time Adaptive Processing, London, UK, 6 April 1998; pp. 2/1–2/6. [Google Scholar]
- Friedlander, B.; Porat, B. VSAR: A high resolution radar system for detection of moving targets. IEE Proc. Radar Sonar Navigat. 1997, 144, 205–218. [Google Scholar] [CrossRef]
- Jansen, R.W.; Raj, R.G.; Rosenberg, L.; Sletten, M.A. Practical Multichannel SAR Imaging in the Maritime Environment. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4025–4036. [Google Scholar] [CrossRef]
- Guo, X.; Gao, Y.; Liu, X. Moving target detection in HRWS mode. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 1169–1172. [Google Scholar]
- Hou, L.; Song, H.; Zheng, M.; Zhang, L.; Qi, L. Clutter suppression for multichannel synthetic aperture radar ground moving target indication system with the capability of high-resolution wide-swath imaging. J. Appl. Remote Sens. 2015, 9, 095054. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M.; Xia, X.; Guo, R.; Liu, Y.; Bao, Z. A Novel Moving Target Imaging Algorithm for HRWS SAR Based on Local Maximum-Likelihood Minimum Entropy. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5333–5348. [Google Scholar] [CrossRef]
- Wang, L.; Wang, D.; Li, J.; Xu, J.; Xie, C.; Wang, L. Ground Moving Target Detection and Imaging Using a Virtual Multichannel Scheme in HRWS Mode. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5028–5043. [Google Scholar] [CrossRef]
- Baumgartner, S.V.; Krieger, G. Simultaneous High-Resolution Wide-Swath SAR Imaging and Ground Moving Target Indication: Processing Approaches and System Concepts. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5015–5029. [Google Scholar] [CrossRef]
- Shu, Y.; Liao, G.; Yang, Z. Design Considerations of PRF for Optimizing GMTI Performance in Azimuth Multichannel SAR Systems with HRWS Imaging Capability. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2048–2063. [Google Scholar]
- Yang, T.; Li, Z.; Suo, Z.; Bao, Z. Ground moving target indication for high-resolution wide-swath synthetic aperture radar systems. IET Radar Sonar Navig. 2014, 8, 227–232. [Google Scholar] [CrossRef]
- Zhang, S.; Xing, M.; Xia, X.; Guo, R.; Liu, Y.; Bao, Z. Robust Clutter Suppression and Moving Target Imaging Approach for Multichannel in Azimuth High-Resolution and Wide-Swath Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 687–709. [Google Scholar] [CrossRef]
- Zheng, H.; Wang, J.; Liu, X. Ground Moving Target Indication for High-Resolution Wide-Swath Synthetic Aperture Radar Systems. IEEE. Geosci. Remote Sens. Lett. 2017, 14, 749–753. [Google Scholar] [CrossRef]
- Kim, J.; Younis, M.; Prats-Iraola, P.; Gabele, M.; Krieger, G. First Spaceborne Demonstration of Digital Beamforming for Azimuth Ambiguity Suppression. IEEE Trans. Geosci. Remote Sens. 2013, 51, 579–590. [Google Scholar] [CrossRef]
- Yang, T.; Li, Z.; Liu, Y.; Bao, Z. Channel Error Estimation Methods for Multichannel SAR Systems in Azimuth. IEEE. Geosci. Remote Sens. Lett. 2013, 10, 548–552. [Google Scholar] [CrossRef]
- Shang, M.; Qiu, X.; Han, B.; Ding, C.; Hu, Y. Channel Imbalances and Along-Track Baseline Estimation for the GF-3 Azimuth Multichannel Mode. Remote Sens. 2019, 11, 1297. [Google Scholar] [CrossRef]
- Jin, T.; Qiu, X.; Hu, D.; Ding, C. An ML-Based Radial Velocity Estimation Algorithm for Moving Targets in Spaceborne High-Resolution and Wide-Swath SAR Systems. Remote Sens. 2017, 9, 404. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, X.; Zhong, L.; Shang, M.; Ding, C. A Simultaneous Imaging Scheme of Stationary Clutter and Moving Targets for Maritime Scenarios with the First Chinese Dual-Channel Spaceborne SAR Sensor. Remote Sens. 2019, 11, 2275. [Google Scholar] [CrossRef]
- Calloway, T.M.; Donohoe, G.W. Subaperture autofocus for synthetic aperture radar. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 617–621. [Google Scholar] [CrossRef]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakowatz, C.V. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Mei, S.; Liu, Q.; Wan, S. A Moving Target Imaging Algorithm Based on Compressive Sensing for Multi-channel in Azimuth HRWS SAR System. In Proceedings of the 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019. [Google Scholar]
- Middleton, R.J.C. Dechirp-on-Receive Linearly Frequency Modulated Radar as a Matched-Filter Detector. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2716–2718. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic Decomposition by Basis Pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Cai, T.T.; Wang, L.; Xu, G. Stable Recovery of Sparse Signals and an Oracle Inequality. IEEE Trans. Inf. Theory 2010, 56, 3516–3522. [Google Scholar] [CrossRef]
- Han, B.; Ding, C.; Zhong, L.; Liu, X.; Qiu, X.; Hu, Y.; Lei, B. The GF-3 SAR Data Processor. Sensors 2018, 18, 835. [Google Scholar] [CrossRef] [PubMed]




| Symbol | Parameter | Value |
|---|---|---|
| Wavelength | 0.055517 m | |
| Signal bandwidth | 120 MHz | |
| Sampling rate | 150 MHz | |
| Pulse width | 30 | |
| Channel number | 6 | |
| Baseline | 1.4 m | |
| Platform velocity | 7508 m/s | |
| Reference slant range | 800 Km | |
| PRF | 1340.7 Hz | |
| Synthetic aperture time | 2.11 s | |
| Dwell time of a burst | 0.52 s | |
| Doppler bandwidth | 5362.9 Hz | |
| Scene folding times | 3 |
| Scene Number | Design Scheme |
|---|---|
| Stationary clutter | |
| Stationary clutter A moving target: | |
| Stationary island A moving target: Static target 1: |
| Point | Whether It Is a Moving Target? | ||||||
|---|---|---|---|---|---|---|---|
| 1 | −568.09 Hz | 0.224 s | 0.225 s | 0.001 s | −0.0846 m/s | No | |
| 2 | −388.20 Hz | 0.153 s | 0.224 s | 0.071 s | −5.0078 m/s | Yes | 1681.792 m |
| 3 | −568.09 Hz | 0.224 s | 0.224 s | 0 s | −0.0142 m/s | No | |
| 4 | −287.83 Hz | 0.113 s | 0.001 s | 0.112 s | 7.9194 m/s | Yes | 7.508 m |
| 5 | 0 Hz | 0 s | 0 | 0 s | 0 m/s | No | |
| 6 | 215.88 Hz | −0.085 s | −0.001 s | 0.084 s | −5.9219 m/s | Yes | −7.508 m |
| 7 | 568.09 Hz | −0.223 s | −0.224 s | 0.001 s | 0.0142 m/s | No | |
| 8 | 208.30 Hz | −0.082 s | −0.225 s | 0.143 s | 10.0719 m/s | Yes | −1689.300 m |
| 9 | 568.09 Hz | −0.224 s | −0.224 s | 0 s | 0.0142 m/s | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Qiu, X.; Shang, M.; Zhong, L.; Ding, C. A Method of Marine Moving Targets Detection in Multi-Channel ScanSAR System. Remote Sens. 2020, 12, 3792. https://doi.org/10.3390/rs12223792
Yang J, Qiu X, Shang M, Zhong L, Ding C. A Method of Marine Moving Targets Detection in Multi-Channel ScanSAR System. Remote Sensing. 2020; 12(22):3792. https://doi.org/10.3390/rs12223792
Chicago/Turabian StyleYang, Junying, Xiaolan Qiu, Mingyang Shang, Lihua Zhong, and Chibiao Ding. 2020. "A Method of Marine Moving Targets Detection in Multi-Channel ScanSAR System" Remote Sensing 12, no. 22: 3792. https://doi.org/10.3390/rs12223792
APA StyleYang, J., Qiu, X., Shang, M., Zhong, L., & Ding, C. (2020). A Method of Marine Moving Targets Detection in Multi-Channel ScanSAR System. Remote Sensing, 12(22), 3792. https://doi.org/10.3390/rs12223792