Estimating Water Reflectance at Near-Infrared Wavelengths for Turbid Water Atmospheric Correction: A Preliminary Study for GOCI-II

Abstract

Atmospheric correction is a fundamental process to remove the atmospheric effect from the top-of-atmosphere level. The atmospheric correction algorithm developed by the Korea Institute of Ocean Science and Technology employs a near-infrared (NIR) water reflectance model to deal with non-negligible NIR water reflectance over turbid waters. This paper describes the NIR water reflectance models using visible bands of the Second Geostationary Ocean Color Imager (GOCI-II). Whereas the previous GOCI uses the 660 nm band to estimate NIR water reflectance (SR660), GOCI-II uses additional 620 and 709 nm bands, which improves estimation of NIR water reflectance. We developed two reflectance models with the additional bands based on a spectral relationship of water reflectance (SR709) and a spectral relationship of inherent optical properties (SRIOP) from red to NIR wavelengths. A preliminary validation of these two reflectance models was performed using both simulations and an in situ dataset. The validation result showed that the mean absolute percentage error of the SR709 model compared with SR660 was reduced by approximately 6% and 10% at 745 and 865 nm, respectively. Moreover, the mean absolute percentage error of the SRIOP model compared with SR660 was reduced by approximately 12% and 16% at 745 and 865 nm, respectively. Note that SR709 produces the most accurate result when there is only one sediment type, and SRIOP shows the most accurate result when various sediment types exist. Users will be able to optionally select the appropriate NIR water reflectance models in the GOCI-II atmospheric correction process to enhance the accuracy of aerosol reflectance correction over turbid waters.

1. Introduction

Atmospheric correction plays an important role in ocean color remote sensing, which estimates water reflectance at the surface from the top of the atmosphere at the satellite level by removing path reflectances, which mainly result from light scattered by the atmosphere [1]. Atmospheric reflectances are the result of multiple scattering by air molecules (Rayleigh scattering) and aerosols, including their interactions. The Rayleigh scattering reflectance can be derived precisely using radiative transfer theory [2,3,4,5,6]. However, estimating the aerosol reflectance is more laborious because the reflectance is a function of aerosol type and optical thickness, which cannot be predicted a priori. The widely used approach was developed by Gordon and Wang [7] and then applied to other ocean color sensors with several modifications [8,9,10,11]. Algorithms of this type consider multiple-scattering reflectances of aerosol at two near-infrared (NIR) wavelengths to determine the appropriate aerosol model and aerosol optical thickness based on the black pixel assumption (BPA) that water reflectance in the NIR is negligible because of the strong water absorption in the NIR [1,7].

Whereas the aerosol correction scheme based on two NIR bands has been used for general atmospheric correction algorithms, water reflectance in the NIR over turbid water becomes non-negligible because of the strong backscattering coefficient of the suspended sediments in water. Therefore, the turbid water and aerosol reflectances should be separated in the NIR when the BPA aerosol correction scheme is applied, and this is also often referred to as the bright pixel atmospheric correction [12,13,14,15,16,17,18,19,20,21,22,23]. For the separation, an iterative optimization scheme has been widely used [14,15,16,17,18,19,21,23]. To estimate the NIR water reflectance iteratively, Siegel et al. [14] use bio-optical models with the retrieved chlorophyll-a concentration. Stumpf et al. [15] and Bailey et al. [17] use semi-analytic optical models with the estimated backscattering and absorption coefficient. Wang et al. [18] use an empirical relationship between the diffuse attenuation coefficient at 490 nm and water reflectances in the NIR. Ahn et al. [19,24] use an empirical relationship between water reflectance at 660 nm and that at NIR wavelengths for the Geostationary Ocean Color Imager (GOCI) atmospheric correction.

This study develops a preliminary NIR water reflectance model that will be implemented for an iteration-based turbid water atmospheric correction algorithm for the Second Geostationary Ocean Color Imager (GOCI-II), launched in 2020, which followed the GOCI mission. The GOCI-II observation bands include the GOCI bands (i.e., 412, 443, 490, 555, 660, 680, 745, and 865 nm) plus the 380, 510, 620, and 709 nm bands [25]. The reflectance models are evaluated using water reflectance datasets from both in situ observations and simulations.

2. Data and Methods

Atmospheric correction is used for the retrieval of water reflectance at the sea surface (ρ_wn) by removing the atmospheric contributions. Ignoring the sunglint, the whitecaps, and the effects of the bidirectional reflectance, the top-of-atmosphere (TOA) reflectance (ρ_TOA) at wavelength λ can be described by [7]:

$${\rho }_{\mathrm{TOA}}\left(\lambda \right)=\raisebox{1ex}{$\pi L_{\mathrm{TOA}}\left(\lambda \right)$}\!\left/ \!\raisebox{-1ex}{$F_0\left(\lambda \right){\mu }_0$}\right.$$

(1)

$${\rho }_{\mathrm{TOA}}\left(\lambda \right)={\rho }_r\left(\lambda \right)+{\rho }_{am}\left(\lambda \right)+t_d^v\left(\lambda \right)t_d^s\left(\lambda \right){\rho }_{wn}\left(\lambda \right)$$

(2)

where L_TOA is the TOA radiance, F₀ is the extraterrestrial solar irradiance, and µ₀ is the cosine of the solar zenith angle. The atmospheric term ρ_r is the Rayleigh reflectance in the absence of aerosols, and ρ_am is the aerosol reflectance in the presence of air molecules. The values $t_d^v$ and $t_d^s$ are the upward and downward diffuse transmittances, respectively. It should be noted that the variables except F₀ are a function of geometric angle, and the geometry notations are omitted in the Equations (1) and (2).

To solve the desired value ρ_wn in Equation (2), the value of ρ_r can be predicted precisely from given solar-sensor angular geometries and the air pressure at the surface through radiative transfer simulation with less than about 1% error [2,3,4,5,6]. The aerosol reflectance in the visible wavelengths is estimated from the observed aerosol reflectance at the two NIR wavelengths based on the BPA by comparing various radiative transfer simulation results stored in a look-up table.

To apply the BPA approach over turbid water, the general atmospheric correction algorithm based on the two NIRs iteratively separates ρ_wn(NIR) and ρ_am(NIR) using the NIR water reflectance model, as shown in Figure 1. This section first introduces the NIR water reflectance model based on the spectral relationships of water reflectance between 660 nm and the two NIRs that have been employed by GOCI (denoted SR660). Then, we could improve the SR660 model by replacing the 660 nm band with a 709 nm band, which has been newly added by the GOCI-II sensor (denoted SR709). We also describe another NIR water reflectance model that uses the spectral relationships of inherent optical properties (IOPs) among wavelengths of 620, 709, 745, and 865 nm (denoted SRIOP).

2.1. Water Reflectance Dataset from Simulations and In Situ Measurements

This study uses a radiative transfer simulation dataset (RTSD) generated by both the Korea Ocean Satellite Center (KOSC) of the Korea Institute of Ocean Science and Technology and the International Ocean-Color Coordinating Group (denoted KOSC RTSD and IOCCG RTSD, respectively) for validation of SR660, SR709, and SRIOP. Shipborne water reflectance data from turbid coastal waters are also used to build the SR709 model and validate SR660, SR709, and SRIOP. For the validation, we use the remote-sensing reflectance (R_rs), which can be described as R_rs(λ) = ρ_wn(λ)/π, instead of the ρ_wn that has been used more widely for in situ measurement protocols.

To simulate the KOSC RTSD, we use the HydroLight radiative transfer code [26,27] with various IOP input values. Measurement of in situ IOP values at NIR wavelengths may be difficult because of low absorption and backscattering coefficients of in-water particles while the water absorption is high [28]. Moreover, the simulation requires consideration of more extreme cases than the usual IOP range of field observations. Therefore, we use model IOP values rather than in situ IOP data.

The input values for the KOSC RTSD are prepared as

Table 1. Inherent optical properties (IOPs) and other parameters prepared for an input of the radiative transfer code.

IOP	Pure sea water	Absorption coefficient: Pope and Fry [29] and Kou et al. [30], without consideration of the temperature effect Scattering coefficient: Smith and Baker [31]
	Phytoplankton and detritus	Concentration range: 0.1–30.0 mg/m3 chlorophyll-a Concentration interval: 0.125 in log10 space chlorophyll-a Specific absorption model: Morel [32], with the specific absorption coefficient set to zero for a wavelength longer than 700 nm. Specific scattering model: Gordon and Morel [33]
	Mineral particles	Concentration range: values covary with the chlorophyll-a concentration based on the in situ measurements (0.1–10,000 g/m3) Concentration interval: 0.5 in log10 space Specific absorption and backscattering (including bb/b) values of four types of mineral particles, red clay, yellow clay, brown earth, and calcareous sand obtained in the laboratory from Ahn [28] The wavelength range of specific absorption and backscattering coefficients described in Ahn is from 400 to 750 nm [28]. Therefore, specific absorption spectra are extrapolated linearly [34], and specific scattering spectra are extrapolated using the power law [35].
	CDOM	aCDOM absorption at 440 nm: values covary with the chlorophyll-a concentration based on the in situ measurements (0.01–1.7783 m−1) Absorption coefficient interval: 0.25 in log10-space Spectral slope of aCDOM: 0.014 [36]
Other parameters		Wavelengths: 355–895 nm at 5 nm intervals Optically infinite depth Geometric angles: 30°, 30°, and 90° for the solar zenith, sensor zenith, and relative azimuth angles, respectively Absorption coefficient interval: 0.25 in log10-space

. It should be noted that the dataset used for establishing the SRIOP is identical to these input IOP values.

Besides the KOSC RTSD, we additionally used the IOCCG RTSD generated in a different way [37] to use validation data separated from the algorithm creation. The simulation input IOP values for the IOCCG RTSD are generated using nine specific absorption models for chlorophyll. The quantity and slope of backscattering and absorption coefficients are randomly generated for detritus, mineral particles, and Colored Dissolved Organic Matter (CDOM). The spectral range of the IOCCG RTSD is 400–800 nm, with 10 nm intervals; therefore, the IOCCG RTSD is used with a spectral interpolation for validation of 745 nm, but not 865 nm.

The in situ shipborne water reflectance dataset over highly turbid waters was obtained by KOSC in October 2015 and 2016 using the above-water radiometer TriOS RAMSES, which measures the total water radiance above the sea surface, sky radiance, and down-welling irradiance simultaneously. The KOSC obtained 39 in situ R_rs spectra over highly turbid waters in the Korean coastal area (Figure 2). The radiometric measurements and data processing methods followed Mobley’s protocol [38] without application of any post-processes to reduce residual error emerging from sky radiance. It should be noted that there was no wind during the measurements. Thus, we could collect reliable R_rs spectra with a lower residual error emerging from sky radiance at the air-sea interface.

2.2. Method 1: Using the Spectral Relationships of Water Reflectance

The GOCI scheme [19] estimates ρ_wn(NIR) using the spectral relationship between ρ_wn(660 nm) and ρ_wn(745 nm) and ρ_wn(865 nm) (SR660) based on the similarity spectrum [39]. For each iterative step, the scheme first estimates ρ_wn(660 nm) by an aerosol correction process and then estimates ρ_wn(745 nm) and ρ_wn(865 nm) using the following equations:

$${\rho }_{wn}\left(745\mathrm{nm}\right)={\displaystyle \sum _{n=0}^5}{j}_n{\rho }_{wn}{(660\mathrm{nm})}^n$$

(3)

$${\rho }_{wn}\left(865\mathrm{nm}\right)={\displaystyle \sum _{n=1}^2}{k}_n{\rho }_{wn}{(745\mathrm{nm})}^n$$

(4)

where j_n and k_n are the coefficients for the polynomial models [24].

The SR660 may be less accurate for highly turbid water because the water reflectance optical saturation issue appears early at shorter wavelengths with increasing turbidity [18,40,41]. Moreover, the relationship between the 660 nm and NIR band water reflectance can vary inconsistently among different composition ratios of suspended sediments and chlorophyll concentrations, because 660 nm is close to the second peak of the chlorophyll absorption spectrum (670–680 nm). Therefore, the GOCI-II atmospheric correction algorithm employs the 709 nm band (SR709), which is affected negligibly by chlorophyll absorption compared with the 660 nm band, moreover the optical saturation issue appears later wavelengths with increasing turbidity. Similar to the GOCI algorithm, the GOCI-II process first derives ρ_wn(709 nm) and then estimates ρ_wn(745 nm) and ρ_wn(865 nm). Thus, the empirical model (Equation (3)) can be replaced with

$${\rho }_{wn}\left(745\mathrm{nm}\right)={\displaystyle \sum _{n=0}^3}{l}_n{\rho }_{wn}{(709\mathrm{nm})}^n$$

(5)

where l_n is the coefficient for the polynomial relationship.

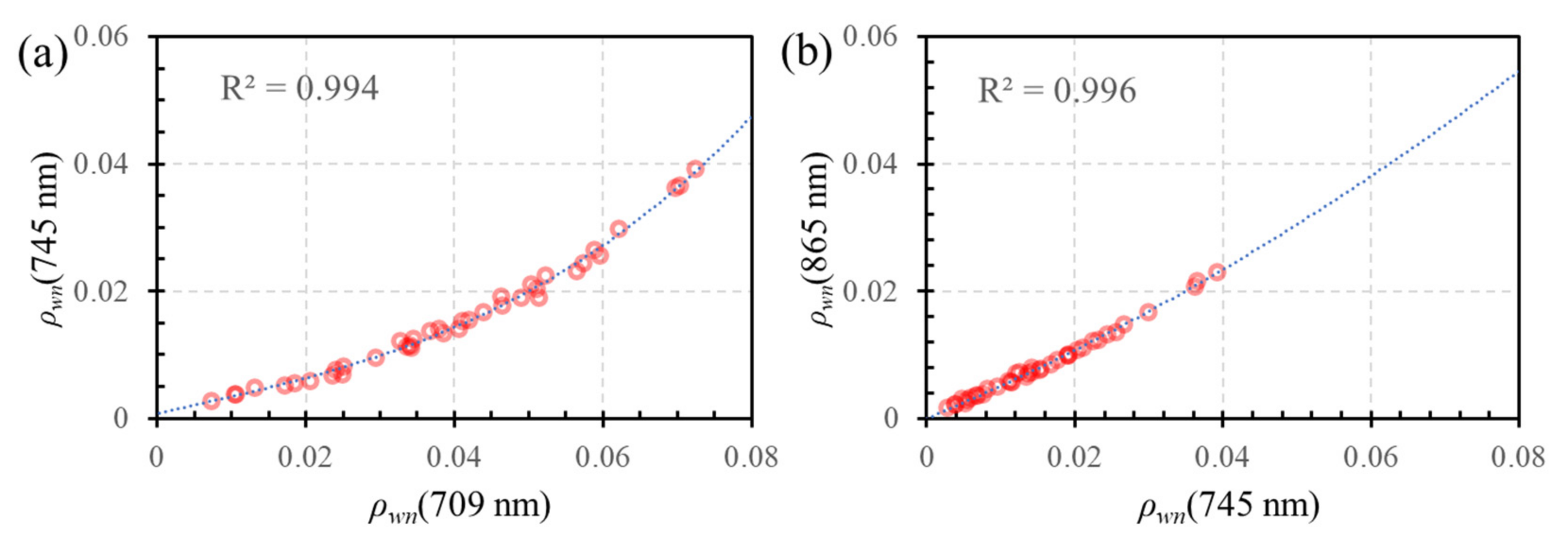
Unlike the relationships for Equations (3) and (4), which are derived from satellite data [19], the new relationship for Equation (5) is derived from in situ R_rs data (Figure 3). Because the model’s coefficients depend on the vicarious calibration gains, they are computed from the satellite-derived ρ_wn. The polynomial coefficients of SR660 and SR709 are summarized in

Table 2. Coefficients of SR660 and SR709 polynomial models for Equations (3)–(5).

	ρwn(VIS) → ρwn(745 nm)	ρwn(745 nm) → ρwn(865 nm)
SR660	−0.00148, 0.486, −22.93, 615.8, −6760.0, 30,210.0	0.5012, 4.0878
SR709	0.00079, 0.2614, 0.1614, 52.333	0.4885, 2.4233

.

2.3. Method 2: Using the Spectral Relationships of IOPs

Another model can estimate ρ_wn(NIR) in a semi-analytical way using the spectral relationship of IOPs (SRIOP). This model also uses the 620 nm GOCI-II band, which has the advantage of being less affected by chlorophyll-a than the 660 nm band and less affected by CDOM than the 555 nm band. To derive NIR water reflectance using the SRIOP model, the atmospheric correction scheme first derives ρ_wn(620 nm) and ρ_wn(709 nm) for each iterative step. Then, the SRIOP estimates IOP values at 620 nm. The water reflectances ρ_wn(745 nm) and ρ_wn(865 nm) can finally be computed from the NIR IOP values extrapolated from IOPs at 620 nm using the SRIOP.

To explain in more detail, the SRIOP model first assumes that spectral relationships for the total absorption (a) and backscattering (b_b) coefficients can be established among the red and NIR bands. For different in-water constituents, we find monotonic spectral relationships for the total absorption (a) and backscattering (b_b) coefficients including water itself among the 620, 709, 745, and 865 nm bands [42] as follows:

$$a\left({\lambda }_2\right)=c_1+c_{2}a\left({\lambda }_1\right)$$

(6)

$$b_b\left({\lambda }_2\right)=d_1{b}_b{({\lambda }_1)}^{d_2}$$

(7)

where c₁, c₂, d₁, and d₂ are coefficients for the relationship model. Their values are described in

Table 3. Coefficients of SRIOP models for Equations (6) and (7).

	Equation	Coefficients (cn and dn)
		620 nm → 709 nm	709 nm → 745 nm	745 nm → 865 nm
a	$a\left({\lambda }_2\right)=c_{1}a\left({\lambda }_1\right)+c_2$	0.577, 0.746	2.060, 0.947	2.162, 0.864
bb	$b_b\left({\lambda }_2\right)=d_1{b}_b{({\lambda }_1)}^{d_2}$	0.835, 1.011	0.933, 1.003	0.884, 1.009

and Figure 4.

Based on Lee et al. [43], water reflectance ρ_wn(λ) can be derived theoretically from b_b(λ)/{a(λ) + b_b(λ)} and vice versa. To solve ρ_wn(NIR), a and b_b at NIR wavelengths should be estimated from a and b_b at 620 or 709 nm. The four unknown values—a(620 nm), a(709 nm), b_b(620 nm), and b_b(709 nm)—can be solved theoretically, because there are two known values and two known constraints, as in

Table 4. List of known values, known constraints, and unknown values to solve.

Unknown Values (4)	Known Values (2)	Known Constraints (2)
a(620 nm) a(709 nm) bb(620 nm) bb(709 nm)	$\frac{b_b\left(620\mathrm{nm}\right)}{a\left(620\mathrm{nm}\right)+b_b\left(620\mathrm{nm}\right)},$ $\frac{b_b\left(709\mathrm{nm}\right)}{a\left(709\mathrm{nm}\right)+b_b\left(709\mathrm{nm}\right)}$	Relationship between a(620 nm) and a(709 nm) (Equation (6)), Relationship between bb(620 nm) and bb(709 nm) (Equation (7))

.

Finally, the desired values of ρ_wn(745 nm) and ρ_wn(865 nm) can be calculated using the NIR IOP values of a(745 nm), a(865 nm), b_b(745 nm), and b_b(865 nm) from the solved values of a(620 nm) and b_b(620 nm) using SRIOP models (Equations (6) and (7)).

3. Results and Discussion

To compare the NIR turbid water reflectance model for the GOCI-II atmospheric correction process with other approaches, we also implemented the scheme of Bailey et al. [17] (denoted B2010). Scheme B2010 was developed for the Sea-viewing Wide Field-of-view Sensor (SeaWiFS) atmospheric correction algorithm and then implemented in the SeaWiFS Data Analysis System (SeaDAS) ocean color processing software, which is used widely in the ocean color community.

The resulting ρ_wn(NIR) values are converted into R_rs values with Equation (2) to validate the NIR water reflectance model. Then, we analyze our evaluation using statistical indices such as the mean absolute percentage error (MAPE), root mean square error (RMSE), and R squared (R²), which are defined as follows:

$$\mathrm{MAPE}\left(\%\right)=\frac{100}{K}{\displaystyle \sum }_{n=1}^K\left(\raisebox{1ex}{$\left|v_n^t-v_n^e\right|$}\!\left/ \!\raisebox{-1ex}{$v_n^t$}\right.\right)$$

(8)

$$\mathrm{RMSE}=\sqrt{\raisebox{1ex}{${{\displaystyle \sum }}_{n=1}^K{\left(v_n^t-v_n^e\right)}^2$}\!\left/ \!\raisebox{-1ex}{$K$}\right.}$$

(9)

$${\mathrm{R}}^2=1-\raisebox{1ex}{$S_{res}$}\!\left/ \!\raisebox{-1ex}{$S_{tot}$}\right.$$

(10)

where K is the total number of match-up pairs and $v_n^t$ and $v_n^e$ are the true and derived values of the n^th match-up entry, respectively. The terms S_res and S_tot are the sum squared regression and the total sum of squares used to calculate the coefficient of determination.

Figure 5 shows the validation results for R_rs(NIR) for the KOSC (blue) and IOCCG (green) RTSD. For the moderately turbid range, when R_rs(745 nm) is less than 0.0012, the validation results at 745 with RTSD are 0.000087, 0.000084, 0.000033, and 0.000148 for SR660, SR709, SRIOP, and B2010, respectively. These values are approximately 0.5–2.3% of the average aerosol reflectance at 745 nm in the Korean coastal area (the aerosol optical thickness at 865 nm is approximately 0.15 within the cloud mask threshold), and these values are expected to be lower than the acceptable range of the NIR accuracy requirements [44]. Errors among models tend to be more different when turbidity is higher. The SR709 model shows a better correlation than the SR660 model because the 709 nm band is affected less by the chlorophyll-a and CDOM absorptions than is the 660 nm band. Both models tend to show differences in deviation according to the sediment type for KOSC RTSD. Despite the four mineral models having a similar spectral shape in NIR with regard to specific absorption and the specific scattering coefficients, these different deviations occur from the different b/b_b in the different sediment models [28]. Validation of the SR660 and SR709 in the yellow clay and calcareous sand models shows underestimated results, whereas the red clay and brown earth model shows better accuracy. The SRIOP model is more robust than others when seawater includes various sediment types, as shown in the validation using the KOSC RTSD. The B2010 model tends to show differences in deviation according to the sediment type, as for the SR660 and SR709; moreover, it underestimates results for the highly turbid range in which R_rs(745 nm) is larger than 0.0012.

Figure 6 shows the validation results of R_rs(NIR) for the in situ data generally obtained from a highly turbid coastal area. The SR709 model showed the best accuracy as expected because this in situ dataset was used to create the SR709 model. The SR660 and B2010 models showed underestimations compared with the SR709 and SRIOP models with increasing turbidity. Note that the validation results using in situ data showed underestimation of the reflectance in the low turbid range for all models. As shown in Figure 1, an iterative scheme based on the underestimated models might cause inaccurate determination of the aerosol type and concentration, even when the water is not highly turbid water. Using the above-water radiometric measurements, residual errors can emerge by sky radiance or microbubbles that cause a lower signal-to-noise ratio in clear water with a smaller reflectance level at NIR. Further investigation and analysis of the error budget will be required in the next study.

Statistical accuracies for all models are summarized in

Table 5. Summary of statistical accuracies for each model.

		Rrs(745 nm)		Rrs(865 nm)
		RMSE	MAPE	R2	RMSE	MAPE	R2
in situ	SR660	0.00457	28.8	0.88	0.00422	41.7	0.82
	SR709	0.00064	5.8	0.99	0.00119	14.7	0.97
	SRIOP	0.00138	11.0	0.99	0.00140	12.4	0.98
	B2010	0.00654	45.0	0.80	0.00506	45.6	0.70
KOSC RTSD	SR660	0.00180	15.2	0.82	0.00164	29.4	0.71
	SR709	0.00240	39.7	0.87	0.00271	25.5	0.73
	SRIOP	0.00038	7.8	0.99	0.00047	10.6	0.98
	B2010	0.00269	58.1	0.83	0.00216	74.0	0.71
IOCCG RTSD	SR660	0.00023	31.0	0.97
	SR709	0.00003	11.3	1.00
	SRIOP	0.00006	19.4	0.99
	B2010	0.00026	13.8	0.88
Color scale for mean absolute percentage error (MAPE).

.

4. Summary and Conclusions

The atmospheric correction algorithm developed for GOCI and GOCI-II is theoretically based on the work of Gordon and Wang [7], which uses two NIR wavelengths (745 and 865 nm for GOCI and GOCI-II) to determine aerosol reflectance in visible bands. The algorithm based on the two NIR bands requires optimization using additional visible bands to handle non-negligible NIR water reflectance over turbid waters; thus, the GOCI-II algorithm employs 620, 660, 709, 745, and 865 nm regions for aerosol correction.

For iterative optimization for the GOCI-II turbid water atmospheric correction algorithm, we developed two candidate NIR water reflectance models using (1) the spectral relationship of water reflectance between 709 nm and two NIR wavelengths (SR709) and (2) the spectral relationships of IOPs (i.e., total absorption and backscattering coefficients; SRIOP). The validation results show that both the SR709 and SRIOP models are more accurate than the SR660 and B2010 models.

The SR709 model is a simple extension of the GOCI scheme (SR660), which is more reliable for different absorptions by chlorophyll and CDOM. The SRIOP model is slightly less accurate than the SR709 model if the validation data are composited with a single sediment type such as the in situ dataset or the IOCCG RTSD. However, SR709 tends to give more robust and versatile results for various sediment types as a validation result using the KOSC RTSD.

Although the SRIOP scheme gives reliable results, the spectral relationships of IOPs used for the scheme have not been verified with the field measured dataset in this study. Further investigation and verification of the IOPs’ spectral relationships based on the in situ data should be done in the future.

Both the SR709 and SRIOP models will be implemented for the Ocean Data Processing System of the GOCI-II Ground Segment by KOSC of the Korea Institute of Ocean Science and Technology. The SR709 is expected to be more accurate in terms of the Northeast Asian Sea, which is the main observation area of GOCI and GOCI-II missions. The SRIOP is expected to be more useful for the full-disk area than the local area (i.e., the newly extended observation mission of GOCI-II), where there are likely various sediment types. Users will be able to select the appropriate model for a given area. Although the SR709 and SRIOP algorithms are designed for GOCI-II, they can also be applied to other ocean color sensors that have similar bands, such as MEdium Resolution Imaging Spectrometer (MERIS), Ocean and Land Colour Instrument (OLCI), Ocean Colour Monitor (OCM)-3, Ocean Color Instrument (OCI), or Geosynchronous Littoral Imaging and Monitoring Radiometer (GLIMR).