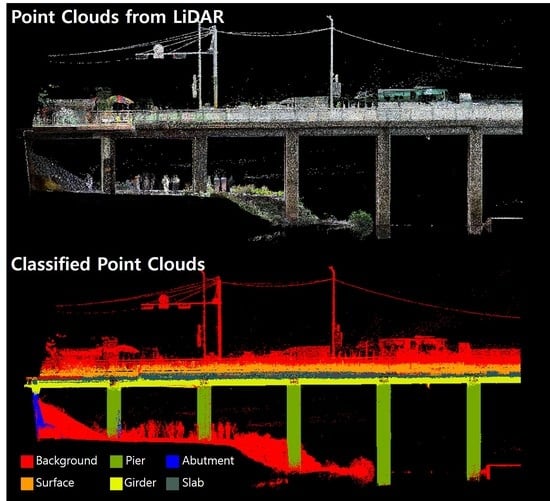
Deep-Learning-Based Classification of Point Clouds for Bridge Inspection
Abstract
1. Introduction
2. Related Work
3. Deep-Learning Algorithms
- -
- They can handle semantic segmentation problems for point cloud data.
- -
- They can use irregular point cloud data without converting it into a regular format.
- -
- They use the same block sampling method introduced by Qi, Su, Mo and Guibas [33].
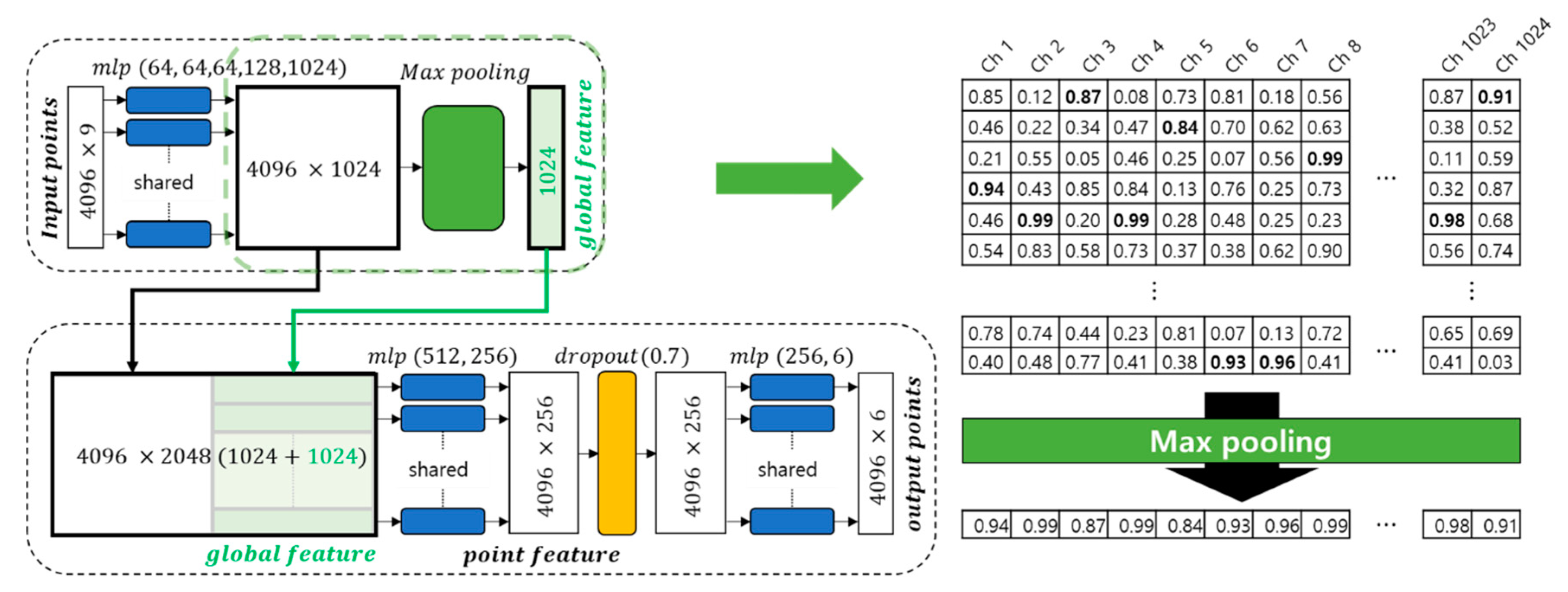
3.1. PointNet
3.2. PointCNN
3.3. DGCNN
4. Methodology
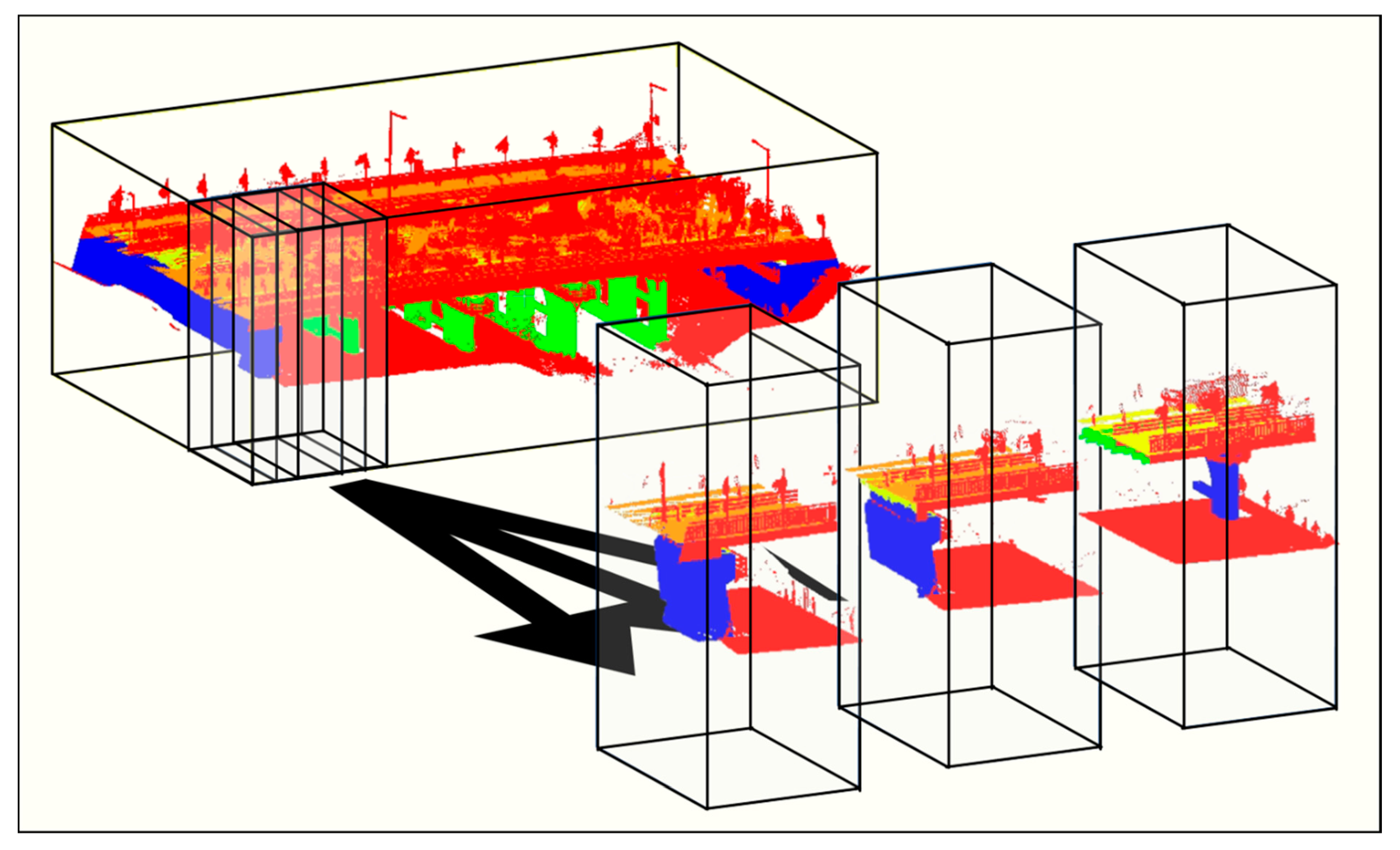
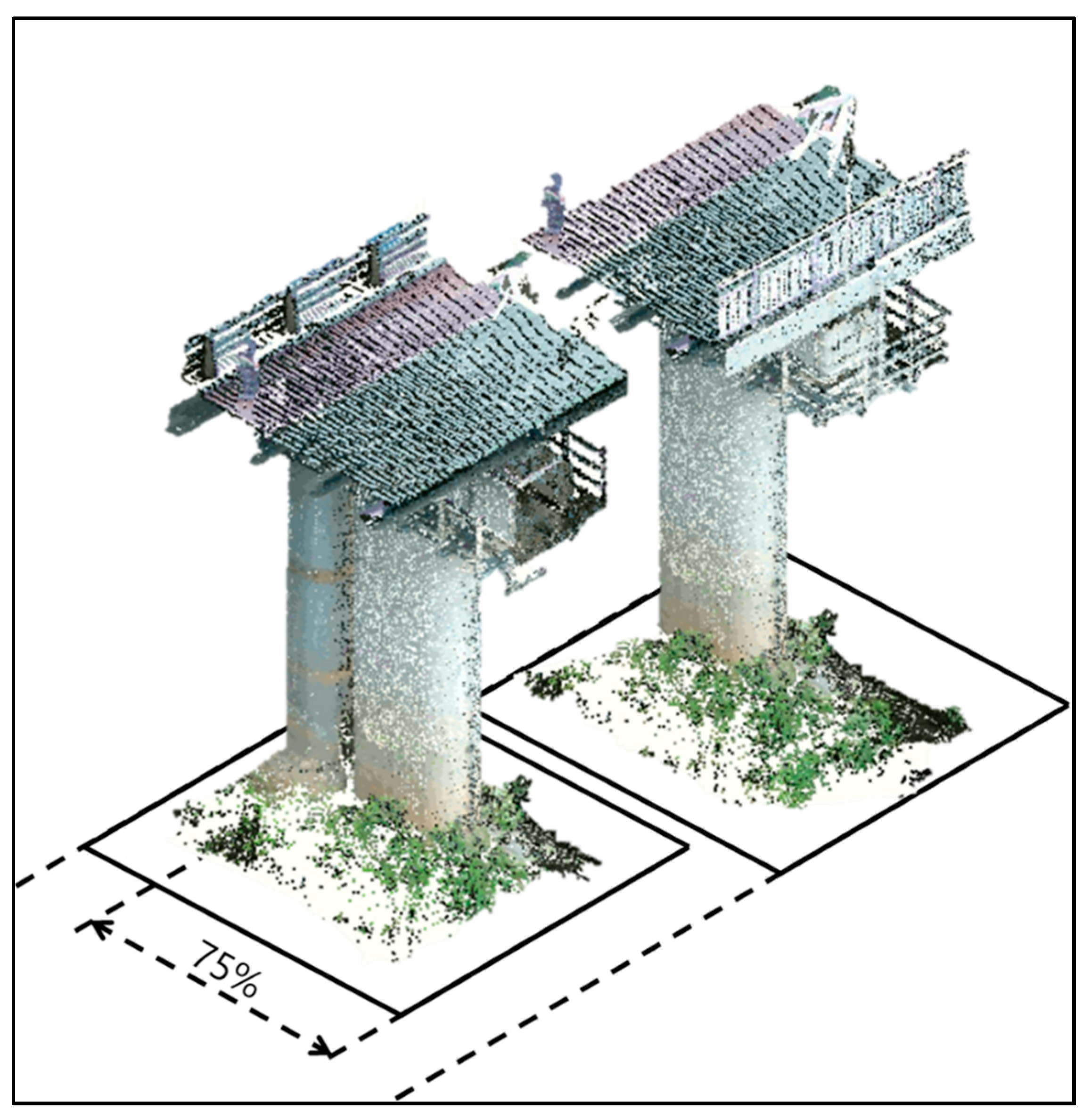
4.1. Block Partitioning for Model Input
4.2. Performance Measures
4.3. Cross-Validation
4.4. Hyperparameter Tuning
5. Experiment and Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rothballer, C.; Lam-Frendo, M.; Kim, H. Strategic Infrastructure Steps to Operate and Maintain Infrastructure Efficiently and Effectively; Forum, I.W.E., Ed.; World Economic Forum: Geneva Canton, Switzerland, 2014. [Google Scholar]
- Musick, N.; Petz, A. Public Spending on Transportation and Water Infrastructure, 1956 to 2014; Congressional Budget Office, Ed.; US Congressional Budget Office: Washington, DC, USA, 2015. [Google Scholar]
- Japanese Public Finance Fact Sheet; Japanese Ministry of Finance, Ed.; Japanese Ministry of Finance: Tokyo, Japan, 2017.
- Strategies for National Infrastructure Intelligence for Innovative Growth. (Smart SOC); Korea National Information Society Agency, Ed.; Korea National Information Society Agency: Seoul, Korea, 2017. [Google Scholar]
- Korea Infrastructure Safety Corporation Status of Public Facility Safety Management; Korea Infrastructure Safety Corporation: Seoul, Korea, 2020.
- The First Basic Plan for Infrastructure Management; Korea Ministry of Land, Infrastructure and Transport, Ed.; Construction Policy Institute of Korea: Seoul, Korea, 2019.
- Yang, Y.-S.; Wu, C.-l.; Hsu, T.T.; Yang, H.-C.; Lu, H.-J.; Chang, C.-C. Image analysis method for crack distribution and width estimation for reinforced concrete structures. Automat. Constr. 2018, 91, 120–132. [Google Scholar] [CrossRef]
- Chen, Z.; Li, H.; Bao, Y.; Li, N.; Jin, Y. Identification of spatio-temporal distribution of vehicle loads on long-span bridges using computer vision technology. Struct. Control Health Monit. 2016, 23, 517–534. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, D.; Shen, X.; Xu, Y.; Pan, Z. A novel computer vision-based monitoring methodology for vehicle-induced aerodynamic load on noise barrier. Struct. Control Health Monit. 2018, 25, e2271. [Google Scholar] [CrossRef]
- Dutton, M.; Take, W.A.; Hoult, N.A. Curvature monitoring of beams using digital image correlation. J. Bridge Eng. 2014, 19, 05013001. [Google Scholar] [CrossRef]
- Hoult, N.A.; Take, W.A.; Lee, C.; Dutton, M. Experimental accuracy of two dimensional strain measurements using digital image correlation. Eng. Struct. 2013, 46, 718–726. [Google Scholar] [CrossRef]
- Lydon, D.; Lydon, M.; Taylor, S.; Del Rincon, J.M.; Hester, D.; Brownjohn, J. Development and field testing of a vision-based displacement system using a low cost wireless action camera. Mech. Syst. Signal Process. 2019, 121, 343–358. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.-C.; Jeong, S.; Lee, Y.-J.; Sim, S.-H. Long-term displacement measurement of full-scale bridges using camera ego-motion compensation. Mech. Syst. Signal Process. 2020, 140, 106651. [Google Scholar] [CrossRef]
- Yoon, H.; Shin, J.; Spencer, B.F., Jr. Structural displacement measurement using an unmanned aerial system. Comput.-Aided Civil Infrastruct. Eng. 2018, 33, 183–192. [Google Scholar] [CrossRef]
- Kim, H.; Ahn, E.; Cho, S.; Shin, M.; Sim, S.-H. Comparative analysis of image binarization methods for crack identification in concrete structures. Cem. Concr. Res. 2017, 99, 53–61. [Google Scholar] [CrossRef]
- Kim, K.; Sohn, H. Dynamic displacement estimation by fusing LDV and LiDAR measurements via smoothing based Kalman filtering. Mech. Syst. Signal Process. 2017, 82, 339–355. [Google Scholar] [CrossRef]
- Lee, J.; Lee, K.C.; Lee, S.; Lee, Y.J.; Sim, S.H. Long-term displacement measurement of bridges using a LiDAR system. Struct. Control Health Monit. 2019, 26, e2428. [Google Scholar] [CrossRef]
- Cabaleiro, M.; Riveiro, B.; Arias, P.; Caamaño, J. Algorithm for the analysis of deformations and stresses due to torsion in a metal beam from LIDAR data. Struct. Control Health Monit. 2016, 23, 1032–1046. [Google Scholar] [CrossRef]
- Jaafar, H.A.; Meng, X.; Sowter, A.; Bryan, P. New approach for monitoring historic and heritage buildings: Using terrestrial laser scanning and generalised Procrustes analysis. Struct. Control Health Monit. 2017, 24, e1987. [Google Scholar] [CrossRef]
- Dai, K.; Li, A.; Zhang, H.; Chen, S.E.; Pan, Y. Surface damage quantification of postearthquake building based on terrestrial laser scan data. Struct. Control Health Monit. 2018, 25, e2210. [Google Scholar] [CrossRef]
- Law, D.W.; Silcock, D.; Holden, L. Terrestrial laser scanner assessment of deteriorating concrete structures. Struct. Control Health Monit. 2018, 25, e2156. [Google Scholar] [CrossRef]
- Sánchez-Rodríguez, A.; Riveiro, B.; Conde, B.; Soilán, M. Detection of structural faults in piers of masonry arch bridges through automated processing of laser scanning data. Struct. Control Health Monit. 2018, 25, e2126. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Vela, P.A. Scan2BrIM: IFC Model Generation of Concrete Bridges from Point Clouds. In Proceedings of the Computing in Civil Engineering 2019: Visualization, Information Modeling, and Simulation, American Society of Civil Engineers, Atlanta, GA, USA, 17–19 June 2019; pp. 455–463. [Google Scholar]
- Lu, R.D.; Brilakis, I.; Middleton, C.R. Detection of Structural Components in Point Clouds of Existing RC Bridges. Comput.-Aided Civil Infrastruct. Eng. 2019, 34, 191–212. [Google Scholar] [CrossRef]
- Kim, H.; Yoon, J.; Sim, S.H. Automated bridge component recognition from point clouds using deep learning. Struct. Control Health Monit. 2020, 27, e2591. [Google Scholar] [CrossRef]
- Ma, L.; Sacks, R.; Kattel, U.; Bloch, T. 3D Object Classification Using Geometric Features and Pairwise Relationships. Comput.-Aided Civil Infrastruct. Eng. 2018, 33, 152–164. [Google Scholar] [CrossRef]
- Dimitrov, A.; Gu, R.; Golparvar-Fard, M. Non-uniform B-spline surface fitting from unordered 3D point clouds for as-built modeling. Comput.-Aided Civil Infrastruct. Eng. 2016, 31, 483–498. [Google Scholar] [CrossRef]
- Walsh, S.B.; Borello, D.J.; Guldur, B.; Hajjar, J.F. Data processing of point clouds for object detection for structural engineering applications. Comput.-Aided Civil Infrastruct. Eng. 2013, 28, 495–508. [Google Scholar] [CrossRef]
- Vo, A.-V.; Truong-Hong, L.; Laefer, D.F.; Bertolotto, M. Octree-based region growing for point cloud segmentation. ISPRS J. Photogramm. Remote Sens. 2015, 104, 88–100. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Xu, Y.; Tuttas, S.; Hoegner, L.; Stilla, U. Voxel-based segmentation of 3D point clouds from construction sites using a probabilistic connectivity model. Pattern Recognit. Lett. 2018, 102, 67–74. [Google Scholar] [CrossRef]
- Laefer, D.F.; Truong-Hong, L. Toward automatic generation of 3D steel structures for building information modelling. Autom. Constr. 2017, 74, 66–77. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.C.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. Proc. Cvpr. IEEE 2017, 77–85. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X.; Chen, Z.; Lu, Z. A Review of Deep Learning-Based Semantic Segmentation for Point Cloud. IEEE Access 2019, 7, 179118–179133. [Google Scholar] [CrossRef]
- Li, Y.Y.; Bu, R.; Sun, M.C.; Wu, W.; Di, X.H.; Chen, B.Q. PointCNN: Convolution On X -Transformed Points. Adv. Neur. Inf. 2018, 31, 820–830. [Google Scholar]
- Wang, Y.; Sun, Y.B.; Liu, Z.W.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. Acm Trans. Graphic 2019, 38. [Google Scholar] [CrossRef]
- Bello, S.A.; Yu, S.; Wang, C.; Adam, J.M.; Li, J. deep learning on 3D point clouds. Remote Sens. 2020, 12, 1729. [Google Scholar] [CrossRef]
- Braga-Neto, U.; Hashimoto, R.; Dougherty, E.R.; Nguyen, D.V.; Carroll, R.J. Is cross-validation better than resubstitution for ranking genes? Bioinformatics 2004, 20, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Kim, J.-H. Estimating classification error rate: Repeated cross-validation, repeated hold-out and bootstrap. Comput. Stat. Data Anal. 2009, 53, 3735–3745. [Google Scholar] [CrossRef]
- Braga-Neto, U.; Dougherty, E. Bolstered error estimation. Pattern Recognit. 2004, 37, 1267–1281. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Datasheet—Trimble TX8 Laser Scanner. Available online: https://de.geospatial.trimble.com/sites/geospatial.trimble.com/files/2019-03/Datasheet%20-%20Trimble%20TX8%20Laser%20Scanner%20-%20English%20A4%20-%20Screen.pdf (accessed on 6 November 2020).
- Trimble RealWorks|Trimble Geospatial. Available online: https://geospatial.trimble.com/products-and-solutions/trimble-realworks (accessed on 6 November 2020).



| Bridge | Lengths of the Piers along the Longitudinal Direction (m) | Width (m) | Length (m) |
|---|---|---|---|
| Bridge1 | 40.00 | 35.73 | 282.23 |
| Bridge2 | 10.00 | 41.42 | 67.28 |
| Bridge3 | 7.00 | 29.65 | 87.45 |
| Fold | Train | Validation |
|---|---|---|
| 1 | Bridge 1–2, Bridge 2–1, Bridge 2–2, Bridge 3–1 | Bridge 1–1, Bridge 3–2 |
| 2 | Bridge 1–1, Bridge 1–2, Bridge 2–2, Bridge 3–2 | Bridge 2–1, Bridge 3–1 |
| 3 | Bridge 1–2, Bridge 2–1, Bridge 2–2, Bridge 3–1 | Bridge 1–2, Bridge 2–2 |
| Model | Hyperparameter | Value |
|---|---|---|
| PointNet | Epoch | 60 |
| Batch size | 36 | |
| Learning rate | 0.001 | |
| PointCNN | Epoch | 60 |
| Batch size | 8 | |
| Learning rate | 0.001 | |
| DGCNN | Epoch | 60 |
| Batch size | 12 | |
| Learning rate | 0.001 |
| Block Size | 50% | 66% | 75% | 80% |
|---|---|---|---|---|
| PointNet | ||||
| 3 m | 70.09% | 79.99% | 88.96% | 93.83% |
| 6 m | 65.65% | 67.17% | 69.48% | 68.31% |
| 9 m | 60.30% | 64.46% | 63.41% | 65.60% |
| 12 m | 61.14% | 59.68% | 62.32% | 64.89% |
| 15 m | 58.25% | 56.51% | 55.42% | 61.22% |
| DGCNN | ||||
| 3 m | 84.69% | 89.67% | 93.44% | 94.49% |
| 6 m | 69.58% | 76.36% | 75.62% | 87.03% |
| 9 m | 54.73% | 64.12% | 74.12% | 69.53% |
| 12 m | 55.08% | 59.33% | 61.97% | 63.00% |
| 15 m | 58.16% | 63.10% | 52.47% | 59.41% |
| PointCNN | ||||
| 3 m | 91.25% | 89.57% | 91.04% | 91.39% |
| 6 m | 92.55% | 91.58% | 91.94% | 92.00% |
| 9 m | 91.14% | 91.07% | 90.49% | 91.23% |
| 12 m | 89.79% | 91.41% | 91.12% | 90.71% |
| 15 m | 90.64% | 90.85% | 91.14% | 90.19% |
| IoU | PointNet | PointCNN | DGCNN |
|---|---|---|---|
| Abutment | 55.47% | 30.87% | 73.78% |
| Slab | 97.90% | 95.69% | 96.39% |
| Pier | 92.22% | 75.45% | 79.11% |
| Girder | 90.96% | 92.18% | 91.71% |
| Surface | 80.59% | 78.45% | 88.38% |
| Background | 88.62% | 88.06% | 91.74% |
| Mean IoU | 84.29% | 76.78% | 86.85% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Kim, C. Deep-Learning-Based Classification of Point Clouds for Bridge Inspection. Remote Sens. 2020, 12, 3757. https://doi.org/10.3390/rs12223757
Kim H, Kim C. Deep-Learning-Based Classification of Point Clouds for Bridge Inspection. Remote Sensing. 2020; 12(22):3757. https://doi.org/10.3390/rs12223757
Chicago/Turabian StyleKim, Hyunsoo, and Changwan Kim. 2020. "Deep-Learning-Based Classification of Point Clouds for Bridge Inspection" Remote Sensing 12, no. 22: 3757. https://doi.org/10.3390/rs12223757
APA StyleKim, H., & Kim, C. (2020). Deep-Learning-Based Classification of Point Clouds for Bridge Inspection. Remote Sensing, 12(22), 3757. https://doi.org/10.3390/rs12223757