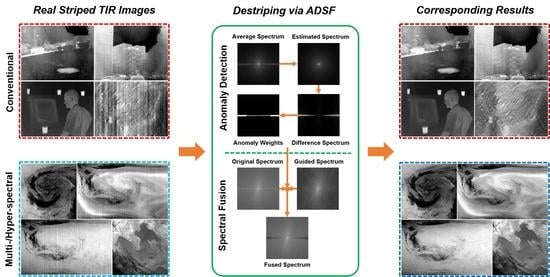
Fourier Domain Anomaly Detection and Spectral Fusion for Stripe Noise Removal of TIR Imagery
Abstract
1. Introduction
1.1. Two Striped TIR Image Cases
1.2. Related Work
1.3. Motivation
- The respective spectral characteristics of TIR images and stripe noise are explored systematically. On this basis, a Fourier domain anomaly detection method is proposed to locate the abnormal frequencies that are likely to be contaminated by stripe noise. As a result, an anomaly weight map is obtained.
- With the anomaly weight map, a fusion strategy between the original spectrum and the spectrum of a stripe-free guidance image is adopted to generate the new Fourier spectrum and then to reconstruct the destriped image. In the implementation, the guidance image is estimated via an adequate de-texture filter.
- Extensive experiments on real striped TIR data including conventional TIR images and remote sensing spectral images are performed. The results demonstrate that the proposed method has better destriping ability and stronger robustness, compared with the state-of-the-art destriping methods in the two fields.
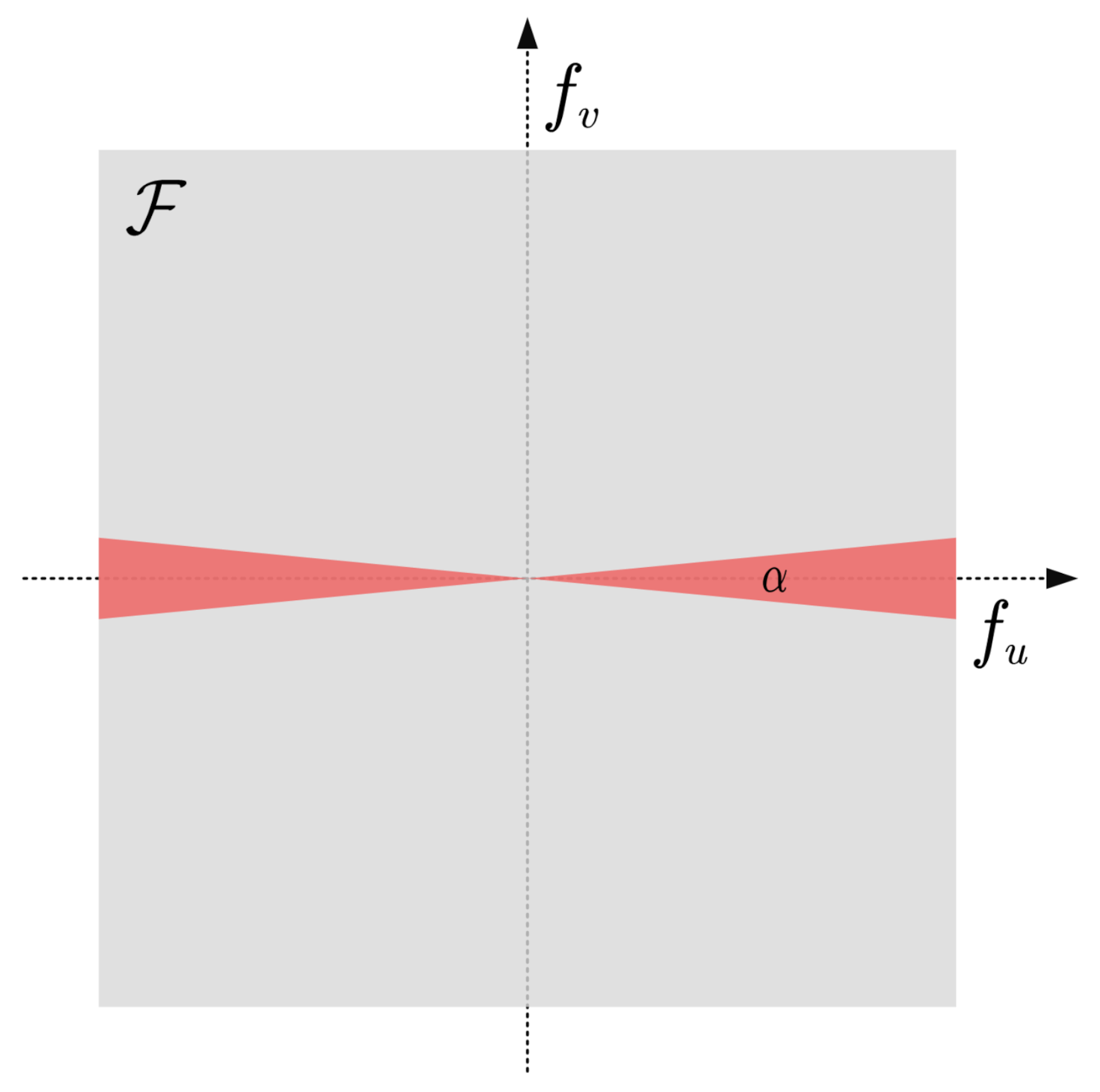
2. Spectral Analysis
2.1. Brief Reminder and Notations
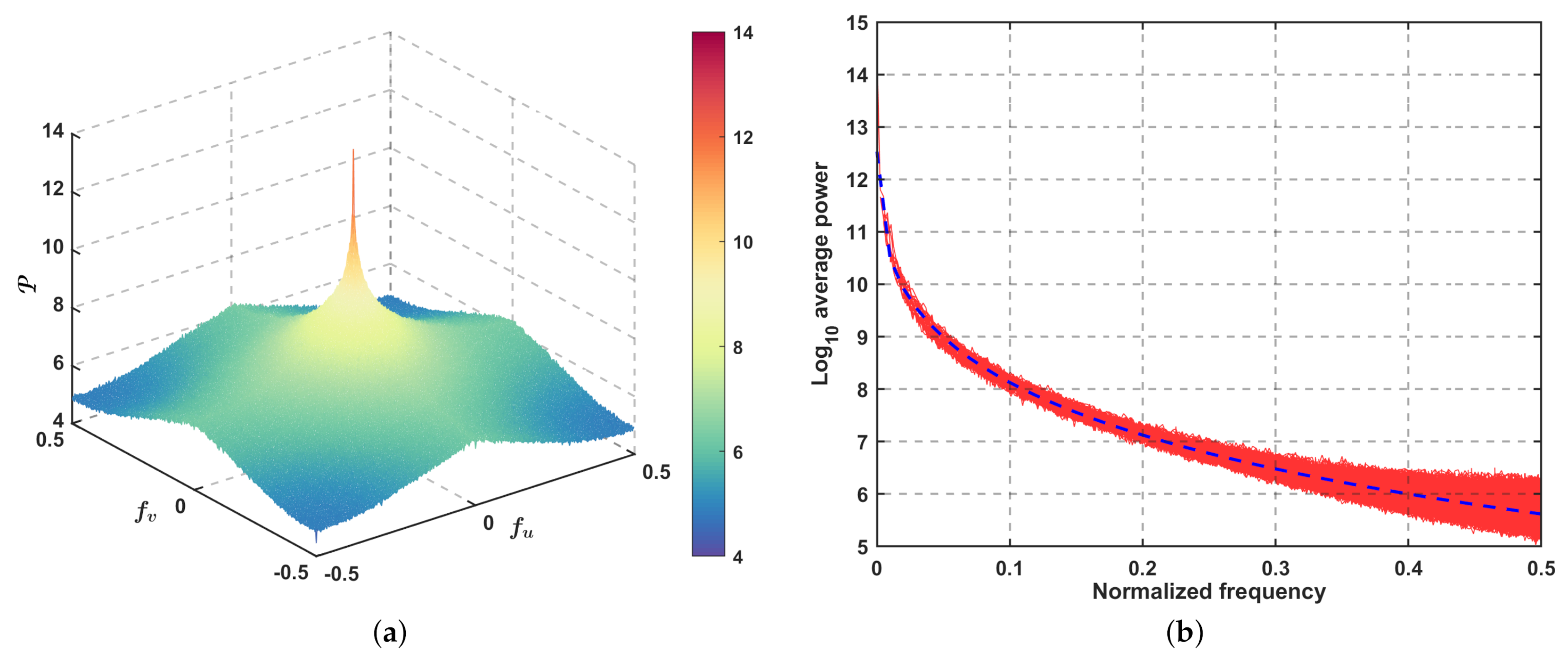
2.2. Spectral Statistics of TIR Images
2.3. Spectral Distribution of Stripe Noise
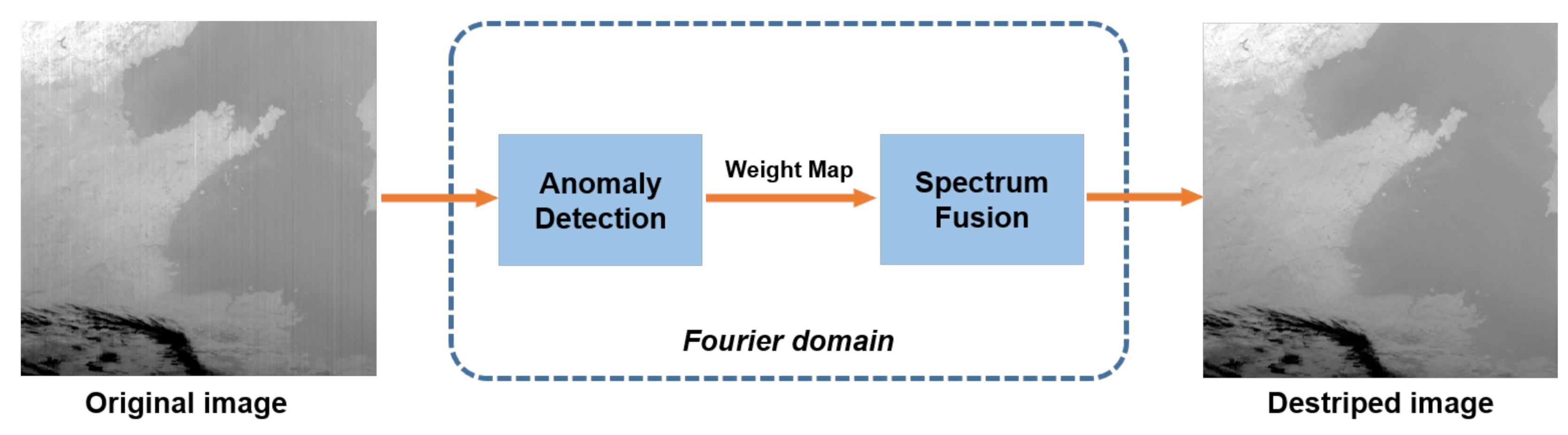
3. Methodology
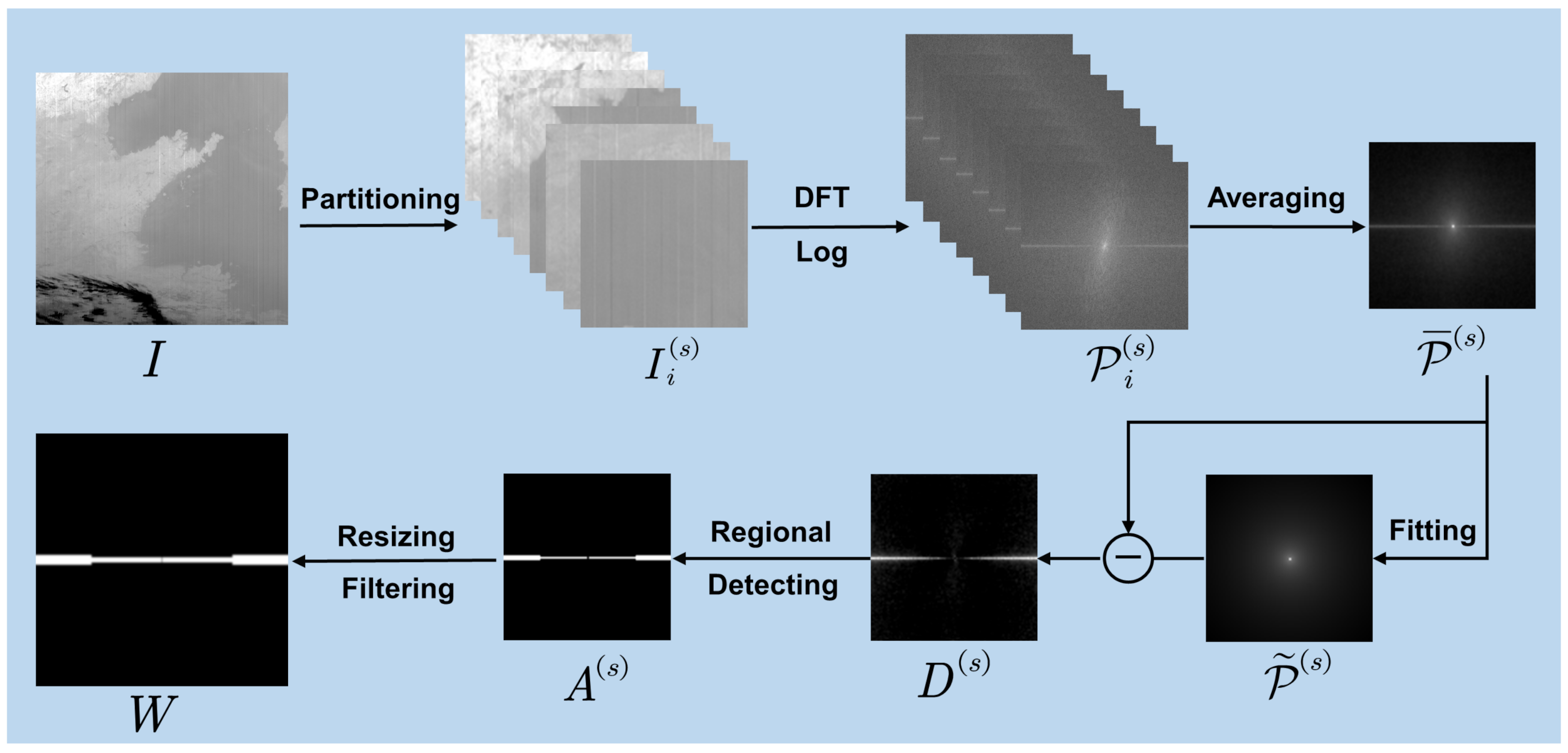
3.1. Anomaly Detection
3.1.1. Spectral Estimation
3.1.2. Regional Detection
3.2. Guidance Image Based Spectrum Fusion
3.2.1. Guidance Image Generation
3.2.2. Fourier Spectrum Fusion
3.3. Practical Considerations
4. Experimental Results and Discussion
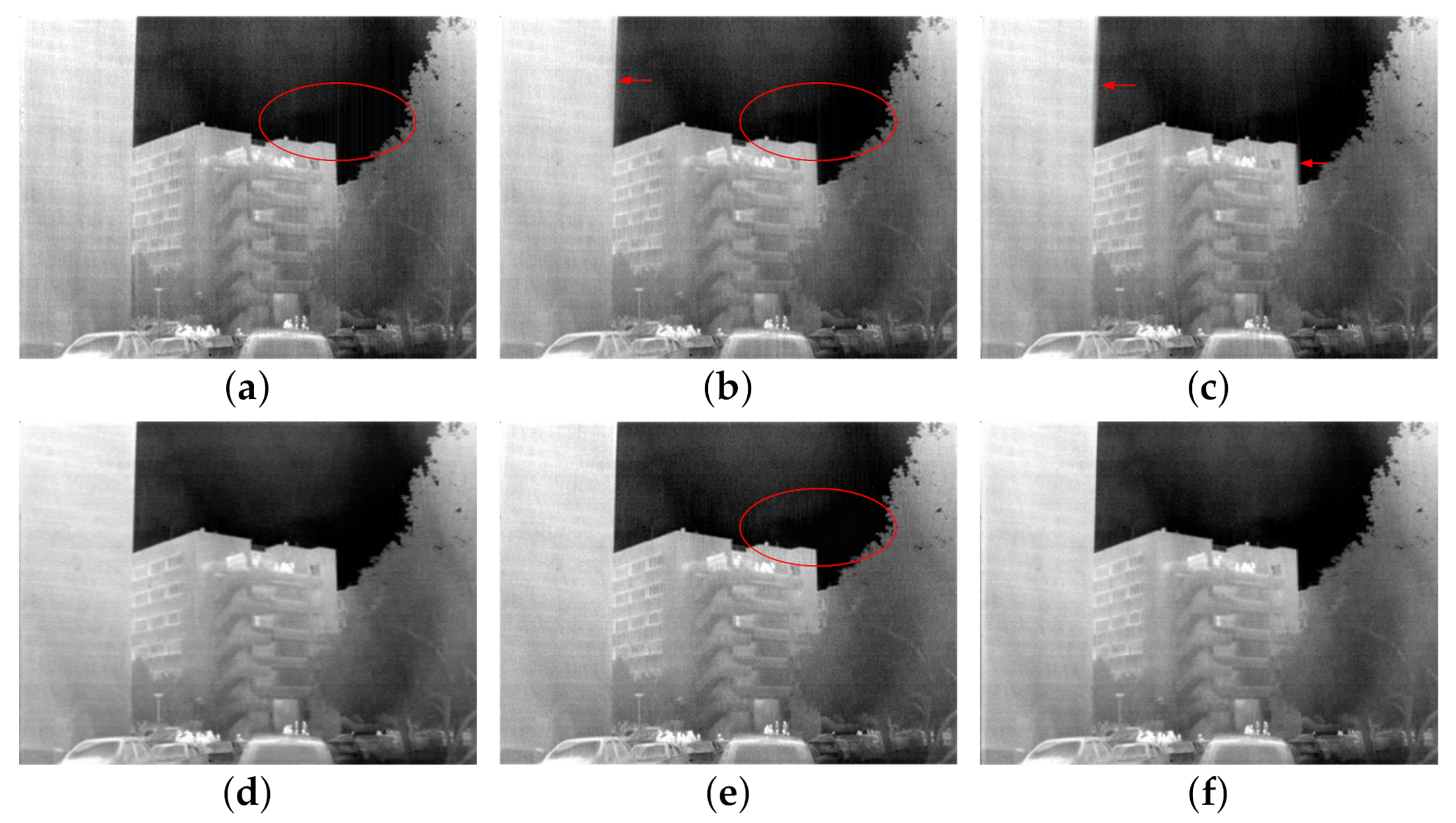
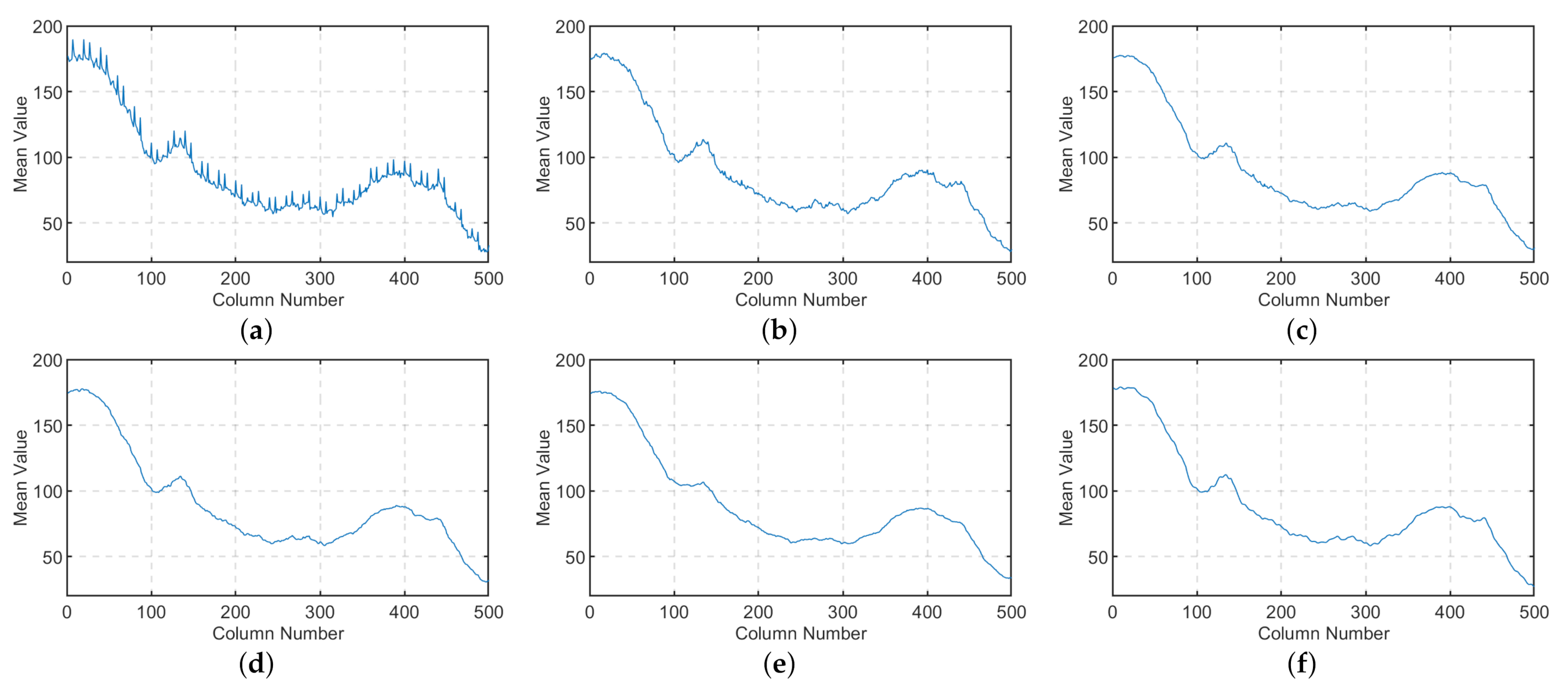
4.1. Experiments on Conventional TIR Images
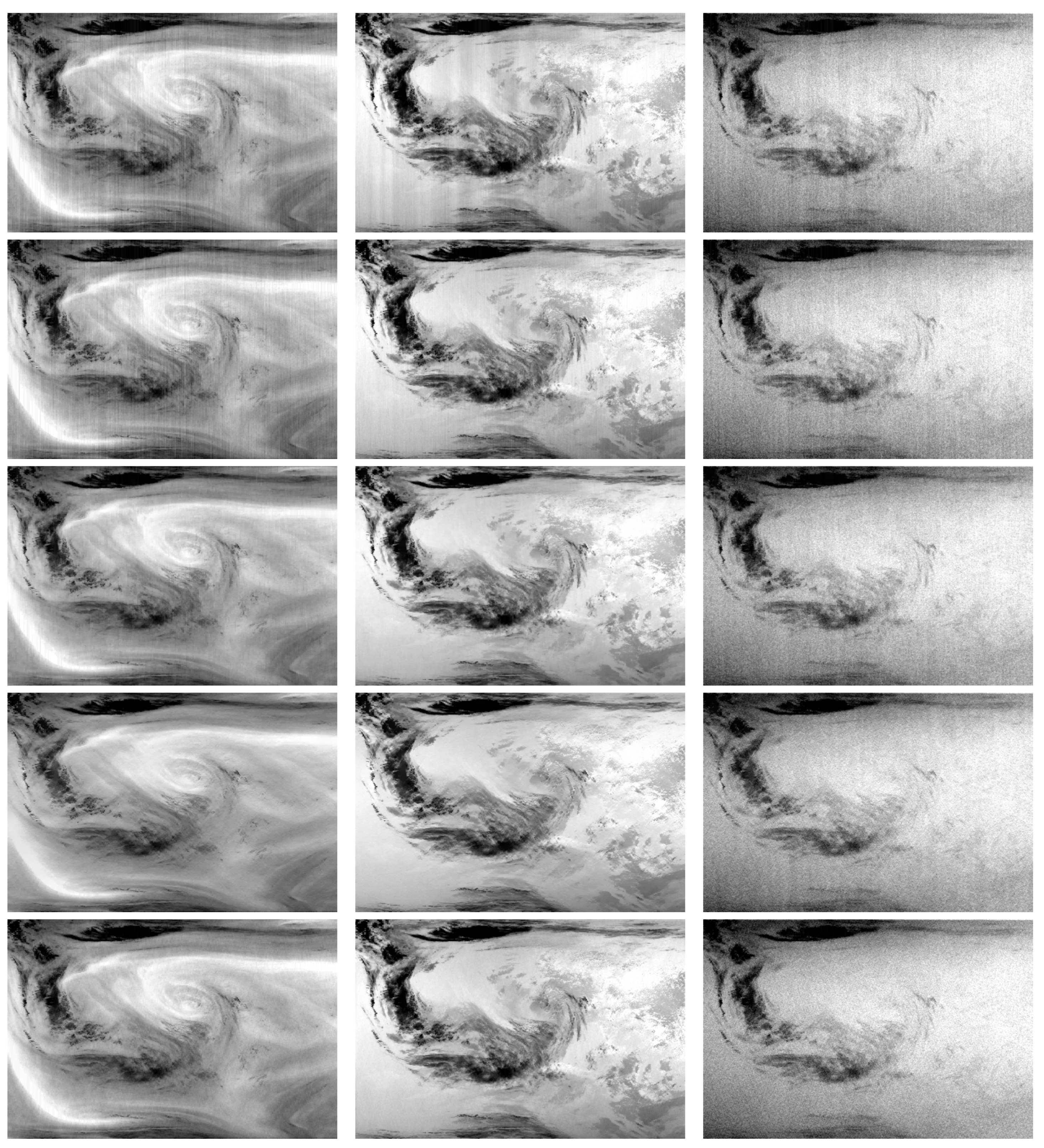
4.2. Experiments on Remote Sensing Spectral Images
4.3. Discussion
4.3.1. Parameter Analysis
4.3.2. Running Time
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sobrino, J.A.; Del Frate, F.; Drusch, M.; Jiménez-Muñoz, J.C.; Manunta, P.; Regan, A. Review of thermal infrared applications and requirements for future high-resolution sensors. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2963–2972. [Google Scholar]
- Tronin, A.A.; Hayakawa, M.; Molchanov, O.A. Thermal IR satellite data application for earthquake research in Japan and China. J. Geodyn. 2002, 33, 519–534. [Google Scholar]
- Blackett, M. An overview of infrared remote sensing of volcanic activity. J. Imaging 2017, 3, 13. [Google Scholar]
- Chen, Y.; Duan, S.; Ren, H.; Labed, J.; Li, Z. Algorithm development for land surface temperature retrieval: Application to Chinese Gaofen-5 data. Remote Sens. 2017, 9, 161. [Google Scholar]
- Stark, B.; Smith, B.; Chen, Y. Survey of thermal infrared remote sensing for unmanned aerial systems. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 1294–1299. [Google Scholar]
- Ren, P.; Meng, Q.; Zhang, Y.; Zhao, L.; Yuan, X.; Feng, X. An unmanned airship thermal infrared remote sensing system for low-altitude and high spatial resolution monitoring of urban thermal environments integration and an experiment. Remote Sens. 2015, 7, 14259–14275. [Google Scholar]
- Rahaghi, A.I.; Lemmin, U.; Sage, D.; Barry, D.A. Achieving high-resolution thermal imagery in low-contrast lake surface waters by aerial remote sensing and image registration. Remote Sens. Environ. 2019, 221, 773–783. [Google Scholar]
- Qian, W.; Chen, Q.; Gu, G.; Guan, Z. Correction method for stripe nonuniformity. Appl. Opt. 2010, 49, 1764–1773. [Google Scholar]
- Cao, Y.; Li, Y. Strip non-uniformity correction in uncooled long-wave infrared focal plane array based on noise source characterization. Opt. Commun. 2015, 339, 236–242. [Google Scholar]
- Goodall, T.R.; Bovik, A.C.; Paulter, N.G. Tasking on natural statistics of infrared images. IEEE Trans. Image Process. 2016, 25, 65–79. [Google Scholar]
- Cao, Y.; He, Z.; Yang, J.; Cao, Y.; Yang, M.Y. Spatially adaptive column fixed-pattern noise correction in infrared imaging system using 1D horizontal differential statistics. IEEE Photonics J. 2017, 9, 1–13. [Google Scholar]
- Gadallah, F.L.; Csillag, F.; Smith, E.J.M. Destriping multisensor imagery with moment matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Stripe noise reduction in MODIS data by combining histogram matching with facet filter. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1844–1856. [Google Scholar]
- Kang, Y.; Pan, L.; Sun, M.; Liu, X.; Chen, Q. Destriping high-resolution satellite imagery by improved moment matching. Int. J. Remote Sens. 2017, 38, 6346–6365. [Google Scholar]
- Jia, J.; Wang, Y.; Cheng, X.; Yuan, L.; Zhao, D.; Ye, Q.; Zhuang, X.; Shu, R.; Wang, J. Destriping algorithms based on statistics and spatial filtering for visible-to-thermal infrared pushbroom hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4077–4091. [Google Scholar]
- Cao, Y.; Yang, M.Y.; Tisse, C.L. Effective strip noise removal for low-textured infrared images based on 1-D guided filtering. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 2176–2188. [Google Scholar]
- Li, F.; Zhao, Y.; Xiang, W. Single-frame-based column fixed-pattern noise correction in an uncooled infrared imaging system based on weighted least squares. Appl. Opt. 2019, 58, 9141–9153. [Google Scholar]
- Carfantan, H.; Idier, J. Statistical linear destriping of satellite-based pushbroom-type images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1860–1871. [Google Scholar]
- Tendero, Y.; Landeau, S.; Gilles, J. Non-uniformity correction of infrared images by midway equalization. Image Process. Line 2012, 2, 134–146. [Google Scholar]
- Shen, H.; Jiang, W.; Zhang, H.; Zhang, L. A piece-wise approach to removing the nonlinear and irregular stripes in MODIS data. Int. J. Remote Sens. 2014, 35, 44–53. [Google Scholar]
- Bouali, M.; Ladjal, S. Toward optimal destriping of MODIS data using a unidirectional variational model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar]
- Chang, Y.; Fang, H.; Yan, L.; Liu, H. Robust destriping method with unidirectional total variation and framelet regularization. Opt. Express 2013, 21, 23307–23323. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zheng, X.; Pan, J.; Wang, B. Unidirectional total variation destriping using difference curvature in MODIS emissive bands. Infrared Phys. Technol. 2016, 75, 1–11. [Google Scholar] [CrossRef]
- Huang, Y.; He, C.; Fang, H.; Wang, X. Iteratively reweighted unidirectional variational model for stripe non-uniformity correction. Infrared Phys. Technol. 2016, 75, 107–116. [Google Scholar] [CrossRef]
- Boutemedjet, A.; Deng, C.; Zhao, B. Edge-aware unidirectional total variation model for stripe non-uniformity correction. Sensors 2018, 18, 1164. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Yan, L.; Wu, T.; Zhong, S. Remote sensing image stripe noise removal: From image decomposition perspective. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7018–7031. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, X.; Ma, T.; Chen, Y.; Huang, T.; Ding, M. Remote sensing images destriping using unidirectional hybrid total variation and nonconvex low-rank regularization. J. Comput. Appl. Math. 2020, 363, 124–144. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Shen, H.; Yuan, Q.; Jiao, Y.; Zhang, L. Stripe noise separation and removal in remote sensing images by consideration of the global sparsity and local variational properties. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3049–3060. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, T.; Deng, L.; Zhao, X.; Wang, M. Group sparsity based regularization model for remote sensing image stripe noise removal. Neurocomputing 2017, 267, 95–106. [Google Scholar] [CrossRef]
- Dou, H.; Huang, T.; Deng, L.; Zhao, X.; Huang, J. Directional l0 sparse modeling for image stripe noise removal. Remote Sens. 2018, 10, 361. [Google Scholar] [CrossRef]
- Xiao, P.; Guo, Y.; Zhuang, P. Removing stripe noise from infrared cloud images via deep convolutional networks. IEEE Photonics J. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- He, Z.; Cao, Y.; Dong, Y.; Yang, J.; Cao, Y.; Tisse, C.L. Single-image-based nonuniformity correction of uncooled long-wave infrared detectors: A deep-learning approach. Appl. Opt. 2018, 57, D155–D164. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Yan, L.; Liu, L.; Fang, H.; Zhong, S. Infrared aerothermal nonuniform correction via deep multiscale residual network. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1120–1124. [Google Scholar] [CrossRef]
- Guan, J.; Lai, R.; Xiong, A.; Liu, Z.; Gu, L. Fixed pattern noise reduction for infrared images based on cascade residual attention CNN. Neurocomputing 2020, 377, 301–313. [Google Scholar] [CrossRef]
- Chang, Y.; Chen, M.; Yan, L.; Zhao, X.L.; Li, Y.; Zhong, S. Toward universal stripe removal via wavelet-based deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2880–2897. [Google Scholar] [CrossRef]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet-Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Pan, J.J.; Chang, C.I. Destriping of Landsat MSS images by filtering techniques. Photogramm. Eng. Remote Sens. 1992, 58, 1417. [Google Scholar]
- Chen, J.; Shao, Y.; Guo, H.; Wang, W.; Zhu, B. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- Torres, J.; Infante, S.O. Wavelet analysis for the elimination of striping noise in satellite images. Opt. Eng. 2001, 40, 1309–1314. [Google Scholar]
- Yang, Z.; Li, J.; Menzel, W.P.; Frey, R.A. Destriping for MODIS data via wavelet shrinkage. Proc. SPIE Appl. Weather Satell. 2003, 4895, 187–199. [Google Scholar]
- Cao, Y.; He, Z.; Yang, J.; Ye, X.; Cao, Y. A multi-scale non-uniformity correction method based on wavelet decomposition and guided filtering for uncooled long wave infrared camera. Signal Process. Image Commun. 2018, 60, 13–21. [Google Scholar] [CrossRef]
- Zeng, Q.; Qin, H.; Yan, X.; Zhou, H. Fourier spectrum guidance for stripe noise removal in thermal infrared imagery. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1072–1076. [Google Scholar] [CrossRef]
- Guan, J.; Lai, R.; Xiong, A. Wavelet deep neural network for stripe noise removal. IEEE Access 2019, 7, 44544–44554. [Google Scholar] [CrossRef]
- Pei, J.; Zou, M.; Zhao, Y. Adaptive comb-type filtering method for stripe noise removal in infrared images. J. Electron. Imaging 2019, 28, 013037. [Google Scholar] [CrossRef]
- Lin, J.; Zuo, H.; Ye, Y.; Liao, X. Histogram-based autoadaptive filter for destriping NDVI imagery acquired by UAV-loaded multispectral camera. IEEE Geosci. Remote Sens. Lett. 2019, 16, 648–652. [Google Scholar] [CrossRef]
- Field, D.J. Relations between the statistics of natural images and the response properties of cortical cells. J. Opt. Soc. Am. A 1987, 4, 2379–2394. [Google Scholar] [CrossRef]
- Yeganeh, H.; Rostami, M.; Wang, Z. Objective quality assessment for image super-resolution: A natural scene statistics approach. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Orlando, FL, USA, 30 September–3 October 2012; pp. 1481–1484. [Google Scholar]
- Sur, F.; Grediac, M. Automated removal of quasiperiodic noise using frequency domain statistics. J. Electron. Imaging 2015, 24, 013003. [Google Scholar] [CrossRef]
- Morris, N.J.; Avidan, S.; Matusik, W.; Pfister, H. Statistics of infrared images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Minneapolis, MN, USA, 17–22 June 2007; pp. 1–7. [Google Scholar]
- Liu, X.; Lu, X.; Shen, H.; Yuan, Q.; Zhang, L. Oblique stripe removal in remote sensing images via oriented variation. arXiv 2018, arXiv:1809.02043. [Google Scholar]
- Zeng, Q.; Qin, H.; Yan, X.; Yang, S.; Yang, T. Single infrared image-based stripe nonuniformity correction via a two-stage filtering method. Sensors 2018, 18, 4299. [Google Scholar] [CrossRef]
- Lee, H.; Jeon, J.; Kim, J.; Lee, S. Structure-texture decomposition of images with interval gradient. Comput. Graph. Forum 2017, 36, 262–274. [Google Scholar] [CrossRef]
- Moisan, L. Periodic plus smooth image decomposition. J. Math. Imaging Vis. 2011, 39, 161–179. [Google Scholar] [CrossRef]
- Sur, F. An a-contrario approach to quasi-periodic noise removal. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 3841–3845. [Google Scholar]
- Zhu, X.; Milanfar, P. Automatic parameter selection for denoising algorithms using a no-reference measure of image content. IEEE Trans. Image Process. 2010, 19, 3116–3132. [Google Scholar] [PubMed]
- Yuan, Y.; Zheng, X.; Lu, X. Spectral–spatial kernel regularized for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3815–3832. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.; Fang, L.; Ma, Y.; Benediktsson, J.A. Spectral–spatial adaptive sparse representation for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2016, 54, 373–385. [Google Scholar] [CrossRef]













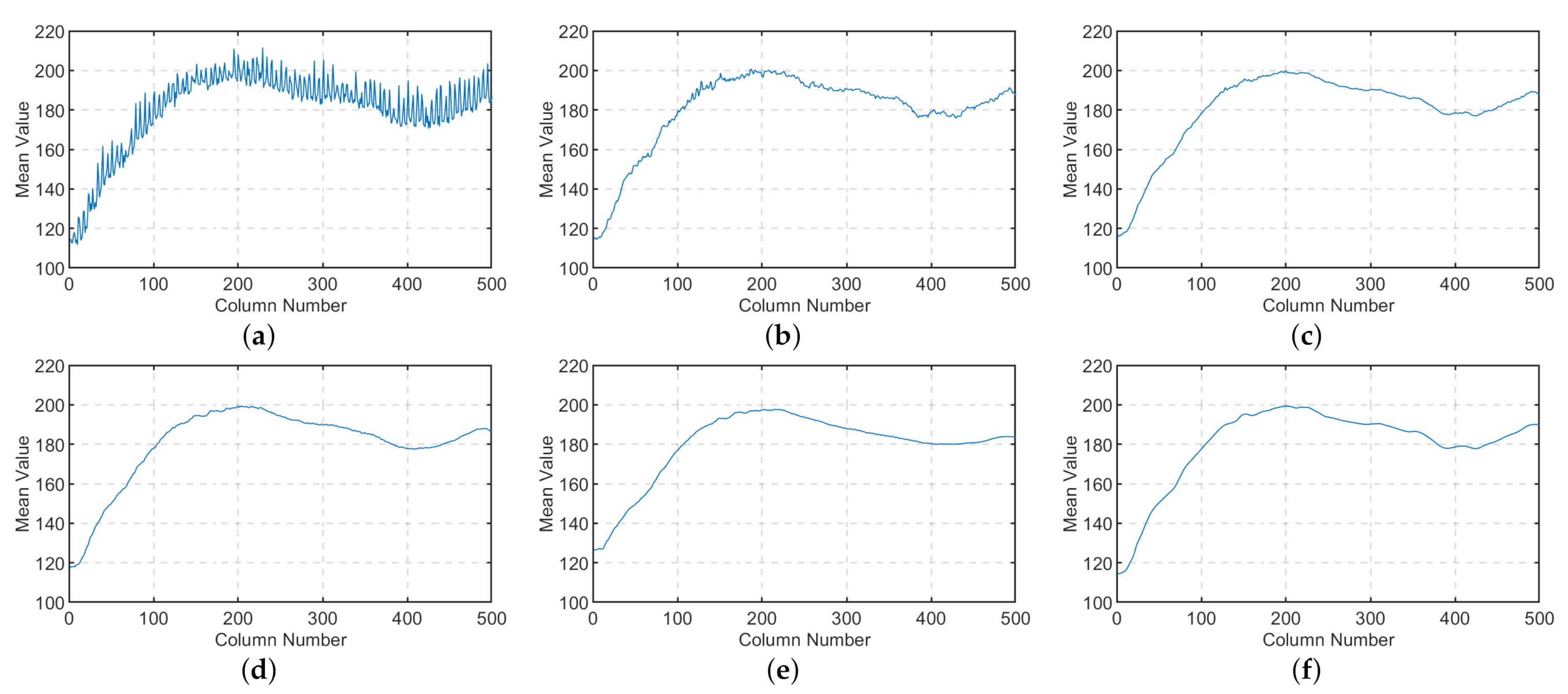

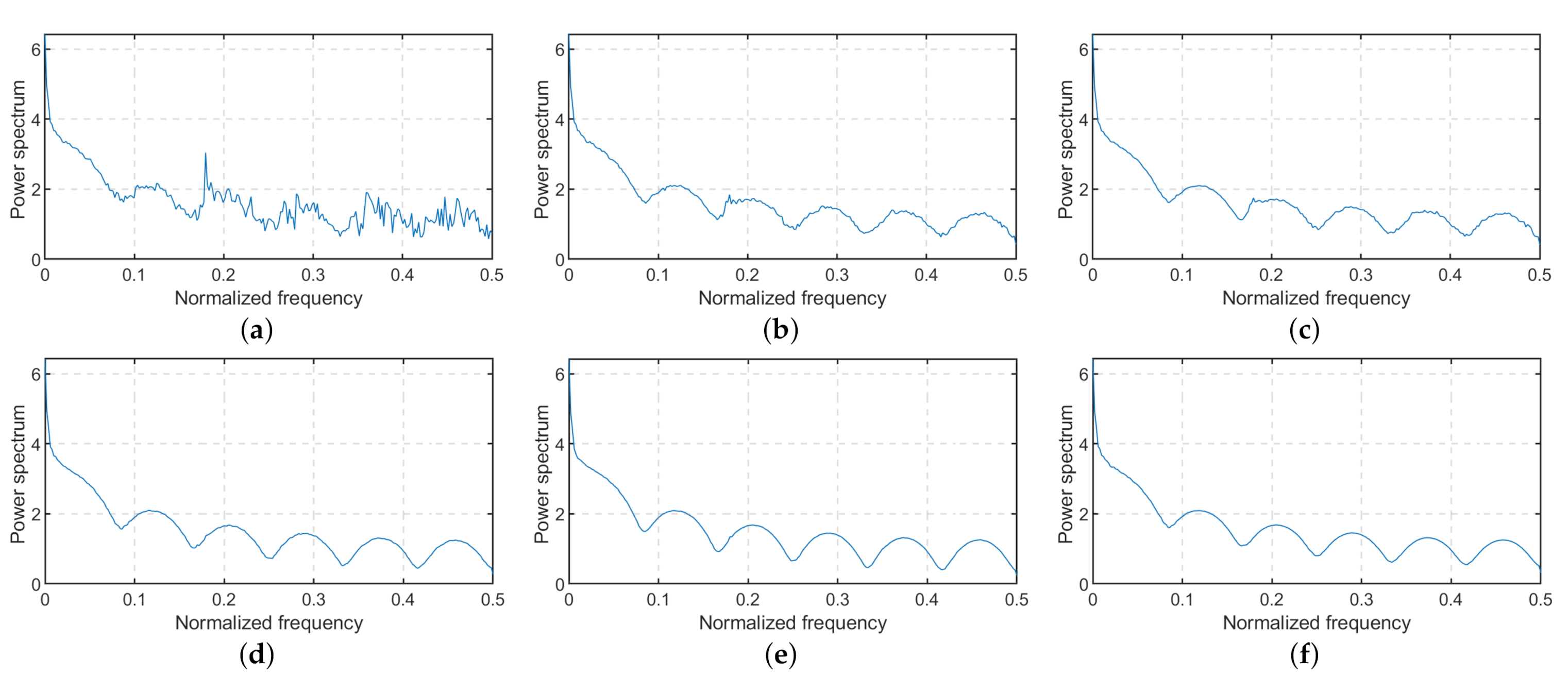

| Method | Experiment 1 | Experiment 2 | Experiment 3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q | RMSE | Q | RMSE | Q | RMSE | |||||||
| MIRE | 0.138 | 0.160 | 9.82 | 0.0217 | 0.125 | 0.328 | 8.66 | 0.0286 | 0.177 | −0.470 | 17.08 | 0.0059 |
| 1D-GF | 0.131 | 0.139 | 9.11 | 0.0209 | 0.120 | 0.223 | 7.83 | 0.0282 | 0.164 | −0.284 | 11.89 | 0.0068 |
| TwSF | 0.131 | 0.149 | 9.09 | 0.0231 | 0.119 | 0.235 | 7.81 | 0.0318 | 0.166 | −0.382 | 12.46 | 0.0056 |
| DLSNUC | 0.100 | 0.499 | 11.05 | 0.0220 | 0.088 | 0.567 | 10.71 | 0.0292 | 0.126 | 0.255 | 18.07 | 0.0057 |
| WDNN | 0.129 | 0.256 | 9.34 | 0.0207 | 0.118 | 0.421 | 8.55 | 0.0281 | 0.166 | −0.021 | 15.70 | 0.0047 |
| Ours | 0.126 | 0.526 | 11.47 | 0.0200 | 0.114 | 0.618 | 11.36 | 0.0271 | 0.162 | 0.283 | 19.32 | 0.0042 |
| Image | Index | Original | WFAF | SLD | LRSID | DSM- | Ours |
|---|---|---|---|---|---|---|---|
| Band 21 | ICV1 | 21.8910 | 28.0554 | 28.0749 | 31.8895 | 36.5370 | 31.4056 |
| ICV2 | 18.5833 | 19.6632 | 21.8711 | 24.0064 | 29.5712 | 24.6683 | |
| MRD1 | - | 0.0167 | 0.0182 | 0.0253 | 0.0376 | 0.0248 | |
| MRD2 | - | 0.0131 | 0.0139 | 0.0157 | 0.0320 | 0.0135 | |
| Band 24 | ICV1 | 3.8014 | 3.8561 | 3.8729 | 3.9096 | 4.4591 | 4.1827 |
| ICV2 | 87.8540 | 122.4623 | 125.2533 | 151.5480 | 154.6837 | 149.2865 | |
| MRD1 | - | 0.0224 | 0.0268 | 0.0350 | 0.0980 | 0.0333 | |
| MRD2 | - | 0.0106 | 0.0087 | 0.0110 | 0.0212 | 0.0101 | |
| Band 27 | ICV1 | 14.5392 | 17.2013 | 16.5835 | 17.8278 | 27.7905 | 18.5027 |
| ICV2 | 38.7568 | 54.0097 | 54.5366 | 65.7343 | 125.2244 | 73.0345 | |
| MRD1 | - | 0.0204 | 0.0211 | 0.0286 | 0.0356 | 0.0258 | |
| MRD2 | - | 0.0259 | 0.0302 | 0.0402 | 0.0544 | 0.0372 | |
| Band 33 | ICV1 | 5.5825 | 5.4789 | 5.5875 | 5.7910 | 8.7910 | 5.6949 |
| ICV2 | 108.4053 | 164.1888 | 166.2775 | 231.5580 | 253.2472 | 212.7835 | |
| MRD1 | - | 0.0102 | 0.0067 | 0.0136 | 0.0169 | 0.0124 | |
| MRD2 | - | 0.0044 | 0.0034 | 0.0074 | 0.0115 | 0.0065 | |
| Band 34 | ICV1 | 14.4918 | 15.4177 | 15.7350 | 15.9210 | 18.2459 | 16.3604 |
| ICV2 | 40.4405 | 54.1095 | 58.4728 | 77.3437 | 127.7196 | 90.1767 | |
| MRD1 | - | 0.0319 | 0.0482 | 0.0651 | 0.1450 | 0.0585 | |
| MRD2 | - | 0.0102 | 0.0110 | 0.0131 | 0.0147 | 0.0126 | |
| Band 35 | ICV1 | 7.8907 | 8.2272 | 8.3232 | 9.5049 | 13.2531 | 10.3291 |
| ICV2 | 60.8430 | 70.1713 | 75.3580 | 92.3648 | 153.1217 | 92.1730 | |
| MRD1 | - | 0.0115 | 0.0151 | 0.0289 | 0.0344 | 0.0252 | |
| MRD2 | - | 0.0084 | 0.0099 | 0.0179 | 0.0414 | 0.0175 | |
| SAM1 | - | 0.0261 | 0.0218 | 0.0293 | 0.0533 | 0.0214 | |
| SAM2 | - | 0.0149 | 0.0124 | 0.0143 | 0.0178 | 0.0121 |
| Image Size | MIRE | 1D-GF | TwSF | DLSNUC | Ours | Image Size | WFAF | SLD | LRSID | DSM- | Ours |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 288 × 384 | 0.07 | 0.06 | 0.01 | 0.46 | 0.38 | 500 × 500 | 0.25 | 0.04 | 16.37 | 34.52 | 1.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Qin, H.; Yan, X.; Yang, T. Fourier Domain Anomaly Detection and Spectral Fusion for Stripe Noise Removal of TIR Imagery. Remote Sens. 2020, 12, 3714. https://doi.org/10.3390/rs12223714
Zeng Q, Qin H, Yan X, Yang T. Fourier Domain Anomaly Detection and Spectral Fusion for Stripe Noise Removal of TIR Imagery. Remote Sensing. 2020; 12(22):3714. https://doi.org/10.3390/rs12223714
Chicago/Turabian StyleZeng, Qingjie, Hanlin Qin, Xiang Yan, and Tingwu Yang. 2020. "Fourier Domain Anomaly Detection and Spectral Fusion for Stripe Noise Removal of TIR Imagery" Remote Sensing 12, no. 22: 3714. https://doi.org/10.3390/rs12223714
APA StyleZeng, Q., Qin, H., Yan, X., & Yang, T. (2020). Fourier Domain Anomaly Detection and Spectral Fusion for Stripe Noise Removal of TIR Imagery. Remote Sensing, 12(22), 3714. https://doi.org/10.3390/rs12223714