Cross-Sensor Quality Assurance for Marine Observatories
Abstract
1. Introduction
1.1. Background
1.2. State-of-the-Art
1.3. Summary of Proposed Solution
- A formalized way to obtain sets of oceanographic data related to similar phenomena.
- A first of its kind cross-sensor scheme to verify the disqualification of identified anomalies.
2. System Model
2.1. Preliminaries for Potential Relationships between Datasets
2.2. Setup and Main Assumptions
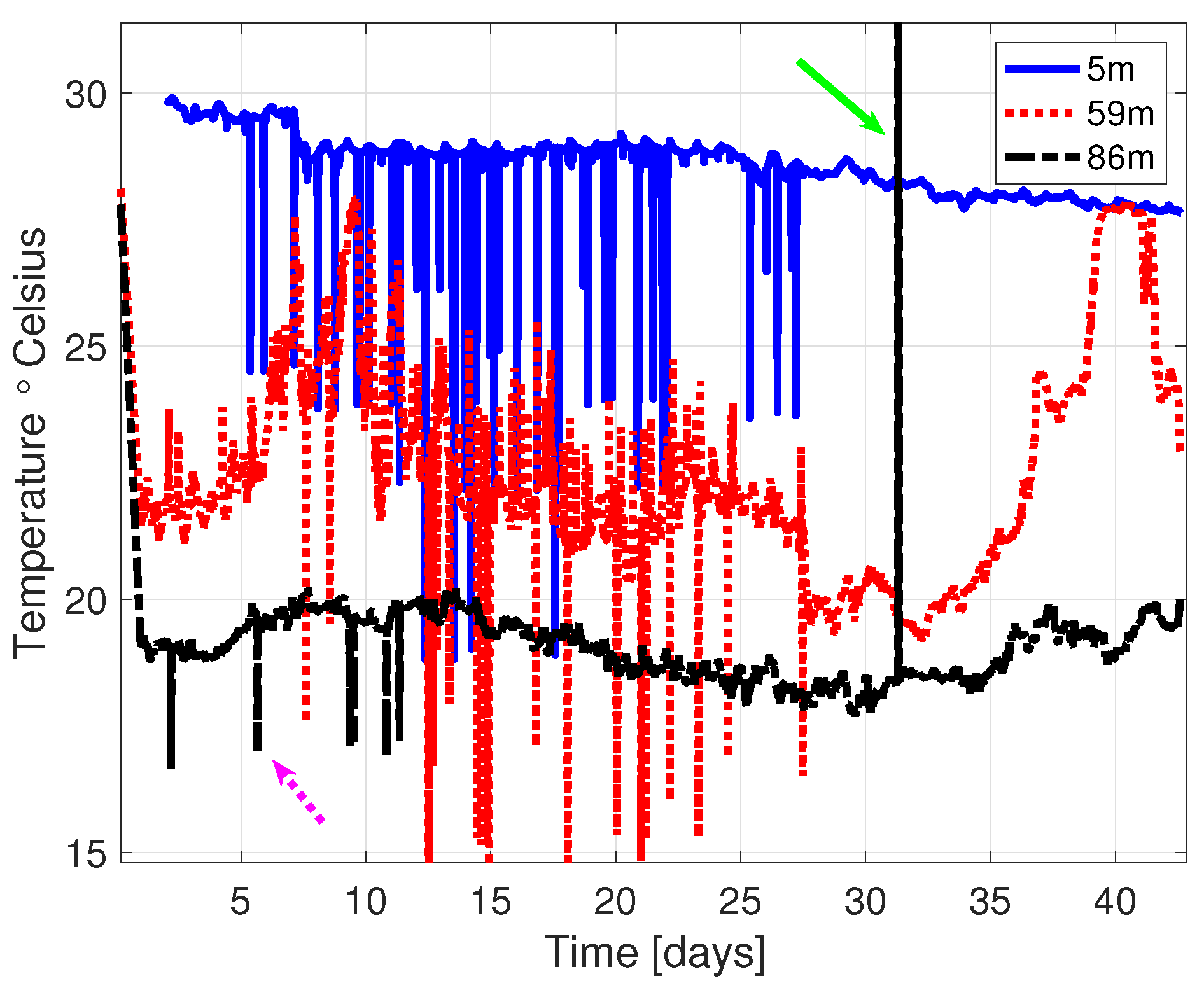
2.3. The Used Datasets
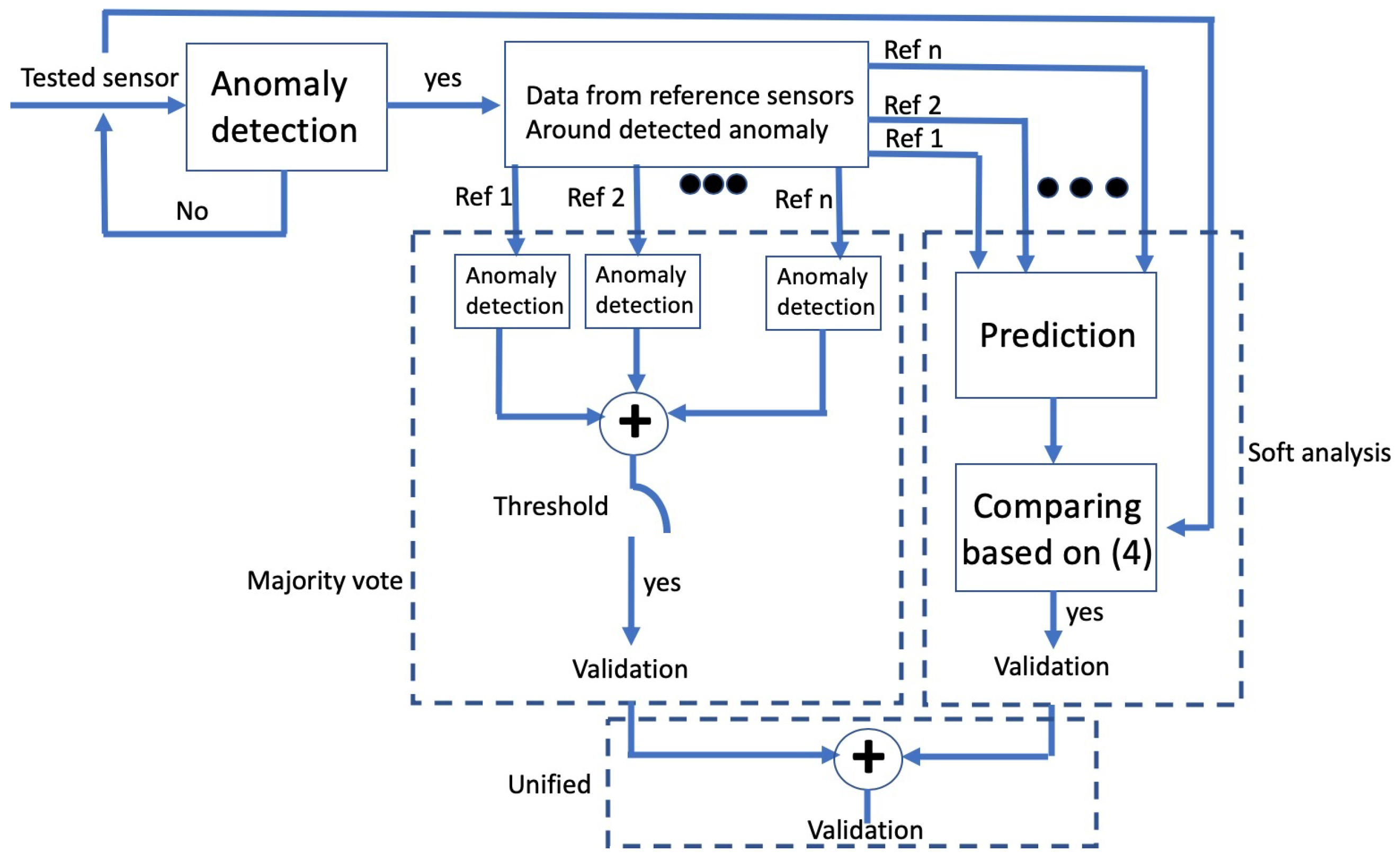
3. The Cross-Sensor QA Method
3.1. Offline: Identification of Related Datasets
3.1.1. Prediction of Datasets
- I
- Prediction always agrees with the original dataset. Such a relationship is relevant for a direct comparison between the datasets.
- II
- Prediction agrees with the original dataset only for transient samples. This similarity refers to rare events that may be falsely identified as outliers.
- III
- Prediction does not agree with the original dataset. This lack of connection means that the datasets used for the prediction cannot be part of the related group.
3.1.2. Comparing Predictions
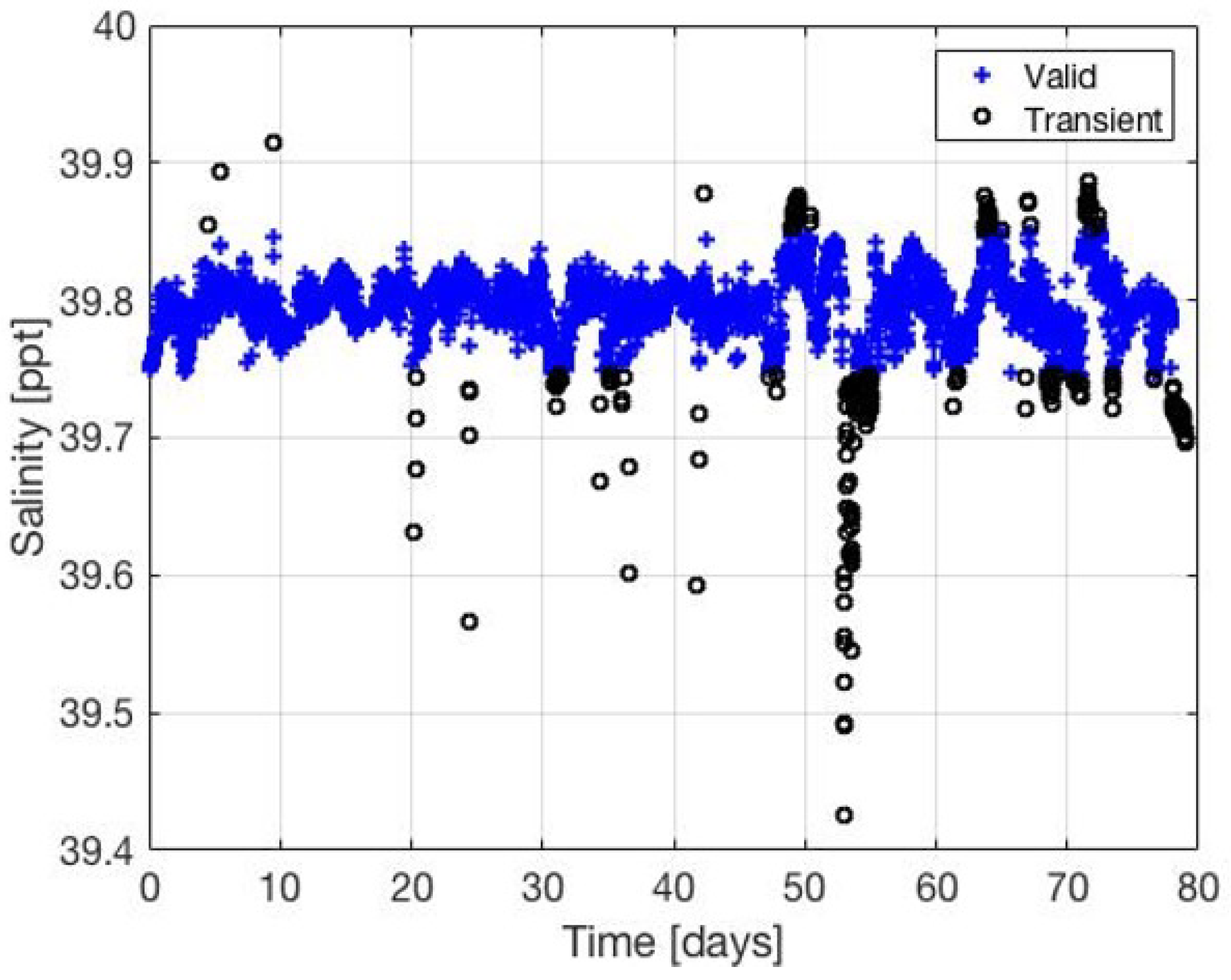
3.2. Online: Identifying Faulty Data Samples
3.2.1. Anomaly Detection
3.2.2. Detection Verification
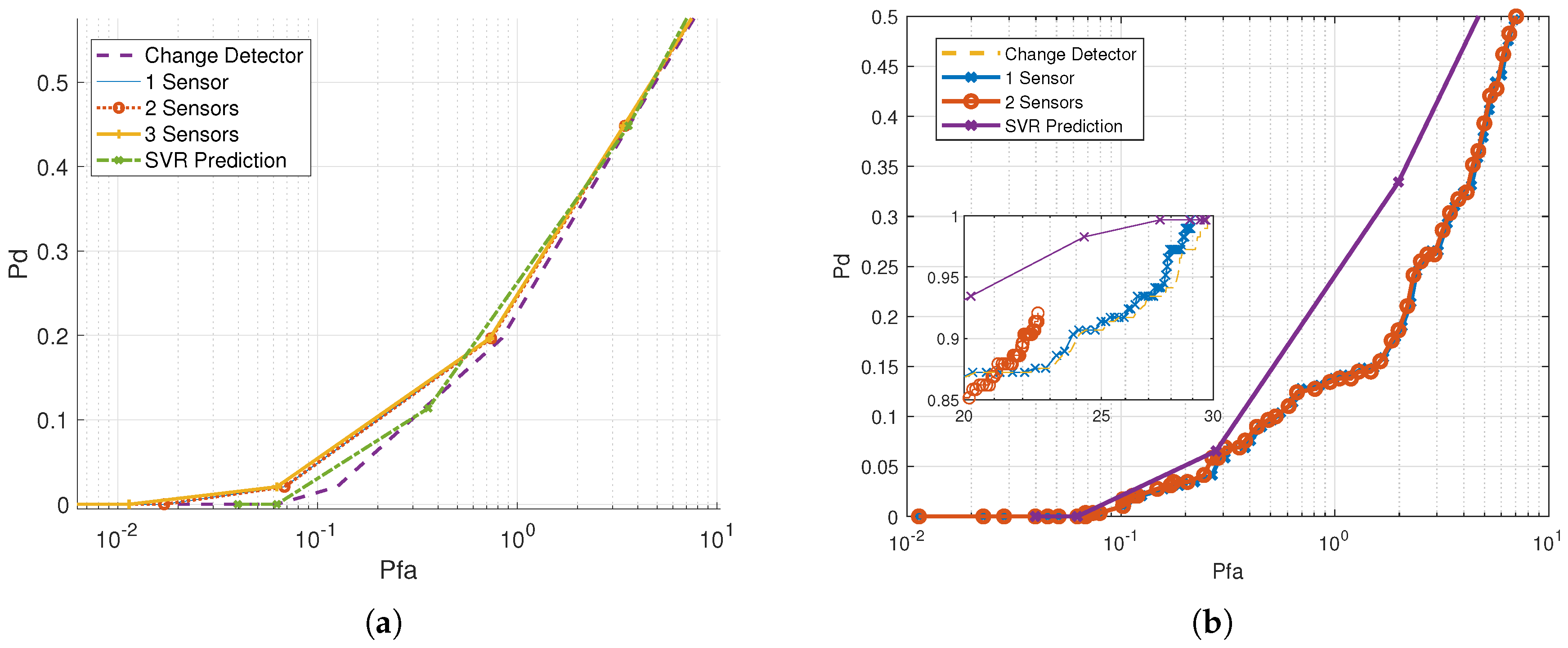
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Guidelines for Anticipating Related Datasets
References
- Walpert, J.; Guinasso, N.; Lee, W.; Liu, D.; Buschang, S. TABS responder—A quick response buoy to supplement the TABS network. In Proceedings of the 2014 Oceans-St. John’s, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–6. [Google Scholar]
- Cooke, S.; Iverson, S.; Stokesbury, M.; Hinch, S.; Fisk, A.; VanderZwaag, D.; Apostle, R.; Whoriskey, F. Ocean Tracking Network Canada: A network approach to addressing critical issues in fisheries and resource management with implications for ocean governance. Fisheries 2011, 36, 583–592. [Google Scholar] [CrossRef]
- Diamant, R.; Knapr, A.; Dahan, S.; Mardix, I.; Walpert, J.; DiMarco, S. THEMO: The Texas A&M-University of Haifa-Eastern Mediterranean Observatory. In Proceedings of the 2018 OCEANS-MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–5. [Google Scholar]
- Koziana, J.; Olson, J.; Anselmo, T.; Lu, W. Automated data quality assurance for marine observations. In Proceedings of the OCEANS 2008, Quebec City, QC, Canada, 15–18 September 2008; pp. 1–6. [Google Scholar]
- Biffard, B.; Morley, M.; Hoeberechts, M.; Rempel, A.; Dakin, T.; Dewey, R.; Jenkyns, R. Adding value to big acoustic data from ocean observatories: Metadata, online processing, and a computing sandbox. J. Acoust. Soc. Am. 2018, 144, 1956. [Google Scholar] [CrossRef]
- Quality Control of Ocean Observatory Initiative. 2018. Available online: https://oceanobservatories.org/quality-contro (accessed on 1 June 2020).
- Abeysirigunawardena, D.; Jeffries, M.; Morley, M.; Bui, A.; Hoeberechts, M. Data quality control and quality assurance practices for Ocean Networks Canada observatories. In Proceedings of the OCEANS 2015-MTS/IEEE Washington, Washington, DC, USA, 19–22 October 2015; pp. 1–8. [Google Scholar]
- Wong, A.; Keeley, R.; Carval, T. Argo Quality Control Manual for CTD and Trajectory Data, Version 3.1; Technical report; IFREMER: Brest, France, 16 January 2018. [Google Scholar] [CrossRef]
- Batsi, E.; Tsang-Hin-Sun, E.; Klingelhoefer, F.; Bayrakci, G.; Chang, E.T.; Lin, J.Y.; Dellong, D.; Monteil, C.; Géli, L. Nonseismic Signals in the Ocean: Indicators of Deep Sea and Seafloor Processes on Ocean-Bottom Seismometer Data. Geochem. Geophys. Geosyst. 2019, 20, 3882–3900. [Google Scholar] [CrossRef]
- Diamant, R.; Dahan, S.; Mardix, I. Communication Operations at THEMO: The Texas A&M - University of Haifa - Eastern Mediterranean Observatory. In Proceedings of the 2018 Fourth Underwater Communications and Networking Conference (UComms), Lerici, Italy, 28–30 August 2018; pp. 1–5. [Google Scholar]
- Howe, B.; Chan, T.; El-Sharkawi, M.; Kenney, M.; Kolve, S.; Liu, C.; Lu, S.; McGinnis, T.; Schneider, K.; Siani, C.; et al. Power System for the MARS Ocean Cabled Observatory. In Proceedings of the Scientific Submarine Cable 2006 Conference, 2006; pp. 7–10. Available online: http://neptunepower.apl.washington.edu/publications/documents/psftmoco.pdf (accessed on 19 October 2020).
- Bushnell, M.; Kinkade, C.; Worthington, H. Manual for Real-Time Quality Control of Ocean Optics Data: A Guide to Quality Control and Quality Assurance of Coastal and Oceanic Optics Observations. 2017. Available online: file:///Users/Downloads/noaa_20938_DS1.pdf (accessed on 1 June 2020).
- Bushnell, M.; Worthington, H. Manual for Real-Time Quality Control of Wind Data: A Guide to Quality Control and Quality Assurance for Coastal and Oceanic Wind Observations. 2017. Available online: https://repository.library.noaa.gov/view/noaa/15487 (accessed on 1 June 2020).
- Timms, G.; Souza, P.D.; Reznik, L.; Smith, D. Automated data quality assessment of marine sensors. Sensors 2011, 11, 9589–9602. [Google Scholar] [CrossRef] [PubMed]
- Lévy, M.; Ferrari, R.; Franks, P.; Martin, A.; Rivière, P. Bringing physics to life at the submesoscale. Geophys. Res. Lett. 2012, 39, 1–13. [Google Scholar] [CrossRef]
- McWilliams, J. Submesoscale currents in the ocean. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160117. [Google Scholar] [CrossRef] [PubMed]
- Talley, L. Descriptive Physical Oceanography: An Introduction; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Datasets Used for Analysis and Their Tagging. 2020. Available online: https://drive.google.com/drive/folders/1SDoV8wejlpYtn3hBrYlw0uej5vmMHJqC?usp=sharing (accessed on 1 October 2020).
- Mamayev, O. Temperature-Salinity Analysis of World Ocean Waters; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Emery, W.; Meincke, J. Global water masses-summary and review. Oceanol. Acta 1986, 9, 383–391. [Google Scholar]
- Rudnick, D.; Ferrari, R. Compensation of horizontal temperature and salinity gradients in the ocean mixed layer. Science 1999, 283, 526–529. [Google Scholar] [CrossRef] [PubMed]
- Rudnick, D.; Martin, J. On the horizontal density ratio in the upper ocean. Dyn. Atmos. Ocean. 2002, 36, 3–21. [Google Scholar] [CrossRef]
- Abraham, E. The generation of plankton patchiness by turbulent stirring. Nature 1998, 391, 577–580. [Google Scholar] [CrossRef]
- Bouman, H.; Platt, T.; Sathyendranath, S.; Li, W.; Stuart, V.; Fuentes-Yaco, C.; Maass, H.; Horne, E.; Ulloa, O.; Lutz, V.; et al. Temperature as indicator of optical properties and community structure of marine phytoplankton: Implications for remote sensing. Mar. Ecol. Prog. Ser. 2003, 258, 19–30. [Google Scholar] [CrossRef]
- Eckart, C. Properties of water, Part II: The equation of state of water and sea water at low temperatures and pressure. Am. J. Sci. 1958, 256, 225–240. [Google Scholar] [CrossRef]
- Bryan, K.; Cox, M. An approximate equation of state for numerical models of ocean circulation. J. Phys. Oceanogr. 1972, 2, 510–514. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Antonino-Daviu, J.; Pineda-Sanchez, M.; Puche-Panadero, R.; Pérez-Cruz, J. A general approach for the transient detection of slip-dependent fault components based on the discrete wavelet transform. IEEE Trans. Ind. Electron. 2008, 55, 4167–4180. [Google Scholar] [CrossRef]
- Abu, A.; Diamant, R. A Statistically-Based Method for the Detection of Underwater Objects in Sonar Imagery. IEEE Sens. J. 2019, 19, 6858–6871. [Google Scholar] [CrossRef]
- Diamant, R.; Campagnaro, F.; de Filippo de Grazia, M.; Casari, P.; Testolin, A.; Sanjuan Calzado, V.; Zorzi, M. On the Relationship Between the Underwater Acoustic and Optical Channels. IEEE Trans. Wirel. Commun. 2017, 16, 8037–8051. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Smola, A.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Kokare, M.; Chatterji, B.; Biswas, P. Comparison of similarity metrics for texture image retrieval. In Proceedings of the Conference on Convergent Technologies for Asia-Pacific Region (TENCON), Bangalore, India, 15–17 October 2003; Volume 2, pp. 571–575. [Google Scholar]





| Description | Sensor Model |
|---|---|
| Barometric pressure [mbars] (3 m above sea surface) | Vaisala (PTB210) |
| Chlorophyll [µg/L] (depth 1 m) | Wet Labs (ECOFLNTUS) |
| Salinity [PSU] (depth 1 m) | CTD microcat (SBE37-SI) |
| Conductivity [S/m] (depth 1 m) | CTD microcat (SBE37-SI) |
| Temperature [C] (depth 1 m) | CTD microcat (SBE37-SI) |
| Air humidity [RH%] (3 m above sea surface) | Rotronics (mp101a) |
| Air temperature [C] (3 m above sea surface) | Rotronics (mp101a) |
| Temperature [C] (depths 5 m, 14 m, 16 m) | Sound-nine (Ulti-Modem) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diamant, R.; Shachar, I.; Makovsky, Y.; Ferreira, B.M.; Cruz, N.A. Cross-Sensor Quality Assurance for Marine Observatories. Remote Sens. 2020, 12, 3470. https://doi.org/10.3390/rs12213470
Diamant R, Shachar I, Makovsky Y, Ferreira BM, Cruz NA. Cross-Sensor Quality Assurance for Marine Observatories. Remote Sensing. 2020; 12(21):3470. https://doi.org/10.3390/rs12213470
Chicago/Turabian StyleDiamant, Roee, Ilan Shachar, Yizhaq Makovsky, Bruno Miguel Ferreira, and Nuno Alexandre Cruz. 2020. "Cross-Sensor Quality Assurance for Marine Observatories" Remote Sensing 12, no. 21: 3470. https://doi.org/10.3390/rs12213470
APA StyleDiamant, R., Shachar, I., Makovsky, Y., Ferreira, B. M., & Cruz, N. A. (2020). Cross-Sensor Quality Assurance for Marine Observatories. Remote Sensing, 12(21), 3470. https://doi.org/10.3390/rs12213470









