Characterizing the Error and Bias of Remotely Sensed LAI Products: An Example for Tropical and Subtropical Evergreen Forests in South China
Abstract
1. Introduction
- (i)
- How well do EO-based estimates of LAI capture temporal dynamics observed in ground measurements?
- (ii)
- How robust are EO LAI error estimates?
2. Materials and Methods
2.1. Study Area
2.2. Field LAI Data Measurements
2.3. Earth Observation LAI Estimates
2.4. Mapping Heterogeneity of Canopy Properties
2.5. Statistical Analysis
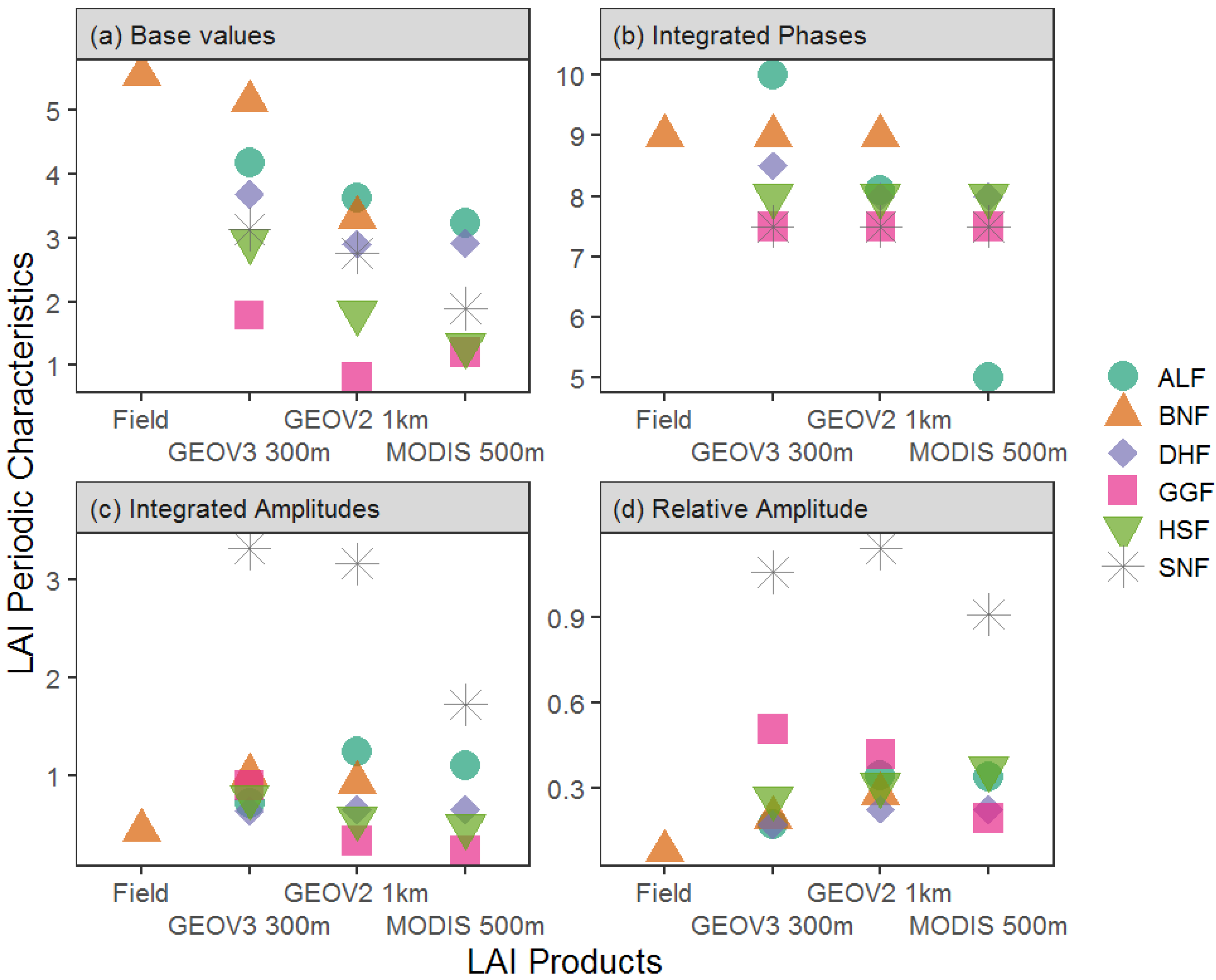
2.6. Calculation of Amplitude, Phases and Periods for LAI Time Series
2.7. Software
3. Results
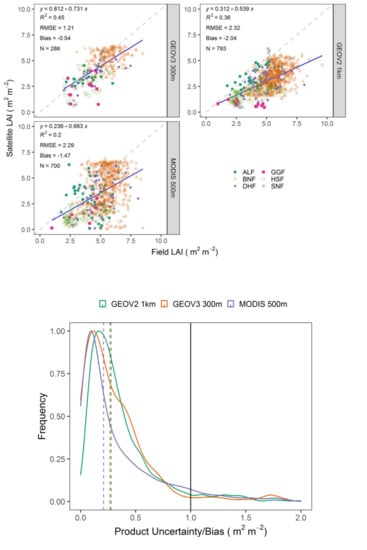
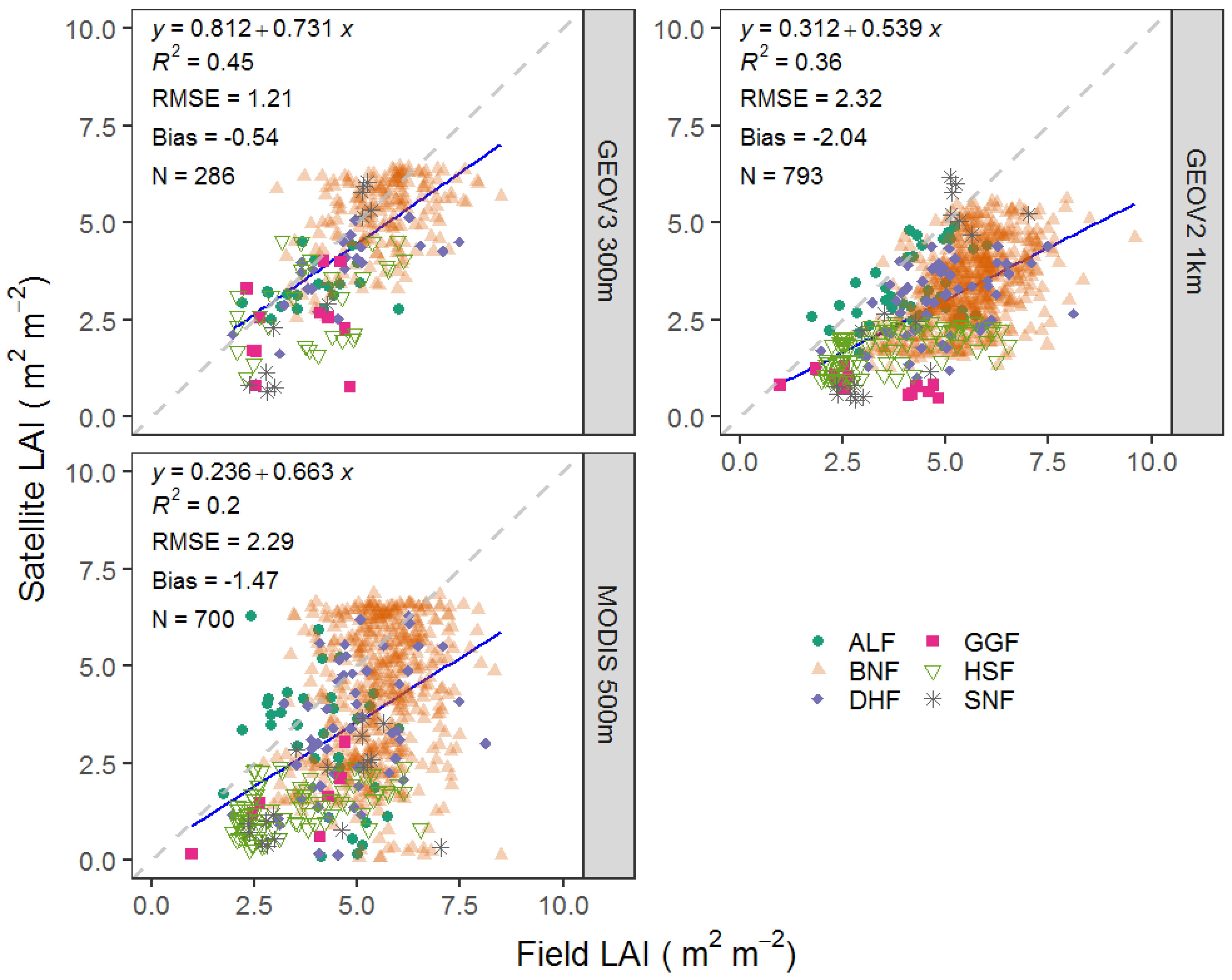
3.1. Accuracy of the LAI Products Magnitude
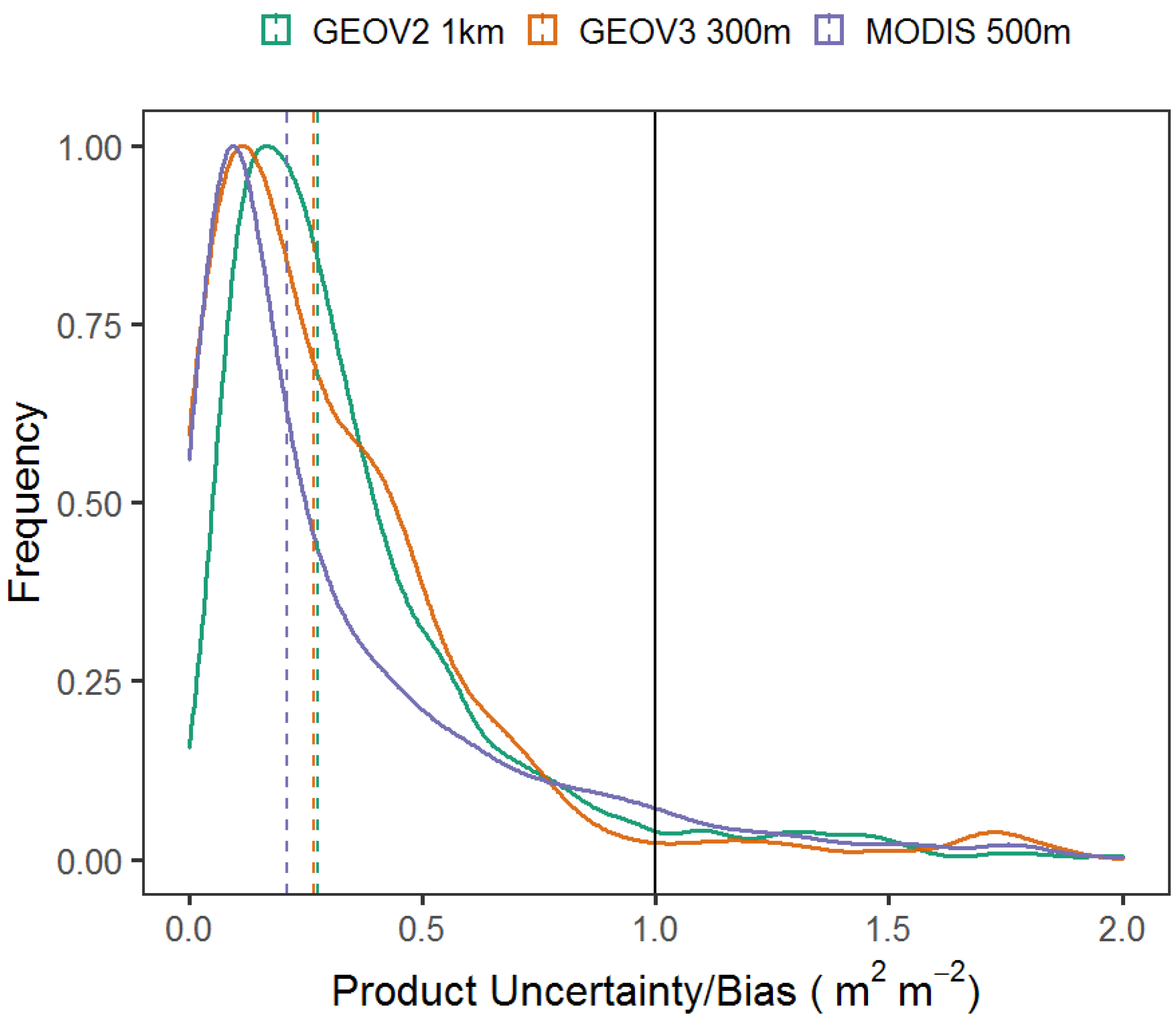
3.2. Robustness of the LAI Products Uncertainty
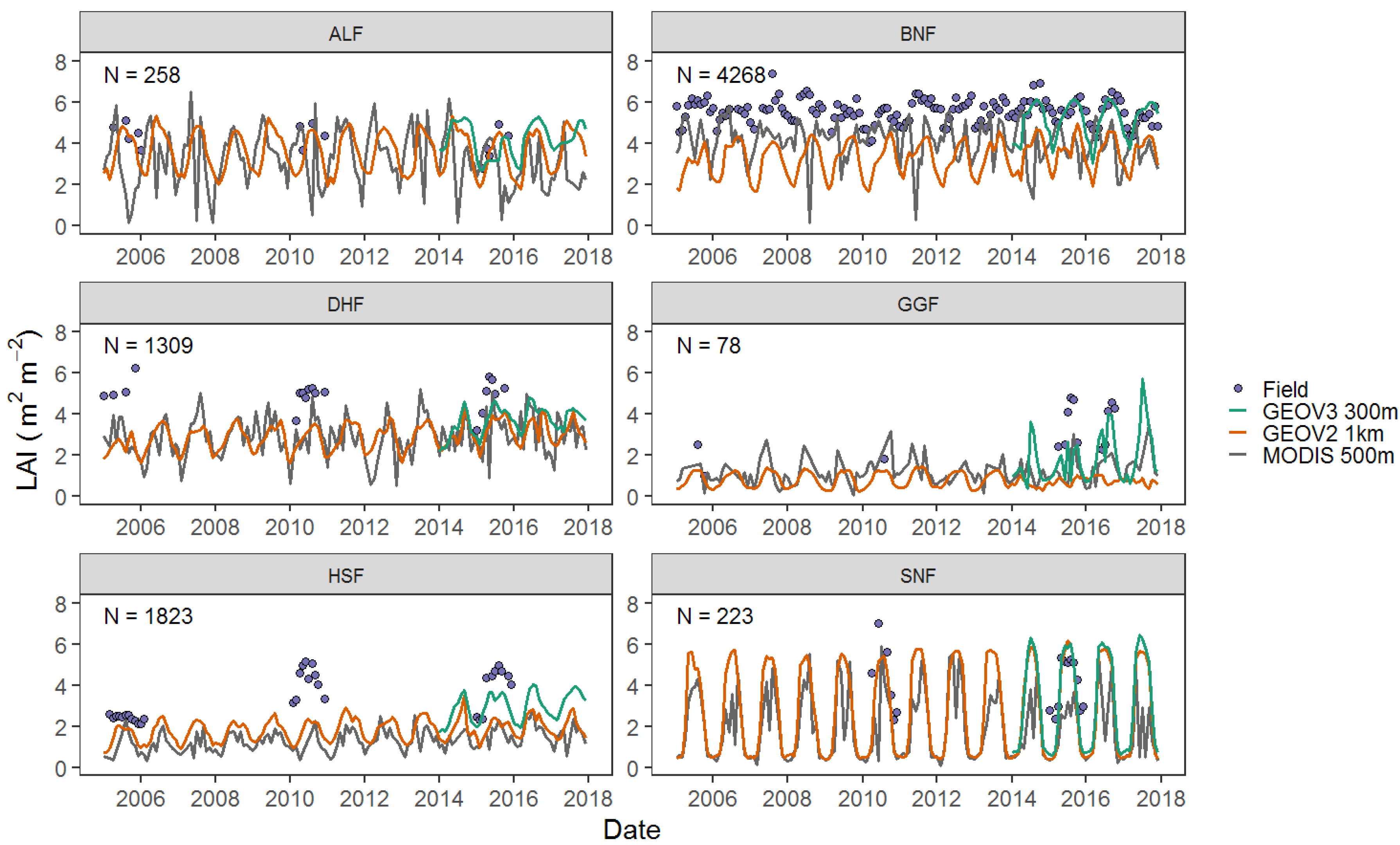
3.3. Validation of the LAI Products Temporal Dynamics
3.4. Evaluation of Landcover Heterogeneity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anav, A.; Murray-Tortarolo, G.; Friedlingstein, P.; Sitch, S.; Piao, S.; Zhu, Z. Evaluation of land surface models in reproducing satellite Derived leaf area index over the high-latitude northern hemisphere. Part II: Earth system models. Remote Sens. 2013, 5, 3637–3661. [Google Scholar] [CrossRef]
- Mahowald, N.; Lo, F.; Zheng, Y.; Harrison, L.; Funk, C.; Lombardozzi, D.; Goodale, C. Projections of leaf area index in earth system models. Earth Syst. Dynam. 2016, 7, 211–229. [Google Scholar] [CrossRef]
- Williams, M.; Richardson, A.D.; Reichstein, M.; Stoy, P.C.; Peylin, P.; Verbeeck, H.; Carvalhais, N.; Jung, M.; Hollinger, D.Y.; Kattge, J. Improving land surface models with FLUXNET data. Biogeosciences 2009, 6, 2785. [Google Scholar] [CrossRef]
- Asner, G.P.; Scurlock, J.M.; Hicke, A.J. Global synthesis of leaf area index observations: Implications for ecological and remote sensing studies. Glob. Ecol. Biogeogr. 2003, 12, 191–205. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G. Integration of MODIS LAI and vegetation index products with the CSM–CERES–Maize model for corn yield estimation. Int. J. Remote Sens. 2011, 32, 1039–1065. [Google Scholar] [CrossRef]
- Richardson, A.D.; Dail, D.B.; Hollinger, D. Leaf area index uncertainty estimates for model–data fusion applications. Agric. For. Meteorol. 2011, 151, 1287–1292. [Google Scholar] [CrossRef]
- Asaadi, A.; Arora, V.K.; Melton, J.R.; Bartlett, P. An improved parameterization of leaf area index (LAI) seasonality in the Canadian Land Surface Scheme (CLASS) and Canadian Terrestrial Ecosystem Model (CTEM) modelling framework. Biogeosciences 2018, 15, 6885–6907. [Google Scholar] [CrossRef]
- Tum, M.; Günther, K.P.; Böttcher, M.; Baret, F.; Bittner, M.; Brockmann, C.; Weiss, M. Global gap-free MERIS LAI time series (2002–2012). Remote Sens. 2016, 8, 69. [Google Scholar] [CrossRef]
- Gonsamo, A.; Chen, J.M. Improved LAI Algorithm Implementation to MODIS Data by Incorporating Background, Topography, and Foliage Clumping Information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1076–1088. [Google Scholar] [CrossRef]
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS/Terra Leaf Area Index/FPAR 8-Day L4 Global 500 m SIN Grid V006 [Data set]. NASA EOSDIS Land Processes DAAC. 2015. Available online: https://doi.org/10.5067/MODIS/MCD15A2H.006 (accessed on 15 September 2020).
- Verger, A.; Baret, F.; Weiss, M. Near Real-Time Vegetation Monitoring at Global Scale. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3473–3481. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Verger, A.; Smets, B. Atbd for Lai, Fapar and Fcover From Proba-V Products at 300m Resolution (Geov3); INRA: Paris, France, 2016. [Google Scholar]
- Williams, M.; Rastetter, E.B.; Shaver, G.R.; Hobbie, J.E.; Carpino, E.; Kwiatkowski, B.L. Primary production of an arctic watershed: An uncertainty analysis. Ecol. Appl. 2001, 11, 1800–1816. [Google Scholar] [CrossRef]
- Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.; Weiss, M.; Nickeson, J.; Fernandes, R.; Plummer, S.; Shabanov, N.; Myneni, R. Validation and intercomparison of global Leaf Area Index products derived from remote sensing data. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and fAPAR CYCLOPES global products derived from VEGETATION. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION: Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Knyazikhin, Y. MODIS Leaf Area Index (LAI) and Fraction of Photosynthetically Active Radiation Absorbed by Vegetation (FPAR) Product (MOD 15) Algorithm Theoretical Basis Document. 1999. Available online: https://modis.gsfc.nasa.gov/data/atbd/atbd_mod15.pdf (accessed on 15 September 2020).
- Pinty, B.; Andredakis, I.; Clerici, M.; Kaminski, T.; Taberner, M.; Verstraete, M.; Gobron, N.; Plummer, S.; Widlowski, J.L. Exploiting the MODIS albedos with the Two-stream Inversion Package (JRC-TIP): 1. Effective leaf area index, vegetation, and soil properties. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Fang, H.; Jiang, C.; Li, W.; Wei, S.; Baret, F.; Chen, J.M.; Garcia-Haro, J.; Liang, S.; Liu, R.; Myneni, R.B.; et al. Characterization and intercomparison of global moderate resolution leaf area index (LAI) products: Analysis of climatologies and theoretical uncertainties. J. Geophys. Res. Biogeosci. 2013, 118, 529–548. [Google Scholar] [CrossRef]
- GCOS. Systematic Observation Requirements for Satellite-Based Products for Climate. 2011 Update Supplemetnatl Details to the Satellite 39 Based Component og the Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (2010 Update); Technical Report; World Meteorological Organisation (WMO) 7 bis: Geneva, Switzerland, 2011. [Google Scholar]
- Revill, A.; Florence, A.; MacArthur, A.; Hoad, S.; Rees, R.; Williams, M. Quantifying Uncertainty and Bridging the Scaling Gap in the Retrieval of Leaf Area Index by Coupling Sentinel-2 and UAV Observations. Remote Sens. 2020, 12, 1843. [Google Scholar] [CrossRef]
- Williams, M.; Bell, R.; Spadavecchia, L.; Street, L.E.; Van Wijk, M.T. Upscaling leaf area index in an Arctic landscape through multiscale observations. Glob. Chang. Biol. 2008, 14, 1517–1530. [Google Scholar] [CrossRef]
- Wang, Q.; Tenhunen, J.; Dinh, N.Q.; Reichstein, M.; Otieno, D.; Granier, A.; Pilegarrd, K. Evaluation of seasonal variation of MODIS derived leaf area index at two European deciduous broadleaf forest sites. Remote Sens. Environ. 2005, 96, 475–484. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.; Wang, X.; Zhang, X. A new algorithm for the estimation of leaf unfolding date using MODIS data over China’s terrestrial ecosystems. ISPRS J. Photogramm. Remote Sens. 2019, 149, 77–90. [Google Scholar] [CrossRef]
- Kou, W.; Liang, C.; Wei, L.; Hernandez, A.J.; Yang, X. Phenology-based method for mapping tropical evergreen forests by integrating of MODIS and landsat imagery. Forests 2017, 8, 34. [Google Scholar]
- Clark, D.A. Sources or sinks? The responses of tropical forests to current and future climate and atmospheric composition. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 477–491. [Google Scholar] [PubMed]
- Miller, S.D.; Goulden, M.L.; Hutyra, L.R.; Keller, M.; Saleska, S.R.; Wofsy, S.C.; Figueira, A.M.S.; da Rocha, H.R.; de Camargo, P.B. Reduced impact logging minimally alters tropical rainforest carbon and energy exchange. Proc. Natl. Acad. Sci. USA 2011, 108, 19431–19435. [Google Scholar] [CrossRef] [PubMed]
- Tang, A.C.I.; Stoy, P.C.; Hirata, R.; Musin, K.K.; Aeries, E.B.; Wenceslaus, J.; Shimizu, M.; Melling, L. The exchange of water and energy between a tropical peat forest and the atmosphere: Seasonal trends and comparison against other tropical rainforests. Sci. Total Environ. 2019, 683, 166–175. [Google Scholar] [CrossRef]
- Heiskanen, J.; Korhonen, L.; Hietanen, J.; Pellikka, P.K.E. Use of airborne lidar for estimating canopy gap fraction and leaf area index of tropical montane forests. Int. J. Remote Sens. 2015, 36, 2569–2583. [Google Scholar] [CrossRef]
- Piao, S.; Liu, Q.; Chen, A.; Janssens, I.A.; Fu, Y.; Dai, J.; Liu, L.; Lian, X.; Shen, M.; Zhu, X. Plant phenology and global climate change: Current progresses and challenges. Glob. Chang. Biol. 2019, 25, 1922–1940. [Google Scholar]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar]
- Chhabra, A.; Panigrahy, S. Analysis of spatio-temporal patterns of leaf area index in different forest types of India using high temporal remote sensing data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, W20. [Google Scholar]
- Olivas, P.C.; Oberbauer, S.F.; Clark, D.B.; Clark, D.A.; Ryan, M.G.; O’Brien, J.J.; Ordonez, H. Comparison of direct and indirect methods for assessing leaf area index across a tropical rain forest landscape. Agric. For. Meteorol. 2013, 177, 110–116. [Google Scholar]
- Fang, H.; Wei, S.; Jiang, C.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar]
- Huete, A.R.; Didan, K.; Shimabukuro, Y.E.; Ratana, P.; Saleska, S.R.; Hutyra, L.R.; Yang, W.; Nemani, R.R.; Myneni, R. Amazon rainforests green-up with sunlight in dry season. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Wagner, F.H.; Hérault, B.; Rossi, V.; Hilker, T.; Maeda, E.E.; Sanchez, A.; Lyapustin, A.I.; Galvão, L.S.; Wang, Y.; Aragao, L.E. Climate drivers of the Amazon forest greening. PLoS ONE 2017, 12, e0180932. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Kobayashi, H.; Stark, S.C.; Meng, R.; Guan, K.; Tran, N.N.; Gao, S.; Yang, W.; Restrepo-Coupe, N.; Miura, T. Biological processes dominate seasonality of remotely sensed canopy greenness in an Amazon evergreen forest. New Phytol. 2018, 217, 1507–1520. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Albert, L.P.; Lopes, A.P.; Restrepo-Coupe, N.; Hayek, M.; Wiedemann, K.T.; Guan, K.; Stark, S.C.; Christoffersen, B.; Prohaska, N. Leaf development and demography explain photosynthetic seasonality in Amazon evergreen forests. Science 2016, 351, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Dubayah, R. Light-driven growth in Amazon evergreen forests explained by seasonal variations of vertical canopy structure. Proc. Natl. Acad. Sci. USA 2017, 114, 2640–2644. [Google Scholar] [CrossRef]
- Yan, D.; Zhang, X.; Yu, Y.; Guo, W. A comparison of tropical rainforest phenology retrieved from geostationary (seviri) and polar-orbiting (modis) sensors across the congo basin. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4867–4881. [Google Scholar] [CrossRef]
- Adole, T.; Dash, J.; Atkinson, P.M. A systematic review of vegetation phenology in Africa. Ecol. Inform. 2016, 34, 117–128. [Google Scholar] [CrossRef]
- Ryan, C.M.; Williams, M.; Grace, J.; Woollen, E.; Lehmann, C.E. Pre-rain green-up is ubiquitous across southern tropical Africa: Implications for temporal niche separation and model representation. New Phytol. 2017, 213, 625–633. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Zhou, L.; Ciais, P.; Zhu, B. Variations in satellite-derived phenology in China’s temperate vegetation. Glob. Chang. Biol. 2006, 12, 672–685. [Google Scholar] [CrossRef]
- Wu, C.; Hou, X.; Peng, D.; Gonsamo, A.; Xu, S. Land surface phenology of China’s temperate ecosystems over 1999–2013: Spatial–temporal patterns, interaction effects, covariation with climate and implications for productivity. Agric. For. Meteorol. 2016, 216, 177–187. [Google Scholar] [CrossRef]
- Liu, Q.; Fu, Y.H.; Zeng, Z.; Huang, M.; Li, X.; Piao, S. Temperature, precipitation, and insolation effects on autumn vegetation phenology in temperate China. Glob. Chang. Biol. 2016, 22, 644–655. [Google Scholar] [CrossRef] [PubMed]
- Ge, Q.; Dai, J.; Cui, H.; Wang, H. Spatiotemporal Variability in Start and End of Growing Season in China Related to Climate Variability. Remote Sens. 2016, 8, 433. [Google Scholar] [CrossRef]
- Zhu, H. The Tropical Forests of Southern China and Conservation of Biodiversity. Bot. Rev. 2017, 83, 87–105. [Google Scholar] [CrossRef]
- Wu, J.; Lin, W.; Peng, X.; Liu, W. A review of forest resources and forest biodiversity evaluation system in China. Int. J. Res. 2013, 2013. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; Ciais, P.; Peylin, P.; Huang, Y.; Sitch, S.; Wang, T. The carbon balance of terrestrial ecosystems in China. Nature 2009, 458, 1009–1013. [Google Scholar] [CrossRef]
- Tang, X.; Zhao, X.; Bai, Y.; Tang, Z.; Wang, W.; Zhao, Y.; Wan, H.; Xie, Z.; Shi, X.; Wu, B. Carbon pools in China’s terrestrial ecosystems: New estimates based on an intensive field survey. Proc. Natl. Acad. Sci. USA 2018, 115, 4021–4026. [Google Scholar] [CrossRef] [PubMed]
- Justice, C.; Belward, A.; Morisette, J.; Lewis, P.; Privette, J.; Baret, F. 2000: Developments in the ‘validation’of satellite sensor products for the study of the land surface. Int. J. Remote Sens. 2000, 21, 3383–3390. [Google Scholar]
- Morisette, J.T.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.E.; Garrigues, S.; Shabanov, N.V.; Weiss, M.; Fernandes, R.A.; Leblanc, S.G. Validation of global moderate-resolution LAI products: A framework proposed within the CEOS land product validation subgroup. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1804–1817. [Google Scholar] [CrossRef]
- Post, H.; Hendricks Franssen, H.J.; Han, X.; Baatz, R.; Montzka, C.; Schmidt, M.; Vereecken, H. Evaluation and uncertainty analysis of regional-scale CLM4.5 net carbon flux estimates. Biogeosciences 2018, 15, 187–208. [Google Scholar] [CrossRef]
- Rüdiger, C.; Albergel, C.; Mahfouf, J.F.; Calvet, J.C.; Walker, J.P. Evaluation of the observation operator Jacobian for leaf area index data assimilation with an extended Kalman filter. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Viskari, T.; Hardiman, B.; Desai, A.R.; Dietze, M.C. Model-data assimilation of multiple phenological observations to constrain and predict leaf area index. Ecol. Appl. 2015, 25, 546–558. [Google Scholar] [CrossRef]
- Fu, B.; Li, S.; Yu, X.; Yang, P.; Yu, G.; Feng, R.; Zhuang, X. Chinese ecosystem research network: Progress and perspectives. Ecol. Complex. 2010, 7, 225–233. [Google Scholar] [CrossRef]
- Yu, G.; Chen, Z.; Piao, S.; Peng, C.; Ciais, P.; Wang, Q.; Li, X.; Zhu, X. High carbon dioxide uptake by subtropical forest ecosystems in the East Asian monsoon region. Proc. Natl. Acad. Sci. USA 2014, 111, 4910–4915. [Google Scholar] [CrossRef] [PubMed]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Eur. Geosci. Union 2007, 4, 439–473. [Google Scholar]
- Li-Cor, I. LAI-2000 Plant Canopy Analyzer Instruction Manual; LI-COR Inc.: Lincoln, NE, USA, 1992. [Google Scholar]
- Wu, D.; Wei, W.; Zhang, S. Protocols for Standard Biological Observation and Measurement in Terrestrial Ecosystems; China Environmental Science Pres: Beijing, China, 2007. [Google Scholar]
- Knyazikhin, Y.; Martonchik, J.; Myneni, R.B.; Diner, D.; Running, S.W. Synergistic algorithm for estimating vegetation canopy leaf area index and fraction of absorbed photosynthetically active radiation from MODIS and MISR data. J. Geophys. Res. Atmos. 1998, 103, 32257–32275. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M. Atbd for Lai, Fapar and Fcover from Proba-V Products Collection 1km Version 2; 2019, Issue I1.41. Available online: https://land.copernicus.eu/global/sites/cgls.vito.be/files/products/CGLOPS1_ATBD_LAI1km-V2_I1.41.pdf (accessed on 15 April 2020).
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett. 2006, 3, 68–72. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Zanter, K.; Department of the Interior, U.S. Geological Survey. Landsat 4-7 Surface Reflectance (LEDAPS) Product Guide. Version 2.0. 2019, EROS, Sioux Falls, South Dakota. Available online: https://www.usgs.gov/media/files/landsat-4-7-surface-reflectance-code-ledaps-product-guide (accessed on 15 September 2020).
- Zanter, K.; Department of the Interior, U.S. Geological Survey. Landsat 8 Surface Reflectance Code (LASRC) Product Guide. Version 2.0. 2019, EROS, Sioux Falls, South Dakota. Available online: https://www.usgs.gov/media/files/land-surface-reflectance-code-lasrc-product-guide (accessed on 15 September 2020).
- USGS. GTOPO30: Global 30 Arc-Seconds Digital Elevation Model [Data Set]. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-global-30-arc-second-elevation-gtopo30?qt-science_center_objects=0#qt-science_center_objects (accessed on 15 September 2020).
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Jun, C.; Ban, Y.; Li, S. Open access to Earth land-cover map. Nature 2014, 514, 434. [Google Scholar] [CrossRef]
- Wu, G.; Anafi, R.C.; Hughes, M.E.; Kornacker, K.; Hogenesch, J.B. MetaCycle: An integrated R package to evaluate periodicity in large scale data. Bioinformatics 2016, 32, 3351–3353. [Google Scholar] [CrossRef]
- Yang, R.; Su, Z. Analyzing circadian expression data by harmonic regression based on autoregressive spectral estimation. Bioinformatics 2010, 26, i168–i174. [Google Scholar] [CrossRef] [PubMed]
- Hughes, M.E.; Hogenesch, J.B.; Kornacker, K. JTK_CYCLE: An efficient nonparametric algorithm for detecting rhythmic components in genome-scale data sets. J. Biol. Rhythms 2010, 25, 372–380. [Google Scholar] [CrossRef] [PubMed]
- Glynn, E.F.; Chen, J.; Mushegian, A.R. Detecting periodic patterns in unevenly spaced gene expression time series using Lomb–Scargle periodograms. Bioinformatics 2006, 22, 310–316. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.r-project.org/ (accessed on 3 December 2018).
- Hijmans, R.J.; Van Etten, J.; Cheng, J.; Mattiuzzi, M.; Sumner, M.; Greenberg, J.A.; Lamigueiro, O.P.; Bevan, A.; Racine, E.B.; Shortridge, A. Package ‘raster’. R package version 2.5-8 (2015).
- Weiss, M.; Baret, F.; Smith, G.; Jonckheere, I.; Coppin, P. Review of methods for in situ leaf area index (LAI) determination: Part II. Estimation of LAI, errors and sampling. Agric. For. Meteorol. 2004, 121, 37–53. [Google Scholar] [CrossRef]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data. Remote Sens. Environ. 2006, 105, 286–298. [Google Scholar] [CrossRef]
- Fuster, B.; Sánchez-Zapero, J.; Camacho, F.; García-Santos, V.; Verger, A.; Lacaze, R.; Weiss, M.; Baret, F.; Smets, B. Quality Assessment of PROBA-V LAI, fAPAR and fCOVER Collection 300 m Products of Copernicus Global Land Service. Remote Sens. 2020, 12, 1017. [Google Scholar] [CrossRef]
- Nagendra, H. Using remote sensing to assess biodiversity. Int. J. Remote Sens. 2001, 22, 2377–2400. [Google Scholar] [CrossRef]
- Liu, Z.; Shao, Q.; Liu, J. The Performances of MODIS-GPP and -ET Products in China and Their Sensitivity to Input Data (FPAR/LAI). Remote Sens. 2015, 7, 135–152. [Google Scholar] [CrossRef]
- Li, X.; Lu, H.; Yu, L.; Yang, K. Comparison of the spatial characteristics of four remotely sensed leaf area index products over China: Direct validation and relative uncertainties. Remote Sens. 2018, 10, 148. [Google Scholar] [CrossRef]
- Shabanov, N.V.; Huang, D.; Yang, W.; Tan, B.; Knyazikhin, Y.; Myneni, R.B.; Ahl, D.E.; Gower, S.T.; Huete, A.R.; Aragão, L.E.O. Analysis and optimization of the MODIS leaf area index algorithm retrievals over broadleaf forests. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1855–1865. [Google Scholar] [CrossRef]
- Yang, W.; Shabanov, N.; Huang, D.; Wang, W.; Dickinson, R.; Nemani, R.; Knyazikhin, Y.; Myneni, R. Analysis of leaf area index products from combination of MODIS Terra and Aqua data. Remote Sens. Environ. 2006, 104, 297–312. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Yan, G.; Chen, C.; Yang, B.; Liu, Z.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Evaluation of MODIS LAI/FPAR Product Collection 6. Part 1: Consistency and Improvements. Remote Sens. 2016, 8, 359. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y.; Fang, H.; Myneni, R.; Claverie, M.; Zhu, Z. Inconsistencies of interannual variability and trends in long-term satellite leaf area index products. Glob. Chang. Biol. 2017, 23, 4133–4146. [Google Scholar] [CrossRef] [PubMed]
- Cammalleri, C.; Verger, A.; Lacaze, R.; Vogt, J. Harmonization of GEOV2 fAPAR time series through MODIS data for global drought monitoring. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Pisek, J.; Chen, J.M.; Alikas, K.; Deng, F. Impacts of including forest understory brightness and foliage clumping information from multiangular measurements on leaf area index mapping over North America. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M. Performances of neural networks for deriving LAI estimates from existing CYCLOPES and MODIS products. Remote Sens. Environ. 2008, 112, 2789–2803. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Y.; Zhang, Y.; Knyazikhin, Y.; Bogaert, J.; Myneni, R.B. Radiative transfer based scaling of LAI retrievals from reflectance data of different resolutions. Remote Sens. Environ. 2003, 84, 143–159. [Google Scholar] [CrossRef]
- Bloom, A.A.; Exbrayat, J.-F.; Van Der Velde, I.R.; Feng, L.; Williams, M. The decadal state of the terrestrial carbon cycle: Global retrievals of terrestrial carbon allocation, pools, and residence times. Proc. Natl. Acad. Sci. USA 2016, 113, 1285–1290. [Google Scholar] [CrossRef]
- Raupach, M.R.; Rayner, P.J.; Barrett, D.J.; DeFries, R.S.; Heimann, M.; Ojima, D.S.; Quegan, S.; Schmullius, C.C. Model–data synthesis in terrestrial carbon observation: Methods, data requirements and data uncertainty specifications. Glob. Chang. Biol. 2005, 11, 378–397. [Google Scholar] [CrossRef]
- Xie, X.; Li, A.; Jin, H.; Tan, J.; Wang, C.; Lei, G.; Zhang, Z.; Bian, J.; Nan, X. Assessment of five satellite-derived LAI datasets for GPP estimations through ecosystem models. Sci. Total Environ. 2019, 690, 1120–1130. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Xiao, J.; Ju, W.; Zhu, G.; Wu, X.; Fan, W.; Li, D.; Zhou, Y. Satellite-derived LAI products exhibit large discrepancies and can lead to substantial uncertainty in simulated carbon and water fluxes. Remote Sens. Environ. 2018, 206, 174–188. [Google Scholar] [CrossRef]
- Xiao, J.; Chevallier, F.; Gomez, C.; Guanter, L.; Hicke, J.A.; Huete, A.R.; Ichii, K.; Ni, W.; Pang, Y.; Rahman, A.F. Remote sensing of the terrestrial carbon cycle: A review of advances over 50 years. Remote Sens. Environ. 2019, 233, 111383. [Google Scholar] [CrossRef]
- Scholze, M.; Buchwitz, M.; Dorigo, W.; Guanter, L.; Quegan, S. Reviews and syntheses: Systematic Earth observations for use in terrestrial carbon cycle data assimilation systems. Biogeosciences 2017, 14, 3401–3429. [Google Scholar] [CrossRef]
- Dietze, M.C. Ecological Forecasting; Princeton University Press: Princeton, NJ, USA, 2017. [Google Scholar]
- López-Blanco, E.; Exbrayat, J.-F.; Lund, M.; Christensen, T.R.; Tamstorf, M.P.; Slevin, D.; Hugelius, G.; Bloom, A.A.; Williams, M. Evaluation of terrestrial pan-Arctic carbon cycling using a data-assimilation system. Earth Syst. Dyn. 2019, 10, 233–255. [Google Scholar] [CrossRef]
- MacBean, N.; Peylin, P.; Chevallier, F.; Scholze, M.; Schuermann, G. Consistent assimilation of multiple data streams in a carbon cycle data assimilation system. Geosci. Model. Dev. 2016, 9, 3569–3588. [Google Scholar] [CrossRef]
- De Kauwe, M.G.; Disney, M.; Quaife, T.; Lewis, P.; Williams, M. An assessment of the MODIS collection 5 leaf area index product for a region of mixed coniferous forest. Remote Sens. Environ. 2011, 115, 767–780. [Google Scholar] [CrossRef]
- Chevallier, F. Impact of correlated observation errors on inverted CO2 surface fluxes from OCO measurements. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Xu, B.; Li, J.; Park, T.; Liu, Q.; Zeng, Y.; Yin, G.; Zhao, J.; Fan, W.; Yang, L.; Knyazikhin, Y. An integrated method for validating long-term leaf area index products using global networks of site-based measurements. Remote Sens. Environ. 2018, 209, 134–151. [Google Scholar] [CrossRef]
- Stark, S.C.; Leitold, V.; Wu, J.L.; Hunter, M.O.; de Castilho, C.V.; Costa, F.R.; McMahon, S.M.; Parker, G.G.; Shimabukuro, M.T.; Lefsky, M.A. Amazon forest carbon dynamics predicted by profiles of canopy leaf area and light environment. Ecol. Lett. 2012, 15, 1406–1414. [Google Scholar] [CrossRef]
- Jucker, T.; Hardwick, S.R.; Both, S.; Elias, D.M.; Ewers, R.M.; Milodowski, D.T.; Swinfield, T.; Coomes, D.A. Canopy structure and topography jointly constrain the microclimate of human-modified tropical landscapes. Glob. Chang. Biol. 2018, 24, 5243–5258. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, S.; Li, H.; Ma, Y.; Wang, J.; Zhang, Y.; Xu, Z.; Xu, T.; Song, L.; Yang, X. Intercomparison of six upscaling evapotranspiration methods: From site to the satellite pixel. J. Geophys. Res. Atmos. 2018, 123, 6777–6803. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Qin, J.; Qu, Y. An upscaling algorithm to obtain the representative ground truth of LAI time series in heterogeneous land surface. Remote Sens. 2015, 7, 12887–12908. [Google Scholar] [CrossRef]
- Hilker, T.; Lyapustin, A.I.; Tucker, C.J.; Sellers, P.J.; Hall, F.G.; Wang, Y. Remote sensing of tropical ecosystems: Atmospheric correction and cloud masking matter. Remote Sens. Environ. 2012, 127, 370–384. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.C.; Malambo, L. Using ICESat-2 to Estimate and Map Forest Aboveground Biomass: A First Example. Remote Sens. 2020, 12, 1824. [Google Scholar] [CrossRef]
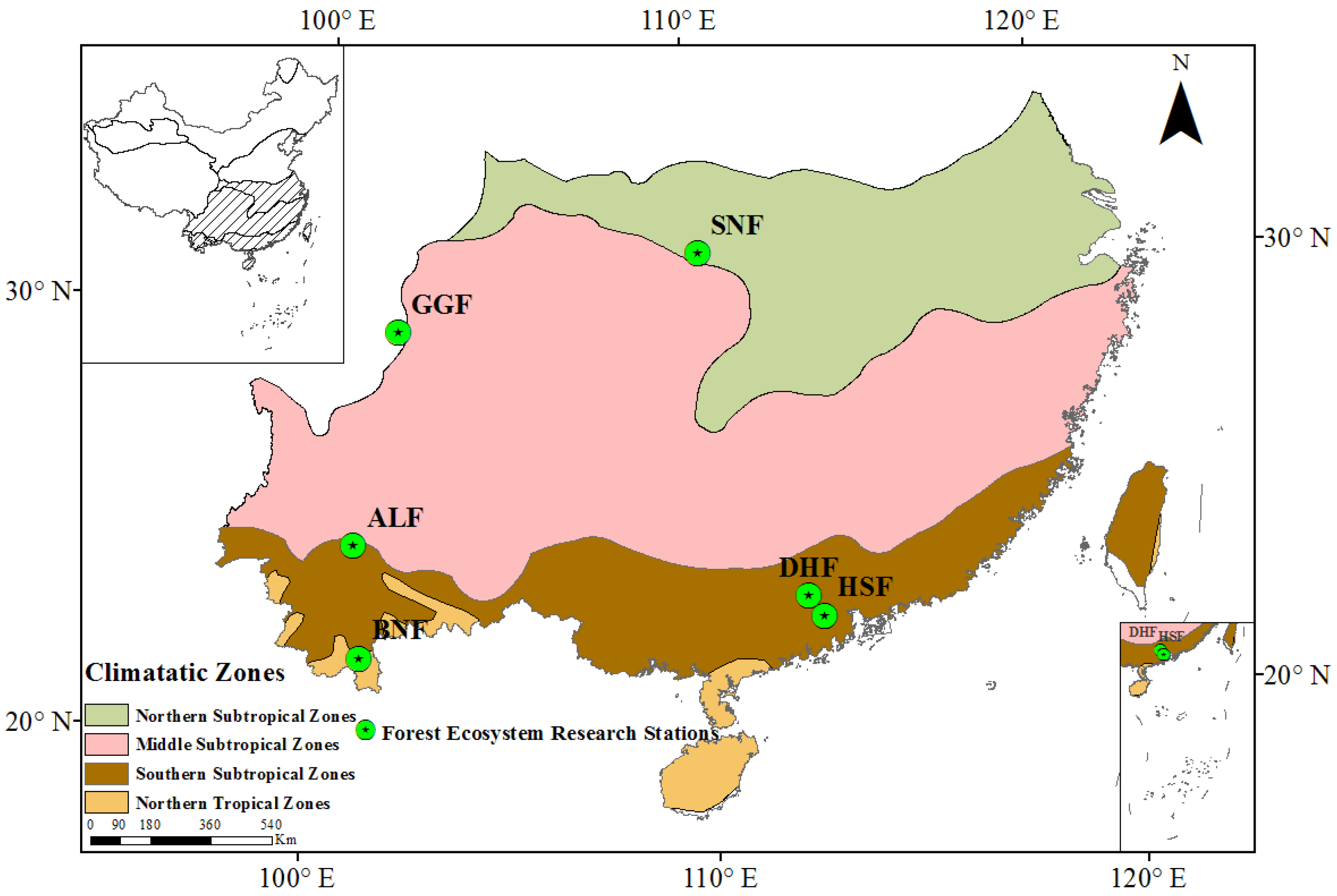
| Sites | Latitude (N) | Longitude (W) | Altitude (m) | MAT (°C) | AP (mm) | Gradient | Forest Types |
|---|---|---|---|---|---|---|---|
| BNF | 21.91 | 101.2 | 730 | 21.8 | 1506 | 18–25° | Tropical seasonal rainforest |
| HSF | 22.67 | 112.89 | 70 | 21.7 | 1761 | 18–23° | Mixed coniferous forest |
| DHF | 23.16 | 112.53 | 300 | 21 | 1996 | 25–35° | Mixed coniferous forest |
| ALF | 24.54 | 101.01 | 2488 | 11 | 1931 | 5–25° | Natural wet evergreen broad-leaved forest |
| GGF | 29.57 | 101.98 | 3160 | 4.2 | 2175 | 30–35° | Subalpine Emei fir forest |
| SNF | 31.3 | 110.47 | 1650 | 10.6 | 1722 | 10–70° | Evergreen and deciduous mixed broad-leaved forest |
| LAI Source | Metric Statics | ALF | BNF | DHF | GGF | HSF | SNF | Overall |
|---|---|---|---|---|---|---|---|---|
| Field (20~100 m) | Mean | 4.18 | 5.55 | 4.90 | 3.18 | 3.44 | 4.11 | 5.1 |
| Measurements error (std) | 0.46 | 0.58 | 0.89 | 0.5 | 0.51 | 0.57 | 0.59 | |
| Relative error (std/mean) | 0.11 | 0.11 | 0.18 | 0.16 | 0.15 | 0.14 | 0.12 | |
| N | 38 | 571 | 57 | 14 | 96 | 17 | 793 | |
| GEOV3 300 m | Mean | 3.28 | 5.15 | 3.82 | 2.38 | 2.94 | 3.34 | 4.50 |
| Product uncertainty (RMSE) | 0.13 | 0.20 | 0.12 | 0.04 | 0.55 | 0.30 | 0.22 | |
| Relative uncertainty (RMSE/Mean) | 0.04 | 0.04 | 0.03 | 0.02 | 0.19 | 0.09 | 0.07 | |
| Bias (mean) | −0.58 | −0.40 | −0.89 | −1.18 | −0.94 | −0.66 | −0.54 | |
| r (median) | 0.17 | 0.24 | 0.09 | 0.65 | 0.45 | 0.36 | 0.26 | |
| R2 | 0.12 | 0.18 | 0.53 | 0.05 | 0.21 | 0.93 | 0.45 | |
| N | 20 | 191 | 23 | 11 | 30 | 11 | 286 | |
| GEOV2 1 km | Mean | 3.3 | 3.35 | 2.92 | 0.82 | 1.72 | 2.96 | 3.07 |
| Product uncertainty (RMSE) | 0.54 | 0.60 | 0.60 | 0.27 | 0.33 | 0.77 | 0.56 | |
| Relative uncertainty (RMSE/Mean) | 0.16 | 0.18 | 0.21 | 0.33 | 0.19 | 0.26 | 0.19 | |
| Bias(mean) | −0.88 | −2.20 | −1.97 | −2.36 | −1.72 | −1.16 | −2.04 | |
| r (median) | 0.56 | 0.28 | 0.37 | 0.16 | 0.22 | 0.58 | 0.28 | |
| R2 | 0.18 | 0.22 | 0.15 | 0.38 | 0.30 | 0.74 | 0.36 | |
| N | 38 | 571 | 57 | 14 | 96 | 17 | 793 | |
| MODIS 500 m | Mean | 3.1 | 4.1 | 3.3 | 1.45 | 1.29 | 1.72 | 3.60 |
| Product uncertainty (std) | 0.45 | 0.38 | 0.48 | 0.66 | 0.16 | 0.40 | 0.37 | |
| Relative uncertainty (std/mean) | 0.15 | 0.09 | 0.14 | 0.44 | 0.12 | 0.23 | 0.10 | |
| Bias (mean) | −0.99 | −1.35 | −1.54 | −1.94 | −2.09 | −2.38 | −1.47 | |
| r (median) | 0.37 | 0.24 | 0.39 | 0.26 | 0.07 | 0.13 | 0.21 | |
| R2 | 0.03 | 0.12 | 0.10 | 0.47 | 0.16 | 0.25 | 0.20 | |
| N | 33 | 506 | 52 | 7 | 85 | 17 | 700 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Chen, X.; Smallman, T.L.; Flack-Prain, S.; Milodowski, D.T.; Williams, M. Characterizing the Error and Bias of Remotely Sensed LAI Products: An Example for Tropical and Subtropical Evergreen Forests in South China. Remote Sens. 2020, 12, 3122. https://doi.org/10.3390/rs12193122
Zhao Y, Chen X, Smallman TL, Flack-Prain S, Milodowski DT, Williams M. Characterizing the Error and Bias of Remotely Sensed LAI Products: An Example for Tropical and Subtropical Evergreen Forests in South China. Remote Sensing. 2020; 12(19):3122. https://doi.org/10.3390/rs12193122
Chicago/Turabian StyleZhao, Yuan, Xiaoqiu Chen, Thomas Luke Smallman, Sophie Flack-Prain, David T. Milodowski, and Mathew Williams. 2020. "Characterizing the Error and Bias of Remotely Sensed LAI Products: An Example for Tropical and Subtropical Evergreen Forests in South China" Remote Sensing 12, no. 19: 3122. https://doi.org/10.3390/rs12193122
APA StyleZhao, Y., Chen, X., Smallman, T. L., Flack-Prain, S., Milodowski, D. T., & Williams, M. (2020). Characterizing the Error and Bias of Remotely Sensed LAI Products: An Example for Tropical and Subtropical Evergreen Forests in South China. Remote Sensing, 12(19), 3122. https://doi.org/10.3390/rs12193122