A Deep Learning Approach to the Detection of Gossans in the Canadian Arctic
Abstract
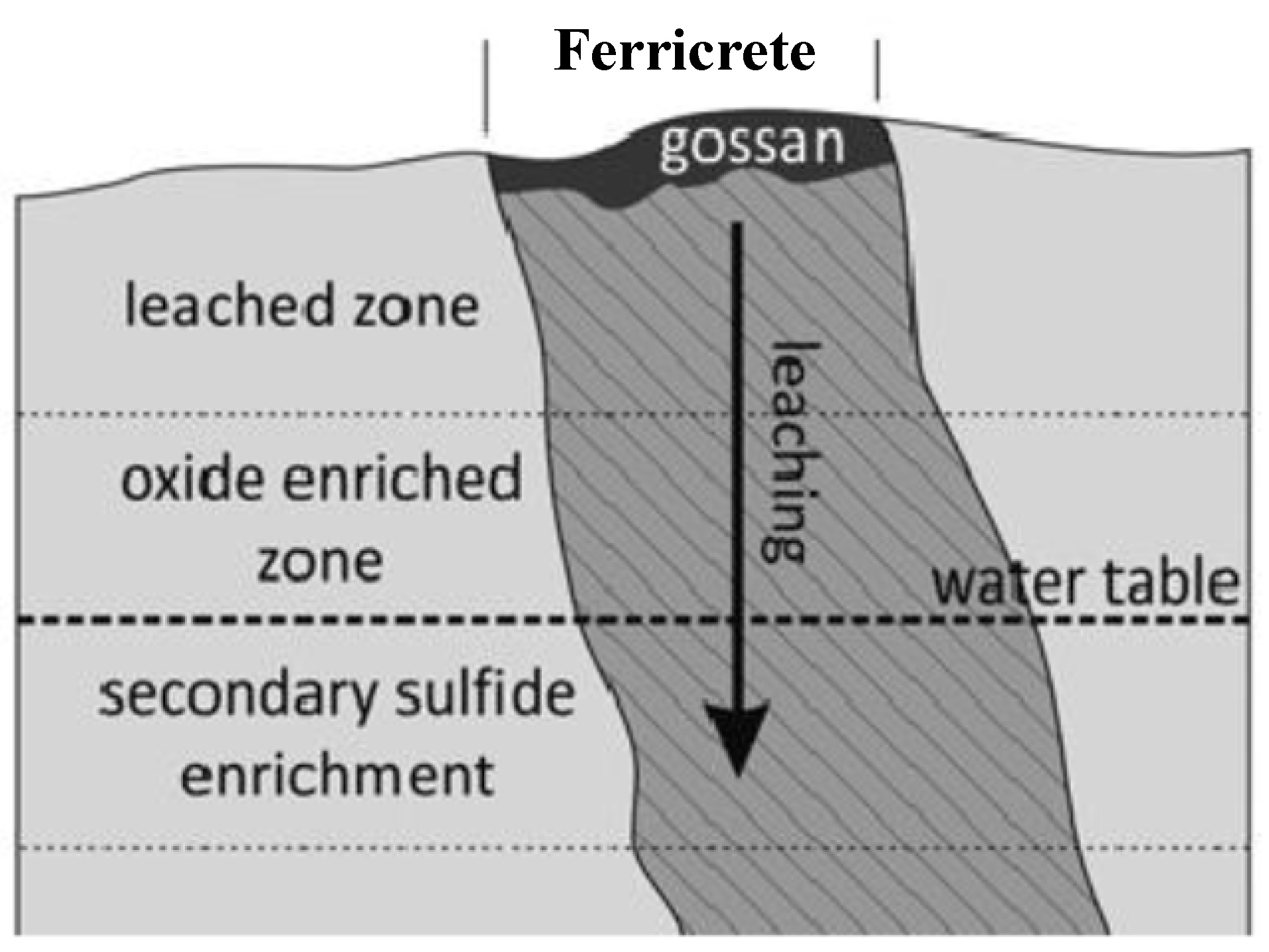
1. Introduction
2. Materials and Methods
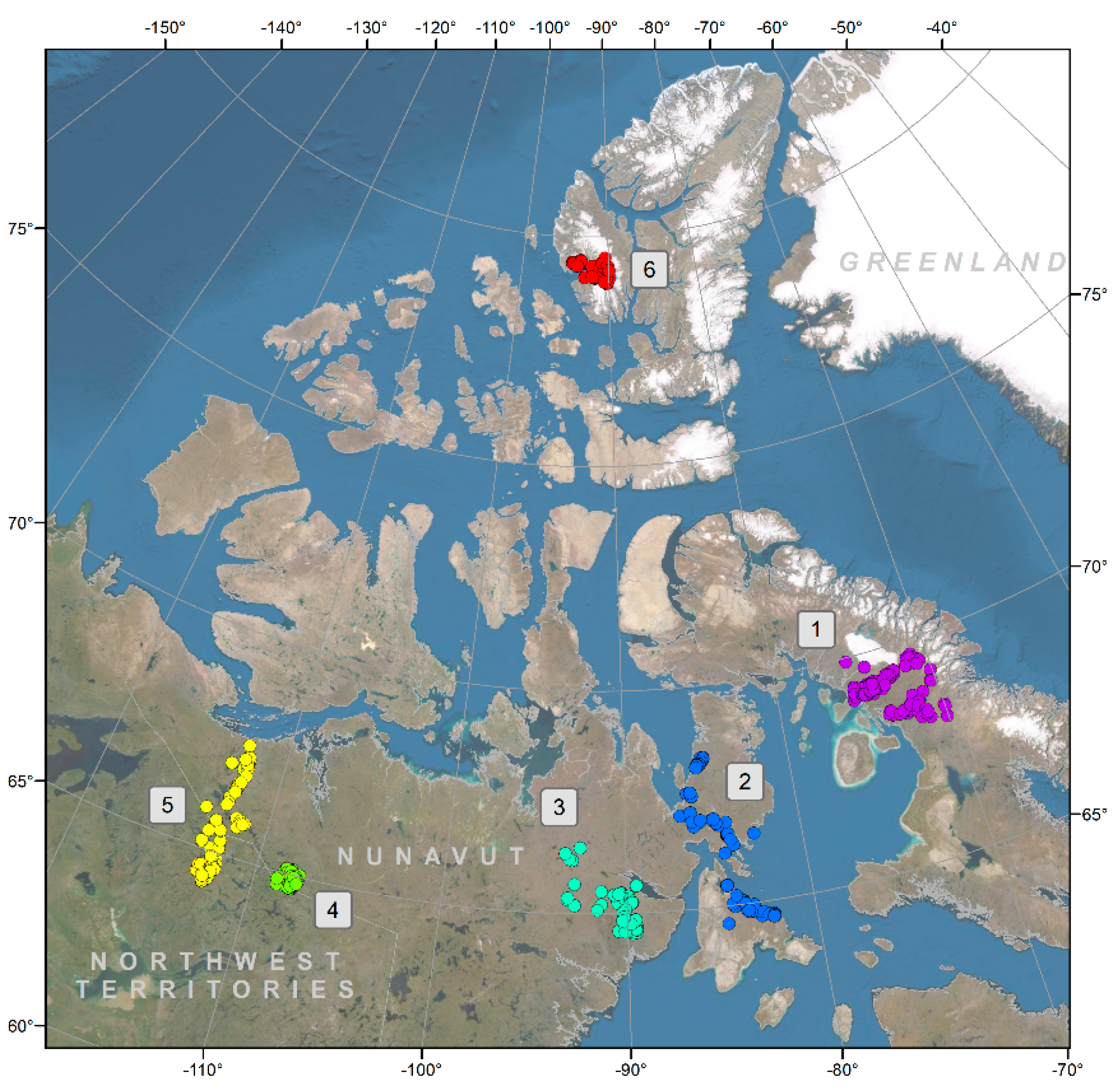
2.1. Region of Study
2.2. Satellite Imagery
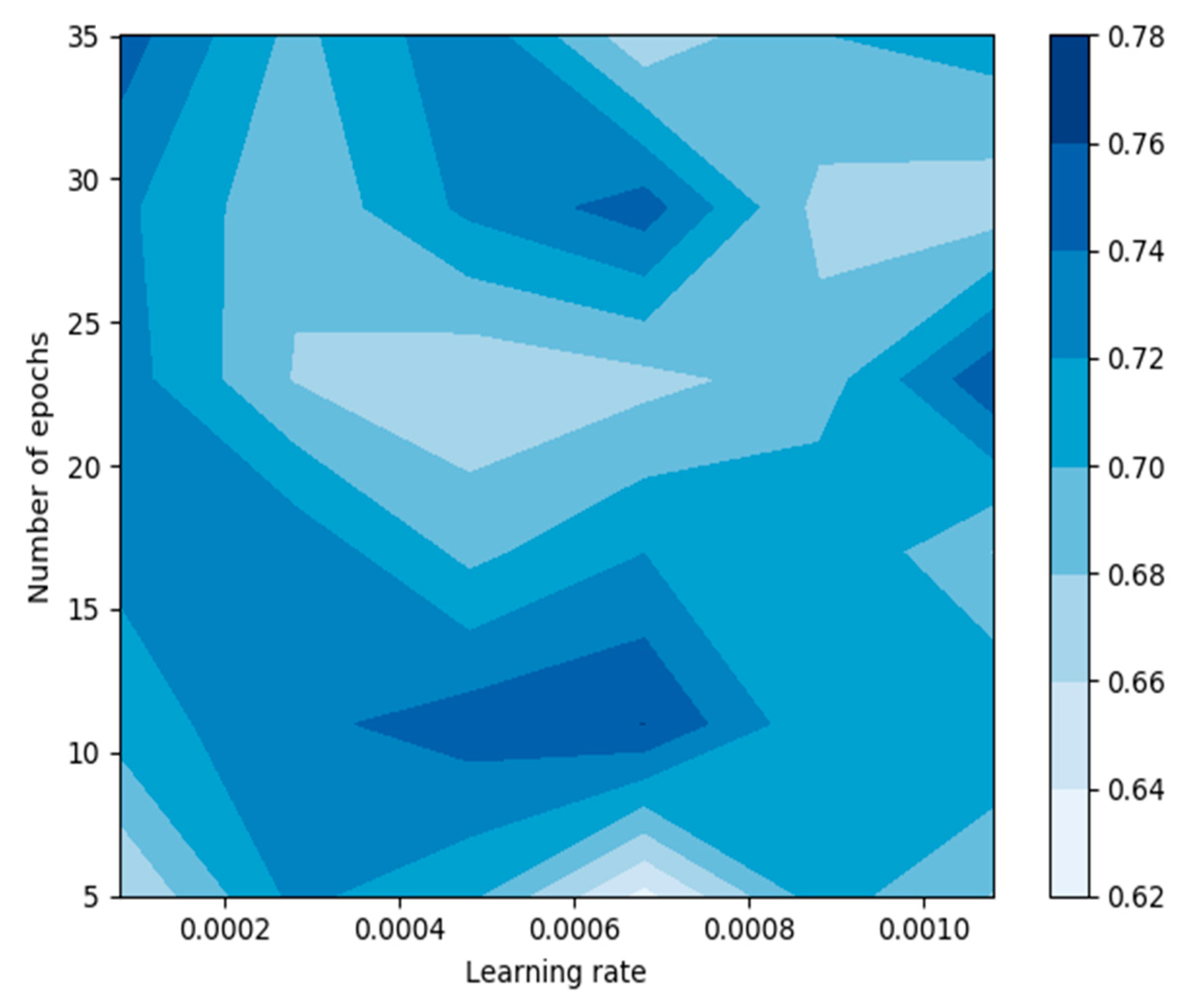
2.3. Methodology
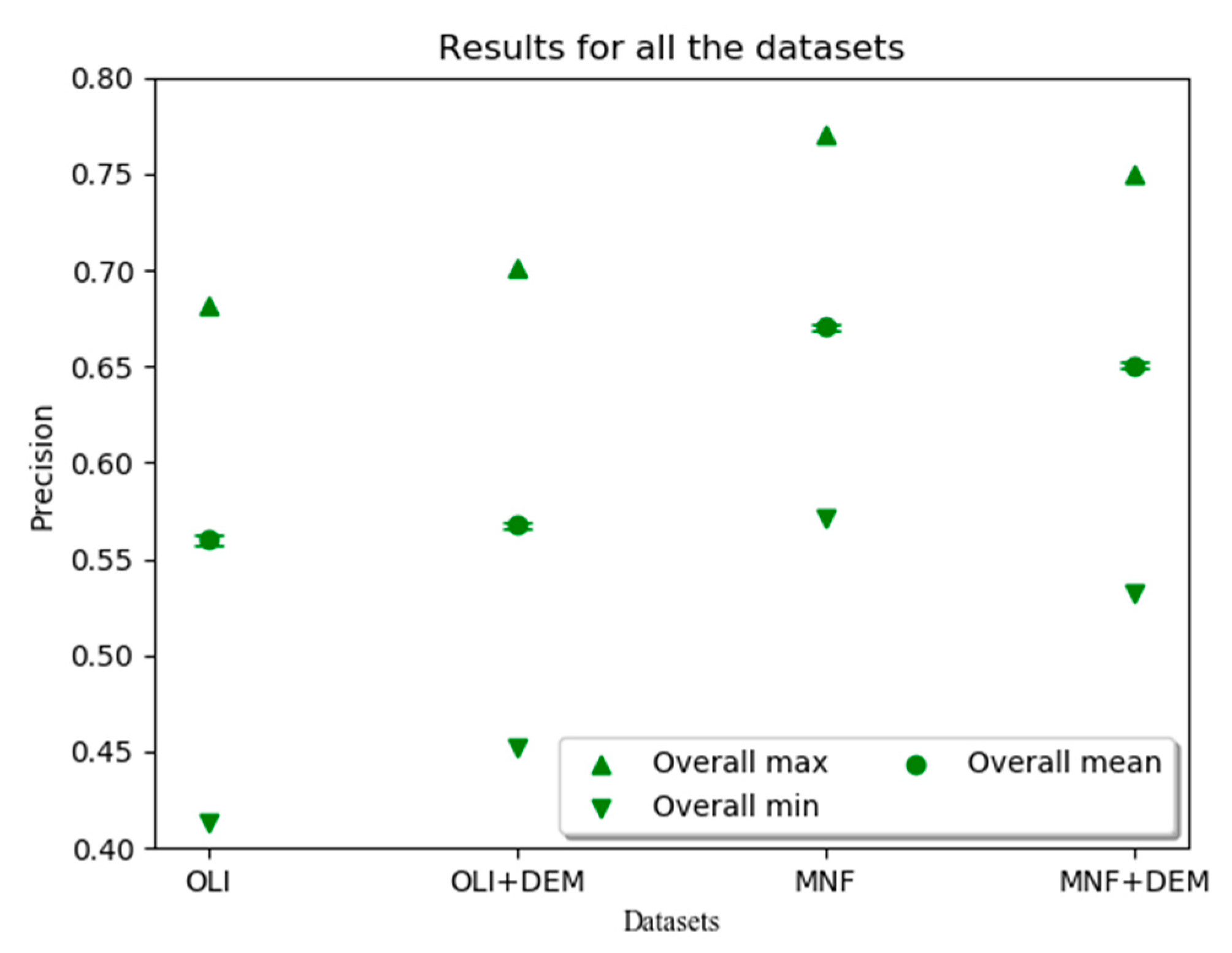
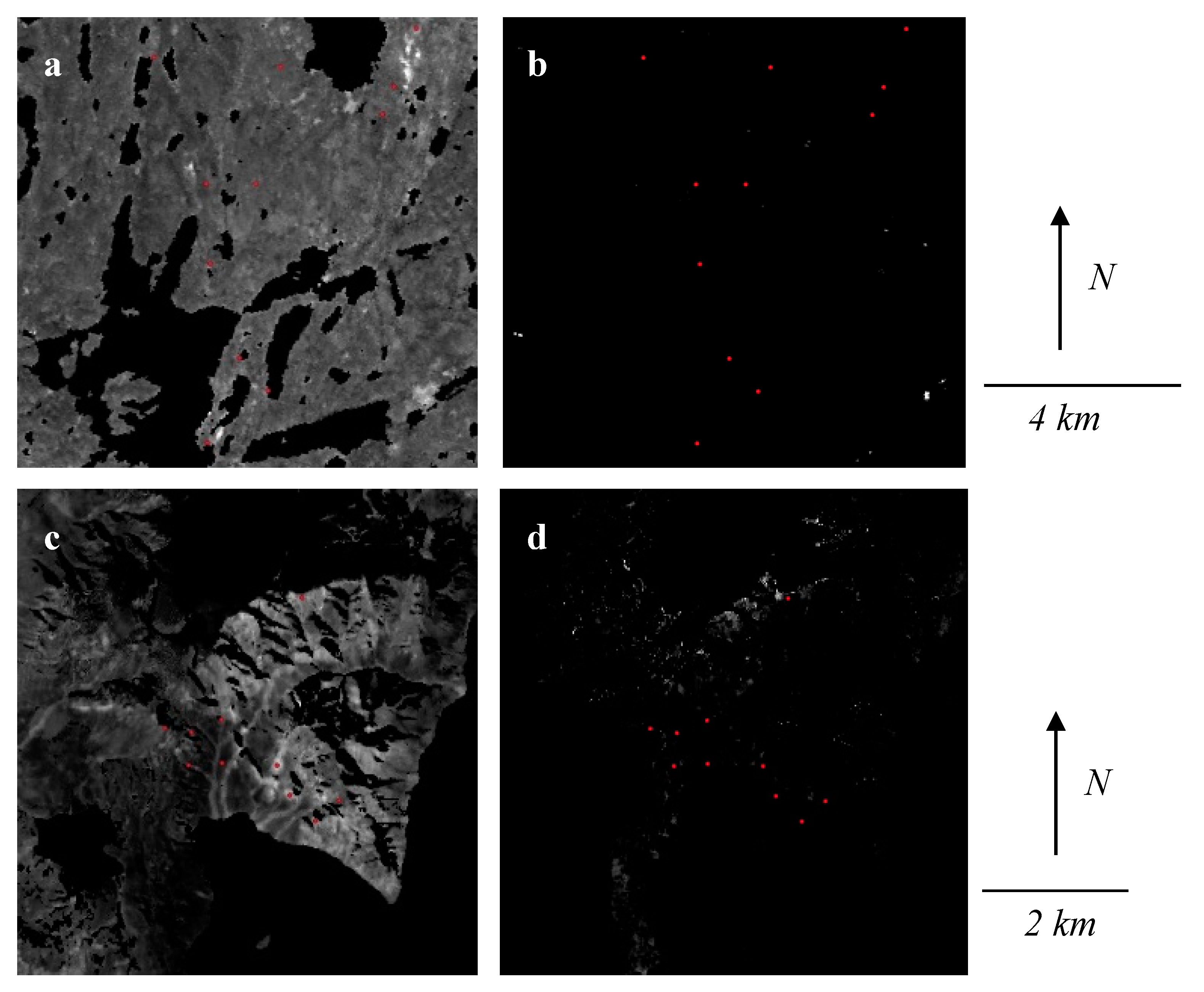
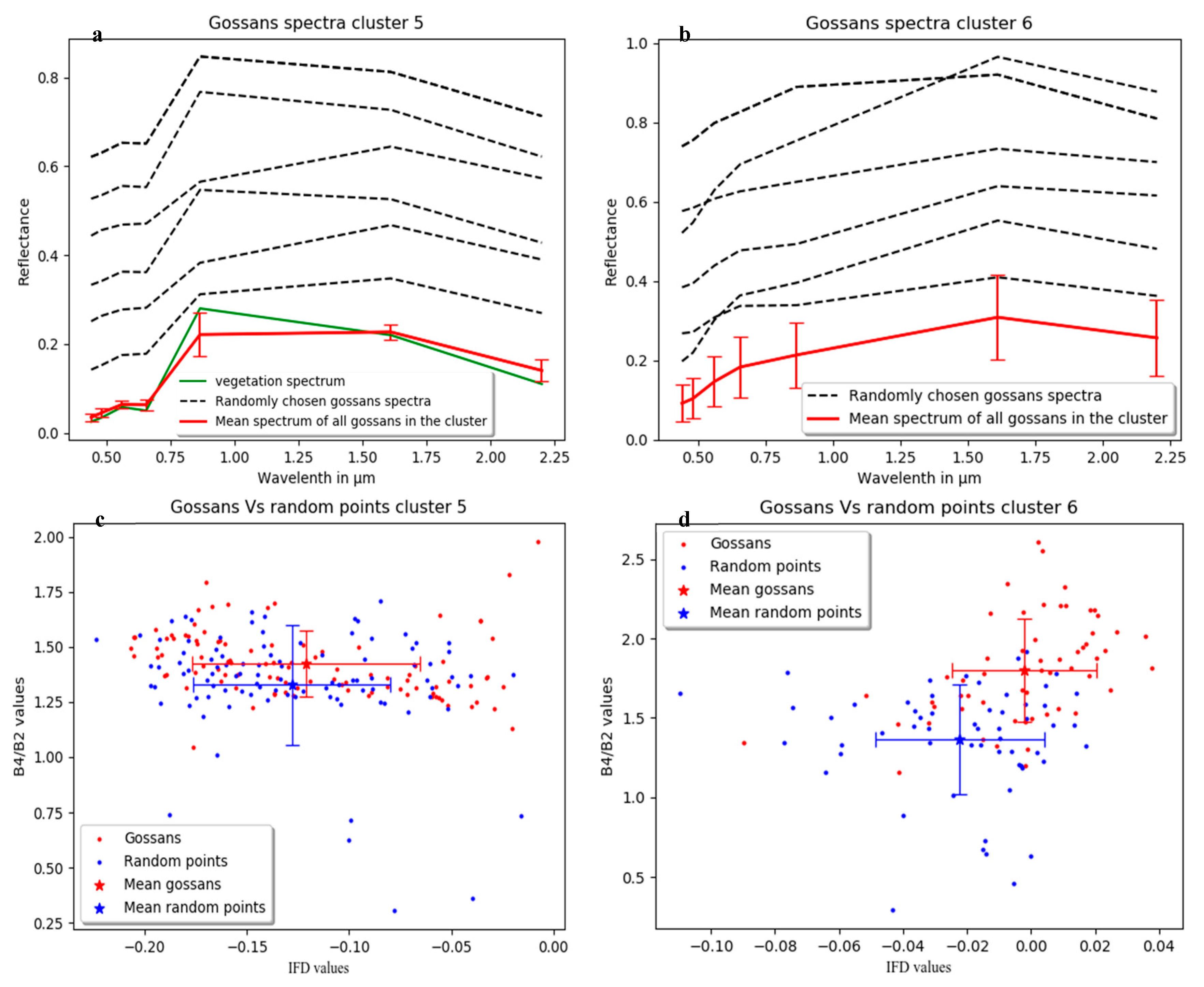
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Velasco, F.; Herrero, J.M.; Suárez, S.; Yusta, I.; Alvaro, A.; Tornos, F. Supergene features and evolution of gossans capping massive sulphide deposits in the Iberian Pyrite Belt. Ore Geol. Rev. 2013, 53, 181–203. [Google Scholar] [CrossRef]
- West, L.; McGown, D.J.; Onstott, T.C.; Morris, R.V.; Suchecki, P.; Pratt, L.M. High Lake gossan deposit: An Arctic analogue for ancient Martian surficial processes? Planet. Space Sci. 2009, 57, 1302–1311. [Google Scholar] [CrossRef]
- Harris, J.R.; Williamson, M.-C.; Percival, J.B.; Behnia, P.; Macleod, R. Detecting and Mapping Gossans Using Remotely-Sensed Data. In Environmental and Economic Significance of Gossans; Geological Survey of Canada: Ottawa, ON, Canada, 2015; p. 7718. [Google Scholar]
- Essalhi, M.; Sizaret, S.; Barbanson, L.; Chen, Y.; Lagroix, F.; Demory, F.; Nieto, J.M.; Sáez, R.; Capitán, M.Á. A case study of the internal structures of gossans and weathering processes in the Iberian Pyrite Belt using magnetic fabrics and paleomagnetic dating. Min. Depos. 2011, 46, 981–999. [Google Scholar] [CrossRef]
- Hunt, J.; Lottermoser, B.G.; Parbhakar-Fox, A.; Van Veen, E.; Goemann, K. Precious metals in gossanous waste rocks from the Iberian Pyrite Belt. Miner. Eng. 2016, 87, 45–53. [Google Scholar] [CrossRef]
- Peterson, R.C.; Williamson, M.-C.; Rainbird, R.H. Gossan Hill, Victoria Island, Northwest Territories: An analogue for mine waste reactions within permafrost and implication for the subsurface mineralogy of Mars. Earth Planet. Sci. Lett. 2014, 400, 88–93. [Google Scholar] [CrossRef]
- Williamson, M.-C. Environmental and Economic Significance of Gossans; Comission Géologique du Canada: Ottawa, ON, Canada, 2015; p. 100. [CrossRef]
- Cruz, C.; Noronha, F.; Santos, P.; Mortensen, J.K.; Lima, A. Supergene gold enrichment in the Castromil-Serra da Quinta gold deposit, NW Portugal. Mineral. Mag. 2018, 82, S307–S320. [Google Scholar] [CrossRef]
- Valente, T.; Rivera, M.J.; Almeida, S.F.P.; Delgado, C.; Gomes, P.; Grande, J.A.; de la Torre, M.L.; Santisteban, M. Characterization of water reservoirs affected by acid mine drainage: Geochemical, mineralogical, and biological (diatoms) properties of the water. Environ. Sci. Pollut. Res. 2016, 23, 6002–6011. [Google Scholar] [CrossRef] [PubMed]
- Santos, E.S.; Abreu, M.M.; Macías, F.; de Varennes, A. Chemical quality of leachates and enzymatic activities in Technosols with gossan and sulfide wastes from the São Domingos mine. J. Soils Sediments 2016, 16, 1366–1382. [Google Scholar] [CrossRef]
- Santos, E.S.; Abreu, M.M.; Macías, F.; Magalhães, M.C.F. Potential environmental impact of technosols composed of gossan and sulfide-rich wastes from São Domingos mine: Assay of simulated leaching. J. Soils Sediments 2017, 17, 1369–1383. [Google Scholar] [CrossRef]
- Santos, E.S.; Abreu, M.M.; Macías, F. Rehabilitation of mining areas through integrated biotechnological approach: Technosols derived from organic/inorganic wastes and autochthonous plant development. Chemosphere 2019, 224, 765–775. [Google Scholar] [CrossRef]
- Shuster, J.; Reith, F.; Izawa, M.; Flemming, R.; Banerjee, N.; Southam, G. Biogeochemical Cycling of Silver in Acidic, Weathering Environments. Minerals 2017, 7, 218. [Google Scholar] [CrossRef]
- Hedrich, S.; Schippers, A. Distribution of Acidophilic Microorganisms in Natural and Man-made Acidic Environments. Curr. Issues Mol. Biol. 2020, 25–48. [Google Scholar] [CrossRef]
- Floyd, M.A.M.; Williams, A.J.; Grubisic, A.; Emerson, D. Metabolic Processes Preserved as Biosignatures in Iron-Oxidizing Microorganisms: Implications for Biosignature Detection on Mars. Astrobiology 2019, 19, 40–52. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.N. Spectroscopy of Rocks and Minerals, and Principles of Spectroscopy. In Manual of Remote Sensing; Remote Sensing for the Earth Sciences; Andrew, N.R., Ed.; John Wiley and Sons: New York, NY, USA, 1999; Volume 3, pp. 3–58. [Google Scholar]
- Laakso, K.; Rivard, B.; Rogge, D. Enhanced detection of gossans using hyperspectral data: Example from the Cape Smith Belt of northern Quebec, Canada. ISPRS J. Photogramm. Remote Sens. 2016, 114, 137–150. [Google Scholar] [CrossRef]
- Beiranvand Pour, A.; S Park, T.Y.; Park, Y.; Hong, J.K.; M Muslim, A.; Läufer, A.; Crispini, L.; Pradhan, B.; Zoheir, B.; Rahmani, O.; et al. Landsat-8, Advanced Spaceborne Thermal Emission and Reflection Radiometer, and WorldView-3 Multispectral Satellite Imagery for Prospecting Copper-Gold Mineralization in the Northeastern Inglefield Mobile Belt (IMB), Northwest Greenland. Remote Sens. 2019, 11, 2430. [Google Scholar] [CrossRef]
- Abrams, M.J.; Ashley, R.P.; Rowan, L.C.; Goetz, A.F.H.; Kahle, A.B. Mapping of hydrothermal alteration in the Cuprite mining district, Nevada, using aircraft scanner images for the spectral region 0.46 to 2.36 µm. Geology 1977, 5, 713–718. [Google Scholar] [CrossRef]
- Abrams, M.J.; Brown, D.; Lepley, L.; Sadowski, R. Remote sensing for porphyry copper deposits in southern Arizona. Econ. Geol. 1983, 78, 591–604. [Google Scholar] [CrossRef]
- Gahlan, H.; Ghrefat, H. Detection of Gossan Zones in Arid Regions Using Landsat 8 OLI Data: Implication for Mineral Exploration in the Eastern Arabian Shield, Saudi Arabia. Nat. Resour. Res. 2018, 27, 109–124. [Google Scholar] [CrossRef]
- Mielke, C.; Muedi, T.; Papenfuss, A.; Boesche, N.K.; Rogass, C.; Gauert, C.D.K.; Altenberger, U.; de Wit, M.J. Multi- and hyperspectral spaceborne remote sensing of the Aggeneys base metal sulphide mineral deposit sites in the Lower Orange River region, South Africa. S. Afr. J. Geol. 2016, 119, 63–76. [Google Scholar] [CrossRef]
- Mielke, C.; Boesche, N.; Rogass, C.; Kaufmann, H.; Gauert, C.; de Wit, M. Spaceborne Mine Waste Mineralogy Monitoring in South Africa, Applications for Modern Push-Broom Missions: Hyperion/OLI and EnMAP/Sentinel-2. Remote Sens. 2014, 6, 6790–6816. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lin, M.; Chen, Q.; Yan, S. Network in Network. Available online: https://arxiv.org/pdf/1312.4400.pdf (accessed on 4 March 2014).
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 580–587. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; He, K.; Sun, J. Instance-Aware Semantic Segmentation via Multi-task Network Cascades. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3150–3158. [Google Scholar]
- Cheng, G.; Yang, C.; Yao, X.; Guo, L.; Han, J. When Deep Learning Meets Metric Learning: Remote Sensing Image Scene Classification via Learning Discriminative CNNs. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2811–2821. [Google Scholar] [CrossRef]
- Liu, Q.; Basu, S.; Ganguly, S.; Mukhopadhyay, S.; DiBiano, R.; Karki, M.; Nemani, R. DeepSat V2: Feature augmented convolutional neural nets for satellite image classification. Remote Sens. Lett. 2020, 11, 156–165. [Google Scholar] [CrossRef]
- Ducart, D.F.; Silva, A.M.; Toledo, C.L.B.; Assis, L.M. de Mapping iron oxides with Landsat-8/OLI and EO-1/Hyperion imagery from the Serra Norte iron deposits in the Carajás Mineral Province, Brazil. Braz. J. Geol. 2016, 46, 331–349. [Google Scholar] [CrossRef]
- Li, S.; Dragicevic, S.; Castro, F.A.; Sester, M.; Winter, S.; Coltekin, A.; Pettit, C.; Jiang, B.; Haworth, J.; Stein, A.; et al. Geospatial big data handling theory and methods: A review and research challenges. ISPRS J. Photogramm. Remote Sens. 2016, 115, 119–133. [Google Scholar] [CrossRef]
- GEM: Geo-mapping for Energy and Minerals. Available online: https://www.nrcan.gc.ca/earth-sciences/resources/federal-programs/geomapping-energy-minerals/18215 (accessed on 22 April 2019).
- Harrison, J.; St-Onge, M.; Petrov, O.; Strelnikov, S.; Lopatin, B.; Wilson, F.; Tella, S.; Paul, D.; Lynds, T.; Shokalsky, S.; et al. Geological Map of the Arctic; Geological Survey of Canada: Ottawa, ON, Canada, 2011. [CrossRef]
- Zanter, K. Landsat 8 Surface Reflectance Code (LASRC) Product Guide; USGS: Sioux Falls, SD, USA, 2019; p. 39.
- Canadian Digital Elevation Model, 1945–2011. Available online: https://open.canada.ca/data/en/dataset/7f245e4d-76c2-4caa-951a-45d1d2051333 (accessed on 29 January 2020).
- Bottou, L. Large-Scale Machine Learning with Stochastic Gradient Descent. In Proceedings of the COMPSTAT’2010, Paris, France, 22–27 August 2010; Lechevallier, Y., Saporta, G., Eds.; Physica-Verlag HD: Heidelberg, Germany; pp. 177–186. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Adivarekar, B. Simple Keras CNN with 95.3% Accuracy. Available online: https://www.kaggle.com/bhumitadivarekar/simple-keras-cnn-with-95-13-accuracy (accessed on 15 January 2020).
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Hutchison, D.; Kanade, T.; Kittler, J.; Kleinberg, J.M.; Mattern, F.; Mitchell, J.C.; Naor, M.; Nierstrasz, O.; Pandu Rangan, C.; Steffen, B.; et al. Learning to Detect Roads in High-Resolution Aerial Images. In Computer Vision – ECCV 2010; Daniilidis, K., Maragos, P., Paragios, N., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6316, pp. 210–223. ISBN 978-3-642-15566-6. [Google Scholar]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; DiBiano, R.; Karki, M.; Nemani, R. DeepSat: A learning framework for satellite imagery. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems - GIS ’15, Seattle, WA, USA, 3–6 November 2015; ACM Press: New York, NY, USA; pp. 1–10. [Google Scholar]
- Perez, L.; Wang, J. The Effectiveness of Data Augmentation in Image Classification using Deep Learning. Available online: https://arxiv.org/pdf/1712.04621.pdf (accessed on 13 December 2017).





| Spectral Range | Spatial Resolution | |
|---|---|---|
| Band 1 Costal aerosol | 0.43–0.45 µm | 30 m |
| Band 2 Blue | 0.450–0.51 µm | 30 m |
| Band 3 Green | 0.53–0.59 µm | 30 m |
| Band 4 Red | 0.64–0.67 µm | 30 m |
| Band 5 Near-Infrared | 0.85–0.88 µm | 30 m |
| Band 6 SWIR 1 | 1.57–1.65 µm | 30 m |
| Band 7 SWIR 2 | 2.11–2.29 µm | 30 m |
| Band 8 Panchromatic | 0.50–0.68 µm | 15 m |
| Band 9 Cirrus | 1.36–1.38 µm | 30 m |
| Min Values Tested | Kept Values | Max Values Tested | |
|---|---|---|---|
| Number of epochs | 1 | 5–35 | 500 |
| Learning rate | 10−5 | 10−4–10−3 | 10−1 |
| Batch size | 16 | 64 | 256 |
| Dropout probability | 0.1 | 0.4–0.7 | 0.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clabaut, É.; Lemelin, M.; Germain, M.; Williamson, M.-C.; Brassard, É. A Deep Learning Approach to the Detection of Gossans in the Canadian Arctic. Remote Sens. 2020, 12, 3123. https://doi.org/10.3390/rs12193123
Clabaut É, Lemelin M, Germain M, Williamson M-C, Brassard É. A Deep Learning Approach to the Detection of Gossans in the Canadian Arctic. Remote Sensing. 2020; 12(19):3123. https://doi.org/10.3390/rs12193123
Chicago/Turabian StyleClabaut, Étienne, Myriam Lemelin, Mickaël Germain, Marie-Claude Williamson, and Éloïse Brassard. 2020. "A Deep Learning Approach to the Detection of Gossans in the Canadian Arctic" Remote Sensing 12, no. 19: 3123. https://doi.org/10.3390/rs12193123
APA StyleClabaut, É., Lemelin, M., Germain, M., Williamson, M.-C., & Brassard, É. (2020). A Deep Learning Approach to the Detection of Gossans in the Canadian Arctic. Remote Sensing, 12(19), 3123. https://doi.org/10.3390/rs12193123






