Abstract
The spatial and temporal scale of rainfall datasets is crucial in modeling hydrological processes. Recently, open-access satellite precipitation products with improved resolution have evolved as a potential alternative to sparsely distributed ground-based observations, which sometimes fail to capture the spatial variability of rainfall. However, the reliability and accuracy of the satellite precipitation products in simulating streamflow need to be verified. In this context, the objective of the current study is to assess the performance of three rainfall datasets in the prediction of daily and monthly streamflow using Soil and Water Assessment Tool (SWAT). We used rainfall data from three different sources: Climate Hazards Group InfraRed Rainfall with Station data (CHIRPS), Climate Forecast System Reanalysis (CFSR) and observed rain gauge data. Daily and monthly rainfall measurements from CHIRPS and CFSR were validated using widely accepted statistical measures, namely, correlation coefficient (CC), root mean squared error (RMSE), probability of detection (POD), false alarm ratio (FAR), and critical success index (CSI). The results showed that CHIRPS was in better agreement with ground-based rainfall at daily and monthly scale, with high rainfall detection ability, in comparison with the CFSR product. Streamflow prediction across multiple watersheds was also evaluated using Kling-Gupta Efficiency (KGE), Nash-Sutcliffe Efficiency (NSE) and Percent BIAS (PBIAS). Irrespective of the climatic characteristics, the hydrologic simulations of CHIRPS showed better agreement with the observed at the monthly scale with the majority of the NSE values ranging between 0.40 and 0.78, and KGE values ranging between 0.62 and 0.82. Overall, CHIRPS outperformed the CFSR rainfall product in driving SWAT for streamflow simulations across the multiple watersheds selected for the study. The results from the current study demonstrate the potential of CHIRPS as an alternate open access rainfall input to the hydrologic model.
1. Introduction
Hydrological models have become efficient tools to understand problems related to water resources and obtain information about the water cycle in a given study area. Among the various components of the water cycle, rainfall plays a significant role and hence forms an indispensable element that constitutes the input dataset for hydrological models. Rainfall, being highly variable with respect to space and time, requires a well-distributed rain gauge network to accurately map variability over the catchment area. Rainfall data, which represent spatio-temporal variability, is an appanage to the distributed and semi-distributed hydrological models. In most cases, sparsely distributed rain-gauge networks fail to capture the spatio-temporal variability in rainfall. Even the existing rain gauge stations might not generate continuous records of data due to technical failure, which can also affect the ability to capture variability. Depending on the geomorphology and geography of the location in question, the Thiessen polygon technique of spatially extrapolating the data may not be an applicable method. In addition, there are situations where reliable datasets are available, but they are not available in the public domain. In this context, satellite-derived estimates of rainfall data have proven to be effective in capturing the spatial heterogeneity in rainfall to a significant extent [1,2,3].
The spatial coverage, proper temporal resolution, and free availability of data in the public domain give satellite-based rainfall datasets an edge over conventional rain gauge observations. Further, reanalysis datasets that combine satellite estimates with observed data constitute the category of gridded datasets of rainfall. The spatial distribution is accounted for by gridded datasets through interpolation and assimilation from rain gauge stations [4,5]. These datasets differ in their spatial and temporal resolutions, domain size, sources, and the method by which they are obtained [6]. Since these datasets are an indirect estimator of rainfall, they need to be evaluated in terms of their effectiveness in capturing the spatio-temporal variability in rainfall when compared to observed rain gauge data [7,8].
The evaluation is usually carried out by either field experiments to quantify the error or in terms of statistical comparison or long term trends of the satellite datasets with observed values [1,9,10,11,12]. The comparisons are made in terms of long-term average rainfall values, the multi-year trend in rainfall across different datasets, and interannual variability in rainfall among the datasets, etc. [12].
Statistically quantifying the ability of different rainfall datasets to simulate streamflow within a hydrological modeling framework provides another method for comparing rainfall data [13,14,15,16,17,18]. These studies focused on applying the gridded rainfall datasets from diverse sources as input to the hydrological model and assessed the datasets based on a comparison between the simulated flows generated by the datasets against the observed streamflows. Many studies have been carried out on the performance of merged satellite precipitation products or open-access satellite products, namely, CFSR, TRMM and CHIRPS precipitation datasets in hydrological modeling [19,20,21,22]. However, in terms of the performance of the datasets in driving hydrological models, studies reported contrasting findings. While CFSR precipitation product yielded satisfactory performance in the case of few watersheds (Lake Tana basin [14], Gumera watershed in Ethiopia [23], small watersheds in the USA [23]); the performance was poor in the case of two other watersheds from USA [24], upstream watersheds of Three Gorges reservoir in China [25], upper Gilgel Abay basin, Ethiopia [26]. Similar to CFSR, the CHIRPS dataset yielded better performance compared to rest of the satellite products in simulating monthly streamflows for Upper Blue Nile Basin [20], Adige basin in Italy [21], Gilgel Abay basin in Ethiopia [26]. Hence, based on the results from the studies carried out on individual basins, it can be stated that the performance of the precipitation dataset in hydrological modeling is specific to the basin [27] or the climatic characteristic which individual basins represent.
Though gridded rainfall datasets have been widely used in hydrological modeling studies, bias/uncertainties associated with the data have been shown to have an impact on the model calibration and subsequently on the hydrological simulations [28,29]. Studies have shown that though the overall rainfall pattern appeared to be similar across the different datasets, differences in terms of quantity were observed in the Wet Tropics, and even higher differences in the case of dry regions [30]. The uncertainty in rainfall among the datasets gets subsequently translated into error in the estimates of streamflow, and the degree of error induced in the hydrological simulations varies with the geographic region [30]. This implies that climatic variability affects the performance of gridded datasets and hence needs to be accounted for in the hydrological modeling. A dataset that might capture the spatial heterogeneity in rainfall in each geographic area may not perform the same in another region.
To the best of our knowledge, no study has been conducted to assess the performance of these datasets across basins belonging to different climate classes or with distinct hydrological characteristics. In this context, the aim of this study is to (1) compare the precipitation values of products, namely, CFSR and CHIRPS along with ground-based rainfall data. (2) To evaluate the effectiveness of the three individual products in streamflow simulation using SWAT for multiple watersheds with distinct climatic characteristics and selected across the continents. The study attempts to arrive at a reliable potential alternative to ground-based measurements of precipitation as input data for hydrological models in regions with limited access to local gauge data.
2. Study Area
The ten watersheds selected for this analysis are distributed across five different continents and eight different climatic regions. Figure 1 shows the location of watersheds over the globe and their descriptions. Two watersheds from each of the following countries, namely, the USA, Brazil, Spain, Ethiopia, and India, were chosen for this study (Table 1), which belongs to different climatic classifications. According to the Koppen classification, the selected watersheds represent tropical monsoon climate (Am), tropical savanna climate (Aw), cold semi-arid (Bsk), humid subtropical (Cfa), temperate oceanic (Cfb), hot summer mediterranean (Csa), warm summer mediterranean (Csb) and hot summer humid continental (Dfa) [31]. The drainage area of the selected watersheds varied from 712 to 32,374 km2. The elevation of these watersheds varies from 0 to 2609 m above mean sea level. The annual rainfall ranges between 520 and 2517 mm for these watersheds. Land cover/land use determines how water is transported, allocated, and modified during residency on the landscape. As can be seen in Table 1, the selected watersheds have agriculture, rangeland, and forest as their dominant land cover/land use.
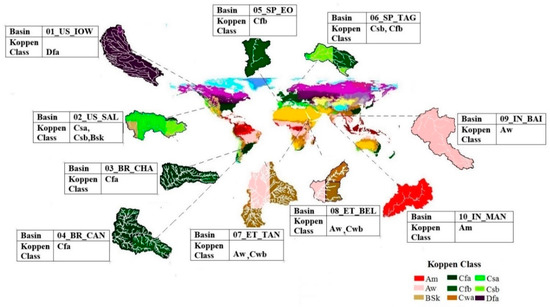
Figure 1.
Koppen classification of the world and the location of the watersheds used in this study along with their characteristics.

Table 1.
List of watersheds used, and the codes used to specify them for this work.
3. Materials and Methods
3.1. Rainfall Datasets
3.1.1. Gauge Rainfall Data
Gauge rainfall data have been taken as the reference dataset for the evaluation of satellite-based rainfall data in this study. For the USA watersheds, the local rainfall data is downloaded from the National Center for Environmental Information (NCEI) website. The local rainfall data for the watersheds in Brazil is downloaded from HidroWeb (http://www.snirh.gov.br/hidroweb/Publico/apresentacao.jsf). A total of 11 (03_BR_CHA) and 15 (04_BR_CAN) rainfall stations managed by the Brazilian National Water Agency (ANA) (www.ana.gov.br, Brasilia (DF), Brazil) were selected. For basins located in Spain, version 2.0 of the State Meteorology Agency (AEMET) (www.aemet.es, Madrid, Spain) grid has been used [32]. This grid has a spatial resolution of 5 km and provides daily rainfall from 1951 to March 2019. It has been produced based on the data from 3236 rainfall gauges, and according to previous studies [33], this grid provides satisfactory results in simulating streamflow. In the case of watersheds from Ethiopia, daily rainfall, and maximum/minimum temperature observations from 11 climatic stations in the Lake Tana and Beles basins are provided by the Ethiopian National Meteorological Agency (NMA) (www.ethiomet.gov.et/, Addis Ababa, Ethiopia) from 1988 to 2005. The SWAT model weather data generator [34] was prepared using observed weather data at the Bahir Dar meteorological gauging station to complete missing data in the rainfall and maximum/minimum temperature and generate data for relative humidity, solar radiation, and wind speed. Streamflow data are provided by the Ethiopian Ministry of Water, Irrigation, and Electricity (http://www.mowie.gov.et/, Addis Ababa, Ethiopia) for the 1990–2005 time span. The gridded rainfall and temperature datasets at a spatial resolution of 0.25° and 1° respectively, developed by the India Meteorological Department (IMD) (www.imdpune.gov.in, Pune, India) using the rain gauge network across India, were employed for the two watersheds in India [35].
3.1.2. Climate Forecast System Reanalysis (CFSR) Data
CFSR is a reanalysis dataset which is a widely used source of weather data and is available at http://globalweather.tamu.edu/. This interpolated dataset is based on the National Weather Service Global Forecast System. The dataset is based on hourly forecasts derived using information from satellite products and the global weather station network [24]. The CFSR datasets are at a spatial resolution of ~38 km and are delivered through the official website of SWAT.
3.1.3. CHIRPS Data
CHIRPS is a 30+ year quasi-global rainfall dataset which blends satellite data of 0.050 spatial resolution with in situ rain gauge station data to generate a time series of gridded rainfall. The dataset incorporates monthly rainfall climatology Climate Hazards Group Rainfall Climatology (CHP Clim), geostationary thermal infrared satellite observations, Tropical Rainfall Measuring Mission (TRMM) 3B42 rainfall product, atmospheric model rainfall fields from NOAA Climate Forecast System and rainfall observations from national or regional meteorological sources [36]. The dataset is available open-source and, for the current study, data for the period 1988–2014 were obtained from http://chg.geog.ucsb.edu/data/chirps/. Since it is available at a fine spatial resolution of 0.050, the dataset can be treated as a potential source of rainfall input for distributed hydrological models.
The authors have created a standalone tool, “Chirps4SWAT” to extract the CHIRPS rainfall data from the FTP server and convert them into the format, which can be used as input for the SWAT model. This tool will be made available in the following link https://swat.tamu.edu/software/. A screenshot of this tool is shown in Figure 2. The user should enter the bounding coordinates of the watersheds, the years for which data are required, and its resolution to obtain the rainfall data in the format to be used in the SWAT model.
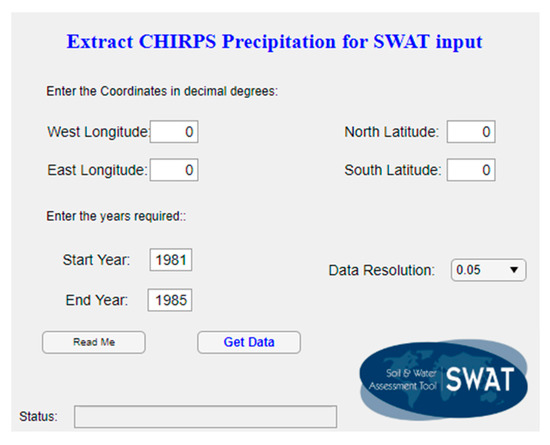
Figure 2.
Screenshot of the Chirps4SWAT tool to extract the Climate Hazards Group InfraRed Rainfall with Station data (CHIRPS) rainfall data.
3.1.4. Evaluation Statistics Used
In this study, the capability of the CFSR and CHIRPS datasets as input to the SWAT model for simulating daily streamflow was evaluated and compared to identify the best of the gridded rainfall products. Firstly, daily ground-based rainfall observations were used to assess the performance of the CFSR and CHIRPS rainfall products. One approach that is commonly used is to compare the nearest grid point of each satellite-based product directly to the gauge observations, but, according to Yong et al. (2014) [37], this approach may lead to evaluation errors because of the differences in scales between them. Meng et al. (2014) [38] suggested that for hydrologic applications, it is recommended to use area-averaged rainfall data to make a comparison between rainfall products and rain gauge data. Following this recommendation, the evaluation was done using the data from 1988 to 2013. The accuracy of the data quality of CHIRPS and CFSR rainfall products were quantified using four basic statistical metrics at a daily and monthly scale. These statistics include root mean square error (RMSE), mean error (ME), correlation coefficient (CC), and relative bias (BIAS). The ability to detect daily rainfall events was also evaluated using the probability of detection (POD), false alarm ratio (FAR), and critical success index (CSI). POD measures the skill of the rainfall product in detecting the occurrence of rainfall, while FAR measures rainfall detections that were false alarms. CSI considers both situations, accurate forecasting and incorrect forecasting, and measures the ratio of actual rainy day count to the total number of rainy days estimated by the CHIRPS and CFSR rainfall products. The expressions of each indicator, unit, and absolute value are shown in Table 2.

Table 2.
Statistical indices used for evaluating climate forecast system reanalysis (CFSR) and CHIRPS precipitation products.
3.2. Hydrological Modelling
The study employed the Soil Water Assessment Tool (SWAT). This semi-distributed, process-based, river basin model operates on a daily time step to model major hydrological processes such as rainfall, surface runoff, evapotranspiration, soil, and root zone infiltration, and baseflow. SWAT incorporates the effects of surface runoff, groundwater flow, evapotranspiration, weather, crop growth, land, and agricultural management practices to assess the hydrological behavior of the watershed. Based on the topographical information about the watershed, SWAT models the watershed as an accumulation of the number of sub-watersheds. Each sub-watershed consists of several Hydrological Response Units (HRU). These HRUs are areas with homogeneous land use, management, topography, and soil characteristics. All the water budget calculation in SWAT happens at the HRU level. SWAT computes water balance at HRU scale, irrespective of the area of the watershed. Studies have shown that in the case of SWAT, spatial scale has little impact on the streamflow simulations [39,40,41]. While water balance is the driving force behind all the processes in SWAT, simulation of watershed hydrology is separated into the land phase, which controls the amount of water, sediment, and nutrient loadings to the main channel in each sub-watershed, and the routing phase, which accounts for the movement of water and sediments through the channel network of the watershed to the outlet.
3.2.1. SWAT Model Setup
SWAT requires data related to topography, land use, soil, weather, and stream discharge as inputs to assess water balance. The study used 30 * 30 m resolution digital elevation model (DEM) data derived from Shuttle Radar Topographic Mission (SRTM) (srtm.csi.cgiar.org) for delineating the watershed as well as for defining the stream network, area, and slope of the sub-watersheds. The input datasets, in the form of land-use and soil maps, are crucial for accurate representation of landcover and soil characteristics.
The input datasets, comprised of DEM, land use, and soil map, were co-registered to the projection of respective catchments for SWAT setup. Apart from DEM, land use and soil data, SWAT requires daily rainfall, minimum and maximum air temperature, solar radiation, wind speed, and relative humidity as input data for hydrological simulation. The details and sources of the datasets are provided in Table 3. DEM, land use, soil map, and reservoir location, along with the database input files for the model, were organized, assembled, and modeled following the guidelines of the interface of SWAT 2012.

Table 3.
Description of the nature and source of datasets employed in the study.
3.2.2. Calibration Process
The SWAT model was run for three scenarios corresponding to (a) observed rainfall data, (b) CFSR gridded rainfall (c) CHIRPS gridded rainfall. The model was run at a daily time step with the initial three years treated as a warm-up period. The period of the simulation was selected, such that all three sources of rainfall covered the common time frame. Excluding the warm-up, 2000–2009 was used for calibration and 2010–2013 was considered for validation. The Sequential Uncertainty Fitting algorithm (SUFI-2) within SWAT-CUP was used to automatically calibrate the model for streamflow [42].
The calibration procedure requires objective functions, which optimizes the search in the parameter space and finds the best combination that reflect the watershed characteristics [43]. These statistical coefficients help the modelers to analyze the simulation results. In this study, the Kling–Gupta Efficiency (KGE) [44] was used as the objective function in the SUFI2 algorithm and for model evaluation
where r is the correlation coefficient between observed and simulated values, α is the measure of relative variability in the simulated and observed values, and β is the bias normalized by the standard deviation in the observed values.
The KGE is composed of three components (α, β, and r), which can be separately considered within each iteration, if necessary. The formulation also allows for the unequal weighting of the three components if one wishes to emphasize certain areas of the aggregate function tradeoff space. The KGE ranges from −∞ to 1. Regarding model performance, Nicolle et al. (2014) [45] consider 0.79 a good model, and Asadzadeh et al. (2016) [46] describes that a value of 0.45 could adequately estimate the daily streamflow.
The Percentage Bias (PBIAS) [47], p-factor and r-factor were metrics used to evaluate the model performance after calibration, through the distinct rainfall scenarios. The PBIAS evaluates the trend that the average of the simulated values has in relation to the observed ones. The ideal value of PBIAS is zero (%); a good model performance could be ±25% for streamflow [48]; positive values indicate a model underestimation and negative values overestimation
where is simulated values; and is observed values.
The p-factor and r-factor are the two uncertainty measures offered by SUFI-2. The p-factor is the percentage of observed data bracketed by the 95 percentage prediction uncertainty (ppu). The r-factor is equal to the average thickness of the 95 ppu band divided by the standard deviation of the observed data. A p-factor above of 0.70 and an r-factor under of 1.5 can be considered satisfactory simulations [49]
where and represent the upper and lower simulated boundaries at the time of the 95 ppu, and n is the number of observed datapoints, M refers to modele, is the simulation time step, stands for the standard deviation of the measured data; and is the number of observed data in the 95 ppu interval.
4. Results and Discussion
4.1. Evaluation of Gridded Rainfall Products
Daily and monthly precipitation estimates from CFSR and CHIRPS precipitation products were compared against the rain gauge data. The daily contingency scores CSI, FAR, and POD and the statistical indices CC, RMSE, ME, and BIAS are calculated and summarized in Table 4. Overall, CHIRPS exhibited the best overall performance for the period 1988–2013. This is especially true for a monthly scale where the values of CC, RMSE, ME, and BIAS indicated that CHIRPS data is in closest agreement with the observed data. The sign of monthly CC indicates that CHIRPS clearly outperforms CFSR, with the largest values in the watersheds located in the USA, Brazil, and Ethiopia. Minimum correlation values and the highest BIAS are found in the headwaters of the Tagus River (Spain). This result coincides with those of Katsanos et al. (2016) [50], which analyzed CHIRPS throughout the Mediterranean area and detected a poor correlation with local data, highlighting the possible lack of observed data over these areas.

Table 4.
Monthly and daily statistical and contingency indices for the CFSR and CHIRPS precipitation products as compared to the rain gauge observations.
Compared to the values of monthly statistical indices, daily CC is significantly lower in all watersheds, and it is difficult to deduce which rainfall product has better performance. This is due to the fact that, on a daily scale, the correlation coefficient is especially insensitive to additive and proportional differences and oversensitive to extreme values [51]. Related to the rainfall detection metrics, CFSR showed better skill at detecting rainfall events with higher CSI and POD values in all the studied basins and lower FAR values in all the basins studied except the one located in the Manimala river.
Based on the comparison of monthly rainfall statistics with that of observation data, high CC and low RMSE, ME and BIAS for CHIRPS data were obtained for almost all watersheds except those in Spain and Ethiopia. IOWA watershed in the USA (01_US_IOW) exhibited the highest CC value and lowest monthly statistics for RMSE, ME, and BIAS.
Though the FAR value for CHIRPS in the Manimala river was slightly higher compared to other watersheds, a higher POD value was also noted for the same watershed. The high POD value specific to the Baitarani river shows the positive skill of the CHIRPS data in detecting rainfall occurrences in the Manimala river. The FAR values for CHIRPS are lower compared to CFSR for all watersheds except the 02_US_SAL watershed. POD and CSI values for CFSR data were found to be higher than CHIRPS data for almost all watersheds except Baitarani river. This clearly indicates that CHIRPS data fare well in the rainfall prediction accuracy, compared with lower FAR values for most of the selected watersheds. In the case of CFSR data, the estimation skill of rainfall is attributed to the higher POD and CSI values.
One of the reasons for the low capacity of CHIRPS in detection metrics is its low number of rainy days compared to observed data. As shown in Table 5, in all the watersheds studied, CHIRPS detects fewer rainy days than those observed with local data. This situation is especially relevant in 02_US_MIN, 05_SP_EO and 06_SP_TAG where, for the period 1988–2013, CHIRPS underestimates the occurrence of rainfall even above 50%. However, when looking at the number of days in which more than 1 mm of rain was recorded, the detection capacity of CHIRPS increases considerably but is still lower than local data. If the threshold is set at 10 mm, the CHIRPS detection capacity of these heavy precipitation events has better agreement with local observations than that of the CFSR. This good capability of detecting the most intense rain events is what makes its flow simulation capability acceptable despite its low detection metrics.

Table 5.
Number of days with precipitation greater than 0 (PD0), 1 (PD1) or 10 (PD10) mm during the study period (1988–2013).
Figure 3 shows the box plot comparison of monthly rainfall from Gauge, CFSR, and CHIRPS over the selected watersheds. In the 01_US_IOW watershed during the snowfall season, which extends from mid-October to mid-April, CFSR presents more snowfall compared to gauge data. However, from June to September, which is the rainy season, CFSR had less rainfall compared to gauge data. In the case of the 02_US_SALwatershed, CFSR data depicted slightly more rainfall during high rainfall months while the performance of CFSR remained on par with the gauge data during low rainfall months. Furthermore, both in Iowa and Salt watersheds, the performance of CHIRPS matches well with the gauge data throughout the year.
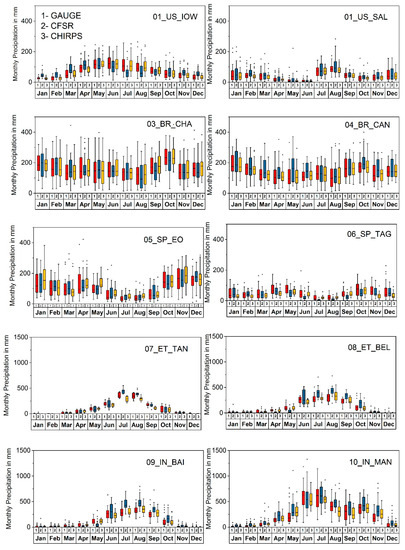
Figure 3.
Box plot comparison of the magnitude of rainfall and its temporal distribution generated by 1. Gauge 2. CFSR, and 3. CHIRPS.
In the Chapecó watershed, CFSR exhibited a slightly lower rainfall magnitude for the September and October months, while in the Canoas watershed, CFSR data slightly overestimated rainfall in some months. However, the Chapecó and Canaos watersheds, which have rainfall throughout the year, had both CFSR and CHIRPS in good agreement with rain gauge data except for in a few months. For the EO watershed, which experiences rainfall throughout the year, the variability range of all the three-rainfall data did not differ much. The Tagus River, which has low annual rainfall distributed across the year, saw the performance of all three rainfall datasets fail to show significant variability over the months. In the 07_ET_TAN and 08_ET_BEL watersheds, CFSR had more rainfall during the high rainfall months, and for rest of the period, the performances of CFSR and CHIRPS were similar to that of gauge data. However, in the 08_ET_BEL watershed, CHIRPS data outperformed CFSR data for almost all the months. In the case of the Baitarani watershed, which has a unimodal rainfall pattern, CFSR data had more rainfall during the rainy season; during the non-rainy season, the three rainfall datasets had almost similar rainfall magnitude. The 10_IN_MAN watershed, with a bimodal rainfall pattern, exhibited slightly higher rainfall by CFSR data during the rainy season, while summer months exhibited similar performance by all the three-rainfall data. Further, CHIRPS data matched well with the gauge data for both Baitarani and Manimala watersheds.
All three datasets were consistent in capturing the seasonal pattern of rainfall for the watersheds 07_ET_TAN, 08_ET_BEL, 09_IN_BAI, and 10_IN_MAN, with rainy months concentrated during the period June–October. Though seasonally consistent, CFSR had more rainfall in comparison with Gauge and CHIRPS for the rainy months. However, for the rest of the months with monthly rainfall less than 200 mm, the pattern and magnitude of rainfall from CFSR, CHIRPS are in agreement with the rain gauge. In the case of watersheds (01_US_IOW, 02_US_MIN, 03_BR_CHA, 04_BR_CAN, 05_SP_EO, and 06_SP_TAG), the rainfall is distributed throughout the year, with the magnitude of rainfall less in comparison with the watersheds belonging to a monsoon climate. Except for the watersheds 04_BR_CAN and 06_SP_TAG, where CFSR reported rains with marginally higher magnitude, a significant difference was not exhibited by the rainfall datasets.
Figure 4 shows the cumulative distribution fraction of the monthly rainfall acquired from local data, CFSR, and CHIRPS averaged over individual study watersheds during the period 1988–2013. The datasets exhibited similarity for values of monthly rainfall up to 100 mm across the watersheds, irrespective of the climatic zone to which they belong. The distribution of CHIRPS and CFSR matches the gauge data for values of monthly rainfall within 100 mm. Overall, CFSR and CHIRPS datasets agreed better with gauge data for the watersheds 01_US_IOW, 02_US_MIN, 03_BR_CHA, 04_BR_CAN, 05_SP_EO and 06_SP_TAG. CHIRPS and CFSR exhibit similar distribution with gauge for all rainfall depths. However, it should be noted that differences among the rainfall products were noteworthy in the case of watersheds belonging to Tropical monsoon (10_IN_MAN), Tropical wet/dry (09_IN_BAI) and Tropical highland monsoon (07_ET_TAN, 08_ET_BEL) climate. Unlike the rest of the watersheds, the box plot comparison of rainfall datasets indicates a monsoon climate with high magnitude rains reported during the monsoon months for the watersheds 07_ET_TAN, 08_ET_BEL, 09_IN_BAI and 10_IN_MAN. In the case of Indian watersheds (09_IN_BAI and 10_IN_MAN), CFSR datasets showed a different probability of occurrence for monthly rains greater than 150 mm. The most considerable difference in the CDFs corresponding to CFSR occurred for higher monthly rainfall depths, which coincides with the monsoon months. This difference in magnitude of rainfall is likely to translate to higher simulated runoff. Overall, it can be observed that CHIRPS is comparable with Gauge datasets, while CFSR shows variability at the higher magnitude of monthly rainfall. Figure 5 shows the cumulative distribution fraction of the daily rainfall.
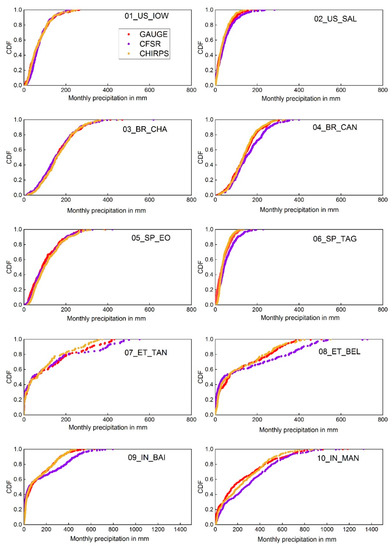
Figure 4.
Cumulative distribution of monthly rainfall of the selected watersheds for 1. Gauge 2. CFSR, and 3. CHIRPS.
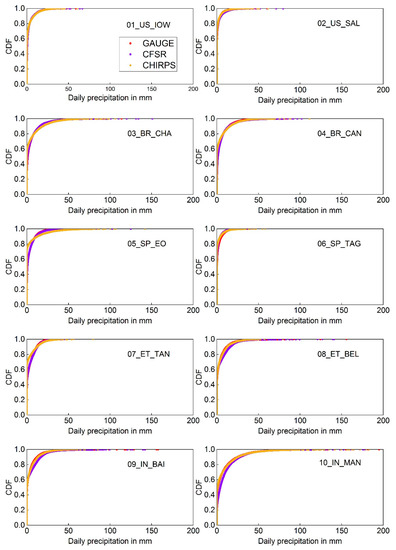
Figure 5.
Cumulative distribution of daily rainfall of the selected watersheds for 1. Gauge 2. CFSR, and 3. CHIRPS.
4.2. Streamflow Evaluation
Hydrological simulations from the SWAT model using three rainfall datasets (rain gauge, CFRS, and CHIRPS) were intercompared to evaluate the hydrological utility of satellite rainfall product-CHIRPS. The performance of the rainfall datasets was assessed based on scatter plots, cumulative probability plots of observed and simulated flows along with statistical indices NSE, KGE, and PBIAS at both daily and monthly scale. Previous studies [19,23,36] have evaluated the performance of reanalysis datasets in hydrologic simulations across watersheds of varying sizes. The CFSR and CHIRPS products used in the current and above-mentioned studies are available at spatial resolutions of 0.25 and 0.05 degree, respectively. Hence, we observe that further downscaling is not a requisite for the use of these data as an input to SWAT.
Table 6 shows the statistical measures employed to evaluate the performance of streamflow simulation at a monthly scale using gauge data, CFSR, and CHIRPS. From Table 6, it can be noted that in the 01_US_IOW watershed, CHIRPS data performed well during calibration and validation periods with respect to observed streamflow. Though the PBIAS was higher, the performance of rain gauge data was equally comparable with CHIRPS in terms of NSE and KGE for both calibration and validation. However, CFSR data gave a lower NS value, which could be due to their lower ability to capture extreme events, which is clear from the high RMSE value of CFSR rainfall data (Table 4). In the 02_US_SAL watershed, CHIRPS data outperformed others, with a high KGE value during both calibration and validation.

Table 6.
Model performance for the calibration and the validation period at the monthly scale.
Furthermore, flow simulations with rain gauge data reported very low KGE value during the validation period. This is due to a localized event that occurred during January 2010, which was not properly translated into flow simulations as the Thiessen polygon rainfall averaging technique employed in rain gauge data was inefficient to restrict it as a local event causing local flow. The performance of CFSR was not satisfactory compared to other rainfall data, which also was confirmed by the high RMSE value obtained during the analysis of CFSR rainfall (Table 4).
In the 03_BR_CHA watershed, CHIRPS and rain gauge data achieved a very good performance during the calibration period, with the CHIRPS model reporting the highest NSE and KGE values of 0.83 and 0.91 for calibration and lowest PBIAS value of 0.40. CFSR-driven simulations reached the level of good performance only due to low PBIAS value (−1.90%). It is observed that for the two watersheds in Brazil, the performance of CFSR is poor, which may be attributed to the high RMSE value of the monthly rainfall statistics (Table 4). While in the 04_BR_CAN watershed, both CHIRPS and rain gauge data performed better, however, a lower PBIAS value of 0.60 was reported for CHIRPS data-based simulations.
The performance of CHIRPS data to simulate the flow is inferior compared to that of gauge and CFSR data for the 05_SP_EO watershed. The high-resolution CHIRPS data were ineffective in improving the simulated flows and it is interesting to note large biases in CHIRPS data (Table 4), which may be translated into flow simulations. This may be attributed to the small size of the watershed. In the 06_SP_TAG watershed, model simulations with rain gauge data as input had a higher performance than CFSR and CHIRPS data. This may be due to the presence of large biases in rainfall estimates of both CFSR and CHIRPS data (Table 4).
In the case of Ethiopian watersheds (07_ET_TAN, 08_ET_BEL) the performance of CFSR was relatively better in comparison with CHIRPS. CHIRPS data performed fairly well in 09_IN_BAI watershed with a relatively low value of PBIAS during the calibration period and slightly higher value of PBIAS during the validation period. In the 09_IN_BAI watershed, the performance of CFSR data was unsatisfactory and can be attributed to the overestimation of rainfall in the watershed (Figure 3 and Figure 4). Further, high values of RMSE, ME, and BIAS were observed for CFSR data (Table 4). In the 10_IN_MAN watershed, CHIRPS outperformed others in streamflow simulation even though there was no high disparity between the performance criteria values of other rainfall data on a monthly scale. However, a low value of NSE was obtained for gauge data during the calibration period; this indicates the inability of the model to capture high flows.
The summary of the model evaluation statistics for all watersheds at the monthly scale shows that gauge and CHIRPS datasets have almost similar performance. The streamflow simulations across the watersheds with gauge data as an input performed well with small PBIAS and NS and KGE values greater than 0.7 in the majority of the watersheds. The results indicate that the monthly streamflow simulations using CHIRPS showed relatively better performance with NS greater than 0.7 and KGE greater than 0.74 for most of the watersheds considered in the study. The statistical measures signified that CHIRPS performed satisfactorily during validation with many of the statistics within the acceptable model performance range. It may be noted that in the case of watersheds 09_IN_BAI, 04_BR_CAN, 02_US_SAL, the performance of CFSR is relatively poor, which can be attributed to the disparity between CFSR and gauge rainfall, wherein CFSR overestimates the rainfall (Figure 4). The overestimation of rainfall, which translates to overestimation in streamflow simulations, is reflected in the high negative PBIAS values for the respective watersheds. The overestimation of CFSR seems to be significant during the validation period, with reportedly high PBIAS for the watersheds.
Table 7 summarises the model evaluation statistics of streamflow simulations at the daily timescale. In 01_US_IOW watershed, CHIRPS data gave more accurate streamflow simulations on a daily timescale compared to the other rainfall inputs. The statistical comparisons showed positive NS and KGE values based on CHIRPS data for both calibration and validation periods, which indicates good skills in the simulations. In the 02_US_SAL watershed, statistical comparisons showed that hydrological simulations with rain gauge data as input had a higher performance during the calibration period than those based on other rainfall inputs. In the 03_BR_CHA, though CHIRPS data obtained a negative NS value, the performance was satisfactory with the highest value of KGE (0.36) obtained during the calibration period at a daily timescale. In the 04_BR_CAN watershed, the NS and KGE values for CHIRPS data were close to that for rain gauge input.

Table 7.
Model performance for the calibration and the validation period at the daily scale.
Moreover, the model simulations based on rain gauge data had higher performance in the two watersheds in Spain than those based on other rainfall inputs for both calibration and validation periods. The performance statistics at daily scale indicate that CFSR outperformed chirps in the case of Ethiopian watersheds (07_ET_TAN, 08_ET_BEL). In the 09_IN_BAI watershed, though the NSE value was slightly lower for CHIRPS data, a KGE value above 0.5 was obtained for both calibration and validation period, which indicated a good skill of CHIRPS data in streamflow simulations. The 10_IN_MAN watershed statistical comparisons showed that the simulations obtained with rain gauge data as input had a higher performance for both calibration and validation periods than those based on other rainfall inputs on a daily timescale.
Thus, taking into consideration the performance during both calibration and validation periods for the selected watersheds, it can be stated that the CHIRPS dataset outpaced CFSR, and the statistical measures were on par with that of gauge data.
Figure 6 shows the scatter plot and histogram comparison between the observed and simulated flows at a monthly scale based on gauge, CFSR, and CHIRPS datasets. In the case of the 01_US_IOW and 02_US_SAL watersheds, the flows simulated by CFSR datasets generated scatter with more spread across the 1:1 line during calibration and validation period. This indicated that the performance of flow simulated by the CHIRPS data is on par with that of gauge data in the case of the selected USA watersheds. The watersheds in Brazil exhibited similar behavior with increased scatter for the CFSR dataset in comparison with CHIRPS during the calibration period, but performance during validation was relatively poor for both CHIRPS and CFSR datasets at monthly scale (Figure 6).
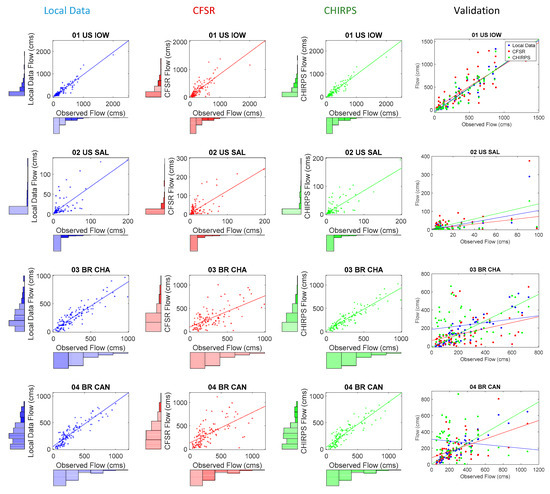
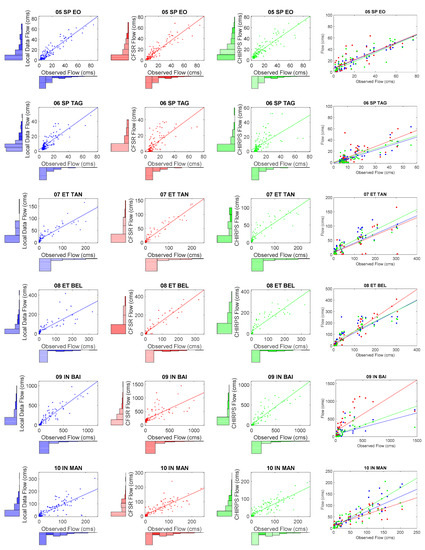
Figure 6.
Relationship between the observed and simulated data for accumulated monthly streamflow. The calibration process and is separate for each rainfall input (local data, CFSR, and CHIRPS, respectively) represented by the combination of the histogram and scatter plots. The scatter plot alone represents the validation process for the three inputs together (for interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).
The scatter plots of two watersheds in Spain (05_SP_EO and 06_SP_TAG) depicted larger scatter for CHIRPS data-based flow simulations. This brings out the relatively poor performance of CHIRPS data in these two watersheds during the calibration period. However, the mixed scatter pattern indicates that all three rainfall datasets performed at a similar level of efficiency to generate the flows during the validation period.
In the case of the 09_IN_BAI watershed, the streamflow simulation with Gauge and CHIRPS outperformed CFSR during calibration and validation at the monthly scale. The scatter plots of simulated vs. observed streamflows at monthly scale show linear trends with less scatter in the case of gauge- and CHIRPS-based simulations, while the points are widely scattered for CFSR-based simulations. All three datasets were consistent in capturing the onset of the flow events (high flows and low flows) during calibration and validation periods, however CFSR simulations over predicted the peak flow events. In the case of the 09_IN_BAI, basin, high flows occurred during the monsoon months (July—September), and overestimation of the simulated streamflows can be attributed to the overestimation of precipitation by CFSR data product. The poor performance arose mainly from the low statistical agreement between CFSR precipitation data products and gauge data.
In the case of the 10_IN_MAN watershed, the scatterplots of simulated flows against observed flow clearly show a linear trend with an almost similar scatter for gauge, CFSR, and CHIRPS data. This indicates that there is not much disparity between the flows simulated based on gauge, CFSR, and CHIRPS data for both calibration and validation period at the monthly scale. However, it can be noted from the histogram plot that medium flows obtained with CFSR data are slightly higher compared to gauge and CHIRPS.
Figure 7 represents the daily Cumulative Probability plots for the calibration and validation period. Calibration graphs show the uncertainty envelope, and the results obtained based on the best parameters after calibration. The values obtained for p factor and r factor evaluation criteria were calculated based on 500 iterations performed during the calibration process. The p factor and r factor assess the degree of uncertainties accounted for in the calibrated model. The degree of deviation of p factor and r factor from the accepted value helps to determine the efficiency of the calibrated model. A large p factor can be obtained only at the expense of a large r factor; hence, a balance must be maintained between these two factors.
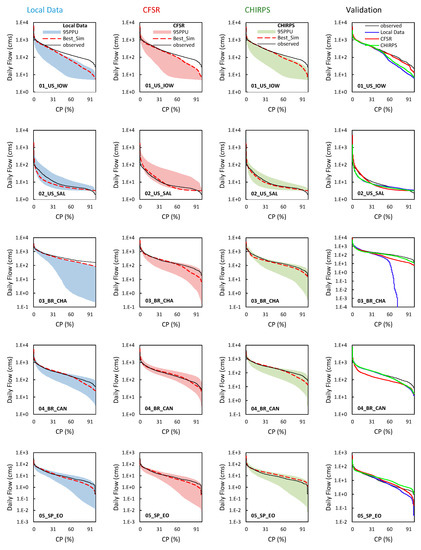
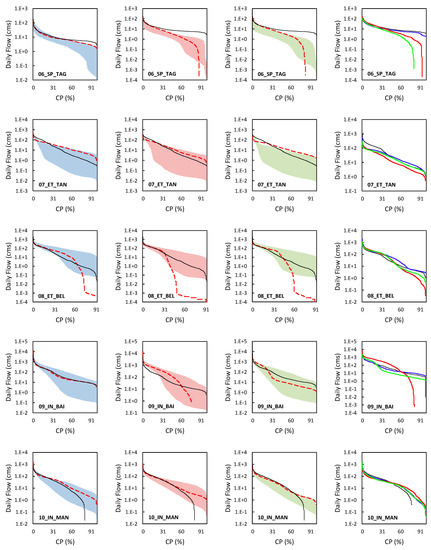
Figure 7.
Daily Cumulative Probability plot for daily streamflow using each of the three rainfall inputs. The graph with the uncertainty range (95 ppu) it refers to the calibration process (local data, CFSR, and CHIRPS, respectively), the red dotted line indicates the best simulation, and the black dots are the observed data. The validation process is represented by the graph with no 95 ppu envelope, the black dots are the observed data, the blue line is the local data, the red line is CFSR, and the green line is CHIRPS. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.).
The results of SWAT calibration at a daily scale for the 01_US_IOW watershed with a p factor value of 0.43 and an r factor value of 0.79 for CHIRPS data show larger uncertainties. Though the performance of CHIRPS data is better compared to CFSR data, the uncertainty band is wider. However, in the 02_US_SAL watershed, the uncertainty band is narrower and comparable with that of gauge data in the case of daily simulations from CHIRPS with an r factor of 0.68. In the 03_BR_CHA watershed, though the value of r factor is less for gauge-based flows, the p factor is also low with a value of 0.31 at a daily timescale for the calibration period. Moreover, the performance of CFSR and CHIRPS based flow simulations were at par compared to gauge data. While in the 04_BR_CAN watershed, the p factor value remained almost the same for all three-rainfall dataset-based streamflows. The gauge data showed the lowest uncertainty in the daily flow simulations. In the case of the 05_SP_EO watershed, the CHIRPS data have the highest uncertainty with the r factor value of 1.01 and lowest p factor value of 0.78. This brings out the inefficiency of high-resolution CHIRPS data in daily flow simulations for a small watershed. The performance of the gauge and CFSR data-based flows were at par during the calibration period. While in the 06_SP_TAG watershed, higher uncertainty was depicted by the gauge-based simulated flows with r factor value of 0.94 though a smaller p factor value in the range of 0.22–0.25 was obtained for CHIRPS and CFSR-data-based flow simulations.
The results from daily simulation for 09_IN_BAI indicate that the datasets performed below a satisfactory threshold, though gauge and CHIRPS performed relatively better in comparison with CFSR. The results of simulation from the 95 ppu plot indicate that, in the case of the gauge dataset, the 95 ppu covered 89% of the observed streamflow during the calibration period with 58% of relative width. In the case of the CHIRPS dataset, the values are 88% and 62%, respectively. The streamflow simulation based on the CFSR dataset resulted in reduced fit quality with the simulated flows covering 79% of the observed daily flows with a relative width of 92%.
The p factor and r factor were found to be 0.54 and 0.59, respectively, for the gauge data in the 10_IN_MAN watershed. The p factor and r factor of the CFSR data were most similar to those of gauge data. The lowest r factor value of 0.55 was obtained for CHIRPS in the basin, which indicated the narrowest uncertainty band with lesser uncertainty.
The size of the uncertainty envelope, r-factor is less than 1.5 for all basins and datasets, except for the 02_US_SAL, where the value of the r-factor is 1.65. The separate analysis for the three rainfall datasets indicated that the gauge data presented gave better results at a daily time scale, followed by CHIRPS and CFSR, respectively. The improvement in the predictive uncertainty was obtained when the CHIRPS data are used, which illustrates the ability of these data to deal with the parameter variations and the process related to each basin. CHIRPS relatively better performance can be attributed to its improved spatial resolution when compared to CFSR. Further, the CHIRPS data product is created by blending with in situ measurements from rain gauge stations, which results in improved performance. Overall, based on the performance statistics, it can be stated that CHIRPS can serve as a potential alternative to ground-based measurements of precipitation, however, conventional gauge datasets continue to be a reliable and accurate source of data in hydrological modeling.
5. Conclusions
The present study was carried out to perform a comparative analysis of open-source rainfall datasets from Climate Forecast System Reanalysis (CFSR) and Climate Hazards Group InfraRed Rainfall with Station data (CHIRPS) against observed rain gauge data. This was achieved by evaluating their effectiveness in simulating the streamflow through hydrological modeling using the Soil Water Assessment Tool (SWAT) over ten watersheds spread across different climatic regions. This study demonstrated the potential of CHIRPS to be used as an input in water budget modeling at the monthly level. CHIRPS outperformed CFSR in most of the watersheds, with a KGE value of 0.5 and above and Nash Sutcliffe value of 0.6 and above. However, for watershed process modeling at daily time scale, CHIRPS demonstrated better ability to predict the streamflow with KGE and NASH values of 0.4 and above. Though local rain gauge measured rainfall is considered the best input source, the way it is distributed by using the Thiessen polygon model cannot be considered an unparalleled method. The contribution of gridded rainfall products becomes crucial in watersheds where rain gauge network is poor or the recorded rainfall data is scarce. This study proved CHIRPS to be a better alternative input for the SWAT model to predict the streamflow in watersheds belonging to diverse climatic conditions. The relatively better performance of the CHIRPS dataset can be attributed to the finer spatial resolution of 0.05°, which improves the effectiveness of the dataset in capturing the spatial heterogeneity in precipitation. Further, as part of this work, authors have developed a standalone tool to download CHIRPS rainfall data and convert it into a SWAT input format. This tool will be made available for free download from https://swat.tamu.edu/software/. Though the direct use of rainfall products enables a more natural way to reduce the errors in the hydrological simulations induced due to rainfall, the exploration of an integrated rainfall dataset from various sources may be analyzed as a part of future work to verify any significant improvement in the flow simulations obtained from hydrological models. The uncertainties associated with satellite data products further translates to unreliable quantification of the hydrological response of basins due to the overestimation or underestimation of simulated streamflows. This can be addressed to an extent through bias correction of the satellite rainfall products with ground-based measurements of rainfall to obtain more realistic flow simulations.
Author Contributions
Conceptualization, Y.D. and R.S.; methodology, Y.D., V.M.B., J.S.-A., T.M.B., E.A., and P.S.S.; software, Y.D. and C.F.; data curation, Y.D., V.M.B., J.S.-A., T.M.B., E.A., and P.S.S.; writing—Original draft preparation, Y.D., V.M.B., J.S.-A., T.M.B., E.A., and P.S.S.; writing—Review and editing, Y.D., V.M.B., J.S.-A., T.M.B., E.A., and P.S.S.; funding acquisition, R.S. All authors have read and agreed to the published version of the manuscript.
Funding
The open access publishing fees for this article have been covered by the Texas A&M University Open Access to Knowledge Fund (OAK Fund), supported by the University Libraries. This publication was made possible through support provided by the Feed the Future Innovation Lab for Small Scale Irrigation through the U.S. Agency for International Development, under the terms of Contract No. AID-OAA-A-13-0005. The opinions expressed herein are those of the authors and do not necessarily reflect the views of the U.S. Agency for International Development. J.S.-A. was supported by a Fulbright Visiting Scholar Fellowship at the Texas A&M University, College Station, USA. T.M.B. would like to thank the CNPq (National Council for Scientific and Technological Development) and PPGEA-UFSC (Environmental Engineering Pos-Graduation Program of Federal University of Santa Catarina) for the Ph.D. financial support.
Acknowledgments
Authors acknowledge Nicolle Norelli for her valuable editorial comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, F.; Zhao, S.; Guo, Z.; Goosse, H.; Yin, Q. Multi-proxy reconstructions of May–September precipitation field in China over the past 500 years. Clim. Past 2017, 13, 1919–1938. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, Y.; Chen, Y.; Yang, Y.; Tang, G.; Yao, Y.; Long, D.; Li, C.; Han, Z.; Liu, R. Performance of Optimally Merged Multisatellite Precipitation Products Using the Dynamic Bayesian Model Averaging Scheme Over the Tibetan Plateau. J. Geophys. Res. Atmos. 2018, 123, 814–834. [Google Scholar] [CrossRef]
- Mantas, V.M.; Liu, Z.; Caro, C.; Pereira, A.J.S.C. Validation of TRMM multi-satellite precipitation analysis (TMPA) products in the Peruvian Andes. Atmos. Res. 2015, 163, 132–145. [Google Scholar] [CrossRef]
- Mishra, A.K.; Gairola, R.M.; Varma, A.K.; Agarwal, V.K. Improved rainfall estimation over the Indian region using satellite infrared technique. Adv. Space Res. 2011, 48, 49–55. [Google Scholar] [CrossRef]
- Kistler, R.; Kalnay, E.; Collins, W.; Saha, S.; White, G.; Woollen, J.; Chelliah, M.; Ebisuzaki, W.; Kanamitsu, M.; Kousky, V.; et al. The NCEP-NCAR 50-Year Reanalysis: Monthly Means CD-ROM and Documentation. Bull. Am. Meteorol. Soc. 2001, 82, 247–268. [Google Scholar] [CrossRef]
- Gampe, D.; Ludwig, R. Evaluation of Gridded Precipitation Data Products for Hydrological Applications in Complex Topography. Hydrology 2017, 4, 53. [Google Scholar] [CrossRef]
- Gao, Y.C.; Liu, M.F. Evaluation of high-resolution satellite precipitation products using rain gauge observations over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 837–849. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long-term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Negrón Juárez, R.I.; Li, W.; Fu, R.; Fernandes, K.; de Oliveira Cardoso, A. Comparison of Precipitation Datasets over the Tropical South American and African Continents. J. Hydrometeorol. 2009, 10, 289–299. [Google Scholar] [CrossRef]
- Blacutt, L.A.; Herdies, D.L.; de Gonçalves, L.G.G.; Vila, D.A.; Andrade, M. Precipitation comparison for the CFSR, MERRA, TRMM3B42 and Combined Scheme datasets in Bolivia. Atmos. Res. 2015, 163, 117–131. [Google Scholar] [CrossRef]
- Rivera, J.A.; Marianetti, G.; Hinrichs, S. Validation of CHIRPS precipitation dataset along the Central Andes of Argentina. Atmos. Res. 2018, 213, 437–449. [Google Scholar] [CrossRef]
- Henn, B.; Newman, A.J.; Livneh, B.; Daly, C.; Lundquist, J.D. An assessment of differences in gridded precipitation datasets in complex terrain. J. Hydrol. 2018, 556, 1205–1219. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.; Sorooshian, S.; Gupta, H.V.; Wagener, T. Intercomparison of Rain Gauge, Radar, and Satellite-Based Precipitation Estimates with Emphasis on Hydrologic Forecasting. J. Hydrometeorol. 2005, 6, 497–517. [Google Scholar] [CrossRef]
- Wilk, J.; Kniveton, D.; Andersson, L.; Layberry, R.; Todd, M.C.; Hughes, D.; Ringrose, S.; Vanderpost, C. Estimating rainfall and water balance over the Okavango River Basin for hydrological applications. J. Hydrol. 2006, 331, 18–29. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Espinoza, J.C.V.; Ronchail, J.; Rotunno Filho, O.C. Assessment of different precipitation datasets and their impacts on the water balance of the Negro River basin. J. Hydrol. 2011, 404, 304–322. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Hydrologic evaluation of satellite and reanalysis precipitation datasets over a mid-latitude basin. Atmos. Res. 2015, 164–165, 37–48. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Hong, Y.; Yang, X.; Ma, M.; Zhang, Y.; Yuan, F. Improvement of Multi-Satellite Real-Time Precipitation Products for Ensemble Streamflow Simulation in a Middle Latitude Basin in South China. Water Resour. Manag. 2014, 28, 2259–2278. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y.-P. Evaluation and hydrological application of precipitation estimates derived from PERSIANN-CDR, TRMM 3B42V7, and NCEP-CFSR over humid regions in China: Evaluation and Hydrological Application of Precipitation Estimates. Hydrol. Process. 2016, 30, 3061–3083. [Google Scholar] [CrossRef]
- Dile, Y.T.; Srinivasan, R. Evaluation of CFSR climate data for hydrologic prediction in data-scarce watersheds: An application in the Blue Nile River Basin. J. Am. Water Resour. Assoc. 2014, 50, 1226–1241. [Google Scholar] [CrossRef]
- Bayissa, Y.; Tadesse, T.; Demisse, G.; Shiferaw, A. Evaluation of Satellite-Based Rainfall Estimates and Application to Monitor Meteorological Drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2017, 9, 669. [Google Scholar] [CrossRef]
- Duan, Z.; Liu, J.; Tuo, Y.; Chiogna, G.; Disse, M. Evaluation of eight high spatial resolution gridded precipitation products in Adige Basin (Italy) at multiple temporal and spatial scales. Sci. Total Environ. 2016, 573, 1536–1553. [Google Scholar] [CrossRef]
- Rahman, K.; Shang, S.; Shahid, M.; Wen, Y. Hydrological evaluation of merged satellite precipitation datasets for streamflow simulation using SWAT: A case study of Potohar Plateau, Pakistan. J. Hydrol. 2020, 587, 125040. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models: Using Cfsr as Weather Input Data for Watershed Models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Radcliffe, D.E.; Mukundan, R. PRISM vs. CFSR Precipitation Data Effects on Calibration and Validation of SWAT Models. J. Am. Water Resour. Assoc. 2017, 53, 89–100. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, G.; Wang, L.; Yu, J.; Xu, Z. Evaluation of Gridded Precipitation Data for Driving SWAT Model in Area Upstream of Three Gorges Reservoir. PLoS ONE 2014, 9, e112725. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.; Tuo, Y.; Liu, J.; Gao, H.; Song, X.; Zhang, Z.; Yang, L.; Mekonnen, D.F. Hydrological evaluation of open-access precipitation and air temperature datasets using SWAT in a poorly gauged basin in Ethiopia. J. Hydrol. 2019, 569, 612–626. [Google Scholar] [CrossRef]
- Tuo, Y.; Duan, Z.; Disse, M.; Chiogna, G. Evaluation of precipitation input for SWAT modeling in Alpine catchment: A case study in the Adige river basin (Italy). Sci. Total Environ. 2016, 573, 66–82. [Google Scholar] [CrossRef]
- Renard, B.; Kavetski, D.; Leblois, E.; Thyer, M.; Kuczera, G.; Franks, S.W. Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation: Decomposing Predictive Uncertainty in Hydrological Modeling. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Mendoza, P.A.; Clark, M.P.; Mizukami, N.; Newman, A.J.; Barlage, M.; Gutmann, E.D.; Rasmussen, R.M.; Rajagopalan, B.; Brekke, L.D.; Arnold, J.R. Effects of Hydrologic Model Choice and Calibration on the Portrayal of Climate Change Impacts. J. Hydrometeorol. 2015, 16, 762–780. [Google Scholar] [CrossRef]
- Fekete, B.Z.M. Uncertainties in Precipitation and Their Impacts on Runoff Estimates. J. Clim. 2004, 17, 11. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Peral-García, C.; Navascués Fernández-Victorio, B.; Ramos Calzado, P. Serie de Precipitación Diaria en Rejilla con Fines Climáticos; Spanish Meterological Agency (AEMET): Madrid, Spain, 2017. [Google Scholar]
- Senent-Aparicio, J.; López-Ballesteros, A.; Pérez-Sánchez, J.; Segura-Méndez, F.; Pulido-Velazquez, D. Using Multiple Monthly Water Balance Models to Evaluate Gridded Precipitation Products over Peninsular Spain. Remote Sens. 2018, 10, 922. [Google Scholar] [CrossRef]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. SWAT 2012 Input/Output Documentation. Texas Water Resources Institute. Available online: http://hdl.handle.net/1969.1/149194 (accessed on 4 March 2013).
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic extremes? J. Hydrol. 2014, 508, 77–87. [Google Scholar] [CrossRef]
- Meng, J.; Li, L.; Hao, Z.; Wang, J.; Shao, Q. Suitability of TRMM satellite rainfall in driving a distributed hydrological model in the source region of Yellow River. J. Hydrol. 2014, 509, 320–332. [Google Scholar] [CrossRef]
- Jha, M.; Gassman, P.W.; Secchi, S.; Gu, R.; Arnold, J. Effect of Watershed Subdivision on Swat Flow, Sediment, and Nutrient Predictions. J. Am. Water Resour. Assoc. 2004, 40, 811–825. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V. Impact of Watershed Subdivision and Soil Data Resolution on SWAT Model Calibration and Parameter Uncertainty. J. Am. Water Resour. Assoc. 2009, 45, 1179–1196. [Google Scholar] [CrossRef]
- Wallace, C.; Flanagan, D.; Engel, B. Evaluating the Effects of Watershed Size on SWAT Calibration. Water 2018, 10, 898. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Y.; Wang, G.; Cui, X.; Yu, J.; Zuo, D.; Xu, Z. Physically based distributed hydrological model calibration based on a short period of streamflow data: Case studies in four Chinese basins. Hydrol. Earth Syst. Sci. 2017, 21, 251–265. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Nicolle, P.; Pushpalatha, R.; Perrin, C.; Francois, D.; Thiéry, D.; Mathevet, T.; Lay, M.L.; Besson, F.; Soubeyroux, J.-M.; Viel, C.; et al. Benchmarking hydrological models for low-flow simulation and forecasting on French catchments. Hydrol. Earth Syst. Sci. 2014, 30. [Google Scholar] [CrossRef]
- Asadzadeh, M.; Leon, L.; Yang, W.; Bosch, D. One-day offset in daily hydrologic modeling: An exploration of the issue in automatic model calibration. J. Hydrol. 2016, 534, 164–177. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of Automatic Calibration for Hydrologic Models: Comparison with Multilevel Expert Calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Abbaspour, K.C. User Manual for SWAT-CUP, SWAT Calibration and Uncertainty Analysis Programs; Eawag: Duebendorf, Switzerland, 2007. [Google Scholar]
- Katsanos, D.; Retalis, A.; Michaelides, S. Validation of a high-resolution precipitation database (CHIRPS) over Cyprus for a 30-year period. Atmos. Res. 2016, 169, 459–464. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).